CM5 ACP
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Page 1 : CM 3 : Analyse multivariée - ACPData explorationAnalyse en Composantes PrincipalesObserver simultanément des individus d'une population sur p2 variablesEtudier le lien entre les variablesFaire une représentation graphique d’un nuage de points à p dimensionsQualifier les observations du jeu de donnée
Page 2 : CM 3 : Analyse multivariée - ACP2ACPNuage de points en dimension p22npnin1kpkik12p2i211p1i11xxxxxxxxxxxxMLKMVariable : p variables n observations Perte d’informationFigure J.P. FenelonUn jeu de données est un tableau avec en ligne les observations et en colonne les variables , … , . On peut donc représenter chaque ligne du tableau comme un point dont les coordonnées sont les valeurs prises par les variables.Si p3, il est impossible de visualiser le nuage de points. L’objectif de l’ACP est de trouver une projection du nuage de points en dimension 2 ou 3 de façon à perdre le moins possible d’information. •Qu’est-ce que l’information?•Si projection alors produit scalaire?•Quel lien avec les variables , … , ?Sur cet exemple chaque point est un pays caractérisé par son espérance de vie, et ses taux de natalité et de mortalité.observation :
Page 3 : CM 3 : Analyse multivariée - ACP3ACPComment mesurer l’information?33Centre de gravitéLe centre de gravité est le point dont les coordonnées sont définies par les valeurs moyennes des variables, = , … , InertieL’information contenue dans un nuage de points correspond à l’inertie de celui-ci, c.-à-d. la somme des distances au carré entre les observations et le centre de gravité du nuage, = où .désigne la norme euclidienne. Propriétés de l’inertieL’inertie peut s’exprimer comme la trace de la matrice de variance-covariance, c.-à-d. la somme des variances des variables, = = où =.La matrice de variance-covariance est symétrique définie positive. L’inertie peut aussi s’écrire comme la somme des valeurs propres de , = + + L' inetrie mesure la dispersion totale du nuage de points.
Page 4 : CM 3 : Analyse multivariée - ACP4ACPCentrer et réduire les variables44L’analyse en composantes principales nécessite de calculer des distances entre observations, = ².Si les variables n’ont pas le même ordre de grandeur, certaines variables à valeurs faibles « disparaitrons » de l’information au profit de celles ayant de fortes valeurs.Pop. milliersTaux nat. pour milleEsp. vieNb. enfantsArgentine4105016,8775,872,19Arménie309915,4774,441,77Australie2173112,5681,991,85Autriche84079,0180,551,4041050-3099²+16,87-15,47²+75,87-74,44²+2,19-1,77²=144027840541050-3099² =1440278401 distance entre l’Argentine et l’ArménieLes variables Taux nat., Esp. vie et Nb. enfants ne comptent pas dans le calcul de la distanceIl est donc important de centrer et réduire les variables ← , i = 1, … , pDe la même façon la quantification de l’information au travers de l’inertie, = , privilégie les variables fortement dispersés.
Page 5 : CM 3 : Analyse multivariée - ACP5ACPQuel produit scalaire?55Le produit scalaire entre deux variables et + est défini par, , + = 1. +,d’où la norme ² = 1. ²Si les variables sont centrées alors , + = /0 et = D’après la formule du cosinus,cos , + 4= , + + =/0 += /0• 56=1 ⇔les variables sont colinéairescorrélées positivement si 56=1 corrélées négativement si 56=-1 • 56 = 0 ⇔les variables sont orthogonales ⇔les variables ne sont pas linéairement corrélées 78 79
Page 6 : CM 3 : Analyse multivariée - ACP6ACPPrincipe de l’ACP6Le principe de l’ACP est de trouver des espaces de petites dimensions sur lesquels les projections des observations minimisent la déformation de la réalité. On cherche donc un sous-espace :; de Rp de dimension q q=2,3,.. sur lequel projeté le nuage de points. Les axes de ce sous-espace sont des combinaisons linéaires des axes d’origine c.-à-d. les variables. Les nouveaux axes s’appellent les composantes principales.X1X2C1C2Principe• La 1ère composante principale C1 doit « capturer » le maximum d’informationIl reste un résidu d’information non expliquée• La 2ème composante principale C2 est calculée sur ce résidu telle queElle capture un maximum d’informationElle soit non corrélée linéairement à C1 orthogonalité• Sur le même principe, calcul de C3, C4, …,CpIl s’agit d’un changement de repère pour passer du repère initial formé par les variables à un repère orthogonale tel que les nouveaux axes sont ordonnés par quantité d’information décroissante. Nb. composantes principales = Nb. variables initiales
Page 7 : CM 3 : Analyse multivariée - ACP7ACPComment perdre le moins d’information possible?7FqekfkgSoit un point du nuage et notons sa projection orthogonale sur le sous-espace :;. On cherche :; tel que la distance entre :; et les individus soit minimale.Minimiser : ²D’après Pythagore, Donc le problème revient à maximiser = ² ²= = = ²car = ne dépend pas de :;autrement dit maximiser l’inertie du nuage projeté. On cherche à garder un maximum de dispersion dans la projection.
Page 8 : CM 3 : Analyse multivariée - ACP8ACPSolution du problèmeLe sous-espace qui minimise l’inertie du nuage projeté est définir par ::; = vectQ, … , Q;où QR est le vecteur propre unitaire de la matrice de variance-covariance associée à la kème plusgrande valeur propre.Les vecteurs propres sont appelés les axes principauxLe premier axe principal Q est associé à la plus grande valeur propre λ1Le deuxième axe principal Q est associé à la deuxième valeur propre λ2Etc…L’ACP est un changement de repère dans lequel les 1ers axes contiennent un maximum d’informationL’inertie du nuage projeté sur Q est L’inertie du nuage projeté sur :; est +…+;L’inertie totale est I=+…+;La projection des individus sur un axe principal est une nouvelle variable appelée composante principaleLa première composante c1 représente les coordonnées des projections des individus sur l’axe QLa deuxième composante c2 représente les coordonnées des projections des individus sur l’axe QEtc…
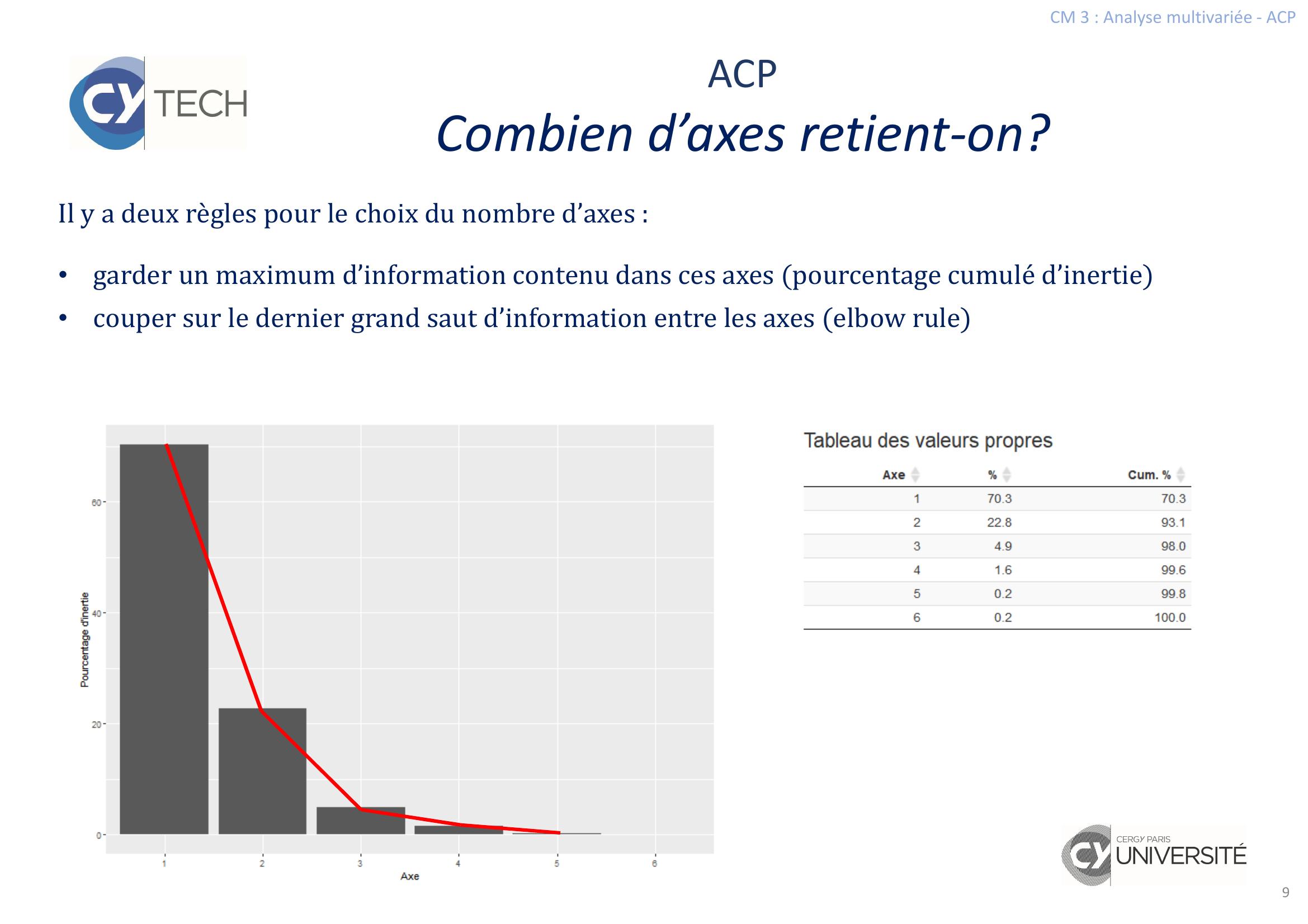
Page 9 : CM 3 : Analyse multivariée - ACP9ACPCombien d’axes retient-on?Il y a deux règles pour le choix du nombre d’axes :•garder un maximum d’information contenu dans ces axes pourcentage cumulé d’inertie•couper sur le dernier grand saut d’information entre les axes elbow rule
Page 10 : CM 3 : Analyse multivariée - ACP10ACPExemple de la démographie mondialePays caractérisés par 4 variables :•TNAT : Taux de natalité•TMORT : Taux de mortalité•EV : Espérance de vie•T65 : Taux 65 ans
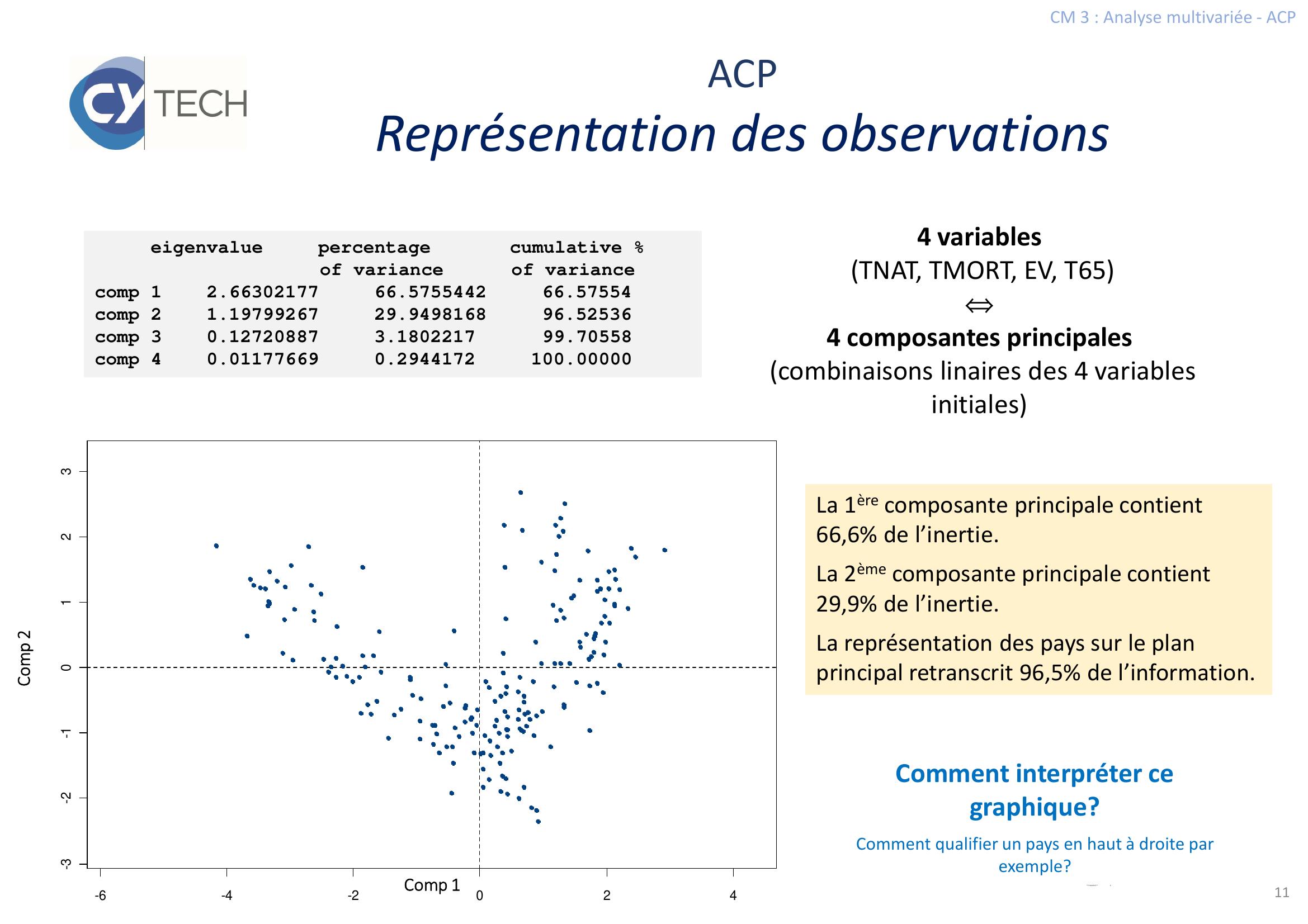
Page 11 : CM 3 : Analyse multivariée - ACP-6-4-2024-3-2-1012311ACPReprésentation des observationsLa 1ère composante principale contient 66,6 de l’inertie.La 2ème composante principale contient 29,9 de l’inertie.La représentation des pays sur le plan principal retranscrit 96,5 de l’information. eigenvaluepercentagecumulative of variance of variancecomp 1 2.6630217766.575544266.57554comp 2 1.1979926729.949816896.52536comp 3 0.127208873.180221799.70558comp 4 0.011776690.2944172100.000004 variablesTNAT, TMORT, EV, T65⇔4 composantes principalescombinaisons linaires des 4 variables initialesComment interpréter ce graphique?Comment qualifier un pays en haut à droite par exemple?Comp 1Comp 2
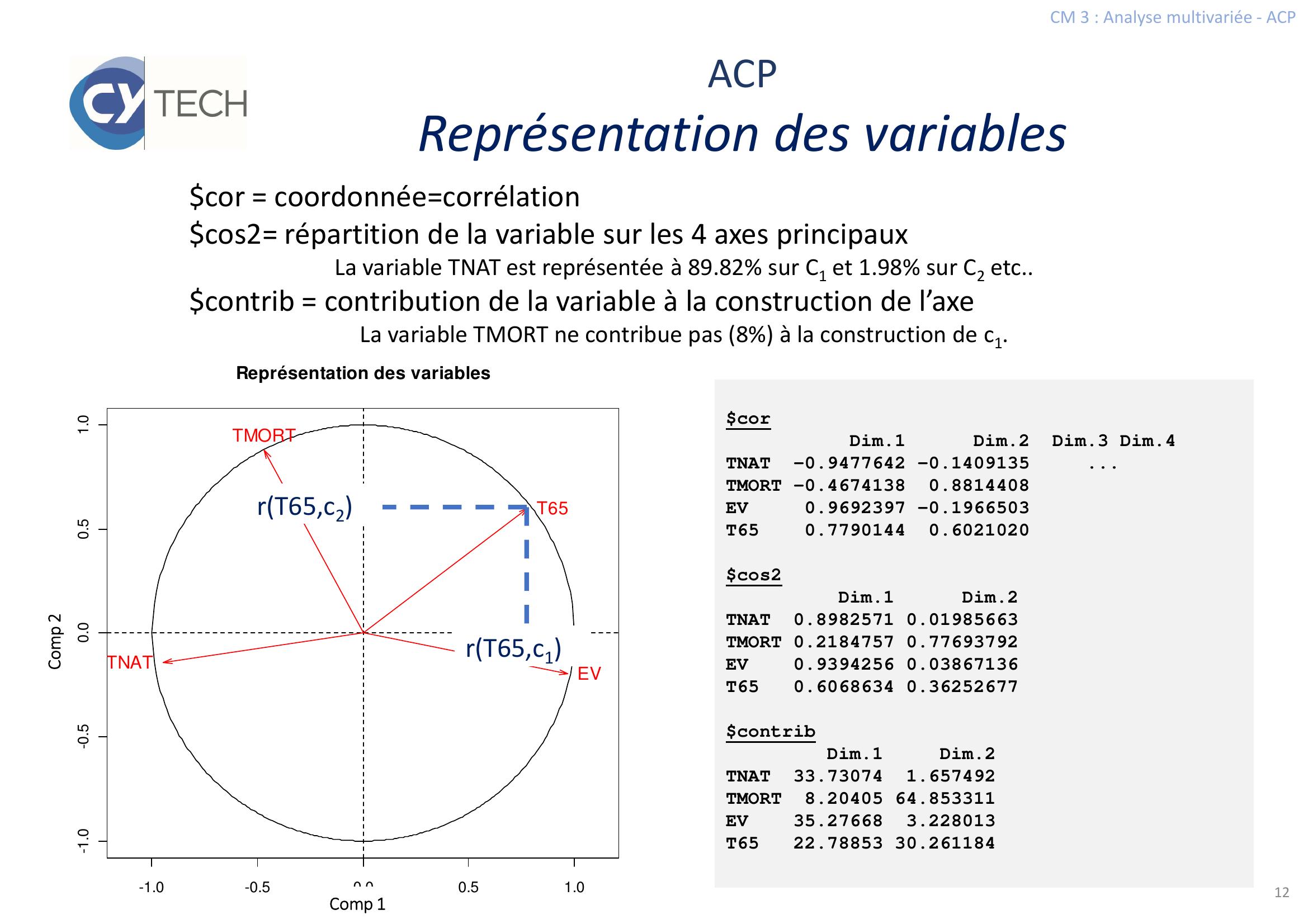
Page 12 : CM 3 : Analyse multivariée - ACP12ACPReprésentation des variablescorDim.1 Dim.2 Dim.3 Dim.4TNAT -0.9477642 -0.1409135 ...TMORT -0.4674138 0.8814408EV 0.9692397 -0.1966503T65 0.7790144 0.6021020cos2Dim.1 Dim.2TNAT 0.8982571 0.01985663TMORT 0.2184757 0.77693792EV 0.9394256 0.03867136T65 0.6068634 0.36252677contribDim.1 Dim.2TNAT 33.73074 1.657492TMORT 8.20405 64.853311EV 35.27668 3.228013T65 22.78853 30.261184-1.0-0.50.00.51.0-1.0-0.50.00.51.0Représentation des variablesTNATTMORTEVT65rT65,c1rT65,c2Comp 2Comp 1cor = coordonnée=corrélationcos2= répartition de la variable sur les 4 axes principaux La variable TNAT est représentée à 89.82 sur C1 et 1.98 sur C2 etc..contrib = contribution de la variable à la construction de l’axeLa variable TMORT ne contribue pas 8 à la construction de c1.
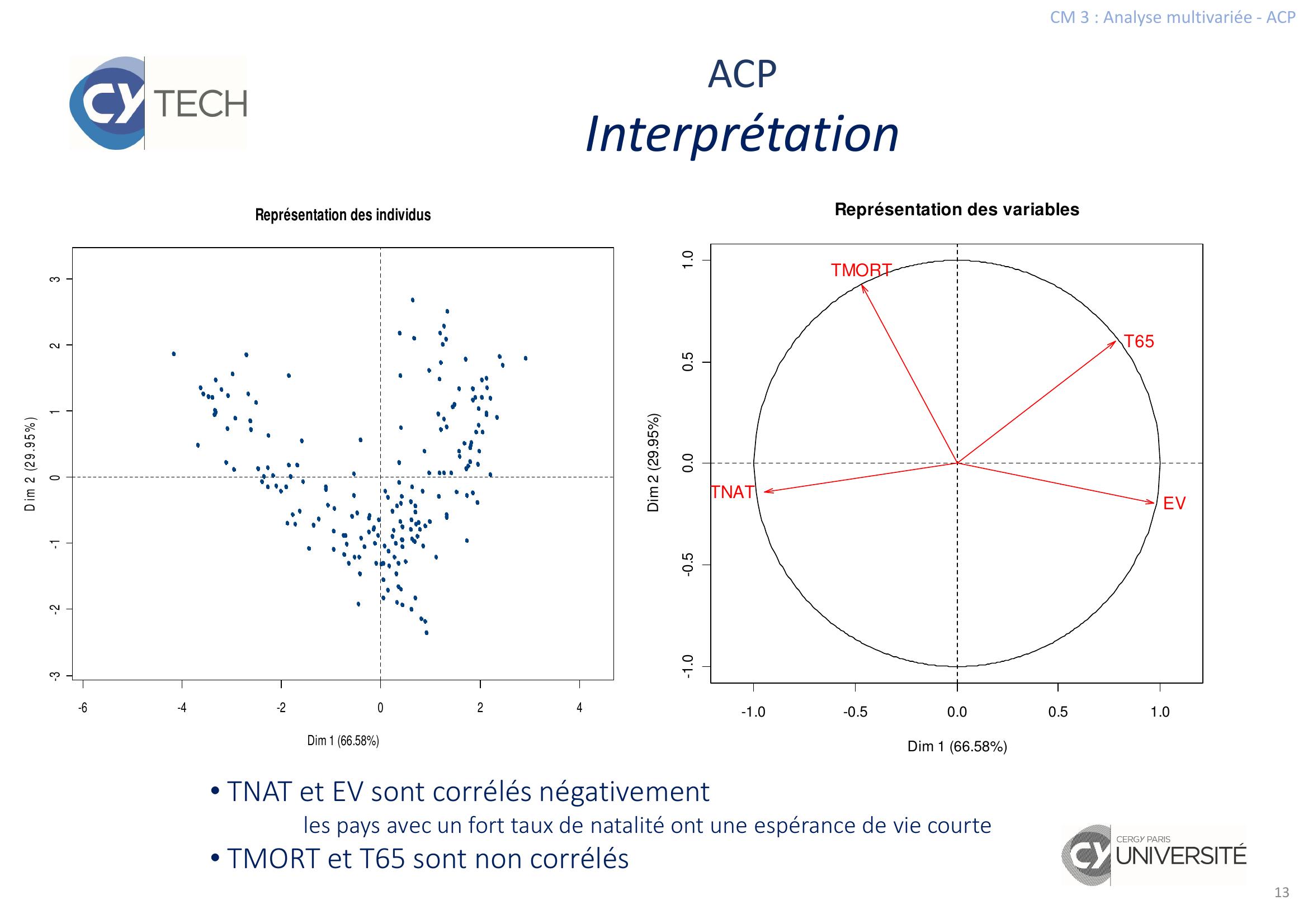
Page 13 : CM 3 : Analyse multivariée - ACP13ACPInterprétation-6-4-2024-3-2-10123Représentation des individusDim 1 66.58D im 2 2 9 .9 5 -1.0-0.50.00.51.0-1.0-0.50.00.51.0Représentation des variablesDim 1 66.58Dim 2 29.95TNATTMORTEVT65• TNAT et EV sont corrélés négativementles pays avec un fort taux de natalité ont une espérance de vie courte• TMORT et T65 sont non corrélés
Page 14 : CM 3 : Analyse multivariée - ACP14ACPValidité des représentations graphiques• La projection perd le moins d’information possible vérifier le d’inertie expliquée pas l’axeconserver le nombre d’axes nécessaire pour avoir une inertie expliquée correcte• Les variables sont bien représentées si elles sont proches du cercle. A contrario celles qui sont proches de l’origine sont peu corrélées avec les axespas d’interprétation possible pour ces variables• Les individus sont bien représentés s’ils ne sont pas trop éloignés de l’axe sur lequel on les projettevérifier le cosinus entre l’individu et l’axe proche de 1valable si l’individu loin du centre de gravité e1e2gckAutre utilisation de l’ACP = réduire la dimension d’un problèmeL’ACP est très souvent utilisée en amont de méthodes de machine learning pour réduire le nombre de variables. L’objectif n’est plus l’interprétation des données sur un graphique.
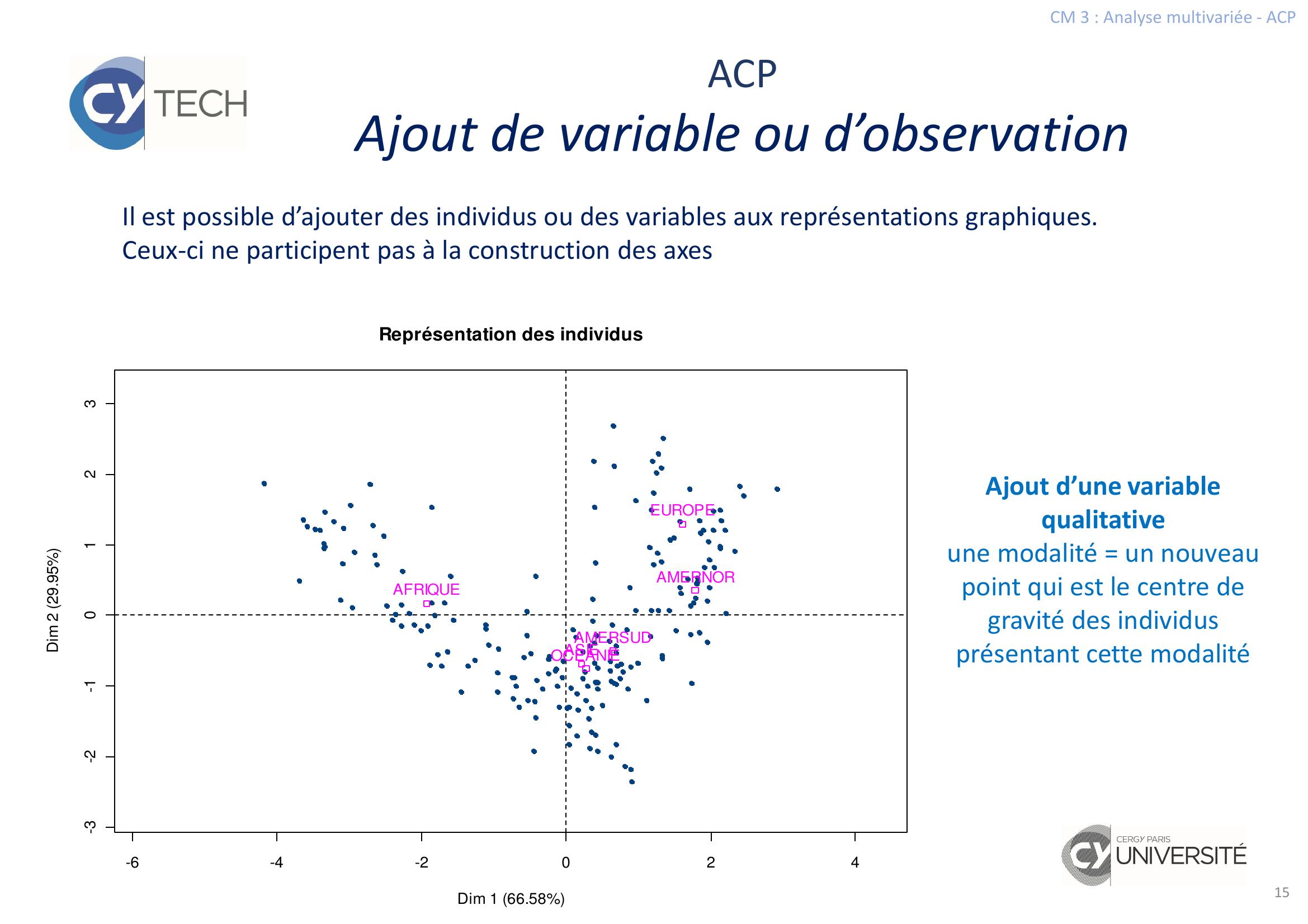
Page 15 : CM 3 : Analyse multivariée - ACP15ACPAjout de variable ou d’observation-6-4-2024-3-2-10123Représentation des individusDim 1 66.58Dim 2 29.95AFRIQUEAMERNORAMERSUDASIEEUROPEOCEANIEAjout d’une variable qualitativeune modalité = un nouveau point qui est le centre de gravité des individus présentant cette modalitéIl est possible d’ajouter des individus ou des variables aux représentations graphiques. Ceux-ci ne participent pas à la construction des axes
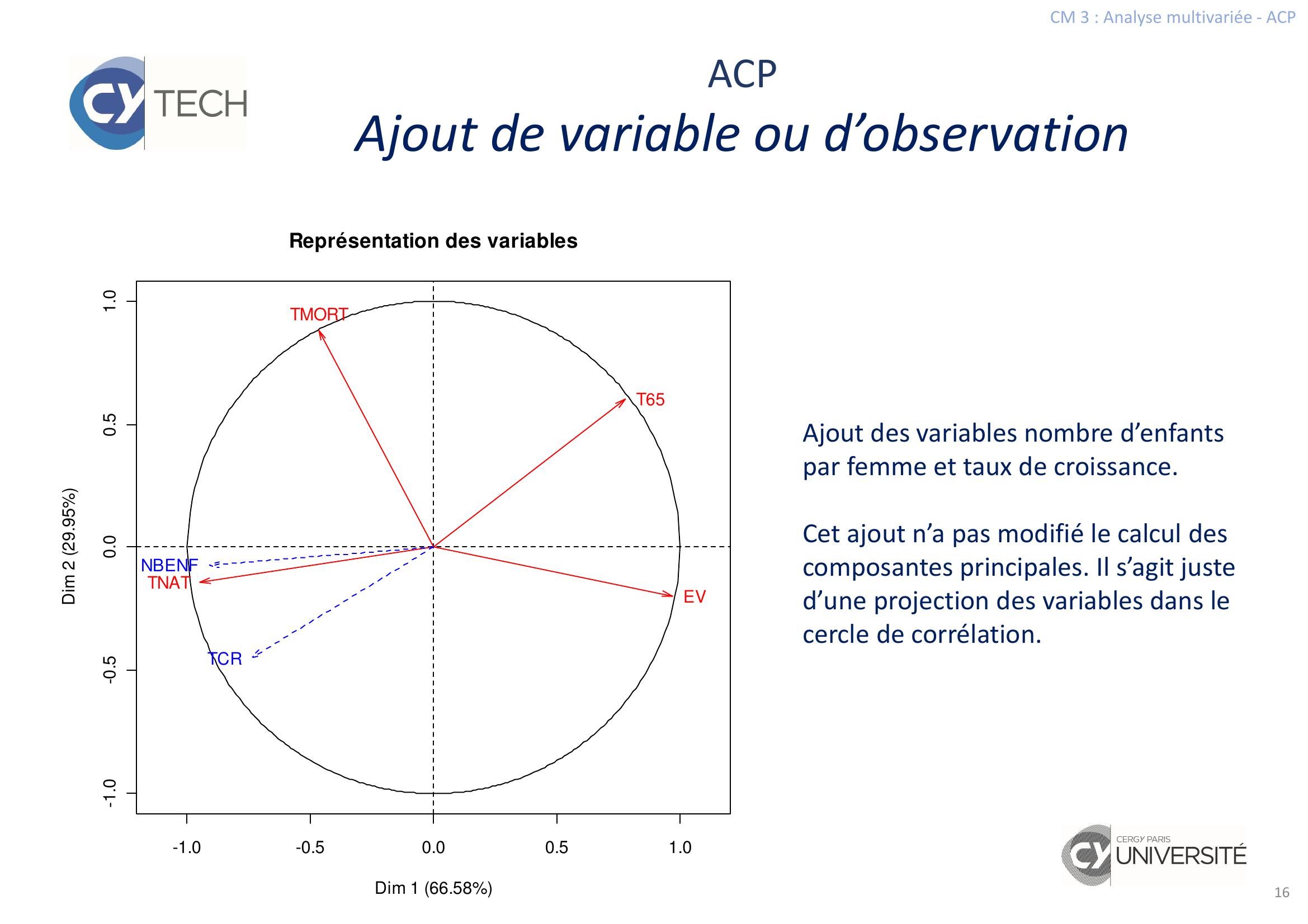
Page 16 : CM 3 : Analyse multivariée - ACP16ACPAjout de variable ou d’observation-1.0-0.50.00.51.0-1.0-0.50.00.51.0Représentation des variablesDim 1 66.58Dim 2 29.95TNATTMORTEVT65NBENFTCRAjout des variables nombre d’enfants par femme et taux de croissance.Cet ajout n’a pas modifié le calcul des composantes principales. Il s’agit juste d’une projection des variables dans le cercle de corrélation.
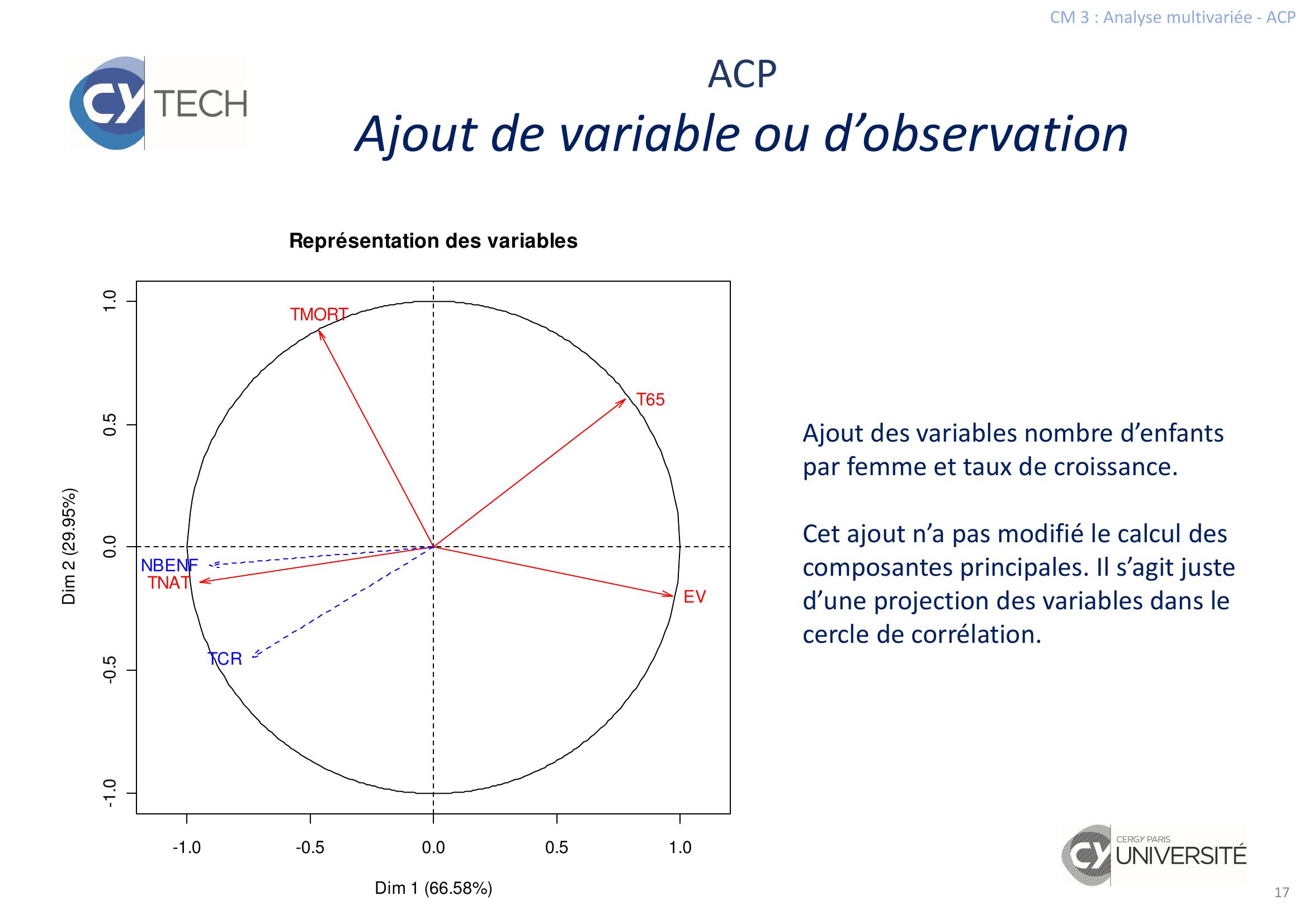
Page 17 : CM 3 : Analyse multivariée - ACP17ACPAjout de variable ou d’observation-1.0-0.50.00.51.0-1.0-0.50.00.51.0Représentation des variablesDim 1 66.58Dim 2 29.95TNATTMORTEVT65NBENFTCRAjout des variables nombre d’enfants par femme et taux de croissance.Cet ajout n’a pas modifié le calcul des composantes principales. Il s’agit juste d’une projection des variables dans le cercle de corrélation.
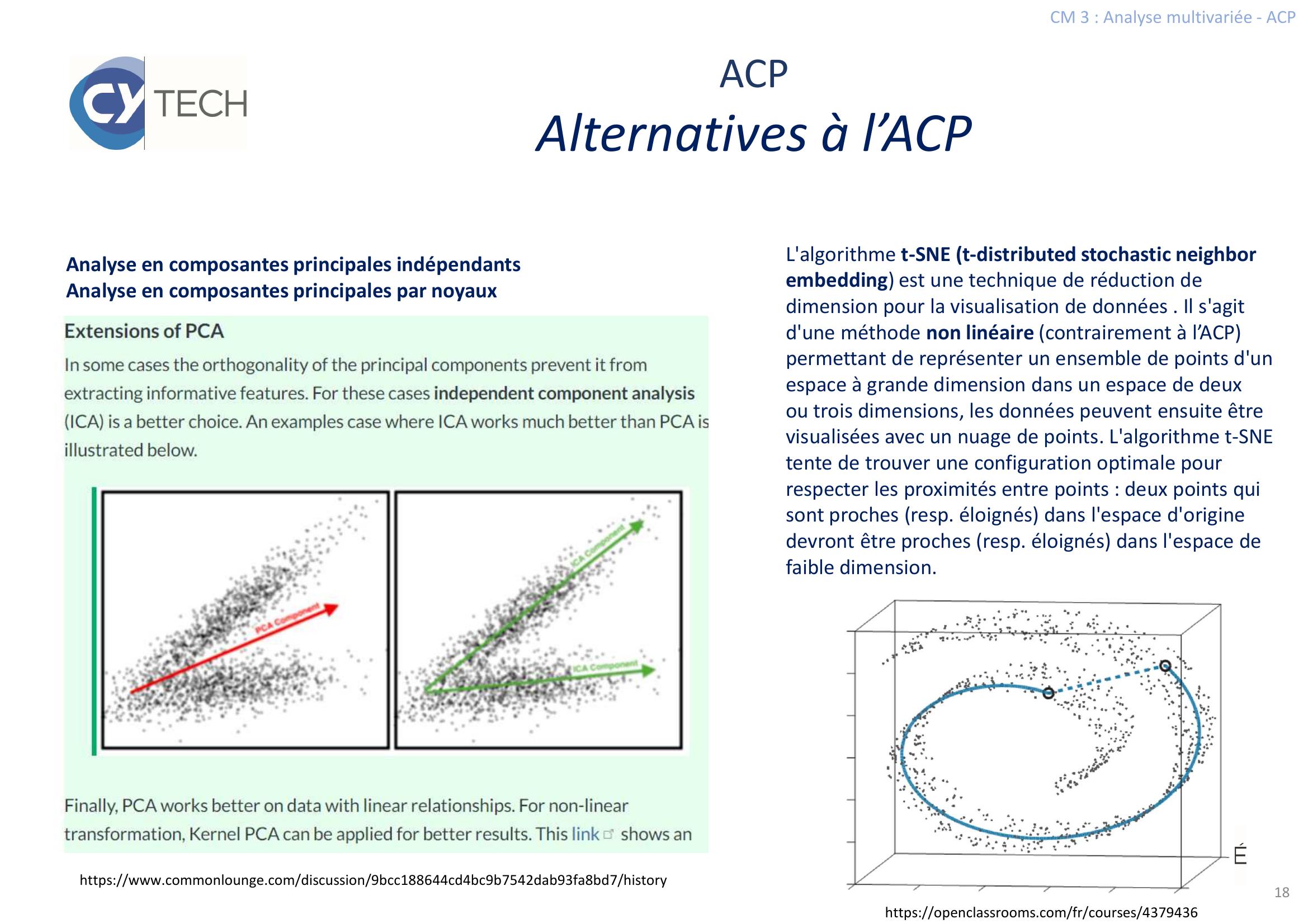
Page 18 : CM 3 : Analyse multivariée - ACP18ACPAlternatives à l’ACPL'algorithme t-SNE t-distributed stochastic neighborembedding est une technique de réduction de dimension pour la visualisation de données . Il s'agit d'une méthode non linéaire contrairement à l’ACP permettant de représenter un ensemble de points d'un espace à grande dimension dans un espace de deux ou trois dimensions, les données peuvent ensuite être visualisées avec un nuage de points. L'algorithme t-SNE tente de trouver une configuration optimale pour respecter les proximités entre points : deux points qui sont proches resp. éloignés dans l'espace d'origine devront être proches resp. éloignés dans l'espace de faible dimension.https://openclassrooms.com/fr/courses/4379436https://www.commonlounge.com/discussion/9bcc188644cd4bc9b7542dab93fa8bd7/historyAnalyse en composantes principales indépendantsAnalyse en composantes principales par noyaux