CM5 AVL

Télécharger le CM5 AVL en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198

Page 1 : INFORMATIQUE 3V. A V LEva ANSERMIN & Renaud VERIN & Romuald GRIGNONv1.01

Page 2 : I. Optimisation de la recherche dans un ABRE.ANSERMIN R.VERIN R.GRIGNON2

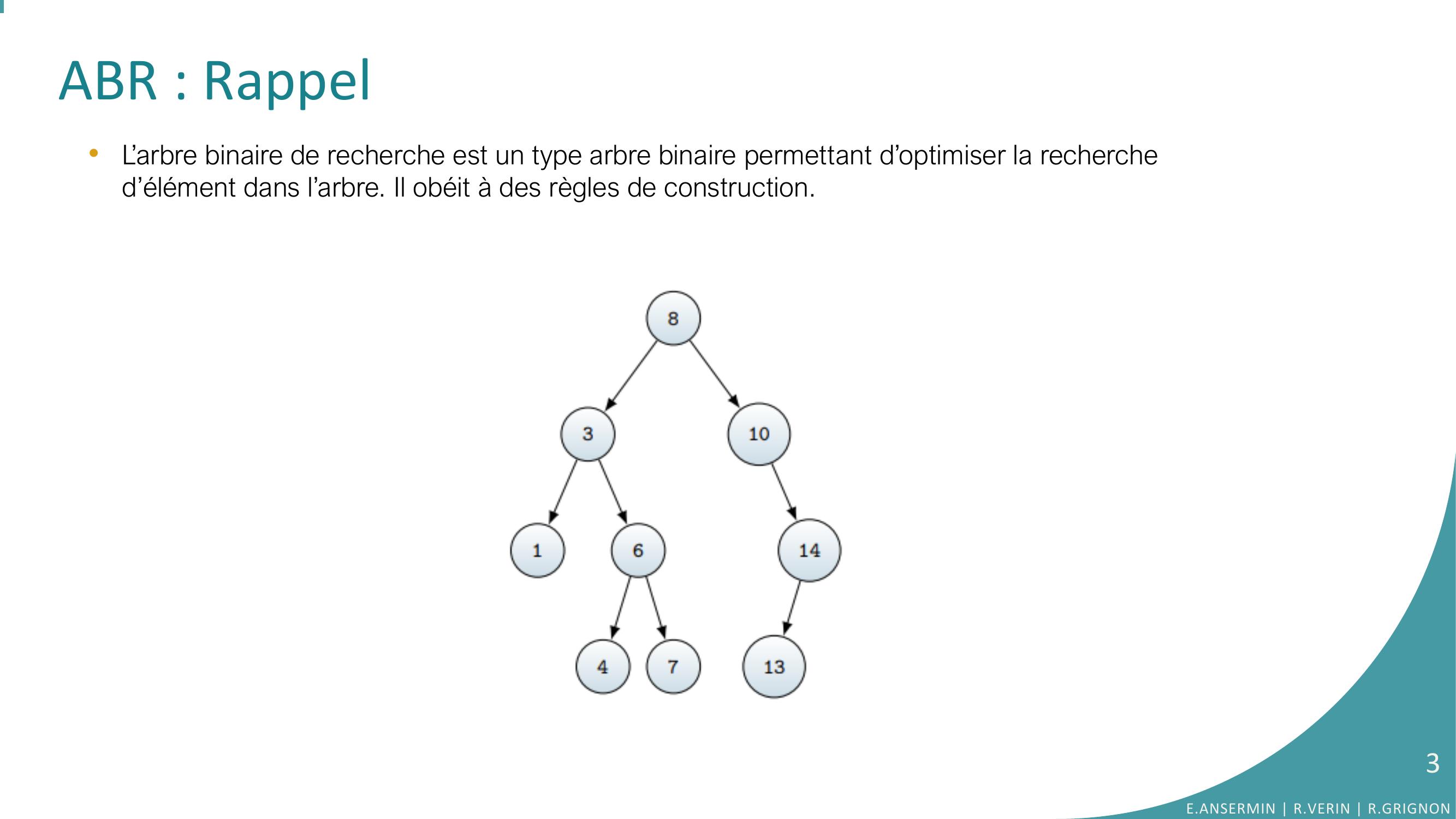
Page 3 : ABR : Rappel•L’arbre binaire de recherche est un type arbre binaire permettant d’optimiser la recherche d’élément dans l’arbre. Il obéit à des règles de construction.E.ANSERMIN R.VERIN R.GRIGNON3

Page 4 : Configuration de l’ABR•Construire un ABR en insérant les éléments suivant dans l’ordre : 1 , 3 , 5 , 8, 9 E.ANSERMIN R.VERIN R.GRIGNON4

Page 5 : Configuration de l’ABR•Construire un ABR en insérant les éléments suivant dans l’ordre : 1 , 3 , 5 , 8, 9E.ANSERMIN R.VERIN R.GRIGNON5

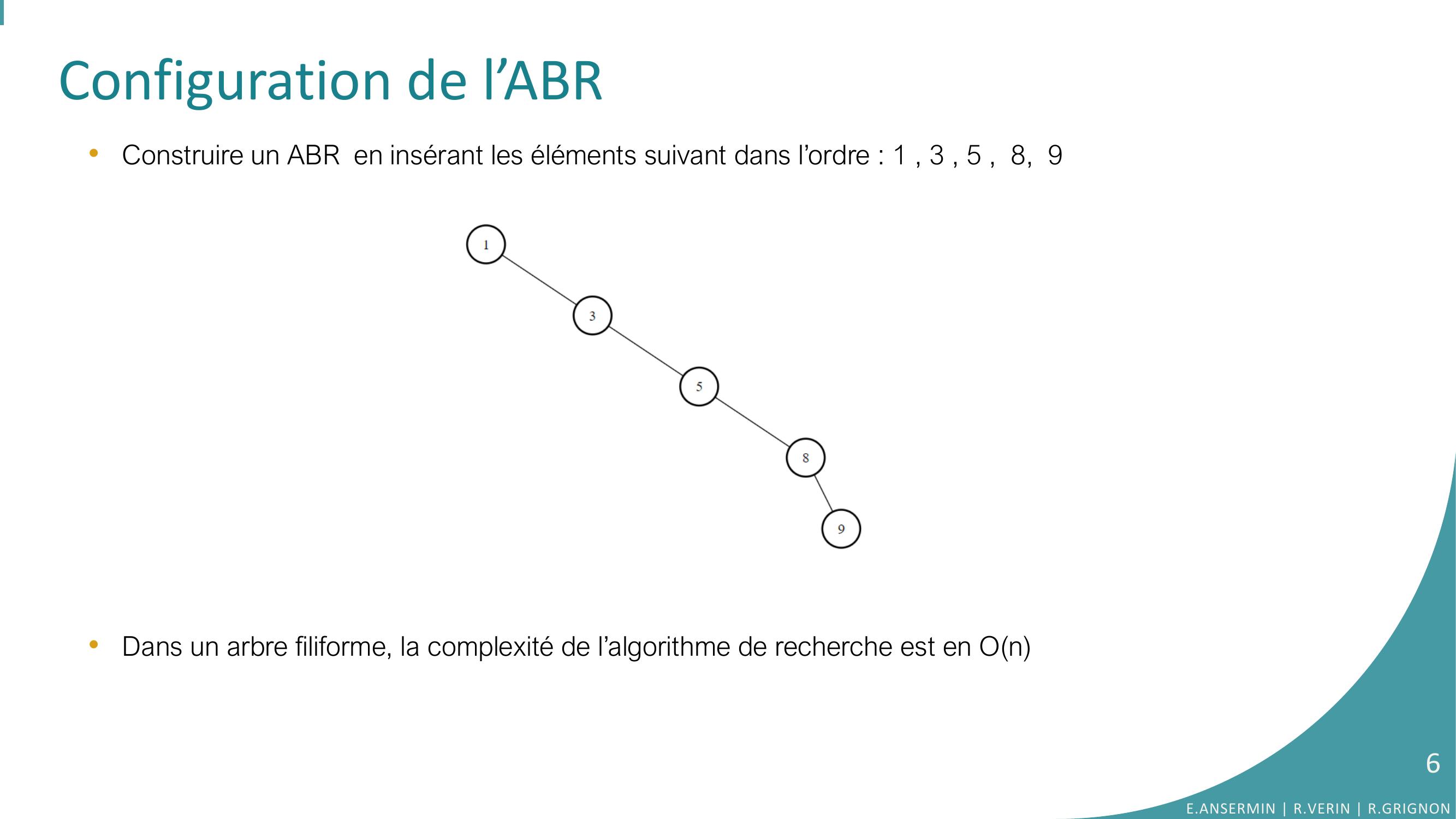
Page 6 : Configuration de l’ABR•Construire un ABR en insérant les éléments suivant dans l’ordre : 1 , 3 , 5 , 8, 9•Dans un arbre filiforme, la complexité de l’algorithme de recherche est en OnE.ANSERMIN R.VERIN R.GRIGNON6

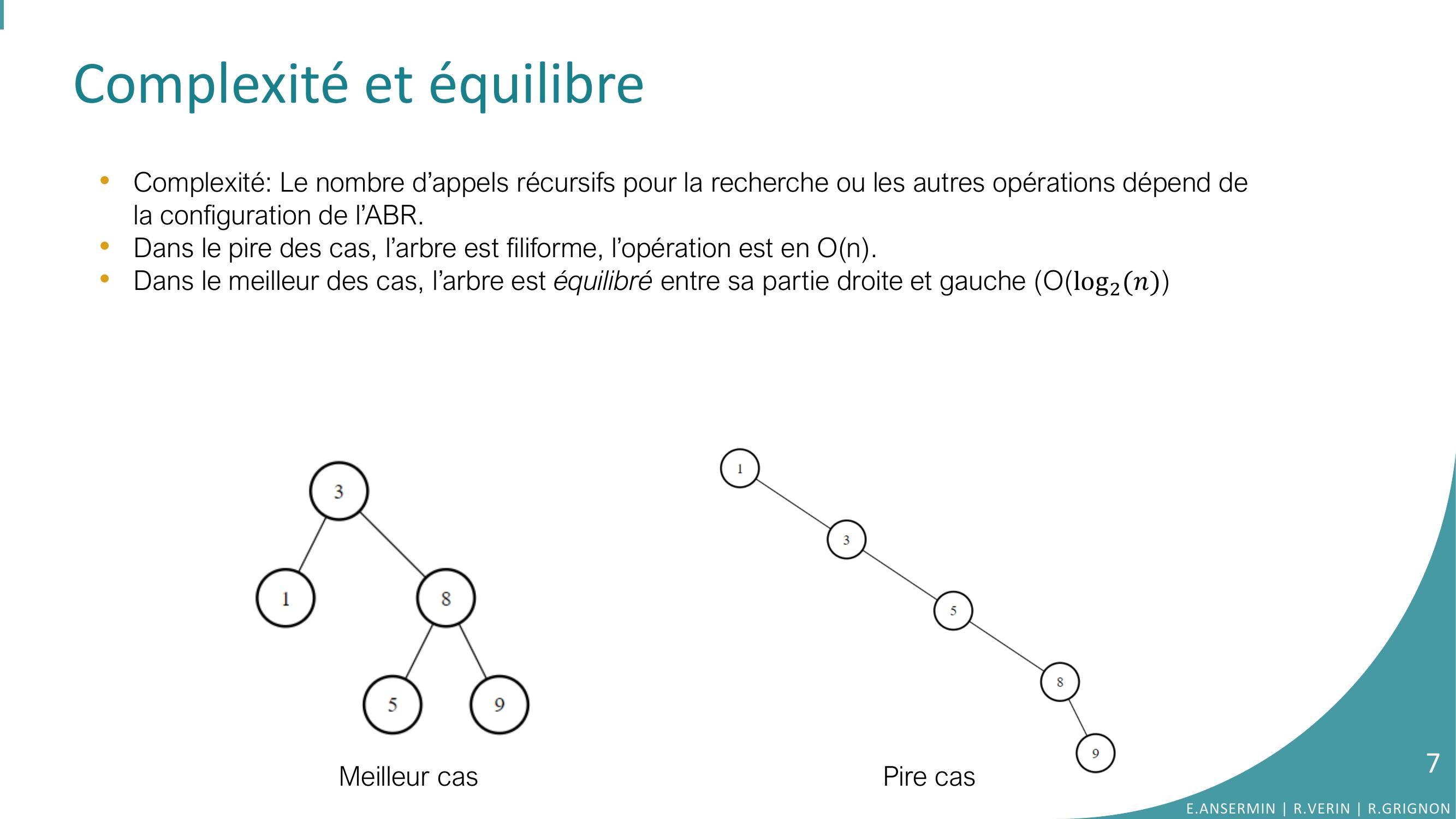
Page 7 : Complexité et équilibre•Complexité: Le nombre d’appels récursifs pour la recherche ou les autres opérations dépend de la configuration de l’ABR.•Dans le pire des cas, l’arbre est filiforme, l’opération est en On.•Dans le meilleur des cas, l’arbre est équilibré entre sa partie droite et gauche Olog2𝑛Meilleur casPire casE.ANSERMIN R.VERIN R.GRIGNON7

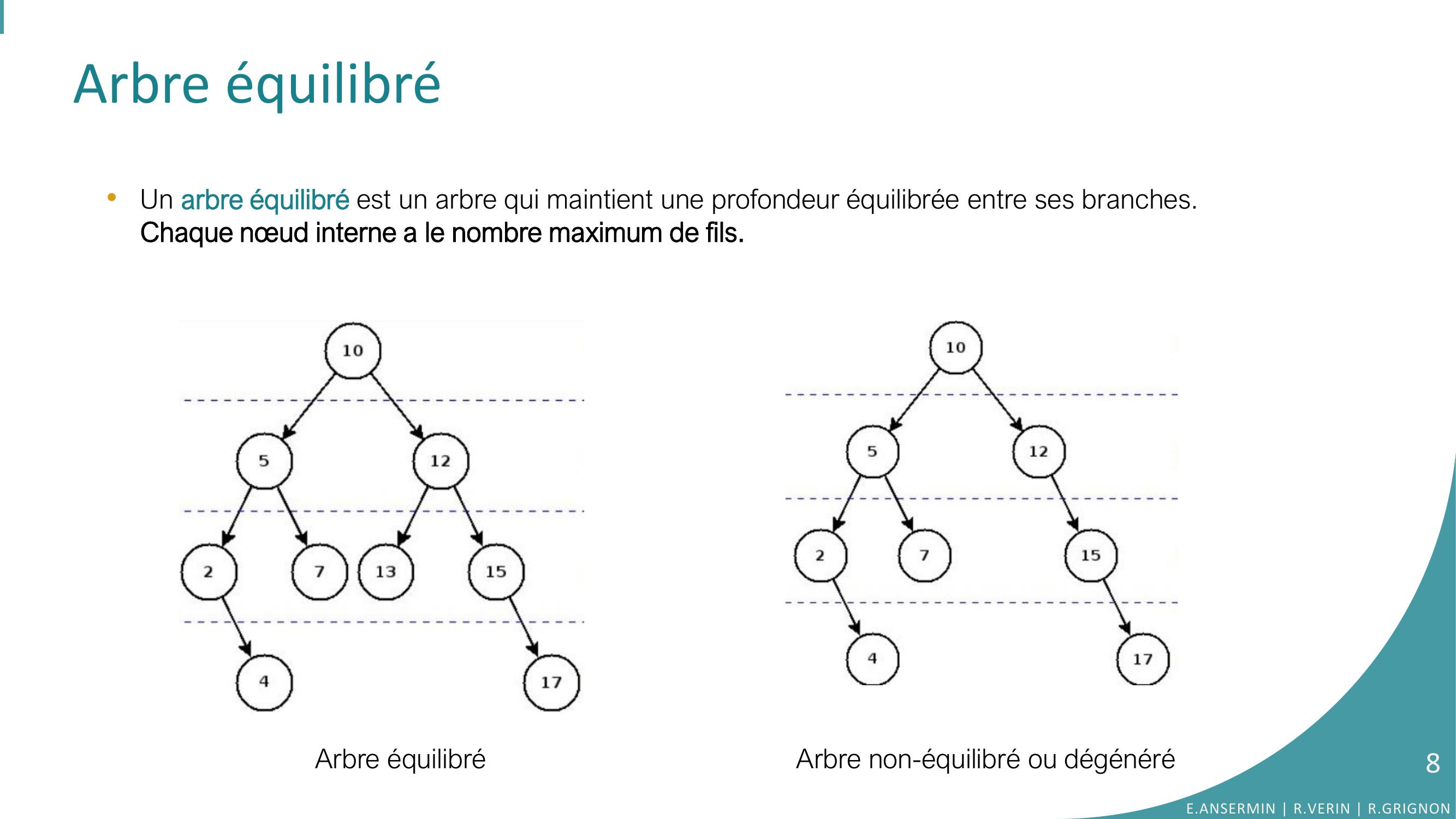
Page 8 : Arbre équilibré•Un arbre équilibré est un arbre qui maintient une profondeur équilibrée entre ses branches. Chaque nœud interne a le nombre maximum de fils. Arbre équilibréArbre non-équilibré ou dégénéréE.ANSERMIN R.VERIN R.GRIGNON8

Page 9 : II. AVL : introductionE.ANSERMIN R.VERIN R.GRIGNON9

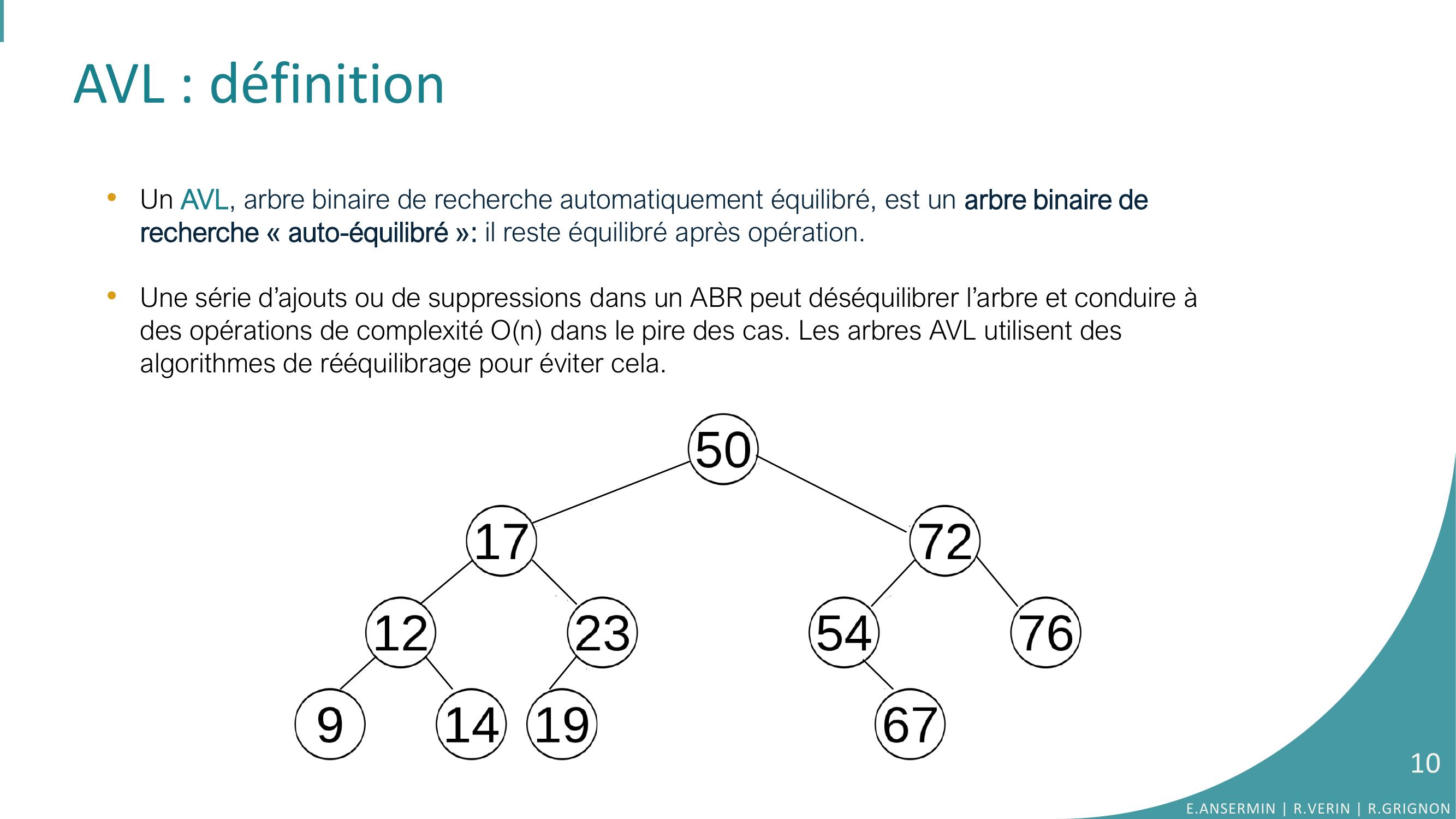
Page 10 : AVL : définition•Un AVL, arbre binaire de recherche automatiquement équilibré, est un arbre binaire de recherche « auto-équilibré »: il reste équilibré après opération. •Une série d’ajouts ou de suppressions dans un ABR peut déséquilibrer l’arbre et conduire à des opérations de complexité On dans le pire des cas. Les arbres AVL utilisent des algorithmes de rééquilibrage pour éviter cela.E.ANSERMIN R.VERIN R.GRIGNON10

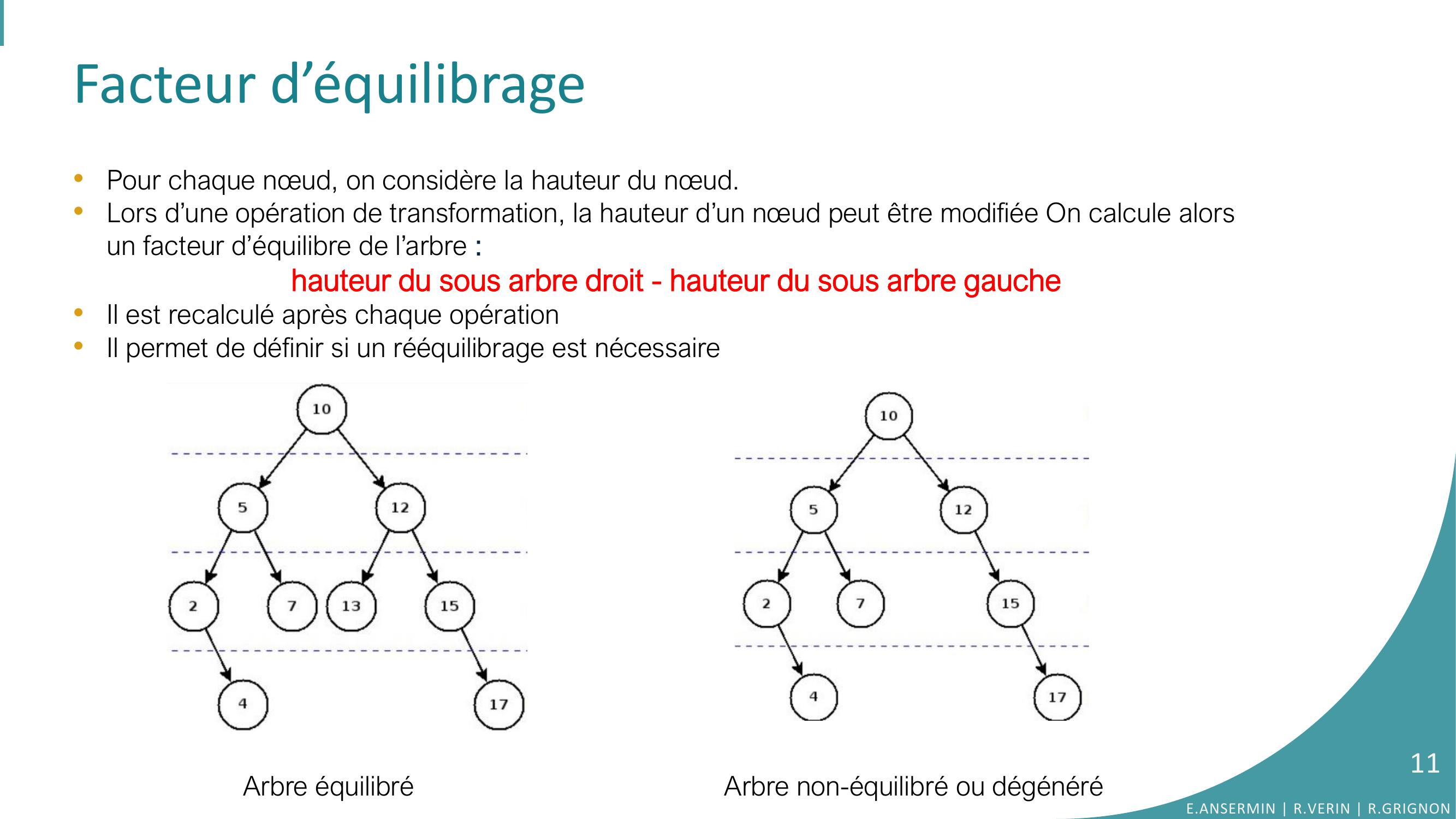
Page 11 : Facteur d’équilibrageArbre équilibréArbre non-équilibré ou dégénéré•Pour chaque nœud, on considère la hauteur du nœud.•Lors d’une opération de transformation, la hauteur d’un nœud peut être modifiée On calcule alors un facteur d’équilibre de l’arbre :hauteur du sous arbre droit - hauteur du sous arbre gauche •Il est recalculé après chaque opération •Il permet de définir si un rééquilibrage est nécessaireE.ANSERMIN R.VERIN R.GRIGNON11

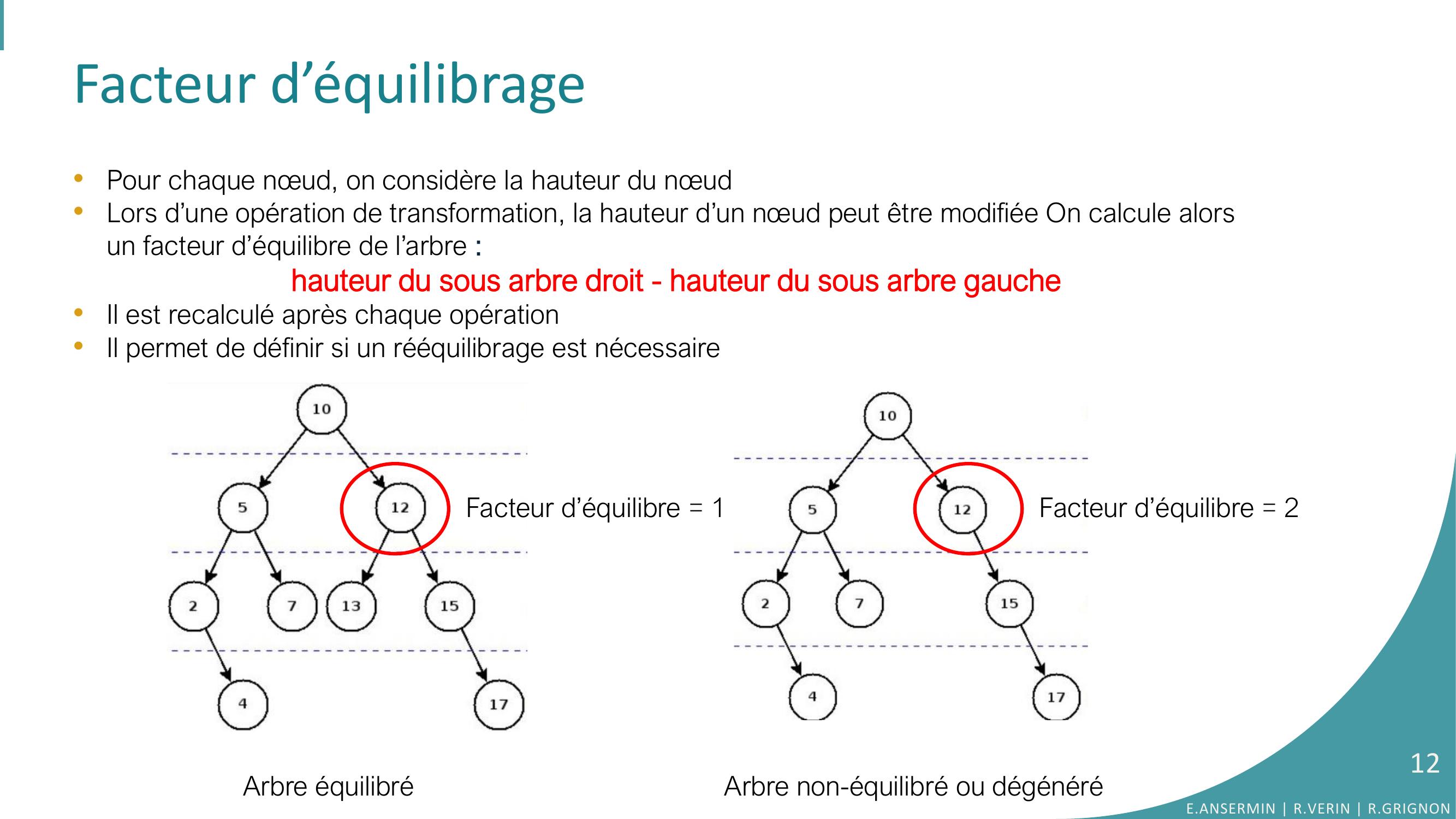
Page 12 : Facteur d’équilibrageArbre équilibréArbre non-équilibré ou dégénéréFacteur d’équilibre = 2•Pour chaque nœud, on considère la hauteur du nœud•Lors d’une opération de transformation, la hauteur d’un nœud peut être modifiée On calcule alors un facteur d’équilibre de l’arbre :hauteur du sous arbre droit - hauteur du sous arbre gauche •Il est recalculé après chaque opération •Il permet de définir si un rééquilibrage est nécessaireFacteur d’équilibre = 1E.ANSERMIN R.VERIN R.GRIGNON12

Page 13 : Facteur d’équilibrage•Pour chaque nœud, on considère la hauteur du nœud•Lors d’une opération de transformation, la hauteur d’un nœud peut être modifiée On calcule alors un facteur d’équilibre de l’arbre :hauteur du sous arbre droit - hauteur du sous arbre gauche •Il est recalculé après chaque opération •Il permet de définir si un rééquilibrage est nécessaire• Un arbre est équilibré  facteur d’équilibre 2 pour tous les nœuds.E.ANSERMIN R.VERIN R.GRIGNON13

Page 14 : Construction d’un AVL• Structure d’un nœud d’un AVL: Structure Arbre :elmt : Element // contenu du nœud fg, fd : pointeur sur structure Arbre // fils gauche et droitequilibre : entier // facteur d’équilibre du nœud = hauteur sous arbre droit – hauteur sous-arbre gauche. E.ANSERMIN R.VERIN R.GRIGNON14

Page 15 : Construction d’un AVL•Déclaration et initialisation d’un nœud FONCTION creerArbrer: Element : ptr sur ArbreVARIABLEnoeud : ptr sur ArbreDEBUTnoeud ←reserverMemoireArbreelmtnoeud ←rfgnoeud ←?? fdnoeud ←??equilibrenoeud ←??RETOURNER noeudFINE.ANSERMIN R.VERIN R.GRIGNON15

Page 16 : Construction d’un AVL•Déclaration et initialisation d’un nœud FONCTION creerArbrer: Element : ptr sur ArbreVARIABLEnoeud : ptr sur ArbreDEBUTnoeud ←reserverMemoireArbreelmtnoeud ←rfgnoeud ←NULL // Le noeud n’a pas de fils à sa créationfdnoeud ←NULLequilibrenoeud ←0 // Le noeud n’a pas de fils: son equilibre est 0RETOURNER noeudFINE.ANSERMIN R.VERIN R.GRIGNON16

Page 17 : III. AVL : opérationsE.ANSERMIN R.VERIN R.GRIGNON17

Page 18 : Opération de recherche•Puisque l’AVL respecte les propriétés d’un ABR, l’algorithme de recherche ne change pas : •Recherche dans le sous-arbre gauche si la valeur recherchée est inférieure au nœud•Recherche dans le sous-arbre droit si la valeur recherchée est supérieure au nœud•L’opération de recherche ne modifie pas l’arbre : pas besoin de rééquilibrage. FONCTION recherchea: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL AlorsRETOURNER NULLSINON SI elementa EST EGAL A e AlorsRETOURNER aSINON SI e EST INF. STRICT. A elementa ALORSRETOURNER recherchefga,eSINONRETOURNER recherchefda,eFIN SIFinE.ANSERMIN R.VERIN R.GRIGNON18

Page 19 : Insertion•1ère étape : l’insertion se déroule de la même manière que pour un ABR : 10528151218•Algorithme :FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINExemple : insertionABRA, 9E.ANSERMIN R.VERIN R.GRIGNON19

Page 20 : Insertion•1ère étape : l’insertion se déroule de la même manière que pour un ABR : 105281512189•Algorithme :FONCTION insertionABRa: pointeur sur Arbre, e: Element : pointeur sur ArbreDEBUTSI a EST EGAL A NULL ALORSRETOURNER creerArbree SINON SI e EST INF. STRICT. A elementa ALORSfga ← insertionABRfga, eSINON SI e SUP. STRICT. A elementa Alorsfda ← insertionABRfda, eFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON20

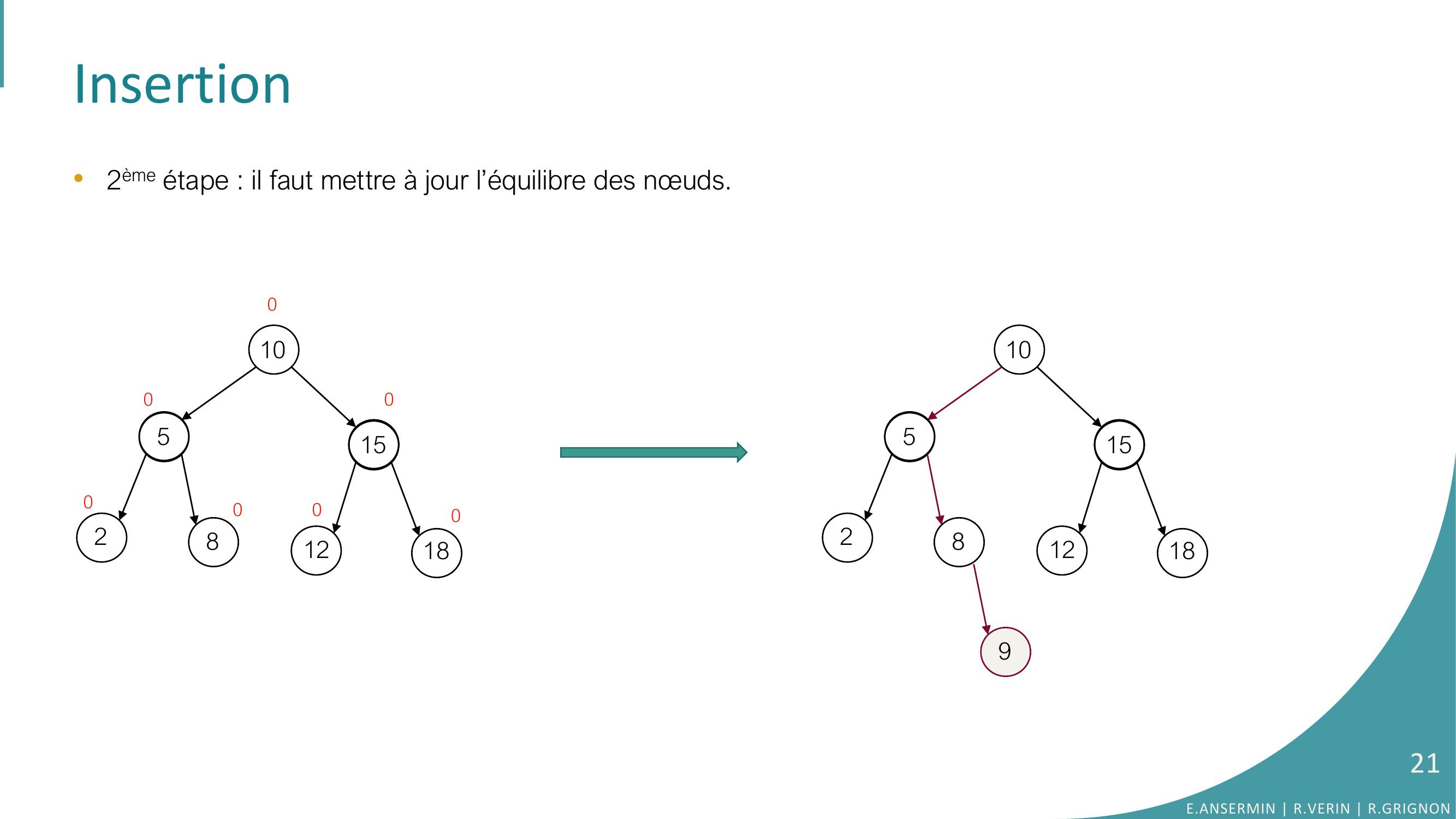
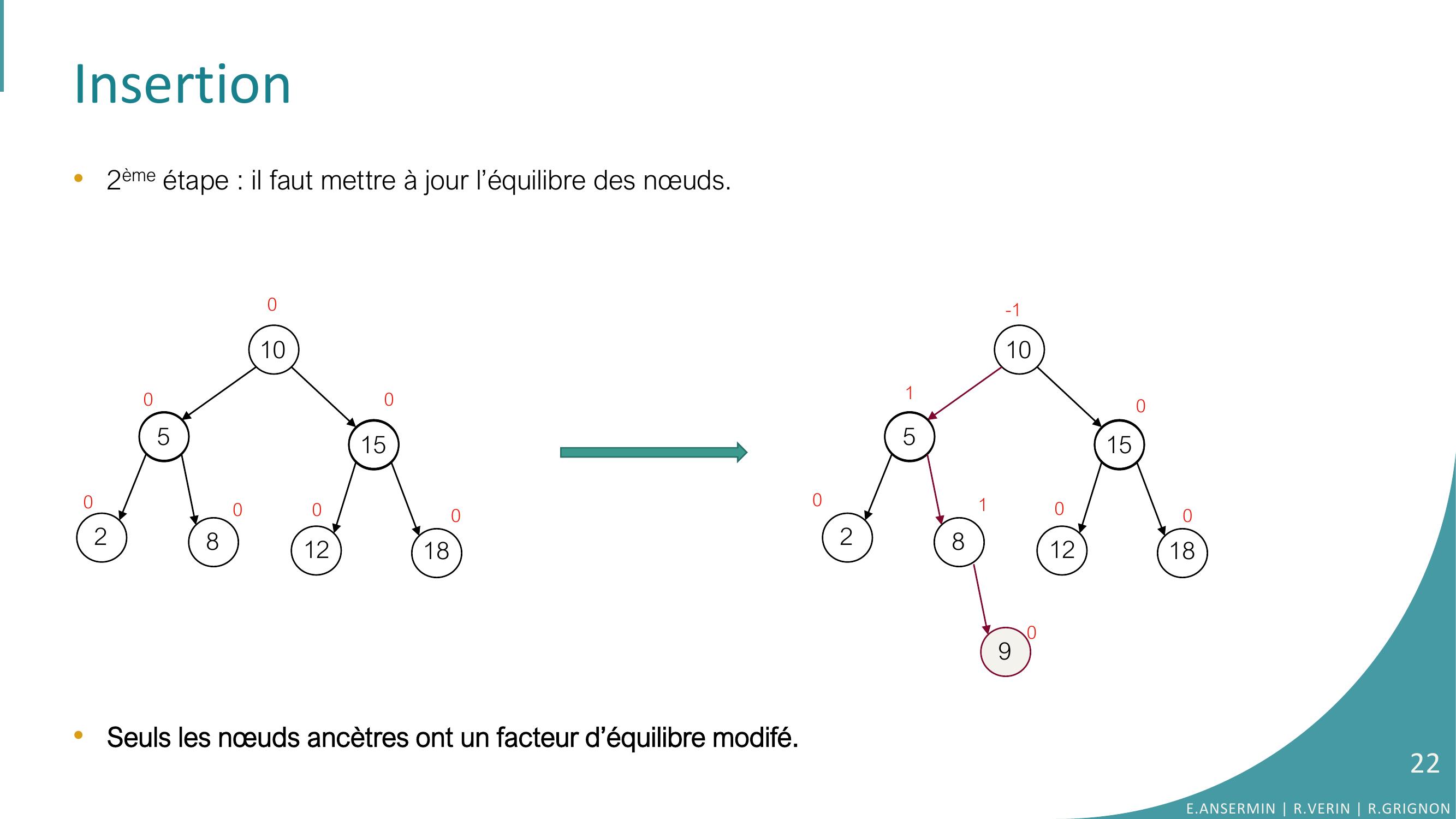
Page 21 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.105281512189105281512180000000E.ANSERMIN R.VERIN R.GRIGNON21

Page 22 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.•Seuls les nœuds ancètres ont un facteur d’équilibre modifé.1052815121891052815121800000000101-1000E.ANSERMIN R.VERIN R.GRIGNON22

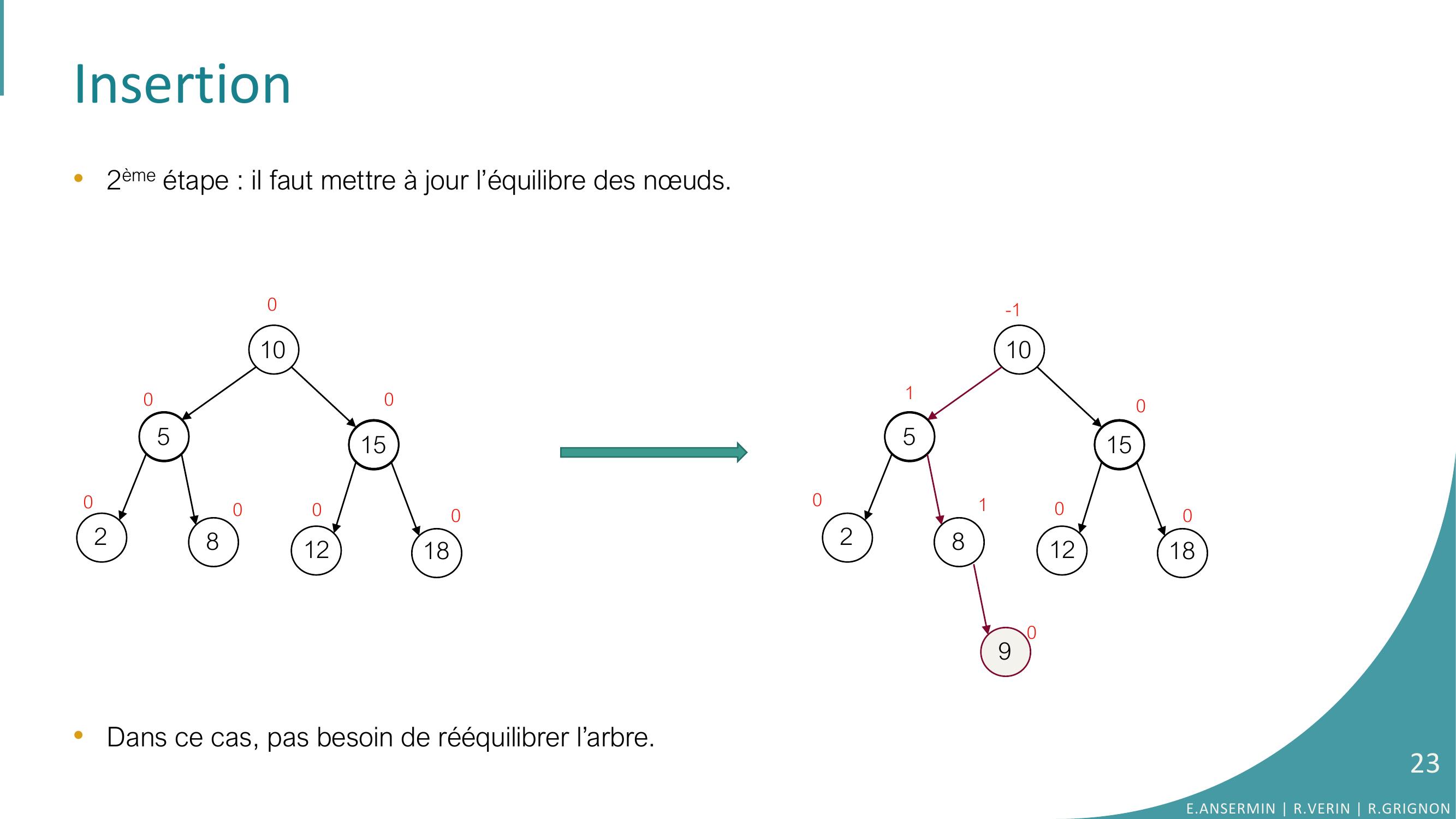
Page 23 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.•Dans ce cas, pas besoin de rééquilibrer l’arbre. 1052815121891052815121800000000101-1000E.ANSERMIN R.VERIN R.GRIGNON23

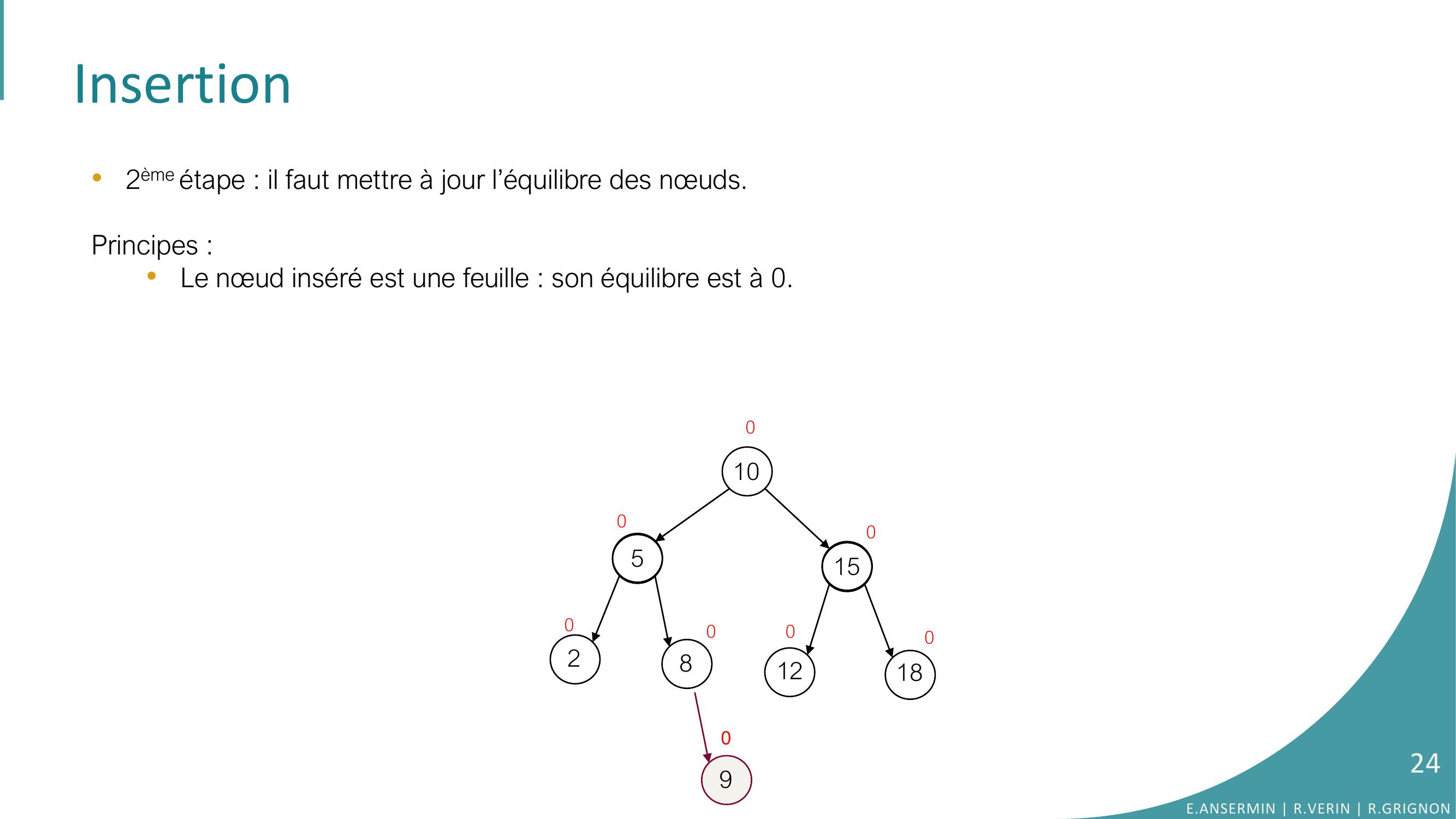
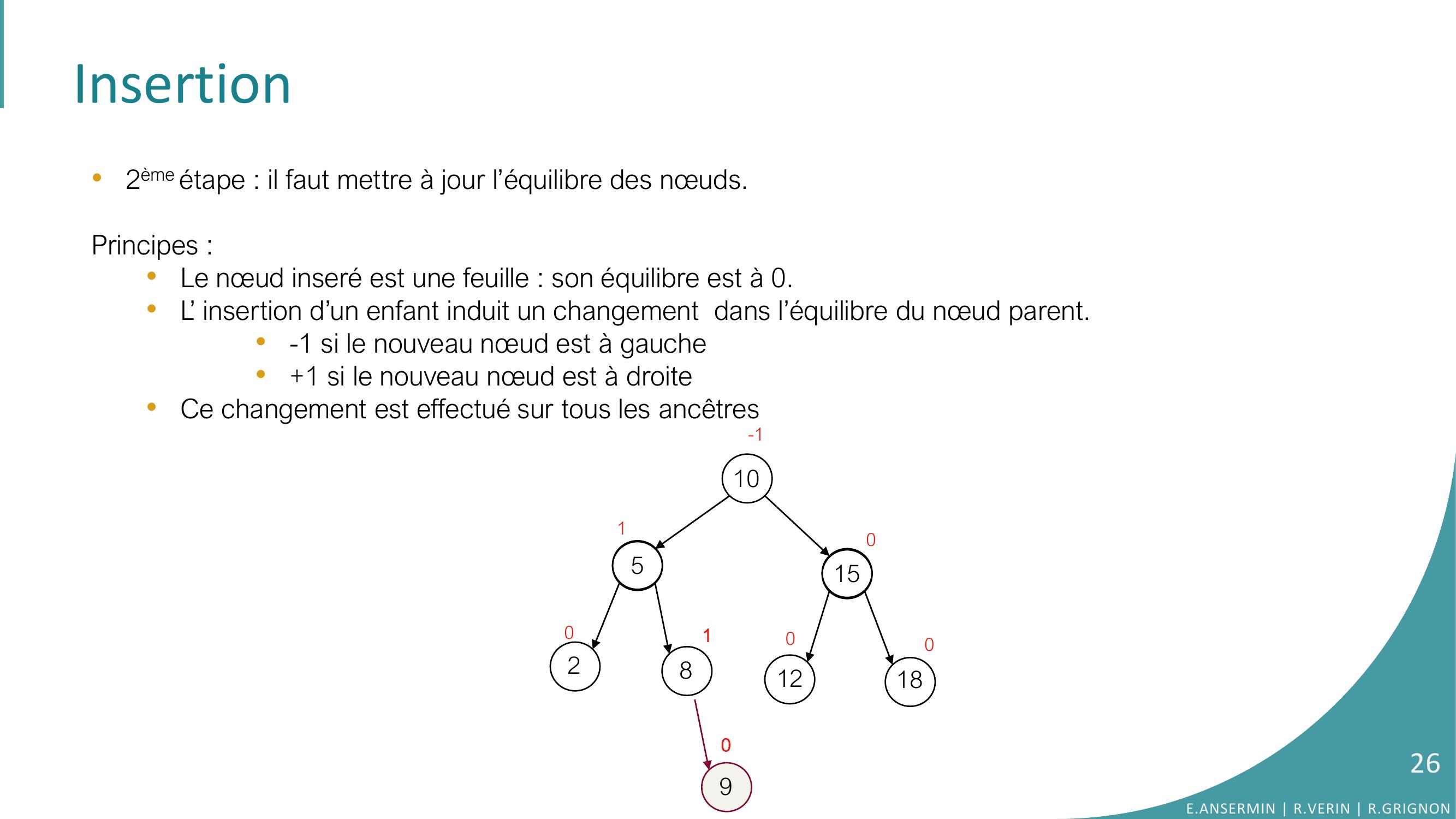
Page 24 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.Principes : •Le nœud inséré est une feuille : son équilibre est à 0. 10528151218000000090E.ANSERMIN R.VERIN R.GRIGNON24

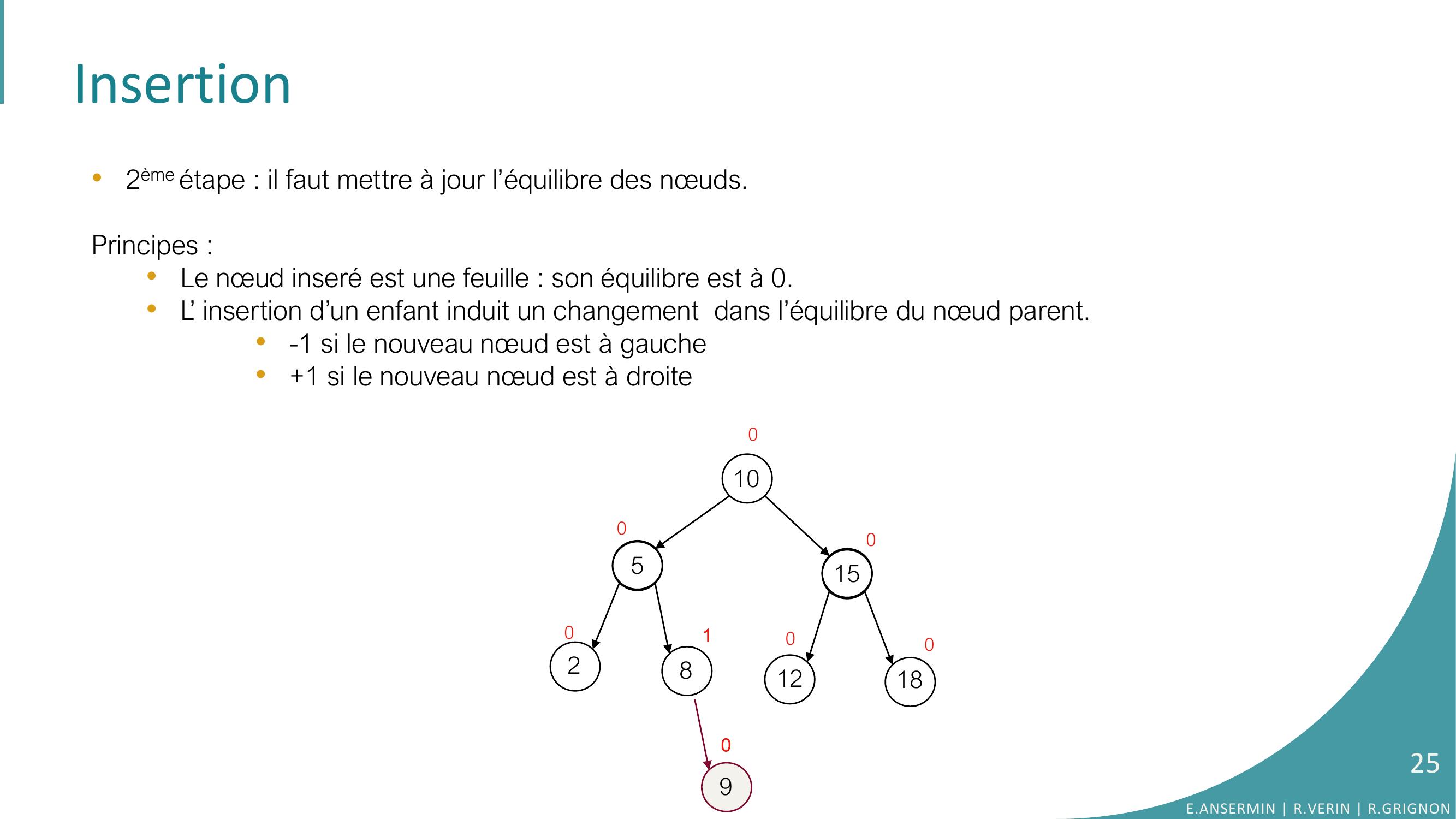
Page 25 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.Principes : •Le nœud inseré est une feuille : son équilibre est à 0. •L’ insertion d’un enfant induit un changement dans l’équilibre du nœud parent.•-1 si le nouveau nœud est à gauche•+1 si le nouveau nœud est à droite 10528151218010000090E.ANSERMIN R.VERIN R.GRIGNON25

Page 26 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœuds.Principes : •Le nœud inseré est une feuille : son équilibre est à 0. •L’ insertion d’un enfant induit un changement dans l’équilibre du nœud parent.•-1 si le nouveau nœud est à gauche•+1 si le nouveau nœud est à droite •Ce changement est effectué sur tous les ancêtres10528151218010010-190E.ANSERMIN R.VERIN R.GRIGNON26

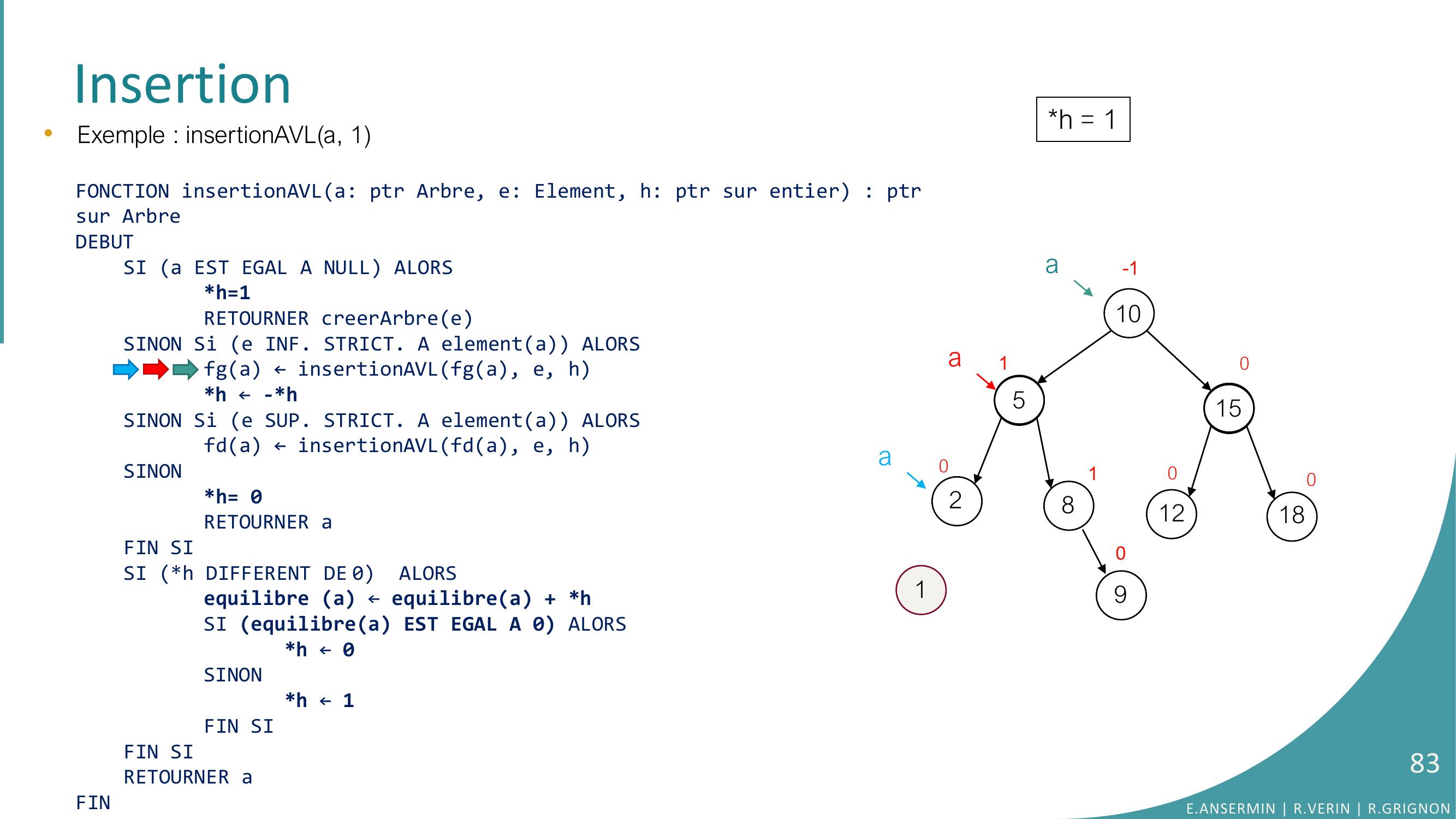
Page 27 : Insertion•2ème étape : il faut mettre à jour l’équilibre des nœud Algorithme :FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1// on ajoute un élément : l’équilibre va changerRETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h // difference de -1 si on insère à gaucheSINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0// cas où l’élément est déjà dans l’arbreRETOURNER a// pas de changement d’équilibreFIN SISI h DIFFERENT DE 0 ALORS// s’il y a changement…equilibre a ← equilibrea + h// … mise à jour du facteur d’équilibreSI equilibrea EST EGAL A 0 ALORS // si arbre équilibré à nouveau…h ← 0// ses ancêtres ne changent pas SINONh ← 1FIN SIFIN SI RETOURNER AFINh : différence d’équilibreE.ANSERMIN R.VERIN R.GRIGNON27

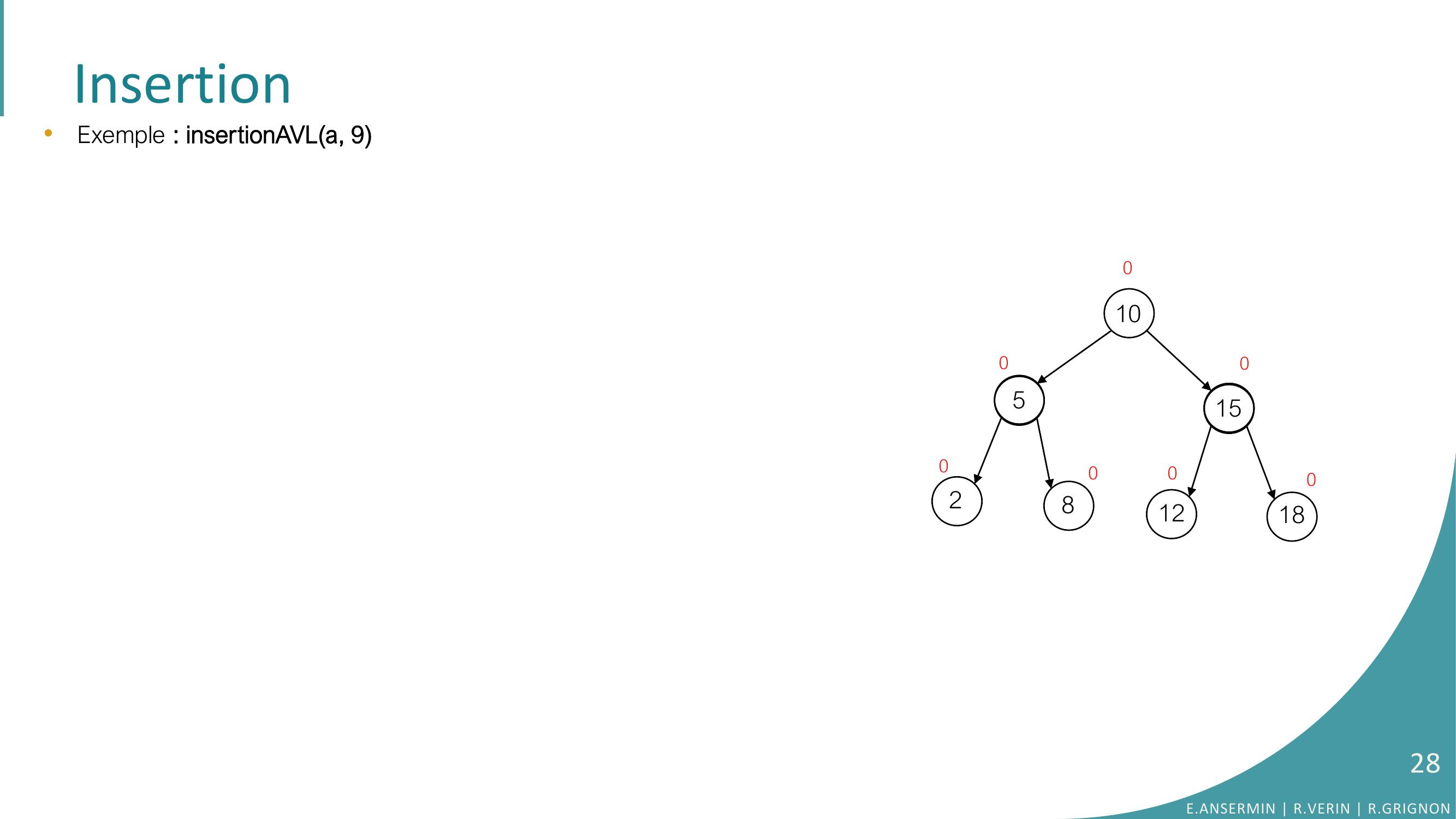
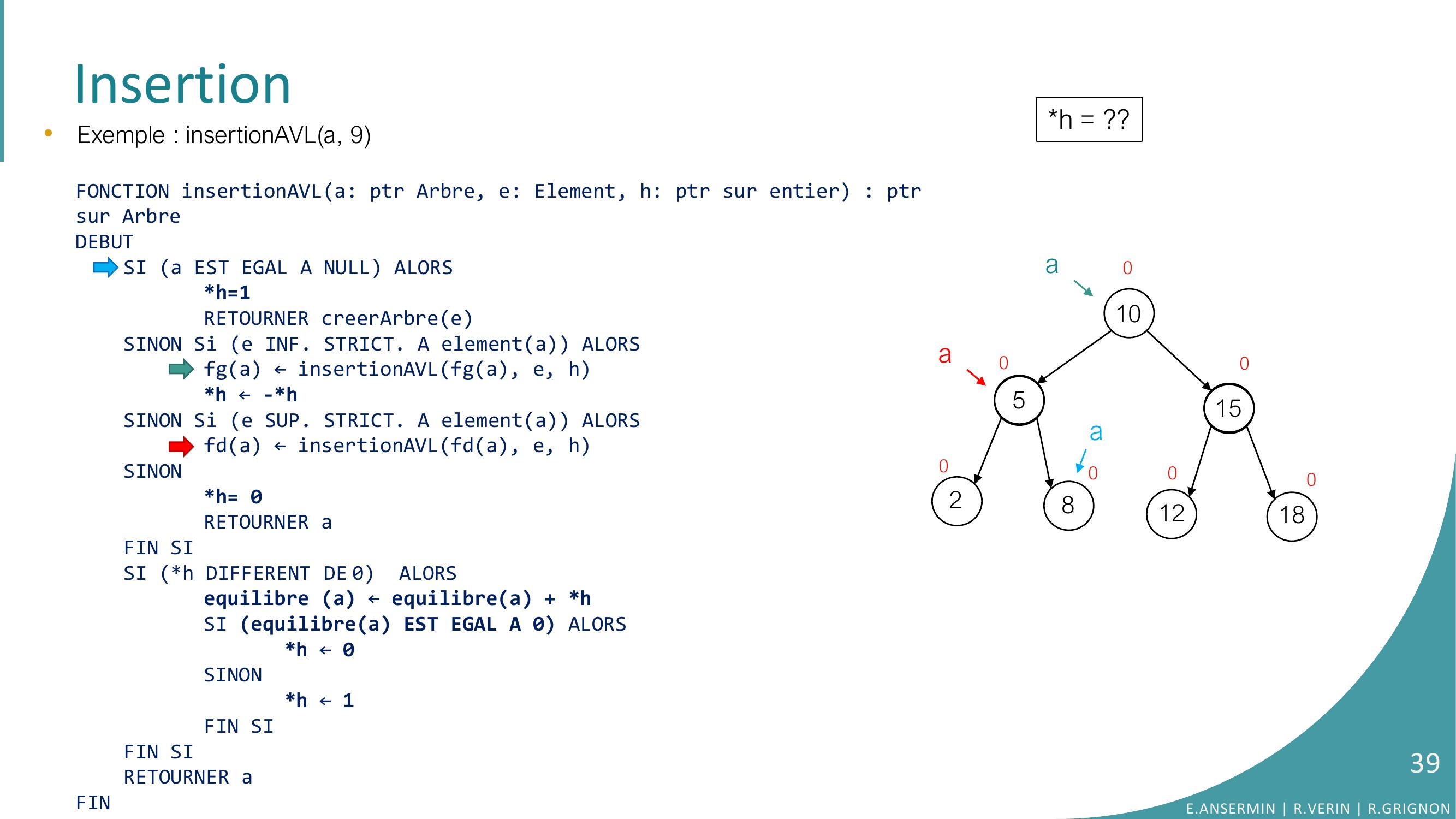
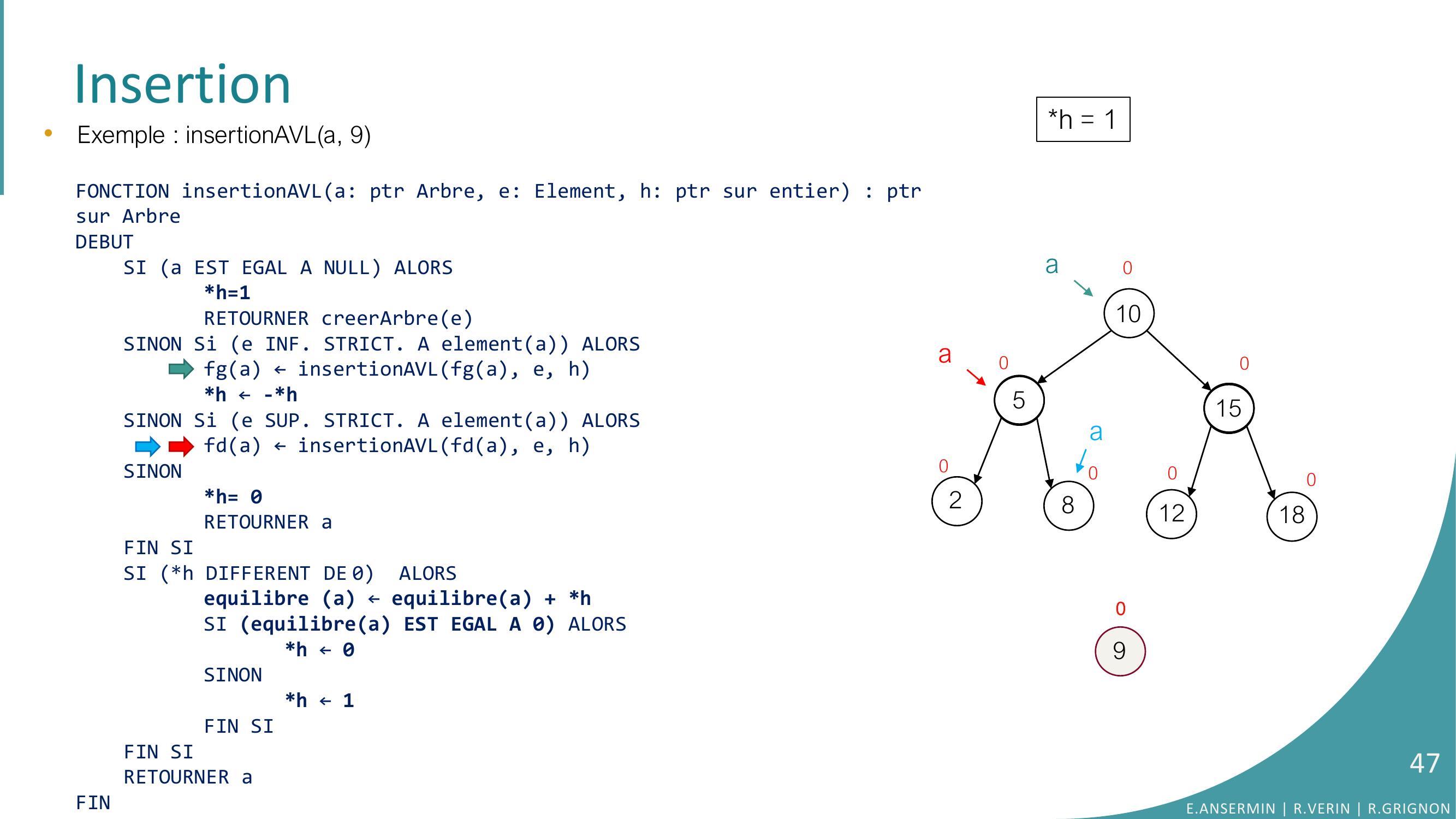
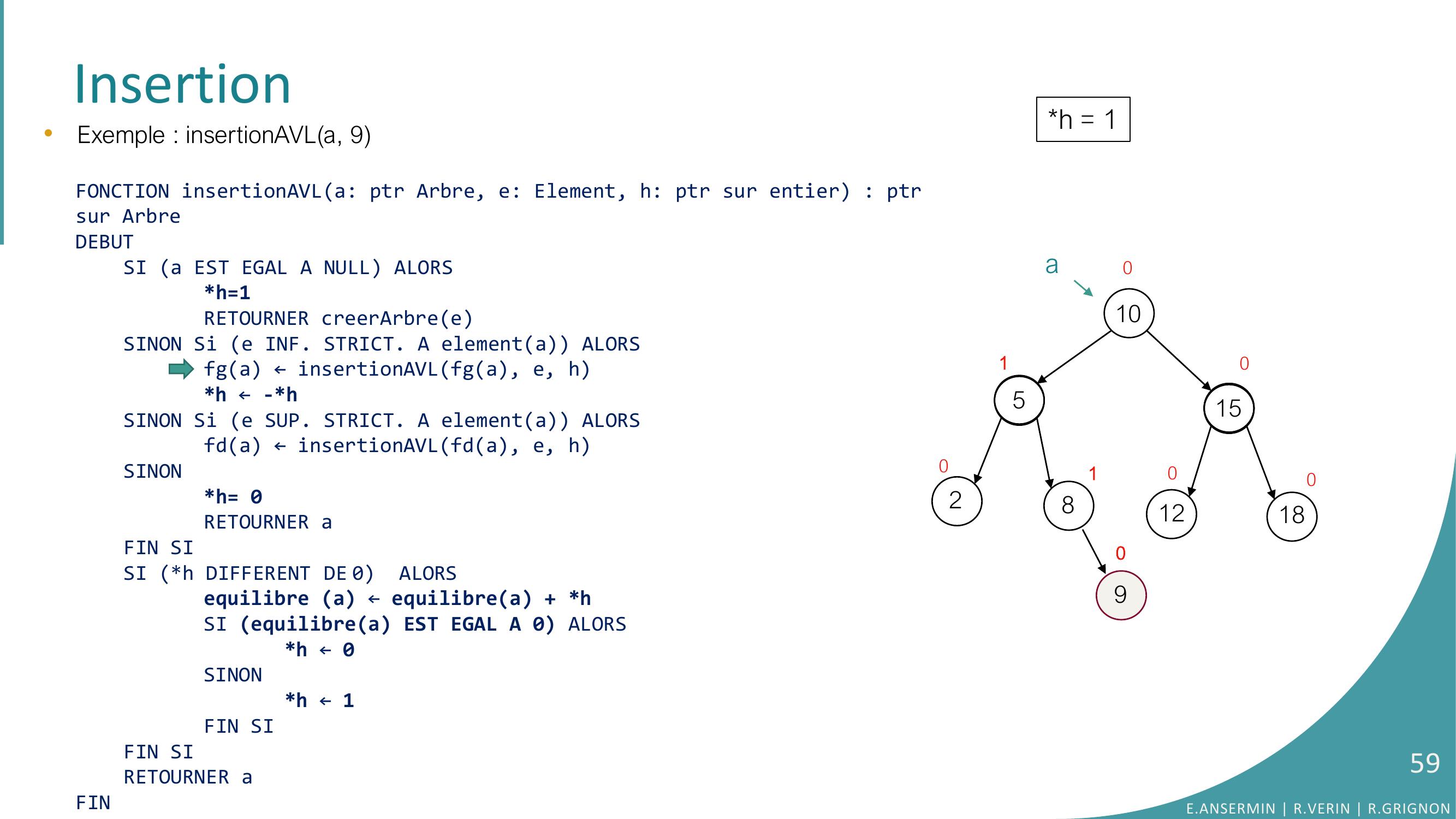
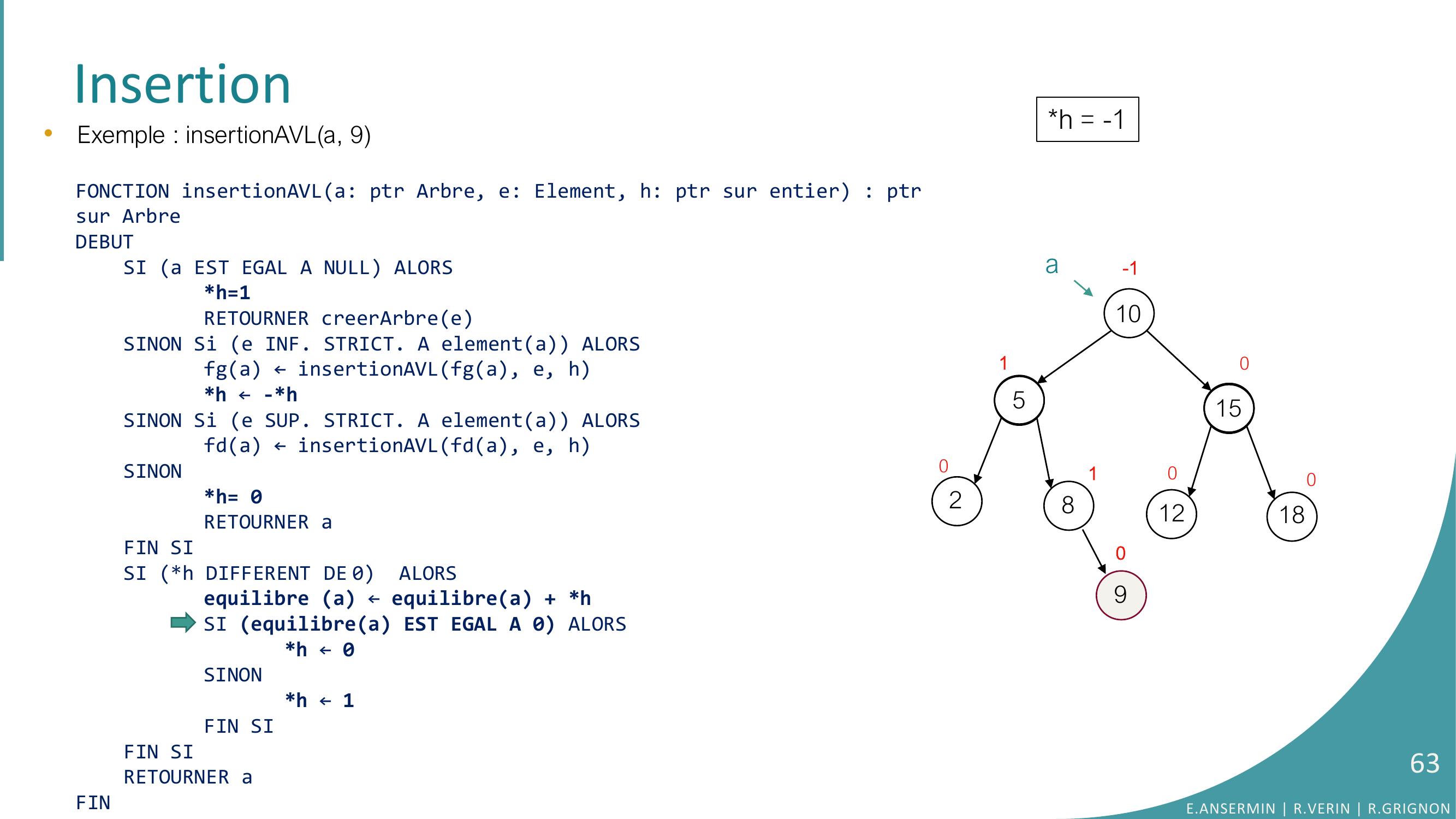
Page 28 : Insertion105281512180000000•Exemple : insertionAVLa, 9E.ANSERMIN R.VERIN R.GRIGNON28

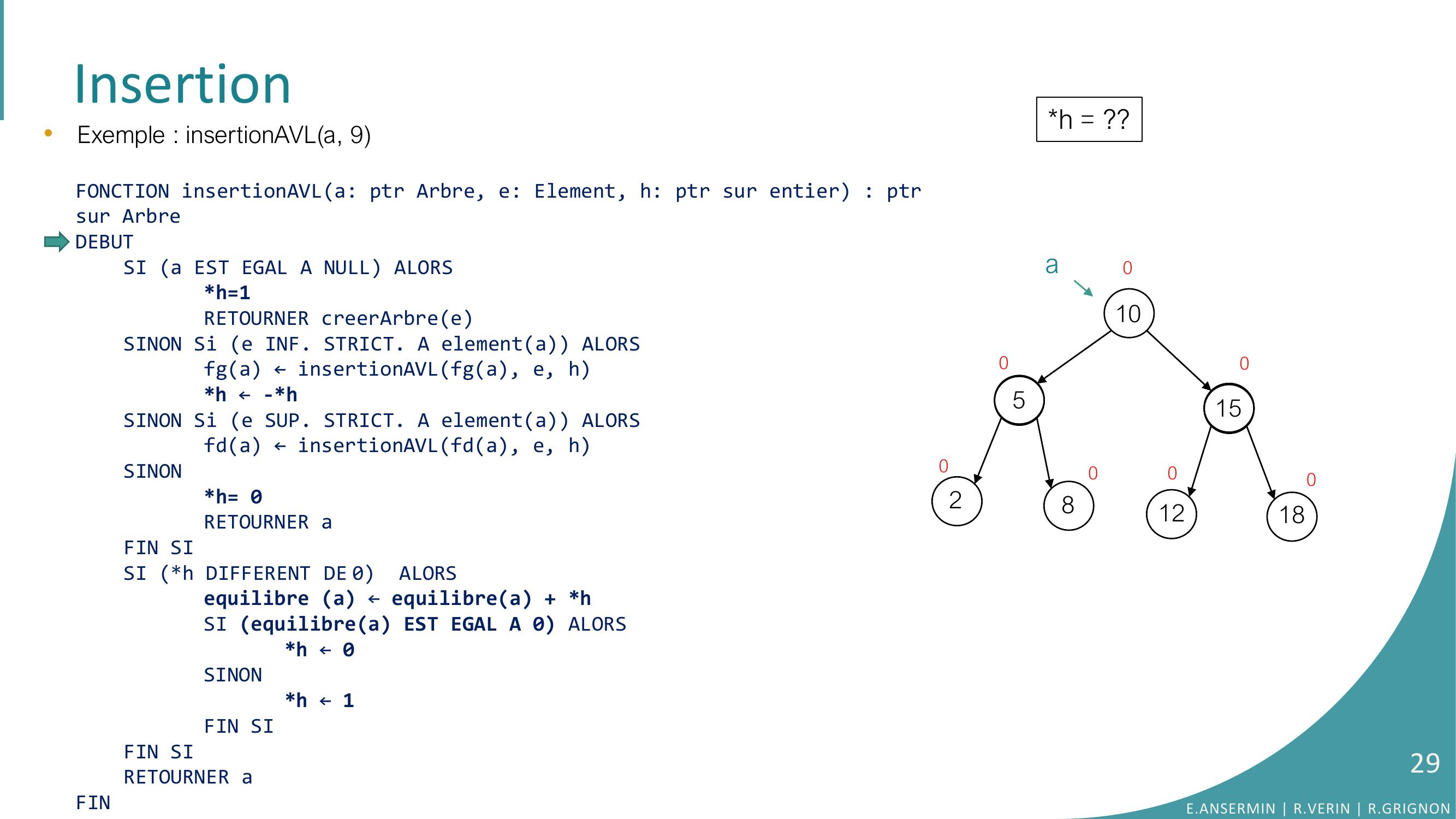
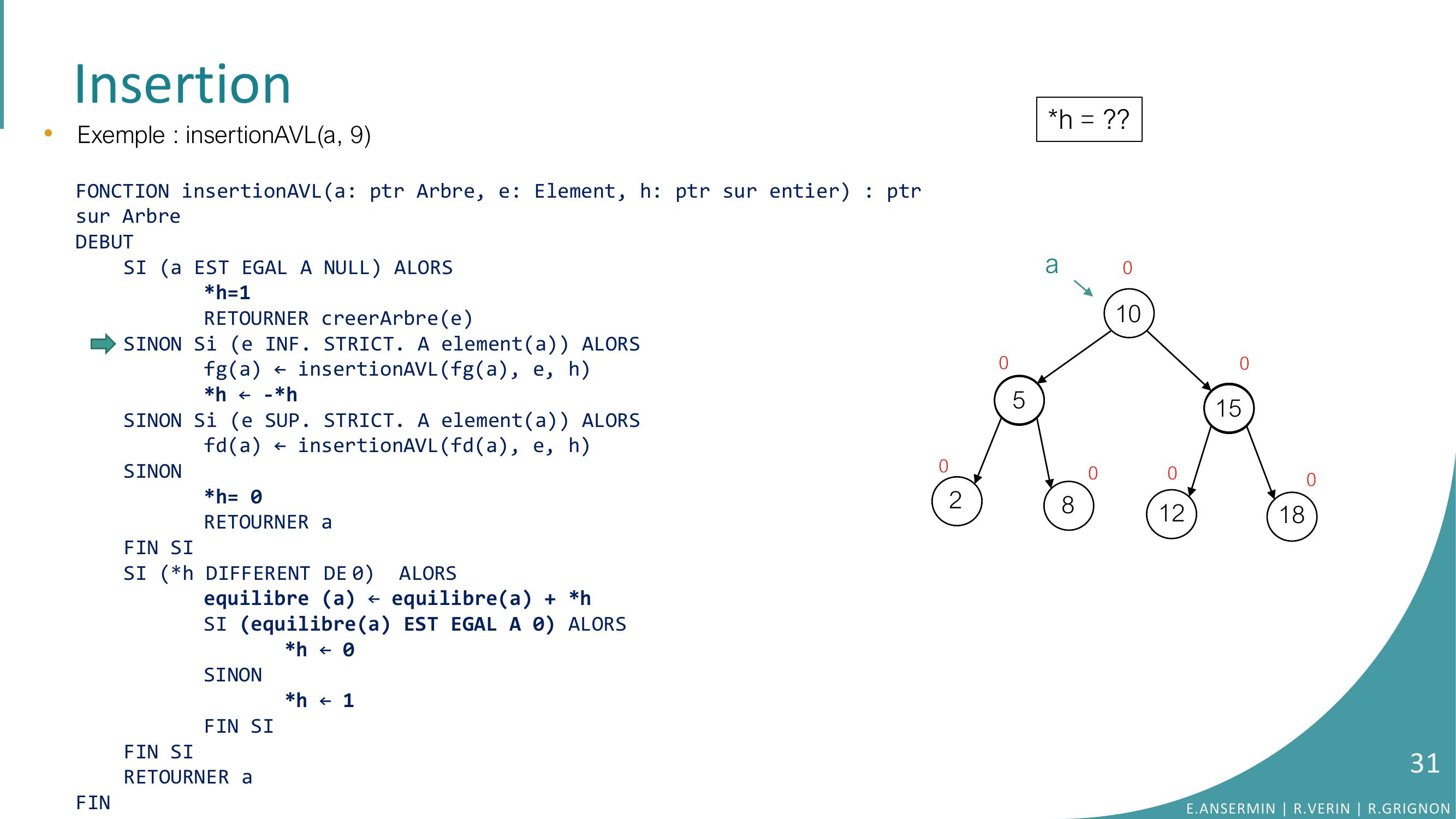
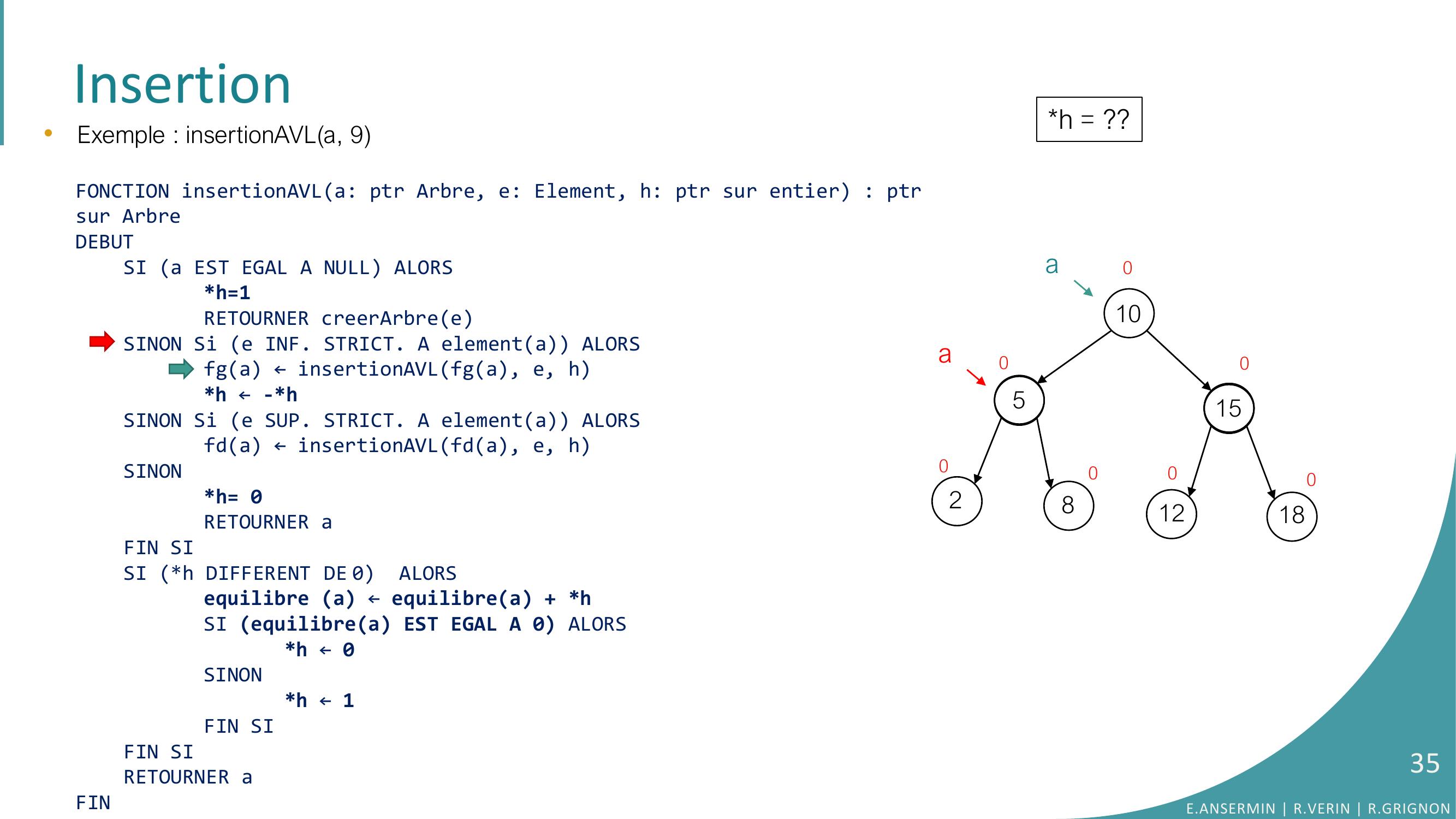
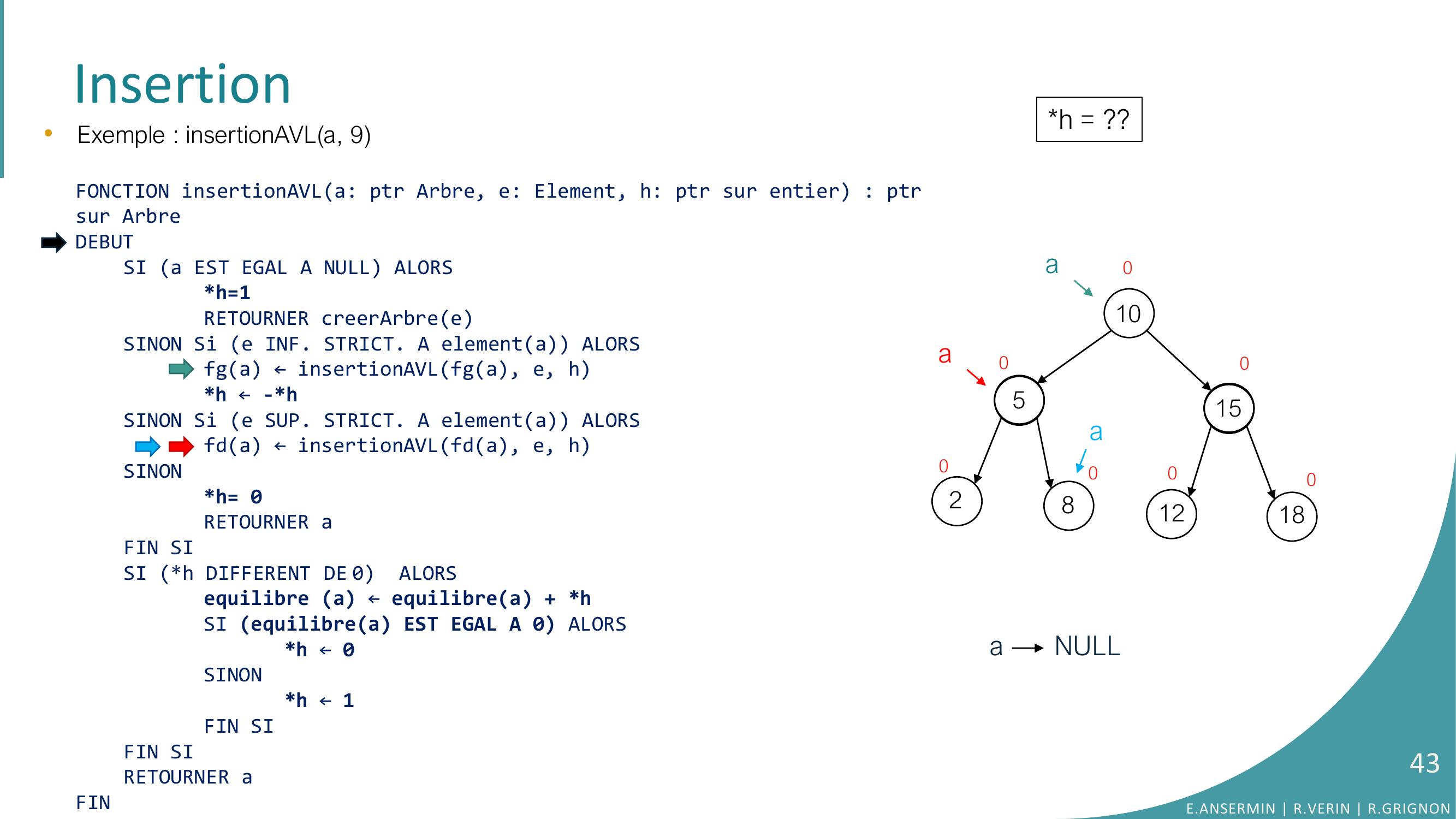
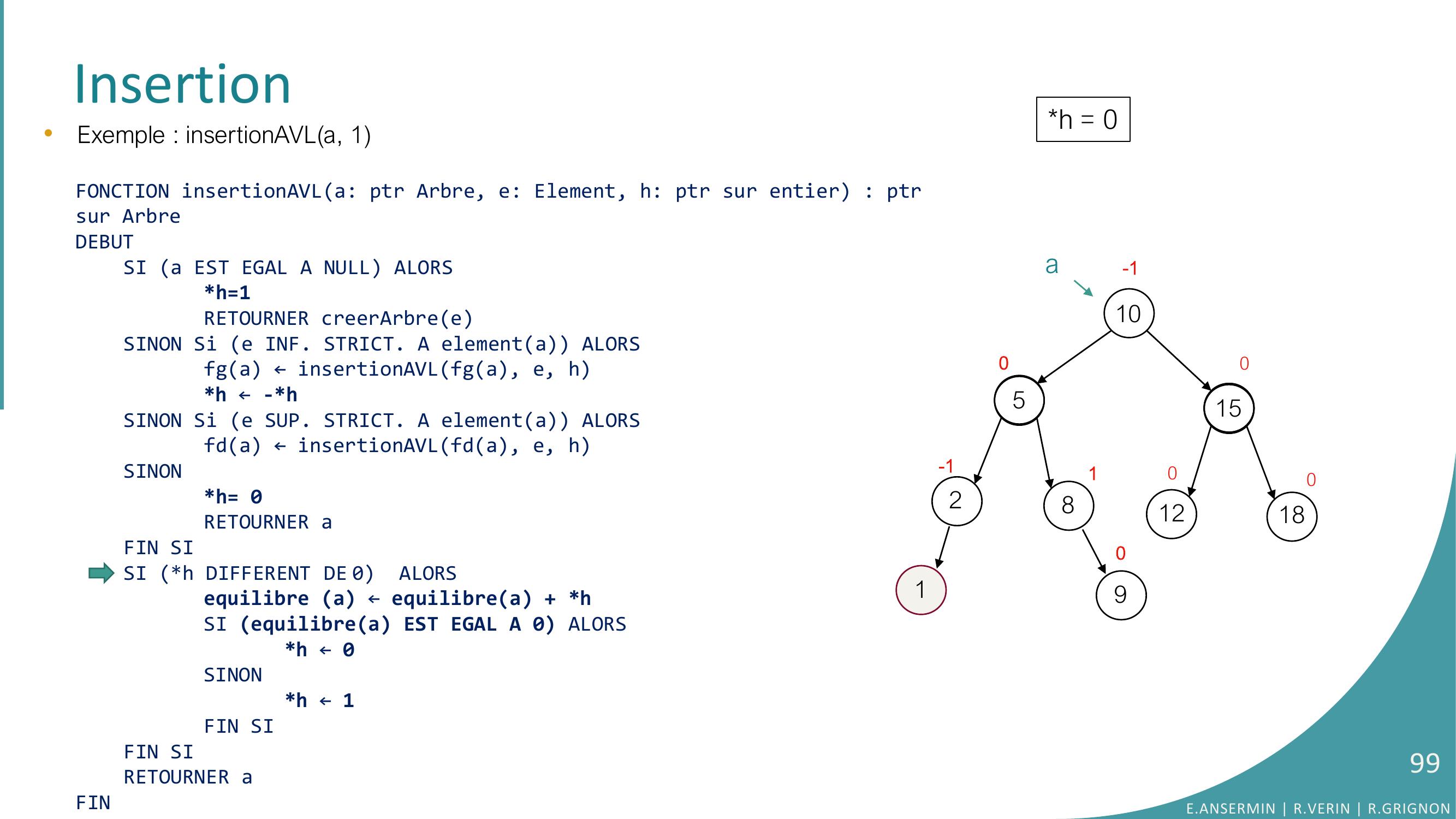
Page 29 : Insertion105281512180000000ah = ??•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON29

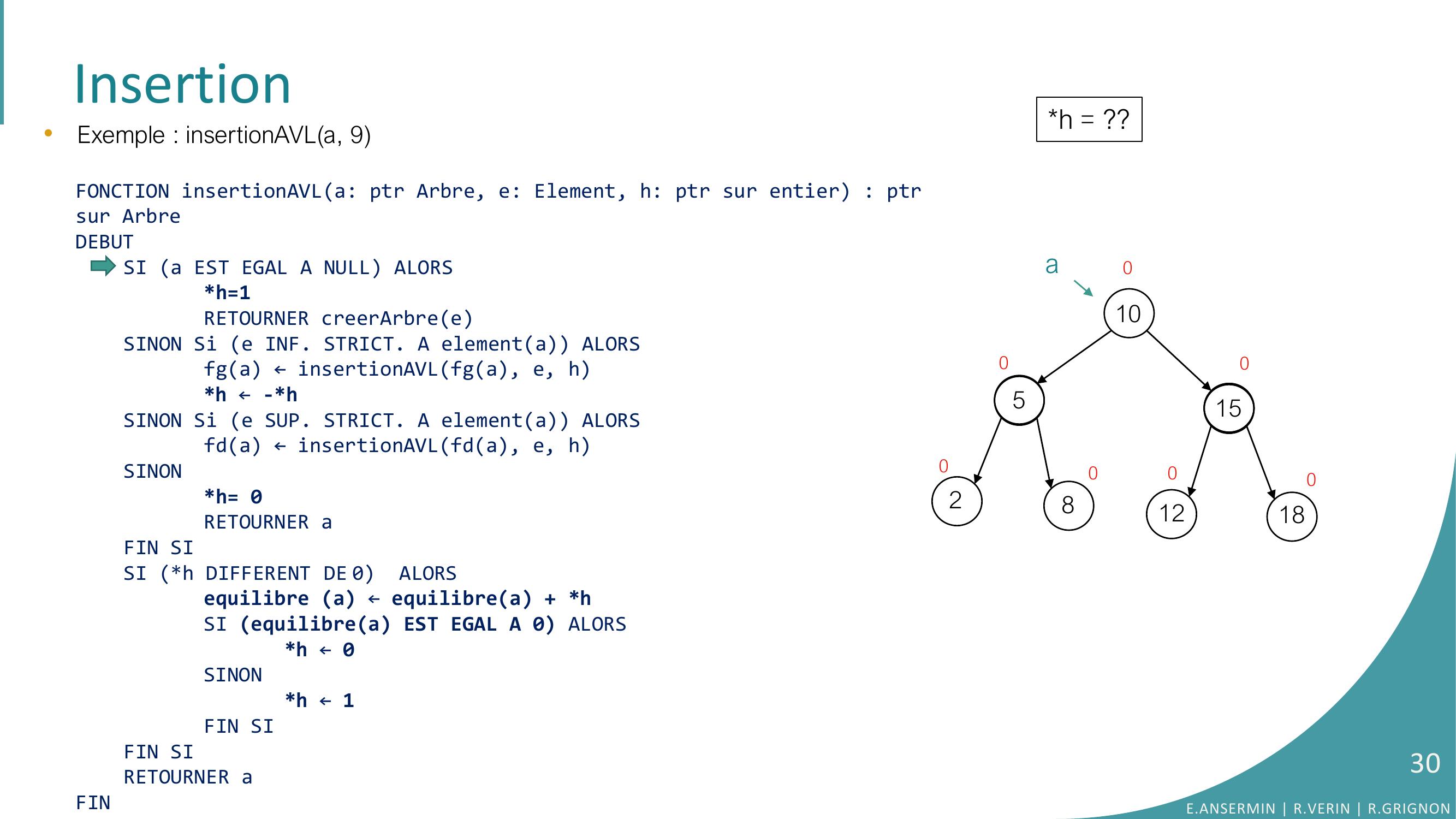
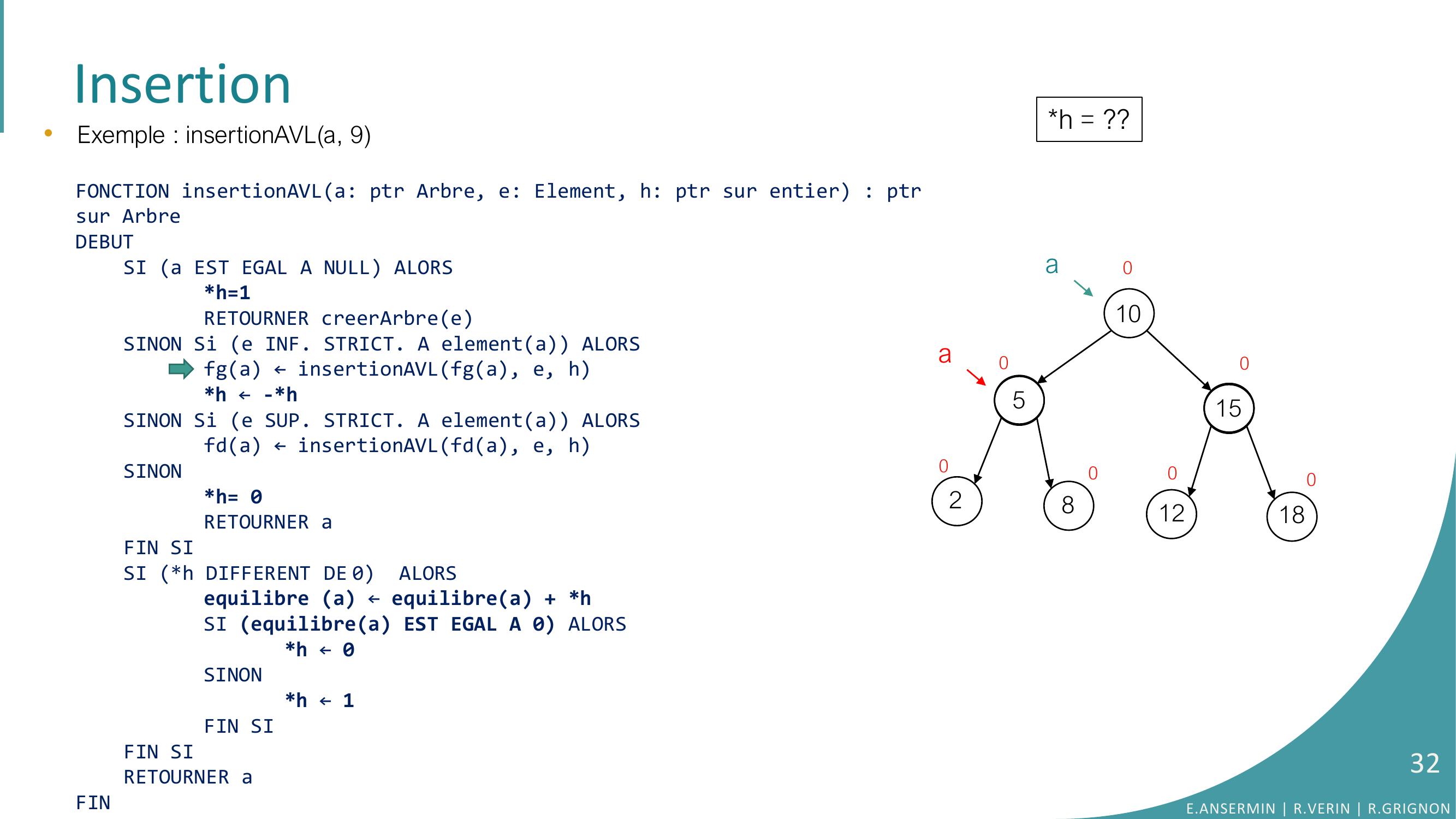
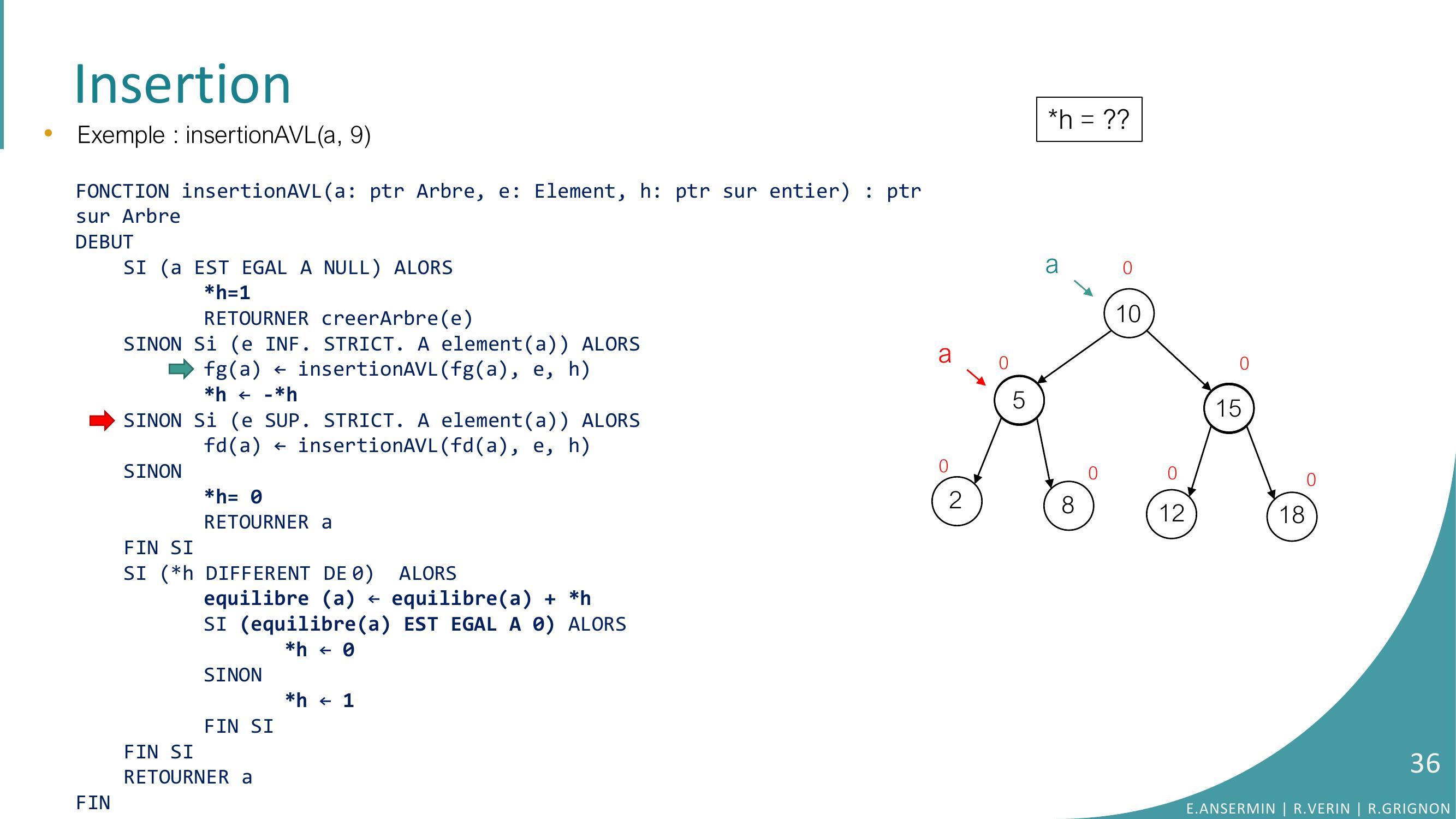
Page 30 : Insertion105281512180000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON30

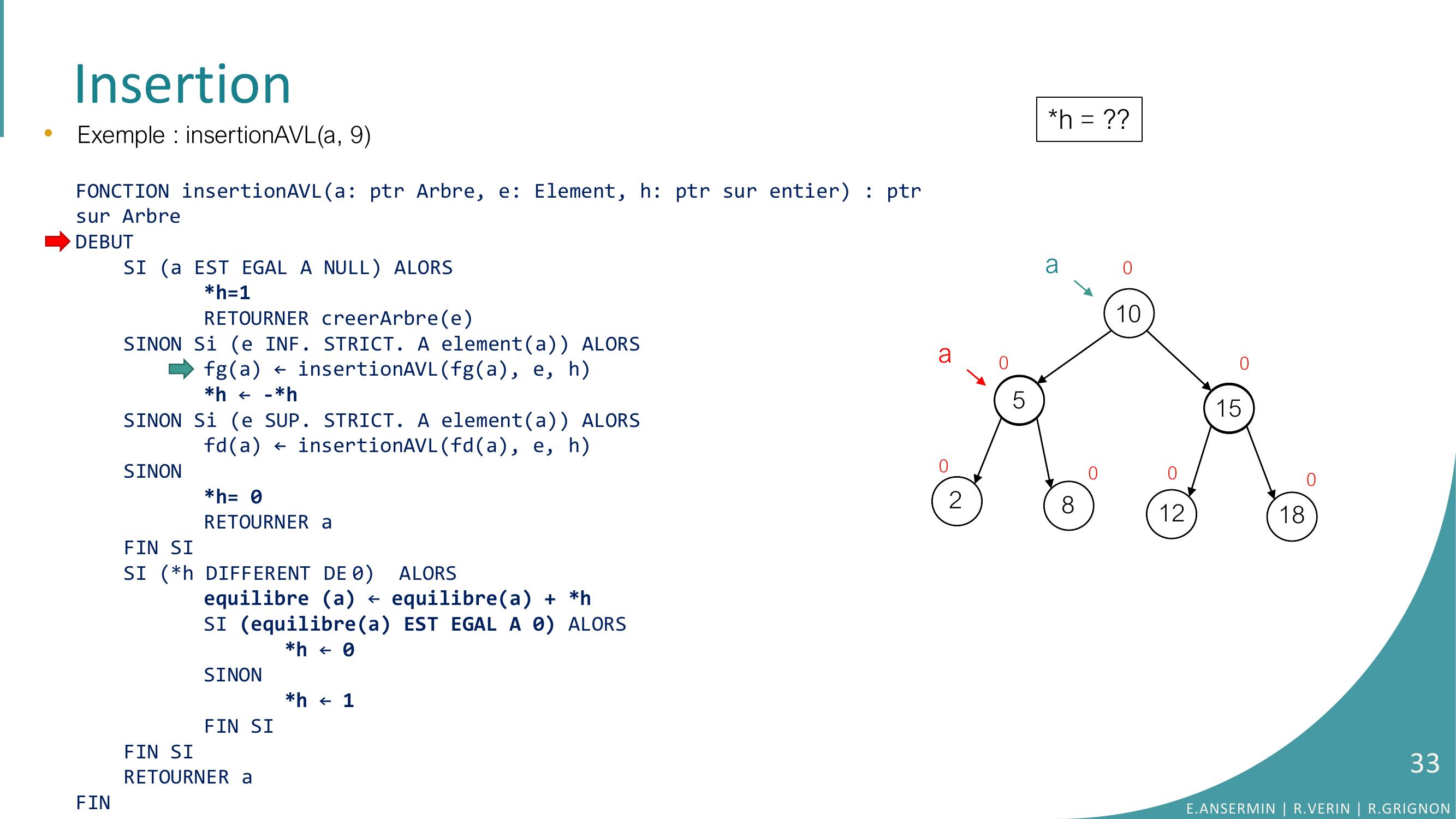
Page 31 : Insertion105281512180000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON31

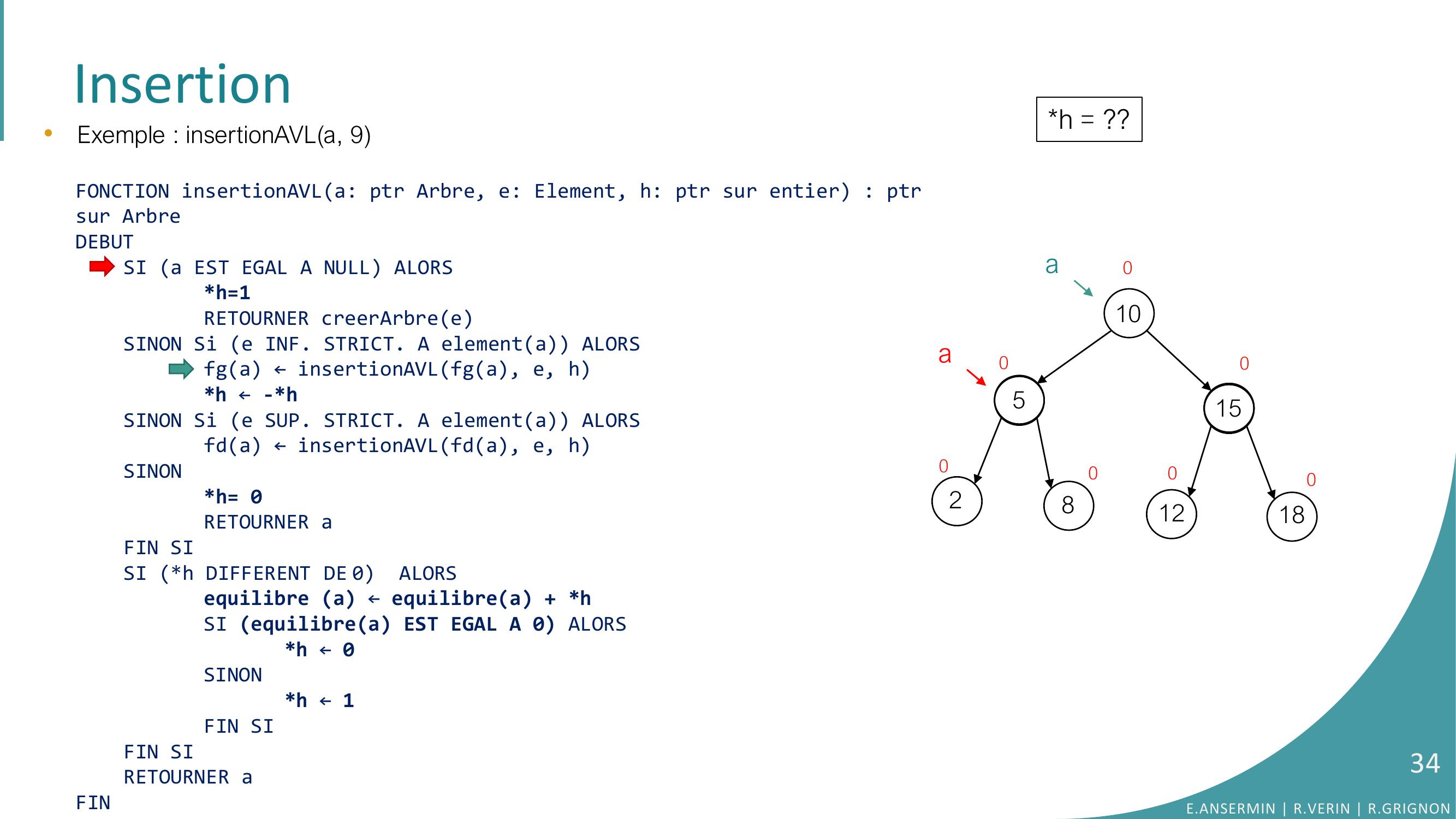
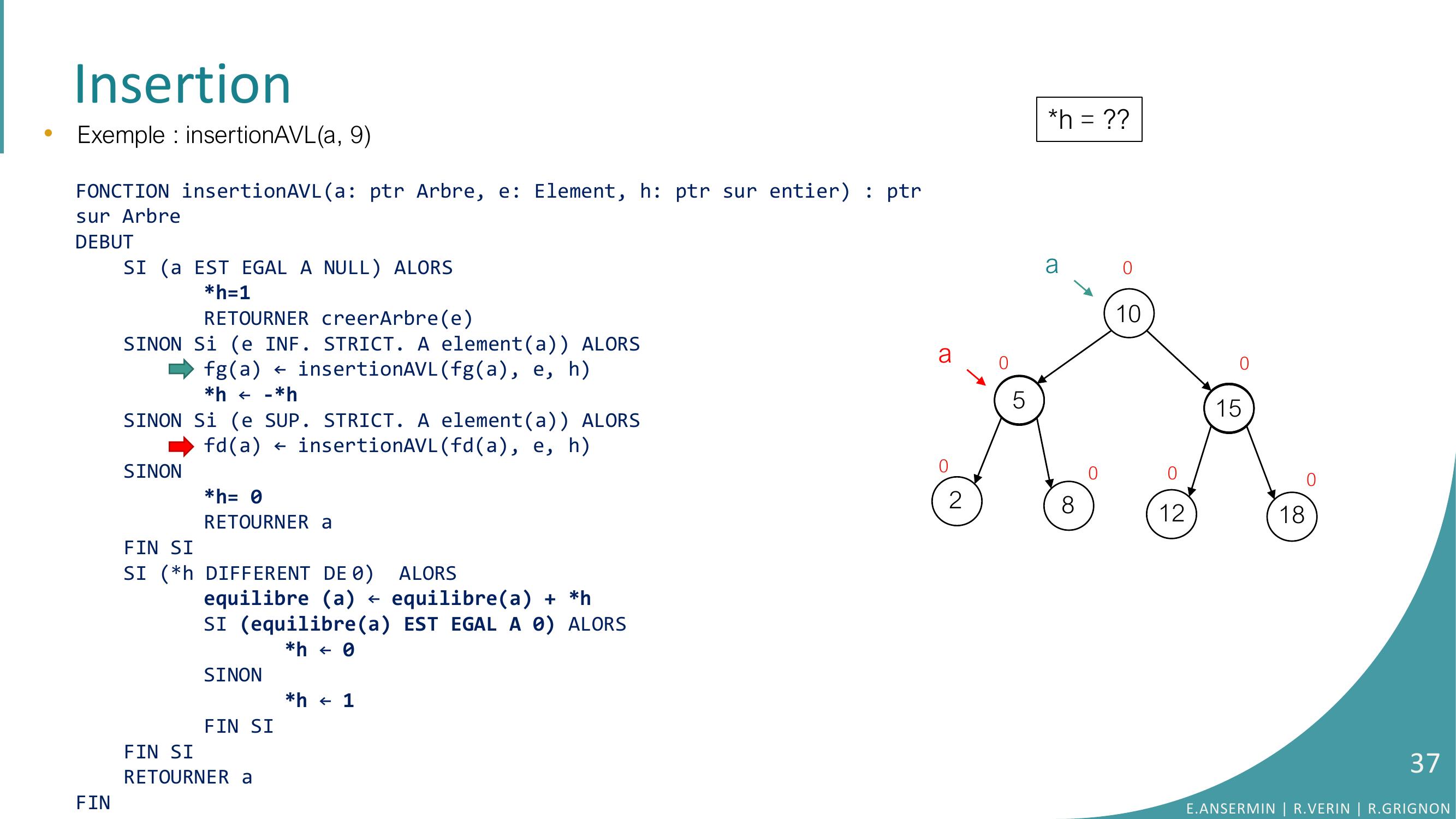
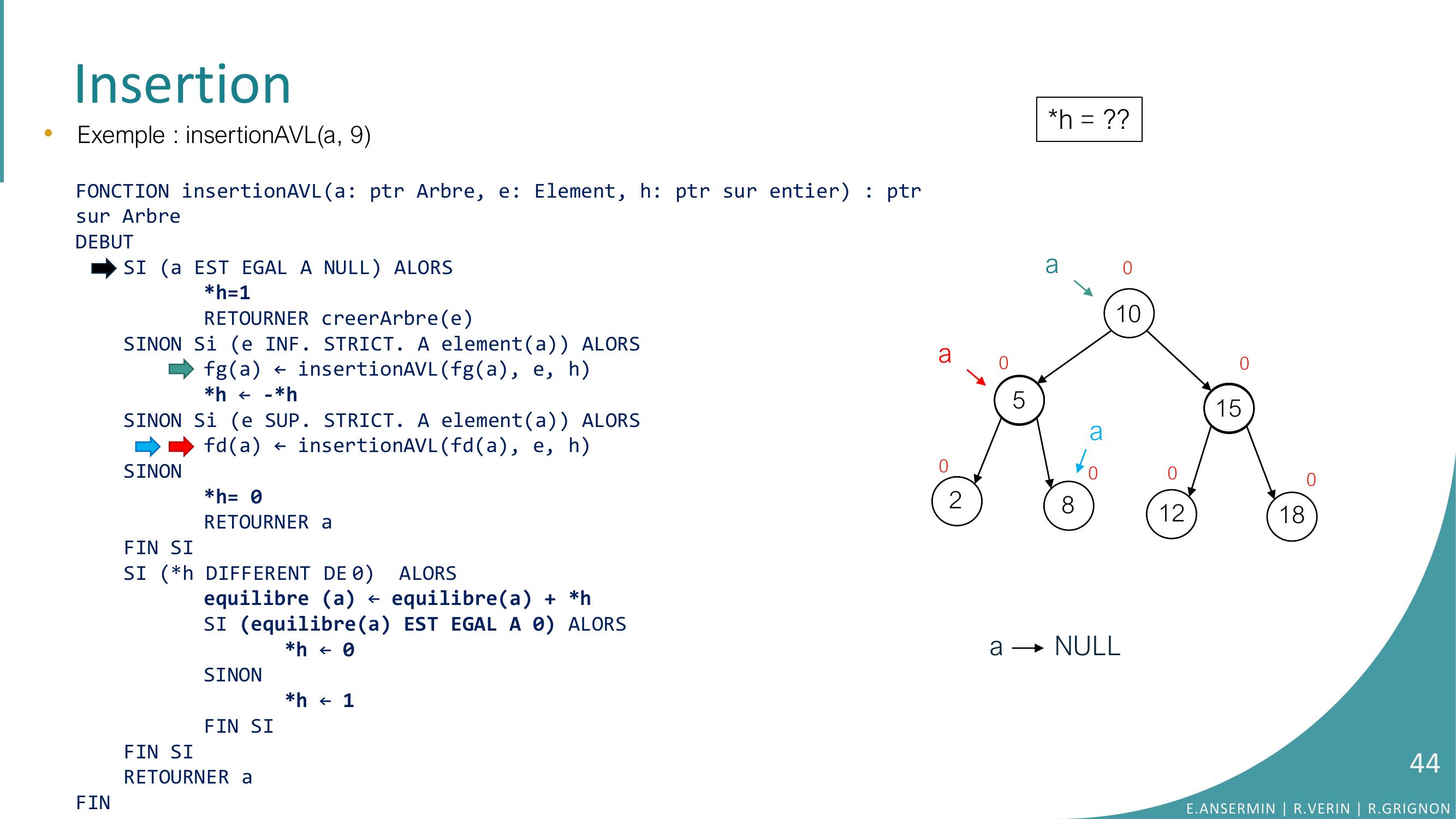
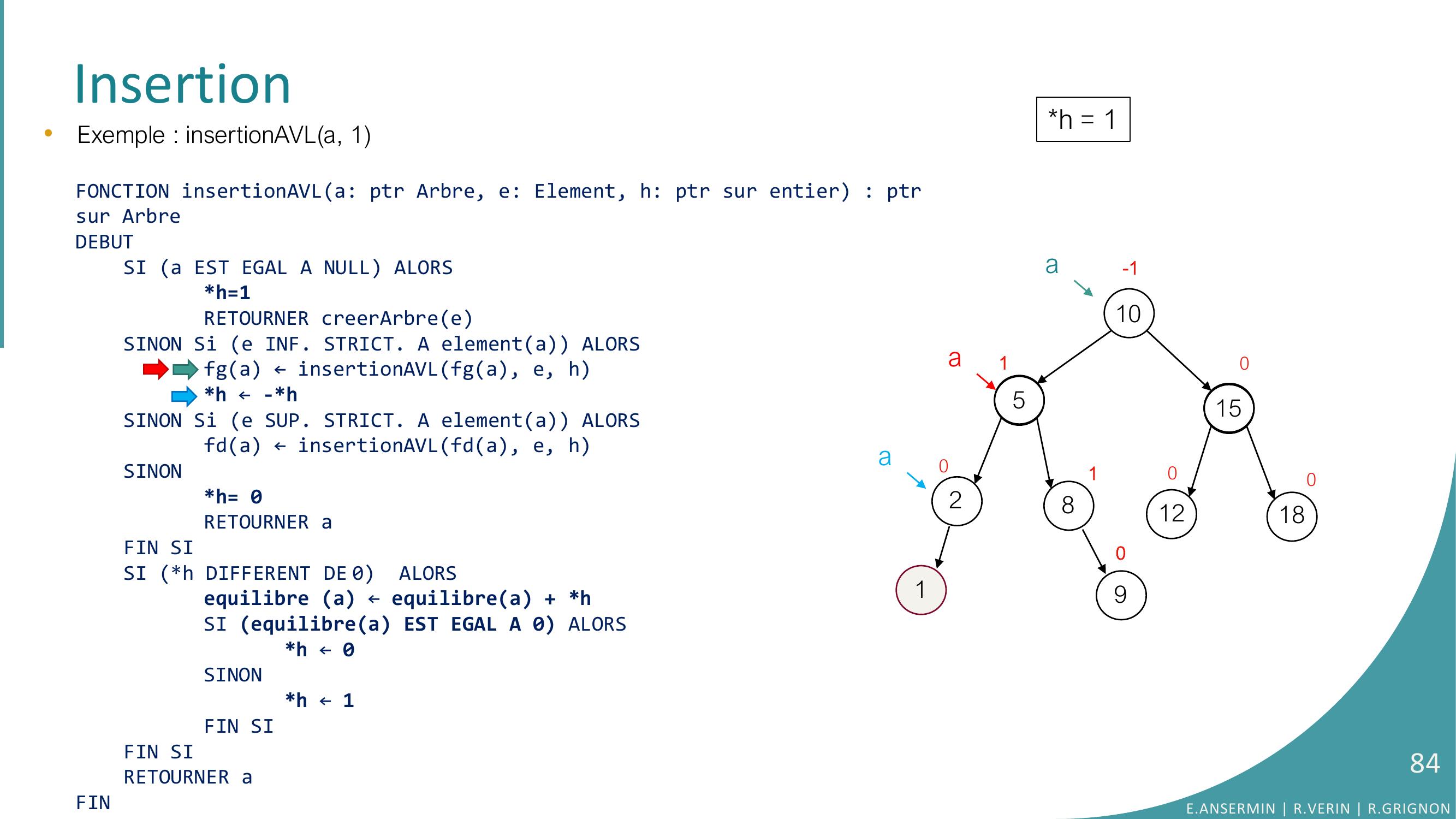
Page 32 : Insertion105281512180000000aa•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON32

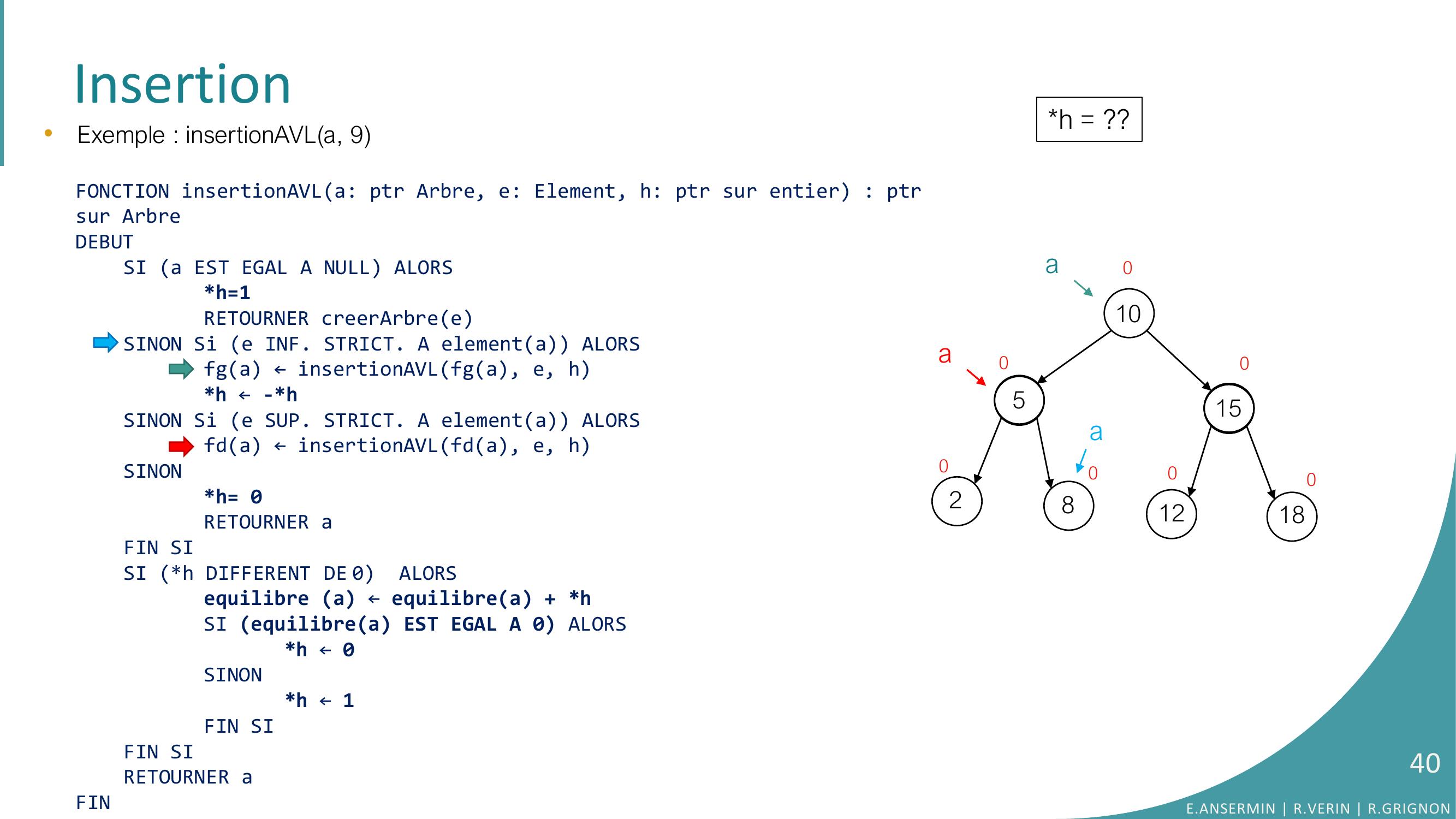
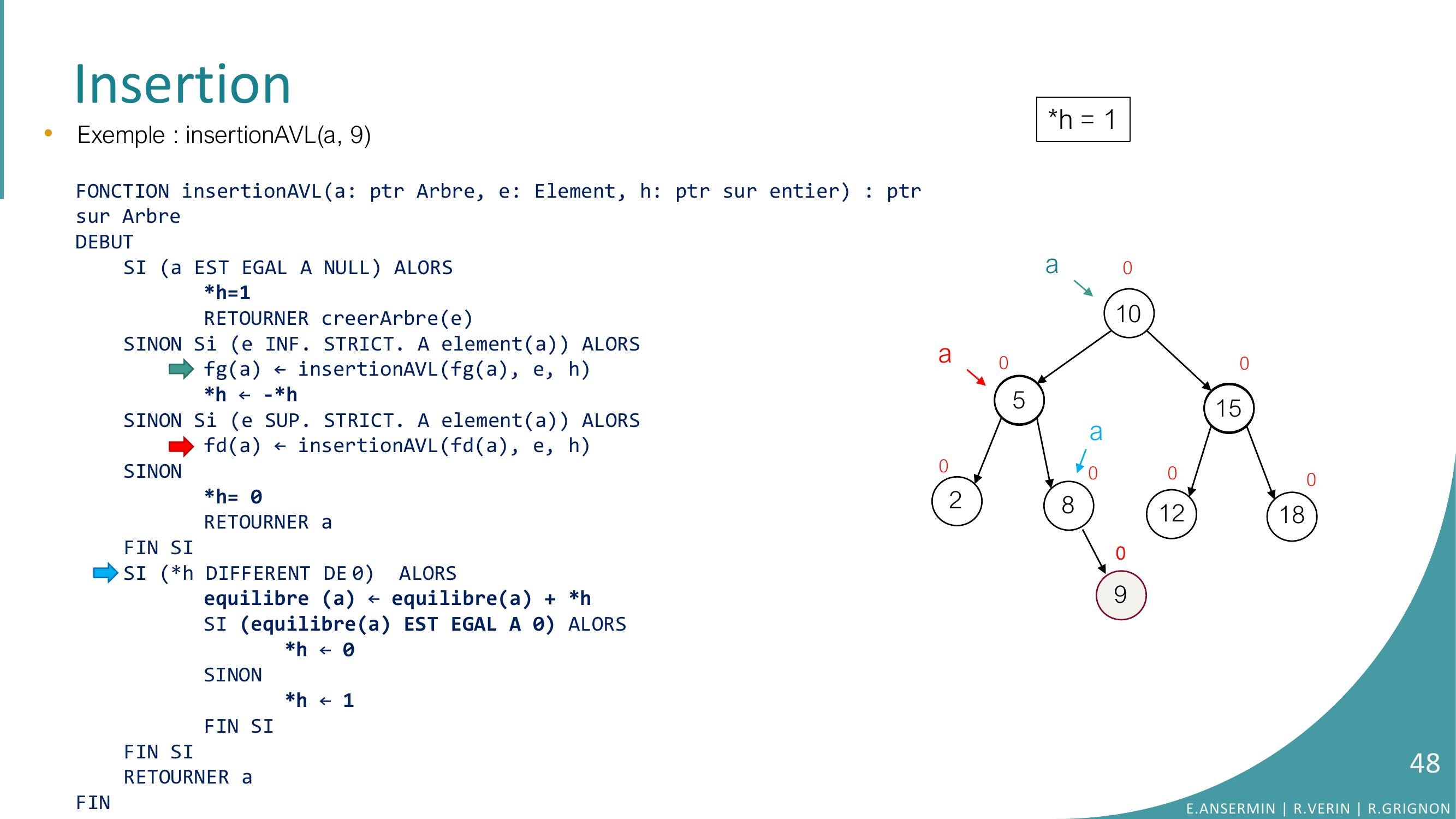
Page 33 : Insertion10528151218000000•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON33

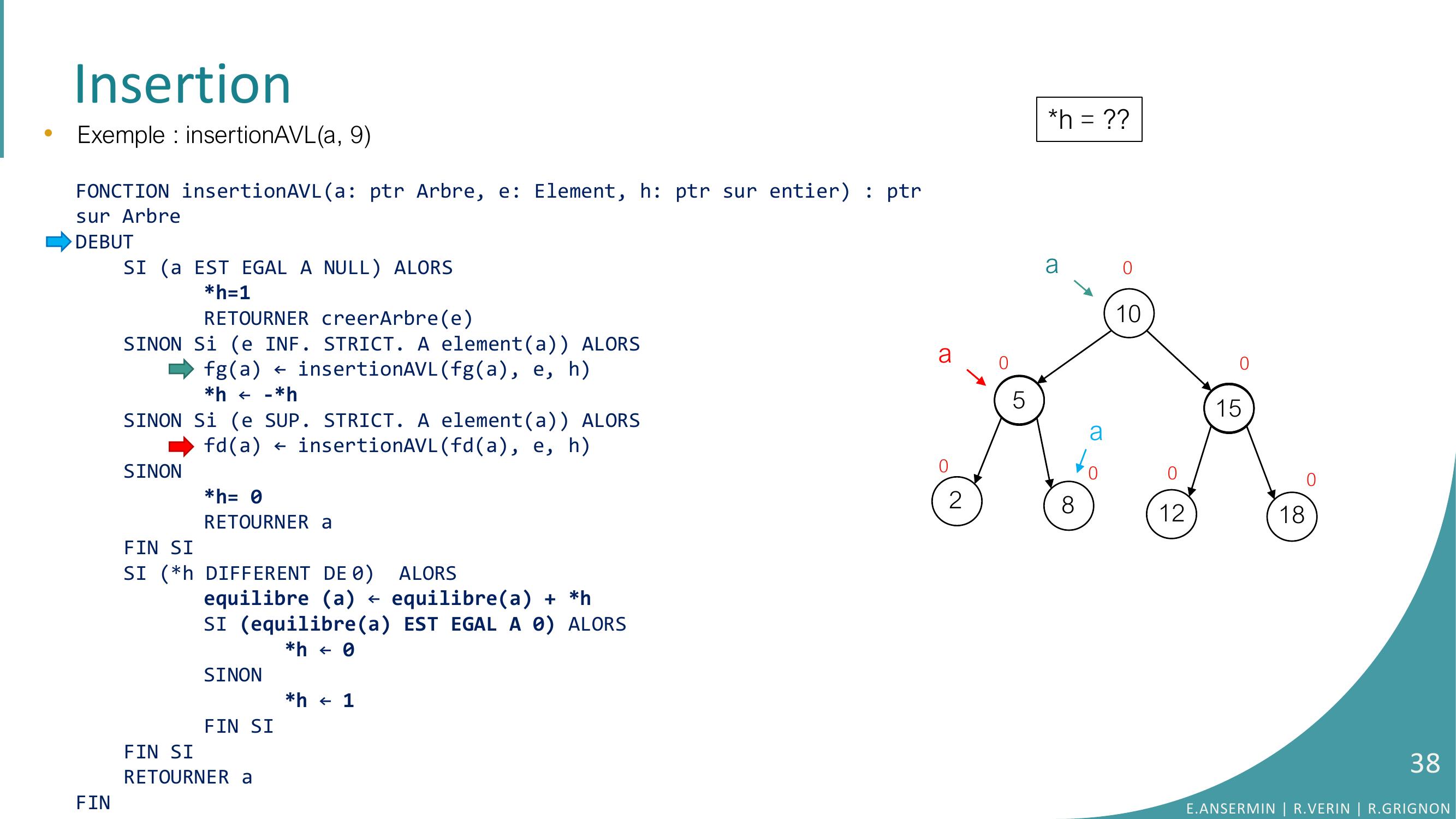
Page 34 : Insertion10528151218000000•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON34

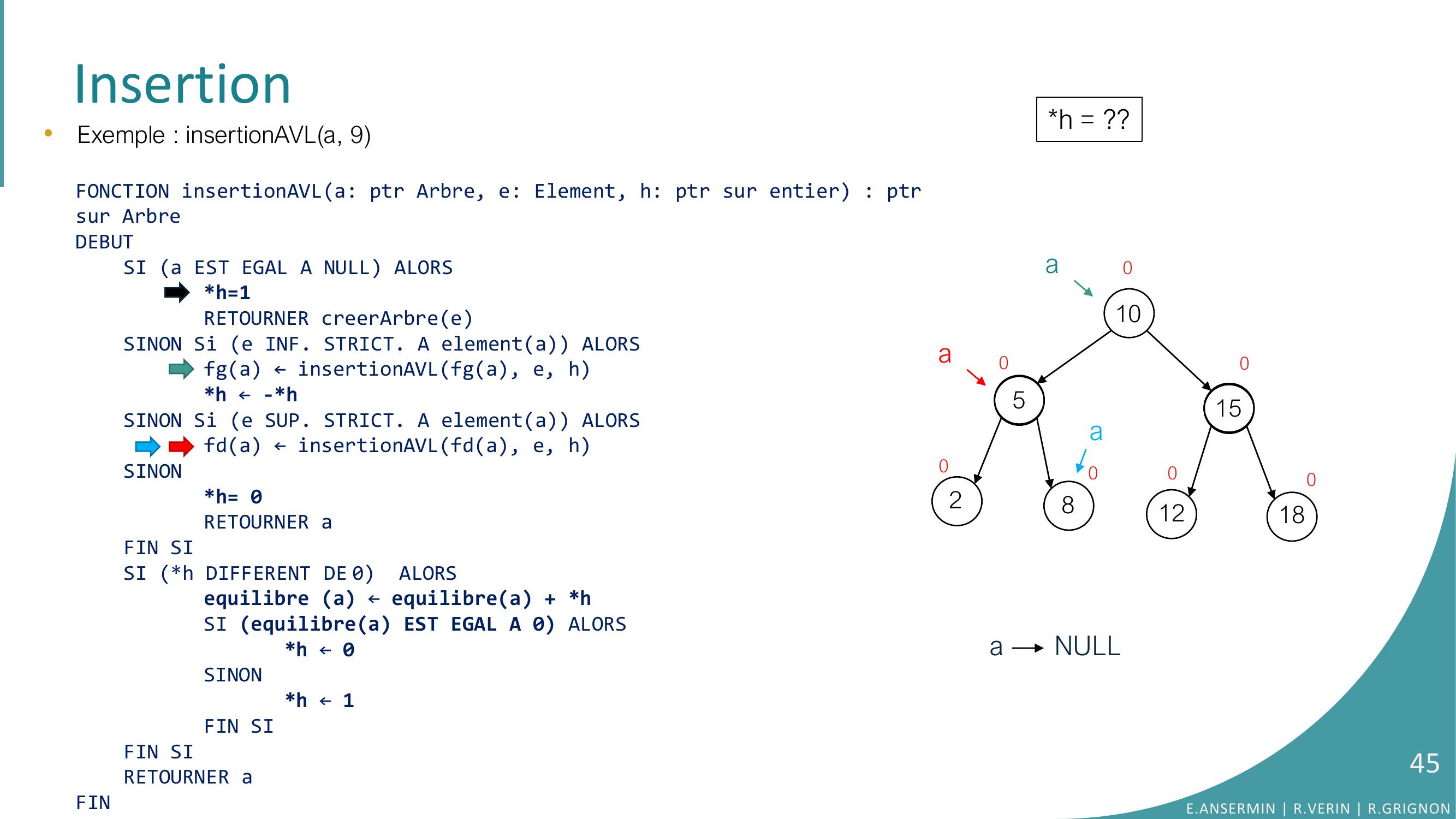
Page 35 : Insertion10528151218000000•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON35

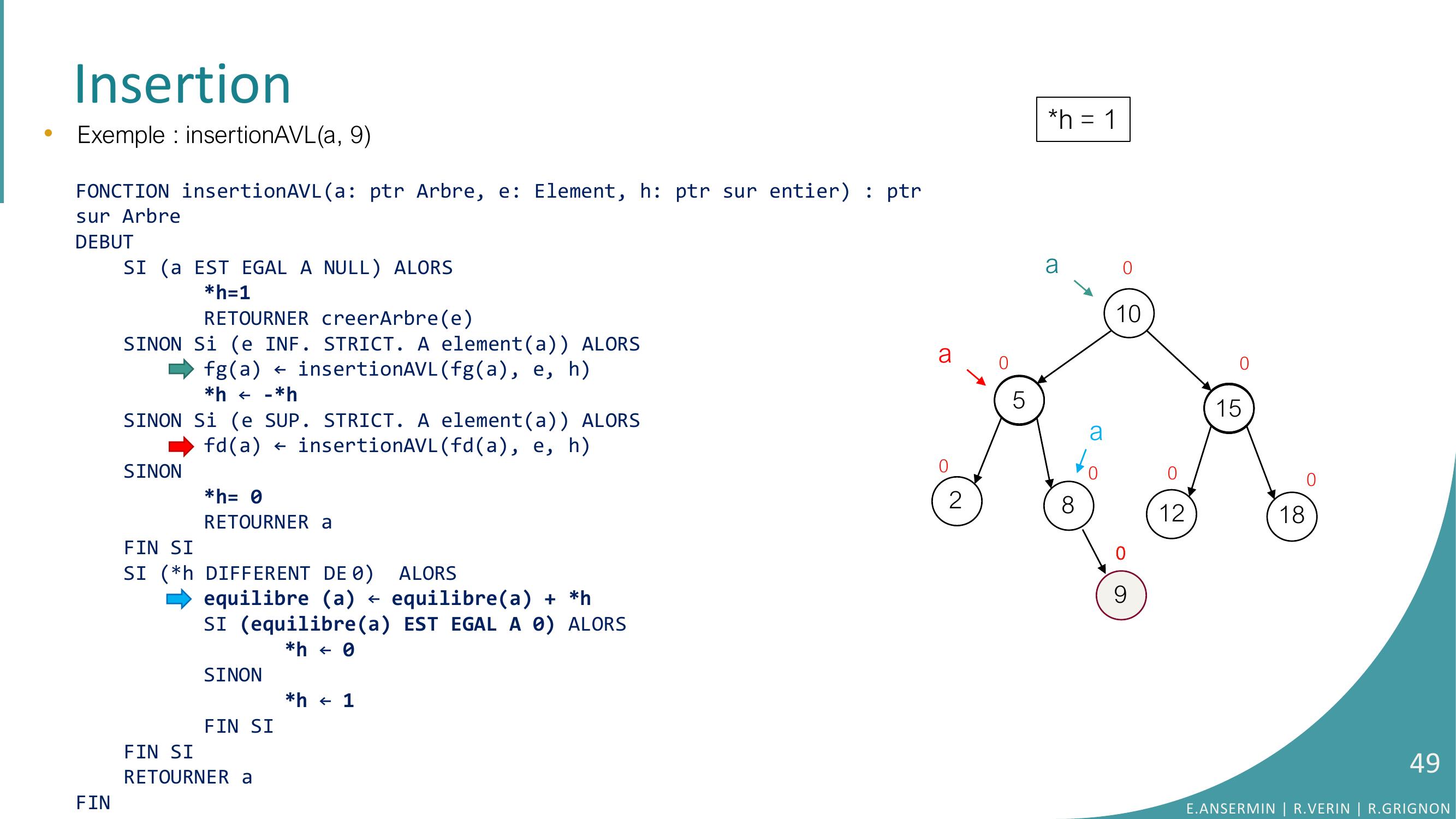
Page 36 : Insertion10528151218000000•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON36

Page 37 : Insertion10528151218000000•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON37

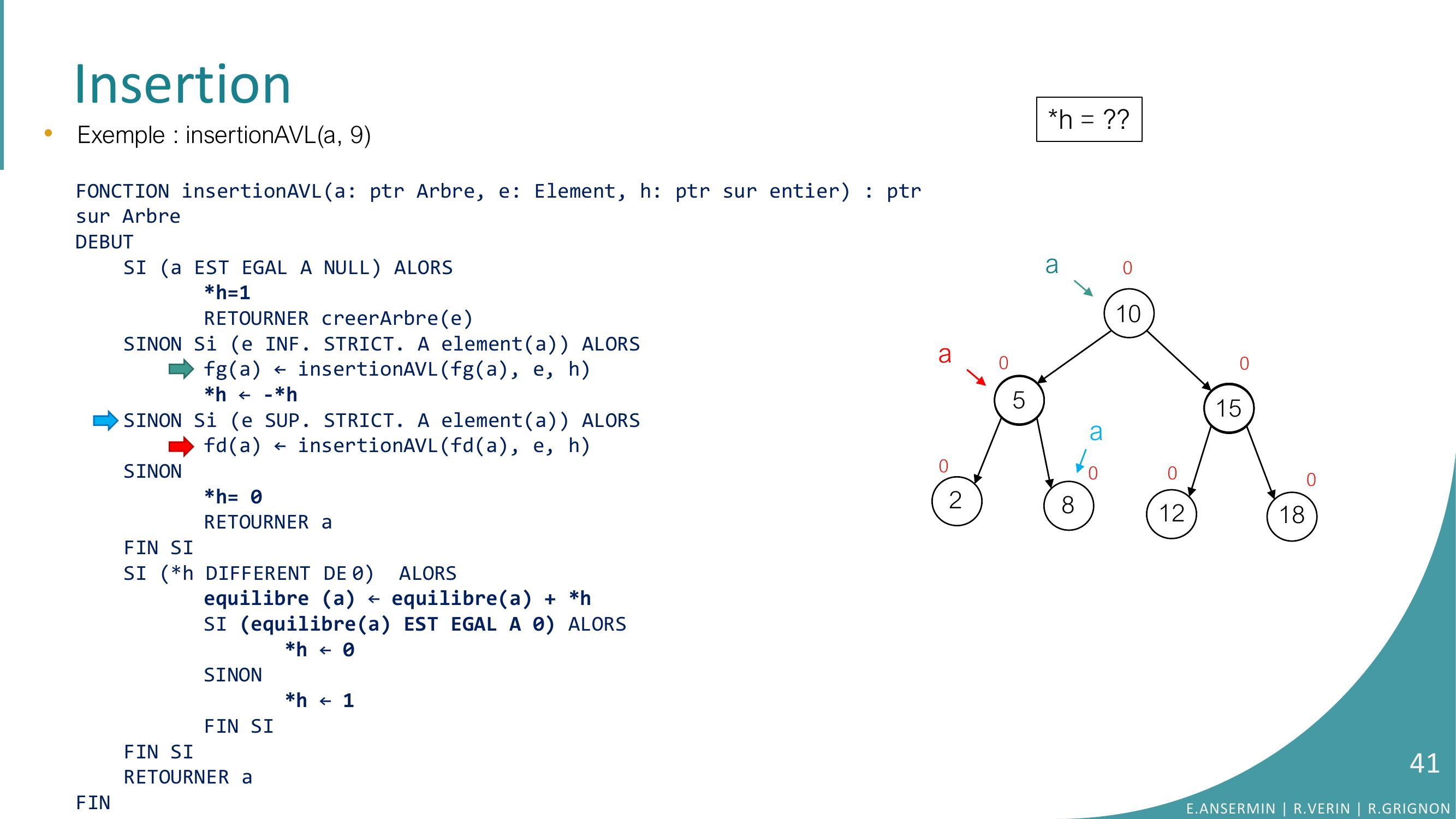
Page 38 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON38

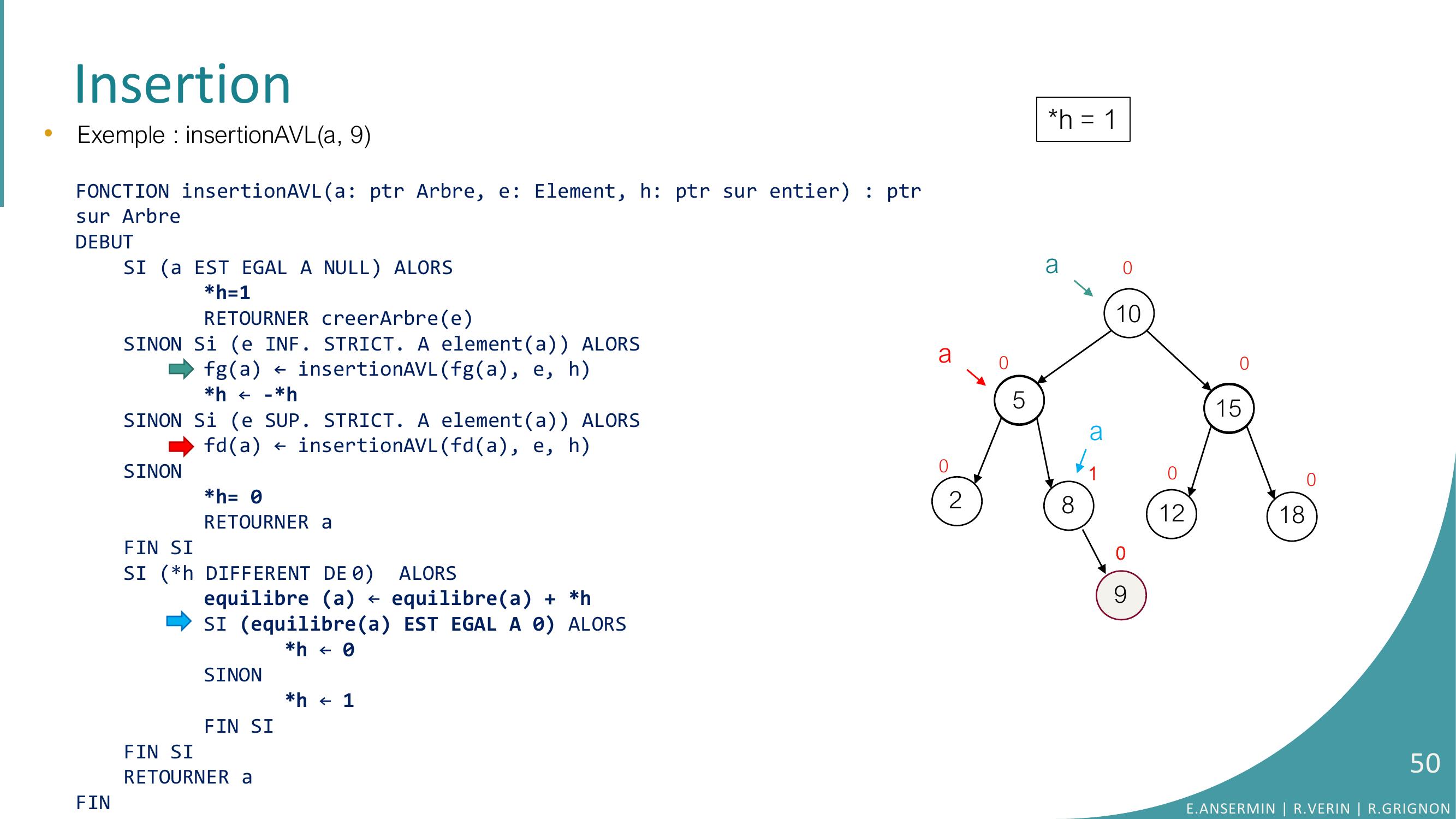
Page 39 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON39

Page 40 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON40

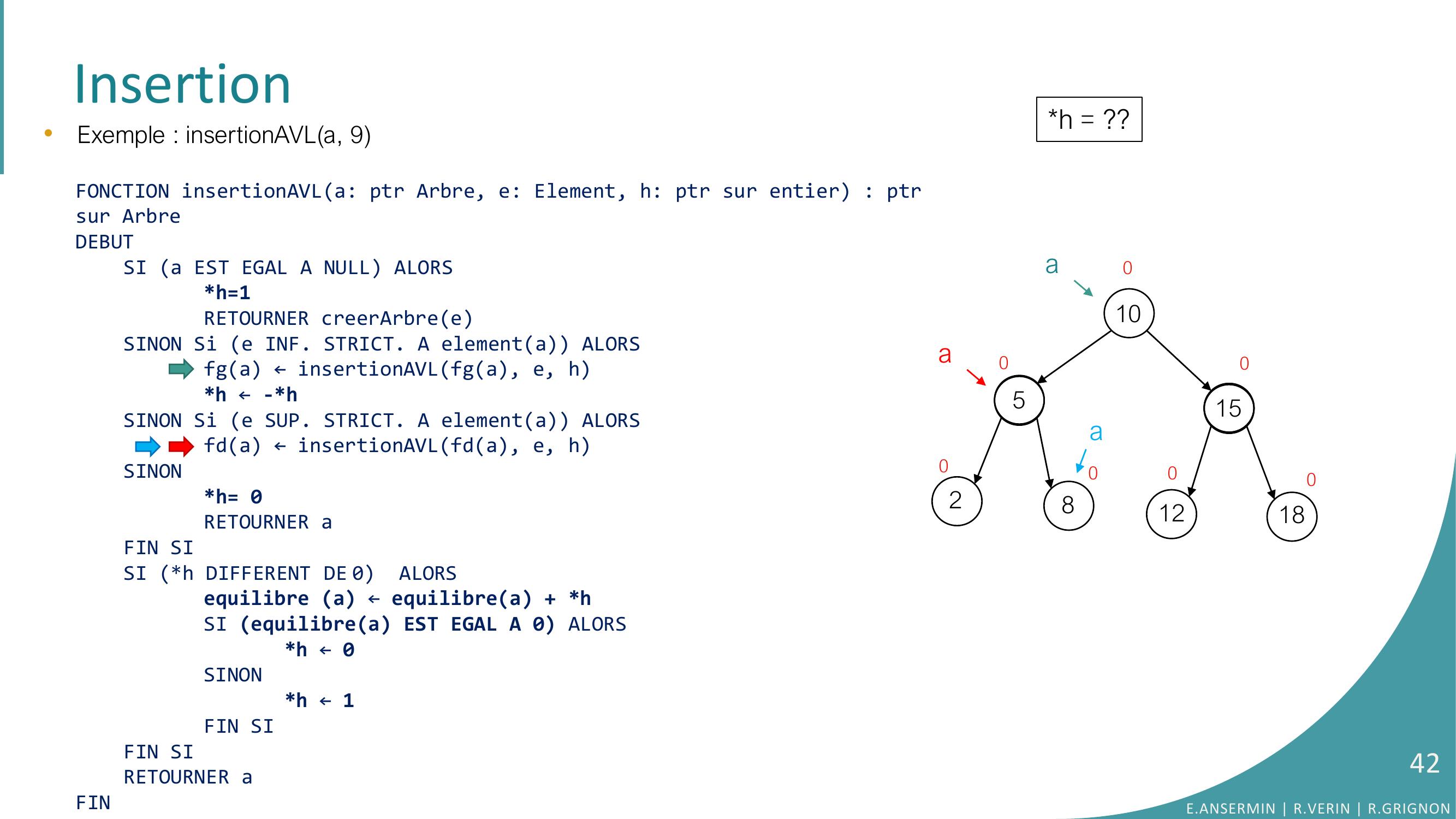
Page 41 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON41

Page 42 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaE.ANSERMIN R.VERIN R.GRIGNON42

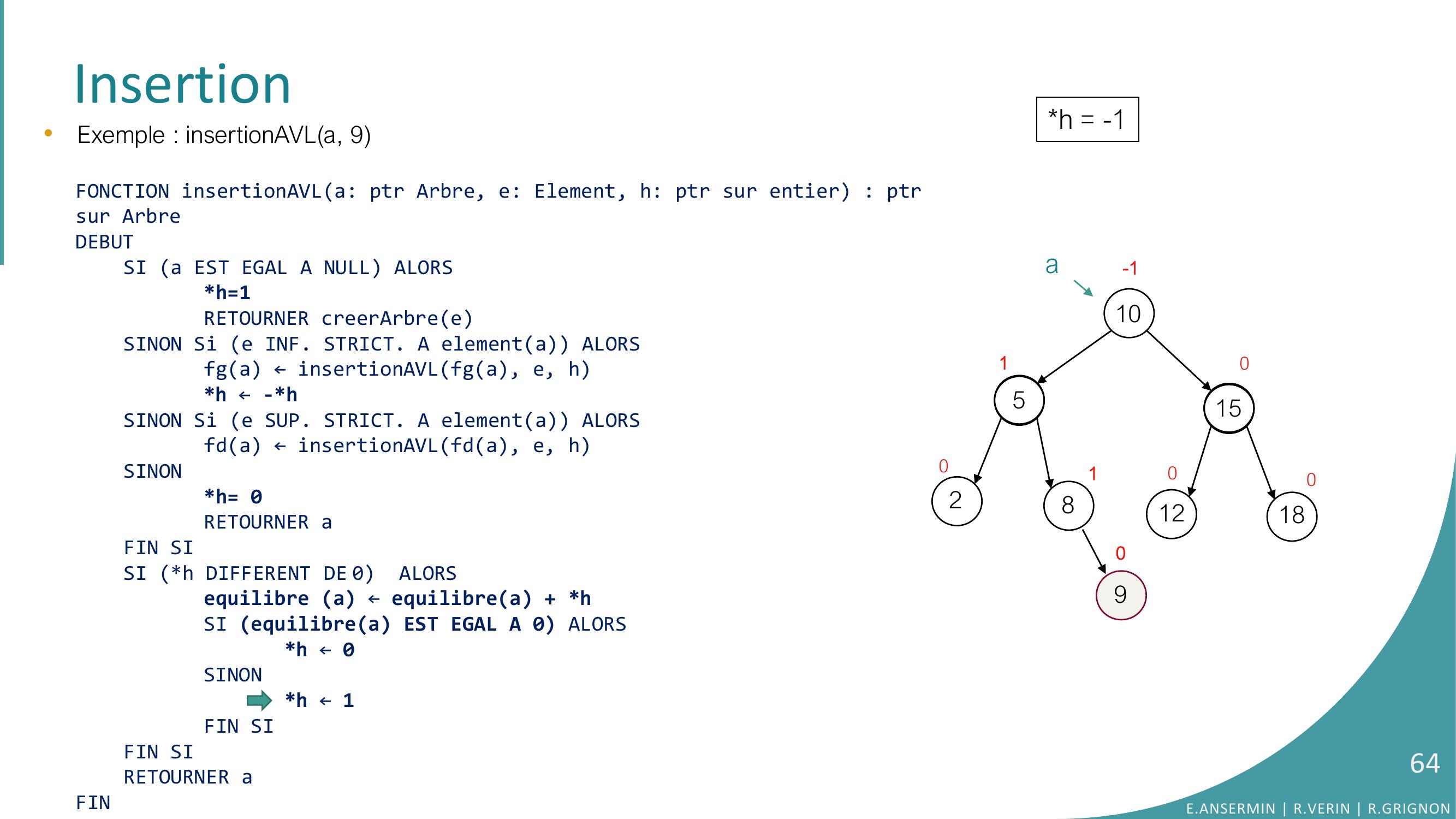
Page 43 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaa NULLE.ANSERMIN R.VERIN R.GRIGNON43

Page 44 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaa NULLE.ANSERMIN R.VERIN R.GRIGNON44

Page 45 : Insertion10528151218000000a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??0aaa NULLE.ANSERMIN R.VERIN R.GRIGNON45

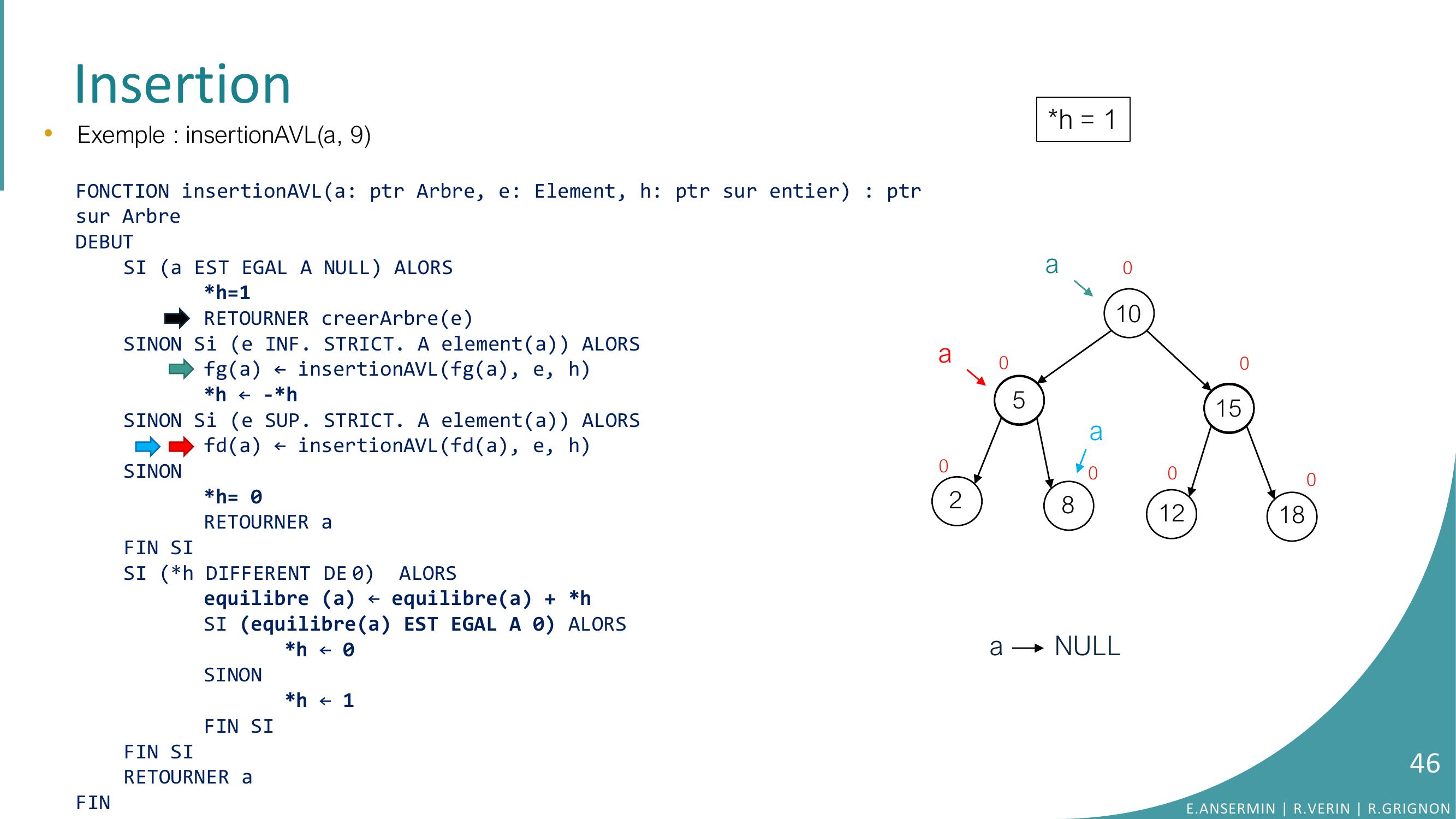
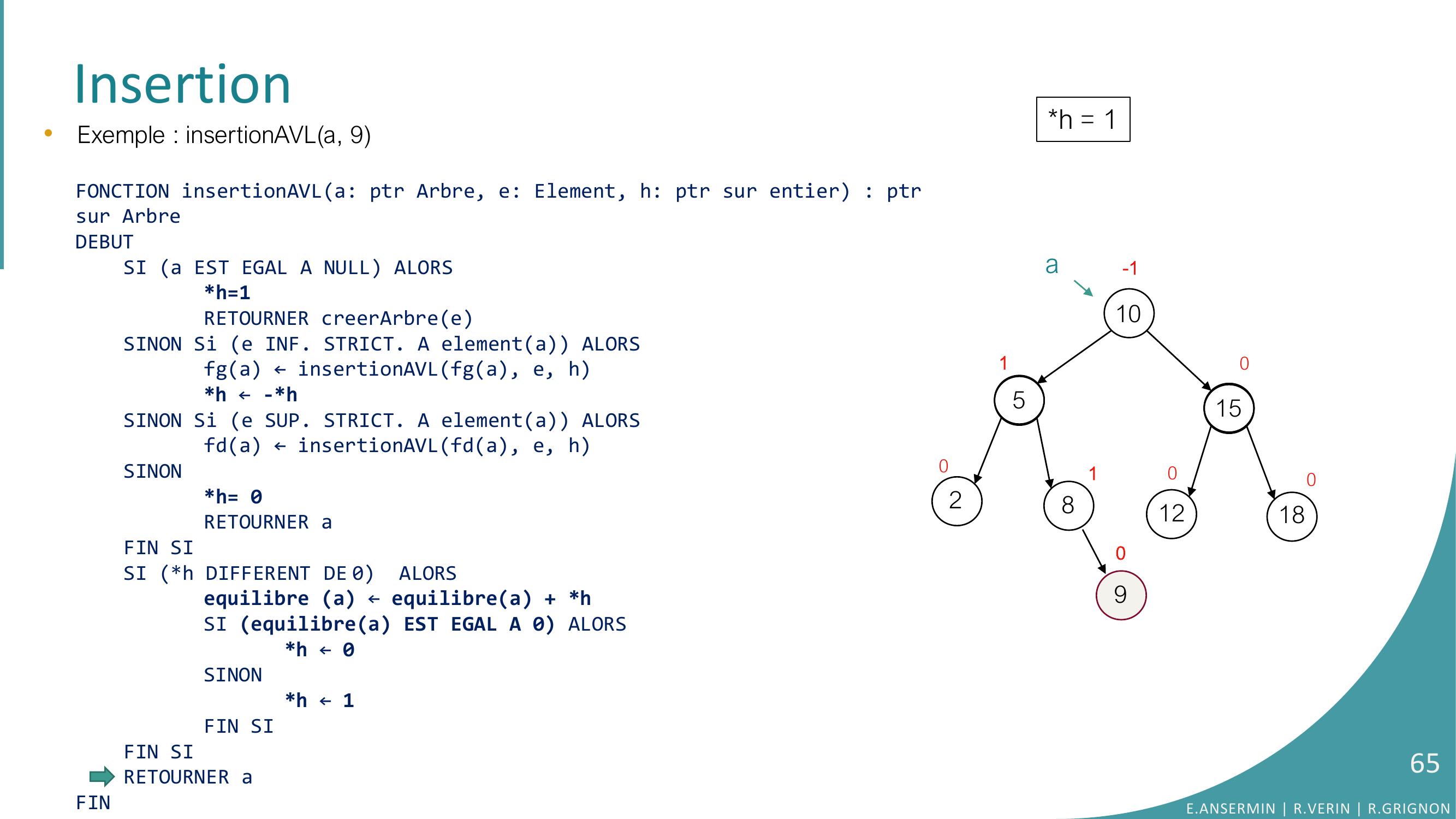
Page 46 : Insertion10528151218000000h = 1a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFIN0aaa NULLE.ANSERMIN R.VERIN R.GRIGNON46

Page 47 : Insertion10528151218000000a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON47

Page 48 : Insertion10528151218000000a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON48

Page 49 : Insertion1052815121800000900a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON49

Page 50 : Insertion1052815121801000090a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON50

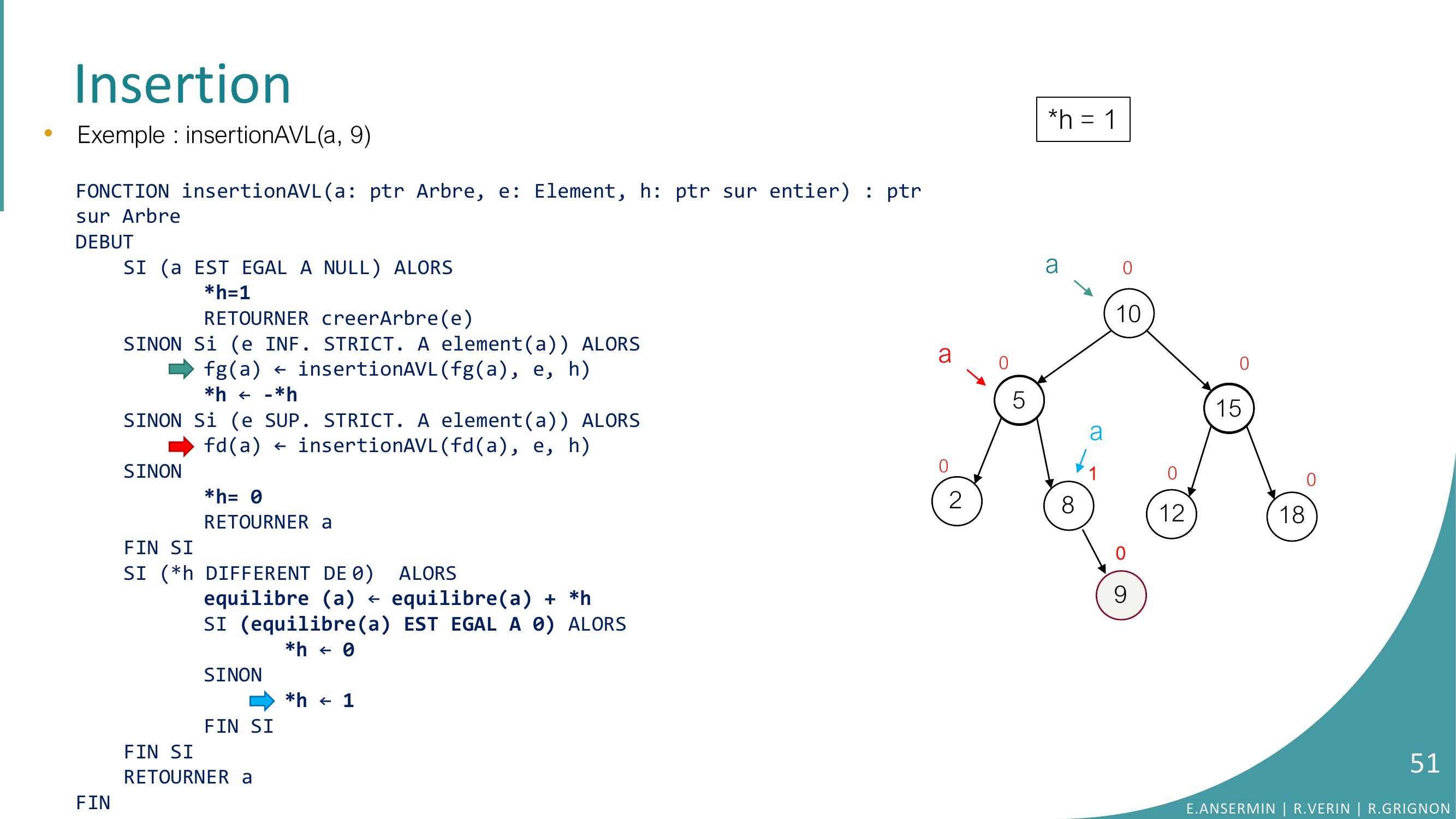
Page 51 : Insertion1052815121801000090a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON51

Page 52 : Insertion1052815121801000090a•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON52

Page 53 : Insertion1052815121801000090•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON53

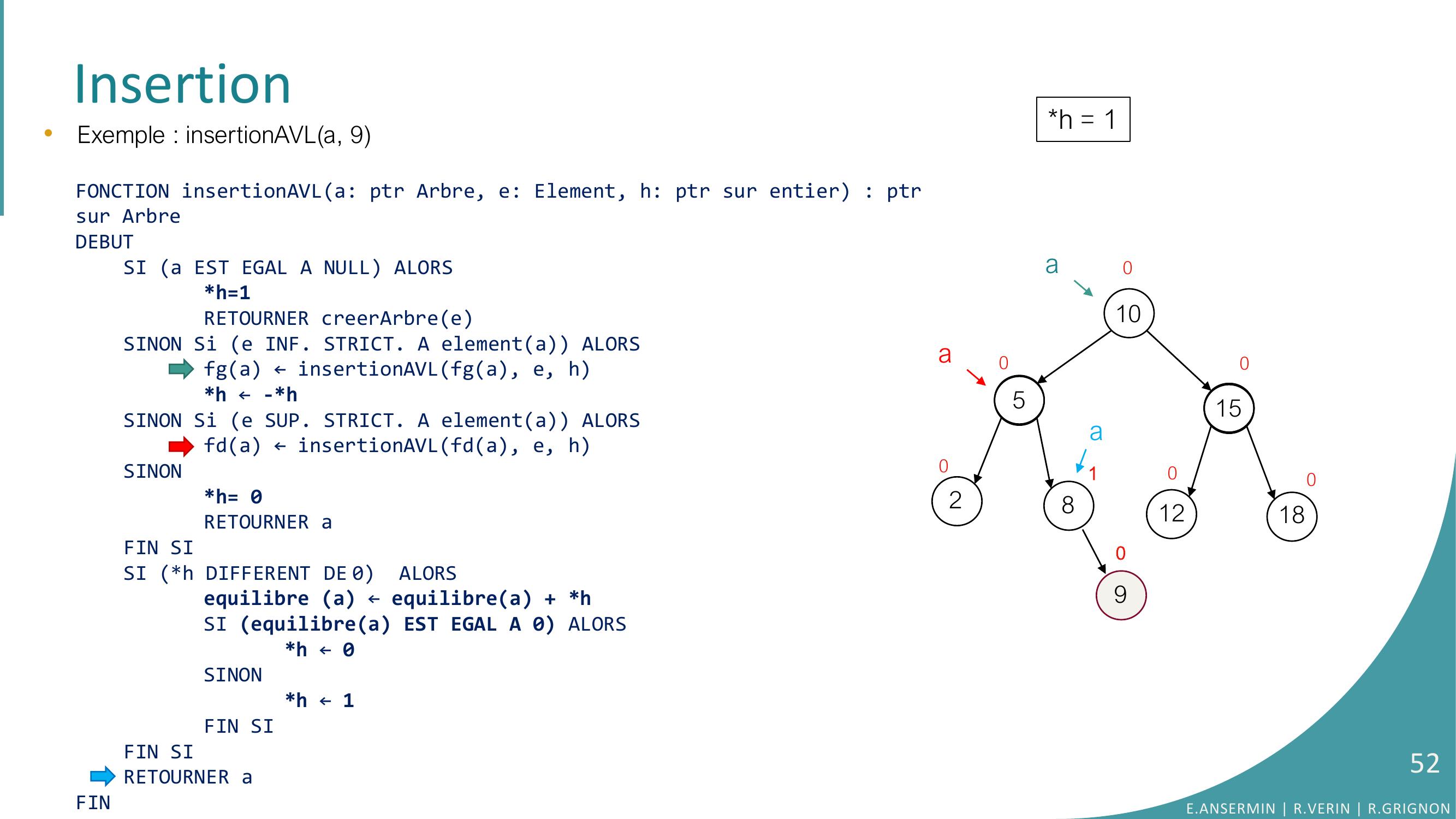
Page 54 : Insertion1052815121801000090•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON54

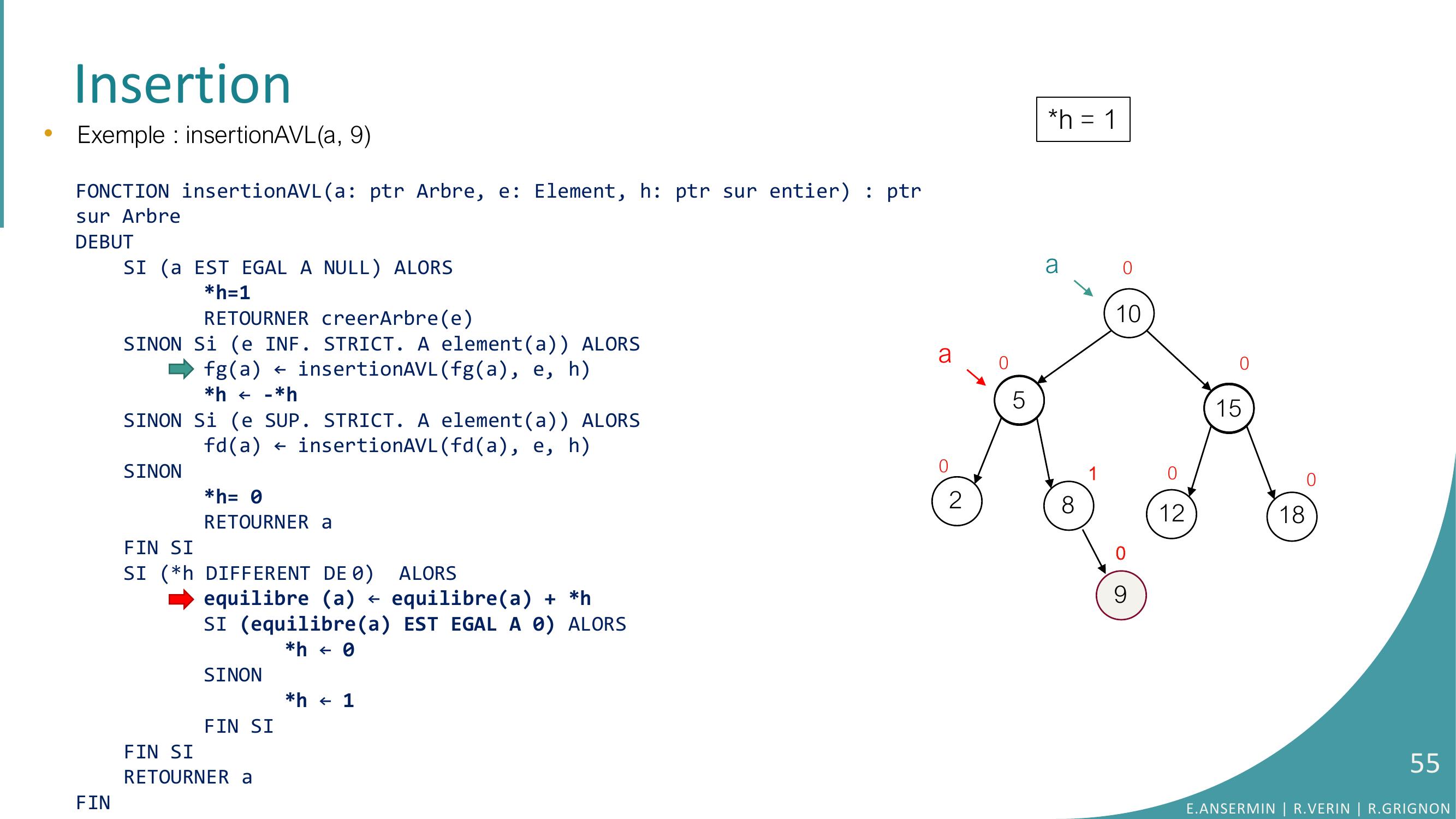
Page 55 : Insertion1052815121801000090•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 10aaE.ANSERMIN R.VERIN R.GRIGNON55

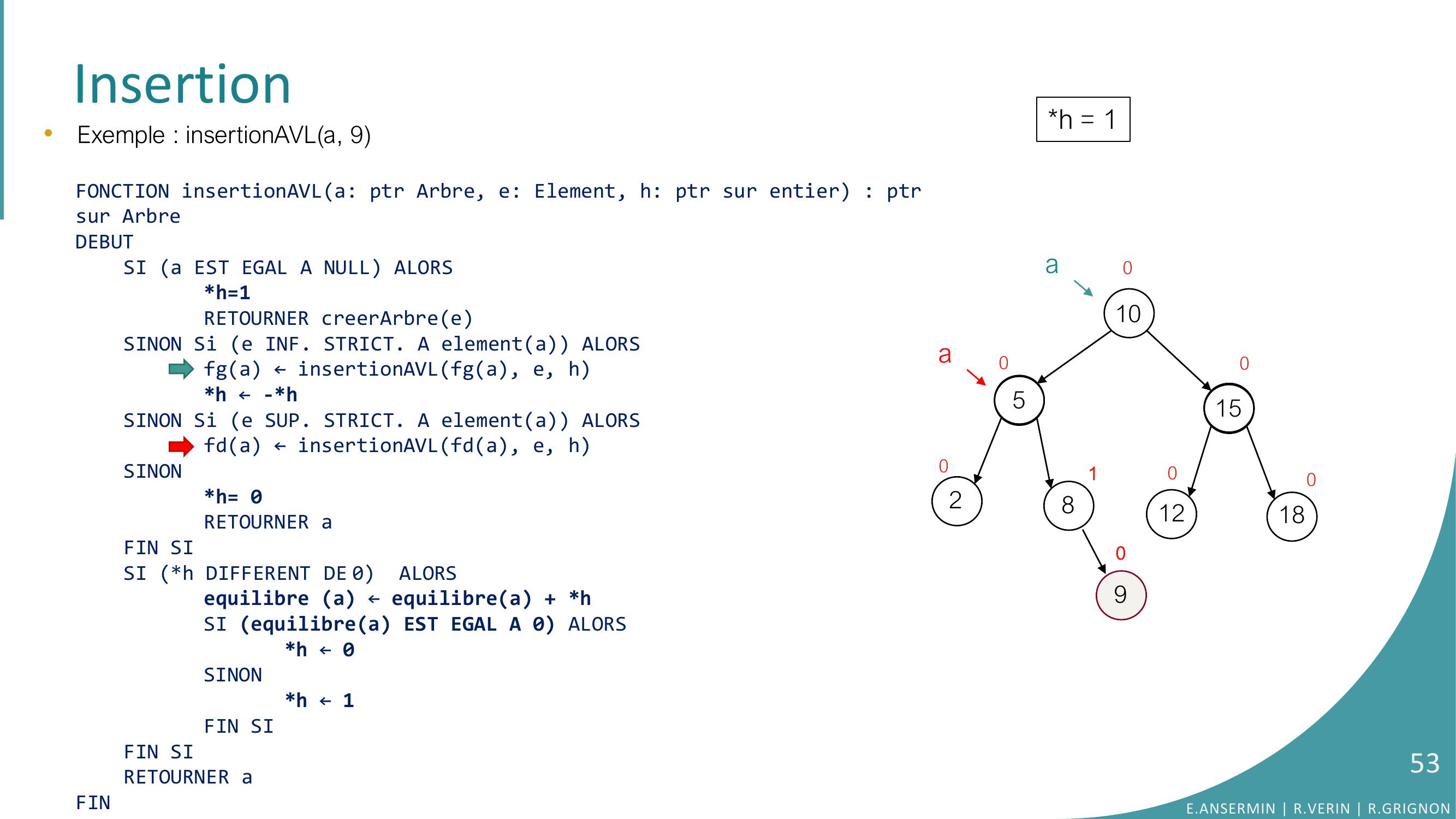
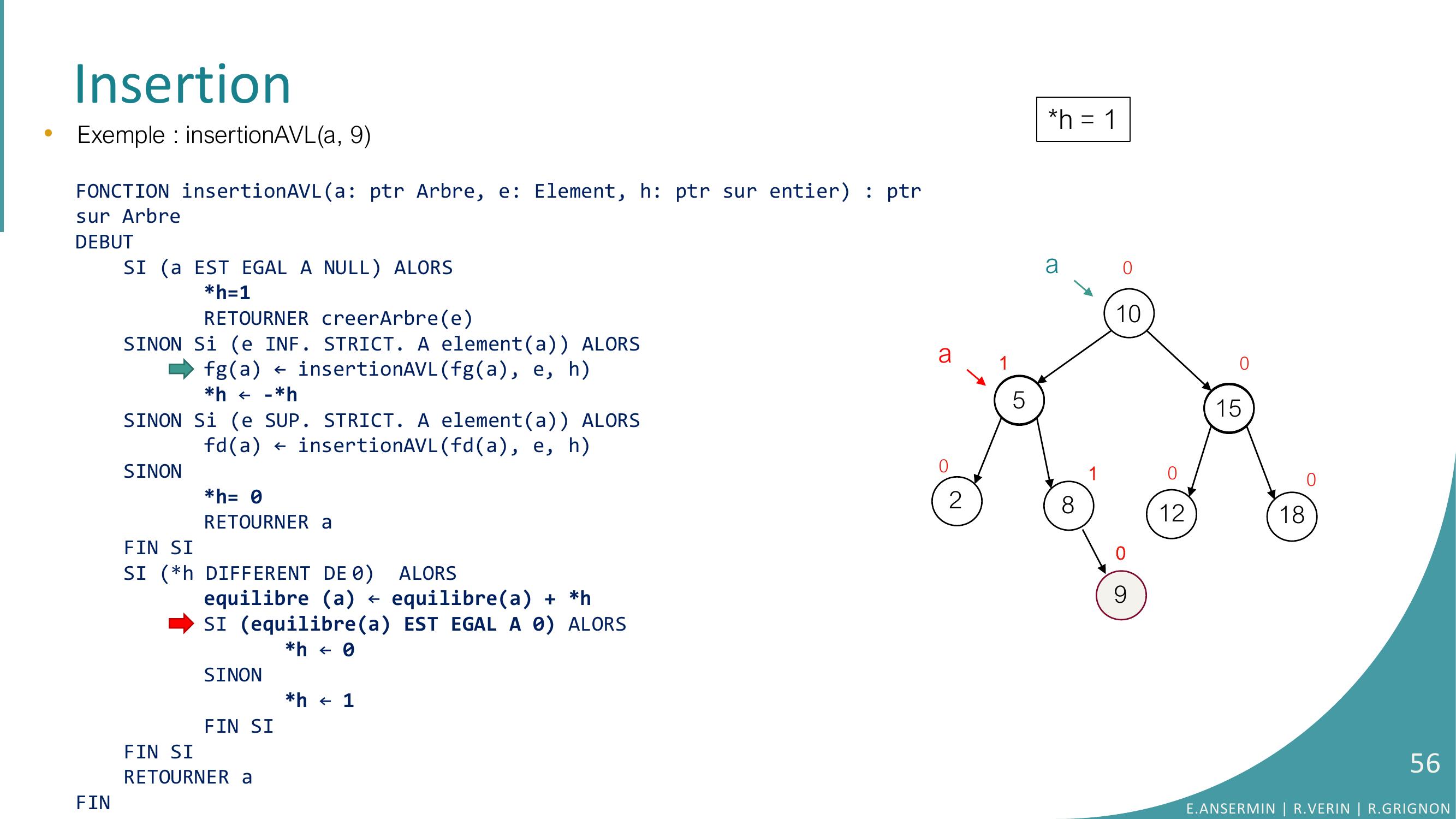
Page 56 : Insertion105281512180100100aa90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 1E.ANSERMIN R.VERIN R.GRIGNON56

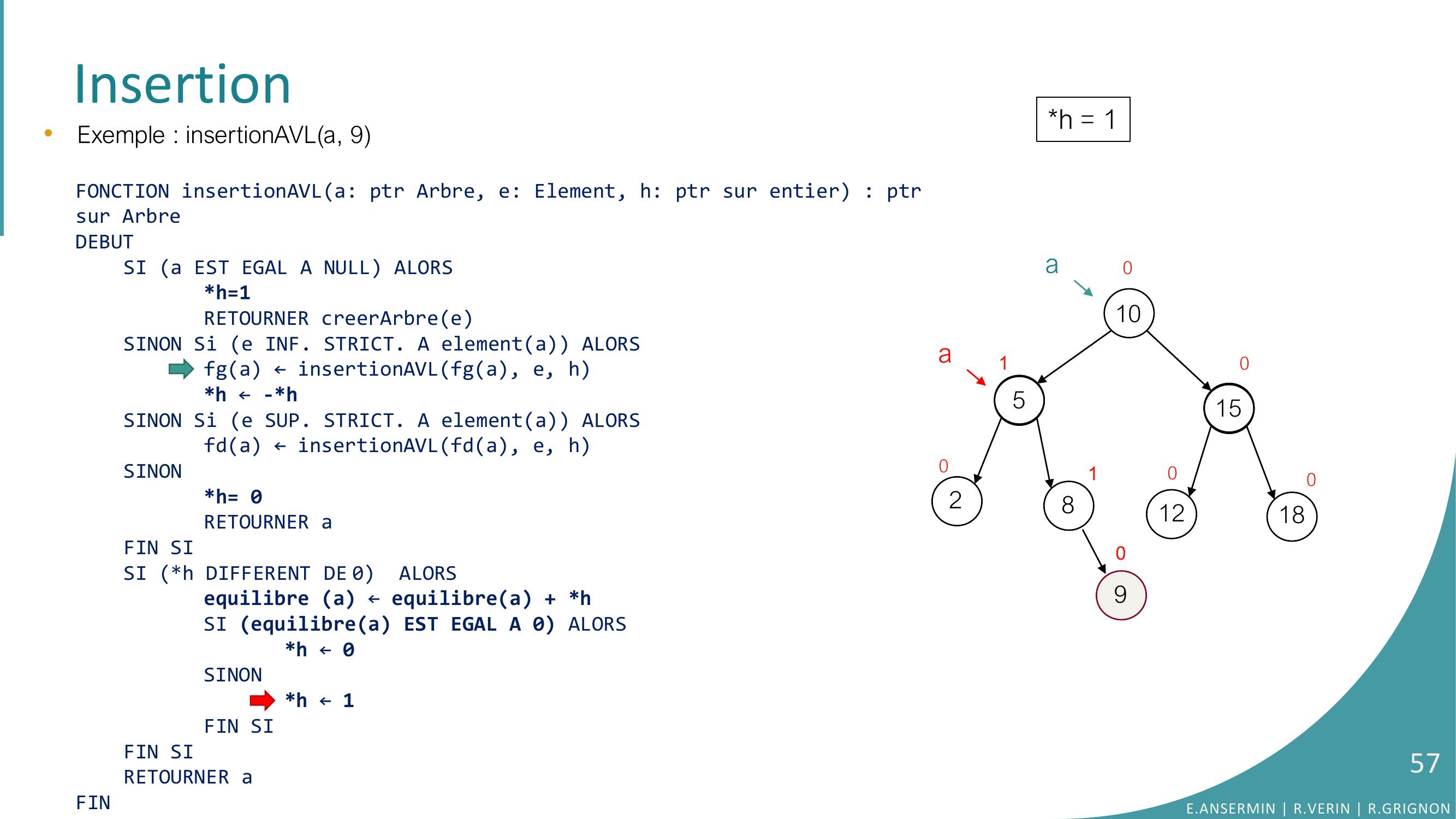
Page 57 : Insertion1052815121801000090•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 11aaE.ANSERMIN R.VERIN R.GRIGNON57

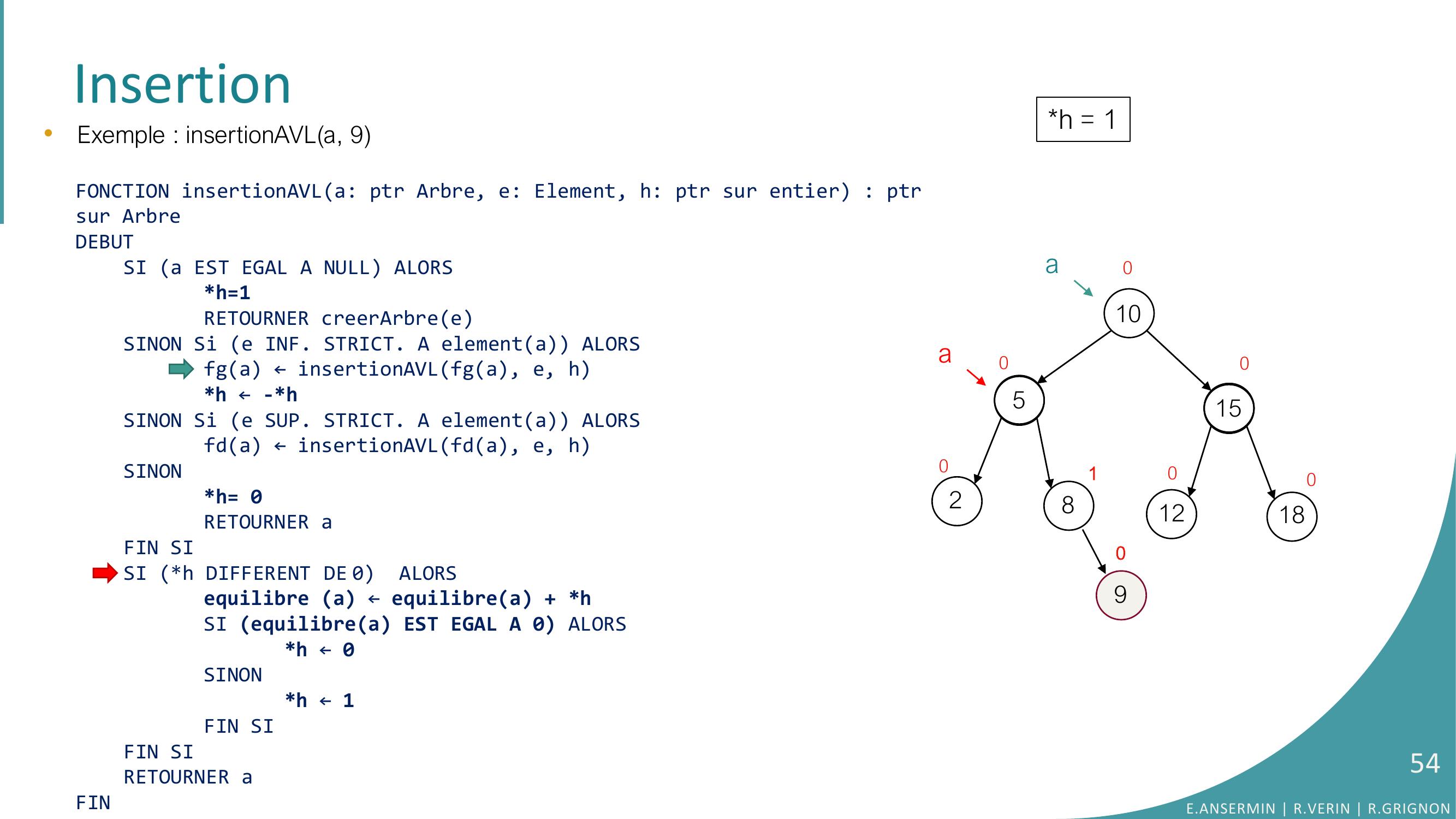
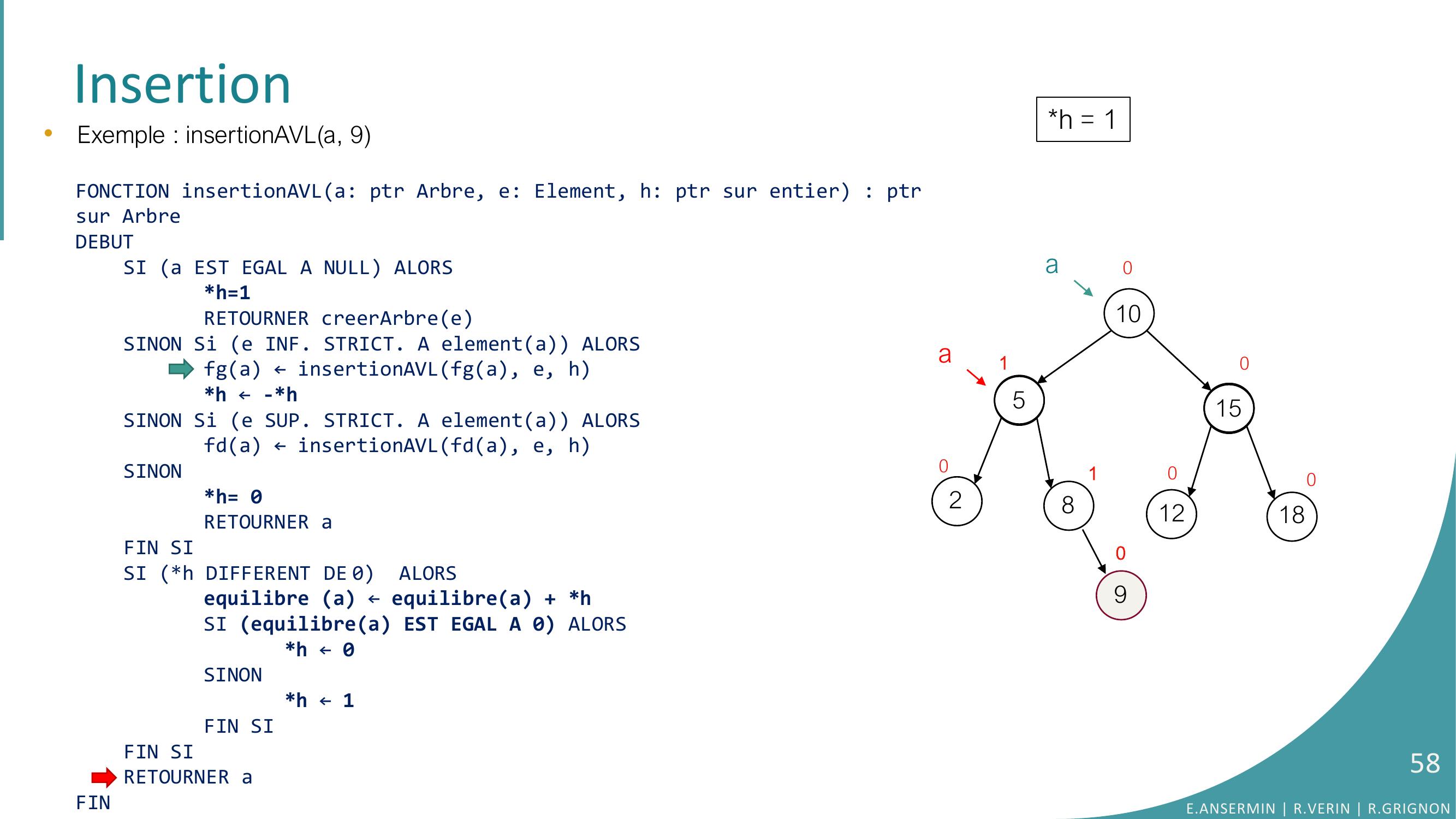
Page 58 : Insertion1052815121801000090•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 11aaE.ANSERMIN R.VERIN R.GRIGNON58

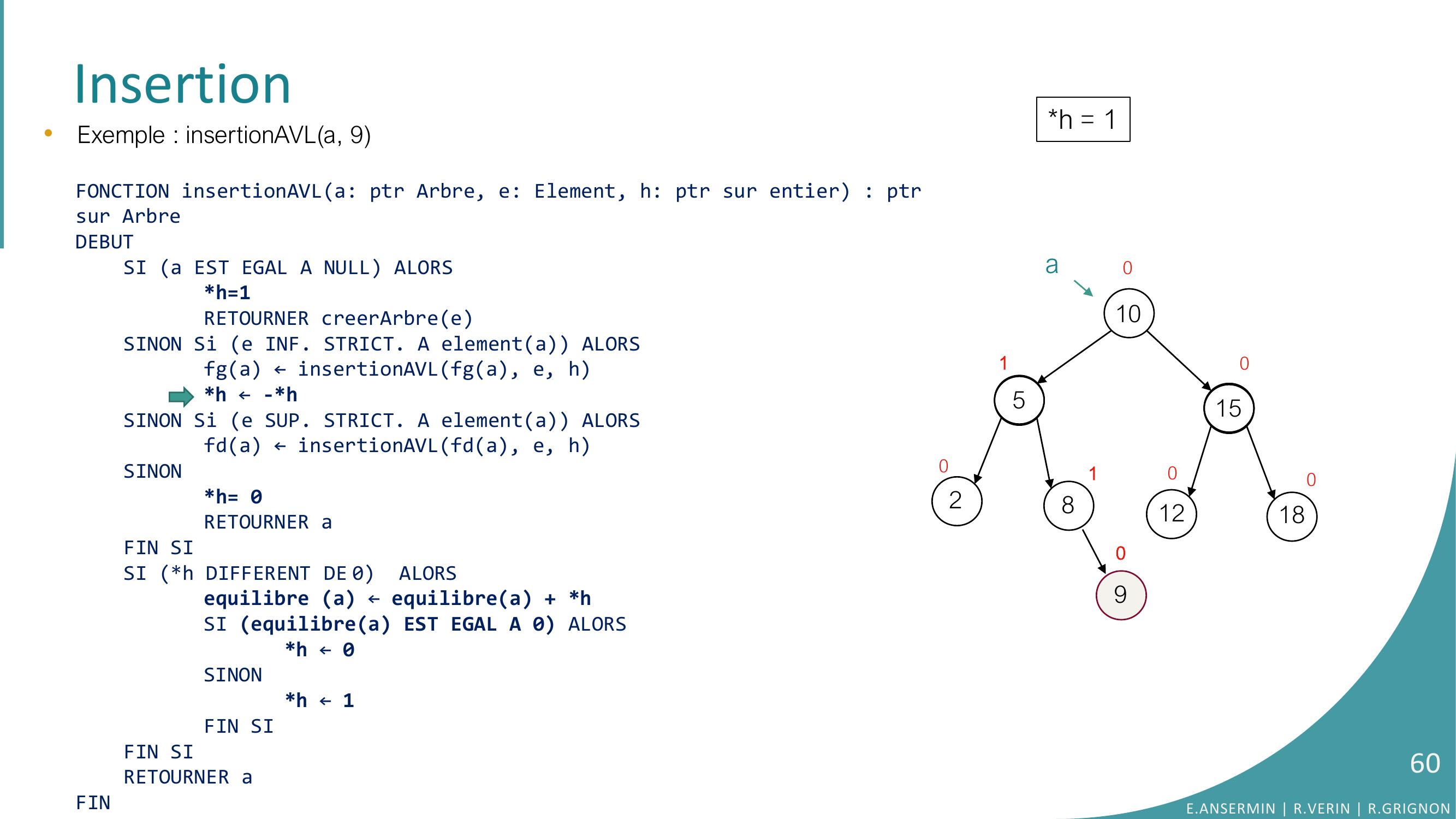
Page 59 : Insertion105281512180100100a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 1E.ANSERMIN R.VERIN R.GRIGNON59

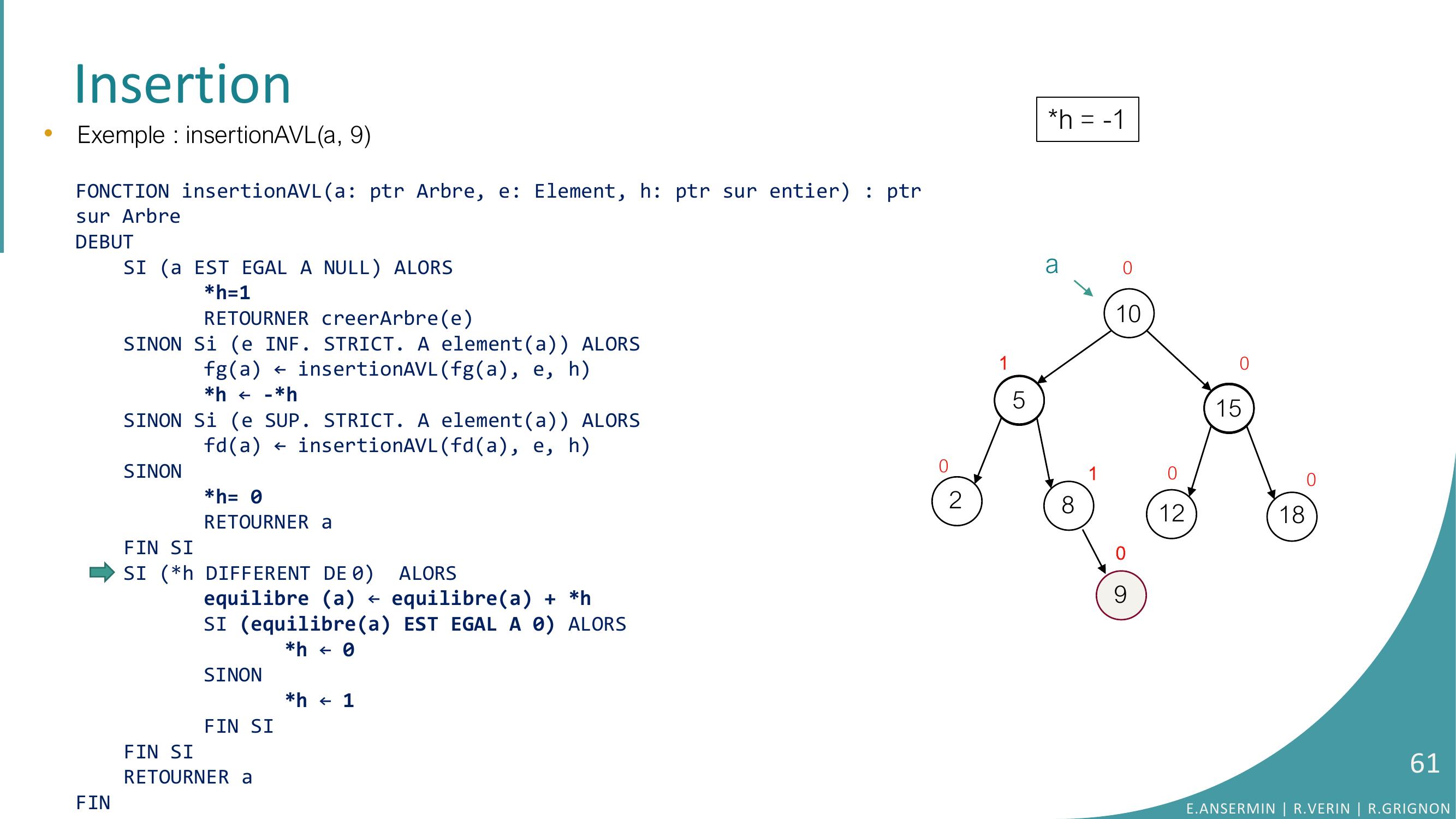
Page 60 : Insertion105281512180100100a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 1E.ANSERMIN R.VERIN R.GRIGNON60

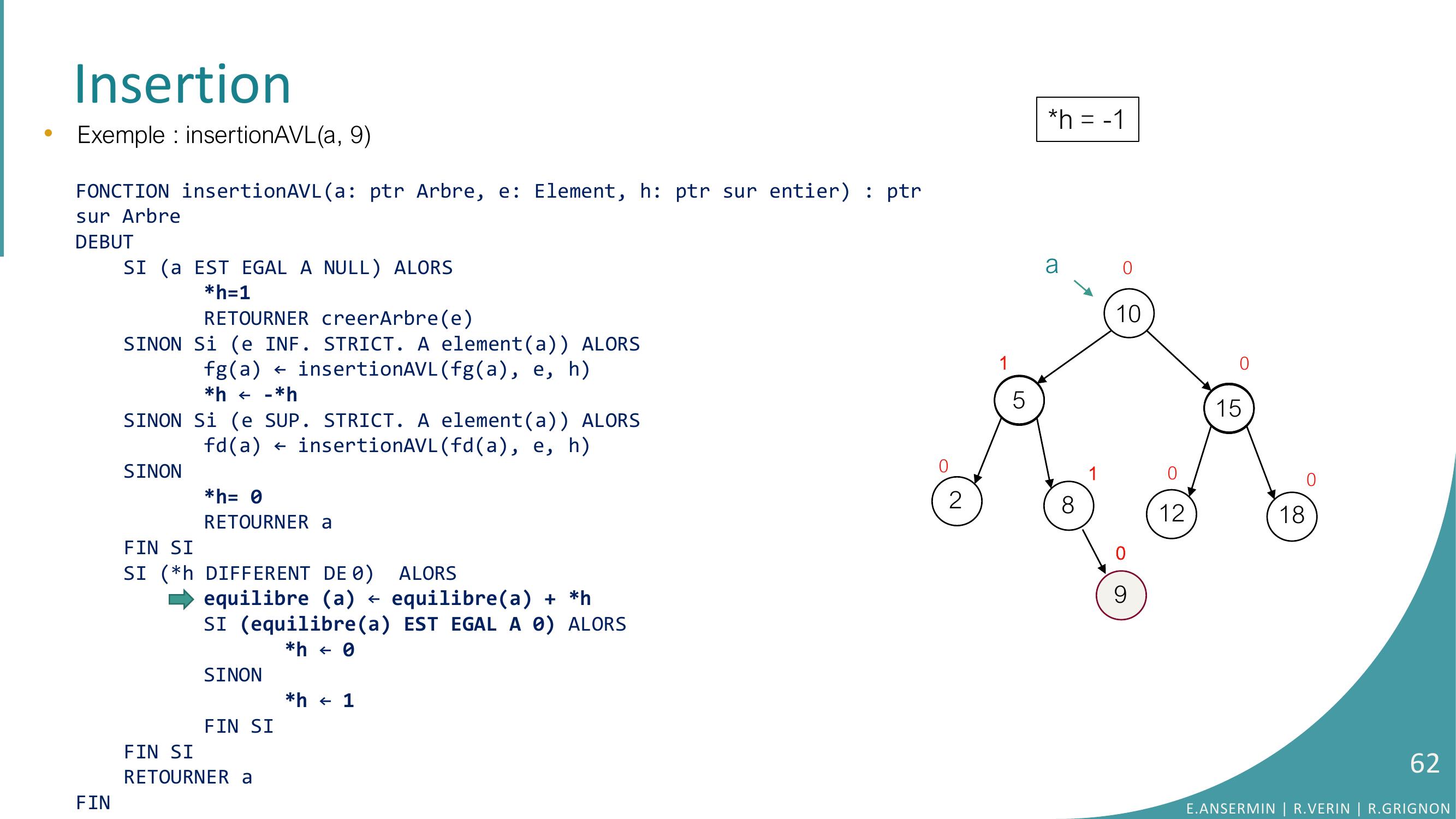
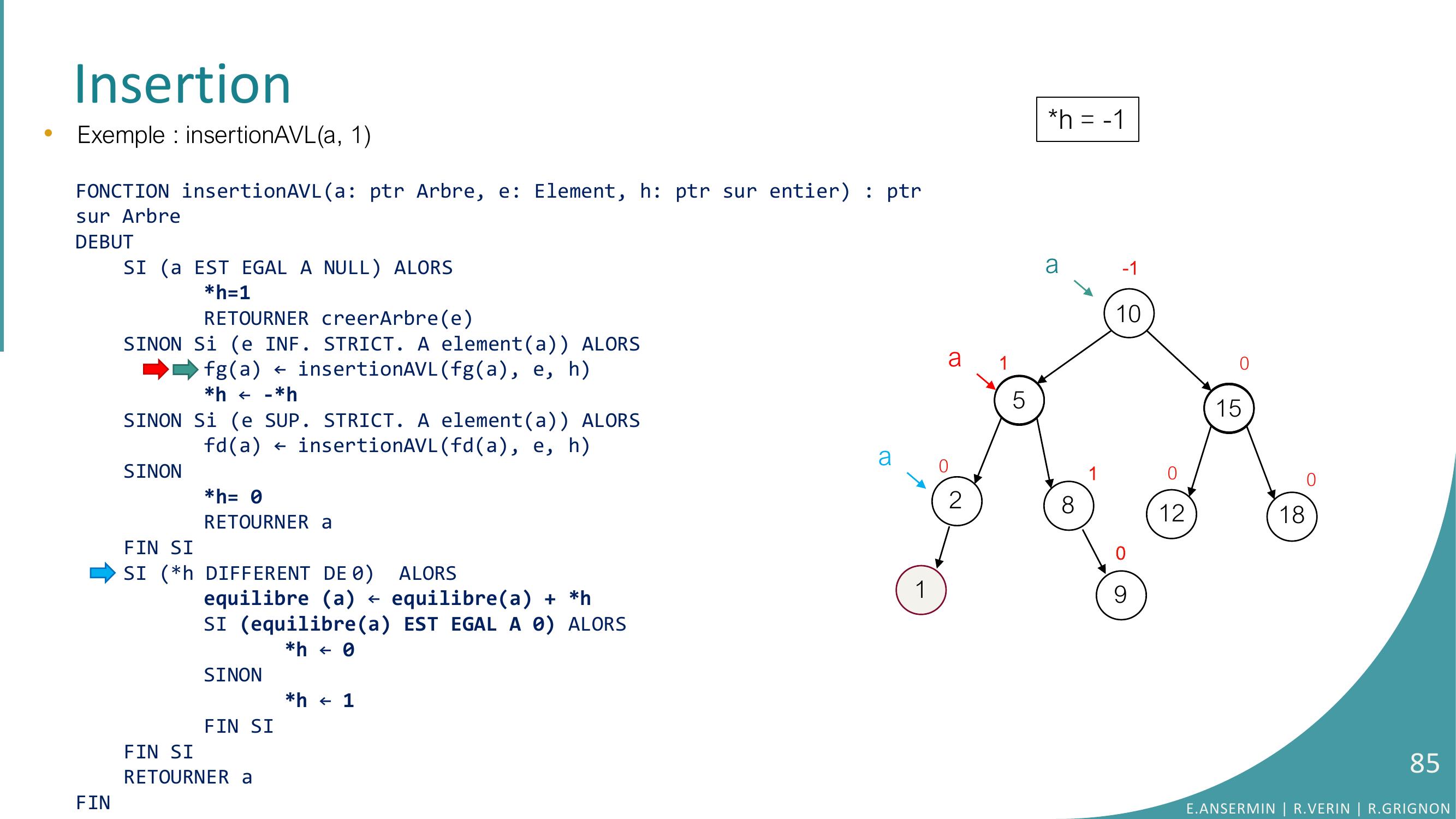
Page 61 : Insertion105281512180100100ah = -190•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON61

Page 62 : Insertion105281512180100100a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -1E.ANSERMIN R.VERIN R.GRIGNON62

Page 63 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -1E.ANSERMIN R.VERIN R.GRIGNON63

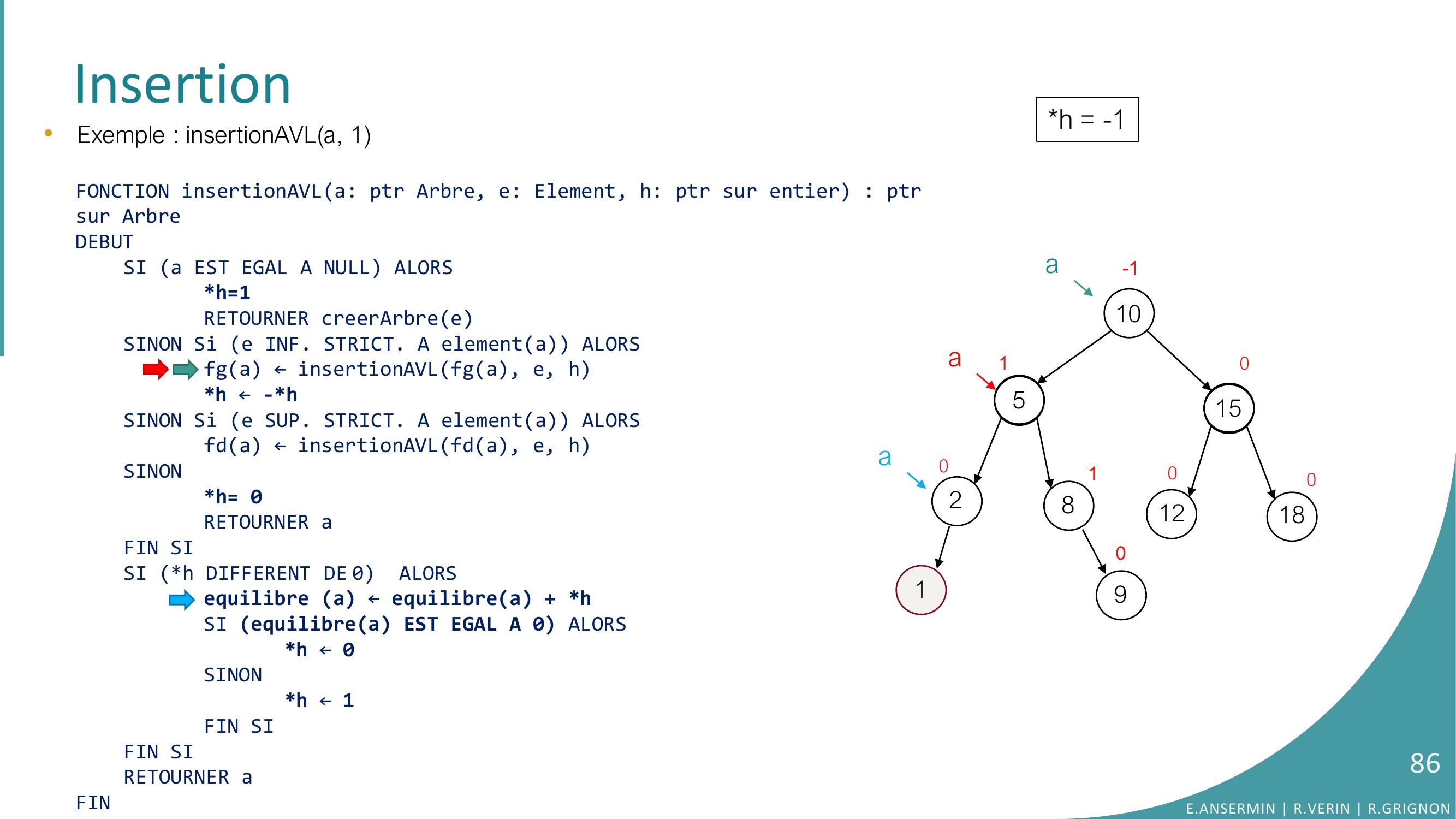
Page 64 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -1E.ANSERMIN R.VERIN R.GRIGNON64

Page 65 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 9FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 1E.ANSERMIN R.VERIN R.GRIGNON65

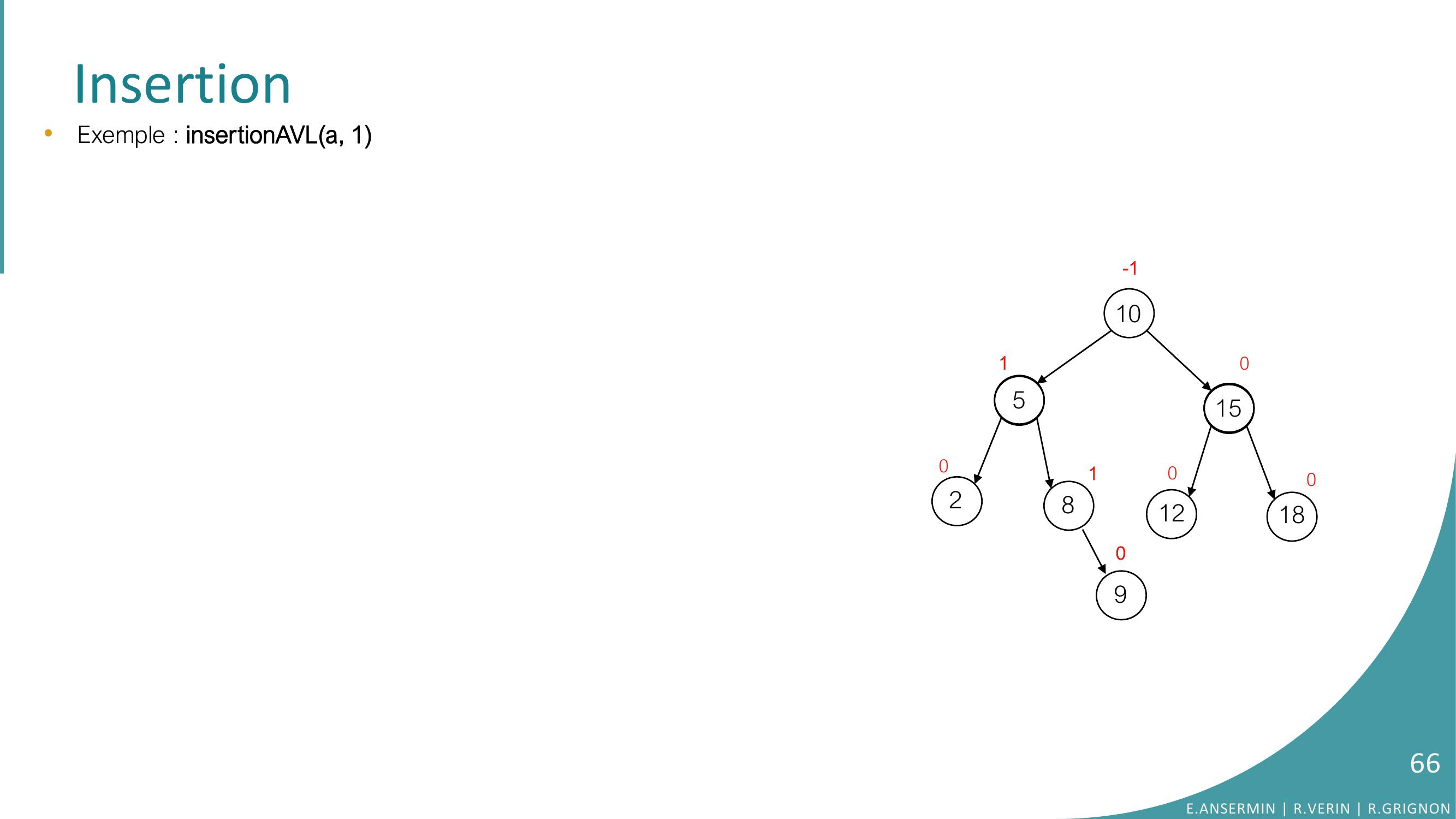
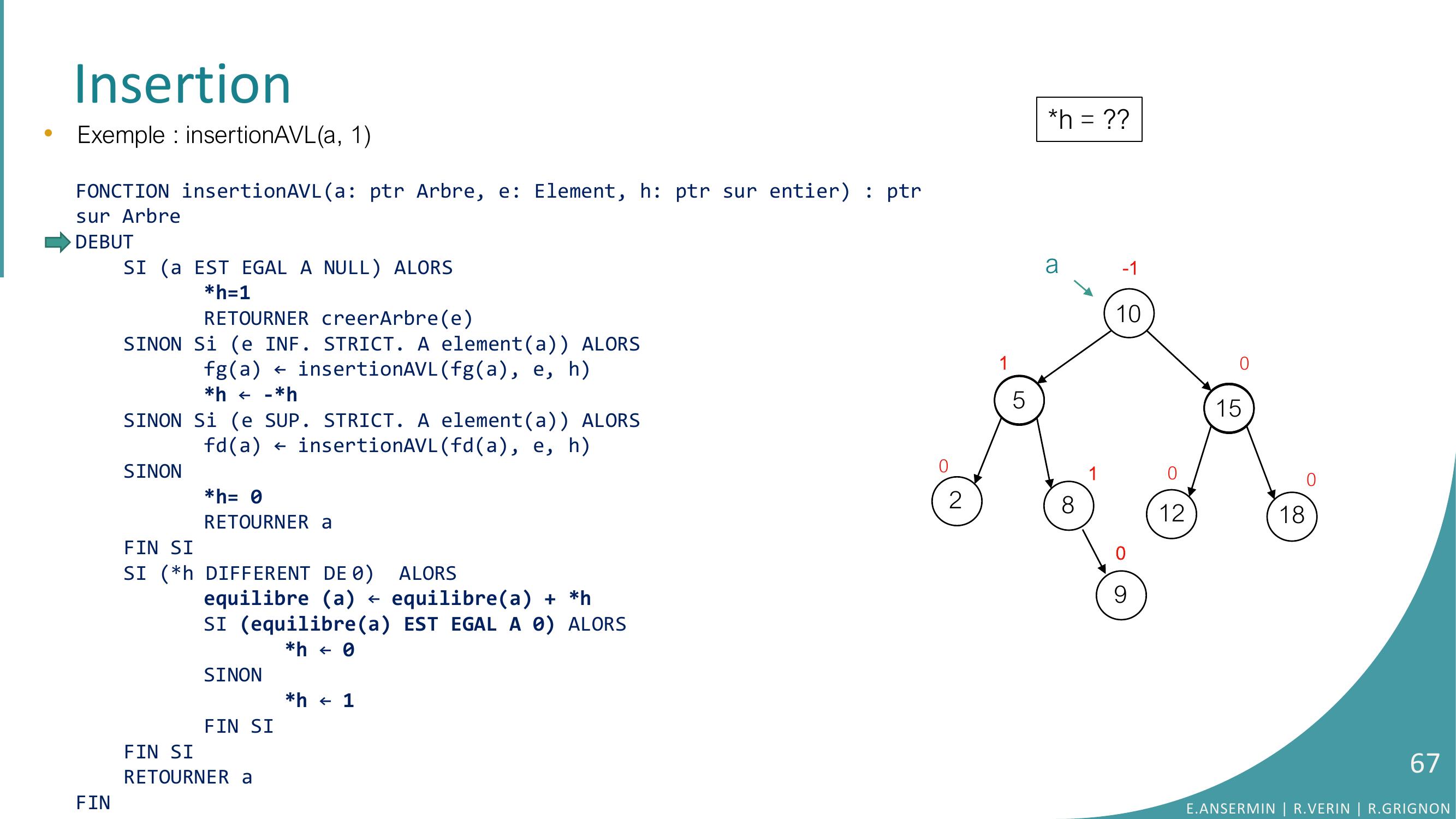
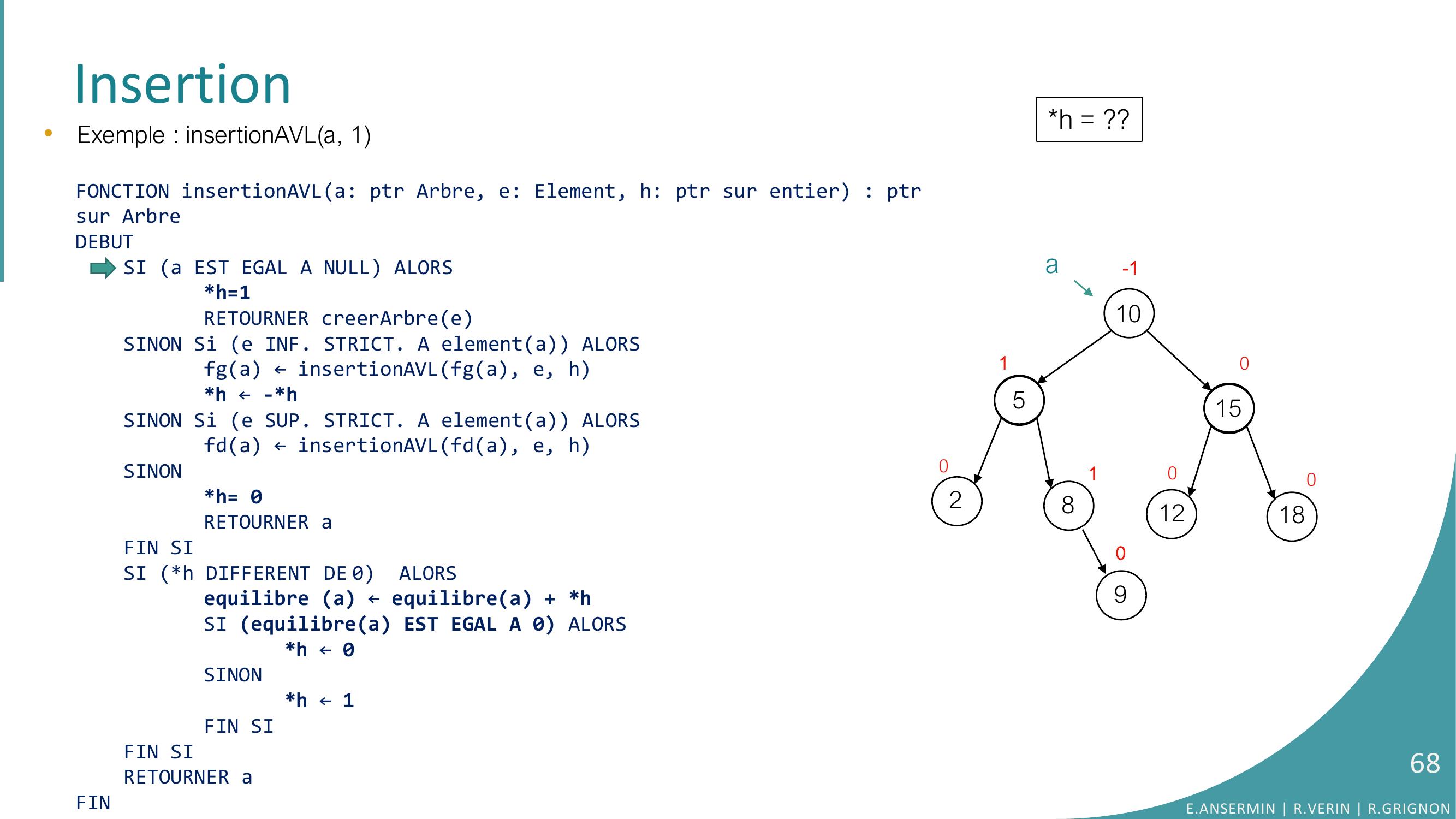
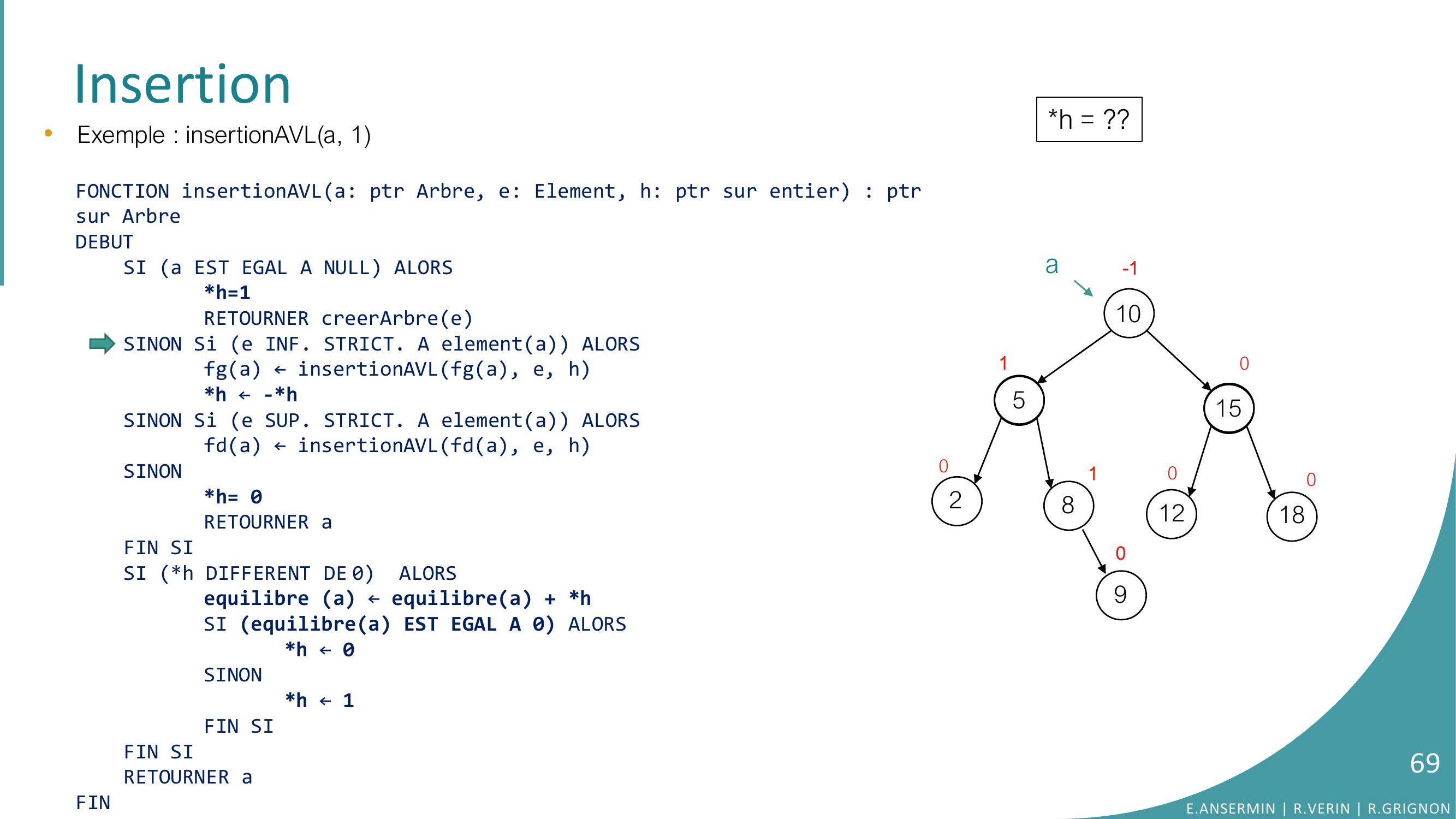
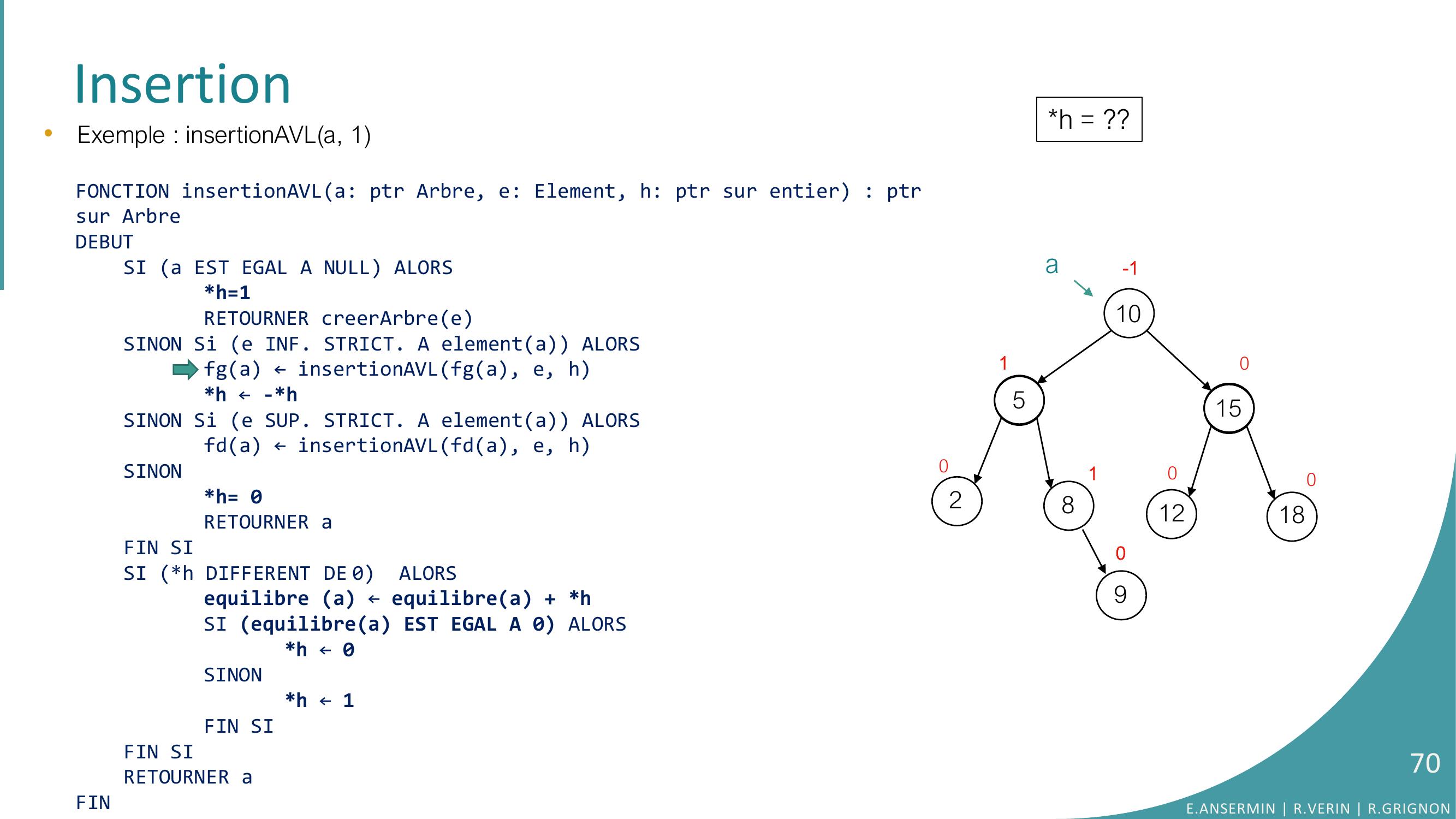
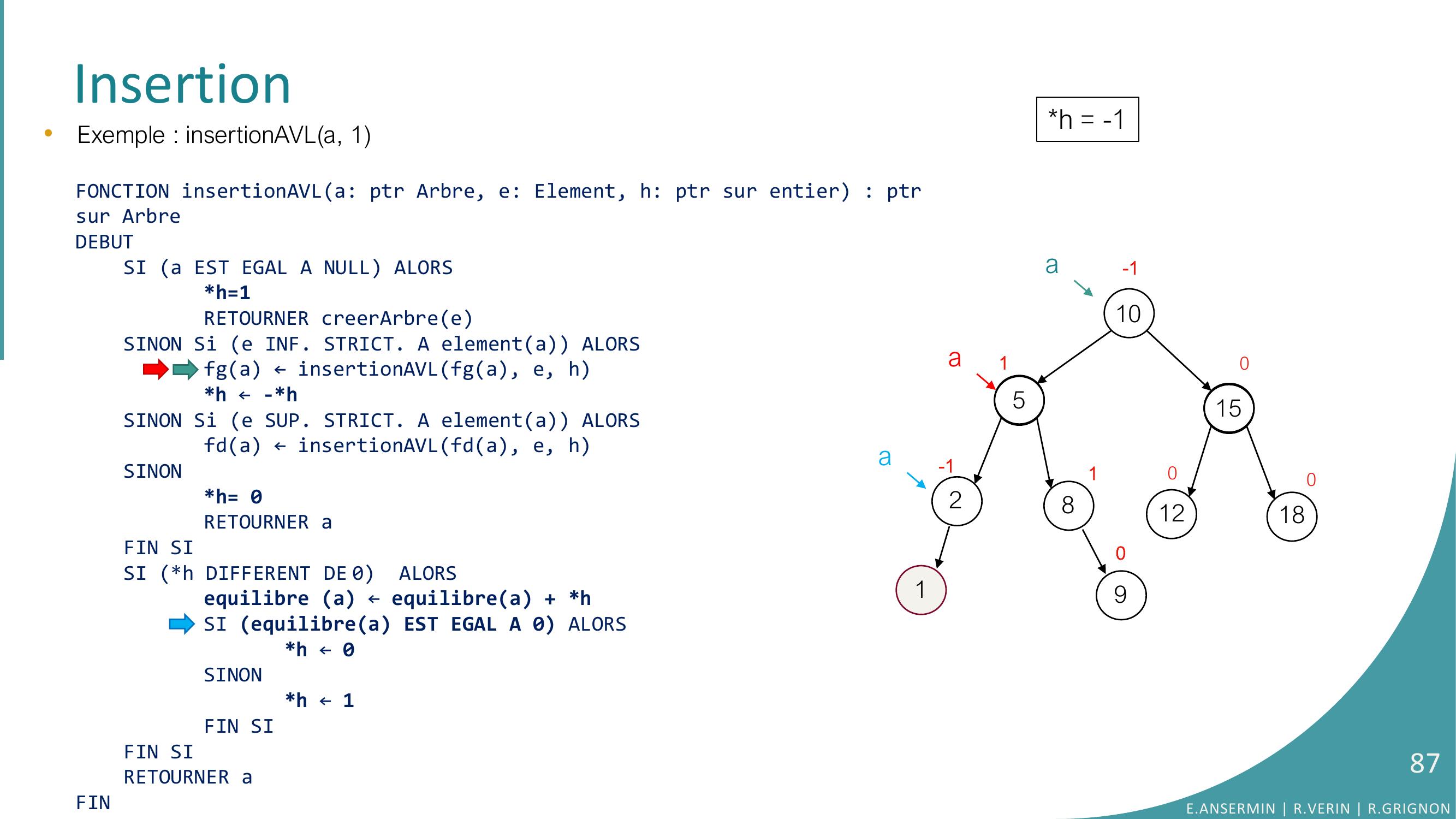
Page 66 : Insertion10528151218010010-190•Exemple : insertionAVLa, 1E.ANSERMIN R.VERIN R.GRIGNON66

Page 67 : Insertion10528151218010010-1ah = ??90•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON67

Page 68 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON68

Page 69 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON69

Page 70 : Insertion10528151218010010-1a90•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??E.ANSERMIN R.VERIN R.GRIGNON70

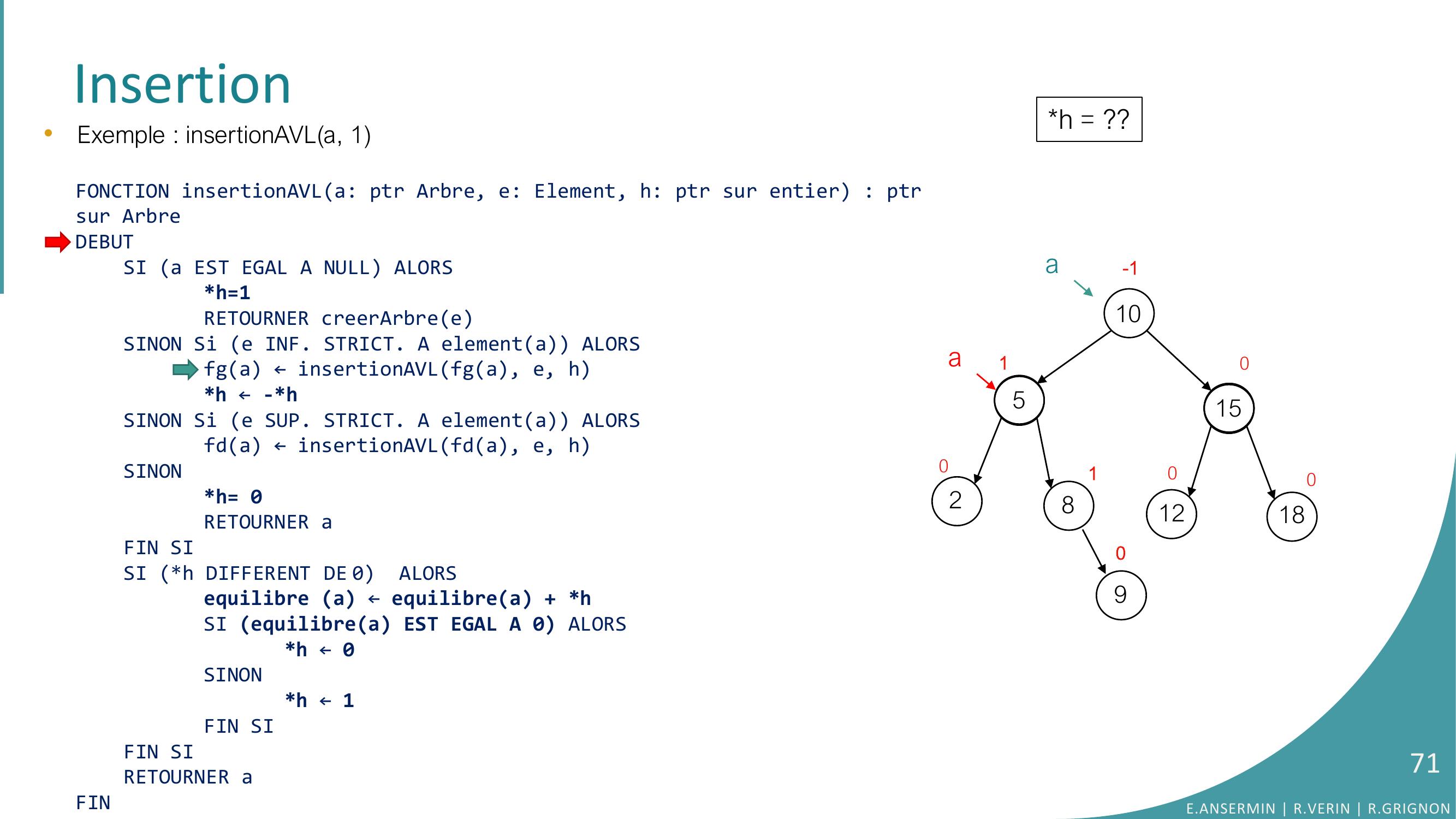
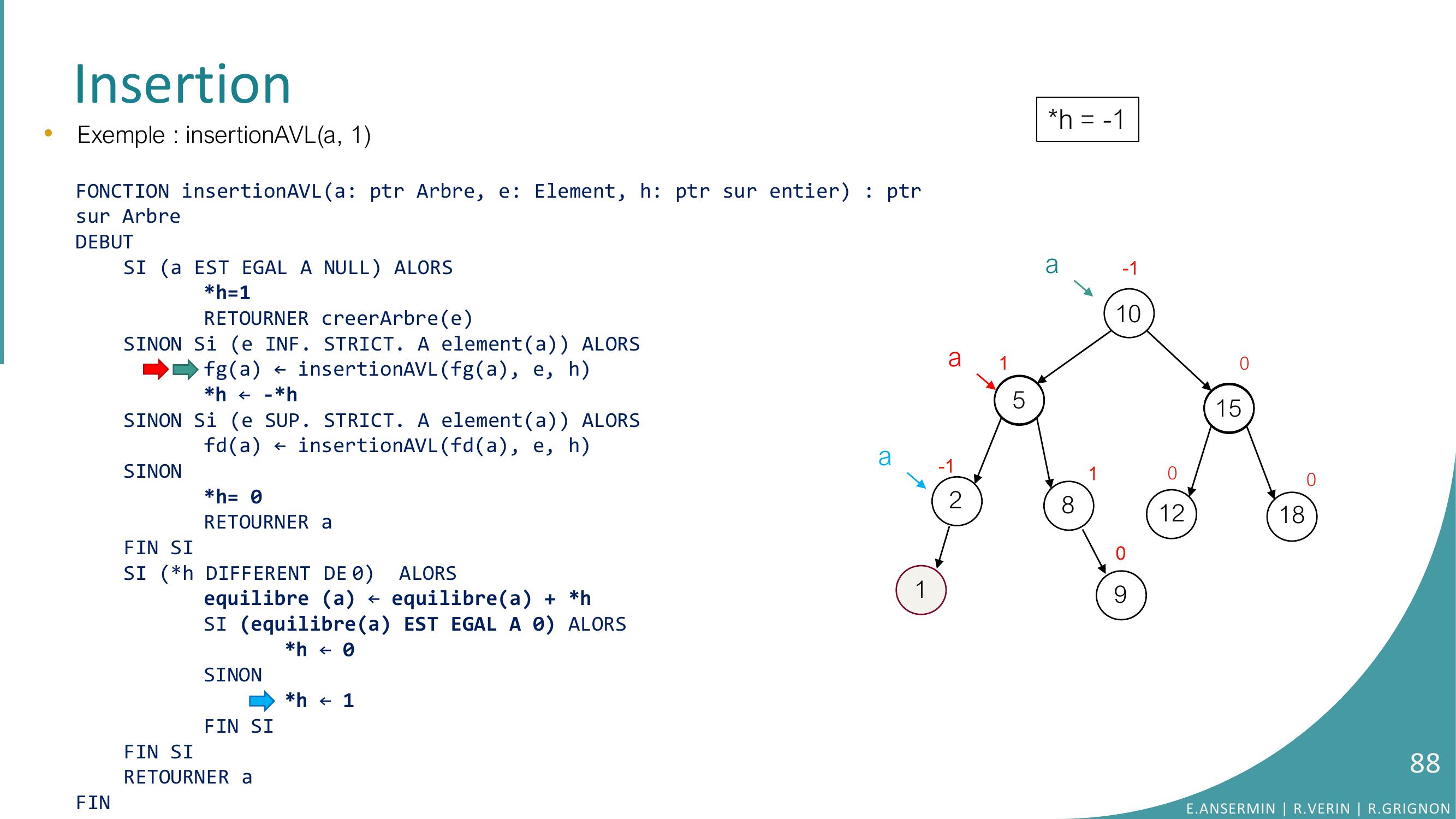
Page 71 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aE.ANSERMIN R.VERIN R.GRIGNON71

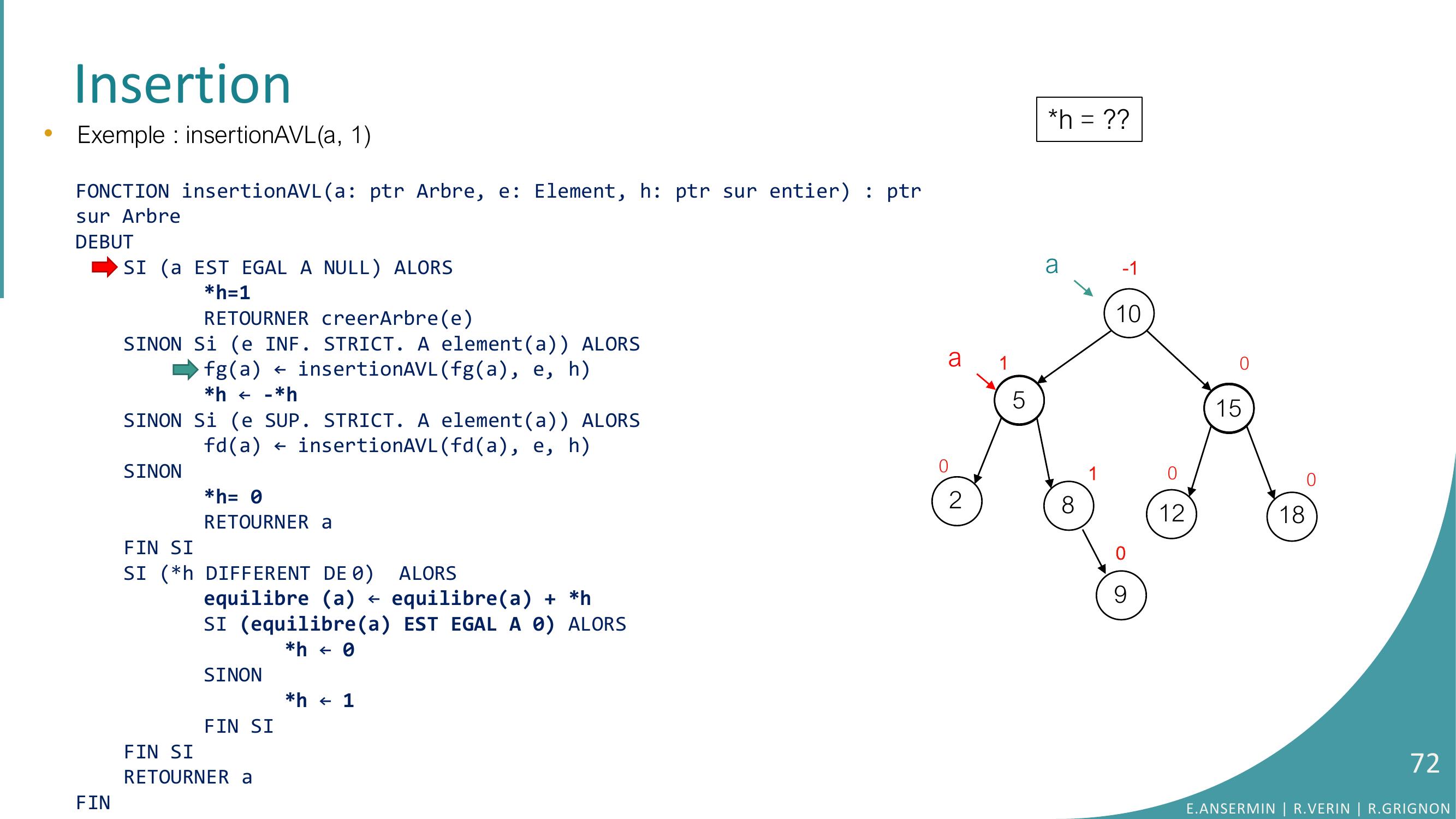
Page 72 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aE.ANSERMIN R.VERIN R.GRIGNON72

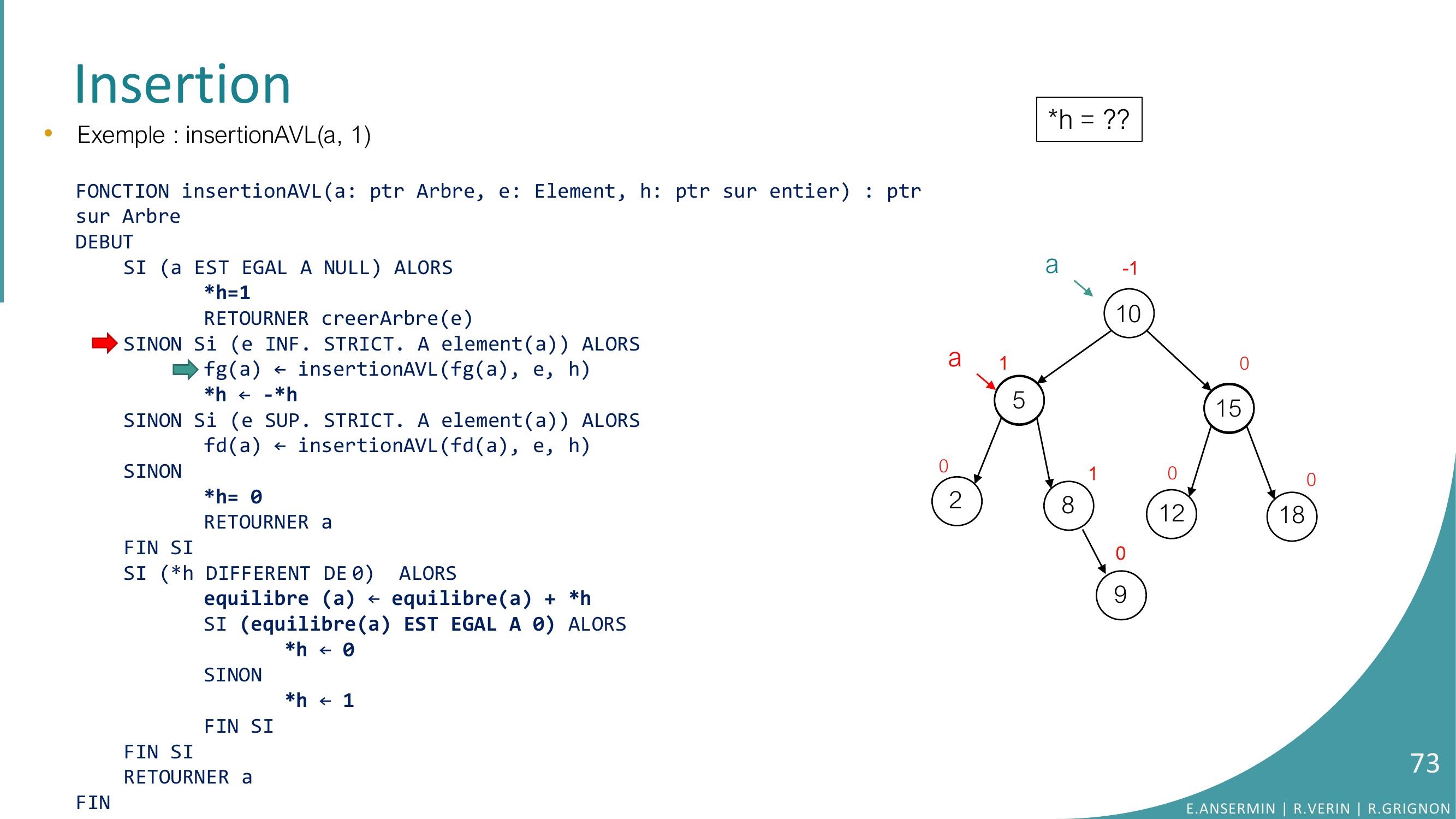
Page 73 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aE.ANSERMIN R.VERIN R.GRIGNON73

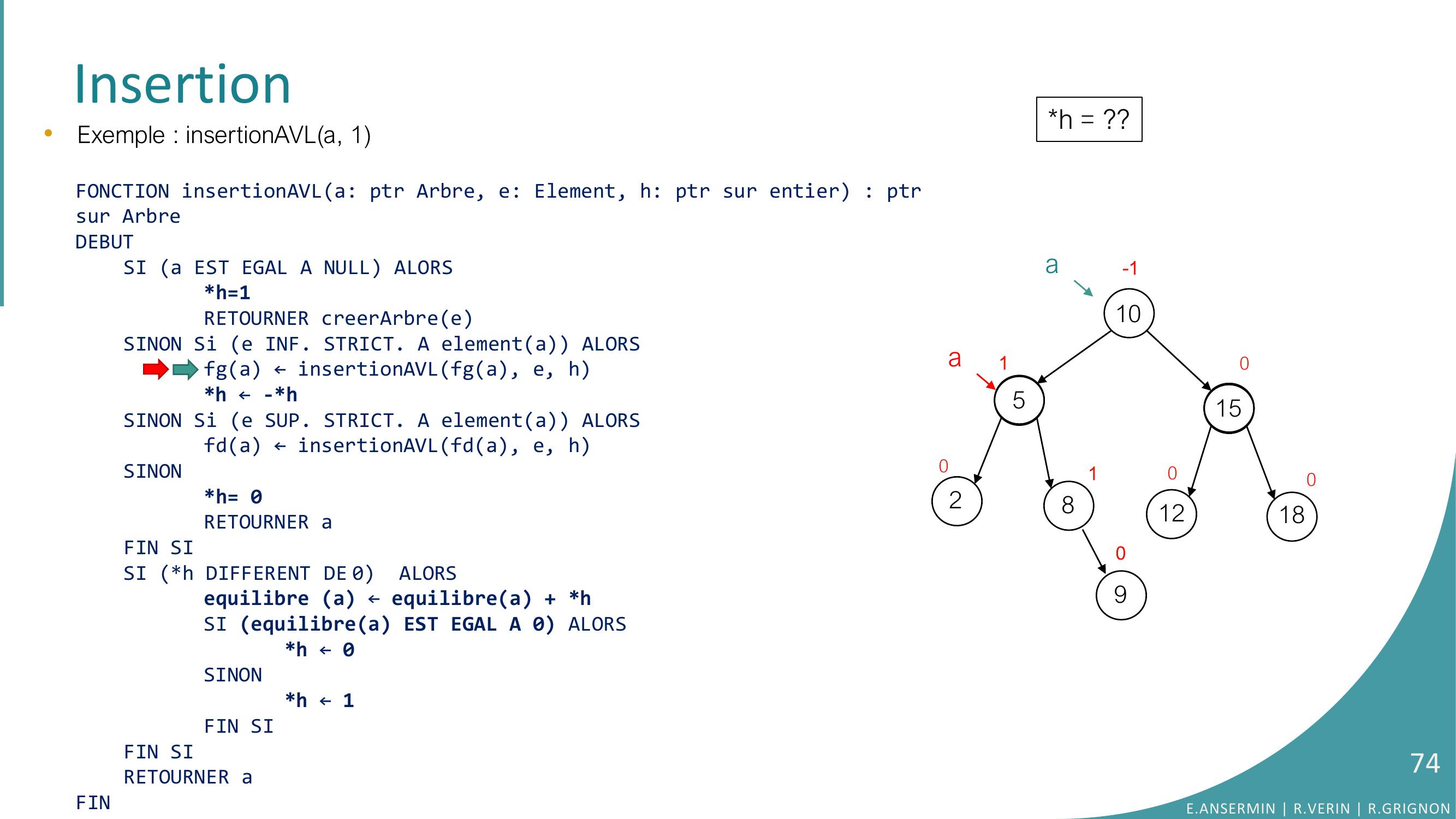
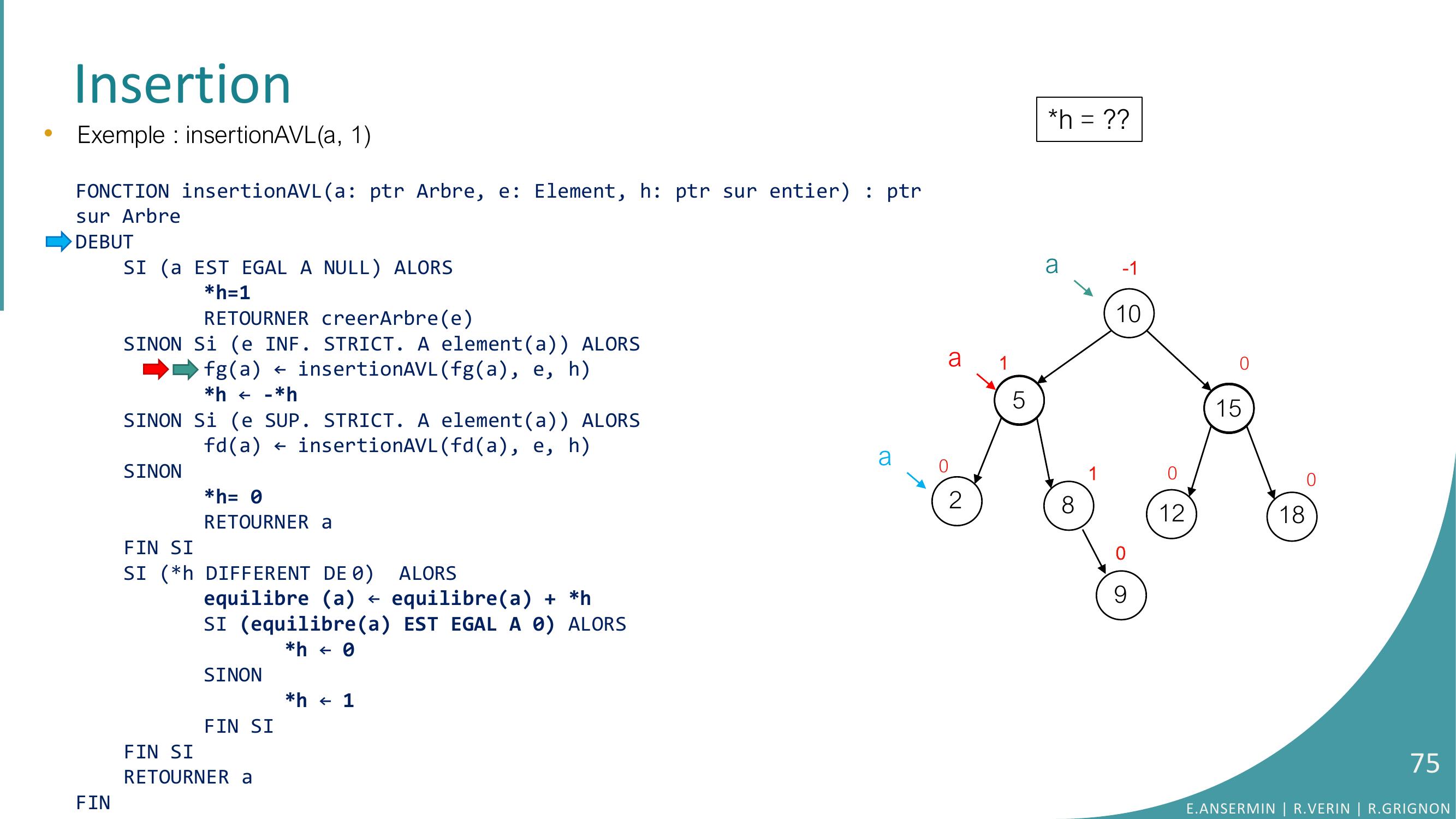
Page 74 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aE.ANSERMIN R.VERIN R.GRIGNON74

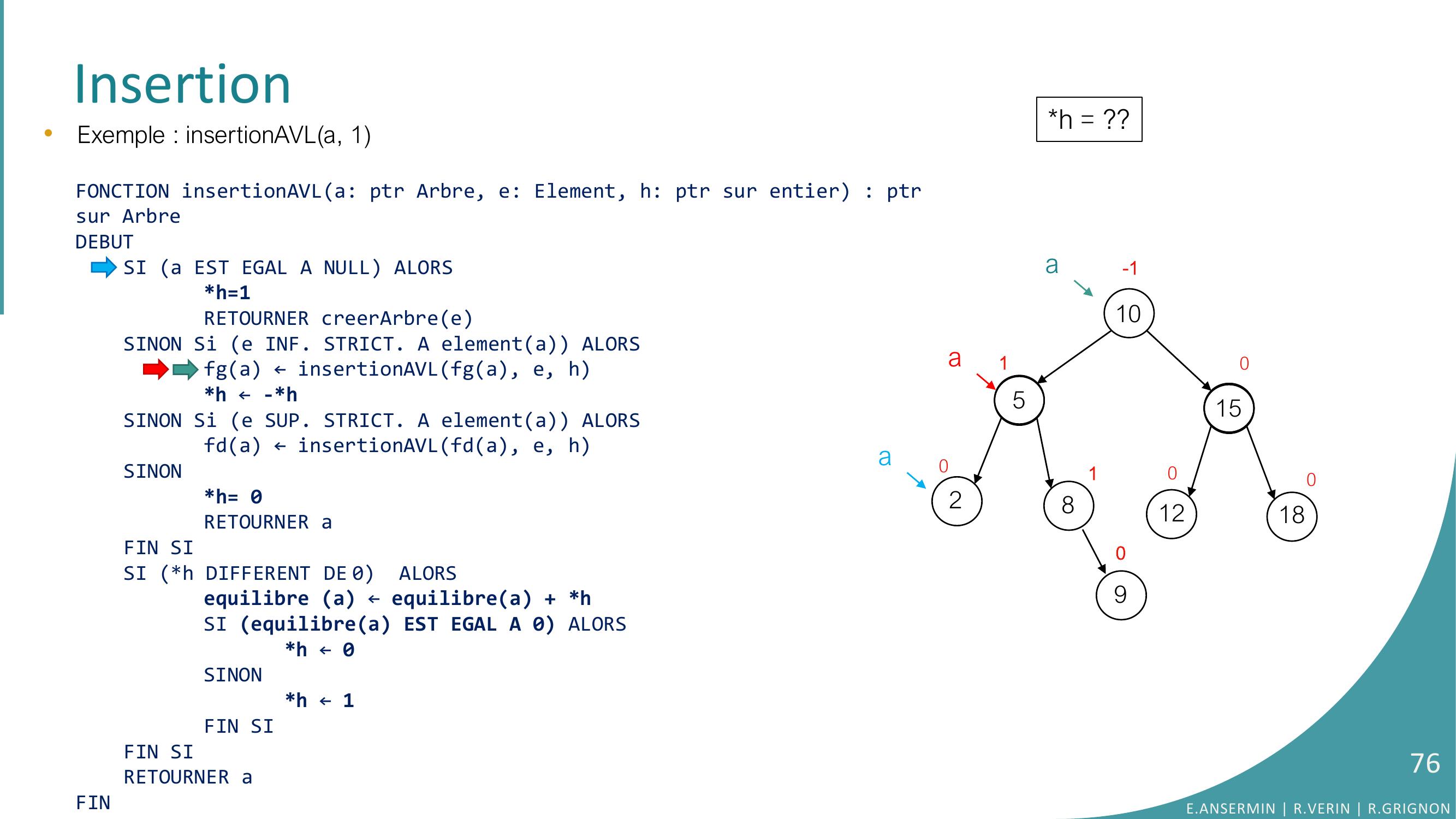
Page 75 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aaE.ANSERMIN R.VERIN R.GRIGNON75

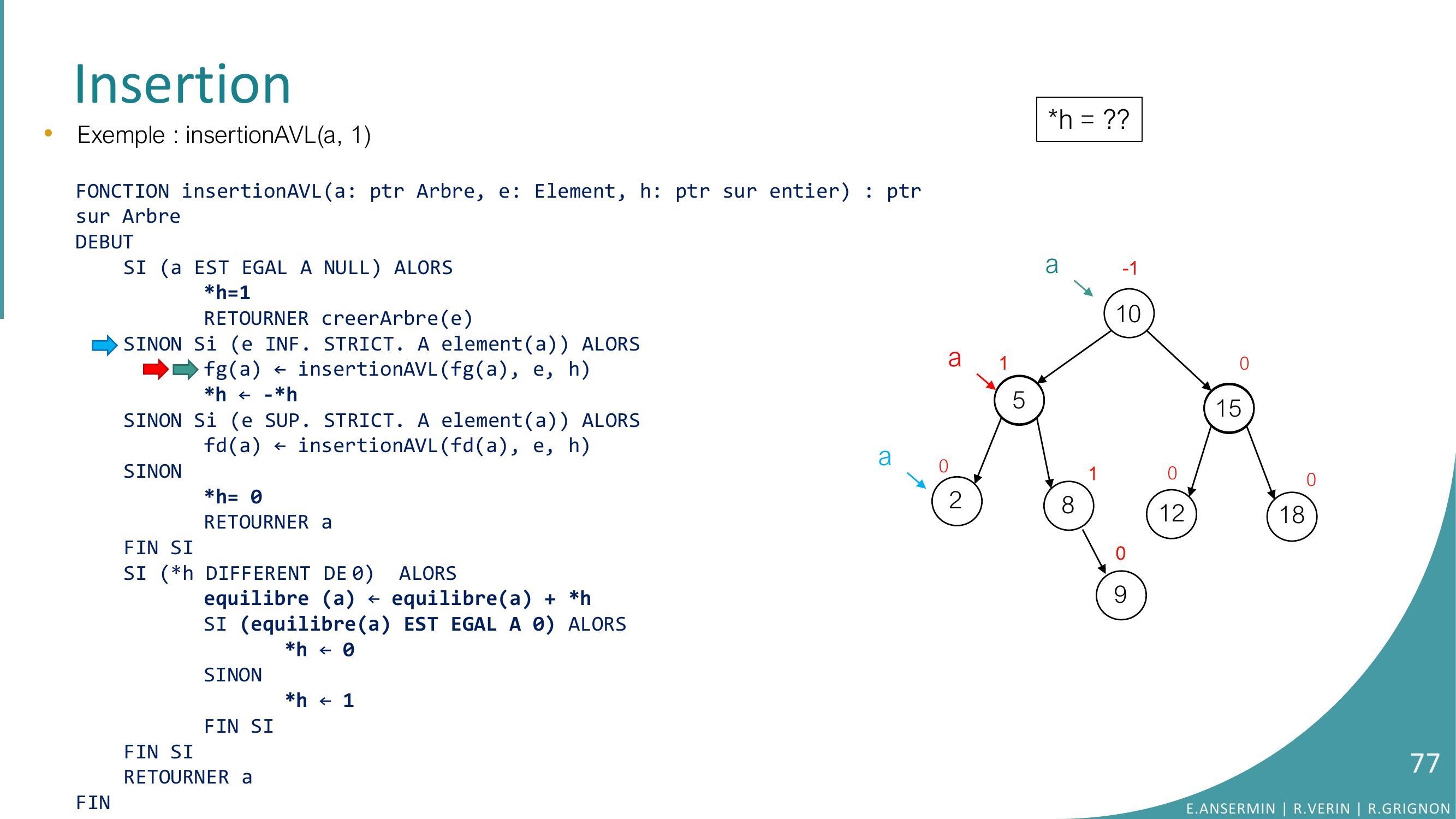
Page 76 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aaE.ANSERMIN R.VERIN R.GRIGNON76

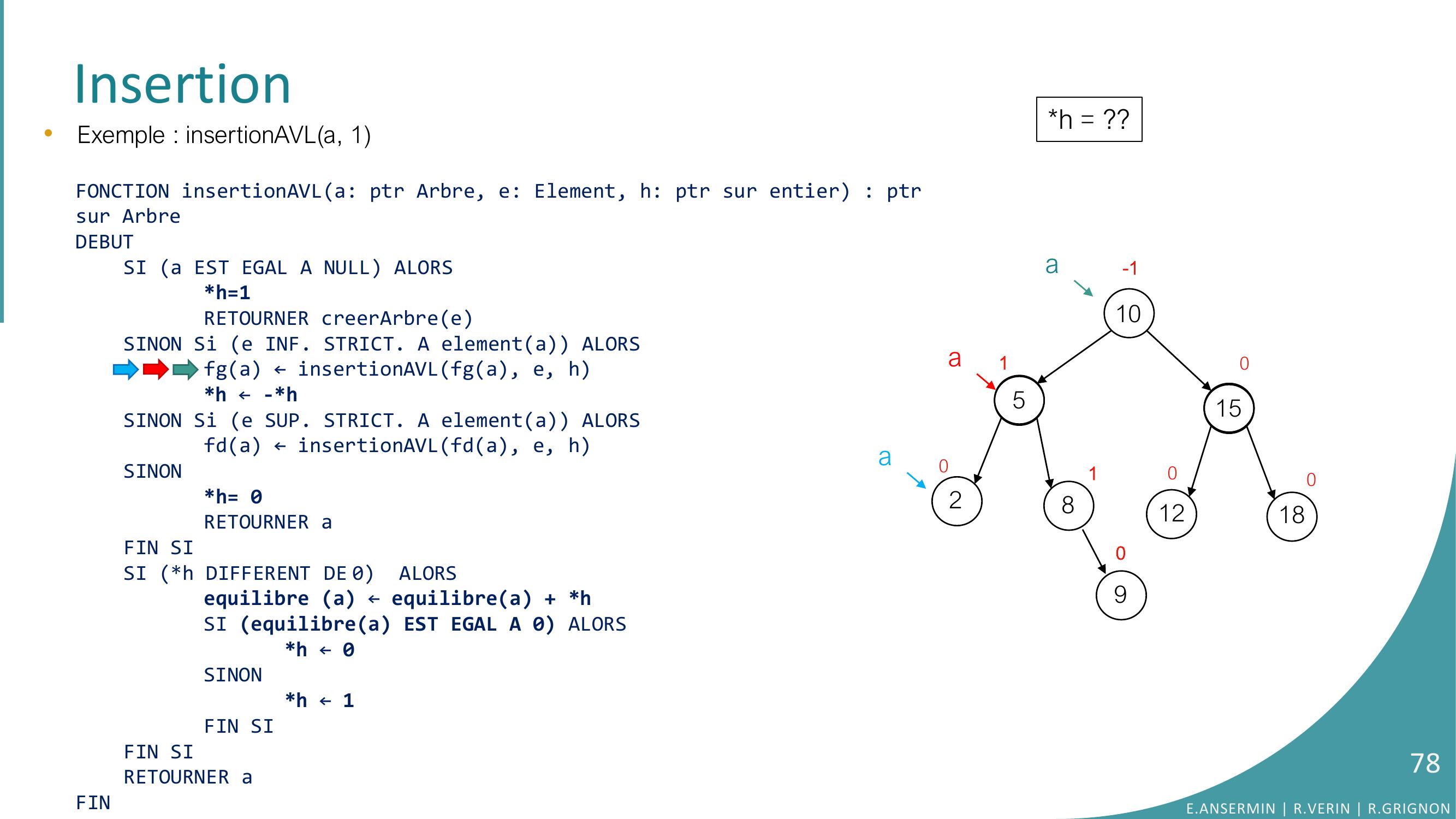
Page 77 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aaE.ANSERMIN R.VERIN R.GRIGNON77

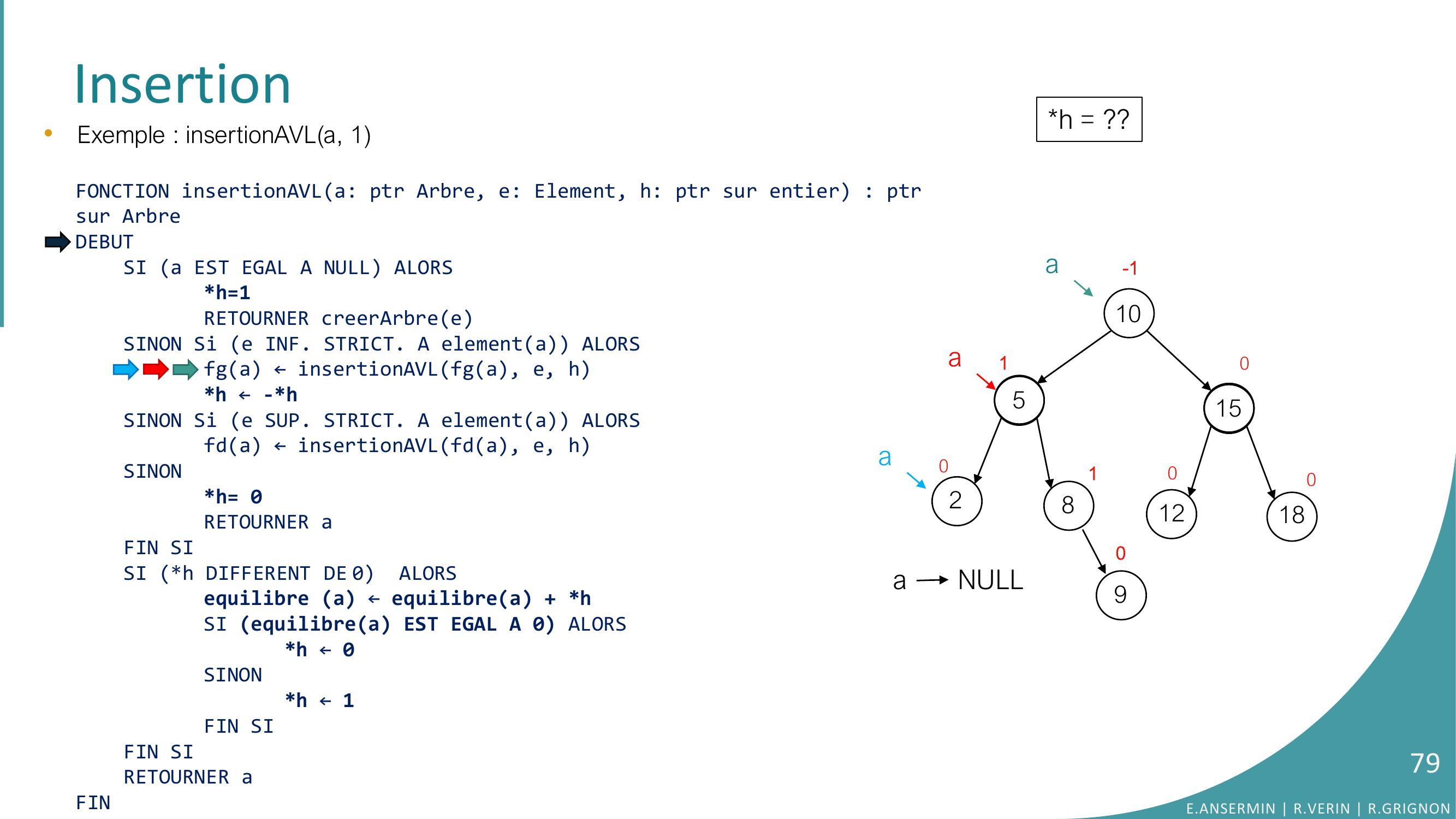
Page 78 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010010-1a90aah = ??E.ANSERMIN R.VERIN R.GRIGNON78

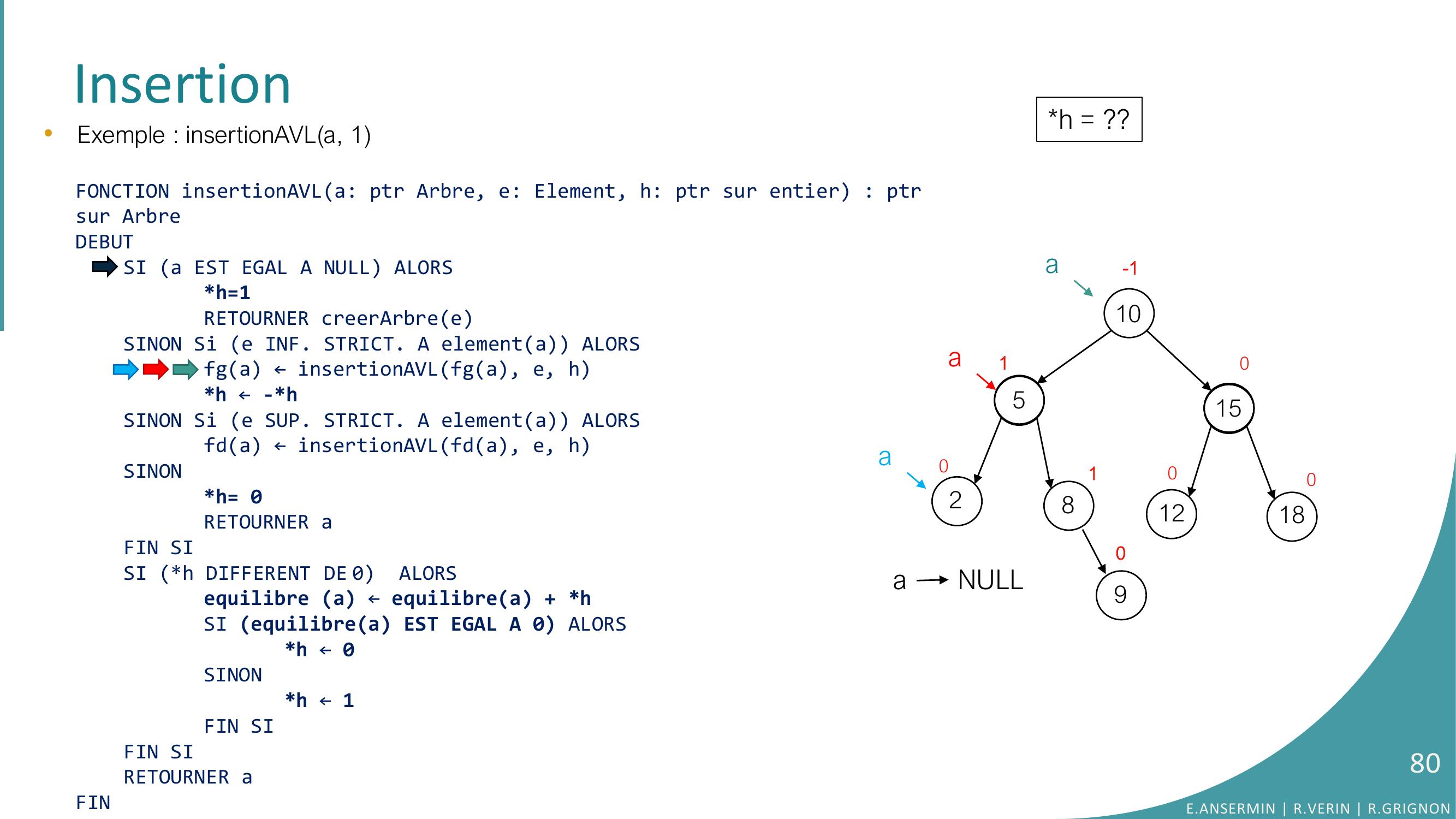
Page 79 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010010-1a90aaa NULLh = ??E.ANSERMIN R.VERIN R.GRIGNON79

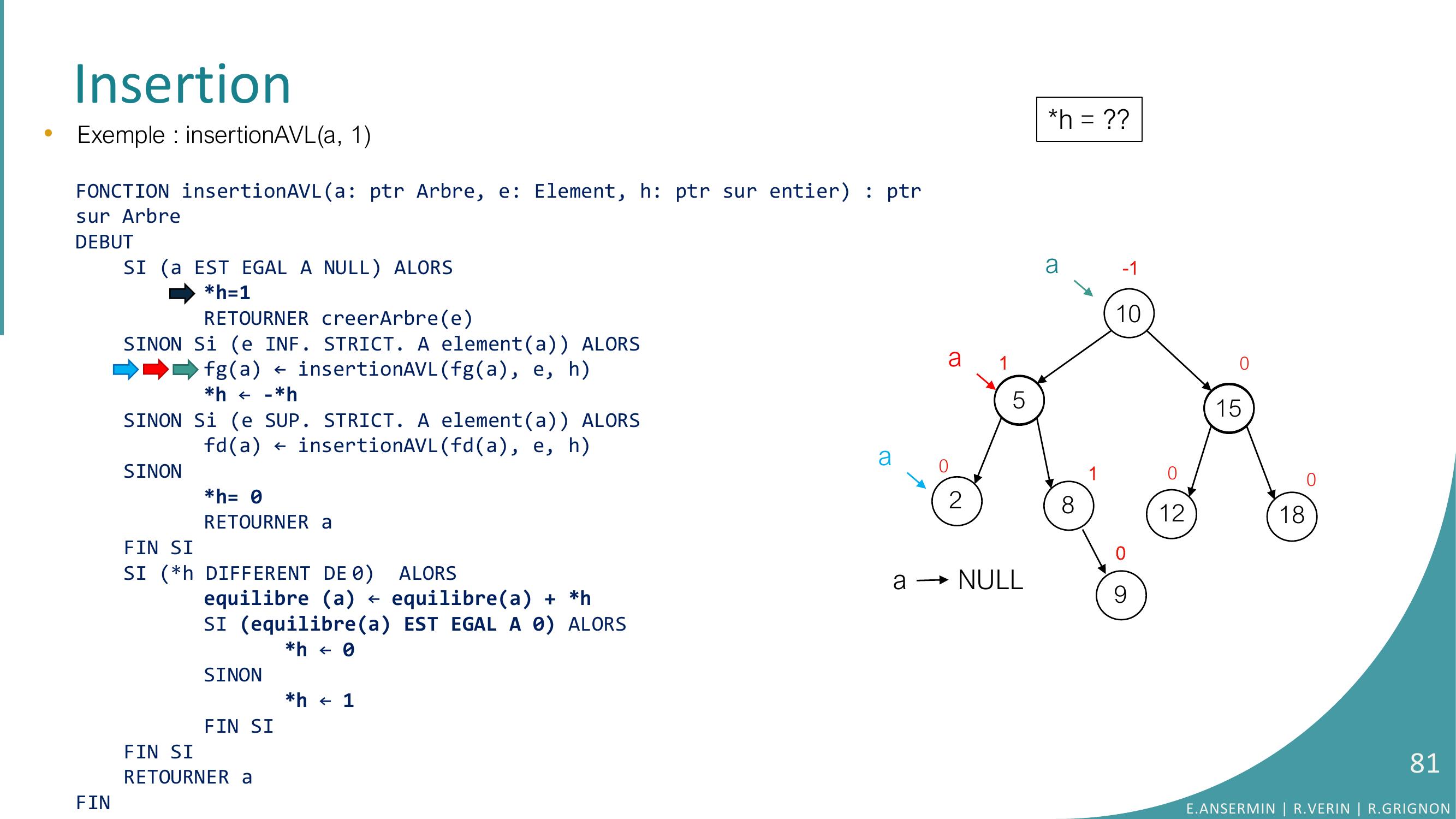
Page 80 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010010-1a90aah = ??a NULLE.ANSERMIN R.VERIN R.GRIGNON80

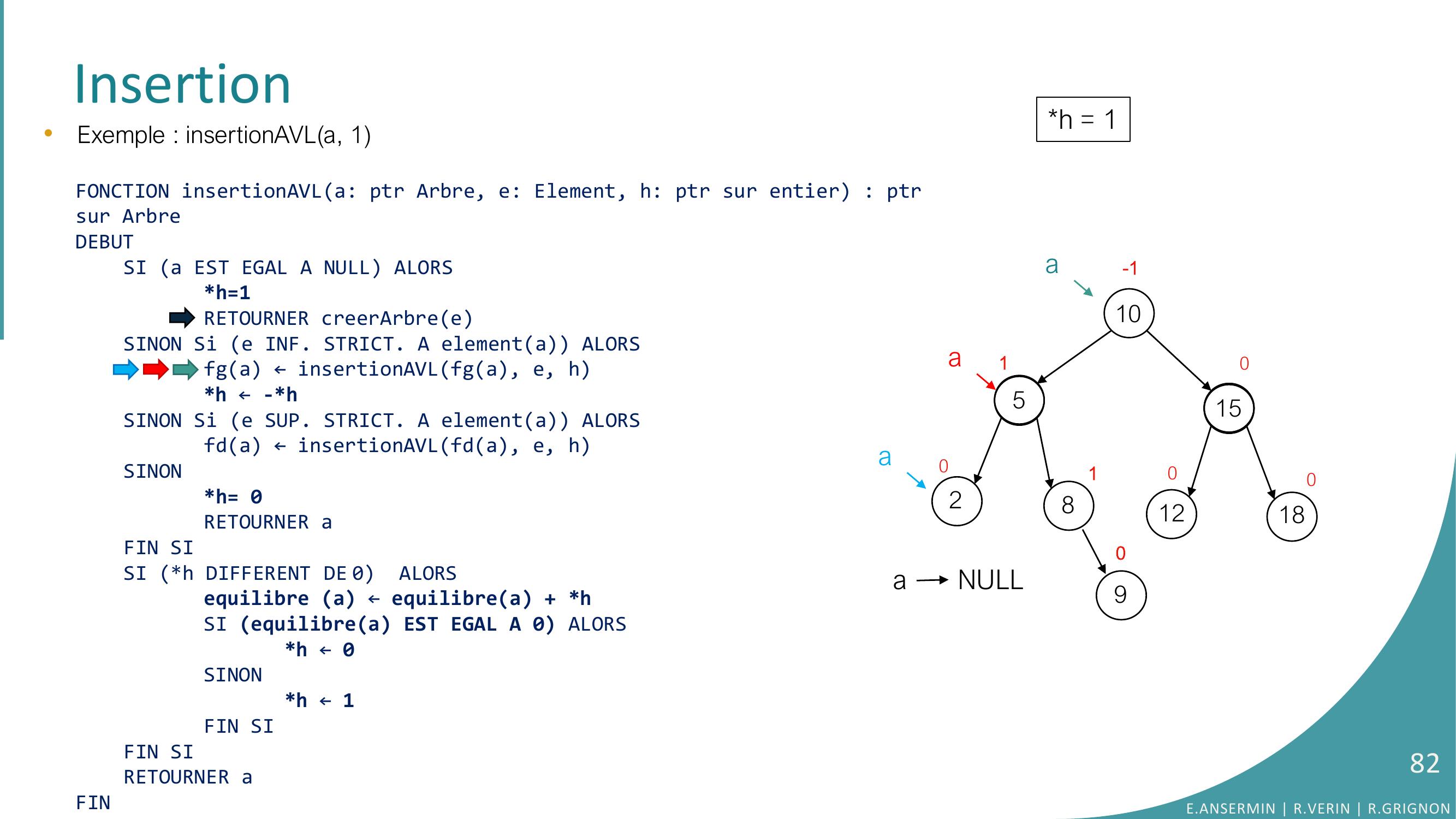
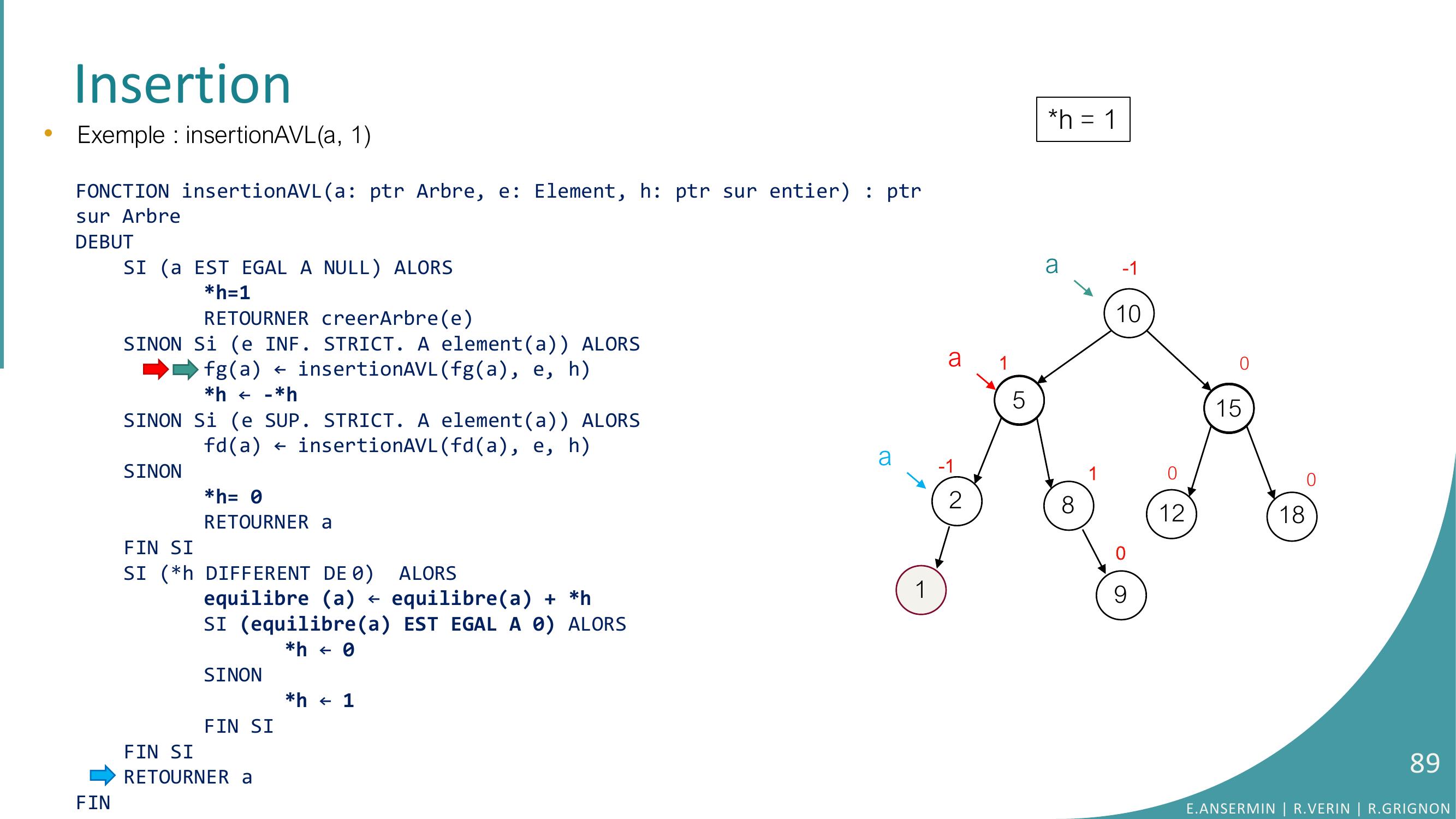
Page 81 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = ??10528151218010010-1a90aaa NULLE.ANSERMIN R.VERIN R.GRIGNON81

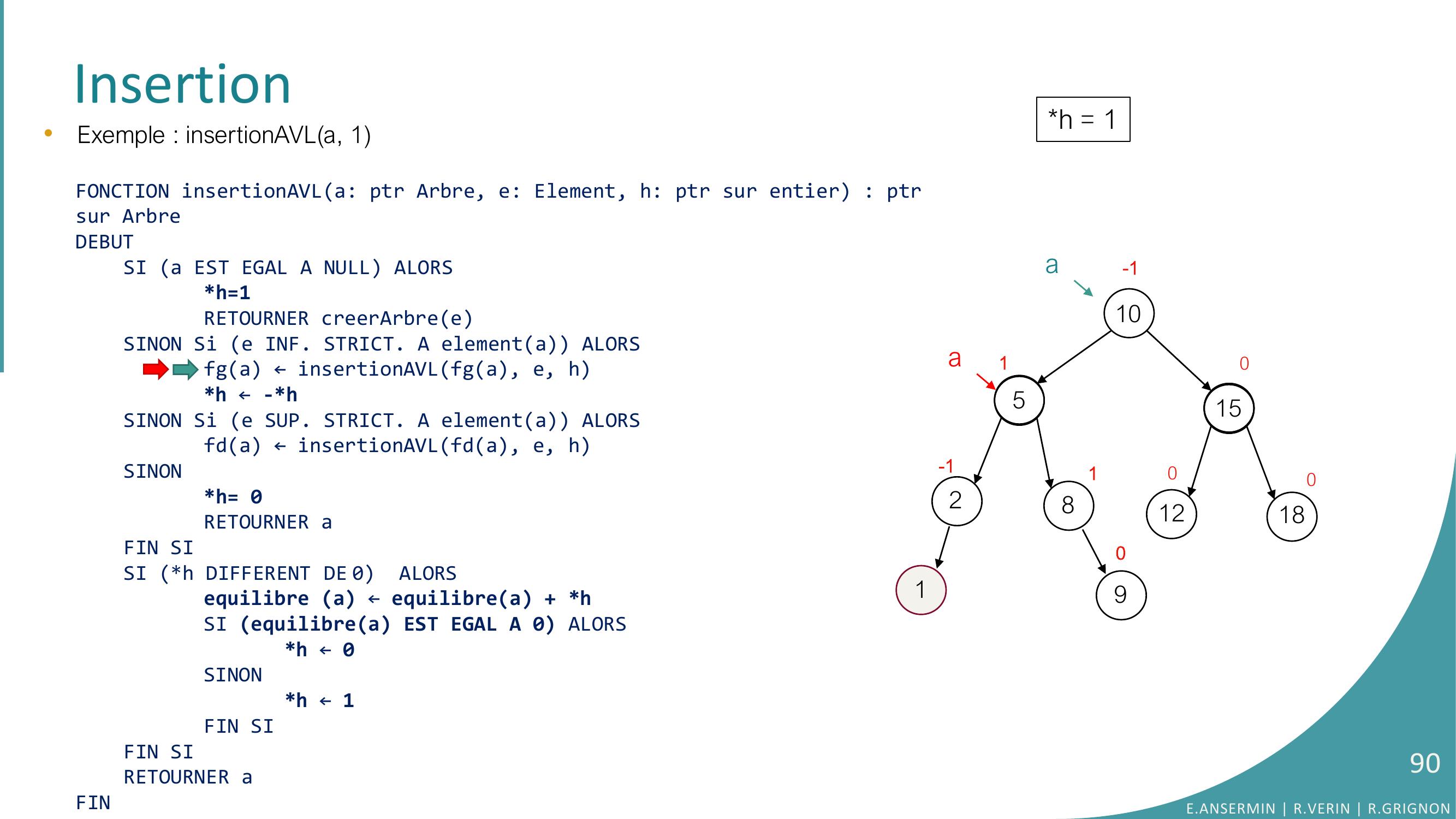
Page 82 : Insertionh = 1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFIN10528151218010010-1a90aaa NULLE.ANSERMIN R.VERIN R.GRIGNON82

Page 83 : Insertion1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 110528151218010010-1a90aaE.ANSERMIN R.VERIN R.GRIGNON83

Page 84 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010010-1a90aa1h = 1E.ANSERMIN R.VERIN R.GRIGNON84

Page 85 : Insertionh = -1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFIN10528151218010010-1a90aa1E.ANSERMIN R.VERIN R.GRIGNON85

Page 86 : Insertion•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -110528151218010010-1a90aa1E.ANSERMIN R.VERIN R.GRIGNON86

Page 87 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010-10-190a1h = -11aaE.ANSERMIN R.VERIN R.GRIGNON87

Page 88 : •Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINInsertion10528151218010-10-190a1h = -11aaE.ANSERMIN R.VERIN R.GRIGNON88

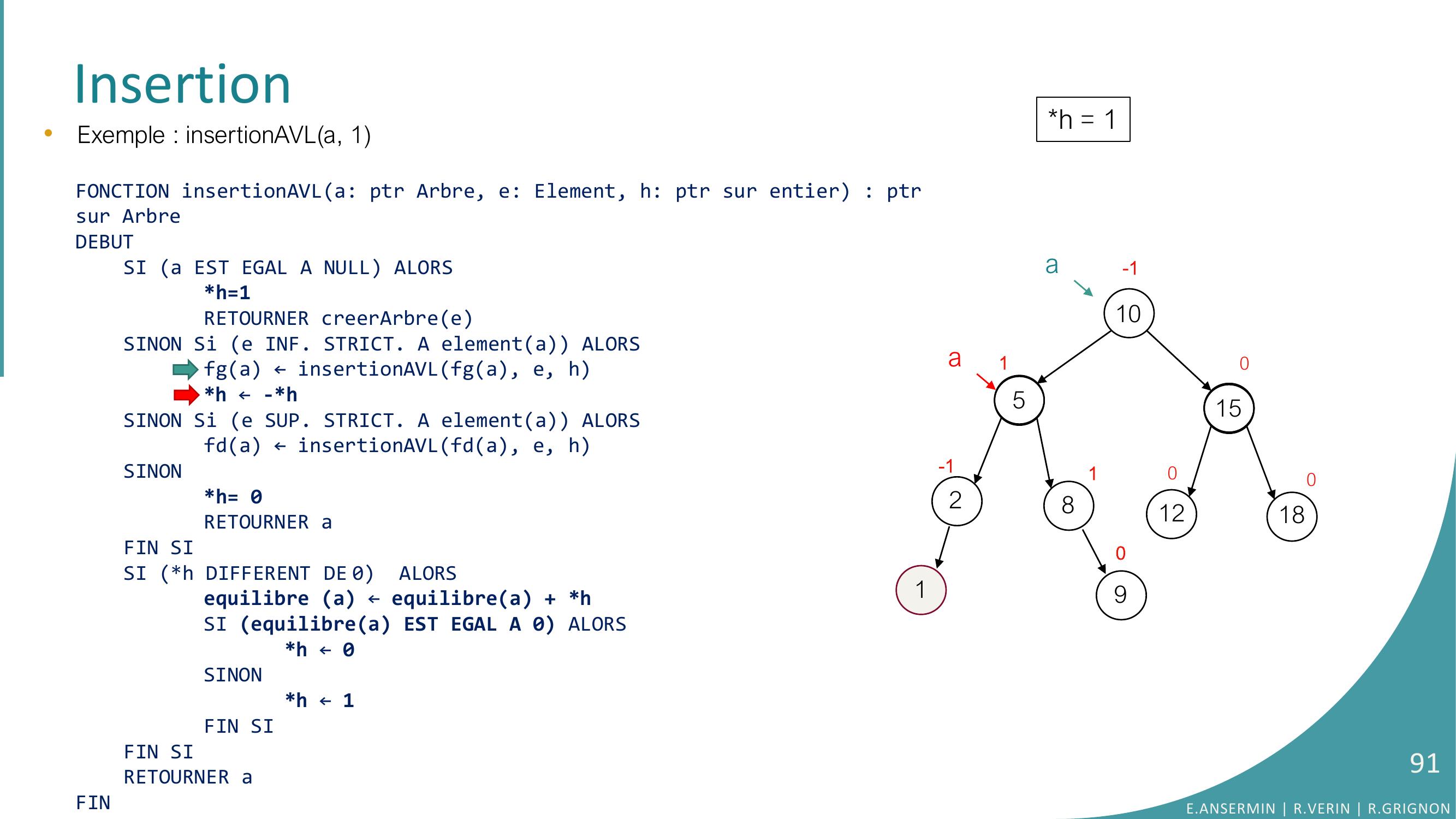
Page 89 : Insertion10528151218010-110-1ah = 190a1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON89

Page 90 : Insertion10528151218010-10-1901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 11aaE.ANSERMIN R.VERIN R.GRIGNON90

Page 91 : Insertion10528151218010-10-1901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 11aaE.ANSERMIN R.VERIN R.GRIGNON91

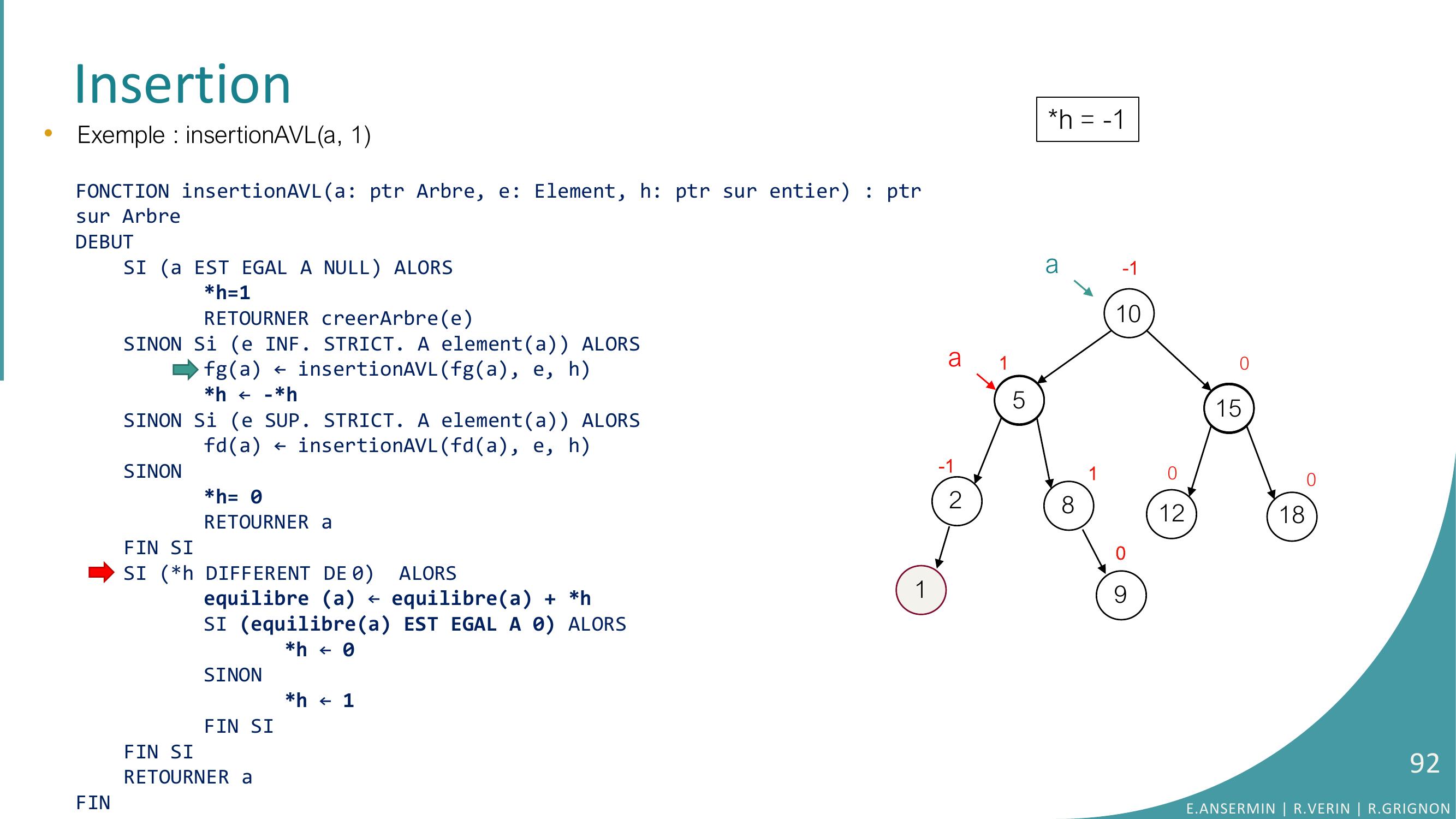
Page 92 : Insertion10528151218010-10-1901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -11aaE.ANSERMIN R.VERIN R.GRIGNON92

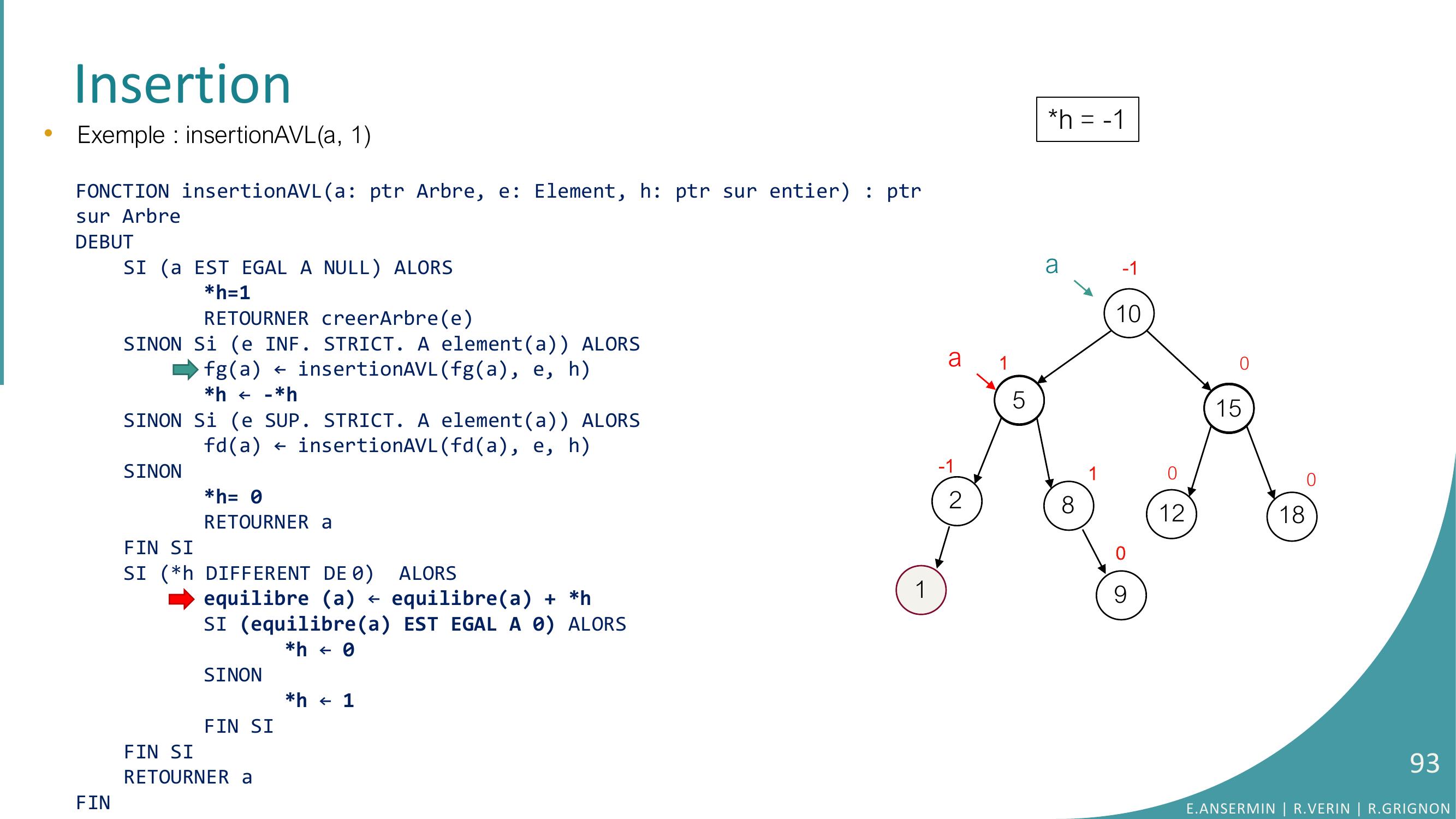
Page 93 : Insertion10528151218010-10-1901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -11aaE.ANSERMIN R.VERIN R.GRIGNON93

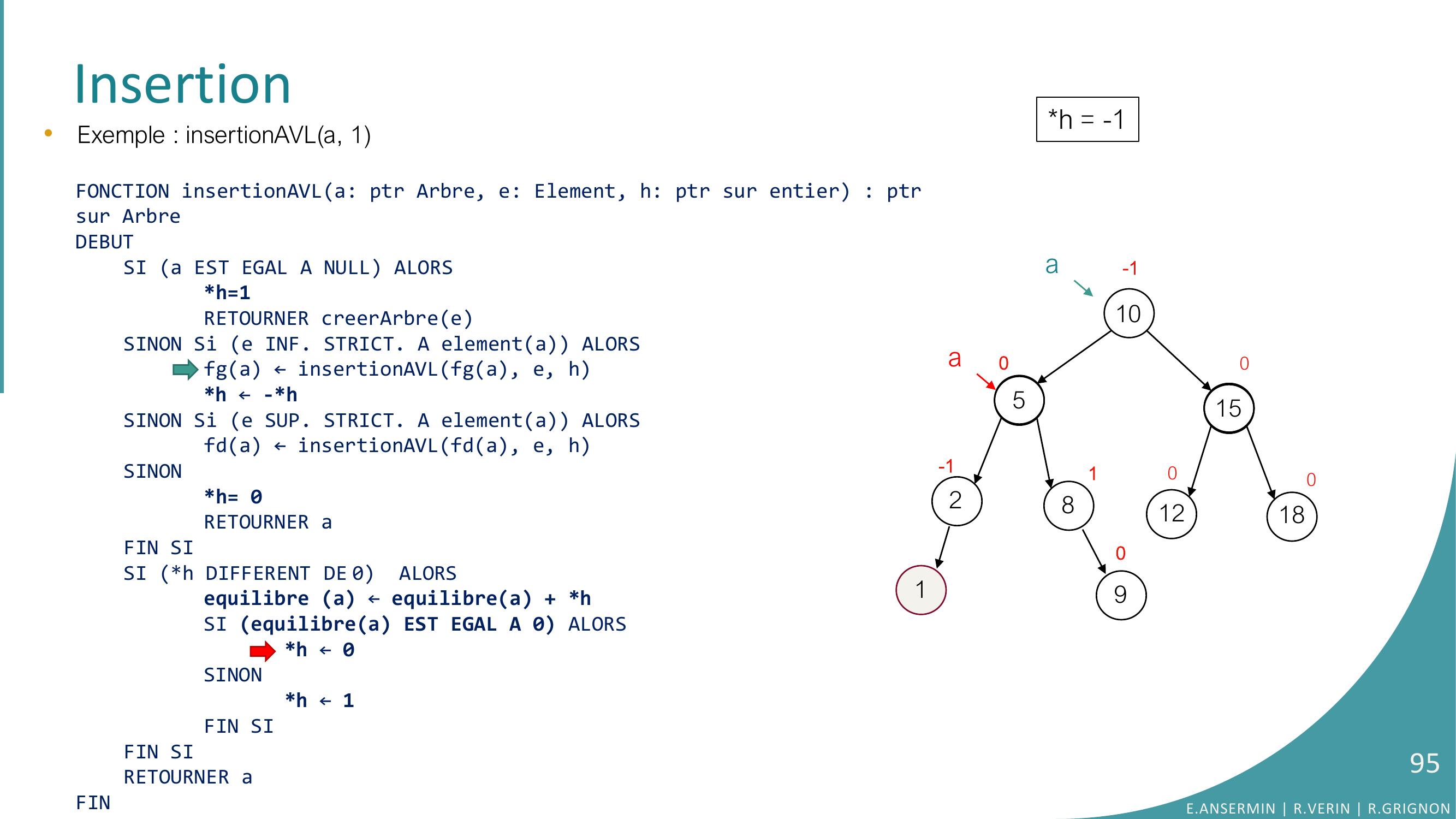
Page 94 : Insertion10528151218010-100-1a90a1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -1E.ANSERMIN R.VERIN R.GRIGNON94

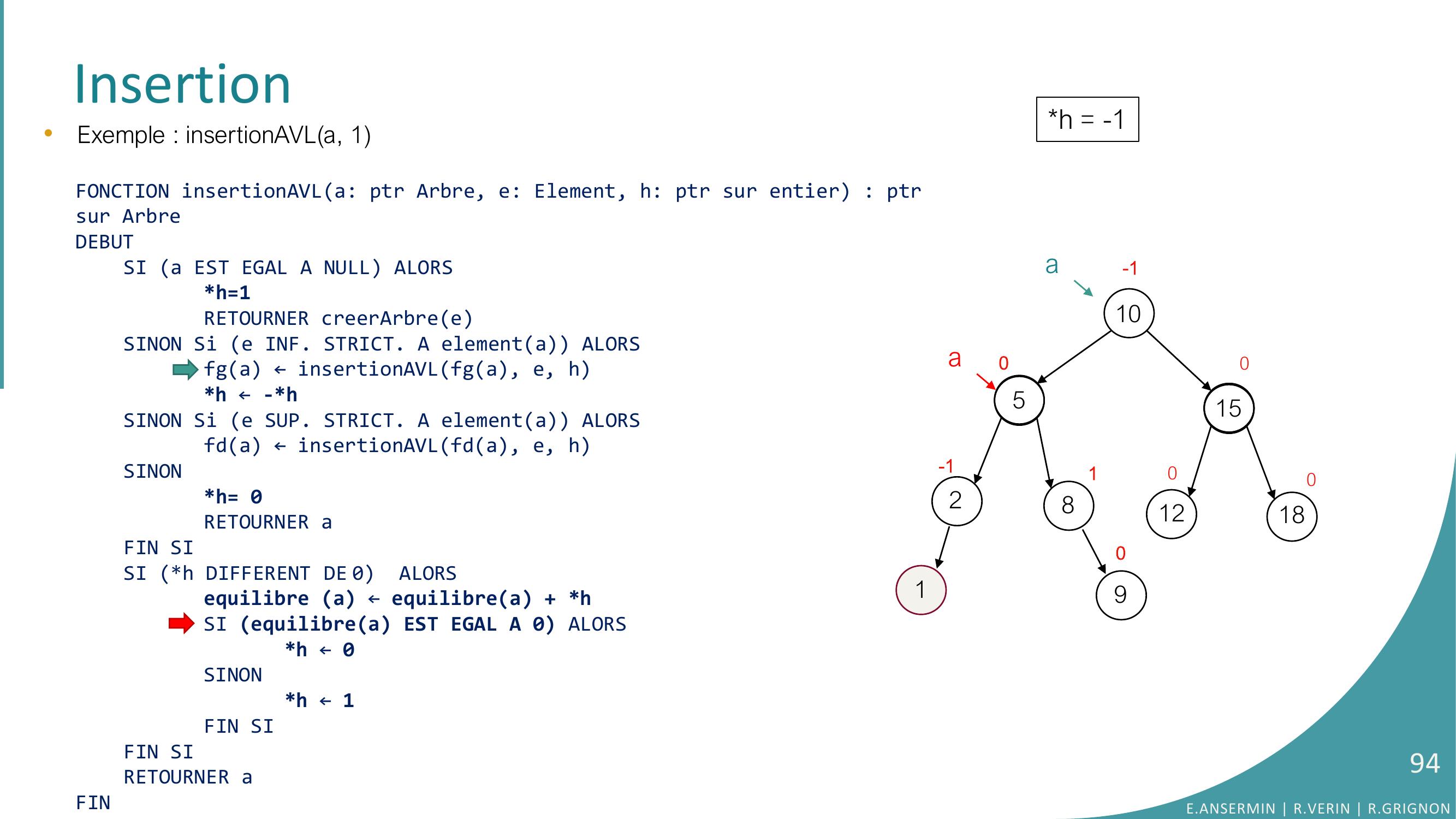
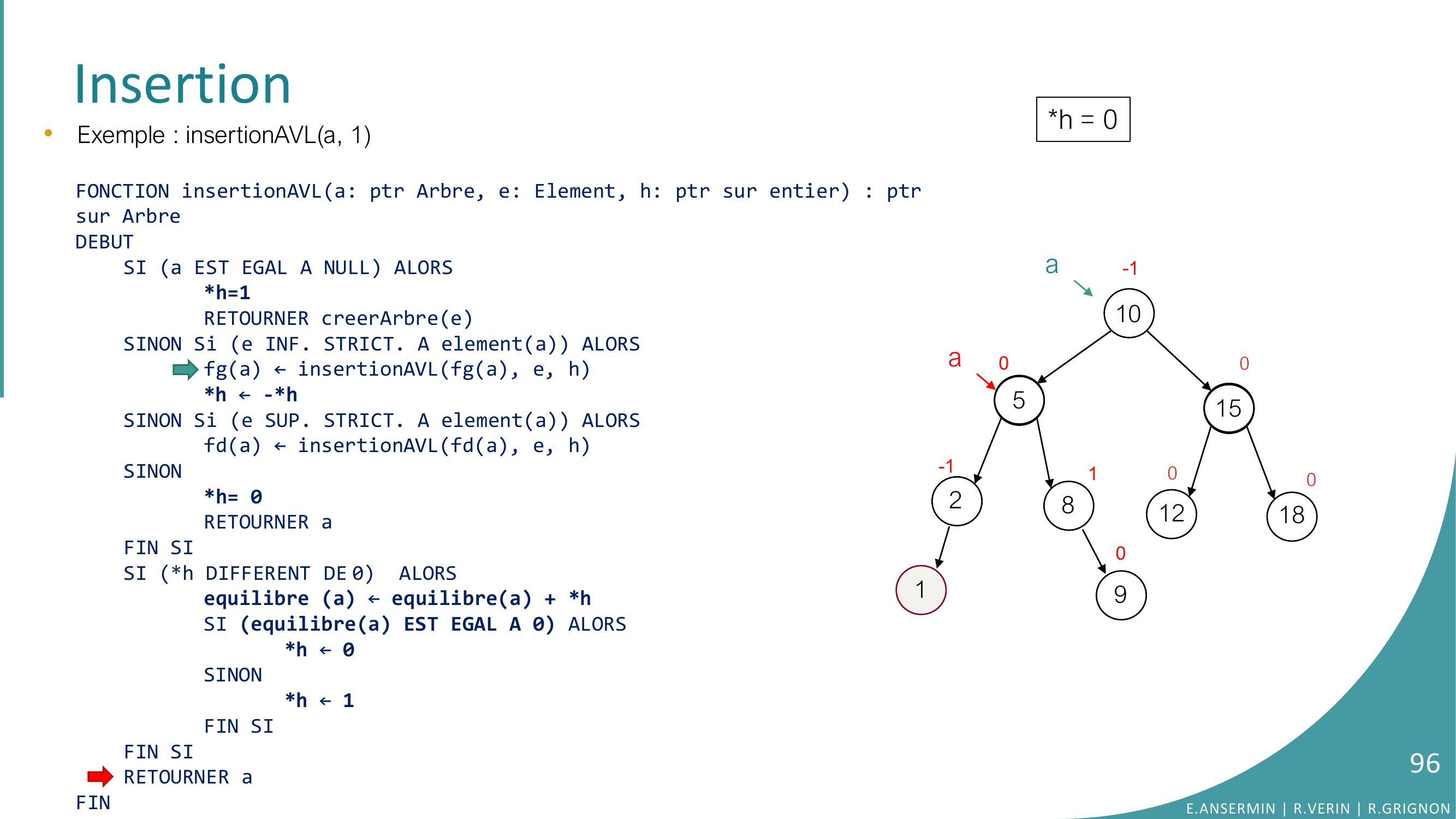
Page 95 : Insertion10528151218010-100-1a90a1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = -1E.ANSERMIN R.VERIN R.GRIGNON95

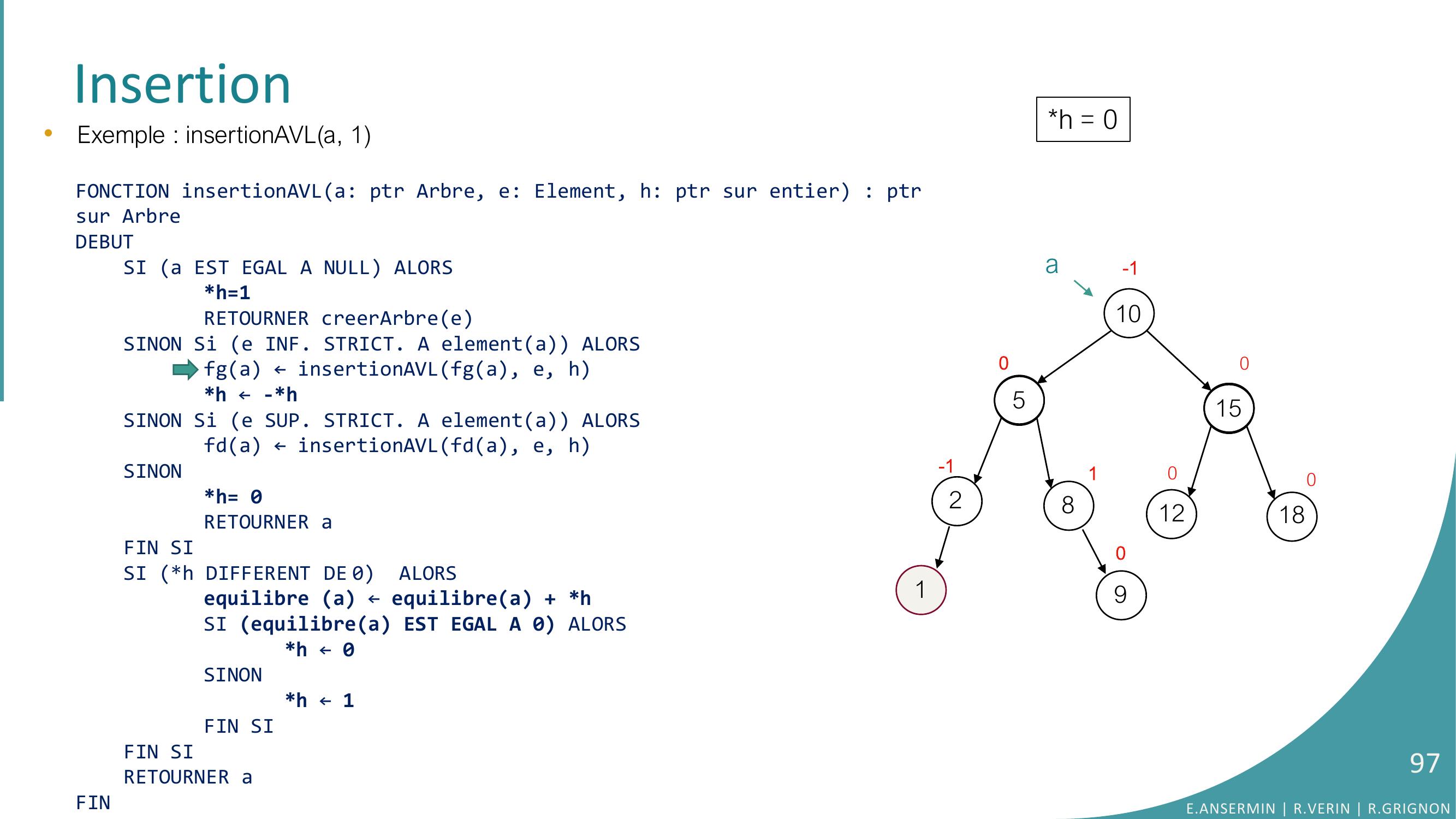
Page 96 : Insertion10528151218010-100-1a90a1•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 0E.ANSERMIN R.VERIN R.GRIGNON96

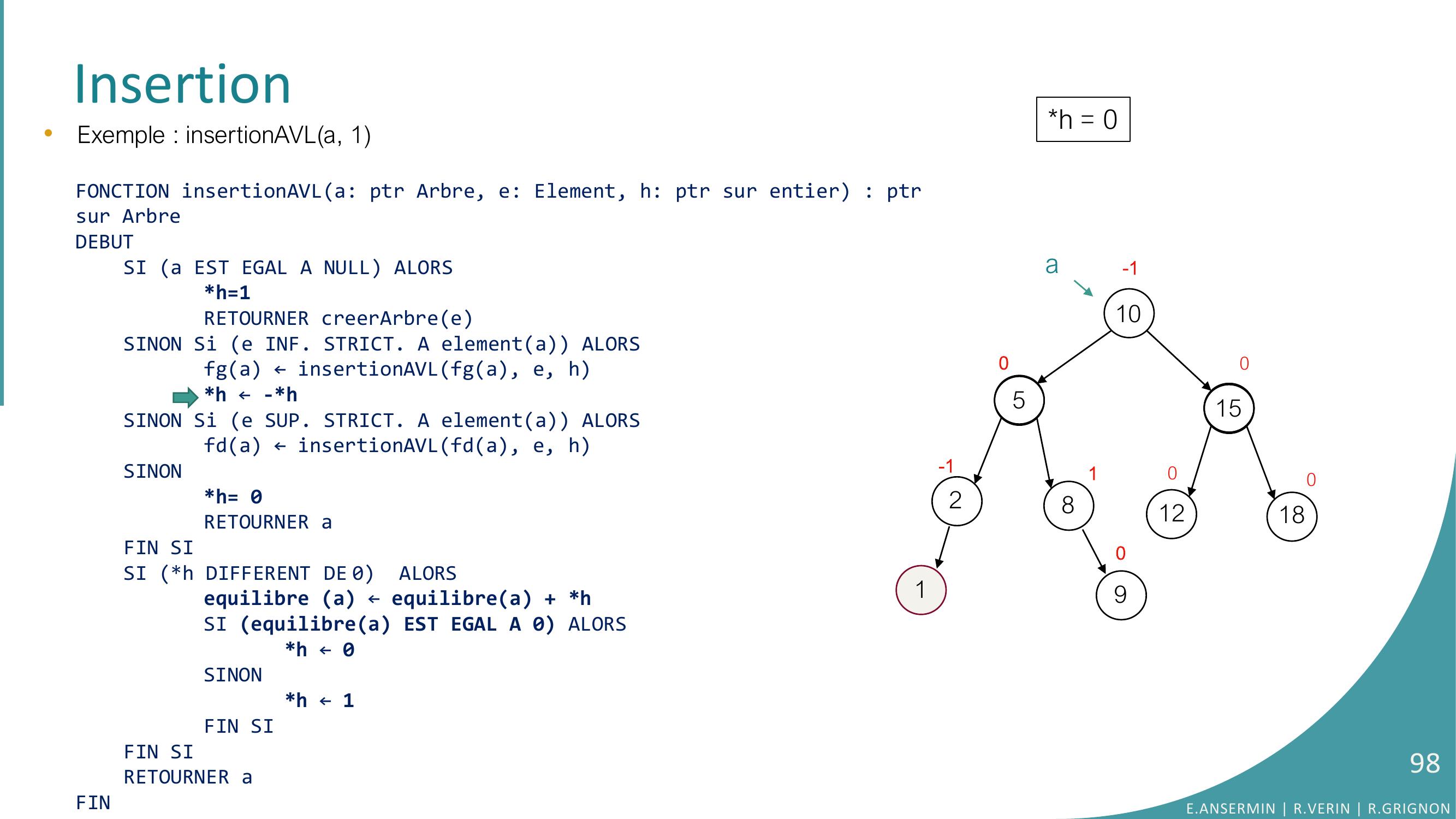
Page 97 : Insertion10528151218010-100-1a901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 0E.ANSERMIN R.VERIN R.GRIGNON97

Page 98 : Insertion10528151218010-100-1a901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 0E.ANSERMIN R.VERIN R.GRIGNON98

Page 99 : Insertion10528151218010-100-1a901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 0E.ANSERMIN R.VERIN R.GRIGNON99

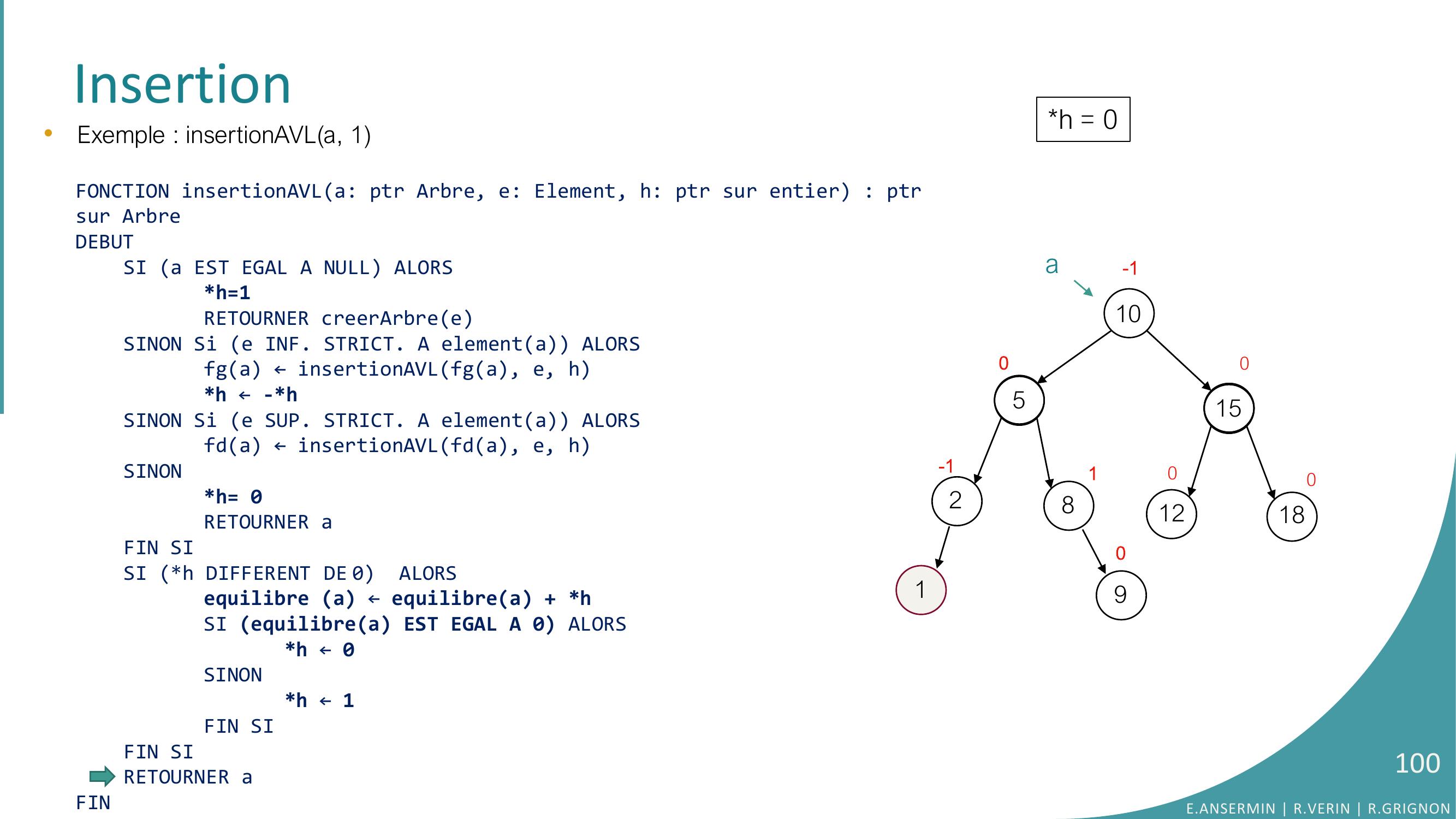
Page 100 : Insertion10528151218010-100-1a901•Exemple : insertionAVLa, 1FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptr sur entier : ptrsur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + hSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINh = 0E.ANSERMIN R.VERIN R.GRIGNON100

Page 101 : Insertion•3ème étape : le rééquilibrage.•Algorithme :FONCTION insertionAVLa: ptr Arbre, e: Element, h: ptrsur entier : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh=1RETOURNER creerArbreeSINON Si e INF. STRICT. A elementa ALORSfga ← insertionAVLfga, e, hh ← -h SINON Si e SUP. STRICT. A elementa ALORSfda ← insertionAVLfda, e, hSINONh= 0RETOURNER aFIN SISI h DIFFERENT DE 0 ALORSequilibre a ← equilibrea + ha ← equilibrageAVLaSI equilibrea EST EGAL A 0 ALORS h ← 0SINONh ← 1FIN SIFIN SI RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON101

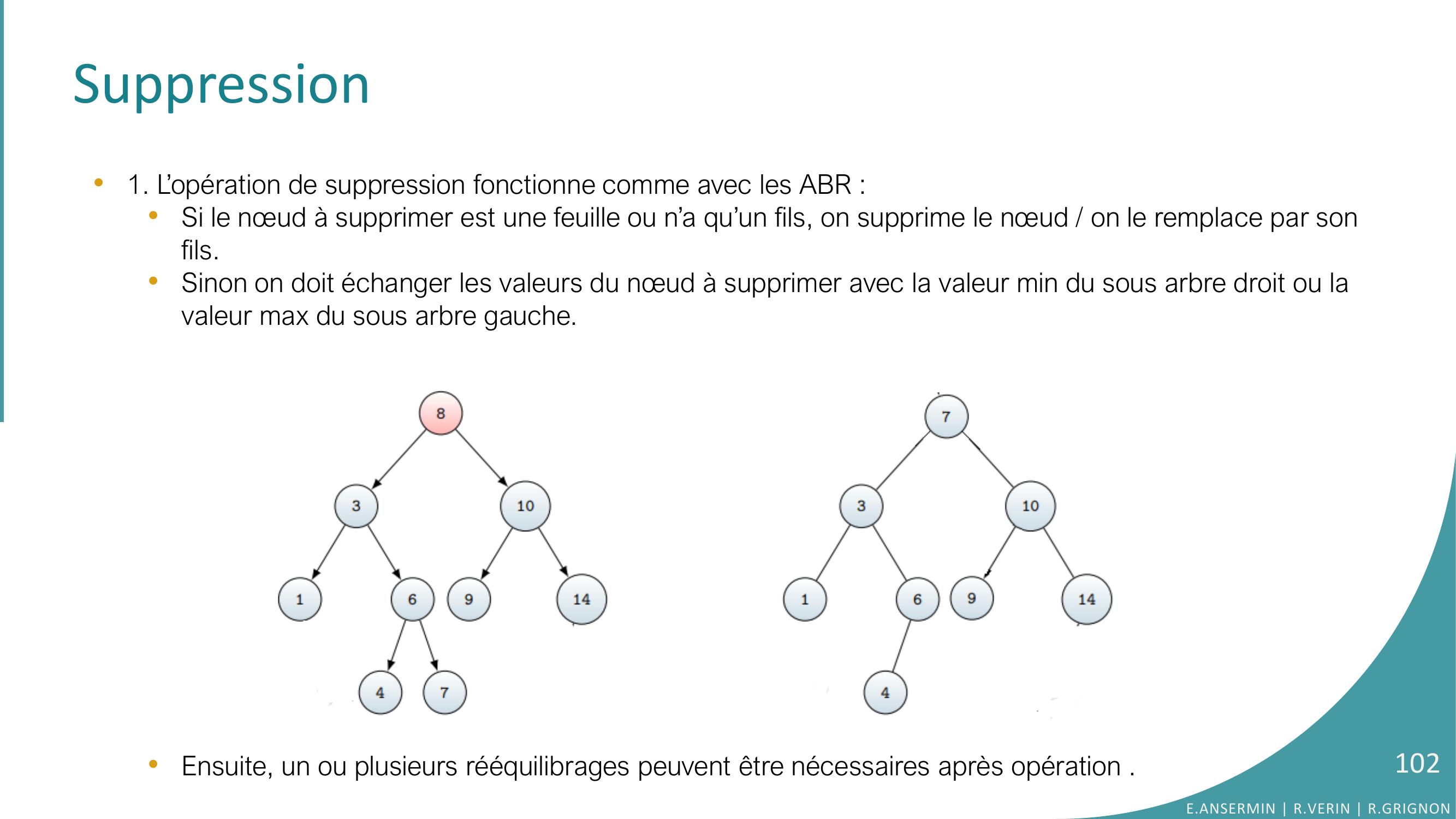
Page 102 : Suppression•Ensuite, un ou plusieurs rééquilibrages peuvent être nécessaires après opération .•1. L’opération de suppression fonctionne comme avec les ABR :•Si le nœud à supprimer est une feuille ou n’a qu’un fils, on supprime le nœud / on le remplace par son fils.•Sinon on doit échanger les valeurs du nœud à supprimer avec la valeur min du sous arbre droit ou la valeur max du sous arbre gauche.E.ANSERMIN R.VERIN R.GRIGNON102

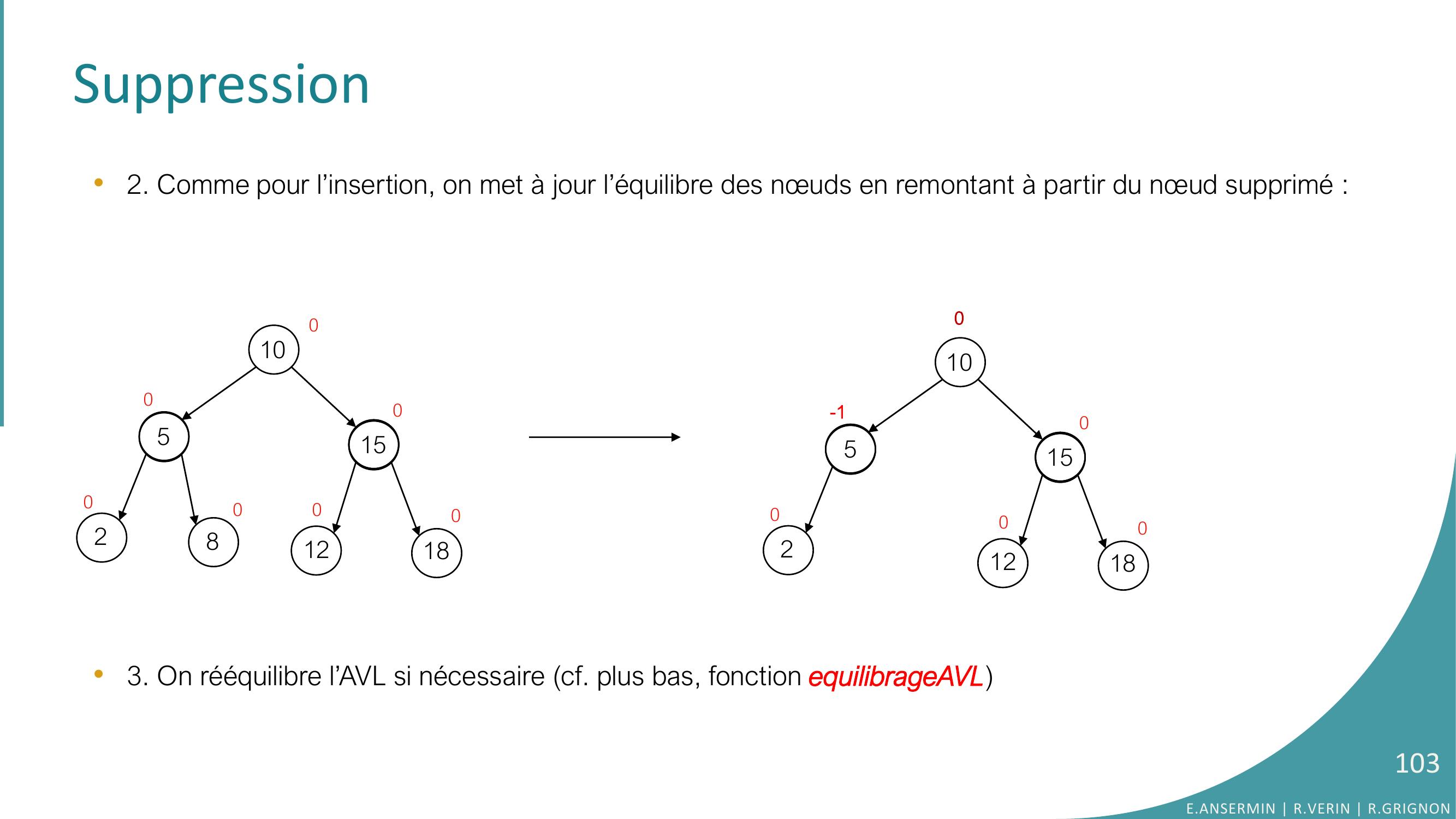
Page 103 : Suppression•2. Comme pour l’insertion, on met à jour l’équilibre des nœuds en remontant à partir du nœud supprimé :•3. On rééquilibre l’AVL si nécessaire cf. plus bas, fonction equilibrageAVL 1052815121800000001052151218000-100E.ANSERMIN R.VERIN R.GRIGNON103

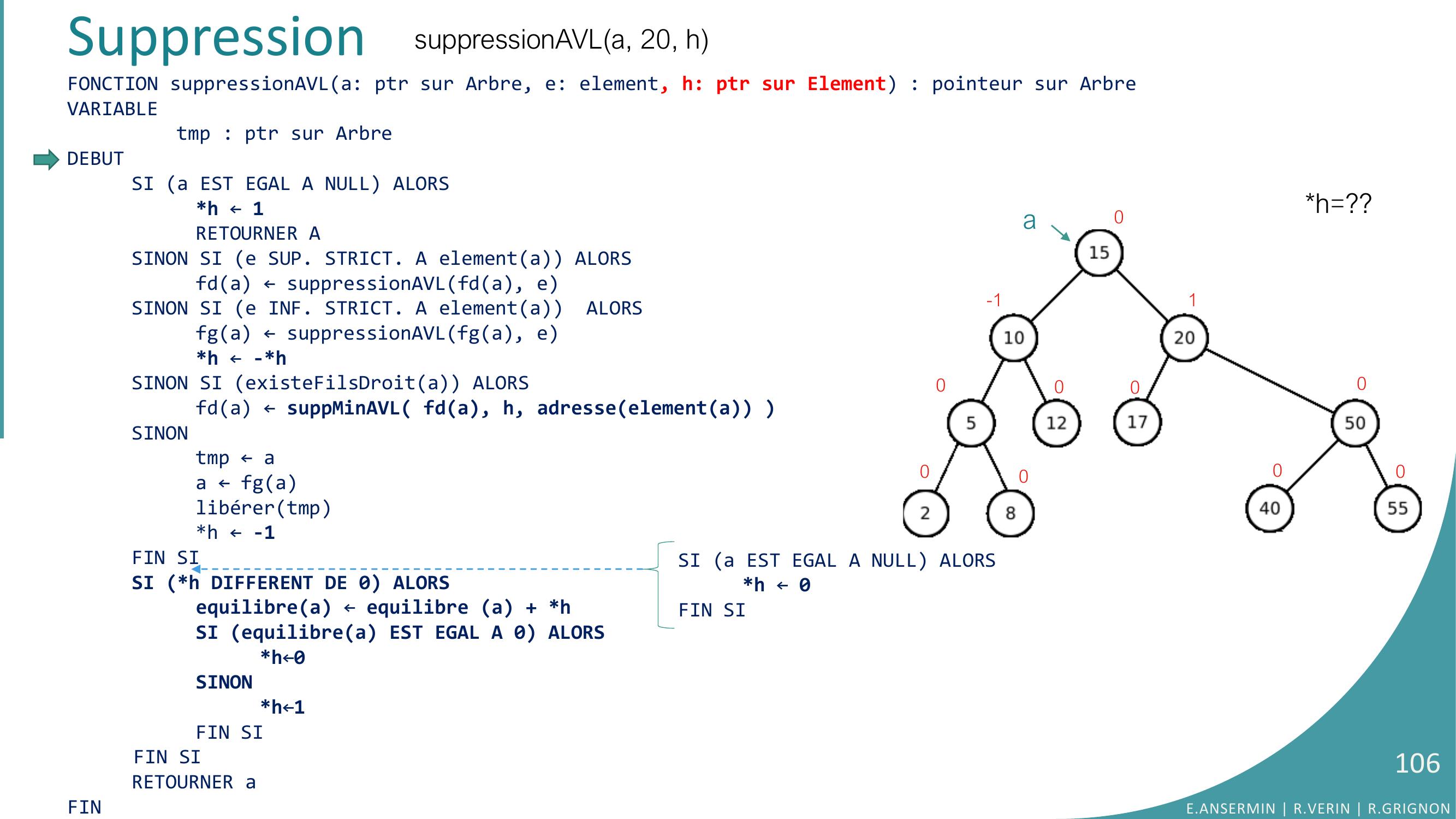
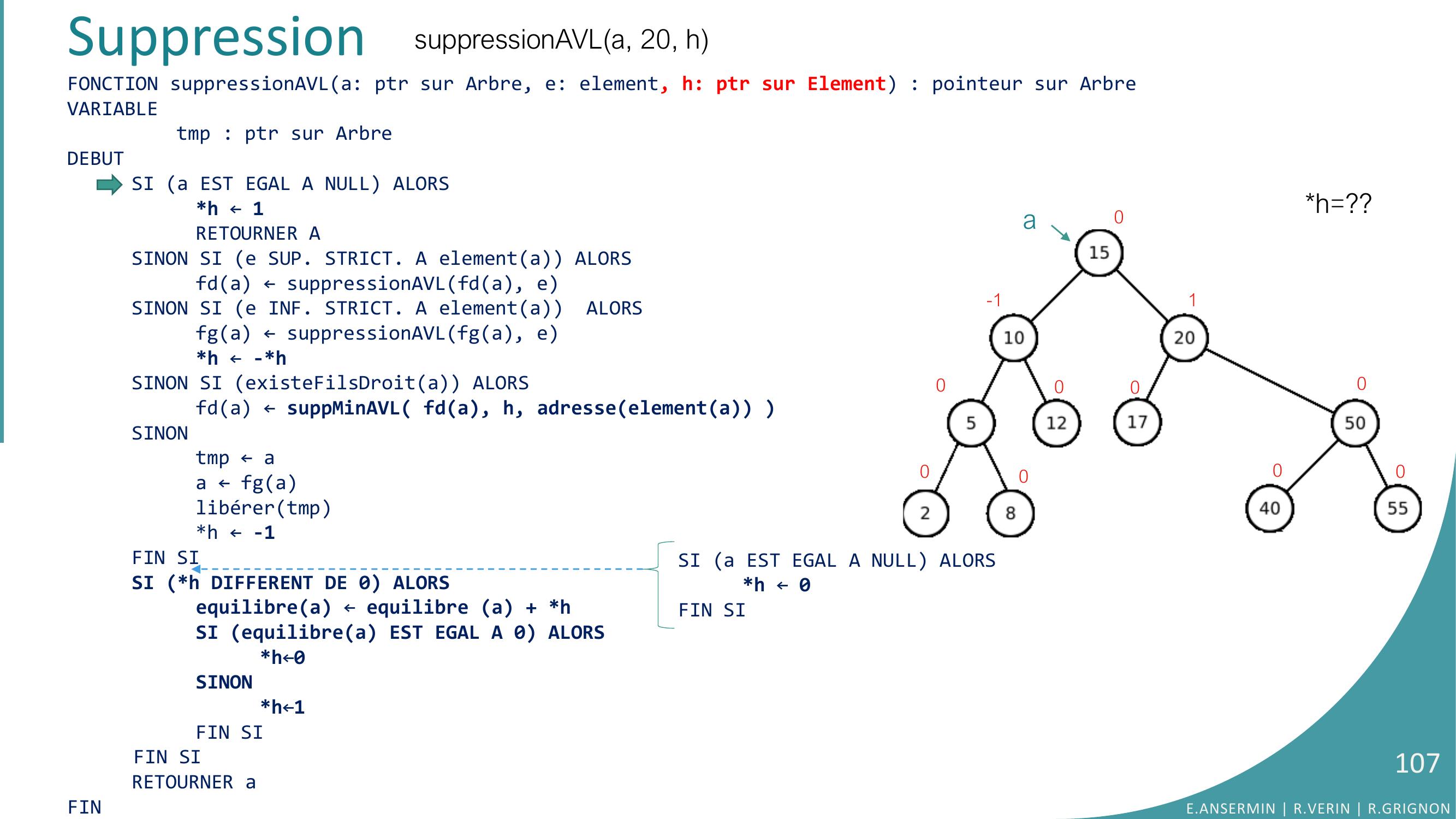
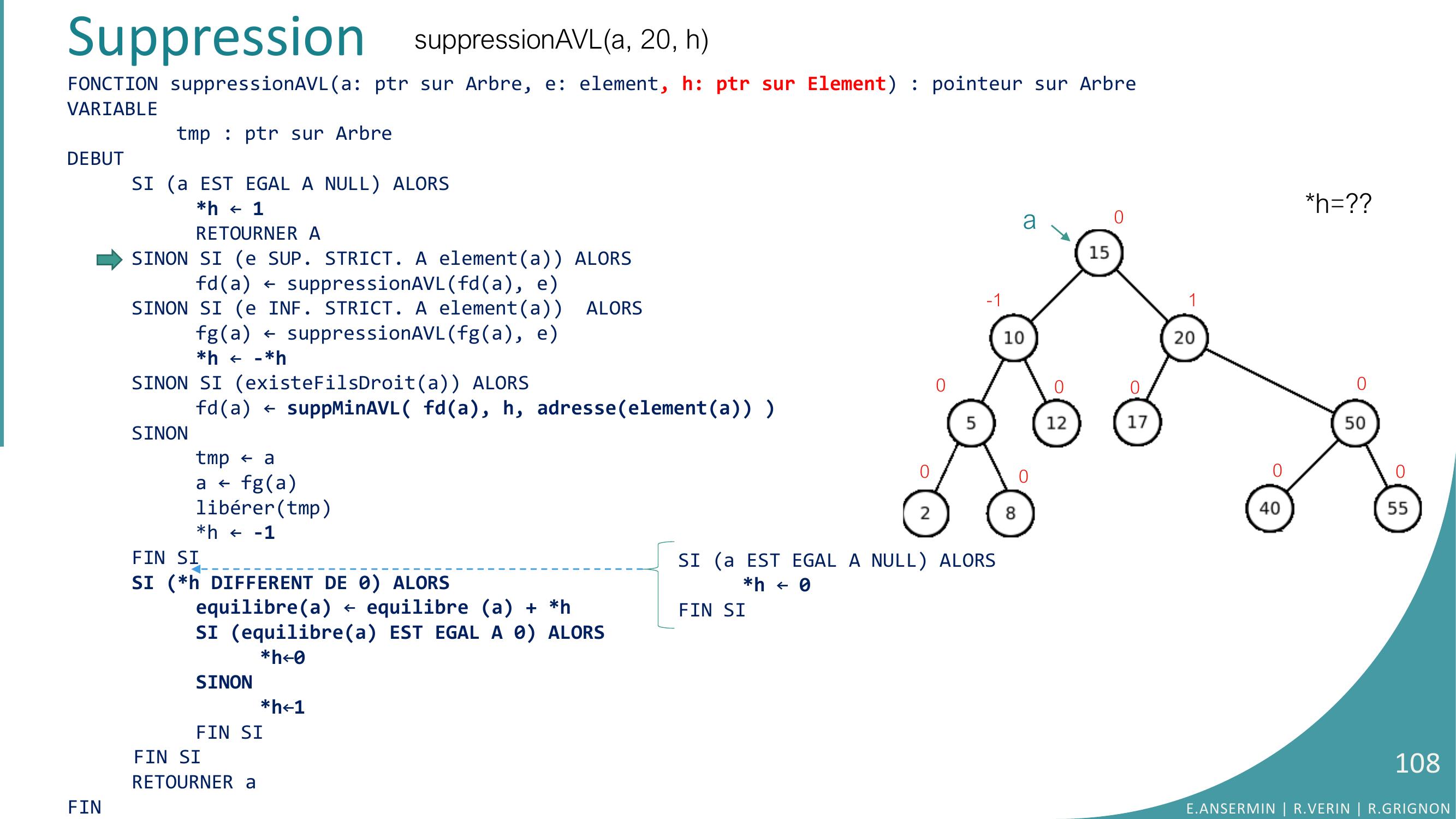
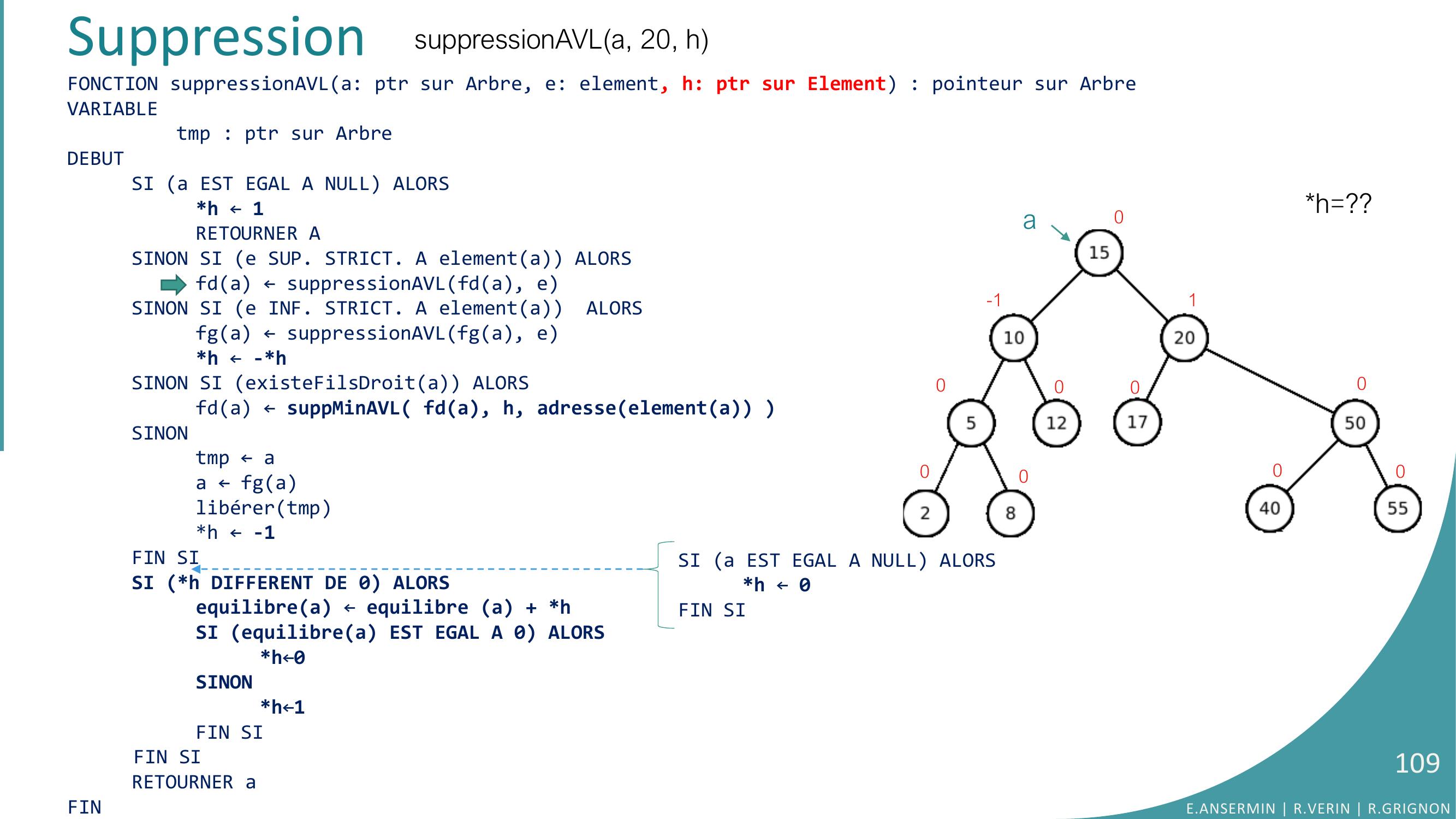
Page 104 : SuppressionFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORS// parcours pour trouver le noeudfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS // si il y a un fils droit…fga ← suppMinAVL fda, h, adresseelementa // … on cherche le minimum dedans SINONtmp ← a// le noeud n’a qu’un fils gauche ou aucun filsa ← fga // échange avec le fils gauche et suppressionlibérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFIN•Algorithme:E.ANSERMIN R.VERIN R.GRIGNON104SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 105 : Suppression•Algorithme:FONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORS// Si il n’y a plus de fils gauche… pe ← elementa// … alors on a trouvé la plus petite valeur de l’arbreh ← -1tmp ← aa ← fda// on remplace le noeud actuel par le fils droit…liberertmp// … et on libère la mémoire du noeudRETOURNERaSINONfga ← suppMinAVLfga, h, pe// appel récursif sur le sous-arbre de gaucheh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + h// mise à jour du facteur d’équilibrageSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON105

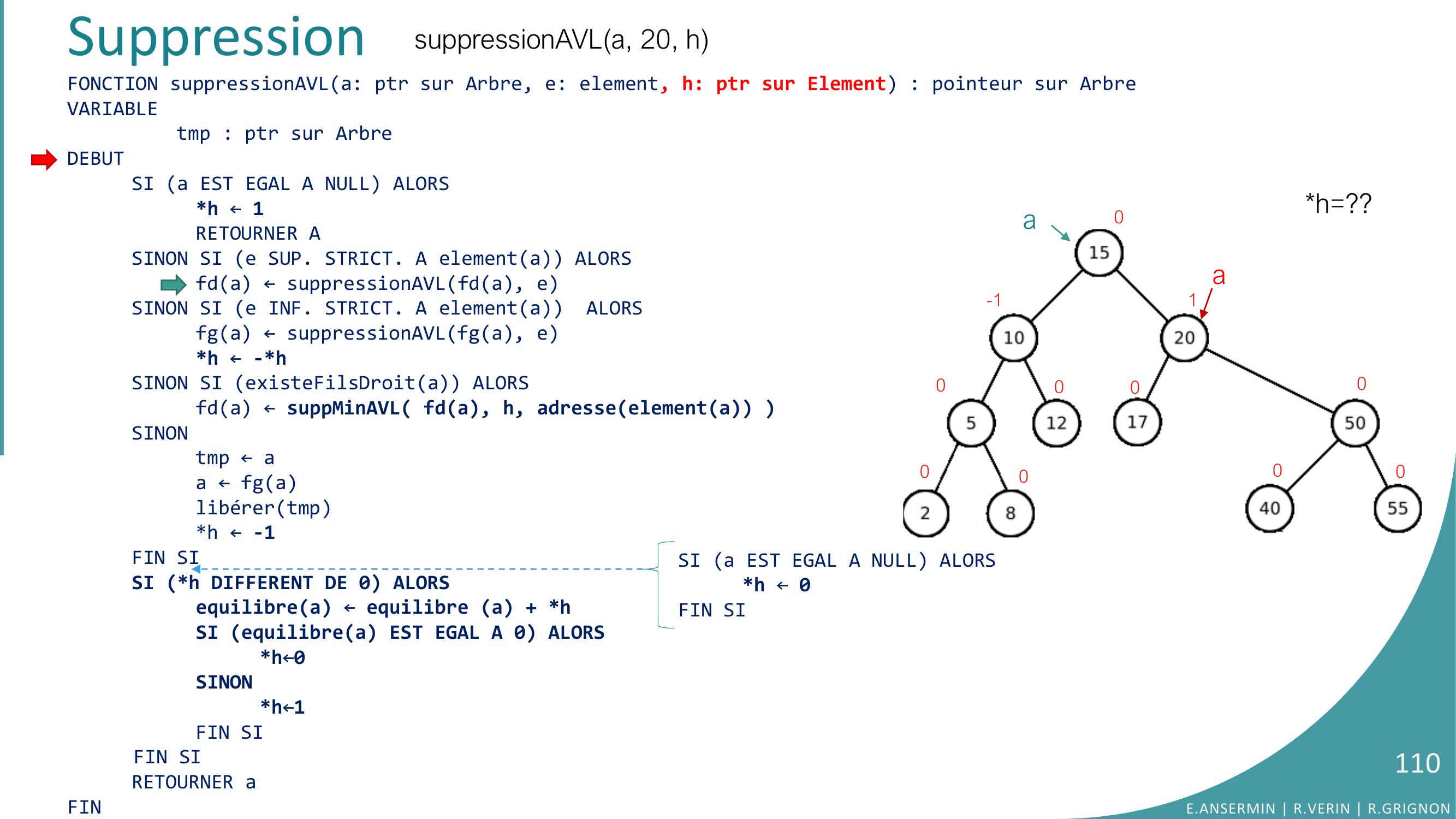
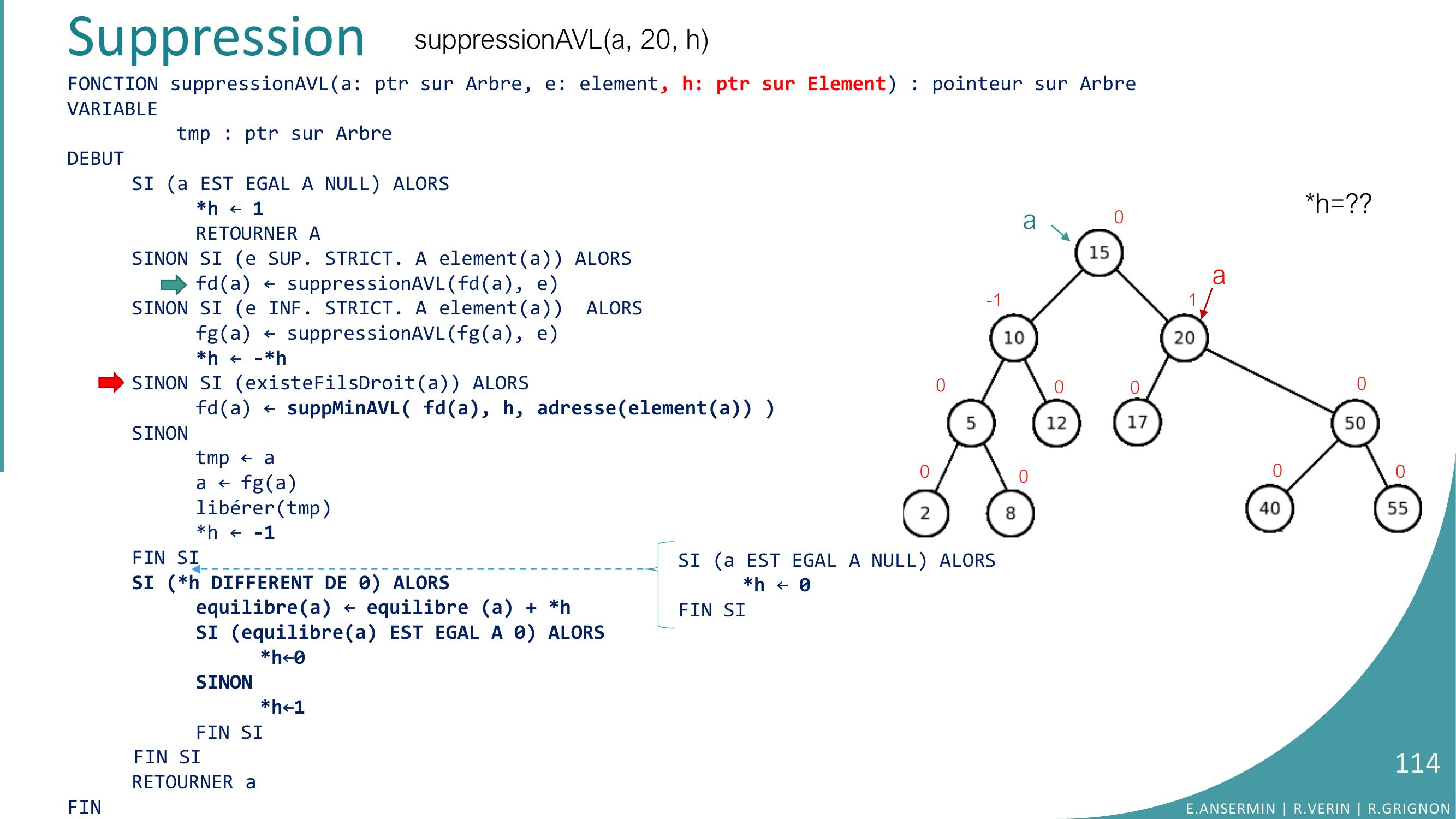
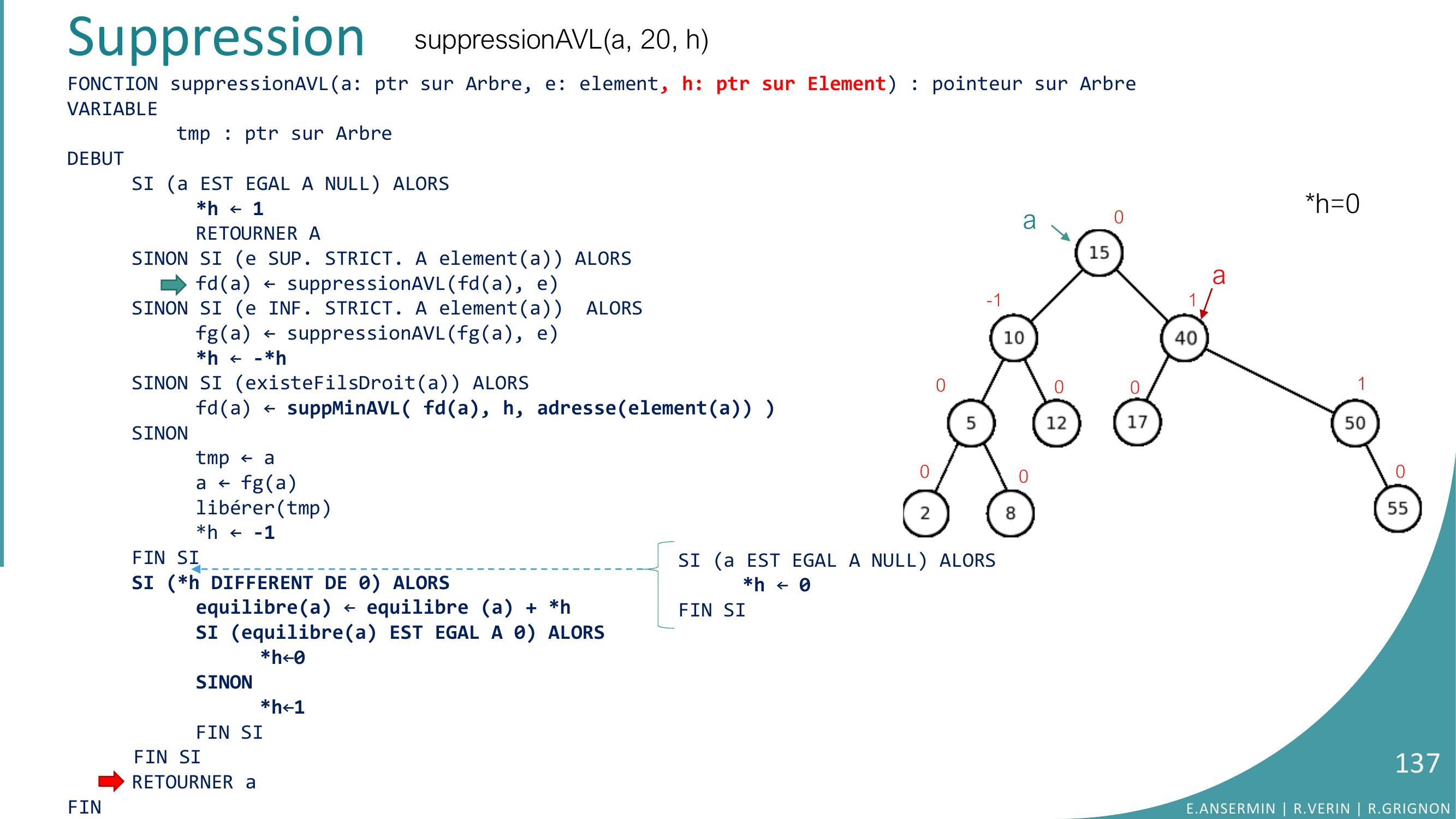
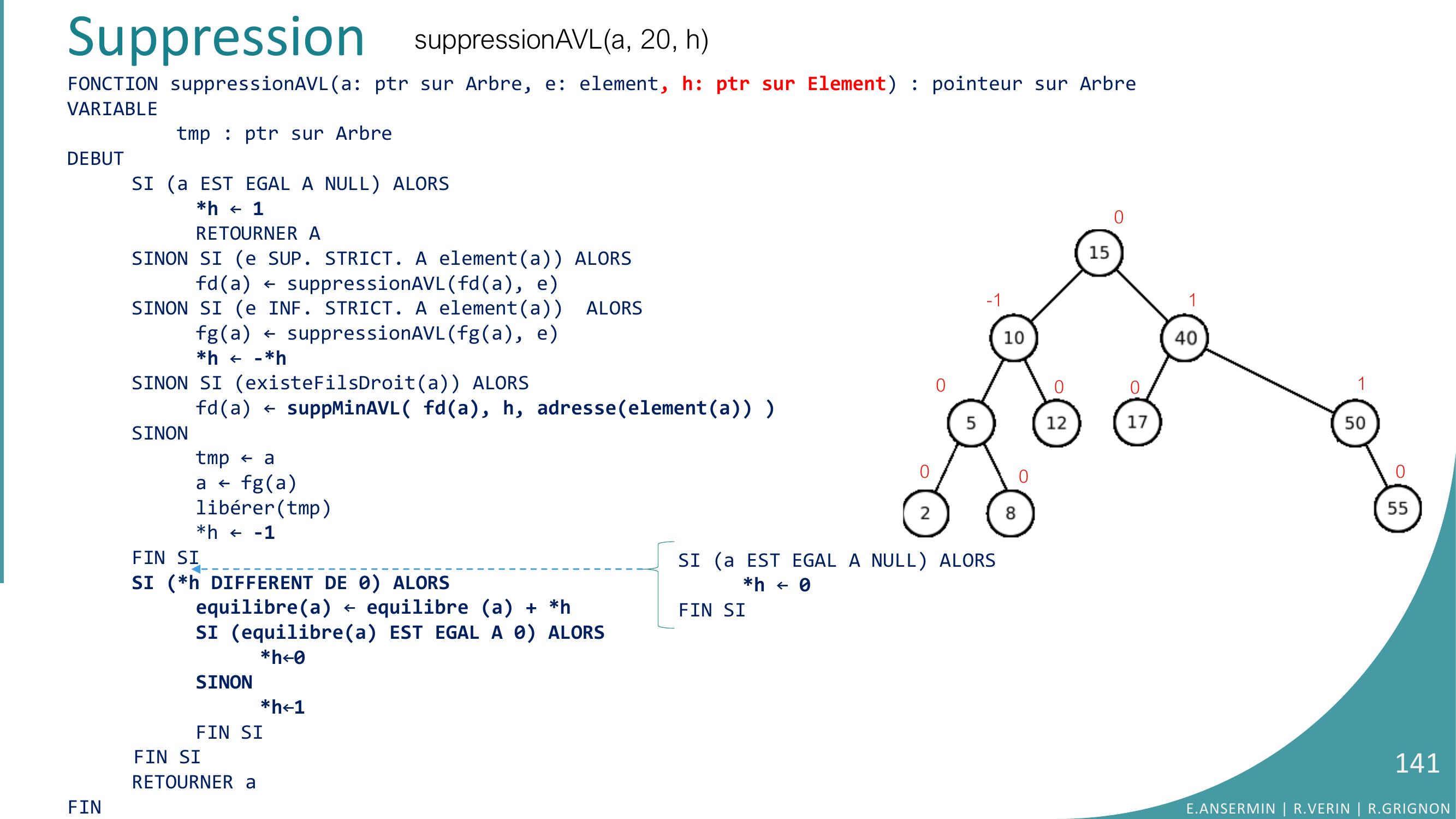
Page 106 : FONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINSuppressionsuppressionAVLa, 20, hh=??a0-1000000001E.ANSERMIN R.VERIN R.GRIGNON106SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 107 : FONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINSuppressionh=??a0-1000000001suppressionAVLa, 20, hE.ANSERMIN R.VERIN R.GRIGNON107SI a EST EGAL A NULL ALORSh ← 0FIN SI

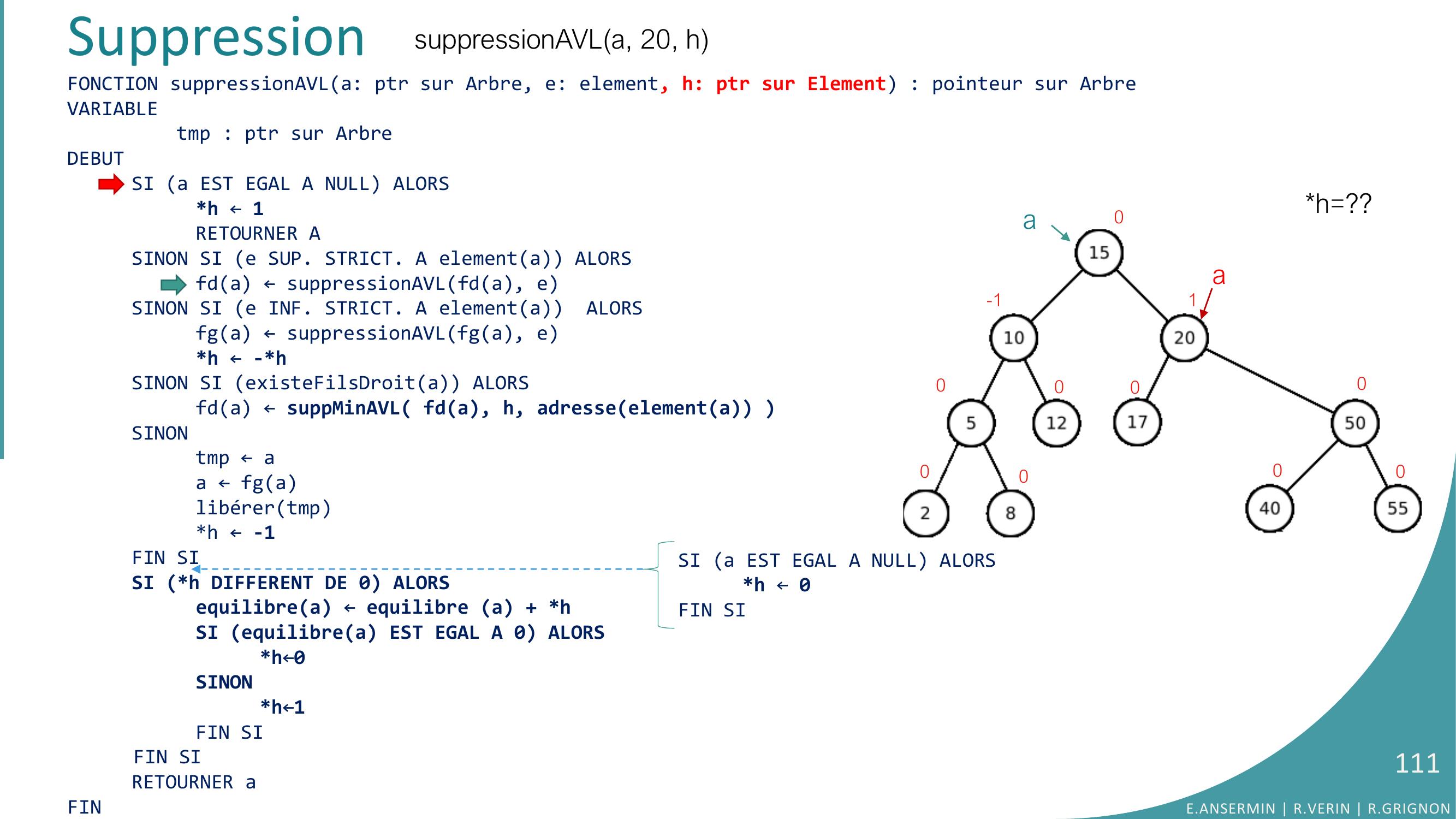
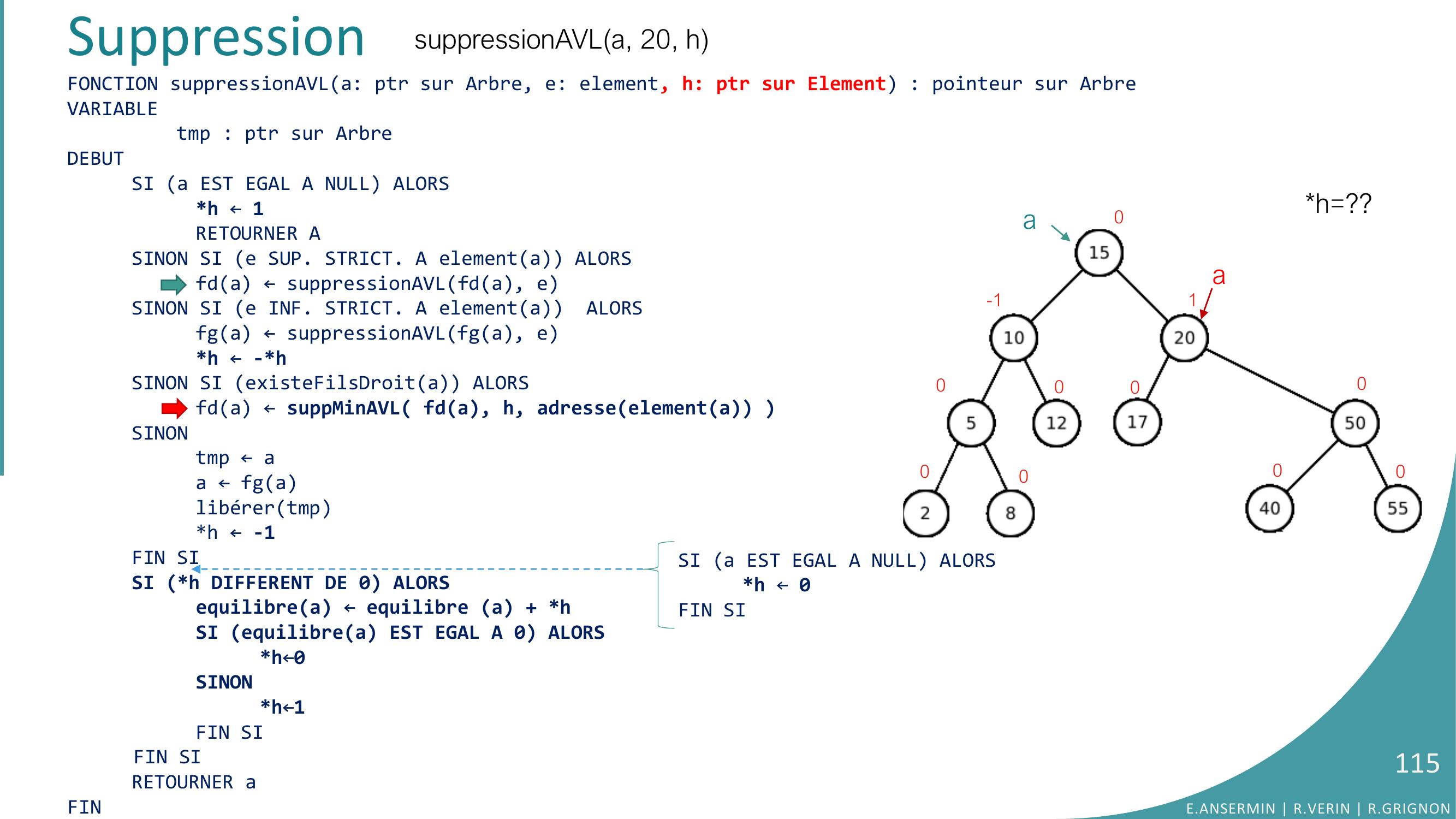
Page 108 : FONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINSuppressionh=??a0-1000000001suppressionAVLa, 20, hE.ANSERMIN R.VERIN R.GRIGNON108SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 109 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON109SI a EST EGAL A NULL ALORSh ← 0FIN SI

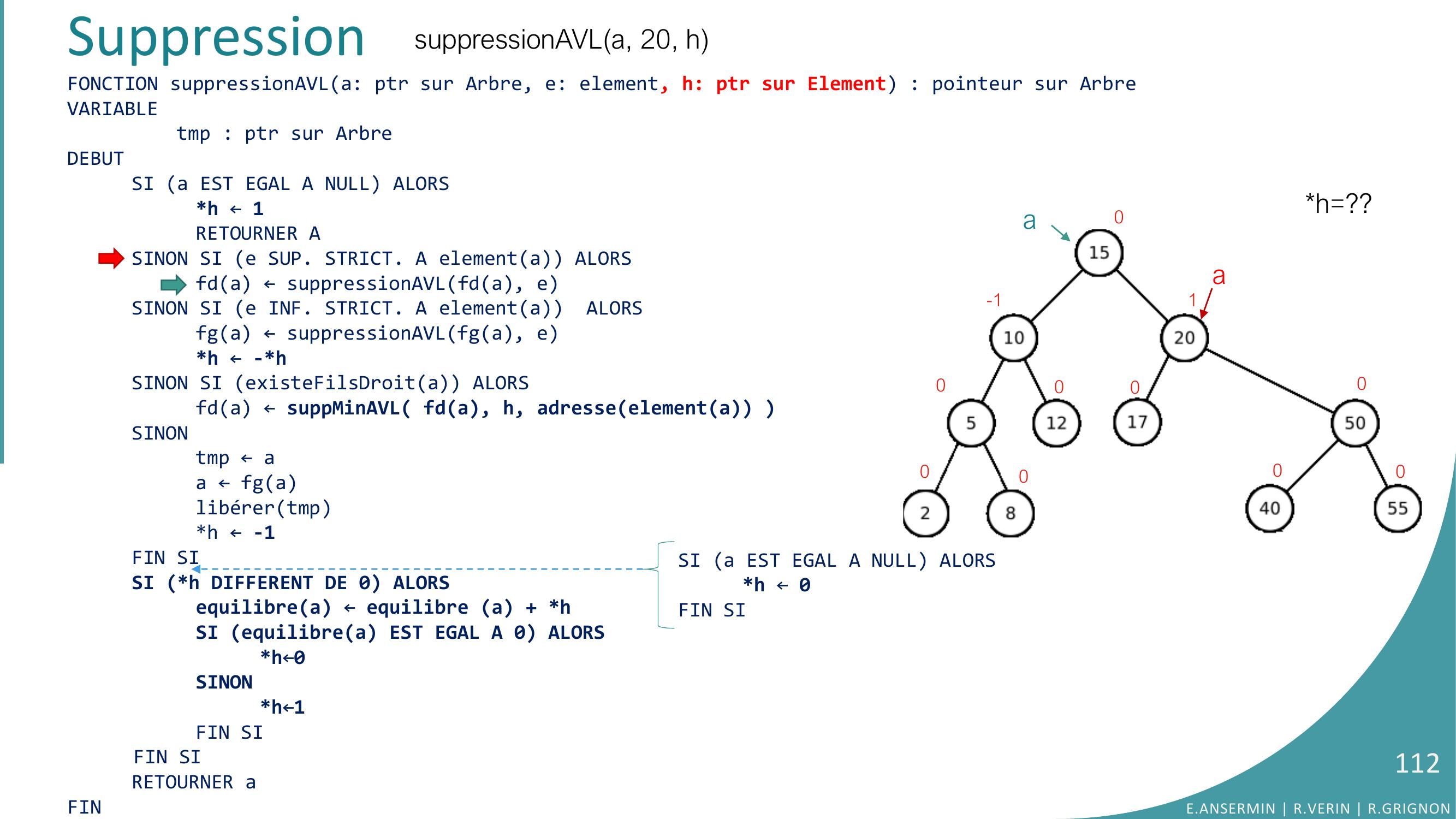
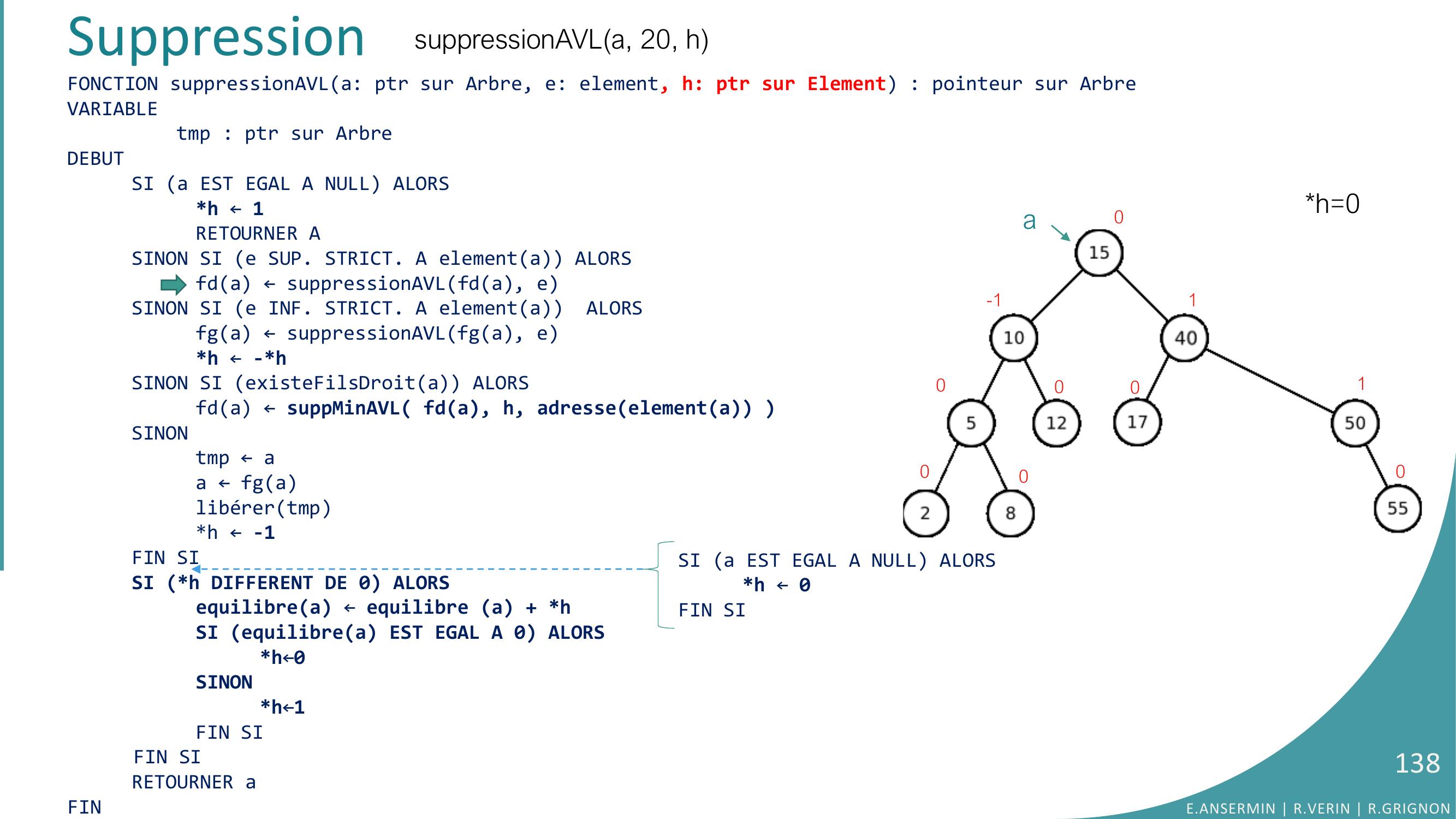
Page 110 : Suppressionh=??a0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON110SI a EST EGAL A NULL ALORSh ← 0FIN SI

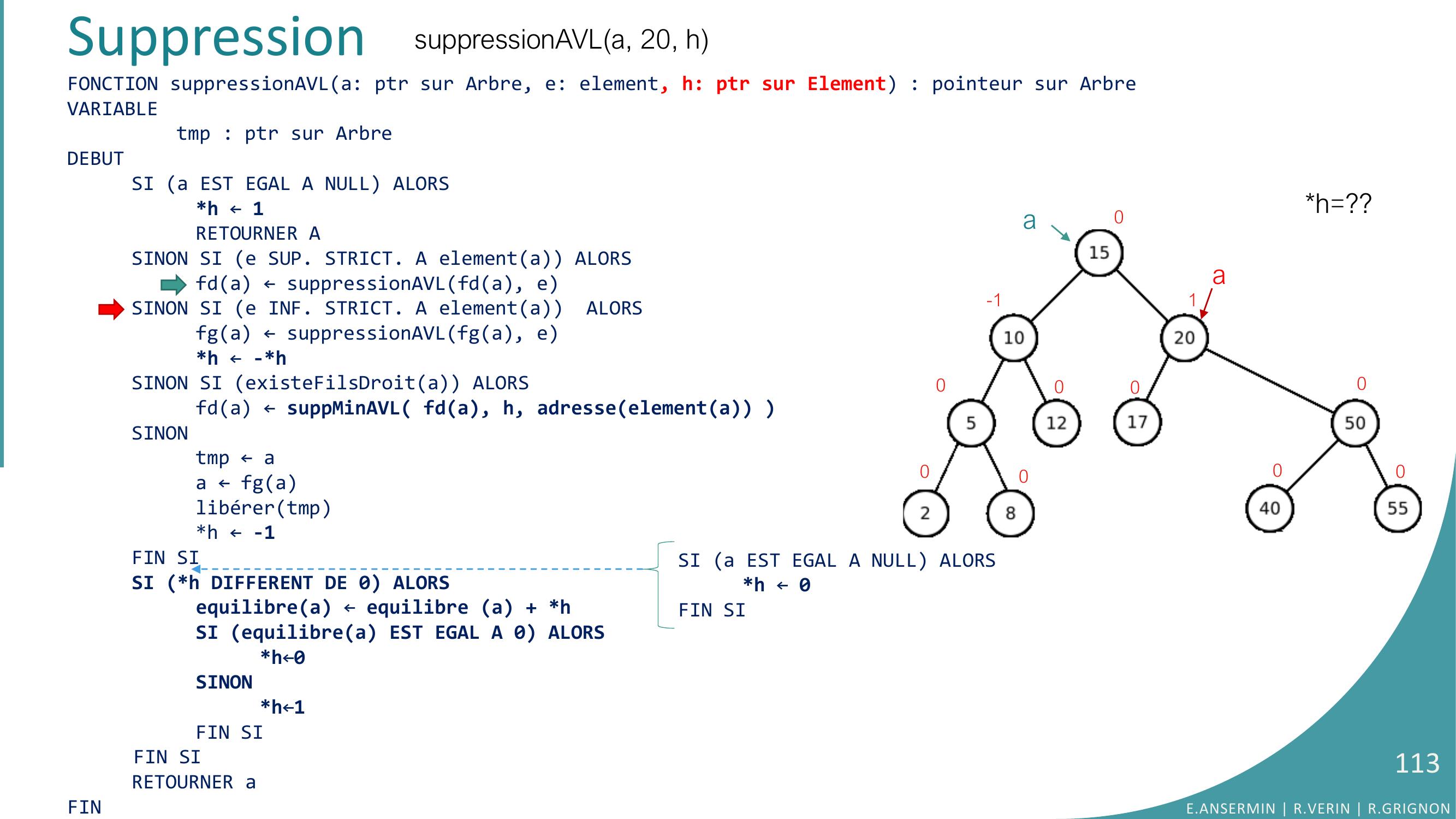
Page 111 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON111SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 112 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON112SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 113 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON113SI a EST EGAL A NULL ALORSh ← 0FIN SI

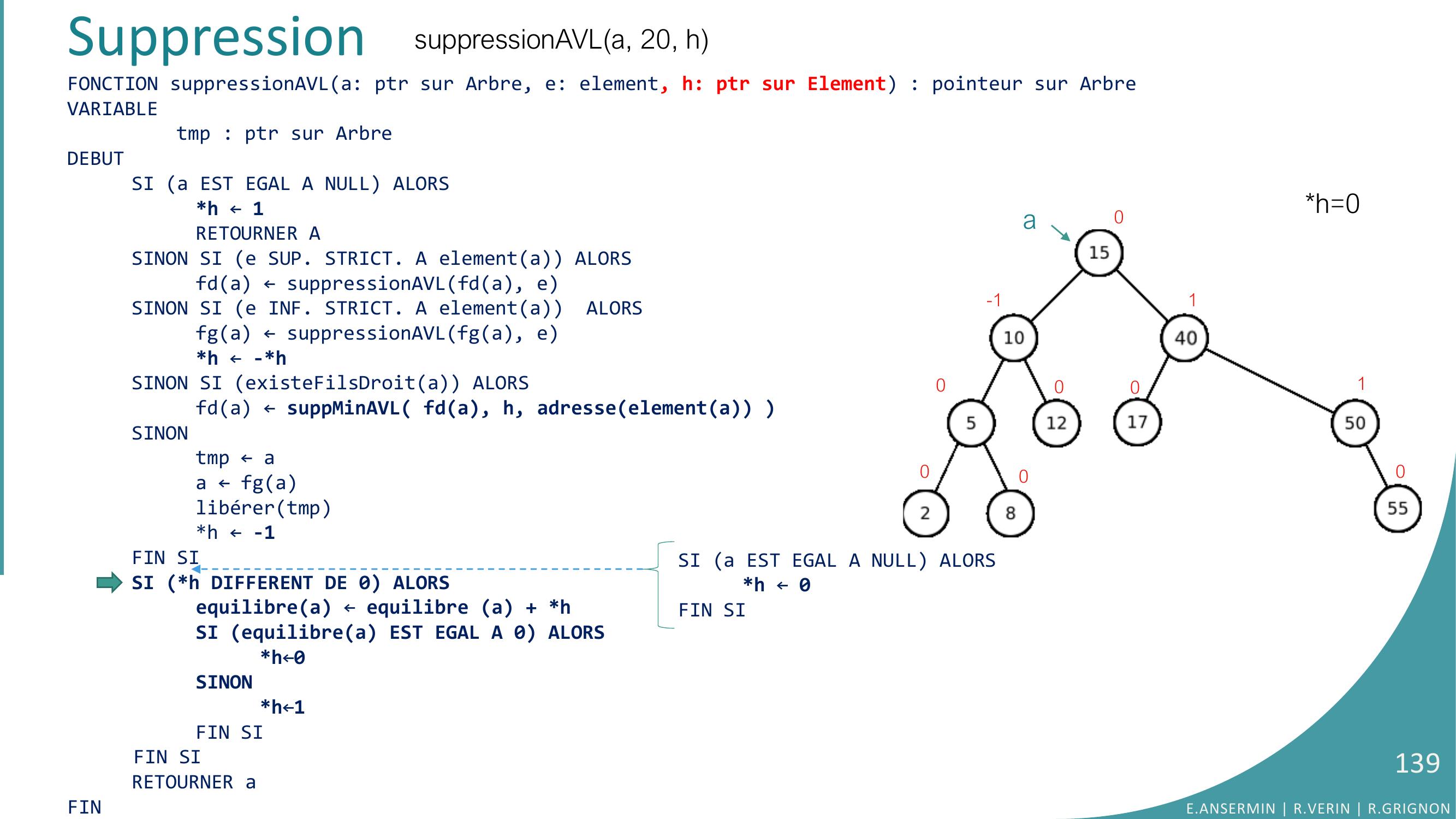
Page 114 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON114SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 115 : Suppressionh=??0-1000000001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON115SI a EST EGAL A NULL ALORSh ← 0FIN SI

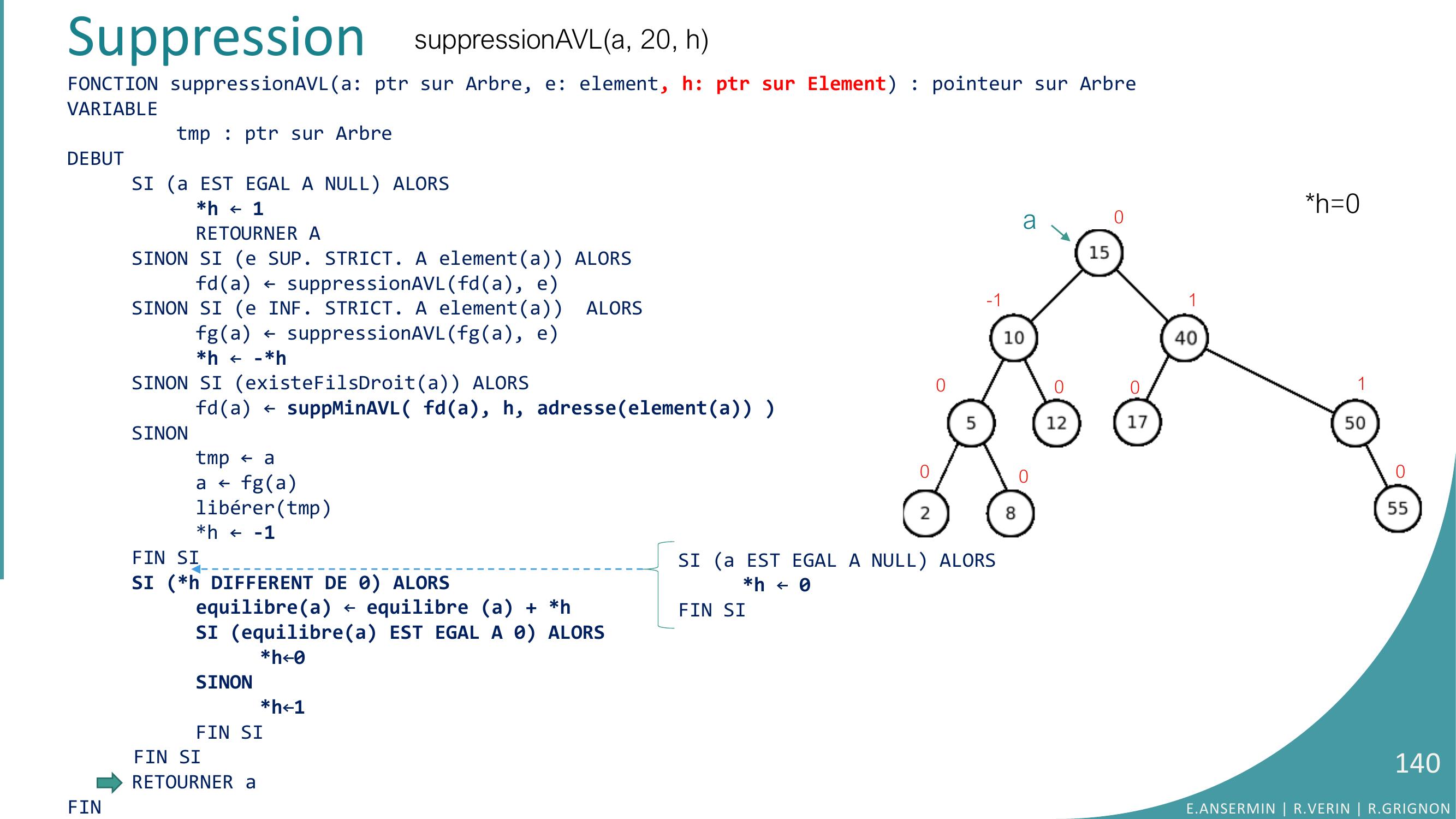
Page 116 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=??pe= 20a0-1000000001E.ANSERMIN R.VERIN R.GRIGNON116

Page 117 : Suppressionh=??pe= 20a0-1000000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON117

Page 118 : Suppressionh=??pe= 20a0-1000000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON118

Page 119 : Suppressionh=??pe= 20a0-1000000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON119

Page 120 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=??pe= 20aa0-1000000001E.ANSERMIN R.VERIN R.GRIGNON120

Page 121 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=??pe= 20aa0-1000000001E.ANSERMIN R.VERIN R.GRIGNON121

Page 122 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=??pe= 20aa0-1000000001E.ANSERMIN R.VERIN R.GRIGNON122

Page 123 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=??pe= 40aa0-1000000001E.ANSERMIN R.VERIN R.GRIGNON123

Page 124 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=-1pe= 40aa0-1000000001E.ANSERMIN R.VERIN R.GRIGNON124

Page 125 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=-1pe= 40aatmp0-1000000001E.ANSERMIN R.VERIN R.GRIGNON125

Page 126 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=-1pe= 40aatmpNULL0-1000000001E.ANSERMIN R.VERIN R.GRIGNON126

Page 127 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=-1pe= 40aaNULL0-100000001tmpE.ANSERMIN R.VERIN R.GRIGNON127

Page 128 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=-1pe= 40a0-100000001E.ANSERMIN R.VERIN R.GRIGNON128

Page 129 : Suppressionh=-1pe= 40a0-100000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON129

Page 130 : Suppressionh=1pe= 40a0-100000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON130

Page 131 : Suppressionh=1pe= 40a0-100000001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON131

Page 132 : Suppressionh=1pe= 40a0-100001001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON132

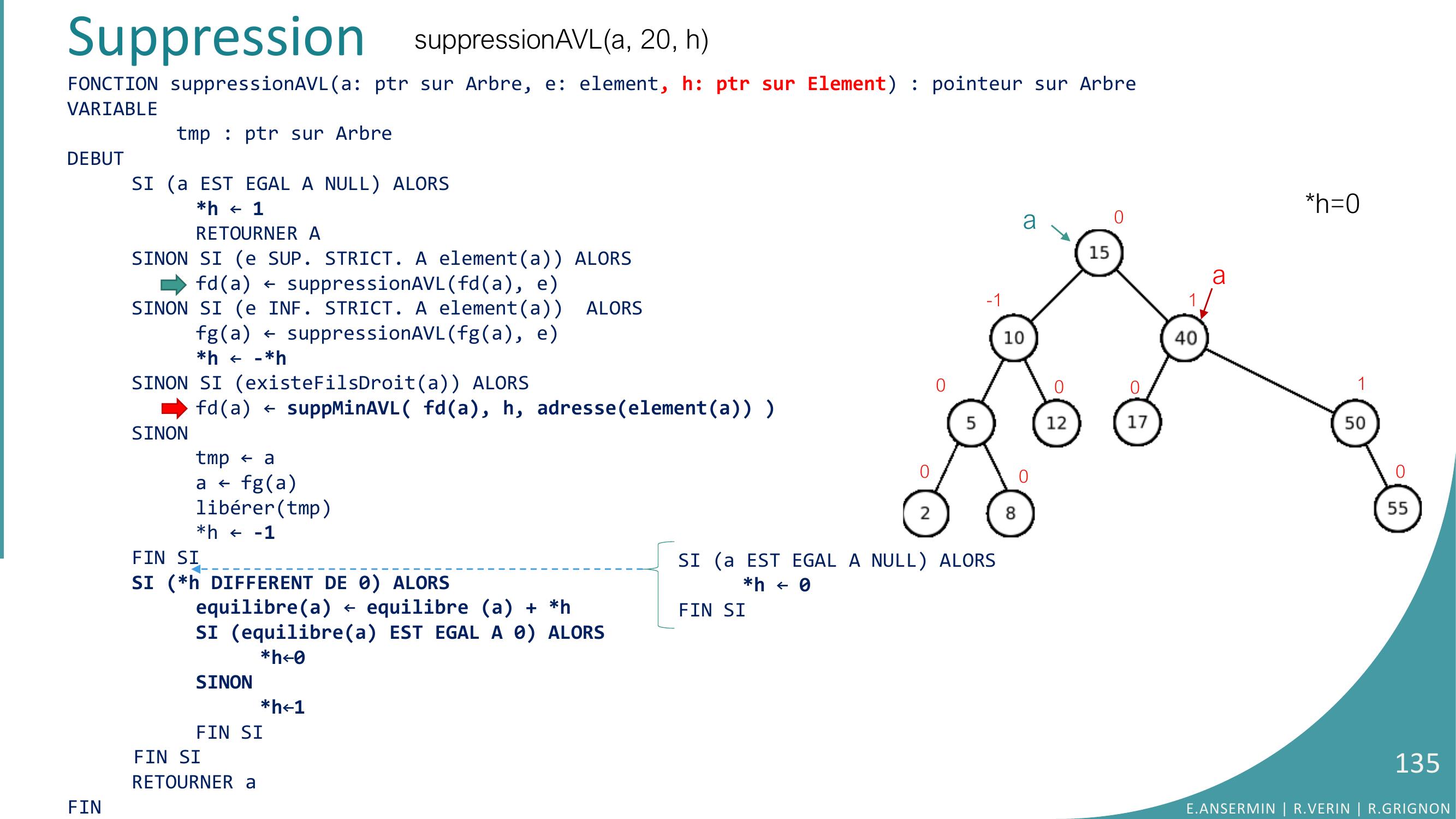
Page 133 : suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINSuppressionh=1pe= 40a0-100001001E.ANSERMIN R.VERIN R.GRIGNON133

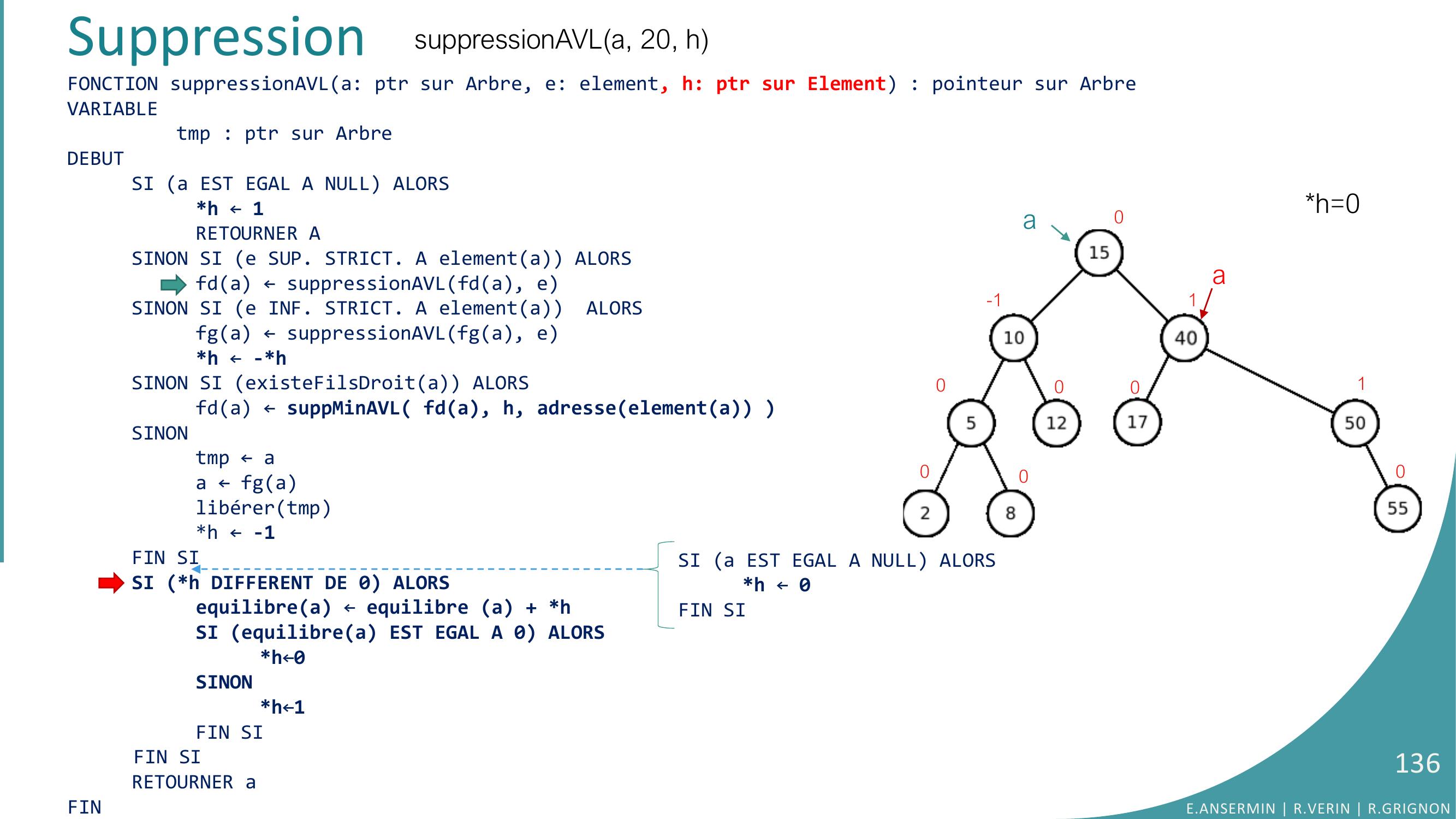
Page 134 : Suppressionh=0pe= 40a0-100001001suppressionAVLA, 20, hFONCTION suppMinAVLa: Arbre; h: pointeur sur entier, pe: ptr sur Element : ptr sur ArbreVARIABLE tmp : ptr sur ArbreDEBUTSI fga EST EGAL A NULL ALORSpe ← elementah ← -1tmp ← aa ← fdaliberertmpRETOURNERaSINONfga ← suppMinAVLfga, h, peh ← -hFIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibrea + hSI equilibrea EST EGAL A 0 ALORSh ← -1SINONh ← 0FIN SIFIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON134

Page 135 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON135SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 136 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON136SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 137 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaaE.ANSERMIN R.VERIN R.GRIGNON137SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 138 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON138SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 139 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON139SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 140 : Suppressionh=00-100001001suppressionAVLa, 20, hFONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINaE.ANSERMIN R.VERIN R.GRIGNON140SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 141 : FONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINSuppression0-100001001suppressionAVLa, 20, hE.ANSERMIN R.VERIN R.GRIGNON141SI a EST EGAL A NULL ALORSh ← 0FIN SI

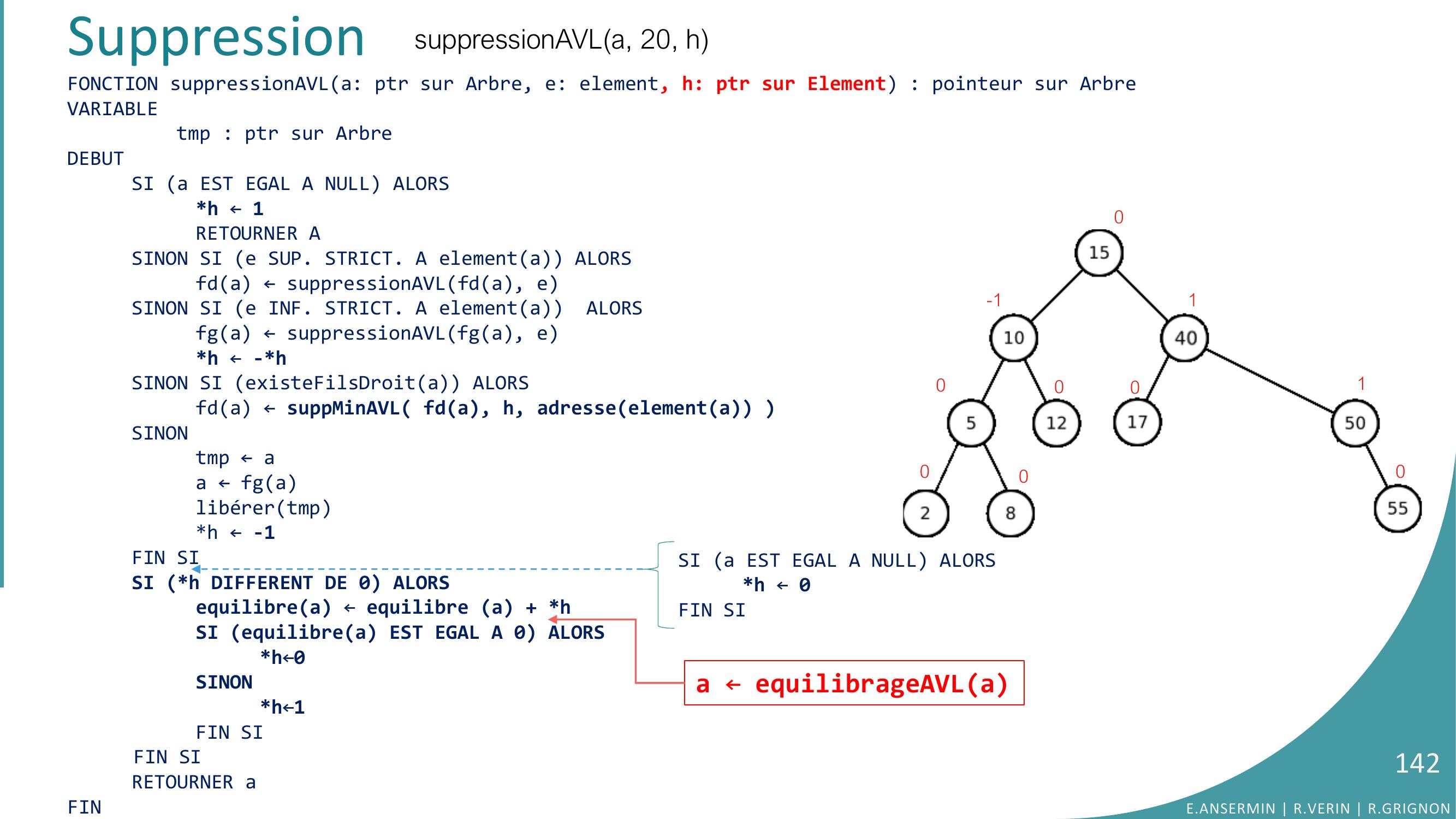
Page 142 : FONCTION suppressionAVLa: ptr sur Arbre, e: element, h: ptr sur Element : pointeur sur ArbreVARIABLEtmp : ptr sur ArbreDEBUTSI a EST EGAL A NULL ALORSh ← 1RETOURNER ASINON SI e SUP. STRICT. A elementa ALORSfda ← suppressionAVLfda, eSINON SI e INF. STRICT. A elementa ALORSfga ← suppressionAVLfga, eh ← -hSINON SI existeFilsDroita ALORS fda ← suppMinAVL fda, h, adresseelementa SINONtmp ← aa ← fga libérertmph ← -1FIN SISI h DIFFERENT DE 0 ALORSequilibrea ← equilibre a + hSI equilibrea EST EGAL A 0 ALORSh←0SINONh←1FIN SIFIN SIRETOURNER aFINSuppression0-100001001suppressionAVLa, 20, ha ← equilibrageAVLaE.ANSERMIN R.VERIN R.GRIGNON142SI a EST EGAL A NULL ALORSh ← 0FIN SI

Page 143 : IV. Equilibrage d’un AVLE.ANSERMIN R.VERIN R.GRIGNON143

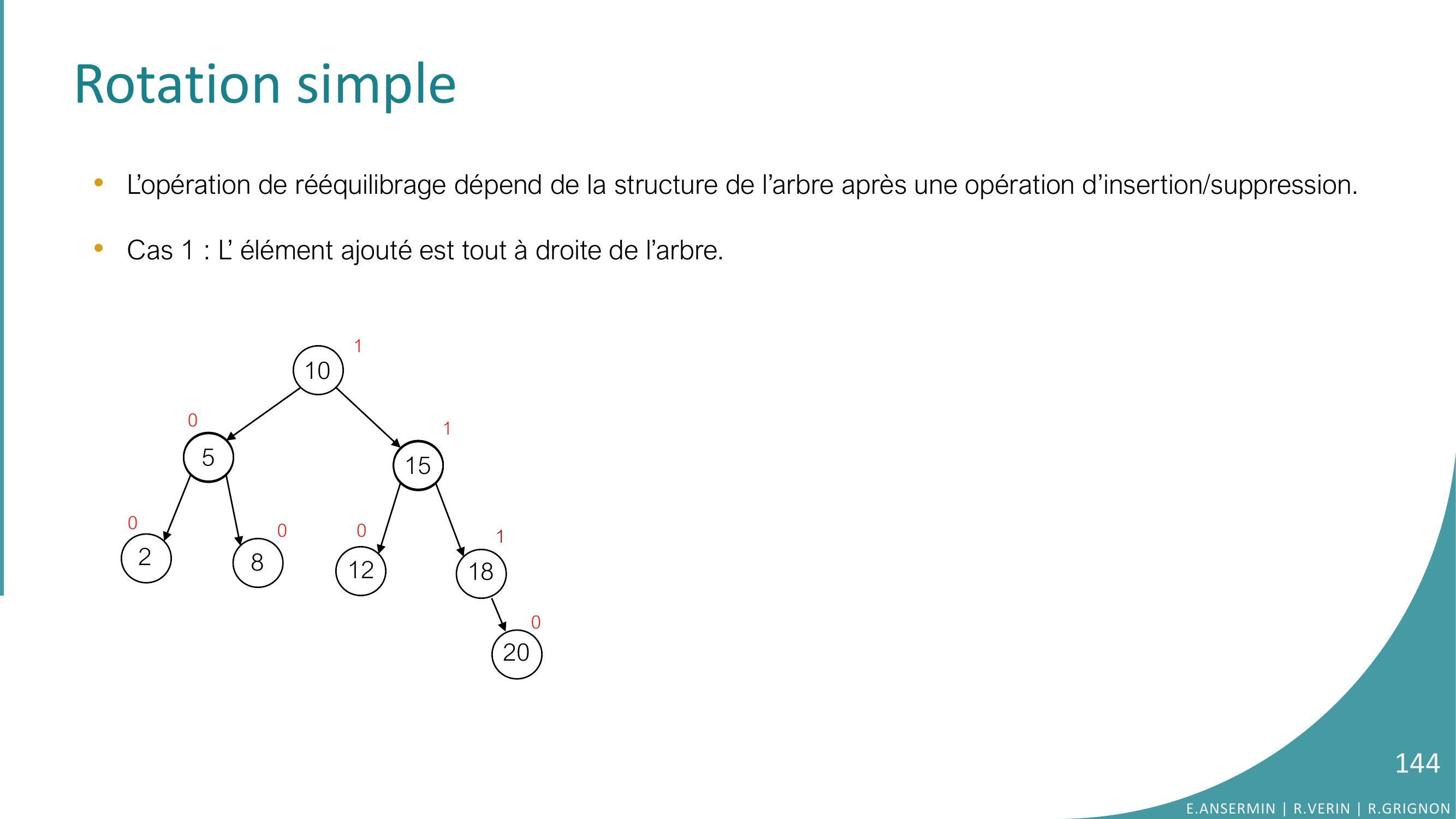
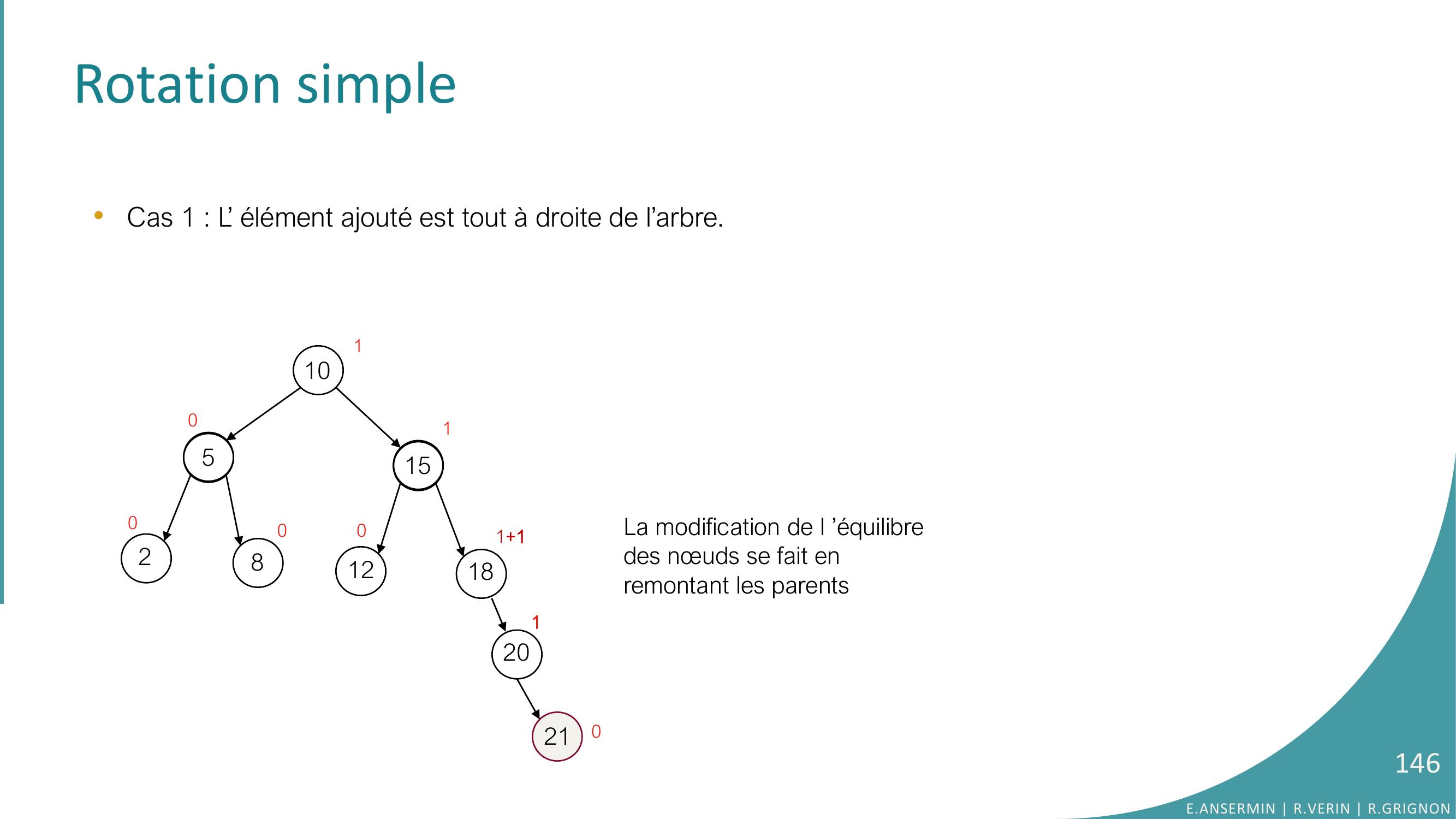
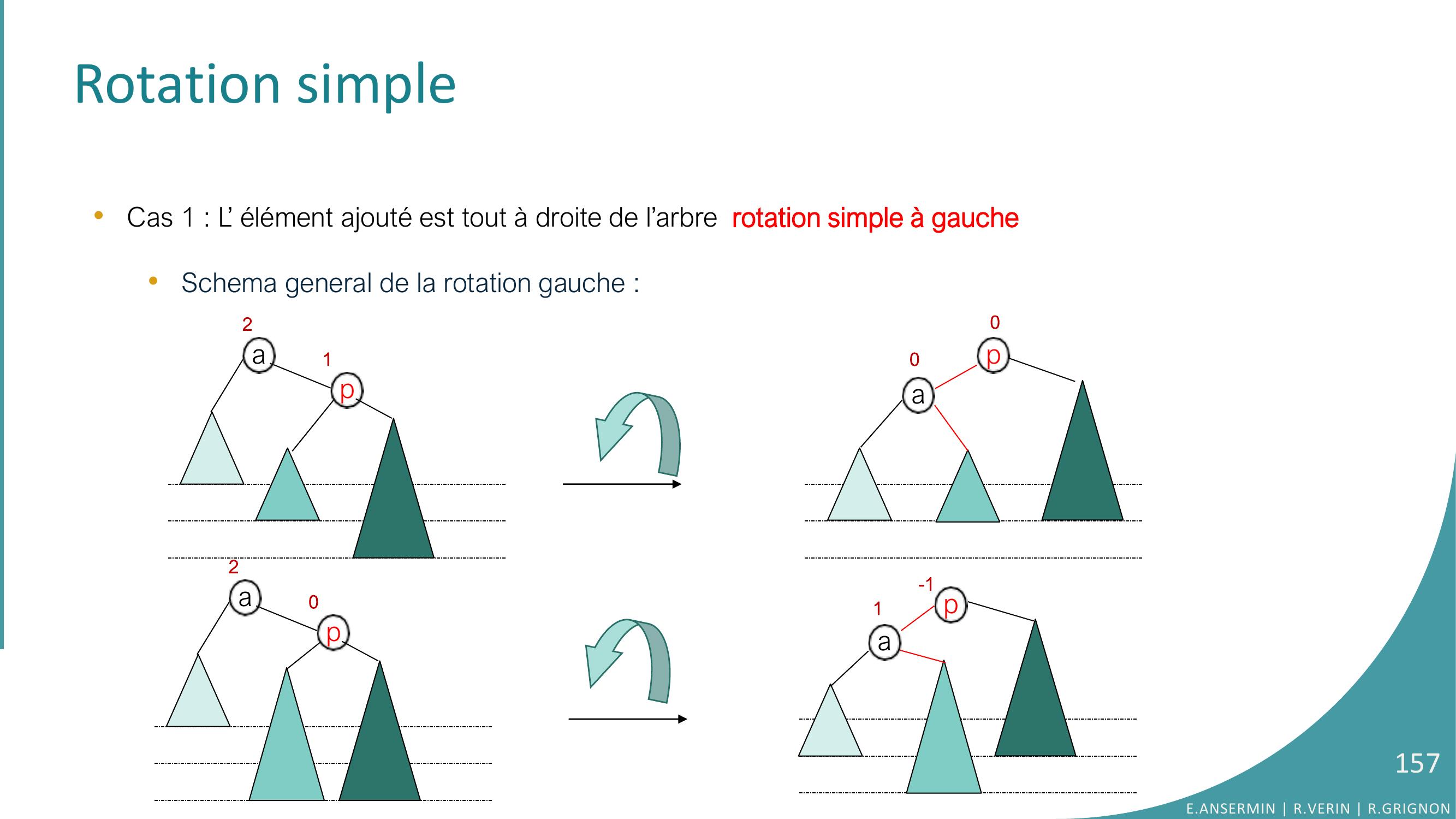
Page 144 : Rotation simple•L’opération de rééquilibrage dépend de la structure de l’arbre après une opération d’insertion/suppression.•Cas 1 : L’ élément ajouté est tout à droite de l’arbre. 105281512181000011200E.ANSERMIN R.VERIN R.GRIGNON144

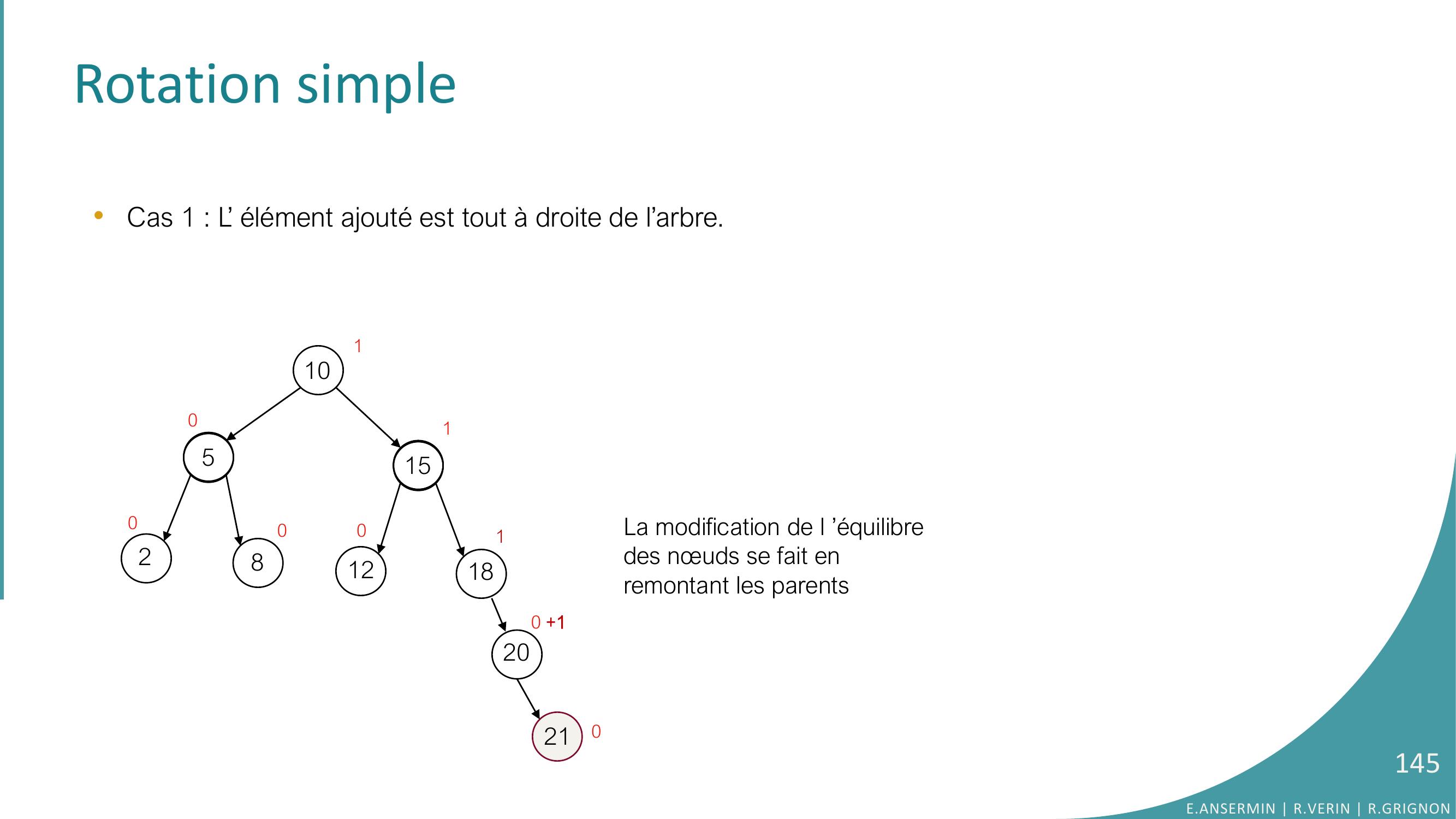
Page 145 : Rotation simple •Cas 1 : L’ élément ajouté est tout à droite de l’arbre. 105281512181000011200 +1210La modification de l ’équilibre des nœuds se fait en remontant les parentsE.ANSERMIN R.VERIN R.GRIGNON145

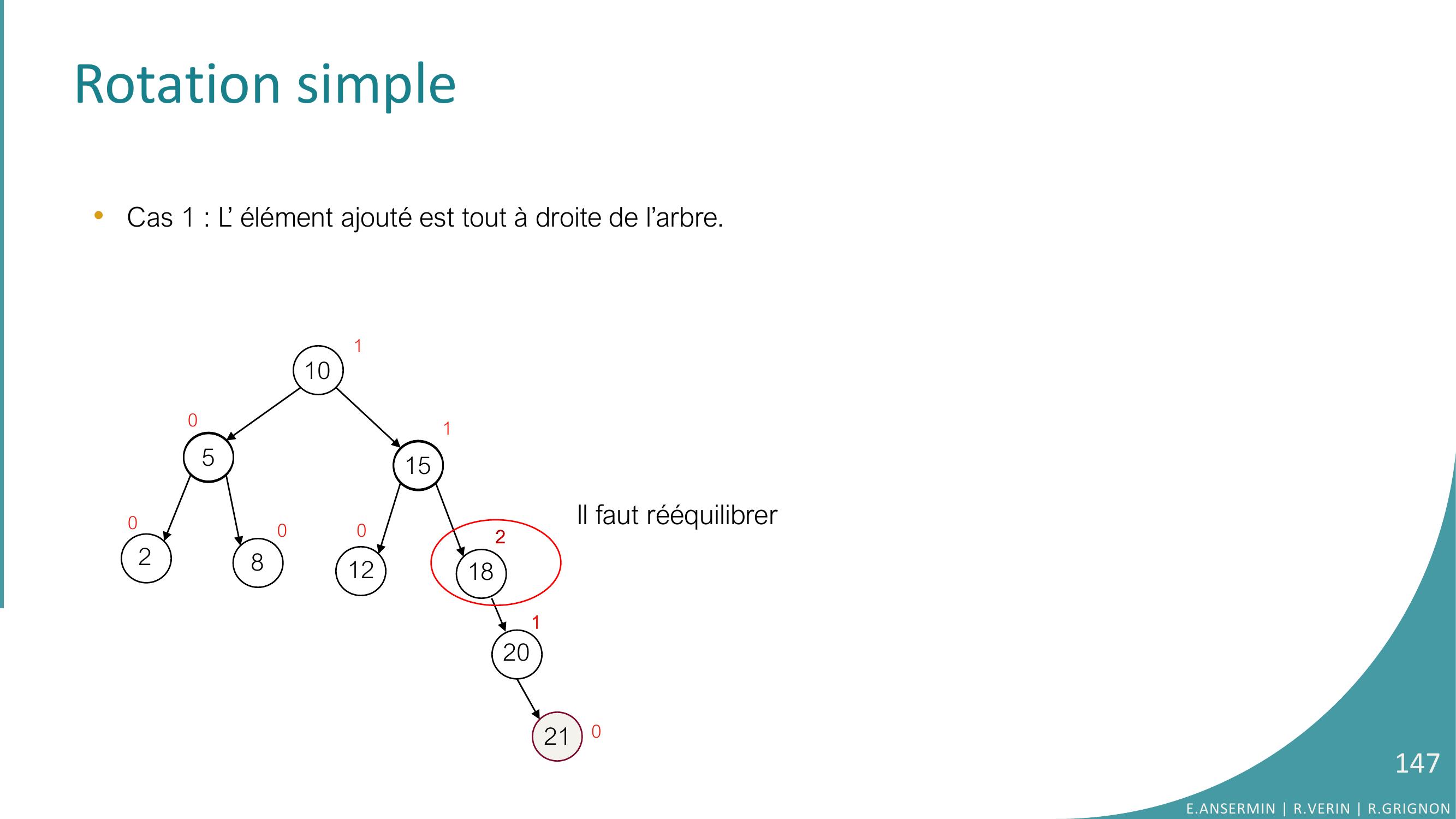
Page 146 : 105281512181+1000011201210La modification de l ’équilibre des nœuds se fait en remontant les parentsRotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre. E.ANSERMIN R.VERIN R.GRIGNON146

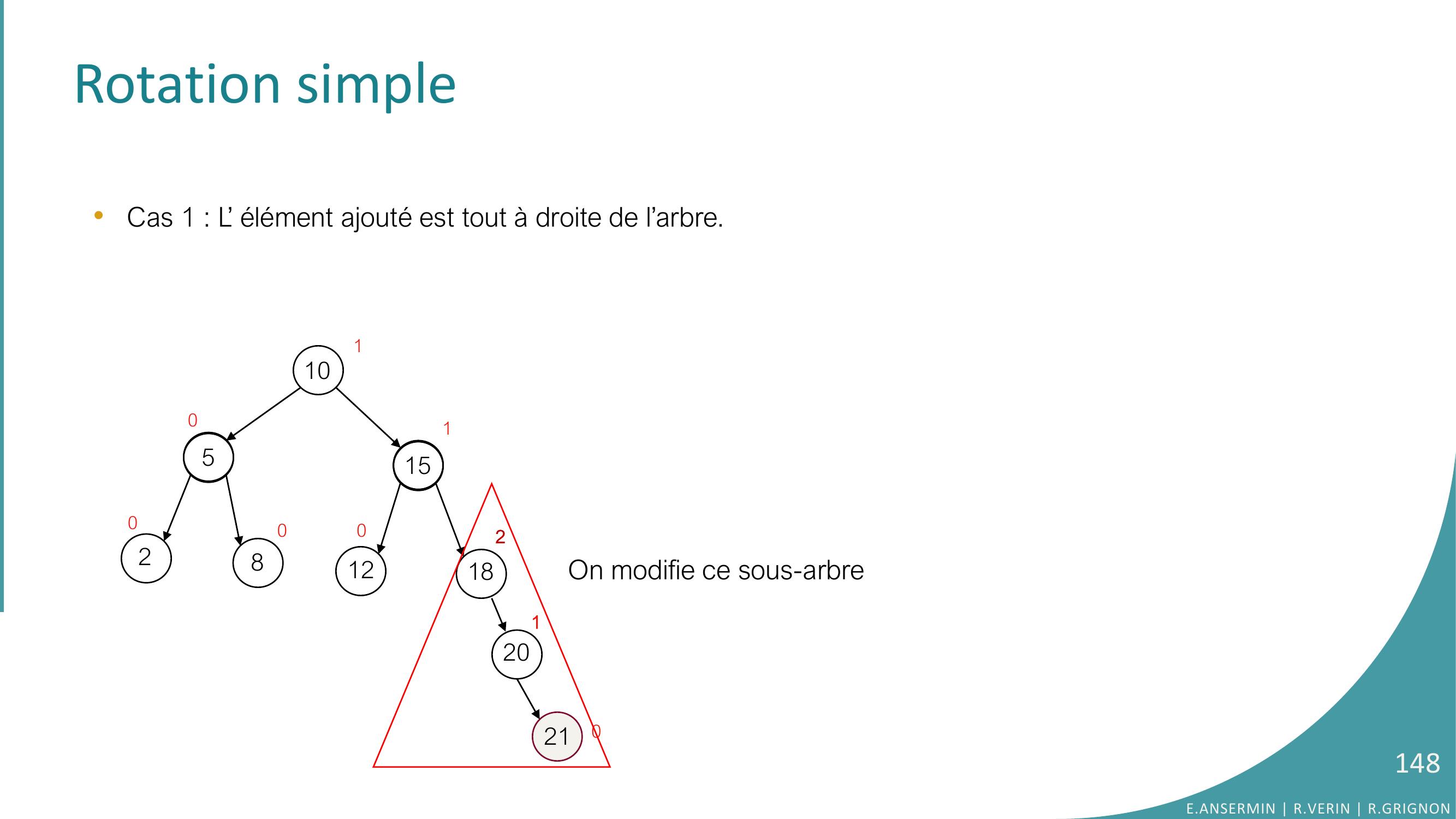
Page 147 : Rotation simple 105281512182000011201210Il faut rééquilibrer•Cas 1 : L’ élément ajouté est tout à droite de l’arbre. E.ANSERMIN R.VERIN R.GRIGNON147

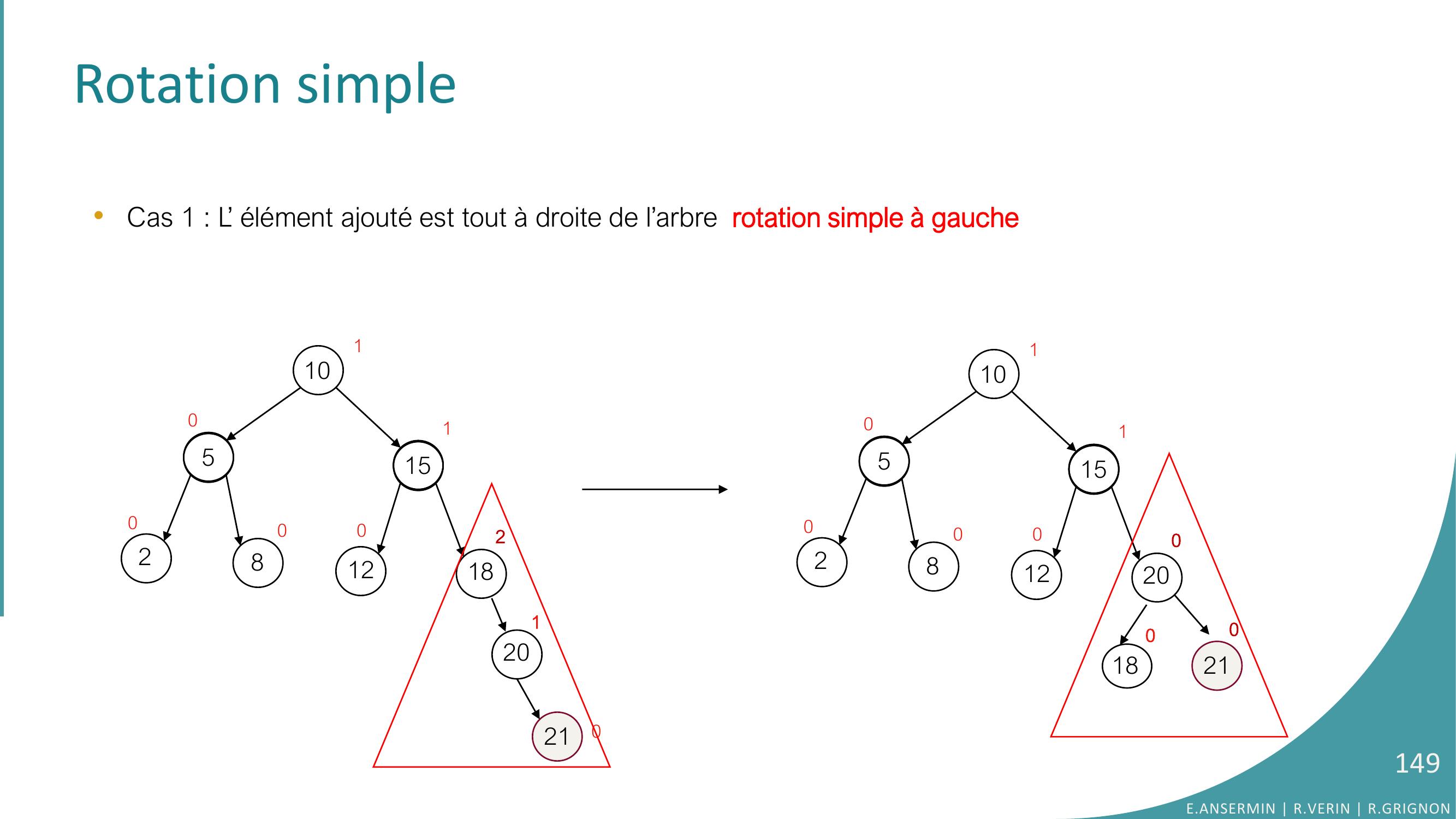
Page 148 : Rotation simple105281512182000011201210On modifie ce sous-arbre•Cas 1 : L’ élément ajouté est tout à droite de l’arbre. E.ANSERMIN R.VERIN R.GRIGNON148

Page 149 : Rotation simple105281512182000011201210105281512200000011180210•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche E.ANSERMIN R.VERIN R.GRIGNON149

Page 150 : Rotation simplea2p1c0pivot•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•L’element intermédiaire doit devenir la racine du sous-arbre équilibré ; l’arbre doittourner autour de cet élément : c’est le pivot.E.ANSERMIN R.VERIN R.GRIGNON150

Page 151 : Rotation simplea2p1c0pivot•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•L’element intermédiaire doit devenir la racine du sous-arbre équilibré ; l’arbre doittourner autour de cet élément : c’est le pivot.a2p1c0On tourne le sous arbre vers la gaucheautour du pivot.E.ANSERMIN R.VERIN R.GRIGNON151

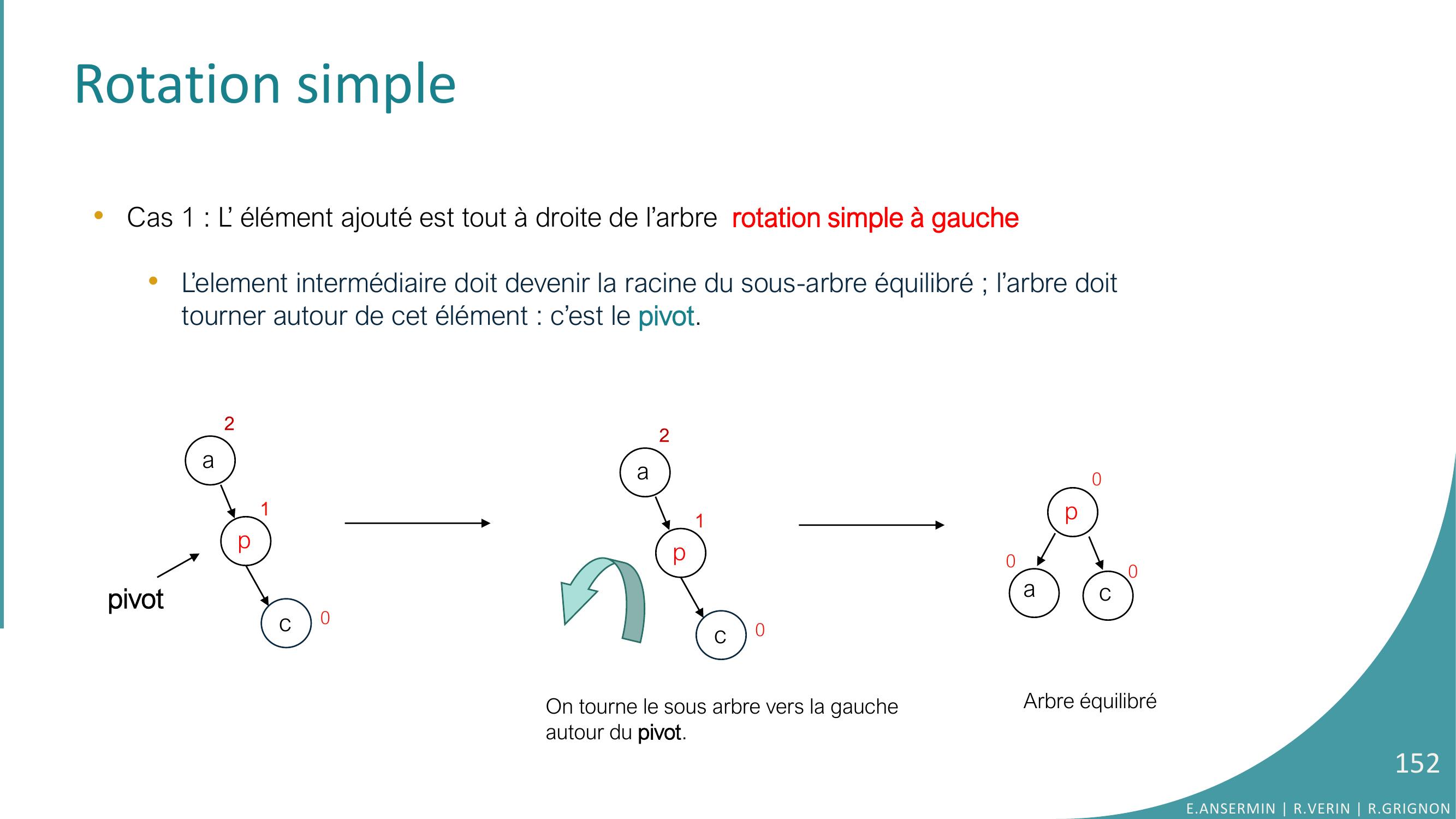
Page 152 : Rotation simplea2p1c0pivot•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•L’element intermédiaire doit devenir la racine du sous-arbre équilibré ; l’arbre doittourner autour de cet élément : c’est le pivot.a2p1c0On tourne le sous arbre vers la gaucheautour du pivot.pacArbre équilibré000E.ANSERMIN R.VERIN R.GRIGNON152

Page 153 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Schema general de la rotation gauche : a12pE.ANSERMIN R.VERIN R.GRIGNON153

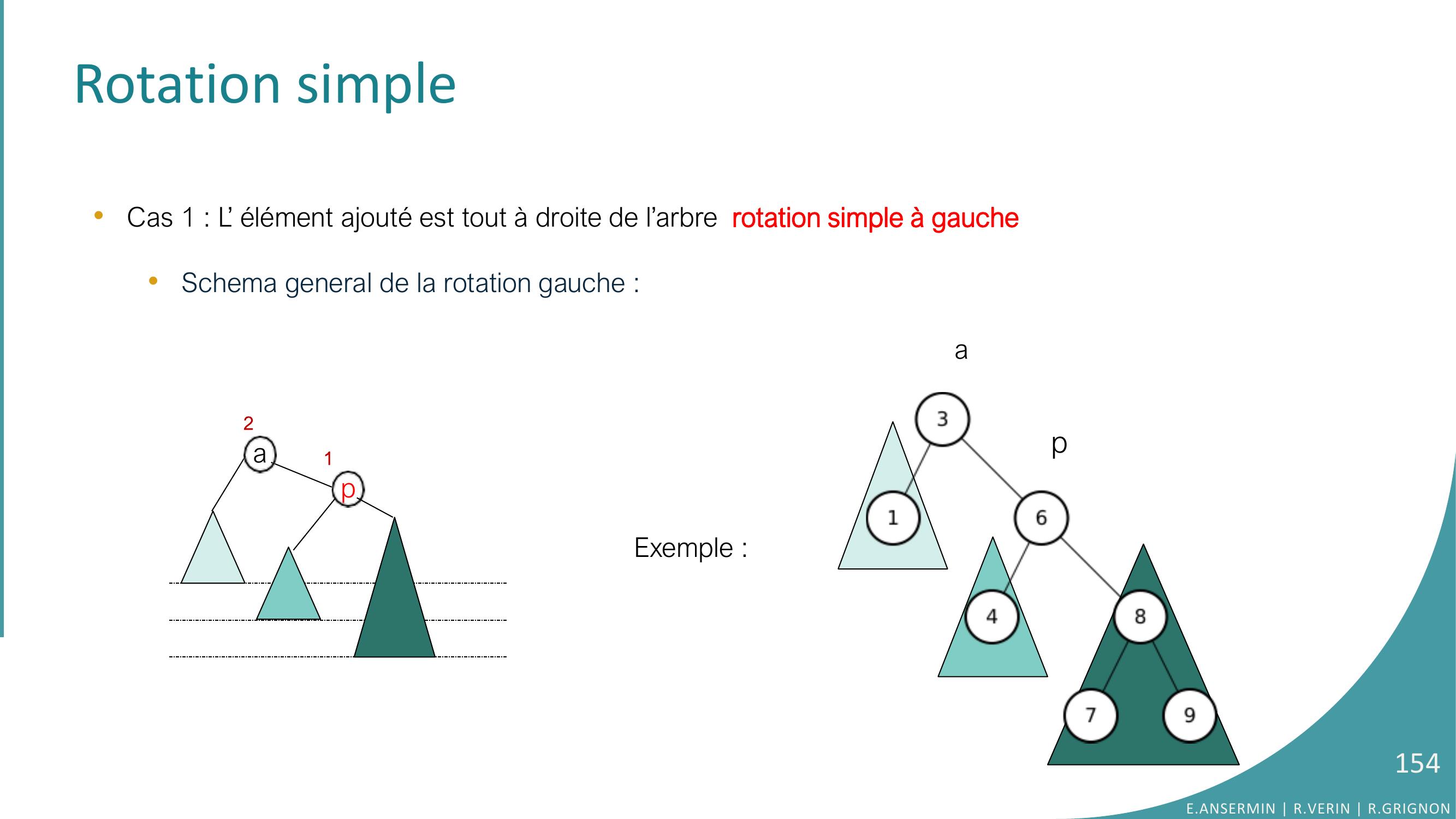
Page 154 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Schema general de la rotation gauche : Exemple :a12papE.ANSERMIN R.VERIN R.GRIGNON154

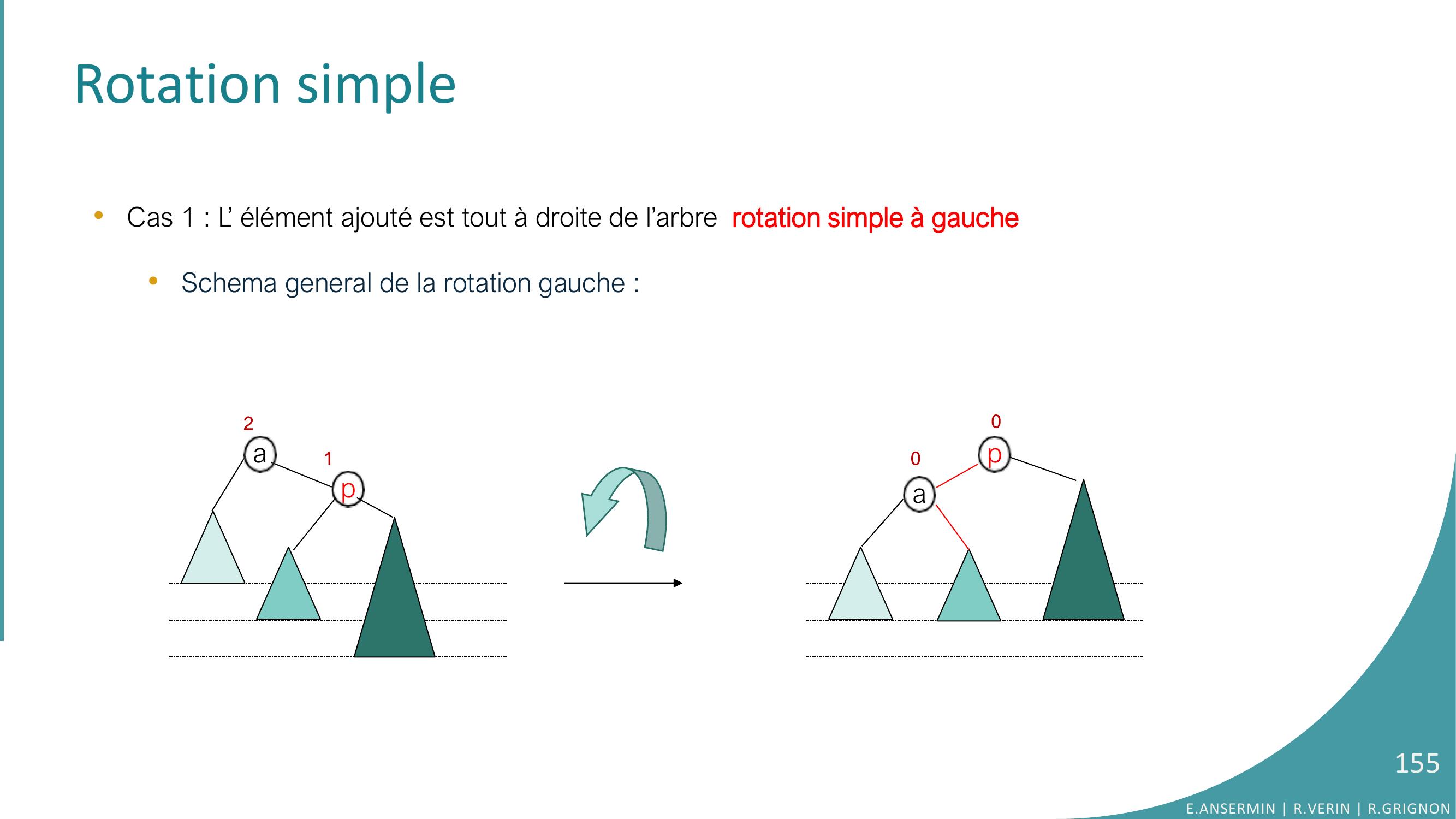
Page 155 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Schema general de la rotation gauche : paa12p00E.ANSERMIN R.VERIN R.GRIGNON155

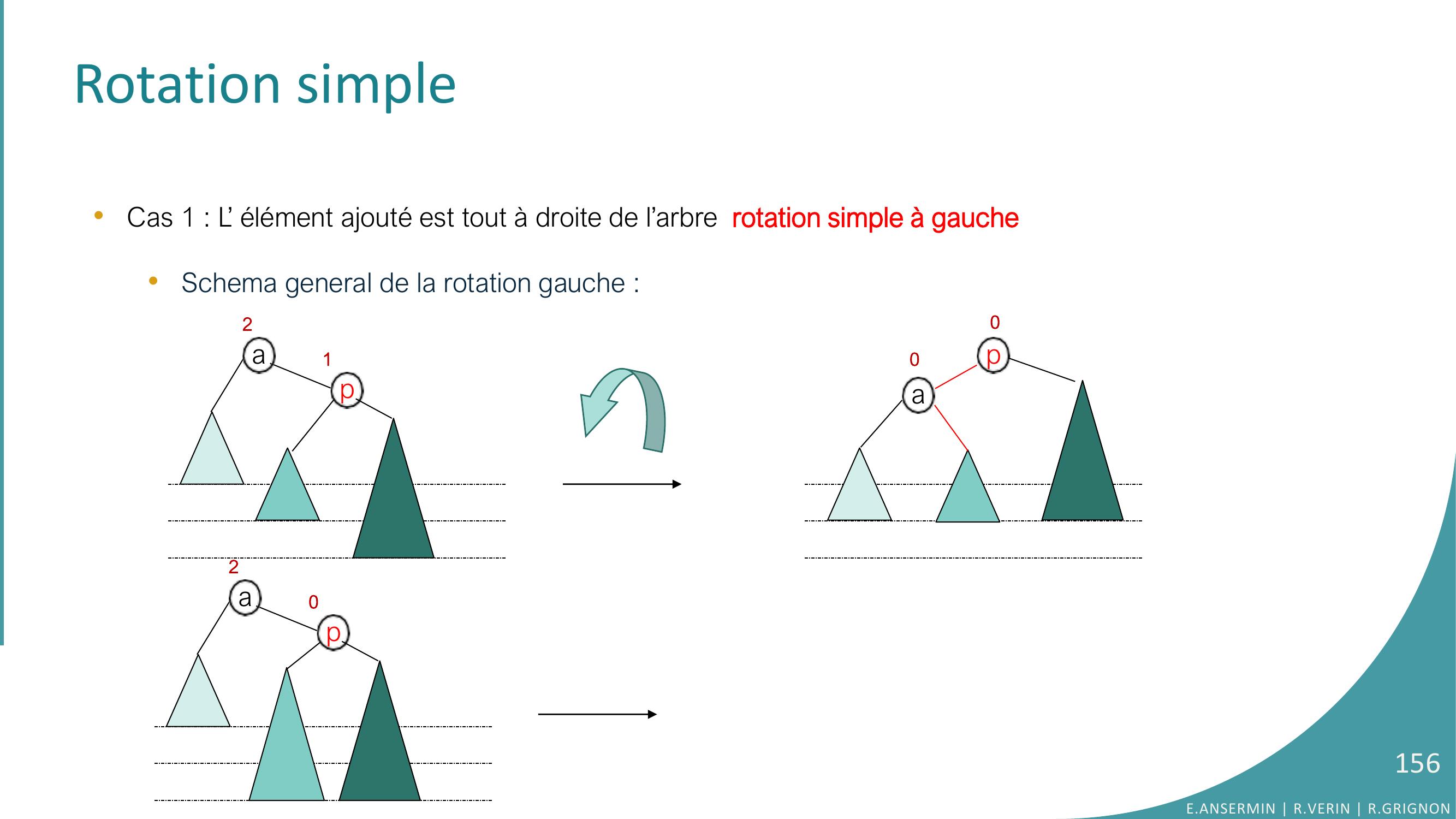
Page 156 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Schema general de la rotation gauche : paa12p00a02pE.ANSERMIN R.VERIN R.GRIGNON156

Page 157 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Schema general de la rotation gauche : paa12p00a02ppa-11E.ANSERMIN R.VERIN R.GRIGNON157

Page 158 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Algorithme: paa12p00FONCTION rotationGauchea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← ???…RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON158

Page 159 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Algorithme: FONCTION rotationGauchea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← fdafda ← fgpivotfgpivot ← a…a ← pivotRETOURNER aFINpaa12p00E.ANSERMIN R.VERIN R.GRIGNON159

Page 160 : Rotation simple•Cas 1 : L’ élément ajouté est tout à droite de l’arbre rotation simple à gauche•Algorithme: FONCTION rotationGauchea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← fdafda ← fgpivotfgpivot ← aeqa← equilibreaeqp← equilibrepivotequilibrea ← eqa - maxeqp, 0 - 1equilibrepivot ← min eqa-2, eqa+eqp-2, eqp-1 a ← pivotRETOURNER aFINpaa12p00E.ANSERMIN R.VERIN R.GRIGNON160

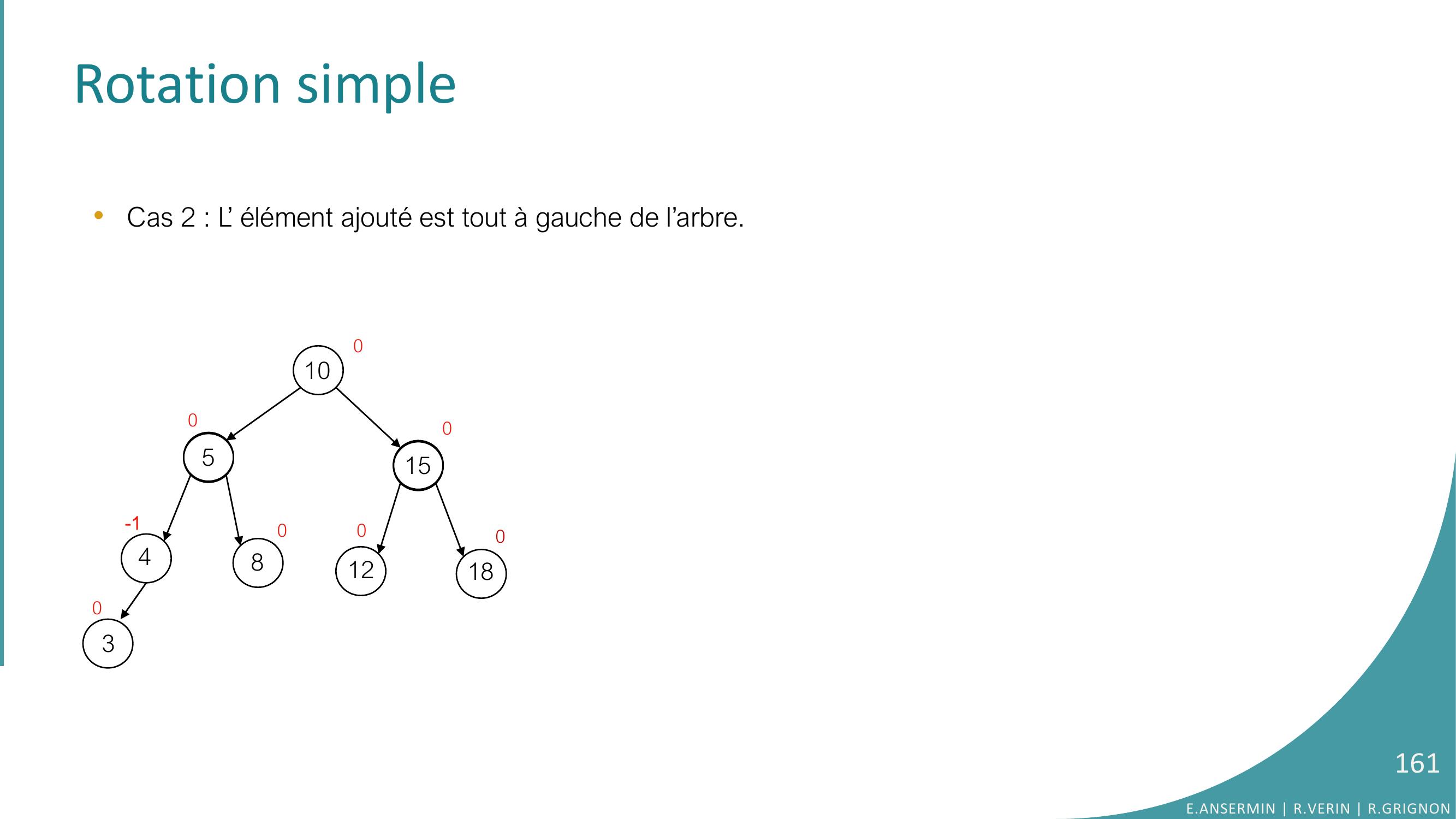
Page 161 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre. 10548151218000-100030E.ANSERMIN R.VERIN R.GRIGNON161

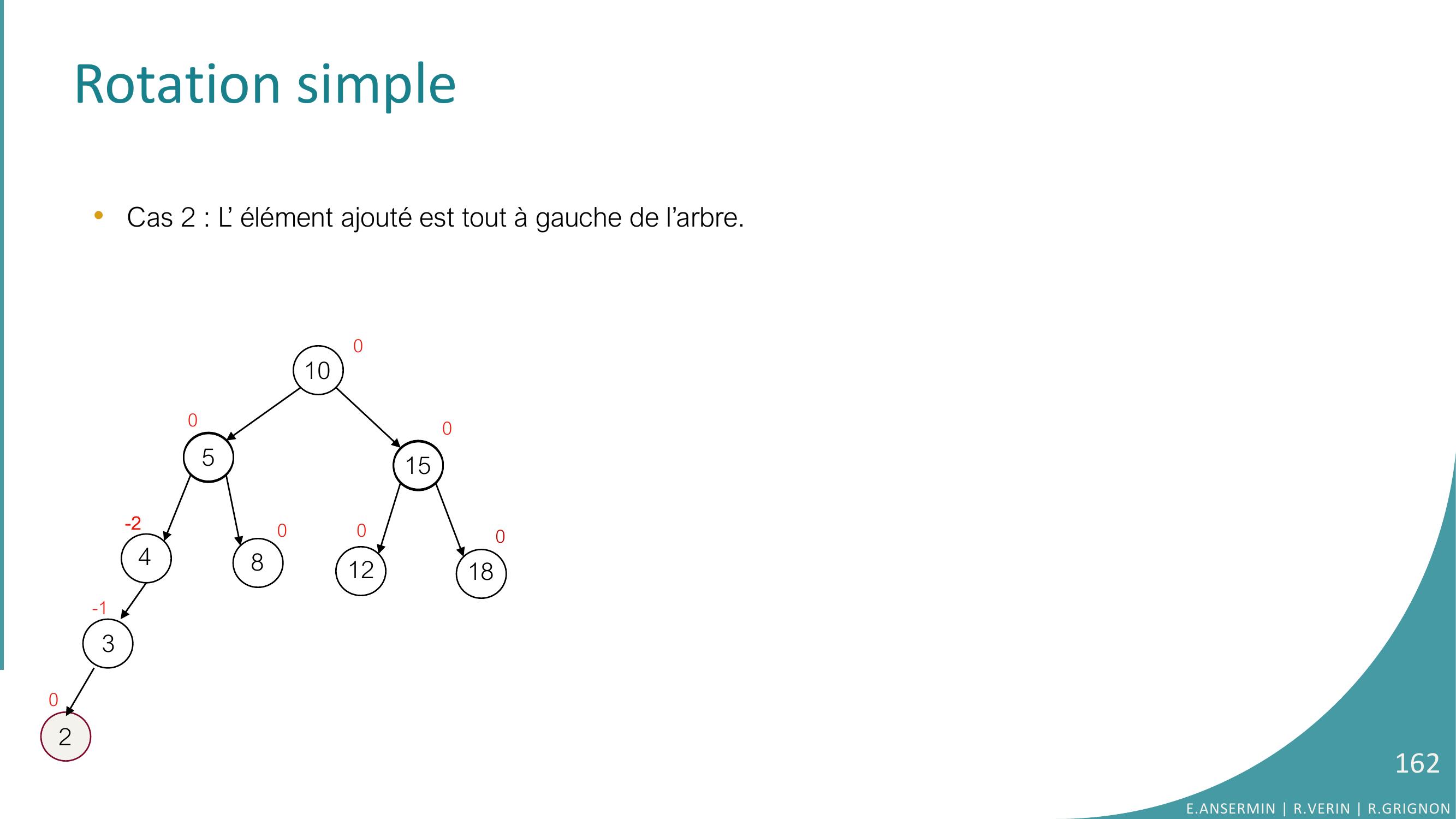
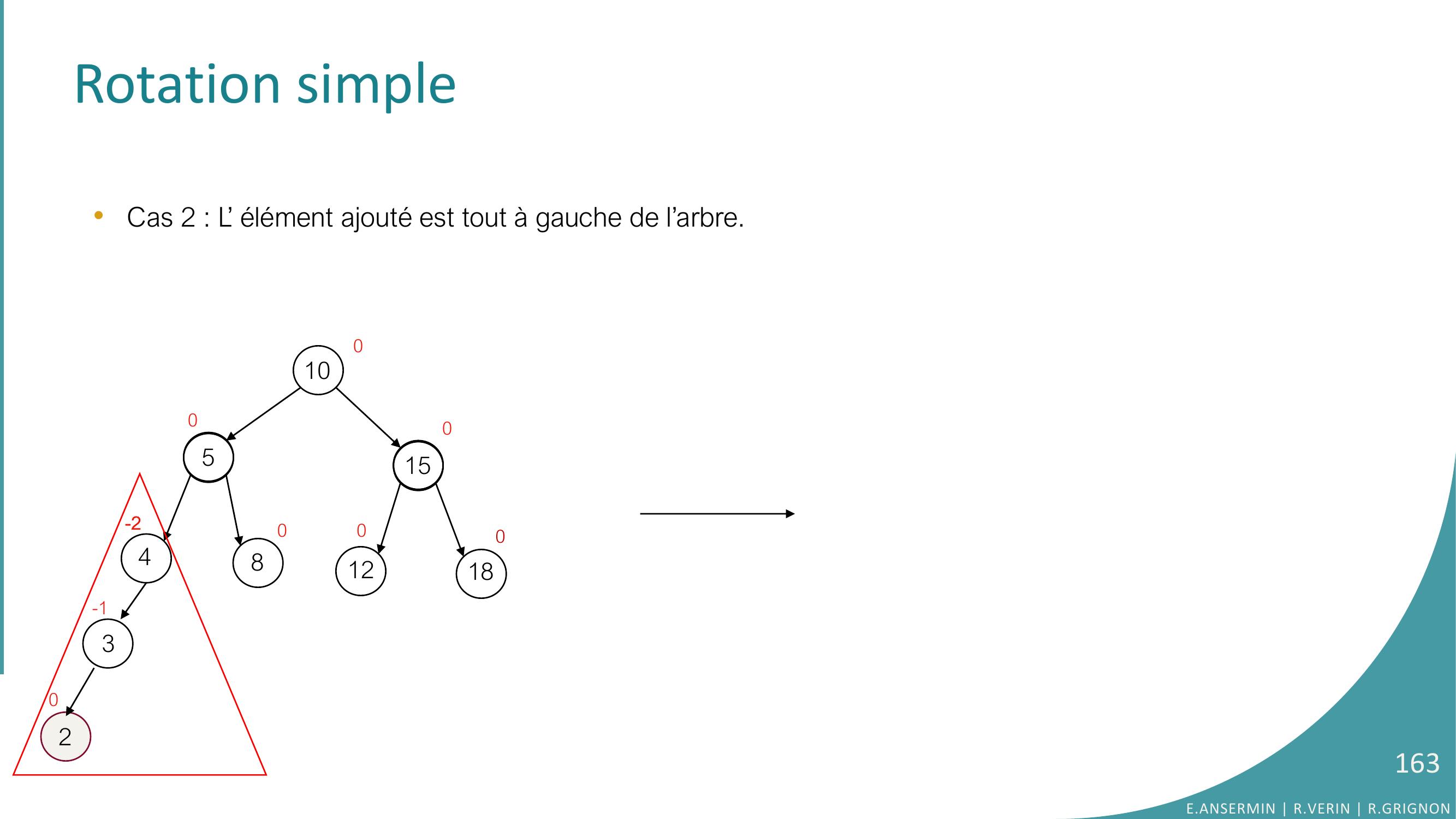
Page 162 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre. 10548151218000-200032-10E.ANSERMIN R.VERIN R.GRIGNON162

Page 163 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre. 10548151218000-200032-10E.ANSERMIN R.VERIN R.GRIGNON163

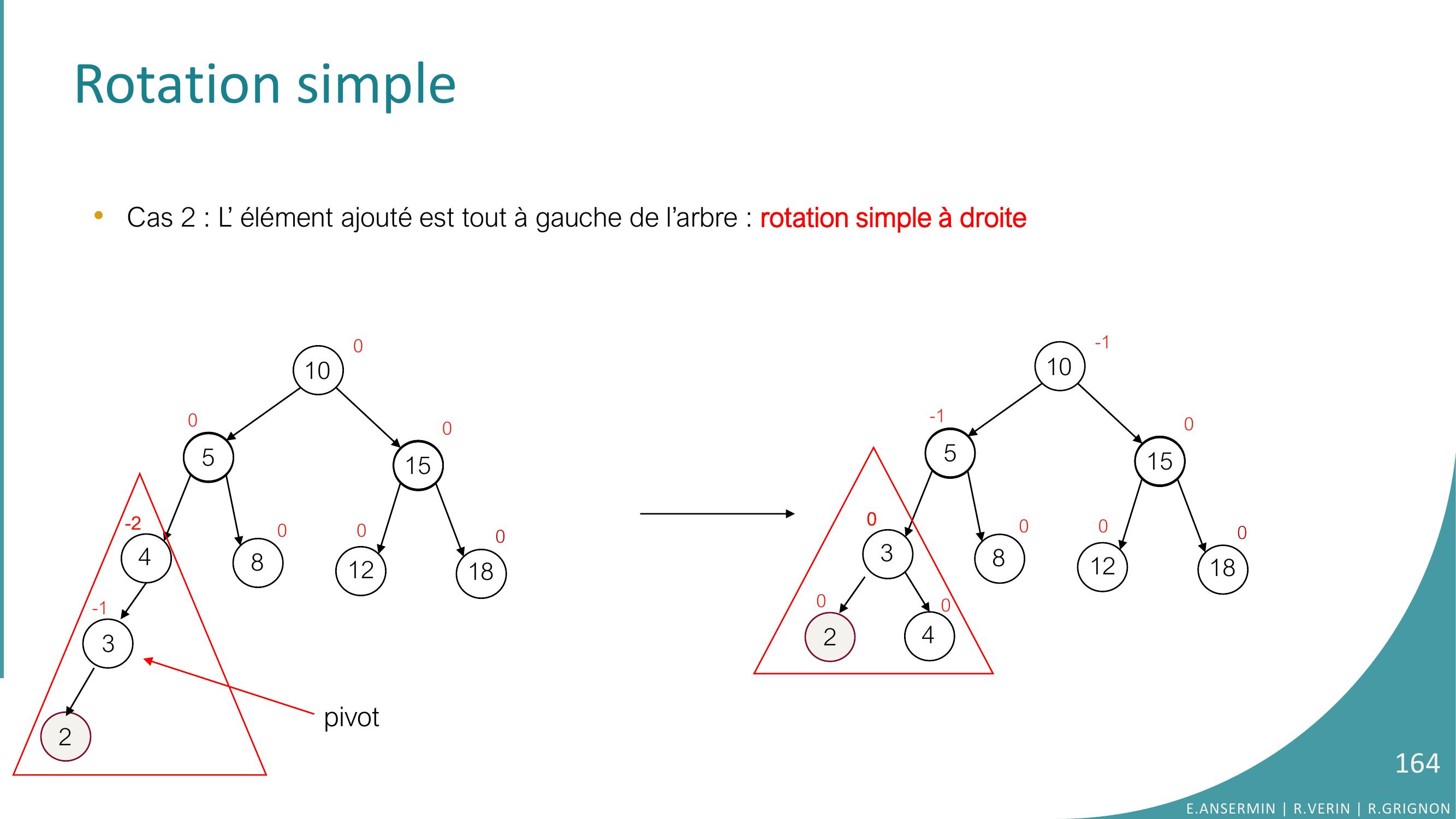
Page 164 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite 10548151218000-200032-10105381512180000-10-1240pivotE.ANSERMIN R.VERIN R.GRIGNON164

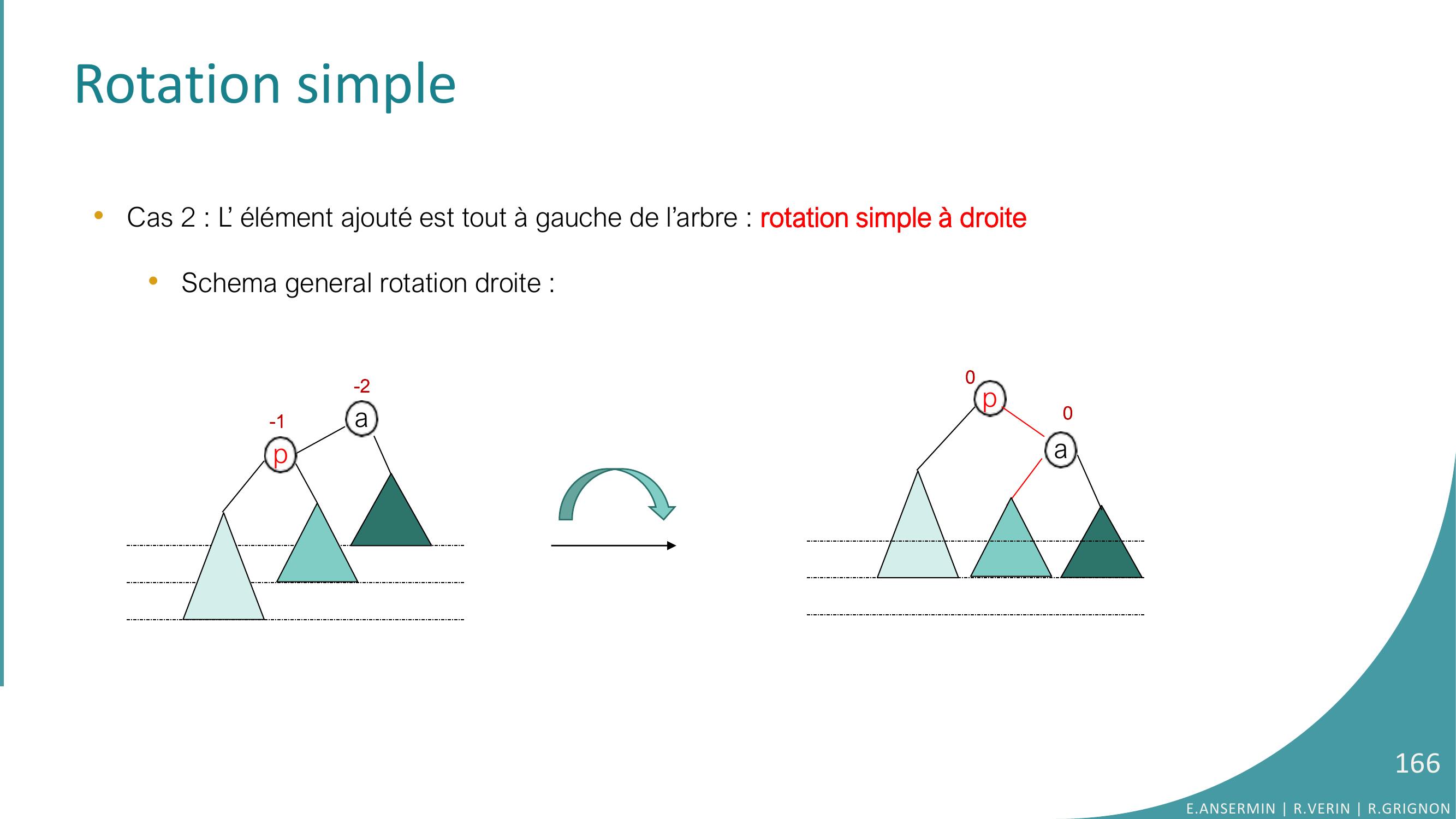
Page 165 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Schema general rotation droite : a-1-2pE.ANSERMIN R.VERIN R.GRIGNON165

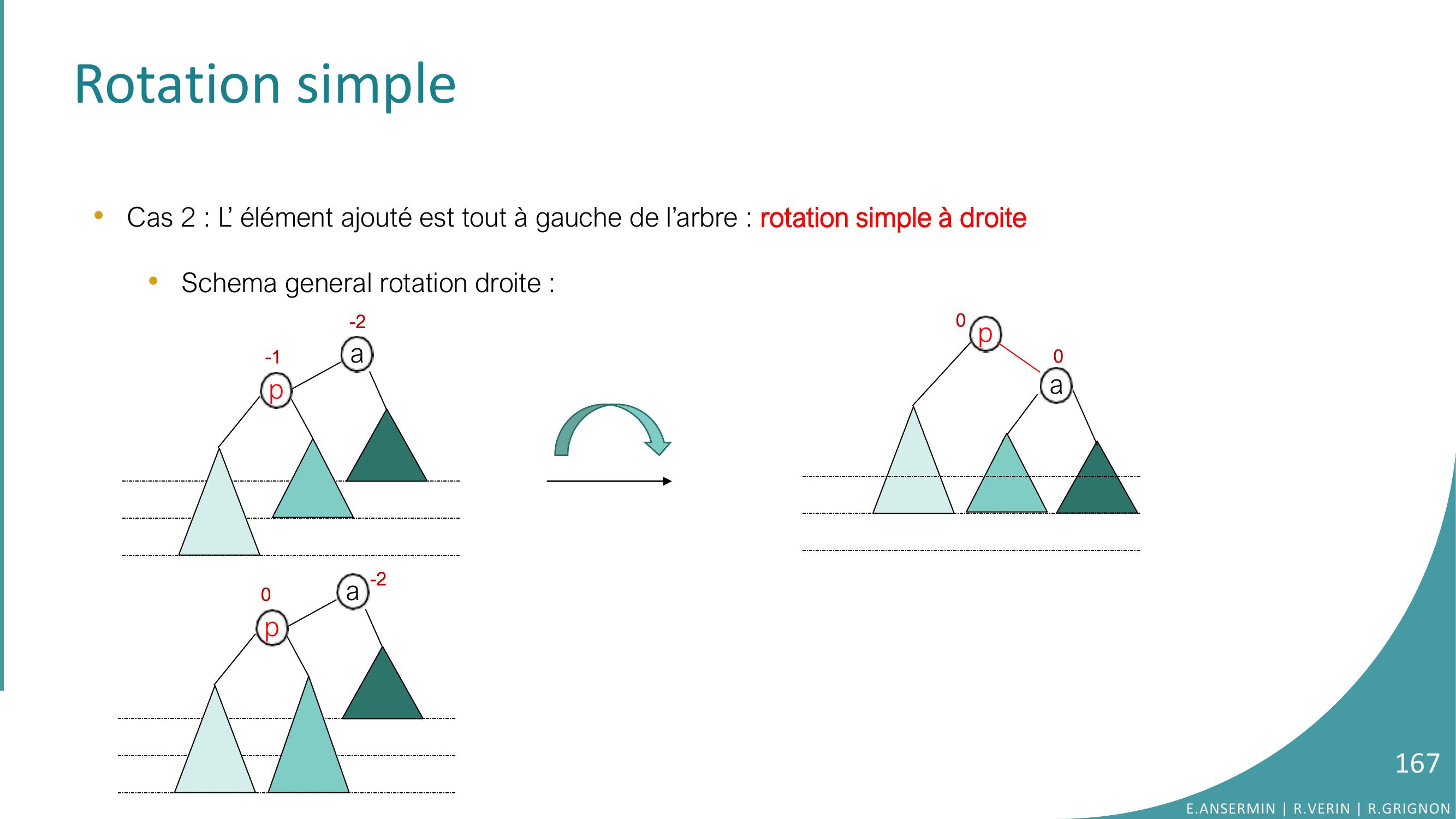
Page 166 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Schema general rotation droite : a-1-2ppa00E.ANSERMIN R.VERIN R.GRIGNON166

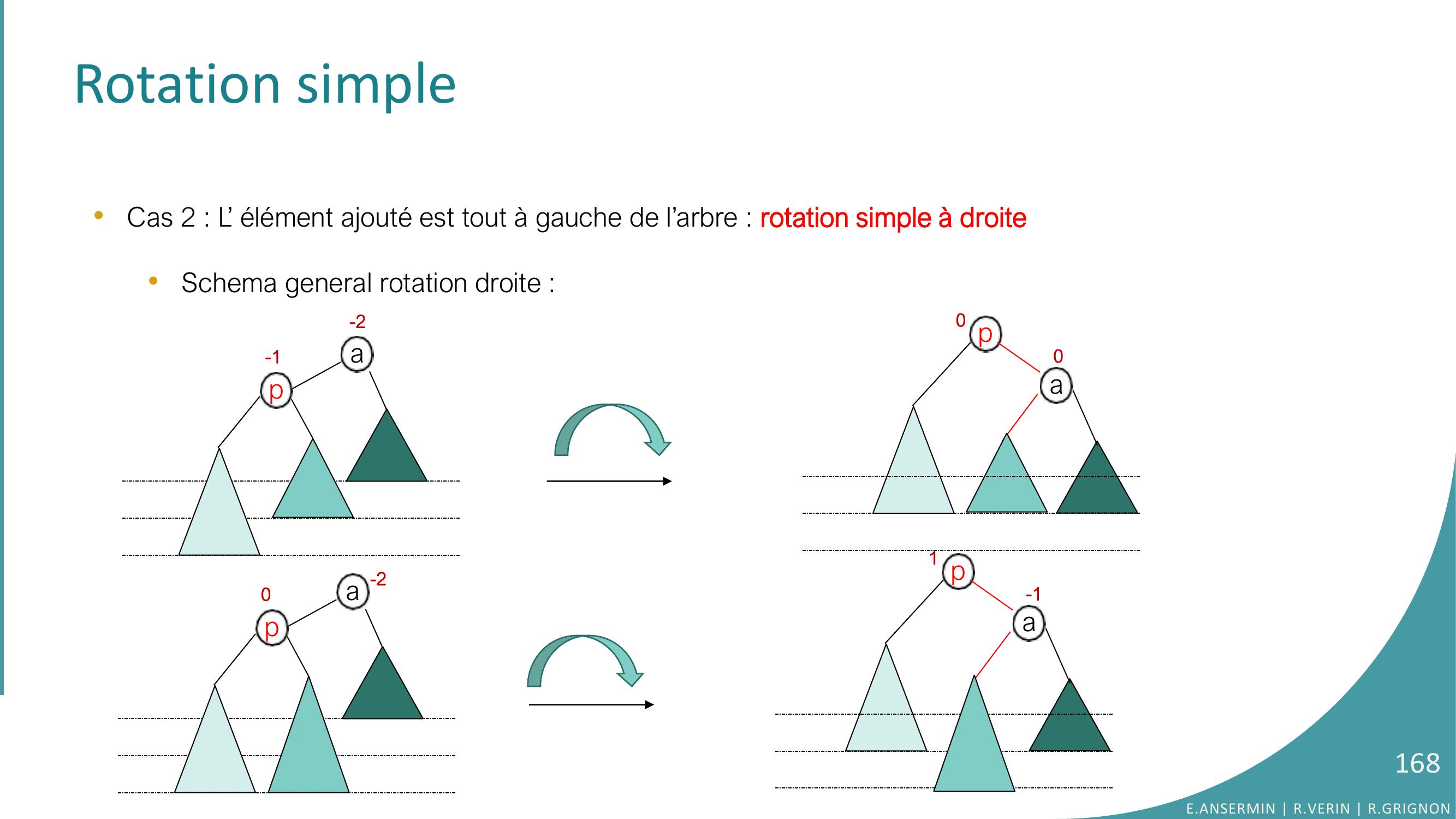
Page 167 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Schema general rotation droite : a-1-2ppa00a0-2pE.ANSERMIN R.VERIN R.GRIGNON167

Page 168 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Schema general rotation droite : a-1-2ppa00a0-2ppa1-1E.ANSERMIN R.VERIN R.GRIGNON168

Page 169 : Rotation simple a-1-2ppa00•Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Algorithme:FONCTION rotationDroitea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← ???…RETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON169

Page 170 : Rotation simple a-1-2ppa00•Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Algorithme:FONCTION rotationDroitea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← fgafga ← fdpivotfdpivot ← a…a ← pivotRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON170

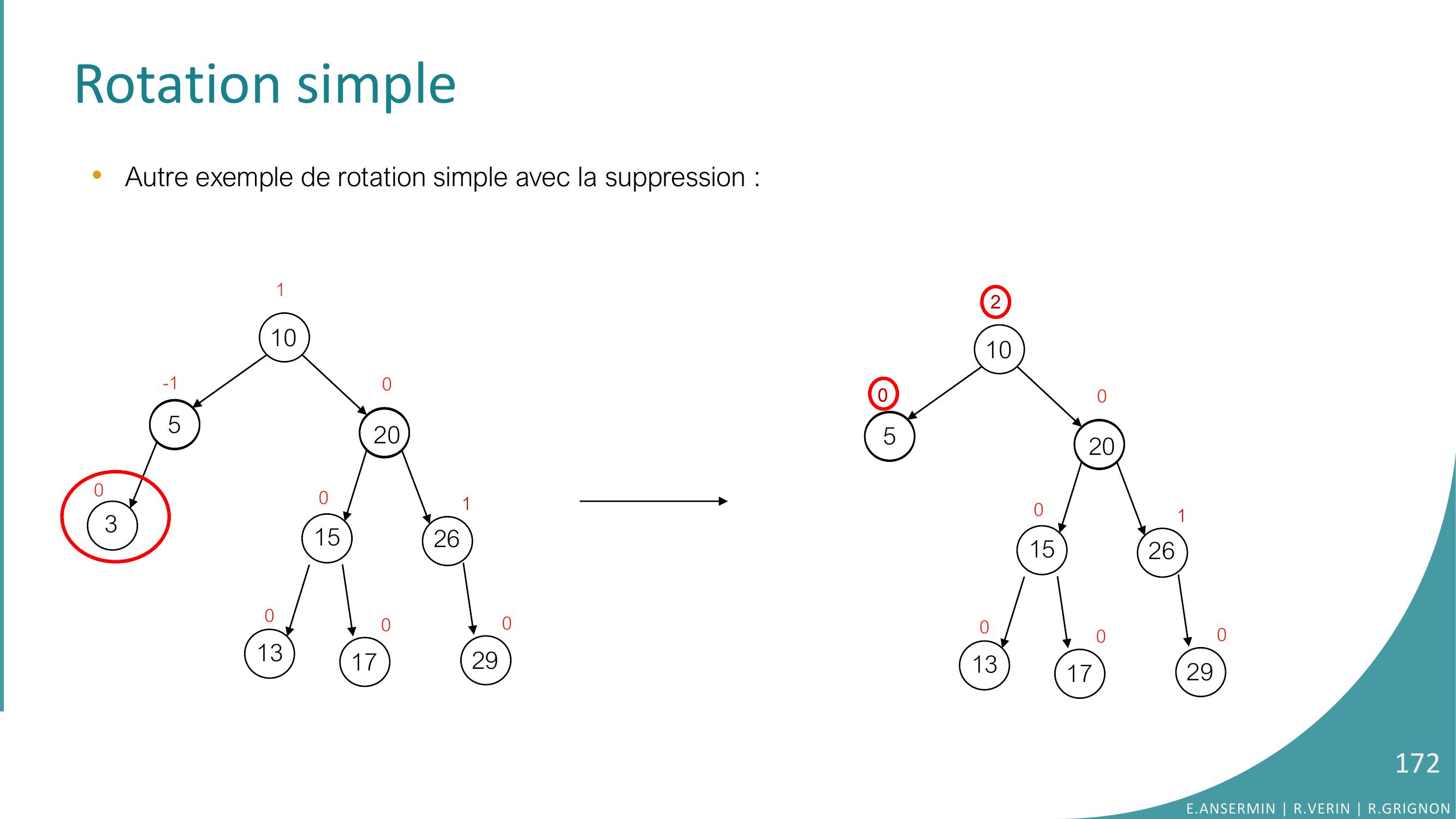
Page 171 : Rotation simple •Cas 2 : L’ élément ajouté est tout à gauche de l’arbre : rotation simple à droite•Algorithme:a-1-2ppa00FONCTION rotationDroitea: ptr sur Arbre : ptr sur ArbreVARIABLE pivot : ptr sur Arbreeqa, eqp: entierDEBUTpivot ← fgafga ← fdpivotfdpivot ← aeqa← equilibreaeqp← equilibrepivotequilibrea ← eqa - mineqp, 0 + 1equilibrepivot ← max eqa+2, eqa+eqp+2, eqp+1 a ← pivotRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON171

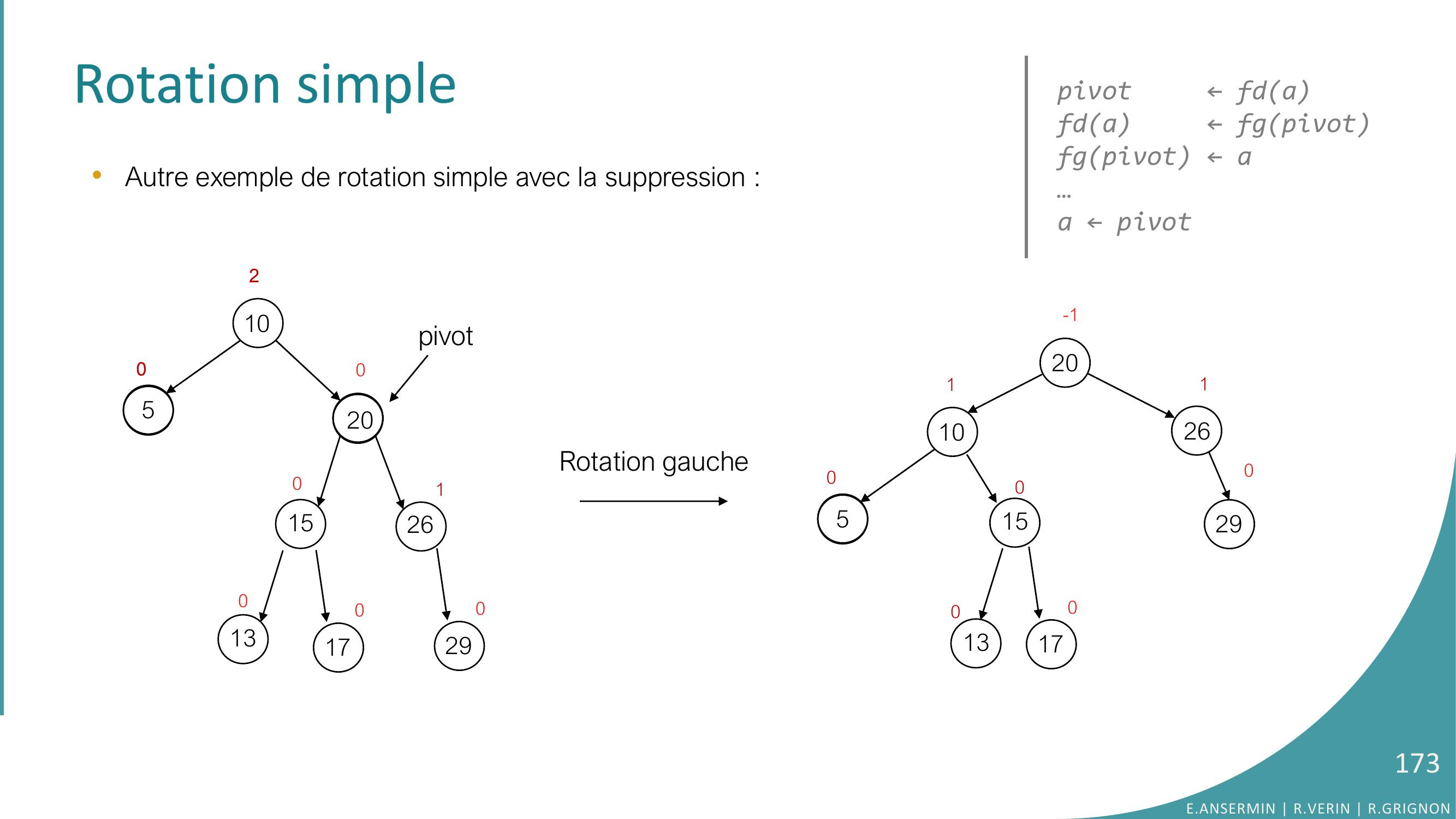
Page 172 : Rotation simple •Autre exemple de rotation simple avec la suppression :10532015261000-1130170129010520152610001301702290E.ANSERMIN R.VERIN R.GRIGNON172

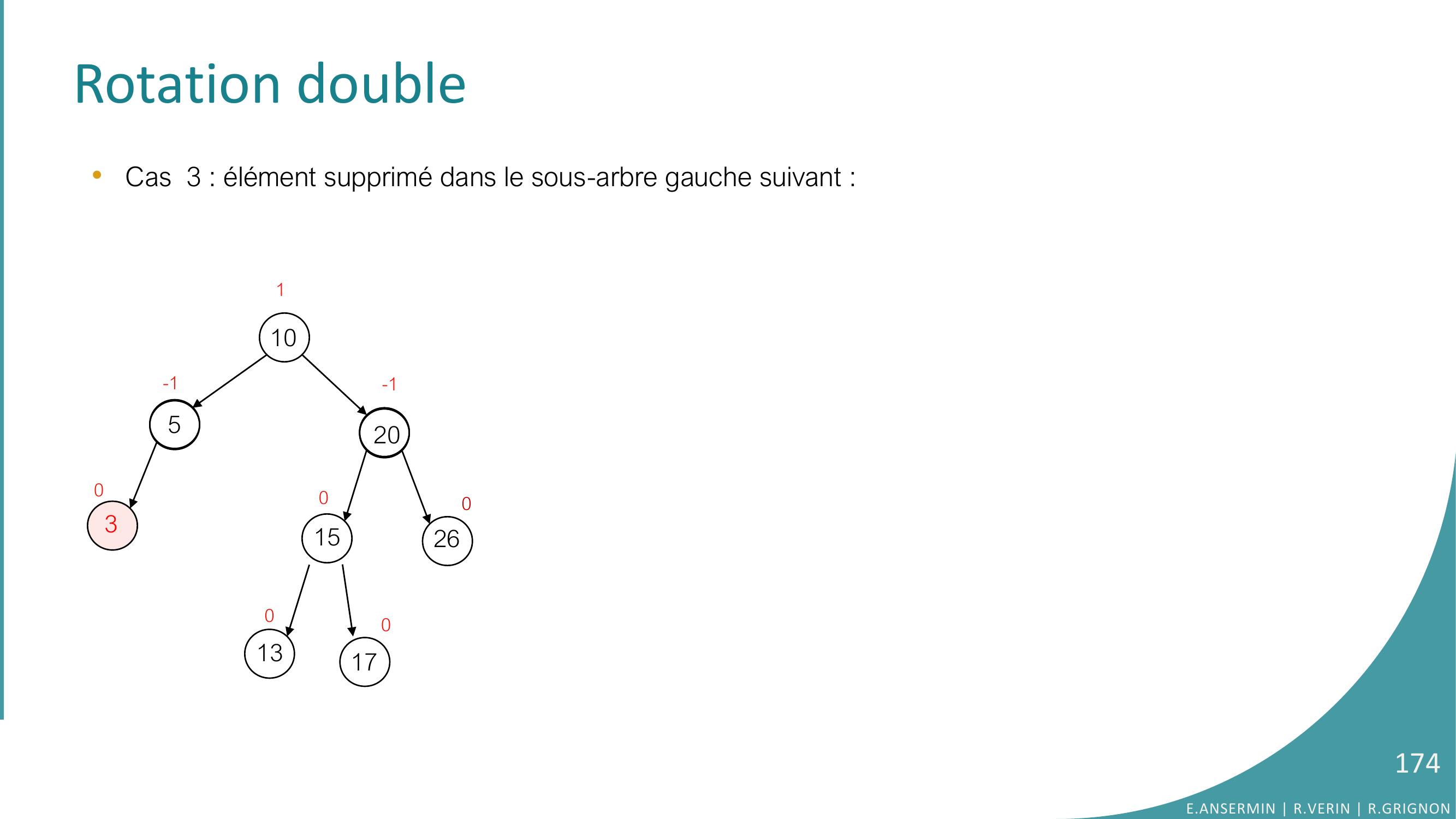
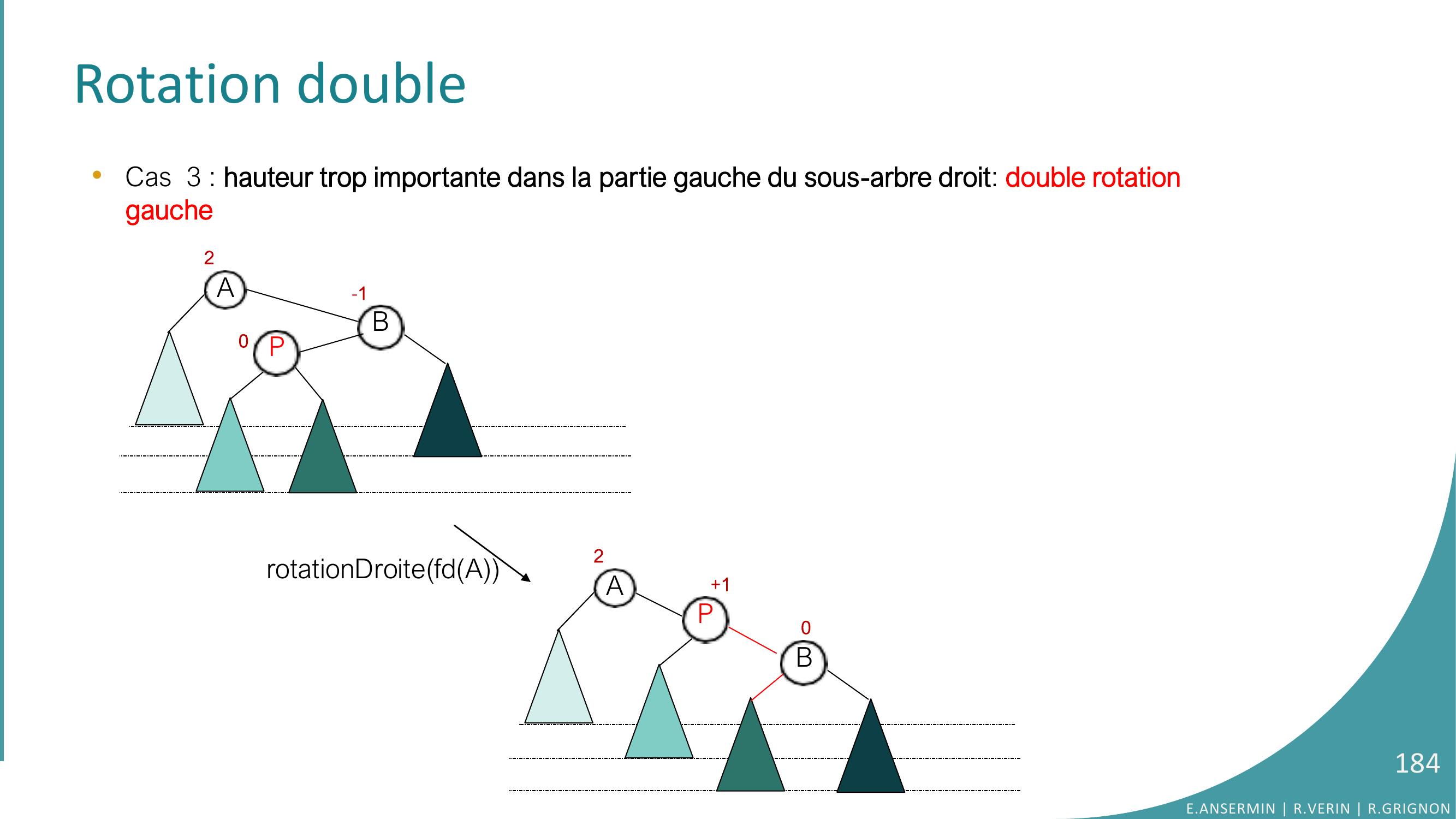
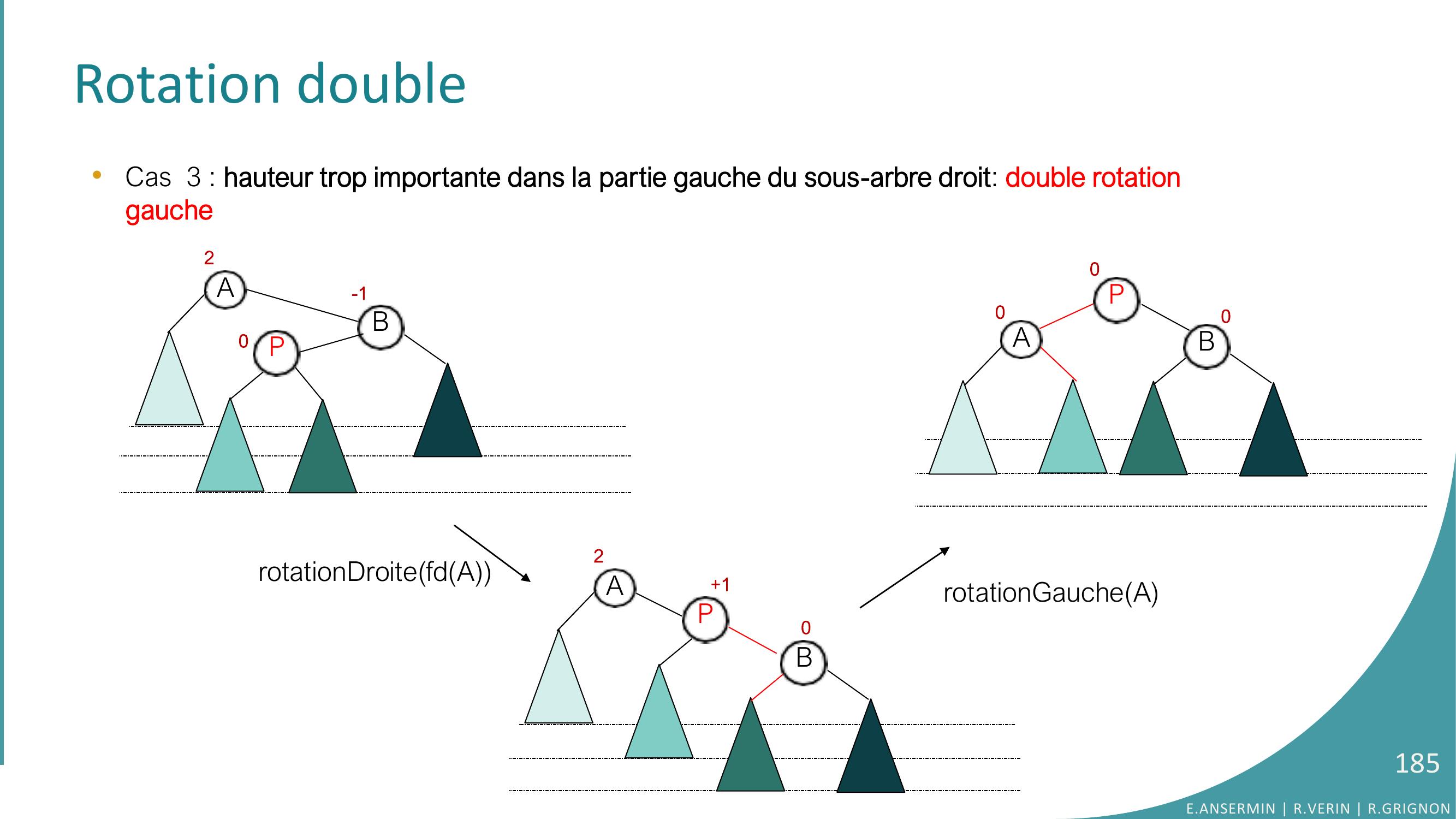
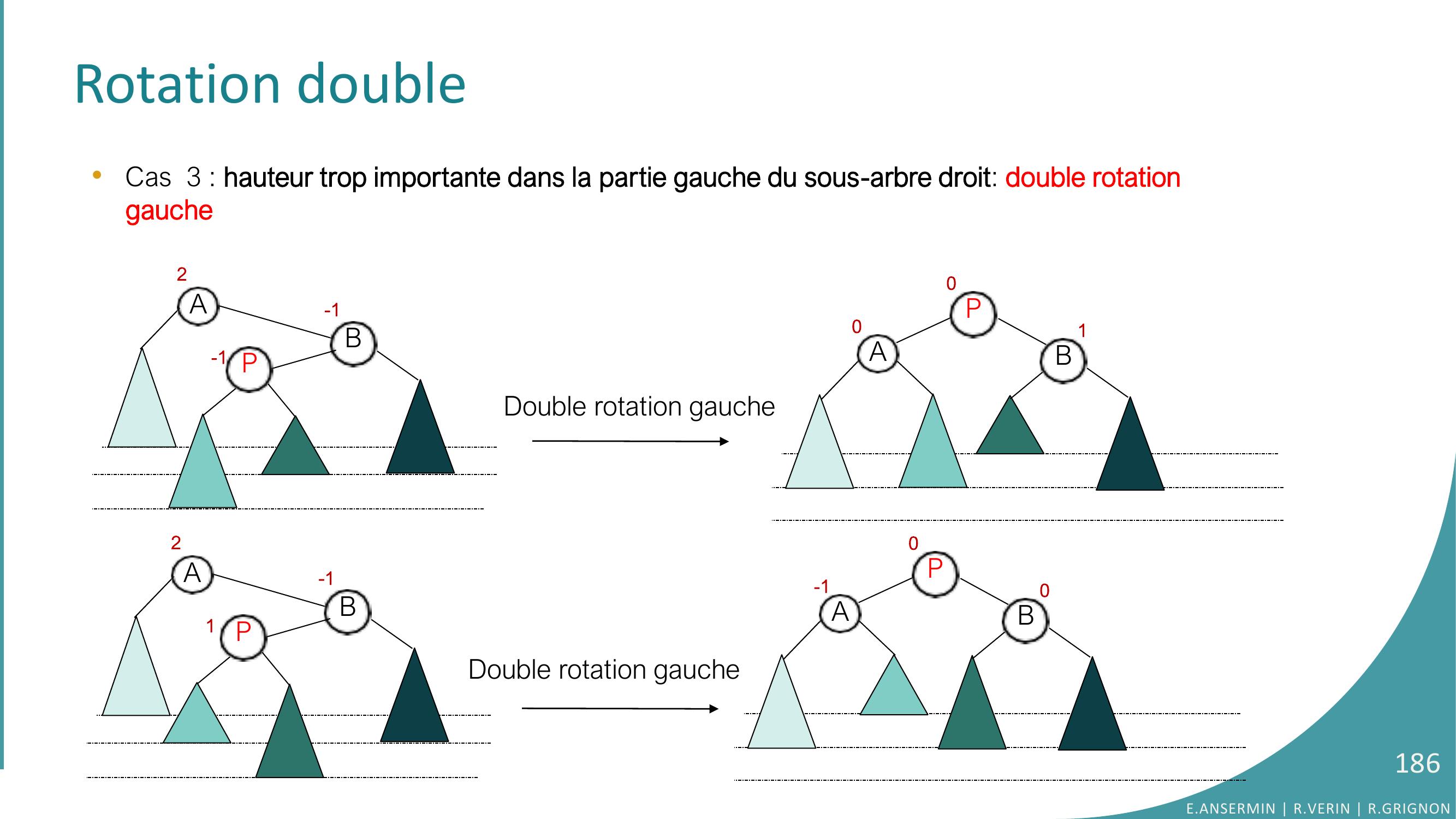
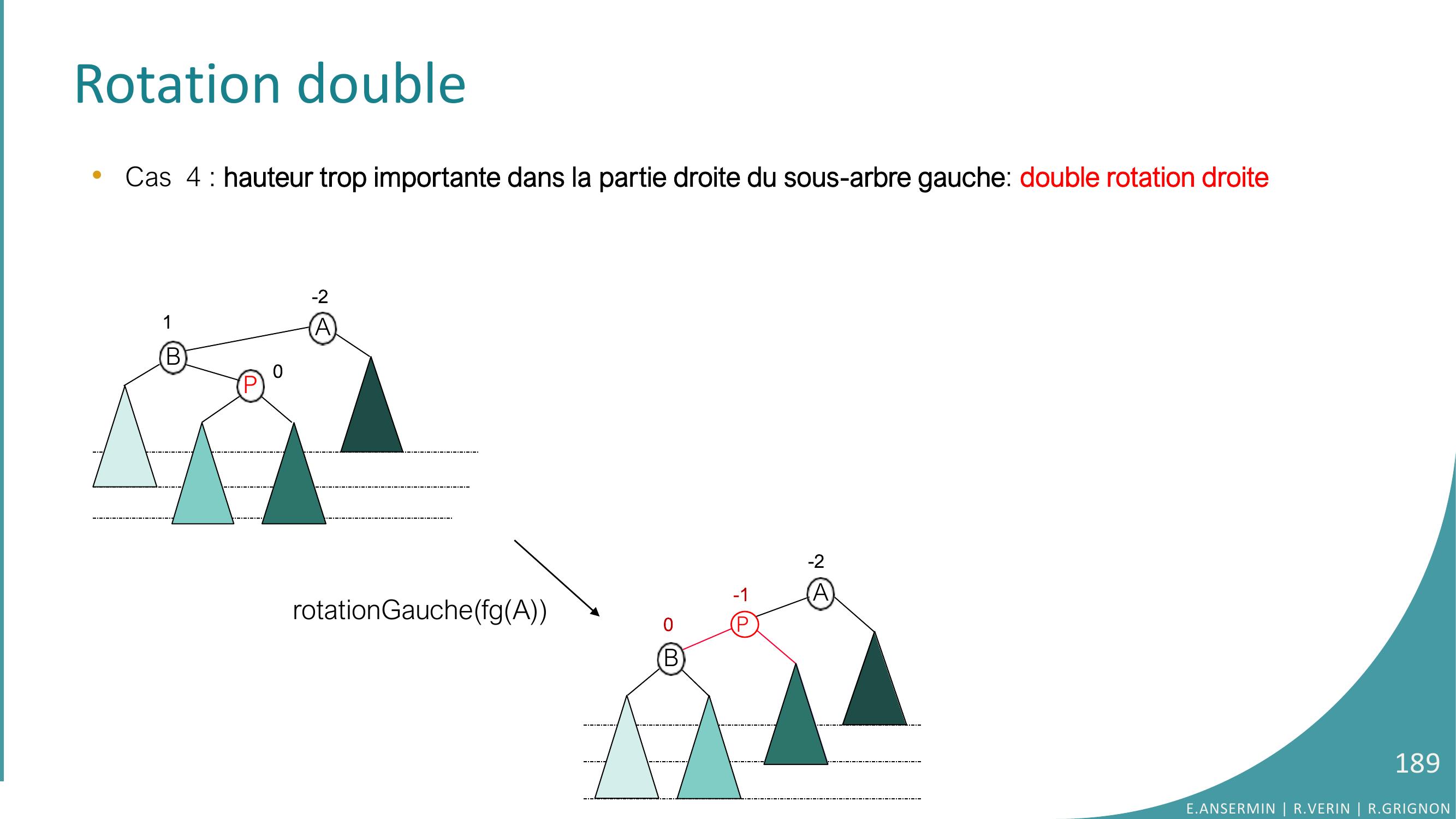
Page 173 : Rotation simple •Autre exemple de rotation simple avec la suppression :1052015261000130170229020-110501513170261290001pivotRotation gauchepivot ← fdafda ← fgpivotfgpivot ← a…a ← pivotE.ANSERMIN R.VERIN R.GRIGNON173

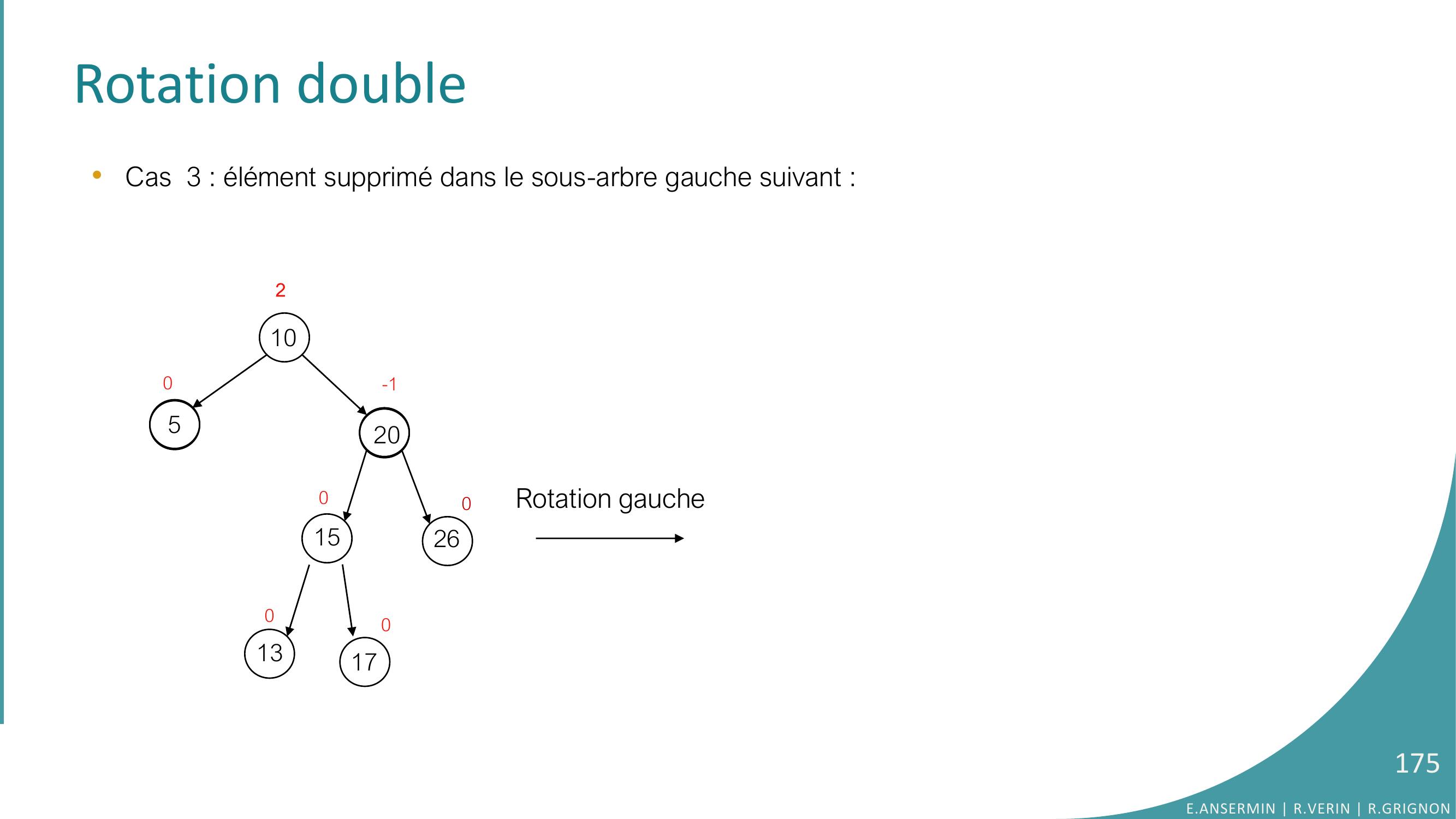
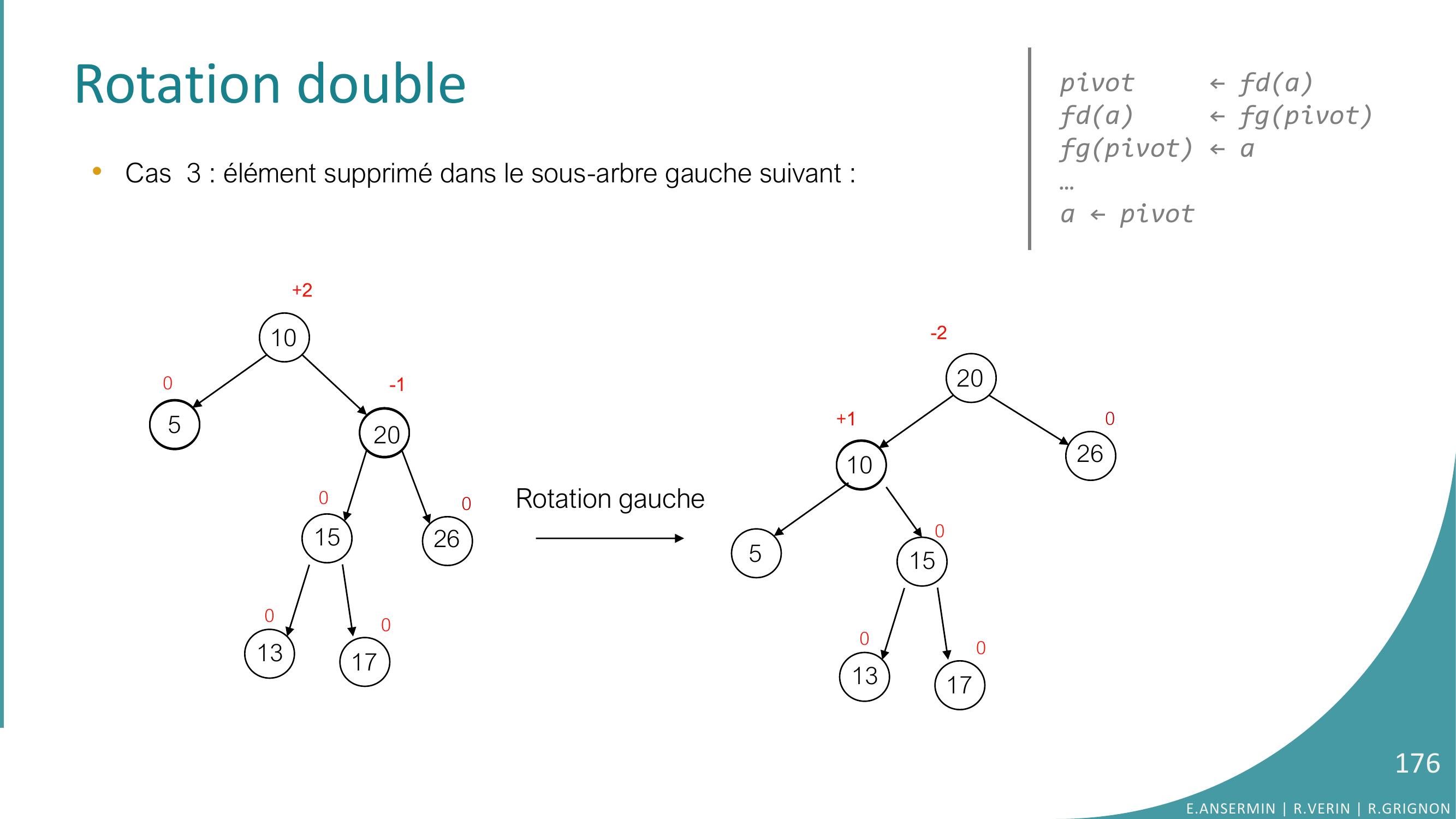
Page 174 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : 1053201526000-1-11301701E.ANSERMIN R.VERIN R.GRIGNON174

Page 175 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : 10520152600-101301702Rotation gaucheE.ANSERMIN R.VERIN R.GRIGNON175

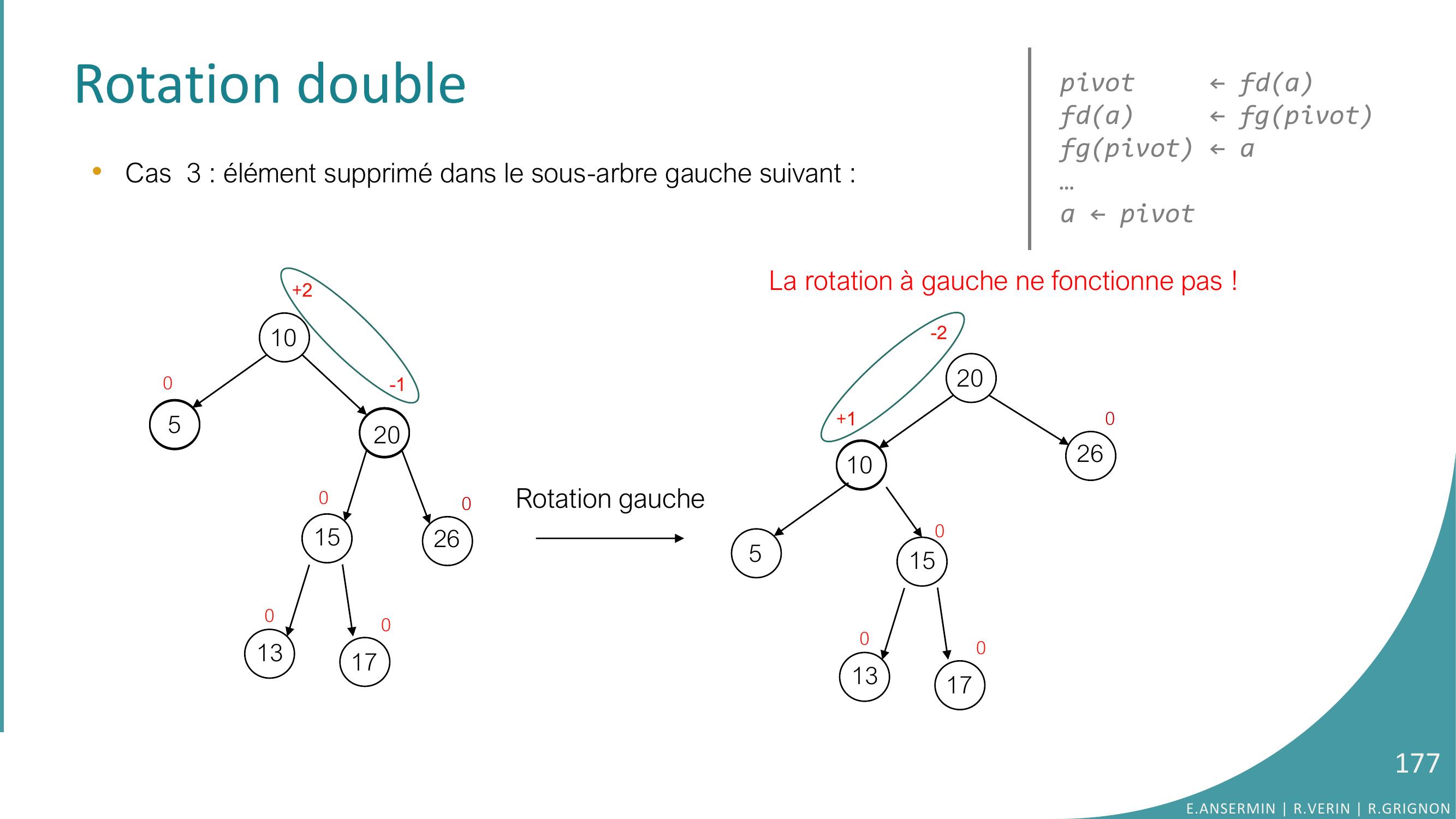
Page 176 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : 10520152600013017020105152601301700pivot ← fdafda ← fgpivotfgpivot ← a…a ← pivotRotation gauche-1+2+1-2E.ANSERMIN R.VERIN R.GRIGNON176

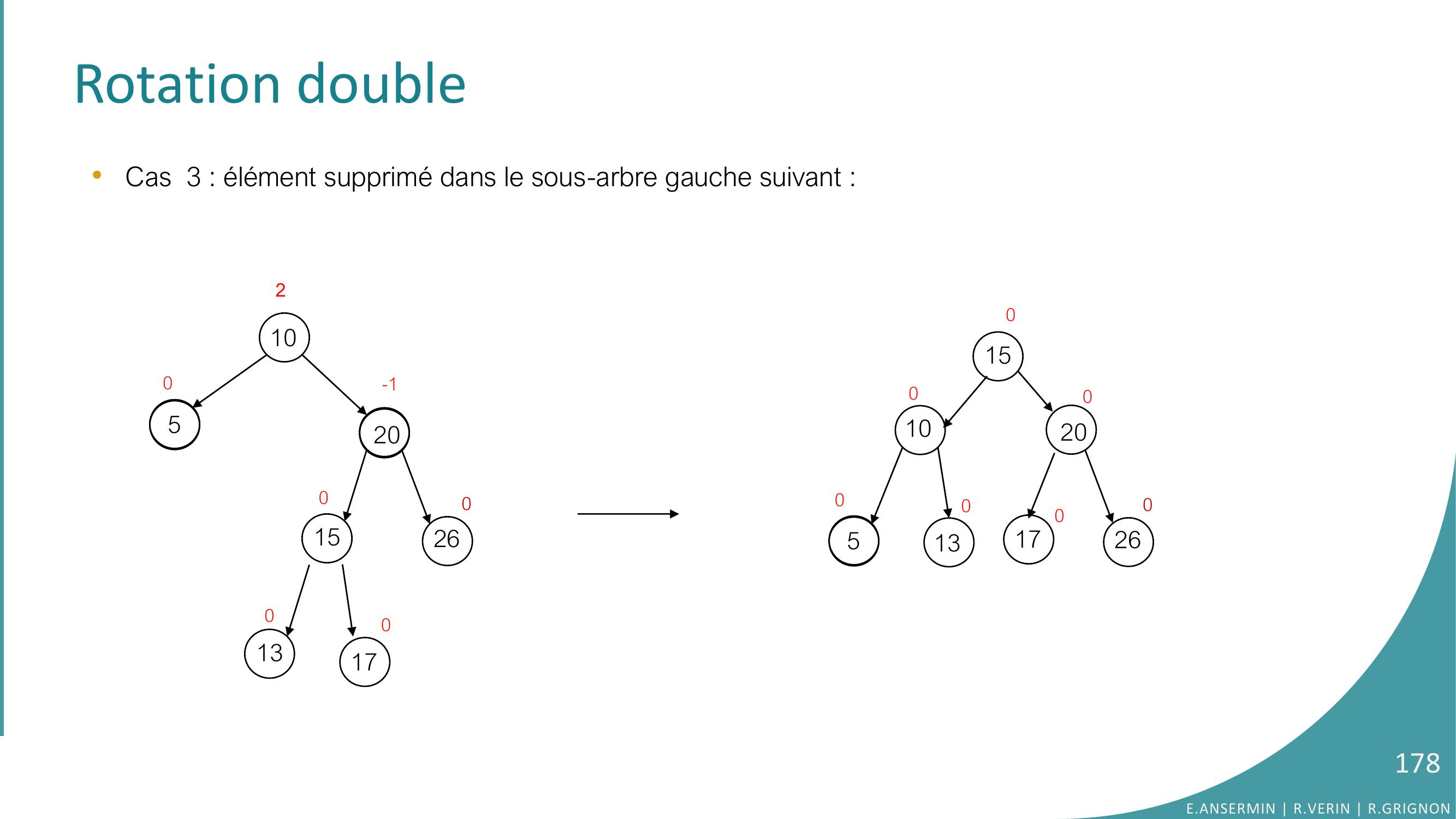
Page 177 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : 10520152600-10130170+2La rotation à gauche ne fonctionne pas !2010+1-25152601301700pivot ← fdafda ← fgpivotfgpivot ← a…a ← pivotRotation gaucheE.ANSERMIN R.VERIN R.GRIGNON177

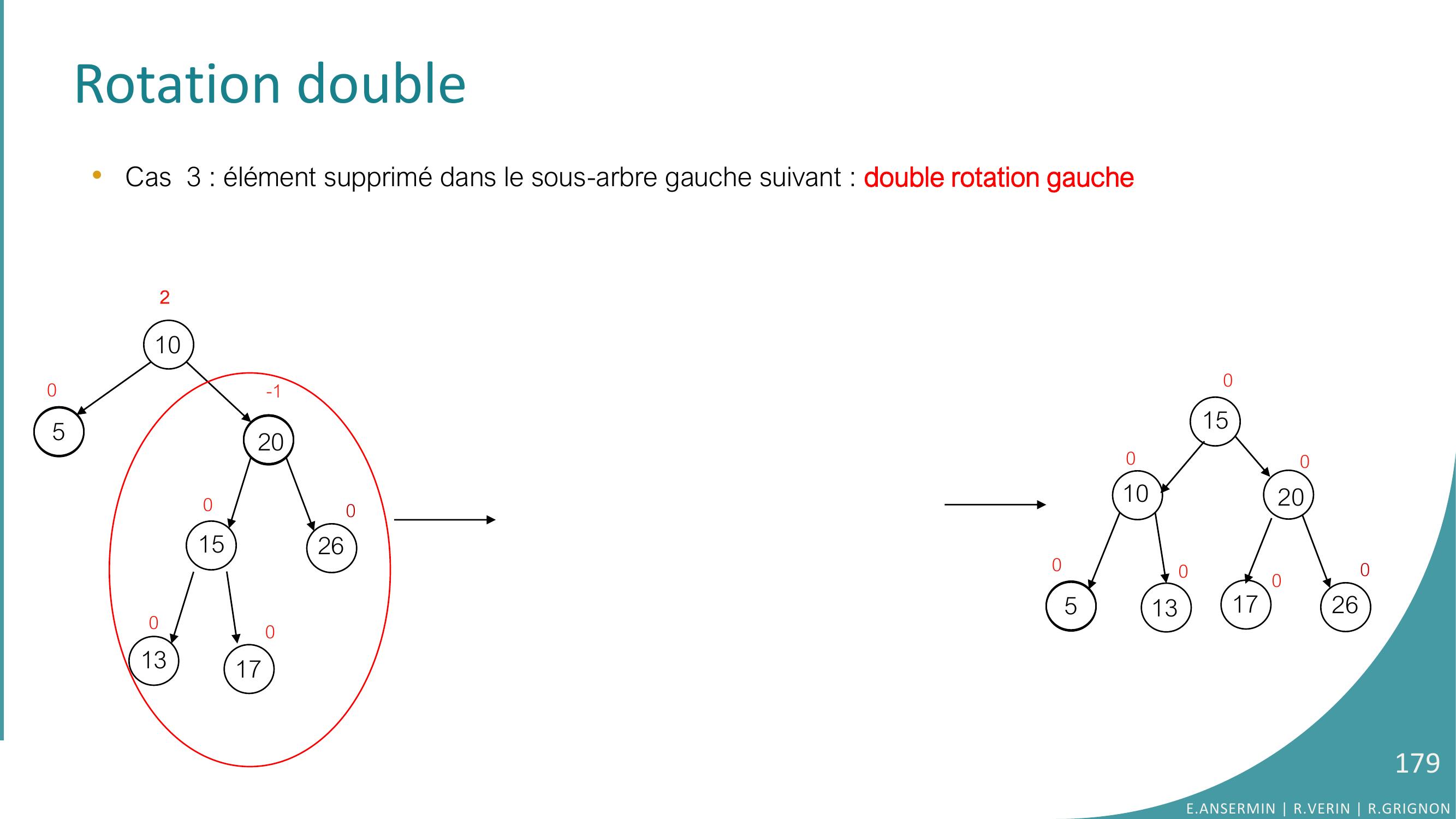
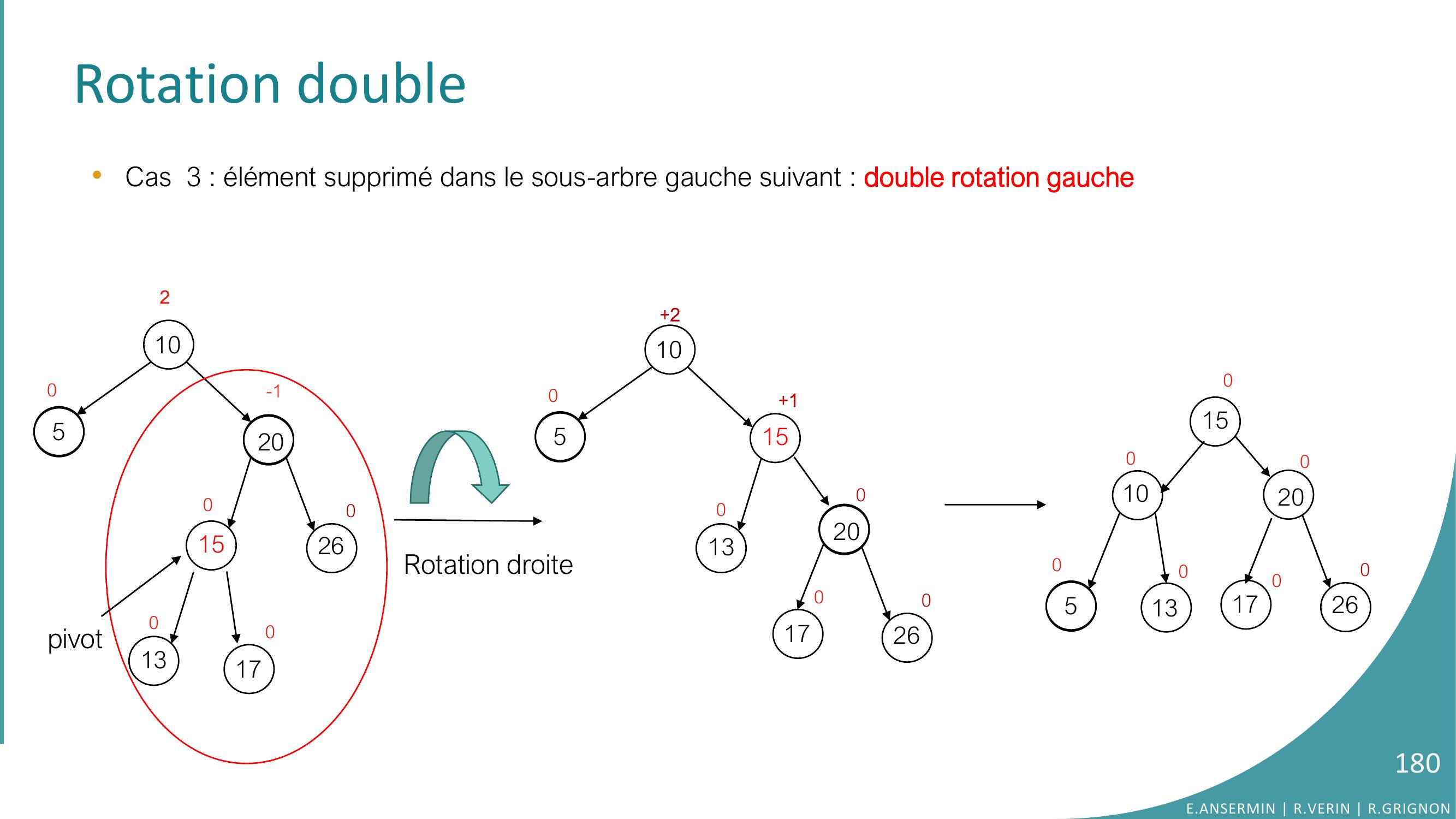
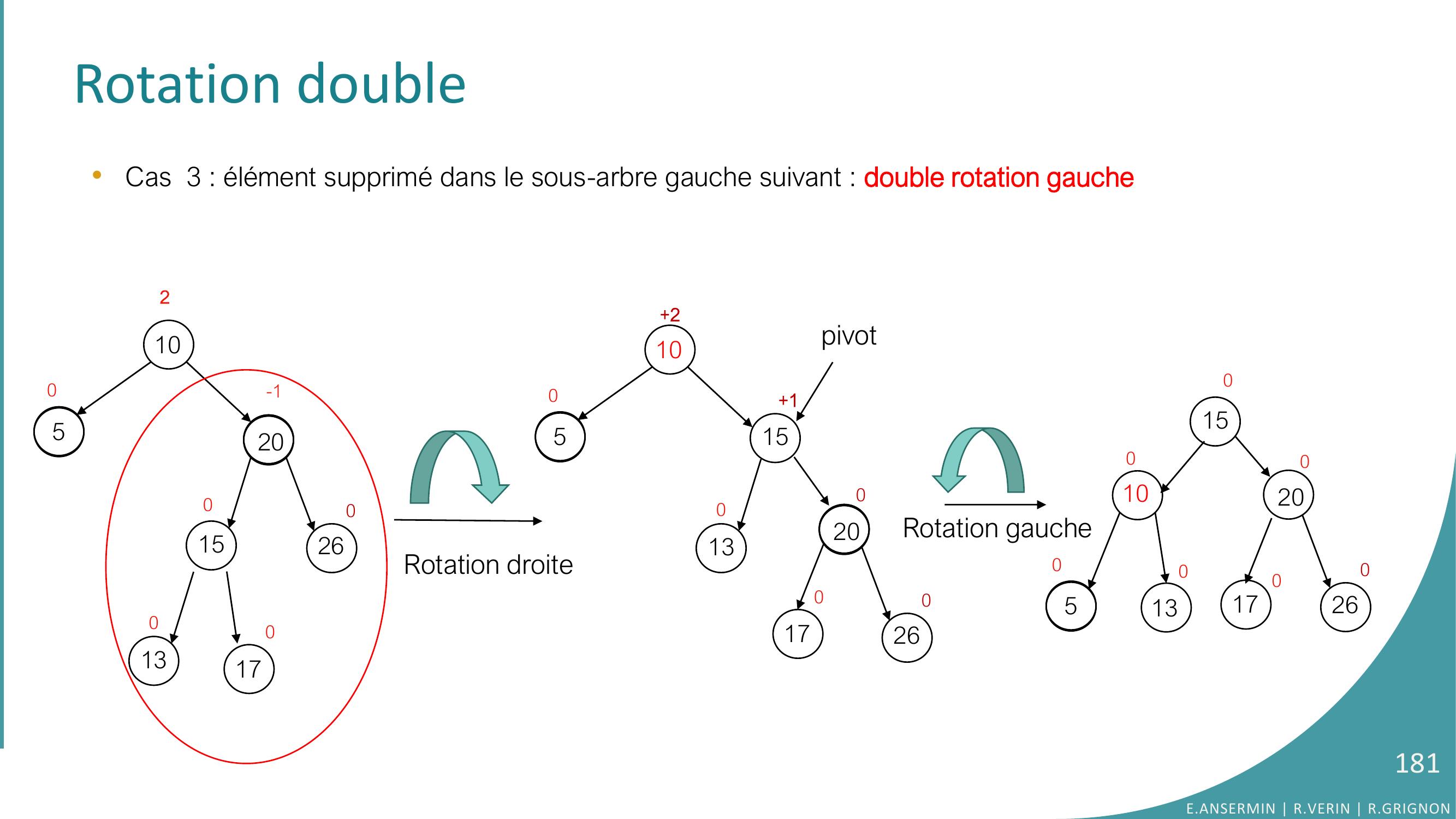
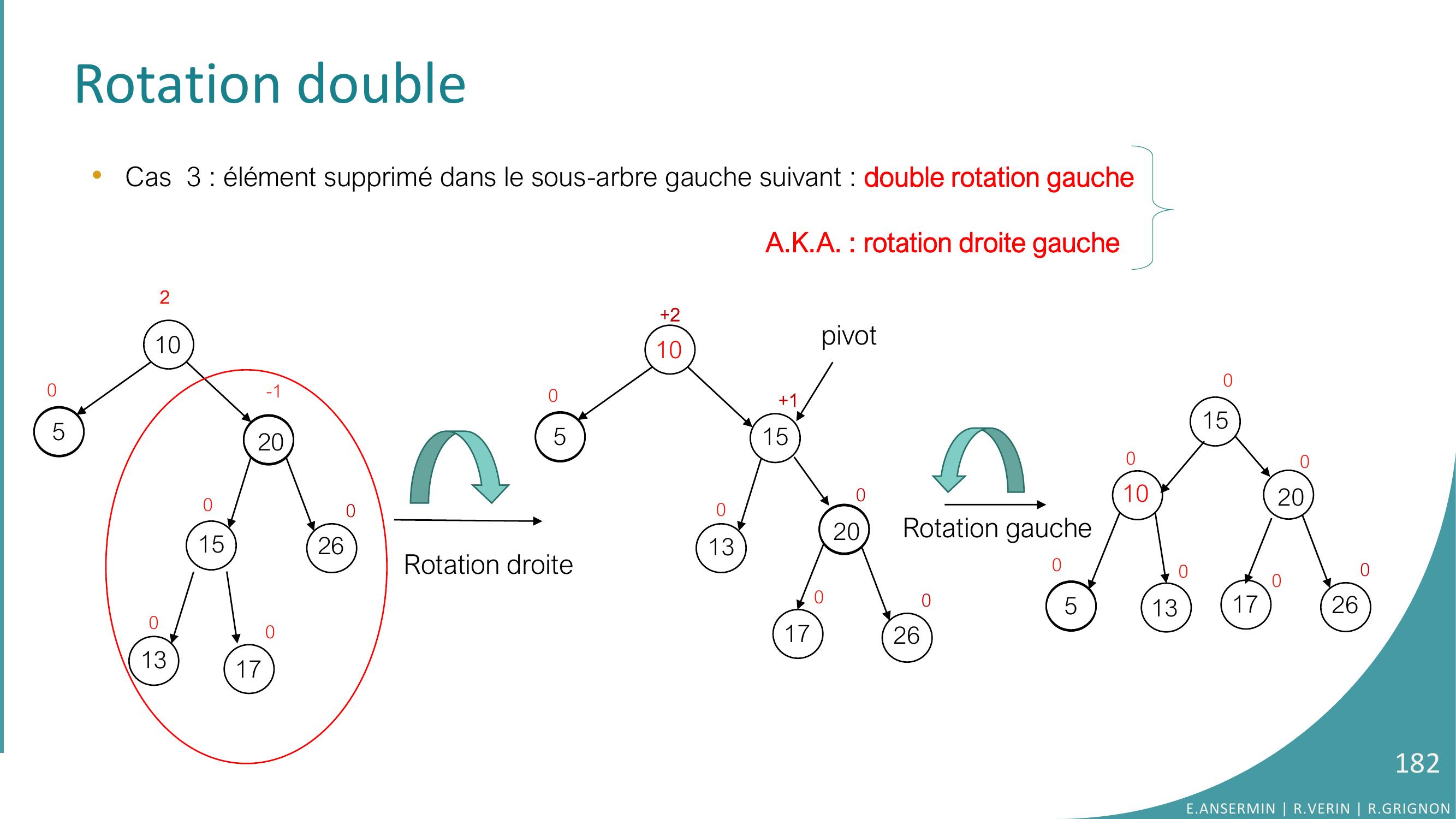
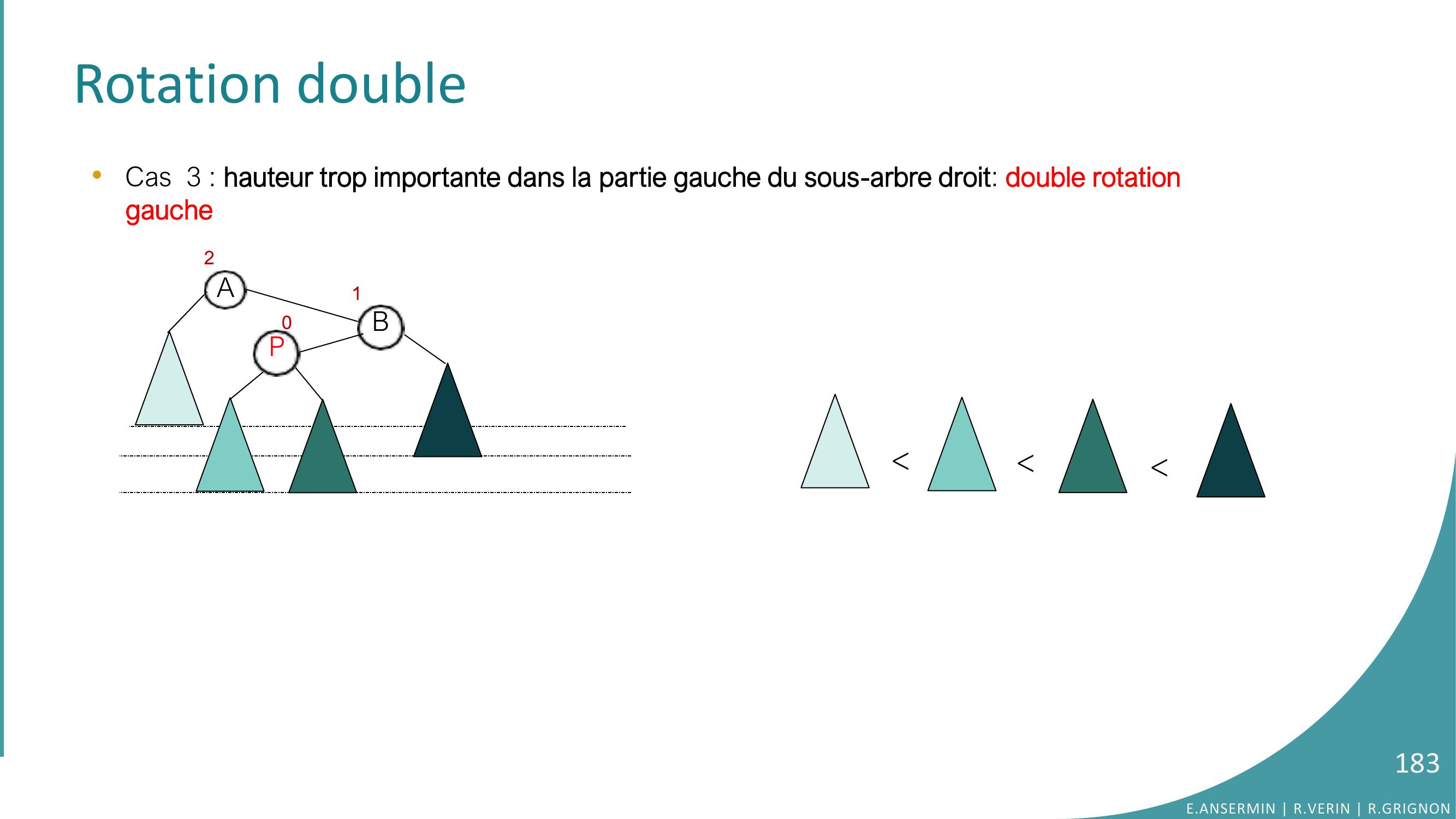
Page 178 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : 10520152600-10130170215105013201702600000E.ANSERMIN R.VERIN R.GRIGNON178

Page 179 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : double rotation gauche 10520152600-10130170215105013201702600000E.ANSERMIN R.VERIN R.GRIGNON179

Page 180 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : double rotation gauche 10520152600-1013017021510501320170260000010501520260170130Rotation droitepivot0+1+2E.ANSERMIN R.VERIN R.GRIGNON180

Page 181 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : double rotation gauche10520152600-1013017021510501320170260000010501520260170130Rotation droitepivotRotation gauche0+1+2E.ANSERMIN R.VERIN R.GRIGNON181

Page 182 : Rotation double•Cas 3 : élément supprimé dans le sous-arbre gauche suivant : double rotation gaucheA.K.A. : rotation droite gauche 10520152600-1013017021510501320170260000010501520260170130Rotation droiteRotation gauchepivot0+1+2E.ANSERMIN R.VERIN R.GRIGNON182

Page 183 : Rotation double•Cas 3 : hauteur trop importante dans la partie gauche du sous-arbre droit: double rotation gauche A12BP0E.ANSERMIN R.VERIN R.GRIGNON183

Page 184 : Rotation double•Cas 3 : hauteur trop importante dans la partie gauche du sous-arbre droit: double rotation gauche A-12BPA+12BProtationDroitefdA00E.ANSERMIN R.VERIN R.GRIGNON184

Page 185 : •Cas 3 : hauteur trop importante dans la partie gauche du sous-arbre droit: double rotation gauche Rotation doubleA-12BPA+12BProtationDroitefdA00ABP000rotationGaucheAE.ANSERMIN R.VERIN R.GRIGNON185

Page 186 : •Cas 3 : hauteur trop importante dans la partie gauche du sous-arbre droit: double rotation gauche Rotation doubleA-12BP-1A-12BP1ABP001ABP-100Double rotation gaucheDouble rotation gaucheE.ANSERMIN R.VERIN R.GRIGNON186

Page 187 : •Cas 3 : hauteur trop importante dans la partie gauche du sous-arbre droit: double rotation gauche Rotation double•Algorithme :FONCTION doubleRotationGauchea: ptr sur Arbre : ptr sur ArbreDEBUT fda ← rotationDroitefdaRETOURNER rotationGaucheaFINE.ANSERMIN R.VERIN R.GRIGNON187

Page 188 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation doubleABP-210E.ANSERMIN R.VERIN R.GRIGNON188

Page 189 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation doubleABPABP-210-10rotationGauchefgA-2E.ANSERMIN R.VERIN R.GRIGNON189

Page 190 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation doubleABPAABPPB-210-10000rotationDroiteArotationGauchefgA-2E.ANSERMIN R.VERIN R.GRIGNON190

Page 191 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation doubleABPAABPPB-210-10000rotationDroiteArotationGauchefgA-2A.K.A. : rotation gauche droiteE.ANSERMIN R.VERIN R.GRIGNON191

Page 192 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation doubleABP-21-1APB001ABP-211APB-100Double rotation droiteE.ANSERMIN R.VERIN R.GRIGNON192

Page 193 : •Cas 4 : hauteur trop importante dans la partie droite du sous-arbre gauche: double rotation droiteRotation double•Algorithme :FONCTION doubleRotationDroitea: ptr sur Arbre : ptr sur ArbreDEBUT fga ← rotationGauchefgaRETOURNER rotationDroiteaFINE.ANSERMIN R.VERIN R.GRIGNON193

Page 194 : Choix de la rotation• La rotation à effectuer dépend de la structure de l’arbre de quel côté se situe le déséquilibre.• Pour connaître la rotation à effectuer, il suffit de regarder l’équilibre de la racinenœud dont l’équilibre vaut +2 ou -2 et de ses fils :• SI equilibreracine EST EGAL A -2 • →rotation droite • SI equilibreracine EST EGAL A +2 → rotation gauche• →rotation gaucheE.ANSERMIN R.VERIN R.GRIGNON194

Page 195 : • La rotation à effectuer dépend de la structure de l’arbre de quel côté se situe le déséquilibre.• Pour connaître la rotation à effectuer, il suffit de regarder l’équilibre de la racinenœud dont l’équilibre vaut +2 ou -2 et de ses fils :• SI equilibreracine EST EGAL A -2 • →rotation droite • SI equilibrefgracine EST INF. OU EGAL A 0• →rotation simple• SINON• →rotation double• SI equilibreracine EST EGAL A +2 → rotation gauche• →rotation gauche• SI equilibrefdracine EST SUP. OU EGAL A 0• →rotation simple• SINON• →rotation doubleChoix de la rotationE.ANSERMIN R.VERIN R.GRIGNON195

Page 196 : Choix de la rotation•Algorithme :FONCTION equilibrerAVLa: ptr sur Arbre : ptr sur ArbreDEBUTSI equilibrea EST SUP. OU EGAL A 2 ALORS// sous-arbre droit plus profondSI equilibrefdA SUP. OU EGAL A 0 ALORSRETOURNER rotationGaucheaSINONRETOURNER doubleRotationGaucheaFIN SISINON SI equilibrea EST INF. OU EGAL A -2 ALORS // sous-arbre gauche plus profondSI equilibrefga INF. OU EGAL A 0 ALORSRETOURNER rotationDroiteaSINONRETOURNER doubleRotationDroiteaFIN SI FIN SIRETOURNER aFINE.ANSERMIN R.VERIN R.GRIGNON196

Page 197 : Complexité de l’AVL• Les opérations de rotations sont à compléxité constante O1• L’opération d’insertion ajoute une hauteur de 1 sur la branche où est inséré l’élément : unerotation suffit pour rééquilibrer l’arbre.• L’opération de suppression peut exécuter une rotation sur chaque ancêtre du nœud supprimé. Mais celles-ci étant en temps constant, le nombre de rotations dépend de la hauteur de l’arbre.• Donc, pour un arbre AVL de n nœuds, le temps total d’ajout ou suppression est : 𝑶𝐥𝐨𝐠𝟐𝒏E.ANSERMIN R.VERIN R.GRIGNON197

Page 198 : Résumé • Le facteur d’équilibre d’un arbre représente la différence de hauteur entre le sous-arbre gauche et droit : il permet de quantifier l’équilibre de l’arbre.• Les AVL sont des arbres auto-équilibrés garantissant une structure de l’arbre permettant d’optimiser les opérations de recherche, d’insertion et de suppression.• L’ AVL exploite des opérations de rotation autour d’un nœud pivot pour rééquilibrer un arbre.• Il existe d’autre types d’arbres auto-équilibrés comme les arbres rouge-noirs!E.ANSERMIN R.VERIN R.GRIGNON198

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198