CM5 Complexes
Télécharger le CM5 Complexes en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
Page 1 : ApplicationsNombres ComplexesAlgebre-Premier semestre 20211Applications2Nombres ComplexesN. Arancibia - relu par D. CransacAlgebre
Page 2 : ApplicationsNombres ComplexesAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre
Page 3 : ApplicationsNombres ComplexesLes Nombres ComplexesIntroduction :L’equationx + 2 = 1n’a pas de solution dans N, mais elle en a dans Z, un ensemble plusgrand que N .L’equation3x = 1n’a pas de solution dans Z, mais elle en a dans Q.L’equationx2 = 1n’a pas de solution dans R.On va donc construire un ensemble plus grand que R dans lequel cetteequation possede des solutions. On appellera cet ensemble C :l’ensemble des nombres complexes.N. Arancibia - relu par D. CransacAlgebre
Page 4 : ApplicationsNombres ComplexesLes Nombres ComplexesOn definit un element particulier de C, note i qui n’est pas reel, tel quei2 = 1.L’equation x2 + 1 = 0 possede alors 2 solutionsx2 + 1 = 0 ⇐⇒x2 i2 = 0⇐⇒x ix + i = 0⇐⇒x = i ou x = iN. Arancibia - relu par D. CransacAlgebre
Page 5 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDonnons la definition de l’ensemble des nombres complexes.DefinitionOn appelle ensemble des nombres complexes et on note C, l’ensemble desnombres de la formea + ibou a et b sont des reels,et ou i est un element qui verifiei2 = 1.N. Arancibia - relu par D. CransacAlgebre
Page 6 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesEtudions quelques proprietes de l’ensemble des nombres complexes.PropositionSoit z C. Alors il existe un unique couple a, b R2tel quez = a + ib.Demonstration.En effet, si a, b R2 et a′, b′ R sont tels quea + ib = z = a′ + ib′=⇒a a′ = ib′ b.En elevant au carre, on obtient une egalite entre nombres reels :a a′2 = b′ b2=⇒a = a′ et b = b′.N. Arancibia - relu par D. CransacAlgebre
Page 7 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesLa proposition precedente nous amene a definir.DefinitionSoit z = a + ib C. On dit que z a pour ecriture algebrique a + ib et ondefinit :a sa partie reelle qu’on noteraRez = a,b sa partie imaginaire qu’on noteraImz = b.Remarques :Les reels sont exactement les nombres complexes de partie imaginairenulle, c’est-a-direR = z C : Imz = 0 = a + 0i : a R C.Un nombre complexe de partie reelle nul est appele un imaginaire pur.L’ensemble des imaginaires purs sera note iR. C’est-a-direiR = z C : Rez = 0 = 0 + ib : b R C.N. Arancibia - relu par D. CransacAlgebre
Page 8 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDefinition Egalite entre nombres complexesDeux nombres complexesz = a + bietz′ = a′ + ib′sont egaux si et seulement si ils ont mˆeme partie reelle et mˆeme partieimaginaire :a + ib = a′ + ib′⇐⇒ a = a′b = b′.En resume :UNE egalite de nombres complexes = DEUX egalites de nombres reelsN. Arancibia - relu par D. CransacAlgebre
Page 9 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesL’ensemble C est muni de deux operations : d’addition et de multiplicationqui generalisent celles que nous connaissons sur R.Definition Addition sur CPour tousz = a + ib Cetz′ = a′ + ib′ Con definitz + z′ = a + a′ + ib + b′.Ce qui signifie queRez + z′ = Rez + Rez′Imz + z′ = Imz + Imz′.N. Arancibia - relu par D. CransacAlgebre
Page 10 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDefinition Multiplication sur CPour tousz = a + ib Cetz′ = a′ + ib′ Con definitz · z′ = aa′ bb′ + i ab′ + a′b. .Ce qui signifie queRezz′ = RezRez′ ImzImz′Imzz′ = RezImz′ + ImzRez′.N. Arancibia - relu par D. CransacAlgebre
Page 11 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDefinitionEnfin, pour tout z = x + iy Con a1z =1x + iy = x iyx2 + y 2 .Remarque :En general :Rezz′ ̸= RezRez′etImzz′ ̸= ImzImz′En particulier :Rez2 ̸= Rez2etImz2 ̸= Imz2.N. Arancibia - relu par D. CransacAlgebre
Page 12 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesPropositionL’applicationf :R2 7→Ca, b 7→z = a + ibrealise une bijection de R2 sur C.DemonstrationL’application f est surjective par la definition de C.Montrons que f est injective : Pour z, z′ C2 avecz = a + ib, a, b R2z′ = a′ + ib′, a′, b′ R2Montrons quez = z′ ⇒a, b = a′, b′Supposons z = z′. Il vienta + ib = a′ + ib′Donc a = a′ et b = b′ et z = z′N. Arancibia - relu par D. CransacAlgebre
Page 13 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesInterpretation geometrique de C :La bijection f : a, b 7→z = a + ib, nouspermet d’identifier l’ensemble des nombrescomplexe au plan usuel muni d’un repereorthonorme direct O,⃗i,⃗j :On associe a z = a + ib C un uniquepoint M du planz = a + ib 7→M = a, b R2,et un unique vecteur ⃗v tel quez 7→v = a⃗i + b⃗j.On dit que z = a + ib est l’affixe du point M et du vecteur ⃗v decoordonnees a, b, et on ecrit Mz et ⃗vz.N. Arancibia - relu par D. CransacAlgebre
Page 14 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDefinitionSoit z = x + iy C.On appelle conjugue de z le nombre complexe z, defini parz = x iyi.e.z = Rez iImz.N. Arancibia - relu par D. CransacAlgebre
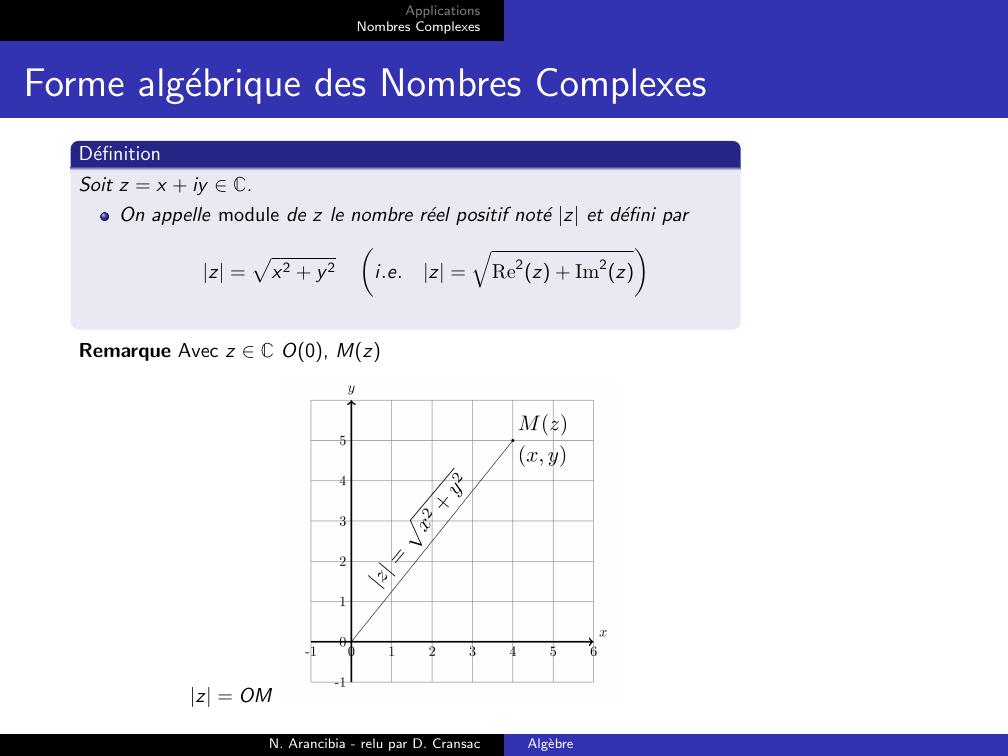
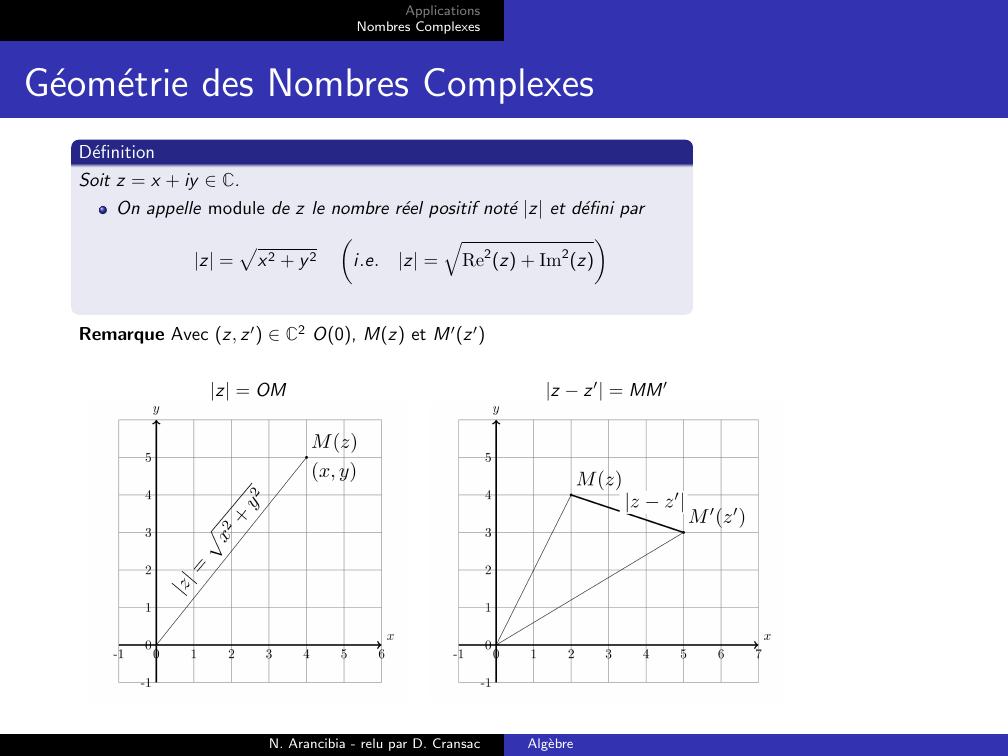
Page 15 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDefinitionSoit z = x + iy C.On appelle module de z le nombre reel positif note z et defini parz =px2 + y 2i.e.z =qRe2z + Im2zRemarque Avec z C O0, Mzz = OMN. Arancibia - relu par D. CransacAlgebre
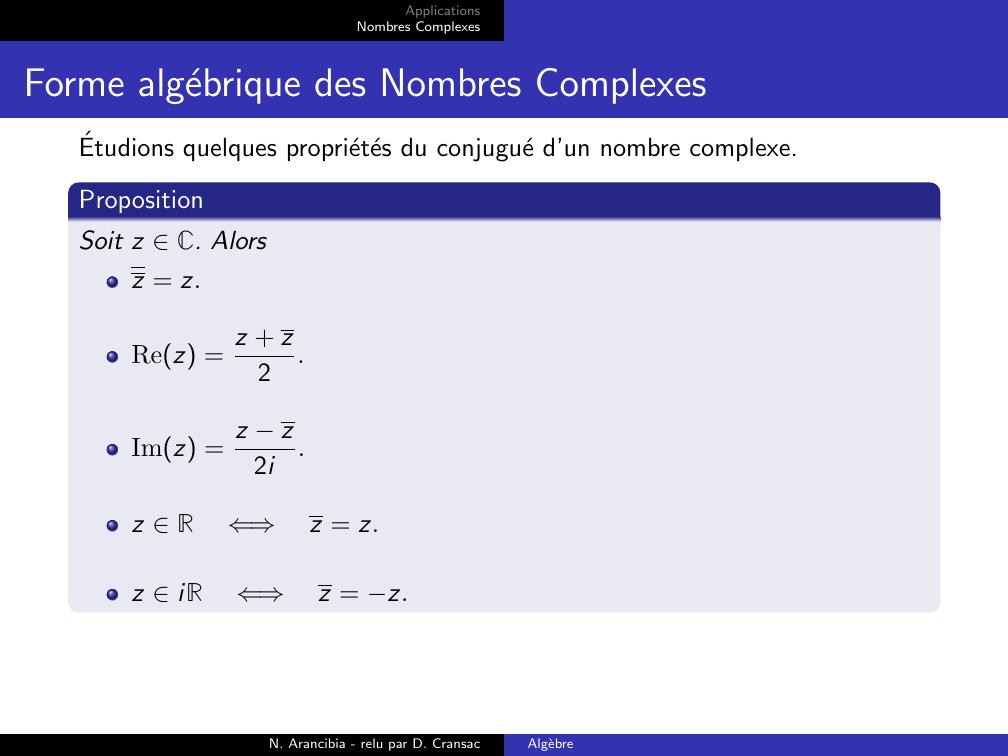
Page 16 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesEtudions quelques proprietes du conjugue d’un nombre complexe.PropositionSoit z C. Alorsz = z.Rez = z + z2.Imz = z z2i.z R⇐⇒z = z.z iR⇐⇒z = z.N. Arancibia - relu par D. CransacAlgebre
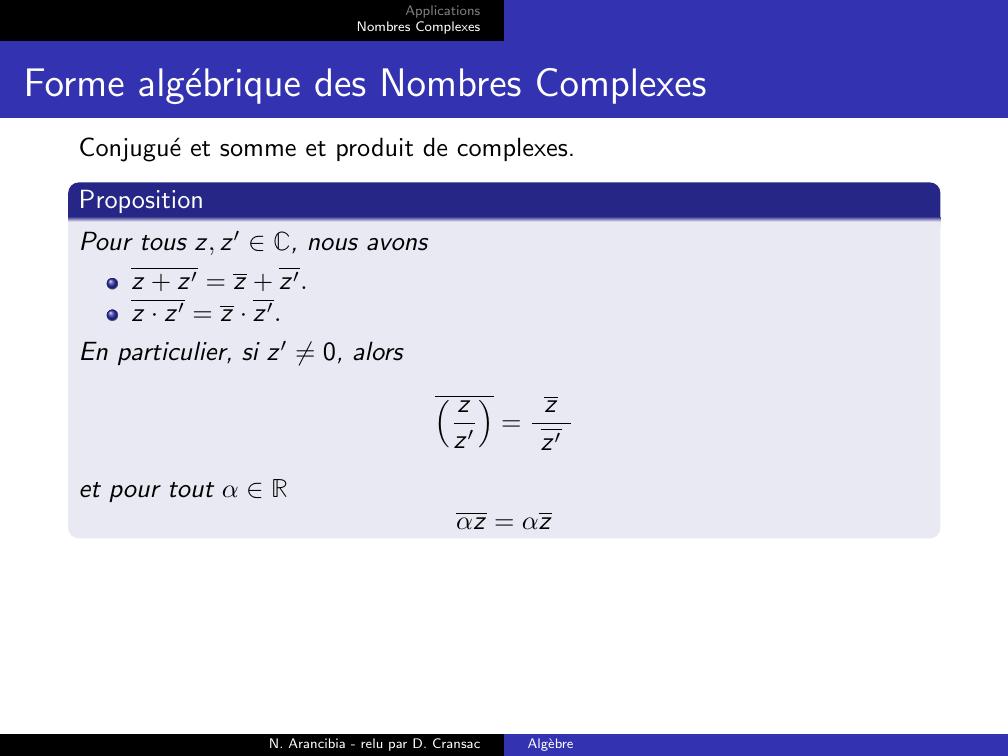
Page 17 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesConjugue et somme et produit de complexes.PropositionPour tous z, z′ C, nous avonsz + z′ = z + z′.z · z′ = z · z′.En particulier, si z′ ̸= 0, alors zz′=zz′et pour tout α Rαz = αzN. Arancibia - relu par D. CransacAlgebre
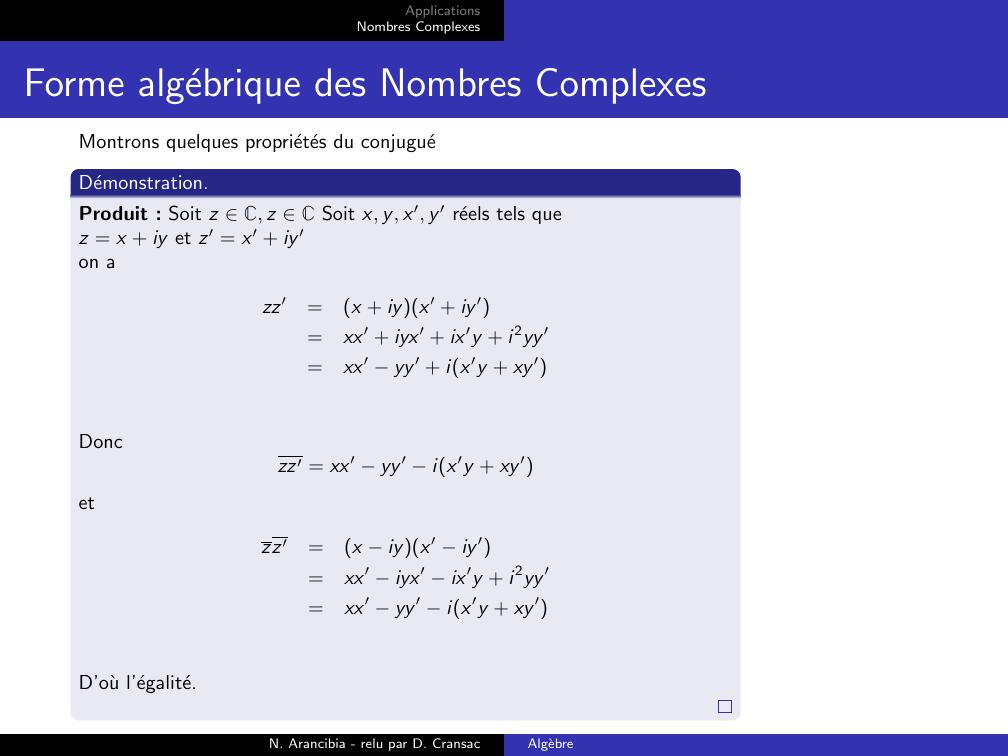
Page 18 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesMontrons quelques proprietes du conjugueDemonstration.Produit : Soit z C, z C Soit x, y, x′, y ′ reels tels quez = x + iy et z′ = x′ + iy ′on azz′=x + iyx′ + iy ′=xx′ + iyx′ + ix′y + i2yy ′=xx′ yy ′ + ix′y + xy ′Donczz′ = xx′ yy ′ ix′y + xy ′etzz′=x iyx′ iy ′=xx′ iyx′ ix′y + i2yy ′=xx′ yy ′ ix′y + xy ′D’ou l’egalite.N. Arancibia - relu par D. CransacAlgebre
Page 19 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDonnons maintenant certaines proprietes du module.PropositionSoient z, z′ C.Proprietes algebriques :z = zzz′ = z z′, et si z′ ̸= 0 alors zz′ = zz′.Proprietes geometriques :z = 0 ⇐⇒z = 0.Rez zetImz z.N. Arancibia - relu par D. CransacAlgebre
Page 20 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesPropositionPour tout z C nous avonszz = Re2z + Im2z = z2.Remarque :L’inverse de z = x + iy Cse calcule donc grˆace a la formulezz = z2. En effetzz = z2=⇒1z =zz2 = x iyx2 + y 2 .N. Arancibia - relu par D. CransacAlgebre
Page 21 : ApplicationsNombres ComplexesForme algebrique des Nombres ComplexesDeux autres proprietes importantes du module sont :PropositionSoient z, z′ C.Inegalite triangulaire :z + z′ z + z′.Inegalite triangulaire generalisee 1 :z z′ z z′ z + z′.Inegalite triangulaire generalisee 2 :z z′ z + z′ z + z′.N. Arancibia - relu par D. CransacAlgebre
Page 22 : ApplicationsNombres ComplexesNombres complexes de module 1On se place dans un repere 0, →u , →v , orthonorme, oriente.DefinitionOn appelle cercle trigonometrique et on note U l’ensemble des nombrescomplexes de module 1 :U = z C : z = 1.Remarque : Geometriquement, U est le circle de centre 0 et rayon 1. Eneffet,x + iy U⇐⇒z =px2 + y 2 = 1⇐⇒x2 + y 2 = 1.N. Arancibia - relu par D. CransacAlgebre
Page 23 : ApplicationsNombres ComplexesNombres complexes de module 1DefinitionSoit z U, Mz et θ = →u , →OM.On definit cos θ et sin θ comme l’abscisse et l’ordonnee de MMcos θ, sin θRemarquePour un point du cercle trigonometrique, on a, en utilisantla definition geometrique rapport des longueurs dans untriangle rectangle du cosinus et du sinuscos θ = x1 = xetsin θ = y1 = y.Cette nouvelle definition du cos et du sin est bien compa-tible avec la definition geometrique et l’etend aux anglessuperieur a π2 et aux angles negatifs.N. Arancibia - relu par D. CransacAlgebre
Page 24 : ApplicationsNombres ComplexesNombres complexes de module 1DefinitionSoit θ R, on appelle exponentielle iθ le nombre complexe defini pareiθ = cos θ + i sin θ.Remarque : Notons que pour tout θ R,eiθ UDe plus,eiθ = 1 eteiθ = cosθ + i sin θ =qcos2θ + sin2θ.Donccos2θ + sin2θ = 1N. Arancibia - relu par D. CransacAlgebre
Page 25 : ApplicationsNombres ComplexesNombres complexes de module 1Les remarques precedentes nous permettent d’enoncer le resultat suivant.TheoremePour tout z Cz U⇐⇒θ R, z = eiθ.En resumeU = eiθ, θ R.Pour tous θ R, θ′ R on aeiθ = eiθ′⇐⇒ cosθ = cosθ′sinθ = sinθ′⇐⇒θ = θ′mod 2π.N. Arancibia - relu par D. CransacAlgebre
Page 26 : ApplicationsNombres ComplexesNombres complexes de module 1Etudions quelques proprietes de l’exponentielle iθ.TheoremeSoient θ, θ′ R et n N.Conjugaison :eiθ = eiθ = 1eiθFormule d’Euler :cosθ = eiθ + eiθ2etsinθ = eiθ eiθ2i.N. Arancibia - relu par D. CransacAlgebre
Page 27 : ApplicationsNombres ComplexesNombres complexes de module 1Demonstration.Conjugaison : Pour tout reel θ R, on aeiθ = cosθ + i sinθ = cosθ i sinθ = cosθ + i sinθ = eiθFormule d’Euler : Ces formules sont evidentes a partir de la definitionde eiθ.N. Arancibia - relu par D. CransacAlgebre
Page 28 : ApplicationsNombres ComplexesNombres complexes de module 1Etudions quelques proprietes de l’exponentielle iθ.TheoremeSoient θ, θ′ R et n N.Transformation des sommes en produits :eiθ+θ′ = eiθ · eiθ′.Formule de De Moivre :cosθ + i sinθn = cosnθ + i sinnθ.N. Arancibia - relu par D. CransacAlgebre
Page 29 : ApplicationsNombres ComplexesNombres complexes de module 1Demonstration.Transformation des sommes en produits : Soit θ R et θ′ R. Alorseiθ · eiθ = cosθ + i sinθcosθ′ + i sinθ′= cosθ cosθ′ sinθ sinθ′ + icosθ sinθ′ + sinθ cosθ′= cosθ + θ′ + i sinθ + θ′ = eiθ+θ′.Formule de De Moivre : Soit θ R. Alors le point precedent nouspermet, grˆace a une recurrence simple, de conclureeiθn = einθ =⇒cosθ + i sinθn =eiθn=einθ = cosnθ + i sinnθ.N. Arancibia - relu par D. CransacAlgebre
Page 30 : ApplicationsNombres ComplexesApplication a la trigonometrieEtudions quelques applications de l’exponentiele iθ a la trigonometrie.Linearisation des puissances de cosinus et sinus : Lineariser uneexpression polynomiale de la formecoskx · sinlxen sinx et cosx, c’est l’exprimer comme une combinaison lineaire decosx, cos2x, cos3x, · · ·etsinx, sin2x, sin3x, · · ·en supprimant toute puissance et tout produit.N. Arancibia - relu par D. CransacAlgebre
Page 31 : ApplicationsNombres ComplexesApplication a la trigonometrieDecrivons la methode avec un exemple : Lineariser cos4x sin2x. Onprocede comme suit :1 On utilise les formules d’Euler pour changer cosx et sinx en eix eteix.cos4x sin2x =eix + eix24 eix eix2i22 On developpe completement, avec le binˆome de Newton.cos4x sin2x = 164e4ix + 4e2ix + 6 + 4e2ix + e4ix·e2ix 2 + e2ix= 164e6ix + 2e4ix e2ix 4 e2ix + 2e4ix + e6ix.3 On regroupe les termes deux a deux conjugues pour reconnaˆıtre descosαx ou sinβx grˆace a la formule d’Euler.cos4x sin2x = 164e6ix + e6ix+ 2e4ix + e4ixe2ix + e2ix4= 132cos6x 2 cos4x + cos2x + 2.N. Arancibia - relu par D. CransacAlgebre
Page 32 : ApplicationsNombres ComplexesApplication a la trigonometrieTechnique de l’angle moitie : Pour factoriser une expression du typeeix + eiyeteix eiy.On procede comme suit :1On commence par noter quex = x + y2+ x y2ety = x + y2x y2.2Donceix + eiy =eix+y2· eixy2+ eix+y2· eixy2= eix+y2eixy2+ eixy2= 2eix+y2cosx y2.De mˆemeeix eiy = eix+y2eixy2eixy2= 2eix+y2i sinx y2.N. Arancibia - relu par D. CransacAlgebre
Page 33 : ApplicationsNombres ComplexesApplication a la trigonometrieLa technique de l’angle de l’angle moitie nous permet de calculerfacilement les expressions suivants :Propositioncosx + cosy = 2 cosx + y2cosx y2cosx cosy = 2 sinx + y2sinx y2sinx + siny = 2 sinx + y2cosx y2sinx siny = 2 cosx + y2sinx y2.Par exemple : En utilisantsinx = Imcosx+i sinx = Imeixetsiny = Imcosy+i siny = Imeiyon deduitsinx + siny = Imeix + eiy=Im2eix+y2cosx y2=2 sinx + y2cosx y2.N. Arancibia - relu par D. CransacAlgebre
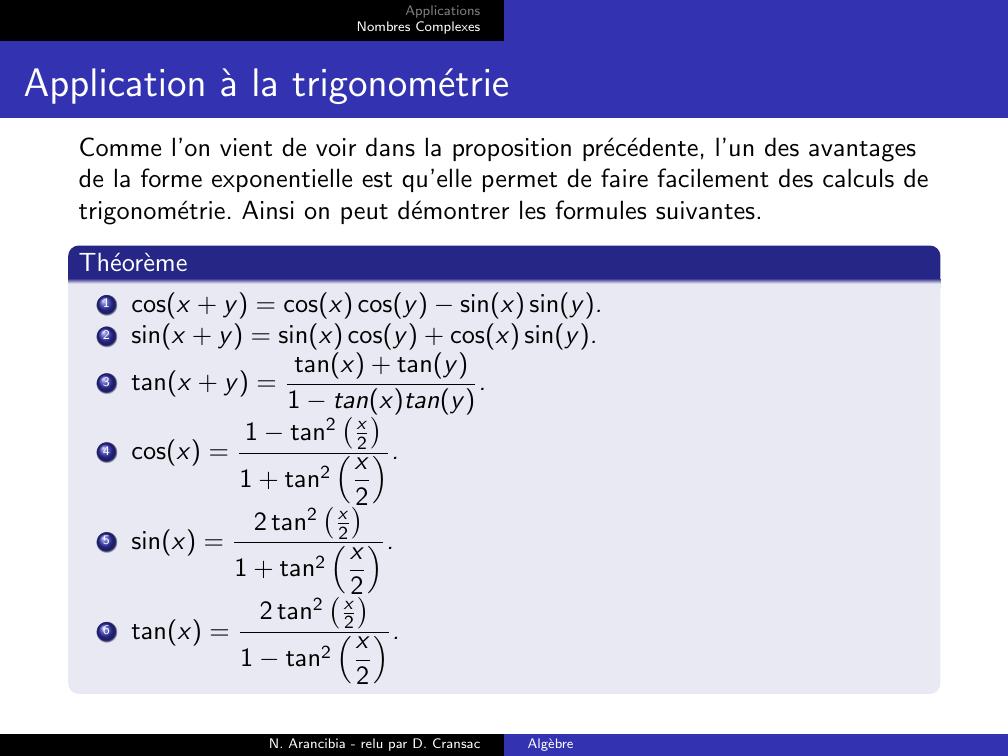
Page 34 : ApplicationsNombres ComplexesApplication a la trigonometrieComme l’on vient de voir dans la proposition precedente, l’un des avantagesde la forme exponentielle est qu’elle permet de faire facilement des calculs detrigonometrie. Ainsi on peut demontrer les formules suivantes.Theoreme1cosx + y = cosx cosy sinx siny.2sinx + y = sinx cosy + cosx siny.3tanx + y = tanx + tany1 tanxtany.4cosx = 1 tan2 x21 + tan2 x2.5sinx =2 tan2 x21 + tan2 x2.6tanx =2 tan2 x21 tan2 x2.N. Arancibia - relu par D. CransacAlgebre
Page 35 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeL’exponentielle iθ nous offre une autre maniere d’exprimer tout nombrecomplexe. Soit z C avec z ̸= 0. Notons que si on calcule le module dezzon obtientzz =z · 1z = z ·1z = z · 1z = zz = 1.Donc pour tout z C avec z ̸= 0, nous avonszz U=⇒θ R,zz = eiθ.Par consequent, tout nombre complexe peut ˆetre ecrit sous la formez = z · eiθ.N. Arancibia - relu par D. CransacAlgebre
Page 36 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeTheoremeTout nombre complexe non nul peut ˆetre ecrit sous la forme :z = reiθavec r R×+ et θ R.Cette forme est dite trigonometrique.Le reel r est unique car : r = z En effet, z = reiθ = r · eiθ = r.Mais θ, appele UN argument de z, et note argz, est seulement uniquea 2π pres.En revanche il existe un et un seul argument de z dans π, π, et celuici est appele l’argument principal de z.Le couple r, θ est aussi appele UN couple de coordonnees polaires dupoint d’image z.N. Arancibia - relu par D. CransacAlgebre
Page 37 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeRemarques :Zero n’a pas de forme trigonometrique, donc pas d’argument.Pour tout z, z′ Cz = z′⇐⇒ z = z′argz = argz′mod 2π.Exemple : Les formes trigonometriques des reels et des imaginaires purssont :Cas des reels : Pour tout x R:x = xei0 si x 0etx = xeiπ si x 0.Cas des imaginaires purs : Pour tout y R:iy = yei π2si y 0etiy = yei π2si y 0.N. Arancibia - relu par D. CransacAlgebre
Page 38 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeEtudions quelques proprietes des arguments.Proposition Proprietes des argumentsPour tous z C, z′ C× nous avonsargzz′ = argz + argz′mod2π.argz = argzmod2π.arg1z= argzmod2π.N. Arancibia - relu par D. CransacAlgebre
Page 39 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeDemonstration.argzz′ = argz + argz′mod2π : Nous avonszz′ = z · ei argzz′ · ei argz′ = zz′ · eiargz+argz′.D’ou on conclut que argzz′ = argz + argz′mod 2π.argz = argzmod2π : Nous avonsz = z · ei argz = z · ei argz = z · ei argz = z · ei argz.D’ou on conclut que argz = argzmod 2π.arg 1z= argzmod2π : Nous avons1z =1z · ei argz = 1z · ei argz.D’ou on conclut que arg 1z= argzmod 2π.N. Arancibia - relu par D. CransacAlgebre
Page 40 : ApplicationsNombres ComplexesForme Trigonometrique d’un nombre complexeSoit z C. Nous avons deux fa¸con d’exprimer z :Forme Algebrique : z = x + iy.Forme Trigonometrique : z = reiθ.Etudions le lien qui existe entre les deux ecritures.Theoreme Lien entre la forme algebrique et les formes trigonometriquesSoit z Cdeforme algebrique : z = x + iyet de forme trigonometrique : z = reiθ.1Forme algebrique en fonction d’une forme trigonometrique :x = r cosθety = r sinθ.2Forme trigonometrique en fonction d’une forme algebrique :r =px2 + y 2etθ = arctan yxmod 2πsi x 0,arctan yx+ πmod 2πsi x 0.N. Arancibia - relu par D. CransacAlgebre
Page 41 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesEtudions quelques equations polynomiales dans C. Commen¸cons par etudierles equations du second degre deux. Notre objectif est de montrer que touteequation de la formeaz2 + bz + c = 0,a C, b C, c Cpossede des solutions sur C.Definition Racines carrees d’un nombre complexeOn appelle racine carree d’un nombre complexe z tout nombre complexe ωverifiantω2 = z.TheoremePour tout z C, l’equation d’inconnue ω C :ω2 = z,possede exactement deux solutions opposees.N. Arancibia - relu par D. CransacAlgebre
Page 42 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesDemonstration.On commence par ecrire z sous forme trigonometriquez = reiθ, r R+, θ R.Posonsζ = reiθ2=⇒ζ2 = z.Nous disposons ainsi d’un exemple de racine carree de z, et grˆace a lui, nousallons trouver toutes les solutions de l’equation ω2 = z.Pour tout ω C, soit seiβ, avec s R+ son ecriture trigonometrique. Alorsω2 = z⇐⇒ω2 = ζ2⇐⇒s2ei2β = reiθ⇐⇒s2 = retei2β = eiθ⇐⇒s = ret2β = θmod 2π⇐⇒s = retβ = θ2mod π⇐⇒ω = rei θ2ouu = rei θ2 +π = rei θ2 .On a donc le resultat voulu.N. Arancibia - relu par D. CransacAlgebre
Page 43 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesAttention :x est une notation autorisee si x R+.z est une notation interdite si z C \ R+.Pourquoi cet interdit ? Parce que nous ne savons pas choisir, tout nombrecomplexe non nul a deux racines carrees distinctes qui se valent l’unel’autre. Il n’y a que dans le cas des reels positifs qu’on sait choisir car lesracines carrees d’un reel positif x sont toutes les deux reelles, l’une positive,l’autre negative, et on choisit de noter x la premiere.N. Arancibia - relu par D. CransacAlgebre
Page 44 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesDe la preuve du theoreme precedent, on sait que si la forme trigonometriquede z est reiθ, alors les deux racines carres de z sontrei θ2etrei θ2 .Le probleme c’est que, tres souvent il est tres difficile de determiner la formetrigonometrique d’un complexe. Dans ce cas, pour trouver les racines carres ilnous faut travailler avec l’ecriture algebrique du nombre complexe.N. Arancibia - relu par D. CransacAlgebre
Page 45 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesPour determiner l’ecriture algebrique des racines carrees, on procederacomme suit :1On cherche les racines de z = a + ib sous la forme w = x + iy.L’equation w 2 = z donne le systemew 2 = z⇐⇒x2 y 2 + i2xy = a + ib⇐⇒ x2 y 2 = a2xy = ben identifiant parties reelle et imaginaire.2On pensera systematiquement a ajouter l’equationw2 = z⇐⇒x2 + y 2 =pa2 + b2pour trouver les valeurs de x2 et y 2.3On prend ensuite les racines carrees, en faisant attention aux signesrelatifs de x et y, donne par l’equation 2xy = b.N. Arancibia - relu par D. CransacAlgebre
Page 46 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesDecrivons la methode avec un exemple :Calculer les racines carres de 24 + 10i.1On cherche les racines de z = a + ib sous la forme w = x + iy.w 2 = 24 + 10i⇐⇒x2 y 2 + i2xy = 24 + i10⇐⇒ x2 y 2 = 242xy = 102w2 = 24 + 10i⇐⇒x2 + y 2 =242 + 102 = 26.Nous avons donc trois equations :x2 + y 2 = 26x2 y 2 = 242xy = 10=⇒x2 = 25y 2 = 1xy = 53Nous avons donc les solutions :x, y = 5, 1oux, y = 5, 1⇐⇒w = 5 + iou w = 5 i.N. Arancibia - relu par D. CransacAlgebre
Page 47 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesMaintenant qu’on a montre que tout nombre complexe possede exactementdeux racines carrees, nous pouvons donner la preuve que toute equation dedegre 2 possede des solutions dans C.TheoremeSoient a, b et c trois nombres complexes avec a ̸= 0. Alors les solutions del’equation d’inconnue z C :az2 + bz + c = 0sontb + δ2aetb δ2a,ou δ est l’une quelconque des deux racines carrees du discriminant= b2 4ac.N. Arancibia - relu par D. CransacAlgebre
Page 48 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesDemonstration.Nous avonsaz2 + bz + c=az2 + ba z + ca=a z + b2a2b2 4ac4a2!.Soit δ l’une de deux racines carres de b2 4ac. Alors b24ac4a2= δ2a2.Ce quinous permet d’ecrireaz2 + bz + c=a z + b2a2 δ2a2!x2 y 2 = x yx + y=az + b2a + δ2a·z + b2a δ2a=az b δ2a·z b + δ2a.Les racines de az2 + bz + c sont doncb δ2aetb + δ2aN. Arancibia - relu par D. CransacAlgebre
Page 49 : ApplicationsNombres ComplexesEquations du second degre a coefficients complexesEn lien avec ce qui precede, la relation triviale :z xz y=z2 x + yz + xynous permet de calculer x et y quand on connaˆıt leur somme x + y et leurproduit xy.Theoreme Systemes somme-produitSoient a, b C.Les solutions du systeme somme-produit d’inconnuesx, y C x + y = bxy = csont les deux racines du polynˆome z2 bz + c eventuellement egales.Remarque : La somme des solutions de az2 + bz + c vaut baet leurproduit ca.N. Arancibia - relu par D. CransacAlgebre
Page 50 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteNous avons decrit les racines carrees de tout complexe non nul z. Faisons lemˆeme avec les racines de degre n. Pour tout z C et n N, nous allonsdonc etudier l’equation :ζn = z.Commen¸cons avec le cas z = 1.Definition Racines n-iemes de l’uniteSoit n N. On appelle racines n-iemes de l’unite tout nombre complexe ζtel queζn = 1On note Un l’ensemble de racines n-iemes de l’unite.Le resultat suivant nous donne une description de l’ensemble de racinesn-iemes de l’unite.TheoremeSoit n N. Alors il existe exactement n racines n-iemes de l’unite, qui sontUn =ne2ikπn:0 k n 1o.N. Arancibia - relu par D. CransacAlgebre
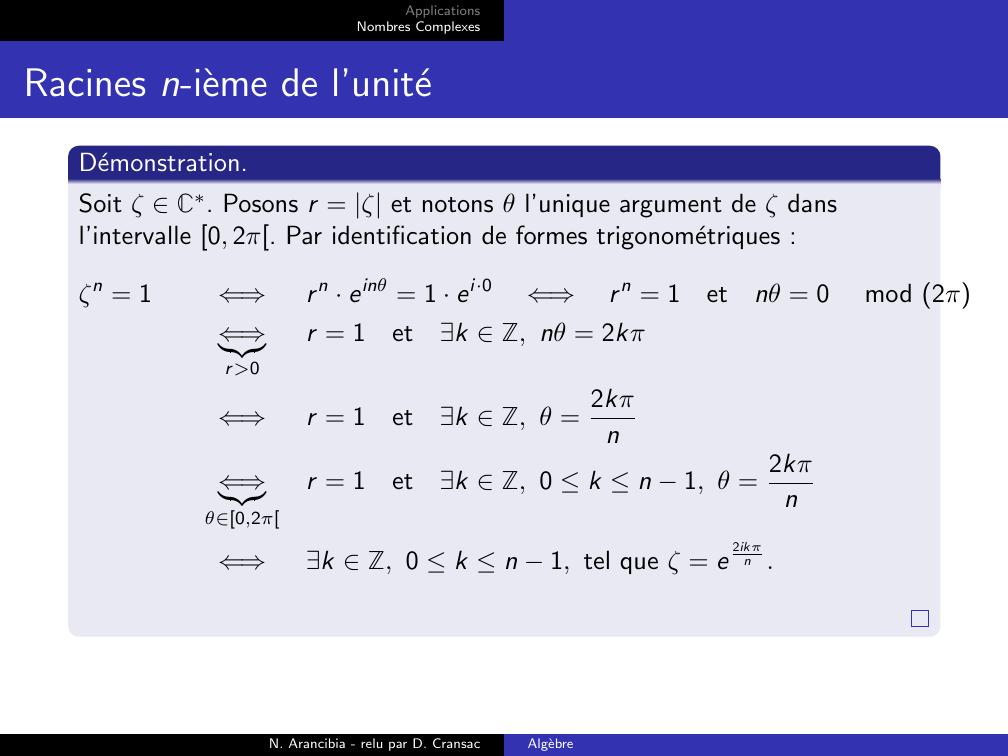
Page 51 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteDemonstration.Soit ζ C. Posons r = ζ et notons θ l’unique argument de ζ dansl’intervalle 0, 2π. Par identification de formes trigonometriques :ζn = 1⇐⇒r n · einθ = 1 · ei·0⇐⇒r n = 1etnθ = 0mod 2π⇐⇒zr0r = 1etk Z, nθ = 2kπ⇐⇒r = 1etk Z, θ = 2kπn⇐⇒zθ0,2πr = 1etk Z, 0 k n 1, θ = 2kπn⇐⇒k Z, 0 k n 1, tel que ζ = e2ikπn .N. Arancibia - relu par D. CransacAlgebre
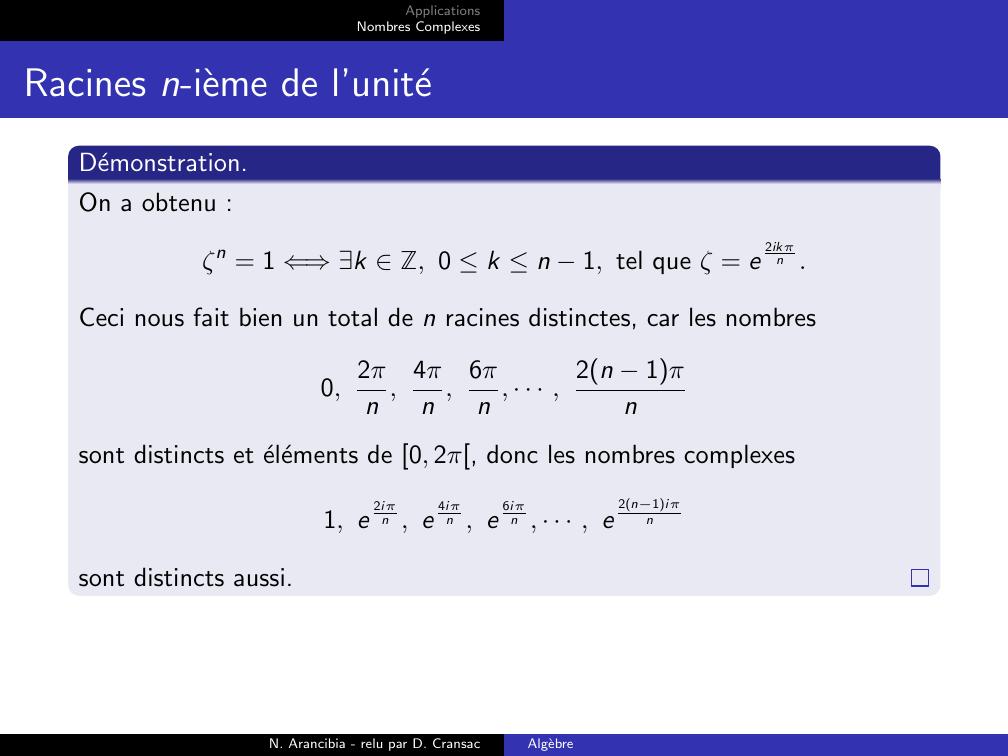
Page 52 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteDemonstration.On a obtenu :ζn = 1 ⇐⇒k Z, 0 k n 1, tel que ζ = e2ikπn .Ceci nous fait bien un total de n racines distinctes, car les nombres0, 2πn , 4πn , 6πn , · · · , 2n 1πnsont distincts et elements de 0, 2π, donc les nombres complexes1, e2iπn , e4iπn , e6iπn , · · · , e2n1iπnsont distincts aussi.N. Arancibia - relu par D. CransacAlgebre
Page 53 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteLes racines de l’unite satisfont la propriete suivante.PropositionSoit n un entier naturel superieur ou egal a 2. La somme des racines n-iemede l’unite est egale e 0. Autrement dit, soit ζ une racine n-ieme de l’unitedifferente de 1, alors1 + ζ + ζ2 + · · · + ζn1 = 0.Demonstration.On reconnaˆıt une suite geometrique de raison . La somme des termes est :1 + ζ + ζ2 + · · · + ζn1 = 1 ζn1 + ζ =01 + ζ = 0N. Arancibia - relu par D. CransacAlgebre
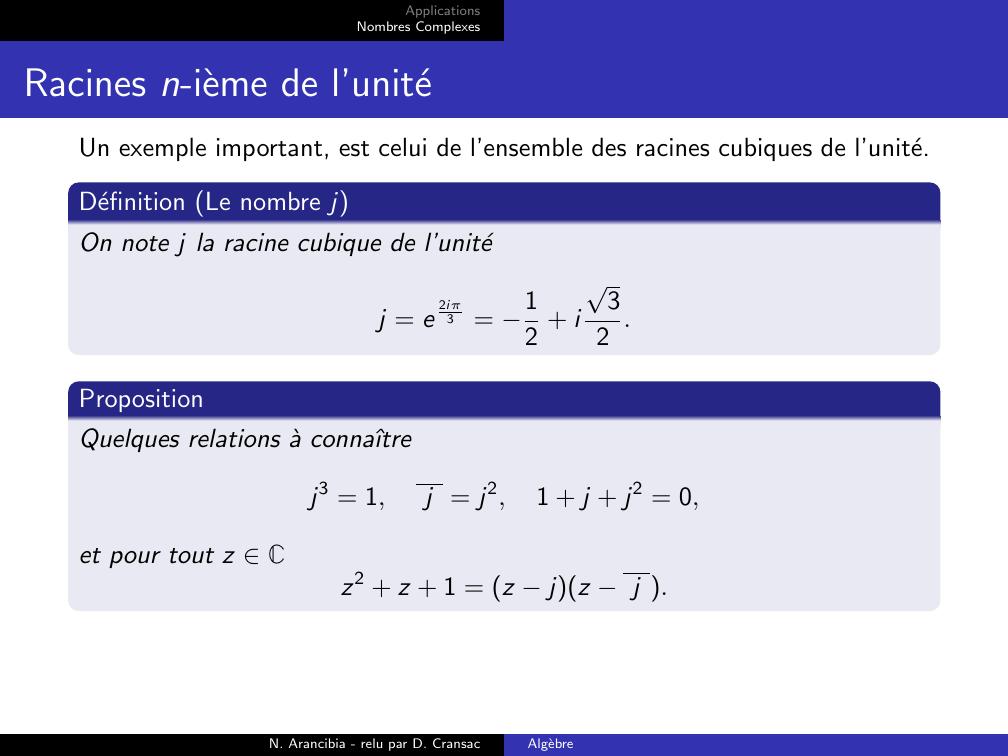
Page 54 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteUn exemple important, est celui de l’ensemble des racines cubiques de l’unite.Definition Le nombre jOn note j la racine cubique de l’unitej = e2iπ3 = 12 + i32 .PropositionQuelques relations a connaˆıtrej3 = 1,j = j2,1 + j + j2 = 0,et pour tout z Cz2 + z + 1 = z jz j .N. Arancibia - relu par D. CransacAlgebre
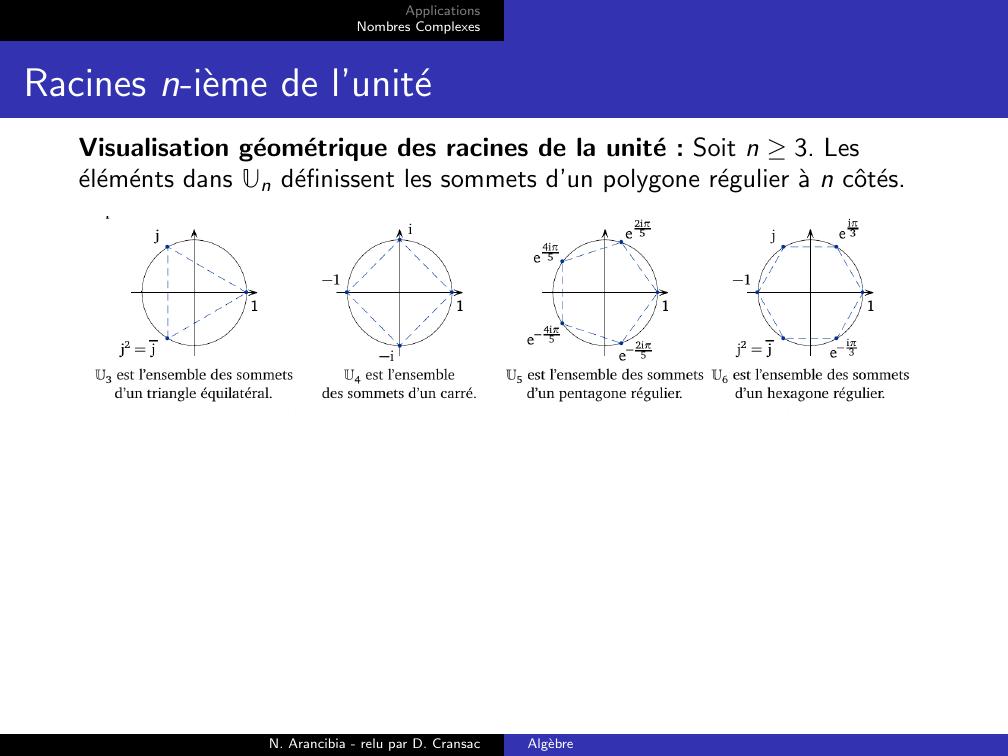
Page 55 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteVisualisation geometrique des racines de la unite : Soit n 3. Leselements dans Un definissent les sommets d’un polygone regulier a n cˆotes.N. Arancibia - relu par D. CransacAlgebre
Page 56 : ApplicationsNombres ComplexesRacines n-iemeEtudions maintenant les racines n-ieme de tout nombre complexe non nul.Definition Racines n-iemesSoit n Net z C non nul. On appelle Racine n-ieme de z tout nombrecomplexe ζ tel quez = ζn.L’ensemble de racines n-iemes de z est decrit dans le resultat suivant.TheoremeSoit n N.1La seule racine n-ieme de 0 est 0. En effet, ζn = 0 ⇐⇒ζ = 0.2Tout nombre complexe z = reiθ Cavec r 0 et θ R possedeexactement n racines n-iemes, a savoir :nr · eiθn + 2ikπn0 k n 1N. Arancibia - relu par D. CransacAlgebre
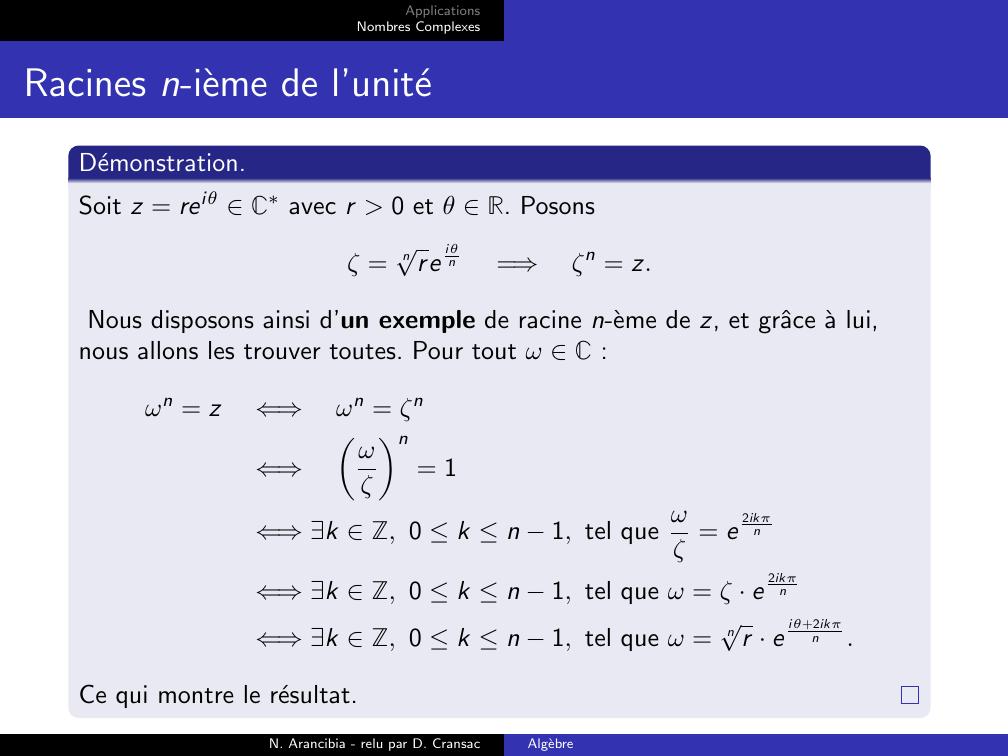
Page 57 : ApplicationsNombres ComplexesRacines n-ieme de l’uniteDemonstration.Soit z = reiθ Cavec r 0 et θ R. Posonsζ =nreiθn=⇒ζn = z.Nous disposons ainsi d’un exemple de racine n-eme de z, et grˆace a lui,nous allons les trouver toutes. Pour tout ω C :ωn = z⇐⇒ωn = ζn⇐⇒ωζn= 1⇐⇒k Z, 0 k n 1, tel que ωζ = e2ikπn⇐⇒k Z, 0 k n 1, tel que ω = ζ · e2ikπn⇐⇒k Z, 0 k n 1, tel que ω =nr · eiθ+2ikπn.Ce qui montre le resultat.N. Arancibia - relu par D. CransacAlgebre
Page 58 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesRegles de calcul sur les affixes :Pour tous vecteurs ⃗u et ⃗v du pland’affixes respectifs z et z′ et pour tousλ, µ R, le vecteur λ⃗v + µ⃗v a pouraffixe :λz + µz′.Pour A et B deux points du plan d’affixesrespectifs z et z′, l’affixe du vecteur ⃗ABestz′ z.Les notions de point, vecteur, coordonnees et nombre complexe sontequivalentes, on prefere d’ailleurs souvent ecrire qu’un point est EGAL a unnombre complexe, qu’un vecteur est EGAL a ses coordonnees.N. Arancibia - relu par D. CransacAlgebre
Page 59 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesDefinitionSoit z = x + iy C.On appelle module de z le nombre reel positif note z et defini parz =px2 + y 2i.e.z =qRe2z + Im2zRemarque Avec z, z′ C2 O0, Mz et M′z′z = OMz z′ = MM′N. Arancibia - relu par D. CransacAlgebre
Page 60 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesOn en deduit que pour tout R 0 :Le cercle de centre a et rayon R estz C : z a = R.Le disque ouvert de centre a et rayon R estz C : z a R.Le disque ferme de centre a et rayon R estz C : z a R.N. Arancibia - relu par D. CransacAlgebre
Page 61 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesL’addition de deux nombres complexes s’interprete geometriquement entermes de translation : En effet soit u C. Alors l’applicationtu : C →Cz 7→z + u.correspond geometriquement a la translation de vecteur ⃗u.L’applicationSO : C →Cz 7→z.correspond, geometriquement, a la symetrie de centre O.N. Arancibia - relu par D. CransacAlgebre
Page 62 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesL’applicationSx : C →Cz 7→z.correspond, geometriquement, a la symetrie d’axe Ox.L’applicationSy : C →Cz 7→z.correspond, geometriquement, a la symetrie d’axe Oy.N. Arancibia - relu par D. CransacAlgebre
Page 63 : ApplicationsNombres ComplexesGeometrie des Nombres ComplexesLe produit de deux nombres complexes s’interprete geometriquement entermes d’homothetie et de rotation. En effet :Soit λ R. Alors l’applicationHλ : C →Cz 7→λz.correspond, geometriquement, a l’homothetie de centre O et de rapportλ.Soit θ R. Alors l’applicationRθ : C →Cz 7→eiθz.correspond, geometriquement, a la rotation de centre O et d’angle θ.Soit ω = ρeiθ. Alors l’applicationHRω : C →Cz 7→ρeiθz.correspond, geometriquement, a la composee d’une rotation de centre Oet d’angle θ avec une homothetie de centre O et de rapport ρsimilitude.N. Arancibia - relu par D. CransacAlgebre
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63