CM6 Clustering

Télécharger le CM6 Clustering en pdf

Pages : 1 2 3 4 5 6 7 8 9 10

Page 1 : Datamining 1 : ClusteringClusteringMéthodes de clustering :•Généralités•K-means•Classification hiérarchique ascendanteLe clustering est la technique non supervisée la plus répandue en datamining.Elle permet de distinguer des groupes homogènes classes, segments, clusters au sein d’un grand volume de données.- De part leur constitution, ces groupes peuvent apporter une information pertinente sur les données, notamment s’ils sont représentés graphiquement à l’aide d’une ACP.- Ils peuvent aussi servir à découper une étude en sous-parties, chacune pouvant bénéficier de traitements particuliers.

Page 2 : Datamining 1 : ClusteringGénéralités2Recherche exhaustive impossibleNotons que le nombres de partitions distinctes de n objets estPar exemple pour 30 objets, on a plus 1023 partitions possibles.Algorithme de recherche performant1kn!kke1L’objectif des méthodes est à la fois, de regrouper les observations ayant des caractéristiques similaires au sein d’une même classe,distance entre observationsà la fois de construire des classes les plus dissemblablespossibles. distance entre classes

Page 3 : Datamining 1 : Clustering3Les métriques sur les observations : variables quantitatives2/1d1i2ii2yxy,xdd1iii1yxy,xddd11yx,...,yxmaxy,xd2/11Tyxyxy,xdPour trouver des similarités entre les observations il faut définir une métrique sur les observations :Distance euclidienne :Distance Manhattan :Atténue l’impact des individus hors norme car pas d’écart au carréDistance infinie :Distance de Mahalanobis :=matrice carrée définie positive permet d’introduire une corrélation entre les variables -11-11

Page 4 : Datamining 1 : Clustering4Les métriques sur les classesDistance de Ward : la plus utilisée, permet de fusionner les deux classes faisant le moins baisser l’inertie inter-classes, tend à produire des classes sphériques de même effectif .4Distance minimale entre deux observations des deux classes : détecte les formes allongées voire sinueuses, sensible à l’effet de de chaîne 2 points éloignés sont considérés comme appartenant à la même classe car reliés par une série de points proches les uns des autresC1C2g1g2y,xdminC,Cd21Cy,Cx21miny,xdmoyenneC,Cd21Cy,Cx21moyg,gdnnnnC,Cd21212121WardDistance moyenne entre deux observations des deux classes : moins sensible au bruit, tend à produire des classes de même variance. Distance maximale entre deux observations des deux classes : très sensible aux observations atypiquesy,xdmaxC,Cd21Cy,Cx21maxPour construire des classes dissemblables il faut définir une métrique sur les classes, c’est-à-dire une distance entre deux ensembles de pointsoù ni et gi sont l’effectif et le centre de gravité de la classe Ci

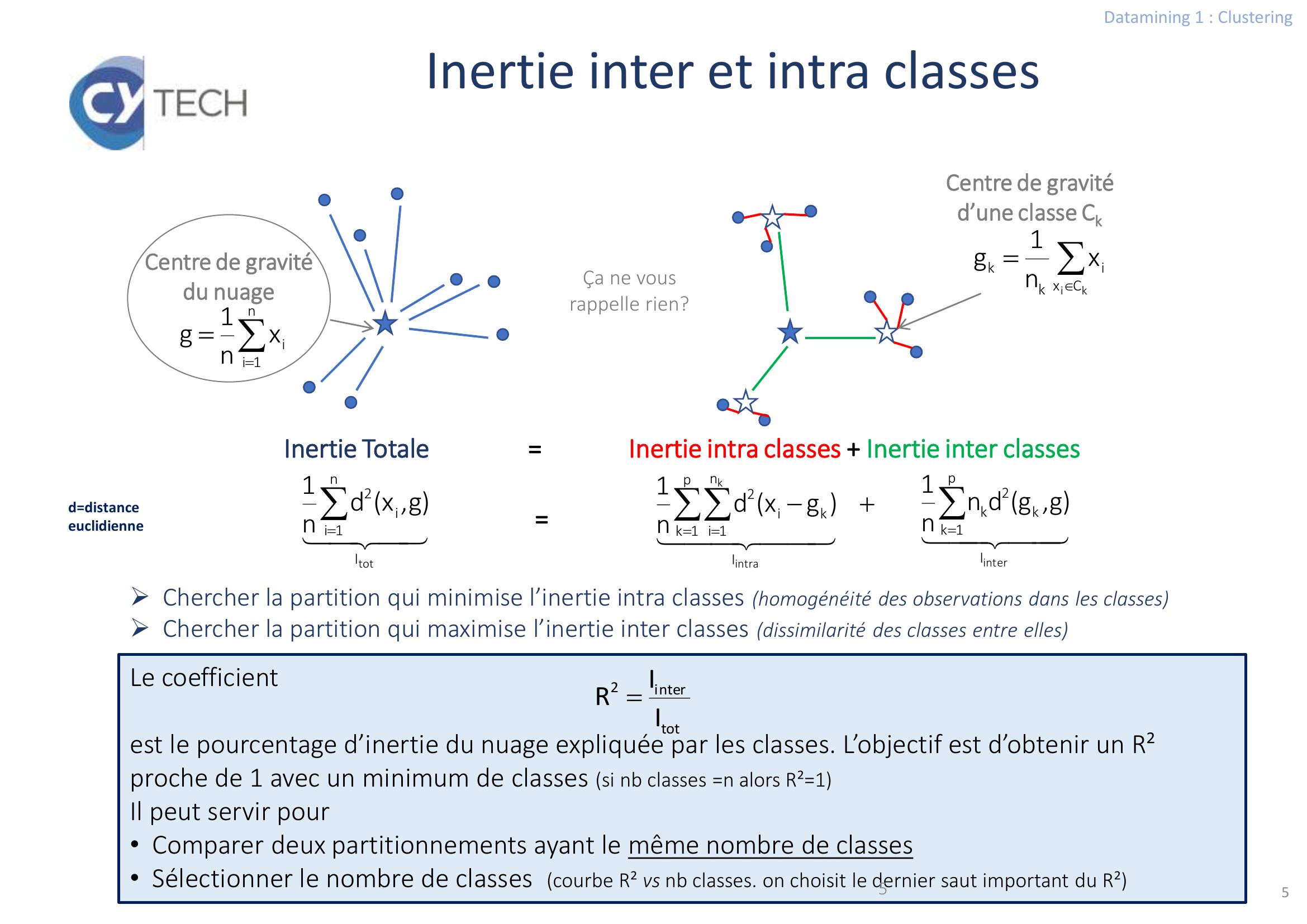
Page 5 : Datamining 1 : Clustering5Inertie inter et intra classesLe coefficientest le pourcentage d’inertie du nuage expliquée par les classes. L’objectif est d’obtenir un R² proche de 1 avec un minimum de classes si nb classes =n alors R²=1Il peut servir pour• Comparer deux partitionnements ayant le même nombre de classes• Sélectionner le nombre de classes courbe R² vs nb classes. on choisit le dernier saut important du R²5n1iixn1gCentre de gravité du nuageki Cxikkxn1gCentre de gravité d’une classe CkInertie Totale = Inertie intra classes + Inertie inter classes erintIp1kk2kg,gdnn1raintkIp1kn1iki2gxdn1totIn1ii2g,xdn1= Chercher la partition qui minimise l’inertie intra classes homogénéité des observations dans les classesChercher la partition qui maximise l’inertie inter classes dissimilarité des classes entre ellestoterint2IIR Ça ne vous rappelle rien?d=distance euclidienne

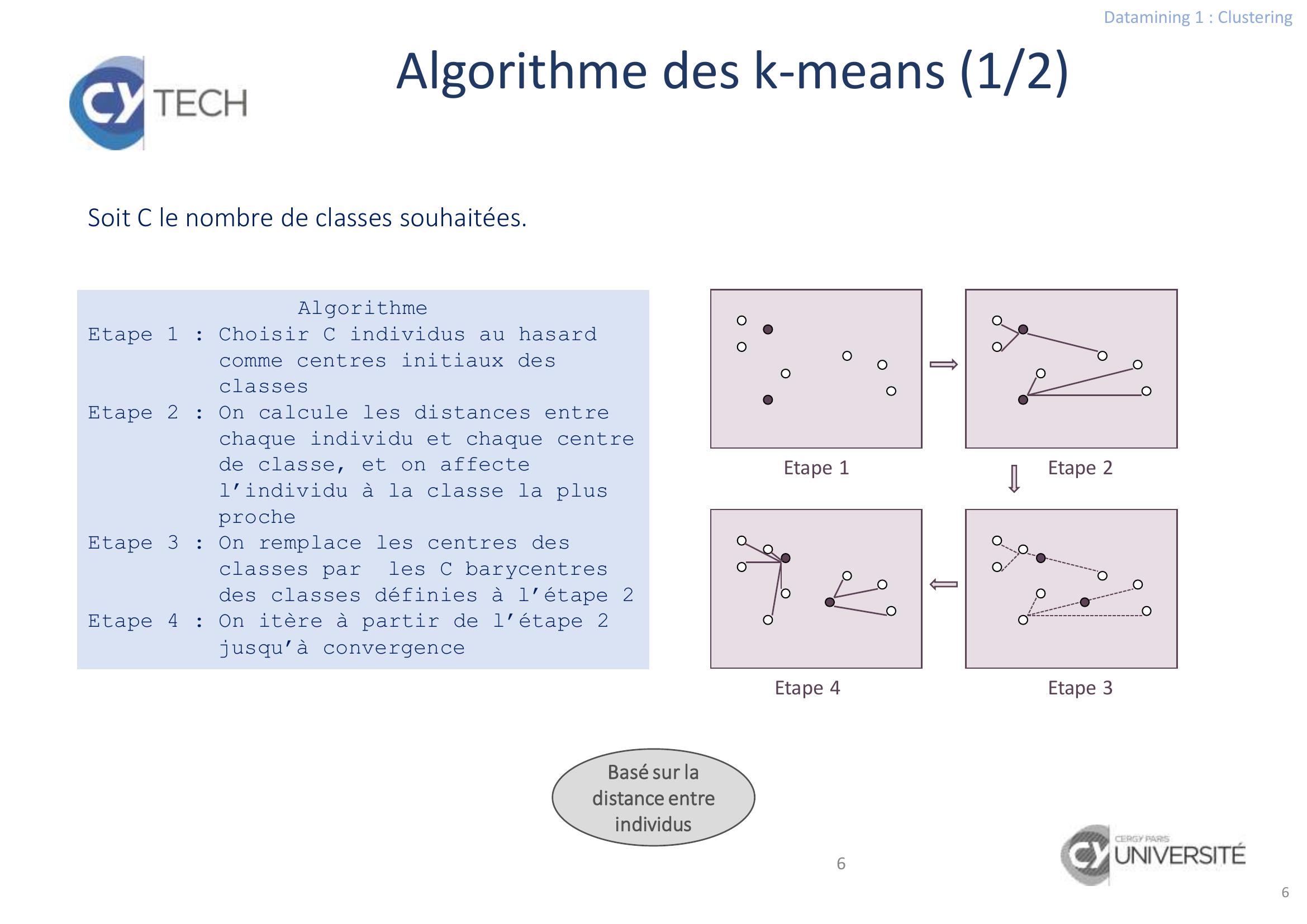
Page 6 : Datamining 1 : Clustering6Algorithme des k-means 1/26AlgorithmeEtape 1 : Choisir C individus au hasard comme centres initiaux des classesEtape 2 : On calcule les distances entre chaque individu et chaque centre de classe, et on affecte l’individu à la classe la plus procheEtape 3 : On remplace les centres des classes par les C barycentres des classes définies à l’étape 2Etape 4 : On itère à partir de l’étape 2 jusqu’à convergenceEtape 1Etape 2Etape 3Etape 4Basé sur la distance entre individusSoit C le nombre de classes souhaitées.

Page 7 : Datamining 1 : Clustering7CaractéristiquesDépend de l’initialisation des centres répéter plusieurs fois l’algorithmeNombre C de classes fixé à l’avance tester plusieurs valeurs de C Un individu atypique est détecté car il forme une classe à lui tout seul en généralComplexité linéaire adapté à de grands volumes de donnéesattention toutefois car il faut tester plusieurs nombres de classes et répéter l’algorithme plusieurs fois pour chaque classeAlgorithme des k-means 2/2

Page 8 : Datamining 1 : Clustering8Classification hiérarchique ascendante1/28AlgorithmeEtape 1 : Chaque individu forme une classe n classesEtape 2 : On calcule les distances entre les classes et on regroupe les deux classes les plus prochesC classes C-1 classesEtape 3 : On itère à partir de l’étape 2 jusqu’à n’avoir qu’une seule classeEtape 4 : Choix du partitionnement à partir de dendrogrammeLedendrogrammereprésentelasuitedepartitions obtenues au cours de l’algorithme.L’axe des ordonnées représente une mesure dedissimilarité/inertie inter-classes R² partiel,….On coupe le dendrogramme où la hauteur desbranches est élevée. Cela permet d’obtenirsimultanément :•Le nombre de classes•La constitution des classesBasé sur la distance entre classes

Page 9 : Datamining 1 : Clustering9Classification hiérarchique ascendante2/2Caractéristiques Regroupe des individus ou des variables dès qu’il y a une notion de distancePas de dépendance à l’initialisationNombre de classes non fixé à l’avanceformes diverses des groupes grâce au choix de la distance A chaque étape le partitionnement dépend de celui obtenu avant Optimum localComplexité exponentielle de l’algorithmique

Page 10 : Datamining 1 : Clustering10Avez-vous des questions?Documents ayant servis à la rédaction des slides et TD :• DataMining et Statistiques décisionnelles, Stéphane Tufféry, Ed. Technip• https://penseeartificielle.fr/choisir-distance-machine-learning/• http://eric.univ-lyon2.fr/ricco/cours/slides/classifcentresmobiles.pdf• https://scikit-learn.org/stable/index.htmlMéthodes non hiérarchiquesIl faut avoir une idée a priori du nombre de classes L’initialisation de l’algorithme peut avoir un impact sur la partition finaleL’algorithme converge assez vite complexité linéaireAlgorithme hiérarchique La complexité de l’algorithme est exponentielleOn n’a pas besoin de connaitre à l’avance le nombre de classesQuand cela est possible confirmer les résultats par plusieurs méthodesConclusion

Pages : 1 2 3 4 5 6 7 8 9 10