CM6 Polynomes

Télécharger le CM6 Polynomes en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Page 1 : PolynˆomesDecomposition en facteurs irreductiblesAlgebre-Premier semestre 20211Polynˆomes2Decomposition en facteurs irreductiblesN. Arancibia - relu par D. CransacAlgebre

Page 2 : PolynˆomesDecomposition en facteurs irreductiblesAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre

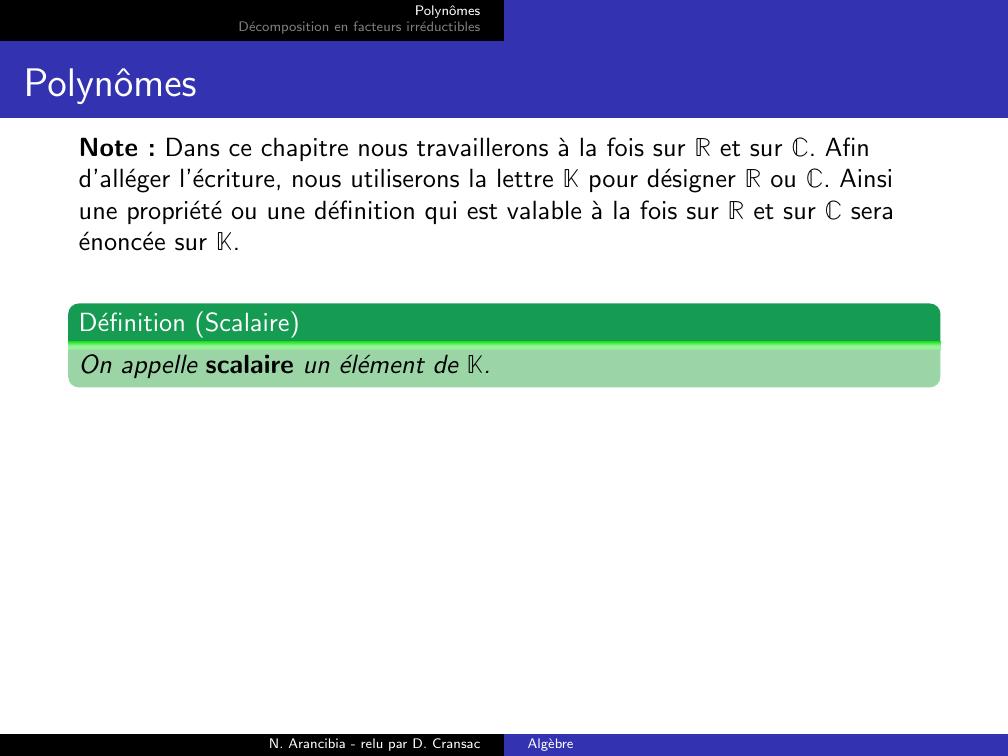
Page 3 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesNote : Dans ce chapitre nous travaillerons a la fois sur R et sur C. Afind’alleger l’ecriture, nous utiliserons la lettre K pour designer R ou C. Ainsiune propriete ou une definition qui est valable a la fois sur R et sur C seraenoncee sur K.Definition ScalaireOn appelle scalaire un element de K.N. Arancibia - relu par D. CransacAlgebre

Page 4 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesDefinition PolynˆomeOn appelle polynˆome P d’indeterminee Xa coefficients dans K touteexpression de la formeP = PX = a0 + a1X + a2X 2 + · · · + anX n =nXk=0akX k.oun N, eta0, a1 , · · · , an sont des elements de K. On les appelle les coefficientsdu polynˆome P.L’ensemble des polynˆomes a coefficients dans K est note KX.Remarque : X N’EST PAS UN NOMBRE !L’objet X est un objet mathematique bien precis que l’on appelleindeterminee. Ce n’est ni une valeur ni une variable.N. Arancibia - relu par D. CransacAlgebre

Page 5 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesDonnons quelques exemples de polynˆomes.DefinitionOn appelle :Polynˆome constant :Tout polynˆome de la forme PX = a0 aveca0 K.Polynˆome unite : Le polynˆome PX = 1.Polynˆome nul : Le polynˆome PX = 0.Monˆome : Tout polynˆome de la forme PX = akX k, ak K.Remarque : Tous les coefficients du polynˆome nul sont nuls.Reciproquement, tout polynˆome ayant tous ses coefficients nuls est lepolynˆome nul.N. Arancibia - relu par D. CransacAlgebre

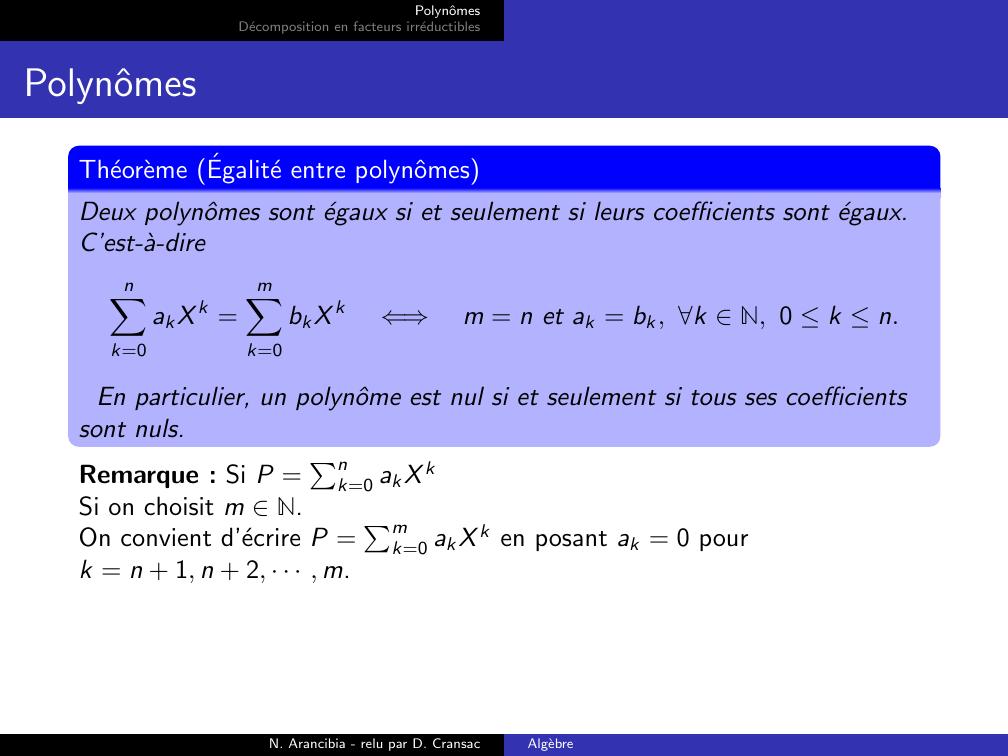
Page 6 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesTheoreme Egalite entre polynˆomesDeux polynˆomes sont egaux si et seulement si leurs coefficients sont egaux.C’est-a-direnXk=0akX k =mXk=0bkX k⇐⇒m = n et ak = bk, k N, 0 k n.En particulier, un polynˆome est nul si et seulement si tous ses coefficientssont nuls.Remarque : Si P = Pnk=0 akX kSi on choisit m N.On convient d’ecrire P = Pmk=0 akX k en posant ak = 0 pourk = n + 1, n + 2, · · · , m.N. Arancibia - relu par D. CransacAlgebre

Page 7 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesSur l’ensemble de polynˆomes nous pouvons definir une addition et unemultiplication.DefinitionSoient PX = Pnk=0 akX k et QX = Pmk=0 bkX k deux polynˆomes acoefficients dans K et λ K.Somme : On definit le polynˆome P + Q parP + QX =maxm,nXk=0ak + bkX k.en convenant que ak = 0 si k n et bk = 0 si k m.N. Arancibia - relu par D. CransacAlgebre

Page 8 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesDefinitionProduit : On definit le polynˆome P · Q parP · QX =m+nXk=0ckX kouck =kXi=0aibki.en convenant que ak = 0 si k n et bk = 0 si k m.Multiplication par λ : On definit le polynˆome λP parλPX =nXk=0λakX k.N. Arancibia - relu par D. CransacAlgebre

Page 9 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesExemples : Considerons les polynˆomesPX = 1 2X X 3etQX = 1 + X 2.AlorsP + QX=2 2X + X 2 X 3.P · QX=1 2X + X 2 3X 3 X 5.N. Arancibia - relu par D. CransacAlgebre

Page 10 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesIntroduisons une derniere operation sur l’ensemble de polynˆomes.Definition CompositionSoient PX = Pnk=0 akX k et QX = Pmk=0 bkX k deux polynˆomes acoefficients dans K.Composee de deux polynˆomes : On definit le polynˆome composeP ◦Q parP ◦QX =nXk=0akQXk.Exemple :1 + X 2 ◦2 + X=1 + 2 + X2 = 5 4X + X 2.2 + X ◦1 + X 2=2 + X 2 + 1 = 1 + X 2.1 + X + X 2 ◦1 + X 3=1 + X 3 + 1 + X 3 + 12 = 3 + 2X 3 + X 6.N. Arancibia - relu par D. CransacAlgebre

Page 11 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesEtudions quelques proprietes de l’addition :TheoremeL’addition dans KX est :associative : Pour tout polynˆome P, Q, R KXP + Q + R = P + Q + R;commutative : Pour tout polynˆome P, Q KXP + Q = Q + P;admet pour element neutre le polynˆome nul : Pour tout polynˆomeP KX0 + P = P + 0 = P.Demonstration.A vous de verifier.N. Arancibia - relu par D. CransacAlgebre

Page 12 : PolynˆomesDecomposition en facteurs irreductiblesPolynˆomesEtudions quelques proprietes du produit :TheoremeLe produit dans KX est :associative : Pour tout polynˆome P, Q, R KXP · Q · R = P · Q · R;commutative : Pour tout polynˆome P, Q KXP · Q = Q · P;admet pour element neutre le polynˆome unite : Pour tout polynˆomeP KX1 · P = P · 1 = P.Demonstration.A vous de verifier.N. Arancibia - relu par D. CransacAlgebre

Page 13 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeAttache a chaque polynˆome on a l’important notion de degre.Definition Degre d’un polynˆomeSoit P = Pnk=0 akX k un polynˆome non nul de KX. On appelle degre dupolynˆome P le plus grand entier k tel queak ̸= 0.On note cet entier degP et on dit que :ak est le coefficient dominant de P. Autrement dit, le coefficientdominant, est le coefficient du monˆome de plus haut degre de PX.P est unitaire ou normalise si son coefficient dominant est egal a 1.Remarque : Par convention, le polynˆome nul est de degre :deg0 = .N. Arancibia - relu par D. CransacAlgebre

Page 14 : PolynˆomesDecomposition en facteurs irreductiblesExemple :X 1515 1 est un polynˆome unitaire, de degre 1515.3X 5 + 2X 4 2x + 1 est un polynˆome de degre 5 , de coefficientdominant 3.5 + 17X + 30X 4 + 6X 7 est un polynˆome de degre 7 , de coefficientdominant 6.N. Arancibia - relu par D. CransacAlgebre

Page 15 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeLe degre satisfait les proprietes suivantes.TheoremeSoient PX et QX deux polynˆomes a coefficients dans K. AlorsdegP + Q maxdegP; degQ.degP · Q = degP + degQ.Pour tout λ K, degλP = degP.Si degQ 1, degP ◦Q = degP · degQ.Demonstration.SoientPX =nXk=0akX ketQX =mXk=0bkX kavec an ̸= 0 et bm ̸= 0.Alors deg P = n et deg Q = m on verifiera sans difficulte que toutes cesproprietes restent vraies dans le cas ou un des 2 polynˆomes est nul......a suivre ...N. Arancibia - relu par D. CransacAlgebre

Page 16 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeDemonstration.SoientPX =nXk=0akX ketQX =mXk=0bkX kavec an ̸= 0 et bm ̸= 0.Alors deg P = n et deg Q = m on verifiera sans difficulte que toutes sesproprietes restent vraies dans le cas ou l’un des 2 polynˆomes est nul.degP + Q maxdegP, degQ :Pour tout k maxm, n, on aak = bk = 0=⇒ak + bk = 0.Ainsi degP + Q maxdegP, degQ.N. Arancibia - relu par D. CransacAlgebre

Page 17 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeDemonstration.degP · Q = degP + degQ : Le terme de plus haut degre de P ·Q estan · bmX n+m.Ainsi degP · Q = m + n.Si degQ 1, degP ◦Q = degP · degQ : Supposons degQ 1.On a par definitionP ◦QX = a0 + a1QX + · · · + anQXn.Maintenant, le point precedent nous permet de conclure que pour tout0 k n, on adegQk = k degQ.Ainsi, le terme de plus haut degre de P ◦Q est anQXn. D’ou onconclutdegP ◦Q = deganQXn = n · degQ = degP · degQ.N. Arancibia - relu par D. CransacAlgebre

Page 18 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeExemple d’inegalite stricte : degP + Q maxdeg P, deg Q :SoitP = X 3 X + 2etQ = X 3 + X 2.AlorsP + QX = X 2 X + 2=⇒degP + Q = 2 3 = maxdeg P, deg Q.Remarque : Si degP ̸= degQ, alorsdegP + Q = maxdegP, degQ.N. Arancibia - relu par D. CransacAlgebre

Page 19 : PolynˆomesDecomposition en facteurs irreductiblesDegre d’un polynˆomeEn utilisant les proprietes du degre, on peut facilement montrer la propositionsuivante.PropositionLe produit de deux polynˆomes non nuls est non nul. Autrement dit :P, Q KX,P · Q = 0 =⇒P = 0ouQ = 0.Demonstration.P · Q = 0=⇒deg P + deg Q = degP · Q = =⇒deg P = oudeg Q = =⇒P = 0 ou Q = 0.N. Arancibia - relu par D. CransacAlgebre

Page 20 : PolynˆomesDecomposition en facteurs irreductiblesDerivation de PolynˆomesUne autre operation que on peut definir sur l’ensemble des polynˆomes, c’estla derivation.Definition Polynˆome deriveSoit P = Pnk=0 akX k un polynˆome dans KX.On appelle derivee formelle du polynˆome P, le polynˆome P′defini parP′X = 0si degP 0Pnk=1 kakX k1 = a1 + 2a2X + · · · + nanX n1si degP 0.On definit par iteration les polynˆomes derives successifs de P parP0=PPk=Pk1′pour tout k 1.N. Arancibia - relu par D. CransacAlgebre

Page 21 : PolynˆomesDecomposition en facteurs irreductiblesDerivation de PolynˆomesExemple : Soit P = 5X 3 + X 2 7X + 3. Alors les derivees successives de Psont :P0X=5X 3 + X 2 7X + 3P1X=15X 2 + 2X 7P2X=30X + 2P3X=30PkX=0,k 4.N. Arancibia - relu par D. CransacAlgebre

Page 22 : PolynˆomesDecomposition en facteurs irreductiblesDerivation de PolynˆomesEtudions quelques proprietes de la derivation.PropositionSoit P un polynˆome dans KX. Alors, si degP 1, on adegP′ = degP 1.Cela vient tout simplement de la definition de la derivee. A vous de verifier.TheoremeSoient PX et QX deux polynˆomes a coefficients dans K.On a P′ = 0 ⇐⇒P est constant.P + Q′ = P′ + Q′.Pour tout λ K, λP′ = λP′.P · Q′ = P′ · Q + P · Q′.P ◦Q′ = Q′ · P′ ◦Q.Demonstration.Cela vient aussi tout simplement des definitions des sommes et produits. Avous de verifier.N. Arancibia - relu par D. CransacAlgebre

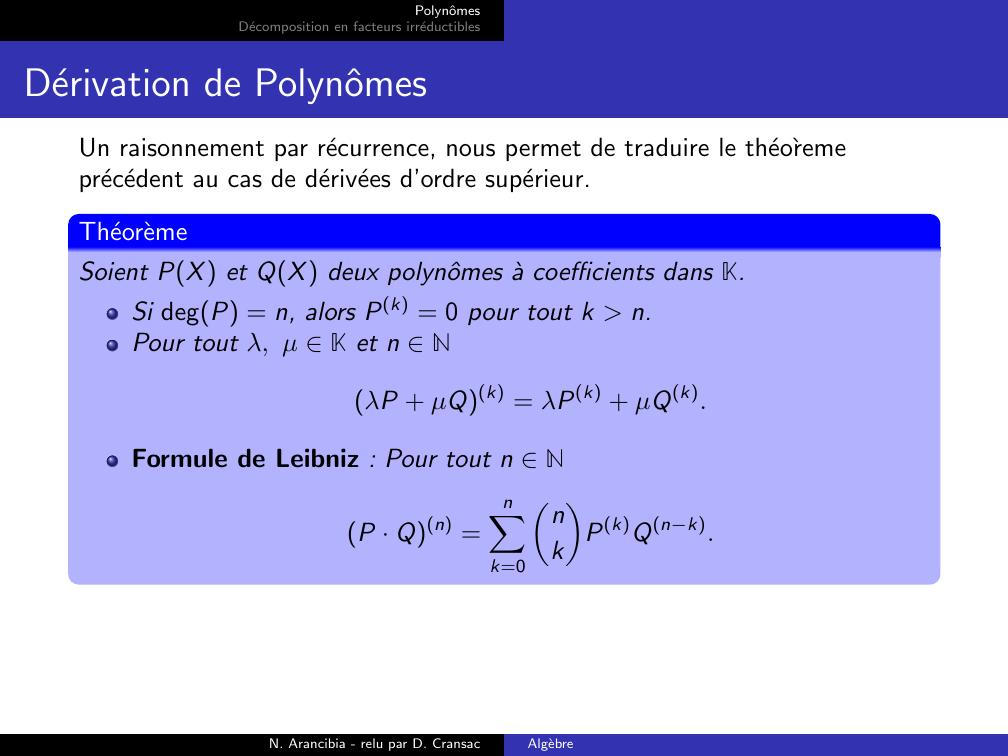
Page 23 : PolynˆomesDecomposition en facteurs irreductiblesDerivation de PolynˆomesUn raisonnement par recurrence, nous permet de traduire le theoremeprecedent au cas de derivees d’ordre superieur.TheoremeSoient PX et QX deux polynˆomes a coefficients dans K.Si degP = n, alors Pk = 0 pour tout k n.Pour tout λ, µ K et n NλP + µQk = λPk + µQk.Formule de Leibniz : Pour tout n NP · Qn =nXk=0nkPkQnk.N. Arancibia - relu par D. CransacAlgebre

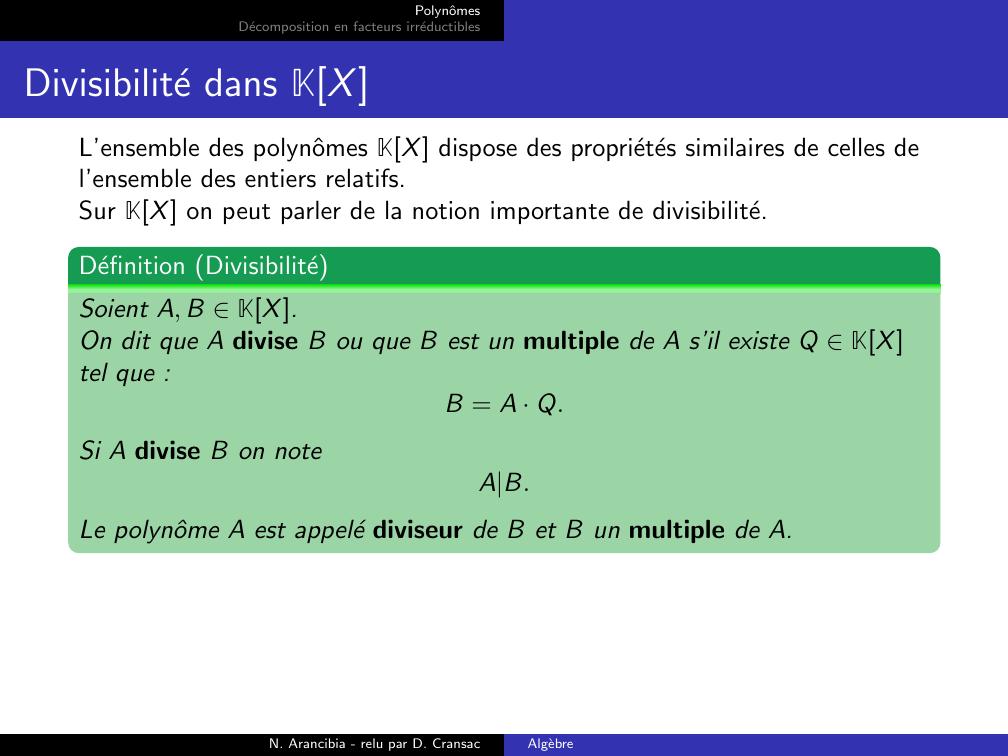
Page 24 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXL’ensemble des polynˆomes KX dispose des proprietes similaires de celles del’ensemble des entiers relatifs.Sur KX on peut parler de la notion importante de divisibilite.Definition DivisibiliteSoient A, B KX.On dit que A divise B ou que B est un multiple de A s’il existe Q KXtel que :B = A · Q.Si A divise B on noteAB.Le polynˆome A est appele diviseur de B et B un multiple de A.N. Arancibia - relu par D. CransacAlgebre

Page 25 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXRemarques :Un polynˆome PX non nul est divisible par les polynˆomes λ et λPXavec λ K. En effet, pour tout λ K, nous avonsPX = λ · λ1PXetPX = λPX · λ1.Reciproquement, un polynˆome de degre 0 polynˆome constant et nonnul divise tous les polynˆomes. En effet, pour tout λ Ket pour toutPX KX, nous avonsPX = λ · λ1PX.Tout polynˆome divise le polynˆome nul. En effet, pour tout PX KX,nous avons 0 = PX · 0.N. Arancibia - relu par D. CransacAlgebre

Page 26 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXEtudions quelques proprietes de la division.PropositionSoit A, B, C et D des polynˆomes dans KX. On a alors :P, Q KXDA et DB=⇒DP · A + Q · BAB et CD=⇒A · CB · D.k N, AB=⇒AkBk.Demonstration.Appliquer les definitionsN. Arancibia - relu par D. CransacAlgebre

Page 27 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXPropositionSoient A, B KX deux polynˆomes non nuls. Alors :AB et BA⇐⇒λ K,A = λBOn dit alors que A et B sont des polynˆomes associes.Demonstration.On raisonne par double implication :⇐=: Immediat=⇒:Si AB et BA, alors il existe C, D KX tels que :B = A · CetA = B · D.Ainsideg B = deg A + deg C deg Aetdeg A = deg B + deg D deg B.D’ou on conclut que deg A = deg B=⇒deg D = deg C = 0. Parconsequent, D est un polynˆome constant D = λ Ket A = λB.N. Arancibia - relu par D. CransacAlgebre

Page 28 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXPropositionSoient PX et QX deux polynˆomes a coefficients dans K. AlorsP · Q = 1si et seulement si P et Q sont des constantes inverses l’une de l’autre.Demonstration.⇐=: Immediat.=⇒: Si P · Q = 1, alors0 = degP · Q = degP + degQ=⇒degP = degQ = 0.D’ou on conclut queP = λetQ = λ′.Or λλ′ = 1. Ce qui implique λ′ = λ1.Remarque : Cela veut dire qu’un polynˆome non nul n’est pas forcementinversible. Les seuls polynˆomes inversibles sont les constantes non nulles.N. Arancibia - relu par D. CransacAlgebre

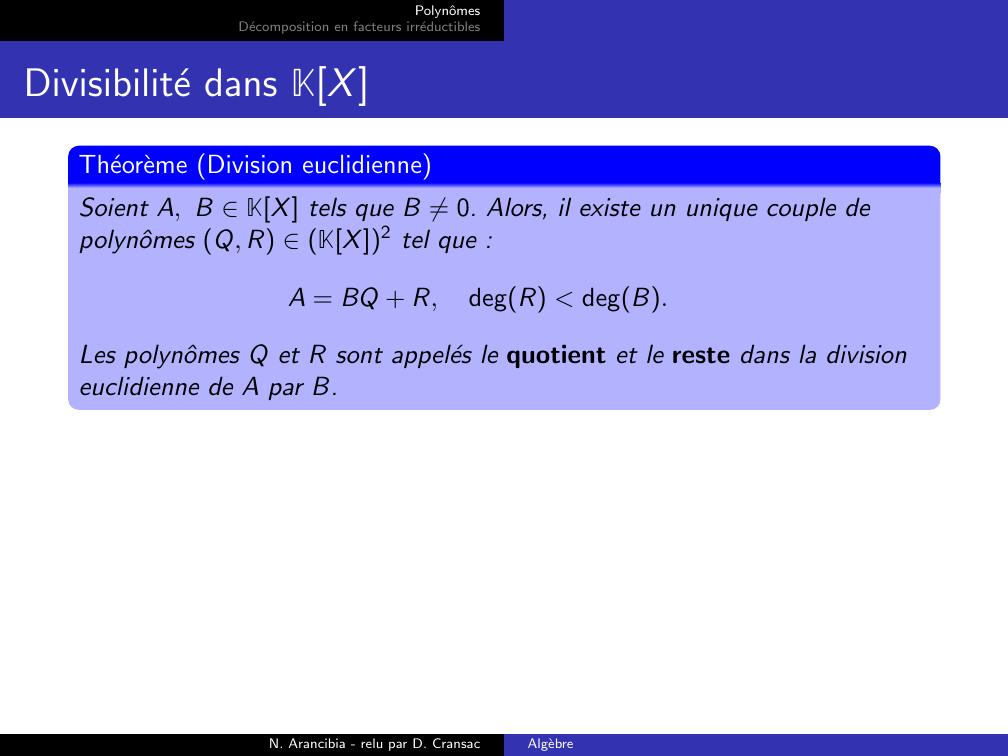
Page 29 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXTheoreme Division euclidienneSoient A, B KX tels que B ̸= 0. Alors, il existe un unique couple depolynˆomes Q, R KX2 tel que :A = BQ + R,degR degB.Les polynˆomes Q et R sont appeles le quotient et le reste dans la divisioneuclidienne de A par B.N. Arancibia - relu par D. CransacAlgebre

Page 30 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXDemonstration.SoitE = AX BXQX KXSoitD = degR, R ESi BA alors la division euclidenne existe. En effetA = BQ + R avec R = 0 et degR debBcar degR = Sinon, minD 0.D etant un sous ensemble de N, il admet un plus petit element r quicorrespond a un polynˆome R et un certain polynˆome Q.N. Arancibia - relu par D. CransacAlgebre

Page 31 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXDemonstration.Montrons que degR degBPar l’absurde : supposons degB degRSoit arX r le monˆome dominant de R et bmX m le monˆome dominant de B.On aRX = arX r +r1Xi=0aiX i et BX = bmX m +m1Xi=0biX iOn poseR′X=RX arbmX rmBX=arX r +r1Xi=0aiX i arbmX rm bmX m +m1Xi=0biX i!.=r1Xi=0aiX i m1Xi=0arbibmX i+rmDonc degR′ r on a donc AX BXQX + arbmX rm= R′Xce qui contredit le fait que r etait le minimum de D.On a bien degB degRN. Arancibia - relu par D. CransacAlgebre

Page 32 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXDemonstration.UniciteSi degB = 0 alors λ K, BX = λ et doncA = BXQX + RX avec Q = 1λA et R = 0Si degB 0, supposons queAX = BXQX + RX = BXQ′X + R′Xavec degR degB et degR′ degB.AlorsBXQX Q′X = RX R′XdoncdegR R′ = degB + degQ Q′or degR R′ maxdegR, degR′ degBL’egalite n’est possible que si R = R′ et Q = Q′Il y donc bien unicite dans les deux cas.N. Arancibia - relu par D. CransacAlgebre

Page 33 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXExemple : Faisons la division euclidienne de A = 2X 4 X 3 2X 2 + 3X 1par B = X 2 X + 1. Notons que on pose une division de polynˆomes commeon pose une division euclidienne de deux entiers. En effet2X 4-X 3-2X 2+3X-1X 2 X + 1-2X 4-2X 3+2X 22X 2+X -3X 3-4X 2+3X-1-X 3-X 2+X-3X 2+2X-1--3X 2+3X-3-X+2Alors on trouveQ = 2X 2 + X 3 QuotientetR = X + 2 Reste.On n’oublie pas de verifier qu’effectivement A = BQ + R.N. Arancibia - relu par D. CransacAlgebre

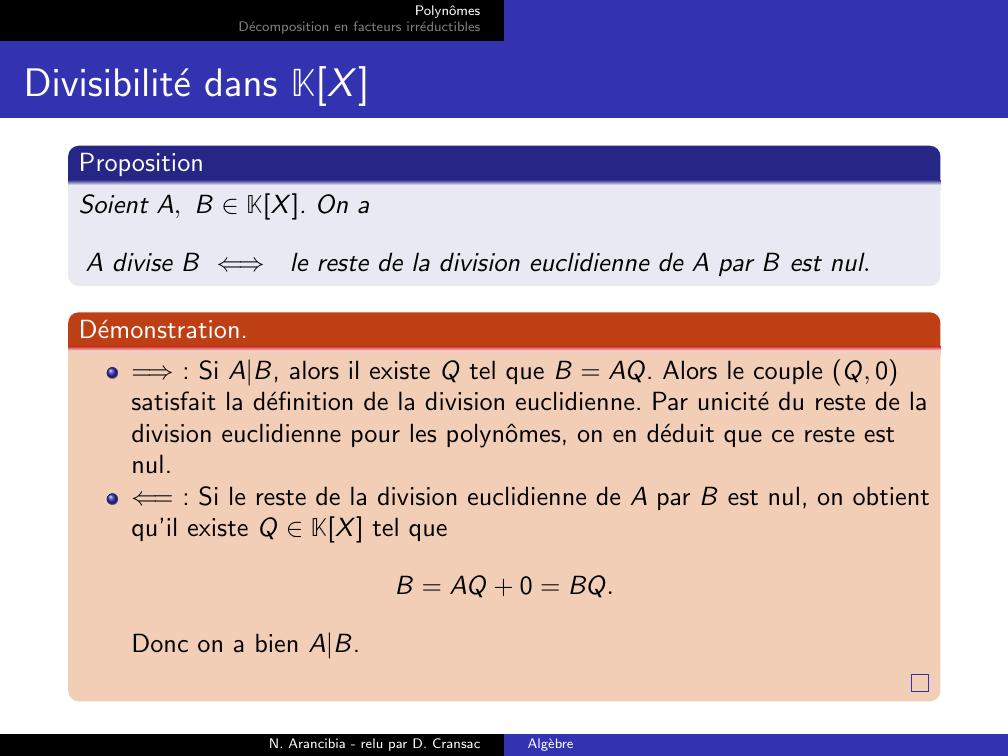
Page 34 : PolynˆomesDecomposition en facteurs irreductiblesDivisibilite dans KXPropositionSoient A, B KX. On aA divise B ⇐⇒le reste de la division euclidienne de A par B est nul.Demonstration.=⇒: Si AB, alors il existe Q tel que B = AQ. Alors le couple Q, 0satisfait la definition de la division euclidienne. Par unicite du reste de ladivision euclidienne pour les polynˆomes, on en deduit que ce reste estnul.⇐= : Si le reste de la division euclidienne de A par B est nul, on obtientqu’il existe Q KX tel queB = AQ + 0 = BQ.Donc on a bien AB.N. Arancibia - relu par D. CransacAlgebre

Page 35 : PolynˆomesDecomposition en facteurs irreductiblesEvaluation polynomialeDefinition Fonction polynomialeSoit P = Pnk=0 akX k KX et λ K. Alors on definitPλ =nXk=0akλkon evalue P en λ.La fonctionK→Kx7→Pxest appelee fonction polynomiale associee au polynˆome P.N. Arancibia - relu par D. CransacAlgebre

Page 36 : PolynˆomesDecomposition en facteurs irreductiblesEvaluation polynomialeL’evaluation polynomiale nous permet d’exprimer les coefficients d’unpolynˆome a l’aide des derivees successives.Theoreme Formule de Taylor en 0Pour tout polynˆome P = Pnk=0 akX k KX de degre n N, on aPX = P0 + P10X + P202!X 2 + · · · + Pn0n!X nCe qui revient aPX =nXk=0Pk0k!X kC’est-a-direak = Pk0k!.N. Arancibia - relu par D. CransacAlgebre

Page 37 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeNous pouvons generaliser la formule de Taylor a tout a K.Theoreme Formule de Taylor en a KPour tout polynˆome P KX de degre n N et a K, nous avons :PX = Pa + P1aX a + P2a2!X a2 + · · · + Pnan!X anCe qui revient aPX =nXk=0Pkak!X ak.N. Arancibia - relu par D. CransacAlgebre

Page 38 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeEtudions les points ou un polynˆome s’annule.Definition RacinesSoit P KX. On dit que a K est une racine ou un zero de P siPa = 0.Exemple :Tout polynˆome de degre 1 a une racine :la racine deaX + b est baEn effeta ·ba+ b = 0L’existence de racines depend de K :par exemple X 2 + 1 n’a pas de racine dans R,il a les racines +i et i dans C.N. Arancibia - relu par D. CransacAlgebre

Page 39 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeDonnons une characterization des racines d’un polynˆome.PropositionSoit α K et P KX. Alorsα est racine de P⇐⇒X αP.Demonstration.On raisonne par double implication :⇐= : Supposons que X αP, alors il existe Q KX tel queP = X αQX. Alors on obtient :Pα = α αQα = 0.N. Arancibia - relu par D. CransacAlgebre

Page 40 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeDemonstration.=⇒: Supposons que α soit racine de P, et ecrivons la divisioneuclidienne de P par X α :il existe Q, R KX tels que :PX = X αQX + RX,degR degX a = 1.Ainsi degR 0, et RX = r K.On evalue alors l’egalite precedente en α :0 = Pα = α αQα + r = r=⇒r = 0.Ainsi PX = X αQX et X α divise P.N. Arancibia - relu par D. CransacAlgebre

Page 41 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeExemple : Considerons le polynˆome P = X 3 X + 6.On voit que 2 est racine de P :23 + 2 + 6 = 0Par la proposition precedente, P se factorise par X + 2. Pour obtenir safactorisation, on peut :soit ecrire P = X + 2aX 2 + bX + c et developper :aX 3 + 2a + bX 2 + 2b + cX + 2cet proceder par identification des coefficients1 = a;0 = 2a + b;1 = 2b + c;6 = 2csoit faire la division euclidienne de P par X + 2 : le quotientcorrespond a l’autre facteur de la factorisation.N. Arancibia - relu par D. CransacAlgebre

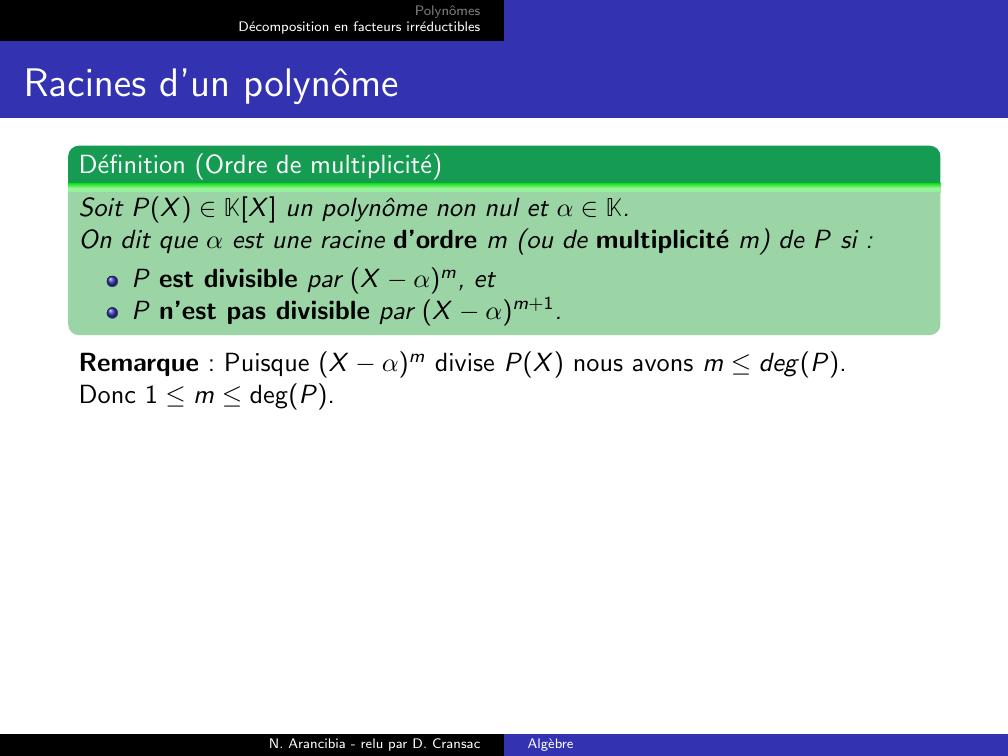
Page 42 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeDefinition Ordre de multipliciteSoit PX KX un polynˆome non nul et α K.On dit que α est une racine d’ordre m ou de multiplicite m de P si :P est divisible par X αm, etP n’est pas divisible par X αm+1.Remarque : Puisque X αm divise PX nous avons m degP.Donc 1 m degP.N. Arancibia - relu par D. CransacAlgebre

Page 43 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeDonnons une caracterisation de l’ordre de multiplicite a l’aide de la derivation.PropositionSoient P KX, α K et m N. On a l’equivalence entre :X αm divise P,Pα = P′α = · · · = Pm1α = 0.Si l’une de ces conditions est satisfaite, on dit alors que α est racine de P demultiplicite au moins m.Demonstration.C’est une consequence directe de la formule de Taylor. A verifier.Exemple : Considerons P = X 5 7X 4 + 19X 3 25X2 + 16X 4.On aP1 = P′1 = P′′1 = 0.Donc 1 est racine de P de multiplicite au moins 3. AinsiX 13diviseX 5 7X 4 + 19X 3 25X2 + 16X 4.N. Arancibia - relu par D. CransacAlgebre

Page 44 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeComme corollaire du resultat precedent on a :TheoremeSoient P KX, α K et m N. Alors α est une racine de multiplicitem de PX si et seulement siPα = P′α = · · · = Pm1α = 0etPmα ̸= 0.Demonstration.Cela decoule tout simplement de la definition de la multiplicite d’une racineet de la proposition precedente.Vocabulaire :Lorsque m 2, on parle de racine multiple.Les racines d’ordre 1,2,3 de P sont respectivement appeles racinessimples, doubles, triples de P.Exemple : Considerons toujours P = X 5 7X 4 + 19X 3 25X2 + 16X 4.On aP1 = P′1 = P′′1 = 0etP31 = 6Donc 1 est racine de P de multiplicite 3 exactement.N. Arancibia - relu par D. CransacAlgebre

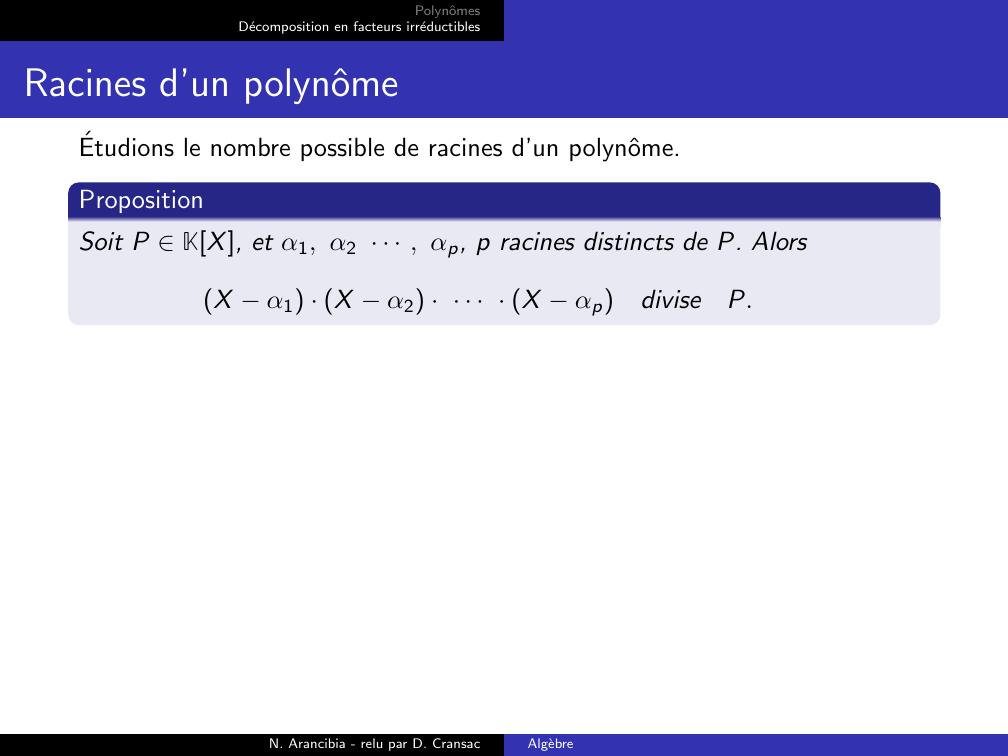
Page 45 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeEtudions le nombre possible de racines d’un polynˆome.PropositionSoit P KX, et α1, α2 · · · , αp, p racines distincts de P. AlorsX α1 · X α2 · · · · · X αpdiviseP.N. Arancibia - relu par D. CransacAlgebre

Page 46 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeComme consequence de cette proposition, on obtient les deux theoremessuivants.TheoremeUn polynˆome de degre n N a au plus n racines distinctes.Demonstration.Soit P un polynˆome et supposons que P admette p racines distinctesα1, · · · , αp.D’apres la proposition precedente, il existe alors Q KX tel que :PX = X α1 · · · · · X αpQX.En prenant les degres dans cette egalite, on en deduit quedegP = p + degQet donc p degP = n.N. Arancibia - relu par D. CransacAlgebre

Page 47 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeTheoremeLe seul polynˆome qui possede une infinite de racines est le polynˆome nul.Demonstration.C’est une consequence directe de la proposition precedente :si P est non nul, il n’a qu’un nombre fini de racines.Remarque :Un polynˆome de degre n, ayant au moins n + 1 racines est le polynˆomenul.N. Arancibia - relu par D. CransacAlgebre

Page 48 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeSi on compte les racines avec leur multiplicite alors on a :TheoremeSoit P KX, et α1, α2 · · · , αp, p racines distincts de P de multipiciterespectives m1, m2, · · · , mp. AlorsX α1m1 · X α2m2 · · · · · X αpmpdiviseP.Comme consequence de cette proposition, on a le resultat suivant.CorollaireUn polynˆome de degre n a au plus n racines comptees avec leurs ordres demultiplicite.N. Arancibia - relu par D. CransacAlgebre

Page 49 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition en facteurs irreductiblesEtudions comme un polynˆome se decompose en produit de polynˆomes plussimples i.e. de degre inferieurDefinition Polynˆome irreductibleSoit PX KX.On dit que PX est irreductible s’il satisfait :deg P 1.les seuls diviseurs de P sont les polynˆomes :λetλPX,avec λ K.C’est-a-dire les polynˆomes constants non nuls et les polynˆomes associesa PX.Autrement dit, PX est irreductible sur K s’il satisfait :A, B KX, PX = AXBX=⇒degA = 0 oudegB = 0.Remarque : Les polynˆomes de degre 1 sont irreductibles.N. Arancibia - relu par D. CransacAlgebre

Page 50 : PolynˆomesDecomposition en facteurs irreductiblesRacines d’un polynˆomeTheoremeTout polynˆome de KX de degre superieur ou egal a 1 se decompose demaniere unique en produit d’une constante non nulle et de polynˆomesirreductibles unitaires a l’ordre des facteurs pres.Definition Polynˆome ScindeOn dit qu’un polynˆome P KX de degre superieur ou egal a 1 est scindes’il peut ˆetre ecrit comme un produit de polynˆomes de degre 1 de KX.N. Arancibia - relu par D. CransacAlgebre

Page 51 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition en facteurs irreductiblesRemarque :Les polynˆomes de degre 1 sont irreductibles.Un polynˆome P KX est scinde et irreductible sur K si et seulement sidegP = 1.Le polynˆome X 2 + 1 est irreductible sur R mais pas sur C puisqu’il peuts’ecrire :X 2 + 1 = X iX + i.La decomposition d’un polynˆome depend de K. Nous allons donc distinguerles decompositions sur CX et sur RX.N. Arancibia - relu par D. CransacAlgebre

Page 52 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans CXTheoreme Theoreme de d’Alembert-GaussTout polynˆome non constant de CX possede au moins une racine dans C.La demonstration est difficile. Le theoreme sera admis dans ce cours.N. Arancibia - relu par D. CransacAlgebre

Page 53 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans CXPropositionTout polynˆome non nul de CX est scinde.Demonstration.Montrons par recurrence la propriete Pn pour n N :Tout polynˆome de CX de degre n est scindeInitialisation : Si deg P = 1, alors P est scinde par definition, doncP1 est vraie.N. Arancibia - relu par D. CransacAlgebre

Page 54 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans CXDemonstration.Heredite : Soit n N et supposons Pn vraie.Soit P de degre n + 1. D’apres le Theoreme de d’Alembert Gauss, Padmet au moins une racine α C. Alors X α divise P et il existeQ KX tel que PX = X αQX. Or degQ = n et parhypothese de recurrence, Q est scinde :Q = λX α1 · · · · · X αn.Ainsi P = λX αX α1 · · · · · X αn est scinde, et Pn + 1 estvraie. On conclut par principe de recurrence.N. Arancibia - relu par D. CransacAlgebre

Page 55 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans CXProposition1Les polynˆomes irreductibles de CX sont les polynˆomes de degre 1.2Tout polynˆome P de CX se factorise de fa¸con unique a l’ordre pres desfacteurs en produit de polynˆomes irreductibles de CX sous la forme :PX = λX α1m1 · X α2m2 · · · · · X αkmk.Demonstration.1On a deja vu que les polynˆomes de degre 1 sont irreductibles.Reciproquement, soit P un polynˆome irreductible. Par le Theoreme ded’Alembert Gauss, il existe α tel que Pα = 0. Il existe doncQ KX tel que P = X aQ. Comme de plus P est irreductible, onen deduit que Q Ket que P est de degre 1.2Soit P un polynˆome de degre superieur ou egal a 1 de CX. D’apres laproposition precedente, P est scinde sur CX, d’ou l’existence d’unetelle factorisation.N. Arancibia - relu par D. CransacAlgebre

Page 56 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans RXPassons maintenant a la decomposition dans RX. Commen¸cons introduitele resultat suivant :LemmeSoit PX RX. Si on considere PX comme un polynˆome de CX etque α C \ R est une racine de PX alors α est aussi une racine complexede PX avec mˆeme multiplicite.Demonstration.Soit PX = Pnk=0 akX k. Puisque les coefficients de P sont reels, nouspouvons ecrire0 = Pα=⇒0 = PαOn a doncPα=nXk=0akαk =nXk=0ak · αk= nXk=0akαk!= 0Donc α est une racine.N. Arancibia - relu par D. CransacAlgebre

Page 57 : PolynˆomesDecomposition en facteurs irreductiblesDecomposition dans RXA l’aide du lemme precedent nous pouvons donner la decomposition dansRX.Theoreme1Les polynˆomes irreductibles de RX sontles polynˆomes de degre 1 ;les polynˆomes de degre 2 a discriminant strictement negatif.2Tout polynˆome P de RX se factorise de fa¸con unique a l’ordre pres desfacteurs en produit de polynˆomes irreductibles de RX sous la forme :PX = λ pYk=1X αkmk! qYk=1X 2 + βkX + γknk!.N. Arancibia - relu par D. CransacAlgebre

Page 58 : PolynˆomesDecomposition en facteurs irreductiblesSomme et produit des racines d’un polynˆomeOn finit le chapitre avec le resultat suivant.Proposition Somme et produit des racines d’un polynˆome scindeSoit P = Pnk=0 akX k KX un polynˆome scinde, α1, α2 · · · , αn, sesracines distinctes ou non. Alorsα1 + α2 + · · · + αn=an1an.α1 · α2 · · · · · αn=1n a0an.Remarque : En particulier, pour n = 2 et PX = c + bX + aX 2, nousavons :α1 + α2=baα1 · α2=caN. Arancibia - relu par D. CransacAlgebre

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58