CM7 Fractions Rationnelles
Télécharger le CM7 Fractions Rationnelles en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
Page 1 : Fractions RationnellesDecomposition des Fractions RationnellesAlgebre-Premier semestre 20211Fractions Rationnelles2Decomposition des Fractions RationnellesN. Arancibia - relu par D. CransacAlgebre
Page 2 : Fractions RationnellesDecomposition des Fractions RationnellesAlgebre-Premier semestre 2021ThemesLogique et raisonnementEnsemblesRelations binairesApplicationsNombres complexesPolynˆomesFractions rationnellesN. Arancibia - relu par D. CransacAlgebre
Page 3 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesDans ce chapitre nous continuons a utiliser K pour designer C ou R.A partir de l’ensemble Z, nous pouvons construire l’ensemble Q. De la mˆememaniere, nous pouvons construire a partir de KX, l’ensemble KX desfractions rationnelles. Dans l’ensemble des fractions rationnelles, il va nousˆetre possible, par exemple, de parler de l’inverse d’un polynˆome. Dans lasuite, nous allons donc voir que les fractions rationnelles sont aux polynˆomesce que les nombres rationnels sont aux entiers relatifs.N. Arancibia - relu par D. CransacAlgebre
Page 4 : Fractions RationnellesDecomposition des Fractions RationnellesDefinition Fractions RationnellesUne fraction rationnelle a coefficients dans K est une expression de laformeR = PQ ,ou P, Q KX sont deux polynˆomes avec Q ̸= 0. Autrement dit, unefraction rationnelle est un quotient entre deux polyˆomes.Si R = PQ est une fraction rationnelle, le couple P, Q s’appelle unrepresentant de la fraction rationnelle R.DefinitionL’ensemble des fractions rationnelles est note KX.Remarque : On identifie tout polynˆome P KX a la fractionrationnelle P1 . Cette identification fait de KX un sous-ensemble deKX.N. Arancibia - relu par D. CransacAlgebre
Page 5 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesDefinition Egalite entre fractions rationnellesSoit A, B, C, D KX avec B ̸= 0 et D ̸= 0. Alors on dit que les deuxfractions rationnelles AB et CD sont egales, si et seulement siA · D = C · B.Exemple :Dans RX, les fractions 1X etX + 1XX + 1 sont egales car :1 · XX + 1 = X · X + 1.N. Arancibia - relu par D. CransacAlgebre
Page 6 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesRemarque : Une fraction rationnelles possede plusieurs representants.Autrement dit, l’ecriture d’une fraction rationelle R KX comme quotientde deux polynomes, n’est pas unique :RX = 1X =X + 1XX + 1 = X + 3X 2 + 1XX + 3X 2 + 1.Entre tous les fa¸cons d’exprimer une fraction rationnelle R, nous allonssurtout ˆetre interesses par la forme irreductible de R.N. Arancibia - relu par D. CransacAlgebre
Page 7 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesAvant de pouvoir parler de la forme irreductible d’une fraction rationnelle,nous devons introduire la notion de polynˆomes premiers.Definition Polynˆomes premiersSoit P, Q KX.On dit que P et Q sont deux polynˆomes premiers entre eux si et seulement siles seuls diviseurs communs a P et Q sont les polynˆomes constants non nuls.Exemples :X 1 et 2X + 4 sont premiers entre eux.X 2 + X + 1 et X 1 sont premiers entre eux.2X 2 + 2X 4 et X 3 1 ne sont pas premiers entre eux.En effet2X 2 + 2X 4=X 12X + 4=⇒X 12X 2 + 2X 4X 3 1=X 1X 2 + X + 1=⇒X 1X 3 1.N. Arancibia - relu par D. CransacAlgebre
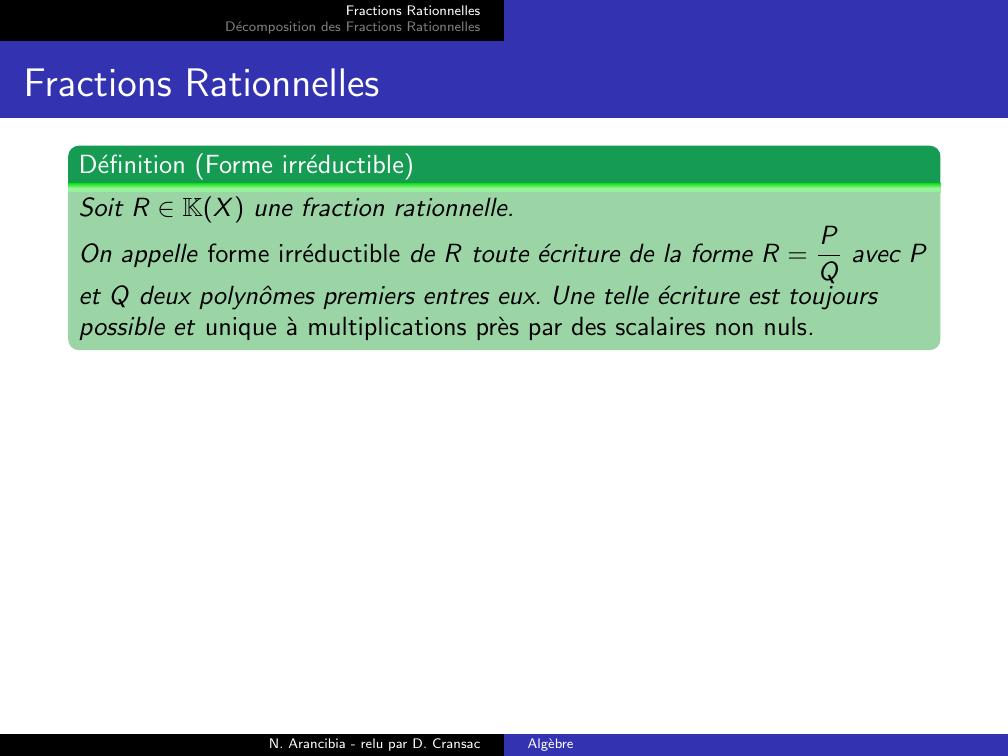
Page 8 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesDefinition Forme irreductibleSoit R KX une fraction rationnelle.On appelle forme irreductible de R toute ecriture de la forme R = PQ avec Pet Q deux polynˆomes premiers entres eux. Une telle ecriture est toujourspossible et unique a multiplications pres par des scalaires non nuls.N. Arancibia - relu par D. CransacAlgebre
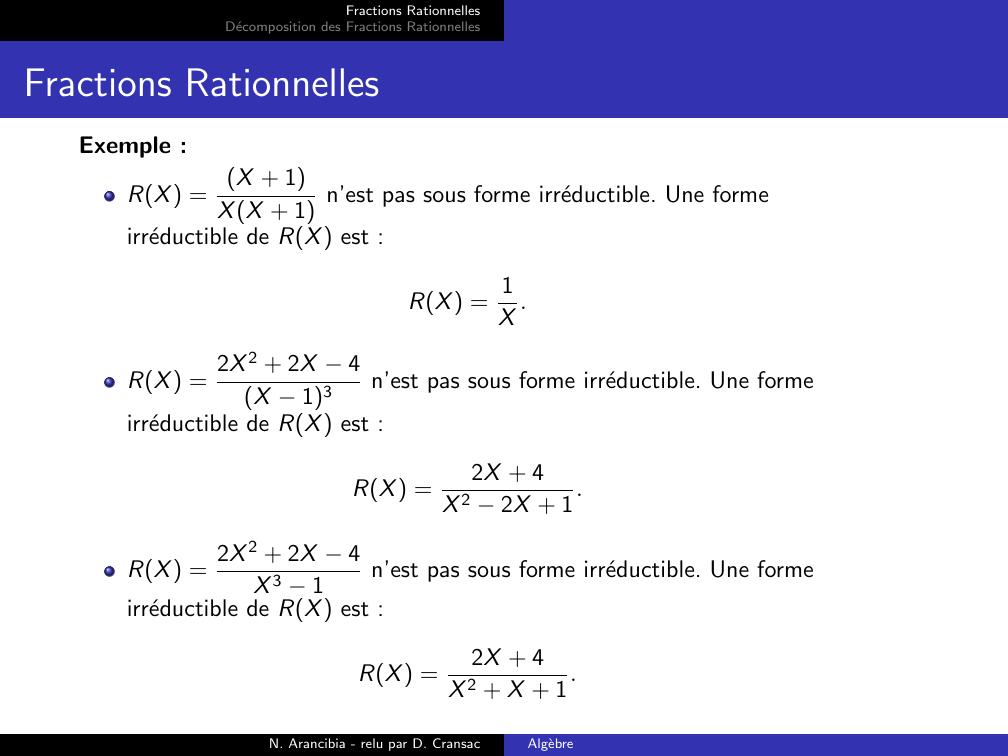
Page 9 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesExemple :RX = X + 1XX + 1 n’est pas sous forme irreductible. Une formeirreductible de RX est :RX = 1X .RX = 2X 2 + 2X 4X 13n’est pas sous forme irreductible. Une formeirreductible de RX est :RX =2X + 4X 2 2X + 1.RX = 2X 2 + 2X 4X 3 1n’est pas sous forme irreductible. Une formeirreductible de RX est :RX =2X + 4X 2 + X + 1.N. Arancibia - relu par D. CransacAlgebre
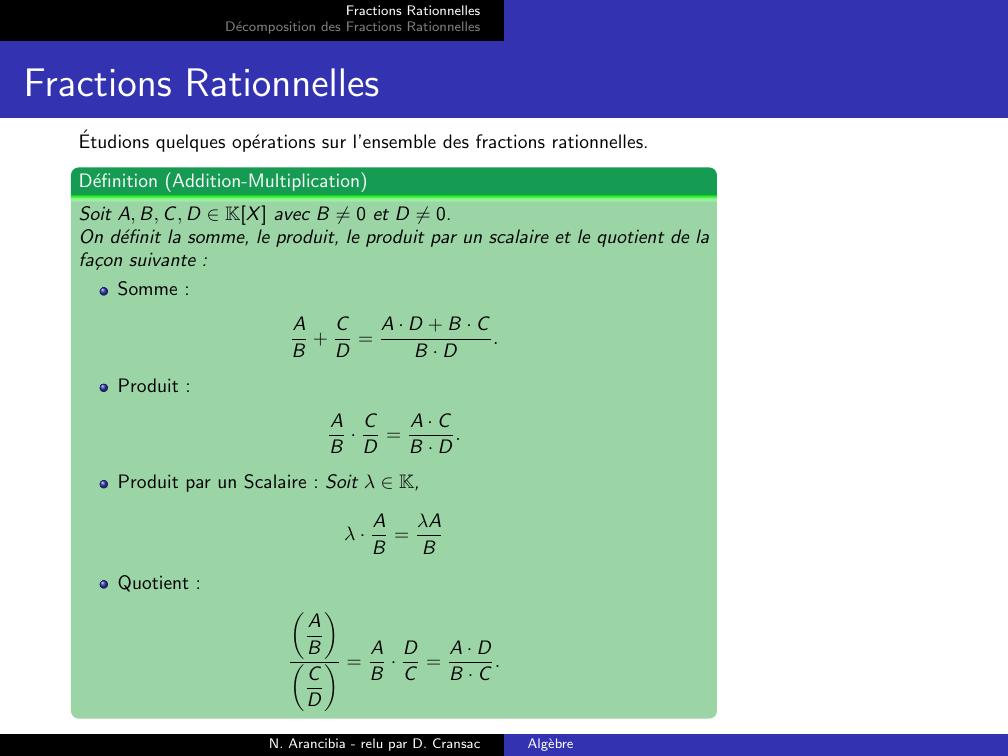
Page 10 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesEtudions quelques operations sur l’ensemble des fractions rationnelles.Definition Addition-MultiplicationSoit A, B, C, D KX avec B ̸= 0 et D ̸= 0.On definit la somme, le produit, le produit par un scalaire et le quotient de lafa¸con suivante :Somme :AB + CD = A · D + B · CB · D.Produit :AB · CD = A · CB · D .Produit par un Scalaire : Soit λ K,λ · AB = λABQuotient : ABCD = AB · DC = A · DB · C .N. Arancibia - relu par D. CransacAlgebre
Page 11 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesRemarque : Les definitions de somme et produit ne dependent pas du choixdes representants propriete indispensable.Definition DeriveeSoit R = PQ KX une fraction rationnelle. On appelle derivee de R lafraction rationnelleR′ = P′Q PQ′Q2Remarque : La derivee de R ne depend pas du choix de P et Q.N. Arancibia - relu par D. CransacAlgebre
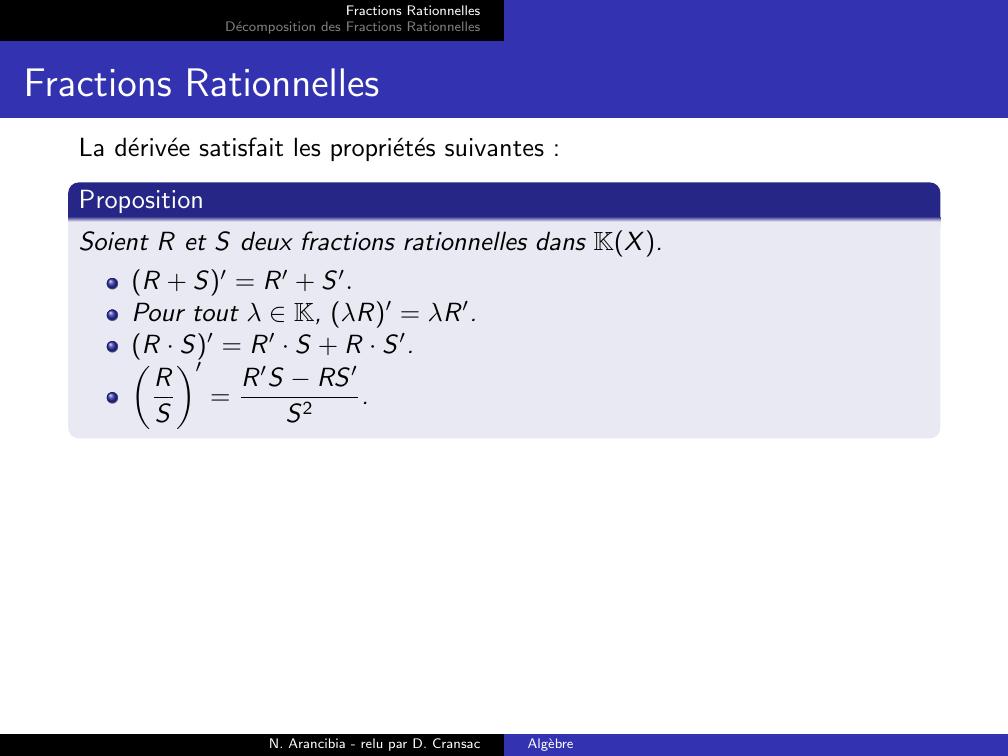
Page 12 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesLa derivee satisfait les proprietes suivantes :PropositionSoient R et S deux fractions rationnelles dans KX.R + S′ = R′ + S′.Pour tout λ K, λR′ = λR′.R · S′ = R′ · S + R · S′.RS′= R′S RS′S2.N. Arancibia - relu par D. CransacAlgebre
Page 13 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesDefinition Degre d’une fraction rationnelleSoit R = PQ KX une fraction rationnelle. On appelle degre de R l’entierrelatif :degR = degP degQ.Remarques :Le degre de R ne depend pas du choix de P et Q.Le degre d’une fraction rationnelle R = PQ est ainsi soit un entier relatifsi P ̸= 0, soit si P = 0.PropositionPour tous R, S KX, nous avonsdegR + S maxdegR, degS.degR · S = degR + degS.N. Arancibia - relu par D. CransacAlgebre
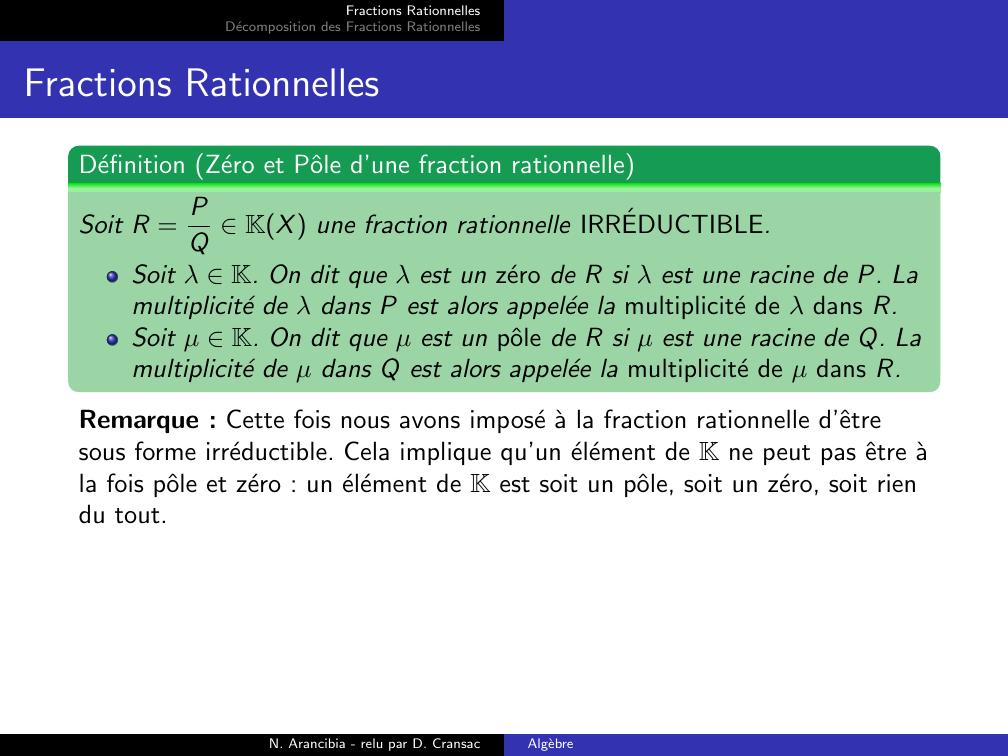
Page 14 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesDefinition Zero et Pˆole d’une fraction rationnelleSoit R = PQ KX une fraction rationnelle IRREDUCTIBLE.Soit λ K. On dit que λ est un zero de R si λ est une racine de P. Lamultiplicite de λ dans P est alors appelee la multiplicite de λ dans R.Soit µ K. On dit que µ est un pˆole de R si µ est une racine de Q. Lamultiplicite de µ dans Q est alors appelee la multiplicite de µ dans R.Remarque : Cette fois nous avons impose a la fraction rationnelle d’ˆetresous forme irreductible. Cela implique qu’un element de K ne peut pas ˆetre ala fois pˆole et zero : un element de K est soit un pˆole, soit un zero, soit riendu tout.N. Arancibia - relu par D. CransacAlgebre
Page 15 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesExemple : Dans RX, la fractionRX=X + 1X 24X 3X 43X + 7X 2 + X + 1X 3X + 12X 3X 4X 52X 2 + 13=X 24X 42X + 7X 2 + X + 1X 3X + 1X 52X 2 + 13.a pour zeros :2 de multiplicite 4.4 de de multiplicite 2.-7 de multiplicite 1.et pour pˆoles :0 de multiplicite 3.-1 de multiplicite 1.5 de de multiplicite 2.3 n’est ni un pˆole ni un zero.N. Arancibia - relu par D. CransacAlgebre
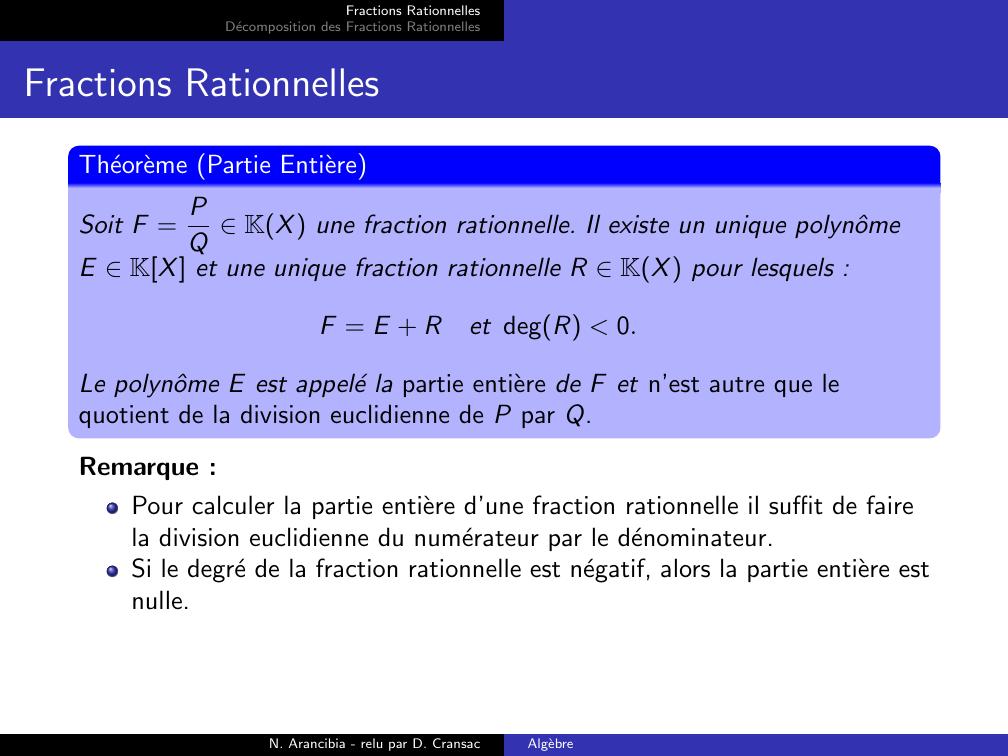
Page 16 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesTheoreme Partie EntiereSoit F = PQ KX une fraction rationnelle. Il existe un unique polynˆomeE KX et une unique fraction rationnelle R KX pour lesquels :F = E + Ret degR 0.Le polynˆome E est appele la partie entiere de F et n’est autre que lequotient de la division euclidienne de P par Q.Remarque :Pour calculer la partie entiere d’une fraction rationnelle il suffit de fairela division euclidienne du numerateur par le denominateur.Si le degre de la fraction rationnelle est negatif, alors la partie entiere estnulle.N. Arancibia - relu par D. CransacAlgebre
Page 17 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesExemple : Soit R = 2X 4 X 3 2X 2 + 3X 1X 2 X + 1. Alors2X 4 X 3 2X 2 + 3X 1 = X 2 X + 12X 2 + X 3 + X + 2D’ou on obtient2X 4 X 3 2X 2 + 3X 1X 2 X + 1=X 2 X + 12X 2 + X 3 + X + 2X 2 X + 1=2X 2 + X 3 +X + 2X 2 X + 1N. Arancibia - relu par D. CransacAlgebre
Page 18 : Fractions RationnellesDecomposition des Fractions RationnellesDecomposition en elements simples dans CXTheoremeSoit R CX de partie entiere E et de pˆoles distincts λ1, · · · , λr demultiplicites respectives m1, · · · , mr. Il existe une unique famille des nombrescomplexesaik1ir,1kmitelles queR =Ezpartie entiere de R+rXi=1miXk=1aikX λikzpartie polaire relative au pole λiCette decomposition de R est appelee decomposition en elements simples surC.N. Arancibia - relu par D. CransacAlgebre
Page 19 : Fractions RationnellesDecomposition des Fractions RationnellesDecomposition en elements simples dans RXTheoremeSoit R = PQ RX sous forme irreductible, de partie entiere E. Soit ladecomposition de Q en facteurs irreductibles :Q = αrYi=1X λimisYj=1X 2 + bjX + cjnj.Alors il existe des familles uniques de reelsaik1ir,1kmi;ujk1js,1knj;vjk1js,1knjtelles queR =Ezpartie entierede R+rXi=1miXk=1aikX λikzpartie polairerelativeau pole λi+sXj=1njXk=1ujkX + vjkX 2 + bjX + cjkCette decomposition de R est appelee decomposition en elements simples surR.N. Arancibia - relu par D. CransacAlgebre
Page 20 : Fractions RationnellesDecomposition des Fractions RationnellesFractions RationnellesNotation : Dans la decomposition de la fraction rationnelle R dans RX :Les fractionsaikX λik sont appelees elements simples de premiereespece.Les fractionsujkX + vjkX 2 + bjX + cjk sont appelees elements simples deseconde espece.N. Arancibia - relu par D. CransacAlgebre
Page 21 : Fractions RationnellesDecomposition des Fractions RationnellesDecomposition en elements simples dans RXCorollaireSoit R = PQ RX sous forme irreductible, de partie entiere E. Soit ladecomposition de Q en facteurs irreductibles :Q=αrYi=1X λimisYj=1X 2 + bjX + cjnjdans RX=αrYi=1X λimisYj=1X µi · X µinjdans CX.Alors il existe des familles uniques aik1ir,1kmi et ηjk1js,1knjtelles queR =Ezpartie entiere de R+rXi=1miXk=1aikX λikzpartie polaire relative au pole λi+sXj=1njXk=1ηjkX µjk +ηjkX µjkzpartie polaire relative au poles µj et µj.C’est la decomposition en elements simples de R dans CX.N. Arancibia - relu par D. CransacAlgebre
Page 22 : Fractions RationnellesDecomposition des Fractions RationnellesProcedure a suivre pour la D.E.SSoientP = 2X 6 + 3X 5 3X 4 3X 3 3X 2 18X 5etQ = X 5 + X 4 2X 3 X 2 X + 2.Nous allons calculer la decomposition en elements simples deF = 2X 6 + 3X 5 3X 4 3X 3 3X 2 18X 5X 5 + X 4 2X 3 X 2 X + 2Donnons la procedure a suivre :1 Partie entiere : Puisque degP degQ, on fait la division euclidiennede P par Q pour extraire la partie entiere de F. Nous avons :F =2X + 1 z partie entiere de F+X 3 21X 7X 5 + X 4 2X 3 X 2 X + 22 Polˆes de F : Determiner les pˆoles de F. Pour faire cela, on factorise lepolynˆome denominateur de F en produit de facteurs irreductibles. Dans notreexemple, nous avons :Q1 = Q′1 = Q2 = 0=⇒X 12X + 2 divise Q.Finalement, en effectuant la division euclidienne de Q par X 12X + 2on obtient :QX=X 12X + 2X 2 + X + 1dans RX.N. Arancibia - relu par D. CransacAlgebre
Page 23 : Fractions RationnellesDecomposition des Fractions RationnellesProcedure a suivre pour la D.E.SEtQX = X 12X + 2X 2 + X + 1 = X 12X + 2X jX jdans CX,ou j = e2iπ3 . Ainsi 1 et 2 sont des pˆoles de F dans R d’ordre 2 et 1respectivement, et le couple j, j sont des pˆoles simples de F sur C.3 Poser la decomposition en elements simples de F : Il existe des reelstels que la decomposition de F dans RX s’ecrit sous la forme :F = 2x + 1 +aX 12 +bX 1zpartie polaire relative au pole 1+cX + 2zpartie polaire relative au pole 2+dX + eX 2 + X + 1.De plus, puisque F est une fraction rationnelle a coefficients reels, ladecomposition de F dans CX s’ecrit sous la forme :F=2x + 1 +aX 12 +bX 1 +cX + 2 +αX j +αX jzpartie polaire relative aux poles j et j.4 Calculer les coefficients intervenant dans la decomposition enelements simples de F : Pour cela nous allons etudier des methodessystematiques et efficaces adaptees a chaque type de pˆole.N. Arancibia - relu par D. CransacAlgebre
Page 24 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S-Pˆoles simples : Multiplication-EvaluationPˆoles simples : Commen¸cons par calculer les coefficients associees a despoles simples. Pour faire cela nous allons introduire la methode dite demultiplication-evaluation.Multiplication-evaluation : Soit λ un pˆole simple de F = PQ , alorsQ = X λQ1avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PQ =αX λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0. La procedure a suivrepour trouver α est la suivante :1Multiplier F par X λ :X λFX = X λPXX λQ1X = X λ ·αX λ + X λF0X.2Simplifier :PQ1= α + X λF0.3Substituer X par λ et calculer le coefficient :PλQ1λ = α + λ λF0=⇒PλQ1λ = α.N. Arancibia - relu par D. CransacAlgebre
Page 25 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S-Pˆoles simples : Multiplication-EvaluationDans notre exemple λ = 2 est un pˆole simple, implementons la methode.Nous avons2X + 1 +X 3 21X 7X 12X + 2X 2 + X + 1 =cX + 2 + F0Multiplions F par X + 2 :X + 2 · 2X + 1 +X + 2 · X 3 21X 7X 12X + 2X 2 + X + 1 = X + 2 ·cX + 2 + X + 2 · F0Simplifions :X + 2 · 2X + 1 +X 3 21X 7X 12X 2 + X + 1 = c + X + 2 · F0.Substituons X par 2 :2 + 2 · 22 + 1 +8 + 42 72 12 · 22 2 + 1 = c=⇒c = 1.N. Arancibia - relu par D. CransacAlgebre
Page 26 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S-Pˆoles doubles : Multiplication-EvaluationEtudions a present le cas des pˆoles doubles.Pˆoles doubles : Soit λ un pˆole double de F = PQ , alorsQ = X λ2Q1,avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PXQX =αX λ2 +βX λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0. La procedure a suivrepour trouver α et β est la suivante :• Premier coefficient : Pour trouver α nous pouvons utiliser le principe demultiplication-evaluation introduit au moment d’etudier les pˆoles simples,mais au lieu de multiplier F par X λ on multiplie F par X λ2 :X λ2 ·PXX λ2Q1X = X λ2 ·αX λ2 + X λ2 ·βX λ + X λ2 · F0.On simplifie :PXQ1X = α + X λβ + X λ2 · F0.Pour finalement substituer X par λ :PλQ1λ = α.N. Arancibia - relu par D. CransacAlgebre
Page 27 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles doubles : Multiplication-EvaluationDans notre exemple λ = 1 est un pˆole d’ordre 2, implementons la methode.Nous avons :2X + 1 +X 3 21X 7X 12X + 2X 2 + X + 1 =aX 12 +bX 1 + F0.Multiplions F par X 12 :X 12 · 2X + 1 +X 12X 3 21X 7X 12X + 2X 2 + X + 1=X 12 ·aX 12+ X 12 ·bX 1 + F0.Simplifions :X 12 · 2X + 1 +X 3 21X 7X + 2X 2 + X + 1 = a + X 1b + X 12 · F0.Subtituons X par 1 :1 12 · 21 + 1 +13 21 71 + 212 + 1 + 1 = 279= 3=⇒a = 3.N. Arancibia - relu par D. CransacAlgebre
Page 28 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles doubles : Soustraction• Deuxieme coefficient : Maintenant que l’on connaˆıt le coefficient α dansF = PXQX =αX λ2 +βX λ + F0,pour calculer β nous allons utiliser la methode dite de soustraction.Soustraction : La procedure a suivre pour trouver β est la suivante :1RamenerαX λ2 a gauche :PXX λ2Q1X αX λ2 =βX λ + F0.2Mettre F1 = F αX λ2 au mˆeme denominateur :PX α · Q1XX λ2Q1X=βX λ + F0,puis simplifier la fraction a gauche. Le numerateur et le denominateur sesimplifient forcement sinon il y a une erreur de calcul et λ devient uneracine simple de F1.3Le coefficient β peut se calculer alors en utilisant le principe demultiplication-evaluation : on multiplie F1 par X λ, on simplifiepuis on substitue X par λ.N. Arancibia - relu par D. CransacAlgebre
Page 29 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles doubles : SoustractionAppliquons cette methode a notre exemple pour calculer b :F=bX 1 3X 12 + F0.1 Ramener3X 12 a gauche :2X + 1 +X 3 21X + 1X + 2X 2 + X + 1X 12 +3X 12 =bX 1 + F0.2 Mettre la fraction a gauche au mˆeme denominateur, puis simplifier :2X + 1 +4X 2 + 13X + 1X + 2X 2 + X + 1X 1zF1=bX 1 + F0.On voit bien que 1 est une pˆole simple pour la fraction rationnelle ainsiobtenue.3 Pour trouver β on multiplie F1 par X 1, on simplifie et finalement onevalue en 1 :F1X =bX 1 + · · ·=⇒zmultiplier par X14X 2 + 13X + 1X + 2X 2 + X + 1 = b + X 1 · · · ·=⇒zsubstituer X par 14 + 13 + 11 + 21 + 1 + 1 = 2 = b.N. Arancibia - relu par D. CransacAlgebre
Page 30 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Elements simples de seconde especeAinsiF=2x + 1 +2X 1 3X 12 +1X + 2 +dX + eX 2 + X + 1dans RX.etF=2x + 1 +2X 1 3X 12 +1X + 2 +αX j +αX jdans CX.Pour trouver les coefficient d et e on dispose de deux methodes :• Passage dans C :On calcule d’abord les coeffiecients α et α, puis onregroupe les elements simples conjugues :F=αX j +αX j+ · · · = αX j + αX jX jX j+ · · ·=α + αX α · j + α · jX 2 + X + 1+ · · ·=⇒α + αX α · j + α · jX 2 + X + 1=dX + eX 2 + X + 1.=⇒d = α + αete = α · j + α · j.N. Arancibia - relu par D. CransacAlgebre
Page 31 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Elements simples de seconde especeCalculons donc α et α. Utilisons pour cela le principe demultiplication-evaluation : on multiplie F par X j, on simplifie etfinalement on substitue X par j :FX =αX j + · · ·=⇒zmultiplier par XjX 3 21X 7X 12X + 2X j = α + X j · · · ·=⇒zsubstituer X par jj3 21j 7j 12j + 2j j = 32 536 i = α=⇒α = 32 + 536 i.Par consequent :d=2Re 32 536 i!= 3e=2Re 32 536 i!· j!= 1.D’ou on obtient :F=2x + 1 +2X 1 3X 12 +1X + 2 +32 536 iX j+32 + 536 iX j=2x + 1 +2X 1 3X 12 +1X + 2 +3X + 1X 2 + X + 1.N. Arancibia - relu par D. CransacAlgebre
Page 32 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Elements simples de seconde especeDeuxieme mˆethode pour trouver les coefficient d et e :Multiplication-evaluation dans C : La procedure a suivre pour trouver d ete est la suivante :1On multiplie F par X 2 + X + 1 :X 2 + X + 1F = X 2 + X + 12X + 1 +X 3 21X 7X 12X + 2 = dX + e + X2Substituer X par l’une des racines de X 2 + X + 1 :j2 + j + 12j + 1 +j3 21j 7j 12j + 2 = dj + e=⇒6 + 21j3j 3 = dj + e.3On calcule d et e en separant les parties reelle et imaginaireA vous de le faire :d = 3ete = 1.N. Arancibia - relu par D. CransacAlgebre
Page 33 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesPˆoles d’ordre superieur ou egal a 3 : Soit λ un pˆole d’ordre n 3 deF = PQ , alorsQ = X λnQ1,avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PXQX =a0X λn +a1X λn1 + · · · +an1X λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0.• Premier coefficient : Pour calculer a0 nous pouvons utiliser le principle demultiplication-evaluation : On multiplie F par X λn pour ensuiteevaluer en λ :X λn · PXQX=a0 + a1X λ + · · · + an1X λn1 + X λnF0.=⇒PλQ1λ=a0.• Tout autre coefficient : Pour calculer les autres coefficients, on peuttoujours appliquer la methode de soustraction introduite dans le cas des pˆolesdoubles. En effet : Pour calculer a1 : on doit suivre les etapes suivants :1Ramenera0X λn a gauche.2Mettre F1 = F a0X λn au mˆeme denominateur puis simplifiernumerateur et denominateur.3Multiplier F1 par X λn1 puis evaluer en λ pour trouver a1.N. Arancibia - relu par D. CransacAlgebre
Page 34 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesPour calculer a2 : on doit suivre les etapes suivants :1Ramenera0X λn +a1X λn1 a gauche.2Mettre F1 = F a0X λn a1X λn1 au mˆeme denominateur puissimplifier numerateur et denominateur.3Multiplier F2 par X λn2 puis evaluer en λ pour trouver a2.Et ainsi de suite pour tout autre coefficient.Notons que au fur et a mesure des soustractions, les fractions se simplifient,mais les calculs restent lourds. Donnons donc une autre methode pourcalculer les coefficients. Cette deuxieme methode est basee sur le principe dedivision selon les puissances croissantes qui nous permet de calculer tousles coefficients d’un pˆole d’un coup.Division selon les puissances croissantes : Nous avons le resultat suivant :Proposition Division selon les puissances croissantesSoit n N, A et B des polynˆomes dans KX. On suppose que le termeconstant de B est non nul. Alors il existe deux polynˆomes C et D verifiant :AX = BX · CX + X n+1DX,degQ n.N. Arancibia - relu par D. CransacAlgebre
Page 35 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesExemple : SoitA = X 5 + 6X 4 + 14X 3 + 16X 2 + 9X + 3etB = X 2 + 4X + 4.1Calculer la division selon les puissances croissantes a l’ordre 2 de A par B.Solution : Le principe est le mˆeme que la division euclidienne, mis a partqu’au lieu d’ordonner les polynˆomes selon les puissances decroissantes, on lesordonne selon les puissances croissantes. Lors de la division, il faut garder entˆete que l’on ne s’interesse qu’aux degres inferieurs ou egaux a 2 :3+9X+16X 2+14X 3+6X 4+X 54 + 4X + X 23+3X+34X 234+32X+3716X 26X+614 X 2+14X 3+6X 4+X 56X+6X 2+32X 3+374 X 2+252 X 3+6X 4+X 5-374 X 2+374 X 2+3716X 4134 X 3+5916X 4+X 5Par consequent :A =32 + 32X + 3716X 2B + X 3134 + 5916X + X 2.N. Arancibia - relu par D. CransacAlgebre
Page 36 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesMaintenant qu’on a introduit la division selon les puissances croissantes,regardons comme elle nous permet de calculer les coefficients d’un pˆole demultiplicite n. Comme precedement, soit λ un pˆole d’ordre n 3 de F = PQ ,alorsQ = X λnQ1,avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PXQX =a0X λn +a1X λn1 + · · · +an1X λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0. La methode a suivre estla suivante :aOn effectue le changement de variable Y = X λ, et on reecrit F enfonction de Y : Ainsi, F se decompose sous la forme :PY Y n · Q1Y = a0Y n +a1Y n1 + · · · + an1Y+ F0Y .Le nouveau pˆole est alors 0, de multiplicite n.bOn multiplie FY par Y n :Y n ·PY Y n · Q1Y = PY Q1Y = a0 + a1Y + · · · + an1Y n1 + Y n · F0Y .cLes n coefficients se trouvent alors en faisant une division selon lespuissances croissantes de P par Q1, que l’on arrˆete des que l’onobtient le ne coefficient.N. Arancibia - relu par D. CransacAlgebre
Page 37 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesImplementons la methode sur l’exemple suivant :Exemple : Decomposer en elements simples la fraction rationnelle :F =X 5 + X 4 + 1X 13X + 12 .Solution :aPartie entiere : Puisque degX 5 + X 4 + 1 = degX 13X + 12,on fait la division euclidienne de X 5 + X 4 + 1 par X 13X + 12 pourextraire la partie entiere de F. Nous avonsF =1zpartie entiere de F+ 2X 4 + 2X 3 2X 2 X + 2X 13X + 12bPˆoles : F possede un pˆole double : 1 et un pˆole triple : 1.cPoser la decomposition en elements simples : La decomposition deF dans CX s’ecrit sous la forme :X 5 + X 4 + 1X 13X + 12 = 1 +aX 13 +bX 12 +cX 1 +dX + 12 +eX + 1.Trouvons la valeur de chaque coefficient.N. Arancibia - relu par D. CransacAlgebre
Page 38 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesDans le cas des pˆoles multiples la methode dite de division selon lespuissances croissantes s’avere tres utile. Implementons cette techniquepour trouver a, b et c :On commence par le changement de variable X 1 = Y , pour ensuitereecrire F en fonction de Y :FY = Y + 15 + Y + 14 + 1Y 3Y + 22= Y 5 + 6Y 4 + 14Y 3 + 16Y 2 + 9Y + 3Y 3Y 2 + 4Y + 4.On multiplie FY par Y 3 :Y 3FY = Y 5 + 6Y 4 + 14Y 3 + 16Y 2 + 9Y + 3Y 2 + 4Y + 4,et on fait la division selon les puissances croissantes deY 5 + 6Y 4 + 14Y 3 + 16Y 2 + 9Y + 3parY 2 + 4Y + 4.Lors de la division, il faut garder en tˆete que l’on ne s’interesse qu’aux degresinferieurs ou egaux a 2 car 1 est pˆole de multiplicite 3. C’est-a-dire on faitune division selon les puissances croissantes a l’ordre 2. Nous avons VoirExemple 1 :Y 5 + 6Y 4 + 14Y 3 + 16Y 2 + 9Y + 3Y 2 + 4Y + 4=34 + 32Y + 3716Y 2+ Y 3 ·134 + 5916Y + Y 2Y 2 + 4Y + 4.Ainsia = 34;b = 32;c = 3716.N. Arancibia - relu par D. CransacAlgebre
Page 39 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Pˆoles MultiplesPar consequentX 5 + X 4 + 1X 13X + 12 = 1 +34X 13 +32X 12 +3716X 1 +dX + 12 +eX + 1.Pour trouver d on utilise la mˆethode de multiplication-evaluation : Onmultiplie F par X + 12, on simplifie et finalement on evalue en 1. Onobtient :d = 18.Finalement pour e, considerons F0 :F0 =05 + 04 + 10 130 + 12 = 1=⇒1 = 3413 +3212 +37161 18 + e.=⇒e = 516.D’ouX 5 + X 4 + 1X 13X + 12 = 1 +34X 13 +32X 12 +3716X 1 18X + 12 516X + 1.N. Arancibia - relu par D. CransacAlgebre
Page 40 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Elements simples de seconde especeElements simples de seconde espece : Soit F = PQ , avec Q un polynomede discriminant negatif tel que :QX=X 2 + aX + bnQ1XetX 2 + aX + b ne divise pas Q1X.Ainsi, F se decompose sous la forme :PXQX =α0X + β0X 2 + aX + bn +α1X + β1X 2 + aX + bn1 + · · · + αn1X + βn1X 2 + aX + b + F0,ou X 2 + aX + b ne divise pas le denominateur de la fraction rationnelle F0.La methode a suivre pour trouver les coefficients est la suivante :• Pour calculer α0 et β0 : nous pouvons utiliser le principle demultiplication -evaluation : On multiplie F par X 2 + aX + bn pourensuite evaluer en une racine complexe λ de X 2 + aX + b :X 2 + aX + bn ·PXX 2 + aX + bnQ1X=α0X + β0 + X 2 + aX + b · · ·=⇒PλQ1λ=α0λ + β0,Ou l’on calcule α0 et β0 en separant les parties reelles et imaginaires.N. Arancibia - relu par D. CransacAlgebre
Page 41 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Elements simples de seconde especePour calculer les autres coefficients, on peut toujours appliquer la methodede soustraction introduite dans le cas des pˆoles doubles. En effet :• Pour calculer α1 et β1 : on doit suivre les etapes suivants :1Ramenerα0X + β0X 2 + aX + bn a gauche.2Mettre F1 = F α0X + β0X 2 + aX + bn au mˆeme denominateur puissimplifier numerateur et denominateur.3Multiplier F1 par X 2 + aX + bn1 puis evaluer en λ pour trouver α1 etβ1.• Pour calculer α2 et β2 :1Ramenerα0X + β0X 2 + aX + bn +α1X + β1X 2 + aX + bn1 a gauche.2Mettre F1 = F α0X + β0X 2 + aX + bn α1X + β1X 2 + aX + bn1 au mˆemedenominateur puis simplifier numerateur et denominateur.3Multiplier F2 par X 2 + aX + bn2 puis evaluer en λ pour trouver α2 etβ2.Et ainsi de suite pour tout autre coefficient.N. Arancibia - relu par D. CransacAlgebre
Page 42 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : DerivationPoles Simples : Dans le cas des pˆoles simples la derivation peut se montrertres utile au moment de calculer les coefficients intervenant dans ladecomposition en elements simples. Etudions cela de plus pres.Derivation : Soit λ un pˆole simple de F = PQ , alorsQ = X λQ1avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PQ =αX λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0. Comme nous avons vuprecedement, ceci implique que :X λ · PXQX = PXQ1X = α + X λF0X=⇒PλQ1λ = α.Notons maintenant que l’egalite QX = X λQ1X implique que :Q′X = X λQ′1X + Q1X=⇒Q′λ = λ λQ′1λ + Q1λ=⇒Q′λ = Q1λ.Ainsiα = PλQ1λ = PλQ′λ.N. Arancibia - relu par D. CransacAlgebre
Page 43 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : DerivationLa derivation est surtout pratique lorsque l’on connaˆıt la forme developpee dudenominateur et que l’on ne veut pas le factoriser. Implementons la methodesur l’exemple suivant :Exemple : Decomposer en elements simples dans CX pour n Nlafraction rationnelle : FX =1X n 1.Solution :aPartie Entiere : Puisque deg1 = 0 degX n 1, la partie entiere deF est 0.bPˆoles : Soit QX = X n 1. Les racines de Q sont les racines n-iemesde l’unite a savoir :ωk = e2iπkn, 0 k n 1=⇒QX =n1Yk=0X ωk.Ainsi F possede n pˆoles simples : ωk = e2iπkn, 0 k n 1.cPosons la decomposition en elements simples : La decompositionde F dans CX s’ecrit sous la forme :1X n 1 =a0X 1 +a1X ω1+ · · · +an1X ωn1=n1Xk=0akX ωk.Trouvons la valeur de chaque coefficient a l’aide de la derivation.N. Arancibia - relu par D. CransacAlgebre
Page 44 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : DerivationComme tous les pˆoles sont simples et le denominateur de F est sous formedeveloppee, la derivation s’avere tres utile :On commence par deriver QX = X n 1 :Q′X = nX n1.Puis pour chaque k N, 0 k n 1, on evalue1Q′X en ωk pourtrouver ak :ak =1Q′ωk =1nωn1k= ωknωnk= ωkn .Ainsi1X n 1 =1nX 1 +ω1nX ω1 + · · · +ωn1nX ωn1 =n1Xk=0ωknX ωk.N. Arancibia - relu par D. CransacAlgebre
Page 45 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : DerivationPoles Doubles : La derivation peut aussi se montrer tres utile au momentde calculer les coefficients associes a un pole double.Derivation : Soit λ un pˆole double de F = PQ , alorsQ = X λ2Q1,avec Q1λ ̸= 0. Ainsi, F se decompose sous la forme :PXQX =αX λ2 +βX λ + F0,ou λ n’est pas un pˆole de la fraction rationnelle F0. Nous allons a presentcalculer β a l’aide de la derivee. Nous avons vu que pour trouver α il suffit demultiplier F par X λ2, simplifier et finalement evaluer en λ :PXQ1X=α + X λ · β + X λ2 · F0X2=⇒PλQ1λ=α.Maintenant en derivant l’equation 2, nous obtenons : PXQ1X′= β + X λ2F0 + X λF ′0.Ainsi, en substituant X par λ on conclut : PQ1′λ = β.N. Arancibia - relu par D. CransacAlgebre
Page 46 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : DerivationCette methode demande d’ˆetre capable de calculer simplement la derivee dela fraction rationnelle PQ1, c’est-a-dire que P et Q1 devront de preference ˆetresous forme developpe.Exemple : Decomposer en elements simples la fraction rationnelle :FX =X 2 + 1X 3 + 2X 2 + X .Solution :aPartie Entiere : Puisque degX 2 + 1 degX 3 + 2X 2 + X, la partieentiere de F est 0.bPˆoles : Nous avons :X 3 + 2X 2 + X = XX 2 + 2X + 1 = XX + 12.F possede alors un pˆole double : -1, et un pˆole simple : 0.cPosons la decomposition en elements simples : La decompositionde F s’ecrit sous la forme :X 2 + 1X 3 + 2X 2 + X =aX + 12 +bX + 1 + cXTrouvons la valeur de chaque coefficient.• Calculons a : On multiplie F par X + 12, on simplifie et finalement onevalue en 1. On obtient :a = 2.N. Arancibia - relu par D. CransacAlgebre
Page 47 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Derivation• Calculons b : Trouvons la valeur de b a l’aide de la derivation. Oncommence par multiplier F par X + 12 :X + 12 ·X 2 + 1XX + 12 = X 2 + 1X,on derive cette derniere fraction rationnelle :X 2 + 1X′= 2X 2 X 2 1X 2= X 2 1X 2,pour finalement evaluer en 1. On obtient :b = 0.• Calculons c : On multiplie F par X, on simplifie et finalement on evalueen 0. On obtient :c = 1.D’ouX 2 + 1X 3 + 2X 2 + X = 2X + 12 + 1X .N. Arancibia - relu par D. CransacAlgebre
Page 48 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.Voyons differentes methodes moins efficaces que les precedentes mais quipeuvent parfois permettre de finir rapidement les calculs. SoitFX = PXQX• Evaluation dans de valeurs particulieres : Quand il reste peu decoefficients a calculer, il peut ˆetre interessant d’evaluer, l’egalite entre F etsa decomposition, en une ou plusieurs valeurs qui ne sont pas de pˆoles de F.Cela permet d’obtenir d’autres relations entre les coefficients et calculer lescoefficients restants.Si F est dans RX, on peut evaluer en une valeur complexe, l’identificationdonnant alors deux relations entre les coefficients reels inconnus.• Methode de la limitelimx→+X · FX : Supposons que le degre de F eststrictement negatif la partie entiere est donc nulle, F se decompose alorssous la forme :FX =rXk=1akX λk +lXk=1bkX + ckX 2 + βkX + γk + F0.ou degF0 2. Le calcul delimx→+X · FX donne alors une relation liantles coeffients ak et bk.Regardons cela plus en detail.N. Arancibia - relu par D. CransacAlgebre
Page 49 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.En effet, puisque degF 0, nous avons :degX · FX 0=⇒limx→+X · FX admet une limite finie L en + .=⇒L=limx→+X · rXk=1akX λk +lXk=1bkX + ckX 2 + βkX + γk + F0!=limx→+ rXk=1akXX λk +lXk=1bkX 2 + ckXX 2 + βkX + γk + X · F0!=rXk=1ak +lXk=1bk +limx→+X · F0=rXk=1ak +lXk=1bkcar degX · F0 1.Cette methode est interessante quand il ne reste plus qu’un ou deuxcoefficients a calculer. Implementons ces deux methodes sur un exemple.Exemple : Decomposer en elements simples dans CX pour n Nlafraction rationnelle :X 2 + 3X 5 3X 4 + 5X 3 7X 2 + 6X 2.N. Arancibia - relu par D. CransacAlgebre
Page 50 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.X 2 + 3X 5 3X 4 + 5X 3 7X 2 + 6X 2.Solution :aPartie entiere : PuisquedegX 2 + 3 degX 5 3X 4 + 5X 3 7X 2 + 6X 2, la partie entierede F est 0.bPˆoles : Trouvons les pˆoles de F. PosonsQX = X 5 3X 4 + 5X 3 7X 2 + 6X 2. Il faut commencer parremarquer que Q1 = 0. On peut alors tester la multiplicite de 1comme racine de P : on s’aper¸coit que 1 est racine triple carQ′1 = Q′′1 = 0.On en deduit que QX est factorisable par X 13. En effectuantensuite la division euclidienne de QX par X 13 on obtient :X 5 3X 4 + 5X 3 7X 2 + 6X 2=X 13X 2 + 2=X 13X 2iX +2i.F possede alors 1 pˆole triple dans R : 1, en plus de deux pˆoles simplesdans C : ±2i.cPoser la decomposition en elements simples : La decomposition deF dans RX s’ecrit sous la forme :X 2 + 3X 13X 2 + 2 =aX 13 +bX 12 +cX 1 + dX + fX 2 + 2 .N. Arancibia - relu par D. CransacAlgebre
Page 51 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.Puisque F est une fraction rationnelle a coefficient reels, la decompostion deF dans CX s’ecrit sous la forme :X 2 + 3X 13X 2 + 2 =aX 13 +bX 12 +cX 1 +αX 2i+αX +2i.Commen¸cons par la decomposition de F en CX. Pour trouver les valeurs dea et α on utilise la methode de multiplication-evaluation :• Calculons a : On multiplie F par X 13, on simplifie et finalement onevalue en 1. On obtient :a = 43.• Calculons α : On multiplie F par X 2i, on simplifie et finalement onevalue en2i. On obtient :α = 127 · 2 52i4=⇒α = 127 · 2 + 52i4.Pour trouver b et c, on commence par considerer la limitelimx→+X · FX.Nous avons :limx→+X ·X 2 + 3X 13X 2 + 2 = 0=⇒0 =limx→+X · aX 13 +bX 12 +cX 1+αX 2i+αX +2i!= c + α + α.N. Arancibia - relu par D. CransacAlgebre
Page 52 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.Ainsic = α + α = 2Reα = 127.Finalement, en considerant F0 on obtient :F0 =03 + 30 130 + 2 = 32=⇒32 =4313 + b 12712 127 · 2 + 52i40 2i+ 127 · 2 + 52i40 +2i=⇒b = 29.D’ouX 2 + 3X 13X 2 + 2=43X 13 29X 12 +127X 1 2 + 52i108X 2i+2 + 52i108X +2iN. Arancibia - relu par D. CransacAlgebre
Page 53 : Fractions RationnellesDecomposition des Fractions RationnellesD.E.S - Autres methodes : Limite et Evaluation.Finalement, pour trouver la decomposition dans RX il suffit de regrouperles termes conjugues :X 2 + 3X 13X 2 + 2=43X 13 29X 12 +127X 1 2 + 52i108X 2i+2 + 5108X +=43X 13 29X 12 +127X 1 X 527X 2 + 2.N. Arancibia - relu par D. CransacAlgebre
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53