CM

Télécharger le CM en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125

Page 1 :

Page 2 : Cycle Préparatoire Sommaire 2

Page 3 : Cycle Préparatoire Sommaire 3 Bibliographie du cours Chapitres 1 à 13: LLLeeesss NNNooouuuvvveeeaaauuuxxx PPPrrréééccciiisss BBBrrréééaaalll ::: PPPhhhyyysssiiiqqquuueee Electromagnétisme MPSI P. KREMPF Bréal Editions Réf. 209.0343 LLLeeesss NNNooouuuvvveeeaaauuuxxx PPPrrréééccciiisss BBBrrréééaaalll ::: PPPhhhyyysssiiiqqquuueee Electromagnétisme MP P. KREMPF Bréal Editions Réf. 209.0359 EEEllleeeccctttrrrooommmaaagggnnnééétttiiisssmmmeee ::: FFFooonnndddeeemmmeeennntttsss eeettt aaappppppllliiicccaaatttiiiooonnnsss Premiers cycles - Licence José-Philippe PEREZ, Robert CARLES, ROBERT FLECKINGER MASSON Sciences DUNOD 4ème édition HHH PPPrrrééépppaaa ::: NNNooouuuvvveeeaaauuu PPPrrrooogggrrraaammmmmmeee Electromagnétisme 2ième année MP-MP-PC-PC-PSI-PSI-PT-PT Jean-Marie BREBEC, Thierry DESMARAIS, Alain FAVIER, Marc MENETRIER, Bruno NOËL, Régine NOËL, Claude Orsini, Jean-Marc VANHAECKE Hachette Supérieur

Page 4 : Cycle Préparatoire Sommaire 4 CHAPITRE 0 : Introduction Générale ................................................................................................ 7 CHAPITRE 1 : Notion de Charge Elémentaire ................................................................................... 9 I. Introduction .................................................................................................................. 9 II. Historique de l'électrostatique : découverte des particules chargées ......................... 10 III. Charges électriques / Loi de Coulomb ....................................................................... 12 CHAPITRE 2 : Etude Générale du Champ Electrostatique ............................................................ 21 I. Introduction ................................................................................................................ 21 II. Loi de Coulomb / Rappels .......................................................................................... 22 III. Champ électrostatique créé par des charges ............................................................... 23 CHAPITRE 3 : Potentiel et Energie Potentielle Electrostatiques .................................................... 41 I. Introduction ................................................................................................................ 41 II. Notion mathématique / Le gradient ou vecteur gradient ......................................... 42 III. Potentiel électrostatique ............................................................................................. 44 IV. Energie potentielle électrostatique ............................................................................. 50 CHAPITRE 4 : Conducteurs en Equilibre Electrostatique dans le Vide ........................................ 57 I. Introduction ................................................................................................................ 57 II. Notion d’isolants et conducteurs / Conservation de l’électricité ............................... 58 III. Grandeurs électrostatiques et propriétés dans la matière conductrice en équilibre électrostatique ............................................................................................................ 59 IV. Champ électrostatique dans le vide, au voisinage immédiat de la surface d’un conducteur. ................................................................................................................. 61 V. Complément sur l'électrisation des conducteurs. ....................................................... 65 VI. Condensateurs électriques .......................................................................................... 69 CHAPITRE 5 : Dipôle Électrostatique ............................................................................................... 77 I. Introduction ................................................................................................................ 77 II. Définitions .................................................................................................................. 78 III. Etude du dipôle actif .................................................................................................. 79 IV. Etude du dipôle passif ................................................................................................ 83 V. Intérêt de la notion de dipôle ...................................................................................... 87

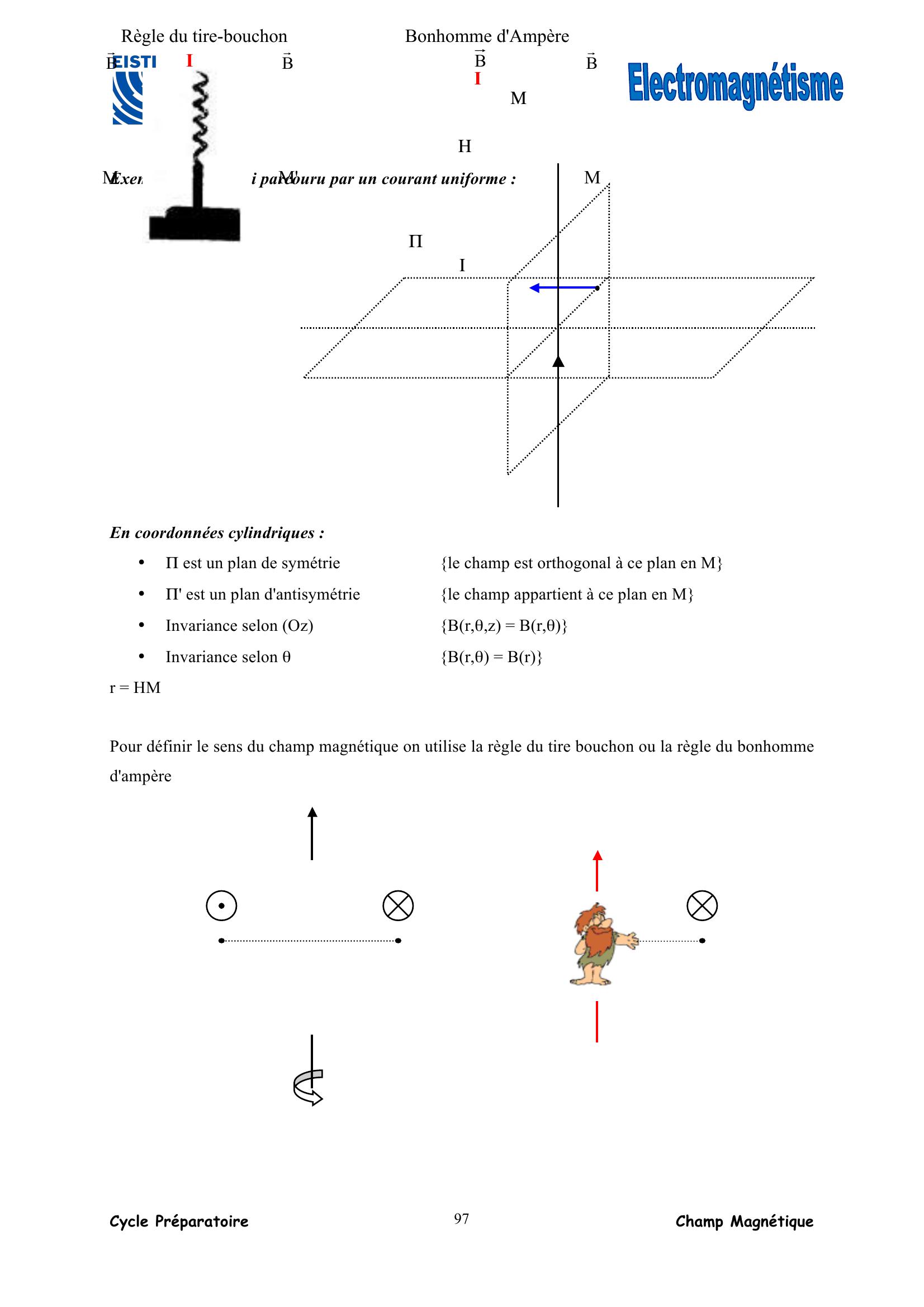
Page 5 : Cycle Préparatoire Sommaire 5 CHAPITRE 6 : Champ Magnétique & Mouvement de Particules Chargées Introduction ....... 94 I. Introduction ................................................................................................................ 94 II. Mise en évidence du champ magnétique ................................................................... 95 III. Lignes de champ ........................................................................................................ 98 IV. Flux et circulation du champ magnétique. ................................................................. 99 V. Théorème d'Ampère. ................................................................................................ 101 VI. Force de Lorentz. ..................................................................................................... 105 VII. Force de Laplace. ..................................................................................................... 107 VIII. Définition Légale de l'Ampère. ................................................................................ 108 CHAPITRE 7 : Mouvements de particules chargées ...................................................................... 110 I. Introduction .............................................................................................................. 110 II. La force de Lorentz .................................................................................................. 111 III. Champ électrostatique uniforme .............................................................................. 112 IV. Champ magnétique uniforme ................................................................................... 115 V. Mise en œuvre .......................................................................................................... 120

Page 6 : Cycle Préparatoire Sommaire 6

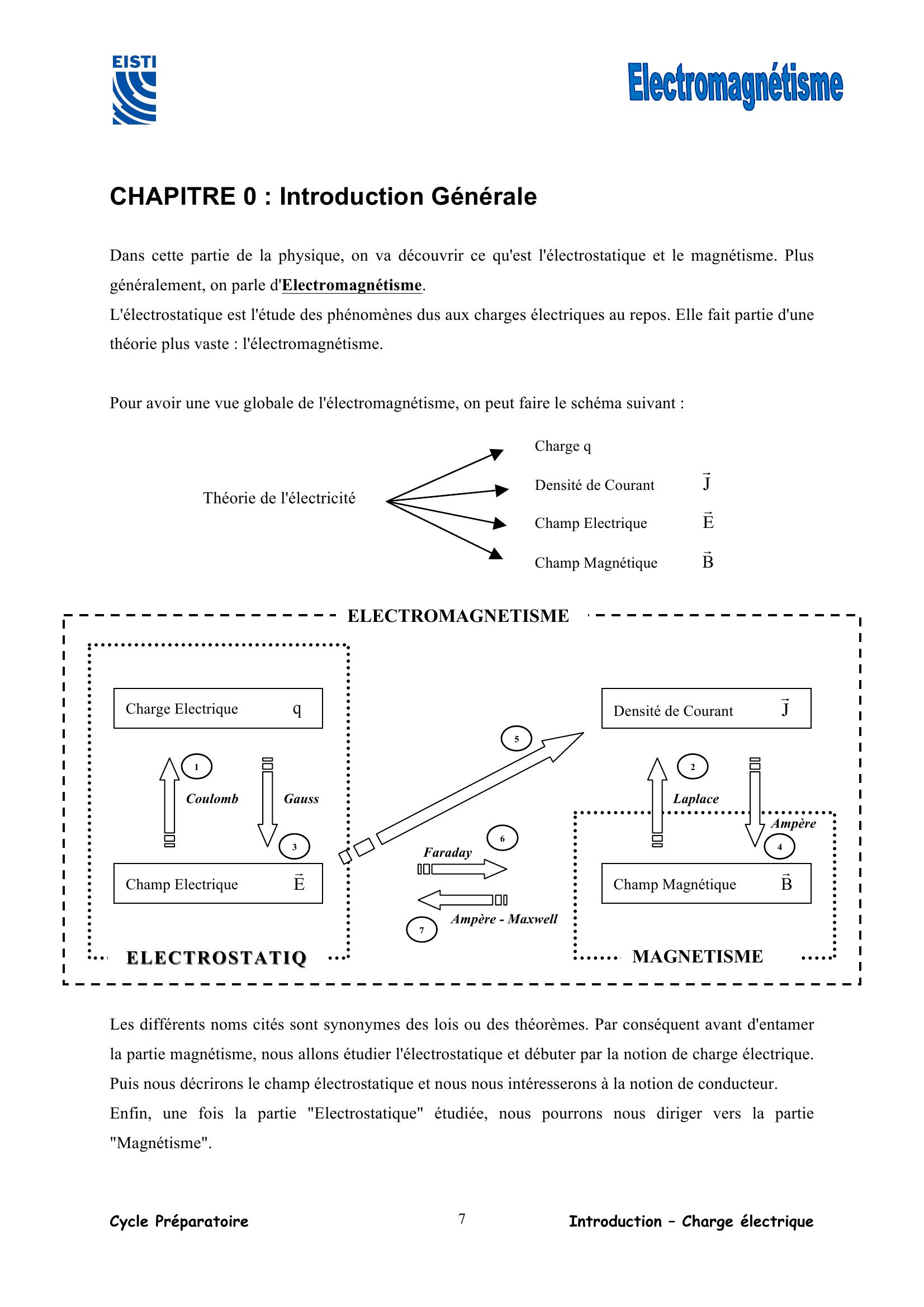
Page 7 : Cycle Préparatoire Introduction – Charge électrique 7 CHAPITRE 0 : Introduction Générale Dans cette partie de la physique, on va découvrir ce qu'est l'électrostatique et le magnétisme. Plus généralement, on parle d'Electromagnétisme. L'électrostatique est l'étude des phénomènes dus aux charges électriques au repos. Elle fait partie d'une théorie plus vaste : l'électromagnétisme. Pour avoir une vue globale de l'électromagnétisme, on peut faire le schéma suivant : Les différents noms cités sont synonymes des lois ou des théorèmes. Par conséquent avant d'entamer la partie magnétisme, nous allons étudier l'électrostatique et débuter par la notion de charge électrique. Puis nous décrirons le champ électrostatique et nous nous intéresserons à la notion de conducteur. Enfin, une fois la partie "Electrostatique" étudiée, nous pourrons nous diriger vers la partie "Magnétisme". Théorie de l'électricité Champ Magnétique B! Champ Electrique E! Densité de Courant J! Charge q Ampère Laplace Coulomb Densité de Courant J! Charge Electrique q Champ Magnétique B! Champ Electrique E! Gauss Faraday Ampère - Maxwell ELECTROSTATIQELECTROSTATIQMAGNETISME ELECTROMAGNETISME 1235674

Page 8 : Cycle Préparatoire Introduction – Charge électrique 8

Page 9 : Cycle Préparatoire Introduction – Charge électrique 9 CHAPITRE 1 : Notion de Charge Elémentaire I. Introduction Dans ce court chapitre, nous allons introduire et étudier succinctement la loi de Coulomb qui traduit l'interaction entre deux charges électriques dites ponctuelles. A partir de cette loi et de la définition de la charge électrique, nous pourrons, au cours des chapitres suivants, établir toute la théorie de l'électrostatique. Pour étudier ce chapitre et les suivants, nous aurons besoin de définir quelques repères mathématiques cartésien, cylindrique et sphérique et d'introduire le calcul d'intégrales multiples.

Page 10 : Cycle Préparatoire Introduction – Charge électrique 10 II. Historique de l'électrostatique : découverte des particules chargées - 600 : Thalès de Milet 625-547, célèbre mathématicien, découvre l'électrisation en frottant un morceau d'ambre jaune avec une peau de chat. Il attribut à ces objets une « âme et un souffle pour expliquer ces phénomènes. 1600 : Le mot électrique est inventé par William Gilbert en souvenir de l'ambre êlecktron en grec. 1600 : Otto Van Guerick 1602-1686 invente une machine électrostatique constituée d'une boule de souffre mise en rotation et sur laquelle vient frotter la main ou un tissus. La boule de souffre est ensuite remplacée par un globe de verre. Début du 18ème siècle : Charles François de Cisternay du Fay 1698-1737 définit l'électricité vitreuse positive et résineuse négatif. 1746 : Invention de la bouteille de Leyde Pays Bas qui permet de stocker les charges électriques. Il s'agit d'un condensateur constitué par une bouteille remplie d'eau dans laquelle on plonge une tige métallique traversant le bouchon. 1776 : Jesse Ramsden 1735-1800 construit une machine électrostatique qui devient très vite populaire. Elle est constituée d'un disque de verre entraîné par une manivelle et sur lequel viennent frotter 4 coussins de cuir remplis de crin. Les charges positives crées sur le disque provoque par influence l'électrisation de deux tubes métalliques creux. 1785 : Charles Augustin de Coulomb, physicien français, 1736-1806, établit les lois fondamentales de l'électrostatique : «les forces électriques entre deux particules chargées sont proportionnelles à leurs charges et inversement proportionnelles au carré de leurs distances.» 20ème siècle : Joseph John Thomson, anglais, 1856-1940 découvre le proton. En 1911, Ernest Rutherford, physicien anglais, 1871-1937, montra l'existence d'un noyau dans les atomes. Environ vingt ans plus tard, il était clair que les noyaux étaient formés de protons de charge électrique positive et de neutrons électriquement neutres comme leur nom l'indique. A cette époque, seulement deux interactions fondamentales la gravitation et l'électromagnétisme étaient connues. Or, aucune des deux ne pouvait expliquer la cohésion du noyau atomique. En effet, la gravitation est beaucoup trop faible et l'interaction électromagnétique ne peut pas assurer la cohésion de particules électriquement neutres comme les neutrons. De plus, la répulsion électrostatique des protons entre eux ils ont tous une charge électrique positive devrait faire exploser le noyau atomique. Il fallut donc introduire une nouvelle force capable d'assurer la cohésion de ces noyaux: la force nucléaire de nucleus=noyau. La première théorie de la force nucléaire fut élaborée par Hideki Yukawa en 1935. Il s'agissait alors d'une interaction entre protons et neutrons par l'intermédiaire d'une particule vecteur lourde appelée pion. Dans cette théorie, la particule vecteur devait avoir une masse non nulle afin d'expliquer pourquoi les effets de la force nucléaire étaient de courte portée. Cette particule fut bien découverte quelques années plus tard, mais la théorie

Page 11 : Cycle Préparatoire Introduction – Charge électrique 11 de Yukawa ne donnait pas de résultats suffisamment satisfaisants. De plus, contre toute attente, de très nombreuses particules sensibles à la force nucléaire furent découvertes. Ainsi, au début des années 1960, la force nucléaire n'était toujours pas décrite par une théorie correcte. En 1964, Murray Gell-Mann et George Zweig émirent l'hypothèse que les protons, les neutrons et les très nombreuses particules récemment découvertes n'étaient pas des particules élémentaires mais plutôt des objets complexes constitués de particules plus petites appelées quarks. Cette nouvelle description des particules sensibles à la force nucléaire changea complètement la façon dont cette force était abordée. Ainsi entre 1967 et 1970, une nouvelle théorie appelée chromodynamique quantique ou QCD vit le jour, donnant une description cohérente de l'interaction forte qui permet de lier les quarks entre eux pour former des particules composites appelées hadrons les protons, les neutrons et les pions sont des exemples de hadrons. La force nucléaire n'est plus alors que le résidu entre hadrons de cette interaction forte, comme sont les forces de van der Waals par rapport à l'interaction électromagnétique. http://www.cerimes.fr/edoc/forces/forte.htm L'électricité a toujours existé. Même avant la vie sur notre planète il y a 4 milliards d'années, de grands éclairs illuminaient déjà le ciel. La foudre est la manifestation la plus effrayante de cette énergie appelée : électricité. Lorsque la vie apparut, l'électricité devint un élément essentiel du monde vivant. Déjà les anciens firent des observations sur ce que nous avons appelé depuis, l'électricité et magnétisme. Les grecs furent les premiers penseurs de la tradition scientifique. Au 17ème siècle, les expériences sur l'électricité se développent mais toujours sans explications pratiques, le but étant simplement le savoir. Ainsi en 1729, l'anglais Stephen Gray 1666-1736 annonça que tout corps qui touche un autre qui est chargé devient lui-même chargé. C'est, la première approche du concept de conductibilité électrique. Mais, l'électricité statique que l'on produit et qui fait l'objet des recherches ne peut plus amener grands progrès. En 1800, la découverte de la pile de Volta permet d'obtenir des courants électriques. Alors, ce fait la jonction de deux catégories : électricité et magnétisme et l'on découvre les courants d'inductivité Foucault vers 1850.

Page 12 : Cycle Préparatoire Introduction – Charge électrique 12 III. Charges électriques / Loi de Coulomb III – 1 Enoncé de la loi de Coulomb La loi de Coulomb décrit l'interaction entre deux charges électriques dites ponctuelles immobiles dans le vide. On assimilera souvent l'air au vide. Enoncé : Soient la charge q1, placée au point M1, et la charge q2, placée au point M2. La force 2/1F! exercée par la charge ponctuelle q1 sur la charge ponctuelle q2 a pour expression : 21212212/1urqqkF→=!! On pose les notations suivantes : 2/1F! force en Newton N de q1 sur q2 q1, q2 charges ponctuelles en Coulomb C r12 = M1M2 distance en Mètre m entre q1 et q2 21u →! vecteur unitaire sans dimension dirigé de M1 vers M2 Cette loi de Coulomb se schématise par la figure suivante : Cette force 2/1F! agit en q2 par la charge q1. La constante k dépend du milieu. Dans le vide elle vaut : 041πε = 9.109 SI avec ε0, permittivité absolue du vide. SI : Kg.m3.s-4.A-2 Le vecteur unitaire 21u →! est orienté de M1 vers M2. q1 2/1F 21u →! M2 M1 q2

Page 13 : Cycle Préparatoire Introduction – Charge électrique 13 On peut écrire la force 1/2F!, force exercée par la charge ponctuelle q2 sur q1, appliquée en M1. 2/1212211212221121/2FurqqkurqqkF!!!!===→→ 2 cas possibles : q1 et q2 sont de même signe q1 et q2 sont de signes opposés Deux charges q1 et q2 de même signe se repoussent. Deux charges q1 et q2 de signes opposés s'attirent. III – 2 Charge Totale d'une Distribution Supposons que nous voulons déterminer la charge d'une distribution, c'est à dire, la répartition des charges électriques dans une région donnée de l'espace. Cet "espace" peut être ponctuel, linéique, surfacique ou volumique. Par conséquent, la charge totale de la distribution peut être ponctuelle pas de calcul, linéique, surfacique ou volumique. Pour cela, on introduira la notion de densité ou densité de charges. On distinguera des densités linéiques, surfaciques ou volumiques. q1 2/1F! 1/2F! M2 M1 q2 q1 2/1F! 1/2F! M2 M1 q2

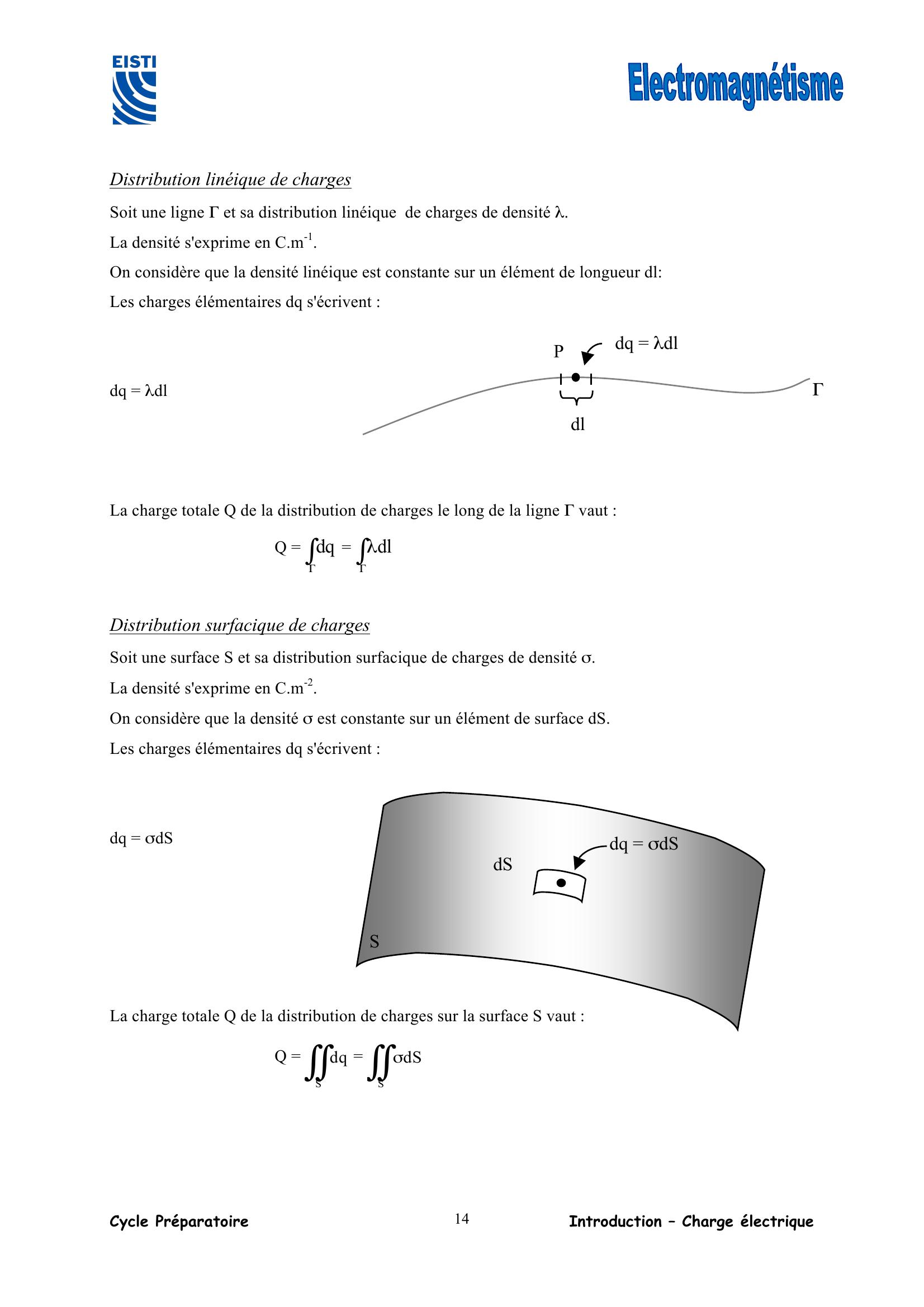
Page 14 : Cycle Préparatoire Introduction – Charge électrique 14 Distribution linéique de charges Soit une ligne Γ et sa distribution linéique de charges de densité λ. La densité s'exprime en C.m-1. On considère que la densité linéique est constante sur un élément de longueur dl: Les charges élémentaires dq s'écrivent : dq = λdl La charge totale Q de la distribution de charges le long de la ligne Γ vaut : Q = Γdq = Γλdl Distribution surfacique de charges Soit une surface S et sa distribution surfacique de charges de densité σ. La densité s'exprime en C.m-2. On considère que la densité σ est constante sur un élément de surface dS. Les charges élémentaires dq s'écrivent : dq = σdS La charge totale Q de la distribution de charges sur la surface S vaut : Q = Sdq = σSdS P Γ dq = λdl dl S dS dq = σdS

Page 15 : Cycle Préparatoire Introduction – Charge électrique 15 Distribution volumique de charges Soit un volume V et sa distribution volumique de charges de densité ρ. La densité s'exprime en C.m-3. On considère que la densité ρ est constante sur un élément de volume dV. Les charges élémentaires dq s'écrivent : dq = ρdV La charge totale Q de la distribution de charges sur le volume total V vaut : Q = Vdq = ρVdV Cas particuliers : On suppose que la densité linéique/surfacique/volumique est uniforme et constante sur toute la distribution : Q = Γdq = Γλdl = Γλ dl = λL pour une ligne de longueur L Q = Sdq = σSdS = σSdS = σS pour une surface d'aire S Q = Vdq = ρVdV = ρVdV = ρV pour un volume de capacité V V dV dq = ρdV

Page 16 : Cycle Préparatoire Introduction – Charge électrique 16 Intégrales multiples : Lorsqu'on intègre sur une surface ou un volume, il est nécessaire de faire varier plusieurs coordonnées. Le calcul d'une telle intégrale dans le cas général est très compliqué. Cependant, si la fonction à intégrer est un produit de fonctions de chacune des coordonnées et que les bornes d'intégration de chaque coordonné sont indépendantes des autres coordonnées, alors l'intégrale multiple est le produit des intégrales simples. =dzzhdyygdxxfdzdydxzhygxf Pour calculer des distributions de charges, on fait appel à des intégrales simples ou multiples doubles ou triples. Dans tous les cas, il faut utiliser un repère pour définir les positions, les longueurs, … . Nous allons rapidement voir trois systèmes ou repères de coordonnées. Coordonnées cartésiennes Le point M de l'espace est repéré par ses coordonnées cartésiennes x, y, z : zyxezeyexOM!!!++= Le volume élémentaire dV est un petit parallélépipède rectangle d'arêtes dx, dy, dz. dV = dx.dy.dz z x y O M dz dy dx O xe! ze! ye!

Page 17 : Cycle Préparatoire Introduction – Charge électrique 17 Coordonnées cylindriques Le point M de l'espace est repéré par ses coordonnées cartésiennes ρ, θ, z : zezeM'M'OMOM!!+ρ=+=ρ Le volume élémentaire dV est un petit parallélépipède rectangle d'arêtes dρ, ρdθ, dz. dV = dρ.ρdθ.dz ze! θe! ρe! z x y O θ M dρ ρ.dθdz ρ M'

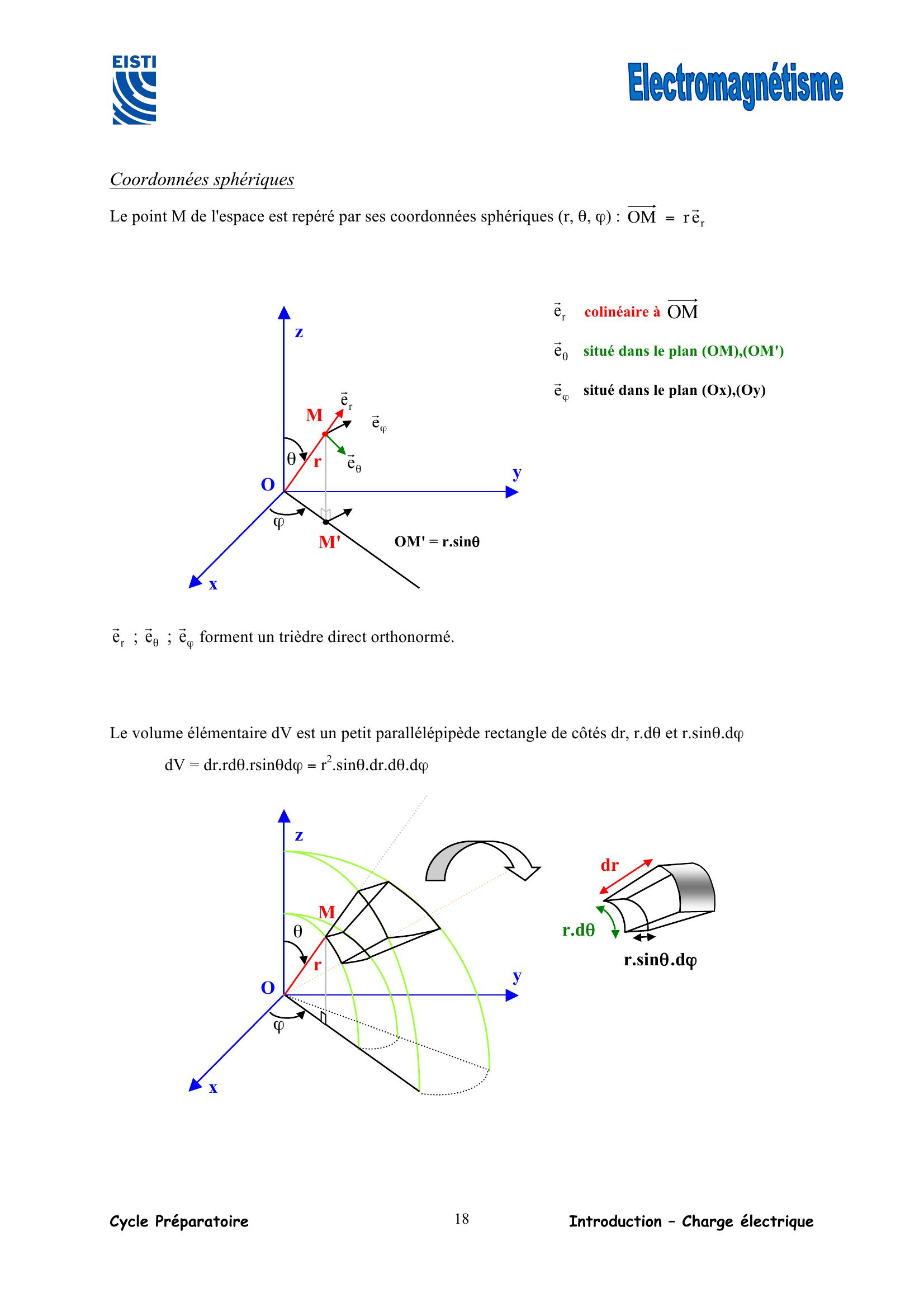
Page 18 : Cycle Préparatoire Introduction – Charge électrique 18 Coordonnées sphériques Le point M de l'espace est repéré par ses coordonnées sphériques r, θ, ϕ : rerOM!= ϕθe;e;er!!! forment un trièdre direct orthonormé. Le volume élémentaire dV est un petit parallélépipède rectangle de côtés dr, r.dθ et r.sinθ.dϕ dV = dr.rdθ.rsinθdϕ = r2.sinθ.dr.dθ.dϕ z x y O ϕ θ M r dr r.dθ r.sinθ.dϕ z x y O ϕ θ M r OM' = r.sinθ M' re! θe! ϕe! re! colinéaire à OM θe! situé dans le plan OM,OM' ϕe! situé dans le plan Ox,Oy

Page 19 : Cycle Préparatoire Introduction – Charge électrique 19 III – 3 Propriétés Fondamentales Liées aux Charges Electriques a Conservation de la charge électrique Considérons un système fermé c'est à dire qu'il n'échange pas de matière avec l'extérieur. La charge électrique d'un système fermé se conserve, c'est à dire qu'elle reste constante et indépendante invariante du référentiel dans lequel on étudie le système. b Principe de superposition La force totale subie par une charge q3 en interaction avec les charges q1 et q2, est la somme des forces 3/1F! et 3/2F! exercées individuellement par q1 et q2. 3/23/1élecFFF!!!+= Autrement dit, la somme des causes produit un effet électrique égal à la somme des effets individuels. q1 3/1F! 3/2F! q3 q2 élecF!

Page 20 : Cycle Préparatoire Introduction – Charge électrique 20 c Charges positives et charges négatives La charge électrique peut exister sous deux formes, l'une qualifiée de positive et l'autre de négative. Le choix d'affecter une charge électrique négative pour l'électron est purement conventionnel. d Extensivité de la charge La charge électrique d'un système est une grandeur extensive : elle peut se mettre sous la forme d'une somme algébrique des charges qui la constituent rejoint le principe de superposition. e Quantification de la charge De nombreuses expériences montrent que la charge électrique d'un système ne peut varier que par de multiples entiers d'une charge élémentaire de valeur e : e = 1,60217733.10-19 1,6.10-19 C L'unité est le coulomb. La charge d'un système s'écrit donc : Q = Z.e avec Z un entier positif ou négatif. Les porteurs stables usuels de ces deux types de charges ont des masses différentes : Electron q = - e me = 0,91091.10-30 Kg Proton q = + e mp = 1,6725.10-27 Kg 2000 fois plus lourd que l'électron

Page 21 : Cycle Préparatoire Champ électrostatique 21 CHAPITRE 2 : Etude Générale du Champ Electrostatique I. Introduction L'interaction électrostatique obéit à des lois quantitatives simples qui ont été interprétées par Coulomb en 1785, à partir de la notion de charge électrique. Plus précisément, la loi de Coulomb met en évidence l'existence du champ électrique ou électrostatique si pas de variation au cours du temps. Ce champ électrostatique pourra être obtenu en utilisant le théorème de Gauss.

Page 22 : Cycle Préparatoire Champ électrostatique 22 II. Loi de Coulomb / Rappels Compte tenu de ce qui a été écrit dans le chapitre précédent, on écrit la force de Coulomb entre deux charges ponctuelles immobiles dans le vide, sous la forme : ABABqq41eABqq41F3BA0r2BA0BAπε=πε=→!! où ABABer =! I.S10.94190=πε avec ε0, permittivité absolue du vide. La norme de la force BAF →! qu'exerce la charge ponctuelle A sur la charge ponctuelle B est inversement proportionnelle au carré de la distance AB qui sépare les deux charges.

Page 23 : Cycle Préparatoire Champ électrostatique 23 III. Champ électrostatique créé par des charges Dans un premier temps, nous allons écrire la définition relative à un champ électrostatique et sa force créés par une charge quelconque. Puis, dans un second temps, on écrira l'expression du champ électrostatique créé par une charge ponctuelle et par une distribution linéique, surfacique ou volumique de charges. III – 1 Définition de Champ Electrostatique Définition : Si une particule ponctuelle de charge q, immobile en un point M de l'espace, est soumise à une force F! autre que son poids et nulle si q est nulle, alors, il existe un champ électrostatique E! au point M tel que : EqF!!×= avec F! : force en Newton N q : charge ponctuelle en Coulomb C E! : champ électrostatique en N.C-1 ou V.m-1 III – 2 Champ Electrostatique Créé par une Charge Ponctuelle Soit une charge q' placée en M et subissant de la part d'une charge ponctuelle q placée en P la force de Coulomb E'qPMPM'q.q41er'q.q41F30PM20!!!×=πε=πε= On dit que la charge q est en interaction coulombienne avec la charge q'.

Page 24 : Cycle Préparatoire Champ électrostatique 24 La charge ponctuelle q, placée en P, crée sur le point M, situé à une distance r de P, le champ électrostatique : PMPMq41erq41E30PM20πε=πε=!! avec E! : champ électrostatique en M q : la charge en P r : distance PM ε0 : permittivité du vide Deux cas se présentent : q positive ou q négative. • Si q est une charge positive, alors E! est de même sens que u! a • Si q est une charge négative, alors E! est de sens opposé à u! b a b q 0 E! u! M P q 0 E! u! M P

Page 25 : Cycle Préparatoire Champ électrostatique 25 III – 3 Champ Electrostatique Créé par un ensemble de Charges Ponctuelles Soit un ensemble de N charges ponctuelles distinctes qi situées respectivement aux points Pi. Grâce au théorème de superposition, additivité vectorielle des forces électrostatiques, il est possible d'écrire au point M, l'expression des champs électrostatiques : ==N1iiMEME!! ==πε=πε=N1i3ii0iN1i2ii0iMPMP4qru4qME!! où iiiiirrMPMPu!!== : vecteur unitaire de la droite PiM dirigé de P vers M

Page 26 : Cycle Préparatoire Champ électrostatique 26 III – 4 Champ Electrostatique Créé par une Distribution Linéique de Charges Il faut reprendre la définition d'une distribution linéique de charge avec la densité linéique λ. On suppose que cette densité est uniforme constante. Soit une distribution linéique de charge : Sur cette ligne Γ, sont disposées avec une densité λ, les charges électriques. Soit un point P sur Γ et dl un élément de longueur de Γ autour de P. Cet élément est considéré comme ponctuel. Pour cet élément dℓ, il existe la charge dq telle que dq = λdℓ. Cet élément ponctuel va créer sur le point M un champ électrostatique d E de valeur : ur4dur4dqEd2020!ℓ!!πελ=πε= avec rrPMPMu!!== : le vecteur unitaire de la droite PM dirigé de P vers M. Le champ total en M de la ligne Γ est la somme de tous les champs élémentaires créés par tous les éléments dℓ formant la ligne Γ, d'où : ΓΓΓπελ=πε==P20P20ur4dur4dqEdME!ℓ!!! avec rrPMPMu!!== P Γ dq = λdℓ dl M Ed!

Page 27 : Cycle Préparatoire Champ électrostatique 27 III – 5 Champ Electrostatique Créé par une Distribution Surfacique de Charges Comme précédemment, on se réfère à la définition de la distribution étudiée. Soit S une distribution surfacique de charges de densité uniforme σ : Sur cette surface S, sont disposées avec une densité σ, les charges électriques. Soit un point P sur S et dS un élément de surface de S autour de P. Cet élément dS est considéré comme ponctuel. Pour cet élément dS, il existe la charge dq telle que dq = σdS. Cet élément ponctuel dS va créer sur le point M un champ électrostatique Ed! de valeur : ur4dSur4dqEd2020!!!πεσ=πε= avec rrPMPMu!!==: le vecteur unitaire de la droite PM dirigé de P vers M. Le champ total en M de la surface S est la somme de tous les champs élémentaires créés par tous les éléments dS formant la surface S, d'où : πεσ=πε==SP20SP20Sur4dSur4dqEdME!!!! avec rrPMPMu!!== S dS dq = σdS Ed! M P

Page 28 : Cycle Préparatoire Champ électrostatique 28 III – 6 Champ Electrostatique Créé par une Distribution Volumique de Charges Soit V une distribution volumique de charges de densité uniforme ρ : Dans ce volume V, sont disposées avec une densité ρ, les charges électriques. Soit un point P de V et dV un élément de volume de V contenant P. Cet élément dV est considéré comme ponctuel. Pour cet élément dV, il existe la charge dq telle que dq = ρdV. Cet élément ponctuel dV va créer sur le point M un champ électrostatique Ed! de valeur : ur4dVur4dqEd2020!!!περ=πε= avec rrPMPMu!!== : le vecteur unitaire de la droite PM dirigé de P vers M. Le champ total en M du volume V est la somme de tous les champs élémentaires créés par tous les éléments dV formant le volume V, d'où : περ=πε==VP20VP20Vur4dVur4dqEdME!!!! avec rrPMPMu!!== V dV dq = ρdV Ed! M P

Page 29 : Cycle Préparatoire Champ électrostatique 29 III – 7 Définition et continuité du Champ Electrostatique Soit une collection de charges ponctuelles. Le champ électrostatique E! créé par cette collection est défini et continu en tout point de l'espace, sauf sur les charges. Soit une distribution linéique de charges. Le champ électrostatique E! créé par cette distribution est défini et continu en tout point de l'espace, sauf sur les points de la distribution. Soit une distribution surfacique de charges. Le champ électrostatique E! créé par cette distribution est défini et continu en tout point de l'espace, sauf sur les points de la distribution ; il est donc discontinu à la traversée de la surface. Soit une distribution volumique de charges. Le champ électrostatique E! créé par cette distribution est défini et continu en tout point de l'espace. III – 8 Champ Electrostatique Créé par une Distribution Quelconque de Charges Considérons le cas le plus général pour la distribution de charges électriques : distribution volumique. Soit P, un point de la distribution et M, hors de la distribution. La densité est variable non uniforme. Le champ E! résultant en M s'écrit alors : ρπε=VP30dVPPMPM41ME! nouveauté

Page 30 : Cycle Préparatoire Champ électrostatique 30 L'intégration porte sur les variables qui caractérisent le point P. Si l'on désigne par r! et 'r! , les vecteurs OM et OP respectivement, il vient : ρπε=VP30dV'r'rr'rr41rE!!!!! III – 9 Propriétés de Symétrie du Champ Electrostatique Du fait que le champ soit un effet créé par une distribution de charges, il contient des informations sur les causes qui lui ont donné origine. Par conséquent, si l'on connaît les propriétés de symétrie d'une distribution de charges, on pourra connaître celles du champ électrostatique associé. Ces propriétés pourront simplifier le calcul du champ électrostatique. Cela correspond au principe de Curie : lorsque certaines causes produisent certains effets, les éléments de symétrie des causes doivent se retrouver dans les effets produits. Donc, on étudie l'effet des isométries transformations qui conservent les distances de l'espace sur la direction du champ. V dV M P r' r 'rr!! O

Page 31 : Cycle Préparatoire Champ électrostatique 31 Règles de symétrie : 1. Invariance par translation : Si S, un système physique est invariant dans toute translation parallèle à un axe Oz du repère cartésien, les effets ne dépendent pas de z. 2. Symétrie axiale : Si S est invariant dans toute rotation θ du repère cylindrique autour d'un axe Oz, alors, ses effets exprimés en coordonnées cylindriques ρ, θ, z ne dépendent pas de θ. 3. Symétrie cylindrique : Si S est invariant par translation le long de l'axe Oz et par rotation autour de ce même axe, alors, ses effets exprimés en coordonnées cylindriques ρ, θ, z ne dépendent que de la distance à l'axe ρ. 4. Symétrie sphérique : Si S est invariant dans toute rotation autour d'un point fixe O, alors, ses effets exprimés en coordonnées sphériques r, θ, ϕ ne dépendent que de la distance au centre r. 5. Plan de symétrie Π : Si S admet un plan de symétrie Π, alors en tout point de ce plan, le champ électrostatique est contenu dans ce plan. 6. Soit deux points M et M' le symétrique de M par rapport à un plan de symétrie Π, alors le champ électrique en M' est le symétrique par rapport à Π du champ électrique en M. 7. Plan d'antisymétrie Π' : Si, par symétrie par rapport à un plan Π', S est transformé en –S, alors en tout point de ce plan, le champ électrostatique lui est perpendiculaire. M Π ME!M' 'ME! M Π' ME!M' 'ME!

Page 32 : Cycle Préparatoire Champ électrostatique 32 Remarques : On verra par la suite et en TD que le champ électrostatique est un vecteur appelé vrai vecteur car son sens ne dépend pas de l'orientation de l'espace. Un vrai vecteur est aussi appelé vecteur polaire. A contrario, nous verrons par la suite que le champ magnétique est un pseudo-vecteur son sens dépend de l'orientation de l'espace. De manière générale, tout produit vectoriel de deux vrais vecteurs est un pseudo-vecteur, alors que le produit vectoriel d'un vrai vecteur par un pseudo-vecteur est un vrai vecteur. III – 10 Calcul du Champ Electrostatique par le Théorème de Gauss Le théorème de Gauss fournit une méthode utile pour calculer le champ E! lorsque celui-ci possède des propriétés de symétrie particulières. Grâce à ce théorème, il est possible de calculer le champ E! sans calculer d'intégrale. Cependant, nous devons dans un premier temps calculer le flux du champ E! à travers une surface. Comme le théorème de Gauss est valable pour une surface quelconque, il nous suffit de trouver une surface S adaptée, c'est à dire respectant les propriétés de symétrie du champ, appelée "surface de Gauss". a Flux élémentaire dφ On considère un élément de surface dS infinitésimal. Le champ E! est considéré uniforme sur dS. Le vecteur surface dS.nSd!!= avec n! le vecteur unitaire de la normale à l'élément dS. Le flux élémentaire dφ du champ E! à travers dS est défini par : dS.n.ESd.Ed!!!!==φ avec dS en m2, dφ en V.m et E! en V.m-1

Page 33 : Cycle Préparatoire Champ électrostatique 33 b Flux total Φ à travers une surface S De la même manière que pour un élément dS, on considère une surface S composée d'éléments dS. Le flux total Φ du champ E! à travers S est défini par la relation : φ=φSd ==φSSdS.n.ESd.E!!!! c Théorème de Gauss Théorème : Le flux Φ du champ E! à travers une surface fermée SGauss, dite "Surface de Gauss", est proportionnel à la charge qint contenue dans le volume V délimité par la Surface de Gauss. ==φGaussGaussSSdS.n.ESd.E!!!! 0intqε=φ avec Φ flux V.m qint charge C ε0 permittivité absolue du vide SI Remarque : Il arrive parfois, pour signaler que la surface est fermée, que l'on note : ==φGaussGaussSSdS.n.ESd.E!!!!

Page 34 : Cycle Préparatoire Champ électrostatique 34 d Quelques exemples : • Champ électrostatique créé par un plan infini uniformément chargé On considère un plan infini Π portant une charge électrique σ uniforme par unité de surface. Déterminer le champ E!. Tous les plans perpendiculaires au plan infini Π passant par M sont des plan de symétrie de celui-ci : E! appartient aux plans de symétrie, il est donc perpendiculaire à Π. ð E! = Ez x,y,z k! au point M Il existe une invariance par translation selon x et y : ð E! = Ez z k! au point M ð On peut donc choisir comme surface de Gauss, un cylindre de sections perpendiculaires aux plans avec des hauteurs symétriques : Aussi, par raison de symétrie, Ez = E-z et zEzE= On calcule le flux total : Φ = SdS.E = dS.n.E1S + dS.n.E2S + dS.n.E3S Φ = Ez.S + E-z.S + 0 = 2ES car zEzE= et 12nn!!= Π S1 n! z S3 S2 n! n! 0 M

Page 35 : Cycle Préparatoire Champ électrostatique 35 Or : Φ = 0intqε = 01ε σSdS = 0Sεσ ð 2ES = 0Sεσ ð Le champ électrostatique créé par un plan infini uniformément chargé vaut E = 02εσ et dirigé suivant l'axe Oz. • Champ électrostatique créé par une distribution linéique uniformément chargée Etablir l'expression du champ E! créé en un point quelconque M de l'espace par une distribution linéique de charge de densité λ uniforme répartie le long d'un fil rectiligne infini. Comme pour l'exemple précédent, on recherche les isométries : Il existe des symétries cylindriques et invariance de translation, par conséquent, le champ E! en M s'exprime en coordonnées cylindriques : ð rurErE!!= E = 02εσ M λ

Page 36 : Cycle Préparatoire Champ électrostatique 36 On recherche ensuite une surface de Gauss qui respecte les considérations de symétrie et d'invariance : choisissons une surface cylindrique en trois parties S1, S2 et S3. On applique le théorème de Gauss sur S1, S2 et S3. Le flux du champ E! pour S1 et S2 est nul car : E 1n! et E 2n! Φ1 = dS.n.E1S1 = 0 Φ2 = dS.n.E2S2 = 0 Calcul du flux à travers la surface S3 Φ3 = dS.n.E3S3 = dS.rE3S = 3SdSrE = Er.2πrh En appliquant le théorème de Gauss, on obtient : Φ = Φ1+ Φ2+ Φ3 = Φ3 = 0intqε = 0hελ ð Er.2πrh = 0hελ ð ou bien encore rE = 0r2επλru S1 1n!λ S3 S2 2n!3n!M h r EEEr = 0r2επλ

Page 37 : Cycle Préparatoire Champ électrostatique 37 • Champ électrostatique créé par une boule uniformément chargée On considère une boule sphère pleine de centre O et de rayon R, chargée avec une distribution volumique de charge de densité ρ. Déterminer le champ E!. Cette distribution possédant une symétrie sphérique, le champ électrostatique qui en résulte aura la même symétrie, donc E! ne dépendra que du rayon r distance du point M au centre O en coordonnées sphériques : ð rurErE!!= On peut prendre comme surface de Gauss une sphère de rayon r : Le flux du champ E! s'écrit alors : Φ = SdS.E = SdS.n.E = SdS.rE = SdS.rE = Er.4πr2 En appliquant le théorème de Gauss, on obtient : Φ = 0intqε = 0Vερ = Er.4πr2 z x y R r M

Page 38 : Cycle Préparatoire Champ électrostatique 38 Deux solution sont possibles Si la sphère de Gauss a un rayon r R Alors, la charge intérieure à la sphère de Gauss est la charge totale Q. 3éeargChSphèreintR34VdVQqπρ=ρ=ρ== Donc, 030int2R34qr4.rEεπρ=ε=π ð Si la sphère de Gauss a un rayon r R Alors, la charge intérieure est la charge contenue dans la sphère de Gauss de rayon r. 3GaussGaussdeSphèreintintr34VdVqetQqπρ=ρ=ρ= Donc, 030int2r34qr4.rEεπρ=ε=π ð Remarque : Le champ électrique E! créé par une boule de centre O sphérique uniformément chargée est le même que celui d'une charge ponctuelle égale, située en O. On constate la continuité du champ électrique E! pour r = R : 03RREερ= e Lignes de champ E! La notion de lignes de champ permet de visualiser l'évolution de E! dans l'espace. Les lignes de champ sont déterminées à partir de la définition suivante : Une ligne de champ d'un champ de vecteur quelconque est une courbe C définie dans l'espace telle qu'en chacun de ses points, le vecteur y soit tangent. Cette définition est équivalente à la relation suivante : 0dE!ℓ!!= dℓ est parallèle à E 0dE!ℓ!!= dℓ est parallèle à E 20320r3Rr4QrEερ=πε=020int3rr4qrEερ=πε=

Page 39 : Cycle Préparatoire Champ électrostatique 39 Dans le repère cartésien, ℓ"d s'écrit : dzdydxd=ℓ" a zyxEdzEdyEdx== Dans le repère de coordonnées cylindriques, ℓ"d s'écrit : dzdddθρρ=ℓ" a zEdzEdEd=θρ=ρθρ Dans le repère de coordonnées sphériques, ℓ"d s'écrit : ϕθθ=dsinrrddrdℓ" a ϕθϕθ=θ=EdsinrErdEdrr Justification du Dans le repère cartésien : dzdydxd=ℓ" zyxEEEE =! Le produit vectoriel donne : 0dE!ℓ!!= on note aussi 0dE!ℓ!!=× Rappel : u.B,Asin.BABA!!!!!!!=

Page 40 : Cycle Préparatoire Champ électrostatique 40 000dxEdyE......dzdydxEEEdEyxzyx===ℓ"" D'où Exdy Eydx = 0 a yxEdyEdx = En faisant le produit vectoriel complet, on trouve : zyxEdzEdyEdx== Exemple : Le champ E! pour une boule chargée uniformément de rayon r considérée comme une charge ponctuelle en O. On retrouve une symétrie sphérique donc, rurErE!!= Ainsi les lignes de champ produites par une charge ponctuelle placée en O sont des droites passant par O. Remarque : Nous allons voir, dans le chapitre suivant, que ces lignes de champ sont fortement liées à la notion de lignes/surfaces équipotentielles et donc à la notion de potentiel électrique. r Lignes de champ O

Page 41 : Cycle Préparatoire Potentiel électrostatique 41 CHAPITRE 3 : Potentiel et Energie Potentielle Electrostatiques I. Introduction Nous avons vu que le champ électrostatique E , introduit à partir de la force de Coulomb, satisfait à une première propriété fondamentale, connue sous le nom de théorème de Gauss, attribuée à la forme en 2r1 de cette force. A partir de la circulation du champ, on va établir une formule permettant de calculer le potentiel électrostatique, en introduisant la notion de gradient. Ensuite, nous pourrons définir les surfaces équipotentielles et, enfin, l’énergie potentielle électrostatique.

Page 42 : Cycle Préparatoire Potentiel électrostatique 42 II. Notion mathématique / Le gradient ou vecteur gradient Prenons un scalaire VM défini en tout point de l’espace on dit un champ scalaire. Une variation dV de ce champ, lorsque l’on passe d’un point M à un point M’ proche de M est défini par la différentielle totale : OMd.VgradxdxVMdVi31ii== = où le vecteur Vgrad est le gradient du champ scalaire V. En coordonnées cartésiennes, on a : kdzjdyidxOMd!!!++= et dzzVdyyVdxxVdV++= donc, le gradient s’écrit : ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=zVyVxVVgrad En coordonnées cylindriques, on obtient : ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧θ=zVVr1rVVgrad

Page 43 : Cycle Préparatoire Potentiel électrostatique 43 Et en coordonnées sphériques, on trouve : ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧ϕθθ=Vsinr1Vr1rVVgrad Une propriété importante du vecteur gradient découle directement de sa définition. Considérons une surface "équipotentielle" S de VM, c’est à dire, une surface telle qu’en tout point M qui lui appartient, VM prend la même valeur V0. Pour un déplacement élémentaire OMd du point M sur S, on a : 0OMd.Vgrad V VdVM 00=== Le vecteur gradient Vgrad est donc normal à la surface équipotentielle passant par M de la fonction scalaire VM.

Page 44 : Cycle Préparatoire Potentiel électrostatique 44 III. Potentiel électrostatique III – 1 Définition de la circulation du champ électrostatique Considérons une courbe Γ liant deux points A et B. La circulation C d'un champ de vecteurs E!, sur cette courbe, de A à B, est définie par : =BAld.EC!! où ld! désigne le déplacement élémentaire le long de la courbe Γ. III – 2 Circulation du champ d'une charge ponctuelle Considérons, dans un premier temps, une charge ponctuelle q, placée en O, et deux points N et M voisins. On a PMNPNM+= ou θθ+=udrurdNMr!! Soit le champ E! créé par q en N ou M car NM = distance infinitésimale : r20ur4qE!!επ= Γ ld r P M O q rdN dr ru!θu!Edθ

Page 45 : Cycle Préparatoire Potentiel électrostatique 45 La circulation élémentaire dC du champ E! vaut : udrurd.ur4qNM.EdCrr20θθ+επ==!!!! En respectant les vecteurs unitaires : ⎟⎟⎠⎞⎜⎜⎝⎛επ=επ=r4qddrr4qdC020 On suppose maintenant 2 points M1 et M2 éloignés avec r1 = OM1 et r2 = OM2 La circulation du champ E est l'intégrale somme des circulations élémentaires dC : 2010rr0MMr4qr4qr4qddCC2121επεπ=⎟⎟⎠⎞⎜⎜⎝⎛πε== On pourrait généraliser pour toute distribution de charges élémentaires en appliquant le théorème de superposition, la circulation C est la somme des circulations élémentaires de chaque élément de charge considéré comme ponctuel. D'où la définition suivante : Définition : La circulation du champ ne dépend que des positions des points de départ et d'arrivée, et non du chemin suivi. On dit que le champ est à circulation conservative.

Page 46 : Cycle Préparatoire Potentiel électrostatique 46 III – 3 Définition du potentiel électrostatique Le champ est à circulation conservative et la fonction potentiel électrostatique est définie par : VgradE=! avec E! champ électrostatique V.m-1 V potentiel V D'après cette relation, on peut écrire la circulation du champ E : ===BABABAdVld.Vgradld.EC!!! C = VA – VB La circulation C se mesure donc en Volts V On définit, donc, le potentiel électrostatique V en un point M créé par une charge q placée en O : rr20urdrdavecrd.ur4qOMd.EMdV!!!!!=επ== drr4qMdV20επ= Après intégration, 00Vr4qMV+επ= VM potentiel en M V V0 constante d'intégration V, généralement choisie comme étant nulle r OM m Vérification : On a vu que C = VM1 – VM2 de M1 à M2 relation du III - 3 ð ⎟⎟⎠⎞⎜⎜⎝⎛+επ+επ=020010Vr4qVr4qC ð 2010r4qr4qCεπεπ= relation du III - 2

Page 47 : Cycle Préparatoire Potentiel électrostatique 47 III – 4 Potentiels pour différents cas de figure de distribution. a Potentiel créé par un ensemble de charges ponctuelles On considère n charges qi. Grâce au principe de superposition, le champ électrostatique vaut : ==n1iiEE!! et donc ==n1iiMVMV tels que la relation VgradE=! soit vérifiée, d’où : 0n1ii0iVr4qMV+επ= = où ri est la distance entre qi et M. Le potentiel électrique est défini et continu en tout point sauf aux points où se trouvent les charges ponctuelles. b Potentiel créé par une distribution linéique de charges Soit une distribution linéique de densité λ : Le potentiel VM du champ E! créé en un point M s’écrit : 0P0Vr4qddVMV+επ==ΓΓ 0P0Vr4dMV+επλ= Γℓ avec r = PM Dans le cas d'une distribution linéique de charges, le potentiel électrique n'est pas défini sur les points où se trouvent les charges. Γ dℓ r dV P M

Page 48 : Cycle Préparatoire Potentiel électrostatique 48 c Potentiel créé par une distribution surfacique de charges Soit une distribution surfacique de densité σ : Le potentiel VM du champ E! créé en un point M s’écrit : 0SP0SVr4qddVMV+επ== 0SP0Vr4SdMV+επσ= avec r = PM Dans le cas d'une distribution surfacique de charges, le potentiel électrique est défini sur la surface chargée et il est continu à la traversée de la surface. d Potentiel créé par une distribution volumique de charges Soit une distribution volumique de densité ρ : Le potentiel VM du champ E! créé en un point M s’écrit : 0vP0vVr4dqdVMV+πε== 0vP0Vr4dMV+πετρ= avec r = PM Dans le cas d'une distribution volumique de charges, le potentiel électrique est défini et continu en tout point de l'espace. Attention !! Ne pas confondre ici V ð pour le potentiel v ð pour le volume S dS r dV P M v dv r dV P M

Page 49 : Cycle Préparatoire Potentiel électrostatique 49 III – 5 Complément sur les lignes de champ et les surfaces équipotentielles. D’après ce qui a été écrit précédemment, on peut énoncer les différentes propriétés suivantes : 1 Les lignes de champ sont telles qu’en chacun de leurs points M, le vecteur E leur est tangent. 2 Une surface équipotentielle est définie par l’ensemble des points où la valeur du potentiel électrostatique est invariante. 3 Les lignes de champ sont en tout point aux équipotentielles car ld.E!! = dV = 0 exemple pour un fil infini chargé avec une densité linéique λ. 4 Si le déplacement a lieu le long d'une ligne de champ et dans le sens du champ depuis un point M1 vers un point M2 alors : 0ld.E21MM!! Donc, VM1 – VM2 0 Ce qui amène VM1 VM2 Le long d’une ligne de champ, le champ E! est dirigé vers les potentiels décroissants : λ λ V cteV cteEE!E!EE!E!E

Page 50 : Cycle Préparatoire Potentiel électrostatique 50 IV. Energie potentielle électrostatique Pour étudier l’énergie potentielle gravitationnelle, on utilise la notion de travail fourni pour déplacer le corps ou le système en question. On va retrouver l’analogie pour l’énergie potentielle électrostatique. IV – 1 Travail de la force électrostatique de Coulomb. Le travail élémentaire de la force EqF!!= lors d’un déplacement ld! de celle-ci est : qVdld.qVgradld.Vgradqld.Eqld.FdW=====!!!!!! Sur un trajet entre A et B A → B, on obtient : ==BABAABdVqqVdW WAB = qVA – VB Ce travail ne dépend pas du chemin suivi. L’énergie potentielle d’interaction entre une charge q et un champ électrostatique E! créant le potentiel V, est : Ep = εp = q.V + K En effet, le travail élémentaire est égal à l’opposé de la variation de l’énergie potentielle : ld.F!! = – dεp Sur un trajet A→B, le travail vaut : WAB = – εpB + εpA = qVA – VB = – Δεp

Page 51 : Cycle Préparatoire Potentiel électrostatique 51 On peut aussi écrire que la force de Coulomb dérive de l’énergie potentielle : pgradFε=! car, εp = q.V + K ð FEqVgradqqVgradKqVgradgradp!!====+=ε Remarque : Energie potentielle d’interaction de deux charges ponctuelles Soient deux charges ponctuelles q1 et q2 en M1 et M2 et M1M2 = r12 Energie potentielle de q1 εp1 = q1V2 + K = 12021r4qqπε + K Energie potentielle de q2 εp2 = q2V1 + K = 12021r4qqπε + K ð εp1 = εp2 L’énergie potentielle d’interaction est le travail fourni par un opérateur pour amener les charges depuis des positions où elles sont infiniment éloignées et n’interagissent pas pas de force de Coulomb entre les charges, jusqu’à des positions de voisinage où chaque charge est soumise au champ créé par l’autre charge : on montre que cf TD ð εp = 12021r4qqπε + K = εp1 = εp2

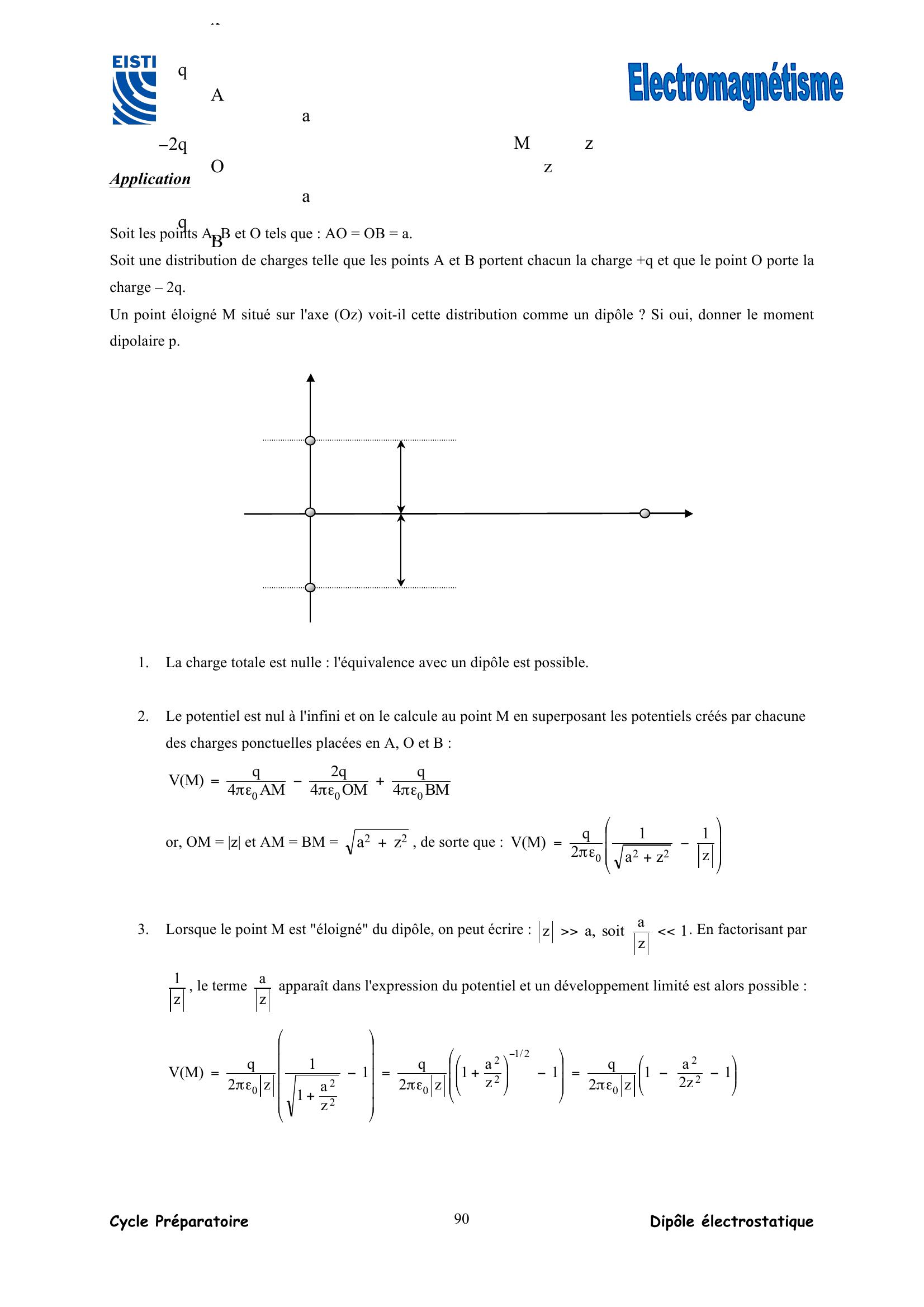
Page 52 : Cycle Préparatoire Potentiel électrostatique 52 Application 1 : Soit un cylindre de rayon R et de hauteur infinie chargé uniformément avec une densité volumique de charges ρ. Déterminer le potentiel créé ce système. Le champ sera déterminé dans la série de TD en utilisant le théorème de Gauss. Dans un système de coordonnées cylindriques, on trouve : r0r02ru2rRrEur2RRrEurEME!!!!!!ερ=ερ== Le potentiel est déterminé par la relation VgradE=!. Elle donne ici : rdVdrVEr==, car r est la seule variable trouvée grâce aux invariances. On a donc : ερ=ερ=dr2rRrVetdrr2RRrV002 Les constantes K et K' sont a priori différentes, car sur chacun de ces domaines, le champ a une expression mathématique différente. Il vient :'K4rRrVetKrln2RRrV0202+ερ=+ερ= La relation entre les constantes est trouvée en écrivant que le potentiel doit être continu en r = R 'K4RKRln2RRrVRrV0202+ερ=+ερ====+ Si l'on garde K', alors Rln2R'K4RK0202ερ++ερ=, et donc : 'K4rRrVet'K4RrRln2RRrV020202+ερ=+ερ⎟⎟⎠⎞⎜⎜⎝⎛ερ= Le calcul direct du potentiel s'obtient en écrivant : KPM4dMVvP0+πετρ= P est un point quelconque du volume. En prenant l'origine O du repère cylindrique sur le projeté orthogonal de M sur l'axe du cylindre et l'axe Ox confondu avec la droite OM, on simplifie au maximum le calcul. Le point P est repéré par sa distance r' à l'axe, l'angle θ et sa cote z. On a : xzyxuruzusin'rucos'rOMPOPM!!!!+θθ=+= D'où, 222222zcos'rr2'rrzsin'rcos'rrPM+θ+=+θ+θ= Le potentiel est donné par le calcul de l'intégrale triple : +θ+πεθρ=VP2220zcos'rr2'rr4dzd'dr'rMV Cette intégrale est absolument incalculable à la main. Il est plus intéressant pour les problèmes à haute symétrie de calculer d'abord le champ électrique en utilisant le théorème de Gauss, puis le potentiel en cherchant la primitive du champ.

Page 53 : Cycle Préparatoire Potentiel électrostatique 53 Application 2 : Déterminer l'énergie potentielle électrostatique d'un ensemble de trois charges identiques q présentes aux sommets A, B et C d'un triangle équilatéral de côté 2a. On fixe la charge en A. On approche la charge suivante pour la placer en B. Enfin on amène la dernière charge pour la placer en C. La seconde charge subit l'action du champ créé par la première. Le potentiel créé au point B par la charge q placée en A vaut : a8qBV0Aπε= L'opérateur doit donc fournir un travail : a8qBVqW02ABπε=×= On approche la troisième charge jusqu'en C. Celle-ci est plongée dans le potentiel électrostatique des deux premières charges placées en A et en B. Le potentiel créé en C par les deux charges présentes en A et en B est la somme des potentiels créés par chacune d'elles : a4qa8qa8qCVCVCV000BAπε=πε+πε=+= Le travail que l'opérateur doit accomplir pour rapprocher cette dernière charge jusqu'en C vaut : a4qCVq'W02Cπε=×= L'énergie potentielle électrostatique d'interaction Ep de ce système de trois charges est égale à la somme des travaux effectués par l'opérateur : a8q3a4qa8q'WWE020202pπε=πε+πε=+= Le cas de l'énergie d'une distribution continue de charges est hors programme. A C B O y 2a

Page 54 : Cycle Préparatoire Potentiel électrostatique 54

Page 55 : Cycle Préparatoire Potentiel électrostatique 55

Page 56 : Cycle Préparatoire Potentiel électrostatique 56

Page 57 : Cycle Préparatoire Conducteurs 57 CHAPITRE 4 : Conducteurs en Equilibre Electrostatique dans le Vide I. Introduction Dans ce chapitre, nous abordons l’étude des conducteurs comme des milieux où l’électrisation ne reste pas localisée mais peut se transmettre. Il s’agit d’examiner comment appliquer aux conducteurs les lois générales de l’électrostatique, exposées aux chapitres 1, 2 et 3 et d’en tirer les conséquences pour ces milieux. Au cours de ce chapitre, on mentionnera aussi les applications des propriétés électrostatiques des conducteurs ex : condensateurs

Page 58 : Cycle Préparatoire Conducteurs 58 II. Notion d’isolants et conducteurs / Conservation de l’électricité Un isolant est un corps dont l’électrisation reste localisée là ou elle est apparue. Un conducteur est un corps dont l’électrisation peut se transmettre hors de la région où elle est apparue. Ces définitions rejoignent bien évidemment celles qui seront évoquées en électronique diodes, diodes Zener, concernant les électrons libres ou pas des matériaux. Une définition ou un principe découle des notions d’isolants et de conducteurs : L’état électrique global d’un corps isolé électriquement est invariable : conservation de l’électricité. Ce principe de conservation de l’électricité ne souffre d’aucune exception. Un conducteur est en équilibre électrostatique lorsque les porteurs de charges libres qu’il contient n’ont aucun mouvement d’ensemble à l’échelle macroscopique. Dans un conducteur en équilibre électrostatique, on appliquera les lois de l’électrostatique dans le vide, comme dans les chapitres 1, 2 et 3.

Page 59 : Cycle Préparatoire Conducteurs 59 III. Grandeurs électrostatiques et propriétés dans la matière conductrice en équilibre électrostatique III – 1 Propriété fondamentale de la matière conductrice en électrostatique : nullité du champ Le vecteur champ électrique est nécessairement uniformément nul en tout point de la matière conductrice en équilibre, sinon, les porteurs de charges libres seraient soumis à des forces électrostatiques leur donnant un mouvement d’ensemble incompatible avec un état d’équilibre. Donc, dans un conducteur en équilibre électrostatique, le vecteur champ électrique est uniformément nul : ð 0E!!= III – 2 Potentiel électrostatique dans un conducteur En tout point intérieur on trouve la relation : 0E!!= Or, le champ électrostatique peut s’exprimer en fonction de V VgradE=! 0Vgrad!= En choisissant par exemple d’exprimer le gradient de V dans le repère cartésien : 0zVyVxVVgrad!=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧= Le potentiel V est uniforme dans tout le volume de la matière conductrice, y compris sur la surface du conducteur. La surface du conducteur est donc une surface équipotentielle.

Page 60 : Cycle Préparatoire Conducteurs 60 III – 3 Charge volumique d’un conducteur en équilibre Considérons une petite surface fermée intérieure à la matière conductrice, délimitant un petit volume dV. Cette surface peut représenter une surface dite de Gauss. D’après le théorème de Gauss, le flux du champ E! sortant de la petite surface est défini par : 00intdVqερ=ε=φ Mais, il peut également s’exprimer par la relation suivante : =φSSd.E!! En fait ce flux est nul car 0E!!= donc, φ = 0 ð ρdV = 0 ð ρ = 0 La charge volumique est nulle en tout point. L’électrisation d’un conducteur en équilibre électrostatique ne peut être que superficielle.

Page 61 : Cycle Préparatoire Conducteurs 61 IV. Champ électrostatique dans le vide, au voisinage immédiat de la surface d’un conducteur. IV – 1 Application du théorème de Coulomb Pour bien comprendre le phénomène du champ électrostatique au voisinage immédiat, on applique la remarque suivante : La surface d’un conducteur électrisé doit être considérée comme une couche caractérisée par une charge surfacique σ, généralement non uniforme. Soit un point M de la surface d’un conducteur et n! le vecteur unitaire normal sortant du conducteur en M, dirigé de la région R1 intérieure au conducteur vers la région extérieure vide R2. On considère deux cas en scindant le point M en deux parties : M1 et M2. Un point M1 R1, intérieur au conducteur : le champ y est nul par définition cf. partie III. 0E1!!= Un point M2 R2 : on pose : 22MElimE!!= pour M2 infiniment voisin de M. vidM1 M2 M R1R2n! S

Page 62 : Cycle Préparatoire Conducteurs 62 En calculant le flux pour une surface autour de M2, on peut exprimer la relation suivante : S1SESd.E022σε==!! en appliquant le théorème de Gauss Donc, on peut écrire : 02Eεσ= et de manière vectorielle nE02!!εσ= pour un point M2 R2 infiniment voisin de M. D’après les relations de E pour M1 et M2, on peut écrire nnEE021012!!!!εσ=εσ=→ C’est la relation de passage à la traversé de S en M Théorème de Coulomb. Il en résulte que : • Les lignes de champ sont normales à la surface du conducteur au voisinage immédiat de celui-ci. • Si σ 0, ces lignes sont orientées vers l’extérieur elles "sortent" du conducteur. • Si σ 0, ces lignes sont orientées vers l’intérieur elles "rentrent" dans le conducteur. Remarque 1 : la "fonction" champ électrostatique E est une fonction non continue. vid+ Conducteσ 0 + + + + + + + + + vid- Conducteσ 0 - - - - - - - - - σ : charge surfacique positive ou négative

Page 63 : Cycle Préparatoire Conducteurs 63 Remarque 2 : s'il existe plusieurs corps en présence, il faut considérer l'ensemble de ces corps pour déterminer le champ électrostatique E le sens. Par conséquent, la charge surfacique σ en M dépend de l'électrisation de tous les corps en présence. Cela est dû au phénomène d'influence. IV – 2 Calcul de la pression électrostatique – Hors Programme Soit une charge dQ = σdS, plongée dans le champ E! d'origine extérieure à dS; elle subit la force extérieure : EQdFd!!= L'expression d'un champ E! pour une surface plane est : n2E0!!εσ=, donc dSn2Fd02 !!εσ= Cette force a une expression analogue à celle de la force pressante exercée par un fluide au contact d'une paroi : dSnpFd!!= avec le vecteur n! unitaire normal à la paroi et sortant du fluide. Par analogie, on pose 022pεσ= : p étant la pression électrostatique. En introduisant le champ au voisinage de M2, on peut écrire , avec E0ε=σ 20 E2pε=

Page 64 : Cycle Préparatoire Conducteurs 64 Application 1 Au voisinage immédiat d'un conducteur, règne un champ de 104 V.m-1. Calculer σ et le nombre surfacique d'électrons correspondant. ------------------------------------------------------ 940103610Eπ=ε=σ = 8,84.10-8 C.m-2 On obtient le nombre d'électrons par cm2 : /cm électrons10.25,5510.6,110.84,8n261912 == ou 5,525.1011 électrons/m2 Application 2 Calculer la pression électrostatique p en un point de la surface d'un conducteur, au voisinage immédiat duquel, le champ est de 104 V.m-1. ------------------------------------------------------ On a la relation suivante : 2002E22pε=εσ= avec 9010.361π=ε On a donc p 18.π.109.σ2 ou 29 E10..721pπ= ð π=π=72011010721p249 en Pascal ð p = 1,4.10-3 Pa Cette pression est très faible par rapport à la pression atmosphérique normale p0 105 Pa.

Page 65 : Cycle Préparatoire Conducteurs 65 V. Complément sur l'électrisation des conducteurs. V – 1 Propriétés des conducteurs creux. Soit un conducteur creux C entourant une cavité dont l'intérieur ne contient aucune charge. A l'intérieur d'une cavité sans charge, le potentiel est uniformément égal à V0, potentiel de la matière du conducteur C. En tout point de la cavité, le champ est nul. En effet, V étant uniforme : 0EVgrad!!== On peut écrire aussi : Le champ dans la cavité 2E! Le champ dans le conducteur 1E! La relation de passage à la traversée du conducteur, côté intérieur, s'écrit : 210i012nEE→εσ=!!! σ0E 0 σ0i = 0 C V0 V0 SOI SOE

Page 66 : Cycle Préparatoire Conducteurs 66 Mais ici, pour le côté intérieur, on a 0Eet0E21!!!!==, d'où σ0i = 0 en tout point de la surface S0I. On dit que la surface S0I limitant la cavité n'est pas électrisée la charge surfacique intérieure σ0i est uniformément nulle. Par conséquent, l'électrisation ne peut apparaître que sur la surface extérieure S0E de C. On dit : L'électrisation du conducteur creux est identique à celle du conducteur plein ayant même surface extérieure. Application Pratique : La Cage de Faraday Un conducteur dont les parois sont un simple treillage se comporte comme un conducteur creux sans lacune avec une approximation d'autant meilleure que le treillage est fin. Il va exister une charge électrostatique sur la surface extérieure du conducteur creux. Un champ électrostatique existe de la surface extérieure vers le vide. A l'intérieur de cette cage, le champ est nul. Cette situation simple de phénomène électrostatique pour un conducteur creux se trouve dans le cas d'une voiture véhicule en présence d'orages. Le véhicule joue le rôle de cage de Faraday. Donc il est préférable de rester à l'abri à l'intérieur de véhicule car il y a un phénomène d'autoprotection dû à la carcasse métallique creuse du véhicule et en plus on reste au sec !. Cage métallique illSocle isolant

Page 67 : Cycle Préparatoire Conducteurs 67 V – 2 Electrisation d'un conducteur seul dans l'espace. Pour cette section, on donnera quelques observations sans les démontrer. On considère un conducteur seul dans l'espace. L'électrisation d'un conducteur seul dans le vide purement superficielle est partout de même signe. La charge Q du conducteur et sa charge surfacique σM ont même signe que son potentiel V. Les deux types d'électrisation sont : 1. V 0, σM 0 et Q 0 2. V 0, σM 0 et Q 0 L'allure des lignes de champ au voisinage immédiat du conducteur est normale entrante pour V 0 ou sortante pour V 0. Les lignes de champ sont orientées vers les potentiels décroissants cf. Chapitre III. C + + + + + + + + + + + + + + + - - - C - - - - - - - - - - - -

Page 68 : Cycle Préparatoire Conducteurs 68 Aucune ligne de champ ne peut relier deux points de la surface du conducteur : la surface du conducteur est une surface équipotentielle. La charge Q est proportionnelle au potentiel V du conducteur. On pose : VQC = C est toujours positif C est la capacité propre du conducteur supposé seul dans l'espace illimité. L'unité de la capacité est le Farad F. La charge surfacique σM n'est pas uniforme, sauf pour la sphère seule dans l'espace. ⎪ σM⎪ est faible dans les régions à faible courbure. ⎪ σM⎪ est grande dans les régions à forte courbure. On appelle ce phénomène, le pouvoir des pointes. Application : Calculer la capacité propre d'une sphère de rayon R. Rechercher le rayon R pour une capacité de 1 Farad ------------------------------------------------------ Le potentiel pour une sphère vaut : R4QV0πε= donc on a R4VQC0επ== ð C = 1 F ð 041Rπε= ð R 9.109 m 9.106 Km ð énorme On utilise des sous multiples du Farad µF, nF. C + + ++ + + + + + + + + + ++ + + + + + + + Faible courbure Forte courbure

Page 69 : Cycle Préparatoire Conducteurs 69 VI. Condensateurs électriques On considère deux conducteurs isolés A et B et l'on admet qu'une charge + Q a été enlevée de l'un deux pour être déposée sur l'autre. Les lignes de champ partent du conducteur chargées positivement pour rejoindre celui de charge négative. Les charges + Q et – Q sont stationnées à la surface des conducteurs. Une telle configuration est appelée condensateur : Chaque conducteur est une armature du condensateur et comme on l'a vu précédemment, chacune des surfaces est une équipotentielle. Si Q est différent de 0, les potentiels des armatures chargée positivement et négativement sont différents. Comme le champ est dirigé de l'armature positive vers l'armature négative, le potentiel de la première est donc plus élevé que celui de la seconde. Nous appellerons tension aux bornes du condensateur la différence de potentiel ddp entre les armatures : U = VA – VB en Volt V - + + + Q + + + + + + + + + + + - - - - Q - - - - - - - - - - - A B

Page 70 : Cycle Préparatoire Conducteurs 70 La charge Q du conducteur, armature chargée positivement et la chute du potentiel U sont liés par la relation d'état du condensateur : Q = C.U avec C la capacité du condensateur en Farad F. C dépend de la configuration géométrique du condensateur forme et dimensions des armatures, distance entre celles-ci ainsi que des propriétés diélectriques du milieu. Pour calculer la capacité d'un condensateur, on décompose le procédé en 4 étapes : 1. A partir de la forme géométrique des armatures, on cherche la répartition de la charge sur ces armatures. 2. On calcule le champ électrique avec la loi de Gauss 3. On calcule le potentiel entre les armatures ℓ""d.EdV= 4. On relie le potentiel, la ddp et la relation d'état du condensateur Exemple : Condensateur plan Un condensateur plan est formé par deux armatures planes de même section A situées à une distance d l'une de l'autre elles sont parallèles entre elles. Si l'on considère un condensateur idéal, les armatures parallèles sont supposées infinies, il n'existe pas d'effets de bord, c'est à dire que toutes les lignes de champ sont parallèles entre elles. ++++++++++- - - - - - - - - - = + -

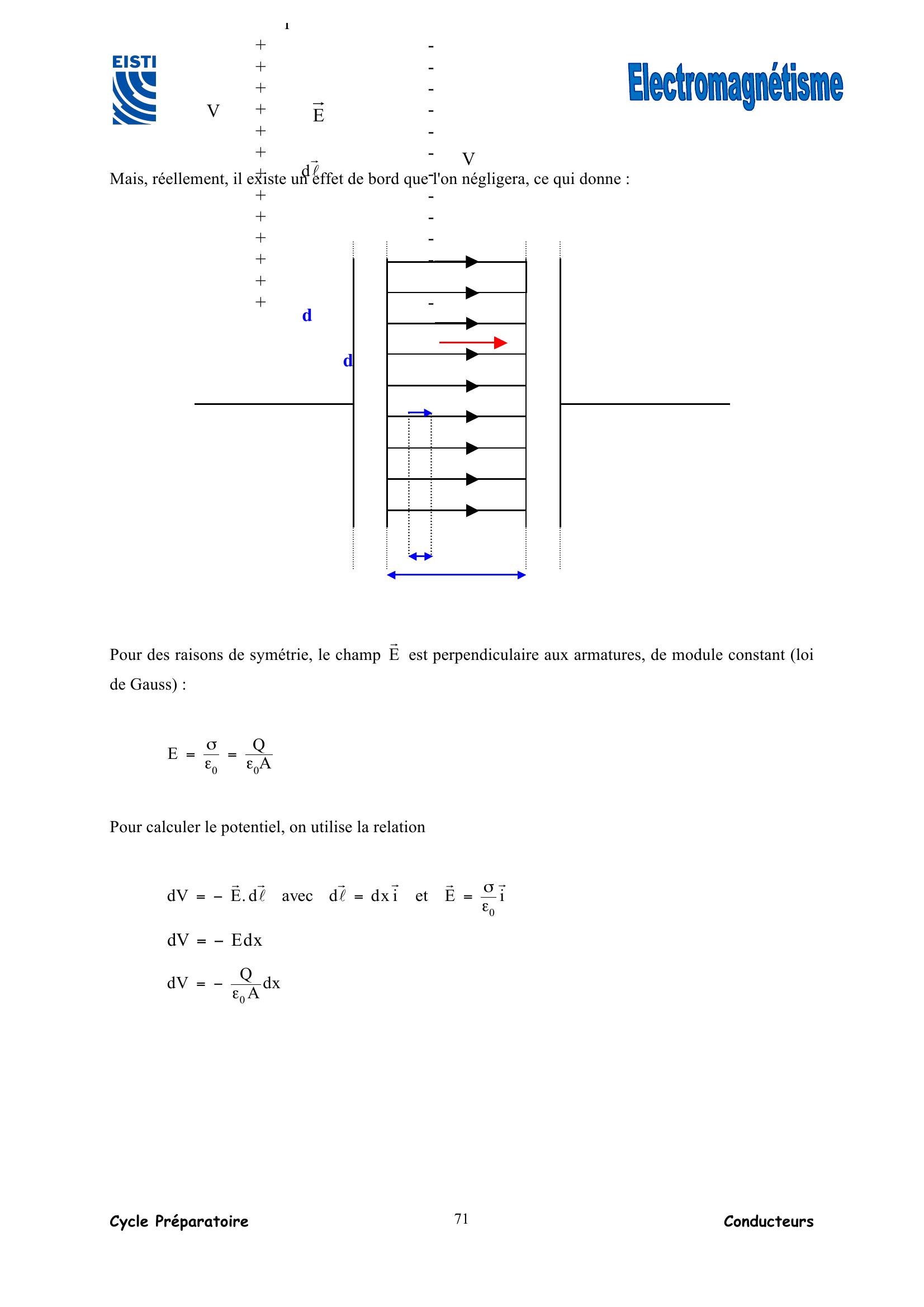
Page 71 : Cycle Préparatoire Conducteurs 71 Mais, réellement, il existe un effet de bord que l'on négligera, ce qui donne : Pour des raisons de symétrie, le champ E! est perpendiculaire aux armatures, de module constant loi de Gauss : AQE00ε=εσ= Pour calculer le potentiel, on utilise la relation iEetixddavecd.EdV0!!!ℓ!ℓ!!εσ=== xdEdV= dxAQdV0ε= ℓ"dVVE+++++++++++++- - - - - - - - - - - - - d di

Page 72 : Cycle Préparatoire Conducteurs 72 Ce qui donne en intégrant : ctexAQxV0+ε= En considérant la ddp U entre les armatures, on a : AdQVVVVU0dx0xBAε===== A partir de la relation Q = C.U, on obtient : dAC0ε= Formule de la capacité d'un condensateur plan idéal. Un condensateur, de capacité C et portant la charge Q, a une ddp U entre ses bornes telle que Q = CU et son énergie potentielle a pour expression : 22pUC21CQ21UQ21E=== Ep = énergie potentielle en Joule J Q = charge en Coulomb C U = tension en Volt V C = capacité en Farad F Remarques : • Il existe aussi des condensateurs cylindriques, sphériques et bifilaires 2 fils chargés, pour lesquels, on peut appliquer la méthode précédente. • On peut rencontrer un diélectrique autre que le vide entre les armatures, c'est à dire, un matériau isolant placé entre les armatures faisant varier la capacité C du condensateur.

Page 73 : Cycle Préparatoire Conducteurs 73 Application : On cherche l'expression de la capacité d'un condensateur cylindrique : les armatures sont des cylindres coaxiaux même axe de rayons R1 et R2 R1, de hauteur h et portent respectivement les charges +q et - q sur leur surface avec une densité surfacique uniforme. On utilisera l'approximation du cylindre infiniment haut. Solution : Le condensateur est cylindrique de rayon R et le champ E! créé par un cylindre ayant une distribution surfacique uniforme de charges de densité σ a été déjà calculé . On en rappelle les résultats : r0urRRrEet0RrE!!!!εσ== dans le système de coordonnées cylindriques. Donc, le cylindre de rayon R2 crée un champ nul dans l'espace inter-armatures et le cylindre de rayon R1 crée le champ : r0111urRE!!εσ= au point M situé à la distance r de l'axe du cylindre , avec R1 r R2. La charge q est uniformément répartie sur le cylindre de rayon R1 et de hauteur h. La surface du cylindre sur laquelle se trouve la charge est S1 = 2πR1h, de sorte que la charge s'écrit : q = σ1.2πR1h puisque la densité surfacique est uniforme La circulation du champ électrostatique doit être calculée de R1 à R2. On choisit la ligne que l'on veut, puisque le champ électrostatique est à circulation conservative. Il est préférable de choisir une ligne pour laquelle E! et ℓd sont colinéaires et de même sens en tout point, c'est à dire une ligne de champ ; une telle ligne est une droite radiale et le déplacement élémentaire s'écrit : ru.drd!ℓ= La circulation est donc : 12011RR011RRrr01121RRlnRrdrRudr.urRd.E2121εσ=εσ=εσ=!!ℓ On sait que la circulation du champ s'exprime aussi en fonction du potentiel électrostatique : UVVdVd.Vgradd.E21212121====ℓℓ Il vient donc : 12011RRlnRUεσ= avec q = σ1.2πR1h soit : h2qR11π=σ Et l'on trouve : 120RRlnh2CsoitCqUεπ==

Page 74 : Cycle Préparatoire Conducteurs 74

Page 75 : Cycle Préparatoire Conducteurs 75

Page 76 : Cycle Préparatoire Conducteurs 76

Page 77 : Cycle Préparatoire Dipôle électrostatique 77 CHAPITRE 5 : Dipôle Électrostatique I. Introduction Le dipôle électrostatique est un dispositif fréquemment utilisé en physique. Il possède une charge électrique nulle mais crée un champ électrostatique non nul. On trouve cette situation lorsque les barycentres des charges positives et négatives sont décalés cas de la molécule d'eau et un grand nombre de distributions de charges de ce type peut être considéré, par analogie, comme un dipôle.

Page 78 : Cycle Préparatoire Dipôle électrostatique 78 II. Définitions Un doublet électrostatique est un ensemble de deux charges opposées + q et – q liées l'une à l'autre invariablement en deux points A – q et B + q. La distance a = AB reste donc constante Un dipôle électrostatique est un doublet électrostatique tel que la distance a entre les deux charges opposées – q et + q est petite. Le dipôle est dit actif lorsque la distance a reste petite devant la distance r = AM = BM du point M où l'on considère le champ électrostatique créé par le doublet A – q et B + q. Le dipôle est dit passif lorsque la distance a reste suffisamment petite pour que l'on puisse considérer le champ dans lequel le doublet se trouve plongé comme uniforme sur l'étendue du doublet. On appelle moment dipolaire le vecteur : ABqp =! Le moment dipolaire p = qa se mesure en coulombs mètre C.m ou en debye D : m.C10.31D129= + q q ABqp =! a B A

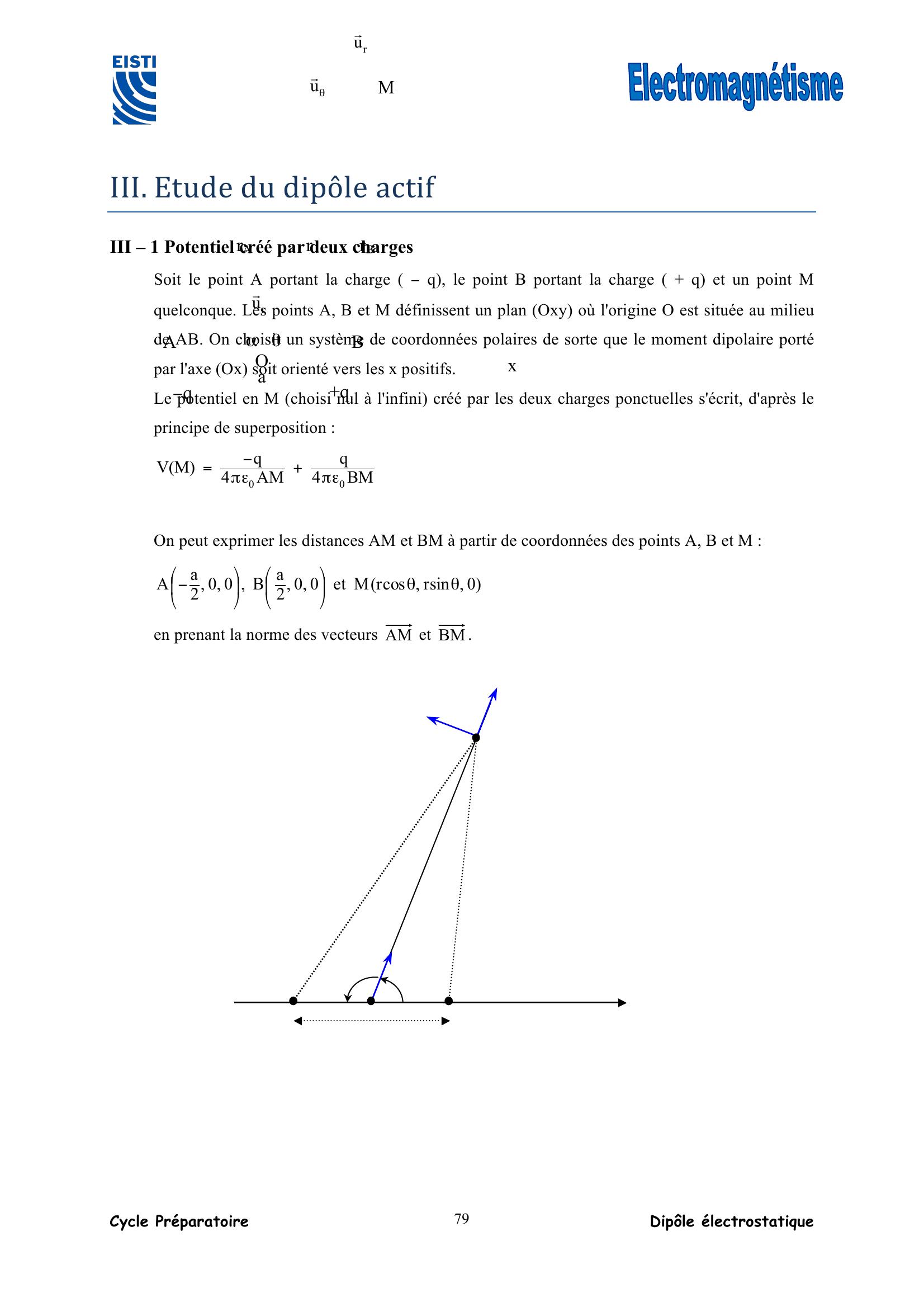
Page 79 : Cycle Préparatoire Dipôle électrostatique 79 III. Etude du dipôle actif III – 1 Potentiel créé par deux charges Soit le point A portant la charge q, le point B portant la charge + q et un point M quelconque. Les points A, B et M définissent un plan Oxy où l'origine O est située au milieu de AB. On choisit un système de coordonnées polaires de sorte que le moment dipolaire porté par l'axe Ox soit orienté vers les x positifs. Le potentiel en M choisi nul à l'infini créé par les deux charges ponctuelles s'écrit, d'après le principe de superposition : BM4qAM4qMV00επ+επ= On peut exprimer les distances AM et BM à partir de coordonnées des points A, B et M : 0,sinr,cosrMet0,0,2aB,0,0,2aAθθ⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛ en prenant la norme des vecteurs AM et BM. rA q r a θ A α O +q B M x rB ru!ru!θu!

Page 80 : Cycle Préparatoire Dipôle électrostatique 80 On peut aussi utiliser le théorème de Pythagore généralisé dans les triangles AOM et BOM. Dans le triangle AOM : AM2 = AO2 + OM2 – 2AO.OM.cosα Or, α = π – θ, OM = r et AO = OB = 2a , donc la relation devient : θ++=cosrar4aAM222 soit θ++=cosrar4aAM22 Dans le triangle BOM : BM2 = BO2 + OM2 – 2BO.OM.cosθ θ+=cosrar4aBM222 soit θ+=cosrar4aBM22 Le potentiel s'écrit ⎟⎠⎞⎜⎝⎛+επ=BM1AM14qMV0 et comme a r, les distances AM et BM sont voisines ; un développement limité en ra est ici adapté pour simplifier cette différence : ⎟⎠⎞⎜⎝⎛θ⎟⎠⎞⎜⎝⎛θ++=⎟⎠⎞⎜⎝⎛θ++=cosr2a1r1cosrar4a1r1cosrar4aAM12/1222/122 De même : ⎟⎠⎞⎜⎝⎛θ+⎟⎠⎞⎜⎝⎛θ+=⎟⎠⎞⎜⎝⎛θ+=cosr2a1r1cosrar4a1r1cosrar4aBM12/1222/122 Et le potentiel VM s'écrit alors : ⎟⎟⎠⎞⎜⎜⎝⎛⎟⎠⎞⎜⎝⎛θ++⎟⎠⎞⎜⎝⎛θεπ⎟⎠⎞⎜⎝⎛+επ=cosr2a1cosr2a1r4qBM1AM14qMV00 02r4cosqaMVεπθ au premier ordre en ra . Le potentiel électrostatique créé par un dipôle actif vaut : 0302r02r4OM.pr4u.pr4cosqaMVεπ=επ=επθ!!!

Page 81 : Cycle Préparatoire Dipôle électrostatique 81 On choisit la constante additive nulle, ce qui rend V nul à l'infini où le champ électrostatique créé par chacune des charges ponctuelles est nul. III – 2 Champ créé La relation VgradE=! permet d'exprimer, en coordonnées polaires, le champ électrostatique créé par le dipôle : θθ=uVr1urVVgradr!!, soit θεπθ+επθ=ur4sinpur4cosp2E30r30!!! Le champ E! à la distance r créé par un dipôle xu.pp!! = placé en O a pour composantes, en coordonnées polaires d'origine O : 30rr4cosp2Eεπθ et 30r4sinpEεπθθ Le vecteur champ est inclus dans le plan Oxy, ce que vérifie le principe de superposition. III – 3 Diagramme électrique Les équipotentielles sont données par : V = cte, soit r2 = k.cosθ où k est une constante qui dépend de la valeur du potentiel : V4pk0επ= L'équipotentielle V = 0 est le plan Oyz, qui se projette selon l'axe Oy dans le plan Oxy. Les lignes de champ sont orthogonales aux équipotentielles. Elles ont pour équation, en coordonnées polaires : Lignes de champ Equipotentielles y x V = 0 ð cosθ = 0 ð θ = ± π/2 axe Oy en coordonnées polaires

Page 82 : Cycle Préparatoire Dipôle électrostatique 82 r = k'.sin2θ, où k' est une constante. démonstration hors programme

Page 83 : Cycle Préparatoire Dipôle électrostatique 83 IV. Etude du dipôle passif On étudie les actions subies par un dipôle électrostatique points Aq et B+q lorsqu'il est plongé dans un champ électrostatique extérieur. On cherche la résultante des forces que le dipôle subit de la part du champ extérieur, puis le moment résultant. IV – 0 Moment d'une force et produit vectoriel Une force F! permet de mettre un système en mouvement de translation, mais elle peut également le faire tourner autour d'un axe ou un point. On définit alors le vecteur moment d'une force par rapport à un point O : FMO = FOM où M désigne le point matériel sur lequel s’applique la force F!. On appelle produit vectoriel de 1V X1, Y1, Z1 et 2V X2, Y2, Z2 le vecteur noté 1V 2V tel que 1V 2V = Y1Z2 – Y2Z1 i! + Z1X2 – Z2X1 j! + X1Y2 – X2Y1 k!. Le produit vectoriel a son support perpendiculaire au plan contenant les deux vecteurs. Son sens est tel que le trièdre formé par 1V , 2V et 1V 2V soit direct. Son module est égal à l’aire du parallélogramme construit à partir des deux vecteurs 1V et 2V ou encore égal à 1V .2V .⎪sinθ⎪ MF! M 0 FM0Règle du tire bouchonRègle du tire bouchon

Page 84 : Cycle Préparatoire Dipôle électrostatique 84 IV – 1 Cas d'un champ extérieur uniforme : force et moment La résultante des forces subies par le dipôle s'écrit : 0EqEqFFFBA!!!!!!=+=+= On calcule le moment de cet ensemble de forces en un point C quelconque. EpEABqEqCBCAFCBFCAMBAC!!!!!!!==+=+= Ce moment ne dépend plus de C, donc du point où on le calcule. On dit que le dipôle subit un couple force nulle et moment non nul. Un dipôle électrostatique plongé dans un champ électrostatique uniforme subit une résultante des forces nulle, le moment de cette force étant non nul et indépendant du point où on le calcule : 0F!!= et EpM!!!= Le sens du moment donne le sens naturel de rotation du dipôle règle du tire-bouchon. Le dipôle ou plutôt son moment dipolaire tend spontanément à s'orienter dans le sens du champ extérieur. IV – 2 Energie du dipôle dans le champ extérieur L'énergie potentielle électrostatique Ep est égale au travail fourni par l'opérateur pour amener le dipôle de l'infini jusqu'à sa position finale chapitres 3 et 4. Soient VA et VB les valeurs du potentiel du champ aux points A et B. Sachant que l'on ne rapproche pas les charges l'une de l'autre, mais que l'on amène le dipôle depuis une position éloignée où le champ extérieur est nul jusqu'à sa position finale, l'expression de l'énergie potentielle électrostatique du dipôle est : Ep = qVA + qVB = qVBVA Or, la circulation du champ extérieur E! entre A et B vaut : AB.Ed.Ed.EBABA!ℓ!!ℓ!!==

Page 85 : Cycle Préparatoire Dipôle électrostatique 85 Et aussi, BABABABAVVdVd.Vgradd.E===ℓ"ℓ"" On en tire : AB.EVVBA!= et E.pAB.EqVVqEABp!!!=== Un dipôle électrostatique plongé dans un champ électrostatique uniforme E! possède l'énergie potentielle électrostatique : E.pVVqEABp!!== IV – 3 Cas d'un champ extérieur non uniforme Même si le champ extérieur E! n'est pas uniforme, la notion de dipôle impose que sur l'étendue du dipôle, le champ extérieur varie très faiblement. On admet alors que : AB.Ed.EBA!ℓ!!, le terme correctif étant négligeable. L'énergie potentielle électrostatique Ep du dipôle plongé dans un champ extérieur non uniforme garde la même expression : E.pVVqEABp!!== Si on ne tient pas compte des variations du champ extérieur E!, alors la force est nulle. Cela revient ici à négliger un terme qui contient les petites variations de E! devant la force totale, c'est à dire zéro ! Il faut donc tenir compte du caractère non uniforme de E! pour déterminer la force que subit le dipôle. La force de Coulomb étant conservative, on a pu définir l'énergie potentielle électrostatique, qui n'est autre que l'énergie potentielle associée à cette force. Lorsqu'une force F! est conservative, elle est reliée à son énergie potentielle associée par la relation pEgradF=! La force F! que le dipôle subit de la part du champ extérieur non uniforme a pour expression : E.pgradEgradFp!!!==

Page 86 : Cycle Préparatoire Dipôle électrostatique 86 Le travail W de cette force depuis la position 1 vers une position 2 est : 21pp21p21p21EEEdd.Egradd.FW====ℓ"ℓ"" Le déplacement est spontané si le travail est moteur, c'est à dire positif, soit lorsque l'énergie potentielle décroît. Lorsque le champ extérieur E! est uniforme, l'énergie potentielle est minimale lorsque p! et E! sont colinéaires et de même sens : le moment dipolaire s'oriente spontanément dans la direction et le sens du champ extérieur E!. Le moment dipolaire p! s'oriente spontanément dans le sens du champ extérieur E!. Lorsque le champ extérieur E! n'est pas uniforme, le moment dipolaire s'oriente spontanément dans la direction et le sens du champ extérieur E!, et le dipôle se déplace de telle manière que le module EE!= du champ augmente, ce qui fait décroître l'énergie potentielle électrostatique. Le dipôle tend à se déplacer spontanément vers les zones de champ extérieur plus intenses.

Page 87 : Cycle Préparatoire Dipôle électrostatique 87 V. Intérêt de la notion de dipôle V – 1 Action d'un système de charges à grande distance Une distribution de charges étudiée "à grande distance", c'est à dire à une distance r très supérieure à son étendue a, est équivalente à un dipôle. Soit un ensemble de N charge qi placées respectivement en des points Oi et soit O un point du voisinage de cet ensemble de charges. On étudie le champ et le potentiel électrostatiques de cet ensemble de charges en un point M éloigné : la distance r = OM doit être très supérieure à chacune des distances OOi = ai. On exprime le potentiel V au point M grâce au principe de superposition : +επ=ii0icter4qV, où ri = OiM. Avec iiOOa =!, on a : 2/122i2i2iirarr.a21r1OMOO1r1⎟⎟⎠⎞⎜⎜⎝⎛+=+=!! On effectue un développement limité du premier ordre approximation dipolaire en : 2i3i2iiru.ar1rr.ar1rr.a1r1r1!!!!!!+=+=⎟⎟⎠⎞⎜⎜⎝⎛+, où rru!! = L'expression du potentiel devient alors : ...r4aq.ur4qr4qV20iii0iiii0i+επ+επ=επ=!! On n'a pas écrit les termes correspondant à l'ordre 2, mais ils restent petits. Le premier terme, s'il n'est pas nul, est évidemment très grand devant le second et ainsi de suite.

Page 88 : Cycle Préparatoire Dipôle électrostatique 88 On peut distinguer plusieurs cas : Cas n°1 : 0Qqii=, la charge totale de la distribution n'est pas nulle et tout se passe comme si on pouvait, depuis le point M éloigné, considérer la distribution comme une charge ponctuelle Q placée en O : En effet : r4QV0επ Cas n°2 : 0qii =, la charge totale de la distribution est nulle donc le premier terme du potentiel aussi. Si 0aqiii!, on pose =iiiaqp!! et le potentiel s'écrit alors : 20r4p.uVεπ!! On reconnaît l'expression du potentiel électrostatique créé à la distance r par un dipôle de moment dipolaire p! . On dit que la distribution de charges est dipolaire, car on peut identifier le potentiel V et le champ qu'elle crée à ceux d'un dipôle de moment dipolaire =iiiaqp!!. Cas n°3 : 0qii = et 0aqpiii!!!== , les deux premiers termes du potentiel sont nuls et on parle de distribution multipolaire cas non étudié.

Page 89 : Cycle Préparatoire Dipôle électrostatique 89 V – 2 Détermination de la structure de molécules On peut avoir de l'information sur les structures moléculaires par la connaissance de la valeur pp!= du moment dipolaire. Les molécules de dioxygène ou de dichlore ne sont pas polaires, mais la molécule d'eau l'est : la connaissance de p permet de remonter à l'angle entre les liaisons OH si on en connaît la longueur. Si on prend par exemple la molécule de dinitro-benzène qui est un explosif plus ou moins puissant selon sa structure moléculaire. Pour l'ortho dinitro-benzène, on mesure p = 5,8 D Pour le méta dinitro-benzène, on mesure p = 3,5 D Pour le para dinitro-benzène, on mesure p = 0

Page 90 : Cycle Préparatoire Dipôle électrostatique 90 Application Soit les points A, B et O tels que : AO = OB = a. Soit une distribution de charges telle que les points A et B portent chacun la charge +q et que le point O porte la charge – 2q. Un point éloigné M situé sur l'axe Oz voit-il cette distribution comme un dipôle ? Si oui, donner le moment dipolaire p. 1. La charge totale est nulle : l'équivalence avec un dipôle est possible. 2. Le potentiel est nul à l'infini et on le calcule au point M en superposant les potentiels créés par chacune des charges ponctuelles placées en A, O et B : BM4qOM4q2AM4qMV000επ+επεπ= or, OM = z et AM = BM = 22za+, de sorte que : ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛+επ=z1za12qMV220 3. Lorsque le point M est "éloigné" du dipôle, on peut écrire : 1zasoit,az. En factorisant par z1 , le terme za apparaît dans l'expression du potentiel et un développement limité est alors possible : ⎟⎟⎠⎞⎜⎜⎝⎛επ=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛+επ=⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛+επ=1z2a1z2q1za1z2q1za11z2qMV2202/1220220 x A O B a a z M z 2q q q

Page 91 : Cycle Préparatoire Dipôle électrostatique 91 202zz4aqMVεπ= 4. Ce potentiel VM est proportionnel à 3z1 , c'est à dire à 3r1 , où r = OM. Or, le potentiel créé par un dipôle est proportionnel à 2r1 , donc cette distribution n'est pas équivalente à un dipôle 5. A titre de vérification, on calcule : 0OBOAqOBqOOq2OAqa.qiii!!=+=+= Nous nous trouvons dans le cas où l'équivalence à un dipôle n'est pas possible. Nous sommes en présence d'une distribution multipolaire.

Page 92 : Cycle Préparatoire Dipôle électrostatique 92

Page 93 : Cycle Préparatoire Dipôle électrostatique 93

Page 94 : Cycle Préparatoire Champ Magnétique 94 CHAPITRE 6 : Champ Magnétique & Mouvement de Particules Chargées Introduction I. Introduction La force de Lorentz met en évidence l'existence du champ magnétique. On va étudier les champs magnétiques créés par les courants électriques indépendants du temps : on parle aussi de magnétostatique comme pour l'électrostatique, pas de variation du champ électrostatique dans le temps. On peut calculer l'expression du champ magnétique par la loi de Biot et Savart. Comme pour le champ électrostatique, il existe des propriétés de symétrie et d'invariance et un théorème Ampère pour calculer d'une autre manière le champ magnétique. En étudiant le mouvement des particules, on arrive à établir, dans un conducteur, la fameuse loi d'Ohm et donc on peut calculer une résistance.

Page 95 : Cycle Préparatoire Champ Magnétique 95 II. Mise en évidence du champ magnétique Soit une charge q, immobile en un point M1 et ne subissant aucune force autre que son poids. Si elle passe au point M avec la vitesse v! et y subit une force f!, alors on peut dire qu'il existe au point M le champ magnétique B! qui satisfait la relation : Bvqf!!!= avec f! force de Lorentz en Newton N q charge en Coulomb C B! champ magnétique en Tesla T v! vitesse m.s-1 Pour calculer le champ magnétique de manière directe, il existe la loi de Biot & Savart pour une distribution linéique. On calcule le champ magnétique sur un élément de longueur ℓ"d et on intègre sur l'ensemble de la distribution : 30PMPMd4IBdBπµ==ΓΓℓ""" PMretMPMPuavecrud4IB20==πµ= Γ!!ℓ!! µ0 = perméabilité du vide = 4π.10-7 SI Le champ magnétique n'est donc pas défini donc ni continu aux points où se trouve un courant filiforme. ℓ"dI P r Γ Bd

Page 96 : Cycle Préparatoire Champ Magnétique 96 En pratique, la loi de Biot & Savart est très difficile à appliquer. Pour essayer de calculer de manière indirecte le champ magnétique, on utilise l'analogie avec le champ électrostatique E! qui consiste à considérer les propriétés de symétrie et d'invariance que l'on va énumérer. 1. La direction du champ magnétique en M est celle de la droite orthogonale à un plan Π de symétrie pour la distribution de courants et passant par M. 2. Le vecteur champ magnétique en M est inclus dans tout plan d'antisymétrie Π' pour la distribution de courants et passant par M. 3. La direction du champ magnétique en un point M est celle de la droite intersection d'au moins deux plans d'antisymétrie Π' et Π'' pour la distribution de courants et passant par M. 4. Si une distribution de courant reste invariante par une translation ou par une rotation, alors la valeur B du champ magnétique en tout point M ne dépend pas de la coordonnée correspondante à cette translation ou rotation. Π' Π'' Μ B Ι

Page 97 : Cycle Préparatoire Champ Magnétique 97 Exemple du fil infini parcouru par un courant uniforme : En coordonnées cylindriques : • Π est un plan de symétrie le champ est orthogonal à ce plan en M • Π' est un plan d'antisymétrie le champ appartient à ce plan en M • Invariance selon Oz Br,θ,z = Br,θ • Invariance selon θ Br,θ = Br r = HM Pour définir le sens du champ magnétique on utilise la règle du tire bouchon ou la règle du bonhomme d'ampère Π' Π Μ B Ι Η Règle du tire-bouchon Bonhomme d'Ampère I B!M M' B!M I B!

Page 98 : Cycle Préparatoire Champ Magnétique 98 III. Lignes de champ Les lignes de champ sont telles qu'en chacun de leurs points M, le champ magnétique B leur est tangent. Exemple du fil infini parcouru par un courant uniforme : θ=urBB!! Comme pour le champ électrostatique, on calcule un flux et une circulation du champ magnétique. I r rB! rB! rB! rB4!r3 Lignes d'un champ magnétique orthoradial et vue du dessus

Page 99 : Cycle Préparatoire Champ Magnétique 99 IV. Flux et circulation du champ magnétique. IV – 1 Flux magnétique Le flux du champ magnétique B! à travers une surface S s'écrit : ==φSSdSn.BSd.B!!!! où n! est le vecteur normal à l'élément de surface dS. Quelques caractéristiques : • Le flux magnétique à travers toute surface fermée est nul, 0Sd.BS=!! • Le flux magnétique à travers une surface ouverte S ne dépend que de la ligne fermée Γ sur laquelle la surface s'appuie. IV – 2 Circulation du champ magnétique Supposons que les considérations de symétrie et d'invariance ont permis de connaître la topographie du champ magnétique B!. En tout point M quelconque de l'espace où l'on cherche le champ magnétique, il passe une ligne de champ connue. On exprime la circulation C du champ magnétique B! sur une ligne fermée Γ définie par : • une ligne de champ si les lignes de champ sont fermées, • par une portion de ligne de champ complétée par une ligne orthogonale à B! en chacun de ces points si les lignes de champ ne sont pas fermées.

Page 100 : Cycle Préparatoire Champ Magnétique 100 Sur une ligne de champ, en notant L la longueur de la ligne de champ considérée et ℓ"d étant un élément de longueur de la ligne dont le sens dépend du choix de l'orientation de Γ, on obtient : Γ=ℓ""d.BC L.Bd.Bd.BC===ΓΓℓℓ"" où la ligne de champ est orientée dans le sens du champ magnétique B! si B est constant sur la ligne de champ. Si la ligne de champ n'est pas fermée, alors la portion Γ n'appartenant pas à la ligne de champ doit être telle que sa contribution soit nulle à la circulation par choix préalables B! et ℓ"d sont orthogonaux voir applications 1 et 2

Page 101 : Cycle Préparatoire Champ Magnétique 101 V. Théorème d'Ampère. Grâce au calcul de la circulation le long d'une courbe Γ fermée, il est possible de déterminer le champ magnétique. Le Théorème d'Ampère relie la circulation C du champ B le long du contour Γ et l'intensité Ialg comptée positivement si elle traverse S dans le sens de sa normale du courant qui traverse toute surface ouverte S s'appuyant sur Γ. µ=ΓId.Blga0ℓ"" Exemple IIId.B3210+µ=Γℓ"" avec Ι1, Ι2, Ι3 positifs Remarques : 1. Forte analogie avec le Théorème de Gauss et E!. 2. On peut calculer la direction de B! par les symétries et les invariances. Pour définir le sens de B!, on utilise la règle dite du tire bouchon ou du bonhomme d'Ampère. I2 I3 I1 Γ S + n!

Page 102 : Cycle Préparatoire Champ Magnétique 102 Application 1: Utilisation du théorème d'Ampère Calculer le champ magnétique créé en un point M quelconque de l'espace par un fil rectiligne infiniment long et défini par l'axe Oz en utilisant le théorème d'Ampère. L'étude déjà effectuée auparavant, a permis de choisir le système de coordonnées cylindriques d'axe Oz confondu avec le fil. Il a alors été trouvé : θ=urBMB! Le champ magnétique étant orthoradial, les lignes de champ sont des cercles centrés sur le fil, et le long d'une ligne de champ, B! reste inchangé car r est constant. Comme la ligne de champ est fermée et que le disque qu'elle délimite est traversée par le fil, on cherche à utiliser le théorème d'Ampère. On prend la ligne de champ comme contour Γ, vu qu'elle est fermée. On l'oriente positivement de telle manière que B et ℓd soient dans le même sens. La surface la plus simple s'appuyant sur ce cercle est un disque, pour lequel on a tracé la normale n! , conforme à l'orientation choisie pour Γ. La circulation du champ magnétique s'écrit alors : Br2dBdBud.uBd.Bπ====ΓΓΓθθΓℓℓ"ℓ"ℓ D'autre part, l'intensité I traverse le disque dans le sens de la normale n! , donc doit être comptée positivement. Le théorème d'Ampère s'écrit : I.Br2d.B0µ=π=Γℓ, soit r2IB0πµ= et finalement, θπµ=ur2IB0! I r ℓdrB! M n

Page 103 : Cycle Préparatoire Champ Magnétique 103 Application 2: Solénoïde infini On montre, voir exercice n°5 Série n°6 en utilisant la loi de Biot & Savart, que le champ magnétique créé par un solénoïde infini cylindrique de section circulaire en tout point M de son axe de révolution Oz vaut : z00u.InBsoitInB!µ=µ= Avec n : le nombre de spires par mètre. Le champ est alors indépendant du rayon du solénoïde. Pour tout point M de l'espace, le système est invariant par translation le long de l'axe Oz et par rotation autour de ce même axe Oz. De plus le plan perpendiculaire à l'axe Oz et passant par le point M est un plan de symétrie : le champ magnétique au point M est donc perpendiculaire à ce plan. zurBz,rB!=θ Le lignes de champ sont donc des cylindres centrés sur l'axe Oz r = constante. Appliquons le théorème d'Ampère : Soit un contour C fermé contenu dans un plan contenant l'axe Oz et constitué de deux parallèles à Oz distantes respectivement de r1 et r2 de l'axe, et de deux perpendiculaires à Oz. Les contributions des deux perpendiculaires à Oz à la circulation du champ magnétique le long de ce contour sont nulles : le champ est perpendiculaire aux déplacements élémentaires. En notant ℓ, la longueur des parallèles à Oz, on obtient : lga021CMIrBrBd.MBµ==ℓℓℓ r1 z ℓ I r2 R sens de parcours

Page 104 : Cycle Préparatoire Champ Magnétique 104 On distingue les trois cas suivants : Si r1 r2 R, Ialg = 0 et on en déduit que Br1 = Br2 Le champ créé à l'intérieur d'un solénoïde infini ne dépend pas de r : il est donc uniforme. On le note Bint. Si R r1 r2, Ialg = 0 et on en déduit que Br1 = Br2 Le champ créé à l'extérieur d'un solénoïde infini ne dépend pas de r : il est donc uniforme. On le note Bext. Si r1 R r2, Ialg = n.I.ℓ compté positivement vu le sens de parcours choisi qui détermine la normale à la surface. Le champ magnétique est orienté dans le sens de zu! . Br1ℓ – Br2ℓ = Bint – Bext.ℓ = µ0.n.I.ℓ Bint – Bext = µ0.n.I Dans le cas d'un solénoïde de section circulaire, on a calculé la valeur du champ sur l'axe et on peut écrire : InB0intµ= On en déduit donc Bext = 0 Le champ magnétique est donc nul à l'extérieur d'un solénoïde infini. Par analogie avec l'exercice 3 de la Série 5, on peut également considérer que le solénoïde est une bobine torique de rayon infini.

Page 105 : Cycle Préparatoire Champ Magnétique 105 VI. Force de Lorentz. La force de Lorentz généralisée, c'est la force qu'exerce un champ électromagnétique E!, B! sur une charge q électrique. Il existe des effets dus à E! et à B!. BvEqf!!!!+= avec f! force de Lorentz en Newton N q charge en Coulomb C B! champ magnétique en Tesla T E! champ électrostatique V.m-1 ou N.C-1 v! vitesse m.s-1 Dans les études, on négligera l'action du poids dont le module reste très faible devant celui de toute force électromagnétique électrique ou magnétique. Une particule plongée dans un champ électrostatique uniforme décrit une trajectoire parabolique si la vitesse initiale et le champ électrostatique ne sont pas colinéaires, une droite décrite de manière uniformément accélérée dans le cas contraire. Utilisation du principe fondamental de la dynamique – TD mécanique La vitesse v de la particule chargée varie au cours de son déplacement, car celui-ci s'effectue dans le champ d'énergie potentielle Ep = qV. Le mouvement d'une particule chargée plongée dans un champ magnétique uniforme et stationnaire s'effectue à vitesse v constante.

Page 106 : Cycle Préparatoire Champ Magnétique 106 Le champ électromagnétique E!, B! exerce sur une particule de charge q et possédant une vitesse v! la force de Lorentz. Si la particule a une vitesse, alors, il existe une densité de courant, j!, décrite par : Ej!!γ= loi d'Ohm locale avec E! champ électrostatique V.m-1 ou N.C-1 j! densité de courant SI γ coefficient de conductivité du conducteur dépend du milieu et de la T° l'unité est le Siemens γ1 résistivité en Ohm.mètre Ω.m Le vecteur densité de courant j! est défini par vvnqjm!!!ρ==, où nq = ρm est la densité volumique de charges des porteurs mobiles de vitesse v! . Si S est une section du conducteur traversée par I, la densité de courant j! est liée à l'intensité I du courant par la relation : Sd.jidISS!!== L'intensité I du courant s'exprime en ampère A La loi d'Ohm globale définit, en régime stationnaire, la résistance R d'un conducteur de section S entre les points A et B par la relation : ==SBABASd.jd.EIVVR!!ℓ!! Remarque : Pour un barreau cylindrique de longueur ℓ, de conductivité γ et de section S : γ=ρρ=1avecSRℓ résistivité du barreau

Page 107 : Cycle Préparatoire Champ Magnétique 107 VII. Force de Laplace. Soit un circuit filiforme parcouru par une intensité I. Si il existe un champ magnétique B!, la force de Laplace 1F! est la force subie par un conducteur parcouru par un courant électrique sous l'action du champ magnétique B! dans lequel il est plongé : BdIFd 1!ℓ!!= On introduit alors la densité volumique de la force de Laplace : BjdFd 1!!!=τ

Page 108 : Cycle Préparatoire Champ Magnétique 108 VIII. Définition Légale de l'Ampère. Elle est basée sur l'interaction entre deux fils conducteurs infinis et parallèles. D'après le calcul effectué plus haut, le fil 1 crée un champ magnétique θπµ=urI2MB101!! en notant r la distance du point M au fil rectiligne et en utilisant les coordonnées cylindriques. Une longueur ℓ du fil 2 subit donc une force magnétique : r21010z221udII2udI2uIF!ℓ!!ℓ!πµ=πµ=θ→ La connaissance du module de la force et des distance ℓ et d permet de définir l'unité d'intensité, l'ampère, en faisant circuler le même courant dans les deux fils. On obtient : L'ampère est l'intensité d'un courant constant qui, maintenu dans deux conducteurs rectilignes, infinis et parallèles, de section circulaire négligeable et distants de 1 m, produit une force d'interaction entre ces deux conducteurs égale à 2.10-7 N par mètre de conducteurs. On fixe en même temps la constante µ0 ou valeur de la perméabilité du vide à 4π.10-7 H.m-1.

Page 109 : Cycle Préparatoire Champ Magnétique 109

Page 110 : Cycle Préparatoire Mouvement des particules chargées 110 CHAPITRE 7 : Mouvements de particules chargées I. Introduction C'est dans les grands accélérateurs de particules que des découvertes fondamentales sur la structure de la matière ont été faîtes : les chocs des particules ont permis de mettre en évidence les quarks dans les années 70. Le but de ce chapitre n'est pas de reprendre une étude des chocs entre particules dans les accélérateurs, mais de comprendre comment les particules chargées se meuvent lorsqu'elles sont plongées dans un champ électromagnétique. La force de Lorentz, très supérieure au poids, met les particules chargées en mouvement ou modifie leurs mouvements. A partir d'hypothèses simplificatrices champs uniformes et stationnaires, ce chapitre permet de comprendre les causes du mouvement des particules chargées.

Page 111 : Cycle Préparatoire Mouvement des particules chargées 111 II. La force de Lorentz C'est la force qu'exerce un champ électromagnétique sur une charge électrique q. Son expression générale comprend les effets du champ électrique E! et ceux du champ magnétique B!. Le champ électromagnétique B,E!! exerce sur une particule de charge q et possédant une vitesse v! la force de Lorentz : Tmagnétiquechamp:Bs.mvitesse:vm.Vtiqueélectrostachamp:ECcoulombeneargch:qNnewtonenforce:BvEq11!!!!!!!!+=ff Pour étudier le comportement des particules chargées sous l'action de cette force, on se place dans le cadre de la mécanique newtonienne, ou classique. Le module de la vitesse des particules reste très petit devant la vitesse de la lumière dans le vide. On appliquera le principe fondamental de la dynamique PFD à la particule dans un référentiel galiléen, et en excluant tout changement de référentiel. Le référentiel terrestre peut être considéré comme galiléen pour ce qui est de l'étude du mouvement de particules chargées. En effet, la durée de cette étude n'excède jamais quelques secondes, durée négligeable devant celle caractéristique de rotation de la Terre. Dans les études suivantes, on négligera l'action du poids dont le module reste négligeable devant celui de toute force électromagnétique électrique ou/et magnétique.

Page 112 : Cycle Préparatoire Mouvement des particules chargées 112 III. Champ électrostatique uniforme La particule chargée est plongée dans un champ électrostatique E! uniforme et on néglige la pesanteur. Ce mouvement est étudié dans le vide. III – 1 Equations horaires et trajectoire On écrit le principe fondamental de la dynamique PFD pour la particule chargée de masse m et de charge q : Eqam!!!== f Soit : mEqa!! =. Le mouvement de la particule est uniformément accéléré. Pour déterminer le vecteur position OMr =! de la particule, on intègre deux fois l'expression précédente, puisque dtvda!! = et dtrdv!! = : Ÿ 0vtmEqv!!!+=, où 0tvv0== !! est la vitesse initiale ; Ÿ 002rtvtm2Eqr!!!!++=, où 0trr0== !! est la position initiale. Comme la force Eq!!=f est uniforme, la trajectoire de la particule reste dans le plan v;;M00!!f, où M0 est le point définissant la position de la particule à l'instant initial. Pour tracer cette trajectoire plane, on peut changer d'origine du repère et choisir M0 comme nouvelle origine, puis prendre comme axe Ox la direction de xuEE:E!!!=, et enfin faire en sorte que l'axeOz soit orthogonal aux vecteurs xuEE!!= et 0v! .

Page 113 : Cycle Préparatoire Mouvement des particules chargées 113 On peut alors projeter la relation vectorielle précédente, avec 0r0!! =, yy0xx00uvuvv!!!+=, et yxuyuxr!!!+=, pour obtenir les équations horaires : ⎪⎪⎩⎪⎪⎨⎧=+=tvtytvtm2qEtxy0x02 On trouve l'équation de la trajectoire par élimination du temps tvtyy0= : tyvvtyvm2qEtxy0x022y0+= Si v0y 0, alors il s'agit d'une parabole : si v0y = 0, alors c'est une droite : l'axe Ox. Une particule chargée plongée dans un champ électrostatique décrit une trajectoire parabolique si la vitesse initiale et le champ électrostatique ne sont pas colinéaires, une droite décrite de manière uniformément accélérée dans le cas contraire. III – 2 Etude énergétique La puissance P de la force de Coulomb vaut : v.EqP!!=. Elle est non nulle : l'énergie cinétique de la particule chargée change lors de son parcours. On rappelle que la variation d'énergie cinétique entre deux points M1 et M2 du parcours est obtenue en intégrant la puissance précédente : f!!!==dtvdmam Or ⎟⎟⎠⎞⎜⎜⎝⎛===2vm21dtdv.dtvdmv.P!!!!!f, soit : 212221221221vm21vm21vm21ddtvm21dtddtP=⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛=!! ffff!!!!!!!Wrd.dtdtrd.dtv.dtP2121212121→==== VVqdVqrd.Vgradqrd.Vgradqrd.EqdtP212121212121=====!!!!

Page 114 : Cycle Préparatoire Mouvement des particules chargées 114 Finalement VVqvm21vm21212122= Si la particule se déplace vers les potentiels décroissants V1 V2, sa charge étant positive q 0, alors la vitesse de la particule augmente, le travail de f! est positif et le déplacement de la particule est spontané. On peut aussi écrire : mpc121222EEEqVvm21qVvm21=+=+=+ On retrouve le fait que l'énergie mécanique est conservée, vu que la seule force qui travaille est la force de Coulomb, conservatrice et associée à l'énergie potentielle électrostatique : Ep = qV, provenant de La vitesse v de la particule chargée varie au cours de son déplacement, car celui-ci s'effectue dans le champ d'énergie potentielle Ep = qV.

Page 115 : Cycle Préparatoire Mouvement des particules chargées 115 IV. Champ magnétique uniforme La particule chargée est plongée dans un champ magnétique B! uniforme et stationnaire ; on néglige la pesanteur. Il n'y a pas de champ électrostatique. Ce mouvement est étudié dans le vide. IV – 1 Equations horaires et trajectoire On choisit le repère de telle façon que le champ magnétique B! uniforme soit porté par l'axe Oz : zuBB!!=, avec B 0. La particule se trouvant au point O à l'origine des dates t = 0. On choisit la position des axes Ox et Oy de telle manière que la vitesse initiale 0tvv0== !! soit un vecteur du plan Oyz. IV – 1.1 Lois horaires du mouvement On écrit le principe fondamental pour la particule chargée de masse m et de charge q : Bvqdtvdmam!!!!!===f Exprimons les vecteurs dans la base cartésienne : ⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛0BvBvB00vvvBv;B00B;dtdvdtdvdtdva;vvvvxyzyxzyxzyx!!!!! Et donc, en les projetant sur les axes : • Sur Ox, yxqBvdtdvm= 1 • Sur Oy, xyqBvdtdvm= 2 • Sur Oz, 0dtdvmz = 3

Page 116 : Cycle Préparatoire Mouvement des particules chargées 116 En dérivant l'équation 1 par rapport au temps et en combinant avec l'équation 2, on obtient l'équation différentielle vérifiée par vx : x22y2x2vmBqdtdvqBdtvdm== Soit : 0vmBqdtvdx2222x2=+ De même, en dérivant 2 et en utilisant 1 : y22x2y2vmBqdtdvqBdtvdm== Soit : 0vmBqdtvdy2222y2=+ Les deux composantes vx et vy, de la vitesse satisfont la même équation différentielle du second ordre à coefficients constants et sans second membre. En posant mqB=ω, grandeur homogène à une pulsation et appelée pulsation cyclotron, les solutions de ces équations s'écrivent : vxt = Acosωt + Hsinωt, vyt = Dcosωt + Fsinωt et vzt = G où A, H, D, F et G sont cinq constantes déterminées à partir des conditions initiales : vxt = 0 = 0, vyt = 0 = v0cosθ et vzt = 0 = v0sinθ Des équations du mouvement 1 et 2, il vient les deux équations : cosv0tv0tdtdv0yxθω==ω== 00tv0tdtdvxy==ω== En utilisant les lois horaires solutions et les conditions initiales, il vient : A = 0, H = D = v0cosθ, F = 0 et G = v0sinθ

Page 117 : Cycle Préparatoire Mouvement des particules chargées 117 Les lois horaires des composantes de la vitesse s'écrivent enfin : vxt = v0cosθsinωt vyt = v0cosθcosωt vzt = v0sinθ Il reste à intégrer ces composantes pour obtenir les coordonnées x, y et z de la particule en fonction du temps lois horaires du mouvement : • Xtcoscosvtxtsincosvdtdxv00x+ωθω=→ωθ== • Ytsincosvtytcoscosvdtdyv00y+ωθω=→ωθ== • Ztsinvtzsinvdtdzv00z+θ=→θ== Où X, Y et Z sont trois nouvelles constantes d'intégration à calculer. Or, à l'instant initial, la particule se trouve à l'origine O du repère, donc : • cosvX0Xcosv0tx00θω=→=+θω== • 0Y0ty=== • 0Z0tz=== Les lois horaires du mouvement prennent donc la forme suivante : • tcos1cosvtx0ωθω= • tsincosvty0ωθω= • tsinvtz0θ=

Page 118 : Cycle Préparatoire Mouvement des particules chargées 118 IV – 1.2 Trajectoire Dans la direction de l'axe Oz, le mouvement est uniforme. Dans le plan Oxy, le temps doit être éliminé. Pour ce faire, on utilise les lois horaires et la relation fondamentale de la trigonométrie. cosvtx1tcos0θω=ω cosvtytsin0θω=ω 1tsintcos22=ω+ω 1cosvtycosvtx12020=⎟⎟⎠⎞⎜⎜⎝⎛θω+⎟⎟⎠⎞⎜⎜⎝⎛θω 1tycosvtxcosvcosv2202020=⎟⎟⎠⎞⎜⎜⎝⎛θω+⎟⎟⎠⎞⎜⎜⎝⎛ωθ⎟⎟⎠⎞⎜⎜⎝⎛θω 20220cosvtycosvtx⎟⎟⎠⎞⎜⎜⎝⎛ωθ=+⎟⎟⎠⎞⎜⎜⎝⎛ωθ En projection dans le plan Oxy, la trajectoire est un cercle de centre C parcouru de manière uniforme avec : 0yetqBcosmvcosvxC00C=θ=ωθ= En reprenant l'ensemble des résultats, on peut écrire le mouvement de la particule chargée dans l'espace. Lorsque sinθ 0, la particule chargée décrit une hélice circulaire de par constant p avec une vitesse angulaire constante mqB=ω. Lorsque sinθ = 0, la particule chargée décrit un cercle de manière uniforme dans un plan orthogonal au champ magnétique. Le rayon R du cercle est qBcosmvcosvR00θ=ωθ=

Page 119 : Cycle Préparatoire Mouvement des particules chargées 119 Lorsque cosθ = 0, B! et v! sont colinéaires et la force est nulle : la trajectoire est rectiligne uniforme suivant l'axe Oy. Compte tenu des équations horaires et du cercle décrit dans le plan Oxy, on voit que ωt représente physiquement l'angle OM,CO, où M est le point auquel se trouve la particule chargée à l'instant t 0. Le pas de l'hélice est la distance parcourue le long de l'axe Oz lorsque le point M a fait un tour : Pour sinqBmv22sinvpz2t00θπ=ωπθ==→π=ω Lorsque sinθ = 0, B! et v! sont orthogonaux, le pas est nul et on retrouve le fait que la trajectoire soit alors circulaire. IV – 2 Etude énergétique La puissance P de la force de Lorentz vaut : 0v.BvqP==!!! En effet, le produit vectoriel Bv!! est orthogonal à chacun des deux vecteurs qui le constitue, donc à v! , et le produit scalaire avec v! est nul. Par conséquent, la force magnétique ne travaille pas et l'application du théorème de l'énergie cinétique entre deux points M1 et M2 de la trajectoire donne : 1221212122vv0PdtWvm21vm21=→===→f! Le mouvement d'une particule chargée plongée dans un champ magnétique uniforme et stationnaire s'effectue à vitesse v constante.

Page 120 : Cycle Préparatoire Mouvement des particules chargées 120 V. Mise en œuvre Comment déterminer le mouvement d'une particule chargée dans un champ électromagnétique ? Soit une particule de masse m et de charge q plongée dans un champ électromagnétique uniforme et stationnaire B,E!!. Compte tenu des conditions initiales données, déterminer la trajectoire décrite par cette particule. Œ Faire un bilan des forces  Ecrire le Principe Fondamental de la Dynamique PFD. Le projeter sur les 3 axes et obtenir l'équation différentielle que satisfait chacune des composantes de la vitesse de la particule. Ž Ecrire la solution générale de chacune des équations différentielles précédentes. Compter les constantes qui sont apparues.  Exprimer les conditions initiales. Vérifier qu'il y en a autant que de constantes d'intégration, puis, déterminer les constantes et écrire les lois horaires de chacune des composantes de la vitesse.  Intégrer ces composantes pour obtenir les lois horaires de la position de la particule. Les trois constantes sont calculées en utilisant la position initiale. ‘ Tracer la trajectoire. Application Déterminer la trajectoire décrite par une particule de masse m et de charge q 0 plongée dans un champ électromagnétique uniforme xuEE!!= et zuBB!!=, sachant qu'à t = 0, elle se trouve à l'origine du repère sans vitesse initiale. Solution Le poids est négligeable devant toute force électromagnétique. La seule force qui s'applique est la force de Lorentz généralisée : BvEq!!!!+=f

Page 121 : Cycle Préparatoire Mouvement des particules chargées 121 Le principe fondamental de la dynamique s'écrit : BvEqdtvdmam!!!!!!+===f Pour projeter cette équation vectorielle sur les axes Ox, Oy et Oz, on projette chacun des vecteurs en les exprimant sous forme de "vecteurs colonne" : ⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎜⎜⎜⎝⎛⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎝⎛0BvBvB00vvvBv;B00B;00EE;dtdvdtdvdtdva;vvvvxyzyxzyxzyx!!!!!! Les projections sur les axes s'écrivent alors : • Sur Ox, qEqBvdtdvmyx+= 1 • Sur Oy, xyqBvdtdvm= 2 • Sur Oz, 0dtdvmz = 3 En dérivant l'équation 2 et en utilisant l'équation 1, on obtient l'équation différentielle vérifiée par vy. ⎟⎟⎠⎞⎜⎜⎝⎛+==mqEqBvqBdtdvqBdtvdmyx2y2 Soit : 22y22y2mEBqvmqBdtvd=⎟⎟⎠⎞⎜⎜⎝⎛+ De même, en dérivant l'équation 1 et en utilisant l'équation 2, on obtient l'équation différentielle vérifiée par vx. 0vmqBdtvdx22x2=⎟⎟⎠⎞⎜⎜⎝⎛+

Page 122 : Cycle Préparatoire Mouvement des particules chargées 122 L'équation 3 est l'équation différentielle satisfaite par vz. La solution générale de l'équation 3 est : vz = A, où A est une constante. L'équation différentielle satisfaite par vx est du second ordre, linéaire, à coefficients constants, homogène et on en connaît la solution générale : ⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=tmqBsin'CtmqBcosCvx ou C et C' sont des constantes. L'équation différentielle satisfaite par vy est du second ordre, linéaire, à coefficients constants, avec un second membre. Sa solution générale vy est la somme de la solution générale vy1 de l'équation homogène associée et d'une solution particulière vy2. La solution particulière est choisie de la même forme mathématique que le second membre, c'est-à-dire une constante. On trouve : BEv 2y= Puis, par analogie avec vx, on obtient ⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=tmqBsin'DtmqBcosDv 1y La solution générale pour vy s'écrit enfin : BEtmqBsin'DtmqBcosDvy⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛= On dénombre alors cinq constantes A, C, C', D et D'. Les conditions initiales portant sur la vitesse sont au nombre de trois : vxt = 0 = vyt = 0 = vzt = 0 = 0

Page 123 : Cycle Préparatoire Mouvement des particules chargées 123 Il manque donc deux équations pour pouvoir déterminer toutes les constantes. Comme on a dérivé les équations du mouvement pour obtenir les équations différentielles, les équations manquantes pourront être obtenues à partir des équations du mouvement. Les équations 1 et 2 à l'instant initial : mqE0tdtdvqE0tqBv0tdtdvmxyx==→+=== 00tdtdv0tqBv0tdtdvmyxy==→=== Elles fournissent les deux équations supplémentaires et on peut calculer les constantes : BE'CdonnemqE0tdtdvet0Cdonne00tvxx======0'Ddonne00tdtdvetBEDdonne00tvyy====== vzt = 0 = 0 donne A = 0 On peut maintenant écrire les lois horaires des composantes de la vitesse : ⎟⎟⎠⎞⎜⎜⎝⎛=tmqBsinBEtvx ⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛=1tmqBcosBEtvy 0tvz= Il reste à intégrer les trois composantes de la vitesse • ⎟⎟⎠⎞⎜⎜⎝⎛==tmqBsinBEtvdtdxx s'intègre en ''CtmqBcosqBmEtx2+⎟⎟⎠⎞⎜⎜⎝⎛= • BEtmqBcosBEtvdtdyy⎟⎟⎠⎞⎜⎜⎝⎛== donne ''DtBEtmqBsinqBmEty2+⎟⎟⎠⎞⎜⎜⎝⎛= • La primitive de 0dtdz = est A" où A", B" et C" sont trois constantes que l'on détermine en utilisant la position initiale.

Page 124 : Cycle Préparatoire Mouvement des particules chargées 124 A l'instant t = 0, le point est à l'origine O du repère, ce qui permet d'obtenir : 0"DqBmE"C0"A2=== Les lois horaires de position sont : • ⎟⎟⎠⎞⎜⎜⎝⎛⎟⎟⎠⎞⎜⎜⎝⎛=tmqBcos1qBmEtx2 • tBEtmqBsinqBmEty2⎟⎟⎠⎞⎜⎜⎝⎛= • 0tz= Les équations horaires ne font pas apparaître une trajectoire classique cercle, ellipse, …. On peut tout de même voir qu'elle est plane, car contenue dans le plan Oxy. On utilise un tableur pour la tracer et on reconnaît une cycloïde.

Page 125 : Cycle Préparatoire Mouvement des particules chargées 125

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125