CM
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189
Page 1 : 1Pourquoi vous enseigne-t-on les mathématiques :1 pour vous sélectionner2 pour la construction de votre esprit3 pour décrire des phénomènes et prédire leurs évolutions acquérir la logique mathématiquel’intelligence d’un individu se mesure à la largesse de sesconnaissances et non à son niveau de spécialisation acquérir la démarche scientifiquephysique, biologie, informatique, chimie, climatologie,... finance, économie, médecine,...sociologie, psychologie2020/2021Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction générale Mathématiques préING 2
Page 2 : 2Problème : :Mais on décrit peu de chose avec des fonctions scalaires d’une variableExemples :En thermodynamique : l’énergie interne U :En électromagnétisme : , : Mathématiques préING 22020/2021Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction généraleVous connaissez parfaitement les fonctions programme d’Analyse préING 1
Page 3 : 3Généralisation aux fonctions de la forme :Or, comme vous l’avez vu en 1ère année, il faut également étudier la structure des ensembles sur lesquels ces fonctions sont définiesTopologie ouvert, fermé,...2020/2021Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction générale Mathématiques préING 2
Page 4 : 4Chapitre 2 :2020/2021Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction générale Mathématiques préING 2
Page 5 : 5Chapitre 3 :Chapitre 4 :1Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction générale2020/2021 Mathématiques préING 2
Page 6 : 6Chapitre 5 :Ph.D. Elian Masnadaa. Objectifs b. PlanChapitre 1 :Introduction générale2020/2021 Mathématiques préING 2
Page 7 : Objectif du cours :Etudier les fonctions de plusieurs variablesGénéralisation des notions de : - limites - continuité - dérivée - dérivabilité - ...ouvert, fermé, ….?Comment généralise-t-on les notions de norme, de distance,d’ouvert, de fermée,… dans le cas d’un espace vectoriel quelconque ? 72020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 2 : Suites d’éléments d’un EVNIntroduction du chapitre 2Partie 1 : Eléments de topologie
Page 8 : Vous connaissez un exemple de norme dans :alors82020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 9 : 9Remarques :1 Si , alors2 Si , alors pour ,2c’est donc la norme que vous connaissezon l’appelle norme euclidienne2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
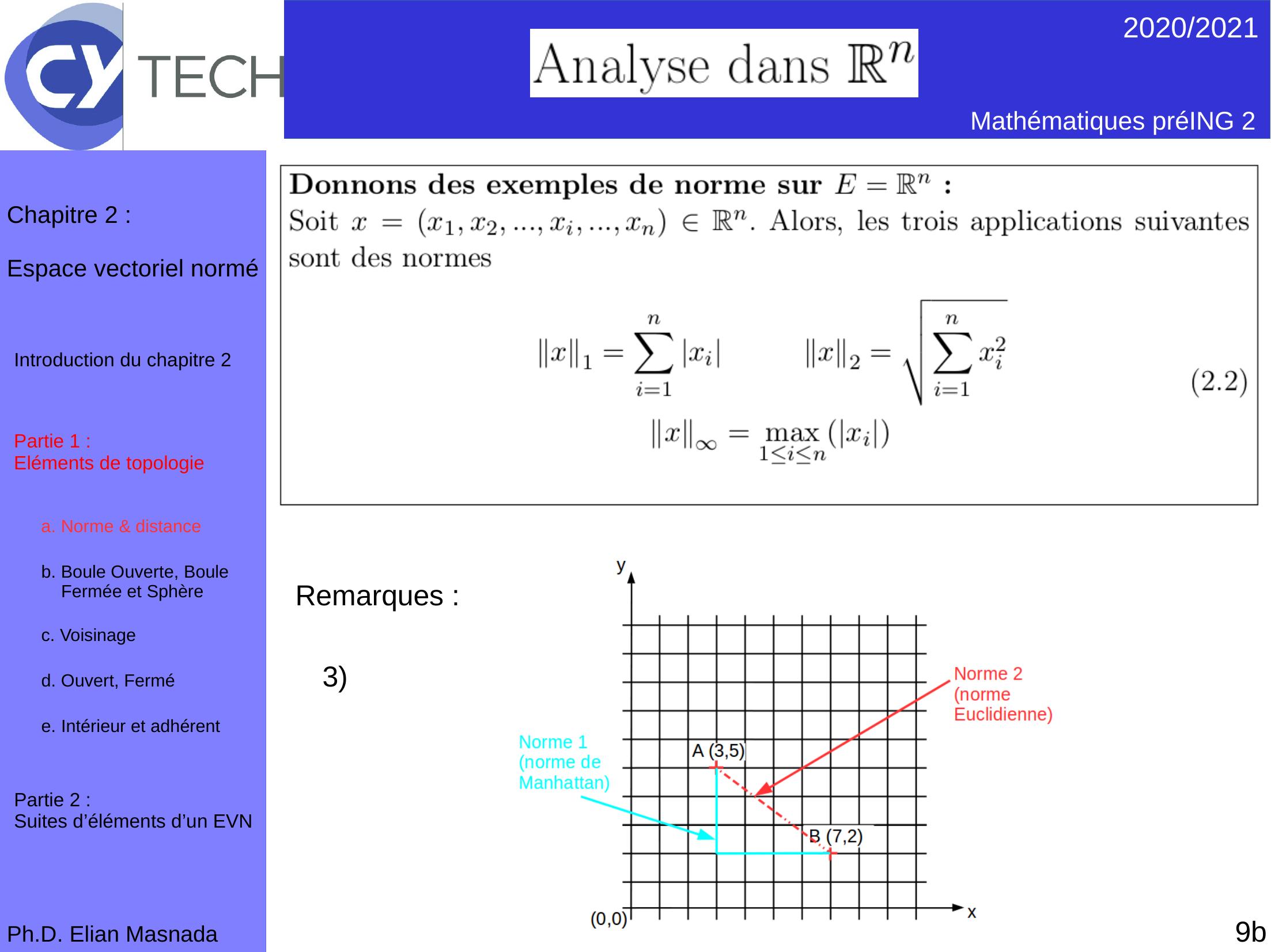
Page 10 : 9bRemarques :3 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 11 : 102020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 12 : NON2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN11
Page 13 : 12ceci n’est en général pas vrai voir polycopié p.132020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 14 : 132020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 15 : 141.2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 16 : 152.2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 17 : 163.:2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 18 : 17Ce théorème va être fondamental dans la suite du cours2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNRéflexif + Transitif + Symétrique = Relation d’équivalence
Page 19 : 182020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 20 : 192020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 21 : 2022020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 22 : 21:2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 23 : 222020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 24 : 23dans notre casRappel2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
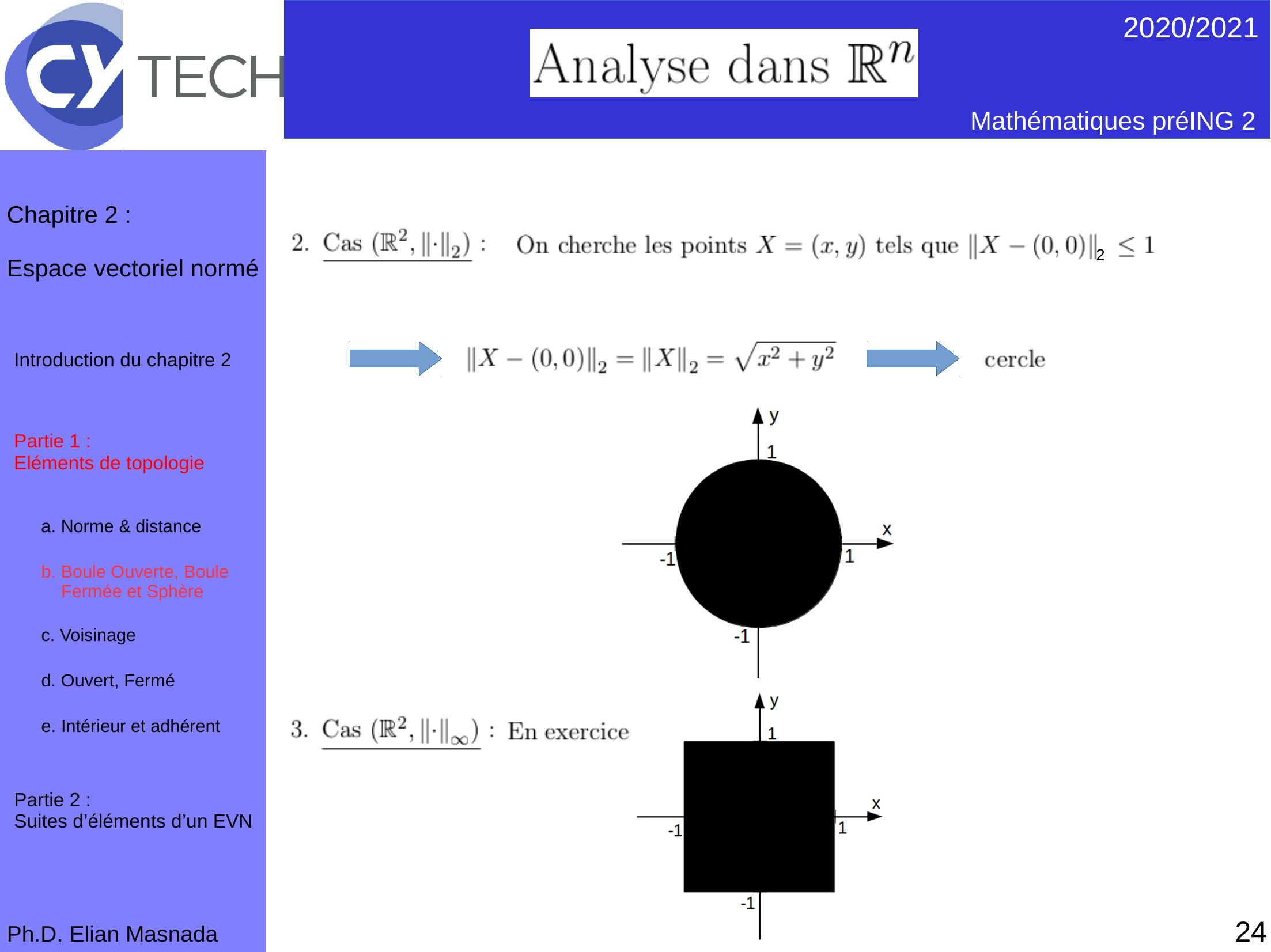
Page 25 : 2422020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 26 : Chapitre 2 :Espace vectoriel normé252020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 27 : 262020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 28 : Chapitre 2 :Espace vectoriel normé272020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 29 : 28V1V22020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 30 : Chapitre 2 :Espace vectoriel normé29,2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 31 : Chapitre 2 :Espace vectoriel normé302020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
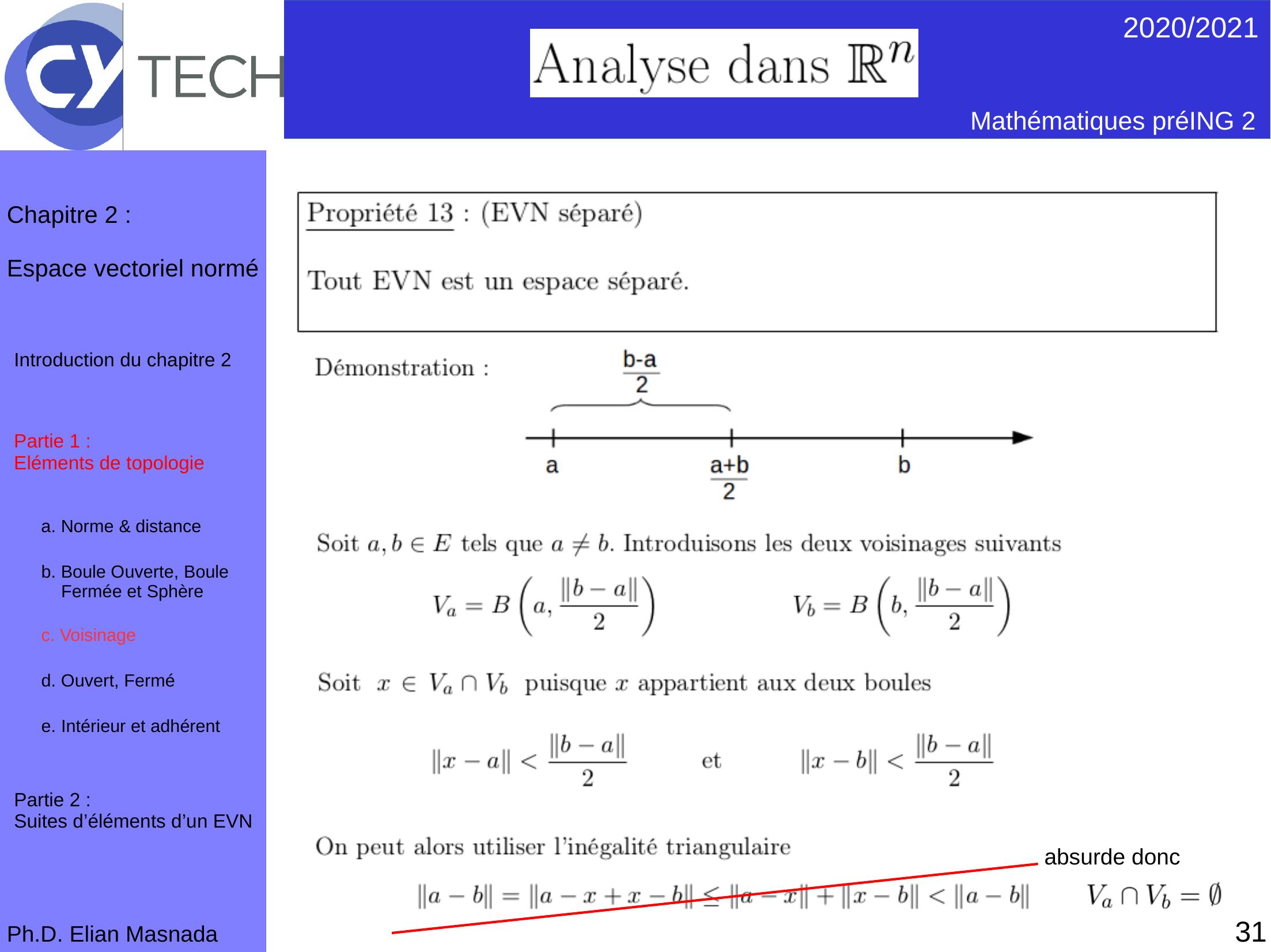
Page 32 : 31absurde donc2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 33 : 32dans la suite, on représentera lescontours d’un ouvert avec des pointillés 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 34 : 332020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
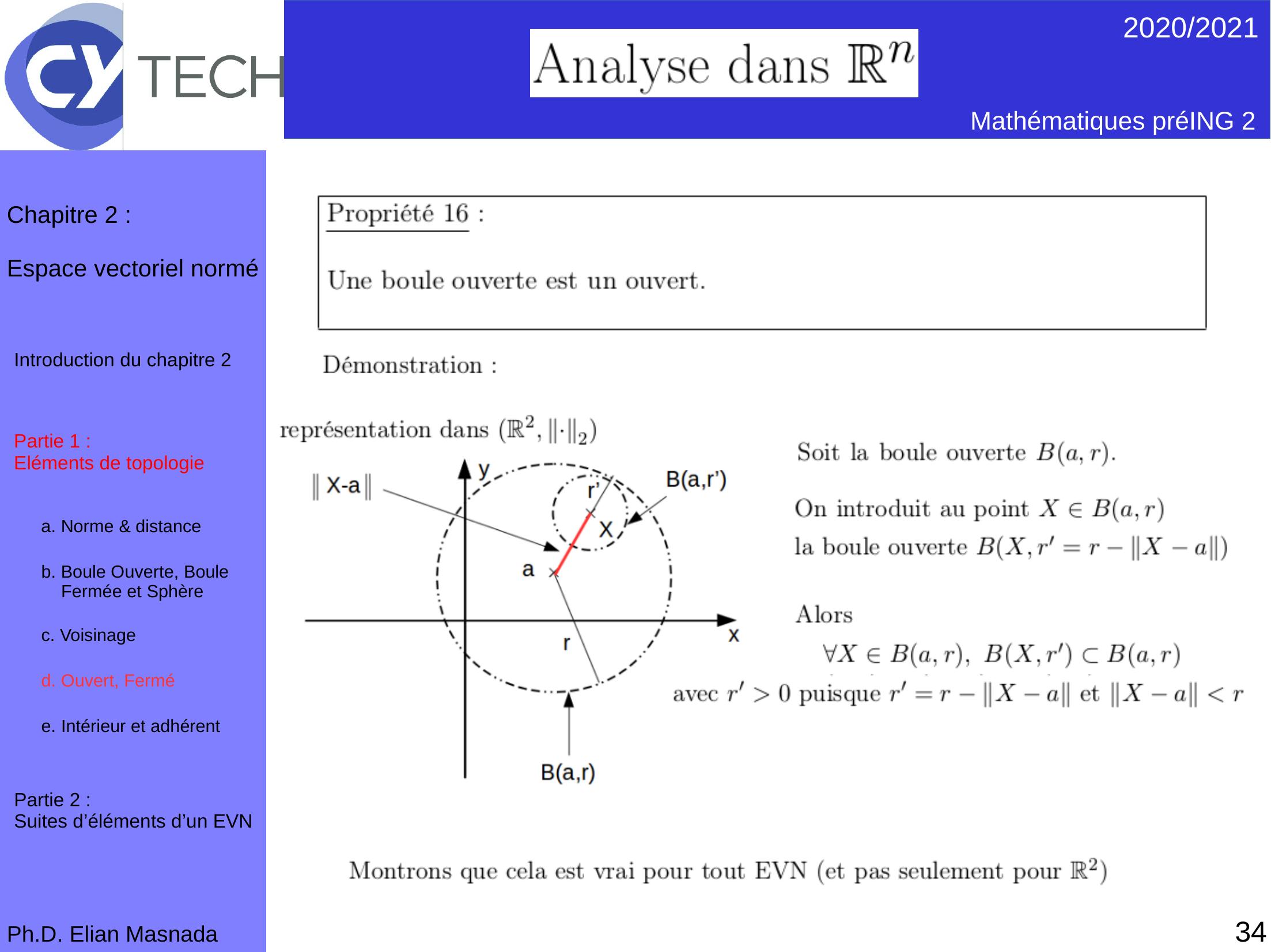
Page 35 : 342020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
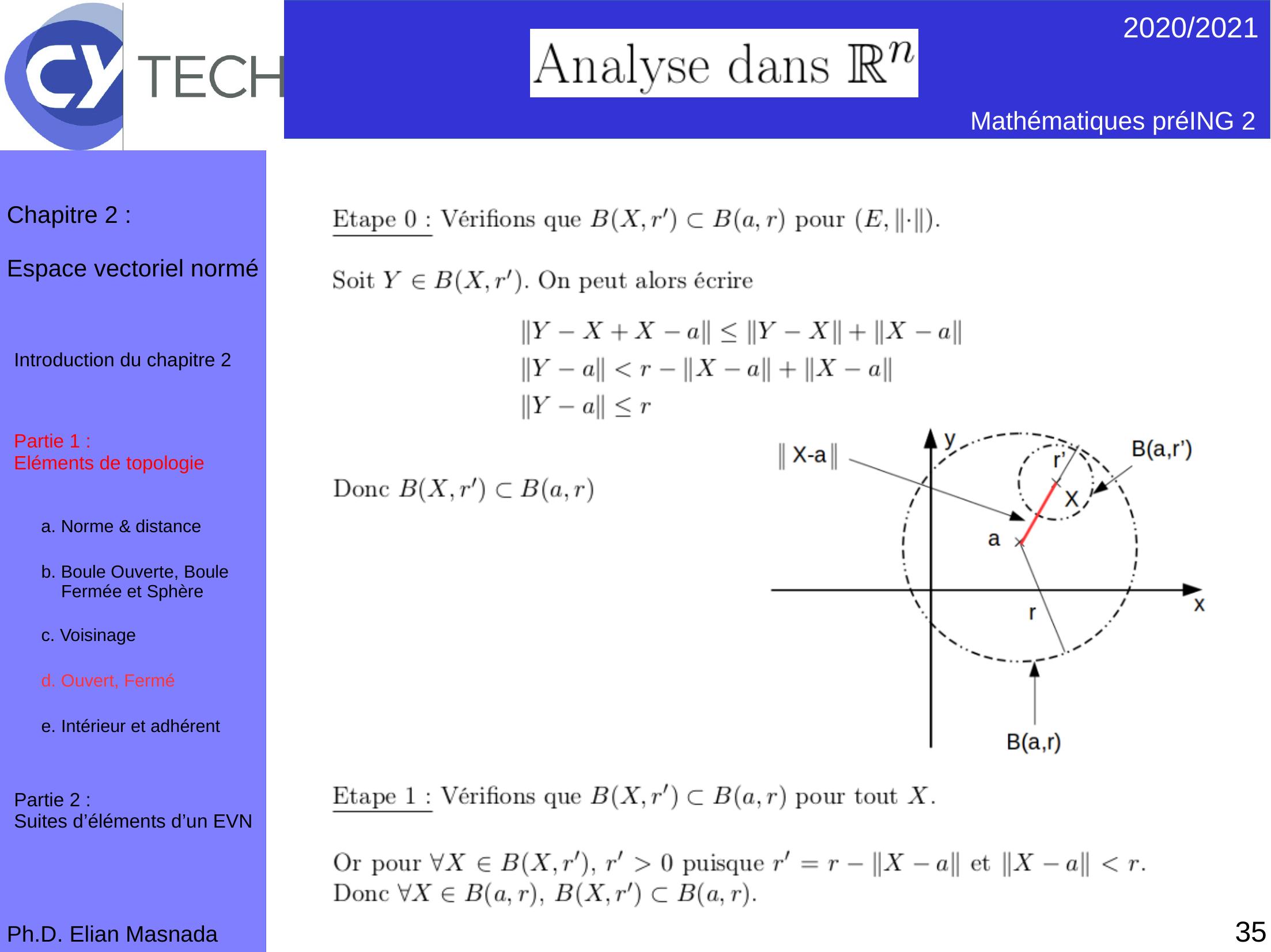
Page 36 : 352020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 37 : Chapitre 2 :Espace vectoriel normé362020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 38 : 372020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 39 : 382020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 40 : 392020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 41 : 402020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNVoir le poly
Page 42 : 412020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 43 : 42Trivial2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 44 : 432020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 45 : 442020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN32
Page 46 : 452020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 47 : 462020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 48 : Chapitre 2 :Espace vectoriel normé47A2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 49 : Chapitre 2 :Espace vectoriel normé482020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 50 : 49Admis2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 51 : Chapitre 2 :Espace vectoriel normé502020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 52 : 5111-1-1A-1;02020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
Page 53 : 5211-1-1A1,02020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologiea. Norme & distance b. Boule Ouverte, Boule Fermée et Sphèrec. Voisinaged. Ouvert, Fermé e. Intérieur et adhérent Introduction du chapitre 2Partie 2 : Suites d’éléments d’un EVN
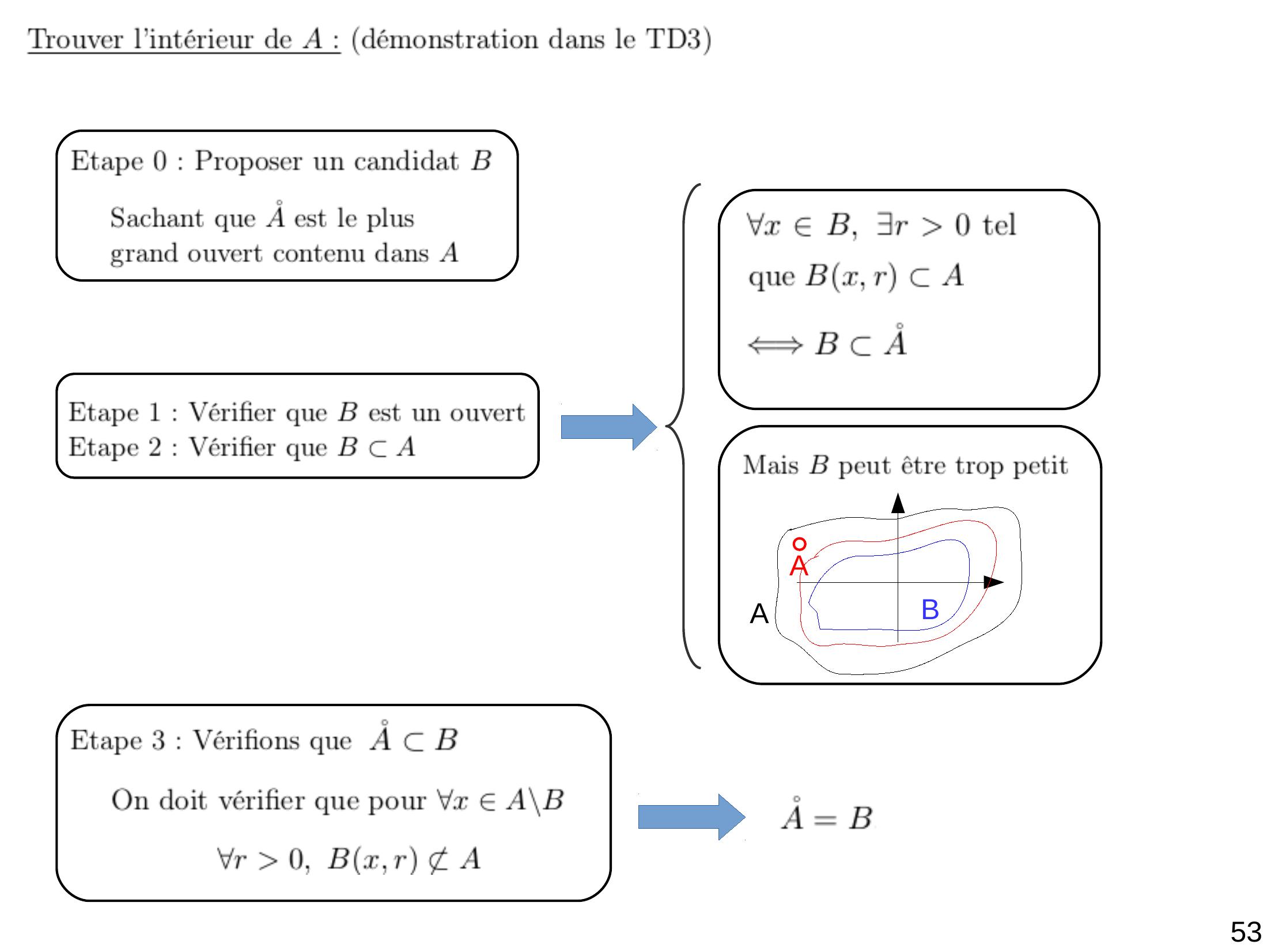
Page 54 : 53ABA
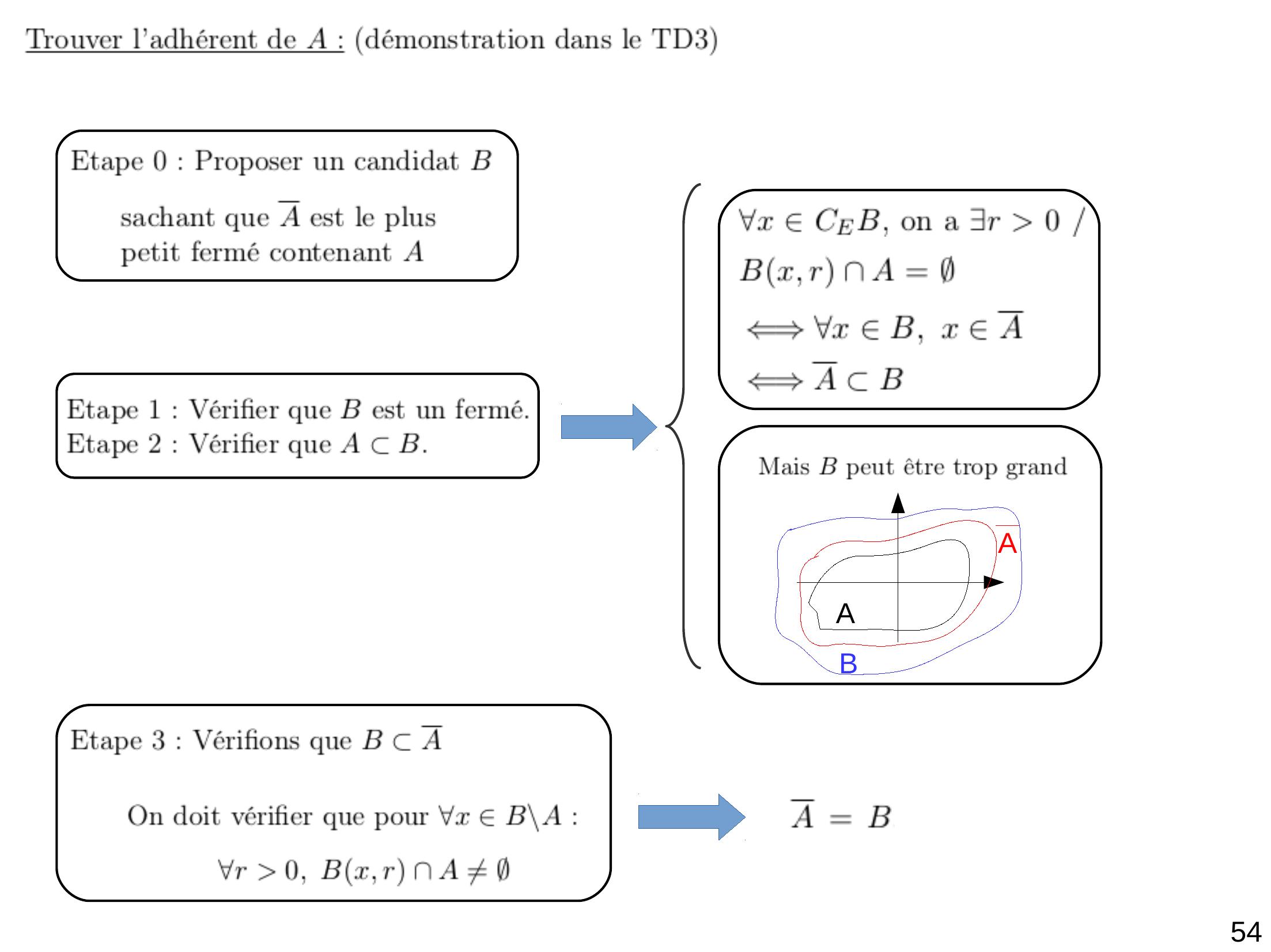
Page 55 : 54ABA
Page 56 : 552020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 57 : 562020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 58 : 572020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 59 : 58402020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 60 : 592020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 61 : 602020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité :
Page 62 : 612020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 63 : 622020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité 42
Page 64 : 632020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 65 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité 64
Page 66 : 652020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité strictement croissante:prop. rang n
Page 67 : 662020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 68 : 672020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 69 : 682020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 70 : 692020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 71 : 702020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 72 : 712020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 73 : 7211-1-1A2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 74 : 732020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 75 : 742020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité 48
Page 76 : 75
Page 77 : 762020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 78 : 772020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 79 : 782020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 80 : 792020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 81 : 802020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 82 : 812020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 83 : 822020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 84 : 832020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 85 : 842020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 86 : 852020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 2 :Espace vectoriel norméPartie 1 : Eléments de topologieIntroduction du chapitre 2Partie 2 : Suites d’éléments d’un EVNa. Généralités b. Suites Convergentes c. Valeurs d’adhérence d. Suites de Cauchy e. Compacité
Page 87 : 862020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 88 : 872020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 89 : 882020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 90 : 892020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 91 : 902020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 92 : 91???2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
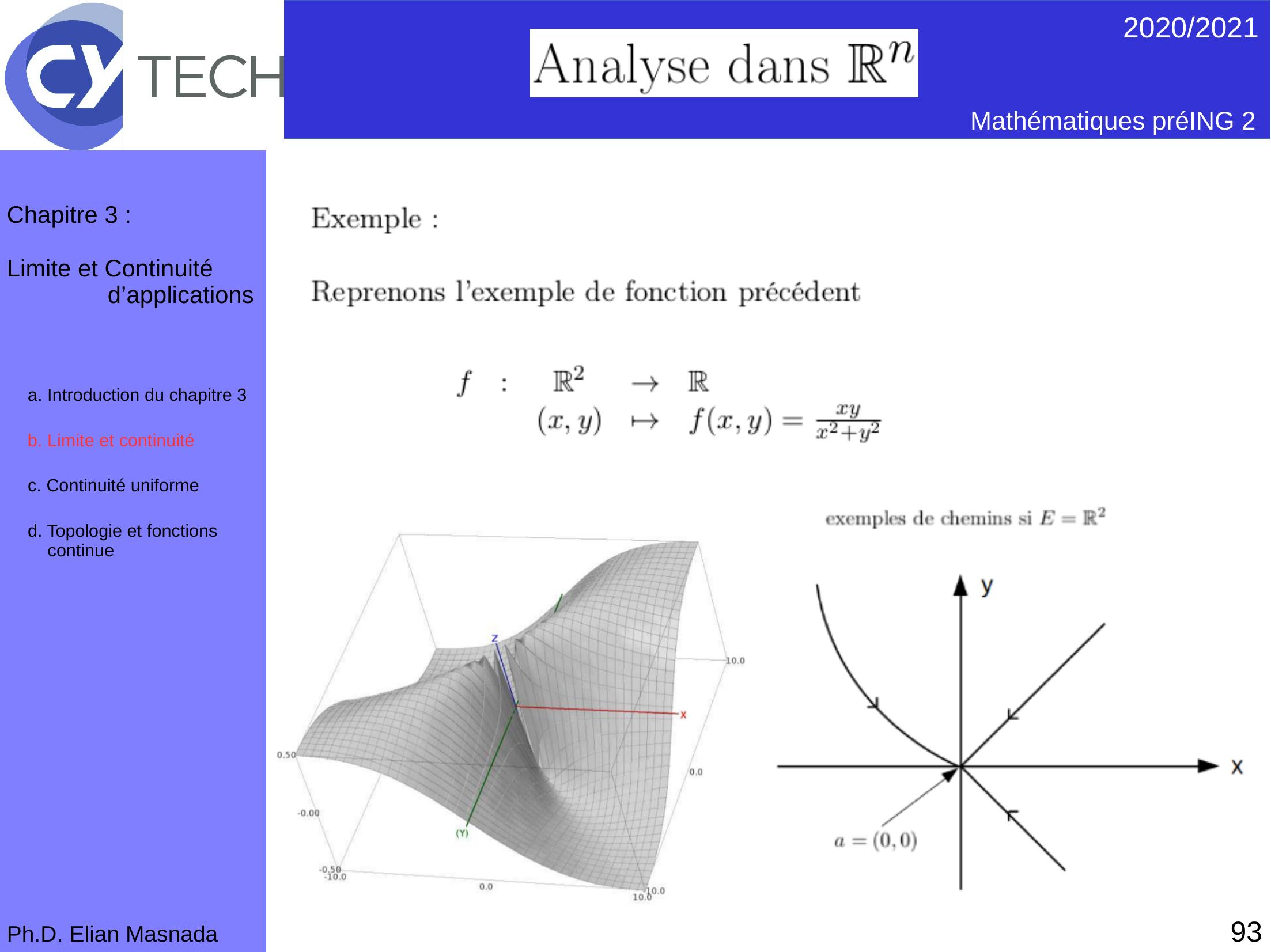
Page 93 : 922020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 94 : 932020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
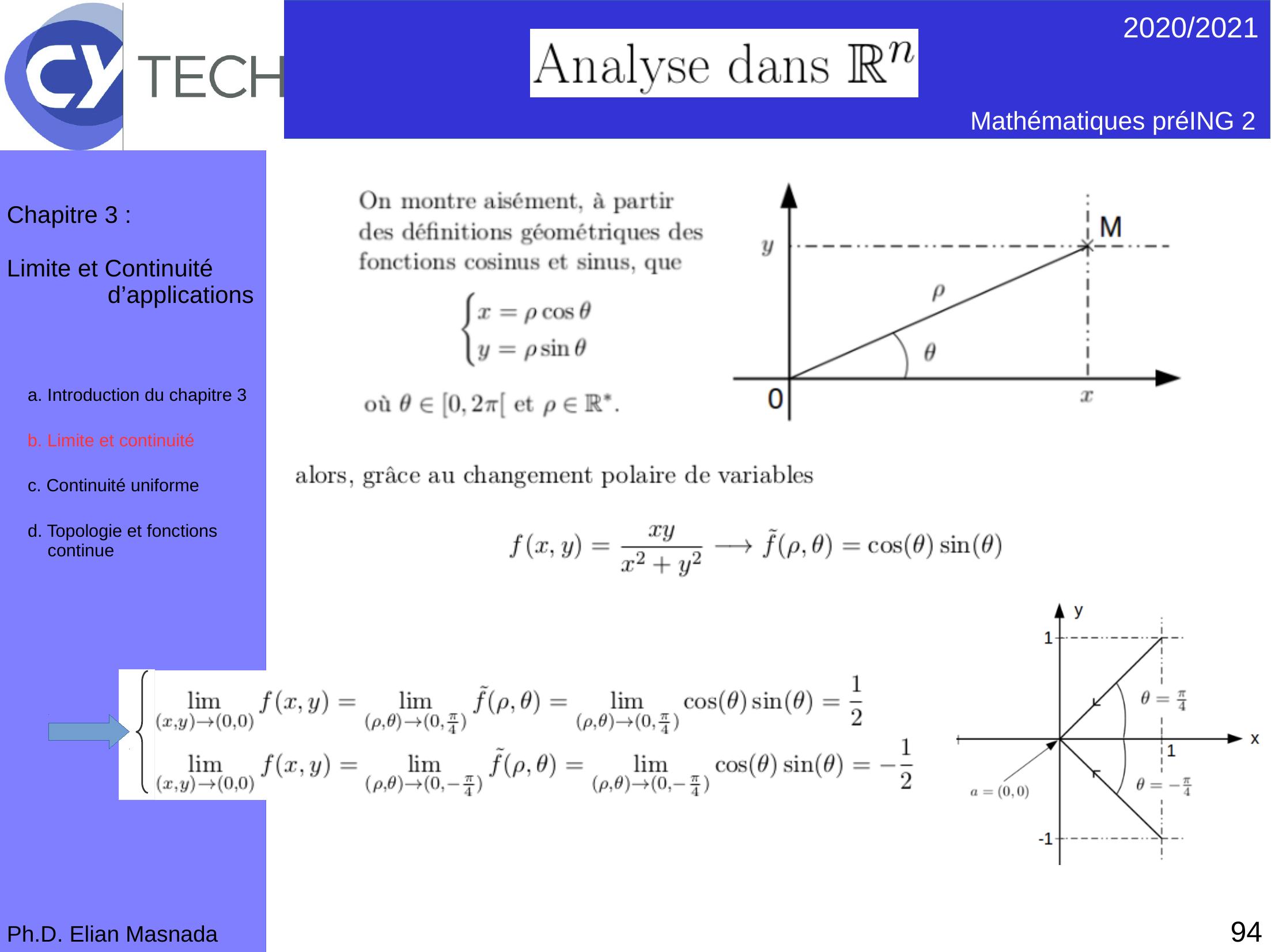
Page 95 : 942020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 96 : 952020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 97 : 962020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 98 : 97?12122020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 99 : 982020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 100 : 992020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 101 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 100
Page 102 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 101
Page 103 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 102
Page 104 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 103
Page 105 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 104Nous allons illustrer la méthodologie sur deux exemples :un qui admet une limite en 0,0 et l’autre pas.
Page 106 : ::111111111105???PAS DE LIMITE
Page 107 : ::2???10622
Page 108 : ::2???10622
Page 109 : 1072020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 110 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 108
Page 111 : 1092020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 112 : 1102020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 113 : 1112020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3
Page 114 : 1122020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 72
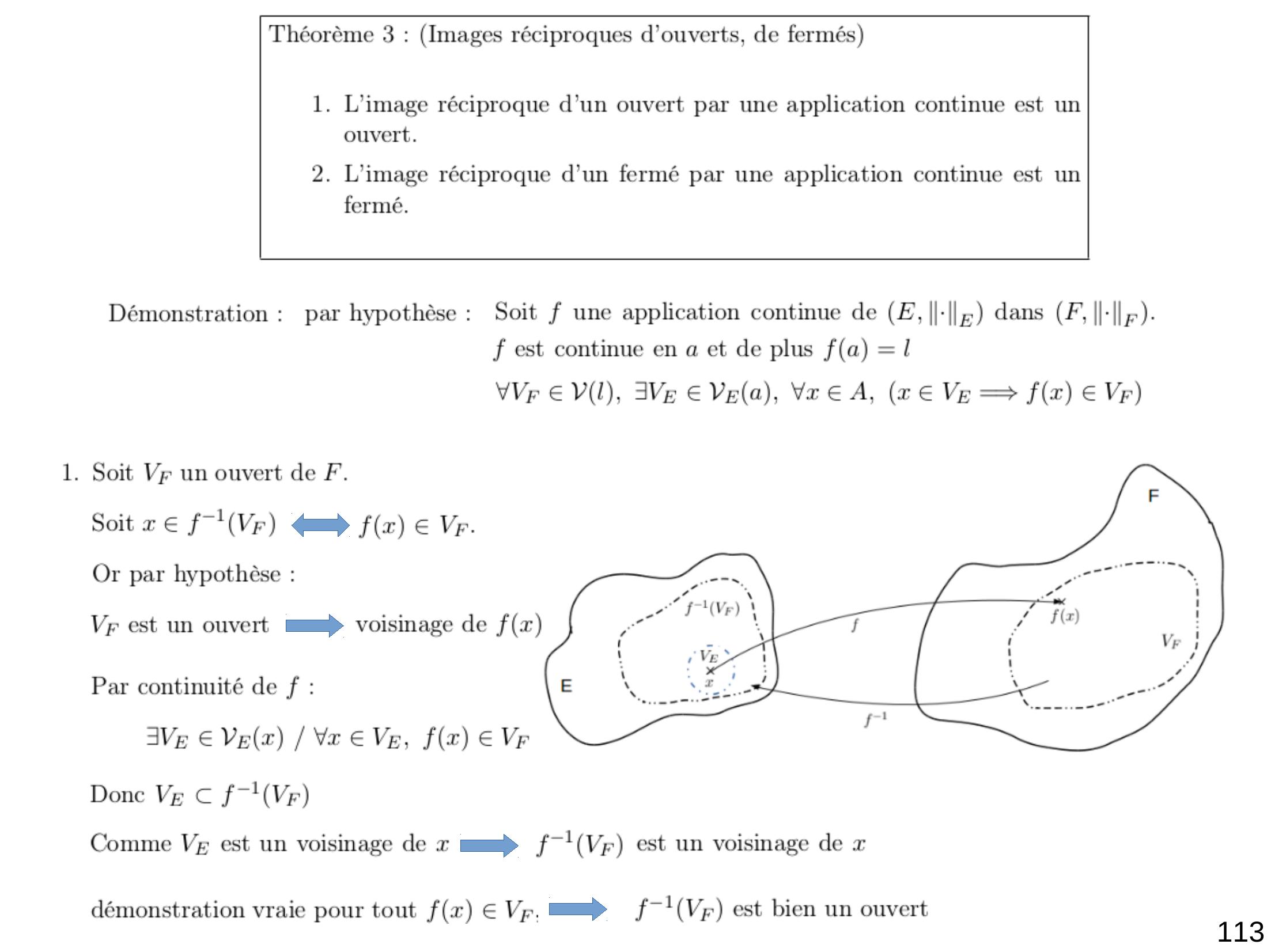
Page 115 : 113
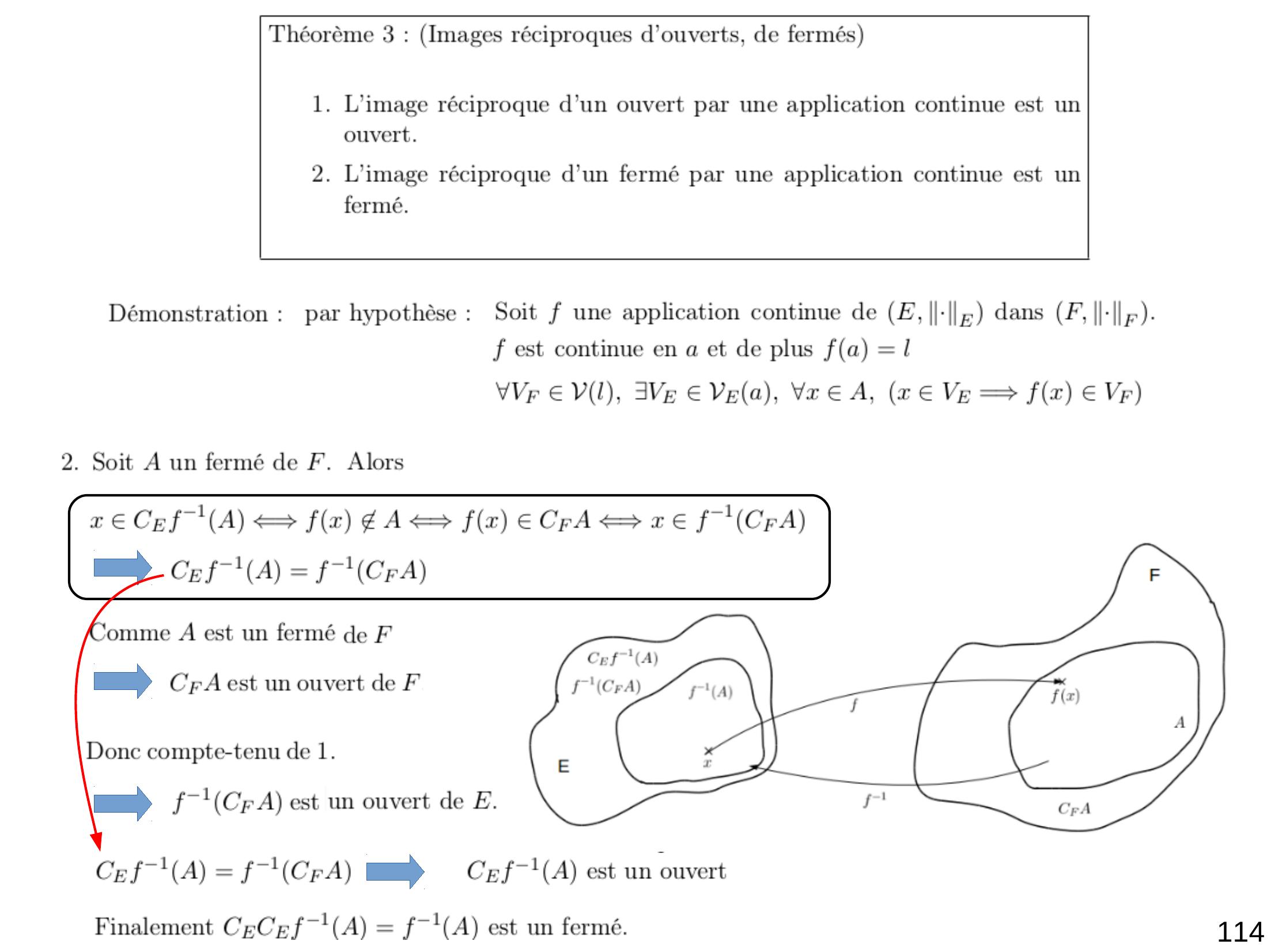
Page 116 : 114
Page 117 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 3 :Limite et Continuité d’applicationsb. Limite et continuité c. Continuité uniformed. Topologie et fonctions continuea. Introduction du chapitre 3 115
Page 118 : 1162020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 119 : 1172020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 120 : 118:2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 121 : 1192020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 122 : 1202020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 123 : 121:Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 124 : 1222020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 125 : 123812020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 126 : 1242020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 127 : 1252020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 128 : 1262020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 129 : 1272020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 130 : 1282020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 131 : 1292020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 132 : 13012020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4 1
Page 133 : 131112020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 134 : 1322020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 135 : 1332020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 136 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4 134
Page 137 : 1352020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 138 : 1362020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 139 : 1372020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 140 : 1382020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 141 : 1392020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4 93
Page 142 : 140
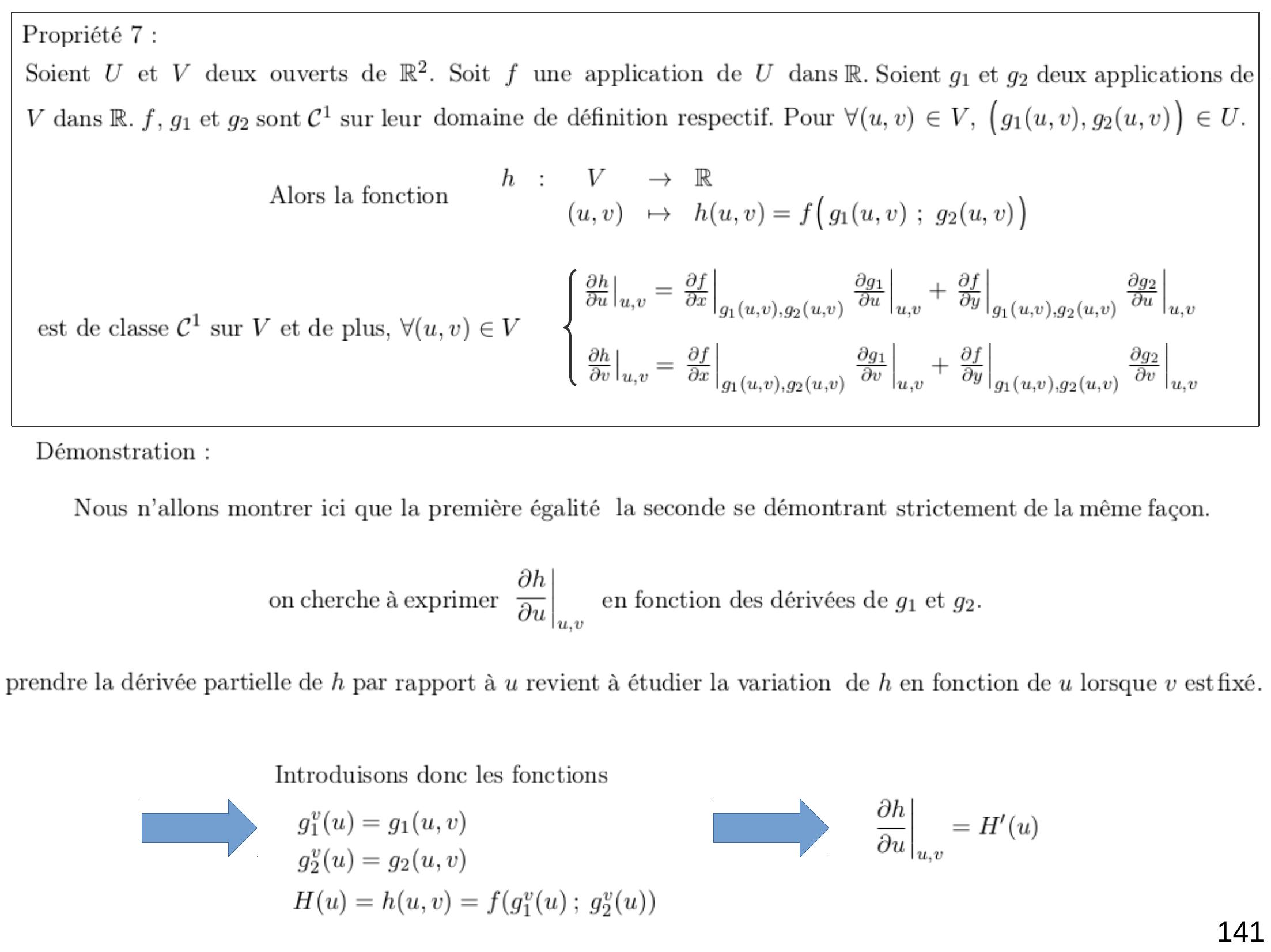
Page 143 : 141
Page 144 : CQFD142
Page 145 : 1432020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 146 : 1442020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 147 : 1452020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 148 : 1462020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 149 : 1472020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 150 : 1482020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 151 : 1492020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 152 : 1502020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 153 : 1512020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 154 : 1522020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 155 : 1532020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 156 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4 154
Page 157 : 155 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 158 : 2019/2020156.Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 159 : 1572020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 160 : 1582020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4 105
Page 161 : 1592020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 162 : 1602020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 163 : 161FAIT A LA MAIN EN CLASSE2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 4 :Calcul différentiel du 1er ordreb. Dérivées partielles du 1er ordre c. Fonctions différentiablesd. EDP du 1er ordre et C^1-difféomorphismea. Introduction du chapitre 4
Page 164 : 1622020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 165 : 1632020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 166 : 1642020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 167 : 1652020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 168 : 16612020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 169 : 1672020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 170 : 1682020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 171 : 1692020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 172 : 1702020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 173 : 1712020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 174 : 1722020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 175 : 1732020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 176 : 174Fait à la main2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 177 : 1752020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 178 : 1762020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 179 : 177Fait à la main en cours2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 180 : 1782020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 181 : 1792020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
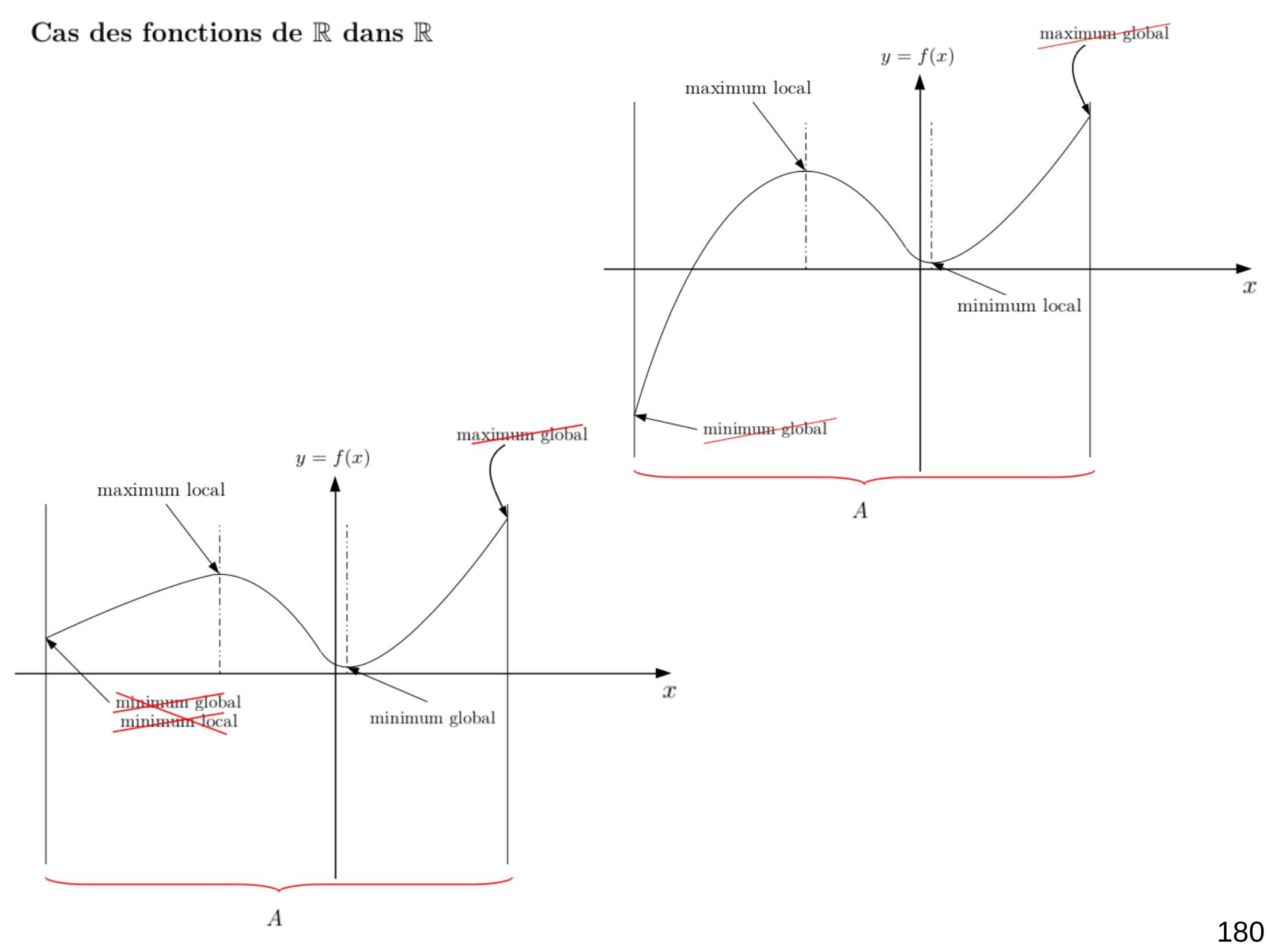
Page 182 : 180
Page 183 : 1812020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 184 : 1822020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 185 : 1832020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 186 : 2020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R184
Page 187 : 1852020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 188 : 1862020/2021 Mathématiques préING 2Ph.D. Elian MasnadaChapitre 5 :Calcul différentiel d’ordre supérieurb. Dérivées partielles d’ordre Supérieur à 1 c. Systèmes d’EDPs d’ordre 1d. EDP d’ordre 2a. Introduction du chapitre 5 e. Extremums de fonctions à valeurs dans R
Page 189 : 187
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189