CM

Télécharger le CM en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Page 1 : Cycle pré-ingénieur 2ème annéeSéries – Notes de coursRomain Dujol2022 – 2023

Page 2 : Table des matières0Comparaison locale des fonctions réelles40.1Négligeabilité. Domination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .40.2Équivalence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .70.3Développements limités au voisinage de 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13Correction des exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15ISéries numériques181Généralités191.1Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .191.1.1Série. Série numérique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .191.1.2Structure algébrique de l’ensemble des séries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .201.2Convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .201.2.1Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .201.2.2Reste d’une série convergente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .211.2.3Condition nécessaire de convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .221.2.4Structure algébrique de l’ensemble des séries convergentes . . . . . . . . . . . . . . . . . . . . . .232Séries numériques à termes réels positifs252.1Lemme fondamental . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .252.2Théorèmes de comparaison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .262.2.1Théorème de majoration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .262.2.2Théorème de minoration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .272.2.3Théorème d’équivalence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .272.3Séries de référence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .282.3.1Séries géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .282.3.2Séries de RIEMANN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .282.3.3Séries de BERTRAND . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .292.4Règles de convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .292.4.1Règle de D’ALEMBERT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .292.4.2Règle de CAUCHY . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .312.4.3Lien entre les deux règles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32Romain Dujol1

Page 3 : 3Séries numériques à termes quelconques333.1Convergence absolue. Semi-convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .333.2Règles de convergence absolue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .343.3Règles de semi-convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .353.3.1Condition de convergence de CAUCHY . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .353.3.2Règle d’ABEL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .363.3.3Séries numériques alternées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .373.4Raisonnement par regroupement de termes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .384Méthodes d’évaluation394.1Calcul de la somme d’une série convergente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .394.1.1Séries géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .394.1.2Par « télescopage » . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .394.2Majoration du reste d’une série convergente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .404.3Comparaison série-intégrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .404.3.1Cas décroissant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .404.3.2Cas croissant . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .43IISuites et séries d’applications455Suites d’applications : convergences465.1Convergence simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .465.2Convergence uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .486Suites d’applications : théorèmes d’interversion516.1Interversion limite-limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .516.2Interversion limite-intégrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .536.3Interversion limite-dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .536.3.1Théorèmes d’interversion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .536.3.2Nécessité des hypothèses du théorème . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .557Séries d’applications : convergences567.1Convergences . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .577.1.1Convergence simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .577.1.2Convergence absolue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .587.1.3Convergence uniforme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .597.1.4Convergence normale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .607.2Théorèmes d’interversion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .657.2.1Interversion somme-limite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .657.2.2Interversion somme-intégrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .667.2.3Interversion somme-dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .67Romain Dujol2

Page 4 : IIISéries entières. Séries de FOURIER698Séries entières : rayon de convergence708.1Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .708.1.1Propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .728.1.2Cas particuliers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .728.2Stabilités opératoires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .738.2.1Structure vectorielle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .738.2.2Produit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .748.2.3Dérivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .748.3Méthodes d’évaluation du rayon de convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .748.3.1Théorèmes de comparaison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .748.3.2Règles de calcul . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .75ADémonstration du théorème 8.2 non exigible77BDémonstration de la proposition 8.4 non exigible799Séries entières : somme et développements809.1Convergence et régularité de la somme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .809.1.1Convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .809.1.2Continuité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .809.1.3Dérivabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .819.2Développement en série entière . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .829.2.1Généralités . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .829.2.2Structure algébrique de l’ensemble des fonctions développables en série entière . . . . . .849.2.3Utilisation des équations différentielles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .85CDémonstration de la théorème 9.1 non exigible87D Développements en série entière en 08810 Séries de FOURIER9010.1 Séries trigonométriques réelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9010.1.1 Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9010.1.2 Convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9010.1.3 Développement en série de FOURIER réel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9110.2 Séries trigonométriques complexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9410.2.1 Définition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9410.2.2 Convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9410.2.3 Développement en série de FOURIER complexe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9510.3 Convergence du développement en série de FOURIER . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9710.3.1 Fonctions périodiques de classe C 1 par morceaux sur R . . . . . . . . . . . . . . . . . . . . . . . .9710.3.2 Théorème de DIRICHLET . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9810.3.3 Théorème de PARSEVAL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .98Romain Dujol3

Page 5 : Thème no 0Comparaison locale des fonctions réelles0.1Négligeabilité. Domination0.1.1NégligeabilitéDéfinition 0.1 Négligeabilité. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I telles que ϕ ne s’annule pas sur I \a.On dit que f est négligeable devant ϕ au voisinage de a si et seulement si il existe une fonction réelleϵ définie sur I telle quelimx→a ϵx = 0etx I , f x = ϵxϕxCette relation se notef = oaϕouf x = ox→aϕxnotation de LANDAUouf a ϕouf x x→a ϕxnotation de HARDYSi il n’y a pas d’ambigüité, on omettra d’indiquer le point a.Remarque. La notation f = oaϕ est impropre, car plusieurs fonctions différentes peuvent être négligeablesdevant une même fonction ϕ au voisinage de a, c’est-à-diref1 = oaϕ,f2 = oaϕavec f1 ̸= f2Exemple.x = ox→+x 2,px = ox→+x 2,sin3 x = ox→0xProposition 0.1 Négligeabilité devant une constante non nulle. Soit I un intervalle de R, a un point de I etf une fonction réelle définie sur I . Alorsf = oa1 ⇐⇒limx→a f x = 0Proposition 0.2 Caractérisation rapide. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I telles que ϕ ne s’annule pas sur I \a.f = oaϕ ⇐⇒limx→af xϕx = 0ϕa = 0 =⇒f a = 0Romain Dujol4

Page 6 : Proposition 0.3 Règles opératoires de oa. Soit I un intervalle de R et a un point de I .Soit f , g et ϕ, ψ des fonctions réelles définies sur I telles que ϕ et ψ ne s’annulent pas sur I \a.1. Si f = oaϕ et g = oaϕ, alors f + g = oaϕ.2. Si f = oaϕ alors pour tout réel λ, λf = oaϕ.3. Si f = oaϕ et g = oaψ, alors f g = oaϕψ.4. Si f = oaϕ et ϕ = oaψ, alors f = oaψ.5. Si h est une fonction réelle définie au voisinage de b R, alors :limx→b hx = af = oaϕ=⇒f ◦h = ob ϕ ◦h0.1.2DominationDéfinition 0.2 Domination. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I telles que ϕ ne s’annule pas sur I \a.On dit que f est dominée par ϕ au voisinage de a si et seulement si il existe une fonction réelle χdéfinie sur I telle queχ est bornée au voisinage de aetx I , f x = χxϕxCette relation se notef = Oaϕouf x = Ox→aϕxnotation de LANDAUouf a ϕouf x x→a ϕxnotation de HARDYSi il n’y a pas d’ambigüité, on omettra d’indiquer le point a.Remarque. La notation f = Oaϕ est impropre, car plusieurs fonctions différentes peuvent être dominées parune même fonction ϕ au voisinage de a, c’est-à-diref1 = Oaϕ,f2 = Oaϕavec f1 ̸= f2Exemple.x = Ox→+x 2,2x 2 = Ox→+x 2,x 2 = Ox→0xProposition 0.4 Domination devant une constante non nulle. Soit I un intervalle de R, a un point de I et fune fonction réelle définie sur I . Alorsf = Oa1 ⇐⇒f est bornée au voisinage de aProposition 0.5 Caractérisation rapide. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I telles que ϕ ne s’annule pas sur I \a.f = Oaϕ ⇐⇒fϕ est bornée au voisinage de aϕa = 0 =⇒f a = 0Romain Dujol5

Page 7 : Proposition 0.6 Règles opératoires de Oa. Soit I un intervalle de R et a un point de I .Soit f , g et ϕ, ψ des fonctions réelles définies sur I telles que ϕ et ψ ne s’annulent pas sur I \a.1. Si f = Oaϕ et g = Oaϕ, alors f + g = Oaϕ.2. Si f = Oaϕ alors pour tout réel λ, λf = Oaϕ.3. Si f = Oaϕ et g = Oaψ, alors f g = Oaϕψ.4. Si f = Oaϕ et ϕ = Oaψ, alors f = Oaψ.5. Si h est une fonction réelle définie au voisinage de b R, alors :limx→b hx = af = Oaϕ=⇒f ◦h = Ob ϕ ◦hProposition 0.7 Régles opératoires communes. Soit I un intervalle de R et a un point de I .Soit f , g et ϕ, ψ des fonctions réelles définies sur I telles que ϕ et ψ ne s’annulent pas sur I \a.1. Si f = oaϕ alors f = Oaϕ.2. Si f = Oaϕ et g = oaψ, alors f g = oaϕψ.3. Si f = oaϕ et ϕ = Oaψ, alors f = oaψ.4. Si f = Oaϕ et ϕ = oaψ, alors f = oaψ.0.1.3Comparaisons de référenceProposition 0.8 Puissances. Soit α et β deux nombres réels. Alorsα β ⇐⇒x α = ox→+x βα β ⇐⇒x α = ox→0+x βProposition 0.9 Comparaisons logarithmes/puissances. Pour tout réel α, on a :β 0, ln xα = ox→+x βγ 0, ln xα = ox→0+x γProposition 0.10 Comparaisons puissances/exponentielles. Pour tout réel α, on a :a 1,+, x α = ox→+a x a 0,1, a x = ox→+x αRomain Dujol6

Page 8 : 0.2ÉquivalenceOn rappelle ici l’intérêt des équivalents pour déterminer rapidement certaines limites dans le cas de formesindéterminées... à condition de les utiliser correctement!0.2.1DéfinitionDéfinition 0.3 Équivalence. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I qui ne s’annulent pas sur I \a.On dit que f est équivalente à ϕ au voisinage de a si et seulement si il existe une fonction réelle ηdéfinie sur I telle quelimx→a ηx = 1etx I , f x = ηxϕxCette relation se notef a ϕouf x x→a ϕxSi il n’y a pas d’ambigüité, on omettra d’indiquer le point a.Exemple.x 2 + xx→+x 2,sin x x→0 xProposition 0.11 Équivalence devant une constante non nulle. Soit I un intervalle de R, a un point de I etf une fonction réelle définie sur I . AlorsℓR, f a ℓ⇐⇒limx→a f x = ℓRemarque. f a 0 impliquerait que f s’annule sur I , ce qui est impossible par hypothèse.f a 0 N’A AUCUN SENS!Proposition 0.12 Caractérisation rapide. Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I qui ne s’annulent pas sur I \a.f a ϕ ⇐⇒limx→af xϕx = 1ϕa = 0 =⇒f a = 00.2.2Règles opératoiresCas généralProposition 0.13 Règles opératoires de a . Soit I un intervalle de R et a un point de I .Soit f , g et ϕ, ψ des fonctions réelles définies sur I qui ne s’annulent pas sur I \a.1. Si f a ϕ et g a ψ, alors f g a ϕψ.2. Si f a ϕ alors 1f a1ϕ .3. Si f a ϕ et g a ψ, alors fg aϕψ.Romain Dujol7

Page 9 : 4. Si f a ϕ et ϕ a ψ, alors f a ψ.5. Si f et ϕ sont positives sur I et f a ϕ, alors f α a ϕα pour tout α R6. Si h est une fonction réelle définie au voisinage de b R, alors : limx→b hx = af a ϕ=⇒f ◦h b ϕ ◦hAdditionRemarque. « Si f a ϕ et g a ψ, alors f + g a ϕ + ψ » est fausse dans le cas géneral.Exemple. Au voisinage de a = 0,x + x 2 0 xx + x 2 0 x. Maisx + x 2 + x + x 2 = 2x 2 ̸00 = x + xON NE PEUT PAS ADDITIONNER DES ÉQUIVALENTS N’IMPORTE COMMENT!On peut toutefois isoler certains cas où cela est possible.Proposition 0.14 Addition d’équivalents. Soit I un intervalle de R et a un point de I .Soit f , g et ϕ, ψ des fonctions réelles définies sur I telles que ϕ et ψ ne s’annulent pas sur I \a et que :f a ϕetg a ψ1. Si ϕ et ψ sont de même signe constant au voisinage de a, alors f + g a ϕ + ψ.2. Si ϕ : x 7→λx α et ψ : x 7→µx β, alors f + g a ϕ + ψ sauf si α = β et λ + µ = 0.Composition par la gaucheLa propriété 5 de la proposition 0.13 assure qu’il est possible de composer les équivalences par la droite.Remarque. La proposition« Si h est une fonction réelle définie au voisinage de ϕa, et f a ϕ alors h ◦f a h ◦ϕ. »est fausse en général.Exemple. Au voisinage de a = +, x + 1x→+x. Mais e x+1̸x→+e x .Proposition 0.15 Composition à gauche par l’exponentielle.Soit I un intervalle de R et a un point de I .Soit f et ϕ deux fonctions réelles définies sur I qui ne s’annulent pas sur I \a. Alorsexp◦f a exp◦ϕ ⇐⇒lima f ϕ = 0Romain Dujol8

Page 10 : Proposition 0.16 Composition à gauche par le logarithme.Soit I un intervalle de R et a un point de I et f et ϕ deux fonctions réelles définies sur I .Si ϕ est strictement positive sur I \a et admet une limite ℓR+\1, alorsf a ϕ =⇒ln◦f a ln◦ϕExemple. Au voisinage de a = 0, 1 + x x→0 1 + 2x. Mais x x→0 ln1 + x ̸x→0ln1 + 2x x→0 2x.ON NE PEUT PAS PRENDRE LE LOGARITHME D’ÉQUIVALENTS N’IMPORTE COMMENT!0.2.3Lien avec oa et OaProposition 0.17. Soit I un intervalle de R et a un point de I .Soit f , ϕ et ψ des fonctions réelles définies sur I qui ne s’annulent pas sur I \a.1. Si f = oaϕ et ϕ a ψ, alors f = oaψ.2. Si f a ϕ et ϕ = oaψ, alors f = oaψ.3. f a ϕ ⇐⇒f ϕ = oaϕ4. Si f = Oaϕ et ϕ a ψ, alors f = Oaψ.5. Si f a ϕ et ϕ = Oaψ, alors f = Oaψ.6. Si f a ϕ alors f = Oaϕ et ϕ = Oaf .Remarque. « Si f = Oaϕ et ϕ = Oaf alors f a ϕ » est fausse en général.Exemple. Au voisinage de a = +, x = Ox→+2x et 2x = Ox→+x. Mais 2x̸x→+x.0.2.4Équivalents usuelsProposition 0.18 Cas simples de calcul d’équivalents.1. Tout polynôme est équivalent à son terme de plus haut degré en +ou .Tout polynôme est équivalent à son terme de plus bas degré en 0.2. Toute fraction rationnelle est équivalente au quotient de ses termes de plus haut degré en ±.Toute fraction rationnelle est équivalente au quotient de ses termes de plus bas degré en 0.3. Si f est dérivable en a et f ′a ̸= 0, alors f x f a x→a f ′a · x a.4. Si f admet un développement limité au voisinage de 0, alors f est équivalente au terme non nul de plusfaible ordre en 0.Exemple.1. x 4 + x 2 + 2xx→+x 4x 4 + x 2 + 2x x→0 2x2.x 3 xx 4 + x 2 + 2xx→+x 3x 4 = 1xx 3 xx 4 + x 2 + 2xx→0x2x = 123. Avec f = exp en a = 0, e x 1 = expx exp0 x→0 exp′0 · x 0 = x.4. sin x = x x 36 + ··· x→0 xRomain Dujol9

Page 11 : Théorème 0.1 Équivalents des fonctions usuelles.e x 1 x→0 xln1 + x x→0 xsin x x→0 xarcsin x x→0 xsh x x→0 xtan x x→0 xarctan x x→0 xth x x→0 x1 cos x x→0x 22ch x 1 x→0x 22Pour tout réel α fixé, 1 + xα 1 x→0 αxRemarque. La plupart des équivalents usuels sont exprimés au voisinage de 0. Pour obtenir des équivalentsau voisinage d’une autre valeur finie a, il suffit d’effectuer un changement de variable du type x = a ± h avech au voisinage de 0.Romain Dujol10

Page 12 : Exercice. Déterminer les limites suivantes :1. limx→0ln1 + 2tan xsin x2.limx→+1 + 1x‹x3.limx→π/4tan xcotan4xSolution.1. Comme limx→02tan x = 0 et ln1 + X X →0 X , on a ln1 + 2tan x x→0 2tan x.Comme tan x x→0 x, il vient que ln1 + 2tan x x→0 2x.De plus sin x x→0 x : on conclut alors que ln1 + 2tan xsin xx→02xx = 2, puis que limx→0ln1 + 2tan xsin x= 2 .2. Passons au logarithme : ln1 + 1x‹x= x ln1 + 1x‹.Commelimx→+1x = 0 et ln1 + X X →0 X , on a ln1 + 1x‹x→+1x . Doncln1 + 1x‹x= x ln1 + 1x‹x→+x · 1x = 1On conclut quelimx→+ln1 + 1x‹x= 1, puis exp étant continue en 1limx→+1 + 1x‹x= e .3. On effectue le changement de variable x = π4 h et on passe au logarithme :lntan xcotan4x= lntan xtan4x =lntanπ4 htanπ 4hÉtudions chacun des termes :· tanπ4 h= 1 tanh1 + tanh , donc lntanπ4 h= ln1 tanh ln1 + tanh. Orln1 tanh h→0 tanh h→0 hetln1 + tanh h→0 tanh h→0 hOn est dans les conditions de la propriété 2 de la proposition 0.14, donclntanπ4 h= ln1 tanh ln1 + tanh h→0 2h· tanπ 4h = tan4h h→0 4hDonc lntan xcotan4x=lntanπ4 htanπ 4hh→02h4h = 12.On conclut que limx→π/4lntan xcotan4x= 12, puis exp étant continue en 1/2 :limx→π/4tan xcotan4x = e 1/2 = peRomain Dujol11

Page 13 : 0.3Développements limités au voisinage de 0e x = 1 + x 11! + x 22! + ··· + x nn! + ox nch x = 1 + x 22! + x 44! + ··· + x 2n2n! + ox 2n+1sh x = x + x 33! + x 55! + ··· +x 2n+12n + 1! + ox 2n+2th x = x x 33 + 2x 515 17x 7315 + ox 8cos x = 1 x 22! + x 44! + ··· + 1n x 2n2n! + ox 2n+1sin x = x x 33! + x 55! + ··· + 1nx 2n+12n + 1! + ox 2n+2tan x = x + x 33 + 2x 515 + 17x 7315 + ox 811 x = 1 + x + x 2 + ··· + x n + ox n11 + x = 1 x + x 2 + ··· + 1n x n + ox n1 + xα = 1 + αx + αα 12!x 2 + ··· + αα 1···α n + 1n!x n + ox np1 + x = 1 + x2 x 28 + ··· + 1n1 1 · 3 · 5···2n 32nn!x n + ox np1 x = 1 x2 x 28 + ··· 1 · 3 · 5···2n 32nn!x n + ox n1p1 + x= 1 x2 + 3x 28+ ··· + 1n 1 · 3 · 5···2n 12nn!x n + ox nln1 x = x + x 22 + x 33 + ··· + x nn + ox nln1 + x = x x 22 + x 33 + ··· + 1n1 x nn + ox narctan x = x x 33 + x 55 + ··· + 1n x 2n+12n + 1 + ox 2n+2arcsin x = x + 12 · x 33 + 38 · x 55 + ··· + 1 · 3 · 5 · ··· ·2n 12nn!· x 2n+12n + 1 + ox 2n+2Romain Dujol12

Page 14 : Chapitre 0. Comparaison locale des fonctions réelles — TDExercice 0.1. Calculer les limites suivantes :1. limt →1t t 11 t + ln1 + t 2. limt →1lntt 13.limx→+xpxpx xExercice 0.2. Calculer les limites suivantes :1. limx→0+11 x x +1x ln x2.limx→+Æx + px pxExercice 0.3. Déterminer des équivalents simples de :1. x + sin x en 0, puis en +2. x sin x en 0, puis en +3. lntan x en 0+, puis en π44. 1x 1tan x en 05.px 2 + x 3px 3 + 2x 2 en 0+, puis en +Exercice 0.4. Déterminer les équivalents en 0 de :1. f1 : x 7→ln1 + x 2x arctan x2. f2 : x 7→1 ch x1 cos x3. f3 : x 7→e x cos x xx ln1 + x4. f4 : x 7→sin2 x x ln1 + xe x + cos x sin x 2Romain Dujol13

Page 15 : Exercice 0.5. Déterminer les équivalents en +de :1. un =e 1/n cos 1n1 vt1 1n22. un =1pn pn sin 1n3. un =lncos anlncos bn‹ avec a réel et b réel non nul4. un = e 1/n e 1/n+15. un = arctann arccos 1n6. un =lnn + 1n + 2‹sin n + 1n2 + 2‹7. un = e ·pn2 n + 1 n1 + 1n‹nExercice 0.6. Pour tout entier naturel supérieur ou égal à deux, on note un =•ln1 + nlnn˜n lnn.1. Déterminer un équivalent de lnun en +.2. En déduirelimn→+un.Romain Dujol14

Page 16 : Chapitre 0. Comparaison locale des fonctions réelles — TD CorrigéExercice 0.1.1.t t 11 t + ln1 + t →t →111 11 1 + ln1 + 1 =0ln2 = 02.lntt 1 = lnt ln1t 1→t →1 ln′1 = 11 = 13. ln xpxpx x = px ln x x lnpx = px ln x x2 ln x =px x2ln xx→+x2 ln xDonclimx→+ln xpxpx x = puis, par continuité de exp sur R,limx→+xpxpx x =limX →e X = 0.Exercice 0.2.1.11 x x +1x ln x =11 e x ln x +1x ln x =11 e y + 1y avec y = x ln xComme limx→0+ x ln x = 0, il vient que x 7→11 x x +1x ln x admet une limite en 0+ si et seulement si y 7→11 e y + 1y admet une limite en 0auquel cas, leurs valeurs sont égales.On a11 e y + 1y = y + 1 e y1 e y y , puis :• y + 1 e y = y + 1 1 + y + y 22 + oy 2= y 22 + oy 2y →0y 22• 1 e y yy →0y · y = y 2D’où11 e y + 1yy →0+y 2/2y 2= 12 puis limx→0+11 x x +1x ln x = limy →011 e y + 1y = 12.2.Æx + px px =vtx1 + 1px‹px = px1 + 1px‹1/2px= px1 + 1px‹1/21x→+px ·12px = 12.Donclimx→+Æx + px px = 12.Remarque. On peut aussi passer par l’expression conjuguée.Exercice 0.3.1. En 0, x + sin x x→0 x + x = 2x.En +, x + sin x = x + oxx→+x.2. En 0, x sin x = x x x 36 + ox 3= x 36 + ox 3 x→0x 36 .En +, x sin x = x oxx→+x.3. En 0+, tan xx→0+ x, donc lntan xx→0+ ln x.En π4 , on note f : x 7→lntan x. Alors fπ4= 0 et f ′x = tan′xtan x= 1 + tan2 xtan x.Donc f ′π4= 1 + 121= 2 ̸= 0 et lntan x = f x fπ4x→π/4 f ′π4·x π4= 2x π4.Remarque. On peut aussi appliquer la formule de TAYLOR-YOUNG à l’ordre un pour ln◦tan en π/4Romain Dujol15

Page 17 : 4. On a 1x 1tan x = tan x xx · tan x , puis :• tan x x =x + x 33 + ox 3x = x 33 + ox 3 x→0x 33• x · tan x x→0 x · x = x 2D’où 1x 1tan xx→0x 3/3x 2= x3 .5. En 0+,px 2 + x 3px 3 + 2x 2x→0+px 3p2x 2 = x 1/2 3p2x 2/3x→0+ x 1/2 = px.En +,px 2 + x 3px 3 + 2x 2 =vtx 2 ·1 + 1x‹3vtx 3 ·1 + 2x‹= x ·1 + 1x‹1/21 + 2x‹1/3= x ·•1 + 12x + o 1x‹‹1 + 23x + o 1x‹‹˜= x ·•12 23‹ 1x + o 1x‹˜= 16 + o1x→+16Exercice 0.4.1. f1x x→0x 2x · x = 12. f2x x→0x 2/2x 2/2 = 13.• e x cos x x =1 + x + x 22 + ox 21 x 22 + ox 2x = x 2 + ox 2 x→0 x 2• x ln1 + x = x x x 22 + ox 2= x 22 + ox 2 x→0x 22D’où f3x x→0x 2x 2/2 = 2.4.• sin2 x =x + ox 22 = x 2 1 + ox2 = x 2 1 + ox = x 2 + ox 3x ln1 + x = x ·x x 22 + ox 2= x 2 x 32 + ox 3Donc sin2 x x ln1 + x = x 32 + ox 3 x→0x 32 .• e x + cos x sin x 2 =1 + x + x 22 + x 36 + ox 3+1 x 22 + ox 3x x 36 + ox 32 = x 33 + ox 3D’où f4x x→0x 3/2x 3/3 = 32.Exercice 0.5. On utilisera le changement de variable h = 1n : ainsi rechercher l’équivalent de un lorsque ntend vers l’infini revient à le chercher lorsque h tend vers 0+.ATTENTION. Il faut alors reconvertir le résultat obtenu en h en remplaçant h par son expression réelle, i.e. 1n .1.• e h cosh = 1 + h + oh 1 + oh = h + ohh→0+ h• 1 p1 h2 = 1 1 h21/2h→0+ 12h2 = h22D’où unh→0+hh2/2 = 2h , c’est-à-dire un 2n.Romain Dujol16

Page 18 : 2.ph 1phsinh =ph 1phh h36 + oh3=ph ph h5/26+ oh5/2= h5/26+ oh5/2h→0+h5/26 .Donc un 16n5/2 .3. Comme limh→0+ cosah = 1, il vient que lncosahh→0+ cosah 1h→0+ah22.De même, lncosb hh→0+b h22. D’où un ah2/2bh2/2 = a 2b 2 .4. e 1/n e 1/n+1 = e 1/n+1 e 1/n1/n+1 1= e 1/n+1 ”e1nn+1 1—•limn→+e 1/n+1 = 1, donc e 1/n+1 1• e1nn+1 1 1nn + 1 1n · n = 1n2D’où un 1n2 .5. arctan 1h arccosh =π2 arctanhπ2 arcsinh= arcsinh arctanh=h + h36 + oh3h h33 + oh3= h32 + oh3h→0+h32 .Donc un 12n3 .6.• Commelimn→+n + 1n + 2 = 1, il vient que ln n + 1n + 2 n + 1n + 2 1 =1n + 2 1n .• Comme n + 1n2 + 2 nn2 = 1n , on alimn→+n + 1n2 + 2 et sin n + 1n2 + 2 n + 1n2 + 2 1n .D’où un 1/n1/n = 1.7. e ·pn2 n + 1 = e ·vtn21 1n + 1n2‹= e n•1 1n + 1n2˜1/2= e n1 12n +12n2 181n + 1n2‹2+ o 1n2‹= e n•1 12n +38n2 + o 1n2‹˜n1 + 1n‹n= n exp•n ln1 + 1n‹˜= n exp•n 1n 12n2 +13n3 + o 1n3‹‹˜= n exp•1 12n +13n2 + o 1n2‹˜= e n exp•12n +13n2 + o 1n2‹˜= e n1 12n +13n2 + 1212n +13n2‹2+ o 1n2‹= e n•1 12n +1124n2 + o 1n2‹˜D’où e ·pn2 n + 1 n1 + 1n‹n= e n• 112n2 + o 1n2‹˜e n · 112n2 = e12n .Exercice 0.6.1. 1 + n n, donc ln1 + n lnn puislimn→+ln1 + nlnn= 1 et :lnun = n lnn ln•ln1 + nlnn˜n lnn•ln1 + nlnn1˜= n lnn · ln1 + n lnnlnn= n ln1 + nn‹= n ln1 + 1n‹n · 1n2. Donclimn→+lnun = 1 puis, par continuité de exp en 1,limn→+un = e 1 = e .Romain Dujol17

Page 19 : Première partieSéries numériquesRomain Dujol18

Page 20 : Thème no 1GénéralitésDans tout le chapitre, E ,· désigne un K-espace vectoriel normé avec K = R ou C.1.1Définition1.1.1Série. Série numériqueDéfinition 1.1 Série. Soit unnN une suite d’éléments de E .La série de terme général un, notéePnNun ouPn0un est le couple unnN,SnnN où la suite SnnNdéfinie par :n N, Sn =nXk=0ukun est le n ème terme ou terme général dePnNun. Sn est la somme partielle d’ordre n dePnNun.Si la suite unnn0 est définie à partir d’un certain rang n0 N, on définit de la même manière la sérienumériquePnn0un avec Sn =nXk=n0uk pour tout n n0.Définition 1.2 Série numérique.Une série numérique est une série à valeurs dans E = K muni de la valeur absolue · .Exemple Séries numériques réelles.1.PnNn est la série de terme général n. La nème somme partielle est calculable : Sn =nXk=0k = nn + 12.2. Soit x un nombre réel.PnNx n est la série de terme général x n. La nème somme partielle est calculable :Sn =nXk=0x k =1 x n+11 xsi x ̸= 1n + 1si x = 13.Pn11n est la série de terme général 1n et la nème somme partielle est Sn =nXk=11k .Romain Dujol19

Page 21 : 1.1.2Structure algébrique de l’ensemble des sériesDéfinition 1.3 Opérations. On munit l’ensemble S des séries à valeurs dans E de deux lois :— la loi interne + :S × S→S PnNun,PnNvn7→PnNun + vn;— la loi externe · :K × S→Sλ,PnNun7→PnNλ · un.Théorème 1.1 Structure algébrique de l’ensemble des séries.L’ensemble des séries à valeurs dans E muni des lois + et · vues en définition 1.3 est un K-espacevectoriel.1.2Convergence1.2.1DéfinitionDéfinition 1.4 Série convergente.Une sériePnNun à valeurs dans E converge si et seulement la suite SnnN de ses sommes partiellesconverge dans E ,· .Auquel cas, on définit la somme de la sériePnNun, notée+Xn=0un, par+Xn=0un = limn→+Sn.Une série diverge si et seulement si elle ne converge pas.Deux séries sont dites de même nature si et seulement si elles convergent toutes les deux ou si ellesdivergent toutes les deux.Exemple avec E = R.• La suite des sommes partielles dePnNn a pour terme général Sn =nXk=0k = nn + 12.Donc SnnN diverge et la sériePnNn diverge.• La suite des sommes partielles dePnNx na pour terme général Sn=1 x n+11 xsi x ̸= 1n + 1si x = 1qui ne converge que si x 1.Donc si x 1, la sériePnNx n converge et+Xn=0x n =11 x . Sinon, elle diverge.Romain Dujol20

Page 22 : Proposition 1.1 Changement d’indice de départ.SoitPnNun une série à valeurs dans E et n0 un entier naturel. AlorsPn0un etPnn0un sont de même nature.Si de plus, les deux séries convergent, alors+Xn=0un =n01Xn=0un ++Xn=n0un.Démonstration. Pour tout entier n supérieur ou égal à n0,nXk=0uk =n01Xk=0uk +nXk=n0uk.• SiPn0un converge, alors la suite de terme généralnXk=0uk converge. On en déduit que la suite de terme généralnXk=n0uk =nXk=0uk n01Xk=0uk converge aussi, puis quePnn0un converge.• SiPnn0un converge, alors la suite de terme généralnXk=n0uk converge. On en déduit que la suite de terme généralnXk=0uk converge, puis quePn0un converge.Remarque. L’indice de départ n’a donc aucune influence sur la convergence d’une série numérique. Lorsquel’étude d’une série se réduit à celle de sa convergence, on pourra noter la série étudiéePnun ouPun lorsqu’iln’y a pas d’ambigüité.IMPORTANT. Tous les résultats de convergence et/ou divergence de cette partie restent donc valables si on changel’indice de départ des séries numériques dans leur énoncé.1.2.2Reste d’une série convergenteDéfinition 1.5 Reste d’ordre n. SoitPnNun une série à valeurs dans E convergente.On appelle reste d’ordre n dePnNun la somme de la sériePkn+1uk, c’est-à-dire+Xk=n+1uk.ATTENTION.Il n’existe pas de reste pour une série divergente!Remarque. Pour simplifier l’écriture, on note souvent :— Sn la somme partielle d’ordre n ;— S la somme lorsque la série numérique converge;— Rn le reste d’ordre n lorsque la série numérique converge.On a alors Rn = S Sn , c’est-à-dire+Xk=n+1uk =+Xk=0uk nXk=0ukProposition 1.2 Convergence du reste.SoitPnNun une série numérique convergente et RnnN la suite de ses restes d’ordre n.Alors RnnN converge vers 0E .Démonstration. CommePnNun converge, la suite SnnN des sommes partielles converge vers la somme S.Donc RnnN = S SnnN converge vers S S = 0E .Romain Dujol21

Page 23 : 1.2.3Condition nécessaire de convergenceThéorème 1.2 Condition nécessaire de convergence.Si la sériePnNun à valeurs dans E converge, alors unnN converge vers 0E .Démonstration. SoitPnNun une série convergente et SnnN la suite de ses sommes partielles.Alors SnnN converge vers une limite notée S.n 1, un = Sn Sn1 : donc unnN converge et limn→+un = S S = 0E .Corollaire Condition nécessaire de convergence. Soit unnN une suite d’éléments de E .Si la suite unnN ne converge pas vers 0E , alorsPnNun diverge.IMPORTANT. Dans un tel cas, on dit quePnNun diverge grossièrement.Exemple Séries numériques réelles.1. Commelimn→+n = +,PnNn diverge grossièrement.2. Soit x un nombre réel.— si x 1, alors x nnN diverge : doncPnNx n diverge grossièrement;— si x = 1, alors x nnN diverge : doncPnNx n diverge grossièrement;— si x = 1, alors x nnN converge vers 1 : doncPnNx n diverge grossièrement;— si x 1,PnNx n converge et x nnN converge vers 0.Remarque. Il ne s’agit que d’une condition nécessaire de convergence.Il existe des sériesPnNun divergentes telles que unnN converge vers zéro.Théorème 1.3 Série harmonique.On appelle série harmonique la série numériquePn11n .Pour tout entier naturel non nul n, on note Hn sa nème somme partielle, c’est-à-dire Hn =nXk=11k .La série harmonique diverge.Démonstration. Supposons par l’absurde quePn11n converge. Alors Hnn1 converge vers une limite H .Soit n un entier naturel non nul. Alors pour tout k Jn,2nK, 12n 1k 1n . Donc :H2n Hn =2nXk=n+11k 2nXk=n+112n = n 12n = 12En passant à la limite dans l’inégalité, il vient que 0 = H H 12, ce qui est impossible.On en conclut que doncPn11n diverge.Romain Dujol22

Page 24 : 1.2.4Structure algébrique de l’ensemble des séries convergentesCas généralThéorème 1.4. L’ensemble Sc des séries à valeurs dans E convergentes est un sous-espace vectoriel del’espace vectoriel des séries à valeurs dans E cf. théorème 1.1.De plus, l’applicationSc→EPnNun7→+Xn=0unest une application linéaire sur Sc.Remarque. Donc :— la somme de deux séries convergentes est convergente;— la somme d’une série convergente et d’une série divergente est divergente.ATTENTION. Il n’existe pas de résultat général pour la somme de deux séries divergentes. En effet :—PnN1 etPnN1 sont grossièrement divergentes etPnN1 + 1 =PnN0 est convergente;—PnN1 est grossièrement divergente etPnN1 + 1 =PnN2 est grossièrement divergente.+conv.div.conv.conv.div.div.div.???Cas des séries numériquesThéorème 1.5 Cas E = C.Une série numérique à valeurs complexesPnNun converge si et seulement si les séries réellesPnNℜeunetPnNℑmun convergent toutes les deux. Auquel cas,+Xn=0un =+Xn=0ℜeun + i+Xn=0ℑmun.IMPORTANT. Autrement dit, on ramène l’étude sur E = C à celle sur E = R.Définition 1.6 Série-produit. On munit l’ensemble S des séries numériques de la loi :× :S × S→S PnNun,PnNvn7→PnN‚ nXk=0uk vnkŒThéorème 1.6. L’ensemble des séries numériques muni des lois + et · définition 1.3 et × définition 1.6est une K-algèbre vectorielle.Romain Dujol23

Page 25 : Cas des séries numériques réellesProposition 1.3 Positivité de la somme.SoitPnNun une série à valeurs dans E = R convergente telle que n N, un 0. Alors+Xn=0un 0.Démonstration. On a donc pour tout entier naturel n,nXk=0uk 0. On conclut en passant à la limite.Proposition 1.4 Croissance de la somme.SoitPnNun etPnNvn deux séries à valeurs dans E = R convergentes telles que n N, un vn.Alors+Xn=0un +Xn=0vn.Démonstration. On a donc pour tout entier naturel n,nXk=0uk nXk=0vk. On conclut en passant à la limite.Romain Dujol24

Page 26 : Thème no 2Séries numériques à termes réels positifsDans tout le reste de cette partie, on considère le cas E = K.2.1Lemme fondamentalProposition 2.1. SoitPnNun une série numérique à termes réels positifs.Alors la suite SnnN de ses sommes partielles est croissante.Démonstration. Pour tout entier naturel n, Sn+1 Sn = un+1 0.Théorème 2.1 Lemme fondamental des séries à termes positifs.SoitPnNun une série numérique à termes réels positifs. AlorsPnNun est convergente si et seulementsi la suite de ses sommes partielles est majorée :XnNun converge ⇐⇒M R+, n N,nXk=0uk MDémonstration. On note SnnN la suite des sommes partielles dePnNun.⇒ CommePnNun converge, SnnN converge, donc est majorée.⇐ D’après la proposition 2.1, SnnN est croissante.Elle est également majorée, donc SnnN converge, puisPnNun converge.Proposition 2.2. SoitPnNun une série numérique à termes réels positifs.1. SiPnNun converge, alors n N,nXk=0uk +Xn=0un.2. SiPnNun diverge, alorslimn→+nXk=0uk = +.Romain Dujol25

Page 27 : Démonstration. On note SnnN la suite des sommes partielles dePnNun : d’après la proposition 2.1, SnnN est une suitecroissante.1.PnNun converge, donc SnnN converge vers la somme S. SnnN est croissante, donc n N, Sn limn→+Sn = S.2.PnNun diverge donc, d’après le lemme fondamental des séries à termes positifs, SnnN n’est pas majorée.SnnN est croissante, donc limn→+Sn = +.2.2Théorèmes de comparaison2.2.1Théorème de majorationThéorème 2.2 Théorème de majoration des séries à termes positifs.SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que n N, un vn.SiPnNvn converge, alorsPnNun converge également.Démonstration. D’après la proposition 2.2, n N,nXk=0uk nXk=0vk +Xk=0vk.DoncPnNun converge d’après le lemme fondamental des séries à termes positifs.Corollaire. SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que un = On→+vn.SiPnNvn converge, alorsPnNun converge également.Démonstration. un = On→+vn, donc N N, C R+, n N , un C vn.PnNvn converge donc :1.PnNvn converge d’après la proposition 1.1;2. puisPnNC vn = C ·PnNvn converge d’après le théorème 1.4;3. puisPnNC vn converge d’après la proposition 1.1;4. enfinPnNun converge d’après le théorème de majoration des séries à termes positifs.Corollaire. SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que un = on→+vn.SiPnNvn converge, alorsPnNun converge également.Démonstration. un = on→+vn, donc un = On→+vn. On conclut en utilisant le corollaire précédent.Romain Dujol26

Page 28 : 2.2.2Théorème de minorationThéorème 2.3 Théorème de minoration des séries à termes positifs.SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que n N, un vn.SiPnNun diverge, alorsPnNvn diverge également.Démonstration. C’est la contraposition du théorème de majoration des séries à termes positifs.On peut donc formuler les contraposées des corollaires précédents.Corollaire. SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que un = On→+vn.SiPnNun diverge, alorsPnNvn diverge également.Corollaire. SoitPnNun etPnNvn deux séries numériques à termes réels positifs telles que un = on→+vn.SiPnNun diverge, alorsPnNvn diverge également.2.2.3Théorème d’équivalenceThéorème 2.4 Théorème d’équivalence des séries numériques.SoitPnNun etPnNvn deux séries numériques réelles telles que unn→+vn.Si la suite vnnN est de signe constant à partir d’un certain rang alorsPnNun etPnNvn sont de mêmenature.Remarque. Ce théorème est en particulier applicable aux séries numériques à termes réels positifs et aux sériesnumériques à termes réels négatifs.Démonstration. On suppose ici que vnn est positive à partir d’un certain rang n0.limn→+unvn= 1 donc N N, n N , 12 unvn32 puis n maxN ,n0, un 0. unn→+vn donc :— un = Ovn etPnNvn converge =⇒PnNun converge d’après le corollaire page 26;— vn = Oun etPnNun converge =⇒PnNvn converge d’après le corollaire page 26.DoncPnNun converge ⇐⇒PnNvn converge.Si vnnN est négative à partir d’un certain rang n0, on applique le raisonnement précédent à vnnN.ATTENTION.Le théorème n’est plus valable si l’hypothèse « vnnN est de signe constant à partir d’un certainrang » n’est plus vérifiée.Exemple. cf. TDRomain Dujol27

Page 29 : Proposition 2.3 Sommation des équivalences. SoitPnNun etPnNvn deux séries numériques réelles de mêmesigne constant à partir d’un certain rang telles que unn→+vn.SiPnNvn converge, alorsPnNun converge et leurs restes sont équivalents :+Xk=n+1unn→++Xk=n+1vnSiPnNvn diverge, alorsPnNun diverge et leurs sommes partielles sont équivalentes :nXk=0unn→+nXk=0vn2.3Séries de référence2.3.1Séries géométriquesThéorème 2.5 Série géométrique. Soit z un nombre complexe.AlorsPnNz n converge si et seulement si z 1 : auquel cas,+Xn=0z n =11 z .Démonstration. La démonstration dans le cas réel a été traitée dans l’exemple page 20.2.3.2Séries de RIEMANNThéorème 2.6 Série de RIEMANN. Soit α un nombre réel.AlorsPn11nα converge si et seulement si α 1.Démonstration. On distingue deux cas selon la valeur de α.— Si α 1, alors pour tout entier naturel non nul n, on a 0 1n 1nα . En appliquant le théorème de minoration desséries à termes positifs, il vient quePn11nα diverge.— Si α 1, t 7→1t α est décroissante sur R+. Donc pour tout entier k 2 :t k 1,k, 1k α 1t αpuis, en intégrant sur k 1,k,1k α =Z kk11k α dt Z kk11t α dtOn en déduit alors que :n 2,nXk=21k α nXk=2Z kk11t α dt =Z n11t α dt =t 1α1 αn1= n1α 11α1 α=1α 11 1nα1‹1α 1Donc n 2,nXk=11k α 1 +1α 1 =αα 1.D’après le lemme fondamental des séries à termes positifs,Pn11nα converge.Romain Dujol28

Page 30 : Proposition 2.4 Règle « nαun ». SoitPnNun une série numérique à termes réels positifs. Alors :α 1,limn→+nαun = 0=⇒XnNun convergeα 1,limn→+nαun = +=⇒XnNun divergeDémonstration.• Donclimn→+un1/nα = 0 puis un = o 1nα‹. α 1 doncXn11nα converge puisPnNun converge d’après le corollairepage 26.• Donc limn→+1/nαun= 0 puis 1nα = oun. α 1 doncXn11nα diverge puisPnNun diverge d’après le corollaire page 27.2.3.3Séries de BERTRANDThéorème 2.7 Série de BERTRAND.Soit α et β deux nombres réels. AlorsPn21nαlnnβ converge si et seulement siα 1ouα = 1 et β 1Démonstration page 42.2.4Règles de convergence2.4.1Règle de D’ALEMBERTThéorème 2.8 Règle de D’ALEMBERT.SoitPnNun une série numérique à termes réels strictement positifs telle que la suiteun+1un‹nNconverge vers ℓR+ = R+ +.— Si ℓ 1, alorsPnNun converge.— Si ℓ 1 ou ℓ= +, alorsPnNun diverge grossièrement.ATTENTION. Le cas ℓ= 1 est indéterminé.Exemple.• Si un = 1n2 , alors un+1un=n2n + 12 →n→+1 etPn1un converge.• Si un = 1n , alors un+1un=nn + 1 →n→+1 etPn1un diverge.Romain Dujol29

Page 31 : Démonstration. Traitons les trois cas ℓ 1, ℓ 1 et ℓ= +séparément.• ℓ 1 D’après la définition de la limite avec ϵ = 1 ℓ2 0,N N, n N ,un+1unℓ 1 ℓ2c’est-à-direN N, n N , 3ℓ12un+1un1 + ℓ2On en déduit que N N, n N , un+1 un ·1 + ℓ2‹.Montrons par récurrence que pour tout n N , un uN ·1 + ℓ2‹N·1 + ℓ2‹n:— si n = N , alors uN uN = uN ·1 + ℓ2‹N·1 + ℓ2‹N;— soit n N tel que un uN ·1 + ℓ2‹N·1 + ℓ2‹n, alorsun+1 un ·1 + ℓ2‹uN ·1 + ℓ2‹N·1 + ℓ2‹n·1 + ℓ2‹= uN ·1 + ℓ2‹N·1 + ℓ2‹n+1Comme 1 + ℓ2 1, la série géométriquePnN1 + ℓ2‹nconverge, ainsi que la sériePnN1 + ℓ2‹n.On en déduit par théorème de majoration des séries à termes positifs quePnNun puisPnNun convergent.• ℓ 1 D’après la définition de la limite avec ϵ = ℓ12 0,N N, n N ,un+1unℓ ℓ12c’est-à-direN N, n N , 1 + ℓ2un+1un3ℓ12On en déduit que N N, n N , un+1 un ·1 + ℓ2‹.Montrons par récurrence que pour tout n N , un uN ·1 + ℓ2‹N·1 + ℓ2‹n:— si n = N , alors uN uN = uN ·1 + ℓ2‹N·1 + ℓ2‹N;— soit n N tel que un uN ·1 + ℓ2‹N·1 + ℓ2‹n, alorsun+1 un ·1 + ℓ2‹uN ·1 + ℓ2‹N·1 + ℓ2‹n·1 + ℓ2‹= uN ·1 + ℓ2‹N·1 + ℓ2‹n+1Comme 1 + ℓ2 1 et uN 0, on en déduit par minoration quelimn→+un = +puis quePnNun diverge grossière-ment.• ℓ= +D’après la définition de la limite, N N, n N , un+1un2.Comme dans le cas précédent, on montre par récurrence que un uN · 2N · 2n pour tout n N eton conclut de manière identique quePnNun diverge grossièrement.IMPORTANT. De manière générale, si un = 1nα , alors un+1un=nn + 1α→n→+1 : donc cette règle ne fait pas ladistinction entre les séries de RIEMANN convergentes et divergentes.Romain Dujol30

Page 32 : Remarque. Il ne s’agit pas d’une condition nécessaire de convergence ou de divergence :— si un = 2 + 1n2n, alors un+1un= 12 · 2 1n2 + 1n est le terme général d’une suite non convergente; comme0 un 32n , il vient quePnNun converge par théorème de majoration des séries à termes positifs.— si un = 2+1n, alors un+1un= 2 1n2 + 1n est le terme général d’une suite non convergente; comme un 1,il vient quePnNun diverge par théorème de minoration des séries à termes positifs.Exercice. Déterminer la nature i.e. convergente ou non de la série de terme général un = n!nn .Solution.PnNun est une série numérique à termes strictement positifs. De plusun+1un=n + 1!n + 1n+1 · nnn! = n + 1!n!·nnn + 1n+1 = n + 1nnn + 1n+1 =nn + 1n=1 + 1n‹nComme ln1 + 1n‹n= n ln1 + 1n‹n→+n · 1n = 1, il vient quelimn→+ln1 + 1n‹n= 1puislimn→+1 + 1n‹n= e 1 1D’après la règle de D’ALEMBERT,PnNun converge.2.4.2Règle de CAUCHYThéorème 2.9 Règle de CAUCHY.SoitPnNun une série numérique à termes réels positifs telle que la suitenpunnNconverge versℓR+ = R+ +.— Si ℓ 1, alorsPnNun converge.— Si ℓ 1 ou ℓ= +, alorsPnNun diverge grossièrement.Remarque. Comme dans le cas de la règle de D’ALEMBERT, le cas ℓ= 1 est aussi indéterminé.IMPORTANT. Si un = 1nα , alors npun = e α lnnn →n→+1 : donc cette règle ne fait pas plus la distinction entre lesséries de RIEMANN convergentes et divergentes que la règle de D’ALEMBERT.Démonstration. Traitons les trois cas ℓ 1, ℓ 1 et ℓ= +séparément.• ℓ 1 D’après la définition de la limite avec ϵ = 1 ℓ2 0,N N, n N , npun ℓ 1 ℓ2c’est-à-direN N, n N , 3ℓ12npun 1 + ℓ2On en déduit que N N, n N , un 1 + ℓ2‹n. Comme 1 + ℓ2 1,PnN1 + ℓ2‹nconverge.On en déduit par théorème de majoration des séries à termes positifs quePnNun puisPnNun convergent.Romain Dujol31

Page 33 : • ℓ 1 D’après la définition de la limite avec ϵ = ℓ12 0,N N, n N , npun ℓ ℓ12c’est-à-direN N, n N , 1 + ℓ2npun 3ℓ12On en déduit que N N, n N , un 1 + ℓ2‹n. Comme 1 + ℓ2 1 on en déduit par minoration que limn→+un =+puis quePnNun diverge grossièrement.• ℓ= +D’après la définition de la limite, N N, n N ,npun 2.Comme dans le cas précédent, on montre que un 2n pour tout n N et on conclut de manière identique quePnNun diverge grossièrement.2.4.3Lien entre les deux règlesProposition 2.5 Lien entre les deux règles.SoitPnNunune série numérique à termes réelsstrictement positifs telle que la suiteun+1un‹nNconverge vers ℓR+.Alors la suitenpunnN converge vers ℓ.Remarque. La réciproque de la proposition 2.5 est fausse en général.Donc si la suiteun+1un‹nNn’a pas de limite, la suitenpunnN peut en avoir une.Remarque. De manière générale, si npun →n→+ℓ, deux cas sont possibles :— la suiteun+1un‹nNn’a pas de limite dans R+ : la règle de D’ALEMBERT est donc inapplicable;— la suiteun+1un‹nNadmet une limite dans R+ : donc cette limite est égale à ℓd’après la proposition 2.5et l’application de la règle de D’ALEMBERT ne donne aucune information supplémentaire.Donc la règle de D’ALEMBERT ne donne pas plus d’information que la règle de CAUCHY.Néanmoins, on priviégiera la règle de D’ALEMBERT si l’expression de un s’y prête.Exercice. Reprendre l’exercice page 31 avec la règle de CAUCHY.Solution. D’après la proposition 2.5, on sait que la limite denpunnN existe et vaut e 1. Néanmoins, le calculdirect de cette limite est bien plus complexe que celle deun+1un‹nN...Romain Dujol32

Page 34 : Thème no 3Séries numériques à termes quelconquesPar «à termes quelconques», on entend «réels ou complexes». L’une des stratégies possibles sera de revenirlorsque cela est possible dans le cadre des séries numériques à termes positifs.3.1Convergence absolue. Semi-convergenceDéfinition 3.1 Convergence absolue.Une série numériquePnNun converge absolument si et seulement siPnNun converge.Théorème 3.1 Convergence absolue et convergence.L’ensemble des séries numériques absolument convergentes est un sous-espace vectoriel de l’es-pace vectoriel des séries numériques convergentes cf. théorème 1.4.De plus, pour toute série numérique absolument convergentePnNun, on a+Xn=0un +Xn=0un.ATTENTION. Il existe des séries numériques convergentes qui ne sont pas absolument convergentes.Exemple. La sériePn11nnconverge mais ne converge pas absolument.Démonstration.Pn11nn =PnN1n est la série harmonique et est donc divergente d’après le théorème 1.3.Pour tout entier naturel non nul n, on note un = 1nnet Sn la nème somme partielle de la série numériquePn1un.Montrons que les suites S2nn1 et S2n+1n0 sont adjacentes :— S2n+1 S2n = u2n+1 =12n + 1, donc limn→+S2n+1 S2n = 0;— S2n+2 S2n = u2n+1 + u2n+2 =12n + 1 +12n + 2 =12n + 12n + 2 0 : donc S2nn1 est une suite décroissante;— S2n+3 S2n+1 = u2n+2 + u2n+3 =12n + 2 12n + 3 =12n + 22n + 3 0 : donc S2n+1n0 est une suite croissante.D’après le théorème des suites adjacentes, S2nn1 et S2n+1n0 convergent : donc Snn1 converge etPn1un converge.Romain Dujol33

Page 35 : Définition 3.2 Série numérique semi-convergente.Une série numérique semi-convergente est une série numérique convergente qui n’est pas absolumentconvergente.Proposition 3.1. SiPnNun etPnNvn sont deux séries numériques convergentes dont l’une des deux convergeabsolument, alors leur série-produit converge a pour somme‚+Xn=0unŒ·‚+Xn=0vnŒ.ATTENTION. L’hypothèse de convergence absolue pour une des deux séries numériques est indispensable.Exemple. cf. TD3.2Règles de convergence absolueThéorème 3.2 Règle de D’ALEMBERT. SoitPnNun une série numérique à termes non nuls à partir d’uncertain rang telle que la suiteun+1unnNconverge vers ℓR+ = R+ +.— Si ℓ 1, alorsPnNun converge absolument.— Si ℓ 1 ou ℓ= +, alorsPnNun diverge grossièrement.Théorème3.3Règle de CAUCHY. SoitPnNun une série numérique telle que la suitenpunnN convergevers ℓR+ = R+ +.— Si ℓ 1, alorsPnNun converge absolument.— Si ℓ 1 ou ℓ= +, alorsPnNun diverge grossièrement.Démonstration des théorèmes 3.2 et 3.3. On applique la règle pour les séries à termes positifs correspondante à la sériePnNun.— Si ℓ 1, alorsPnNun converge : doncPnNun converge absolument.— Si ℓ 1 ou ℓ= +, alorsPnNun diverge grossièrement. Donc unnN ne converge pas vers 0, et unnN neconverge donc pas vers 0. On en conclut quePnNun diverge grossièrement.IMPORTANT. Comme dans le cas des séries à termes positifs :— le cas ℓ= 1 est indéterminé pour les deux régles;— la règle de D’ALEMBERT n’apporte pas plus d’information que la règle de CAUCHY, mais elle doit êtrepréférée si l’expression de un s’y prête.Romain Dujol34

Page 36 : Exercice. Déterminer la nature de la série de terme général un = 1n lnnnn .Solution.• Utilisons la règle de D’ALEMBERT :un+1un = lnn + 1n + 1n+1 · nnlnn = lnn + 1lnn·nnn + 1n+1 =1n + 1lnn + 1lnn·nn + 1n— On alimn→+1n + 1 = 0.— On a n + 1 n etlimn→+n + 1 = limn→+n = +: donc lnn + 1 lnn etlimn→+lnn + 1lnn= 1.— On a vu dans l’exercice page 31 quelimn→+nn + 1n= 1e .On en conclut donc quelimn→+un+1un = 0 1 et quePnNun converge absolument.• Utilisons la règle de CAUCHY :nÆun =nplnnn= 1n explnlnnn‹Comme ln x = ox→+x, il vient par composition que lnlnn = olnn. De plus lnn = on, donc lnlnn =on par transitivité de o· etlimn→+lnlnnn= 0, puislimn→+explnlnnn‹= 1.Commelimn→+1n = 0, on en conclut quelimn→+nÆun = 0 1 et quePnNun converge absolument.• On a n 2, un = lnnnn lnnn2 .Pn2lnnn2 =Pn21n2lnn1 est une série de BERTRAND convergente d’après le théorème 2.7 donc, par théo-rème de majoration des séries à termes positifs,Pn2un puisPnNun convergent absolument.• Par croissance comparée, n2un = lnnnn2 →n→+0.D’après la ??,Pnun converge absolument.3.3Règles de semi-convergence3.3.1Condition de convergence de CAUCHYThéorème 3.4 Condition de convergence de CAUCHY.Une série numériquePnNun converge si et seulement si :ϵ 0, N N, p N , q N ,qXk=p+1uk ϵDémonstration.PnNun converge si et seulement si sa suite des sommes partielles SnnN converge, c’est-à-dire si etseulement si SnnN est une suite de CAUCHY.Romain Dujol35

Page 37 : Remarque. Un terme du typeqXk=p+1uk est parfois appelé paquet de CAUCHY en référence à ce résultat.Corollaire. SoitPnNun une série numérique.Si il existe deux suites à valeurs entières pnnN et qnnN telles que :— n N, pn qn ;—limn→+pn = limn→+qn = +;— la suite qnXk=pnuk!nNne converge pas vers 0;alorsPnNun diverge.Démonstration. C’est la contraposition de la condition de convergence de CAUCHY.3.3.2Règle d’ABELThéorème 3.5 Règle d’ABEL. Soit ϵnnN et vnnN deux suites numériques telles que :— ϵnnN est une suite réelle positive, décroissante telle quelimn→+ϵn = 0;— la suite numérique‚ nXk=0vkŒnNest bornée.AlorsPnNϵnvn converge.Démonstration. Pour tout entier naturel n, on note Vn =nXk=0vk et Sn =nXk=0ϵk vk. Soit M = supnNVn. Alors :Sn =nXk=0ϵk vk = ϵ0v0 +nXk=1ϵk vk = ϵ0v0 +nXk=1ϵkVk Vk1 = ϵ0v0 +nXk=1ϵkVk nXk=1ϵkVk1=nXk=0ϵkVk n1Xk=0ϵk+1Vk = ϵnVn +n1Xk=0ϵk ϵk+1Vk· Comme la suite ϵnn converge vers 0 et que la suite Vnn est bornée, il vient que la suite ϵnVnn converge vers 0.· Pour tout n N,n1Xk=0ϵk ϵk+1 · Vk =n1Xk=0ϵk ϵk+1 · Vk =n1Xk=0ϵk ϵk+1 · VkMn1Xk=0ϵk ϵk+1 = Mn1Xk=0ϵk ϵk+1 = M ϵ0 ϵn M ϵ0D’aprèslelemmefondamentaldessériesàtermespositifs,ilvientquelasérienumériquePnNϵn ϵn+1 · Vn converge puis quePnNϵn ϵn+1 · Vn converge.On en déduit que SnnN converge puis quePnNϵnvn converge.Romain Dujol36

Page 38 : 3.3.3Séries numériques alternéesDéfinition 3.3. Une série numérique réellePnn0un est dite alternée si et seulement sin n0, un = 1nunoun n0, un = 1nunRemarque. Une série alternée est donc une série pour laquelle le terme général change de signe à chaque rang.Ainsi :un =1nsi n est le carré d’un entier1nnsinonn’est pas le terme général d’une série alternée et ce, à partir de n’importe quel rang.Théorème 3.6 Théorème spécial à certaines séries alternées.SoitPnNun une série numérique alternée telle que unnN soit une suite réelle positive décrois-sante qui converge vers zéro. AlorsPnNun converge.De plus, n N, Rn est du signe de un+1 et Rn =+Xk=n+1uk un+1.Démonstration. On suppose ici que n N, un = 1nun.On note Sn la somme partielle d’ordre n dePnNun. Montrons que S2nnN et S2n+1nN sont adjacentes :— S2n+1 S2n = u2n+1 = u2n+1, donc limn→+S2n+1 S2n = 0;— S2n+2 S2n = u2n+1 + u2n+2 = u2n+1 + u2n+2 0 : donc S2nnN est une suite décroissante;— S2n+3 S2n+1 = u2n+2 + u2n+3 = u2n+2 u2n+3 0 : donc S2n+1nN est une suite croissante.D’après le théorème des suites adjacentes, S2nnN et S2n+1nN convergent vers une limite commune S : donc SnnNconverge vers S etPnNun converge vers S.Les monotonies des deux suites partielles assurent que n N, S2n+1 S S2n. Donc :— n N, R2n = S S2n 0, or u2n+1 = u2n+1 0— n N, R2n+1 = S S2n+1 0, or u2n+2 = +u2n+1 0.Donc, pour tout entier naturel n, Rn et un+1 sont de même signe. De plus :— n N, R2n = S2n S S2n S2n+1 = u2n+1 = u2n+1;— n N, R2n+1 = S S2n+1 S2n+2 S2n+1 = u2n+2 = u2n+2.Donc n N, Rn un+1.Si n N, un = 1nun, on applique le raisonnement précédent àPnNun, dont la suite des restes est RnnN,pour obtenir que :— pour tout entier naturel n, Rn et un+1 sont de même signe : donc il en est de même pour Rn et un+1 ;— n N, Rn un+1 : donc n N, Rn un+1.Remarque. Le résultat de convergence de ce théorème est une application directe de la règle d’ABEL avecϵn = un et vn = ±1n.Romain Dujol37

Page 39 : Corollaire Séries de RIEMANN alternées.Soit α un nombre réel. AlorsPn11nnαconverge si et seulement si α 0.Démonstration. On distingue trois cas selon la valeur de α.• Si α 0, la suite de terme général 1nnαne converge pas, doncPn11nnαdiverge grossièrement.• Si α 0,1, alors1nnα = 1nα est le terme général d’une suite décroissante qui converge vers 0.CommePn11nnαest une série altérnée, on conclut qu’elle converge d’après le théorème spécial à certaines sériesalternées.• Si α 1, alors1nnα = 1nα est le terme général d’une série convergente : doncPn11nnαconverge absolument.3.4Raisonnement par regroupement de termesExemple. On considère la série de terme général un = 1n : il s’agit d’une série grossièrement divergente.Toutefois la série de terme général vn = u2n + u2n+1 = 0 est une série convergente.Donc la nature d’une série obtenue par regroupement de termes n’a rien à voir avec la nature de la sérieoriginale. Ces considérations font l’objet de résultats qui dépassent le cadre de ce cours. On retiendra que :Il ne faut pas regrouper les termes d’une série pour en déterminer la nature!Remarque. Après et uniquement après avoir établi qu’une série converge, on peut envisager de regrouper lestermes d’une série pour déterminer la valeur de sa somme.Romain Dujol38

Page 40 : Thème no 4Méthodes d’évaluation4.1Calcul de la somme d’une série convergente4.1.1Séries géométriquesOn rappelle le théorème 2.5.Théorème 4.1 Série géométrique. Soit z un nombre complexe.AlorsPnNz n converge si et seulement si z 1 : auquel cas,+Xn=0z n =11 z .4.1.2Par « télescopage »Proposition 4.1. Soit annn0 une suite numérique.AlorsPnn0an+1 an converge si et seulement si annn0 converge : auquel cas,+Xn=n0an+1 an =limn→+anan0.Démonstration. Soit n n0. Alors Sn =nXk=n0ak+1 ak =nXk=n0ak+1 nXk=n0ak =n+1Xk=n0+1ak nXk=n0ak = an+1 an0.DoncPnn0an+1 an converge si et seulement si an+1 an0nn0 converge, donc si et seulement si annn0 converge.Si annn0 converge vers ℓ, on en déduit que Snnn0 converge vers ℓan0, d’où le résultat annoncé.Exemple. On considère la série de terme général un =1nn + 1 = 1n 1n + 1.Avec an = 1n , il vient que n 1, un = an+1 an et ℓ= limn→+an = 0.D’où+Xn=11nn + 1 = 0 a1 = 0 11‹= 1.Remarque. Ce résultat peut être étendu aux séries numériques à valeurs dans un espace vectoriel normé.Romain Dujol39

Page 41 : 4.2Majoration du reste d’une série convergenteIl s’agit ici de borner le reste Rn par une expression plus simple. Cette borne pourra alors être utilisée pourdéterminer la qualité de Sn comme approximation de S.Proposition 4.2 Vitesse de convergence du reste d’une série « sous-géométrique ».SoitPnNun une série réelle strictement positive telle que :λ 0,1, N N, n N , 0 un+1unλAlorsPnNun converge et :n N , Rn uNλN 1 λλn+1Démonstration. On montre aisément par récurrence que n N , 0 un λnN uN . Donc pour tout n N :0 Rn =+Xk=n+1uk +Xk=n+1λkN uN = λN uN+Xk=n+1λk = λN uN+Xk=0λk+n+1 = λn+1N uN+Xk=0λk= λn+1N uN1 λExemple. On considère la série de terme général un = 1n! : on rappelle que+Xn=0un = e .Donner un ordre n assurant que Sn est une approximation de e à 106 près.n 1, un+1un=1n + 1 12. Donc d’après ce qui précède, Rn u11/2 · 1/212‹n+1=12n1 .Donc il suffit que12n1 106 ⇔n 1ln2 6ln10 ⇔n 1 6ln10ln2 19,9 ⇔n 21.Reste d’une série alternéeOn rappelle que si la série numériquePnNun vérifie les hypothèses du théorèmespécial à certaines séries alternées, alors son reste Rn d’ordre n vérifie Rn un+1.4.3Comparaison série-intégraleOn présente dans cette section une méthode d’encadrement qui permet d’étudier le comportement de lasérie de terme général f n pour n n0.4.3.1Cas décroissantThéorème 4.2 Comparaison série-intégrale.Soit n0 un entier naturel et f : n0,+→R+ une application décroissante.Alors pour tout n n0,Z n+1n0f xdx nXk=n0f k f n0 +Z nn0f xdx.Romain Dujol40

Page 42 : Démonstration. Soit k n0. Alors :x k,k + 1,f k + 1 f xf kZ k+1kf k + 1dx Z k+1kf xdxZ k+1kf kdxen intégrant sur k,k + 1f k + 1 Z k+1kf xdxf kSoit n n0. On note Sn =nXk=n0f k et on somme la double inégalité pour k entre n0 et n :nXk=n0f k + 1 nXk=n0Z k+1kf xdx nXk=n0f kn+1Xk=n0+1f k Z n+1n0f xdxnXk=n0f kSn+1 f n0 Z n+1n0f xdxSnConsidérons les deux inégalités séparément :— celle de gauche permet d’établir que Sn f n0 +Z nn0f xdx pour tout n n0on notera que la relation est également vérifiée pour n = n0;— celle de droite permet d’établir queZ n+1n0f xdx Sn pour tout n n0.Finalement, pour tout n n0,Z n+1n0f xdx nXk=n0f k f n0 +Z nn0f xdx.Remarque. C’est la technique utilisée pour démontrer le cas convergent du théorème 2.6.Exemple f : x 7→x 1. Soit n 1. On note Hn =nXk=11k .f : 1,+→R+ est décroissante donc :Z n+11dxx nXk=11k f 1 +Z n1dxxln xn+11Hn1 +ln xn1lnn + 1 ln1 Hn1 + lnn ln1lnn + 1lnnHnlnn1 + lnnlnnOrlimn→+lnn + 1lnn=limn→+1 + lnnlnn= 1 : donc d’après le théorème d’encadrement des limites, il vient quelimn→+Hnlnn = 1. Finalement,Pn11n diverge et Hn =nXk=11kn→+lnn.Romain Dujol41

Page 43 : Cette technique permet de démontrer certains cas du théorème 2.7.Théorème Série de BERTRAND.Soit α et β deux nombres réels. AlorsPn21nαlnnβ converge si et seulement siα 1ouα = 1 et β 1Démonstration. On note un =1nαlnnβ et on distingue deux cas selon la valeur de α.• Si α ̸= 1, on note γ = 1 + α2. Alors nγun = n1α/2lnnβ :— si α 1, alors γ 1 et limn→+nγun = 0; doncPn2un converge d’après la règle « nαun »;— si α 1, alors γ 1 et limn→+nγun = +; doncPn2un diverge d’après la règle « nαun ».• Si α = 1 et β 0, alors un 1n pour tout n 3 : doncPn2un diverge d’après le théorème de minoration des séries àtermes positifs.• Si α = 1 et β 0, alors x 7→1xln xβ est décroissante sur 2,+. En appliquant la comparaison série-intégraleavec n0 = 2 :n 2,Z n+12dxxln xβ nXk=2uk 12ln2β +Z n2dxxln xβCalculons In =Z n2dxxln xβ en posant le changement de variable strictement croissant u = ln x : alors x = e u etdx = e udu. D’où In =Z n2dxxln xβ =Z lnnln2e udue uuβ =Z lnnln2duuβ .Il faut alors distinguer deux cas selon la valeur de β :— si β ̸= 1, alors In =Z lnnln2uβ du =uβ+1β + 1lnnln2= lnnβ+1β + 1ln2β+1β + 1:· si β 1, alorsnXk=2uk 12ln2β + In =12ln2β +1β 1•1ln2β1 1lnnβ1˜12ln2β +1β 11ln2β1doncPn2un converge d’après le lemme fondamental des séries à termes positifs;· si β 1, alorsnXk=2uk In+1 = lnn + 11β ln21β1 β: donc limn→+In+1 = +et on en déduit par mino-ration que limn→+nXk=2uk = +puis quePn2un diverge.— si β = 1, alors In =Z lnnln2duu =”lnu—lnnln2 = lnlnn lnln2. DoncnXk=2uk In+1 = lnlnn + 1 lnln2.Comme limn→+In+1 = +et on en déduit par minoration que limn→+nXk=2uk = +puis quePn2un diverge.Romain Dujol42

Page 44 : 4.3.2Cas croissantThéorème 4.3 Comparaison série-intégrale.Soit n0 un entier naturel et f : n0,+→R+ une application croissante.Alors pour tout n n0, f n0 +Z nn0f xdx nXk=n0f k Z n+1n0f xdx.Démonstration. Soit k n0. Alors :x k,k + 1,f k f xf k + 1Z k+1kf kdx Z k+1kf xdxZ k+1kf k + 1dxen intégrant sur k,k + 1f k Z k+1kf xdxf k + 1Soit n n0. On note Sn =nXk=n0f k et on somme la double inégalité pour k entre n0 et n :nXk=n0f k nXk=n0Z k+1kf xdx nXk=n0f k + 1nXk=n0f k Z n+1n0f xdxn+1Xk=n0+1f kSn Z n+1n0f xdxSn+1 f n0Considérons les deux inégalités séparément :— celle de gauche permet d’établir que Sn Z n+1n0f xdx pour tout n n0 ;— celle de droite permet d’établir que f n0 +Z nn0f xdx Sn pour tout n n0on notera que la relation est également vérifiée pour n = n0.Finalement, pour tout n n0, f n0 +Z nn0f xdx nXk=n0f k Z n+1n0f xdx.Exemple f : x 7→ln x. Soit n 1. On note Sn =nXk=1lnk.f : 1,+→R+ est croissante donc f 1 +Z n1ln x dx nXk=1lnk Z n+11ln x dx, c’est-à-dire :Romain Dujol43

Page 45 : ln1 +x ln x xn1 Snx ln x xn+11n lnn n 1ln1 1 Snn + 1lnn + 1 n + 1 1ln1 1n lnn n 1 Snn + 1lnn + 1 nn lnn n 1n lnnSnn lnn n + 1lnn + 1 nn lnn1 1lnn +1n lnn Snn lnn 1 + 1n‹ lnn + 1lnn1lnnOrlimn→+1 1lnn +1n lnn =limn→+1 + 1n‹ lnn + 1lnn1lnn = 1 : donc d’après le théorème d’encadrement deslimites, il vient quelimn→+Snn lnn = 1. FinalementPn1lnn diverge etnXk=1lnkn→+n lnn.Remarque. En remarquant quenXk=1lnk = ln‚ nYk=1kŒ= lnn!, il vient que lnn!n→+n lnn.Romain Dujol44

Page 46 : Deuxième partieSuites et séries d’applicationsRomain Dujol45

Page 47 : Thème no 5Suites d’applications : convergencesDans tout le chapitre, X est un ensemble non vide et K désigne R ou C.Définition 5.1 Opérations. On munit l’ensemble E des suites d’applications de X dans K de :— la loi interne + :E × E→EfnnN,gnnN7→fn + gnnN;— la loi interne × :E × E→EfnnN,gnnN7→fn · gnnN;— la loi externe · :K × E→Eλ,fnnN7→λ · fnnN.Théorème 5.1 Structure algébrique. L’ensemble E des suites d’applications de X dans K muni des lois+, · et × vues en définition 5.1 est une K-algèbre vectorielle.5.1Convergence simpleDéfinition 5.2 Convergence simple. Soit fnnN une suite d’applications de X dans K.Soit f une application de X dans K. On dit que fnnN converge simplement sur X vers f , ce que l’onnote fnCS→n→+f , si et seulement si la suite numériquefnxnN converge vers f x pour tout élement xde X , c’est-à-dire :fnCS→n→+f ⇐⇒x X ,limn→+fnx = f x⇐⇒x X , ϵ 0, N N, n N , fnx f x ϵOn dit alors que f est la limite simple de fnnN.On dit que fnnN converge simplement sur X si et seulement si il existe une application f de X dansK telle que fnnN converge simplement vers f .Romain Dujol46

Page 48 : Proposition 5.1. Si une suite d’applications converge simplement, alors il y a unicité de la limite simple.Démonstration. Pour tout x de X , il y a unicité de la limite f x de la suite numériquefnxnN.Exemple. Pour tout n N, on définitfn :0,1→Rx7→max1 nx,0 =1 nxsi x •0, 1n˜0si x • 1n ,1˜.Calculons la limite simple f de fnn1 si elle existe. On distingue deux cas pour la valeur de x.— Si x = 0, alors fn0 = 1, donclimn→+fn0 = 1.— Sinon N , n N , 1n x. Donc pour tout n N , fnx = 0 : on en déduit quelimn→+fnx = 0.On en conclut que la limite simple de fnn1 estf :0,1→Rx7→¨1si x = 00si x ̸= 0.Remarque. La limite simple d’une suite de fonctions continues peut ne pas être continue.Proposition 5.2. Soit fnnN une suite d’applications de X dans K convergeant simplement sur X .Alors pour tout sous-ensemble X ′ de X , fn X ′nN converge simplement sur X ′.Définition 5.3 Domaine de convergence. Soit fnnN une suite d’applications de X dans K.L’ensemble des élements x de X pour lesquels la suite numériquefnxnN converge est appelé do-maine de convergence de fnnN.Exemple. Pour tout entier naturel n, on définit l’applicationfn :R+→Rx7→nnx + 1.Déterminons le domaine de convergence de la suite d’applications fnnN :— Si x = 0, fn0nN = nnN ne converge pas.— Si x 0, fnxn→+nn x = 1x . Donc fnxnN converge.Donc le domaine de convergence de fnnN est R+ et sa limite simple sur R+ est x 7→1x .Théorème 5.2 Structure algébrique.L’ensemble des suites d’applications de X dans K qui convergent simplement sur X est une sous-algèbre vectorielle de l’ensemble des suites d’applications de X dans K.De plus, l’application qui à toute suite d’applications de X dans K convergeant simplement sur Xassocie sa limite simple est linéaire sur E .Proposition 5.3. Soit fnnN une suite d’applications de X dans K et f une application de X dans K.Alors fnnN converge simplement sur X vers f si et seulement si fn f nN converge simplement sur Xvers la fonction nulle.Romain Dujol47

Page 49 : 5.2Convergence uniformeDéfinition 5.4 Convergence uniforme. Soit fnnN une suite d’applications de X dans K.Soit f une application de X dans K. On dit que fnnN converge uniformément sur X vers f , ce quel’on note fnCU→n→+f si et seulement si :fnCU→n→+f ⇐⇒ϵ 0, N N, n N , x X , fnx f x ϵOn dit alors que f est la limite uniforme de fnnN.On dit que fnnN converge uniformément sur X si et seulement si il existe une application f de Xdans K telle que fnnN converge uniformément vers f .Théorème 5.3 Structure algébrique. L’ensemble des suites d’applications de X dans K qui convergentuniformément sur X est un sous-espace vectoriel de l’ensemble des suites d’applications de X dans Kqui convergent simplement.De plus, l’application qui à toute suite d’applications de X dans K convergeant simplement sur Xassocie sa limite uniforme est une restriction de l’application qui associe sa limite simple.Démonstration. Comparons la convergence simple et la continuité uniforme de fnnN :— convergence uniforme de fnnN : ϵ 0, N N, n N , x X , fnx f x ϵ— convergence simplede fnnN : x X , ϵ 0, N N, n N , fnx f x ϵRemarque. Donc, lorsque la convergence est uniforme, ϵ et N ne dépendent plus de x mais N dépend tou-jours de ϵ.Proposition 5.4. Soit fnnN une suite d’applications de X dans K convergeant uniformément sur X .Alors pour tout sous-ensemble X ′ de X , fn X ′nN converge uniformément sur X ′.Théorème 5.4 Caractérisation rapide de la convergence uniforme.Soit fnnN une suite d’applications de X dans K et f une application de X dans K. Alors :fnCU→n→+f ⇐⇒¨N N, n N , fn f est une application bornéelimn→+fn f = 0Démonstration. fnCU→n→+f ⇐⇒ϵ 0, N N, n N , x X , fnx f x ϵ⇐⇒ϵ 0, N N, n N , supxXfnx f x ϵ⇐⇒ϵ 0, N N, n N , fn f ϵ ⇐⇒limn→+fn f = 0Remarque. Soit BX ,K l’ensemble des applications de X dans K bornées.Alors la convergence uniforme sur X est la convergence dans l’espace vectoriel normé BX ,K, · .Romain Dujol48

Page 50 : Exemple. On reprend l’exemple page 47.Pour tout entier naturel n, fn est bornée ainsi que f . Donc fn f est bornée et :fn f = supx0,1 fnx f x fn 12n‹f 12n‹Or fn 12n‹= 12 et f 12n‹= 0. Donc pour entier naturel non nul n, fn f 12 et ne peut donc pas être leterme général d’une suite convergente vers 0.Donc fnn1 ne converge pas uniformément sur X vers f .Remarque. La technique précédente pour montrer la non-convergence uniforme est à retenir.IMPORTANT. Il existe donc des suites d’applications qui convergent simplement sans converger uniformé-ment.Corollaire. Soit fnnN une suite d’applications de X dans K et f une application de X dans K.Alors fnnN converge uniformément sur X vers f si et seulement si fn f nN converge uniformémentsur X vers la fonction nulle.Proposition 5.5. Soit fnnN une suite d’applications de X dans K et f une application de X dans K.Soit unnN une suite numérique telle que :n N, x X , fnx f x unetlimn→+un = 0alors fnnN converge uniformément sur X vers f .Démonstration. Alors n N, fn f = supxXfnx f x un. On en déduit que limn→+fn f = 0 par théorèmed’encadrement des limites.Exemple. Pour tout entier naturel non nul n, on définit l’application :gn :0,1→Rx7→max 1n x,0‹=1n xsi x •0, 1n˜0si x • 1n ,1˜.Pour tout entier naturel non nul n, pour tout x 0,1, on a 0 gnx 1n puis 0 gnx 0 1n . DoncgnnN converge uniformément sur 0,1 vers la fonction nulle.Théorème 5.5 Condition de convergence de CAUCHY.Soit fnnN une suite d’applications de X dans K. La suite d’applications fnnN converge unifor-mément sur X si et seulement si :ϵ 0, N N, p N , q N , x X ,fpx fqx ϵDéfinition 5.5 Convergence localement uniforme.Soit I un intervalle de R et fnnN une suite d’applications de I dans K.On dit que fnnN converge localement uniformément sur I si et seulement si fnnN converge uni-formément sur tout segment inclus dans I .Romain Dujol49

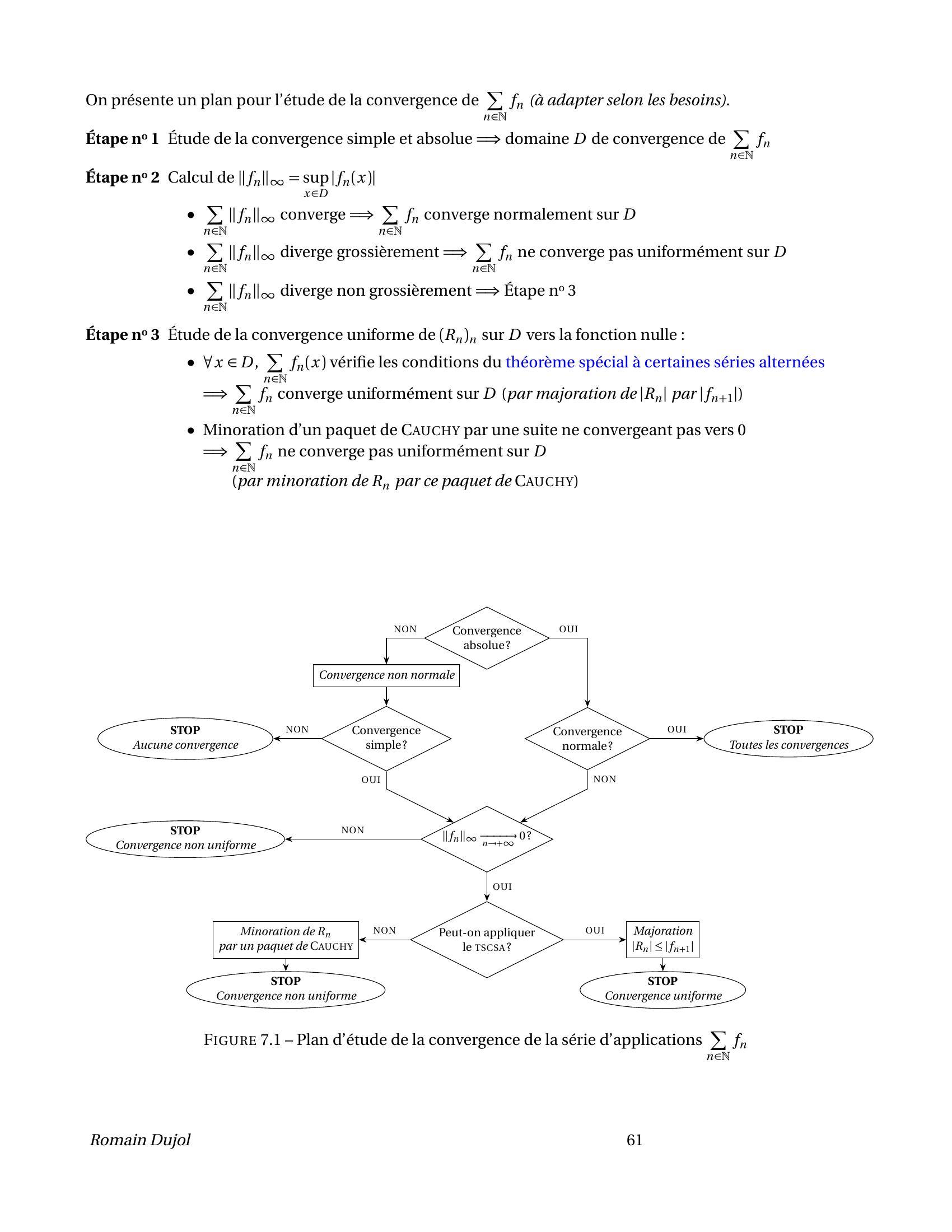
Page 51 : Proposition 5.6. Soit I un intervalle de R et fnnN une suite d’applications de I dans K.• Si fnnN converge uniformément sur I , alors fnnN converge localement uniformément sur I .• Si I est un segment, alors fnnN converge uniformément localement sur I si et seulement si fnnNconverge localement sur I .Démonstration.• Comme fnnN converge uniformément sur I , elle converge uniformément sur tout sous-ensemble de I , donc surtout segment inclus dans I d’après la proposition 5.4.• Comme I est un segment inclus dans I , il vient alors que fnnN converge uniformément sur I .Proposition 5.7. Soit I un intervalle de R et fnnN une suite d’applications de I dans K.Si fnnN converge localement uniformément sur I , alors fnnN converge simplement sur I .Démonstration. Soit x I : alors il existe un segment a,b inclus dans I contenant x.Or fnnN converge uniformément sur a,b donc simplement sur a,b et en particulier en x.On présente un plan pour l’étude de la convergence de fnnN à adapter selon les besoins.Étape no 1 Étude de la convergence simple=⇒domaine D de convergence de fnnN=⇒limite simple f sur DÉtape no 2 Calcul de fn f = supxDfnx f x• fn f n’est pas définie à partir d’un certain rang=⇒fnnN ne converge pas uniformément vers f sur D• fn f nN ne converge pas vers zéro=⇒fnnN ne converge pas uniformément vers f sur D• fn f nN converge vers zéro=⇒fnnN converge uniformément vers f sur DRomain Dujol50

Page 52 : Thème no 6Suites d’applications : théorèmesd’interversion6.1Interversion limite-limiteThéorème 6.1 Théorème d’interversion des limites. Soit a X .Soit fnnN une suite d’applications de X dans K et f une application de X dans K telles que :1. pour tout entier naturel n, fn admette une limite ℓn en a ;2. fnnN converge uniformément sur X vers f .Alors la suite ℓnnN est convergente, f admet une limite finie en a etlimn→+ℓn = limx→a f x.Remarque. C’est-à-dire quelimn→+limx→a fnx = limx→alimn→+fnx.Démonstration. Comme fnnN converge uniformément sur X vers f , on utilise le théorème 5.5.ϵ 0, N N, p N , q N , x X ,fpx fqx ϵ⇒ϵ 0, N N, p N , q N , limx→afpx fqx ϵ⇒ϵ 0, N N, p N , q N , ℓp ℓq ϵIl vient que la suite ℓnnN est une suite de CAUCHY, puis qu’elle est convergente : on note ℓsa limite.Soit ϵ un réel strictement positif. Alors :N1 N, n N1, x X , fnx f x ϵ3convergence uniforme de fnnNN2 N, n N2, ℓn ℓ ϵ3convergence de ℓnnNη 0, x X ,x a η ⇒fN x ℓN ϵ3fN admet une limite en a pour N = maxN1,N2Donc il existe un réel strictement positif η tel que pour tout x vérifiant x a η :f x ℓ f x fN x + fN x ℓN + ℓN ℓ f x fN x + fN x ℓN + ℓN ℓ ϵ3 + ϵ3 + ϵ3 = ϵFinalement ϵ 0, η 0, x X ,x a η ⇒f x ℓ ϵ: on en conclut que limx→a f x = ℓ= limn→+ℓn.Romain Dujol51

Page 53 : Exemple. Pour tout entier naturel non nul n, on définit φn :0,1/2→Rx7→ln1 xnx.Vérifions les hypothèses du théorème d’interversion des limites.1. n N, φnx = ln1 xn xx→0 xn x = 1n : donc ℓn = limx→0φnx = 1n .2. Comme φ1 admet une limite en 0, elle admet un prolongement par continuité φ1 en 0.Comme φ1 est continue sur 0,1/2, elle y est bornée : donc φ1 est également bornée sur 0,1/2.n N, φn = 1n φ1 : donc φn 0= φn= 1n φ1→n→+0.On en déduit que φnnN converge uniformément sur X vers φ = 0.Alors ℓnn1 convergelimn→+ℓn = 0, φ admet une limite en 0 qui est 0 et limx→0φx = limx→00 = 0.Théorème 6.2. Soit a X .Soit fnnN une suite d’applications de X dans K et f une application de X dans K telles que :1. pour tout entier naturel n, fn est continue en a ;2. fnnN converge uniformément sur X vers f .Alors f est continue en a.Démonstration. Vérifions les hypothèses du théorème d’interversion des limites.1. pour tout n N, fn est continue en a donc admet ℓn = fna comme limite en a ;2. fnnN converge uniformément sur X vers f .On applique le théorème d’interversion des limites avec la suite ℓnnN = fnanN :— fnnN converge uniformément donc simplement sur X et donc en a : donc limn→+fna = f a;— f admet une limite finie ℓen a et ℓ= limn→+fna = f a.On en conclut que limx→a f x = f a puis que f est continue en a.Remarque. Le cas traité dans l’exemple page 47 montre que la convergence simple n’est pas une conditionsuffisante de conservation de la continuité.Corollaire. Soit fnnN une suite d’applications de X dans K et f une application de X dans K telles que :1. pour tout entier naturel n, fn est continue sur X ;2. fnnN converge uniformément sur X vers f .Alors f est continue sur X .Démonstration. On applique le théorème précédent en tout point a de X .Remarque. On utilise régulièrement la contraposée de ce théorème pour établir une absence de convergenceuniforme.Corollaire. Soit I un intervalle de R.Soit fnnN une suite d’applications de I dans K et f une application de I dans K telles que :1. pour tout entier naturel n, fn est continue sur I ;2. fnnN converge localement uniformément sur I vers f .Alors f est continue sur I .Démonstration. Tout point de I est inclus dans un segment inclus dans I .Donc on conclut en appliquant le corollaire précédent sur tout segment inclus dans I .Romain Dujol52

Page 54 : 6.2Interversion limite-intégraleThéorème 6.3 Théorème d’interversion limite-intégrale. Soit a et b deux réels tels que a b .Soit fnnN une suite d’applications de a,b dans K et f une application de a,b dans K telles que :1. pour tout entier naturel n, fn est continue sur a,b ;2. fnnN converge uniformément sur a,b vers f .Alors f est continue sur a,b et la suite‚Z bafnxdxŒnNconverge versZ baf xdx.Remarque. C’est-à-dire quelimn→+Z bafnxdx =Z bahlimn→+fnxidx.Démonstration. D’après le corrolaire page 52, f est continue sur a,b comme limite uniforme d’une suite d’applicationscontinues. Donc, pour tout entier naturel n, fn f est continue sur a,b et y est donc bornée :Z bafnxdx Z baf xdx =Z bafn f xdx Z bafn f xdx Z bafn f dx = b afn f Comme fnnN converge uniformément sur a,b vers f , il vient que limn→+fn f = 0.Par théorème d’encadrement des limites, il vient que limn→+Z bafnxdx Z baf xdx = 0.6.3Interversion limite-dérivation6.3.1Théorèmes d’interversionThéorème 6.4 Théorème d’interversion limite-dérivation. Soit a et b deux réels tels que a b.Soit fnnN une suite d’applications de a,b dans K et g une application de a,b dans K telles que :1. pour tout entier naturel n, fn est de classe C 1 sur a,b;2. f ′nnN converge uniformément sur a,b vers g ;3. il existe x0 de a,b tel quefnx0nN converge.Alors :1. fnnN converge uniformément sur a,b vers une application notée f ;2. f est une application de classe C 1 sur a,b ;3. f ′ = g .Démonstration. On note C = limn→+fnx0 et on définit l’applicationf :a,b →Kx7→C +Z xx0g t dt.Comme f ′nnN est une suite d’applications continues qui converge uniformément sur a,b vers g , il vient que g estcontinue. Donc f est de classe C 1 sur a,b en tant que primitive de g et f ′ = g .Romain Dujol53

Page 55 : Remarquons que pour tout élément x de a,b , fnx = fnx0 +Z xx0f ′nt dt . Alors :n N, fnx f x =fnx0 +Z xx0f ′nt dt C Z xx0g t dt fnx0 C +Z xx0f ′nt dt Z xx0g t dtfnx0 C +Z xx0f ′n g t dt fnx0 C +Z xx0f ′n g t dtfnx0 C +Z xx0f ′n g dt = fnx0 C + x x0f ′n g fnx0 C + b af ′n g Comme limn→+fnx0 = C et limn→f ′n g = 0, il vient que limn→fnx0 C + b af ′n g = 0.D’après la proposition 5.5, on en conclut que fnnN converge uniformément sur a,b vers f .Exemple. Pour tout entier naturel non nul n, on définit φn :1/4,3/4→Rx7→ln1 xnx.Vérifions les hypothèses du théorème d’interversion limite-dérivation.1. Pour tout entier naturel non nul n, φn est de classe C 1 sur 1/4,1/2.2. φ′1 est continue sur 1/4,3/4, donc bornée. On en déduit que φ′n=φ′1n=φ′1n→n→+0 puisque φ′nn1 converge uniformément sur 1/4,1/2 vers g = 0.3. n 1, φn1/2 = ln1/2n/2= 2ln2n: doncφn1/2n1 converge vers 0.Alors φnn1 converge uniformément sur 1/4,1/2 vers une application φ de classe C 1 sur 1/4,1/2 telle queφ′ = 0 et φ12‹= limn→+φn12‹= 0 : donc φ = 0.Théorème 6.5 Théorème d’interversion limite-dérivation. Soit I un intervalle de R.Soit fnnN une suite d’applications de I dans K et g une application de I dans K telles que :1. pour tout entier naturel n, fn est de classe C 1 sur I ;2. f ′nnN converge localement uniformément sur I vers g ;3. il existe x0 de I tel quefnx0nN converge.Alors :1. fnnN converge localement uniformément sur I vers une application notée f ;2. f est une application de classe C 1 sur I ;3. f ′ = g .Démonstration. On applique le théorème 6.4 sur tout segment inclus dans I .ATTENTION. Si I n’est pas un segment, l’énoncé obtenu en enlevant « uniformémement » dans les hypothèseset dans la conclusion n’est pas valable.Romain Dujol54

Page 56 : 6.3.2Nécessité des hypothèses du théorèmeConvergence uniforme de la suite des dérivéesL’hypothèse de convergence uniforme de la suite des dérivées est nécessaire.Exemple. Pour tout entier naturel non nul n, on définitfn :1,1→Rx7→vtx 2 + 1n.— Pour tout entier naturel non nul n, fn est de classe C 1 sur a,b et f ′nx =xvtx 2 + 1n.—limn→+f ′nx =1si x 00si x = 0+1si x 0: donc la limite simple de f ′nnN n’est pas continue en 0 et la convergencene peut donc pas être uniforme sur X .Les hypothèses du théorème d’interversion limite-dérivation ne sont donc pas satisfaites.De pluslimn→+fnx = x : donc la limite simple de fnnN n’est pas de classe C 1 sur 1,1.Hypothèse de convergence simple de la suite d’applications en un pointL’hypothèse de convergence simple de la suite d’applications en au moins un point de leur ensemble dedéfinitions est nécessaire.Exemple. Pour tout entier naturel non nul n, on définitfn :0,1→Rx7→n.1. Pour tout entier naturel non nul n, fn est de classe C 1 sur 0,1.2. f ′nnN = 0nN converge uniformément sur 0,1 vers la fonction nulle.3. fnnN ne converge simplement en aucun point de 0,1.Comme la suite d’applications fnnN ne converge pas simplement sur 0,1, elle n’y converge pas uniformé-ment.Romain Dujol55

Page 57 : Thème no 7Séries d’applications : convergencesDéfinition 7.1 Série d’applications. Soit fnnN une suite d’applications de X dans K.Laséried’applicationsdetermegénéralfn,notéePnNfnouPn0fn,lecouplefnnN,SnnNoù la suite SnnN définie par :n N, Sn =nXk=0fkfn est le n ème terme ou terme général dePnNfn. Sn est la n ème somme partielle dePnNfn.Si la suite d’applications fnnn0 est définie à partir d’un certain rang n0 N, on définit de la mêmemanière la série d’applicationsPnn0fn avec Sn =nXk=n0fk pour tout n n0.Définition 7.2 Opérations. On munit l’ensemble E des séries d’applications de X dans K de :— la loi interne + :E × E→E PnNfn,PnNgn7→PnNfn + gn;— la loi interne × :E × E→E PnNfn,PnNgn7→PnN‚ nXk=0fkgnkŒ ;— la loi externe · :K × E→Eλ,PnNfn7→PnNλ · fn.Théorème 7.1. L’ensemble E des séries d’applications de X dans K muni des lois +, × et · vues en défi-nition 7.2 est une K-algèbre vectorielle.Romain Dujol56

Page 58 : Tout comme les séries numériques sont des suites numériques particulières, les séries d’applications sontdes suites d’applications particulières. On peut donc appliquer tous les résultats des thèmes précédents auxséries d’applications7.1Convergences7.1.1Convergence simpleGénéralitésDéfinition 7.3 Convergence simple.Une sériePnNfn d’applications de X dans K converge simplement sur X si et seulement si la suited’applications SnnN de ses sommes partielles converge simplement sur X .Auquel cas, on définit la somme de la sériePnNfn, notée+Xn=0fn comme la limite simple de SnnN.Proposition 7.1 Caractérisation rapide de la convergence simple.Soit fnnN une suite d’applications de X dans K.AlorsPnNfn converge simplement sur X si et seulement siPnNfnx convergente pour tout x X .Démonstration.XnNfn converge simplement sur X ⇐⇒SnnN converge simplement sur X⇐⇒x X , SnxnN =‚ nXk=0fkxŒnNconverge⇐⇒x X ,XnNfnx convergeDéfinition 7.4 Domaine de convergence. Soit fnnN une suite d’applications de X dans K.L’ensemble des élements x de X pour lesquels la série numériquePnNfnx converge est appelé do-maine de convergence dePnNfn.Proposition 7.2. SoitPnNfn une série d’applications de X dans K convergeant simplement sur X .Alors pour tout sous-ensemble X ′ de X ,PnNfn X ′ converge simplement sur X ′.Reste d’une série d’applications convergenteDéfinition 7.5 Reste d’ordre n.Soit fnnN une suite d’applications de X dans K convergeant simplement sur X .On appelle reste d’ordre n dePnNfn la somme de la sériePkn+1fk, c’est-à-dire+Xk=n+1fk.ATTENTION.Il n’existe pas de reste pour une série d’applications qui ne converge pas simplement!Romain Dujol57

Page 59 : Remarque. Pour simplifier l’écriture, on note souvent :— Sn la somme partielle d’ordre n ;— S la somme lorsque la série converge simplement;— Rn le reste d’ordre n lorsque la série converge simplement.On a alors Rn = S Sn , c’est-à-dire+Xk=n+1fk =+Xk=0fk nXk=0fk.Proposition 7.3 Convergence du reste.Soit fnnN une suite d’applications de X dans K telle quePnNfn converge simplement sur X .Alors la suite RnnN de ses restes d’ordre n converge simplement vers la fonction nulle.Condition nécessaire de convergenceProposition 7.4 Condition nécessaire de convergence simple.Soit fnnN une suite d’applications de X dans K.SiPnNfn converge simplement sur X , alors fnnN converge simplement sur X vers la fonction nulle.Démonstration. On note SnnN la suite des sommes partielles dePnNfn. Alors SnnN converge simplement vers S =+Xn=0fn.Or fnn1 = Sn Sn1n1. Comme Snn1 et Sn1n1 convergent simplement vers S, il vient d’après le théorème 5.2que fnn1 converge simplement vers S S = 0.Théorème 7.2 Structure algébrique.L’ensemble E des séries d’applications de X dans K convergeant simplement sur X est un sous-espace vectoriel de l’ensemble des séries d’applications de X dans K cf. théorème 7.1.De plus, l’applicationE→FX ,KPnNfn7→+Xn=0fnest une application linéaire sur E .7.1.2Convergence absolueDéfinition 7.6 Convergence absolue.Une sériePnNfn d’applications de X dans K converge absolument sur X si et seulement siPnNfnxconverge absolument pour tout x X .Proposition 7.5. SoitPnNfn une série d’applications de X dans K convergeant absolument sur X .Alors pour tout sous-ensemble X ′ de X ,PnNfn X ′ converge absolument sur X ′.Théorème 7.3 Structure algébrique. L’ensemble des séries d’applications de X dans K convergeantabsolument sur X est un sous-espace vectoriel de l’ensemble des séries d’applications de X dans Kconvergeant simplement sur X .Romain Dujol58

Page 60 : 7.1.3Convergence uniformeDéfinition 7.7 Convergence uniforme.Une sériePnNfn d’applications de X dans K converge uniformément sur X si et seulement si la suited’applications SnnN de ses sommes partielles converge uniformément sur X .Proposition 7.6. Soit fnnN une suite d’applications de X dans K.AlorsPnNfn converge uniformément sur X si et seulement siPnNfn converge simplement sur X et que lasuite d’applications RnnN converge uniformément vers la fonction nulle.Proposition 7.7 Condition nécessaire de convergence uniforme.Soit fnnN une suite d’applications de X dans K.SiPnNfn converge uniformément sur X , alors la suite d’applications fnnN converge uniformément surX vers la fonction nulle.Démonstration. On note SnnN la suite des sommes partielles dePnNfn. Alors SnnN converge uniformément vers S.Or fnn1 = Sn Sn1n1. Comme Snn1 et Sn1n1 convergent uniformément vers S, il vient d’après le théo-rème 5.3 que fnn1 converge uniformément vers S S = 0.Proposition 7.8. SoitPnNfn une série d’applications de X dans K convergeant uniformément sur X .Alors pour tout sous-ensemble X ′ de X ,PnNfn X ′ converge uniformément sur X ′.Théorème 7.4 Structure algébrique. L’ensemble des séries d’applications de X dans K convergeantuniformément sur X est un sous-espace vectoriel de l’ensemble des séries d’applications de X dans Kconvergeant simplement sur X .Théorème 7.5 Condition de convergence de CAUCHY.Soit fnnN une suite d’applications de X dans K.La série d’applicationsPnNfn converge uniformément sur X si et seulement si :ϵ 0, N N, p N , q N , x X ,qXk=p+1fkx ϵDéfinition 7.8 Convergence localement uniforme. Soit I un intervalle de R.Une sériePnNfn d’applications de I dans K converge localement uniformémement sur I si et seule-ment siPnNfn converge uniformément sur tout segment inclus dans I .Proposition 7.9. Soit I un intervalle de R et fnnN une suite d’applications de I dans K.SiPnNfn converge uniformément sur I , alorsPnNfn converge localement uniformément sur I .SiPnNfn converge localement uniformément sur I , alorsPnNfn converge simplement sur I .Romain Dujol59

Page 61 : 7.1.4Convergence normaleDéfinition 7.9 Convergence normale.Une sériePnNfn d’applications de X dans K converge normalement sur X si et seulement si les deuxconditions suivantes sont vérifiées :1. il existe un entier naturel N tel que fn soit bornée sur X pour tout n N ;2. la série numériquePnNfnconverge.Proposition 7.10. SoitPnNfn une série d’applications de X dans K convergeant normalement sur X .Alors pour tout sous-ensemble X ′ de X ,PnNfn X ′ converge sur X ′.Proposition 7.11. Soit fnnN une suite d’applications de X dans K.Soit unnN une suite numérique telle que :n N, x X , fnx unetPnNun convergealorsPnNfn converge normalement sur X .Démonstration. Remarquons tout d’abord que :n N, x X , fnx un ⇐⇒n N, supxXfnx un ⇐⇒n N, fnunOrPnNun converge, donc d’après le théorème de minoration des séries à termes positifs, il vient quePnNfnconverge. On conclut quePnNfn converge normalement.Théorème 7.6 Structure algébrique. L’ensemble des séries d’applications de X dans K convergeantnormalement sur X est un sous-espace vectoriel :— de l’ensemble des séries d’applications de X dans K convergeant absolument sur X ;— de l’ensemble des séries d’applications de X dans K convergeant uniformément sur X .Définition 7.10 Convergence localement normale. Soit I un intervalle de R.Une sériePnNfn d’applications de I dans K converge localement normalemement sur I si et seule-ment siPnNfn converge normalement sur tout segment inclus dans I .Proposition 7.12. Soit I un intervalle de R et fnnN une suite d’applications de I dans K.SiPnNfn converge normalement sur I , alorsPnNfn converge localement normalement sur I .Romain Dujol60

Page 62 : On présente un plan pour l’étude de la convergence dePnNfn à adapter selon les besoins.Étape no 1 Étude de la convergence simple et absolue =⇒domaine D de convergence dePnNfnÉtape no 2 Calcul de fn= supxDfnx•PnNfnconverge =⇒PnNfn converge normalement sur D•PnNfndiverge grossièrement =⇒PnNfn ne converge pas uniformément sur D•PnNfndiverge non grossièrement =⇒Étape no 3Étape no 3 Étude de la convergence uniforme de Rnn sur D vers la fonction nulle :• x D,PnNfnx vérifie les conditions du théorème spécial à certaines séries alternées=⇒PnNfn converge uniformément sur D par majoration de Rn par fn+1• Minoration d’un paquet de CAUCHY par une suite ne convergeant pas vers 0=⇒PnNfn ne converge pas uniformément sur Dpar minoration de Rn par ce paquet de CAUCHYConvergenceabsolue?Convergence non normaleConvergencesimple?STOPAucune convergenceConvergencenormale?STOPToutes les convergencesfn→n→+0?STOPConvergence non uniformePeut-on appliquerle TSCSA?Minoration de Rnpar un paquet de CAUCHYSTOPConvergence non uniformeMajorationRn fn+1STOPConvergence uniformeNONNONOUIOUIOUINONNONOUINONOUIFIGURE 7.1 – Plan d’étude de la convergence de la série d’applicationsPnNfnRomain Dujol61

Page 63 : Exercice. Étudier la convergence des séries d’applicationsPnNfn définies par :1. pour tout n 1fn :R→Rx7→sinn xn22. pour tout n 1,fn :R+→Rx7→n xe nx3. pour tout n 1,fn :R+→Rx7→1n ln•1 + arctan xn˜4. pour tout n 1,fn :R+→Rx7→1n + n3x 2Solution.1. On a n 1, x R, fnx 1n2 .Pn11n2 converge doncPn1fn converge normalement sur R.2. Soit x R+.• Si x = 0, alors fn0 = 0 pour tout n 1 : doncPn1fn0 converge absolument.• Si x 0, alors e x 1.limn→+n2fnx = limn→+n3xe nx = limn→+n3xe x n = 0 par croissance comparéeD’après la règle « nαun »,Pn1fnx converge absolument.On en conclut quePn1fn converge absolument sur R+.Soit n 1. fn est dérivable sur R+ comme produit de fonctions dérivables sur R+.x R+, f ′nx = ne nx + x ·ne nx = ne nx 1 nxDonc f ′nx 0 si et seulement si 1 nx 0, i.e. x 1n .De plus fn0 = 0 etlimx→+fnx = limx→+nxe nx = 0 par croissance comparée.Enfin, fn 1n‹=n · 1n · e 1 = 1e . On en déduit le tableau de variations suivant :xf ′nfn01n++001e1e0+0+fn est une fonction positive sur R+ donc fn= supxR+fnx = supxR+fnx = fn 1n‹= 1e .fnn1 ne converge pas vers 0 doncPn1fn ne converge ni uniformément ni normalement sur R+.Romain Dujol62

Page 64 : 3. Soit x R+ : alors 1 + arctan xn1 puis ln•1 + arctan xn˜0.Donc n 1, fnx = ln•1 + arctan xn˜0 etPn1fnx est une série alternée.n 1,1n + 1 1n=⇒arctan xn + 1arctan xn=⇒1 + arctan xn + 11 + arctan xn.Donc fn+1x fnx pour tout n 1 : la suite fnxn1 est décroissante.De plus, fnxn→+arctan xn: donclimn→+fnx = 0. D’après le TSCSA,Pn1fnx converge.On en conclut quePn1fn converge simplement sur R+.Remarque. fnxn→+arctan xn: doncPn1fnx diverge sauf en x = 0.Pn1fn ne converge donc pas absolument ni normalement sur R+.Soit n 1. fn est dérivable sur R+ comme composée de fonctions dérivables.x R+, fn′x =11 + arctan xn·• 1n ·11 + x 2˜0Donc fn est croissante sur R+. De plus,limx→+arctan x = π2 : donclimx→+fnx = ln1 + π2n.Donc fn= supxRfnx = limx→+fnx = ln1 + π2n.D’après le TSCSA, n 1, x R+, Rnx =+Xk=n+1fkx fn+1x fn+1= ln•1 +π2n + 1˜.limn→+ln•1 +π2n + 1˜= 0 donc Rnn1 converge uniformément sur R+ vers la fonction nulle puisPn1fn converge uniformément sur R+.4. Soit x R+.• Si x = 0, fn0 = 1n pour tout n 1 : doncPn1fn0 diverge.• Si x 0, fnxn→+1n3x 2 .Pn11n3x 2 converge donc, par théorème d’équivalence,Pn1fnx converge absolument.On en conclut quePn1fn converge absolument sur son domaine de convergence R+.Soit n 1. Alors fn est dérivable sur R+ comme fraction rationnelle dont le dénominateur ne s’annulepas sur R+ et x R+, f ′nx =2n3xn + n3x 22 0.Donc fn est décroissante et positive sur R+ et fn= supxR+fnx = supxR+fnx = limx→0 fnx = 1n .On en déduit quePn1fn ne converge pas normalement sur R+.Romain Dujol63

Page 65 : Soit n 1 et x R+. Alors Rnx =+Xk=n+1fkx 2nXk=n+1fkx.Soit k 1, alors k k + 1 : donc k 3 k + 13 puis k 3x 2 k + 13x 2.D’où k + k 3x 2 k + 1 + k + 13x 2 puis fk+1x fkx.Donc Rnx 2nXk=n+1fkx 2nXk=n+1f2nx = n f2nx puis :n 1, Rn= supxR+Rnx = supxR+Rnx Rn 1n‹n f2n 1n‹=n2n + 8n3 · 1n2= 110Donc Rnn1 ne converge pas 0 puis Rnn1 ne converge pas uniformément sur R+ vers la fonctionnulle. On en conclut quePn1fn ne converge pas uniformément sur R+.Romain Dujol64

Page 66 : 7.2Théorèmes d’interversion7.2.1Interversion somme-limiteThéorème 7.7 Théorème d’interversion somme-limite.Soit a X etPnNfn une série d’applications de X dans K telle que :1. pour tout entier naturel n, fn admette une limite ℓn en a ;2.PnNfn converge uniformément sur X .AlorsPnNℓn converge, S =+Xn=0fn admet une limite finie en a et limx→a Sx =+Xn=0ℓn.Remarque. C’est-à-dire que limx→a–+Xn=0fnx™=+Xn=0hlimx→a fnxi.Démonstration. Vérifions que SnnN vérifie les hypothèses du théorème d’interversion des limites :1. Sn=nXk=0fk admet une limite en a comme somme finie d’applications admettant une limite en a etσn = limx→a Snx =nXk=0limx→a fnx =nXk=0ℓk ;2.PnNfn converge uniformément sur X donc SnnN converge uniformément sur X vers S.D’après ce théorème :1. σnnN =‚ nXk=0ℓkŒnNconverge : doncPnNℓn converge;2. S = limn→+Sn admet une limite fine en a ;3. limx→a Sx = limn→+σn =+Xn=0ℓn.Théorème 7.8. Soit a X etPnNfn une série d’applications de X dans K telle que :1. pour tout entier naturel n, fn est continue en a ;2.PnNfn converge uniformément sur X .Alors+Xn=0fn est continue en a.Démonstration. Vérifions les hypothèses du théorème d’interversion somme-limite.1. pour tout n N, fn est continue en a donc admet ℓn = fna comme limite en a ;2.PnNfn converge uniformément sur X vers S.Romain Dujol65

Page 67 : On applique le théorème d’interversion somme-limite avec la suite ℓnnN = fnanN :—PnNfn converge uniformément donc simplement sur X et donc en a ;— S admet une limite finie σ en a et σ =+Xn=0fna = Sa.On en conclut que limx→a Sx = Sa puis que S est continue en a.Corollaire. SoitPnNfn une série d’applications de X dans K telle que :1. pour tout entier naturel n, fn est continue sur X ;2.PnNfn converge uniformément sur X .Alors+Xn=0fn est continue sur X .Démonstration. On applique le théorème précédent en tout point a de X .Remarque. On utilise régulièrement la contraposée de ce théorème pour établir une absence de convergenceuniforme.Corollaire. Soit I un intervalle de R etPnNfn une série d’applications de I dans K telle que :1. pour tout entier naturel n, fn est continue sur I ;2.PnNfn converge localement uniformément sur I .Alors+Xn=0fn est continue sur I .Démonstration. Tout point de I est inclus dans un segment inclus dans I .Donc on conclut en appliquant le corollaire précédent sur tout segment inclus dans I .7.2.2Interversion somme-intégraleThéorème 7.9 Théorème d’interversion somme-intégrale.Soit a et b deux réels tels que a b etPnNfn une série d’applications de a,b dans K telle que :1. pour tout entier naturel n, fn est continue sur a,b ;2.PnNfn converge uniformément sur a,b.Alors S =+Xn=0fn est continue sur a,b et la sériePnNZ bafnxdx converge versZ baSxdx.Démonstration. Vérifions que SnnN vérifie les hypothèses du théorème d’interversion limite-intégrale :1. Sn =nXk=0fk est continue sur a,b comme somme finie d’applications continues sur a,b;2.PnNfn converge uniformément sur X donc SnnN converge uniformément sur X vers S.Romain Dujol66

Page 68 : D’après ce théorème :1. S est continue sur a,b ;2.‚Z baSnxdxŒnN=‚Z banXk=0fkxdxŒnN=‚ nXk=0Z bafkxdxŒnNconverge versZ baSxdx : doncPnNZ bafnxdxconverge versZ baSxdx.7.2.3Interversion somme-dérivationThéorème 7.10 Théorème d’interversion somme-dérivation.Soit a et b deux réels tels que a b etPnNfn une série d’applications de a,b dans K telle que :1. pour tout entier naturel n, fn est de classe C 1 sur a,b;2.PnNf ′n converge uniformément sur a,b vers S1 ;3. il existe x0 de a,b tel quePnNfnx0 converge.Alors :1.PnNfn converge uniformément sur a,b vers une application notée S ;2. S est une application de classe C 1 sur a,b ;3. S′1 = S.Démonstration. Vérifions que SnnN vérifie les hypothèses du théorème d’interversion limite-dérivation :1. Sn =nXk=0fk est de classe C 1 sur a,b comme somme finie d’applications de classe C 1 sur a,b ;2.PnNf ′n converge uniformément sur a,b donc‚ nXk=0f ′kŒnN=‚‚ nXk=0fkŒ′ŒnN= S ′nnN converge uniformément sura,b vers S1 ;3.PnNfnx0 converge donc‚ nXk=0fkx0ŒnN= Snx0nN converge.D’après ce théorème :1. SnnN converge uniformément sur a,b vers S doncPnNfn converge uniformément sur a,b vers S ;2. S est de classe C 1 sur a,b ;3. S ′ = S1.Romain Dujol67

Page 69 : Théorème 7.11 Théorème d’interversion somme-dérivation.Soit I un intervalle de R etPnNfn une série d’applications de I dans K telles que :1. pour tout entier naturel n, fn est de classe C 1 sur I ;2.PnNf ′n converge localement uniformément sur I vers S1 ;3. il existe x0 de I tel quePnNfnx0 converge.Alors :1.PnNfn converge localement uniformément sur I vers une application notée S ;2. S est une application de classe C 1 sur I ;3. S′ = S1.Démonstration. On applique le théorème précédent sur tout segment inclus dans I .ATTENTION. Si I n’est pas un segment, l’énoncé obtenu en enlevant « uniformémement » dans les hypothèseset dans la conclusion n’est pas valable.Romain Dujol68

Page 70 : Troisième partieSéries entières. Séries de FOURIERRomain Dujol69

Page 71 : Thème no 8Séries entières : rayon de convergenceDéfinition 8.1 Série entière. Soit annN une suite complexe.On appelle série entière de coefficient an la série d’applications de C dans CPnNz 7→anz n.Théorème 8.1 Structure algébrique. L’ensemble des séries entières est une sous-algèbre vectorielle del’ensemble des séries d’applications de C dans C.En effet, siPnNz 7→anz n etPnNz 7→bnz n sont deux séries entières, alors :XnNz 7→anz n +XnNz 7→bnz n =XnNz 7→an + bnz nXnNz 7→anz n ×XnNz 7→bnz n =XnN–z 7→‚ nXk=0ak bnkŒz n™λ C,λ ·XnNz 7→anz n =XnNz 7→λanz n8.1DéfinitionLemme Lemme d’ABEL. SoitPnNz 7→anz n une série entière et z0 un nombre complexe non nul tel que lasuite anz n0 n soit bornée. Alors :z C,‚z z0 =⇒XnNanz n converge absolumentŒDémonstration. On note M un majorant de la suite anz n0 n : n N,anz n0 M . Alors :n N,anz n =anz n0 · z nz n0 =anz n0 ·z nz n0 M zz0‹nSi z z0, alors zz0 1 etPnN zz0‹nest une série géométrique convergente. D’après le théorème de majoration desséries à termes positifs, il vient quePnNanz n converge absolument.Romain Dujol70

Page 72 : Théorème 8.2 Rayon de convergence. Pour toute série entièrePnNz 7→anz n, il existe un unique éle-ment R 0,+ tel que :z C,z R=⇒PnNanz n converge absolumentz R=⇒PnNanz n diverge grossièrementR est appelé le rayon de convergence dePnNz 7→anz n.Le disque de convergence dePnNz 7→anz n le disque ouvert de centre 0 et de rayon R.L’intervalle de convergence dePnNz 7→anz n l’ensemble R,R.Démonstration page 77.Remarque.• Une série entière de rayon de convergence nul a un domaine de convergence réduit à 0.• Une série entière de rayon de convergence infini converge en tout point de C.Remarque. Il est impossible d’énoncer un résultat général lorsque z = R. En effet, des séries entières de mêmerayon de convergence R peuvent se comporter de manière différente lorsque z = R.C’est pourquoi on appelle souvent cercle d’incertitude le cercle de centre 0 et de rayon R.Exemple. Les séries entièresPnNz 7→z n,Pn1z 7→z nn‹etPn1z 7→z nn2‹ont un rayon de convergence égal à 1.Pourtant :— la série numériquePnNz n diverge pour tout z C tel que z = 1;Démonstration.limn→+z n = 1 donc z nnN ne tend pas vers zéro, etPnNz n diverge grossièrement.— la série numériquePn1z nn est semi-convergente pour tout nombre complexe z tel que z = 1 sauf z = 1où elle diverge.Démonstration.— Si z = 1,Pn1z nn =Pn11n diverge.— Sinon, z = e iθ avec θ /2πZ etPnz nn =Pn1cosnθn+ iPn1sinnθn.Les deux séries sont semi-convergentes d’après la règle d’ABEL.— la série numériquePn1z nn2 est absolument convergente pour tout z C tel que z = 1.Démonstration. n 1,z nn2 1n2 : d’où la convergence absolue dePn1z nn2 .Romain Dujol71

Page 73 : 8.1.1PropriétésCorollaire. SoitPnNz 7→anz n une série entière de rayon de convergence R et z0 un nombre complexe nonnul tel que la suite anz n0 n soit bornée. Alors R z0.Démonstration. Supposons par l’absurde que R z0. Soit z un nombre complexe tel que z R,z0 :— comme z z0, il vient d’après le lemme d’ABEL quePnNanz n converge absolument;— comme z R, il vient d’après la définition du rayon de convergence quePnNanz n diverge grossièrement.Il y a contradiction : donc R z0.Corollaire. SoitPnNz 7→anz n une série entière de rayon de convergence R. Alors :z C,PnNanz n converge=⇒z RPnNanz n diverge=⇒z RDémonstration. C’est la contraposée du théorème précédent.8.1.2Cas particuliersProposition 8.1. Soit a un nombre complexe non nul.Alors la série entièrePnNz 7→a nz n a pour rayon de convergence R = 1a etz C,‚z 1a =⇒+Xn=0a nz n =11 a zŒDémonstration. Soit z un nombre complexe.— Si z 1a, alors a z 1 etPnNa zn =PnNa nz n converge absolument.— Si z 1a, alors a z 1 etPnNa zn =PnNa nz n diverge grossièrement.On déduit de la définition du rayon de convergence que R = 1a.Proposition 8.2. Soit α un nombre réel.Alors la série entièrePn1z 7→z nnα‹a pour rayon de convergence R = 1.Démonstration. Soit z un nombre complexe.— Si z 1, alors n2 ·z nnα = n2αzn →n→+0 par croissance comparée.D’après la règle « nαun »,Pn1z nnα converge absolument.— Si z 1, alors limn→+znnα = +par croissance comparée. Doncz nnαn1ne converge pas vers zéro puis z nnα‹n1ne converge pas vers zéro etPn1z nnα diverge grossièrement.On déduit de la définition du rayon de convergence que R = 1.Romain Dujol72

Page 74 : 8.2Stabilités opératoires8.2.1Structure vectorielleThéorème 8.3. SoitPnNz 7→anz n une série entière de rayon de convergence R de somme S.Pour tout nombre complexe λ non nul, la série entièrePnNz 7→λanz n a pour rayon de convergenceR et sa somme Sλ vérifie :z C,”z R =⇒Sλz = λ ·Sz—Théorème 8.4 Domaine de convergence de la somme de deux séries entières.SoitPnNz 7→anz n de rayon de convergence Ra et de somme Sa.SoitPnNz 7→bnz n de rayon de convergence Rb et de somme Sb .On note R le rayon de convergence etS la somme de leur série entière somme. Alors R minRa,Rb etz C,”z minRa,Rb =⇒Sz = Saz +Sb z—De plus, si Ra ̸= Rb , alors R = minRa,Rb .Exemple. Soit a 0,1.Alors les séries entières coefficients an = 1 + a n et bn = 1 ont pour rayon de convergence 1.Mais leur série entière somme de coefficient an +bn = a n a pour rayon de convergence 1a ou +si a = 0.Définition 8.2 Séries entières disjointes.Les séries entièresPnNz 7→anz n etPnNz 7→bnz n sont dites disjointes si et seulement si anbn = 0pour tout entier naturel n.Proposition 8.3 Somme de deux séries disjointes.SoitPnNz 7→anz n etPnNz 7→bnz n deux séries entières disjointes de rayons de convergence respectifsRa et Rb . Alors leur série entière sommePnNz 7→an + bnz n a pour rayon de convergence R = minRa,Rb .Exemple. Calcul du rayon de convergence dePnNz 7→n1n z nPnNz 7→n1n z n=PpNz 7→2pz 2p+PpNz 7→z 2p+12p + 1est la somme de deux séries entières disjointes.Pour z C et p N, on note up = 2pz 2p.Si z = 0, alorsPpNup =PpN0 converge.Si z ̸= 0, alors p 1, up ̸= 0 etup+1up =2p + 2z 2p+22pz 2p = p + 1p· z2 →p→+z2.Romain Dujol73

Page 75 : D’après la règle de D’ALEMBERT :— si z2 1 ⇒z 1, alorsPpNup =PpN2p · z 2p converge;— si z2 1 ⇒z 1, alorsPpNup =PpN2p · z 2p diverge.Par unicité du rayon de convergence, R = 1.De même, le rayon de convergence dePpNz 7→z 2p+12p + 1vaut 1.Donc le rayon de convergence dePnNz 7→n1n z nest min1,1 = 1.8.2.2ProduitThéorème 8.5 Domaine de convergence du produit de deux séries entières.SoitPnNz 7→anz n de rayon de convergence Ra et de somme Sa.SoitPnNz 7→bnz n de rayon de convergence Rb et de somme Sb .On note R le rayon de convergence et S la somme de leur série entière produit. AlorsR minRa,Rb etz C,”z minRa,Rb =⇒Sz = Saz ·Sb z—8.2.3DérivationDéfinition 8.3 Sérieentièredérivée.Onappellesérie entière dérivée de la série entièrePnNz 7→anz n la série entièrePnNz 7→n + 1an+1z n.Proposition 8.4. Une série entière et sa série entière dérivée ont même rayon de convergence.Démonstration page 79.Corollaire. Une série entière et ses séries dérivées à tout ordre ont le même rayon de convergence.8.3Méthodes d’évaluation du rayon de convergence8.3.1Théorèmes de comparaisonThéorème 8.6 Théorème de majoration des séries entières.SoitPnNz 7→anz n etPnNz 7→bnz n deux séries entières de rayons de convergence respectifs Ra etRb tels que an bn pour tout entier naturel n. Alors Ra Rb .Romain Dujol74

Page 76 : Démonstration. Supposons par l’absurde que Ra Rb . Soit z un nombre complexe tel que z Ra,Rb :— comme z Rb , il vient quePnNbnz n converge absolument : doncPnNanz n converge absolument par théorèmede majoration des séries à termes positifs;— comme z Ra, il vient quePnNanz n diverge.Il y a contradiction : donc Ra Rb .Corollaire. SoitPnNz 7→anz n etPnNz 7→bnz n deux séries entières de rayons de convergence respectifs Raet Rb tels que an = Obn. Alors Ra Rb .Remarque. Le résultat est donc valable si an = obn.Corollaire Théorème d’équivalence des séries entières. SoitPnNz 7→anz n etPnNz 7→bnz n deux sériesentières de rayons de convergence respectifs Ra et Rb tels que an bn. Alors Ra = Rb .Démonstration. Comme an bn, alors an = Obn et bn = Oan. D’où le résultat.Exemple. Déterminer le rayon de convergence des séries entières suivantes :1.Pnz 7→e sinnz n2.Pn•z 7→§1 + 1n‹neªz n˜8.3.2Règles de calculThéorème 8.7 Règle de D’ALEMBERT. SoitPnNz 7→anz n une série entière de rayon de convergence Rtelle que il existe un entier naturel N tel quen N , an ̸= 0etan+1annNconverge vers ℓ0,+Alors R = 1ℓavec la convention 10 = +et1+= 0.Démonstration. Pour z C et n N, on note un = anz n.Si z = 0, alors un = 0 etPnNun converge absolument. Sinon, pour tout n N , un ̸= 0 et :un+1un =an+1z n+1anz n =an+1an ·z n+1z n =an+1an · z• ℓ0,+ Alors limn→+un+1un = ℓz. D’après la règle de D’ALEMBERT pour les séries numériques :— si ℓz 1, c’est-à-dire z 1ℓ, alors la série numériquePnNun =PnNanz n converge absolument;— si ℓz 1, c’est-à-dire z 1ℓ, alors la série numériquePnNun =PnNanz n diverge.Par unicité du rayon de convergence, R = 1ℓ.Romain Dujol75

Page 77 : • ℓ= 0 Alorslimn→+un+1un = 0. D’après la règle de D’ALEMBERT pour les séries numériques,PnNun =PnRanz n converge.On déduit de la définition du rayon de convergence que R = +est la seule valeur possible.• ℓ= +Alorslimn→+un+1un = +. D’après la règle de D’ALEMBERT pour les séries numériques,PnNun =PnNanz n di-verge. On déduit de la définition du rayon de convergence que R = 0 est la seule valeur possible.Remarque. Afin de différencier cette règle et son homonyme du chapitre précédent, on indiquera « règle deD’ALEMBERT pour les séries entières » ou « règle de D’ALEMBERT pour les séries numériques ».Théorème 8.8 Règle de CAUCHY. SoitPnNz 7→anz n une série entière de rayon de convergence R tellequenpann1 converge vers ℓ0,+.Alors R = 1ℓavec la convention 10 = +et1+= 0.Démonstration. Pour z C et n N, on note un = anz n.nÆun =nÆanz n =nÆanzn =nÆan ·z• ℓ0,+ Donc limn→+nÆun = ℓz. D’après la règle de CAUCHY pour les séries numériques :— si ℓz 1, c’est-à-dire z 1ℓ, alors la série numériquePnNun =PnNanz n converge absolument;— si ℓz 1, c’est-à-dire z 1ℓ, alors la série numériquePnNun =PnNanz n diverge.Par unicité du rayon de convergence, R = 1ℓ.• ℓ= 0 Alorslimn→+nÆun = 0. D’après la règle de CAUCHY pour les séries numériques,PnNun =PnNanz n converge. Ondéduit de la définition du rayon de convergence que R = +est la seule valeur possible.• ℓ= +Alors limn→+nÆun = +. D’après la règle de CAUCHY pour les séries numériques,PnNun =PnNanz n diverge.On déduit de la définition du rayon de convergence que R = 0 est la seule valeur possible.Remarque. Afin de différencier cette règle et son homonyme du chapitre précédent, on indiquera « règle deCAUCHY pour les séries entières » ou « règle de CAUCHY pour les séries numériques ».Exemple. Déterminer le rayon de convergence des séries entières suivantes :1.PnNz 7→e nn z n2.PnNz 7→nz 2nRomain Dujol76

Page 78 : Annexe ADémonstration du théorème 8.2 non exigibleSoitPnNz 7→anz n une série entière.On note A l’ensemble des nombres complexes z0 tels que la suite numérique anz n0 n est bornée, puis ondéfinit A = A = z0, z0 A l’ensemble des modules des éléments de A : remarquons que A est une partiede R+ par construction.Comme 0 est un élément de A , il vient que 0 = 0 est un élément de A : donc A est une partie non vide de R.Le lemme d’ABEL se formule alors de la manière suivante :z0 A =⇒z C, z z0 ⇒z A A.1Soit r0 est un élément de A : alors il existe un nombre complexe z0 de module r0 qui appartient à A . Donc sir 0,r0, alors il existe un nombre complexe z de module r r0 = z0 qui appartient à A . l’équation A.1permet de alors de déduire que z A , puis que r A. On vient de montrer que 0,r0 A. Finalement, on al’implication suivante :r0 A =⇒0,r0 AA.2Autrement dit : si un réel positif appartient à A, tous les réels positifs qui lui sont inférieurs y sont également.Pour montrer que R existe, on distingue deux cas selon que A est une partie majorée ou non.• Supposons que A ne soit pas majorée : montrons que A = R+.Soit r R+ : comme A n’est pas majorée, il existe un élément r1 de A tel que r1 r . D’après la rela-tion A.2, il vient que r 0,r1A : donc r A. On en déduit que R+ A : comme A est une partie deR+, on en conclut que A = R+.Soit z Cet z0 = 2·z. Comme z0 R+ = A, il vient que la suite anz n0 n est bornée. Puisque z 2·z =z0 = z0, le lemme d’ABEL permet de conclure que la série numériquePnNanz n converge absolument.Donc la série numériquePnNanz n converge pour tout nombre complexe z et R = +vérifie la conditiondemandée.Romain Dujol77

Page 79 : • Supposons que A est majorée : comme A est non vide, elle admet donc une borne supérieure. Montronsque supA est la valeur recherchée.· Soit z C tel que z supA : alors z n’est pas un élément de A.Donc z n’est pas un élément de A et la suite anz nn n’est pas bornée et donc ne converge pas.On en déduit que la série numériquePnNanz n diverge grossièrement.· Soit z C tel que z supA. Alors il existe un réel ϵ 0 tel que z supA ϵ et tel que supA ϵsoit un élément de A.Donc il existe un nombre complexe z0 tel que z0 = supA ϵ et la suite anz n0 n est bornée.On en déduit d’après le lemme d’ABEL, la série numériquePnNanz n converge absolument.R = supA est bien la valeur qui vérifie la valeur demandée.L’unicité de R vient directement de sa définition.Romain Dujol78

Page 80 : Annexe BDémonstration de la proposition 8.4 nonexigibleOn note R le rayon de convergence de la série entièrePnn0z 7→anz n et R ′ le rayon de convergence de sasérie entière dérivéePnn0z 7→n + 1an+1z n.Pour tout entier naturel n strictement ou égal à n0, on a an+1 n + 1 · an+1.Comme les rayons de convergence dePnn0z 7→an+1z n etPnn0z 7→anz n sont égaux, on en déduit d’aprèsle théorème de majoration des séries entières que R R ′.Soit z un nombre complexe que z R : alors la série numériquePnn0anz n converge absolument.Soit r = z + R2z,R. Alors n n0, n + 1an+1z n = n + 1rz nr n · an+1r n+1.Comme z r , on azr = zr 1 : donclimn→+n + 1rz nr n =limn→+n + 1rzrn= 0 par croissance comparée.Donc la suiten + 1rz nr n‹nn0est bornée. On note M un majorant de cette suite et :n n0, n + 1an+1z n M an+1r n+1 = M an+1r n+1Comme les rayons de convergence dePnn0z 7→an+1z n+1etPnn0z 7→anz n sont égaux et que r R, la sérienumériquePnn0M an+1r n+1 est convergente.D’après le théorème de majoration des séries à termes positifs, il vient que la série numériquePnn0n + 1an+1z n est également convergente.La définition du rayon de convergence permet alors d’en déduire que z R ′.On vient donc de montrer que pour tout réel r strictement positif, r R ⇒r R ′, i.e. R R ′.On en conclut donc que R = R ′.Romain Dujol79

Page 81 : Chapitre 9Séries entières : somme et développements9.1Convergence et régularité de la somme9.1.1ConvergenceThéorème 9.1 Convergence d’une série entière.SoitPnNz 7→anz n une série entière de rayon de convergence R.Alors la série d’applicationsPnNz 7→anz n converge normalement sur toute partie compacteincluse dans le disque ouvert de centre 0 et de rayon R.Démonstration page 87.9.1.2ContinuitéThéorème 9.2 Continuité de la somme.SoitPnNz 7→anz n une série entière de rayon de convergence R et de somme S. Alors S est continuesur le disque ouvert de centre 0 et de rayon R.Démonstration. Pour tout entier naturel n, z 7→anz n est continue.D’après le théorème précédent, la série d’applicationsPnNz 7→anz n converge localement normalement, donc locale-ment uniformément sur le disque ouvert de centre 0 et de rayon R. Donc sa somme S y est continue.Proposition 9.1 Étude aux bornes de l’intervalle de convergence.SoitPnNz 7→anz n une série entière de rayon de convergence R et de somme S.Si la série numériquePnNanR n converge absolument, alors la série entière converge normalement sur ledisque fermé de centre 0 et de rayon R, et S y est continue en particulier en R et en R.Si la série numériquePnNanR n converge, alors la série entière converge uniformément sur 0,R et S estcontinue en R.Si la série numériquePnNanRn converge, alors la série entière converge uniformément sur R,0 et Sest continue en R.Romain Dujol80

Page 82 : 9.1.3DérivabilitéThéorème 9.3 Dérivabilité de la somme.SoitPnNz 7→anz n une série entière de rayon de convergence R non nul et de somme S.Alors S est de classe C sur R,R etp N, x R,R, Spx =+Xn=pn!n p!an x np =+Xn=0n + p!n!an+p x nExemple. On peut ainsi évaluer les dérivées de la série géométrique.En effet, pour tout x de 1,1, Sx =+Xn=01 · x n =11 x . Donc :11 x2 = S′x =+Xn=1n!n 1! x n1 =+Xn=1nx n1 =+Xn=0n + 1x n21 x3 = S′′x =+Xn=2n!n 2! x n2 =+Xn=2nn 1x n2 =+Xn=0n + 2n + 1x nCorollaire. SoitPnNz 7→anz n une série entière de de rayon de convergence non nul et de somme S.Alors pour tout entier naturel p, ap = Sp0p!.Corollaire Unicité du développement en série entière.SoitPnNz 7→anz n etPnNz 7→bnz n deux séries entières de rayons de convergence respectifs Ra et Rb nonnuls tels que :z R,–z minRa,Rb =⇒+Xn=0anz n =+Xn=0bnz n™Alors an = bn pour tout entier naturel n.Corollaire Développement en série entière de la somme.SoitPnNz 7→anz n une série entière de rayon de convergence R non nul et de somme S.Alors x R,R, Sx =+Xp=0Sp0p!x p.Romain Dujol81

Page 83 : 9.2Développement en série entière9.2.1GénéralitésDéfinition 9.1. Soit I un intervalle de R et f une application de I dans C.L’application f est dite développable en série entière en 0 si et seulement si 0 �I et il existe une sérieentièrePnNz 7→anz n de rayon de convergence R non nul telle que :x I R,R, f x =+Xn=0an x nAuquel cas, cette relation constitue le développement en série entière de f en 0.Soit x0 un élément de I . L’application f est dite développable en série entière en x0 si et seulement six0 �I et il existe une série entièrePnNz 7→anz n de rayon de convergence R non nul telle que :x I x0 R, x0 + R, f x =+Xn=0anx x0nAuquel cas, cette relation constitue le développement en série entière de f en x0.Théorème 9.4. Soit I un intervalle de R et f une application de I dans C développable en série entièreen 0 avec le développement :x I R,R, f x =+Xn=0an x nAlors f est de classe C sur I R,R et an = f n0n!pour tout entier naturel n.ATTENTION. Toute fonction de classe C au voisinage de 0 n’est pas développable en série entière.Exemple. Soit f : t 7→e 1/t 2. Alors on montre que pour tout entier naturel n, f n0 = 0 : donc si f étaitdéveloppable en série entière en 0, alors f serait nulle, ce qui n’est pas le cas.Proposition 9.2. Soit I un intervalle de R et f une application de I dans C développable en série entière en 0avec le développement :x I R,R, f x =+Xn=0an x nSi f est paire, alors a2p+1 = 0 pour tout entier naturel p.Si f est impaire, alors a2p = 0 pour tout entier naturel p.Démonstration. x I R,R, f x =+Xn=0anxn =+Xn=01nan x n— Si f est paire, alors x I R,R,+Xn=0an x n = f x = f x =+Xn=01nan x n.Par unicité du développement en série entière, il vient que an = 1nan pour tout entier naturel n.En particulier, si n = 2p + 1 est impair, a2p+1 = a2p+1 i.e. a2p+1 = 0.— Si f est impaire, alors x I R,R,+Xn=0an x n = f x = f x =+Xn=01nan x n.Par unicité du développement en série entière, il vient que an = 1nan pour tout entier naturel n.En particulier, si n = 2p est pair, a2p = a2p i.e. a2p = 0.Romain Dujol82

Page 84 : Proposition 9.3 avec le reste intégral.Soit I un intervalle de R et f une application de classe C de I dans C.Alors f est développable en série entière au voisinage de 0 si et seulement si il existe un réel strictementpositif α tel que α,α I etx α,α,limn→+Z x0x t nn!f n+1t dt = 0Exemple Développement en série entière de l’exponentielle.On note f : x 7→e x : alors f ′ = f et par suite f n = f pour tout entier naturel.Soit x un nombre réel quelconque. Alors :Z x0x t nn!f n+1t dt =Z x0x t nn!e t dtmax1,e x Z x0x t nn!dt = max1,e x x t n+1n + 1!x0 = max1,e x x n+1n + 1! = max1,e x xn+1n + 1!Orlimn→+xnn! = 0, puislimn→+Z x0x t nn!f n+1t dt = 0.Évaluons le rayon de convergence de la sériePnNz 7→f n0n!z n=PnNz 7→1n!z n‹en utilisant la règle deD’ALEMBERT pour les séries entières :1n + 1! ·n! = 1n →n→+0. Il vient donc le rayon de convergence est infini.On en conclut que la fonction exponentielle est développable en série entière en 0 et :x R, e x =+Xn=0x nn!Théorème 9.5 Condition suffisante d’existence.Soit I un intervalle de R et f une application de classe C de I dans C telle que :M 0, n N, supxIf nx MAlors f est développable en série entière en 0.Exemple Développement en série entière du cosinus et du sinus.Pour tout nombre réel x, on a :cos′x = sinx = cosx + π2etsin′x = cosx = sinx + π2Il vient alors par récurrence que :cosnx = cosx + n π2etsinnx = sinx + n π2Donc pour tout entier naturel n et tout réel x, cosnx 1 et sinnx 1. On en déduit que cos et sin sontdéveloppables en série entière en 0.Romain Dujol83

Page 85 : Calculons les coefficients du développpement en série entière :cosn0 = cosn π2=¨1n/2si n est pair0si n est impairet sinn0 = sinn π2=¨0si n est pair1n1/2si n est impairOn étudie la série entièrePnNz 7→cosn0n!z n=PpN•z 7→1p2p! z 2p˜.Pour z C et p N, on pose up = 1p2p! z 2p. Si x = 0, alors up = 0 etPpup converge absolument.Sinon, up ̸= 0 etup+1up = z2p+22p + 2! · 2p!z2p =z22p + 12p + 2. Donclimp→+up+1up = 0 1 etPpNup convergeabsolument.Par unicité du rayon de convergence, celui de la série entièrePp•z 7→1p2p! z 2p˜a un rayon de convergenceinfini.Onmontredemanièreidentiquequ’ilenestdemêmepourlasérieentièrePpN•z 7→1p2p + 1!z 2p+1˜. On en conclut que x R, cos x =+Xn=01n x 2n2n!et sin x =+Xn=01n x 2n+12n + 1!.9.2.2Structure algébrique de l’ensemble des fonctions développables en série entièreThéorème 9.6 Somme et produit de fonctions développables en série entière.L’ensemble des fonctions développables en série entière en 0 une sous-algèbre de l’ensemble desfonctions de classe C sur un voisinage de 0.De plus, l’application qui à toute fonction développable en série entière en 0 associe son dévelop-pement est un morphisme d’algèbres vectorielles.Exemple Développement en série entière du cosinus et du sinus hyperbolique.La fonction x 7→e x est développable en série entière et x R, e x =+Xn=01nn!x n.Alors ch : x 7→e x + e x2est développable en série entière en 0. Ce développement est valable sur R commesomme de développements valables sur R et dont le terme général du coefficient est :12• 1n! + 1nn!˜= 1 + 1n2· 1n! =1n!si n est pair0si n est impairOn montre de même que sh : x 7→e x e x2est développable en série entière en 0, que son développementest valable sur R et que le terme général du coefficient de son développement est :12• 1n! 1nn!˜= 1 1n2· 1n! =0si n est pair1n!si n est impairx R, ch x =+Xn=0x 2n2n! et sh x =+Xn=0x 2n+12n + 1!Romain Dujol84

Page 86 : Théorème 9.7. Soit I un intervalle de R et f une application de I dans C.Si f est une fonction développable en série entière en 0, alors f ′ est développable en série entièreen 0 et son développement est la série entière dérivée du développement de f .Si f est une fonction développable en série entière en 0, alors toute primitive de f est développableen série entière en 0 et son développement admet le développement de f pour série dérivée.Exemple Développement en série entière du logarithme.On rappelle que x 7→11 x est développable en série entière en 0 et que son développement est valablesur 1,1 :x 1,1,11 x =+Xn=0x nOr x 7→ln1 x est la primitive de x 7→11 x qui s’annule en 0. Donc x 7→ln1 x est développableen série entière en 0 avec pour développement :x 1,1, ln1 x =+Xn=0x n+1n + 1 =+Xn=1x nnEn étudiant la série entièrePn1z 7→z nn‹, on établit successivement que :— son rayon de convergence est égal à un en utilisant la règle de D’ALEMBERT pour les séries entières;— elle converge uniformément sur 1,0 car la série numériquePn11nnest une série de RIEMANN alter-née convergente.Donc la somme de la série entière est en continue en 1 et :x 1,1, ln1 x = +Xn=1x nnpuis en appliquant le changement de variable x ↔x :x 1,1, ln1 + x =+Xn=11n+1x nnOn en déduit alors que ln2 = ln1 + 1 =+Xn=11n+1n.9.2.3Utilisation des équations différentiellesLes équations différentielles et les séries entières peuvent interagir de deux manières différentes.• Étant donné une équation différentielle, trouver des solutions développables en série entière.• Étant donnée une fonction développable en série entière, trouver l’expression de son développement àl’aide d’une équation différentielle qu’elle vérifie.Romain Dujol85

Page 87 : Exemple. Soit α un nombre réel fixé etfα : 1,+→Rx7→1 + xα.Alors fα est de classe C sur 1,+ et x 1,+, f ′αx = α1 + xα1 = α1 + xα1 + x=α1 + x fαx.Donc fα est solution sur 1,+ de l’équation différentielle 1 + xy ′ αy = 0E .Soit y une solution de E développable en série entière en 0. Alors il existe R 0 tel que :x 1,+ R,R, y x =+Xn=0an x nAlors y ′x =+Xn=0n + 1an+1x n =+Xn=1nan x n1. On réinjecte les expressions de y et y ′ dans E :0 = 1 + xy ′ αy = y ′ + x y ′ αy=+Xn=0n + 1an+1x n + x+Xn=1nan x n1 α+Xn=0an x n =+Xn=0n + 1an+1x n ++Xn=1nan x n +Xn=0αan x n=+Xn=0n + 1an+1x n ++Xn=0nan x n +Xn=0αan x n =+Xn=0n + 1an+1 + n αanx nPar unicité du développement en série entière de x 7→0, on déduit que n + 1an+1 + n αan = 0 pour toutentier naturel n, c’est-à-dire que an+1an= α nn + 1 .Montrons par récurrence que pour tout entier naturel n non nul, an = αα 1···α n + 1n!a0 :— si n = 1, a1 = α 00 + 1 a0 = αa0 = α1!a0 ;— si n est un entier naturel non nul tel que an = αα 1···α n + 1n!a0, alors d’après la relation de récur-rence établie plus haut, an+1 = α nn + 1 an = α nn + 1αα 1···α n 1n!a0 = αα 1···α nn + 1!a0.On en déduit donc que an = αα 1···α n + 1n!a0 pour tout entier naturel non nul n.Commelimn→+an+1an =limn→+α nn + 1 = 1, il vient d’après la règle de D’ALEMBERT pour les séries entièresque le rayon de convergence dePnNz 7→anz n est R = 1.Réciproquement, la somme S de cette série entière est de classe C sur 1,1 et constitue une solutionde l’équation différentielle 1 + xy ′ αy = 0 sur 1,1.La théorie des équations différentielles linéaires homogènes du premier ordre assure que toute solutionde cette équation différentielle est de la forme x 7→C e g x où C est une constante réelle quelconque et g uneprimitive de x 7→α1 + x . Ainsi, toute solution est de la forme x 7→C e αln1+x = C · 1 + xα.Il est en donc de même pour S : il existe une constante réelle C telle quex 1,1, Sx = a0–1 ++Xn=1αα 1···α n + 1n!x n™= C · 1 + xαEn imposant a0 = 1, il vient que 1 = S0 = C ·1+0α = C et x 1,1, 1 + xα = 1 ++Xn=1αα 1···α n + 1n!x n .Romain Dujol86

Page 88 : Annexe CDémonstration de la théorème 9.1 nonexigibleRemarque. Cette démonstration utilise des notions traitées dans le module « Analyse dans Rn ».Montrons d’abord que pour tout réel r de 0,R, la série d’applicationsPnNz 7→anz n converge normalement sur ledisque fermé Dr de centre 0 et de rayon r , i.e. Dr = z C, z r .Soit r 0,R. Comme r R, la série numériquePnNanr n converge absolument.Soit alors z Dr : alors z r et anz n an · zn an · r n = anr n pour tout n.Chaque application z 7→anz n est donc bornée sur Dr par un = anr n qui est le terme général d’une série absolumentconvergente : la série d’applicationsPnNz 7→anz n converge normalement sur Dr .Soit K un compact inclus dans le disque ouvert de centre 0 et de rayon R. L’application · module complexe estcontinue sur K , donc elle y est bornée et y atteint ses bornes. C’est-à-dire que :€zM K , supzKz = zM Š⇐⇒€zM K , z K ,z zM Š⇐⇒€zM K , K DzM ŠComme zM est un élément de K , il vient que zM R. D’après ce qui précède, la série d’applicationsPnz 7→anz nconverge normalement sur DzM et donc sur K .Romain Dujol87

Page 89 : Annexe DDéveloppements en série entière en 0x R,e x =+Xn=0x nn!x R,ch x =+Xn=0x 2n2n!x R,sh x =+Xn=0x 2n+12n + 1!x R,cos x =+Xn=01n x 2n2n!x R,sin x =+Xn=01n x 2n+12n + 1!x 1,1,1 + xα = 1 ++Xn=1αα 1···α n + 1n!x nvalable sur R si α Nx 1,1,11 x =+Xn=0x nx 1,1,11 x2 =+Xn=0n + 1x n=+Xn=1nx n1x 1,1,21 x3 =+Xn=0n + 2n + 1x n=+Xn=2nn 1x n2x 1,1,11 + x =+Xn=01n x nx 1,1,ln1 x =+Xn=1x nnx 1,1,ln1 + x =+Xn=11n+1x nnx 1,1,arctan x =+Xn=01n x 2n+12n + 1Romain Dujol88

Page 90 : x 1,1,argth x = 12 ln1 + x1 x‹=+Xn=0x 2n+12n + 1x 1,1,arcsin x =+Xn=01 · 3 · ··· ·2n 12 · 4 · ··· ·2nx 2n+12n + 1=+Xn=02n!2nn!2x 2n+12n + 1x 1,1,argsh x =+Xn=01n 1 · 3 · ··· ·2n 12 · 4 · ··· ·2nx 2n+12n + 1 =+Xn=01n 2n!2nn!2x 2n+12n + 1Romain Dujol89

Page 91 : Chapitre 10Séries de FOURIERLors de l’étude de sytèmes analogiques filtres, ..., on se ramène souvent à l’étude de termes purementsinusoïdaux. Dans le cas où le système est linéaire, la stratégie est décomposer l’entrée en signaux sinusoïdaux,appliquer le système à chacun des termes de la décomposition et générer la sortie en sommant les termesobtenus c’est la propriété dite « de superposition ».10.1Séries trigonométriques réelles10.1.1DéfinitionDéfinition 10.1 Série trigonométrique réelle.On appelle série trigonométrique réelle toute série d’applications de la formeXnNt 7→an cosnωt + bn sinnωt où annN et bnnN sont deux suites numériques à valeurs réelles et ω un nombre réel strictement positif.10.1.2ConvergenceProposition 10.1. Soit α R tel quePnNt 7→an cosnωt + bn sinnωt converge simplement sur•α,α + 2πω•.Alors elle converge simplement sur R et sa somme est une fonction à valeurs réelles 2πω -périodique.Démonstration. Pour n N, on définitfn :R→Rt7→an cosnωt + bn sinnωt et T = 2πω . Alors :t R, fnt + T = an cosnωt + T + bn sinnωt + T = an cosnωt + nωT + bn sinnωt + nωT = an cosnωt + 2nπ + bn sinnωt + 2nπ = an cosnωt + bn sinnωt = fnt .Donc fn est T -périodique pour tout n N. Soit t R, alors :— R est archimédien, donc il existe p N et η 0,T tel que t α = pT + η;— alors fnt = fnpT + α + η = fnα + η par T -périodicité.Comme α + η α,α + T ,PnNfnα + η converge : doncPnNfnt converge. DoncPnNfn converge simplement sur R.Romain Dujol90

Page 92 : Notons S la somme dePnNfn. Comme pour tout entier naturel n, fn est une fonction T -périodique, on a :t R, St + T =+Xn=0fnt + T =+Xn=0fnt = St Donc S est T -périodique.Proposition10.2. Soit α R tel quePnNt 7→an cosnωt + bn sinnωt converge uniformément sur•α,α + 2πω•.Alors elle converge uniformément sur R et sa somme est une fonction à valeurs réelles 2πω -périodique.Démonstration. Pour n N, on définitfn :R→Rt7→an cosnωt + bn sinnωt et T = 2πω .D’après le théorème précédent,PnNfn converge simplement sur R et S =+Xn=0fn est T -périodique.Soit n N. Alors Rn =+Xk=n+1fk est la somme d’une série trigonométrique réelle. Donc, d’après le théorème précédent,Rn est T -périodique. Soit t R, alors :— R est archimédien, donc il existe p N et η 0,T tel que t α = pT + η;— alors Rnt = RnpT + α + η = Rnα + η par T -périodicité.Comme α + η α,α + T , il vient que Rnt = Rnα + η supxα,α+T Rnx.CommePnNfn converge uniformément, RnnN converge uniformément sur α,α + T puis limn→+supxα,α+T Rnx=0. On conclut donc quePnNfn converge uniformément sur R.10.1.3Développement en série de FOURIER réelLemme. Soit n N, ω R+ et T = 2πω . AlorsZ T0sinnωt dt = 0 etZ T0cosnωt dt =¨Tsi n = 00si n ̸= 0.Démonstration. Soit n N.• t 7→cosnωt est 2π-périodique et paire doncZ T0cosnωt dt =Z T /2T /2cosnωt dt = 2Z T /20cosnωt dt .· Si n = 0, alorsZ T /20cosnωt dt = 2Z T /20dt = T .· Si n ̸= 0, alorsZ T /20cosnωt dt = 2•sinnωt nω˜T /20= 0.• t 7→sinnωt est T -périodique et impaire doncZ T0sinnωt dt =Z T /2T /2sinnωt dt = 0.Lemme. Soit n,m N2, ω R+ et T = 2πω . AlorsZ T0cosnωt · sinmωt dt = 0 etZ T0cosnωt · cosmωt dt =Tsi n = m = 0T/2si n = m ̸= 00si n ̸= metZ T0sinnωt · sinmωt dt =0si n = m = 0T/2si n = m ̸= 00si n ̸= mRomain Dujol91

Page 93 : Démonstration. Soit n,m N2.• t 7→cosnωt ·sinmωt est T -périodique et impaire. DoncZ T0cosnωt ·sinmωt dt =Z T /2T /2cosnωt ·sinmωt dt = 0.• t 7→cosnωt · cosmωt est T -périodique et paire. Donc :Z T0cosnωt · cosmωt dt =Z T /2T /2cosnωt · cosmωt dt = 2Z T /20cosnωt · cosmωt dt= 2Z T /20cosn mωt + cosn + mωt 2dt=Z T /20cosn mωt dt +Z T /20cosn + mωt dt =Tsi n = m = 0T/2si n = m ̸= 00si n ̸= m• t 7→sinnωt · sinmωt est T -périodique et paire. Donc :Z T0sinnωt · sinmωt dt =Z T /2T /2sinnωt · sinmωt dt = 2Z T /20sinnωt · sinmωt dt= 2Z T /20cosn mωt cosn + mωt 2dt=Z T /20cosn mωt dt Z T /20cosn + mωt dt =0si n = m = 0T/2si n = m ̸= 00si n ̸= mThéorème 10.1. SoitPnNt 7→an cosnωt + bn sinnωt une série trigonométrique réelle qui convergeuniformément sur R. On note S sa somme et T = 2πω sa période. Alors a0 = 1TZ T0St dt etn 1,an = 2TZ T0St cosnωt dtetbn = 2TZ T0St sinnωt dtDémonstration. Pour n N, on définitfn :R→Rt7→an cosnωt + bn sinnωt : fn est continue sur R.De plus,PnNfn converge uniformément sur R, donc sur 0,T . Soit m un entier naturel :— pour tout n N, t 7→fnt cosmωt et t 7→fnt sinmωt sont continues sur R;— n N, t R,+Xk=n+1fkt cosmωt =Rnt cosmωt Rnt RnComme RnnN converge uniformément sur R vers la fonction nulle, il vient quelimn→+Rn= 0 puis quePnNt 7→fnt cosmωt converge uniformément sur R.De même, on montre quePnNt 7→fnt sinmωt converge uniformément sur R.Romain Dujol92

Page 94 : On peut donc appliquer le théorème d’interversion somme-intégrale et les lemmes précédents :Z T0St dt =Z T0¨+Xn=0an cosnωt + bn sinnωt «dt =+Xn=0¨Z T0an cosnωt + bn sinnωt «dt=+Xn=0anZ T0cosnωt dt + bnZ T0sinnωt dt= a0 · Tm 1,Z T0St cosmωt dt =Z T0¨+Xn=0an cosnωt cosmωt + bn sinnωt cosmωt «dt=+Xn=0¨Z T0an cosnωt cosmωt + bn sinnωt cosmωt «dt=+Xn=0–anZ T0cosnωt cosmωt dt + bnZ T0sinnωt cosmωt dt™= am · T2m 1,Z T0St sinmωt dt =Z T0¨+Xn=0an cosnωt sinmωt + bn sinnωt sinmωt «dt=+Xn=0¨Z T0an cosnωt sinmωt + bn sinnωt sinmωt «dt=+Xn=0–anZ T0cosnωt sinmωt dt + bnZ T0sinnωt sinmωt dt™= bm · T2Remarque. Le coefficient a0 est donc égale à la valeur moyenne de S sur une période.Définition 10.2 Développement en série de FOURIER réel.Soit T un réel strictement positif et f une application T -périodique sur R.On définit le développement en série de FOURIER réel de f comme la série trigonométriquePnNt 7→an cosnωt + bn sinnωt avec ω = 2πT , a0 = 1TZ T0f t dt etn 1,an = 2TZ T0f t cosnωt dtetbn = 2TZ T0f t sinnωt dtLes suites annN et bnn1 sont appelées coefficients de FOURIER réels de f .Proposition 10.3.Soit Tun réel strictement positif etfune application T -périodique sur R.On note annN et bnn1 les coefficients de FOURIER réels de f .Si f est paire, alors a0 = 2TZ T /20f t dt etn 1,an = 4TZ T /20f t cosnωt dtetbn = 0Si f est impaire, alors a0 = 0 etn 1,an = 0etbn = 4TZ T /20f t sinnωt dtRomain Dujol93

Page 95 : Démonstration. Les fonctions f , t 7→cosnωt et t 7→sinnωt sont T -périodiques.• Si f est impaire, alors t 7→f t cosnωt est paire et t 7→f t sinnωt est impaire :a0 = 1TZ T0f t dt = 1TZ T /2T /2f t dt = 2TZ T /20f t dtn 1, an = 2TZ T0f t cosnωt dt = 2TZ T /2T /2f t cosnωt dt = 4TZ T /20f t cosnωt dtn 1, bn = 2TZ T0f t sinnωt dt = 2TZ T /2T /2f t sinnωt dt = 0• Si f est impaire, alors t 7→f t cosnωt est impaire et t 7→f t sinnωt est paire :a0 = 1TZ T0f t dt = 1TZ T /2T /2f t dt = 2TZ T /20f t dtn 1, an = 2TZ T0f t cosnωt dt = 2TZ T /2T /2f t cosnωt dt = 0n 1, bn = 2TZ T0f t sinnωt dt = 2TZ T /2T /2f t sinnωt dt = 4TZ T /20f t sinnωt dt10.2Séries trigonométriques complexes10.2.1DéfinitionDéfinition 10.3 Série trigonométrique complexe.On appelle série trigonométrique complexe toute «série» d’applications de la formePnZt 7→cne inωt où cnnZ est une suite complexe indexée sur Z et ω est un nombre réel strictement positif.10.2.2ConvergenceProposition 10.4. Soit α R tel quePnZt 7→cne inωt converge simplement sur•α,α + 2πω•.Alors elle converge simplement sur R et sa somme est une fonction 2πω -périodique.Démonstration. Pour n Z, on définitfn :R→Ct7→cne inωtet T = 2πω . Alors :t R, fnt + T = cne inωt +T = cne inωt +inωT = cne inωt +2inπ = cne inωt e 2inπ = cne inωt = fnt Donc fn est T -périodique pour tout n N.Soit t R, alors :— R est archimédien, donc il existe p N et η 0,T tel que t α = pT + η;— alors fnt = fnpT + α + η = fnα + η par T -périodicité.Comme α + η α,α + T ,PnNfnα + η converge : doncPnNfnt converge. DoncPnNfn converge simplement sur R.Romain Dujol94

Page 96 : Notons S la somme dePnNfn. Comme pour tout entier naturel n, fn est une fonction T -périodique, on a :t R, St + T =+Xn=fnt + T =+Xn=fnt = St Donc S est T -périodique.Proposition 10.5. Soit α R tel quePnZt 7→cne inωt converge uniformément sur•α,α + 2πω•.Alors elle converge uniformément sur R et sa somme est une fonction 2πω -périodique.Démonstration. Pour n N, on définitfn :R→Rt7→cne inωtet T = 2πω .D’après le théorème précédent,PnNfn converge simplement sur R et S =+Xn=0fn est T -périodique.Soit n N. Alors Rn =+Xk=n+1fk est la somme d’une série trigonométrique complexe. Donc, d’après le théorème pré-cédent, Rn est T -périodique. Soit t R, alors :— R est archimédien, donc il existe p N et η 0,T tel que t α = pT + η;— alors Rnt = RnpT + α + η = Rnα + η par T -périodicité.Comme α + η α,α + T , il vient que Rnt = Rnα + η supxα,α+T Rnx.CommePnNfn converge uniformément, RnnN converge uniformément sur α,α + T puis limn→+supxα,α+T Rnx=0. On conclut donc quePnNfn converge uniformément sur R.10.2.3Développement en série de FOURIER complexeLemme. Soit n,m N2, ω R+ et T = 2πω . AlorsZ T0e inωt e imωt dt =¨Tsi n = m0si n ̸= m.Démonstration. Soit n,m N2.• Si n = m, alorsZ T0e inωt e imωt dt =Z T0dt = T .• Si n ̸= m, alorsZ T0e inωt e imωt dt =e inmωtn mωT0= e 2inmπ 1n mω= 0.Théorème 10.2. SoitPnZt 7→cne inωt une série trigonométrique complexe qui converge uniformé-ment sur R. On note S : t 7→+Xn=cne inωt et T = 2πω sa période. Alorsn Z, cn = 1TZ T0St e inωt dtRomain Dujol95

Page 97 : Démonstration. Pour n Z, on définitfn :R→Rt7→cne inωt: fn est continue sur R.De plus,PnZfn converge uniformément sur R, donc sur 0,T . Soit m un entier naturel :— pour tout n Z, t 7→fnt e imωt est continue sur R;— n N, t R,+Xk=n+1fkt e imωt +n1Xk=fkt e imωt =Rnt e imωt Rnt RnComme RnnN converge uniformément sur R vers la fonction nulle, il vient quelimn→+Rn= 0 puis quePnNt 7→fnt e imωt converge uniformément sur R.On peut donc appliquer le théorème d’interversion somme-intégrale et les lemmes précédents :m Z,Z T0St e imωt dt =Z T0+Xn=cne inωt e imωt dt =+Xn=cnZ T0e inωt e imωt dt = cn · TDéfinition 10.4 Développment en série de FOURIER.Soit T un réel strictement positif et f une application de R dans C T -périodique.On définit le développement en série de FOURIER complexe de f comme la série trigonométriquePnNt 7→cne inωt avec ω = 2πT et cn = 1TZ T0f t e inωt dt pour tout n Z.La suite cnnZ est appelée coefficients de FOURIER complexes de f .Proposition 10.6. Soit T un réel strictement positif et f une application de R dans C T -périodique.On note cnnZ les coefficients de FOURIER complexes de f .Si f est exclusivement à valeurs réelles, alors cn = cn pour tout entier relatif n.Démonstration. n Z, cn = 1TZ T0f t e inωt dt = 1TZ T0f t e inωt dt = 1TZ T0f t e inωt dt = cnProposition 10.7 Relations entre coefficients de FOURIER réels et complexes.Soit f une application T -périodique sur R. On note annN et bnn1 ses coefficients de FOURIER réels etcnnZ ses coefficients de FOURIER complexes.• c0 = a0 et n 1,cn = an i bn2cn = an + i bn2• a0 = c0 et n 1,an =cn + cn =2ℜecnbn = icn cn = 2ℑmcnRomain Dujol96

Page 98 : Démonstration. Notons que c0 = 1TZ T0f t e i0ωt dt = 1TZ T0f t dt = a0• n N, cn = 1TZ T0f t e inωt dt = 1TZ T0f t cosnωt i sinnωt dt= 1TZ T0f t cosnωt dt i 1TZ T0f t sinnωt dt = an2 i bn2cn = 1TZ T0f t e inωt dt = 1TZ T0f t cosnωt i sinnωt dt= 1TZ T0f t cosnωt dt + i 1TZ T0f t sinnωt dt = an2 + i bn2• n N, an = 2TZ T0f t cosnωt dt = 2TZ T0f t e inωt + e inωt2dt= 1TZ T0f t e inωt dt + 1TZ T0f t e inωt dt = cn + cnbn = 2TZ T0f t sinnωt dt = 2TZ T0f t e inωt + e inωt2idt = iTZ T0f t e inωt e inωt dt= iTZ T0f t e inωt dt iTZ T0f t e inωt dt = icn cn10.3Convergence du développement en série de FOURIER10.3.1Fonctions périodiques de classe C 1 par morceaux sur RDéfinition 10.5 Discontinuité de première espèce.Soit I un intervalle ouvert de R, t0 un point de I et f une application définie sur I \t0.On dit que f possède une discontinuité de première espèce en t 0 si et seulement f admet une limitefinie à gauche en t0 et une limite finie à droite en t0. Auquel cas, on note :ft 0= limt →t 0f t etft +0= limt →t +0f t Définition 10.6 Fonction de classe C 1 par morceaux. Soit a et b deux réels tels que a b.Une application f est dite C 1 par morceaux sur a,b si et seulement si il existe une subdivisionσ = t0 = a,t1,...,tn1,tn = b de a,b telle que pour tout entier naturel i J1,nK :1. f est de classe C 1 sur ti1,ti;2. la restriction de f à ti1,ti se prolonge sur ti1,ti en une application de classe C 1.Romain Dujol97

Page 99 : Proposition 10.8 Caractérisation rapide. Soit a et b deux nombres réels tels que a b .Une application fest C 1 par morceaux sur a,b si et seulement si il existe une subdivisionσ = t0 = a,t1,...,tn1,tn = b de a,b telle que pour tout entier naturel i J1,nK :1. f est de classe C 1 sur ti1,ti;2. f et f ′ admettent une discontinuité de première espèce en ti.Exemple. Soitf :0,2π→Rt7→¨tsi x 0,π2π tsi x π,2πMontrons que f est de classe C 1 par morceaux sur 0,2π :— sur les intervalles 0,π et π,2π, f est polynômiale donc de classe C 1 ;— on a f 0+ = f 2π = 0 et f π = f π+ = π : donc toutes les discontinuités de f sont de premièreespèce;— on a f ′0+ = f ′π = 1 et f ′π+ = f ′2π = 1 : donc toutes les discontinuités de f ′ sont de premièreespèce.Donc f est de classe C 1 par morceaux sur 0,2π. Notons que f est de plus continue sur 0,2π.Définition 10.7 Fonction périodique de classe C 1 par morceaux.Soit T un réel strictement positif et f une application T -périodique sur R.f est dite périodique C 1 par morceaux sur R si et seulement si il existe un nombre réel α tel que f soitde classe C 1 par morceaux sur α,α + T .10.3.2Théorème de DIRICHLETThéorème 10.3 Théorème de DIRICHLET.Soit T un réel strictement positif et f une application T -périodique de classe C 1 par morceaux surR. Alors les développements en série de FOURIER réel et complexe de f converge simplement sur R versl’application Sf :R→Rt7→f t + f t +2.IMPORTANT. f et Sf coïncident en tout point de continuité de f .10.3.3Théorème de PARSEVALThéorème 10.4 Théorème de PARSEVAL.Soit T un réel strictement positif et f une application T -périodique de classe C 1 par morceauxsur R. On note annN et bnn1 ses coefficients de FOURIER réels et cnnZ ses coefficients de FOURIERcomplexes. Alors :1TZ T0f t 2 dt = a 20 ++Xn=1a 2n + b 2n2=+Xn=cn2Romain Dujol98

Page 100 : RappelsComme cosx + π = cos x et sinx + π = sin x pour tout x R, on a par récurrence que :n N, cosx + nπ = 1n cos xetsinx + nπ = 1n sin xEn particulier, en x = 0, cosnπ = 1n cos0 = 1n et sinnπ = 1n sin0 = 0.Soit n N. Pour calculer sin nπ2 , on distingue deux cas :— si n est pair, alors n = 2p et sin nπ2 = sin 2pπ2= sinpπ = 0;— si n est impair, alors n = 2p + 1 et sin nπ2 = sin 2p + 1π2= sinpπ + π2= 1p sin π2 = 1p.Autrement dit,sin nπ2nN = 0,1,0,1,0,1,0,1,0,1,....Interprétation physiqueSi f est T -périodique, continue et de classe C 1 par morceaux et que annN et bnn1 sont ses coefficientsde FOURIER réels, alors t R, f t = a0 ++Xn=1an cosnωt + bn sinnωt .En reprenant le vocabulaire utilisé en physique, f est un signal périodique avec :— sa période T , sa pulsation ω = 2πT et sa fréquence 1T = ω2π ;— sa valeur moyenne a0 = 〈f 〉= 1TZ T0f t dt ;— son harmonique de rang n fn : t 7→an cosnωt + bn sinnωt ; l’harmonique de rang un est appeléfondamental car sa période est égale à celle de f .Soit n un entier naturel. Si an,bn ̸= 0,0, il existe un unique couple An,ϕn R+ ×iπ2 , π2htel que :t R, an cosnωt + bn sinnωt = An cosnωt ϕnPlus précisément :— si an = 0 et bn 0, alors An = bn et ϕn = π2 ;— si an = 0 et bn 0, alors An = bn et ϕn = π2 ;— si an ̸= 0, alors An =Æa 2n + b 2n et ϕn = arctan bnan‹.Les valeurs An et ϕn sont respectivement l’amplitude et la phase de l’harmonique de rang n.La représentation graphique de n 7→An est appelée spectre de fréquence du signal f .Remarque. La formule de PARSEVAL se réécrie 1TZ T0f t 2 dt = a 20 + 12+Xn=1A2n.En remarquant que la puissance du signal fn:t7→an cosnωt + bn sinnωt est égal àA2n2 =a 2n + b 2n2, la formule de PARSEVAL traduit la conservation de la puissance : la puissance du signal est laseule somme des puissances de toutes les harmoniques qui la composent il n’y a pas de termes croisés.Romain Dujol99

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100