CM

Télécharger le CM en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231

Page 1 : CM Algèbre 2Cycle pré-ingénieur 1Mohamed Ali DEBYAOUIFlorian DUSSAPThi Hien NGUYEN2023-2024Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20241 / 231

Page 2 : ÉvaluationVous aurez 4 notes :DS1 25 : 1h en TD, semaine du 04/03/2024.DS2 25 : 1h en TD, semaine du 01/04/2024.Examen 40 : 2h, semaine du 03/06/2024.TD 10 : au cours du semestre.On calcule une moyenne pondérée M de ces notes :M = 0,25 DS1 + DS2 + 0,4 E + 0,1 TD.La note finale NF est le maximum entre la moyenne M et l’examen E :NF = maxM, E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20242 / 231

Page 3 : Chapitres1Groupes et morphismes2Systèmes linéaires3Espaces vectoriels4Applications linéaires5Matrices et inverses de matrices6Déterminants7Représentation matricielle et changements de basesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20243 / 231

Page 4 : Groupes et morphismesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20244 / 231

Page 5 : Contenu1Groupes et morphismesLois de composition interneGroupesMorphismesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20245 / 231

Page 6 : Contenu1Groupes et morphismesLois de composition interneGroupesMorphismesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20246 / 231

Page 7 : Lois de composition interneDéfinitionSoit E un ensemble. Une loi de composition interne sur E est uneapplication :: E × E→Ex, y7→x y.On appelle magma tout couple E, formé d’un ensemble E et d’une loide composition interne sur E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20247 / 231

Page 8 : Lois de composition interneQuestions1 Sur R, les opérations +, , ×, ÷ sont-elles des lois de compositioninterne ?2 La soustraction est-elle une loi de composition interne sur N ? sur Z ?sur Q ? sur R ? sur C ?3 Donner une loi de composition interne sur l’ensemble FE, E desapplications d’un ensemble E dans lui-même.Réponses1 Les opérations +, et × sont des lois de compositions internes sur R,mais pas ÷. En revanche, ÷ est une loi de composition interne sur R.2 La soustraction n’est pas une loi de composition interne sur N. C’estune loi de composition interne sur Z, Q, R et C.3 La composition ◦est une loi de composition interne sur FE, E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20248 / 231

Page 9 : Associativité et commutativitéDéfinitionSoit E, un magma.On dit que est associative si x, y, z E, x y z = x y z.On dit que est commutative si x, y E, x y = y x.ExempleSur R, l’addition et la multiplication sont associatives et commutatives.Sur R, la soustraction n’est ni associative ni commutative.Sur FE, E, la composition d’applications est associative :f , g, h FE, E,f ◦g ◦h = f ◦g ◦h,mais pas commutative sauf si CardE 1 :f ◦g ̸= g ◦fen général.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-20249 / 231

Page 10 : DistributivitéDéfinitionSoit E un ensemble et soient et △deux lois de composition interne sur E.On dit que est distributive à gauche par rapport à △si :x, y, z E,x y △z = x y △x z.On dit que est distributive à droite par rapport à △si :x, y, z E,x △y z = x z △y z.On dit que est distributive par rapport à △si elle est distributive àgauche et à droite par rapport à △.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202410 / 231

Page 11 : DistributivitéExempleDans R, la multiplication est distributive par rapport à l’addition.Soit E un ensemble. Dans l’ensemble PE des parties de E,l’intersection est distributive par rapport à la réunion :A, B, C PE,A B C = A B A C,A B C = A C B C.La réunion est également distributive par rapport à l’intersection :A, B, C PE,A B C = A B A C,A B C = A C B C.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202411 / 231

Page 12 : Élément neutreDéfinitionSoit E, un magma et soit e E. On dit que e est un élément neutrepour si :x E,x e = e x = x.ExempleDans N, +, l’élément neutre est 0.Dans R, ×, l’élément neutre est 1.Dans 2Z, ×, il n’y a pas d’élément neutre.Dans FE, E, ◦, l’élément neutre est idE.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202412 / 231

Page 13 : Élément neutreProposition unicité de l’élément neutreSoit E, un magma. Si possède un élément neutre, alors il est unique.Démonstration.Soient e et e′ des éléments neutres de E, . Puisque e est neutre pour ,on a :e e′ = e′.Mais puisque e′ est aussi neutre pour , on a :e e′ = e.Par conséquent, on a e = e′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202413 / 231

Page 14 : Symétrique d’un élémentDéfinitionSoit E, un magma possédant un élément neutre e et soit x E.On dit que x admet un symétrique à droite s’il existe x′ E tel quex x′ = e.On dit que x admet un symétrique à gauche s’il existe x′ E tel quex′ x = e.On dit que x est symétrisable s’il existe x′ E qui est à la foissymétrique à droite et à gauche.Vocabulaire. On emploie aussi le terme « inversible » à la place de« symétrisable ».Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202414 / 231

Page 15 : Symétrique d’un élémentExempleDans R, +, le symétrique d’un nombre x est son opposé x.Dans R, ×, un nombre x est symétrisable si et seulement si x ̸= 0.Dans ce cas, le symétrique de x est son inverse 1x .Dans FE, E, ◦, une application f est symétrisable si et seulementsi f est bijective. Dans ce cas, le symétrique de f est son applicationréciproque f 1.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202415 / 231

Page 16 : Symétrique d’un élémentProposition unicité du symétriqueSoit E, un magma associatif possédant un élément neutre et soit x E.1 Si x′ est un symétrique à droite et si x′′ est un symétrique à gauchede x, alors x′ = x′′.2 Si x est symétrisable, alors son symétrique est unique.Démonstration.Soit x E et soient x′, x′′ les symétriques à droite et à gauche de x,c.-à-.d. x x′ = e et x′′ x = e où e est l’élément neutre de E, . Parassociativité de , on a :x′ = e x′ = x′′ x x′ = x′′ x x′ = x′′ e = x′′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202416 / 231

Page 17 : Symétrique d’un produitPropositionSoit E, un magma associatif possédant un élément neutre. Si x, y Esont symétrisables de symétriques x1 et y1, alors x y est symétrisablede symétrique :x y1 = y1 x1.Remarque. Si n’est pas commutative, l’ordre des symétriques ci-dessusest important.Démonstration.Notons e l’élément neutre de E, . On a par associativité de :x y y1 x1 = x y y1 x1 = x e x1 = x x1 = e,donc y1 x1 est le symétrique à droite de x y. On procède de mêmepour montrer que c’est le symétrique à gauche.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202417 / 231

Page 18 : Simplification par un élément symétrisablePropositionSoit E, un magma associatif possédant un élément neutre et soitx E. Si x est symétrisable, alors :y, z E,x y = x z =⇒y = zy, z E,y x = z x =⇒y = z.Attention !Ces implications sont fausses en général si x n’est pas inversible. Parexemple, dans le magmaPR, , on a :0, 1 0, 2 = 0, 1 1, 2mais0, 2 ̸= 1, 2.Un autre contre-exemple important est le produit matriciel, cf. chapitre 5.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202418 / 231

Page 19 : Itérés d’un élémentDéfinitionSoit E, un magma associatif possédant un élément neutre e. Si x Eet n N, on note xn l’itéré n-ième de x qu’on définit par récurrence par :x0 = exn = x xn1si n 1.Autrement dit, si n 1 alors :xn = x · · · xzn fois.Remarque. Pour une loi additive +, l’élément neutre se note 0E et l’itérén-ième de x se note nx.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202419 / 231

Page 20 : Itérés d’un élémentPropositionSoit E, un magma associative possédant un élément neutre e. Si x Epossède un symétrique x1, alors pour tout n N, xn est symétrisable et :xn1 =x1n .Dans ce cas, on note xn le symétrique de xn. On définit ainsi xk pourtout k Z.Remarque. Pour une loi additive +, le symétrique de x se note x. Laproposition précédente s’écrit nx = nx. On note nx le symétriquede nx, ce qui permet de définir kx pour tout k Z.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202420 / 231

Page 21 : Itérés d’un élémentExempleOn considère le magma FE, E, ◦. L’itéré n-ième d’une application f estdéfinie par :f n =idEsi n = 0,f ◦· · · ◦fzn foissi n 1.Si f est bijective, alors on note f n l’itéré n-ième de f 1.Attention !Si f : R →R, alors f 2 peut avoir un sens différent selon le contexte :f 2 peut désigner l’itéré 2e de f , c’est-à-dire l’application x 7→f f x.f 2 peut désigner le carré de f , c’est-à-dire l’application x 7→f x2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202421 / 231

Page 22 : Applications à valeurs dans un magmaPropositionSoit E et F des ensembles non vides et soit une loi de compositioninterne sur F. On définit la loi de composition interne sur FE, F par :x E,f gx = f x gx.De plus :1 si est associative ou commutative, l’est aussi.2 si e est l’élément neutre pour , alors l’application constante égale à eest l’élément neutre pour .En pratique, on note aussi la loi de FE, F. C’est ainsi qu’on définit lasomme et le produit de fonctions à valeurs réelles :f + gx = f x + gxetfgx = f xgx.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202422 / 231

Page 23 : Contenu1Groupes et morphismesLois de composition interneGroupesMorphismesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202423 / 231

Page 24 : GroupesDéfinitionSoit G, un magma. On dit que G, est un groupe si :1 la loi est associative ;2 la loi admet un élément neutre ;3 tout élément de G est symétrisable pour .Si de plus la loi est commutative, on dit que G, est un groupecommutatif ou abélien.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202424 / 231

Page 25 : GroupesExempleZ, +, Q, +, R, + et C, + sont des groupes abéliens.Q, ×, R, × et C, × sont des groupes abéliens.N, +, Z, × et R, × ne sont pas des groupes.Soit E un ensemble et soit SE l’ensemble des applications bijectivesde E dans E. Alors SE, ◦ est un groupe, non abélien si E possèdeau moins trois éléments. Ce groupe est appelé groupe symétrique deE, ou groupe des permutations de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202425 / 231

Page 26 : Groupe produitDéfinitionSoient E1, 1, . . . , En, n des magmas. On définit sur E = E1 × · · · × Enune loi de composition interne appelée loi produit par :x1, . . . , xn E, y1, . . . , yn E,x1, . . . , xn y1, . . . , yn = x1 1 y1, . . . , xn n yn.Proposition à faire chez vousSoient G1, 1, . . . , Gn, n des groupes d’éléments neutres e1, . . . , en.Alors G = G1 × · · · × Gn est un groupe pour la loi produit, d’élémentneutre e1, . . . , en. De plus, le symétrique d’un élément x1, . . . , xn Gest l’élément x11 , . . . , x1n où x1iest le symétrique de xi dans Gi, i.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202426 / 231

Page 27 : Sous-groupesDéfinitionSoient G, un groupe et H une partie de G. On dit que H est unsous-groupe de G si H, un groupe.ExemplePour tout groupe G d’élément neutre e, les parties e et G sont dessous-groupes de G. Un sous-groupe de G différent de e et G est appelésous-groupe propre de G.LemmeSoient G, un groupe d’élément neutre e et H un sous-groupe de G.Alors :1 e est l’élément neutre de H, .2 H est stable par passage à l’inverse : h H,h1 H.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202427 / 231

Page 28 : Sous-groupesDémonstration.1 Soit H un sous-groupe de G, . Alors H, est un groupe, notonseH son élément neutre. Alors on a eH eH = eH et eH e = eH, donceH eH = eH e. En simplifiant à gauche par eH, on obtient eH = e.2 Soit h H, soit h′ H son inverse dans H et soit h1 son inversedans G. Alors on a :h′ = e h′ = h1 h h′ = h1 h h′ = h1 e = h1.Donc h1 H.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202428 / 231

Page 29 : Caractérisation des sous-groupesPropositionSoient G, un groupe et H une partie de G. Alors H est un sous-groupede G si et seulement si :1 H est non vide ;2 H est stable par produit et passage à l’inverse :x, y H,x y1 H.En pratique, pour vérifier que H est non vide, on regarde si l’élémentneutre e de G appartient à H :si e H, alors H est non vide. Il reste à vérifier la propriété destabilité pour montrer que H est un sous-groupe.si e /H, alors H n’est pas un sous-groupe.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202429 / 231

Page 30 : Caractérisation des sous-groupesDémonstration.Ces conditions sont évidemment nécessaires, montrons qu’elles sontsuffisantes.Puisque H est non vide, soit x H. Par stabilité, on ae = x x1 H. Puisque e est neutre pour dans G, il l’est aussidans H.Si x H, alors par stabilité x1 = e x1 H. Donc le symétriquede x pour appartient à H.Si x, y H, alors y1 H d’après le point précédent, donc parstabilité on a x y = x y11 H. Ainsi, H est sable par .La loi étant associative sur G, elle l’est à fortiori sur H.On a montré que est une loi de composition interne associative sur H,possède un élément neutre dans H et que tout élément de H possède unsymétrique dans H. Donc H est un sous-groupe de G, .Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202430 / 231

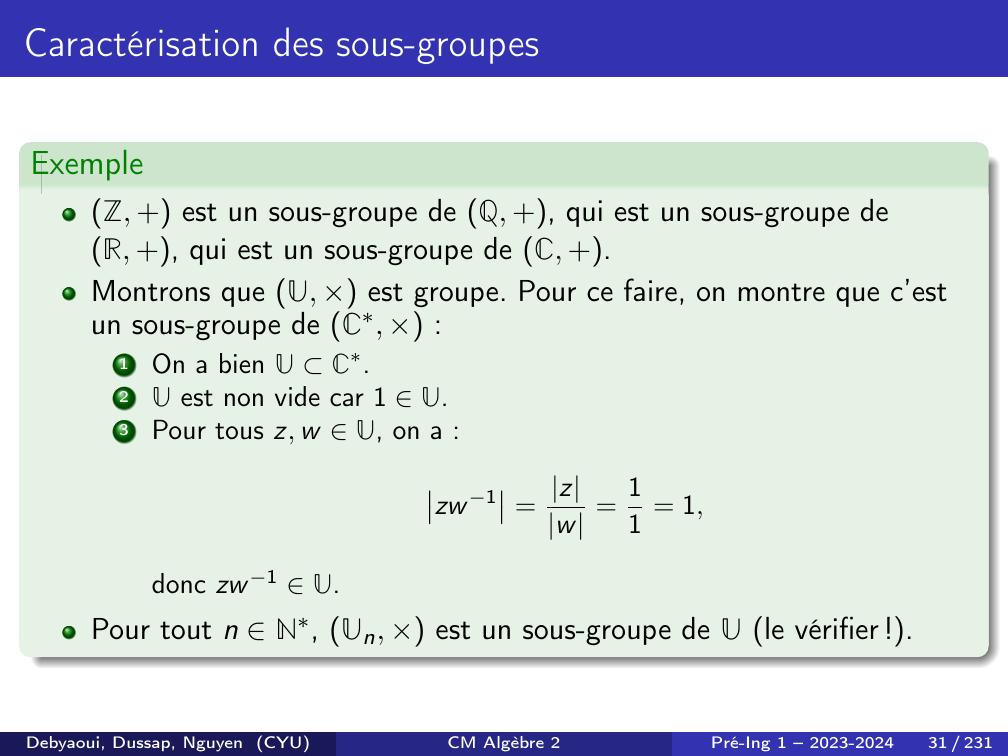
Page 31 : Caractérisation des sous-groupesExempleZ, + est un sous-groupe de Q, +, qui est un sous-groupe deR, +, qui est un sous-groupe de C, +.Montrons que U, × est groupe. Pour ce faire, on montre que c’estun sous-groupe de C, × :1On a bien U C.2U est non vide car 1 U.3Pour tous z, w U, on a :zw 1 = zw = 11 = 1,donc zw 1 U.Pour tout n N, Un, × est un sous-groupe de U le vérifier !.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202431 / 231

Page 32 : Contenu1Groupes et morphismesLois de composition interneGroupesMorphismesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202432 / 231

Page 33 : MorphismesDéfinitionSoient E, et F, △ deux magmas et f une application de E dans F. Ondit que f est un morphisme ou homomorphisme de E, dans F, △ si :x, y E,f x y = f x △f y.Si E, et F, △ sont des groupes, on dit que f est un morphisme degroupes.Un peu de vocabulaire :Un morphisme de E, dans lui-même est appelé un endomorphisme.Un morphisme bijectif est appelé un isomorphisme.Un endomorphisme bijectif est appelé un automorphisme.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202433 / 231

Page 34 : MorphismesExemplePour tout λ R, l’application linéaire :f : R→Rx7→λx,est un endomorphisme du groupe R, +. Si λ ̸= 0, c’est unautomorphisme.L’exponentielle est un isomorphisme de groupes de R, + dansR+, ×. En effet, pour tous x, y R, on a :expx + y = expx × expy,donc exp est un morphisme de groupe, et on sait que l’exponentielleest bijective de R dans R+.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202434 / 231

Page 35 : Composition de morphismesPropositionLa composée de deux morphismes est un morphisme.Démonstration.Soient E, , F, △ et G, ♡ des magmas, et soient f : E →F etg : F →G des morphismes. Alors pour tous x, y E, on a :g ◦f x y = gf x y= gf x △f y= gf x♡gf y= g ◦f x ♡g ◦f y.Par conséquent, g ◦f est un morphisme de E, dans G, ♡.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202435 / 231

Page 36 : Application réciproque d’un isomorphismePropositionL’application réciproque d’un isomorphisme est un isomorphisme.Démonstration.Soient E, et F, △ des magmas et soit f : E →F un isomorphisme.L’application f est bijective, donc elle possède une application réciproquef 1 : F →E également bijective. Montrons que f 1 est un morphisme.Pour tous x, y F, on a :ff 1x f 1y= ff 1x△ff 1y= x △y,donc f 1x f 1y = f 1x △y. Par conséquent, f 1 est unisomorphisme.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202436 / 231

Page 37 : Calculs avec un morphisme de groupesPropositionSoient G, et G ′, △ deux groupes d’éléments neutres respectifs e Get e′ G ′. Si f : G →G ′ est un morphisme, alors :1 f e = e′.2 x G, f x1 = f x1.3 x G, n Z, f xn = f xn.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202437 / 231

Page 38 : Calculs avec un morphisme de groupesDémonstration.1 On a e = e e, donc :f e = f e e =⇒f e = f e △f e=⇒f e △f e1 = f e △f e △f e1=⇒e′ = f e.2 Soit x G, alors on a :e′ = f e = f x x1 = f x △f x1.Par conséquent, f x1 est le symétrique de f x.3 Par récurrence à faire chez soi.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202438 / 231

Page 39 : Image directe/réciproque d’un sous-groupePropositionSoient G, et G ′, △ deux groupes et soit f : G →G ′ un morphisme.1 Si H est un sous-groupe de G, , alors f H est un sous-groupe deG ′, △.2 Si H′ est un sous-groupe de G ′, △, alors f 1H′ est un sous-groupede G, .Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202439 / 231

Page 40 : Image directe/réciproque d’un sous-groupeDémonstration de 1.L’ensemble f H est non vide car H est non vide. Soient y1, y2 f H,alors il existe x1, x2 H tels que f x1 = y1 et f x2 = y2. Montrons quey1 △y12f H. On a :y1 △y12= f x1 △f x21 = f x1 x12 .Or, x1 x12H car H est un sous-groupe de G, , doncy1 △y12f H. Ainsi, on a montré que f H est un sous-groupe deG ′, △.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202440 / 231

Page 41 : Image directe/réciproque d’un sous-groupeDémonstration de 2.On a f e = e′ H′, donc e f 1H′. Par conséquent, f 1H′ est nonvide. Soient x1, x2 f 1H′, montrons que x1 x12f 1H′. On a :f x1 x12 = f x1 △f x21 H′,car f x1 H′, f x2 H′ et H′ est un sous-groupe de G ′, △. Parconséquent, x1 x12f 1H′. Ainsi, on a montré que f 1H′ est unsous-groupe de G, .Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202441 / 231

Page 42 : Noyau et image d’un morphisme de groupesDéfinitionSoient G, et G ′, △ deux groupes et soit f : G →G ′ un morphisme.On note e′ l’élément neutre de G ′.f G est appelé l’image de f et on le note Im f .f 1e′ est appelé le noyau de f et on le note ker f .PropositionSi f : G →G ′ est un morphisme de groupe, alors ker f est un sous-groupede G et Im f est un sous-groupe de G ′.C’est la conséquence de la proposition précédente.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202442 / 231

Page 43 : Injectivité d’un morphisme de groupesLemmeSoient G, et G ′, △ deux groupes et soit f : G →G ′ un morphisme.Pour tous x, y G, on a l’équivalence :f x = f y ⇐⇒x y1 ker f .Démonstration.Soit e′ l’élément neutre de G ′ et soient x, y G. Alors on a :f x = f y ⇐⇒f x △f y1 = e′⇐⇒f x y1 = e′f est un morphisme⇐⇒x y1 ker f .Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202443 / 231

Page 44 : Injectivité d’un morphisme de groupesThéorèmeSoit G, un groupe d’élément neutre e et soit G ′, △ un groupe. Alorsun morphisme f : G →G ′ est injectif si et seulement si ker f = e.Démonstration.On procède par double implication. =⇒ Supposons que f est injective. Soit x ker f , alors on a :f x = e′ = f e,donc x = e par injectivité de f . Par conséquent, ker f = e. ⇐= Supposons que ker f = e. Soient x, y E tels que f x = f y,alors d’après le lemme précédent, on a x y1 ker f . Puisque ker f = e,alors x y1 = e, c’est-à-dire x = y. Par conséquent, f est injective.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202444 / 231

Page 45 : Systèmes linéairesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202445 / 231

Page 46 : Contenu2Systèmes linéairesDéfinitionsSystèmes équivalentsAlgorithme de GaussRésolution d’un système linéaireDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202446 / 231

Page 47 : Contenu2Systèmes linéairesDéfinitionsSystèmes équivalentsAlgorithme de GaussRésolution d’un système linéaireDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202447 / 231

Page 48 : Système d’équations linéairesDans ce chapitre, K désigne l’ensemble R ou l’ensemble C, et n et p sontdes entiers naturels non nuls.DéfinitionOn appelle système de n équations linéaires à p inconnues x1, . . . , xp unsystème de la forme :a1,1 x1 + a1,2 x2 + · · · + a1,p xp = b1a2,1 x1 + a2,2 x2 + · · · + a2,p xp = b2...an,1 x1 + an,2 x2 + · · · + an,p xp = bn,où les ai,j K sont les coefficients du système et les bi K sont le secondmembre. Une solution de ce système est un vecteur s1, . . . , sp Kpvérifiant simultanément chaque équation du système. Si tous les bi sontnuls, on dit que le système est homogène.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202448 / 231

Page 49 : Matrice associée à un systèmeDéfinitionSoit S un système linéaire :a1,1 x1 + a1,2 x2 + · · · + a1,p xp = b1a2,1 x1 + a2,2 x2 + · · · + a2,p xp = b2...an,1 x1 + an,2 x2 + · · · + an,p xp = bn.On appelle matrice associée au système S le tableau de nombres :a1,1a1,2a1,pa2,1a2,2a2,pan,1an,2an,p.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202449 / 231

Page 50 : Matrice augmentéeDéfinitionSoit S un système linéaire de matrice A et notons B le vecteur colonneformé par le second membre :A =a1,1a1,pan,1an,p,B =b1bn.On appelle matrice augmentée du système S la matrice obtenue enjuxtaposant A et B :a1,1a1,pb1an,1an,pbn.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202450 / 231

Page 51 : ExempleSoit le système de 5 équations à 3 inconnues :3x1 + 2x2 + 5x3 = 72x1+ 2x3 = 4x1 + x2 3x3 = 24x1 2x2= 323x2 + 5x3 = 4.La matrice associée A et la matrice augmentée M sont :A =325202113420035,M =3257202411324203/20354.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202451 / 231

Page 52 : Contenu2Systèmes linéairesDéfinitionsSystèmes équivalentsAlgorithme de GaussRésolution d’un système linéaireDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202452 / 231

Page 53 : Opérations élémentairesDéfinitionOn appelle opération élémentaire sur les lignes d’un système ou d’unematrice l’une des opérations suivantes :1 Li ↔Lj : échanger les lignes Li et Lj.2 Li ←λLi λ ̸= 0 : multiplication de la ligne Li par un scalaire λ K.3 Li ←Li + λLj i ̸= j : ajouter λLj à la ligne Li.Remarque. Les opérations élémentaires sont inversibles :1 Li ↔Lj est son propre inverse.2 L’inverse de Li ←λLi est Li ←1λLi.3 L’inverse de Li ←Li + λLj est Li ←Li λLj.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202453 / 231

Page 54 : Équivalence en lignesDéfinitionOn dit que deux systèmes sont équivalents si on peut passer de l’un àl’autre par une suite finie d’opérations élémentaires sur les lignes.On dit que deux matrices M et M′ sont équivalentes en lignes si onpeut passer de l’une à l’autre par une suite finie d’opérationsélémentaires sur les lignes. Dans ce cas, on note : M L M′.Remarques.1 Si on passe d’un système S1 à un système S2 par une suited’opérations élémentaires O1, O2, . . . , Om, alors on passe de S2 àS1 par la suite O1m , . . . , O12 , O11 . Ainsi, si S1 est équivalent àS2, alors S2 est équivalent à S1. L’équivalence en lignes est unerelation d’équivalence.2 Effectuer des opérations élémentaires sur un système revient à leseffectuer sur sa matrice augmentée.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202454 / 231

Page 55 : Équivalence et ensemble de solutionsLemmeSi S1 est un système linéaire et S2 est le système obtenu à partir deS1 après une opération élémentaire, alors les solutions de S1 sont dessolutions de S2.Démonstration.Soit s = s1, . . . , sp une solution de S1.Si l’opération élémentaire pour passer à S2 est un échange de lignesou la multiplication d’une ligne par une constante non nulle, il estévident que s est solution de S2.Si l’opération élémentaire est Li ←Li + λLj, alors puisque s estsolution de Li et de Lj, il est aussi solution de λLj et de Li + λLj,donc s est solution de S2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202455 / 231

Page 56 : Équivalence et ensemble de solutionsPropositionDeux systèmes équivalents ont le même ensemble de solutions.Démonstration.Soient S1 et S2 des systèmes linéaires équivalents. Puisqu’on passe deS1 à S2 par des opérations élémentaires, les solutions de S1 sont dessolutions de S2 d’après le lemme précédent. Réciproquement, desopérations élémentaires permettent de passer de S2 à S1, donc lessolutions de S2 sont aussi des solutions de S1. Les systèmes S1 etS2 ont donc les mêmes solutions.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202456 / 231

Page 57 : Contenu2Systèmes linéairesDéfinitionsSystèmes équivalentsAlgorithme de GaussRésolution d’un système linéaireDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202457 / 231

Page 58 : Matrice échelonnée en lignesDéfinitionUne matrice est échelonnée en lignes si elle vérifie les deux propriétéssuivantes :1 Si une ligne est nulle, toutes les lignes suivantes le sont aussi.2 À partir de la 2e ligne, dans chaque ligne non nulle, le premiercoefficient non nul à partir de la gauche est situé strictement àdroite du premier coefficient non nul de la ligne précédente.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202458 / 231

Page 59 : Matrice échelonnée en lignesExemple1 La matrice123000213n’est pas échelonnée en lignes.2 La matrice123450678900012est échelonnée en lignes.3 La matrice123450045607891n’est pas échelonnée en lignes.4 La matrice12003004560078000009n’est pas échelonnée en lignes.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202459 / 231

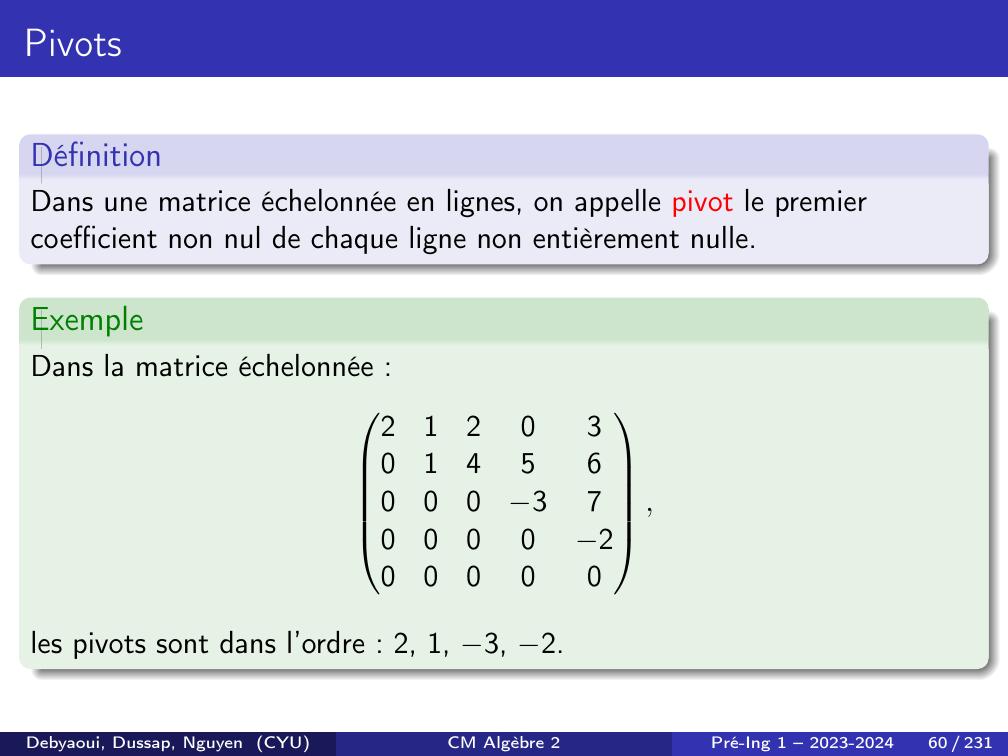
Page 60 : PivotsDéfinitionDans une matrice échelonnée en lignes, on appelle pivot le premiercoefficient non nul de chaque ligne non entièrement nulle.ExempleDans la matrice échelonnée :2120301456000370000200000,les pivots sont dans l’ordre : 2, 1, 3, 2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202460 / 231

Page 61 : Algorithme du pivot de GaussProposition admiseToute matrice est équivalente en lignes à une matrice échelonnée en lignes.La démonstration repose sur l’algorithme du pivot de Gauss, quiconsiste à effectuer des opérations élémentaires sur les lignes d’unematrice pour mettre à zéro petit à petit des coefficients jusqu’àobtenir une matrice échelonnée équivalente.Le système associé à une matrice échelonnée en lignes peut ensuiteêtre résolu facilement par « remontée ».Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202461 / 231

Page 62 : ExempleOn considère le système de 3 équations à 4 inconnues :2x1 + 7x2 + 11x3 + 15x4 = 193x1 + 5x2 + 8x3 + 11x4 = 14x1 + x2 + 2x3 + 3x4 = 4.SLa matrice augmentée de S est :M =27111519358111411234.On commence par échanger les lignes 1 et 3 car il est plus facile d’effectuerles calculs avec un pivot qui vaut 1 ou 1.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202462 / 231

Page 63 : M L11234L1↔L3358111427111519L1↔L3L1123402222L2←L23L1057911L3←L32L1L1123401111L2←12 L2057911L112340111100246L3←L35L2L112340111100123L3←12 L3Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202463 / 231

Page 64 : Le système S est donc équivalent au systèmex1 + x2 + 2x3 + 3x4 = 4x2 + x3 + x4 = 1x3 + 2x4 = 3.S′On passe l’inconnue x4 dans le second membre et on la traite comme unparamètre. Le système est alors triangulaire en x1, x2, x3, on le résout par« remontée » : la dernière équation donne la valeur de x3, ce qui permet detrouver la valeur de x2 dans la 2e équation, ce qui permet de trouver lavaleur de x1 dans la 1re équation.x1 + x2 + 2x3 = 4 3x4x2 + x3 = 1 x4x3 = 3 2x4⇐⇒x1 + x2 + 2x3 = 4 3x4x2= 2 + x4x3 = 3 2x4⇐⇒x1= 0x2= 2 + x4x3 = 3 2x4.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202464 / 231

Page 65 : Finalement, on obtient une description paramétrique des solutions dusystème : on a exprimé les inconnues x1, x2, x3 en fonction de l’inconnue x4qui n’est pas contrainte et peut prendre n’importe quelle valeur dans R. Lessolutions de S sont donc tous les vecteurs de la forme :0, 2 + x4, 3 2x4, x4,avec x4 R une variable libre. L’ensemble des solutions s’écrit :S =0, 2 + x4, 3 2x4, x4 : x4 R.Remarque. Géométriquement, on interprète S comme la droite dans unespace à 4 dimensions ! passant par le point de coordonnées 0, 2, 3, 0et dirigée par le vecteur de coordonnées 0, 1, 2, 1.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202465 / 231

Page 66 : Lignes nulles d’une matrice échelonnéeSoit M la matrice augmentée échelonnées en lignes d’un système linéaire.Les lignes entièrement nulle de M correspondent à des équations« 0 = 0 ». Elles peuvent être supprimées du système sans changer lessolutions.Après avoir enlever les lignes nulles, si le pivot de la dernière lignes estdans la dernière colonne, alors le système contient une équation de laforme « 0 = b » avec b ̸= 0 le pivot. Dans ce cas, le système n’a pasde solutions.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202466 / 231

Page 67 : Contenu2Systèmes linéairesDéfinitionsSystèmes équivalentsAlgorithme de GaussRésolution d’un système linéaireDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202467 / 231

Page 68 : Rang d’une matrice/d’un système linéaireProposition admiseSoient M1 et M2 deux matrices échelonnées en lignes. Si M1 et M2 sontéquivalentes en lignes, alors le nombre de pivots de M1 est égal au nombrede pivots de M2.Cette proposition implique que peu importe la façon d’échelonner en lignesune matrice, le nombre de pivots est toujours le même.DéfinitionOn appelle rang d’une matrice M, et on note rgM, le nombre depivots obtenus après avoir échelonné en lignes M.On appelle rang d’un système linéaire le rang de sa matrice associée.Remarque. Le rang est toujours plus petit que le nombre de lignes et lenombre de colonnes de la matrice.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202468 / 231

Page 69 : Inconnues principales/secondairesDéfinitionSoit S un système linéaire à p inconnues, de rang r et dont la matriceassociée est échelonnée en lignes.On appelle inconnues principales les r inconnues correspondant auxcolonnes contenant les pivots.On appelle inconnues secondaires les p r inconnues restantes.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202469 / 231

Page 70 : Système compatible/incompatibleDéfinitionOn dit qu’un système est incompatible s’il n’admet aucune solution.On dit qu’il est compatible s’il admet au moins une solution.ExempleSoit Sα,β le système linéaire :x1 3x2 + 5x3 = 42x1 + x2 4x3 = 13x1 2x2 + x3 = α4x1 5x2 + 6x3 = βSα,βDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202470 / 231

Page 71 : ExempleSa matrice augmentée est :Mα,β =13542141321α456β.En appliquant l’algorithme du pivot de Gauss, on obtient la matriceéchelonnée :M′α,β =13540121000α + 5000β + 9.Le système est compatible si et seulement si α = 5 et β = 9. Dans cecas, le système est de rang 2, les inconnues principales sont x1, x2 etl’inconnue secondaire est x3.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202471 / 231

Page 72 : Existence et unicité des solutions en fonction du rangPropositionSoit un système de n équations à p inconnues, de rang r, et soit A B samatrice augmentée.Si r = n, alors le système est compatible quel que soit B.Si r n, toute forme échelonnée de A contient n r lignes nulles. Lesystème est compatible ssi ces lignes sont entièrement nulles dans laforme échelonnée de la matrice augmentée.Dans le cas où le système est compatible :Si r = p, alors le système admet une unique solution.Si r p, alors le système admet une infinité de solutions dépendantde p r paramètres.CorollaireSi r = n = p, alors quel que soit B, le système admet une unique solution.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202472 / 231

Page 73 : Structure de l’ensemble des solutionsProposition admiseLes solutions d’un système linéaire s’obtiennent en faisant la somme d’unesolution particulière du système avec toutes les solutions du systèmehomogène associé.solution généraledu système=une solutionparticluière du système+ solution généraledu sys. homogèneRemarque. L’ensemble des solutions d’un système linéaire homogène estun espace vectoriel, voir chapitre suivant.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202473 / 231

Page 74 : ExempleSoit un système linéaire à 5 inconnues, compatible et de rang 3. Supposonsqu’après résolution et après suppression des lignes « 0 = 0 », on obtiennele système :x2 =3 + 2x1 + x3x4 =2 + x1 + 2x3x5 = 2 + 2x1 x3.On a 3 inconnues principales : x2, x4 et x5, et 2 inconnues secondaires : x1et x3. L’ensemble des solutions s’écrit :S =x1, 3 + 2x1 + x3, x3, 2 + x1 + 2x3, 2 + 2x1 x3 : x1, x3 R.Tout élément s S peut s’écrire :s = 0, 3, 0, 2, 2zsolution particulière+ x11, 2, 0, 1, 2 + x30, 1, 1, 2, 1zsolution générale du sys. homogène,avec x1, x3 R.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202474 / 231

Page 75 : Espaces vectorielsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202475 / 231

Page 76 : Contenu3Espaces vectorielsEspaces et sous-espaces vectorielsFamilles de vecteursDimension d’un espace vectorielDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202476 / 231

Page 77 : Contenu3Espaces vectorielsEspaces et sous-espaces vectorielsFamilles de vecteursDimension d’un espace vectorielDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202477 / 231

Page 78 : Vecteurs géométriques rappels de lycéeDans le plan ou l’espace, on définit deux opérations sur les vecteurs :1 l’addition vectorielle ;2 la multiplication par un scalaire.Pour additionner deux vecteurs de même origine, on utilise la règle duparallélogramme.O⃗u⃗v⃗u + ⃗vO⃗uλ⃗uDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202478 / 231

Page 79 : Vecteurs géométriques rappels de lycéeFixons un repère de l’espace. On associe à tout vecteur un tripletx, y, z de nombres réels appelés coordonnées du vecteur.⃗ȷ⃗k⃗ızyx⃗uSi ⃗u et ⃗v ont pour coordonnées x, y, z et x′, y′, z′, alors ⃗u + ⃗v etλ⃗u où λ R ont pour coordonnées :x + x′, y + y′, z + z′etλx, λy, λz.On définit ainsi deux opérations sur R3 :▶une loi de composition interne + addition vectorielle ;▶une loi de composition externe · multiplication par un scalaire.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202479 / 231

Page 80 : L’espace RnGénéralisons les opérations + et · précédentes à Rn et étudions leurspropriétés algébriques.DéfinitionSur Rn, on définit une loi de composition interne + par :⃗x = x1, . . . , xn Rn,⃗y = y1, . . . , yn Rn,⃗x + ⃗y = x1 + y1, . . . , xn + yn.Proposition à vérifier chez vousRn, + est un groupe commutatif, d’élément neutre ⃗0 = 0, . . . , 0, et lesymétrique d’un n-uplet x1, . . . , xn est le n-uplet x1, . . . , xn.Remarque. On définit l’addition de la même façon sur Cn, avec les mêmespropriétés.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202480 / 231

Page 81 : DéfinitionSur Rn, on définit une loi de composition externe · application de R × Rndans Rn par :λ R,⃗x = x1, . . . , xn Rn,λ · ⃗x = λx1, . . . , λxn.En pratique, le symbole de la multiplication est omis : on note λ⃗x = λ · ⃗x.Proposition à vérifier chez vousLa loi · de Rn vérifie :1 ⃗x Rn, 1⃗x = ⃗x.2 λ, µ R, ⃗x Rn, λµ⃗x = λµ⃗x.3 λ R, ⃗x, ⃗y Rn, λ⃗x + ⃗y = λ⃗x + λ⃗y.4 λ, µ R, ⃗x, λ + µ⃗x = λ⃗x + µ⃗x.Remarque. On définit la multiplication par un nombre complexe de lamême façon sur Cn, avec les mêmes propriétés.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202481 / 231

Page 82 : D’autres exemples de « vecteurs »On connait d’autres objets mathématiques pour lesquels des opérationsd’addition et de multiplication par un nombre sont définies et vérifient lesmêmes propriétés que dans Rn. Par exemple :les fonctions définies sur un même intervalle a, b ;les polynômes à coefficients réels ;les suites numériques réelles ;. . . cherchez si vous connaissez d’autres exemples.Les ensembles Rn, Fa, b, R, RX, FN, R, etc, sont des exemplesd’espaces vectoriels réels.Plus généralement, on appelle espace vectoriel n’importe quel ensembledans lequel sont définies des lois + et · satisfaisant les mêmes propriétésalgébriques que dans Rn.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202482 / 231

Page 83 : ScalairesJusqu’à présent, on a toujours utilisé les nombres réels comme scalairesdans le calcul vectoriel, mais rien n’empêche d’utiliser les nombrescomplexes à la place.DéfinitionDans ce chapitre, K désigne soit R, soit C. Les éléments de K sont appelésles scalaires.Remarque. Plus généralement, dans la plupart des énoncés de ce cours, Kpeut être n’importe quel corps.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202483 / 231

Page 84 : Espace vectorielDéfinitionOn appelle K–espace vectoriel K–e.v. un ensemble E dont les élémentssont appelés vecteurs, muni d’une loi de composition interne + et d’une loide composition externe · application de K × E dans E telles que :1 E, + est un groupe commutatif. De plus :▶l’élément neutre est noté 0E et est appelé vecteur nul de E.▶le symétrique d’un vecteur u est noté u et est appelé vecteur opposéde u.2 La loi de composition externe vérifie :1u E, 1 · u = u.2λ, µ K, u E, λ · µ · u = λ × µ · u.3λ K, u, v E, λ · u + v = λ · u + λ · v.4λ, µ K, u E, λ + µ · u = λ · u + µ · u.Lorsqu’il n’y a pas d’ambiguïté sur les lois utilisées, on note simplement El’espace vectoriel, sinon on le note E, +, ·.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202484 / 231

Page 85 : Espace vectorielRemarque. Dans un espace vectoriel, le vecteur nul est unique et l’opposéd’un vecteur est unique.PropositionSoit E un K–espace vectoriel. Pour tout u E, on a :1 0 · u = 0E.2 1 · u = u.Démonstration.Soit u E.1 0 · u = 0 + 0 · u = 0 · u + 0 · u, donc en ajoutant 0 · u àchaque membre, on obtient 0E = 0 · u.2 u + 1 · u = 1 · u + 1 · u = 1 + 1 · u = 0 · u = 0E,donc 1 · u = u par unicité du vecteur opposé de u.Notation. À partir de maintenant, on note λu + v le vecteur λ · u + v.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202485 / 231

Page 86 : Espace vectorielExempleR, R2 et R3 sont des R–e.v.Plus généralement, Kn est un K–e.v. Le vecteur nul de Kn est len-uplet 0, . . . , 0.C est à la fois un R–e.v. et un C–e.v. Le vecteur nul de C est lenombre 0.KX et KX sont des K–e.v. Le vecteur nul de KX et de KX estle polynôme nul.Si A est un ensemble, alors FA, K est un K–e.v. pour les opérationsd’addition d’applications et de multiplication d’une application par unscalaire. Le vecteur nul de FA, K est l’application nulle applicationconstante égale à 0. En particulier :▶l’ensemble des fonctions définies sur un même intervalle est un K–e.v.▶l’ensemble des suites numériques réelles ou complexes est un K–e.v.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202486 / 231

Page 87 : Espace vectoriel produitProposition à vérifier chez vousSoient E1, +1, ·1, . . . , En, +n, ·n des K–e.v. et soit E = E1 × · · · × En.On définit sur E :une loi de composition interne + par loi produit :u1, . . . , un + v1, . . . , vn = u1 +1 v1, . . . , un +n vn;une loi de composition externe · par :λ · u1, . . . , un = λ ·1 u1, . . . , λ ·n un;où ui, vi Ei et λ K. Alors E, +, · est un K–e.v.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202487 / 231

Page 88 : Combinaisons linéairesDéfinitionSoit E un K–espace vectoriel. On appelle famille finie de vecteurs de E toutn-uplet u1, . . . , un E n.Remarque. Une famille peut comporter plusieurs fois le même vecteur etl’ordre des vecteurs dans la famille est important.DéfinitionSoit E un K–espace vectoriel et soit u1, . . . , un une famille de vecteurs.On dit que u E est une combinaison linéaire de la famille u1, . . . , un s’ilexiste des scalaires λ1, . . . , λn K tels que :u =nXi=1λiui = λ1u1 + · · · + λnun.Cette écriture est appelée décomposition de u sur la famille u1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202488 / 231

Page 89 : Combinaisons linéairesExempleDans R3, soient ⃗u1 = 1, 1, 0, ⃗u2 = 3, 1, 1 et ⃗u3 = 1, 3, 1. Alorsle vecteur ⃗v = 5, 3, 2 est combinaison linéaire de ⃗u1, ⃗u2, ⃗u3. En effet, ona par exemple ⃗v = ⃗u1 + ⃗u2 ⃗u3, ou encore ⃗v = ⃗u1 + 2⃗u2 + 0⃗u3.Remarque. La décomposition d’un vecteur sur une famille n’est pas uniqueen général.Proposition combinaison linéaire de combinaisons linéairesSoit E un K–espace vectoriel et soit u1, . . . , un une famille de vecteurs. Siv1, . . . , vp E sont des combinaisons linéaires de u1, . . . , un, alors toutecombinaison linéaire de v1, . . . , vp est une combinaison linéaire deu1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202489 / 231

Page 90 : Combinaisons linéairesDémonstration.Par hypothèse, il existes des scalaires λi,k K tels que :i J1, pK,vi =nXk=1λi,kuk.Soit u = Ppi=1 αivi une combinaison linéaire de v1, . . . , vp. Alors on a :u =pXi=1αi nXk=1λi,kuk!=pXi=1nXk=1αiλi,kuk=nXk=1pXi=1αiλi,kuk =nXk=1 pXi=1αiλi,k!uk =nXk=1βkuk,où βk = Pni=1 αiλi,k pour tout k J1, nK.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202490 / 231

Page 91 : Sous-espace vectorielDéfinitionSoit E, +, · un K–espace vectoriel. On dit que F est un sous-espacevectoriel s.e.v. de E si :1 F E ;2 F, +, · est un K–espace vectoriel.ExempleDans un espace vectoriel E, les ensembles 0E et E sont des s.e.v. de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202491 / 231

Page 92 : Caractérisation d’un sous-espace vectorielPropositionSoit E un K–espace vectoriel. Une partie F de E est un sous-espacevectoriel de E si et seulement si :1 0E F ;2 F est stable par combinaisons linéaires :u, v F, λ, µ K, λu + µv F.Remarques.Noter la ressemblance avec le critère pour montrer qu’un ensemble estun sous-groupe cf. chapitre 1.Si 0E /F, alors F ne peut pas être un sous-espace vectoriel touts.e.v. de E contient nécessairement le vecteur nul.En général, pour montrer qu’un ensemble F est un espace vectoriel,on montre que c’est un s.e.v. d’un espace vectoriel E connu.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202492 / 231

Page 93 : ExempleMontrons que D =x, y R2 2x y = 0est un s.e.v. de R2.1 2 × 0 0 = 0 donc 0, 0 D.2 Soient ⃗u = x, y D, ⃗v = x′, y′ D et λ, µ R, alors x, y, x′, y′vérifient 2x y = 0 et 2x′ y′ = 0.Montrons que λ⃗u + µ⃗v D. Les composantes de ce vecteur sontλ⃗u + µ⃗v = λx + µx′, λy + µy′. Calculons :2λx + µx′ λy + µy′ = λ2x y z =0 + µ2x′ y′ z =0 = 0,donc λ⃗u + µ⃗v D.Par conséquent D est un s.e.v. de R2.Remarque. Géométriquement, D est une droite passant par l’origine durepère. Plus généralement, toutes les droites et les plans passant parl’origine sont des s.e.v. de R3.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202493 / 231

Page 94 : Intersection de sous-espaces vectorielsPropositionL’intersection de deux s.e.v. d’un K–espace vectoriel E est un s.e.v. de E.Démonstration.Soient F et G des s.e.v. d’un K–espace vectoriel E.1 0E F et 0E G car F et G sont des s.e.v. de E, donc 0E F G.2 Soient u, v F G et λ, µ K. Montrons que λu + µv F G :▶λu + µv F par stabilité de F par combinaisons linéaires.▶λu + µv G par stabilité de G par combinaisons linéaires.Donc λu + µv F G.Par conséquent, F G est un s.e.v. de E.PropositionToute intersection finie ou infinie de s.e.v. d’un K–espace vectoriel E estun s.e.v. de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202494 / 231

Page 95 : Sous-espace vectoriel engendré par une famillePropositionSoit E un K–espace vectoriel et soit u1, . . . , un une famille de vecteurs.L’ensemble des combinaisons linéaires de cette famille est un s.e.v. de E,appelé sous-espace vectoriel engendré par la famille u1, . . . , un. On notecet ensemble Vectu1, . . . , un.Démonstration.Notons F = Vectu1, . . . , un.1 On a 0E = 0u1 + · · · + 0un donc 0E F.2 Si u, v F et λ, µ K, alors λu + µv F d’après une propositionprécédente combinaison linéaire de combinaisons linéaires.Par conséquent, F est un s.e.v. de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202495 / 231

Page 96 : Sous-espace vectoriel engendré par une famillePropositionSoit E un K–espace vectoriel et soit u1, . . . , un une famille de vecteurs.Alors Vectu1, . . . , un est le plus petit espace vectoriel au sens del’inclusion contenant les vecteurs u1, . . . , un. On a alors :Vectu1, . . . , un =\F s.e.v. de Eu1,...,unFF.Démonstration.Soit F un s.e.v. de E contenant les vecteurs u1, . . . , un. Montrons queVectu1, . . . , un F.Soit u Vectu1, . . . , un, alors il existe λ1, . . . , λn K tels queu = λ1u1 + · · · + λnun. Puisque u1, . . . , un F et que F est un s.e.v., on au F stabilité par combinaisons linéaires. Par conséquent, on a montréque Vectu1, . . . , un F.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202496 / 231

Page 97 : Sous-espace vectoriel engendré par une partieDéfinitionSoient E un K–espace vectoriel et A une partie de E. L’intersection de tousles sous-espaces de E qui contiennent A est un sous-espace vectoriel de E.On l’appelle le sous-espace vectoriel engendré par A et on le note VectA.Remarque. Si A = u1, . . . , un, alors VectA = Vectu1, . . . , un.PropositionSoient E un K–espace vectoriel et A une partie de E. Alors VectA est leplus petit s.e.v. de E contenant A.Démonstration.Par définition, VectA est un s.e.v. de E. De plus, si F est un s.e.v. quicontient A, alors VectA F puisque VectA est l’intersection de F avecd’autres sous-espaces.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202497 / 231

Page 98 : Sous-espace vectoriel engendré par une partiePropositionSoit E un K–espace vectoriel et soient A et B des parties de E. Si A Balors VectA VectB.Démonstration.On a A B VectB. Ainsi, VectB est un espace vectoriel quicontient A,donc VectA VectB.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202498 / 231

Page 99 : Somme de sous-espaces vectorielsSi F et G sont des s.e.v. d’un espace vectoriel E, alors F G n’est pas uns.e.v. en général il n’est pas stable pour l’addition.ExempleDans R2, soient F =x, y R2 y = 0et G =x, y R2 x = 0.Alors F et G sont des s.e.v. de R2, mais pas F G : on a⃗u = 1, 0 F G et ⃗v = 0, 1 F G, mais ⃗u + ⃗v = 1, 1 /F G.PropositionSoit E un K–e.v. et soient F et G des s.e.v. de E. L’ensemble :F + G = u + v : u F et v G ,est le plus petit s.e.v. qui contient F G. Ce sous-espace est appelé lasomme des sous-espaces F et G.Remarque. Autrement dit, on a F + G = VectF G.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-202499 / 231

Page 100 : Démonstration.Notons S = F + G. Montrons que S est un s.e.v. de E.1 On a 0E = 0E + 0E avec 0E F et 0E G, donc 0E S.2 Soient w, w′ S et λ, µ K. Alors il existe u, u′ F et v, v′ G telsque w = u + v et w′ = u′ + v′. Alors :λw + µw′ = λu + v + µu′ + v′ = λu + µu′zF+ λv + µv′zGS.Ainsi, on a montré que S est un s.e.v. de E.Montrons à présent que F + G est le plus petit s.e.v. contenant F G,c’est-à-dire que F + G = VectF G. On procède par double inclusion :On a clairement F + G VectF G.Puisque F F + G et G F + G, on a F G F + G. Ainsi,F + G est un espace vectoriel qui contient F G, doncVectF G F + G.Par conséquent, F + G = VectF G.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024100 / 231

Page 101 : Sous-espaces vectoriels en somme directeDéfinitionSoit E un K–e.v. et soient F et G des s.e.v. de E. On dit que F et G sonten somme directe si tout élément de F + G se décompose de manièreunique comme somme d’un élément de F et d’un élément de G. Dans cecas, on note F G la somme de F et de G.Exemple contre-exempleDans R3, soient F =x, y R3 x = yet G =x, y R3 y = z.Le vecteur ⃗u = 1, 3, 2 se décompose de 2 façons différentes sur F + G :⃗u = 1, 1, 0 + 0, 2, 2 = 2, 2, 1 + 1, 1, 1.PropositionSoit E un K–e.v. et soient F et G des s.e.v. de E. Alors F et G sont ensomme directe si et seulement si F G = 0E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024101 / 231

Page 102 : Sous-espaces vectoriels en somme directeOn démontre la proposition par double implication.Démonstration =⇒.Supposons que F et G sont en somme directe. Soit u F G, alors on ales décompositions :u =uzF+ 0EzG= 0EzF+uzG.Par unicité de la décomposition, on a u = 0E. Ainsi, F G = 0E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024102 / 231

Page 103 : Sous-espaces vectoriels en somme directeDémonstration ⇐= .Supposons que F G = 0E. Soit u F + G, montrons que ladécomposition de u comme somme de vecteurs de F et G est unique.Soient v, v′ F et w, w′ G tels que u = v + w = v′ + w′. Alors :v v′ z F= w′ w z G,donc v v′ et w′ w appartiennent à F G = 0E. Par conséquent,v v′ = 0E et w′ w = 0E, c’est-à-dire v = v′ et w = w′.Ainsi, ladécomposition de u est unique.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024103 / 231

Page 104 : Sous-espaces supplémentairesDéfinitionSoit E un K–e.v. et soient F et G des s.e.v. de E. On dit que F et G sontsupplémentaires dans E si tout vecteur de E se décompose de manièreunique comme la somme d’un vecteur de F et d’un vecteur de G :u E,!v, w F × G,u = v + w.PropositionSoit E un K–e.v. et soient F et G des s.e.v. de E. Alors F et G sontsupplémentaires dans E si et seulement si :1 F + G = E ;2 F et G sont en somme directe.Dans ce cas, on note F G = E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024104 / 231

Page 105 : Sous-espaces supplémentairesDémonstration.Le point 1 est équivalent à l’existence d’une décomposition des vecteurs deE comme somme de vecteurs de F et de G, et le point 2 est équivalent àl’unicité d’une telle décomposition.ExempleDans R3, tout plan F passant par 0, 0, 0 et toute droite G non contenuedans F passant par 0, 0, 0 sont supplémentaires.F⃗0G⃗u⃗v⃗wDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024105 / 231

Page 106 : Contenu3Espaces vectorielsEspaces et sous-espaces vectorielsFamilles de vecteursDimension d’un espace vectorielDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024106 / 231

Page 107 : Familles génératricesDéfinitionSoit E un K–e.v. et soit u1, . . . , un une famille de vecteurs de E. On ditque u1, . . . , un est une famille génératrice de E ou que u1, . . . , unengendrent E si tout vecteur de E est combinaison linéaire des vecteursu1, . . . , un, c’est-à-dire si Vectu1, . . . , un = E.ExempleLes vecteurs 1, 0, 0, 0, 1, 0 et 0, 0, 1 engendrent R3, de même que lesvecteurs 1, 0, 0, 1, 1, 0 et 1, 1, 1.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024107 / 231

Page 108 : Familles génératricesPropositionSoit E un K–e.v. Toute sur-famille d’une famille génératrice de E estgénératrice.Démonstration.Si un vecteur est combinaison linéaire d’une famille u1, . . . , un, il est àfortiori combinaison linéaire de la famille u1, . . . , un, un+1, . . . , un+p.PropositionSoit E un K–e.v. et soit u1, . . . , un une famille génératrice de E. Alorsu1, . . . , up1, up+1, . . . , un est une famille génératrice de E si etseulement si up Vectu1, . . . , up1, up+1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024108 / 231

Page 109 : Familles génératricesDémonstration.On procède par double implication. =⇒ Supposons que u1, . . . , up1, up+1, . . . , un est génératrice.Puisque up E, alors up est combinaison linéaire deu1, . . . , up1, up+1, . . . , un par définition d’une famille génératrice. ⇐= Supposons que up est combinaison linéaire deu1, . . . , up1, up+1, . . . , un. Les vecteurs u1, . . . , un sont combinaisonslinéaires de u1, . . . , up1, up+1, . . . , un, donc toute combinaison linéairede u1, . . . , un, c.-à-d. tout élément de E, est combinaison linéaire deu1, . . . , up1, up+1, . . . , un d’après une proposition précédentecombinaison linéaire de combinaisons linéaires.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024109 / 231

Page 110 : Familles liéesPropositionSoit E un K–e.v. et soit u1, . . . , un une famille de vecteurs de E. Lesassertions suivantes sont équivalentes :1 L’un des vecteurs ui est combinaison linéaire des autres.2 Il existe λ1, . . . , λn K non tous nuls tels que λ1u1 + · · · + λnun = 0E.Dans ce cas, on dit que la famille u1, . . . , un est liée.Remarques.1 Toute famille contenant le vecteur nul est liée.2 Une famille u, v est liée si et seulement si u et v sont colinéaires.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024110 / 231

Page 111 : Familles liéesDémonstration de 1 =⇒2.Supposons que ui0 Vectui : i ̸= i0. Alors il existe des scalaires λi Ktels que :ui0 =nXi=1i̸=i0λiui.Par conséquent :λ1u1 + · · · + λi01ui01 + 1ui0 + λi0+1ui0+1 + · · · + λnun = 0E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024111 / 231

Page 112 : Familles liéesDémonstration de 2 =⇒1.Supposons qu’il existe λ1, . . . , λn K non tous nuls tels que :λ1u1 + · · · + λnun = 0E.Soit i0 tel que λi0 ̸= 0, alors on a :λi0ui0 =nXi=1i̸=i0λiui,doncui0 =nXi=1i̸=i0λiλi0ui.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024112 / 231

Page 113 : Familles libresDéfinitionSoit E un K–e.v. et soit u1, . . . , un une famille de vecteurs de E. On ditque la famille est libre si elle n’est pas liée. On dit alors que les vecteursu1, . . . , un sont linéairement indépendants.PropositionSoit E un K–e.v. et soit u1, . . . , un une famille de vecteurs de E. Lesassertions suivantes sont équivalentes :1 La famille u1, . . . , un est libre.2 Aucun vecteur de la famille n’est combinaison linéaire des autres.3 λ1, . . . , λn K, λ1u1 + · · · + λnun = 0E =⇒λ1 = · · · = λn = 0.Démonstration.Prendre la négation des assertions de la proposition précédente.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024113 / 231

Page 114 : Familles libresExempleDans R4, soient ⃗u1 = 1, 1, 0, 2, ⃗u2 = 1, 2, 2, 1 et ⃗u3 = 2, 0, 1, 1.Cherchons si ⃗u1, ⃗u2, ⃗u3 est libre. Soient λ1, λ2, λ3 R tels que :λ1⃗u1 + λ2⃗u2 + λ3⃗u3 = ⃗0.Cette égalité est équivalente au système linéaire :λ1 + λ2 + 2λ3 = 0λ1 + 2λ2= 02λ2 λ3 = 02λ1 + λ2 + λ3 = 0.En résolvant ce système p. ex. pivot de Gauss, on trouve que l’uniquesolution est λ1 = λ2 = λ3 = 0. Ainsi, la famille ⃗u1, ⃗u2, ⃗u3 est libre.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024114 / 231

Page 115 : Familles libresProposition à faire chez vousToute sous-famille d’une famille libre est libre.PropositionSoit E un K–e.v. et soit u1, . . . , un une famille libre. Soit u E, alors lafamille u1, . . . , un, u est libre si et seulement si u /Vectu1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024115 / 231

Page 116 : Familles libresDémonstration.On procède par double implication. =⇒ Par contraposée, si u Vectu1, . . . , un alors la familleu1, . . . , un, u est liée. ⇐= Par contraposée, supposons que u1, . . . , un, u est liée. Alorsil existe λ1, . . . , λn, λ K non tous nuls tels que :λ1u1 + · · · + λnun + λu = 0E.Si on avait λ = 0, alors serait une combinaison linéaire nulle de lafamille u1, . . . , un, donc par liberté de cette famille, tous les λiseraient nuls, contradiction. Par conséquent, λ ̸= 0 et on a :u =nXi=1λiλui Vectu1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024116 / 231

Page 117 : BasesDéfinitionSoit E un K–e.v. et soit u1, . . . , un une famille de vecteurs de E. On ditque u1, . . . , un est une base de E si c’est famille à la fois libre etgénératrice.Exemple1 Dans Kn, les vecteurs :⃗e1 = 1, 0 . . . , 0,⃗e2 = 0, 1, 0, . . . , 0,. . . ,⃗en = 0, . . . , 0, 1,forment une base appelée la base canonique de Kn.2 Dans KnX, les polynômes 1, X, X 2, . . . , X n forment une base appeléela base canonique de KnX.Si a K, alors les polynômes 1, X a, X a2, . . . , X an formentégalement une base de KnX formule de Taylor.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024117 / 231

Page 118 : BasesExempleDans R4, soit F =x, y, z, t R4 2x y + z + 3t = 0. Alors F estun s.e.v. de R4. Cherchons une base de F. Soit ⃗u = x, y, z, t R4, on a :⃗u F ⇐⇒2x y + z + 3t = 0⇐⇒y = 2x + z + 3t⇐⇒⃗u = x, 2x + z + 3t, z, t⇐⇒⃗u = x⃗u1 + z⃗u2 + t⃗u3,avec ⃗u1 = 1, 2, 0, 0, ⃗u2 = 0, 1, 1, 0 et ⃗u3 = 0, 3, 0, 1. Ainsi, on aF = Vect⃗u1, ⃗u2, ⃗u3, c.-à-d. la famille ⃗u1, ⃗u2, ⃗u3 est génératrice de F. Onvérifie facilement qu’elle est libre le vérifier !, donc c’est une base de F.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024118 / 231

Page 119 : Coordonnées d’un vecteur dans une baseThéorèmeSoit E un K–e.v. et soit u1, . . . , un une base de E. Alors tout vecteur deE s’écrit de manière unique comme combinaison linéaire de u1, . . . , un :u E,!λ1, . . . , λn Kn,u = λ1u1 + · · · + λnun.Cet unique n-uplet λ1, . . . , λn Kn est appelé les coordonnées de u dansla base u1, . . . , un.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024119 / 231

Page 120 : Coordonnées d’un vecteur dans une baseDémonstration.Une base est une famille génératrice, donc tout vecteur de E s’écrit commecombinaison linéaire de u1, . . . , un. Il reste à montrer l’unicité de cettecombinaison. Soit u E et soient λ1, . . . , λn, µ1, . . . , µn K tels que :u = λ1u1 + · · · + λnun = µ1u1 + · · · + µnun.Alors on a λ1 µ1u1 + · · · + λn µnun = 0E. Puisque la familleu1, . . . , un est libre, tous les coefficients de cette combinaison linéairesont nuls, c.-à-d. λi = µi pour tout i, d’où l’unicité.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024120 / 231

Page 121 : Familles infinies de vecteursDéfinitionSoit E un K–e.v.Une famille infinie de vecteurs de E est une famille uiiI où I est unensemble infini.On dit qu’un vecteur u E est combinaison linéaire de uiiI si u estcombinaison linéaire d’une sous-famille finie de uiiI, c.-à-d. s’ilexiste i1, . . . , in I tels que u est combinaison linéaire de ui1, . . . , uin.Attention !En algèbre linéaire, on ne manipule que des sommes finies de vecteurs.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024121 / 231

Page 122 : Familles infinies de vecteursDéfinitionSoit E un K–e.v. et soit uiiI une famille infinie de vecteurs de E.On dit que uiiI est une famille génératrice si tout vecteur de E estcombinaison linéaire de uiiI, c’est-à-dire si :u E,i1, . . . , in I,u Vectui1, . . . , uin.On dit que uiiI est une famille libre si toute sous-famille finie deuiiI est libre, c’est-à-dire si :i1, . . . , in I,ui1, . . . , uin est libre.ExempleDans KX, la famille X nnN est libre et génératrice : c’est une base deKX appelée la base de canonique de KX.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024122 / 231

Page 123 : Contenu3Espaces vectorielsEspaces et sous-espaces vectorielsFamilles de vecteursDimension d’un espace vectorielDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024123 / 231

Page 124 : Espace vectoriel de dimension finieDéfinitionSoit E un K–e.v. On dit que E est de dimension finie s’il existe une famillegénératrice finie de E. Sinon, on dit que E est de dimension infinie.Lemme admisSoit E un K–e.v. Si E possède une famille libre de p vecteurs et une famillegénératrice de m vecteurs, alors p m la taille d’une famille libre esttoujours inférieure à la taille d’une famille génératrice.Exemple1 Kn est dimension finie.2 KnX est de dimension finie.3 KX est dimension infinie car il possède une famille libre infinie, doncaucune famille génératrice ne peut être finie d’après le lemme.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024124 / 231

Page 125 : Existence de basesThéorème de la base incomplèteSoit E un K–e.v. de dimension finie. Si u1, . . . , up est une famille libre etsi viiI est une famille génératrice finie ou infinie de E, alors il existeune base de E de la forme :u1, . . . , up, vi1, . . . , vin,avec n = 0 si u1, . . . , up est déjà une base de E.CorollaireSoit E un K–e.v. non nul de dimension finie.1 Il existe une base de E.2 De toute famille génératrice viiI de E, on peut extraire une basevi1, . . . , vin.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024125 / 231

Page 126 : Existence de basesDémonstration du théorème de la base incomplète.On construit par récurrence une suite de familles libres par ajouts successifsde vecteurs de la famille viiI, en s’arrêtant quand on obtient une base.Posons L0 = u1, . . . , up. C’est une famille libre par hypothèse.Soit n N. Supposons que Ln = u1, . . . , up, vi1, . . . , vin est libre. SiLn est génératrice, alors c’est une base ; le théorème est démontré.Sinon, il existe in+1 I tel que vin+1 /Vectu1, . . . , up, vi1, . . . , vin.Posons Ln+1 = u1, . . . , up, vi1, . . . , vin, vin+1. Cette famille est libred’après une proposition précédente.Montrons qu’il existe n tel que Ln soit une base de E. Par l’absurde, si cen’était pas le cas, on aurait une suite LnnN de familles libres de taillesstrictement croissantes. Or d’après le lemme précédent, la taille d’unefamille libre est toujours inférieure à la taille d’une famille génératrice de E.Puisque E est de dimension finie, la taille des familles libres est majorée,donc elle ne peut pas croître indéfiniment ; contradiction.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024126 / 231

Page 127 : Dimension d’un espace vectorielThéorèmeSi E est un K–e.v. non nul de dimension finie, alors toutes les bases de Eont le même nombre de vecteurs. Ce nombre est appelé la dimension de Eet on le note dimE. Si E = 0E, on convient que dimE = 0.Démonstration.Soient B et B′ deux bases de E, de tailles respectives n et n′. Puisque Best une famille libre et que B′ est une famille génératrice, on a n n′. Enéchangeant les rôles de B et B′, on obtient l’inégalité contraire n′ n. Parconséquent, n = n′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024127 / 231

Page 128 : Dimension d’un espace vectorielExemple1 dimKn = n.2 dimKnX = n + 1.3 dimC = 2 si C est vu comme un R–e.v.mais dimC = 1 si C est vucomme un C–e.v.PropositionSoit E un K–e.v. de dimension n et soit F une famille de p vecteurs de E.1 Si F est libre alors p n, avec égalité si et seulement si F est unebase de E.2 Si F est génératrice alors p n, avec égalité si et seulement si F estune base de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024128 / 231

Page 129 : Dimension d’un sous-espace vectorielProposition admisSoit E un K–e.v. de dimension finie. Si F est un s.e.v. de E, alors F est dedimension finie et dimF dimE. De plus, dimF = dimE si etseulement si F = E.DéfinitionSoit E un K–e.v. de dimension n et soit F un s.e.v. de E.Si dimF = 1, on dit que F est une droite vectorielle de E.Si dimF = 2, on dit que F est un plan vectoriel de E.Si dimF = n 1, on dit que F est un hyperplan vectoriel de E.ExempleDans R4, soit F =x, y, z, t R4 2x y + z + 3t = 0. On a vuprécédemment que F possède une base de 3 vecteurs, donc dimF = 3.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024129 / 231

Page 130 : Rang d’une famille de vecteursDéfinitionSoit E un K–e.v. et soient u1, . . . , un une famille de vecteurs. On appellerang de u1, . . . , un, et on note rgu1, . . . , un, la dimension finie dus.e.v. Vectu1, . . . , un.Remarque. Le rang d’une famille est le nombre maximal de vecteurslinéairement indépendants de cette famille.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024130 / 231

Page 131 : Dimension d’une sommeThéorème formule de GrassmannSoient F et G des s.e.v. de dimensions finies d’un K–e.v. Alors :dimF + G = dimF + dimG dimF G.CorollaireSoient F et G des s.e.v. de dimensions finies d’un K–e.v. Alors :dimF + G dimF + dimG,avec égalité si et seulement si F et G sont somme directe.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024131 / 231

Page 132 : Caractérisation des supplémentaires en dimension finiePropositionSoit E un K–e.v. de dimension finie et soient F et G des s.e.v. de E. Lesassertions suivantes sont équivalentes :1 E = F G c.-à-d. F et G sont supplémentaires dans E.2 dimE = dimF + dimG et F G = 0E.3 dimE = dimF + dimG et E = F + G.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024132 / 231

Page 133 : Caractérisation des supplémentaires en dimension finieDémonstration.On montre que 1 =⇒2 =⇒3 =⇒1.1 =⇒2 Si E = F G, alors dimE = dimF + dimG d’après laformule de Grassmann. De plus, F et G sont en somme directe doncF G = 0E.2 =⇒3 Si dimE = dimF + dimG et F G = 0E, alors d’aprèsla formule de Grassmann, on a dimE = dimF + G, donc E = F + G.3 =⇒1 Si dimE = dimF + dimG et E = F + G, alors d’après laformule de Grassmann, on a dimF G = 0, donc F G = 0E. Parconséquent F et G sont en somme directe, d’où E = F G.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024133 / 231

Page 134 : Existence de supplémentairesPropositionSoit E un K–e.v. de dimension finie et soit F un s.e.v. de E. Alors il existeun s.e.v. G tel que F et G sont supplémentaires dans E.Démonstration.Posons n = dimE. Soit e1, . . . , ep une base de F, que l’on complèteavec des vecteurs ep+1, . . . , en tels que e1, . . . , en soit une base de E.Posons G = Vectep+1, . . . , en. On a donc dimF = p etdimG = n p, d’où dimE = dimF + dimG. Enfin, pour toutvecteur u E, il existe λ1, . . . , λn K tels que :u = λ1e1 + · · · + λpepzF+ λp+1ep+1 + · · · + λnenzG,donc E = F + G. D’après la proposition précédente, E = F G.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024134 / 231

Page 135 : Applications linéairesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024135 / 231

Page 136 : Contenu4Applications linéairesDéfinitions et propriétésApplications linéaires particulièresFormes linéairesEndomorphismeIsomorphismeAutomorphismeNoyau et image d’une application linéaireFeuille d’exercices-Espaces vectoriels et sous-espaces vectorielsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024136 / 231

Page 137 : Contenu4Applications linéairesDéfinitions et propriétésApplications linéaires particulièresFormes linéairesEndomorphismeIsomorphismeAutomorphismeNoyau et image d’une application linéaireFeuille d’exercices-Espaces vectoriels et sous-espaces vectorielsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024137 / 231

Page 138 : DéfinitionsDéfinitionSoient E, +, . et F, +, . deux K-espaces vectoriels.On dit que f : E →F est linéaire ou est un morphisme d’espace vectorielsi :1 x, y E, on a f x + y = f x + f y ;2 λ K, x E, on a f λx = λf x.On note L E, F l’ensemble des applications de E dans F.Proposition Caractérisation usuelle des applications linéairesSoit f : E →F. L’application f est linéaire, si et seulement si , λ, K,x, y E, f λx + y = λf x + f y.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024138 / 231

Page 139 : ExempleSoit f : E →F définie par f : x 7→0F. L’application f est linéaire.PropositionSoient E, E1, . . . En, n N des K espaces vectoriels. L’applicationf:E→E1 × · · · × Enx7→f1x, . . . , fnx.f est linéaire de E dans E1 × · · · × En, si et seulement si, f1, . . . , fn sont desapplications linéaires de respectivement de E dans E1, . . . , de E dans En.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024139 / 231

Page 140 : ExempleMontrons que f : R2 →R3 définie par f x, y = x + y, x y, 2y est uneapplication linéaire. Soient λ, R, et a = x, y, b = x′, y′ R2,f λa + b=f λx + x′, λy + y′=λx + x′ + λy + y′, λx + x′ λy y′, 2λy + 2y′=λx + y, x y, 2y + x′ + y′, x′ y′, 2y′=λf a + f b.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024140 / 231

Page 141 : PropositionSoient E, +, ., F, +, ., G, +, . des K- espaces vectoriels.1 Si l’application f : E →F est linéaire alors f 0E = 0F ;2 Si f : E →F et g : F →G sont linéaires alors g ◦f : E →G estlinéaire.3 Si u1, . . . , un sont des vecteurs de E alors λ1, . . . , λn K :f nXk=1λkuk!=nXk=1λkf uk.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024141 / 231

Page 142 : Contenu4Applications linéairesDéfinitions et propriétésApplications linéaires particulièresFormes linéairesEndomorphismeIsomorphismeAutomorphismeNoyau et image d’une application linéaireFeuille d’exercices-Espaces vectoriels et sous-espaces vectorielsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024142 / 231

Page 143 : Formes linéairesDéfinitionOn appelle forme linéaire sur un K-espace vectoriel E, toute applicationlinéaire de E dans K. On note E , au lieu de L E, K, l’ensemble desformes linéaires sur E.ExemplePour a1, . . . , an K fixé, l’application f : Kn →K définie parf : x1, . . . , xn 7→a1x1 + · · · + anxn est une forme linéaire sur Kn. En effet,c’est une application de Kn vers K et c’est aussi une application linéaire caron vérifie aisement que λ, K, x, y Kn, on af λx + y = λf x + f y.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024143 / 231

Page 144 : EndomorphismeDéfinitionOn appelle endomorphisme de E, toute applicatin linéaire de E dans luimême. On note L E ou EndE, au lieu de L E, E, l’ensemble desendomorphismes de E.ExempleL’application identité IdE : E →E est un endomorphisme de E.PropositionSi f et g deux endomorphismes de E, alors g ◦f est aussi unendomorphisme de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024144 / 231

Page 145 : IsomorphismeDéfinitionOn appelle isomorphisme d’un K espace vectoriel E vers un K-espacevectoriel F toute application linéaire bijective de E vers F. On noteisoE, F l’ensemble des isomorphismes de E dans F.ExempleL’application f : R2 →C définie par f a, b = a + ib est un isomorphismede R-espace vectoriel. En effet, cette application est R-linéaire et bijective.PropositionSi f : E →F et g : F →G sont des isomorphismes alors la composéeg ◦f : E →G est un isomorphisme.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024145 / 231

Page 146 : PropositionSi f : E →F est un isomorphisme alors son application réciproquef 1 : F →E est un isomorphisme.ExempleL’application g : C →R2 définie par g : z 7→ℜz, ℑz estl’isomorphisme réciproque de l’application f : a, b R2 7→a + ib C.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024146 / 231

Page 147 : AutomorphismeDéfinitionOn appelle automorphisme de E, tout endomorphisme bijectif de E. Onnote GlE l’ensemble d’automorphisme de E.PropositionSi f : E →E et g : E →E sont des automorphismes de E alors lacomposée g ◦f : E →E est un automorphisme.PropositionSi f : E →E est un automorphisme alors son application réciproquef 1 : E →E est un automorphisme.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024147 / 231

Page 148 : Contenu4Applications linéairesDéfinitions et propriétésApplications linéaires particulièresFormes linéairesEndomorphismeIsomorphismeAutomorphismeNoyau et image d’une application linéaireFeuille d’exercices-Espaces vectoriels et sous-espaces vectorielsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024148 / 231

Page 149 : ThéorèmeSoit f : E →F une application linéaire.1 Si V est un sous-espace vectoriel de E alors f V est un sous-espacevectoriel de F.2 Si W est un sous-espace vectoriel de F alors f 1W est unsous-espace vectoriel de E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024149 / 231

Page 150 : Noyau et image d’une application linéaireDéfinitionSoit f : E →F une application linéaire.1 On appelle image de f l’espace Im f = f E = f x, x E.2 On appelle noyau de f l’espaceker f = f 10F = x E f x = 0F.Proposition1 Im f est un sous-espace vectoriel de F.2 ker f est un sous-espace vectoriel de E.ThéorèmeSi f : E →F est une application linéaire alors1 f est surjective, si et seulement si, Im f = F2 f est injective, si et seulement si, ker f = 0E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024150 / 231

Page 151 : Remarque1 Pour déterminer l’image d’une application linéaire f , on détermine lesvaleurs prises par f , i.e., les y F tels qu’il existe x E pour lequely = f x. En pratique, l’image de f est engendré par l’image d’unebase de E. C’est-à-dire pour toute B = u1, . . . , un une base de EImf = Vect f u1, . . . , f un2 Pour déterminer le noyau d’une application linéaire f , on résoutl’equation f x = 0F d’inconnue x E.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024151 / 231

Page 152 : RangDéfinitionSoient E et F deux K-espaces vectoriels et f L E, F. On appelle Rangde f la dimension du sous-espaces vectoriel Imf . On le note rgf .CorollairePour toute application linéaire f de L E, F. On a rgf ⩽dimE.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024152 / 231

Page 153 : ExempleDéterminons le noyau et l’image de l’application linéaire f : R2 →R2définie par f : x, y 7→x y, x + y. On a :ker f = 0, 0Im f = x, x + y, y x, y R = Vect 1, 1, 1, 1 = R2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024153 / 231

Page 154 : Théorème du rangThéorème Théorème du rangSoient E et F deux K-espaces vectoriels et f de E dans F linéaire. On adimE = dimkerf + rgf Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024154 / 231

Page 155 : Exercice 1.Soit E un R-espace vectoriel.On munit le produit cartésien E × E de l’addition usuelle :x, y + x′, y′ = x + x′, y + y′ et de la multiplication externe par lescomplexes définie par : a + i.b x, y = a.x b.y, a.y + b.x.Montrer que E × E est alors un C-espace vectoriel.Celui-ci est appelé complexifié de E.Exercice 2. Soit R+ muni de la loi interne définie para b = a.b, a, b R+ et de la loi externe telle que :λ a = aλ, a R+, λ R.Montrer que R+, , est un R-espace vectoriel.Exercice 3. Sur R2, on définit les deux lois suivantes : pour tousx, y, x′, y′ R2 et λ R, on posex, y + x′, y′ = x + x′, y + y′etλ x, y = λx, 0.Le triplet R2, +, est-il un espace vectorielsur R ?Exercice 4. Les parties suivantes sont-elles des sous-espaces vectoriels deR2 ?a x, y R2 x ⩽y ;Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024155 / 231

Page 156 : Matrices et inverses de matricesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024156 / 231

Page 157 : Contenu5Matrices et inverses de matricesDéfinitionMn,pK, +, . est un K-espace vectorielOpérationsDimensionSous-espaces des matrices diagonales et triangulairesPropriétés du produit matricielPuissance d’une matriceMatrices inversiblesDétermination pratique de l’inverse d’une matrice carrée inversibleDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024157 / 231

Page 158 : DéfinitionDéfinitionSoient n, p N. On appelle matrice à n lignes et p colonnes à coefficientsdans K, un tableau à n lignes et p colonnes d’éléments de K. On note unetelle matriceM = aij1in1jp=a11a12· · ·a1Pa21a22· · ·a2p............an1an2· · ·anp.• On dit que M est une matrice colonne si p = 1.• On dit que M est une matrice ligne si n = 1.• On dit que M est une matrice carrée si n = p.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024158 / 231

Page 159 : Notation :• On note Mn,pK l’ensemble des matrices à n lignes et p colonnes àcoefficients dans K.• Si p = n, on note MnK l’ensemble des matrices carrées à n lignes età n colonnes.• Un élément de MnK est dit matrice carrée de taille n.• Soit M = aij1in1jp , alors aij est le coefficient situé sur la iièmeligne et la jième colonne de la matrice M.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024159 / 231

Page 160 : Matrice triangulaire supérieureDéfinitionSoit M = aij1i,jn une matrice carrée de taille n. On dit que :M est une matrice triangulaire supérieure resp. triangulaire strictementsupérieure si aij = 0 pour tout i j resp. i j. C’est-à-dire :M =a11a12· · ·a1n0a22· · ·a2n............0· · ·0ann, resp.M =0a12· · ·a1n..................an1,n0· · ·· · ·0.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024160 / 231

Page 161 : Matrice triangulaire inférieureDéfinitionSoit M = aij1i,jn une matrice carrée de taille n. On dit que :M est une matrice triangulaire inférieure resp. triangulaire strictementinférieure si aij = 0 pour tout i j resp. i j. C’est-à-dire :M =a110· · ·0a21a22· · ·0............an1· · ·an,n1ann, resp.M =00· · ·0a21...............0an1· · ·an,n10.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024161 / 231

Page 162 : Matrice diagonaleDéfinitionSoit M = aij1i,jn une matrice carrée de taille n. On dit que :M est une matrice diagonale si aij = 0 pour tout i ̸= j. C’est-à-dire :M =a110· · · 00...............an1,n100· · ·...ann.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024162 / 231

Page 163 : Matrice symétrique/ antisymétriqueDéfinitionSoit M = aij1i,jn une matrice carrée de taille n. On dit que :M est symétrique resp. antisymétrique si aij = aji resp. aij aji pourtout 1 i, j n. C’est-à-dire :M =a11a12· · ·a1na12a22· · ·a2n............a1na2n· · ·ann, resp. M =a11a12· · ·a1na12a22· · ·a2n............a1na2n· · ·ann.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024163 / 231

Page 164 : Matrice transposéeDéfinitionSoit M = aij1i,jn une matrice carrée de taille n. On dit que :Soit M = aij1in1jpMn,pK. On appelle transposée de M la matricetM = bij1ip1jn Mp,nK où bij = aij. c’est-à-dire :tM =a11a21· · ·an1a12a22· · ·an2............a1pa2p· · ·anp.Autrement dit, les n lignes de M sont les n colonnes de tM et les pcolonnes de M sont les p lignes de tM.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024164 / 231

Page 165 : Remarque1 Une matrice carrée M est symétrique, si et seulement si, tM = M.2 Une matrice carrée M est antisymétrique, si et seulement si,tM = M.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024165 / 231

Page 166 : Somme de matricesDéfinitionSoit A = aij1in1jpMn,pK et B = bij1in1jpMn,pK. Ondéfinit la matrice A + B Mn,pK de la façon suivante :A + B = aij + bij1in1jpMn,pK. AinsiA + B=a11a12· · ·a1Pa21a22· · ·a2p............an1an2· · ·anp+b11b12· · ·b1Pb21b22· · ·b2p............bn1bn2· · ·bnp=a11 + b11a12 + b12· · ·a1P + b1pa21 + b21a22 + b22· · ·a2p + b2p............an1 + bn1an2 + bn2· · ·anp + bnp.Remarque On ne somme que des matrices de même types.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024166 / 231

Page 167 : Multiplication par un scalaireDéfinitionSoit M = aij1in1jpMn,pK et soit λ K. On définit la matrice λAde Mn,pK par λA = λaij1in1jp . AinsiλA =λa11λa12· · ·λa1Pλa21λa22· · ·λa2p............λan1λan2· · ·λanpDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024167 / 231

Page 168 : ThéorèmeMn,pK, +, . est un K-espace vectoriel d’élément nul0 = 0Mn,pK =0· · ·0...· · ·0· · ·0Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024168 / 231

Page 169 : DéfinitionSoit 1 i n et 1 j p.On appelle matrice élémentaire d’indice i, j de Mn,pK la matrice Eij,dont tous les coefficients sont nuls sauf à la iième ligne et la jième colonnequi vaut 1.ExempleDans M2K, les matrices élémentaires sontE11 = 1000E12 = 0100E21 = 0010E22 = 0001.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024169 / 231

Page 170 : ExempleDans Mn,1K les matrices élémentaires sont :E11 =10...0, . . . , En1 =0...01.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024170 / 231

Page 171 : ThéorèmeLa famille B = Eij, 1 ⩽i n, 1 ⩽j ⩽p est une base de Mn,pK.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024171 / 231

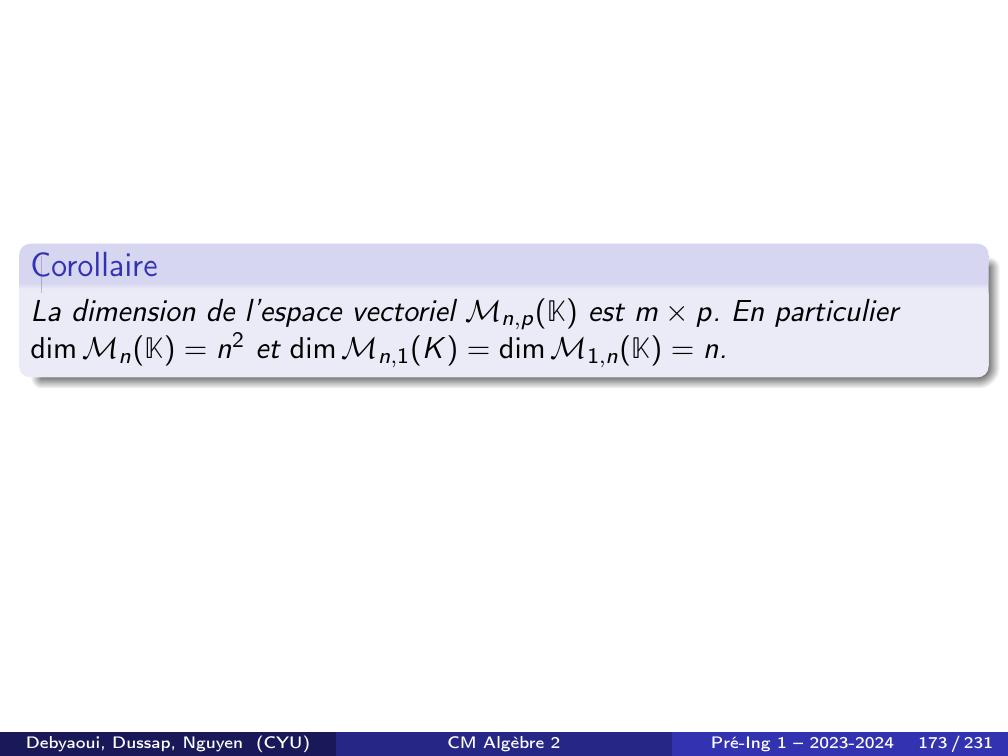
Page 172 : Démonstration.Pour toute matrice X = aij1⩽i⩽n1⩽j⩽pMn,pK, on a X =X1⩽i⩽n1⩽j⩽paijEij. Donc Best une famille génératrice de Mn,pK. Montrons maintenant que B est libre.Soient λij K, 1 ⩽i ⩽n et 1 ⩽j ⩽p tel queX1⩽i⩽n1⩽j⩽pλijEij = 0Mn,pK etmontrons que λij = 0, 1 ⩽i ⩽n et 1 ⩽j ⩽p. On aX1⩽i⩽n1⩽j⩽pλijEij = 0Mn,pK estéquivalent àλ11· · ·λ1p......λn1· · ·λnp=0· · ·0......0· · ·0.Par identification on obtient le résultat λij = 0, 1 ⩽i ⩽n, 1 ⩽j ⩽p.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024172 / 231

Page 173 : CorollaireLa dimension de l’espace vectoriel Mn,pK est m × p. En particulierdim MnK = n2 et dim Mn,1K = dim M1,nK = n.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024173 / 231

Page 174 : ExempleSoient A1, A2, A3, A4 les matrices de M2R suivantes :A1 = 1001A2 = 1001A3 = 1111A4 = 0110.Montrons que B = A1, A2, A3, A4 est une base de M2R.Nous remarquons que CardB = 4 = dim M2R.Donc pour que B soit une base de M2R il suffit que B soit libre surM2R.Soient λ1, . . . , λ4 R, tel que λ1A1 + λ2A2 + λ3A3 + λ4A4 = 0. Montronsque λ1 = · · · = λ4 = 0.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024174 / 231

Page 175 : ExempleOn a λ1A1 + λ2A2 + λ3A3 + λ4A4 = 0 est équivalent à λ1 + λ2 + λ3λ3 λ4λ3 + λ4λ1 λ2 + λ3= 0000.Qui est équivalent àλ1 + λ2 + λ3 = 0,λ3 λ4 = 0,λ3 + λ4 = 0,λ1 λ2 + λ3 = 0.On déduit facilement que λ1 = λ2 = λ3 = λ4 = 0.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024175 / 231

Page 176 : ExempleMontrons que :F = a + ba b2a + ba + 2b a, b Kest un sous-espace vectoriel de M2K. On aF= aa2aa+ bbb2b a, b K=a 1121+ b 1112 a, b K=vect 1121, 1112.Par suite F est un sous-espace vectoriel de M2K.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024176 / 231

Page 177 : ExempleSoit H = abcd a + b + c + d = 0, avec a, b, c, d K.Montrons que H est un sous-espace vectoriel de M2K.Soit f l’application suivantef:M2K→K abcd7→a + b + c + d.Il est facile à vérifier que f est une application linéaire, c’est-à-dire, pourtous λ, b K, A, B M2K on a f λA + bB = λf A + bf B.On aker f=M M2K f M = 0= abcd a + b + c + d = 0On remarque que ker f = H et on sait que le noyau d’une applicationlinéaire est un sous-espace vectoriel. On déduit alors que H est unDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024177 / 231

Page 178 : Sous-espaces des matrices diagonales et triangulairesPropositionDnK l’ensemble des matrices diagonales de MnK est un sous-espacevectoriel de MnK de dimension n.Remarque Une base deDnK =M MnK M =a110...0ann, aij KestB1 = E11, . . . , Enn.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024178 / 231

Page 179 : Proposition1 L’ensemble des matrices triangulaires supérieures resp. triangulairesinférieures est un sous-espace vectoriel de MnK de dimensionnn+12.2 L’ensemble des matrices traingulaires strictement supérieures resp.triangulaires strictement inférieures est un sous-espace vectoriel deMnK de dimension nn12.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024179 / 231

Page 180 : Remarque1 vectEij, 1 i j n est l’ensemble des matrices triangulairessupérieures.2 vectEij, 1 i j n est l’ensemble des matrices traingulairesstrictement supérieures3 vectEij, 1 j i n est est l’ensemble des matrices triangulairesinféreiures.4 vectEij, 1 j i n est l’ensemble des matrices traingulairesstrictement strictement inférieures.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024180 / 231

Page 181 : ExerciceMontrer que :1 T ⩾n K T n K = MnK.2 T ⩽n K T n K = MnK.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024181 / 231

Page 182 : Propriétés du produit matricielDéfinitionSoient A = aij1⩽i⩽n1⩽j⩽pMn,pK, B = bij1⩽i⩽p1⩽j⩽qMp,qK. On définitla matrice C = A × B = AB = cij1in1jqMn,qK, par1 i n, 1 j q, cij = Ppk=1 aikbkj.Exemple Vérifier que pour tous Eij, Ekl MnK, on a EijEkl = δjkEil.Attention : Pour que cette multiplication matricielle soit possible il estnecessaire que le nombre de colonnes de A soit egal au nombre de ligne deB. On apprend : “typen,p× typep,q=typen,q.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024182 / 231

Page 183 : Exemple1211 100211=1 × 1 + 2 × 20 + 2 × 10 + 2 × 11 × 1 + 1 × 20 + 1 × 10 + 1 × 1= 522111Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024183 / 231

Page 184 : Remarque Si les types de A et B permettent de calculer AB et BA, alorsen général on n’a pas AB = BA. Par exemple : 1000 0100= 0100 0100 1000= 0000Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024184 / 231

Page 185 : Proposition1 Pour tout A Mn,pK, B Mp, qK, C Mq, m, on aABC = ACB ;2 pour tous A, B Mn,pK et C Mp, qK, on aA + BC = AC + BC ;3 pour tous A Mn,pK et B, C Mp, qK, on aAB + C = AB + AC ;4 Pour tout A Mn,pK, B Mp, qK, et pour tout λ K, on aλAB = λAB = AλB.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024185 / 231

Page 186 : Remarque Dans l’ensemble des matrices MnK des matrices carrées, lamultiplications est une loi de composition interne. Elle admet commeélément neutre la matrice diagonaleIn =10...01Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024186 / 231

Page 187 : Puissance d’une matriceDéfinitionSoit A MnK, on noteA0 = In, A1 = A, A2 = A × A, . . . , Am = A × · · · × A m termes.Attention : A + B2 = A2 + AB + BA + B2 ̸= A2 + 2AB + B2A + B3 = A3 + A2B + ABA + BA2 + AB2 + BAB + B2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024187 / 231

Page 188 : Contenu5Matrices et inverses de matricesDéfinitionMn,pK, +, . est un K-espace vectorielOpérationsDimensionSous-espaces des matrices diagonales et triangulairesPropriétés du produit matricielPuissance d’une matriceMatrices inversiblesDétermination pratique de l’inverse d’une matrice carrée inversibleDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024188 / 231

Page 189 : Matrices inversiblesDéfinitionUne matrice A MnK est dite inversible s’il existe B MnK vérifiantAB = BA = In.Cette matrice B est alors unique, c’est l’inverse de A noté A1.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024189 / 231

Page 190 : ExempleLa matrice In est inversible et I 1n= In.PropositionSoient A, B MnK.1 Si A et B sont inversibles alors AB1 = B1A1.2 Si A est inversible alors A1 est inversible et A11 = A.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024190 / 231

Page 191 : DéfinitionOn note GLnK l’ensemble des matrices inversibles de MnK.PropositionGLnK, × est un groupe.ExempleSoit A = 1234. On vérifie par le calcul que A2 5A = 2I2. Par suiteA12A 52I2 = I2. On conclut alors que A1 = 12A 52I2.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024191 / 231

Page 192 : Remarque La somme de deux matrice inversible n’est pas toujours unematrice inversible. Par example : 1001+ 1001= 0000Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024192 / 231

Page 193 : LemmeSoient A, B Mn,pK si AX = BX, X Mp,1K alors A = B.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024193 / 231

Page 194 : Comment chercher l’inverse d’une matrice carréeA GLnK :Soit A = aij1⩽i⩽n1⩽j⩽n GLnK. On introduit X =x1...xnMn,1K etY =y1...yn= AX Mn,1K. On ay1...yn=a11· · ·a1n......an1· · ·annx1...xn.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024194 / 231

Page 195 : Le système est équivalent ày1=a11x1 + a12x2 + · · · + a1nxn.........yn=an1x1 + an2x2 + annxn.Si cela est possible, on résout ce système dont les inconnues sont x1, . . . , xnet on obtient :S :x1=b11y1 + b12y2 + · · · + b1nyn.........xn=bn1y1 + bn2y2 + · · · + bnnyn.Soit B = bij1in1jn GLnK.Le système S est équivalent à X = BY . AinsiInX = BAX, X Mn,1K, on a donc In = BA donc A1 = BDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024195 / 231

Page 196 : ExempleSoit A =011101110M3R. Déterminons A1. SoientX =x1x2x2, Y =y1y2y3M3,1R tel que Y = AX. On a :y1 = x2 + x3y2 = x1 + x3y3 = x1 + x2⇔x2 = y1 x3x3 = 12y2 y3 + y1x1 = y3 y1 + x3⇔x2 = 12y1 y2 + y3x3 = 12y1 + y2 y3x1 = 12y1 + y2 + y3On déduit alors que A1 = 12111111111Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024196 / 231

Page 197 : Algorithme de Gauss JordanPropositionAlgorithme de Gauss-Jordan Soit A une matrice carrée de taille ninversible. L’inverse A1 de A se calcule de la manière suivante :1 On forme la matrice augmentée n × 2n suivante B = AIn.2 On applique l’algorithme de Gauss à B.3 Une fois le système échelonné obtenu, on continue sur le mêmeprincipe que l’algorithme de Gauss afin d’obtenir une matrice de laforme InC.4 L’inverse est A1 = C.Démonstration. Admis.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024197 / 231

Page 198 : ExempleInverser la matrice A :A =123234346Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024198 / 231

Page 199 : 123100234010346001123100012210023301L2 ←L2 2L1L3 ←L3 3L1123100012210001121L2 ←L2L3 ←L3 + 2L2120263010032001121L1 ←L1 3L3L2 ←L2 2L3100201010032001121L1 ←L1 2L2Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024199 / 231

Page 200 : L’inverse de A est doncA1 =201032121Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024200 / 231

Page 201 : DéterminantsDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024201 / 231

Page 202 : Dans cette section, on suppose que A = aij est une matrice carrée detaille n × nDéfinition Mineure d’une matricePour tout couple i, j 1; n2, on appelle mineure d’indice i, j la matricede taille n 1 × n 1 obtenue en supprimant la i e ligne et la je colonnede A.ExempleSoit A =12345678910111213141516.La mineure d’indice 2, 3 est : A2,3 =12491012131416Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024202 / 231

Page 203 : Définition Déterminant d’une matrice carréePour tout i, j 1; n2, Aij la matrice obtenue en supprimant la i e ligneet la je colonne de A. On appelle déterminant de A le nombre défini par :Si n = 2, detA =a11a12a21a22 = a11a22 a21a12Si n 2, detA =nPi=11i+1ai1 det Ai1Exemple2552 = 4 25 = 21112231125= 13125+21225+11231 = 152+254+16 = 10Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024203 / 231

Page 204 : Proposition1 det A = detA2 Soit Bj la matrice obtenue en intervertissant la première et la jecolonne ou ligne de A. Alorsdet Bj = detA3 Échanger deux colonnes ou deux lignes de A a pour effet demultiplier le déterminant par 1.4 Le déterminant d’une matrice ayant deux colonnes ou deux ligneségales est nul.5 Multiplier une colonne ou une ligne d’une matrice par λ R,multiplie son déterminant par λ.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024204 / 231

Page 205 : Proposition6 Soit A et B deux matrice de taille n × n et λ R. Alorsdet λA = λn detAdetAB = detA × detBdetA1=1detA si A inversible ⇔detA ̸= 07 Ajouter à une colonne ou une ligne une combinaison linéaire desautres colonnes ou ligne ne modifie par le déterminant.8 Développement selon une ligne et une colonnedetA =nXk=11k+jakj det Akj développement selon la colonne jdetA =nXk=11i+kaik det Aik développement selon la ligne iDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024205 / 231

Page 206 : Exempledéveloppement selon la première ligne102345567= 14567 + 23456 = 28 30 + 218 20 = 6combinaison linéaire des lignes111211456=111300456= 11+2×31156 = 365 = 3deux lignes identiques1163252212= 2116325116= 0Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024206 / 231

Page 207 : Proposition9 Le déterminant d’une matrice triangulaire/diagonale est égal auproduit des coefficients de la diagonale.10 Soit A la matrice définie parA =BC0Dici, B, C, D sont des matrices carrés. Alors detA = detB × detDExempleA =1234567891000abc00def0000g=1267 ×abcdef00g= 5gae bd.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024207 / 231

Page 208 : Définition Déterminant de n vecteursSoit B = e1, e2, · · · , en une base de Rn. Soit u1 =a11a21...an1, u2 =a12a22...an2,. . ., un =a1na2n...ann, n vecteurs de Rn dont les coordonnées sont donnéesdans la base B. Soit A = aij la matrice n × n construites à partir desvecteurs ui. On définit le déterminant de la famille u1, u2, · · · , un dans labase B pardet Bu1, u2, · · · , un = detADebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024208 / 231

Page 209 : Proposition Caractérisation d’une famille liéeSoit u1, u2, · · · , un une famille de n vecteurs de Rn. Il y a équivalenceentre les assertions suivantes :1 La famille u1, u2, · · · , un est liée.2 Pour toutes bases B de Rn, on a det Bu1, u2, · · · , un = 03 Il existe une base B de Rn telle que det Bu1, u2, · · · , un = 0Proposition Caractérisation d’une baseSoit u1, u2, · · · , un une famille de n vecteurs de Rn. Il y a équivalenceentre les assertions suivantes :1 La famille u1, u2, · · · , un est une base.2 Pour toutes bases B de Rn, on a det Bu1, u2, · · · , un ̸= 03 Il existe une base B de Rn telle que det Bu1, u2, · · · , un ̸= 0Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024209 / 231

Page 210 : Proposition Formules de CramerSoit B une matrice colonne de taille n × 1. Alors le système linéaireAX = B possède une unique solution dont les composantes sont donnéespar :i 1; n, xi = det C1, . . . , Ci1, B, Ci+1, . . . , CndetAoù C1, C2, · · · , Cn sont les colonnes de A.ExempleRésoudre2x y + z=0x 2y z=33x + y + 2z=1On a detA =211121312= 6. D’oùx =0113211126= 2;y =2011313126= 1;z =2101233116= 3Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024210 / 231

Page 211 : Représentation matricielle et changements de basesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024211 / 231

Page 212 : Dans cette section, on suppose que E est un K-espace vectoriel dedimension finie n, F est un espace vectoriel de dimension finiDéfinition Matrice d’une famille finie de vecteurs dans une base finieSoit B = e1, e2, · · · , en une base de E et X = X1, e2, · · · , Xp unefamille finie de vecteurs de E. Pour tout j 1; p on note a1j, . . . , anjles coordonnées de Xj dans la base B. La matrice aij1in1jp, notéeMatBX, est appelée matrice de X dans la base B.MatBX =X1XjXp↓↓↓a11. . .a1j. . .a1p←e1.........ai1. . .aij. . .aip←ei.........an1. . .anj. . .anp←enDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024212 / 231

Page 213 : Théorème Bases et matrices inversiblesSoit B une base de E et F une famille de n vecteurs de E. Alors F est unebase de E si et seulement si MatBF est inversible.PropositionSoit E ̸= 0E, B une base de E et X une famille de vecteurs de E. AlorsrgX = rg MatBXDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024213 / 231

Page 214 : Définition Matrice d’une application linéaire dans des bases finiesSoit dimE = p et dimF = n, B = e1, e2, · · · , ep une base de E,C = κ1, κ2, · · · , κn une base de F et f LE, F. On appelle matrice def dans B et C et on note MatB,Cf la matrice de la famillef B = f e1, . . . , f ep dans la base C.Si E = F et B = C, la matrice MatB,Bf est simplement notée MatBf .MatB,Cf = MatCf B =f e1f ejf ep↓↓↓a11. . .a1j. . .a1p←κ1.........ai1. . .aij. . .aip←κi.........an1. . .anj. . .anp←κnCoordonnées de f ej dans C écrites en colonnesDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024214 / 231

Page 215 : ExempleSi B est une base de E, alors MatBIdE = In.Soit T l’endomorphisme P 7→X 2P′′ + P1 de R3X etB3 = 1, X, X 2, X 3 la base canonique de R3X. AlorsT1 = 1TX = 1TX 2 = 2X 2 + 1TX 3 = 6X 3 + 1MatB3T =T1TXTX 2TX 3↓↓↓↓1111←10000←X0020←X 20006←X 3Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024215 / 231

Page 216 : Proposition Rang d’une application linéaireSoit B une base de E, C une base de F et f LE, F. Alorsrgf = rg MatB,Cf Démonstration.rg MatB,Cf = rg MatC f B= rg f B = dim Vectf B = dim Im f = rgf Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024216 / 231

Page 217 : Théorème Calcul matriciel de l’image d’un vecteur par uneapplication linéaireSoit E ̸= 0E et F ̸= 0F deux K-espace vectoriels de dimension finie, Bune base de E, C une base de F, u LE, F et x E. AlorsMatC ux = MatB,Cu × MatBxDémonstration.Soit B = e1, e2, · · · , ep, C = f1, f2, · · · , fn. Posons X = MatBx etU = MatB,Cu.ux = upXj=1xjej=pXj=1xjuej =pXj=1xjnXi=1uijfi =nXi=1pXj=1uijxjfiDonc les coordonnées de ux dans C sontpXj=1u1jxj, . . . ,pXj=1unjxj,c’est-à-dire le produit U × X.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024217 / 231

Page 218 : Proposition Lien entre LE, F et Mn,pKSoit E et F deux K-espaces vectoriels de dimensions finies respectives p etn, B une base de E et C une base de F. L’application f 7→MatB,Cf estun isomorphisme de LE, F sur Mn,pK.Proposition Matrice d’une composéeSoit E, F, G trois K-espaces vectoriels de dimensions finies non nulles debases respectives B, C, D et f LE, F et g LF, G. Alors,MatB,Dg ◦f = MatC,Dg × MatB,Cf Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024218 / 231

Page 219 : Proposition Matrice d’un isomorphismeSoit E et F deux K-espaces vectoriels de mêmes dimensions finies nonnulles de bases respectives B, C et f LE, F. Alors f est unisomorphisme de E sur F si et seulement si MatB,Cf est inversible. Dansce cas,MatC,Bf 1= MatB,Cf 1Démonstration.⇒Si f est bijective et si on pose n = dimF, on aMatB,Cf × MatC,Bf 1 = MatCIdF = In.⇐si A = MatB,Cf est inversible, notons g l’unique application linéairede F dans E pour laquelle MatC,Bg = A1. Dans ces conditions,MatBg ◦f = MatC,Bg × MatBCf = A1A = In. De même,MatC,B = In. Donc g ◦f = IdE et f ◦g = IdF et f est bijective de Esur F.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024219 / 231

Page 220 : Changement de baseDéfinition Matrice de passageSoit B = e1, e2, . . . , en et B′ = e′1, e′2, . . . , e′n deux bases de E. Onappelle matrice de passage de la base B à la base B′ la matrice del’application IdE relativement aux bases B′ et B. On la note :PBB′= MatBB′ = MatB′,BIdEDebyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024220 / 231

Page 221 : ExempleSoit E = R2X, B =1, X, X 2et B′ =1, X 1, X 12. On a alors1 = 1 donc IdE1 = 1 + 0X + 0X 2X 1 = 1 + X, donc IdEX 1 = 1 + 1X + 0X 2X 12 = 1 2X + X 2 donc IdEX 12 = 1 2X + 1X 2La matrice de passage de B à B′ est donc :PBB′= !111←1012←X001←X 2↑↑↑1X 1X 12Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024221 / 231

Page 222 : PropositionSi P = PB B′, alors P est inversible et P1 = PB′ BPropositionUne matrice P est inversible si et seulement si il existe deux bases B et B′de E telles que P = PBB′ = MatB′,BIdE.PropositionSoit B, B′ et B′′ trois bases de E. Alors PB B′′ = PB B′ × PB′ B′′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024222 / 231

Page 223 : Proposition Matrice de passage et coordonnéesSoit vecteur x E, B et B′ deux bases de E, et P = PB B′. On note XBla matrice colonne des coordonnées de x dans la base B et X ′B′ la matricecolonne des coordonnées de x dans la base B′. Alors :XB = PX ′B′Démonstration.x = IdEx, donc le résultat découle simplement de la définition de lamatrice de passage.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024223 / 231

Page 224 : ExempleSoit X = 1, 2, 3 dans la base canonique Bc, soitB′ = e1, e1 + e2, e3 e2 3e1 est une base de R3. Déterminer lescoordonnées de X dans la base B′.Sans utiliser la formule.ε1= e1ε2= e1 + e2ε3= e3 e2 3e1⇔e1= ε1e2= ε2 ε1e3= ε3 + ε2 + 2ε1Ainsi, de X = e1 + 2e2 + 3e3, nous arrivons à X = 5ε1 + 5ε2 + 3ε3En utilisant la formule de changement de bases. Nous avonsXBc = PXB′, d’où XB′ = P1XBc. Il faut donc calculer l’inverse de PP1 =1130110011=112011001. Et on retrouveXB′ = 5, 5, 3.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024224 / 231

Page 225 : Matrices équivalentesDéfinitionSoit A, B Mn,p K. On dit que B est équivalente à A s’il existe deuxmatrices carrées inversibles Q GLn K, P GLp K telles que :B = Q1APPropositionLa relation « est équivalente à » sur Mn,pK est une relationd’équivalence.Démonstration.Réflexivité : Nous avons simplement A = I 1n AIp.Symétrie : Nous avons B = Q1AP, donc A = QBP1. En posantQ′ = Q1 et P′ = P1, on a bien A = Q′1BP′.Transitivité : Nous avons C = Q1BP et B = Q′1AP′. En posantQ′′ = Q′Q et P′′ = P′P nous obtenons C = Q′′1AP′′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024225 / 231

Page 226 : PropositionSoit A et B deux matrices de Mn,p K. Les matrices A et B sontéquivalentes si et seulement si rgA = rgB.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024226 / 231

Page 227 : Matrices semblablesDéfinitionSoit A, B Mn K. On dit que B est semblable à A s’il existe une matriceinversible P GLn K telle queB = P1APPropositionLa relation « est semblable à » sur MnK est une relation d’équivalence.Démonstration.Réflexivité : Nous avons simplement A = I 1n AIn.Symétrie : Nous avons B = P1AP, donc A = PBP1. En posantP′ = P1, on a bien A = P′1BP′.Transitivité : Nous avons C = P1BP et B = P′1AP′. En posantP′′ = P′P nous obtenons C = P′′1AP′′.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024227 / 231

Page 228 : PropositionSi deux matrices A et B sont semblables alors elles sont équivalentessemblables ⇒équivalentes.Attention ! ! La réciproque est fausse.ExempleIn est la seule matrice semblable à In alors que toute matrice inversible estéquivalente à In.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024228 / 231

Page 229 : Proposition Matrices de passage et matrices semblablesSoit f une application linéaire de E dans E, B et B′ deux bases de E. Onnote :P = PBB′Soit A la matrice de f relativement à la base B et B la matrice de frelativement à la base B′. On a alors :B = P1APPropositionSoit A, B MnK. Alors A et B sont semblables si et seulement si A et Bsont les deux matrices d’une même application linéaire dans deux basesdifférentes.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024229 / 231

Page 230 : Proposition Invariance du déterminant et de la traceDeux matrices carrées semblables ont le même déterminant et la mêmetrace. Pour toute matrice carrée A et toute matrice carrée inversible P, ona :detP1AP= detATrP1AP= TrADémonstration.Nous allons utiliser les deux propriété detAB = detA detB etTrAB = TrBAAttention ! La réciproque est fausseExemple1101et1001Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024230 / 231

Page 231 : Définition Trace d’un endomorphismeSoit E ̸= 0E et f LE. On appelle trace de f et l’on note Trf latrace d’une matrice de f dans une base de E.Proposition tracePour tout f , g LE,Pour tout λ K, Trλf + g = λTrf + Trg.Trf ◦g = Trg ◦f Démonstration.Il suffit de revenir aux matrices et utiliser les propriétés précédentes.Debyaoui, Dussap, Nguyen CYUCM Algèbre 2Pré-Ing 1 – 2023-2024231 / 231

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231