CM

Posté le 07/02/2025

Chargé de TD/CM : N. Arancibia.

132 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281

Page 1 : Analyse 1 - Premier semestre 2023 - 2024Analyse 1 - Premier semestre 2023 - 2024Responsable CM :Nicolas Arancibia RobertBureau : Site St Martin, Bâtiment E, cinquième étage,Bureau 552e-mail : nat@cy-tech.fr - nicolas.arancibia-robert@cyu.frÉvaluation :• DS 1 : Semaine du 13/11/202325• DS 2 : Semaine du 11/12/202325• Examen : Semaine du 22/01/202340• Note TD : 10Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20241 / 277

Page 2 : Modalités d’ÉvaluationVous aurez 4 notes :▶2 contrôles continus : DS1 et DS2, durée 1h, en séance de TD,▶Algèbre 1 : Semaines du 23 Octobre et du 27 Novembre.▶Analyse 1 : Semaines du 13 Novembre et du 11 Décembre.▶1 Examen de ﬁn de semestre : E, durée 2h, semaine du 22 Janvier.▶1 note de TD : TD, donnée par l’enseignant.On calcule alors une moyenne pondérée MM = 0.25 × DS1 + DS2 + 0.4 × E + 0.1 × TDVotre note ﬁnale NF est le max entre la moyenne M et la note de l’examen ENF = maxM, E.1 of 4

Page 3 : ExemplesMoyenne : M = 0.25 × DS1 + DS2 + 0.4 × E + 0.1 × TD▶Exemple 1DS1 = 8 DS2 = 17 E = 9 TD = 19On calcule la moyenne :M = 0.25 × 8 + 17 + 0.4 × 9 + 0.1 × 19 = 11.75La note ﬁnale est le max entre M et E donc NF = 11.75▶Exemple 2DS1 = 15 DS2 = 2 E = 13 TD = 12On calcule la moyenne :M = 0.25 × 15 + 2 + 0.4 × 13 + 0.1 × 12 = 10.65La note ﬁnale est le max entre M et E donc NF = 13.2 of 4

Page 4 : Rattrapage pour AbsenceEn cas d’absence justiﬁée ou injustiﬁée la note correspondante dans laformule de la moyenne sera 0.Il y aura à la ﬁn de semestre une épreuve de rattrapage pour les absences.Attention ! C’est un rattrapage pour les absences uniquement,indépendante des notes que vous avez obtenues.Si vous êtes absent.e à l’examen vous devez obligatoirement passer l’épreuvede rattrapage.Si vous êtes absent.e à DS1 ou DS2 vous pouvez passer l’épreuve de rattrapagesi vous le souhaitez.⇒Remarque : il y aura une unique épreuve de rattrapage qui durera 2h etportera sur l’ensemble du semestre, même si vous la passez pour une absenceau DS1 ou DS2.La note R obtenue au rattrapage remplacera le 0 dans le calcul de la noteﬁnale.3 of 4

Page 5 : Exemples▶Exemple 1DS1 = 11 DS2 = 15 E =ABS TD = 16Rattrapage OBLIGATOIRE. Vous obtenez R = 12 qui remplace EM = 0.25 × 11 + 15 + 0.4 × 12 + 0.1 × 16 = 12.9La note ﬁnale est le max entre M et E = R = 12 donc NF = 12.9▶Exemple 2DS1 = 12 DS2 = ABS E = 13 TD = 15On peut calculer la moyenne :M = 0.25 × 12 + 0 + 0.4 × 13 + 0.1 × 15 = 9.7La note ﬁnale est le max entre M et E donc a priori NF = 13.Rattrapage optionnel. Vous décidez de passer le rattrapage et obtenezR = 14, on recalcule alorsM ′ = 0.25 × 12 + 14 + 0.4 × 13 + 0.1 × 15 = 13.2La note ﬁnale est le max entre M ′ et E donc NF = 13.2.4 of 4

Page 6 : Plan• Chapitre 0 : Mise en jambes - Rappel.• Propriétés elementaires de l’ensemble R : relation d’ordre - valeur absolue -equations - inéquations.• Utilisation des symboles Σ et Π : Déﬁnitions et opérations - sommes etproduits télescopiques - sommes et produits usuels.• Fonctions trigonométriques : Formules usuelles - Equations trigonométriques.• Chapitre 1 : L’ensemble R.• Majorants - Minorants - Min - Max - Borne supérieure - Borne inférieur.• R est archimédien - partie entière - approximation décimale.• Densité de Q dans R.• Chapitre 2 : Suites numériques.• Généralités : déﬁnitions - opérations sur les suites.• Limites de suites : Déﬁnitions - opérations - théorèmes d’existence de limite• Suites récurrentes.• Extension aux suites complexes.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20242 / 277

Page 7 : Plan• Chapitre 3 : Limites et continuité de fonctions• Limite d’une fonction : limite en un point - limite à droite, à gauche -opérations - théorèmes d’existence de limites.• Continuité : déﬁnitions - prolongement par continuité - caractérisationséquentielle de la continuité - opérations• Les grands théorèmes de la continuité : Théorème des valeurs intermédiaires -Image d’un segment - Théorème de la bijectionNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20243 / 277

Page 8 : Propriétés élémentaires de l’ensemble RCommencons avec notre étude de l’ensemble R. On commence par introduirel’ensemble de nombres réels et ses sous-ensembles.Déﬁnition• Entiers naturels :N = 0, 1, 2, 3, · · · .• Entiers relatifs :Z = · · · , 2, 1, 0, 1, 2, · · · .Introduisons aussiN=1, 2, 3, · · · Z=· · · , 2, 1, 1, 2, · · · .L’ensemble Z a le gros défaut suivant : seuls n = 1 et n = 1 admettent uninverse, c’est-à-dire un élément m Z tel quenm = 1.Nous remédions à ce problème en introduisant l’ensemble des nombres rationnels.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20244 / 277

Page 9 : Propriétés élémentaires de l’ensemble RDéﬁnition L’ensemble QL’ensemble des nombres rationnels estQ =pq : p Z, q Z.avec des opérations + et × déﬁnis parpq + p′q′ = pq′ + p′qqq′etpq × p′q′ = pp′qq′ .Exemple : Un exemple important de nombre rationnel, sont les nombresdécimaux, c’est-à-dire les nombres de la formep10n , p Z, n N.On peut choisir comme exemple :• 1, 375 = 1375 × 103 = 13751000.• 0, 1375 = 1375 × 104 =137510000.• 0, 001375 = 1375 × 106 =13751000000.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20245 / 277

Page 10 : Propriétés élémentaires de l’ensemble REn d’autre termes, un nombre est décimal s’il admet une écriture décimale ﬁnie.Le résultat suivant nous donne une caractérisation de Q.PropositionUn nombre est rationnel si et seulement si il admet une écriture décimalepériodique ou ﬁnie.Exemple : Les nombres suivants sont de rationnels :0, 8 = 450, 1111 · · · = 1923, 12505505505 · · · = 23, 12505.Nous n’allons pas démontrer la proposition, mais voyons comment le sens ⇐=marche sur un exemple : Montrons que r = 23, 12505 est rationnel.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20246 / 277

Page 11 : Propriétés élémentaires de l’ensemble RL’idée est d’abord de faire apparaître la partie périodique juste après la virgule. Icila période commence deux chiﬀres après la virgule, on multiplie par 100 :100r = 2312, 505505505 · · · .1Maintenant on va décaler tout vers la gauche de la longueur d’une période, doncici on multiplie encore par 1000 pour décaler de 3 chiﬀres :1000 × 100r = 2312505, 505505505 · · · .2Les parties après la virgule des deux lignes 1 et 2 sont les mêmes, si on lessoustrait en faisant 2 - 1 les parties décimales s’annulent :1000 × 100r 100r = 2312505 2312.Donc 99900r = 2310193 etr = 231019399900=⇒23, 12505 = 231019399900 .Remarque : on peut aussi utiliser la somme d’une suite géométrique !Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20247 / 277

Page 12 : Propriétés élémentaires de l’ensemble RRemarque : La notion de nombre permet de compter ; c’est le cas bien sûr pourles entiers naturels, pour les entiers relatifs qui peuvent « compter desdettes », pour les rationnels qui permettent de former des « parts égales »d’une même quantité.Depuis longtemps, elle est également utilisée pour mesurer des longueurs. Vousavez l’habitude d’attacher à chaque segment de droite une longueur et deconsidérer que cette longueur est un nombre ; il est alors naturel d’additionner deslongueurs, de les multiplier pour obtenir des aires, etc.On peut alors s’appuyer sur les théorèmes de la géométrie pour calculer certaineslongueurs. Dans ce contexte, le Théorème de Pythagore a une conséquencecélèbre : la longueur de la diagonale d’un carré dont les côtés ont pourlongueur un mètre, doit être donnée par un « nombre » dont le carré vaut12 + 12 = 2.Théorème Irrationnalité de2Il n’existe pas de nombre rationnel dont le carré soit égal à 2. L’equation p2 = 2n’a donc pas de solution dans Q.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20248 / 277

Page 13 : Nombres élémentaires de l’ensemble RLe théorème précédent a été découvert au moins cinq siècles avant notre ère; onl’attribue en général aux pythagoriciens. Il y a au moins deux réactions possiblesà ce fait :1. Considérer que le mot « nombre » doit être réservé aux rationnels et séparertout ce qui se rapporte à la notion de longueur en géométrie de ce qui serapporte à l’arithmétique.2. étendre la signiﬁcation donnée au mot « nombre » pour que ce mot puissedésigner la longueur de « tout » segment de droite.La première réaction n’est pas absurde : elle fut longtemps dominante. De ladeuxième réaction est issue la notion de nombre réel à laquelle vous êtes habitués.DéﬁnitionNous notons par R l’ensemble des nombres réels. L’ensemble de nombresirrationnels I est déﬁni parI = R \ Q.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/20249 / 277

Page 14 : Nombres élémentaires de l’ensemble RExemple : Les nombres suivants sont irrationnels :•2 = 1, 4142 · · · ,• π = 3, 14159265 · · ·• e = 2, 718 · · ·Les diﬀérents ensembles introduis jusqu’à maintenant, sont liés par les inclusionsN Z Q R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202410 / 277

Page 15 : Propriétés élémentaires de l’ensemble RFinalement, notons par• Ql’ensemble Q privé de 0.• Rl’ensemble R privé de 0.• R+ l’ensemble des réels positifs ou nuls.• Rl’ensemble des réels négatifs ou nuls.• R+ l’ensemble des réels strictement positifs.• Rl’ensemble des réels strictement négatifs.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202411 / 277

Page 16 : Propriétés élémentaires de l’ensemble RPassons maintenant à une étude plus détaillé de R. Plus précisément nous allonsdéﬁnir une relation d’ordre sur R. Ça nous permettra :• déﬁnir la valeur absolue.• étudier le comportement de certaines fonctions par rapport aux inégalités.• parler de majorant, minorant et surtout introduire la très importante notionde borne supérieure et inférieure.• introduire la notion d’intervalle.• déﬁnir la fonction partie entière.• introduire la notion d’ensemble dense dans R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202412 / 277

Page 17 : Relation d’ordre dans ROn commence par introduire une relation d’ordre sur l’ensemble des nombres réels.Déﬁnition R est muni d’une relation de comparaison déﬁni comme suit : pour toutecouple x, y R on déﬁnit :x y←→y x R+x y←→x yetx ̸= y.L’ordre est une relation d’ordre total, c’est à dire qu’elle possède lespropriétés suivantes :• Réﬂexivité : pour tout x R, x x.• Antisymétrie : pour tout x, y R, x y et y x=⇒x = y.• Transitivité : pour tout x, y, z R, x y et y z =⇒x z.• Elle est totale : x, y R, on a nécessairement x y ou y x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202413 / 277

Page 18 : Relation d’ordre dans RÉtudions la compatibilité de la relation d’ordre avec l’addition et la multiplication.Proposition SommeSoit a, b, c, d des nombres réels.• Somme :• Nous avonsa bsi et seulement sia + c b + c.• Si a b et c d, alorsa + c b + d.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202414 / 277

Page 19 : Relation d’ordre dans RProposition ProduitSoit a, b, c, d des nombres réels.• Produit :• Pour tout c 0, nous avonsa bsi et seulement siac bc.• Pour tout c 0, nous avonsa bsi et seulement siac bc.• Si 0 a b et 0 c d, alorsac bd.• Passage à l’inverse : Si a, b R+ ou a, b Rtels que a b, alors1a 1b .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202415 / 277

Page 20 : Relation d’ordre dans RExemples :• Pour x y, montrer l’inégalité 1 x 1 y.Réponse : Comme x y on a y x, d’où on obtient1 y 1 x=⇒1 x 1 y.• Pour x y 0, 1, montrer l’inégalitéx1x y1y.Réponse : On a x y, donc1 x 1 y 0car y 1par passage à l’inverse0 11 x 11 y .Comme 0 x y, en multipliant les deux derniers inégalités, on obtientx1 x y1 y .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202416 / 277

Page 21 : Relation d’ordre dans RRemarque :• Majorer une fraction de réels positifs, c’est majorer son numérateur et minorer sondénominateur.• Minorer une fraction de réels positifs, c’est minorer son numérateur et majorer sondénominateur.Exemple : Soit x 1, 2. On souhaite encadrer grossièrement le réel2x + 13x2 + 4par un calcul simple.Réponse :• Comme 1 x 2 on obtient 2 2x 4 d’où 3 2x + 1 5.• Comme 1 x 2 on obtient 1 x2 4, puis 3 3x2 12. D’où7 3x2 + 4 16.Enﬁn, par passage à l’inverse, on conclut316 2x + 13x2 + 4 57.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202417 / 277

Page 22 : Intervalles de RMaintenant qu’on a déﬁni une relation d’ordre sur R, rappelons la notiond’intervalle.Déﬁnition Intervalle de ROn appelle intervalle de R toute partie I de R vériﬁant la propriété suivantex, y I, t R, x t y=⇒t I.Remarque : De une manière plus géométrique, les intervalles sont les parties de Rqui « n’ont pas de trou ».Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202418 / 277

Page 23 : Intervalles de RLa proposition suivant nous donne une caractérisation des « parties sans trou »de R.Proposition Classiﬁcation des intervallesSoit a, b R tels que a b. Les intervalles de R sont exactement les ensembles :• Segment ou intervalle fermé :a, b=x R : a x b.• Intervalle ouvert :a, b=x R : a x ba, +=x R : a x + , b=x R : x b , +=R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202419 / 277

Page 24 : Intervalles de RProposition Classiﬁcation des intervalles Continuation • Intervalle semi-ouvert à droite :a, b=x R : a x b,a, +=x R : a x +.• Intervalle semi-ouvert à gauche :a, b=x R : a x b, b=x R : x b.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202420 / 277

Page 25 : Valeur AbsoluePassons maintenant à étudier la notion de valeur absolue.Déﬁnition Valeur absolueSoit x R. La valeur absolue de x est le nombre réel noté x déﬁni par :x = x,si x 0,x,si x 0.Ce réel est positif ou nul, et nul seulement si x = 0.Remarque : La déﬁnition même de · nous indique comment prouver quex a.Il faut montrer que x a et x a, c’est-à-dire ils nous faut montrera x a.Cette astuce utile est à retenir : une inégalité invoquant une valeurabsolue se montre en montrant deux inégalités.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202421 / 277

Page 26 : Valeur AbsolueNous avons le résultat suivant.PropositionSoit a un réel quelconque et r un réel strictement positif. Alors :• x a r est équivalent à x a r, a + r. C’est-à-direx a rsi et seulement sia r x a + r• x a r est équivalent à x , a r ou x a + r, +. C’est-à-direx a rsi et seulement six a roua + r x.Remarque :• Ces propriétés sont encore vraies en remplaçant les inégalités larges par desinégalites strictes et les intervalles fermés par des intervalles ouverts.• Interprétation géométrique : La valeur absolue d’un réel représente sadistance à 0. Si a et x sont deux réels, x a est la distance de a à x. Sir 0, l’inégalité x a r signiﬁe que x est à une distance de a inférieureou égale à r.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202422 / 277

Page 27 : Valeur AbsolueExemple : Trouver une expression de x 3 x + 2 qui ne fasse apparaître aucunevaleur absolue.Réponse : On ax 3 =x 3si x 3x 3si x 3etx + 2 =x + 2si x 2x + 2si x 2.La quantité x 3 x + 2 nous oblige donc à distinguer trois intervalles : , 2,2, 3 et 3, +. Par conséquent• Si x , 2 alorsx 3 x + 2 = x 3 + x + 2 = 5.• Si x 2, 3 alorsx 3 x + 2 = x 3 x + 2 = 1 2x.• Si x 3, + alorsx 3 x + 2 = x 3 x + 2 = 5.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202423 / 277

Page 28 : Valeur AbsolueExemple : Résoudre l’équation : x 4 = 2x + 10 d’inconnue x R.Réponse : On a deux cas à étudier• Pour tout x 4 :x 4 = 2x + 10 ⇐⇒x 4 = 2x + 10 ⇐⇒x = 14.Or :14 /4, +, l’équation n’a donc pas de solution sur 4, +.• Pour tout x 4 :x 4 = 2x + 10 ⇐⇒4 x = 2x + 10 ⇐⇒3x = 6 ⇐⇒x = 2.Comme 2 , 4, 2 est bien solution. C’est ﬁnalement la seulesolution sur R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202424 / 277

Page 29 : Valeur AbsolueÉtudions l’eﬀet de la valeur absolue sur la somme et le produitPropositionPour tous réels x, y on a1. x = 0 alors x = 0.2.xy = x · y.3. Inégalité triangulaire :x + yx + yx yx yNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202425 / 277

Page 30 : Valeur AbsolueDémonstration.1. Puisque x = 0, nous avons x 0 et x 0, i.e. x 0 et x 0. Ainsi,x = 0.2. Traitons diﬀérents cas selon les signes de x et y. Si x, y 0, nous obtenonsx = xety = yet l’égalité est claire. Si x, y 0, nous obtenonsx = xety = yet l’égalité est également claire. Les cas x 0 et y 0 ou x 0 et y 0suivent aussi facilement.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202426 / 277

Page 31 : Valeur AbsolueSuite.3.• Commençons par la première inégalité. Les inégalités x x et y yimpliquentx + y x + y.De même, x x et y y impliquentx + y x + y.Ainsi, x + y x + y x + y, d’où x + y x + y.• Pour la deuxième inégalité, appliquons la première inégalité triangulairex = x y + y x y + y.Donc, x y x y. Par la symétrie du rôle de x et y, on ay x x y.Ainsi, x y x y x y, d’où on obtientx y x y.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202427 / 277

Page 32 : Valeur AbsolueExemple : Pour x, y 1, 1, montrer que x+y1+xy 1.Solution : Puisque0 x 1et0 y 1on déduit en multipliant les inégalités0 x · y 1=⇒0 xy 1.Ainsi1 xy 1=⇒0 1 + xy.Pour x, y 1, 1, on a donc :x + y1 + xy 1⇐⇒x + y 1 + xy = 1 + xy⇐⇒1 xy x + y 1 + xy⇐⇒0 x + y + xy + 1et0 1 + xy x y⇐⇒0 1 + x1 + yet0 1 x1 yNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202428 / 277

Page 33 : Valeur AbsolueMaintenant0 1 + x1 + yest vrai carx 1ety 10 1 x1 yest vrai carx 1ety 1.En remontant les équivalences, on a donc prouvé l’inégalité voulue.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202429 / 277

Page 34 : Rappel sur les puissances et les racines carréesDéﬁnition PuissanceSoit x R et n N.• On appelle x puissance n le nombre xn déﬁni parxn = x × x × · · · × xzn foisavecx0 = 1 par convention.• Si x ̸= 0, on appelle x puissance -n le nombre xn déﬁni parxn = 1xn= 1xn= 1x × 1x × · · · × 1x.On a les règles de calcul suivants : pour tous x, y R et m, n Nxn+m=xnxmxnm=xnmxyn=xnyn.Ces formules sont encore vraies si m ou n est négatif à condition que x et y soient nonnuls.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202430 / 277

Page 35 : Rappel sur les puissances et les racines carréesDéﬁnition Racine carréesSoit x 0. Il existe un et un seul réel r 0 pour lequelx = r2.On l’appelle la racine carrée de x et on le note x. On a les règles de calculsuivants : pour tous x, y 0xy=xyx2=x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202431 / 277

Page 36 : Rappel sur les puissances et les racines carréesÉtudions le comportement des carrés et racines carrées par rapport aux égalités.PropositionPour tous a, x, y R, on aax = ay⇐⇒a = 0 ou x = y.Si a R, alorsax = ay⇐⇒x = y.Pour tous a, b R :a2 = b2⇐⇒a = b ou a = b⇐⇒a = b.Pour a 0x = a⇐⇒x2 = a et x 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202432 / 277

Page 37 : Rappel sur les puissances et les racines carréesExemples :Résoudre l’équation : x 2 = 2x + 1 d’inconnu x R.Réponse : Pour tout x R, nous avonsx 2 = 2x + 1⇐⇒x 22 = 4x + 12⇐⇒x2 4x + 4 = 4x2 + 8x + 4⇐⇒0 = 3x2 + 12x = 3xx + 4⇐⇒0 = xx + 4 ⇐⇒x = 0 ou x = 4.Résoudre l’équation : x + 8 = x + 2 d’inconnu x 8, +.Réponse : Pour tout x 8, +, nous avonsx + 8 = x + 2⇐⇒x + 8 = x + 22etx + 2 0⇐⇒x2 + 3x 4 = 0etx 2⇐⇒x 4, 1etx 2⇐⇒x = 1.Donc x = 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202433 / 277

Page 38 : Rappel sur les puissances et les racines carréesÉtudions le comportement des racines carrées par rapport aux inégalités.Attention : Pour x, a Rx an’implique pasx2 a2De même,x2 a2n’implique pasx aPar exemple, nous avons2 1 et 22 1.De même1 22 et 1 2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202434 / 277

Page 39 : Rappel sur les puissances et les racines carréesPar contre nous avons le résultat suivant.PropositionPour tous x, a R, on ax2 a2⇐⇒x a.Pour x, a 0x a⇐⇒x2 a2.Et pour x 0 seulementx a⇐⇒x2 a2eta 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202435 / 277

Page 40 : Rappel sur les puissances et les racines carréesExemple : Résoudre l’inéquation : x 1 2x + 1 d’inconnu x R.Réponse : Pour tout x R, nous avonsx 1 2x + 1⇐⇒x 12 2x + 12⇐⇒x2 2x + 1 4x2 + 4x + 1⇐⇒0 3x2 + 6x = 3xx + 2⇐⇒0 xx + 2.Par conséquent, x est solution de l’inéquation si x , 2 0, +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202436 / 277

Page 41 : Le symbole ΣPassons maintenant à étudier plus en profondeur la somme et le produit.Déﬁnition Le symbole ΣSoit m et n deux entiers naturels avec m n. Alors pour tous am, · · · , an R lasommeam + am+1 + · · · + ansera notéenXi=mai = am + am+1 + · · · + anLa notationnXi=mai se lit par exemple :somme pour i variant de m à n des aiNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202437 / 277

Page 42 : Le symbole ΣRemarques :• La lettre i est une variable muette, autrement dit on peut la changer parn’importe quelle autre lettre sans changer la valeur de la somme. C’est-à-direnXi=mai =nXk=mak.On choisit traditionnellement les lettres i, j, k, etc. pour les indices desommes.• La sommenXi=mai comporte n m + 1 termes.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202438 / 277

Page 43 : Le symbole ΣExemples :• Calculern+1Xi=21=1 + 1 + · · · + 1zn+12+1fois=n.• CalculernXi=1i.Réponse : Nous allons voir un peu plus tard que la valeur de cette somme estnn + 12.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202439 / 277

Page 44 : Le symbole ΠNous avons parlé de la somme, parlons maintenant du produit.Déﬁnition Le symbole ΠSoit m et n deux entiers naturels avec m n. Alors pour tous a1, · · · , an R, leproduitam × am+1 × · · · × ansera notéenYi=mai = am × am+1 × · · · × an.Comme pour la somme nous avons les remarques suivants :Remarque :La lettre i est une variable muette, autrement dit on peut la changer parn’importe quelle autre lettre sans changer la valeur du produit.La produitnYi=mai comporte n m + 1 termes.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202440 / 277

Page 45 : Le symbole ΠUn exemple important de produit, est donné par la factorielle.Déﬁnition FactoriellePour tout n N, on déﬁnit la factorielle de n parn!=nYk=1k=1 × 2 × 3 × · · · × n.On lit « factorielle n ». D’après la convention sur le produit vide0! = 1.Remarque : Si n 1, nous avonsn! = nn 1!.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202441 / 277

Page 46 : Le symboles Σ et ΠLa somme et le produit satisfont la propriété suivant.Proposition Relation de ChaslesSoit m, n et p trois entiers naturels avec m p n. AlorsnXk=mak=pXk=mak +nXk=p+1ak.De mêmenYk=mak= pYk=mak!·nYk=p+1ak.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202442 / 277

Page 47 : Méthodes de calculs pour la somme et le produitÉtudions quelques méthodes de calculs pour la somme et le produit.Méthode 1 : Règles de calcul pour la somme.Proposition Linéarité de la sommeSoit m et n deux entiers naturels avec m n etam, · · · , an;bm, · · · , bndeux familles de nombres réels. AlorsnXi=mai + bi=nXi=mai +nXi=mbi.et pour tout λ RnXi=mλai=λnXi=mai.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202443 / 277

Page 48 : Méthodes de calculs pour la somme et le produitRemarque : Si on combine les deux propriétés précédentes, on anXi=mλai + βbi=λnXi=mai + βnXi=mbi.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202444 / 277

Page 49 : Méthodes de calculs pour la somme et le produitMéthode 1 : Règles de calcul pour le produit.PropositionMultiplicativité :nYi=maibi=nYi=mainYi=mbiPassage à la puissance :nYi=mapi= nYi=mai!p,p N.Constante : Pour tout λ RnYk=mλ · ak=λnm+1nYk=mak.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202445 / 277

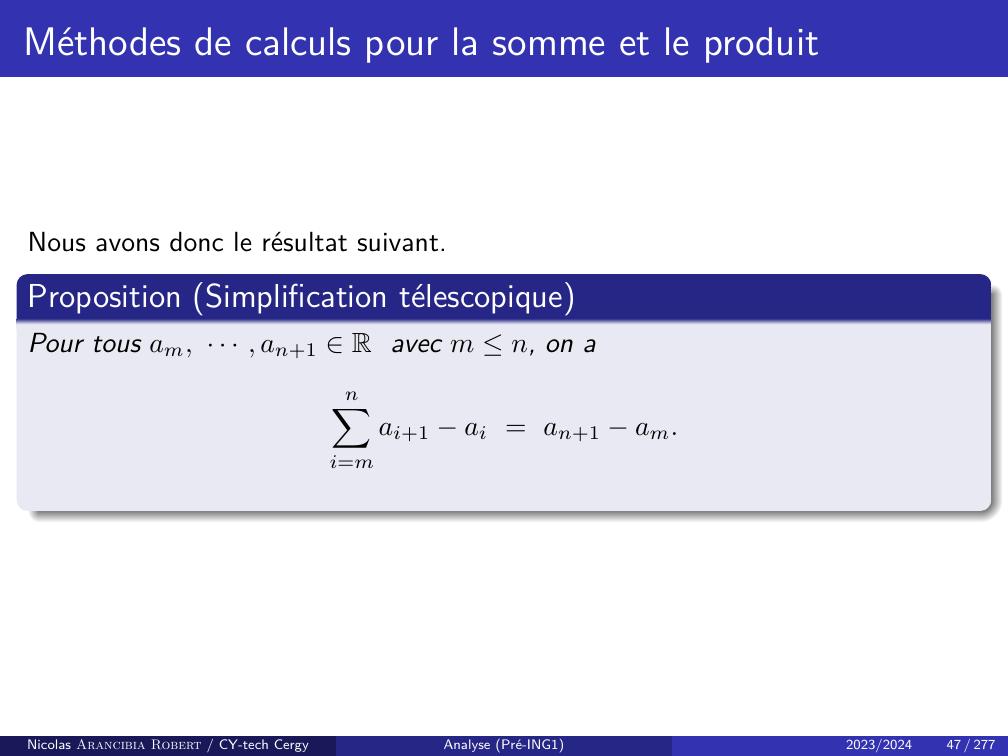
Page 50 : Méthodes de calculs pour la somme et le produitMéthode 2 : Simpliﬁcation télescopique cas de la somme.DéﬁnitionOn appelle somme télescopique toute somme du type suivantnXi=mai+1 ai.Ces sommes se calculent merveilleusement bien. En eﬀetnXi=mai+1 ai =am+1 am+am+2 am+1+am+3 am+2...+an an1+an+1 an=an+1 am.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202446 / 277

Page 51 : Méthodes de calculs pour la somme et le produitNous avons donc le résultat suivant.Proposition Simpliﬁcation télescopiquePour tous am, · · · , an+1 R avec m n, on anXi=mai+1 ai = an+1 am.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202447 / 277

Page 52 : Méthodes de calculs pour la somme et le produitMéthode 2 : Simpliﬁcation télescopique cas du produit.Proposition Simpliﬁcation télescopiquePour tous am, · · · , an+1 Rtous non nuls avec m n, on anYi=mai+1ai= an+1am.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202448 / 277

Page 53 : Méthodes de calculs pour la somme et le produitRemarque : La vraie diﬃculté n’est pas de calculer, mais de repérer les sommeset les produits télescopiques en les mettant sous la bonne forme.Exemple : Calculer156Yk=542k + 32k + 1.Solution : Soit ak = 2k + 1, alors2k + 3 = 2k + 1 + 1 = ak+1.Donc156Yk=542k + 32k + 1 =156Yk=54ak+1ak= a156+1a54= a157a54= 2 × 157 + 12 × 54 + 1 = 315109.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202449 / 277

Page 54 : Méthodes de calculs pour la somme et le produitMéthode 3 : Changement d’indices cas de la somme.Commençons par un exemple :nXk=0k + 12=12 + 22 + · · · + n2 + n + 12=n+1Xj=1j2.Nous avons changé d’indice : au lieu de calculer pour k entre 0 et n, nous avonsposé j = k + 1 qui est entre 1 et n + 1, ce qui simpliﬁe l’expression de la somme.k J0, nK⇐⇒j=k+1j J1, n + 1K.Remarque : Comme l’indice est muet, on peut garder la lettre k dans la secondesomme. On n’est pas obligé de la remplacer par j même si c’est plus facile audébut.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202450 / 277

Page 55 : Méthodes de calculs pour la somme et le produitOn peut procéder à un changement d’indice pour deux types de raison :• Décalage d’indice : Le décalage d’indice revient à utiliser un indice translaté d’unevaleur ﬁxe. Par exemple, en posant j = k + p avec p m, on obtientnXk=mak+p =n+pXj=m+paj.• On repère le changement d’indice que l’on souhaite réaliser, par exemple j = k + pdans le cas ci-dessus pour transformer ak+p en aj.• On cherche les premières et dernières valeurs de la somme. Dans notre exemple, lapremière commence par k = m, ainsik = m=⇒j = m + p.Il faut donc que la nouvelle somme commence à j = m + p. La première somme setermine avec k = n, ainsik = n=⇒j = n + p.Il faut donc que la nouvelle somme ﬁnisse avec j = n + p.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202451 / 277

Page 56 : Méthodes de calculs pour la somme et le produitLa deuxième raison qui nous amème à realiser un changement d’indice est :• Inversion de l’ordre de sommation : Pour inverser l’ordre de sommation lirela somme en sens contraire pour k variant de 0 à n, on remplace k par j = n kqui varie de 0 à n.nXk=0ank =nXj=0aj.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202452 / 277

Page 57 : Méthodes de calculs pour la somme et le produitMéthode 3 : Changement d’indices cas du produit. Comme pour la somme, onpeut procéder à un changement d’indice pour deux types de raison :• Décalage d’indice : Le décalage d’indice revient à utiliser un indice translatéd’une valeur ﬁxe. Par exemple, en posant j = k + p avec p m, on obtientnYk=mak+p =n+pYj=m+paj.• Inversion de l’ordre de multiplication : Pour inverser l’ordre de multiplicationlire le produit en sens contraire pour k variant de 0 à n, on remplace k parj = n k qui varie de 0 à n.nYk=0ank =nYj=0aj.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202453 / 277

Page 58 : Méthodes de calculs pour la somme et le produitMéthode 4 : Indices pairs/impairs.Séparation des termes d’indices pairs et impairs : Lorsque le signe change en fonctionde la parité de n, il est parfois intéressant de séparer la somme des indices pairs de celledes indices impairs.Exemple : Calculer2nXk=11kk=2nXk=1k pair1kk +2nXk=1k impair1kk=2nXk=1k pairk 2nXk=1k impairk=X22i2n2i X12i12n12i 1!=nXi=12i nXi=12i 1!=nXi=12i nXi=12i +nXi=11 = n.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202454 / 277

Page 59 : Sommes usuellesÉtudions quelques sommes classiques.Proposition Somme de constantesSoit a R, soient m n deux entiers. AlorsnXk=ma=n m + 1a=nombre de termes × a.Proposition Somme arithmétiquesSoient m et n deux entiers avec m n. AlorsnXk=mk=n m + 1m + n2.En particuliernXk=0k=nn + 12.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202455 / 277

Page 60 : Sommes usuellesProposition Somme géométriqueSoit q ̸= 1. Soient m et n deux entiers avec m n. AlorsnXi=mqi=qm · 1 qnm+11 q.En particuliernXi=0qi=1 qn+11 q.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202456 / 277

Page 61 : Sommes usuellesComme dernier exemple étudions les sommes binomiales. Pour cela, on commencepar introduire les coeﬃcients binomiaux.Déﬁnition Coeﬃcient binomialPour tout n, k N avec k n, on appelle coeﬃcient binomial de paramètresn, k, le nombrenk=n!k!n k!.Le nombrenkse lit : k parmi n. Par convention : si n k, alorsnk= 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202457 / 277

Page 62 : Sommes binomialesDonons quelques propriétés des coeﬃcients binomiauxProposition Propriétés des coeﬃcients binomiauxSoit n N, k N avec k n.• Symétrie :nk=nn k.• Pour k ̸= 0 :k ·nk= n ·n 1k 1.• Triangle de Pascal :nk=n 1k+n 1k 1.Remarque : La dernière formule à l’immense intérêt de donner une relationsommatoire entre les coeﬃcients binomiaux. Elle permet d’obtenir facilement lescoeﬃcients binomiaux par récurrenceNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202458 / 277

Page 63 : Sommes binomialesElle s’illustre et se mémorise à travers le triangle de Pascal.Pour trouver un coeﬃcient binomial, on fait la somme de celui juste au dessus et de celuiau dessus à gauche. Et si l’un des deux n’existe pas pour la somme, on prend seulementla valeur de celui qui existe. Par exemple, pour obtenir 51, on fait la somme du 1 et du4 au dessus eux-mêmes obtenus à partir des éléments supérieurs. Cela revient à faire lecalcul :51= 40+ 41= 1 + 4 = 5.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202459 / 277

Page 64 : Sommes binomialesLe triangle de Pascal nous permet de conclure le résultat suivant.CorollaireLes coeﬃcients binomiaux sont des entiers.Maintenant que nous avons introduit les coeﬃcients binomiaux, parlons dessommes binomiales.Théorème Formule du binômePour tous n N et x, y R, nous avonsnXk=0nkxnkyk=x + yn.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202460 / 277

Page 65 : Sommes binomialesExemple : En utilisant la formule du binôme nous pouvons écrire2n = 1 + 1n=nXk=0nk1nk1k=nXk=0nket0 = 1 + 1n=nXk=0nk1nk1k=nXk=0nk1k.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202461 / 277

Page 66 : Rappel sur les fonctions trigonométriquesNous allons ﬁnir ce chapitre revision avec un courte étude d’une famille trèsimportante de fonctions : les fonction trigonométriques.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202462 / 277

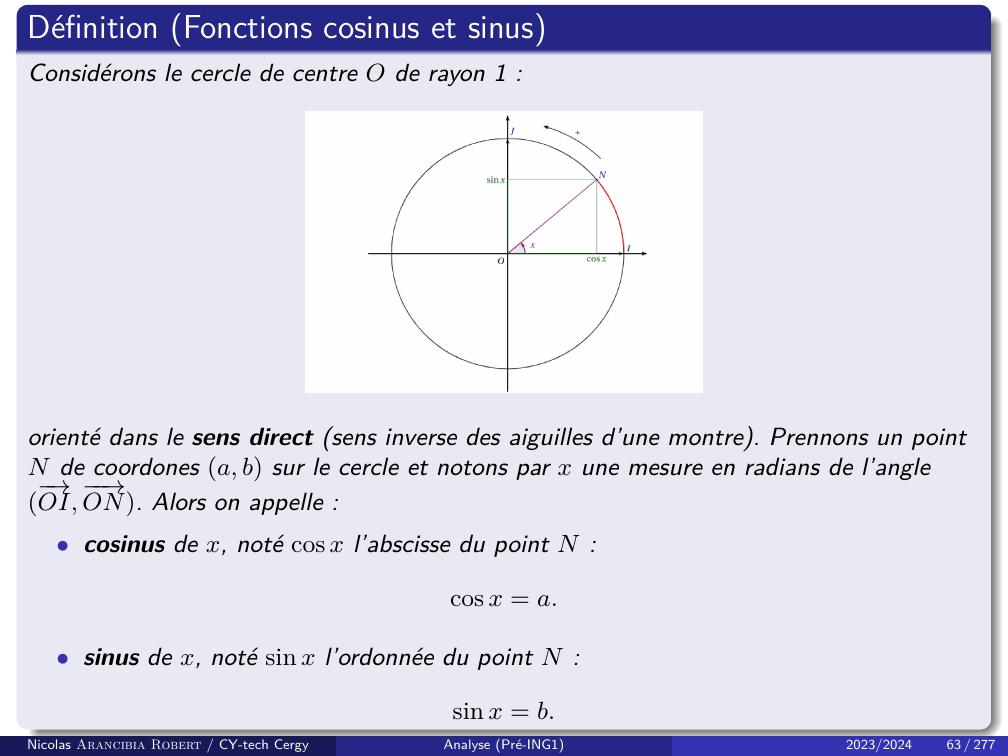
Page 67 : Déﬁnition Fonctions cosinus et sinusConsidérons le cercle de centre O de rayon 1 :orienté dans le sens direct sens inverse des aiguilles d’une montre. Prennons un pointN de coordones a, b sur le cercle et notons par x une mesure en radians de l’angle→OI, →ON. Alors on appelle :• cosinus de x, noté cos x l’abscisse du point N :cos x = a.• sinus de x, noté sin x l’ordonnée du point N :sin x = b.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202463 / 277

Page 68 : Rappel sur les fonctions trigonométriquesRemarque : Puisque pour tout point a, b du cercle trigonométrique, nous avons1 a 1,1 b 1eta2 + b2 = 1,on conclut1 cos x 1,1 sin x 1etcos2 x + sin2 x = 1.La notation suivante va se montrer utile par la suite.Notation : Soit θ R. Pour tous x, y R, on dit quex est congru à y modulo θ,ce qu’on note :x y θ,s’il existe k Z tel quex y = k · θ⇐⇒x = y + k · θ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202464 / 277

Page 69 : Fonctions TrigonométriquesNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202465 / 277

Page 70 : Fonctions sinus et cosinusDonnons quelques propriétés des fonctions cosinus et sinus.Proposition Propriétés• Les fonctions sin et cos sont 2π-périodiques, c’est-à-dire, pour tout x R,nous avonssinx + 2π = sinxetcosx + 2π = cosx.• La fonction sinus est impaire :sinx = sin xet la fonction cosinus est paire :cosx = cos x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202466 / 277

Page 71 : Rappel sur les fonctions sinus et cosinusEn étudiant le cercle trigonométrique, on peut facilement veriﬁer la parité desfonctions trigonométriques.La parité des fonctions trigonométriques nous permet de montrerPropositionRésolution d’équations : pour tous x, y R, nous avonssin x = sin y⇐⇒x y 2πoux π y 2π.cos x = cos y⇐⇒x y 2πoux y 2π.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202467 / 277

Page 72 : Rappel sur les fonctions sinus et cosinusGrâce au cercle trigonométrique, et avec des considérations géométriques simples,on peut aussi voir que les fonctions sinus et cosinus satisfont les relationssuivantes.Proposition Transformations aﬃnesPour tout x R, on asinx + π = sinx;sinπ x = sinxcosx + π = cosx;cosπ x = cosxetsinx + π2= cosx;sinπ2 x= cosxcosx + π2= sinx;cosπ2 x= sinxNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202468 / 277

Page 73 : Fonctions sinus et cosinusEn eﬀet, en regardant le cercle cercle trigonométrique on conclut :Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202469 / 277

Page 74 : Fonctions sinus et cosinusExemple : Résoudre l’équationsin x = cos xSolution : Nous avonssin x = cos x⇐⇒sin x = sinπ2 x⇐⇒x π2 x 2πoux π π2 x2π⇐⇒2x π2 2πou0 π2 2πzimpossibleDonc sin x = cos x si et seulement si2x π2 2π⇐⇒x π4 π.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202470 / 277

Page 75 : Fonctions sinus et cosinusLes fonctions sinus et cosinus satisfont aussi les propriétés suivantes.Proposition Formules d’additionPour tous x, y R, on asinx + y = sin x cos y + cos x sin ycosx + y = cos x cos y sin x sin yLa parité des fonctions trigonométriques nous permet d’écriresinx y = sin x cos y cos x sin ycosx y = cos x cos y + sin x sin yPour x = y, ces relations s’appellent formules de duplication :sin2x=2 sin x cos xcos2x=cos2 x sin2 x = 2 cos2 x 1 = 1 2 sin2 x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202471 / 277

Page 76 : Fonctions sinus et cosinusEn additionant les formules d’addition on obtient les formules de produit :Proposition Formules de produitPour tous x, y R, on acos x cos y=12cosx + y + cosx ysin x sin y=12cosx y cosx + ysin x cos y=12sinx + y + sinx y.Les formules d’addition et de duplication doivent être connues PARCOEUR - et ce même si les secondes découlent des premières. Enrevanche, vous devez juste savoir retrouver vite et bien les formules deproduit, si possible de tête.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202472 / 277

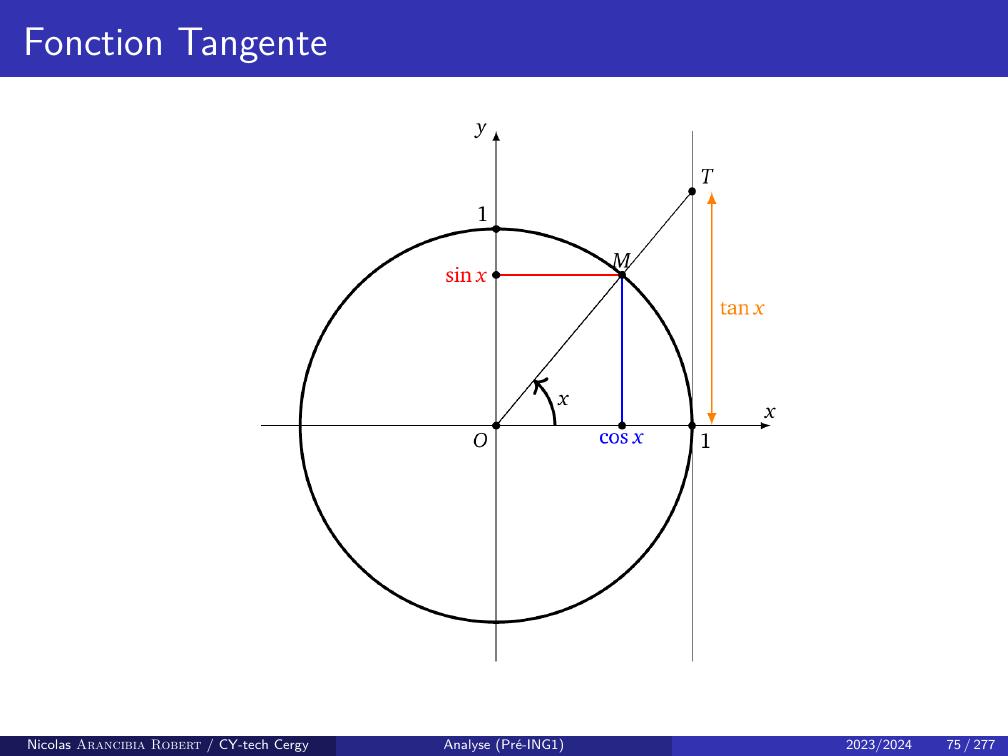
Page 77 : Fonction TangenteFinissons ce rappel des fonctions trigonométriques avec un étude de la fonctiontangente. Pour cela déﬁnissonsiπ2 , π2h+ πZ=nx R : k Z, x ̸= π2 + kπo=R \n· · · , π2 2π, π2 π, π2 , π2 , π2 + π, π2 + 2π, · · ·o.Déﬁnition TangenteOn appelle fonction tangente la fonction déﬁnie suriπ2 , π2h+ πZpar la relationtan x = sin xcos x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202473 / 277

Page 78 : Fonction TangenteDonnons quelques propriétés de la fonction tangente.Proposition PropriétésRésolution d’équations : pour tous x, y π2 , π2+ πZtan x = tan y⇐⇒x = y π.En particulier, la fonction tan est π-périodique.La fonction tan est impaire :tanx=tan x.Formules d’addition et de duplication :tanx + y=tan x + tan y1 tan x tan ytanx y=tan x tan y1 + tan x tan ytan 2x=2 tan x1 tan2 x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202474 / 277

Page 79 : Fonction TangenteNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202475 / 277

Page 80 : Fonctions TrigonométriquesValeurs remarquables du sinus, du cosinus et de la tangente :Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202476 / 277

Page 81 : Chapitre 1 - Nombres réels continuationOn connait très bien maintenant l’ensemble des réels, nous avons étudié :• ses sous-ensembles les plus importantes.• l’addition et la multiplication sur R.• la relation d’ordre et ses propriétés.• la valeur absolue et quelques fonctions importantes.Vous savez donc presque tout sur les réels mais pas tout. Alors que vousmanipulez des inégalités depuis assez longtemps, il y a tout de même unepropriété de la relationsur Rque vous ne connaissez pas :dite propriété de la borne supérieure et qui revêt une importance fondamentale. Cette section vise principalement àmotiver et vous présenter cette propriété.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202477 / 277

Page 82 : Majorant et MinorantCommençons par donner quelques déﬁnitions.Déﬁnition Majorant-MinorantSoit A une partie de R.A est majorée s’il existe M R tel que pour tout x A nous avonsx M.On dit alors que M est un majorant de A.A est minorée s’il existe m R tel que pour tout x A nous avonsx m.On dit alors que m est un minorant de A.A est bornée lorsque A est à la fois majorée et minorée. C’est-à-dire, s’ilexiste m R et M R tel que pour tout x A nous avonsm x M.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202478 / 277

Page 83 : Majorant et MinorantRemarques :• On ne parle jamais « du » majorant d’une partie majorée de R mais bientoujours d’UN majorant car une telle partie en possède toujours plein. Eneﬀet, si A est une partie majorée de R et si M est un majorant de A, alorstout nombre supérieur ou égal à M est aussi un majorant de A. Parconséquent, si une partie de R admet au moins un majorant, alors elle enadmet une inﬁnité. Tout réel supérieur ou égal à un majorant est lui-mêmeun majorant. Même chose à dire sur les minorants.• La partie A est bornée si et seulement si :m R+ tel que x A, x m.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202479 / 277

Page 84 : Majorant et MinorantExemples :• L’ensemble A = 10, 4, 24, 2500 est majoré par tout réel supérieur ouégale à 2500. A est minoré par tout réel inférieur ou égale à -10. L’ensembleA est donc borné.• L’ensemble A = Q0, 1 est majoré et le nombre 1 en est un majorant.Les intervalles a, b, a, b, a, b et a, b ont les mêmes majorants et lesmême minorants.• L’ensemble N est minorée par 0 et tout réel inférieur à 0, mais il n’est pasmajorée.• L’intervalle 3, + est minoré par 3, MAIS AUSSI par 2, e, 0, 1,10,100, · · · . Il n’est pas majoré en revanche.• Les ensembles Z, Q et R ne sont ni majorées, ni minorées.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202480 / 277

Page 85 : Maximum et MinimumUn majorant ou minorant de une partie A de R, n’appartient pas necéssairement àA. Quand il appartient à l’ensemble on dit :Déﬁnition Maximum-Minimum• Plus grand élément : On appelle plus grand élément de A ou maximumde A tout élément de A qui majore A. C’est-à-dire,tout majorant de A qui est dans A.• Plus petit élément : On appelle plus petit élément de A ou minimum deA tout élément de A qui minore A. C’est-à-dire,tout minorant de A qui est dans A.Exemples :• Dans l’ensemble A = 10, 4, 24, 2500, 2500 est un maximun et 10 est unminimum.• Le nombre 0 est un minimum de N.• Dans l’intervalle a, b, b est un maximun et a est un minimum.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202481 / 277

Page 86 : Maximum et MinimumExemple : Montrer que l’intervalle a, b admet a pour plus petit élément mais n’a pasde plus grand élément.Solution : Soit I = a, b.• On va tout d’abord montrer que a est un minimum de I. Par déﬁnition de a, b,pour tout x I, nous avonsa x.Ainsi a est un minorant de I. De plus, a I, donc a est un minimum de I.• Montrons maintenant que I n’admet pas un plus grand élément. Tout d’abord, bn’est pas un maximum de I car b ̸I. Raisonnons en suite par l’absurde etsupposons que b′ est un maximum de I. Alors pour tout x I, nous avonsx b′car b′ est un majorant de I.Posonsb′′ = b + b′2=⇒b + b′2I.car a b′ b et donc a b′′ bDe plus b′ b′′, donc b′ n’est pas un majorant de I. Contradiction ! Parconséquent, I ne possede pas de plus grand élémént.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202482 / 277

Page 87 : Maximum et MinimumDes exemples précédents on peut déduire le résultat suivant.Théorème UnicitéSi A possède un plus grand resp. petit élément, celui-ci est UNIQUE. On peut doncl’appeler LE plus grand resp. petit élément de A et le notermax Aresp.min A.Démonstration.Soit M, M ′ R. Si M et M ′ sont deux plus grands éléments de A, alorsM′ Mcar M majore A et M ′ A, et de mêmeM M′car M ′ majore A et M A. Par conséquentM′ MetM M′=⇒M = M′.Ainsi le maximum est unique. Même preuve permet de conclure que le plus petitélément est unique aussi.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202483 / 277

Page 88 : Maximum et MinimumAttention : On ne peut écrire max A que si on a déjà démontré que A admet unplus grand élément, ou si on se trouve dans un contexte où l’existence du plusgrand élément ne fait pas de doute.Au contraire, si A est une partie donnée de R, il n’y a aucune raison de penserqu’elle a un plus grand élément si on n’a pas d’information supplémentaire : c’estune erreur grave de parler de max A ou de s’en servir dans des exercices si onn’a pas déjà étudié l’existence d’un plus grand élément pour A ou si cetteexistence n’est pas évidente d’après le contexte.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202484 / 277

Page 89 : Maximum et MinimumLe résultat suivant nous donne une caractérisation des ensemble de N possédantun plus petit élément ou un plus grand élément.Théorème• Toute partie non vide de N possède un plus petit élément minimum.• Toute partie non vide majorée de N possède un plus grand élémentmaximum.Démonstration.Voir le cours d’algèbre.Remarque : Comme vous avez vu dans le cours d’algèbre, cette propriété est labase du Raisonnement par Récurrence.Remarque : Dans le cas de Z nous avons :• Toute partie non vide majorée de Z possède un maximum.• Toute partie non vide minorée de Z possède un minimum.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202485 / 277

Page 90 : Borne supérieure - Borne inférieureNous avons vu que l’intervallea, bn’a pas de plus grand élément, pourtant sa borne b est quelque chose de cet ordre mais quoi ? Comment décrire conceptuellement ce réel qui n’est pas dans a, b mais quin’est pas n’importe qui pour a, b?Ce qui rend le majorant b si particulier pour a, b, c’est qu’il est le meilleur majorantqu’on pouvait espérer :LE PLUS PETIT POSSIBLE.Nous allons donc le donner un nom au plus petit majorant et au plus grand minorant.Déﬁnition Borne supérieure/inférieure• Borne supérieure : S’il existe, le plus petit majorant de A est appelé la bornesupérieure de A et notésupA.• Borne inférieure : S’il existe, le plus grand minorant de A est appelé la borneinférieure de A et notéinfA.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202486 / 277

Page 91 : Borne supérieure - Borne inférieureExemple : Les intervalles a, b, a, b, a, b et a, b ont a pour borne inférieur et bpour borne supérieur.Montrons proprement que a, b admet b pour borne supérieure.Solution : Pour commencer, b est un majorant de a, b. Nous devons doncmontrer que b est le plus petit majorant de a, b, c’est-à-dire, montrer que toutréel strictement inférieur à b ne majore pas l’intervalle. Soit x b un tel réel.• Si x a, alors clairement x ne majore pas a, b car x a.• Si x a, posonsx′ = x + b2.Alors x′ a, b et x x′, donc x ne majore pas a, b.Ainsi, b est le plus petit majorant de a, b. En résumé, a, b possède une bornesupérieure, mais PAS de plus grand élément.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202487 / 277

Page 92 : Borne supérieure - Borne inférieureLa diﬀérence essentielle entre plus grand élément et borne supérieure, c’est que la bornesupérieure, quand elle existe, n’appartient pas forcement à la ensemble consideré.Inversement, nous avons le résultat suivant.Théorème Lien entre les notions de plus grand/petit élément etborne supérieure/inférieureSi A possède un plus grand resp. petit élément, alors A possède une borne supérieureresp. inférieure et :supA = maxAresp. infA = minA.Démonstration.Supposons que A possède un plus grand élément et montrons que max A est la bornésupérieur de A. Nous avons deux choses à vériﬁer :1. que : max A est un majorant de A, or par déﬁnition max A majore A,2. que : max A est le plus petit de majorants, or par déﬁnition max A A, doncmax A M pour tout majorant M de A.Puisque max A vériﬁe les deux points précédents, on conclut sup A = max A.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202488 / 277

Page 93 : Borne supérieure - Borne inférieureEn conclusion, nous avons :PropositionSoit A une partie non vide et majorée de R. Alors il y a équivalence entre :• A admet un plus grand élément ;• supA A.De même, si A est une partie non vide et minorée de R. Alors il y a équivalenceentre :• A admet un plus petit élément ;• infA A.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202489 / 277

Page 94 : Borne supérieure - Borne inférieureOn a deja donné quelques exemples de parties de R possèdant une bornesupérieure. On voudrais aller plus loin et déterminer toutes les parties de R quipossèdent une borne supérieure. Le théorème suivant nous donne la réponse.Propriété Propriété de la borne supérieure/inférieure• Toute partie non vide majorée de R possède une borne supérieure.• Toute partie non vide minorée de R possède une borne inférieure.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202490 / 277

Page 95 : Borne supérieure - borne inférieureLa caractérisation suivante de la borne supérieur et inférieur va se montrer trèsutile dans la suite.Propriété Caractérisation de la borne supérieureSoit A une partie non vide et majorée de R.M = supA⇐⇒ M est un majorant de A,pour tout M ′ majorant de A, M M ′.⇐⇒ M est un majorant de A,pour tout b M, b n’est pas un majorant de A.⇐⇒ M est un majorant de Apour tout y M, il existe x A tel que y x.⇐⇒ M est un majorant de Apour tout ϵ 0, x A tel que M ϵ x.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202491 / 277

Page 96 : Borne supérieure - borne inférieurePropriété Caractérisation de la borne inférieureSoit A une partie non vide et minorée de R.m = infA⇐⇒ m est un minorant de A,pour tout m′ minorant de A, m′ m.⇐⇒ m est un minorant de A,pour tout a m, a n’est pas un minorant de A.⇐⇒ m est un minorant de Apour tout y m, il existe x A tel que y x.⇐⇒ m est un minorant de Apour tout ϵ 0, x A tel que x m + ϵ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202492 / 277

Page 97 : Borne supérieure - borne inférieureExemple Nous avonsNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202493 / 277

Page 98 : Borne supérieure - borne inférieureExemple : Trouvons le max, min, inf et sup dans le cas de l’ensemble :A = 1n : n N.Solution : On commence par noter quen N, 1 n=⇒1n 1.Ainsi 1 est un majorant de A. De plus1 = 11=⇒1 A=⇒max A = 1.Comme A possède 1 comme plus grand élémént, on conclut1 = sup A.Maintenant, pour tout 0 n m nous avons1m 1n.L’ensemble A ne possède donc pas un plus petit élément.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202494 / 277

Page 99 : Borne supérieure - borne inférieureFinalementn N, 0 1nAinsi, 0 est un minorant de A, montrons que 0 est la borne inférieure de A.D’après la propriété dite de, caractérisation de la borne inférieure, il ne nousreste qu’à vériﬁer quepour tout y 0, il existe x A tel que x y.Pour montrer cela, notons que comme l’ensemble N n’est pas bornée, pour touty 0, il existe n N, tel que1y n=⇒1n y.Par conséquent, 0 satisfait les deux propriétés caractérisant la borne inférieur, d’oùon conclutinf A = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202495 / 277

Page 100 : Borne supérieure - borne inférieureAutre Méthode : Par déﬁnition de la borne inférieure, pour tout n Non a1n infA.Donc par passage à la limite la limite preserve les inégalités, on obtient0 =limn→+1n limn→+infA = infA.Or 0 est un minorant de A, donc 0 infA. Par conséquentinfA = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202496 / 277

Page 101 : Borne supérieure - Borne inférieureThéorème Opérations sur les bornes supérieuresOn suppose que A et B possèdent chacune une borne supérieure.• Si : A B, alorssupA supB.• L’ensemble A B possède une borne supérieure etsupA B = maxsupA, supB.• L’ensemble A + B = a + b : a A et b B possède une borne supérieureetsupA + B = supA + supB.• Pour tout λ 0, l’ensembleλ · A = λa : a A.possède une borne supérieur et supλ · A = λ · sup A.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202497 / 277

Page 102 : Propriété d’ArchimèdeContinuons avec notre étude de l’ensemble des nombres réels. La dernière propriété del’ensemble des nombres réels que nous allons étudier est la propriété dite d’Archimède :Proposition Propriété d’ArchimèdePour tout nombre réel x, il existe un unique entier relatif n Z vériﬁantn x n + 1.Démonstration.Soit x R, et considérons l’ensembleB = k Z k x.Alors B est une partie non vide et majorée de Z. On sait alors qu’elle possède un plusgrand élément n. D’après la déﬁnition du maximum, on conclut :n B=⇒n xn + 1 ̸B=⇒x n + 1Ainsi, n x n + 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202498 / 277

Page 103 : Propriété d’ArchimèdeUnicité de n.Montrons à présent l’unicité : supposons n1, n2 tels que :n1 x n1 + 1etn2 x n2 + 1.Alors n2 1 x n2 et par somme on obtientn1 n2 1 0 n1 n2 + 1.Ainsi1 n1 n2 1.Puisque n1 n2 Z, on en déduit que n1 n2 = 0. C’est-à-diren1 = n2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/202499 / 277

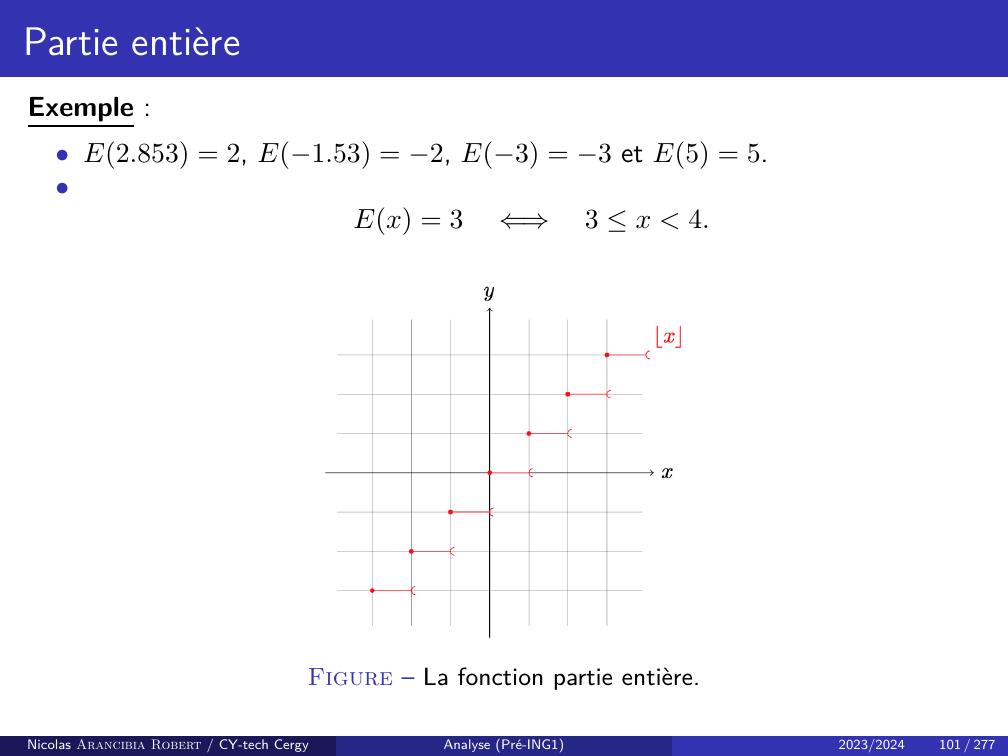
Page 104 : Partie entièreLa propriété d’Archimède peut sembler évidente, elle est pourtant essentielle, ellenous permet par exemple de déﬁnir la partie entière d’un nombre réel.Déﬁnition partie entièreSoit x R. L’unique entier n vériﬁantn x n + 1,s’appelle la partie entière de x et est notéEx ou ⌊x⌋.Remarque : La partie entière de x est donc le plus grand entier relatif inférieur ouégal à x, c’est-à-direx 1 ⌊x⌋x ⌊x⌋+ 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024100 / 277

Page 105 : Partie entièreExemple :• E2.853 = 2, E1.53 = 2, E3 = 3 et E5 = 5.•Ex = 3⇐⇒3 x 4.Figure – La fonction partie entière.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024101 / 277

Page 106 : DensitéFinissons ce chapitre en introduisant la notion de densité.Déﬁnition Partie dense dans ROn dit que A est dense dans R si pour tous x, y R avec : x y, il existe a Atel quex a y.Autrement dit, si l’intervalle x, y contient un élément de A.Nous avons l’exemple suivant.Théorème Densité des rationnels et des irrationnelsLes ensembles Q et R \ Q sont denses dans R.Remarque : Il y a ainsi toujours un rationnel entre deux irrationnels distincts etun irrationnel entre deux rationnels distincts. Les ensembles Q et R \ Q sontimbriqués l’un dans l’autre.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024102 / 277

Page 107 : DensitéDonnons une idée de la preuve de la densité de Q, pour cela on introduit la notiond’approximation décimal.Déﬁnition Approximations décimalesSoit x R et n N. Alorspn = ⌊10nx⌋est l’unique entier tel que :pn 10nx pn + 1=⇒pn10n x pn + 110n .Le nombre décimalpn10n est appelé approximation décimale par défaut de x à laprécision 10n. Le nombre pn+110nest appelé approximation décimale par excèsde x à la précision 10n.Exemple1.1414 2 1.1415 à 104 près, 3.1415 π 3.1416 à 104 près.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024103 / 277

Page 108 : DensitéIdée de preuve : Soit x R. Pour tout n N, notonsun = pn + 110nl’approximation décimale par excès de x. On a alors0 un x 10npour tout n N. Par passage à la limite, on obtient la limite preśerve lesinégalités quelimn un = x.On a ainsi obtenu une suite unn de nombres rationnel qui tend vers x R. Enparticulier, pour tout y R avec x y, il existe n N tel quex un y.Ce qui montre que Q est dense dans R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024104 / 277

Page 109 : DensitéProposition Caractérisation de la densité en termes de voisinagesSoit U une partie de R. Les propriétés suivantes sont équivalentes :i. U est dense dans R,ii. x R, ϵ 0, u Utel queu x ϵ.Remarque :Ainsi, dire que U est dense dans R, c’est dire que tout point de ladroite réelle peut être« approché d’aussi près qu’on veut »par des éléments de U.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024105 / 277

Page 110 : Chapitre 2 - Suites numériquesSuites numériques :• Généralités :• Déﬁnition.• Propriétés.• Opérations sur les suites.• Limites de suites :• Déﬁnition.• Opérations sur les limite.• Théorèmes d’existence de limite.• Suites adjacentes et récurrentes.• Extension aux suites complexes.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024106 / 277

Page 111 : Suites numériquesDéﬁnition Suite réelleUne suite réelle u est une fonction de N dans Ru : N→Rn7→un.Pour tout n N, on préfère noterun le réel unet on l’appele le n-ième terme de la suite ou terme général de la suite.La suite est notée u, ou plus souvent unnN ou unn0, ou simplement un.Remarque : On prendra garde à bien distinguer la suite unn0 avec son n-ièmeterme un.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024107 / 277

Page 112 : Suites numériquesUne suite peut être déﬁnie de trois manières diﬀérentes :• par une formule explicite : chaque terme de la suite est donné directementen fonction de n, soit un = fn. Par exemplen N,un =1n2 + 1.• par une formule de récurrence : un est exprimé en fonction de n et destermes précédents : un1, . . . , u0. Par exempleu0 = 1 et n 0, un+1 = un + 2 relation de récurrence d’ordre 1nous pouvons donner aussi comme exemplev0 = 1, v1 = 1, et n 1, vn+2 = vn+1 + vn relation de récurrence d’odre 2• par une formule implicite : le terme général un de la suite est solution d’uneéquation dépendant de n. Par exemplen N,un est l’unique solution réel de l’équation x3 + x 1 = n.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024108 / 277

Page 113 : Suites numériquesSur les suites on peut déﬁnir les opérations suivants.Déﬁnition Opérations sur les suitesSoient u = unnN et v = vnnN deux suites réelles.• La somme de u et v est la suite notée u + v déﬁnie par :n N,u + vn = un + vn.• Le produit de u et v est la suite notée u · v déﬁnie par :n N,u · vn = un · vn.• Le produit de u par un scalaire λ R est la suite notée λ · u déﬁnie par :n N,λ · un = λ · un.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024109 / 277

Page 114 : Suites réelles et relation d’ordreÉtudions quelques propriétés éventuelles des suites numériques.Déﬁnition suite majorée, minorée, bornéeSoit unnN une suite réele.• On dit que unnN est majorée, s’il existe M R tel quen N, un M.• On dit que unnN est minorée, s’il existe m R tel quen N, m un.• On dit que unnN est bornée, si elle est majorée et minorée, c’est-à-dire,s’il existe m R, M R tel quen N, m un M.Ce qui peut aussi être dite parM 0, n N,un M.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024110 / 277

Page 115 : Suites réelles et relation d’ordreDéﬁnitionSoit unnN une suite réele.• On dit que unnN est croissante sin N, un un+1.• On dit que unnN est strictement croissante sin N, un un+1.• On dit que unnN est décroissante sin N, un un+1.• On dit que unnN est strictement décroissante sin N, un un+1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024111 / 277

Page 116 : Suites réelles et relation d’ordreDéﬁnition• On dit que unnN est monotone si elle est croissante ou décroissante.• On dit que unnN est strictement monotone si elle est strictement croissanteou strictement décroissante.Remarque : Pour montrer qu’une suite unnN est monotone, deux méthodescourantes :• étudier le signe de un+1 un. Ainsisi un+1 un 0=⇒un est croissantesi un+1 un 0=⇒un est décroissante• si n N, un 0, étudier la position de de un+1unpar rapport à 1. Ainsisiun+1un1=⇒un est croissantesiun+1un1=⇒un est décroissanteCette méthode est intéressante surtout lorsque un est déﬁni par des produits et desquotients et qu’on peut espérer des simpliﬁcations.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024112 / 277

Page 117 : Suites réelles et relation d’ordreExemple : Étudions la monotonie de la suite déﬁnie parn N, un = n!nn .Solution : Nous avons un 0. Pour décrire la monotonie de unnN il suﬃtdonc d’étudier la position de un+1unpar rapport à 1. Nous avonsun+1un=n+1!n+1n+1n!nn=n + 1!nnn! · n + 1n+1 =n + 1nnn + 1n+1 =nn + 1n.Ornn + 1 1=⇒nn + 1n 1.Donc unnN est strictement décroissante.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024113 / 277

Page 118 : Suites réelles et relation d’ordreFinalement, introduisons.Déﬁnition suites constantesOn dit que unnN est constante sin N, un+1 = un⇐⇒n N, un = u0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024114 / 277

Page 119 : Propriétés à partir d’un certain rangCe qu’une suite a d’intéressant pour nous dans ce chapitre, ce ne sont pas sespremiers termes mais son comportement asymptotique, c’est-à-dire soncomportement à l’inﬁni. Si par exemple tous ses termes sont majorés par 1 saufles 30 premiers, on a bien envie de dire que la suite est« presque » majorée par 1.On dit qu’elle est majorée par 1 à partir d’un certain rang.Ce qui nous amène à déﬁnir.DéﬁnitionOn dit qu’une suite unnN satisfait la propriété Pn à partir d’un certain rangs’il existe n0 N tel quen n0,Pnest vraie.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024115 / 277

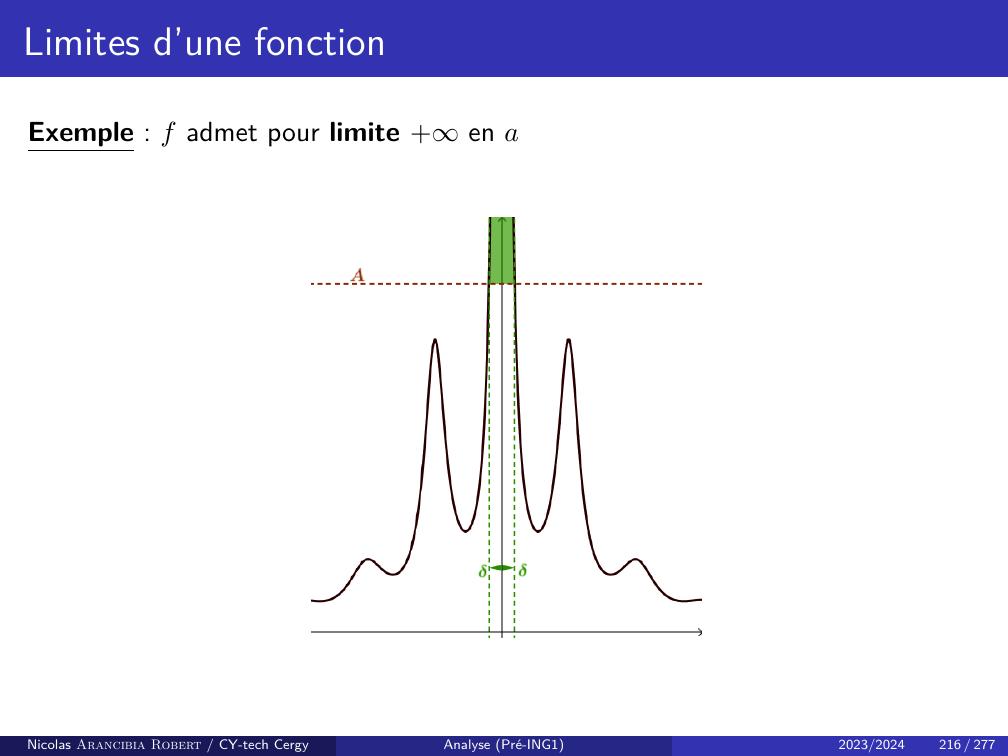
Page 120 : Suites numériquesPar exemple on dit :Déﬁnition suite stationnaireLa suite unnN est dite stationnaire si elle est constante à partir d’un certainrang i.e sin0 : n n0, un = un0.Exemple : Considérons la suite unnN déﬁnie parn N, un =nYk=0100 k.Alors pour tout n 100 nous avonsnYk=0100 k=100 · 100 1 · · · 100 99 · 100 100 · · · 100 n=0Ainsi, unnN est stationnaire, constante égale à 0 à partir du rang n = 100.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024116 / 277

Page 121 : Limite d’une suite réelleNous allons nous intereser maintenant à l’une des notions le plus importantes enmathématiques, la notion de convergence de une suite ou limite de une suite.Déﬁnition ProvisoireSoit unnN une suite réelle. On dit queunnN a pour limite le réel ℓRsi unnN est proche d’aussi près que l’on veux de ℓpour n suﬃsamment grand i.e. àpartir d’un certain rang.Exemple : Avec cette déﬁnition, étudions le cas de la suite unnN déﬁnie pour toutn Nparun = 3 + 1n.Vraisemblablementquand n tend vers l’inﬁni, la suite un tend vers 3Selon notre déﬁnition provisoire, pour montrer la convergence de la suite vers 3, on doitvériﬁer que un est proche d’aussi près que l’on veux de 3 à partir d’un certain rang.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024117 / 277

Page 122 : Limite d’une suite réellePar exemple, supposons qu’on veut que un soit à une distance de110 de 3. Pourcela, on doit avoir3 110 un 3 + 110,ce qui est équivalent àun 3 110.Et cette dernière inégalité est vraie, si et seulement si3 + 1n 3 110 ⇐⇒1n 110 ⇐⇒10 n.Notons qu’il n’a rien de spécial sur110, si l’on veut queun 3 ϵpour ϵ un réel positif,il suﬃt quen 1ϵ .Ainsi, on vient de démontrer que unnN est proche d’aussi près que l’on veux de3 pour n suﬃsamment grand.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024118 / 277

Page 123 : Limite d’une suite réelleFormalisons notre déﬁnition provisoire de limite, on commence par faire plusprécise la notion :« d’être proche de »Dans notre exemple, nous avons vu que pour que unnN soit proche de 3, il fautque la distanceun 3soit petit.Ainsi, le premier changement qu’on va faire à notre déﬁnition provisoire est :Déﬁnition Provisoire 2Soit unnN une suite réelle. On dit queunnN a pour limite le réel ℓRsi un ℓ est aussi petit que l’on veut pour n suﬃsamment grand i.e. à partird’un certain rang.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024119 / 277

Page 124 : Limite d’une suite réelleMaintenant, dans notre exemple nous avons vu que, pour queun 3 soit aussi petit que l’on veut,pour tout ϵ 0, on doit avoirun 3 ϵa partir d’un certain rang.Le deuxième changement qu’on va faire à notre déﬁnition provisoire est donc :Déﬁnition Provisoire 3Soit unnN une suite réelle. On dit queunnN a pour limite le réel ℓRsi pour tout ϵ 0, on aun ℓ ϵpour n suﬃsamment grand i.e. à partir d’un certain rang.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024120 / 277

Page 125 : Limite d’une suite réelleIl ne nous reste donc qu’a faire plus précise la phrase :« pour n suﬃsamment grand »Dans notre exemple, nous avons vu queun 3 110⇐⇒n 10.Ainsi, la propriété est vraie à partir de N = 10. De même, pour tout ϵ 0 nousavonsun 3 ϵ⇐⇒n 1ϵ .Donc pour tout ϵ 0, il existe un entierN N,il suﬃt de prendre N = E1ϵ+ 1,pour que pour tout n N la propriété est vraie.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024121 / 277

Page 126 : Limite d’une suite réelleOn est à présent prêt pour donner la déﬁnition de la limite d’une suite.Déﬁnition Limite d’une suiteSoit unnN une suite réelle. On dit queunnN converge vers un réel ℓRou queunnN a pour limite ℓsi : pour tout ϵ 0 existe un entier N N, tel que si n N alorsun l ϵ.Ce que on peut exprimer à l’aide de quantiﬁcateurs parϵ 0, N N, n N, n N =⇒un ℓ ϵ .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024122 / 277

Page 127 : Limite d’une suite réelleOn constate que le rang en question dépend en général de ϵ : de manière vague, onpeut penser que typiquement, « plus ϵ est petit, plus il faudra attendre un grandrang N avant de voir la distance entre un et ℓrester systématiquement ϵ ».Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024123 / 277

Page 128 : Limite d’une suite réelleRemarque :• Si unnN converge vers ℓ, on pourra aussi dire que :la suite unnN tend vers ℓ,et on notelimn→+un = ℓ,ouun→n→+ℓ.• Noter que dans la phrase logiqueϵ 0, N N, n N, n N ⇒un l ϵ .N dépend de ϵ et qu’on ne peut pas échanger l’ordre du « pour tout » etdu « il existe ».• D’après la déﬁnition de la limite, unnN converge vers ℓsi et seulement silimn→+un ℓ = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024124 / 277

Page 129 : Limite d’une suite réelleExemple : Soit unnNdéﬁnie pour tout n Nparun = 3 + 1n.Montrons que unnN converge vers 3.Solution : Soit ϵ 0, on cherche N N tel quen N,un 3 ϵ.C’est-à-dire, on cherche N N tel quen N,ϵ 1n ϵ⇐⇒n N,0 1n ϵ⇐⇒n N,1ϵ n.Posons N = E 1ϵ+ 1, alors pour n N, nous avonsn N 1ϵ=⇒1n ϵ=⇒un 3 ϵ.Ainsi,limn→+un = 3.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024125 / 277

Page 130 : Limite d’une suite réelleSi elle existe, on va pouvoir parler de la limite, car il y a unicité :Proposition Unicité de la limiteSi la suite réelle unnN converge, alors sa limite est unique.Démonstration.Raisonnons par l’absurde et supposons quelimn→+un = ℓ1etlimn→+un = ℓ2 avec ℓ1 ̸= ℓ2.Soit ϵ = ℓ1ℓ22 0. Par déﬁnition de la limite, on aN1 N tel que n N1,un ℓ1 ϵ/2N2 N tel que n N2,un ℓ2 ϵ/2Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024126 / 277

Page 131 : Limite d’une suite réelleDémonstration.Soit N = maxN1, N2, alors pour tout n N, nous avonsun ℓ1 ϵ2etun ℓ2 ϵ2.Ainsi, par l’inégalité triangulaireℓ1 ℓ2=ℓ1 un + un ℓ2ℓ1 un + un ℓ2ϵ2 + ϵ2=ϵ = ℓ1 ℓ22.Contradiction ! Donc ℓ1 = ℓ2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024127 / 277

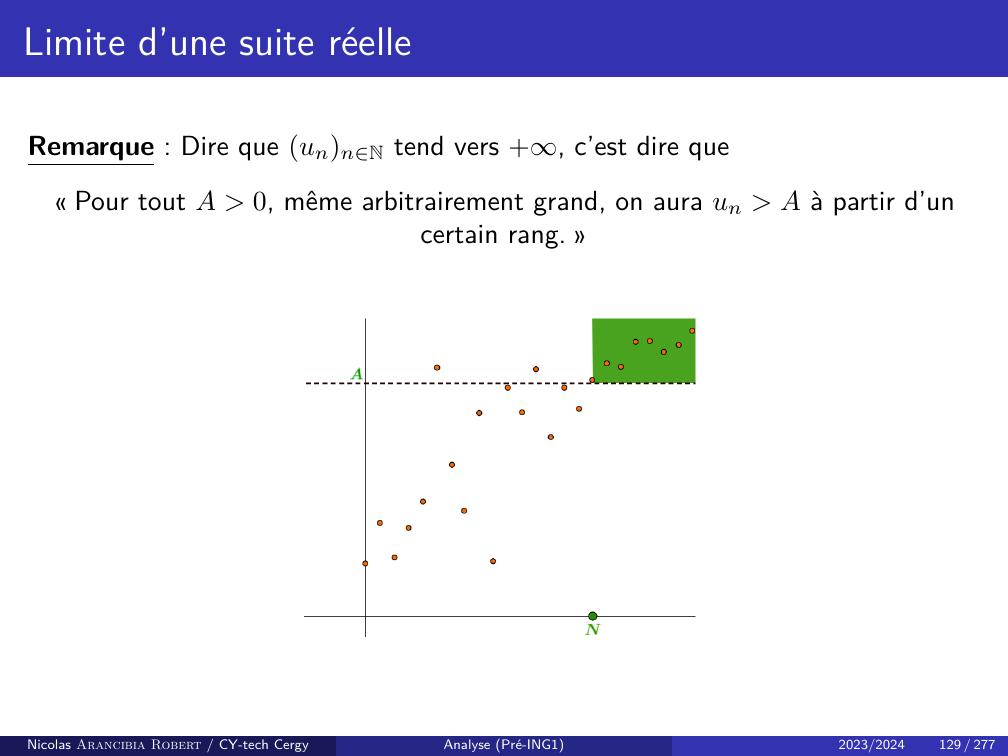
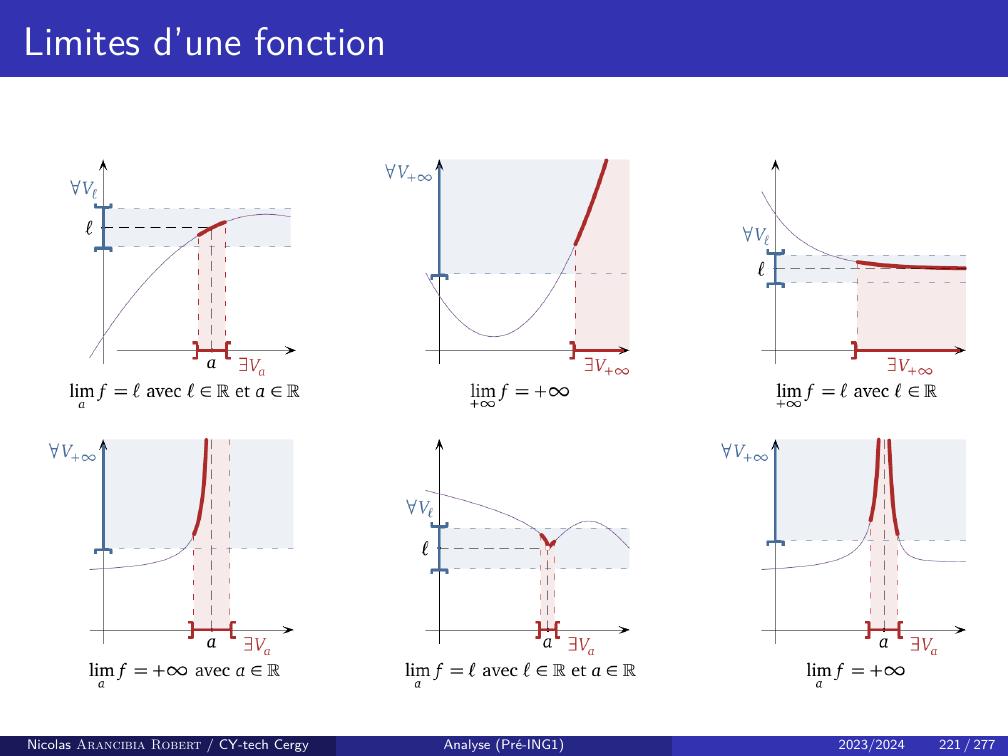
Page 132 : Limite d’une suite réelleDéﬁnitionSoit unnN une suite réelle.• On dit que unnN tend vers +siA R, N N, n N,n N =⇒un A .• On dit que unnN tend vers siA R, N N, n N,n N =⇒un A .Remarque :• Si unnN tend vers ±, on notelimn→+un = ±.• Nous avonslimn→+un = ⇐⇒limn→+un = +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024128 / 277

Page 133 : Limite d’une suite réelleRemarque : Dire que unnN tend vers +, c’est dire que« Pour tout A 0, même arbitrairement grand, on aura un A à partir d’uncertain rang. »Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024129 / 277

Page 134 : Limite d’une suite réelleRemarque : Soit unnN une suite réelle et ℓun nombre réel. En niant ladéﬁnition, l’aﬃrmation « unnN ne converge pas vers ℓ» s’écrit avec desquantiﬁcateurs :ϵ 0, N N, n N,n N etun ℓ ϵ.Pour dire qu’une suite n’admet pas de limite ﬁnie, on doit veriﬁer qu’elle neconverge vers aucun réel : ainsi, si unnN est une suite réelle, l’aﬃrmation« unnN n’est pas convergente » s’écrit avec des quantiﬁcateurs :ℓR, ϵ 0, N N, n N,n N etun ℓ ϵ.Déﬁnition Convergence - Divergence• Une suite est dite convergente si elle admet une limite ﬁnie.• Elle est divergente sinon. C’est-à-dire, une suite est divergente si ellen’admet pas de limite ﬁnie. En particulier, une suite est divergente si elle tendvers ±.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024130 / 277

Page 135 : Limite d’une suite réelleNous avons donc :Limite ﬁnieLimite ±Pas de limiteConvergenceDivergenceDivergenceExemples :• La suite de terme général n sinnn2+4est convergente, sa limite est 0.• La suite de terme général n2 + 1nn est divergente, elle tend vers +.• La suite de terme général 1n est divergente, elle n’admet pas de limite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024131 / 277

Page 136 : Limite d’une suite réelleÉtudions quelques propriétés des suites convergentes.PropositionToute suite réelle convergente est bornée.Démonstration.Soit unn une suite convergente vers un réel ℓR. Posons ϵ = 1 0, pardéﬁnition de la limite, il existe N N tel que :n N, un ℓ 1.Pour tout n N, on a doncun = un ℓ+ ℓun ℓ + ℓℓ + 1 +.Posons alorsM = maxu0, . . . , uN, 1 + ℓ.Ainsi, pour tout n N, nous avons un M.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024132 / 277

Page 137 : Limite d’une suite réelleRemarques :• La réciproque est fausse, la suite de terme général1n + 4est bornée entre 3 et 5 sans être convergente.• Une suite non bornée n’admet pas forcément +ou pour limite. Lasuite de terme général1nn3 + 1,n’est pas bornée et n’a pas de limite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024133 / 277

Page 138 : Limite d’une suite réelleLe lemme suivant peut se montrer utile pour vériﬁer la valeur d’une limite.LemmeConsidérons la suite unnN et soit ℓR. Supposons αnnN une suite réelle positivetendant vers 0 telle quen N,un ℓ αn.Alors, la suite unnN est convergente de limite lim un = ℓ.Démonstration.Soit ϵ 0. Par déﬁnition de la convergence, il existe N1 N tel quen N1,αn ϵ.De plus, il existe N2 N tel quen N2,un ℓ αn.Posons, N = maxN1, N2. Pour tout n N, on a : un ℓ αn ϵ. Ainsi, unconverge vers ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024134 / 277

Page 139 : Limite d’une suite réelleRemarque : Pour montrer qu’une suite unnN converge vers ℓ, on peut tenterde majorerun ℓpar une suite qui converge vers 0.PropositionSoit unn une suite convergente vers un réel ℓR. Alorslimn→+un = ℓ.Démonstration.Voir T.D.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024135 / 277

Page 140 : Opérations sur les limitesNous avons vu que sur l’ensemble des suites on peut déﬁnir une addition et unproduit. Étudions le comportement de la convergence par rapport a ces deuxopérations.Proposition Cas de deux limites ﬁniesSoient unnN et vnnN deux suites qui convergent respectivement vers ℓet ℓ′.• Somme : Nous avonslimn→+un + vn = ℓ+ ℓ′.• Produit : Nous avonslimn→+un · vn = ℓ· ℓ′.• Multiplication par un réel : Soit λ R, alorslimn→+λ · un = λ · ℓ.Remarque : Si on combine les points un et trois du résultat précédent, on aλ, µ R2,limn→+λun + µvn = λℓ+ µℓ′.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024136 / 277

Page 141 : Opérations sur les limitesDémonstration.• Somme : Supposons quelimn→+un = ℓetlimn→+vn = ℓ′.Soit ϵ 0. Nous voulons montrer qu’il existe N N, tel que pour tout n N, nousavonsun + vn ℓ+ ℓ′ ϵ.Maintenant, par déﬁnition de la limiteN1 N tel que n N1,un ℓ ϵ/2N2 N tel que n N2,vn ℓ′ ϵ/2Posons N = maxN1, N2. Alors pour tout n N, on peut, à l’aide de l’inégalitétriangulaire, conclureun + vn ℓ+ ℓ′ = un ℓ + vn ℓ′ un ℓ + vn ℓ′ ϵ2 + ϵ2 = ϵ.Par conséquent, un + vnnN converge vers ℓ+ ℓ′.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024137 / 277

Page 142 : Opérations sur les limitesDémonstration.• Produit : Supposons quelimn→+un = ℓetlimn→+vn = ℓ′.Soit ϵ 0. Nous voulons montrer qu’il existe N N, tel que pour tout n N,nous avonsunvn ℓℓ′ ϵ.Maintenant, pour tout n N, on peut, à l’aide de l’inégalité triangulaire, conclureunvn ℓℓ′ = unvn ℓvn + ℓvn ℓℓ′=un ℓvn + ℓvn ℓ′un ℓvn + ℓvn ℓ′un ℓ · vn + ℓ · vn ℓ′Or vnnN est convergente donc bornée, disons par K. C’est-à-diren N,vn K.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024138 / 277

Page 143 : Opérations sur les limitesDémonstration.De plus, par déﬁnition de la limiteN1 N tel que n N1,un ℓ ϵ2KN2 N tel que n N2,vn ℓ′ ϵ21 + ℓPosons N = maxN1, N2. Alors pour tout n N, nous avonsunvn ℓℓ′un ℓ · vn + ℓ · vn ℓ′ϵ2K · K + ℓ ·ϵ21 + ℓϵ2 + ϵ2 = ϵ.Par conséquent, un · vnnN converge vers ℓ· ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024139 / 277

Page 144 : Opérations sur les limitesProposition Cas des limites inﬁniesSoit vnnN une suite qui tend vers +.• Si unnN est une suite minorée, alorslimn→+un + vn = +.En particulier, si unnN est convergente, alorslimn→+un + vn = +.• Si unnN est une suite minorée par un réel strictement positif à partird’un certain rang, alorslimn→+un · vn = +.En particulier, silimn→+un = ℓR+, alorslimn→+un · vn = +.Remarque : On a de résultats similaires quand on supposelimn→+vn = comme on verra dans un instant.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024140 / 277

Page 145 : Opérations sur les limitesProposition Cas du quotient• Si un converge vers ℓR et vn converge vers ℓ′ R, alors la suite unvnnNest déﬁnie à partir d’un certain rang etlimn→+unvn=ℓℓ′ .• Si unnN diverge vers +, alors la suite 1unnN est déﬁnie à partir d’uncertain rang etlimn→+1un= 0.• Si unnN converge vers 0 et est strictement positif resp. strictement négatif àpartir d’un certain rang, alors la suite 1unnN est déﬁnie à partir d’un certain rangetlimn→+1un= +resp.limn→+1un= .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024141 / 277

Page 146 : Opérations sur les limitesDémonstration.Montrons le première point de la proposition précédente. Soit ϵ 0. Nous voulonsmontrer qu’il existe N N, tel que pour tout n N, nous avonsunvn ℓℓ′ ϵ.Maintenant, comme vn →ℓ′ ̸= 0, on conclut vn →ℓ′ 0. Ainsi, il existe N0 0,tel que pour tout n N0, nous avons vn m. Alors pour tout n N0, on peut, àl’aide de l’inégalité triangulaire, conclureunvnℓℓ′ =unℓ′ vnℓvnℓ′ =unℓ′ ℓℓ′ + ℓℓ′ vnℓvnℓ′=un ℓℓ′ ℓvn ℓ′vnℓ′un ℓℓ′vnℓ′ +ℓvn ℓ′vnℓ′=un ℓvn+ ℓ · vn ℓ′vn · ℓ′un ℓm+ ℓ · vn ℓ′m · ℓ′Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024142 / 277

Page 147 : Opérations sur les limitesDémonstration.Or par déﬁnition de la limiteN1 N tel que n N1,un ℓ ϵ · m2N2 N tel que n N2,vn ℓ′ ϵ · m · ℓ′21 + ℓPosons N = maxN0, N1, N2. Alors pour tout n N, nous avonsunvn ℓℓ′un ℓm+ ℓ · vn ℓ′m · ℓ′ϵ · m2m+ϵ · m · ℓ · ℓ′2m · 1 + ℓ · ℓ′ϵ2 + ϵ2 = ϵ.Par conséquent, unvnnN converge versℓℓ′ .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024143 / 277

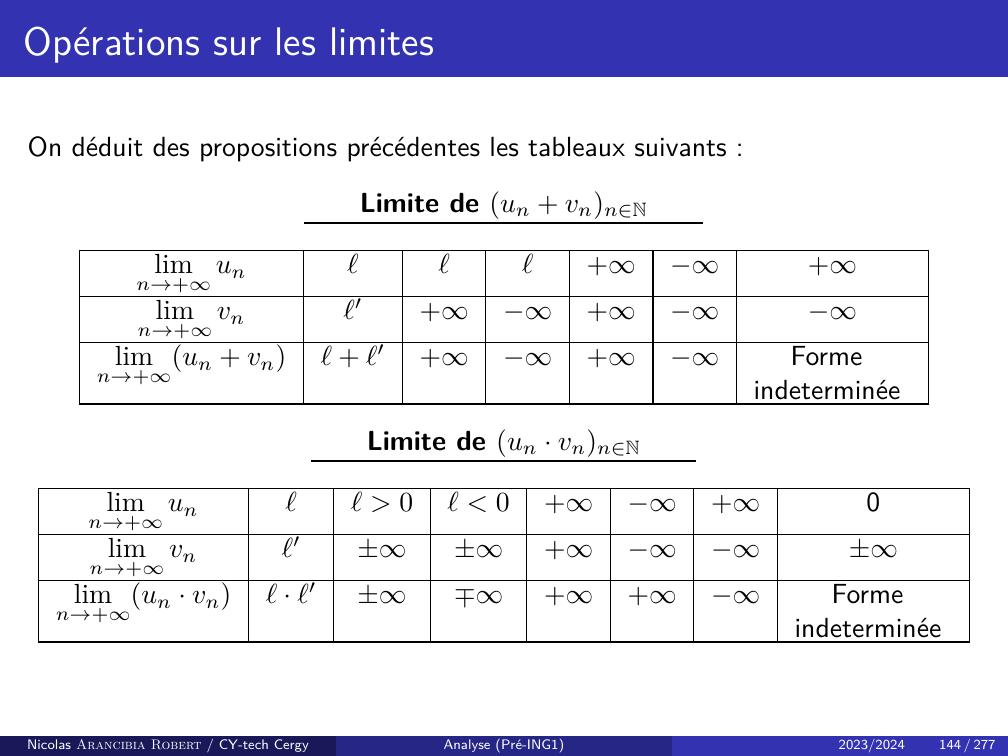
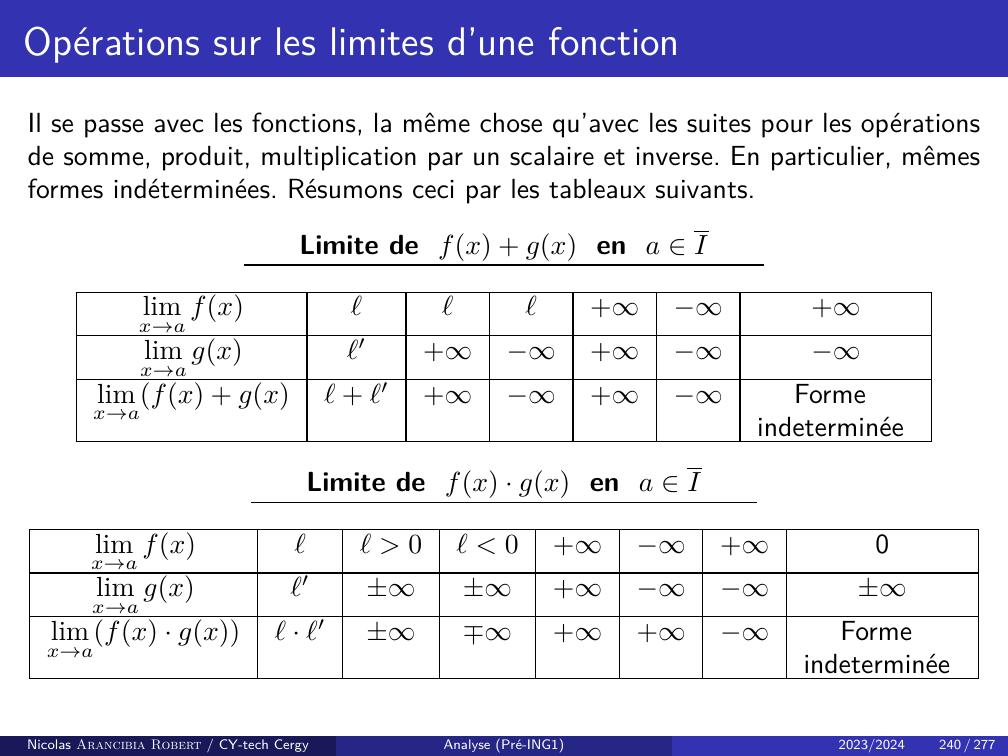
Page 148 : Opérations sur les limitesOn déduit des propositions précédentes les tableaux suivants :Limite de un + vnnNlimn→+unℓℓℓ++limn→+vnℓ′++limn→+un + vnℓ+ ℓ′++FormeindeterminéeLimite de un · vnnNlimn→+unℓℓ 0ℓ 0++0limn→+vnℓ′±±+±limn→+un · vnℓ· ℓ′±++FormeindeterminéeNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024144 / 277

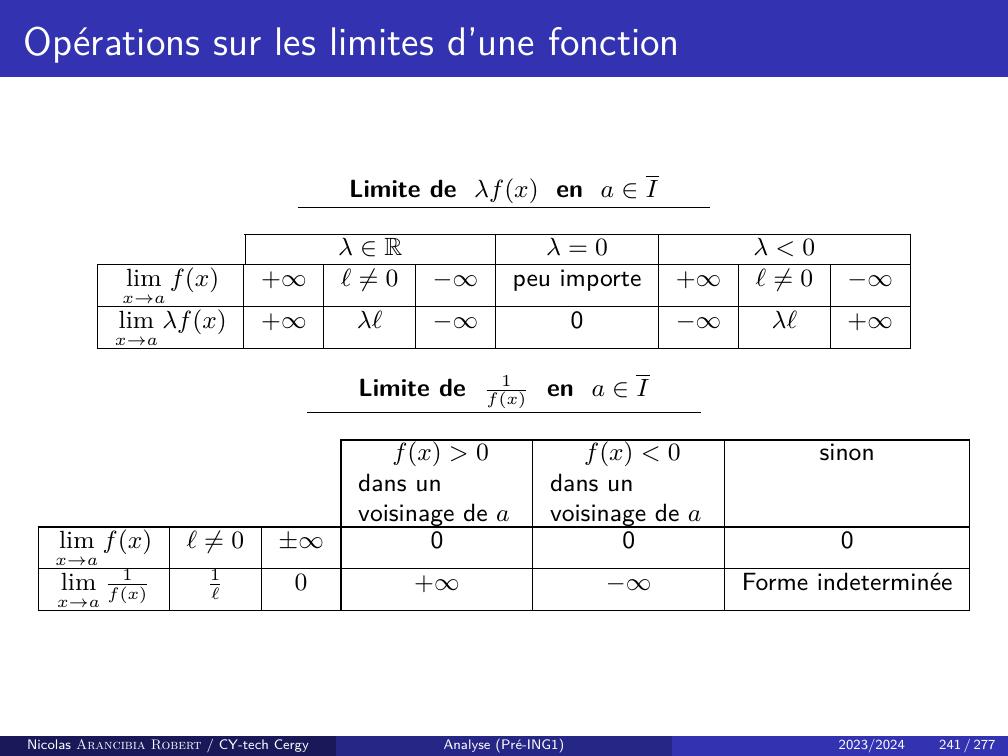
Page 149 : Opérations sur les limitesLimite de λunnNλ 0λ = 0λ 0limn→+un+ℓ̸= 0peu importe+ℓ̸= 0limn→+λun+λℓ0λℓ+Limite de 1unnNun 0àpartird’uncertain rangun 0àpartird’uncertain rangsinonlimn→+unℓ̸= 0±000limn→+1un1ℓ0+Forme indeterminéeRemarque : Forme indéterminée, signiﬁe que c’est une forme à déterminer. C’est-à-dire,en eﬀectuant une opération + + ou 0 × +, on peut tomber a priori surn’importe quel résultat.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024145 / 277

Page 150 : Opérations sur les limitesExemples :Cas de la forme indéterminée + + :• Nous avonslimn→+3n2 + 1 = +etlimn→+3n2 = +,maislimn→+3n2 + 1 3n2 = 1.• Nous avonslimn→+3n2 + 1 = +etlimn→+2n2 = +,maislimn→+3n2 + 1 2n2 = +.• Nous avonslimn→+3n2 + 1n = +etlimn→+3n2 = +,mais 3n2 + 1n 3n2 = 1n n’as pas de limite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024146 / 277

Page 151 : Opérations sur les limitesExemples :Cas de la forme indéterminée 0 × +:• Nous avonslimn→+1n2 + 1 = 0etlimn→+4n2 = +,maislimn→+1n2+1 · 4n2 = 4.• Nous avonslimn→+1n + 1 = 0etlimn→+4n2 = +,maislimn→+1n+1 · 4n2 = +.• Nous avonslimn→+1nn2 + 1 = 0etlimn→+n2 + 1 = +,maislimn→+1nn2+1 · n2 + 1 = 1n n’as pas de limite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024147 / 277

Page 152 : Opérations sur les limitesLa dernière opération sur les limites que nous avons étudier, c’est la composition àgauche par une fonction.Théorème Composition à gauche par une fonctionSoient I un intervallef : I →Rune fonction, ℓR, +, , L R, +, et unnN une suite àvaleurs dans I. Silimn→+un = ℓetlimx→ℓfx = L,alorslimn→+fun = L.Remarque : Si f : I →R est une fonction continue, d’après le théorèmeprécédente nous pouvons conclurelimn→+fun = flimn→+un.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024148 / 277

Page 153 : Passage à la limite dans une inégalitéÉtudions le comportement des limites par rapport à la relation d’ordre sur R.Proposition Passage à la limite dans les inégalités strictesSoit unnN une suite réelle possedant une limite ℓ, et soient m, M R.• Si ℓ M, alorsun Mà partir d’un certain rang.• Si ℓ m, alorsun mà partir d’un certain rang.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024149 / 277

Page 154 : Passage à la limite dans une inégalitéDémonstration.Prouvons le première point, le deuxieme point se montre de la même façon.Supposons ℓ M.• Si ℓ= , alors par déﬁnition de la limiteN N tel que n N,un M.C’est-à-dire, un M à partir d’un certain rang.• Si ℓR, sachant que M ℓ 0 on peut, d’après la déﬁnition de la limite,conclureN N tel que n N,un ℓ M ℓAinsin N,ℓM un ℓ M ℓ=⇒un M.C’est-à-dire, un M à partir d’un certain rang.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024150 / 277

Page 155 : Passage à la limite dans une inégalitéThéorème Passage à la limite dans les inégalités largesSoient unnN et vnnN deux suites convergentes vers ℓet ℓ′ respectivement.Siun vnà partir d’un certain rang, alorslimn→+un limn→+vn.C’est-à-dire, ℓℓ′.Remarque : On retiendra que les inégalités strictes deviennent larges enpassant à la limite. Par exemple, pour tout n N,1n+1 0, maislimn→+1n + 1 = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024151 / 277

Page 156 : Passage à la limite dans une inégalitéDémonstration.Par l’absurde. Supposons donc que un vn à partir d’un certain rang, et quelimn→+un limn→+vn=⇒limn→+un vn 0.Or la proposition précédent montre queun vn 0=⇒un vnà partir d’un certain rang. Contradiction ! Par conséquent,limn→+un limn→+vn.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024152 / 277

Page 157 : Théorèmes d’existence d’une limiteL’existence d’une limite n’est jamais acquise. Jusqu’à maintenant, nous avonssurtout étudié des théorèmes de CALCUL, de manipulation des limites. Lesquatre théorèmes suivants nous donnent de conditions pour conclure l’existenced’une limite, ils nous fournissent donc pas tant la VALEUR d’une limite mais sonEXISTENCE.Théorème Théorème d’encadrementSoit unnN, vnnN et wnnN trois suites rééls et ℓR. Supposonslimn→+un = ℓ=limn→+wnet qu’il existe N N, tel que pour tout n N, nous avonsun vn wn.Alors vnnN converge etlimn→+vn = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024153 / 277

Page 158 : Théorèmes d’existence d’une limiteDémonstration.Soit ϵ 0. Nous voulons montrer qu’il existe N N, tel que pour tout n N,nous avonsvn ℓ ϵ.Par hypothèse, il existe N N tel que pour tout n N, nous avonsun vn wn.Maintenant, par déﬁnition de la limiteN1 N tel que n N1,un ℓ ϵ=⇒ϵ un ℓϵ,N2 N tel que n N2,wn ℓ ϵ=⇒ϵ wn ℓϵ.Posons N3 = maxN1, N2, N. Ainsi, pour tout n N3, on aϵ un ℓvn ℓwn ℓϵ.Donc vn ℓ ϵ et on a montré que vnnN converge vers ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024154 / 277

Page 159 : Théorèmes d’existence d’une limiteExemple : Pour tout n N, on poseun =nXk=1nn2 + k .Calculerlimn→+un.Solution : Il suﬃt de remarquer que, pour tout 1 k n, nous avonsnn2 + n nn2 + k nn2 + 1=⇒nXk=1nn2 + n un nXk=1nn2 + 1.MaintenantnXk=1nn2 + n =nn + 1etnXk=1nn2 + 1 =n2n2 + 1.Ainsin N,nn + 1 un n2n2 + 1.Or, limn→+nn+1 = 1 et limn→+n2n2+1 = 1. Le Théorème d’encadrement permetd’aﬃrmer que la suite unnNtend vers 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024155 / 277

Page 160 : Théorèmes d’existence d’une limiteThéorème Théorème de Minoration/MajorationSoit unnN et vnnN deux suites réelles.• Silimn→+un = +et il existe N N tel que pour tout n N, nous avonsun vn,alorslim vn = +.• Silimn→+vn = et il existe N N tel que pour tout n N, nous avonsun vn,alorslim un = .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024156 / 277

Page 161 : Théorèmes d’existence d’une limiteExemple : Pour tout n N, on poseun =nXk=11k.Étudier la limite de unnN.Solution : Notons quek N, 1 k n,1n 1k=⇒nXk=11n nXk=11k= un.MaintenantnXk=11n =nn = n.Ainsin un.Or, limn→+n = +. Le Théorème de Majoration nous permet d’aﬃrmer quela suite unnNtend vers +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024157 / 277

Page 162 : Théorèmes d’existence d’une limiteNotre troisième théorème d’existence est l’important Théorème de la limitemonotone.Théorème Théorème de la limite monotone• Toute suite réel unnN croissante et majorée est convergent, et apour limite :limn→+un = supun : n N.Toute suite réel unnN croissante non-majorée diverge vers +.• Toute suite réel un décroissante et minorée converge, et a pour limite :limn→+un = infun : n N.Toute suite réel unnN décroissante et non-minorée diverge vers .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024158 / 277

Page 163 : Théorèmes d’existence d’une limiteDémonstration.Montrons le premier point. Supposons unnN majorée. L’ensembleA = un : n Nest alors une partie non vide majorée de R, donc possède une borne supérieure ℓdans R d’après la propriété de la borne supérieure.Montrons quelimn→+un = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024159 / 277

Page 164 : Théorèmes d’existence d’une limiteDémonstration.Soit ϵ 0, puisque ℓest la bornée supérieure de A, ℓϵ ne majore pas unnN,doncuN ℓϵ pour un certain N N.Or la suite est croissante, alors pour tout n N, nous avonsℓϵ uN unzcar ℓmajore Aℓ=⇒ℓϵ un ℓ+ ϵ.Ainsi un ℓ ϵ et on a montré que unnN converge vers ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024160 / 277

Page 165 : Théorèmes d’existence d’une limiteDémonstration.Supposons maintenant que unnN est non majorée. Soit M 0. PuisqueunnN est non majorée, il existe N N tel queuN M.Or, par hypothèse, la suite est croissante, donc pour tout n N, on aun uN M.Nous avons donc montré que unnN tend vers +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024161 / 277

Page 166 : Théorèmes d’existence d’une limiteExemple : Pour tout n N, on poseun =nXk=11k2 .Étudier la convergence de unnN.Solution : Commeun+1 un =n+1Xk=11k2 nXk=11k2 =1n + 12 +nXk=11k2 nXk=11k2 =1n + 12 0.la suite unnN est strictement croissante. De plusun = 1 +nXk=21k2 1 +nXk=21kk 1=1 +nXk=21k 1 1k=1 + 1 1n = 2 1n 2.Donc la suite unnNest majorée. Par le Théorème de la limite monotone,elle converge. Notons que ça limite est π26 !.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024162 / 277

Page 167 : Théorèmes d’existence d’une limiteNotre dérnier théorème d’existence est le Théorème des suites adjacentes.Commençons donc par introduire la notion de suites adjacentes.Déﬁnition Suites adjacentesOn dit que deux suites unnN et vnnN sont adjacentes si :• unnN est croissante ;• vnnN est décroissante ;•limn→+vn un = 0.Remarque : Deux suites adjacentes sont deux suites qui viennent à la rencontrel’une de l’autre, l’une en croissant, l’autre en décroissant, et qui ﬁnissent pars’écraser l’une contre l’autre.« Il faut bien qu’elles s’écrasent QUELQUE PART ! »nous dit le théorème des suites adjacentes.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024163 / 277

Page 168 : Théorèmes d’existence d’une limiteThéorème Théorème des suites adjacentesSoient unnN et vnnN deux suites adjacentes, avecunnN croissanteetvnnN décroissante.Alors unnN et vnnN convergent vers la même limite ℓ, c’est-à-direlimn→+un = ℓ=limn→+vn.De plus, pour tout n N, nous avonsun ℓvn.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024164 / 277

Page 169 : Théorèmes d’existence d’une limiteDémonstration.Soient unnN et vnnN deux suites adjacentes, avecunnN croissanteetvnnN décroissante.Notons que pour tout n N, nous avonsvn+1 un+1 vn un =vn+1 vnz0, car vn est décroissanteun+1 unz0, car un est croissante0.La suite vn unnN est donc décroissante. Comme, par hypothèse, elle converge vers0, on obtient que pour tout n N, nous avonsvn un 0=⇒un vn.Pour tout n N, on a doncu0 un vn v0.Ainsi, unnN est croissante et majorée par v0 et vnnN est décroissante et minoréepar u0. D’après le Théorème de la limite monotone, ces deux suites convergent, disonsvers ℓ1 et ℓ2. Il ne nous reste qu’à montrer l’égalité ℓ1 = ℓ2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024165 / 277

Page 170 : Théorèmes d’existence d’une limiteDémonstration.Commelimn→+un = ℓ1etlimn→+vn = ℓ2Par soustraction sur les limites, on conclutlimn→+vn un = ℓ2 ℓ1.Orlimn→+vn un = 0.Ainsi, par unicité de la limite, on obtient ℓ2 ℓ1 = 0, doncℓ1 = ℓ2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024166 / 277

Page 171 : Théorèmes d’existence d’une limiteExemple : Pour tout n N, on poseun =nXk=01k!etvn = un +1nn!.Établir que ces suites sont adjacentes.Solution :• On aun+1 un =n+1Xk=01k! nXk=01k! =1n + 1! +nXk=01k! nXk=01k! =1n + 1! 0.Donc la suite unnNest croissante.• On a aussivn+1 vn = un+1 un +1n + 1 · n + 1! 1n · n!=1nn + 1n + 1! 0.Donc la suite vnnNest décroissante.• vn unnN=1n·n!nNconverge clairement vers 0.Donc les suites unnNet vnnNsont adjacentes, donc convergent vers lamême limite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024167 / 277

Page 172 : Suites extraitesDéﬁnition ExtractionLorsque ϕ est une application de N dans N strictement croissante, on dit que ϕest une extraction.On vériﬁe par récurrence que toute extraction vériﬁe la propriété suivant.PropositionSi ϕ : N →N est strictement croissante, alors on a la propriétén N, ϕn n.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024168 / 277

Page 173 : Suites extraitesDéﬁnition Suite extraiteOn appelle suite extraite ou encore sous-suite de unnN toute suite de laformeuϕnnNoù ϕ : N →N est une extraction, c’est-à-dire, une fonction strictementcroissante.Exemple : L’application ϕ : n 7→n2 + 1 est une extraction ; la sous-suiteuϕnnN est la suite dont les termes sont : u1, u2, u5, u10, u17, etc.Une sous-suite de unnN est obtenue en sélectionnant une inﬁnité de termes deunnN, dans l’ordre, mais « pas forcément tous ».Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024169 / 277

Page 174 : Suites extraitesExemples :• Les suites5n + 3nnN et nnN sont deux suites extraites de la suite determe général n, associées respectivement aux extractions n 7→5n + 3n etn 7→n2.• Les suites constantes égales à 1 et 1 respectivement sont deux suitesextraites de la suite de terme général 1n, associées respectivement auxextractions n 7→2n et n 7→2n + 1.• Plus généralement, les suites u2nnN et u2n+1nN sont deux suitesextraites de unnN appelées suites extraites paire et impaire.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024170 / 277

Page 175 : Suites extraitesProposition Limites de suites extraitesSoit unnN une suite réelle et ℓR, +, .• Silimn→+un = ℓ, alors pour toute fonction ϕ : N →N strictementcroissante, nous avonslimn→+uϕn = ℓ.Autrement dit, toute suite extraite d’une suite unnN convergente,converge vers la même limite que unnN.• Silimn→+u2n =limn→+u2n+1 = ℓ, alorslimn→+un = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024171 / 277

Page 176 : Suites extraitesDémonstration.Montrons le premier point. Supposons ℓR. Soit ϵ 0. Par déﬁnition de lalimite, il existe N N tel quen N, n N un ℓ ϵ.Or pour tout n N, on aϕn n N=⇒uϕn ℓ ϵ=⇒limn→+uϕn = ℓ.Montrons le cas ℓ= +Même raisonnement dans le cas ℓ= . Pardéﬁnition de la limite, pour tout M R, il existe N N tel quen N, n N, un M.Or pour tout n N, on aϕn n N=⇒uϕn M=⇒limn→+uϕn = +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024172 / 277

Page 177 : Suites extraitesDémonstration.Montrons le point deux. Supposonslimn→+u2n =limn→+u2n+1 = ℓ. Soit ϵ 0. Pardéﬁnition de la limiteN1 N tel que n N1,u2n ℓ ϵ.N2 N tel que n N2,u2n+1 ℓ ϵ.Posons N = max2N1, 2N2 + 1, et soit n N.• Si n = 2k est pair avec k N, alors n = 2k N 2N1. Ce qui implique k N1,doncun ℓ = u2k ℓ ϵ.• Si n = 2k + 1 est impair avec k N, alors n = 2k + 1 N 2N2 + 1. Ce quiimplique k N2, doncun ℓ = u2k+1 ℓ ϵ.Dans le deux casun ℓ ϵ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024173 / 277

Page 178 : Suites extraitesRemarque : Ce théorème est souvent utilisé pour montrer qu’une suite n’a pasde limite. En eﬀet, si on trouve deux suites extraites de unnN qui neconvergent pas vers la même limite, alors unnN diverge.Exemples :• La suite un = 1nnN n’a pas de limite carlimn→+u2n =limn→+12n = 1par contrelimn→+u2n+1 =limn→+12n+1 = 1.• La suite vn =cosn π2n’a pas de limite carlimn→+v4n =limn→+cos 2nπ = 1par contrelimn→+v4n+1 =limn→+cosπ2 + 2nπ= 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024174 / 277

Page 179 : Suites récurrentes de la forme un+1 = funNous allons nous intéreser à présent aux suites récurrentes déﬁnies par :un+1 = fun,avec f une fonction à valeurs réelles déﬁnie sur un intervalle I.Remarque : Une telle relation de récurrence ne permet pas toujours de biendéﬁnir une suite. Par exemple, il n’existe pas de suite déﬁnie paru0 = 1etun+1 = fun = 2 + 1 un.En eﬀet, commefu0 = f1 = 2 +1 1 = 2,on peut poser u1 = 2. Mais ensuite f2? La fonction2 +1 xn’est pas déﬁnié en 2.Quelle valeur alors pour u2? La suite unnN n’est donc pas déﬁnie.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024175 / 277

Page 180 : Suites récurrentes de la forme un+1 = funLa proposition qui suit, nous donne une condition qui permet de garantirl’existence de suites récurrentes du type un+1 = fun.PropositionSoit f : I →R telle que I est stable par f, c’est à direfI I.Soit a I, alors il existe une unique suite unnN vériﬁant :u0=an N, un+1=fun.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024176 / 277

Page 181 : Suites récurrentes de la forme un+1 = funÉtudions quelques propriétés des suites récurrentes. Étudions d’abord lamonotonie d’une telle suite.Proposition MonotonieSoit f : I →R avec I stable par f et unnN déﬁnie paru0=a I,n N, un+1=fun.Nous avons :1. Si f est croissante sur I, alors la suite un est monotone :• Si fu0 u0 0, alors un est croissante.• Si fu0 u0 0, alors un est décroissante.2. Si f est décroissante sur I, alors les suites extraites u2nnN et u2n+1nNsont monotones et de monotonie contraire. Leurs sens de variationdépendent donc de la position de u0 par rapport de u2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024177 / 277

Page 182 : Suites récurrentes de la forme un+1 = funFigure – Suites récurrentes par une fonction croissante gauche et décroissantedroite.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024178 / 277

Page 183 : Suites récurrentes de la forme un+1 = funRemarques :• Pour déterminer la monotonie de unnN, il peut parfois être intéressantd’étudier le signe de x 7→fx x sur I. En eﬀet, supposons par exemplex I, fx x 0.Alors, pour tout n N, nous avonsun+1 un = fun un 0.Ainsi, unnN est croissante.• Pour tout n N, nous avonsfu2n = u2n+1=⇒u2n+2 = f ◦fu2n.Ainsi, u2nnN est récurrente associée à la fonction f ◦f. Même chosepour u2n+1nN.• Si f est décroissante alors f ◦f est croissante.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024179 / 277

Page 184 : Suites récurrentes de la forme un+1 = funDémonstration Monotonie.1 Supposons f est croissante. Si fu0 u0 0, alors u1 u0. Puisque f estcroissante, la relationun+2 un+1 = fun+1 funpermet alors de montrer par récurrence que unnN est croissante. En eﬀet,u1 u0=⇒u2 = fu1 fu0 = u1...=⇒un+1 = fun fun1 = un=⇒un+2 = fun+1 fun = un+1.De même, si fu0 u0 0, alors u1 u0. La relationun+1 un+2 = fun fun+1,nous permet comme dans le cas précédent de conclure que unnN estdécroissante.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024180 / 277

Page 185 : Suites récurrentes de la forme un+1 = funDémonstration Monotonie.2 Supposons f est décroissante. Posonsg = f ◦f.Cette application est croissante sur I. Soitvn = u2netwn = u2n+1.Alorsvn+1 = u2n+2 = fu2n+1 = ffu2n = gu2n = gvn.De mêmewn+1 = gwn.Ainsi, vnnN est récurrente associée à la fonction g. Même chose pourwnnN. Le point 1, permet alors d’en déduire que chacune des suites vnnNet wnnN est monotone.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024181 / 277

Page 186 : Suites récurrentes de la forme un+1 = funDémonstration Monotonie.Si par exemple nous supposons que vnnN est croissante. On peut donc écrire,pour toutn N,vn vn+1.Maintenant comme f décroissante, on en déduitfvn fvn+1.Or u2n = vn et u2n+2 = vn+1, doncu2n+1 = fu2n fu2n+2 = u2n+3=⇒wn wn+1.La suite wnnN est donc décroissante.Finalement, si l’on suppose que vnnN est décroissante, le même raisonnementnous permet de déduire que wnnN est croissante.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024182 / 277

Page 187 : Suites récurrentes de la forme un+1 = funÉtudions maintenant la convergence des suites récurrentes.Proposition ConvergenceSoit f : I →R avec I stable par f et unnN déﬁnie paru0=a I,n N, un+1=fun.Si f est continue sur I et si unnN converge vers ℓ, alorsfℓ = ℓ.On dit que ℓest un point ﬁxe de f.Remarque : Pour déterminer les points ﬁxes de f, il peut parfois être intéressantd’étudier les points d’annulation dex 7→fx x sur I.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024183 / 277

Page 188 : Suites complexesDans le cours d’algèbre vous avez commence à étudier l’ensemble des nombrescomplexes C. Dans cette section nous allons étendre la notion de suite réel auxnombres complexes.Déﬁnition Suite complexeUne suite complexe u est une fonction de N dans Cu : N→Cn7→un.Pour tout n N, on préfère noterun le complexe un.La suite est notée u, ou plus souvent unnN ou unn0, ou simplement un.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024184 / 277

Page 189 : Suites complexesOn peut se demander dans quelle mesure les déﬁnitions et les théorèmes de cechapitre peuvent-ils être étendus aux suites complexes. En tout cas, nous n’avonspas droit aux inégalités dans C, donc une suite complexe ne peut pas êtremajorée, minorée ou motonone. Par contre, les propriétés faisant intervenir lavaleur absolue seront étendues en la remplaçant par le module.Déﬁnition Suite bornéeSoit unnN une suite complexe. On dit que unnN est bornée s’il existeM 0 tel que pour tout n N, nous avonsun M.où un est le module du complexe un.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024185 / 277

Page 190 : Suites complexesÀ l’aide du module nous pouvons étendre la notion de limite aux suites complexes.Déﬁnition Limite d’une suite complexeSoit unnN une suite complexe. On dit que unnN converge vers ℓC siϵ 0, N N, n Nn N =⇒un l ϵ.Le théorème d’unicité de la limite est encore valable, ce qui autorise la notationlimn→+un = ℓ.Remarques :• Il n’existe pas de limite inﬁnie. En eﬀet, la notion de limite inﬁnie n’a aucunsens pour une suite complexe. Ils sont où et +dans C ?• Nous avonslimn→+un = ℓdans C⇐⇒limn→+un ℓ = 0 dans R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024186 / 277

Page 191 : Suites complexesThéorème Caractérisation de la limite par les parties réelle etimaginaireSoit unnN une suite complexe et ℓC. Nous avonslimn→+un = ℓ.si et seulement silimn→+Reun = Reℓ etlimn→+Imun = Imℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024187 / 277

Page 192 : Suites complexesDémonstration.Supposons limn→+un = ℓ. Pour tout n N, nous avons0 Reun Reℓ = Reun ℓ un ℓ,orlimn→+un ℓ = 0, donclimn→+Reun = Reℓ,par le Théorème d’encadrement. Même raisonnement pour conclurelimn→+Imun = Imℓ.Supposonslimn→+Reun = Reℓ etlimn→+Imun = Imℓ, alors par des opérationssur les limites réelsun ℓ =qReun Reℓ2 + Imun Imℓ2→n→+p02 + 02 = 0,donc, limn→+un = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024188 / 277

Page 193 : Suites complexesGrâce au résultat précédent nous pouvons conclure :• Il est toujours vrai qu’une suite convergente est bornée.• Les opérations d’addition, produit, multiplication par un scalaire etinverse sur les limites donnent lieu aux mêmes résultats que dans le cas réel,à ceci près que les symboles +et sont bannis. Nous avons de plus lerésultat suivant :Silimn→+un = ℓ,alorslimn→+un = ℓ.• Le résultats sur les suites extraites sont intégralement maintenus.En résumé :Ce qui reste valable :Ce qui n’est plus valable :Unicité de la limiteMajorant/minorantUne suite convergente est bornéeMonotonieOpérations sur les limitesLimites inﬁniesSuites extraitesPassage à la limite des inégalitésThéorème d’EncadrementThéorème de la limite monotoneSuites adjacentesNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024189 / 277

Page 194 : Chapitre 3 - Limites et continuité de fonctions• Généralités sur les fonctions.• Limite d’une fonction :• Limite en un point.• Limite à droite, à gauche.• Opérations sur les limites.• Théorèmes d’existence de limites.• Continuité :• Déﬁnition.• Prolongement par continuité.• Caractérisation séquentielle de la continuité.• Opérations sur les fonctions continues.• Les grands théorèmes de la continuité :• Théorème des valeurs intermédiaires.• Image d’un segment.• Théorème de la bijection.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024190 / 277

Page 195 : Généralités sur les fonctionsTout ce que vous avez étudié sur les applications dans le cours d’algèbre, nousallons l’appliquer dans ce chapitre. Rappelons certaines notions.DéﬁnitionSoit E une partie de R etf : E →Rx 7→fx,une fonction à valeurs réels.• L’ensemble E est appelé l’ensemble de départ ou domaine de déﬁnitionde f.• Pour tous x E et y R, si y = fx, on dit que :• y est l’image de x par f.• x est un antécédent de y par f pas forcément unique.Remarque : Étant donné une fonction f, il faudra toujours commencer parpréciser le domaine de déﬁnition de f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024191 / 277

Page 196 : Généralités sur les fonctionsRappelons du cours d’algèbre, les notions d’image directe et image reciproque.Déﬁnition Image directe - Image reciproqueSoit f : E →R une fonction à valeurs réels.• Pour toute partie A de E, on appelle image directe de A par f, notée fA,l’ensemble :fA = y R : a A, y = fa = fa : a A.• L’image de E tout entier est simplement appelée l’image de f et est notéegénéralementImf plutôt que fE.• Soit B une partie de R. Si toute valeur de f est élément de Bi.e. Imf B. Alorson dit que f est à valeurs dans B.• Pour toute partie B de R, on appelle image réciproque de B par f, notée f 1B,l’ensemble des éléments de E dont l’image est dans B :f 1B = x E, fx B.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024192 / 277

Page 197 : Généralités sur les fonctionsSur l’ensemble des fonctions réels nous pouvons déﬁnir les opérations suivants.Déﬁnition Opérations sur le fonctions réelsSoit f et g deux fonctions déﬁnies sur un intervalle commun I.• La somme de f et g est la fonction notée f + g déﬁnie pour tout x I parf + gx = fx + gx.• Le produit de f et g est la fonction notée f · g déﬁnie pour tout x I parf · gx = fx · gx.• Supposons de plus que g ne s’annule pas sur I. Le quotient de f par g est lafonction notée fg déﬁnie pour tout x I par :fgx = fxgx .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024193 / 277

Page 198 : Généralités sur les fonctionsLa dernière opération à introduire sur l’ensemble de fonctions est la composition.Déﬁnition CompositionSoit E et F deux parties de R etf : E →Retg : F →Rdeux fonctions. On suppose f à valeurs dans F. On appelle composée de fsuivie de g la fonction g ◦f déﬁnie sur E par :g ◦fx = gfx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024194 / 277

Page 199 : Généralités sur les fonctionsRemarques :• La composition, en général, n’est possible que dans un seul sens, et quandelle est possible dans les deux, on n’a aucune raison d’avoir :f ◦g = g ◦f.• La composition est associative : Soitf : E →R;g : F →R;h : G →Rtrois fonction à valeurs réels avecImf FetImg G.Alors :h ◦g ◦f = h ◦g ◦f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024195 / 277

Page 200 : Fonction paire, Fonction impaireRappelons la notion de fonction paire/impaire.Déﬁnition Partie SymétriqueSoit A une partie de R. Alors on dit que A est symétrique par rapport à 0, six A,x A.Déﬁnition Fonction paire, Fonction impaireSupposons A est une partie symétrique de R. Soit f : A →R une fonction.• On dit que f est paire six A,fx = fx.• On dit que f est impaire six A,fx = fx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024196 / 277

Page 201 : Fonction paire, Fonction impaireExemples :• Les fonctionsx 7→x2;x 7→x;x 7→cos xsont paires.• Les fonctionsx 7→3x;x 7→x3;x 7→1/x;x 7→sin xsont impaires.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024197 / 277

Page 202 : Fonction paire, Fonction impaireRemarques :• Si f est paire, alors le graphe de f est symétrique par rapport à l’axe desordonnées.• Si f est impaire, alors le graphe de f est symétrique par rapport à l’origine.• Pas besoin d’étudier une fonction f : A →R paire ou impaire sur A toutentier, une étude sur A R+ suﬃt.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024198 / 277

Page 203 : Fonction périodiqueRappelons maintenant la notion de fonction périodique.Déﬁnition Partie T-périodiqueSoit T 0 et A une partie de R. Alors on dit que A T-périodique, six A,x + T Aetx T A.Déﬁnition Fonction périodiqueSoit T 0 et A une partie de R, T-périodique. Soit f : A →R une fonction. Ondit que f est T-périodique ou périodique de période T six A,fx + T = fx.Le réel T est alors appelé une période de f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024199 / 277

Page 204 : Fonction périodiqueExemple :• Les fonctions cosinus et sinus sont 2π-périodiques, la fonction tangente estπ-périodique.• La fonctionx 7→x Exest périodique de période 1.Remarque : Pas besoin d’étudier une fonction f : A →R périodique sur A toutentier, une étude sur une période suﬃt, par exemple sur l’ensembleA T, T.C’est-à dire, si la fonction est T-périodique, on restreindra son étude à unsegment de longueur T et on complétera la courbe par translation.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024200 / 277

Page 205 : Fonctions et relation d’ordreÉtudions quelques propriétés eventuelles des fonctions à valeurs réels.Commençons par nous intéresser à des fonctions qui préservent ou inversent larelation d’ordre usuel sur R.Déﬁnition Fonction croissante, Fonction décroissanteSoit A une partie de R et f : A →R une fonction.• On dit que f est croissante resp. strictement croissante, six A, y A,x y =⇒fx fyresp. fx fy.• On dit que f est décroissante resp. strictement croissante, six A, y A,x y =⇒fx fyresp. fx fy.• On dit que f est resp. strictement monotone, si f est resp. strictementcroissante ou décroissante.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024201 / 277

Page 206 : Fonctions et relations d’ordreExemples :• La fonction x 7→2x + 1 est strictement croissant sur R.• La fonction x 7→3x + 1 est strictement décroissant sur R.• La fonction x 7→1/x est strictement décroissant sur 0, +.• La fonction x 7→x2 est strictement croissant sur 0, + et strictementdécroissant sur , 0.• La fonction x 7→ex est strictement croissant sur R.• La fonction x 7→ln x est strictement croissant sur 0, +.• La fonction cosinus est strictement décroissante sur tout intervalle de la forme2kπ, 2k + 1π, k Zet strictement croissante sur tout intervalle de la forme2k + 1π, 2k + 2π, k Z.Mais elle n’est pas monotone sur R.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024202 / 277

Page 207 : Fonctions et relations d’ordreDéﬁnition Majorée, Minorée, BornéeSoit A une partie de R et f : A →R une fonction.• On dit que f est majorée sur A siexiste M R, tel que pour tout x A, fx M.Le réel M est appelé un majorant de f.• On dit que f est minorée sur A siexiste m R, tel que pour tout x A, fx m.Le réel m est appelé un minorant de f.• On dit que f est bornée sur A, si f est à la fois majorée et minorée sur A.Exemple :• Les fonctions cosinus et sinus sont majorées par 1 et minorées par -1.• La fonction x 7→11+x2 est majorée par 1 et minorée par 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024203 / 277

Page 208 : Fonctions et relations d’ordreDéﬁnition Maximum, MinimumSoit A une partie de R, f : A →R une fonction et x0 I A.• On dit que f admet un maximum global en x0, si pour tout x Afx fx0.• On dit que f admet un minimum global en x0 si pour tout x Afx fx0.• On dit que f admet un maximum local en x0, si pour tout x Ifx fx0.• On dit que f admet un minimum local en x0, si pour tout x Ifx fx0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024204 / 277

Page 209 : Fonctions et relation d’ordreExemples :• La fonction cosinus admet un maximun global, en tout point de la forme :x = 2kπ, k Z.• La fonction sinus admet un minimun global, en tout point de la forme :x = 3π2 + 2kπ, k Z.• La fonctionfx =11 + x2 ,admet un maximum global en 0. En eﬀetx R,11 + x2 f0 = 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024205 / 277

Page 210 : Limites d’une fonctionPassons maintenant à étudier la notion de limite de une fonction. Pour cela,dans tout ce qui suit, l’ensemble I désignera un intervalle de R non vide et nonréduit à un point. On notera :•◦I = I \ extrémités de I.• ¯I = I extrémités de I.Exemples :• Nous avons◦a, b = a, b;◦a, b = a, b;◦a, b = a, b.• Nous avonsa, b = a, b;a, b = a, b;a, b = a, b.• Nous avons◦a, + =◦a, + = a, +eta, + = a, + = a, ++.• Nous avons◦R = R;R = R , +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024206 / 277

Page 211 : Limites d’une fonctionCommençons par donner une déﬁnition provisoire mais très intuitive de la limitede une fonction.Déﬁnition ProvisoireSoit f : I →R et a un réel appartenant à I. On dit quef admet une limite ﬁnie ℓR en asi fx est proche d’aussi près que l’on veux de ℓpour x suﬃsamment prochede a.Avec cette déﬁnition, étudions la limite de la fonctionf : x 7→x2.en a = 3. Vraisemblablementquand x tend vers 3, la fonction fx = x2 tend vers 9.Selon notre déﬁnition provisoire, pour montrer la convergence de la fonction vers9 en 3, on doit vériﬁer que x2 est proche d’aussi près que l’on veux de 9, lorsque xest suﬃsamment proche de 3.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024207 / 277

Page 212 : Limites d’une fonctionPar exemple, supposons qu’on veut que x2 soit à une distance de1100 de 9. Pourcela, on doit avoir9 1100 fx 9 +1100,ce qui est équivalent àfx 9 1100.Et cette dernière inégalité est vraie, si et seulement six2 9 1100 ⇐⇒x 3 · x + 3 1100Maintenant, comme on se intéresse ici à x proche de 3, nous pouvons supposerx 3 1=⇒1 x 3 1=⇒2 x 4=⇒5 x + 3 7.Ainsix2 9 = x 3 · x + 3 7 x 3 .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024208 / 277

Page 213 : Limites d’une fonctionPar conséquent, six 3 1700alorsx2 9 7700 =1100.Notons qu’il n’a rien de spécial sur1100, si l’on veut quex2 9 ϵpour ϵ un réel positif,il suﬃt quex 3 ϵ7.Ainsi, on vient de démontrer que fx est proche d’aussi près que l’on veux de 9,lorsque x est suﬃsamment proche de 3.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024209 / 277

Page 214 : Limites d’une fonctionFormalisons notre déﬁnition provisoire de limite, on commence par faire plusprécise la notion :« d’être proche de »Dans notre exemple, nous avons vu que pour que fx soit proche de 9, il fautque la distancefx 9soit petit.Ainsi, le premier changement qu’on va faire à notre déﬁnition provisoire est :Déﬁnition Provisoire 2Soit f : I →R et a un réel appartenant à I. On dit quef admet une limite ﬁnie ℓR en asi fx ℓ est aussi petit que l’on veut pour x suﬃsamment proche de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024210 / 277

Page 215 : Limites d’une fonctionMaintenant, dans notre exemple nous avons vu que, pour quefx 9 soit aussi petit que l’on veut,pour tout ϵ 0, on doit avoirfx 9 ϵlorsque x est suﬃsament proche de 3.Le deuxième changement qu’on va faire à notre déﬁnition provisoire est donc :Déﬁnition Provisoire 3Soit f : I →R et a un réel appartenant à I. On dit quef admet une limite ﬁnie ℓR en asi pour tout ϵ 0, on afx ℓ ϵ,lorsque x est suﬃsamment proche de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024211 / 277

Page 216 : Limites d’une fonctionIl ne nous reste donc qu’a faire plus précise la phrase :« pour x suﬃsamment proche de 3 »Dans notre exemple, nous avons vu quefx 9 1100⇐⇒x 3 1700.Ainsi, la propriété est vraie pour tout x R, avec x 3 1700. De même, pourtout ϵ 0, nous avonsfx 9 ϵ⇐⇒x 3 ϵ7.Donc pour tout ϵ 0, il existe un réel strictement positifδ 0,il suﬃt de prendre δ = ϵ7,tel que pour tout x R, x 3 δ la propriété est vraie.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024212 / 277

Page 217 : Limites d’une fonctionOn est à présent prêt pour donner la déﬁnition de la limite d’une fonction.Déﬁnition Limite en un pointSoit f : I →R et a un réel appartenant à I. On dit que :• f admet une limite ﬁnie ℓR en a, siϵ 0, δ 0, x I, x a δ =⇒fx ℓ ϵ.• f admet pour limite +en a, siM 0, δ 0, x I, x a δ =⇒fx M.• f admet pour limite en a, siM 0, δ 0, x I, x a δ =⇒fx M.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024213 / 277

Page 218 : Limites d’une fonctionRemarque : Dire que f tend vers ℓen a, c’est dire quePour tout ϵ 0, l’écart entre fx et ℓest strictement inférieur à ϵ dès que x estassez proche de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024214 / 277

Page 219 : Limites d’une fonctionRemarque :• l’écart δ dépend de ϵ : intuitivement, « plus ϵ est petit, plus il faudra que xsoit proche de a pour avoir fx ℓ ϵ ».• l’écart δ dépend aussi de a : intuitivement, si f a des variations « brusques »au voisinage de a, l’écart δ nécessaire n’est pas le même que si f a desvariations « douces » au voisinage de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024215 / 277

Page 220 : Limites d’une fonctionExemple : f admet pour limite +en aNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024216 / 277

Page 221 : Limites d’une fonctionÉtendons la déﬁnition de limite de une fonction au cas ou a = +.Déﬁnition Limite en +Soit f : I →R. On suppose que +est une extrémité de I. On dit que :• f admet une limite ﬁnie ℓR en +, siϵ 0, A 0, x I, x A =⇒fx ℓ ϵ.• f admet pour limite +en +, siM 0, A 0, x I, x A =⇒fx M.• f admet pour limite en +, si :N 0, A 0, x I, x A =⇒fx N.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024217 / 277

Page 222 : Limites d’une fonctionExemples :• Soitfx =x2x2 + 1.Alors f admet 1 comme limite en +.• Soitfx =exx3 + 3x.Alors f admet +comme limite en +.• Soitfx = lnxx.Alors f admet 0 comme limite en +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024218 / 277

Page 223 : Limites d’une fonctionFaisons de même lorsque a = .Déﬁnition Limite en Soit f : I →R. On suppose que est une extrémité de I. On dit que :• f admet une limite ﬁnie ℓR en , siϵ 0, B 0, x I, x B =⇒fx ℓ ϵ.• f admet pour limite +en , siM 0, B 0, x I, x B =⇒fx M.• f admet pour limite en , siN 0, B 0, x I, x B =⇒fx N.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024219 / 277

Page 224 : Limites d’une fonctionExemples :• Soitfx =x3x2 + 1.Alors f admet comme limite en .• Soitfx = ex.Alors f admet 0 comme limite en .• Soitfx = x5 + 1x3 + 1.Alors f admet +comme limite en .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024220 / 277

Page 225 : Limites d’une fonctionNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024221 / 277

Page 226 : Limites d’une fonctionRemarque : Soit f : I →R et a ¯I. Supposons ℓR. Alorsfx →x→a ℓ⇐⇒fx ℓ →x→a 0.En particulierfx →x→a 0⇐⇒fx →x→a 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024222 / 277

Page 227 : Unicité de la limiteSi elle existe, on va pouvoir parler de la limite, car il y a unicité :Proposition Unicité de la limiteSoit f : I →R, a I. Si f admet une limite en a, cette limite est alors uniqueet notéelimx→a fxoulima f.Notation : Pour tout ℓR, la relation limx→a fx = ℓest souvent notée :fx →x→a ℓouf →aℓNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024223 / 277

Page 228 : Unicité de la limiteDémonstration.On fait la preuve dans le cas où a R et la limite et ﬁnie. Elle s’adapte facilementaux autres cas.Raisonnons par l’absurde et supposons que f admet deux limites ℓ1 et ℓ2distinctes en a. Posonsϵ = ℓ1 ℓ23 0.Par déﬁnition de la limite en a, nous avonsδ1 0, x I, x a δ1=⇒fx ℓ1 ϵδ2 0, x I, x a δ2=⇒fx ℓ2 ϵSoit δ0 = minδ1, δ2. Alors pour tout x I avec x a δ0, nous avonsfx ℓ1 ϵetfx ℓ2 ϵ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024224 / 277

Page 229 : Propriétés de la limite d’une fonctionDémonstration.Ainsi, à l’aide de l’inégalité triangulaire, nous pouvons écrireℓ1 ℓ2=ℓ1 fx + fx ℓ2fx ℓ1 + fx ℓ2ϵ + ϵ=2ℓ1 ℓ23.Ce qui est absurde. Par conséquent, ℓ1 = ℓ2. D’où le résultat.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024225 / 277

Page 230 : Propriétés de la limite d’une fonctionÉtudions quelques propriétés de la limite.PropositionSoit f : I →R, a ¯I et ℓR. Si limx→a fx = ℓ, alorslimx→a fx = ℓ.Démonstration.On fait la preuve dans le cas où a R. Elle s’adapte facilement aux autres cas.Supposons a R, et soit ϵ 0. Par déﬁnition de la limite en a, nous avonsη 0, x I, x a η=⇒fx ℓ ϵ.Ainsi, d’après l’inégalité triangulaire, pour tout x Ia η, a + η, nous avons fx ℓ fx ℓ ϵ=⇒limx→a fx = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024226 / 277

Page 231 : Propriétés de la limite d’une fonctionAvant de continuer avec notre étude de la limite, introduisons la notion de voisinage.Déﬁnition VoisinageSoit a I. Si a R, alors on dit qu’une fonction f : I →R satisfait la propriété Pxdans un voisinage de a, siδ 0, x a δ, a + δ I=⇒Px est vraie.c’est-à-direδ 0, x I, x a δ=⇒Px est vraie.Si a = +, alors on dit qu’une fonction f : I →R satisfait la propriété Px dans unvoisinage de a, siA 0, x I, x A=⇒Px est vraie.Si a = , alors on dit qu’une fonction f : I →R satisfait la propriété Px dans unvoisinage de a, siB 0, x I, x B=⇒Px est vraie.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024227 / 277

Page 232 : Propriétés de la limite d’une fonctionPropositionSoit f : I →R et a I. Si f admet une limite ﬁnie en a, alors f est bornée auvoisinage de a, c’est-à-dire :• si a R alorsm R, M R, δ 0, x I, x a δ=⇒m fx M.• si a = +alorsm R, M R, A 0, x I, x A=⇒m fx M.• si a = alorsm R, M R, B 0, x I, x B=⇒m fx M.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024228 / 277

Page 233 : Propriétés de la limite d’une fonctionDémonstration.On fait la preuve dans le cas où a R. Elle s’adapte facilement aux autres cas.Notons ℓ= limx→a fx. D’après la déﬁnition de la limite, pour ϵ = 1, nous avonsδ 0, x I, x a δ=⇒fx ℓ 1.Ainsi, pour x Ia δ, a + δ, nous pouvons écrirefx = fx ℓ+ ℓfx ℓ + ℓinégalité triangulaire1 + ℓ.Par conséquent, f est bien bornée au voisinage de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024229 / 277

Page 234 : Propriétés de la limite d’une fonctionRemarques :• Si f : I →R admet une limite ℓ 0 en a R, alors f est minorée auvoisinage de a par un nombre strictement positif :m 0, δ 0, x I, x a δ=⇒fx m.• Si f : I →R admet une limite ℓ 0 en a R, alors f est majorée auvoisinage de a par un nombre strictement negatif :m 0, δ 0, x I, x a δ=⇒fx m.• Si f : I →R admet une limite non nulle en a R, alors f est non nulle auvoisinage de a :δ 0, x I, x a δ=⇒fx ̸= 0.On a les mêmes résultats lorsque a = ±.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024230 / 277

Page 235 : Limites à gauche - Limites à droiteDéﬁnition Limites à gauche et à droiteSoit f : I →R et a ◦I.• On dit que f admet une limite à gauche en a, si la restrictionfI,aadmet une limite en a. Cette limite est alors notée :limx→afxoulimx→axafx.• On dit que f admet une limite à droite en a, si la restrictionfIa,+admet une limite en a. Cette limite est alors notée :limx→a+ fxoulimx→axafx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024231 / 277

Page 236 : Limites à gauche - Limites à droiteRemarque : Les limites à gauche/à droite ne sont jamais que des limites au sensinitial du chapitre mais appliquées à des restrictions. Cela justiﬁe leur unicité et lapossibilité que nous avons de leur accorder une notation. Ainsi• Pour tout ℓR, dire que : ℓ= limx→af revient donc à dire que :ϵ 0, δ 0, x I, a δ x a=⇒fx ℓ ϵsi ℓR,A 0, δ 0, x I, a δ x a=⇒A fxsi ℓ= +,B 0, δ 0, x I, a δ x a=⇒fx Bsi ℓ= .• Pour tout ℓR, dire que : ℓ= limx→a+ f revient donc à dire que :ϵ 0, δ 0, x I, a x a + δ=⇒fx ℓ ϵsi ℓR,A 0, δ 0, x I, a x a + δ=⇒A fxsi ℓ= +,B 0, δ 0, x I, a x a + δ=⇒fx Bsi ℓ= .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024232 / 277

Page 237 : Limites à gauche - Limites à droitePropositionSoit f : I →R et a ◦I. Supposons ℓR, alorslimx→a fx = ℓ⇐⇒limx→afx = limx→a+ fx = ℓetfa = ℓ.Remarque : Dans l’implicationlimx→afx = limx→a+ fx = ℓet fa = ℓ=⇒limx→a fx = ℓ,l’hypothèse ℓ= fa est primordial. Si on ne suppose pas ℓ= fa, alorsl’implicationlimx→afx = limx→a+ fx = ℓ=⇒limx→a fx = ℓ,est fausse.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024233 / 277

Page 238 : Limites à gauche - Limites à droiteEn eﬀet, considérons f déﬁnie sur R parfx = 0si x R1si x = 0.On a bienlimx→0fx = limx→0+ fx = 0.Ainsi, par la proposition précédente, si f a une limite en 0, celle ci doitnécessairement être 0. Posons ϵ = 12. Alors pour tout δ 0, on a0 = 0 0 δ,alors quef0 0 = 1 ϵ.La fonction f n’admet donc pas 0 comme limite et n’admet donc pas de limite en0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024234 / 277

Page 239 : Caractérisation séquentielle de la limiteLes limites d’une fonction peuvent être exprimé à l’aide de la limite de suites numériques.Théorème Caractérisation séquentielle de la limiteSoit f : I →R, ℓR et a ¯I. Les assertions suivantes sont équivalentes :• limx→a fx = ℓ.• Pour toute suite unnN à valeurs dans I, tel quelimn→+un = a, nous avonslimn→+fun = ℓ.Remarques :• Le théorème précédente contient en particulier le théorème « Composition àgauche par une fonction » de notre précédent chapitre.• Notons que pour utiliser l’implication ⇐= du théorème, il ne suﬃt pas de montrerque c’est vrai pour une seule suite, mais pour toutes les suites. Cela rend cetteimplication diﬃcile à utiliser sauf dans le cadre d’exercices « théoriques ». Cethéorème est surtout utile pour étendre certaines propriétés étudiées dans lechapitre limite d’une suite au cas de limites d’une fonction.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024235 / 277

Page 240 : Caractérisation séquentielle de la limiteDémonstration.On fait la preuve dans le cas où a R. Elle s’adapte facilement aux autres cas.=⇒Supposons que limx→a fx = ℓ. Fixons ϵ 0. D’après la déﬁtion de la limiteη 0, x I, x a η=⇒fx ℓ ϵ.Soit unnN telle quelimn→+un = a. Maintenant, par déﬁnition de la limited’une suiteN N, n N, n N=⇒un a η=⇒fun ℓ ϵ.Ainsilimn→+fun = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024236 / 277

Page 241 : Caractérisation séquentielle de la limiteDémonstration.⇐= Pour montrer la réciproque, nous allons procéder par contraposition.Supposons donc que f ne tend pas vers ℓquand x tend vers a. Ainsiϵ 0, η 0, x I, x a η et fx ℓ ϵ.3On doit montrer qu’il existe une suite xnnN telle quelimn→+xn = a, alors quefxnnN ne converge pas vers ℓ.Puisque f ne tend pas vers ℓquand x tend vers a, on peut d’après 3, pourchaque n N, trouver xn I, tel quexn a 1net fxn ℓ ϵ.Considérons la suite xnnN ainsi déﬁnie, alors il est clair quefxnnN ne converge pas vers ℓ.Ce qui montre la contraposé de notre implication.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024237 / 277

Page 242 : Caractérisation séquentielle de la limiteRemarque : La caractérisation séquentielle de la limite est souvent utilisépour montrer qu’une fonction n’admet pas de limite en a. En eﬀet, si on trouvedeux suites xnnN et ynnN qui tendent vers a et telles quefxnnNetfynnNont deux limites diﬀérentes, alors la fonction f n’a pas de limite en a.Exemples :• La fonctionx 7→fx = cosxn’a pas de limite en +. En eﬀet, les suitesxnnN = 2πnnNetynnN = π + 2nπnNdivergent vers +, maislimn→+fxn=limn→+cos2πn = 1etlimn→+fyn=limn→+cosπ + 2πn = 1Donc, f n’a pas de limite en +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024238 / 277

Page 243 : Caractérisation séquentielle de la limite• La fonctionx 7→fx = 1x sin 1xn’a pas de limite en 0+. En eﬀet, pour tout n 1, posonsun =1π/2 + 2nπetvn =12nπ .Alorslimn→+un =limn→+vn = 0, maisf1π/2 + 2nπ=π/2 + 2nπ · sin π/2 + 2nπ = π/2 + 2nπf 12nπ=2nπ · sin 2nπ = 0Donclimn→+fun = +etlimn→+fvn = 0.Donc, f n’a pas de limite en 0+.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024239 / 277

Page 244 : Opérations sur les limites d’une fonctionIl se passe avec les fonctions, la même chose qu’avec les suites pour les opérationsde somme, produit, multiplication par un scalaire et inverse. En particulier, mêmesformes indéterminées. Résumons ceci par les tableaux suivants.Limite de fx + gx en a Ilimx→a fxℓℓℓ++limx→a gxℓ′++limx→afx + gxℓ+ ℓ′++FormeindeterminéeLimite de fx · gx en a Ilimx→a fxℓℓ 0ℓ 0++0limx→a gxℓ′±±+±limx→afx · gxℓ· ℓ′±++FormeindeterminéeNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024240 / 277

Page 245 : Opérations sur les limites d’une fonctionLimite de λfx en a Iλ Rλ = 0λ 0limx→a fx+ℓ̸= 0peu importe+ℓ̸= 0limx→a λfx+λℓ0λℓ+Limite de1fxen a Ifx 0dans unvoisinage de afx 0dans unvoisinage de asinonlimx→a fxℓ̸= 0±000limx→a1fx1ℓ0+Forme indeterminéeNicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024241 / 277

Page 246 : Opérations sur les limites d’une fonctionLa dernière opération à étudier sur les limites, est la composition.Proposition Composition des limitesSoit f : I →R et g : J →R telles que fI J, et a I. Silimx→a fx = betlimy→b gy = calorslimx→ag ◦fx = c.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024242 / 277

Page 247 : Opérations sur les limites d’une fonctionDémonstration.Faisons la preuve dans le cas où a, b et c sont des réels. Elle s’adapte facilementaux autres cas.Soit ϵ 0. Par déﬁnition de la limite de g, nous avonsδ 0, y J, y b δ=⇒gy c ϵ.Maintenant, par déﬁnition de la limite de f, on aη 0, x I, x a η=⇒fx b δ.On a donc pour tout x I avec x a η , l’inégalitégfx c ϵ.Par conséquentlimx→ag ◦fx = c.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024243 / 277

Page 248 : Passage à la limite dans une inégalitéComme pour les suites, nous pouvons décrire le comportement des limites d’unefonction par rapport à la relation d’ordre sur R.Proposition Passage à la limite dans les inégalités strictesSoit a I et f : I →R une fonction possedant une limite ℓen a. Soientm, M R.• Si ℓ M, alorsfx M,dans un voisinage de a.• Si ℓ m, alorsfx m,dans un voisinage de a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024244 / 277

Page 249 : Passage à la limite dans une inégalitéDémonstration.Prouvons le première point, le deuxieme point se montre de la même façon.Suppsons ℓ M.• Si ℓ= , alors par déﬁnition de la limiteδ 0, x I, x a δ=⇒fx M.C’est-à-dire, fx M dans le voisinage de a donné par a δ, a + δ I.• Si ℓR, sachant que M ℓ 0 on peut, d’après la déﬁnition de la limite,conclureδ 0, x I, x a δ=⇒fx ℓ M ℓ.Ainsix I, x a δ,ℓM fx ℓ M ℓ=⇒fx M.C’est-à-dire, fx M dans le voisinage de a donné par a δ, a + δ I.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024245 / 277

Page 250 : Passage à la limite dans une inégalitéProposition Passage à la limite dans les inégalités largesSoient f et g deux fonctions déﬁnies sur I à valeurs dans R et a I. Supposons• limx→a fx = ℓRetlimx→a gx = ℓ′ R,• fx gx dans un voisinage de a.Alors ℓℓ′, c’est-à-direlimx→a fx limx→a gx.Remarque : On retiendra que les inégalités strictes deviennent larges en passant àla limite. Par exemple, pour toutx R,11 + x2 0,maislimx→+11 + x2 = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024246 / 277

Page 251 : Passage à la limite dans une inégalitéDémonstration.Faisons la preuve dans le cas où a est un réel. Elle s’adapte facilement aux autres cas.Par l’absurde. Supposons doncδ 0, x I, x a δ,fx gx.etlimx→a fx limx→a gx.Ainsi, fx gx 0 dans un voisinage de a etlimx→a fx gx 0.Or la proposition sur le passage à la limite dans les inégalités strictes montre quefx gx 0dans un voisinage de a. Contradiction ! Par conséquent, limx→a fx limx→a gx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024247 / 277

Page 252 : Théorèmes d’existence de limitesLes théorèmes• d’Encadrement,• de Minoration/Majoration,• de la limite monotone,que nous avons vu dans le chapitre sur les suites réels, restent valides dans le casde limites d’une fonction.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024248 / 277

Page 253 : Théorèmes d’existence de limitesThéorème Théorème d’encadrementSoient f, g et h trois fonctions de I dans R, ℓR et a I. Supposons• limx→a fx = ℓ= limx→a hx,• fx gx hx dans un voisinage de a.Alorslimx→a gx = ℓ.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024249 / 277

Page 254 : Théorèmes d’existence de limitesComme corollaire du Théorème d’encadrement nous avons le resultat suivant.CorollaireSoient f et g deux fonctions de I dans R et a I. Supposons• fx →x→a 0.• il existe m R, M R, tel que m gx M dans un voisinage de ai.e. g est bornée au voisinage de a.Alorslimx→a fx · gx = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024250 / 277

Page 255 : Théorèmes d’existence de limitesExemple : Déterminer si elle existe la limite en 0 def : R→Rx 7→x sin 1x.Solution : Nous avons :• La fonction x 7→x tend vers 0 lorsque x tend vers 0.• La fonction x 7→sin 1xest une fonction bornée au voisinage de 0.Ainsi, d’après la proposition précédente, on en déduit l’égalitélimx→0 fx = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024251 / 277

Page 256 : Théorèmes d’existence de limitesThéorème Théorème de Minoration/MajorationSoient f et g deux fonctions de I dans R et a I.• Si limx→a gx = +, etfx gxdans un voisinage de a, alorslimx→a fx = +.• Si limx→a gx = , etfx gx,dans un voisinage de a, alorslimx→a fx = .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024252 / 277

Page 257 : Théorèmes d’existence de limitesThéorème Théorème de la limite monotone cas f croissanteSoient a, b R avec a b et f : a, b→R.Supposons que f est croissante.• Si f est majorée, alors f admet une limite ﬁnie en b, etlimx→bfx = supxa,bfx.Sinon, on a limx→bfx = +.• Si f est minorée, alors f admit une limite ﬁnie en a, etlimx→a+ fx =infxa,b fx.Sinon, on a limx→a+ fx = .Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024253 / 277

Page 258 : Théorèmes d’existence de limitesThéorème Théorème de la limite monotone cas f décroissanteSoient a, b R avec a b et f : a, b→R.Supposons que f est décroissante.• Si f est minorée, alors f admet une limite ﬁnie en b etlimx→bfx =infxa,b fx.Sinon, limx→bfx = .• Si f est majorée, alors f admet une limite ﬁnie en a etlimx→a+ fx = supxa,bfx.Sinon, limx→a+ fx = +.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024254 / 277

Page 259 : Théorèmes d’existence de limitesComme corollaire du Théorème de la limite monotone, nous avons le résultatsuivant.CorollaireSoit f : I →R une fonction monotone et a ◦I. Alors, f admet des limitesﬁnies à gauche et à droite en a et on a :si f est croissante alorslimx→afx fa limx→a+ fx.si f est décroissante alorslimx→a+ fx fa limx→afx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024255 / 277

Page 260 : ContinuitéDéﬁnition ContinuitéSoit I un intervalle, f : I →R une fonction et a I. On dit que f est continueen a silimx→a fx = fa.Autrement dit, f est continue en a si et seulement siϵ 0, η 0, x I, x a η=⇒fx fa ϵ.Remarque : Géométriquement, une fonction est continue si son graphe se trace« sans lever le crayon ».Figure – Continuité en un point.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024256 / 277

Page 261 : ContinuitéExemple : La fonction x 7→x est continue en 2.Solution : Nous devons montrer quelimx→2x =2.Pour cela, notons que pour tout x R+, nous avonsx 2 =x 2x +2 x 2.Ainsi, pour tout ϵ 0, prenonsη = ϵ.Si x 2 ϵ, alorsx 2 ϵ=⇒limx→2x =2.La fonction x 7→x est donc continue en 2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024257 / 277

Page 262 : Continuité sur un intervalleDéﬁnition Continuité sur un intervalleOn dit que f : I →R est continue sur l’intervalle I si elle est continue enchaque point de I.On note C0I, R ou CI, R, l’ensemble des fonctions continues sur I dans R, i.e.continues en tout point de I.Exemple : Les fonctionsx 7→x;x 7→exp x;x 7→cos x;x 7→sin xsont continues sur R. La fonctionx 7→xest continues sur R0. Finalement, la fonctionx 7→lnxest continues sur R0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024258 / 277

Page 263 : ContinuitéDéﬁnition Continuité à gauche/à droite en un pointSoient f : I →R une fonction et a I.• Continuité à gauche : On dit que f est continue à gauche en a si fa estla limite à gauche de f en a, i.e.limx→afx = fa.• Continuité à droite : On dit que f est continue à droite en a si fa est lalimite à droite de f en a, i.e.limx→a+ fx = fa.Remarque : Une fonction f est continue en a si et seulement si f est continueà droite et à gauche en a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024259 / 277

Page 264 : ContinuitéExemple : La fonction partie entièrex 7→Exest continue à droite en tout point de R mais elle n’est continue à gauche qu’auxpoints de R\Z.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024260 / 277

Page 265 : ContinuitéDéﬁnition Prolongement par continuitéSoit a I et f : I\a →R une fonction. On dit que f est prolongeable parcontinuité en a s’il existe une fonction˜f : I →Rcontinue en a et telle que˜fI\a = f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024261 / 277

Page 266 : ContinuitéPropositionSoit a I et f : I\a →R une fonction.La fonction f est prolongeable par continuité en a si et seulement si f admetune limite ﬁnie ℓen a. Dans ce cas, un tel prolongement ˜f : I →R est unique,et donné par :˜f : x 7→ fxsi x ̸= a,ℓsi x = a.On l’appelle le prolongement par continuité de f en a qu’on notera souvent fsans distinction par abus de notation.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024262 / 277

Page 267 : ContinuitéDémonstration.=⇒Supposons que f est prolongeable par continuité en a. Par déﬁnition, il existedonc˜f : I →Rcontinue en a et telle que˜fI\a = f.Par continuité de ˜f en a, nous avons˜fa = limx→a˜fx = limx→a+ ˜fx.Or ˜fI\a = f, doncfa = limx→afx = limx→a+ fx.Ainsi f admet une limite ℓen a avec ℓ= ˜fa. Ceci prouve également l’unicités’il existe du prolongement par continuité de f en a.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024263 / 277

Page 268 : ContinuitéDémonstration.⇐= Supposons que f admet une limite ﬁnie ℓen a. Posons alors˜f : x 7→ fxsi x ̸= aℓsi x = a .La fonction ˜f prolonge bien f, et est continue en a puisque˜fa = limx→a˜fx = limx→a+ ˜fx.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024264 / 277

Page 269 : ContinuitéExemples :• Considérons la fonctionf : x 7→sinxxdéﬁnie sur R. Puisquelimx→0sinxx= limx→0sinx sin0x 0= sin′0 = cos0 = 1.On peut donc prolonger f par continuité en 0 en posant f0 = 1.• Fonctions puissances : Soit α R. On rappelle que la fonction puissanced’exposant α, notée pα, est déﬁnie sur R+ parpαx = xα = eα lnx.On alimx→0 xα =+si α 00si α 0. .Ainsi, si α 0, la fonction pα peut être prolongeable par continuité en 0 enposant pα0 = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024265 / 277

Page 270 : ContinuitéLe résultat suivant est la version continue du résultat analogue sur les limitesd’une fonction.Théorème Caractérisation séquentielle de la continuité en un pointSoit f : I →R et a I. Les assertions suivantes sont équivalentes• f est continue en a.• Pour toute suite unnN à valeurs dans I, tel quelimn→+un = a,nous avonslimn→+fun = fa.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024266 / 277

Page 271 : ContinuitéRemarques :• En résumé, pour une fonction continué f et pour tout suite unnNconvergent, nous avonsflimn→+un=limn→+fun• Ce théorème a déjà souvent été utilisé dans le contexte des suites récurrentesun+1 = fun.Si unnN converge vers un réel ℓet si f est déﬁnie et continue en ℓ,alorsfℓ = flimn→+un=limn→+fun =limn→+un+1 = ℓ.C’est-à-dire, ℓest un point ﬁxe de f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024267 / 277

Page 272 : Opérations sur les fonctions continuesProposition Somme et produit sur les fonctions continuesSoient f et g deux fonctions continues sur I et λ, µ R2.1. Les fonctions λf + µg, f × g sont continues sur I.2. Si de plus, g ne s’annule pas sur I, alors fg est continue sur I.Démonstration.Ces résultats découlent immédiatement des résultats analogues que nous avons vudans le chapitre limites de fonctions.Exemples :• Les fonctions polynomiales sont continues sur R en tant que sommes etproduits de fonctions continues.• Pour tout k Z, la fonction tan est continue sur π2 + kπ, π2 + kπ en tantque quotient de fonctions continues.• La fonction rationnelle x 7→P xQx est continue sur R privé de ses pôles,c’est-à-dire des racines de son dénominateur Q.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024268 / 277

Page 273 : Opérations sur les fonctions continuesLe dernière opération à étudier sur les fonctions continues est la composition.Proposition Composition sur les fonctions continuesSoit f : I →R une fonction continue sur I, et g : J →R une fonctioncontinue sur J avec fI J. Alors, la fonctiong ◦fest continue sur I.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024269 / 277

Page 274 : Les Grands Théorèmes de la ContinuitéPassons maintenant à étudier quelques propriétés fondamentales des fonctionscontinues.Théorème Théorème des valeurs intermédiaires TVISoit f : I →R une fonction continue et a, b I, tels quefafb 0.Alors il existe c compris entre a et b tel quefc = 0.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024270 / 277

Page 275 : Les Grands Théorèmes de la ContinuitéDémonstration.Supposons que a b. On construit par récurrence deux suites adjacentesannNetbnnNd’éléments de a, b dont la limite commune c vériﬁe fc = 0. ConstruisonsannN et bnnN. On pose a0 = a et b0 = b.Pour n N, nous allons déﬁnir anet bn de façon d’avoirbn an = b a2netfanfbn 0.Pour cela, posons mn = an+bn2. Ainsi• si fan · fmn 0, on pose an+1 = an et bn+1 = mn.• si fan · fmn 0, on pose an+1 = mn et bn+1 = bn.Dans chacun de ces deux cas, on obtientfan+1fbn+1 0etbn+1 an+1 = bn an2= b a2n+1Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024271 / 277

Page 276 : Les Grands Théorèmes de la ContinuitéDémonstration.Montrons que les suites annN et bnnN sont adjacentes. Par construction• annN est croissante, et• bnnN est décroissante.• De plus, par construction, pour tout n N, nous avonsbn+1 an+1 = b a2n+1=⇒limn→+bn an = 0.Les suites annN et bnnN sont donc adjacentes et convergent vers la mêmelimite c a, b.Comme f est continue, en passant à la limite dans l’inégalité fanfbn 0, onobtientfc2 = flimn→+anflimn→+bn=limn→+fanfbn 0.Ainsi, f 2c 0. Donc fc = 0 et le théorème est démontré.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024272 / 277

Page 277 : Les Grands Théorèmes de la ContinuitéThéorème Théorème des valeurs intermédiaires, version « existenced’un antécédent »Soit a, b R avec a b et f : a, b →R une fonction continue sur a, b. Alorspour tout y entre fa et fb, il existe c a, b tel quefc = y.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024273 / 277

Page 278 : Les Grands Théorèmes de la ContinuitéDémonstration.Soit y entre fa et fb et posons gx = fx y. Alors• La fonction g est continue, et• ga et gb sont de signes contraires, c’est-à-dire ga · gb 0.Par le théorème des valeurs intermédiaires, il existe donc c a, b, tel quefc = y.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024274 / 277

Page 279 : Les grands théorèmes de la continuitéComme corollaire du résultat précédent nous avons le théorème suivant.Théorème Théorème des valeurs intermédiaires, version « image d’unintervalle »Si I est un intervalle et si f est continue sur I, alors fI est un intervalle.Remarque : Si I est un intervalle et f : I →R une fonction continue, cetteversion du TVI aﬃrme que fI est également un intervalle, mais pas que I etfI sont de même nature. Il se peut que I soit ouvert et fI un segmentintervalle fermé et borné, ou bien que I soit semi-ouvert et fI ouvert, etc.Exemples :fx = sinxetf π, π = 1, 1;gx = x2etg 1, 1 = 0, 1.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024275 / 277

Page 280 : Les Grands Théorèmes de la ContinuitéThéorème Théorème des bornes atteintes• Toute fonction continue sur un segment intervalle fermé et borné y estbornée et atteint ses bornes. Autrement dit, si f : a, b →R est continuesur a, b, alors il existe c a, b et d a, b tels que pour tout x a, b,nous avonsfc fx fd.• L’image d’un segment par une fonction continue est un segment.Remarques :• Nous avons vu que la continuité ne préserve pas la forme des intervalles engénéral, mais en tout cas une chose est sûre, un segment est toujourstransformé en un segment.• Sur un intervalle borné qui n’est pas un segment, une fonction continue n’aaucune raison d’être bornée en général. Par exemple, la fonction tangente surπ2 , π2.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024276 / 277

Page 281 : Les Grands théorèmes de la ContinuitéOn ﬁni ce chapitre en étudiant la réciproque d’une fonction continue.ThéorèmeSoit f : I →R une fonction continue. Alors f est injective sur I si etseulement si f est strictement monotone.Théorème Continuité d’une réciproqueToute fonction f continue et strictement monotone sur un intervalle I réalise unebijection de I sur l’intervalle fI. Sa réciproque est de plus continue etstrictement monotone sur l’intervalle fI de même monotonie que f.Nicolas Arancibia Robert / CY-tech CergyAnalyse Pré-ING12023/2024277 / 277

PREING1 S1, Analyse1

Le contenu de cet article est la propriété exclusive de son auteur.

Tags tendance