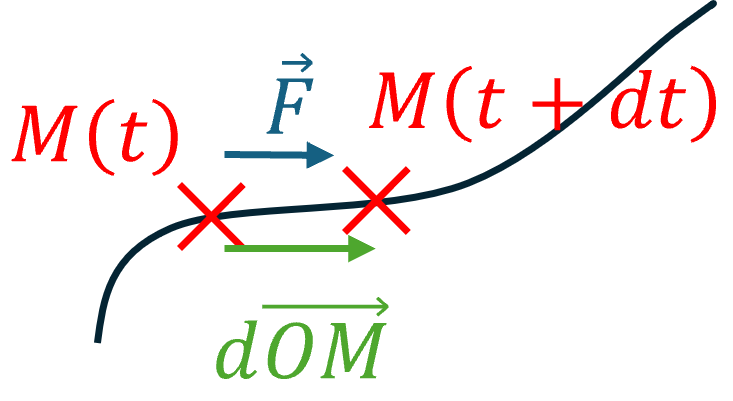CM Mecanique du point
Mécanique du point
Liens Utiles :
En particulier, pour le module de Mécanique du point:
Chapitre I : Introduction
3 Partie de la dynamique :
Dynamique :
- Autres appellations :
- $q^{té}$ de mouvement
- énergie
- mouvement cinétique
- Étude du mouvement en lien avec ses cause
- Autres appellations :
Mécanique :
- étude du mouvement sans liens avec ses cause
Concept de point
- Approximation : néglige l’extention spatial du système
- exact : on peut décrire certaine propriétés du mouvement d’un ensemble de points materiels en se ramenant au mouvement d’un seul point : centre d’inertie
- point materiel : a une masse inertielle
- Cadre cinématique : Galiléen
- L’espace et le temps :
- absolue (ne dépende pas du referentiel)
- indépendant l’un de l’autre
- L’espace et le temps :
Chapitre II : Dynamique en terme de $q^{té}$ de mouvement
I - Les 3 Lois de NEWTON
1. principe d’inertie
- il existe une classe privilégiée de referentiels dit \(\Biggl\{\begin{matrix} \text{inertielle} \\\ \text {galiléen} \end{matrix}\) dans lesquels tout système isolé a un mouvement rectiligne uniforme
- système isolé : système qui n’a aucune interaction avec le reste de l’univers
- L’état de la vitesse chez Galilée : vecteur vitesse constant dans $\mathcal{R}_{galiléen}$
- mouvement rectiligne uniforme : $\overrightarrow{v} = \overrightarrow{c^{st}}$
- $\Longrightarrow$ le mouvement à $\overrightarrow{v} = \overrightarrow{c^{st}}$ par rapport a un referentiel
- galiléen est un état de mouvement
- pas besoin d’être crée ni entretenue
- $\overrightarrow{v} = \overrightarrow{0}$ par rapport a un $\mathcal{R}_{galiléen}$ en est un cas particulier
2. Principe fondamental de la dynamique (PFD)
Dans un $ \mathcal{R}_{galiléen} $, le mouvement d’un système materiel est tel que :
- Masse inertielle :
- definition : Qui fait persister dans on état
- Caractérise la résistance du système à la modification de sont état de mouvement
- $m^{(i)} = \sum \overrightarrow{F}_{exterieur \rightarrow s}$
- avec $\overrightarrow{a} = \frac{d \overrightarrow{v}}{dt}$
- $\text{scalaire} \ge 0$
- additive : \(m^{(i)}_{\{A + B\} } = m^{(i)}_{\{A\}} + m^{ (i) }_ { \{B\} }\)
- invariante par changement de référentiel
- conservée : il n’éxiste pas de source de création/suppression de la masse dans l’univers
- $m^{(i)}_{{système férmé} } = c^{st}$
- Concept de force :
- concept de unificateur de l’interaction entre deux système physiques (ex en mouvement) de l’autre ; et réciproquement
- Vecteur plus point d’application
- Linéarité : \(\overrightarrow{F}_{total} = \sum_{i}^{} \overrightarrow{F}_{i}\)
- $\overrightarrow{F}_{interne}$ : force entre 1 élément d’un système et un autre élément du même système
- $\overrightarrow{F}_{externe}$: force entre unélément externe d’un système et un élément interne du système
si système = un point matériel $\Rightarrow$ pas de $\overrightarrow{F}_{interne}$
Concept de \(\Biggl\{ \begin{matrix} q^{té} \text{de mouvement} \\\text{impulsion} \\ \text{mouvement linéaire} \end{matrix}\) : \(\overrightarrow{p} = m^{(i)}\overrightarrow{v}\)
- \(\frac{d \overrightarrow{p}}{dt} = \frac{d m^{(i)}}{dt}\overrightarrow{v} + \frac{d \overrightarrow{v}}{dt} m^{(i)} = \overrightarrow{a} = m^{(i)}\overrightarrow{a} = \overrightarrow{F}_{exterieur \rightarrow S}\)
- Conséquences : système S \(\Biggl\{\begin{matrix} \text{isolé} \\\ \text{pseudo isolé} \end{matrix} \Longrightarrow\) \(\begin{matrix} \underbrace{\sum\overrightarrow{F}_{exterieur \rightarrow S}}\\\ \text{eq. méca} \end{matrix}= \overrightarrow{0}\)
- \(\Longrightarrow \overrightarrow{p} = c^{st}\)
- plus fondamental : $\Longleftrightarrow$ espace physique homogène (Mme NOETHER)
- principe d’inertie :
- $\Longrightarrow$ les $\mathcal{R}_{galiléen}$ sont en mouvement rectiligne uniforme les un par rapport aux autres
3. principe des actions reciproques
\[\overrightarrow{F}_{A \longrightarrow B} = -\overrightarrow{F}_{B \longrightarrow A}\]Conséquences : concept de centre d’inertie
Soient : un système $S_{1} = $ point materiel $M_{1}$ de $m^{(i)}_{1} $
\[S = \{ S_{1} + S_{2} \}\]Dans un $\mathcal{R}_{galiléen}$ : PFD
\[m^{(i)}_{1}\overrightarrow{a}_{1} + m^{(i)}_{2}\overrightarrow{a}_{2} = \sum \overrightarrow{F}_{ext \longrightarrow S_{1}} + \overrightarrow{F}_{ext \longrightarrow S_{2}}\] \[= \sum \overrightarrow{F}_{ext sans S_{2} \longrightarrow S_{1}} + \overrightarrow{F}_{S_{2} \longrightarrow S_{1}} + \sum \overrightarrow{F}_{ext sans S_{1} \longrightarrow S_{2}} + \overrightarrow{F}_{S_{1} \longrightarrow S_{2}}\] \[\overrightarrow{F}_{S_{1} \longrightarrow S_{2}} = \overrightarrow{F}_{S_{2} \longrightarrow S_{1}} = \overrightarrow{0}\] \[\Longrightarrow\sum \overrightarrow{F}_{ext sans S_{2} \longrightarrow S_{1}} + \sum \overrightarrow{F}_{ext sans S_{1} \longrightarrow S_{2}}\] \[= m^{(i)}_{s}\overrightarrow{a_{s}}\] \[= \left[ m^{(i)}_{1} + m^{(i)}_{2} \right] \overrightarrow{a_{s}}\]Soit le centre d’inertie $I$ de $S$ tel que $\forall o$ origine du repère
\[m^{(i)}_{1} \overrightarrow{OM_{1}} + m^{(i)}_{2} \overrightarrow{OM_{2}} = \left[ m^{(i)}_{1} + m^{(i)}_{2} \right] \overrightarrow{OI}\] \[m_{1}^{(i)}\overrightarrow{v_{1}} + m_{2}^{(i)}\overrightarrow{v_{2}} = \left\lbrack m_{1}^{(i)} + m_{2}^{(i)} \right\rbrack\overrightarrow{v_{i}}\] \[m_{1}^{(i)}\overrightarrow{a_{1}} + m_{2}^{(i)}\overrightarrow{a_{2}} = \left\lbrack m_{1}^{(i)} + m_{2}^{(i)} \right\rbrack\overrightarrow{a_{i}}\] \[\Longrightarrow \overrightarrow{a_{i}} = \overrightarrow{a_{s}}\]- Si $S$ est isolé : \(\sum \overrightarrow{F_{ext \rightarrow S}} = \overrightarrow{0}\) \(\Longrightarrow \overrightarrow{a} = \overrightarrow{0} \Longrightarrow \Biggl \{ \begin{matrix} \overrightarrow{v_{i}} = \overrightarrow{c^{st}} \\ \overrightarrow{p_{i}} = \overrightarrow{c^{st}} \end{matrix} \text{ different de } \mathcal{R}_{galiléen}\) \(\Longrightarrow \text{le référentiel } \mathcal{R}\) liée à I est galiléen
Résultat est galiléen pour tout nombre de sous système de \(S\)
II - Force et exemples
1. Interaction fondamentales : toutes à distance
| Interaction | Particules fondamentales | Portée | exemples |
|---|---|---|---|
| gravitation | ayant une masse gravitationnel | \(+\infty\) | mouvement des planètes |
| électromagnétisme | ayant une charge électrique | \(+\infty\) | stabilité de l’atome aux reactions chimiques |
| interaction faible | nucleons \(\Biggl \{ \begin{matrix} \text{protons} \\ \text{neutrons} \end{matrix}\) | \(10^{-18}m\) | radioactivité \(\beta\) |
| interaction forte | Quarks | \(10^{-15}m\) | stabilité du noyau |
Dans ce cours : échelle macro \(\Longrightarrow\) 2 types de forces :
- à distance : fondamentales (gravitation, électromagnétisme)
- de contact : non-fondamentales Modèle macroscopique réunissant un ensemble d’effet fondamentaux (Rappel : élastique, frottement)
2. Forces à distances
a) Gravitation
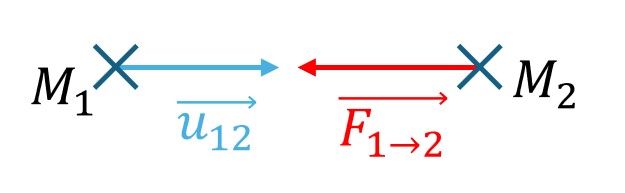
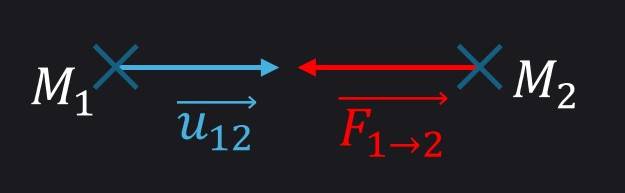
- Soit $M_{1}$ de masse gravitationnel $m^{(g)}_{1} \ge 0$
- Soit $M_{2}$ de masse gravitationnel $m^{(g)}_{2} \ge 0$
- $G$ La $c^{st}$ gravitationnel universelle $> 0$ (toujours attractive)
- $\overrightarrow{u_{12}}$ le vecteur unitaire de 1 vers 2
Remarque : Principe d’équivalence
Formulé par Einstein.
La masse inertielle $m^{(i)}$ d’un corps est égale à la masse gravitationnelle $m^{(g)}$ de ce même corps. Ex : si nous sommes dans une capsule fermée et que nous sommes plongés dans un champ de gravitation. Si on a un chapeau et qu’on l’enlève, le chapeau reste à côté de nous.
Dans le cas de la chute libre, PFD d’un système uniquement soumis à la gravitation :
- Une des théories principales ayant contribué à la théorie de la relativité générale. Selon Einstein, la gravitation n’est plus une force, elle déforme l’espace-temps de la même façon pour tous les corps.
Lien entre gravitation et pesanteur
- Pesanteur : Dans l’exemple de la Terre, la force de pesanteur (ou poids) d’un système de masse $m$ est la force opposée à celle qui le maintient en équilibre (\({\overrightarrow{a}}_{\mathcal{/R}_{T}} = \overrightarrow{0}\)) immobile (\({\overrightarrow{v}}_{\mathcal{/R}_{T}} = \overrightarrow{0}\)) dans le référentiel terrestre $\mathcal{R}_{T}$.
3. approximations :
On suppose que le référentiel terrestre est « à peu près » galiléen
La distribution de la masse dans la Terre est « à peu près » à symétrie sphérique (même densité à deux points de même distance au centre)
Les variations d’altitude pour les mouvements décrits sont très petites devant le rayon de la Terre ($R_{T}$)
Le champ de gravitation terrestre :
b) La force électrostatique :
Cas particulier de l’électromagnétisme, interaction uniquement électrique et dans un régime indépendant du temps.
Soit deux points $M_{1}$ et $M_{2}$ de charges électriques $q_{1}$ et $q_{2}$.
- Où $\epsilon_{0}$ est la permittivité du vide ($\epsilon_{0} > 0$)
- où \({\overrightarrow{E}}_{1}\left( M_{2} \right)\) est le champ électrique créé par $q_{1}$ en $M_{2}$
La charge $q$ est une grandeur scalaire positive, négative ou nulle.
La charge $q$ est quantifiée par la charge élémentaire $e \approx 1.6\ 10^{- 19}C$ (charge du proton).
La charge est une quantité additive, conservée et invariante par changement de référentiel (voir I. 2.).
Si $q_{1}$ et $q_{2}$ sont de même signe, $q_{1}q_{2} > 0$ : la force est répulsive.
Si $q_{1}$ et $q_{2}$ sont de signes opposés, $q_{1}q_{2} < 0$ : la force est attractive.
3. Forces de contact
a. Contact avec un solide
a. 1. Tension d’un fil
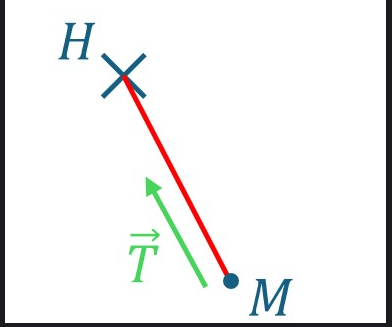
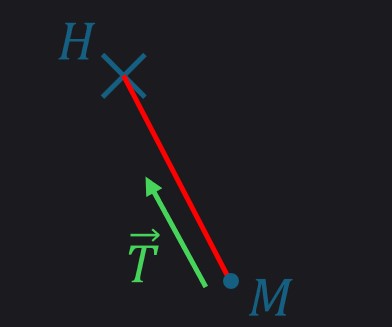
- Fil inextensible et de masse négligeable.
La force $\overrightarrow{T}$ agit en réaction aux autres forces appliquées sur $M$.
$\Vert \overrightarrow{T} \Vert$ est à priori indéterminé. Dépend des autres forces sur $M$.
Si le fil n’est pas tendu, $\overrightarrow{T} = \overrightarrow{0}$
a. 2. Force de rappel élastique
Ex : Ressort
Ressort de masse négligeable.
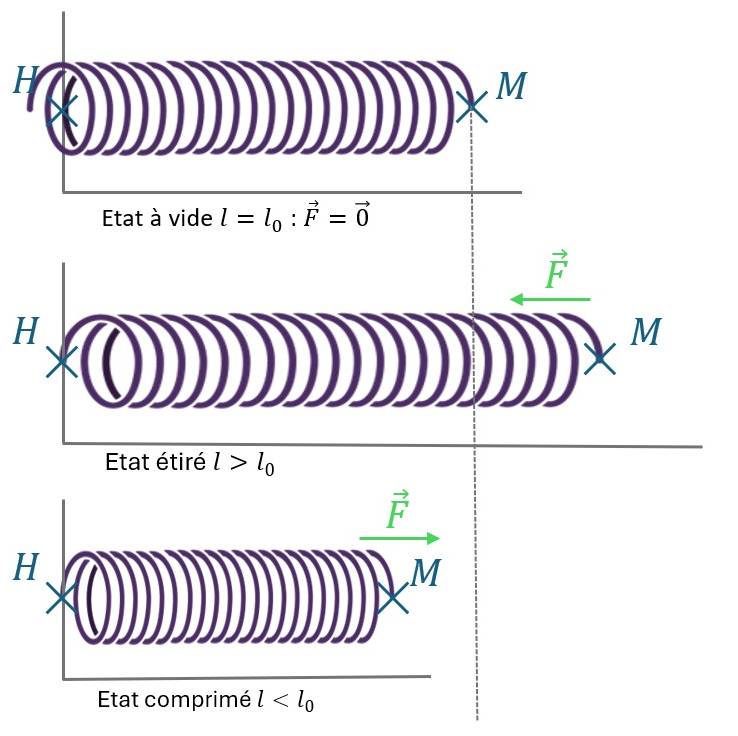
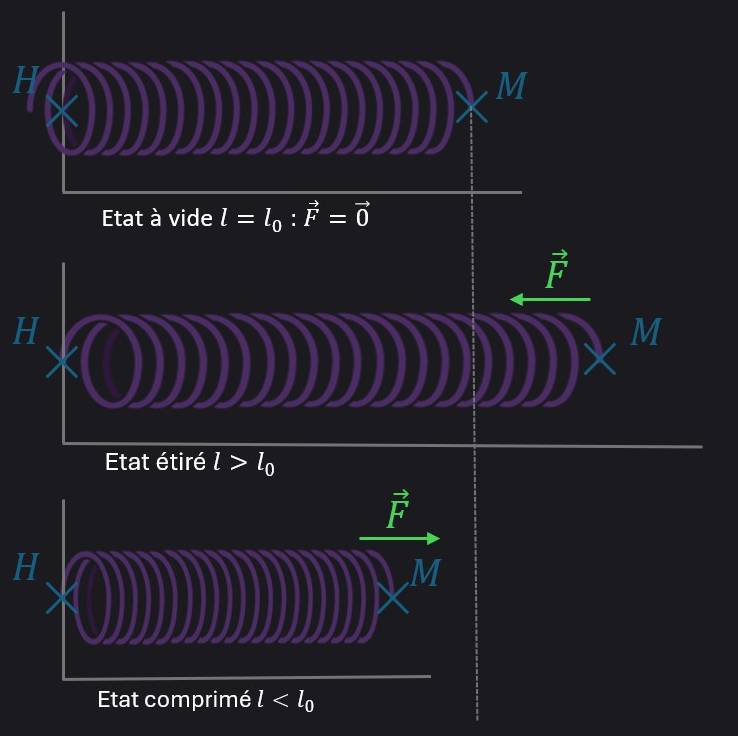
Ressort idéal (pour toute élongation ou compression subie, il peut revenir à son état initial/état à vide) Comportement purement élastique.
$k$ : la raideur du ressort ($> 0$)
$l_{0}$ : longueur du ressort à vide
$l$ : longueur du ressort à l’instant considéré
- $\overrightarrow{F}$ tend toujours à ramener le ressort vers son état à vide.
a. 3. Force de contact entre deux solides
Soit un solide assimilé à un point $M$ de masse $m$ en contact avec un autre solide.
Ex : Bloc posé sur un support
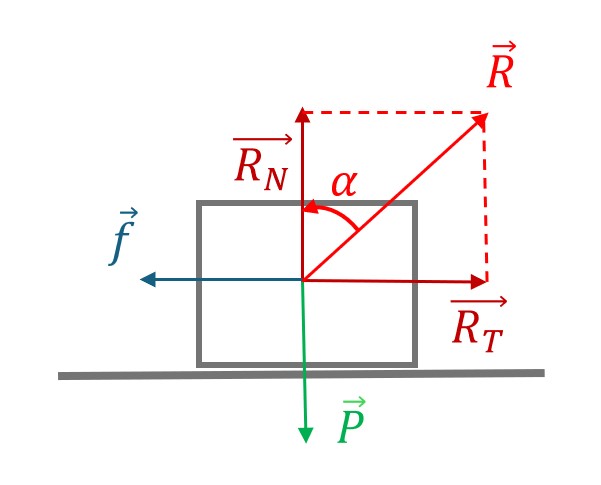
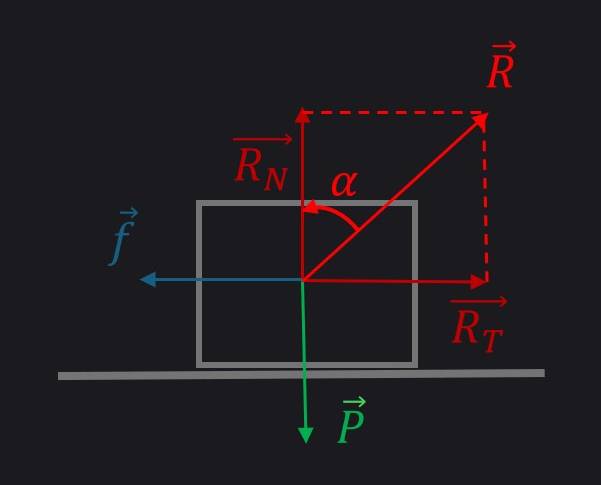
La force de contact entre ces deux objets est appelée force de réaction $\overrightarrow{R}$ sur $M$
Avec $\overrightarrow{R_{N}}$ : réaction normale du support, toujours perpendiculaire au plan du support et orientée du support vers $M$.
La norme de $\overrightarrow{R_{N}}$ est à priori indéterminée, elle dépend des autres forces s’exerçant sur $M$
$\overrightarrow{R_{T}}$ : réaction tangentielle au support. Elle appartient au plan de contact entre les deux solides. Elle est orientée de façon opposée au mouvement du bloc $M$ par rapport au support.
Détails sur $\overrightarrow{R_{T}}$
Dans le référentiel $\mathcal{R}$ lié au support, supposé galiléen.
Initialement, $M$ est immobile par rapport à $\mathcal{R}$.
On applique une force $\overrightarrow{f}$ sur $M$ parallèlement au support pour essayer de mettre $M$ en mouvement. Comment se comporte $\overrightarrow{R_{T}}$ ?
On distingue deux régimes :
Régime d’adhérence/de non-glissement/de frottement statique
Tant que $\Vert \overrightarrow{f} \Vert$ est suffisamment faible, $\Vert \overrightarrow{R_{T}} \Vert$ s’adapte et $\overrightarrow{R_{T}}$ compense $\overrightarrow{f}$.
Ce régime est valable tant que $\Vert \overrightarrow{f} \Vert = \Vert \overrightarrow{R_{T}} \Vert < \max\Vert \overrightarrow{R_{T}} \Vert$
Où \(\max\Vert \overrightarrow{R_{T}} \Vert\) est le frottement statique \({R_{T}}_{S} = \mu_{S}\Vert \overrightarrow{R_{N}} \Vert\) avec $\mu_{S}$ le coefficient de frottement statique qui dépend des surfaces en contact.
Régime de glissement/de frottement dynamique
\(\Vert \overrightarrow{f} \Vert > {R_{T}}_{S}\)
et \({\overrightarrow{a}}_{M} \neq \overrightarrow{0}\Longrightarrow M\) est mis en mouvement par rapport au support.
Alors $\Vert \overrightarrow{R_{T}} \Vert = \mu_{D}\Vert \overrightarrow{R_{N}} \Vert$ avec $\mu_{D}$ le coefficient de frottement dynamique. (Généralement, $\mu_{D} < \mu_{S}$)
$\Longrightarrow$ La force de frottement est indépendante de ${\overrightarrow{v}}_{M}$ par rapport au support.
Transition entre les deux régimes
- $M$ est à l’équilibre dans le référentiel $\mathcal{R}$ tant que $\Vert \overrightarrow{f} \Vert = \Vert \overrightarrow{R_{T}} \Vert < \mu_{S}\Vert \overrightarrow{R_{N}} \Vert$
- Tant que $\tan\alpha < \mu_{S}$
b. Contact avec un fluide
1. Poussée d’Archimède
Soit un objet de masse volumique $\rho$, de volume $V$ immergé dans un fluide de masse volumique $\rho_{f}$, le tout dans un champ de pesanteur $\overrightarrow{g}$
Dans un référentiel galiléen $\mathcal{R}_{gal}$, d’après le PFD, on a
$m\overrightarrow{a} = \overrightarrow{P} + \sum\overrightarrow{F}$ où $\overrightarrow{F}$ sont les forces de pression dues au fluide.
Si l’on remplace l’objet par le fluide, d’après le PFD sur le fluide mis à la place de l’objet, on a
$\overrightarrow{0} = \overrightarrow{P_{f}} + \sum\overrightarrow{F}$ car le fluide est à l’équilibre mécanique dans lui-même.
Dans les deux cas $\sum_{}^{}\overrightarrow{F}$ est identique car l’environnement reste le même.
On obtient alors $\sum\overrightarrow{F} = - \overrightarrow{P_{f}} = {\overrightarrow{\Pi}}_{f}$ : poussée d’Archimède.
La poussée d’Archimède est une force verticale orientée du bas vers le haut. Elle est égale à l’opposée du poids du fluide dépassée par l’objet.
Ainsi,
- Avec : $m = \rho V$ et $m_{f} = \rho_{f}V$
$\Rightarrow$ si $\rho > \rho_{f}$, $\overrightarrow{a}$ est dans le même sens que $\overrightarrow{g}$ et l’objet coule
$\Rightarrow$ si $\rho < \rho_{f}$, $\overrightarrow{a}$ est dans le sens opposé à $\overrightarrow{g}$ et l’objet remonte
$\Rightarrow$ si $\rho = \rho_{f}$, $\overrightarrow{a} = \overrightarrow{0}$ et l’objet est en équilibre
Remarque : l’eau est l’un des seuls éléments tels que
- $\rho_{s} < \rho_{f}$
2. La force de trainée
Force de frottement fluide toujours opposée au mouvement de l’objet par rapport au fluide.
Elle est toujours proportionnelle à l’opposé du vecteur vitesse de l’objet par rapport au fluide
On distingue deux régimes :
$\overrightarrow{f} = - k_{1}\overrightarrow{v}$ si $v$ est suffisamment faible
$\overrightarrow{f} = - k_{2}\Vert \overrightarrow{v} \Vert\overrightarrow{v}$ sinon
Avec $k_{1} > 0,\ k_{2} > 0$
3. La portance
- Cette force est perpendiculaire au vecteur vitesse ${\overrightarrow{v}}_{objet/fluide}\ \ \ $
Chapitre III : Dynamique en termes d’énergie
Considérations générales
Qu’est-ce que l’énergie ?
L’énergie est une grandeur scalaire
L’énergie est conservée pour un système isolé
Plus fondamentalement, par analogie à la conservation de la quantité de mouvement, la conservation de l’énergie est liée à l’homogénéité du temps. Exemple du théorème de NOETHER.
Exemples de forme d’énergie :
Energie cinétique
Energie potentielle
Energie mécanique
Ce sont les trois formes d’énergie étudiées dans ce cours.
Autres exemples d’énergie :
- Energie de rayonnement
Dans la relativité, on a aussi : $E = mc^{2}$ : introduit une équivalence entre énergie et masse.
En mécanique du point, le concept d’énergie est lié au concept de travail d’une force
Travail et puissance d’une force
Le travail
Soit un point matériel $M$ en mouvement dans un référentiel $\mathcal{R}$, soumis à une force $\overrightarrow{F}$
a. Travail élémentaire de $\overrightarrow{F}$
Entre $M(t)$ et $M(t + dt)$ par rapport à $\mathcal{R}$ :
\[\delta W\left( \overrightarrow{F} \right) = \overrightarrow{F}.d\overrightarrow{OM}\]Note : Le symbole $\delta$ est utilisé pour les variations d’une fonction qui (à priori) n’est pas une fonction d’état (ne dépend pas seulement de l’état du système à un instant $t$, dépend de la différence entre deux états).
Ex : La distance entre deux villes est une fonction d’état, mais le chemin parcouru est variable.
- A priori, la grandeur $W\left( \overrightarrow{F} \right)$ n’est pas une fonction d’état, sa valeur n’est pas définie par l’état du système. Seules les variations de $W\left( \overrightarrow{F} \right)$ entre deux états du système sont des choses définies.
b. Dimension physique
- Le travail à la même dimension qu’une énergie.
- Unité SI : $kg \cdot m^{2} \cdot s^{- 2} = J$ (joule)
c. Travail moteur, travail résistant, travail nul
Si $\delta W\left( \overrightarrow{F} \right) > 0 \Longrightarrow$ travail moteur. La force « aide » le déplacement.
Si $\delta W\left( \overrightarrow{F} \right) < 0 \Longrightarrow$ travail résistant. La force « résiste/s’oppose » au déplacement.
Si $\delta W\left( \overrightarrow{F} \right) = 0 \Longrightarrow \ $ travail nul.
d. Propriétés de linéarité
- Soient deux forces $\overrightarrow{F_{1}}$ et $\overrightarrow{F_{2}}$
- Soit $\lambda\mathbb{\in R}$
e. Travail total de $\overrightarrow{F}$
- Entre $A$ et $B$ par rapport à $\mathcal{R}$
- Où $\mathcal{C}_{A \rightarrow B}$ est le chemin parcouru de $A$ à $B$.
Deux exemples :
1. $\overrightarrow{F} = \overrightarrow{cte}$
\[W_{A \rightarrow B}\left( \overrightarrow{F} \right) = \int_{\mathcal{C}_{A \rightarrow B}}^{}{\overrightarrow{F} \cdot d\overrightarrow{OM}} = \overrightarrow{F} \cdot \int_{\mathcal{C}_{A \rightarrow B}}^{}{d\overrightarrow{OM}} = \overrightarrow{F} \cdot \overrightarrow{AB}\ \ \forall\mathcal{C}_{A \rightarrow B}\]Dans ce cas, $W$ est une fonction d’état, ne dépend pas du chemin.
Exemple : Le poids
2. Soit $\overrightarrow{F}$ une force de frottement fluide.
- $\overrightarrow{F} = - \alpha\overrightarrow{v}$ avec $\alpha > 0$
- Or $\overrightarrow{v} = \frac{d\overrightarrow{OM}}{dt}$
Ce travail est forcément de signe négatif $\forall d\overrightarrow{OM}$
Le travail est donc résistant.
\(W_{A \rightarrow B} \left( \overrightarrow{F} \right)\) \(= - \alpha \int_{\mathcal{C}_{A \rightarrow B}}\Vert \overrightarrow{v} \Vert^{2}dt\) \(= - \alpha\int_{\mathcal{C}_{A \rightarrow B}}\frac{\Vert d\overrightarrow{OM} \Vert^{2}}{dt}\)
- Ce travail dépend à priori du chemin $\mathcal{C}_{A \rightarrow B}$
La puissance
a. Puissance instantanée d’une force $\overrightarrow{F}$
- Entre $M(t)$ et $M(t + dt)$ par rapport à $\mathcal{R}$
b. Dimension physique
\[\lbrack puissance\rbrack = \frac{\lbrack énergie\rbrack}{\lbrack temps\rbrack} = ML^{2}T^{- 3}\]- Unité SI : $kg \cdot m^{2} \cdot s^{- 3} = W$ (watt)
c. Mêmes propriétés de linéarité pour puissance et travail
Théorème de l’énergie cinétique
Démonstration
Conséquence du PFD.
Dans un référentiel galiléen, on considère un point matériel $M$ de masse $m$.
D’après le PFD : $m\overrightarrow{a} = \sum{\overrightarrow{F}}_{ext}$
- Avec
- et
Exemple : Dans le plan muni d’un repère cartésien,
\[\overrightarrow{v} = \left( \begin{matrix} v_{x} \\ v_{y} \end{matrix} \right) \text{, }d\overrightarrow{v} = \left( \begin{matrix} dv_{x} \\ dv_{y} \end{matrix} \right)\] \[d\overrightarrow{v} \cdot \overrightarrow{v} = dv_{x}.v_{x} + dv_{y}.v_{y} = d\left( \frac{1}{2}v_{x}^{2} + cte \right) + d\left( \frac{1}{2}v_{y}^{2} + cte \right)\] \[d\overrightarrow{v} \cdot \overrightarrow{v} = d\left( \frac{1}{2}\left( v_{x}^{2} + v_{y}^{2} \right) + cte \right) = d\left( \frac{1}{2}v^{2} + cte \right)\] \[m\ d\overrightarrow{v} \cdot \overrightarrow{v} = d\left( \frac{1}{2}mv^{2} + cte \right)\]N.B. : \(\frac{d\left( \frac{1}{2}v_{x}^{2} + cte \right)}{dv_{x}} = v_{x}\)
- donc
- Ainsi,
Posons $E_{c} = \frac{1}{2}mv^{2} + cte$
Théorème de l’énergie cinétique (local) : \(dE_{c} = \sum\delta W\left( {\overrightarrow{F}}_{ext} \right)\)
Théorème de l’énergie cinétique (global) : \(\Delta E_{c} = \sum W\left( {\overrightarrow{F}}_{ext} \right)\)
Remarque : En mécanique, toutes les énergies sont définies à une constante près car on s’intéresse aux variations d’énergie.
Cette constante étant arbitraire, pour l’énergie cinétique, cette constante vaut 0 par convention.
\[E_{c} = \frac{1}{2}mv^{2}\]Choisir entre PFD et théorème de l’énergie cinétique
Nous avons vu que le PFD et le th. $E_{c}$ sont équivalents (ne demande pas d’introduire de postulat supplémentaire).
Le PFD est une équation vectorielle (donne $d$ équations scalaires pour $d$ dimensions de l’espace).
Le théorème de l’énergie cinétique est une équation scalaire (donne toujours une seule équation scalaire).
Si la dynamique du système peut être décrite avec $N = 1$ paramètre (nombre de degrés de liberté), une équation suffit (on peut utiliser le PFD ou le théorème de l’$E_{c}$).
Si $N > 1$ paramètres, le théorème de l’énergie cinétique seul ne suffit pas, il faut utiliser le PFD.
Forces conservatives et non-conservatives
Une force est dite conservative (${\overrightarrow{F}}_{c}$) si son travail est indépendant du chemin suivi dans le référentiel considéré.
Une force est dite non-conservative (${\overrightarrow{F}}_{nc}$) si son travail est dépendant du chemin suivi dans le référentiel considéré.
Conséquence :
\(\delta W\left( {\overrightarrow{F}}_{c} \right) = d\left( \text{fonction de la position} \right) = - dE_{p}\) où $E_{p}$ est l’énergie potentielle du système (par définition).
\[{\overrightarrow{F}}_{c} \cdot d\overrightarrow{OM} = - dE_{p}\]\({\overrightarrow{F}}_{c} = - \overrightarrow{grad}(E_{p})\) où $\overrightarrow{grad}$ est l’opérateur gradient traduisant la dérivée dans l’espace d’une grandeur scalaire.
Exemple : Dans le plan muni d’un repère cartésien, $E_{p}(x,y)$
\[\overrightarrow{grad}\left( E_{p} \right) = \frac{\partial E_{p}}{\partial x}\overrightarrow{u_{x}} + \frac{\partial E_{p}}{\partial y}\overrightarrow{u_{y}}\] \[\text{Où }\frac{\partial E_{p}}{\partial x}\text{ est la dérivée partielle de }E_{p}\text{ par rapport à }x\] \[\frac{\partial E_{p}}{\partial x}\text{ est la dérivée de }E_{p}\text{ par rapport à }x\ \text{en gardant }y\ \text{constant}\]N.B. :
\[\delta W\left( {\overrightarrow{F}}_{c} \right) = - dE_{p}\ \text{(forme locale)}\] \[W\left( {\overrightarrow{F}}_{c} \right) = - \Delta E_{p}\ \text{(forme globale)}\]Conséquences :
Sur un chemin fermé (le point de départ est la même que le point d’arrivée), $W\left( {\overrightarrow{F}}_{c} \right) = 0$
\(W_{A \rightarrow B}\left( {\overrightarrow{F}}_{c} \right) = - W_{B \rightarrow A}\left( {\overrightarrow{F}}_{c} \right)\)
Remarque :
\[\delta W\left( {\overrightarrow{F}}_{nc} \right) \neq d(\ldots)\]Pas d’énergie potentielle associée.
- Exemples de forces conservatives et énergie potentielle associée :
1. La force de gravitation
- On considère un point $O$ de masse $m_{O}$, un point $M$ de masse $m_{M}$.
- Dans le repère sphérique centré sur $O$, avec $OM = r$,
\(\delta W = - dE_{p}\mathcal{= - G}\frac{m_{O}m_{M}}{r^{2}}\overrightarrow{u_{r}} \cdot dr\ \overrightarrow{u_{r}}\) car les autres composantes de $d\overrightarrow{OM}$ ont un produit scalaire nul avec $\overrightarrow{u_{r}}$
\[\delta W = - dE_{p}\mathcal{= - G}m_{O}m_{M}\frac{dr}{r^{2}} = d\left( \mathcal{G}\frac{m_{O}m_{M}}{r} + cte \right)\]- Ainsi,
2. La pesanteur
Dans le référentiel géocentrique supposé galiléen, la distribution de la masse de la Terre supposée homogène, et les variations d’altitude supposées négligeables devant le rayon de la Terre.
\[\delta W = - dE_{p}\mathcal{= - G}\frac{m_{T}m_{M}}{R_{T}^{2}}\overrightarrow{u_{r}} \cdot dr\ \overrightarrow{u_{r}}\] \[\delta W = - dE_{p} = - m_{M}g\ dr\]- En négligeant la rotondité de la Terre, on considère le plan tangent à la Terre :
3. La force électrostatique
\[\delta W = - dE_{p} = \frac{1}{4\pi\epsilon_{0}}\frac{q_{O}q_{M}}{r^{2}}\overrightarrow{u_{r}} \cdot dr\ \overrightarrow{u_{r}}\] \[- dE_{p} = - d\left( \frac{1}{4\pi\epsilon_{0}}\frac{q_{O}q_{M}}{r} + cte \right)\] \[E_{p} = \frac{1}{4\pi\epsilon_{0}}\frac{q_{O}q_{M}}{r} + cte\]4. La force de rappel élastique
Soit un ressort d’extrémités $H$ et $M$
\[\delta W = - dE_{p} = - k\left( l - l_{0} \right)\overrightarrow{u_{HM}} \cdot d\overrightarrow{OM}\] \[\delta W = - dE_{p} = - k\left( l - l_{0} \right)\overrightarrow{u_{HM}} \cdot dl\ \overrightarrow{u_{HM}}\] \[- dE_{p} = - k\left( l - l_{0} \right)d\left( l - l_{0} \right)\] \[- dE_{p} = - k\ d\left\lbrack \frac{\left( l - l_{0} \right)^{2}}{2} + cte \right\rbrack\] \[- dE_{p} = \ - d\left\lbrack \frac{k}{2}\left( l - l_{0} \right)^{2} + cte \right\rbrack\] \[E_{p} = \frac{k}{2}\left( l - l_{0} \right)^{2} + cte\]Exemple de force non conservative : la force de frottement fluide
${\overrightarrow{F}}_{NC} = - \alpha\overrightarrow{v}$ ($\alpha > 0$)
$\delta W \neq - dE_{p}$ car la force n’est pas conservative.
\[\delta W = - \alpha\overrightarrow{v} \cdot d\overrightarrow{OM}\ \text{où}\ \overrightarrow{v} = \frac{d\overrightarrow{OM}}{dt}\] \[\delta W = - \alpha\Vert \overrightarrow{v} \Vert^{2}dt = - \frac{\alpha\Vert d\overrightarrow{OM} \Vert^{2}}{dt}\]$\delta W < 0$ donc le travail est bien résistant.
Théorème de l’énergie mécanique
Autre écriture du théorème de l’énergie cinétique.
Dans un référentiel galiléen, d’après le théorème de l’énergie cinétique :
- Où \({\overrightarrow{F}}_{ext} = {\overrightarrow{F}}_{C}\) ou \({\overrightarrow{F}}_{NC}\)
Théorème de l’énergie mécanique (local) : \(dE_{m} = \sum\delta W\left( {\overrightarrow{F}}_{NC} \right)\)
Théorème de l’énergie mécanique (global) : \(\Delta E_{m} = \sum W\left( {\overrightarrow{F}}_{NC} \right)\)
Conséquences :
Pour un système isolé (ni \({\overrightarrow{F}}_{C}\) ni \({\overrightarrow{F}}_{NC}\)), \(dE_{m} = dE_{c} = 0 \Longrightarrow\) l’énergie mécanique/cinétique est conservée au cours du temps.
Pour un système non isolé, en absence de forces non conservatives, $dE_{m} = 0 \Longrightarrow \ $ l’énergie mécanique est conservée au cours du temps. Transferts entre $E_{c}$ et $E_{p}$ mais leur somme reste constante.
I - Analyse du mouvement : profil énergétique
1. Limites du mouvement
On se place dans un référentiel galiléen et on considère le mouvement d’un point $M$ de masse $m$.
Dans un premier temps, on se limite à 1 dimension $(Ox)$ et on suppose que $M$ est soumis uniquement à une force conservative $\overrightarrow{F}$ associée à une énergie potentielle $E_{p}$.
D’après le théorème de l’énergie mécanique :
\[dE_{m} = d\left( E_{c} + E_{p} \right) = 0\ \text{: conservation de l'énergie mécanique}\] \[E_{m} = cte = E_{c} + E_{p}\] \[E_{m} - E_{p} = E_{c} = \frac{1}{2}mv^{2} \geq 0\ (1)\]Cette inégalité $(1)$ conditionne les limites du mouvement.
Si $(1)$ est vérifiée, le mouvement est autorisé. Si $(1)$ n’est pas vérifiée, le mouvement est interdit.
Le mouvement est donc autorisé tant que $E_{m} \geq E_{p}$ et interdit si $E_{m} < E_{p}$
En particulier,
- $E_{m} = E_{p} \Rightarrow E_{c} = 0 \Rightarrow v = 0\ :M\ \text{atteint un point d’arrêt dans le référentiel}$
Aussi appelé point limite du mouvement. Le point $M$ s’arrête et repart dans le sens opposé.
- $E_{m} = cte \Rightarrow \min E_{c} \leftrightarrow \max E_{p}\text{et }\max E_{c} \leftrightarrow \min E_{p}$
Exemple :
Imaginons un ressort horizontal attaché à une masse $M$. Si on écarte le ressort de sa position à vide ($E_{p}$ augmente) puis on lâche, le ressort se recomprime ($E_{p}$ diminue), on repasse à la position à vide ($E_{p} = 0$, $E_{c}$ maximal), la masse passe de l’autre côté, atteint un point d’arrêt ($E_{c} = 0$), retourne dans l’autre sens, le ressort s’étire jusqu’à arriver à l’autre point d’arrêt…
À une dimension, s’il y a deux points d’arrêt, le mouvement est limité à une région finie de l’espace (ici, un segment de droite). On dit alors que le mouvement est fini ou que l’état de mouvement de $M$ est lié ($M$ ne peut pas partir, il est lié).
À une dimension, $M$ fait les allers-retours entre les deux points limites (mouvement oscillant).
S’il y a $< 2$ points d’arrêts, le mouvement est non limité à une région finie de l’espace. C’est alors un mouvement infini (dans le sens : $M$ peut parcourir une région infinie), l’état de mouvement de $M$ est non lié, un état libre ou un état de diffusion.
Exemple :
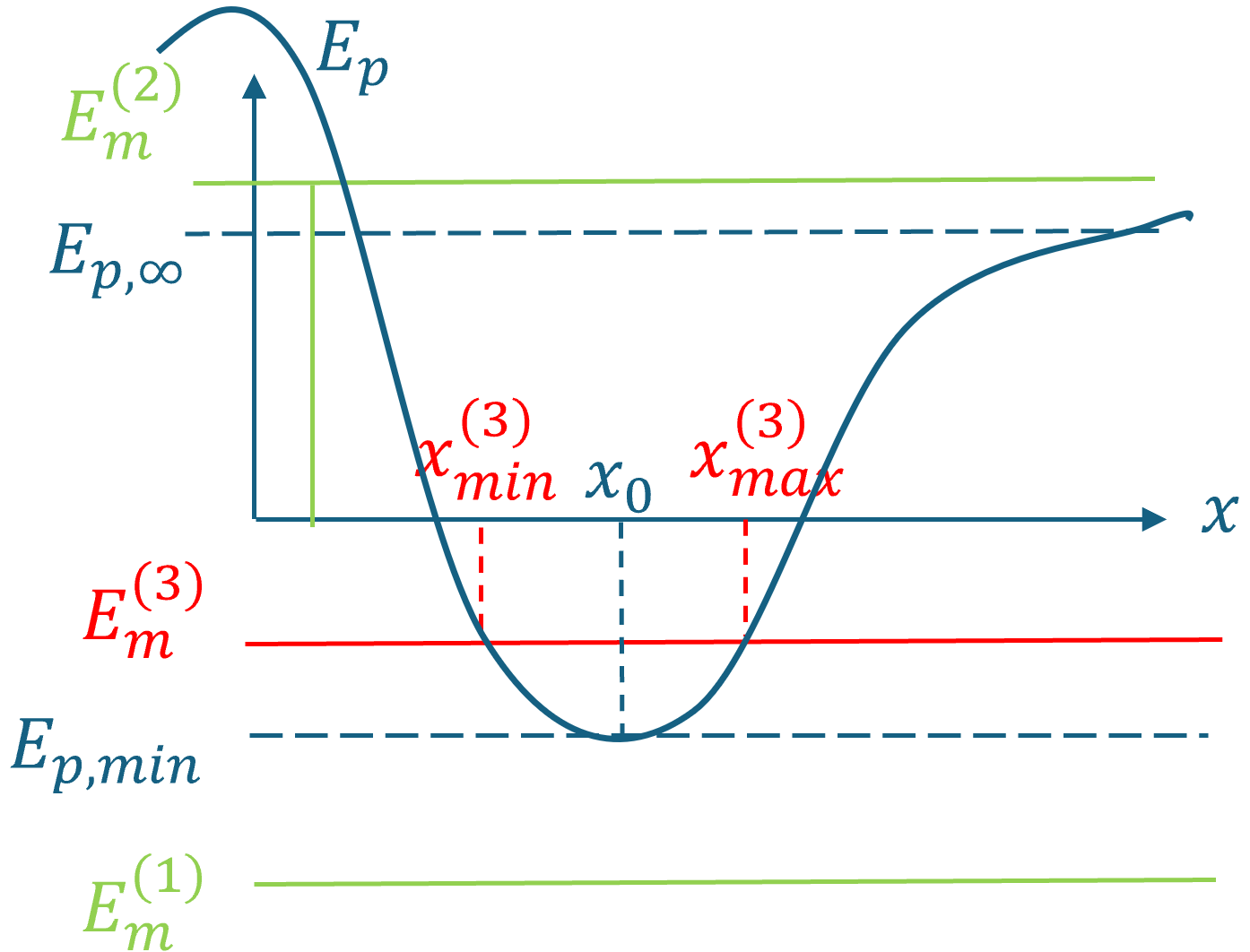
3 cas :
Prenons $E_{m}^{(1)} < E_{p,min}$. Impossible.
Prenons $E_{m}^{(2)} > E_{p,\infty}$. 1 point d’arrêt en $x_{\min}^{(2)}$. Etat non lié : $x_{\min}^{(2)} \leq x < + \infty$
Prenons $E_{p,min} < E_{m}^{(3)} < E_{p,\infty}$. $x_{min\ }^{3} \leq x \leq x_{max\ }^{3}$
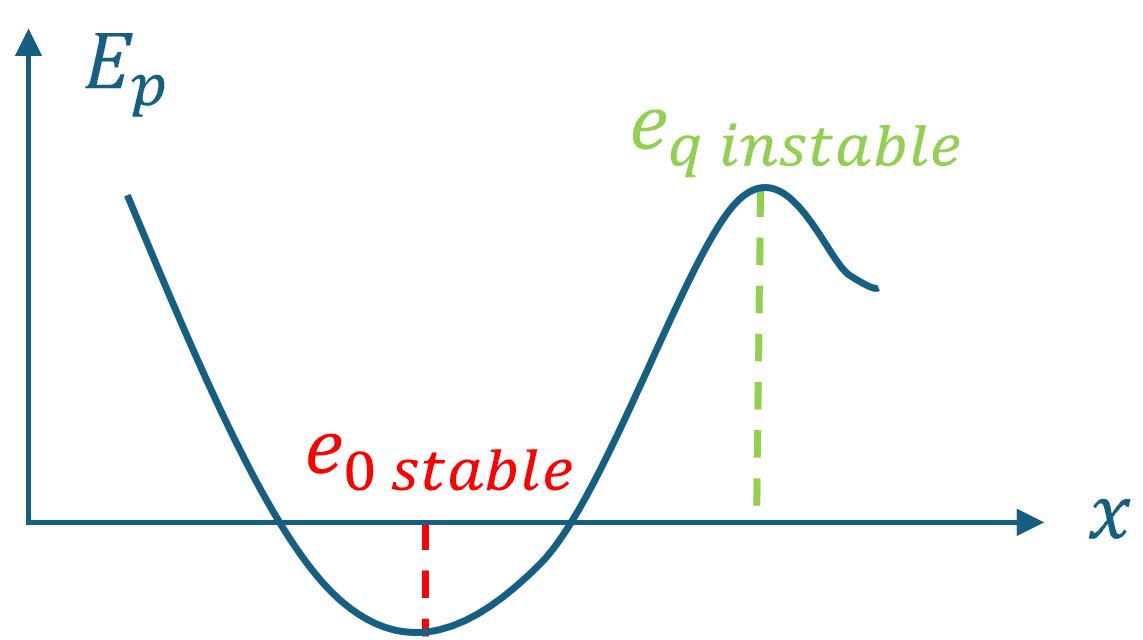
Si $E_{m} = E_{p,min}$, $M$ est au repos ($E_{c} = 0$) à $x = x_{0}$. $M$ est à l’équilibre mécanique par rapport à tout référentiel galiléen.
2. Equilibre mécanique stable/instable
Même contexte que le 1.
Rappels :
- $\overrightarrow{F}$ est conservative, donc $\overrightarrow{F} = - \overrightarrow{grad}\left( E_{p} \right)$.
- À l’équilibre mécanique, dans un référentiel galiléen, $\overrightarrow{a} = \overrightarrow{0} = \sum{\overrightarrow{F}}_{ext} = \overrightarrow{F}$
On déplace $M$ en $x_{eq} + dx$ ($dx \geq 0$ ou $\leq 0$).
On fait un développement limité de $F_{x}$ en $x_{eq}$ à l’ordre 1. (Voir formule de Taylor-Young dans le CM d’analyse).
\[F_{x}\left( x_{eq} + dx \right) = F_{x}\left( x_{eq} \right) + \frac{dF_{x}}{dx}\left. \ \right \vert _{x_{eq}}\left( x_{eq} + dx - x_{eq} \right)\] \[F_{x}\left( x_{eq} + dx \right) = F_{x}\left( x_{eq} \right) - \frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}}dx\] \[F_{x}\left( x_{eq} + dx \right) = - \frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}}dx\]On dit que l’équilibre est stable si, lorsque $M$ est écarté de $x_{eq}$, $\overrightarrow{F}$ tend à l’y ramener.
On dit que l’équilibre est instable si, lorsque $M$ est écarté de $x_{eq}$, $\overrightarrow{F}$ tend à l’en éloigner.
\[\text{Stable si }dx \gtrless 0\text{ et }F_{x}\left( x_{eq} + dx \right) \lessgtr 0 \Rightarrow \frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}} > 0\ \text{soit}\ E_{p}\ \text{atteint un minimum en }x_{eq}\]Instable dans le cas contraire.
3. Approximation harmonique
Même contexte que 1. et 2. :
On se place dans un référentiel galiléen et on considère le mouvement d’un point $M$ de masse $m$.
On se limite à 1 dimension $(Ox)$ et on suppose que $M$ est soumis uniquement à une force conservative $\overrightarrow{F} = F_{x}\overrightarrow{u_{x}}$ associée à une énergie potentielle $E_{p}$.
Soit $x_{eq}$ une position d’équilibre stable pour $M$.
On écrit un développement limité autour de $x_{eq}$.
\[F_{x}(x) = F_{x}\left( x_{eq} \right) + \frac{dF_{x}}{dx}\left. \ \right \vert _{x_{eq}}\left( x - x_{eq} \right) + \ldots\] \[E_{p}(x) = E_{p}\left( x_{eq} \right) + \frac{dE_{p}}{dx}\left. \ \right \vert _{x_{eq}}\left( x - x_{eq} \right) + \frac{1}{2}\frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}}\left( x - x_{eq} \right)^{2} + \ldots\]Or \(F_{x}\left( x_{eq} \right) = \frac{dE_{p}}{dx}\left. \ \right \vert _{x_{eq}} = 0\) (car $M$ est à l’équilibre).
\[\text{Aussi},\ \frac{dF_{x}}{dx}\left. \ \right \vert _{x_{eq}} < 0\ \text{et}\ \frac{dE_{p}}{dx}\left. \ \right \vert _{x_{eq}} > 0\]Ainsi, avec $\alpha > 0$,
\[F_{x}(x) \approx - \alpha\left( x - x_{eq} \right) + \ldots\] \[E_{p}(x) \approx \frac{\alpha}{2}\left( x - x_{eq} \right) + cte\]Ces expressions sont analogues à celles du rappel élastique d’un ressort de raideur
\[k = \alpha = - \frac{dF_{x}}{dx}\left. \ \right \vert _{x_{eq}} = \frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}} > 0\]Exemple :
Cette approximation s’appelle « l’approximation harmonique ».
Exemple : Modèle de Lennard-Jones
Modèle d’interaction entre un électron et le noyau atomique. $(x > 0)$
\[E_{p}(x) = 4\epsilon\left\lbrack \left( \frac{\sigma}{x} \right)^{12} - \left( \frac{\sigma}{x} \right)^{6} \right\rbrack + cte\]Où $\lbrack\epsilon\rbrack = \lbrack énergie\rbrack$, $\epsilon > 0$
Et $\lbrack\sigma\rbrack = L$, $\sigma > 0$
- Le graphe de $E_{p}$ ressemble au schéma précédent.
Cherchons le point $x = x_{eq}$ où la dérivée s’annule.
\[x_{eq} = 2^{\frac{1}{6}}\sigma\]- Vérifions si l’équilibre est stable
Donc l’équilibre est stable. On peut faire l’approximation harmonique du modèle de Lennard-Jones.
\[x_{eq} = 2^{\frac{1}{6}}\sigma\] \[\text{Raideur du ressort associée}\ :k = \frac{d^{2}E_{p}}{dx^{2}}\left. \ \right \vert _{x_{eq}} = \frac{36\epsilon}{\sigma^{2}}\]Chapitre IV : Dynamique en termes de moment cinétique
I - Définition
Le moment cinétique d’un point matériel $M$ de masse $m$ par rapport à un point $A$ dans un référentiel $\mathcal{R}$ est noté $\overrightarrow{L_{A\mathcal{,R}}}$.
\[\overrightarrow{L_{A\mathcal{,R}}}(M) = \overrightarrow{AM} \land \overrightarrow{p_{\mathcal{R}}}(M)\ \text{où} \land \ \text{est le produit vectoriel}\] \[\overrightarrow{L_{B}}(M) = \overrightarrow{BM} \land \overrightarrow{p}(M) = \left( \overrightarrow{BA} + \overrightarrow{AM} \right) \land \overrightarrow{p}(M) = \overrightarrow{BA} \land \overrightarrow{p}(M) + \overrightarrow{AM} \land \overrightarrow{p}(M) = \overrightarrow{BA} \land \overrightarrow{p}(M) + \overrightarrow{L_{A}}(M)\] \[\overrightarrow{L_{B}}(M) \neq \overrightarrow{L_{A}}(M)\ \text{en général}\]Si les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{p}$ sont colinéaires, alors $\overrightarrow{L_{A}}(M) = \overrightarrow{0}$
Dimension physique :
\[\left\lbrack \overrightarrow{L} \right\rbrack = \left\lbrack \overrightarrow{AM} \right\rbrack\left\lbrack \overrightarrow{p} \right\rbrack = ML^{2}T^{- 1}\]Unité SI correspondante : $kg.m^{2}.s^{- 1}$
II - Produit vectoriel
Soit $E$ un espace vectoriel orienté de dimension 3.
Soit $\overrightarrow{w}$ le produit vectoriel de $\overrightarrow{u}$ et $\overrightarrow{v} \in E$
Alors $\overrightarrow{w} = \overrightarrow{u} \land \overrightarrow{v}\ \text{(notation française)} = \overrightarrow{u} \times \overrightarrow{v}\ \text{(notation anglo-saxonne)}$
\[\overrightarrow{w} \in E\]$\overrightarrow{w}$ est orthogonal à $\overrightarrow{u}$ et à $\overrightarrow{v}$
$\left( \overrightarrow{u},\overrightarrow{v},\overrightarrow{w} \right)\ \text{est dans le sens direct}$
N.B. : selon la règle de la main droite
\[\overrightarrow{p}ouce = \overrightarrow{i}ndex \land ma\overrightarrow{j}eur\]- $\left \Vert \overrightarrow{w} \right \Vert = \left \Vert \overrightarrow{u} \right \Vert .\left \Vert \overrightarrow{v} \right \Vert .\left \vert \sin\left( \overrightarrow{u},\overrightarrow{v} \right) \right \vert $
Propriétés :
Si $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires, alors $\overrightarrow{w} = \overrightarrow{0}$
$\overrightarrow{u} \land \overrightarrow{v} = - \left( \overrightarrow{v} \land \overrightarrow{u} \right)$
Le produit vectoriel est distributif : $\overrightarrow{u} \land \left( \overrightarrow{v} + \overrightarrow{w} \right) = \overrightarrow{u} \land \overrightarrow{v} + \overrightarrow{u} \land \overrightarrow{w}$
Produit par un scalaire : $\overrightarrow{u} \land \lambda\overrightarrow{v} = \lambda\left( \overrightarrow{u} \land \overrightarrow{v} \right)$
Le produit vectoriel n’est [pas associatif : $\overrightarrow{u} \land \left( \overrightarrow{v} \land \overrightarrow{w} \right) \neq \left( \overrightarrow{u} \land \overrightarrow{v} \right) \land \overrightarrow{w}$ en général
Interprétation géométrique :
Si $\overrightarrow{w} = \overrightarrow{u} \land \overrightarrow{v}$, alors $\left \Vert \overrightarrow{w} \right \Vert = \text{aire du parallélogramme construit par}\ \overrightarrow{u}\ \text{et}\ \overrightarrow{v}$
Coordonnées :
L’espace vectoriel $E$ est muni d’une base orthonormée directe $\left( \overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}} \right)$
\[\overrightarrow{e_{1}} \land \overrightarrow{e_{2}} = \overrightarrow{e_{3}}\] \[\overrightarrow{e_{2}} \land \overrightarrow{e_{1}} = - \overrightarrow{e_{3}}\] \[\overrightarrow{e_{1}} \land \overrightarrow{e_{3}} = - \overrightarrow{e_{2}},\ \ \overrightarrow{e_{3}} \land \overrightarrow{e_{1}} = \overrightarrow{e_{2}}\] \[\overrightarrow{e_{2}} \land \overrightarrow{e_{3}} = \overrightarrow{e_{1}},\ \ \overrightarrow{e_{3}} \land \overrightarrow{e_{2}} = - \overrightarrow{e_{1}}\] \[\overrightarrow{w} = \overrightarrow{u} \land \overrightarrow{v}\] \[\left( \begin{array}{r} w_{1} \\ w_{2} \\ w_{3} \end{array} \right) = \left( \begin{array}{r} u_{1} \\ u_{2} \\ u_{3} \end{array} \right) \land \left( \begin{array}{r} v_{1} \\ v_{2} \\ v_{3} \end{array} \right) = \left( \begin{array}{r} u_{2}v_{3} - u_{3}v_{2} \\ u_{3}v_{1} - u_{1}v_{3} \\ u_{1}v_{2} - u_{2}v_{1} \end{array} \right)\]III - Théorème du moment cinétique
Conséquence du PFD.
Dans un référentiel galiléen, par application du PFD au point matériel $M$ de masse $m$,
\[\frac{d\overrightarrow{p}}{dt} = m\frac{d\overrightarrow{v}}{dt} = \sum_{}^{}{\overrightarrow{F_{ext}}(M)}\ \text{où}\ \overrightarrow{p} = m\overrightarrow{v}\]Soit un point quelconque $O$ fixe dans ce référentiel.
\[\overrightarrow{OM} \land \frac{d\overrightarrow{p}}{dt} = m\overrightarrow{OM} \land \frac{d\overrightarrow{v}}{dt} = \overrightarrow{OM} \land \sum_{}^{}{\overrightarrow{F_{ext}}(M)}\] \[\text{Or}\ \overrightarrow{OM} \land \frac{d\overrightarrow{p}}{dt} = \frac{d\overrightarrow{L_{O}}(M)}{dt}\]En effet,
\[\frac{d\overrightarrow{L_{O}}(M)}{dt} = \frac{d}{dt}\left( \overrightarrow{OM} \land \overrightarrow{p} \right) = \frac{d}{dt}\left( \overrightarrow{OM} \land m\overrightarrow{v} \right) = m\left( \frac{d\overrightarrow{OM}}{dt} \land \overrightarrow{v} + \overrightarrow{OM} \land \frac{d\overrightarrow{v}}{dt} \right)\] \[\text{Or}\frac{d\overrightarrow{OM}}{dt} = \overrightarrow{v}\text{ donc}\frac{d\overrightarrow{OM}}{dt} \land \overrightarrow{v} = \overrightarrow{v} \land \overrightarrow{v} = \overrightarrow{0}\] \[\frac{d\overrightarrow{L_{O}}(M)}{dt} = m\overrightarrow{OM} \land \frac{d\overrightarrow{v}}{dt} = \overrightarrow{OM} \land \frac{d\overrightarrow{p}}{dt}\]Aussi,
\[\overrightarrow{OM} \land \sum_{}^{}{\overrightarrow{F_{ext}}(M)} = \sum_{}^{}{\overrightarrow{OM} \land \overrightarrow{F_{ext}}(M)} = \sum_{}^{}{\overrightarrow{\mathcal{M}_{O}}\left( \overrightarrow{F_{ext}} \right)}\ \text{où}\ \overrightarrow{\mathcal{M}_{O}}\ \text{est le moment de la force par rapport à}\ O\]Donc,
\[\frac{d\overrightarrow{L_{O}}(M)}{dt} = \sum_{}^{}{\overrightarrow{\mathcal{M}_{O}}\left( \overrightarrow{F_{ext}} \right)}\]Conséquence :
Si $M$ est un système isolé,
\[\sum_{}^{}{\overrightarrow{\mathcal{M}_{O}}\left( \overrightarrow{F_{ext}} \right)} = \overrightarrow{0} \Longrightarrow \overrightarrow{L_{0}}(M) = cte\]Concept lié à l’isotropie de l’espace : toutes les directions de l’espace sont équivalentes.
Chapitre V : Synthèse
En 1918, E. NOETHER montre qu’à toute transformation laissant invariant un système physique correspond une quantité conservée.
Propriété Invariance des lois physiques par Quantité conservée pour un système isolé dans R_gal Homogénéité du temps Translation dans le temps E Homogénéité de l’espace Translation dans l’espace p ⃗ Isotropie de l’espace Rotation dans l’espace L ⃗
| Propriété | Invariance des lois physiques par | Quantité conservée pour un système isolé dans $\mathfrak{R}_{galiléen}$ |
|---|---|---|
| Homogénéité du temps | Translation dans le temps | \(E\) |
| Homogénéité de l’espace | Translation dans l’espace | \(\overrightarrow{p}\) |
| Isotropie de l’espace | Rotation dans l’espace | \(\overrightarrow{L}\) |
Chapitre VI : Le problème à deux corps
I - Position du problème
On souhaite étudier le mouvement de deux points matériels $M_{1}$ et $M_{2}$ de masses respectives $m_{1}$ et $m_{2}$. Ces deux points sont en interaction mutuelle conservative, pas d’autre interaction.
Problème très important en mécanique classique. Historiquement apparu dans le contexte de la gravitation (KEPLER et NEWTON). Par exemple, on peut prendre $M_{1}$ le Soleil et $M_{2}$ une planète du système solaire.
Problème très important en mécanique quantique également (exemple : $M_{1} = \ \text{noyau}$ et $M_{2} = \ \text{électron}$).
Cas particulier du problème à $N$ corps. Avec $N = 2$, le problème est résolvable exactement. Pour $N = 3$, le problème est résolvable exactement mais quasi-impossible d’écrire la solution générale à cause d’une grande sensibilité aux conditions initiales (chaos).
Si on augmente encore $N$, on ne peut plus le résoudre exactement. On utilise essentiellement des solutions numériques approximes.
II - Réduction du problème de deux corps vers « un corps »
Propriétés :
- Conservation de \({\overrightarrow{p}}_{I}\) avec $I$ centre d’inertie du système isolé \(\left\{ M_{1} + M_{2} \right\}\)
- Le référentiel $\mathcal{R}_{I}$ lié à $I$ ($I$ immobile dans ce référentiel) et n’ayant pas de rotation par rapport à tout référentiel galiléen est un référentiel galiléen
Pour simplifier l’étude, et sans perte de généralité, on se place dans $\mathcal{R}_{I}$ et on prend l’origine du repère au point $I$.
- $m_{1}\overrightarrow{r_{1}} + m_{2}\overrightarrow{r_{2}} = \overrightarrow{0}$ avec $\overrightarrow{r_{i}}$ le vecteur position de $M_{i}$ dans $\mathcal{R}_{I}$ (1)
Dans \(\mathcal{R}_{I}\), on applique le PFD à \(M_{1}\) et \(M_{2}\).
$m_{1}\ddot{\overrightarrow{r_{1}}} = {\overrightarrow{F}}_{2 \rightarrow 1}$ (2)
\(m_{2}\ddot{\overrightarrow{r_{2}}} = {\overrightarrow{F}}_{1 \rightarrow 2}\) où \({\overrightarrow{F}}_{2 \rightarrow 1} = - {\overrightarrow{F}}_{1 \rightarrow 2}\)
On pose $\overrightarrow{r} = \overrightarrow{r_{2}} - \overrightarrow{r_{1}} = \overrightarrow{M_{1}M_{2}}$ (3)
En combinant (1) et (3), on forme (4) :
\[\overrightarrow{r_{1}} = - \frac{m_{2}}{m_{1} + m_{2}}\overrightarrow{r}\] \[\overrightarrow{r_{2}} = \frac{m_{1}}{m_{1} + m_{2}}\overrightarrow{r}\]On prend l’équation (2) et l’équation (4) pour former l’équation (5)
\[m_{2}\ddot{\overrightarrow{r_{2}}} - m_{1}\ddot{\overrightarrow{r_{1}}} = 2{\overrightarrow{F}}_{1 \rightarrow 2}\] \[2\frac{m_{1}m_{2}}{m_{1} + m_{2}}\ddot{\overrightarrow{r}} = 2{\overrightarrow{F}}_{1 \rightarrow 2}\] \[\frac{m_{1}m_{2}}{m_{1} + m_{2}}\ddot{\overrightarrow{r}} = {\overrightarrow{F}}_{1 \rightarrow 2} = F_{r}(r)\overrightarrow{u_{r}}\ \text{où}\ \overrightarrow{u_{r}} = \overrightarrow{u_{12}}\]Ne dépend que de $r$ car l’espace est isotrope.
Ainsi, le mouvement de $M_{1}$ et $M_{2}$ se réduit au mouvement d’un point matériel fictif de masse $\frac{m_{1}m_{2}}{m_{1} + m_{2}}$ notée $\mu$ : masse réduite du système \({ M_{1} + M_{2} }\) et soumis à $F_{r}(r)\overrightarrow{u_{r}}$ une force centrale (toujours orientée par $\overrightarrow{u_{r}}$) et conservative.
Mouvement d’un point matériel dans un champ de force centrale conservative
On considère un point matériel $M$ de masse $\mu$. Soit $O$ le centre du champ de force.
Dans le référentiel $\mathcal{R}_{I}$ galiléen, d’après le théorème du moment cinétique sur $M$ :
\[\frac{d\overrightarrow{L_{O}}}{dt} = \overrightarrow{\mathcal{M}_{O}}\left( \overrightarrow{F} \right) = \overrightarrow{OM} \land \overrightarrow{F} = r\overrightarrow{u_{r}} \land F_{r}(r)\overrightarrow{u_{r}} = \overrightarrow{0}\] \[\frac{d\overrightarrow{L_{O}}}{dt} = \overrightarrow{0}\ \text{donc le moment cinétique est conservé}\] \[\overrightarrow{L_{O}}(M) = \overrightarrow{OM} \land \overrightarrow{p} = \overrightarrow{OM} \land \mu\overrightarrow{v} = \overrightarrow{cte}\]Conséquence :
- $\overrightarrow{OM}\bot\overrightarrow{L_{O}}(M)$
Le mouvement de $M$ se fait dans le plan perpendiculaire au moment cinétique.
On se place dans un système de coordonnées cylindriques. Soit l’axe $(Oz)$ selon $\overrightarrow{L_{O}}(M)$
\[\overrightarrow{OM} = r\overrightarrow{u_{r}}\] \[\overrightarrow{v} = \dot{r}\overrightarrow{u_{r}} + r\dot{\theta}\overrightarrow{u_{\theta}}\] \[\overrightarrow{L_{O}}(M) = \overrightarrow{OM} \land \overrightarrow{p} = \mu\left( \overrightarrow{OM} \land \overrightarrow{v} \right) = \mu\left( r\overrightarrow{u_{r}} \land \left( \dot{r}\overrightarrow{u_{r}} + r\dot{\theta}\overrightarrow{u_{\theta}} \right) \right)\] \[\overrightarrow{L_{O}}(M) = \mu r^{2}\dot{\theta}\overrightarrow{u_{z}} = \overrightarrow{cte}\]Ainsi, $\dot{\theta}$ augmente quand $r$ diminue et $\dot{\theta}$ diminue quand $r$ augmente.
Soit $L = \left \Vert \overrightarrow{L_{O}}(M) \right \Vert = \mu r^{2}\dot{\theta}$
Conséquences : « Loi des aires »
On définit la vitesse aréolaire comme l’aire couverte par le vecteur $\overrightarrow{OM}$ par unité de temps.
\[= \frac{d\mathcal{A}}{dt} = \dot{\mathcal{A}}\] \[= \frac{1}{2}\frac{\left( \text{aire du parallélogramme construit par}\ \left( \overrightarrow{r},d\overrightarrow{r} = \overrightarrow{v}dt \right) \right)}{dt}\] \[= \frac{1}{2}.\frac{\overrightarrow{r} \land d\overrightarrow{r}}{dt}.\overrightarrow{u_{z}}\] \[= \frac{1}{2}\left( \overrightarrow{r} \land \overrightarrow{v} \right)\overrightarrow{u_{z}} = \frac{\overrightarrow{L_{O}}(M).\overrightarrow{u_{z}}}{2\mu} = \frac{L}{2\mu} = cte\]