CM

Posté le 07/02/2025

Chargé de TD/CM : N. Arancibia.

121 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276

Page 1 : Algebre 1 - Premier semestre 2024 - 2025Algebre 1 - Premier semestre 2024 - 2025Responsable CM :Nicolas Arancibia RobertBureau : Site St Martin, Bˆatiment E, cinquieme etage,Bureau 552e-mail : nat@cy-tech.fr - nicolas.arancibia-robert@cyu.frEvaluation :• DS 1 : Semaine du 21/10/202425• DS 2 : Semaine du 25/11/202425• Examen : Semaine du 13/01/202540• Note TD : 10Algebre1 / 269

Page 2 : Modalités d’Évaluations en MathématiquesPréing 1CYTech2024-2025

Page 3 : Modalités d’ÉvaluationVous aurez 4 notes :▶2 Contrôles continus : CC1 et CC2, durée 1h, en séance de TD▶Algèbre 1 : Semaines du 21 Octobre et du 25 Novembre.▶Analyse 1 : Semaines du 12 Novembre et du 9 Décembre.▶1 Contôle continu Final : CCF, durée 2h, semaine du 13 Janvier.▶1 note de TD : TD, donnée par l’enseignant.On calcule alors une moyenne pondérée MM = 0.25 × CC1 + CC2 + 0.4 × CCF + 0.1 × TDVotre note ﬁnale NF est le max entre la moyenne M et le CCFNF = maxM, CCF.2 of 6

Page 4 : ExemplesMoyenne : M = 0.25 × CC1 + CC2 + 0.4 × CCF + 0.1 × TD▶Exemple 1CC1 = 8 CC2 = 17 CCF = 9 TD = 19On calcule la moyenne :M = 0.25 × 8 + 17 + 0.4 × 9 + 0.1 × 19 = 11.75La note ﬁnale est le max entre M et CCF donc NF = 11.75▶Exemple 2CC1 = 15 CC2 = 2 CCF = 13 TD = 12On calcule la moyenne :M = 0.25 × 15 + 2 + 0.4 × 13 + 0.1 × 12 = 10.65La note ﬁnale est le max entre M et CCF donc NF = 13.3 of 6

Page 5 : Rattrapage pour AbsenceEn cas d’absence justiﬁée ou injustiﬁée la note correspondante dans laformule de la moyenne sera 0.Il y aura à la ﬁn de semestre une épreuve de rattrapage pour les absences quidurera 2h et portera sur l’ensemble du programme du semestre.Attention ! C’est un rattrapage pour les absences uniquement,indépendant des notes que vous avez obtenues.Si vous êtes absent.e à l’examen vous devez obligatoirement passer l’épreuvede rattrapage.Si vous êtes absent.e à CC1 ou CC2 vous pouvez passer l’épreuve derattrapage si vous le souhaitez. Il y aura une unique épreuve de rattrapage quiportera sur l’ensemble du semestre, même si vous la passez pour une absenceau CC1 ou CC2.La note R obtenue au rattrapage remplace le 0 dansle calcul de la moyenne M et de la note ﬁnale NF .4 of 6

Page 6 : Exemples▶Exemple 1CC1 = 10 CC2 = 15 CCF =ABS TD = 16Rattrapage OBLIGATOIRE. Vous obtenez R = 12 qui remplace CCFM = 0.25 × 10 + 15 + 0.4 × 12 + 0.1 × 16 = 12.65La note ﬁnale est le max entre M et CCF = R = 12 donc NF = 12.65▶Exemple 2CC1 = 12 CC2 = ABS CCF = 13 TD = 15On peut calculer la moyenne :M = 0.25 × 12 + 0 + 0.4 × 13 + 0.1 × 15 = 9.7La note ﬁnale est le max entre M et CCF donc a priori NF = 13.Rattrapage optionnel. Vous décidez de passer le rattrapage et obtenezR = 14, on recalcule alorsM ′ = 0.25 × 12 + 14 + 0.4 × 13 + 0.1 × 15 = 13.2La note ﬁnale est le max entre M ′ et CCF donc NF = 13.2.5 of 6

Page 7 : DéfaillanceVous serez déclaré Défaillant dans les 2 cas suivants :▶Vous avez été absent.e 2 fois parmi les épreuves CC1, CC2 et CCFinal.▶Vous avez été absent.e au CC Final et au Rattrapage.En cas de défaillance les jurys de ﬁn de semestre et de ﬁn d’année étudierontvotre dossier et prendront une décision sur la suite de vos études.6 of 6

Page 8 : Algebre 1 - Premier semestre 2023 - 2024Themes• Logique et raisonnement• Ensembles• Relations binaires• Applications• Nombres complexes• Polynˆomes• Fractions rationnellesAlgebre2 / 269

Page 9 : Logique et raisonnementCe chapitre regroupe les diﬀerents points de vocabulaire, notations etraisonnement necessaires pour la conception et la redaction eﬃcace d’unedemonstration mathematique. Nous allons donc apprendre a bien ecrire et a bienargumenter en mathematiques.Themes detailles• Rudiments de Logique• Propositions.• Quantiﬁcateurs.• Implication, contraposition, equivalence.• Modes de Raisonement• Contraposition• Par l’absurde• Par analyse-synthese• RecurrenceAlgebre3 / 269

Page 10 : Rudiments de LogiqueDeﬁnition PropositionOn appelle proposition ou assertion toute phrase P dont on peut dire si elleest vraie V ou fausse F.Autrement dit, on appelle proposition toute phrase P au sujet de laquelle on peutposer la question :P est-elle vraie ? Exemples :•3 × 3 = 9 est une proposition vraie.•7 est pair est une proposition fausse.•l’entier 49 est un carre est une proposition vraie 72 = 49.•Les zeros non triviaux de la fonction zˆeta de Riemann ont tous une partiereelle egale a 1/2 Hypothese de Riemann est une proposition dont on nesait pas s’il est vraie ou fausse. ConjectureAlgebre4 / 269

Page 11 : Rudiments de LogiqueRemarque : La plupart des phrases grammaticalement correctes sont despropositions, mais par exemple :•Dis-le-moi ! ,•Bonjour ,•Quelle heure est-il ? , ou•Comment vas-tu ? n’en sont pas, la question :Est-il vrai que bonjour ? n’a aucun sens.Algebre5 / 269

Page 12 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une propostion, c’estpour aﬃrmer qu’elle est vraie, et qu’on va la demontrer.On a plusiers types de propositions.Deﬁnition• Un Axiome est une proposition qui n’est pas demontrable mais que l’on considerevraie et que ce sera l’un de nos points de depart pour faire des mathematiques.Exemple : Axiomes d’Euclide, axiomes de Peano.• Un Theoreme est une proposition vraie particulierement important.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.• Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus important.Exemple : Lemme de Zorn, Lemme de Schwarz.• Un Corollaire est une proposition vraie, consequence immediate d’une autreproposition vraie.• Une Conjecture est une proposition qu’on pense generalement vraie, sans en avoirla preuve.Exemple : Conjecture de Riemann, Conjecture de Goldbach.Algebre6 / 269

Page 13 : Rudiments de LogiqueRemarque : Dans un cours de mathematiques, lorsqu’on enonce une propostion, c’estpour aﬃrmer qu’elle est vraie, et qu’on va la demontrer.On a plusiers types de propositions.Deﬁnition• Un Axiome est une proposition qui n’est pas demontrable mais que l’on considerevraie et que ce sera l’un de nos points de depart pour faire des mathematiques.Exemple : Axiomes d’Euclide, axiomes de Peano.• Un Theoreme est une proposition vraie particulierement important.Exemple : Theoreme Pythagore, Theoreme de Fermat-Wiles.• Un Lemme est une proposition vraie, utile a la demonstration d’une propositionplus important.Exemple : Lemme de Zorn, Lemme de Schwarz.• Un Corollaire est une proposition vraie, consequence immediate d’une autreproposition vraie.• Une Conjecture est une proposition qu’on pense generalement vraie, sans en avoirla preuve.Exemple : Conjecture de Riemann, Conjecture de Goldbach.2024-09-10AlgebreRudiments de LogiqueTheoreme de Fermat-Wiles :Il n’existe pas de nombres entiers strictement positifs x, y et z tels que :xn + y n = zn pour n N, n 2Lemme de Zorn :si un ensemble ordonne est tel que toute chaˆıne sous-ensemble totalementordonne possede un majorant, alors il possede un element maximal.Conjecture de Goldbach :Tout nombre entier pair superieur a 3 peut s’ecrire comme la somme de deuxnombres premiers.

Page 14 : Rudiments de LogiqueNotation : Lorsque une proposition depend d’une variable x appartenant a un ensembleE, on pourra la noter Px. L’ensemble E sera pour la plupart donne par N, Z, Q, R ouC, ou d’un sous-ensemble de l’un de ces ensembles.Exemples :• Si on pose Px : x 1, alorsP2est vraieP1est fausse.• On rappelle qu’un nombre premier est un entier naturel p 2 qui n’est divisible quepar 1 et par lui mˆeme.Si on posePn :n est un nombre premier alorsP7est vraieP8est fausseP6700417est vraieProuve par L. Euler 1732 .Algebre7 / 269

Page 15 : Rudiments de LogiqueNous disposons de deux types d’outils pour fabriquer des nouvelles propositions :• les operations sur les propositions :• Equivalence ⇐⇒• Negation non• Conjonction et• Disjonction ou• Implication =⇒et les quantiﬁcateurs :• Pour tout • Existe Algebre8 / 269

Page 16 : Rudiments de LogiqueLa premiere operation sur les propositions que nous allons etudier est l’equivalence.Deﬁnition EquivalenceSoient P et Q deux propositions. On deﬁnit la proposition P est equivalent a Q,noteeP ⇐⇒Q,comme la proposition etant vraie si P et Q ont la mˆeme valeur de verite, et faussesinon.Ce qui peut ˆetre resume par le tableau suivant, appele table de veritePQP ⇐⇒QVVVVFFFVFFFVVocabulaire : Lorsque P et Q sont equivalentes, on dit queP est vraie si et seulement si Q est vraie.Algebre9 / 269

Page 17 : Rudiments de LogiqueExemples :• Si x est un nombre reel, les enoncesx 8, 5 etx + 8x 5 0 sont equivalents.• L’aﬃrmationx = 3⇐⇒x + 2 = 5 est une aﬃrmation vraie pour tout reel x.• L’aﬃrmationx = 1⇐⇒x2 = 1 est une aﬃrmation qui n’est pas vraie pour tout reel x.Remarque : Deux propositions P et Q sont equivalentes si elles ont les mˆemestables de verites. En comparant les tables de verites nous pourrons donc veriﬁerla veracite d’une proposition.Algebre10 / 269

Page 18 : Rudiments de LogiqueLa deuxieme operation sur les propositions est la negation.Deﬁnition NegationLa proposition contraire de P, notee non P, et appelee negation de P, est laproposition deﬁnie comme etant vraie lorsque P est fausse et fausse lorsque P est vrai.On resume ceci par la table de verite suivantePnon PVFFVExemple :• La negation de mon chat est noir est mon chat n’est pas noir .• La negation de tous les chats sont noirs est il existe un chat qui n’est pasnoir .• La negation de x 0est x 0et non pas x 0.• La negation de f est la fonction nulle est f n’est pas la fonction nulle ouencore f ne s’annule pas en au moins un point Algebre11 / 269

Page 19 : Rudiments de LogiqueExemple : La negation de dans tous les pays, tous les musiciens sont mortels est il existe au moins un pays dans lequel on peut trouver au moins un musicienimmortel et non il existe un pays ou tous les musiciens sont immortels .Remarque : Nous allons voir un peu plus tard que les deux propositions suivantessont contraires l’une de l’autre•Quel que soit x, Px est vraie. etIl existe un x tel que Px estfaux .Algebre12 / 269

Page 20 : Rudiments de LogiqueLa negation veriﬁe la propriete suivant.Theoreme Double negationPour tout proposition P, on a l’equivalenceP⇐⇒non non P.Demonstration.On ecrit les tables de verite :Pnon Pnon non PVFVVFVFVFFVFPuisque la table de verite de P est la mˆeme que celle de non non P , onconclut que les deux aﬃrmations sont equivalents.Algebre13 / 269

Page 21 : Rudiments de LogiquePassons a etudier maintenant la conjonction et la disjonction de deux propositions.Deﬁnition Conjonction etA deux propositions P et Q, on peut associer la conjonction de P et Q, noteeP et Q ou P Qqui est• vraie si les deux propositions P et Q sont vraies ;• fausse si l’une au moins des deux propositions P ou Q est fausse.On resume ceci par la table de verite suivantePQP et QVVVVFFFVFFFFAlgebre14 / 269

Page 22 : Rudiments de LogiqueExemples :• Soit ABCD un rectangle. La propositionL’angle ABC est droit et les diagonales AC et BD se coupent en leurmilieu est vraie ou fausse ? Elle est vraie. En eﬀet•L’angleABC est droit est une proposition vraie.•Les diagonales AC et BD se coupent en leur milieu est une propositionvraie.• Soit ABC un triangle. La propositionAB AC + CBetABC+CAB+ dBCA = π est vraie ou fausse ? Elle est fausse. En eﬀet•AB AC + CB est une proposition fausse.•ABC+CAB+ dBCA = π est une proposition vraie.Algebre15 / 269

Page 23 : Rudiments de LogiqueDeﬁnition Disjonction ouA deux propositions P et Q, on peut associer la disjonction de P et Q, noteeP ou Q ou P Qqui est• vraie lorsque l’une au moins des deux propositions P ou Q est vraie ;• fausse si les deux propositions P et Q sont fausses.On resume ceci par la table de verite suivantePQP ou QVVVVFVFVVFFFExemple : Soit ABC un triangle. La propositionAB AC + CBouABC+CAB+ dBCA = π est Vraie.Algebre16 / 269

Page 24 : Rudiments de LogiqueRemarque : On prendra garde au fait que le ou logique est un ou inclusif,contrairement au ou du langage courant qui lui est en general exclusif.Distinguer :1. le ou exclusif de la langue fran¸caise : Fromage ou Dessert.On ne peut pas avoir les deux.2. le ou logique ou inclusif : On recrute un enseignant qui sait parlerl’allemand ou l’espagnolou On recrute un informaticien qui sait coder enC++ ou en Python.On peut avoir les deux.Algebre17 / 269

Page 25 : Rudiments de LogiqueEtudions comme la negation modiﬁe les conjonction et les disjonctions.Theoreme Lois de MorganSoit P et Q deux enonces. Alors• Conjonction : non P et Q ⇐⇒non P ou non Q.• Disjonction : non P ou Q ⇐⇒non P et non Q.Demonstration.Negation d’une conjonction : On ecrit les tables de verite :Pnon PQnon QP et Qnon P et Qnon P ou non QVFVFVFFVFFVFVVFVVFFVVFVFVFVVPuisque la table de verite de non P et Q est la mˆeme que celle de nonP ou non Q , on conclut que les deux aﬃrmations sont equivalents.Negation d’une disjonction : Mˆeme methode, voir TD pour les details.Algebre18 / 269

Page 26 : Rudiments de LogiqueDeﬁnition ImplicationEtant donnees deux propositions logiques P et Q, on deﬁnit la proposition Pimplique Q, noteeP =⇒Qcomme la proposition etant fausse dans le seul cas ou P est vraie et Q fausse. Onappelle P son antecedent et Q son consequent.On resume ceci par la table de verite suivantePQP =⇒QVVVVFFFVVFFVAlgebre19 / 269

Page 27 : Rudiments de LogiqueRemarque : Contrairement a P ou Q et P et Q, la table de verite deP =⇒Q n’est pas totalement intuitive. En eﬀet, si P est fausse, alorsl’implication est necessairement vraie. C’est-a-direFaux implique n’importe quoi .En particulier, faux implique faux est considere comme vraie en mathematique.Ce choix est en fait raisonnable. Imaginons par exemple l’assertion suivante :P =⇒Q : J’ai eu une discussion avec mon chien implique mon chien parle.Bien entendu, cette implication est juste, mais niP : J’ai eu une discussion avec mon chienniQ : mon chien parlene le sont.Algebre20 / 269

Page 28 : Rudiments de LogiqueExemples :•n est pair =⇒n est divisible par 2 est une proposition vraie.• Soient a et b deux reels. Alors• a = b =⇒a2 = b2 est vraie, mais• a2 = b2 =⇒a = b est fausse en general. En eﬀeta2 = a2zVrai=⇒a = a z FauxzFaux• a = b =⇒a = b est fausse en general. En eﬀeta = azVrai=⇒a = a z FauxzFauxAlgebre21 / 269

Page 29 : Rudiments de LogiqueVocabulaire : Nous utiliserons souvent le vocabulaire suivant, si P =⇒Q estvraie, nous dirons :si P alors Q.La assertion P est alors appeleeune condition suﬃsante de Q.Pour que Q soit vraie, il suﬃt que P soit vraie. Autrement dit, savoir que P estvraie permet de conclure que Q est vraie. En mˆeme temps, la assertion Q estappeleeune condition necessaire de P.Pour que P soit vraie, il faut que Q soit vraie. Autrement dit, si Q n’est pasvraie, alors P ne peut pas ˆetre vraie.Algebre22 / 269

Page 30 : Rudiments de LogiqueDistinguer :1. Pour aller visiter la Tour Eiﬀel,• Il faut que je prenne le Metro et que je marche.Faux : je peux prendre le bus.• Il suﬃt que je prenne le Metro et que je marche.Vrai2. Pour montrer que 231 n’est pas premier• Il suﬃt que je le decompose en produit de nombres premiers.Vrai : 231 = 3 × 7 × 11 suﬃt pour montrer que 231 n’est pas premier.• Il faut que je le decompose en produit de nombres premiers.Faux : je peux aussi ecrire 231 = 3 × 77.Algebre23 / 269

Page 31 : Rudiments de LogiqueDeﬁnition Reciproque, contraposee• On appelle reciproque de l’implication : P =⇒Q, la proposition :Q =⇒P.• On appelle contraposee de l’implication : P =⇒Q, la proposition :non Q =⇒non P.Exemple : Considerons la propositionP : La nuit, tous les chats sont gris• Sa reciproque est : Si tous les chats sont gris, alors il fait nuit.• Sa contraposee est : Si au moins un chat n’est pas gris, alors il fait jour.Remarque : Si une implication est vraie, sa reciproque n’est pas forcement vraie.Algebre24 / 269

Page 32 : Rudiments de LogiquePar contre toute implication est equivalente a sa contraposee.TheoremeSoit P et Q deux propositions. AlorsP =⇒Q⇐⇒non Q =⇒non P.Demonstration.On ecrit la table de verite de la proposition non Q =⇒non P.Pnon PQnon Qnon Q =⇒non PP =⇒QVFVFVVVFFVFFFVVFVVFVFVVVOn retrouve la mˆeme table de verite que la proposition P =⇒Q . Laproposition P =⇒Q et la proposition non Q =⇒non P sont doncequivalentes.Algebre25 / 269

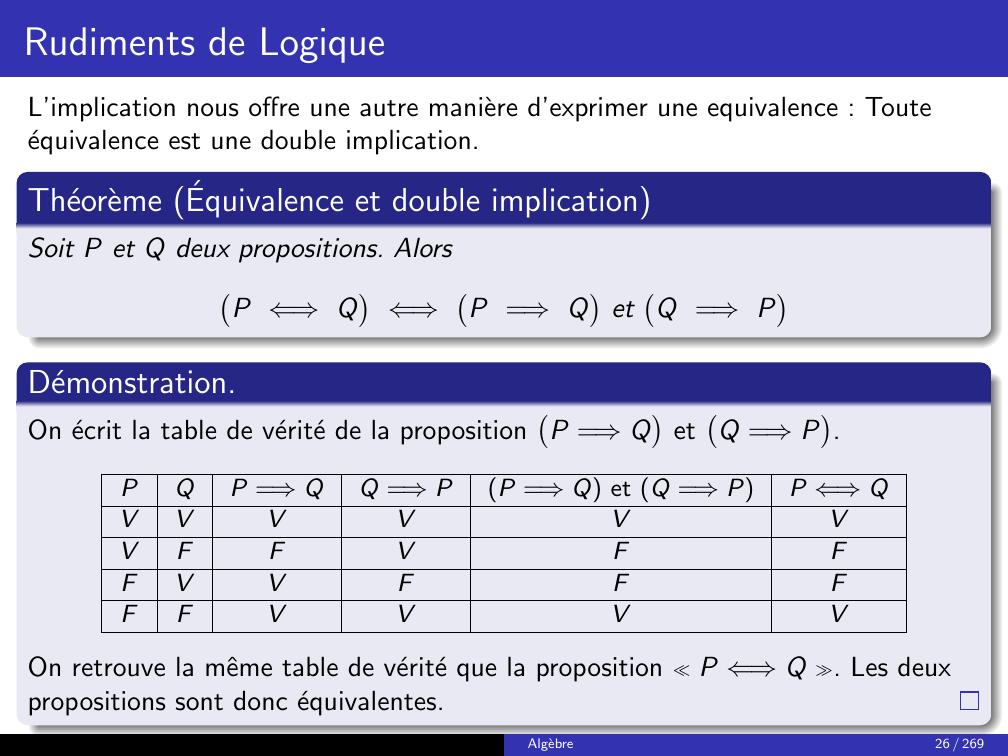
Page 33 : Rudiments de LogiqueL’implication nous oﬀre une autre maniere d’exprimer une equivalence : Touteequivalence est une double implication.Theoreme Equivalence et double implicationSoit P et Q deux propositions. AlorsP ⇐⇒Q⇐⇒P =⇒QetQ =⇒PDemonstration.On ecrit la table de verite de la propositionP =⇒QetQ =⇒P.PQP =⇒QQ =⇒PP =⇒Q et Q =⇒PP ⇐⇒QVVVVVVVFFVFFFVVFFFFFVVVVOn retrouve la mˆeme table de verite que la proposition P ⇐⇒Q . Les deuxpropositions sont donc equivalentes.Algebre26 / 269

Page 34 : Rudiments de LogiqueRemarque - Vocabulaire : Nous avons vu que, si P =⇒Q est vraie, alorsl’assertion P est appeleeune condition suﬃsante de Qet la assertion Q est appeleeune condition necessaire de P.Dans le cas ou P ⇐⇒Q, nous avons a la foisP =⇒QetQ =⇒P.Autrement dit, nous pouvons dire que P est une condition necessaire etsuﬃsante de Q. Ou encore que pour que Q soit vraie, il faut et il suﬃt que Psoit vraie.Algebre27 / 269

Page 35 : Rudiments de LogiqueLa proposition suivant nous donne une autre carecterisation de l’implication etnous indique comme l’implication est modiﬁee par la negation.PropositionSoit P et Q deux propositions. AlorsP =⇒Q⇐⇒non P ou Q,De plus par negation, on obtientnon P =⇒Q ⇐⇒P et non Q.Demonstration.Voir TD pour les details.Algebre28 / 269

Page 36 : QuantiﬁcateursUn autre outil pour deﬁnir des nouvelles propositions est la notion dequantiﬁcateur.Deﬁnition Quantiﬁcateur universel Le symbole place devant une variable x signiﬁe pour tout x , quelquesoit x . Ainsi la proposition :x E, Px,se litPour tout x appartenant a l’ensemble E on a Px.La proposition : x E, Px est donc• vraie si tout objet dans E a la propriete P, et• fausse sinon, c’est-a-dire si au moins un objet dans E n’a pas la propriete P.Algebre29 / 269

Page 37 : QuantiﬁcateursExemples :• x R, x2 ̸= 1 est une proposition vraie, car le carre d’un reel est toujourspositif.• x R, sin x 1 est une proposition vraie.• x R, x 1x 3 0, est une proposition fausse, puisque, par exemple,pour x = 2, on a x 1x 3 0.Algebre30 / 269

Page 38 : QuantiﬁcateursDeﬁnition Quantiﬁcateur existentiel Le symbole place devant une variable x signiﬁe il existe au moins un x .La propositionx E, Pxse lit doncIl existe un element x de E tel que Px.La proposition : x E, Px est donc• vraie si au moins un objet dans E a la propriete P, et• fausse sinon, c’est-a-dire si aucun objet dans E a la propriete P.Finalement, Le symbole ! place devant une variable x signiﬁeil existe un unique x.Algebre31 / 269

Page 39 : QuantiﬁcateursExemples :•z C, z2 = 1 est une proposition vraie car par example i2 = 1.• x R, x 1x 3 0, est une proposition vraie, puisque pour x = 4,l’inegalite est veriﬁee.•r Q, p N, pr Z est une proposition vraie.•n 2, 3, 4, · · · , n ̸= 23 et 23/n N est une proposition fausse.•!n N, 1 2n 3 est une proposition vraie. En eﬀet 1 est le seulentier satisfaisant la proposition.Algebre32 / 269

Page 40 : QuantiﬁcateursRemarque : L’ordre des quantiﬁcateurs est important. Il permet notamment dedeterminer quelles variables peuvent dependre des autres .On peut le constater en comparant par exemple les propositions :• x R, y R+, x2 = y, est une proposition vraie, car le carre de toutnombre reel est un reel positif.• y R+, x R, x2 = y, est une proposition fausse. En eﬀet, s’il existait unreel y veriﬁant x R, x2 = y alors on pourrait appliquer cette aﬃrmationavecx = 0etx = 1,et on obtiendrait02 = 12,ce qui est impossible.Algebre33 / 269

Page 41 : Rudiments de LogiqueTheoreme Negation des quantiﬁcateurs• La negation de : x E, Px estx E, non Px.• La negation de : x E, Px estx E, non Px.Remarque : C’est-a dire, pour nier une proposition contenant des quantiﬁcateurs,on change les en et reciproquement, puis on nie la conclusion. La negation dex, y, Px, yestx, y, non Px, y.Algebre34 / 269

Page 42 : Rudiments de LogiqueExemples : Ecrire les negation des propositions suivantes :• x R, sin x2 + cos x2 = 1.Solution : x R, sin x2 + cos x2 ̸= 1.• x R, x2 + x 2 = 0.Solution : x R, x2 + x 2 ̸= 0.• M R+, x R, f x M.Solution : M R+, x R, f x MAlgebre35 / 269

Page 43 : Rudiments de LogiqueEcriture : Mentionnons que, l’usage des symboles et est restreint auxassertions mathematiques. Ces symboles sont des quantiﬁcateurs, ils n’ont leurplace qu’a l’interieur d’une assertion. Dans une phrase en fran¸cais, nousprefererons l’usage de pour tout et il existe. De mˆeme, nous n’utiliserons pas=⇒mais les termes alors ou donc.Algebre36 / 269

Page 44 : Modes de raisonnementNous avons introduis la notion de proposition et donne une liste d’outils pour, apartir de propositions simples, construire des propositions plus complexes. Mais ildemeure une question important, comme on fait pour veriﬁer la veracite d’uneproposition ? Pour cela nous allons a present :• Introduire diﬀerents modes de raisonnement que vont nous permettre demontrer ou, au moins, de rendre plus facile la preuve de une assertion.Algebre37 / 269

Page 45 : Modes de raisonnement : ImplicationPour montrer une implication :P =⇒Q,plusieurs types de raisonnement peuvent ˆetre mis en oeuvre, donnons trois :• Raisonnement direct : On montre que si la proposition P est vraie alors laproposition Q est vraie. Quand on procede ainsi pour montrer que P =⇒Q, onecrit sans reﬂechir :Supposons P vraie. Montrons que Q est vraie....Preuve de Q.Algebre38 / 269

Page 46 : Modes de raisonnement : ImplicationExemple : Montrer que si n est un entier pair, alors n2 est pair.Preuve : Soit n N. On suppose que n est un entier pair. Montrons que n2 estpair. Comme n est un entier pair, il existe k N tel quen = 2k.Doncn2 = 4k2 = 22k2.C’est-a-dire n2 est pair.Algebre39 / 269

Page 47 : Modes de raisonnement : Implication• Raisonnement par contraposition : non Q =⇒non P. Rappelons que sila propositionnon Q =⇒non Pest vraie,alors la propositionP =⇒Qest vraie.C’est-a-dire, pour montrer P =⇒Q il suﬃt de montrernon Q =⇒non P.Pour cela on ecrit sans reﬂechir :Supposons non Q vraie. Montrons que non P est vraie....Preuve de nonP.Algebre40 / 269

Page 48 : Modes de raisonnnement : ImplicationExemple : Montrer par un raisonnement par contraposition que, si n2 est pair,alors n est pair.Preuve : Nous devons montrer la propositionsi n n’est pas pair, alors n2 n’est pas pair.C’est-a-dire, nous devons montrer la propositionsi n est impair, alors n2 est impair.Comme n est un entier impair, il existe k Z tel quen = 2k + 1.Doncn2 = 2k + 12 = 4k2 + 4k + 1 = 22k2 + 2k + 1.C’est-a-dire n2 est impair.Algebre41 / 269

Page 49 : Modes de raisonnement : Implication• Un type de raisonnement qui va se montrer tres utile dans la suite est leraisonnement par l’absurde. Pour pouvoir l’introduire, appelons d’abordcontradiction toute proposition de la forme :Q et non Q.Le principe du raisonnement par l’absurde s’enonce alors ainsi :Si d’une proposition on arrive a tirer une contradiction, c’est qu’elle estFAUSSE.Donc, quand on veut montrer qu’une proposition P est vraie, on peut raisonnerpar l’absurde de la maniere suivante :Faisons l’hypothese que P est fausseou que non P est vraie....Obtention d’une contradiction.Si on obtient une contradiction, c’est donc parce que l’hypothese de depart etaitfausse. Par consequent P est vraie.Algebre42 / 269

Page 50 : Modes de raisonnementExemple : On sait que π est irrationnel. Montrer que π3 est irrationnel. Preuve : Supposons par l’absurde que π3 est rationnel. Ecrivons-le donc sous formeπ3 = pqavec p Z et q N. Ainsiπ = 3pq .Par consequent, π est rationnel. C’est absurde donc π3 est irrationnel .Algebre43 / 269

Page 51 : Modes de raisonnement : ImplicationExemple :Montrer que2 est irrationnel.Preuve : Supposons par l’absurde que2 est rationnel et ecrivons-le donc sous formeirreductible :2 = pqavec p, q N× et p et q premiers entre eux n’ont pas de diviseur commun. L’egalite :p2 = 2q2 = 2q2montre que p2 est pair, et donc que p est pair d’apres l’exemple precedent. Ainsip = 2p′,pour un certain p′ Z.Par consequentq2 = p22=2p′22= 4p′22= 2p′2.Ceci montre que q2 est pair et donc que q est pair. Disonsq = 2q′, pour un certain q′ Z.Algebre44 / 269

Page 52 : Modes de raisonnement : ImplicationNous avions suppose la fraction pq irreductible, mais ﬁnalement nous l’avonsreduitepq = 2p′2q′ = p′q′ .Contradiction ! Donc la hypothese de depart est fausse. Comme voulu,2 estirrationnel.Algebre45 / 269

Page 53 : Modes de raisonnementRemarque : Le raisonnement par l’absurde nous donne une autre fa¸con demontrer l’implicationP =⇒Q.En eﬀet, comme P =⇒Q est equivalent a la propositionnon P ou Q,on en deduit que si la propositionP et non Q= nonnon P ou Qconduit a une contradiction, alors P =⇒Q est vraie.Algebre46 / 269

Page 54 : Modes de raisonnement : ImplicationExercice : Demontrer, en raisonnant par l’absurde, que si n N×, alors n2 + 1n’est pas le carre d’un entier naturel.Indication : Supposer que n est un entier positif strictement positif et quen2 + 1 est le carre d’un entier naturel a. Trouver une contradiction.Algebre47 / 269

Page 55 : Modes de raisonnement : EquivalencePour montrer une equivalence :P ⇐⇒Q,deux strategies sont possibles :• Double Implication : Soit on raisonne par double implication et on montreseparement les propositionsP =⇒QetQ =⇒P.C’est-a-dire, on ecritSupposons P vraie. Montrons que Q est vraie....Preuve de Q.ReciproquementSupposons Q vraie. Montrons que P est vraie....Preuve de P.Algebre48 / 269

Page 56 : Modes de raisonnement : EquivalenceExemple : On a vu que :• Si n est un entier pair, alors n2 est pair.• Si n2 est pair, alors n est pair.Donc n est pair si et seulement si n2 est pair.Algebre49 / 269

Page 57 : Modes de raisonnement : EquivalenceExemple : Montrer quex, y R,x2 + y 2 = 0 ⇐⇒x = y = 0.Preuve : Soient x, y R. L’implicationx2 + y 2 = 0 ⇐= x = y = 0est triviale, car si x = y = 0 alorsx2 = y 2 = 0et doncx2 + y 2 = 0.Pour la implication reciproque,x2 + y 2 = 0 =⇒x = y = 0;si x2 + y 2 = 0, alors :x20 = y 20,doncx2 = y 2 = 0et enﬁn : x = y = 0.Algebre50 / 269

Page 58 : Modes de raisonnement : Equivalence• De maniere directe : Soit on raisonne directement par equivalence enchangeant peu a peu P en Q :P ⇐⇒· · · ⇐⇒· · · ⇐⇒Q.Attention :• Cette strategie n’est pas toujours disponible et lorsqu’elle est utilisable il fautle faire avec precaution. En eﬀet, dans une chaˆıne d’equivalences, toutel’information doit ˆetre preservee d’une etape a l’autre, il faut donc lefaire soigneusement.• Dans la plupart de case c’est mieux de montrer des implications plutˆot quedes equivalences. Le raisonnement par equivalence est souvent inutile etgenerateur d’erreurs logiques.Algebre51 / 269

Page 59 : Modes de raisonnement : EquivalenceRemarque : Le raisonnement par equivalence permet de montrer qu’uneproposition est vraie en montrant qu’elle est equivalente a une proposition dont onsait deja qu’elle est vraie.Donnos un exemple de cette derniere remarque.Exemple : Montrer que pour tout x, y R2, xy 12x2 + y 2.Preuve : Soit x, y R2, on axy 12x2 + y 2⇐⇒2xy x2 + y 2⇐⇒0 x2 2xy + y 2⇐⇒0 x y2.La derniere proposition etant vraie, la premiere l’est egalement.Algebre52 / 269

Page 60 : Modes de raisonnement : Quantiﬁcateur universel Pour demontrer qu’une proprietex E, Pxest vraie,on doit etudier les diﬀerentes situations selon les valeurs de x. On procedetoujours comme suit : on ecrit sans reﬂechir :Soit x E. Montrons que Px...Preuve de Px.Exemple : Montrer que x R,x1+x2 12.Preuve : Soit x R. Montrons quex1+x2 12. On a0 x 12 = x2 2x + 1.Donc2x x2 + 1=⇒2xx2 + 1 1=⇒xx2 + 1 12.Algebre53 / 269

Page 61 : Modes de raisonnement : Quantiﬁcateur universel Remarque : Pour montrer qu’une assertion du typex E,Px,est fausse, on peut donner un contre-exemple, c’est-a-dire un exemple de x pourlequel Px n’est pas veriﬁee.Algebre54 / 269

Page 62 : Modes de raisonnement : Quantiﬁcateur universel Quand on veut montrer quex E, Pxet qu’on a deja en tˆete un exemple d’objet x E qui a la propriete P, on ecritsans reﬂechir :Posons x = · · ·l’exemple qu’on a en tˆete.Veriﬁons que Px....Veriﬁcations que x satisfait Px.Exemple : Montrer que x R, y R, z R, z x + y.Preuve : Soient x R, y R. Apres reﬂexion, posons :z = x + y + 1.Alors comme voulu : z x + y.Algebre55 / 269

Page 63 : Modes de raisonnement : Quantiﬁcateur universel La diﬃculte, bien sˆur, ne consiste souvent pas a veriﬁer que x a la propriete P,mais a avoir l’idee d’un exemple de tel objet x. Il n’existe helas pas de reglegenerale pour avoir des idees. Donnons tout de mˆeme une methode qui peuts’averer utile pour trouver x.Pour determiner les solutions d’un probleme, ou plus precisement l’ensemble deselements d’un ensemble E qui satisfont une propriete P, on raisonne souvent paranalyse-synthese.Algebre56 / 269

Page 64 : Modes de raisonnement : Analyse - Synthese• Analyse : On suppose que le probleme est resolu et on en deduit desconditions necessaires que la solution doit satisfaire. Pour cela on ecrit : Soitx E. Faisons l’hypothese que Px est vraie....On part na¨ıvement d’un element x de propriete P et onessaie de le faire parler pour savoir qui il est. Quellessont les possible valeurs de x ?• Synthese : On montre que ces conditions obtenues sont suﬃsantes, et onresout le probleme. Pour cela, on posex = · · ·Ici, les possibles valeurs de x trouvees dans l’analyse.On doit veriﬁer que x E et que Px est vraie :...Veriﬁcation que x appartient a E et satisfait la propriete P.Algebre57 / 269

Page 65 : Modes de raisonnement : Analyse - SyntheseEn Resume :• Dans l’analyse, on restraint le nombre des solutions possibles.• Dans la synthese, on veriﬁe que les possibilites obtenues dans l’analyse sonten fait des solutions.Algebre58 / 269

Page 66 : Modes de raisonnement : Analyse - SyntheseExemple : Determiner les solutions reelles de l’equationx + 6 = x.Solution :• Analyse : Supposons que x est solution de cette equation. Alorsx + 6 = x =⇒x + 6 = x2 =⇒x2 x 6 = 0.Doncx = 3oux = 2.Nous avons ainsi montre que si x est solution de x + 6 = x, alors necessairementx = 3 ou x = 2.• Synthese : On teste a present les valeurs obtenues : 2 ne convient pas puisque2 + 6 = 2 ̸= 2,mais 3 convient car on a bien3 + 6 = 3.Nous avons ainsi montre que l’equation x + 6 = x admet une unique solution x = 3.Algebre59 / 269

Page 67 : Raisonnement par recurrenceOn connait tres bienN = 0, 1, 2, 3, · · · l’addition, la multiplication sur N, ainsi que les relations, et .Dans cette section on s’interesse a une autre propriete de l’ensemble N, qui estessentielle : toute partie non vide A de l’ensemble N a un plus petit elementm. Ceci signiﬁe :• d’une part que m est un element de A N,• d’autre part que m est inferieur ou egal a tout element de A, c’est a direx A,m x.Cette propriete est la base du Raisonnement par Recurrence.Algebre60 / 269

Page 68 : Raisonnement par recurrenceProposition Recurrence SimpleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :• Initialisation : P0 est vraie,• Heredite : pour tout n N, si Pn est vraie, alors Pn + 1 est vraie.Alors la propriete Pn est vraie pour tout n N.Remarque : L’initialisation peut commencer a un entier k0 N arbitraire pasnecessairement 0 et dans ce cas la propriete n’est demontree vraie qu’a partir durang k0 : Si• Pk0 est vraie,• Pour tout entier n superieur ou egal a k0, Pn est vraie, alors Pn + 1 estvraie.Alors la propriete Pn est vraie pour tout entier superieur ou egal a k0.Algebre61 / 269

Page 69 : Raisonnement par recurrenceDemonstration.SoitA = n N : Pn est vraie.Pour montrer que A = N, on raisonne par l’absurde. Supposons donc A ̸= N, dans cecas, le complementaire Ac de la partie A dans N est non vide. Elle admet donc un pluspetit element que l’on note p. Puisque 0 A, on ap 1.De plus, comme p est le plus petit element de Ac, on deduit quep 1 0ne peut appartenir au complementaire de A. On a donc p 1 A. Ainsi Pp 1 estvraie, ce qui implique que Pp est vraie, et donc que p appartient a A. Finalement,p Aetp Ac.Contradiction ! ! Par consequent, A = N, est la proposition est vraie pour toutn N.Algebre62 / 269

Page 70 : Raisonnement par recurrenceQuand on veut montrer par recurrence quen N, Pn,on redige ainsi :• Initialisation : Veriﬁcation que P0 est vraie ou plus generalement Pk0si l’initialisation commence a k0.• Heredite : Soit n N. Supposons Pn vraie. Montrons que Pn + 1 estvraie :...Preuve que Pn + 1 est vraie.Algebre63 / 269

Page 71 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 2n n.Initialisation : On a 20 = 1 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire,2n n.Montrons que 2n+1 n + 1 est vraie. On a2n+1 = 2 · 2n = 2n + 2n.Ainsi, par hypothese de recurrence, on en deduit2n+1 = 2n + 2n n + 2n.Maintenant, pour tout n N on a2n 1.Par consequent2n+1 n + 2n n + 1.C’est-a-dire 2n+1 n + 1. Fin de la recurrence. Par consequent pour tout entier natureln, 2n n.Algebre64 / 269

Page 72 : Raisonnement par recurrenceExemple : Montrer que pour tout entier naturel n, 3n 1 est pair.Initialisation : On a 30 1 = 1 1 = 0, donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire3n 1 est pair=⇒3n 1 = 2k,k Z=⇒3n = 2k + 1.Montrons que 3n+1 1 est pair. On a3n+1 1= 3 · 3n 1 = 32k + 1 1 = 6k + 3 1 = 23k + 1.C’est-a-dire 3n+1 1 est pair. Fin de la recurrence. Par consequent, pour toutentier naturel n, 3n 1 est pair.Algebre65 / 269

Page 73 : Raisonnement par recurrenceIl arrive parfois qu’on ne sache pas deduire Pn + 1 de Pn, maisseulementPn + 2dePn et Pn + 1.Le principe du raisonnement par recurrence prend dans ce cas la forme suivante.Proposition Recurrence DoubleOn considere une propriete Pn dependant de l’entier n N, et on supposeque :• P0 et P1 sont vrais,• pour tout n N, si Pn et Pn + 1 sont vrais, alors Pn + 2 est vraie.Alors la propriete Pn est vraie pour tout n N.Remarque : Les recurrences classiques sont dites simples et il existe bien entendudes recurrences triples, etc.Algebre66 / 269

Page 74 : Raisonnement par recurrenceQuand on veut montrer par recurrence double quen N, Pn,on redige ainsi :• Initialisation : Veriﬁcation que P0 et P1 sont vrais.• Heredite : Soit n N. Supposons Pn et Pn + 1 sont vrais.Montronsque Pn + 2 est vraie....Preuve que Pn + 2 est vraie.Algebre67 / 269

Page 75 : Modes de raisonnementTheoreme Recurrence forteOn considere une propriete Pn dependant de l’entier n N, et on supposeque :• P0 est vraie,• pour tout n N, si Pk est vraie pour k n, alors Pn + 1 est vraie.Alors la propriete Pn est vraie pour tout n N.Exemple : Montrer que tout entier n 2 se decompose en produit de nombrespremiers.Algebre68 / 269

Page 76 : Ensembles• Introduction a la theorie des ensembles :• Deﬁnition et exemples.• Inclusion, Egalite.• Ensemble des parties• Operation sur les ensembles :• Intersection, Union.• Diﬀerence, Complementaire.• Partition d’un ensemble.• Produit Cartesien.Algebre69 / 269

Page 77 : EnsemblesDeﬁnition EnsembleUn ensemble E est une collection ou un groupement d’objets distincts. Lesobjets x de E s’appellent les elements de E.• Si E est un ensemble et si x est un element de E, on dit que x appartient aE ou que x est dans E et on ecritx E.• Dans le cas contraire, si x n’est pas un element de E, on dit que xn’appartient pas a E ou que x n’est pas dans E et on ecritx /E.Remarque :• Il existe un unique ensemble ne contenant aucun element. C’est l’ensemblevide note .• Un ensemble qui ne contient qu’un seul element est appele singleton.Algebre70 / 269

Page 78 : EnsemblesPour deﬁnir un ensemble, on peut le decrire :• Par extension : en donnant la liste complete explicite de tous ses elements.On note cette liste entre accolades, l’ordre des elements listes n’ayant aucuneimportance.Exemple :• 1, 1, 4, 1, 4, 9 et1, 4, 9, 11 = 9, 4, 11, 1.• 2N = 0, 2, 4, · · · : L’ensemble des entiers naturels pairs.• 2N + 1 = 1, 3, 5, · · · : L’ensemble des entiers naturels impairs.Algebre71 / 269

Page 79 : Ensembles• Par comprehension : en donnant une propriete P que ses elements veriﬁentet sont seuls a veriﬁer. On notex E : Pxoux E Pxl’ensemble des elements de E qui veriﬁent P.Exemple :• 2N = n N : k N, n = 2k : L’ensemble des entiers naturels pairs.• 2N + 1 = n N : k N, n = 2k + 1 : L’ensemble des entiers naturelsimpairs.• Q =x R : p Z, q N, x = pq: L’ensemble des rationnels.• a, b = x R : a x b : l’intervalle semi-ouverte a droite.Algebre72 / 269

Page 80 : EnsemblesDeﬁnition InclusionSoient E et F deux ensembles. On dit que E est inclus dans F , ou que F contient E, ouque E est une partie de F, ce qu’on noteE Fsi tout element de E est element de F, c’est-a-direx,x E =⇒x F.Exemple :• On a la suite d’inclusions1 1, 4 1, 4, 9 1, 4, 9, 11.• On a2N Net2N + 1 N.• On a la suite d’inclusionsN Z Q R C.• On aa, bR.Algebre73 / 269

Page 81 : EnsemblesAttention ! : Ne pas confondre appartenance et inclusion.• On a bien0 Nmais0 ̸N.Neanmoins0 N.Un element appartient a un ensemble.Par rapport a N, 0 est donc une bille dans un sac et non un sac dans un sac.• On a bienN ZmaisN /Z.Un ensemble est contenu dans un ensemble.Par rapport a Z, N est donc un sac dans un sac et non une bille dans un sac.Algebre74 / 269

Page 82 : EnsemblesQuand on veut montrer une inclusion :E F,on ecrit sans reﬂechir :Soit x E. Montrons que x F est vraie....Preuve que x F.Exemple : Montrer quex R : y R+, x y R+.Preuve : Soit x R. On suppose qu’il existe y R+ tel que x y. Montrons quex R+. Or y 0 par hypothese et x y, doncx 0.Ainsi, x R : y R+, x y R+.Algebre75 / 269

Page 83 : EnsemblesExemple : Montrer queE = kk + 1 : k N 2N.Preuve : Soit n E, alorsn = kk + 1pour un certain k N.Montrons que n 2N. On peut aﬃrmer que k est pair ou impair, et si k estimpair alors k + 1 est pair. Dans tous les caskouk + 1est pair.Par produit, n = kk + 1 l’est aussi, donc n 2N. Par consequent, E 2N.A faire chez soi :• Soit E l’ensemble des entiers naturels multiples de 6 et F l’ensemble desentiers naturels pairs. Montrer que E F.• Soit E = 2, 3 et F = x R : x2 3x 10 0. Montrer que E F.Algebre76 / 269

Page 84 : EnsemblesDeﬁnition EgaliteSoient E et F deux ensembles. Les ensembles E et F sont egaux s’ils ontexactement les mˆemes elements, i.e. si :x,x E ⇐⇒x F.Exemples :• Nous avonsx R : x2 3x 10 0 = 2, 5.• Nous avons0, 1 = n N : n2 = n.TheoremeSoient E et F deux ensembles. Alors :E = Fsi et seulement siE Fet F E.Algebre77 / 269

Page 85 : EnsemblesPour montrer une egalite d’ensembles :E = F,deux strategies sont possibles :• Soit on raisonne par double inclusion : En montrant d’abord E F :Soit x E. Montrons que x F est vraie....Preuve que x F.Puis, en montrant F E :Soit x F. Montrons que x E est vraie....Preuve que x E.• Soit on raisonne directement par equivalence :x :x E ⇐⇒· · · ⇐⇒· · · ⇐⇒x F.Algebre78 / 269

Page 86 : EnsemblesExemple : Montrer queR= x R : y R+x y.Preuve : On raisonne par double inclusion• MontronsRx R : y R+x y.Soit x R. Nous devons montrer que y R+, x y, mais par hypothesex 0. Doncx 0 y.• Montronsx R : y R+x y R.Soit x R tel que y R+, x y. Alors en particulier, pour y = 0 on ax 0. C’est-a-dire x R.Algebre79 / 269

Page 87 : EnsemblesDeﬁnition Ensemble des parties d’un ensembleSoit E un ensemble. On note PE l’ensemble des parties de EPE = A : A E.Remarque : Pour tout ensemble A :A PE⇐⇒A E, i.e. la notation A E a la mˆeme signiﬁcation quela notation A PE.a E ⇐⇒a E ⇐⇒a PE.PEetE PE.Exemple : Determiner l’ensemble des parties de E lorsque :• E = a, b :PE = , a, b, a, b.• E = a, b, c :PE = , a, b, c, a, b, b, c, a, c, a, b, c.Algebre80 / 269

Page 88 : Operations sur les ensemblesEtudions certaines operations sur les ensembles.Deﬁnition IntersectionSoit E un ensemble, et soient A et B deux sous-ensembles de E.• L’intersection de A et B est l’ensemble, note A B, deﬁni par :A B = x E : x Aetx B.En d’autres termes, l’intersection de A et de B est l’ensemble des elementsqui sont a la fois dans A et dans B.Diagramme de Venn :Algebre81 / 269

Page 89 : Operations sur les ensemblesExemple :• 1, 4, 7 3, 5, 7, 11 = 7.• Z Q = Z.•1, 5 0, 7 4, 9 = 0, 5 4, 9 = 4, 5.• On ax, y R2 : x2 + y 2 = 1 x, y R2 : x = y= 22 , 22!, 22 ,22!.• R+ R= 0.• 2N 2N + 1 = .Algebre82 / 269

Page 90 : Operations sur les ensemblesDeﬁnition Ensembles disjointsSoient A et B deux ensembles. On dit que A et B sont disjoints siA B = .Autrement dit si A et B n’ont aucun element commun.Algebre83 / 269

Page 91 : Operations sur les ensemblesDeﬁnition UnionSoit E un ensemble, et soient A et B deux sous-ensembles de E.• L’union de A et B est l’ensemble, note A B, deﬁni par :A B = x E : x Aoux B.En d’autres termes, l’union de A et de B est l’ensemble des elements quiappartiennent a A ou a B. Le ou utilise ici est inclusif : x est unelement de A ou un element de B ou un element de A et de B.Diagramme de Venn :Algebre84 / 269

Page 92 : Operations sur les ensemblesExemple :• 3, 4, 7, 9 2, 7, 9, 10, 21, 84 = 2, 3, 4, 7, 9, 10, 21, 84.• R+ R= R.• Q I = R.• 1, 1 1, 1 = 1, 1.Remarque :• Si A B. AlorsA B = AetA B = B.• Soient A et B deux ensembles. Alors on a toujours les inclusions suivantes :A B A A BetA B B A B.Algebre85 / 269

Page 93 : Operations sur les ensemblesL’union et l’intersection se generalisent facilement au cas de plus de deux ensembles.DeﬁnitionSoit E un ensemble et n un entier superieur ou egale a 2. Supposons donnes nsous-ensemblesA1, A2, · · · , An,de E.• Union :A1 A2 · · · An =i1,2,··· ,nAi = x E : i 1, 2, · · · , n, x Ai.i.e. l’ensemble des objets qui appartiennent a l’un des Ai.• Intersection :A1 A2 · · · An =\i1,2,··· ,nAi = x E : i 1, 2, · · · , n, x Ai.i.e. l’ensemble des objets qui appartiennent a tous les Ai.Algebre86 / 269

Page 94 : Operations sur les ensemblesL’union et l’intersection satisfont les proprietes suivants.TheoremeSoit E un ensemble, et considerons trois sous-ensembles A, B, C de E.• L’intersection et l’union sont commutatives :A B = B AetA B = B A.• L’intersection et l’union sont associatives :A B C = A B C = A B C,A B C = A B C = A B C.• Pour tout sous-ensemble A de E on aA E = A.• Pour tout sous-ensemble A de E on aA = A.Algebre87 / 269

Page 95 : Operations sur les ensemblesTheoremeSoit E un ensemble, et considerons trois sous-ensembles A, B, C de E.• L’intersection et la reunion sont distributives l’une par rapport a l’autre :A B C=A B A C,A B C=A B A C.Demonstration.Voir TD.Algebre88 / 269

Page 96 : Operations sur les ensemblesDeﬁnition DiﬀerenceSoit E un ensemble, et soient A et B deux sous-ensembles de E.• La diﬀerence de A avec B, note A \ B, est l’ensemble de tous les elementsde A qui ne sont pas dans B, i.e.A \ B = x E : x A et x /B.Diagramme de Venn :Algebre89 / 269

Page 97 : Operations sur les ensemblesDeﬁnition Diﬀerence SymetriqueSoit E un ensemble, et soient A et B deux sous-ensembles de E.• La diﬀerence symetrique de A avec B, note AB, est l’ensemble deselements qui sont dans un et un seul des deux ensembles A et B, i.e.AB = A B \ A B = A \ B B \ A.Diagramme de Venn :Algebre90 / 269

Page 98 : Operations sur les ensemblesDeﬁnition ComplementSoient E un ensemble et A une partie de E.• Le complementaire de A dans E est l’ensemble, note C EA , de tous leselements de E qui ne sont pas dans A,i.e.C EA = x : x E et x /A = E \ A.Diagramme de Venn :Remarque : S’il n’y a pas d’ambig¨uite sur l’ensemble E, on privilegiera lanotation Ac pour C EA .Algebre91 / 269

Page 99 : Operations sur les ensemblesLe passage au complementaire satisfait les proprietes suivantes.TheoremeSoient A et B deux parties de E.1. Acc = Aetc = EetE c = .2. Si A B, alorsBc Ac.3. Lois de Morgan :A Bc = Ac BcetA Bc = Ac Bc.Demonstration.Voir TD.Algebre92 / 269

Page 100 : Partition d’un ensembleDeﬁnition PartitionUne partition d’un ensemble E est un ensembleA1, A2, · · · , Anconstitue de parties de E veriﬁant :• Pour tout k 1, · · · , n, Ak ̸= , i.e. aucun Ak ne doit ˆetre vide.•nk=1Ak = E, i.e. la reunion des Ak est egale a E.• Pour tout couple Ai, Aj avec Ai ̸= Aj on a Ai Aj = , i.e. les Ai sont deux a deuxdisjoints.Diagramme de Venn :Algebre93 / 269

Page 101 : Partition d’un ensembleExemples :• L’ensemble 2N, 2N + 1 deﬁnit une partition de N.• L’ensemble Q, I deﬁnit une partition de R.• L’ensemble 0, 12, 12, 32, 32, 2 deﬁnit une partition de 0, 2.Exercice : Donner toutes les partitions de l’ensembleE = a, b, c.Solution :• P0 = E = a, b, c.• P1 = a, b, c.• P2 = a, b, c et P′2 = b, a, c et P′′2 = a, b, c.Algebre94 / 269

Page 102 : Produit CartesienOn ﬁnit ce chapitre en rappelant la deﬁnition du produit cartesien.Deﬁnition Produit CartesienSoient A et B deux parties de E. Le produit cartesien de A et B est l’ensemble,noteA × B,constitue de tous les couples x, y oux Aety B.On a donc :A × B =x, y : x A et y B.Exemple : Soit A = a, b et B = 1, 2, alorsA × B = a, 1, a, 2, b, 1, b, 2.Algebre95 / 269

Page 103 : Produit CartesienExemple : AvecC = 1, 2etD = 1, 2, 3on aC × D = 1, 1, 1, 2, 1, 3, 2, 1, 2, 2, 2, 3.Remarque : On ne confond pas les couples a, b et b, a qui designent deuxobjets diﬀerents, alors que a, b et b, a designent le mˆeme ensemble.L’exemple montre que le premier et le deuxieme terme du couple n’appartiennentpas au mˆeme ensemble.Algebre96 / 269

Page 104 : Produit CartesienLe produit cartesien se generalise au cas de plus de deux ensembles.Deﬁnition Produit cartesien d’une famille ﬁnie d’ensemblesSoit n un entier superieur ou egale a 2. Supposons donnes n ensemblesA1, A2, · · · , An.Alors le produit cartesien de A1, A2, · · · , An est l’ensemble deﬁni parA1 × A2 × · · · × An=x1, x2, · · · , xn : x1 A1, x2 A2, · · · , xn An=x1, x2, · · · , xn : i 1, · · · , n, xi Ai.L’element x1, x2, · · · , xn est appele un n-tuple de composants x1, x2, · · · , xn.Remarque :• Lorsque A = B, on noteA × A = A2.et on generalise cette notation pour l’ensembleAn = A × A × · · · × A.produit cartesien de n facteurs egaux a A.• La diagonale de A2 est l’ensemble = x, x, x A.Algebre97 / 269

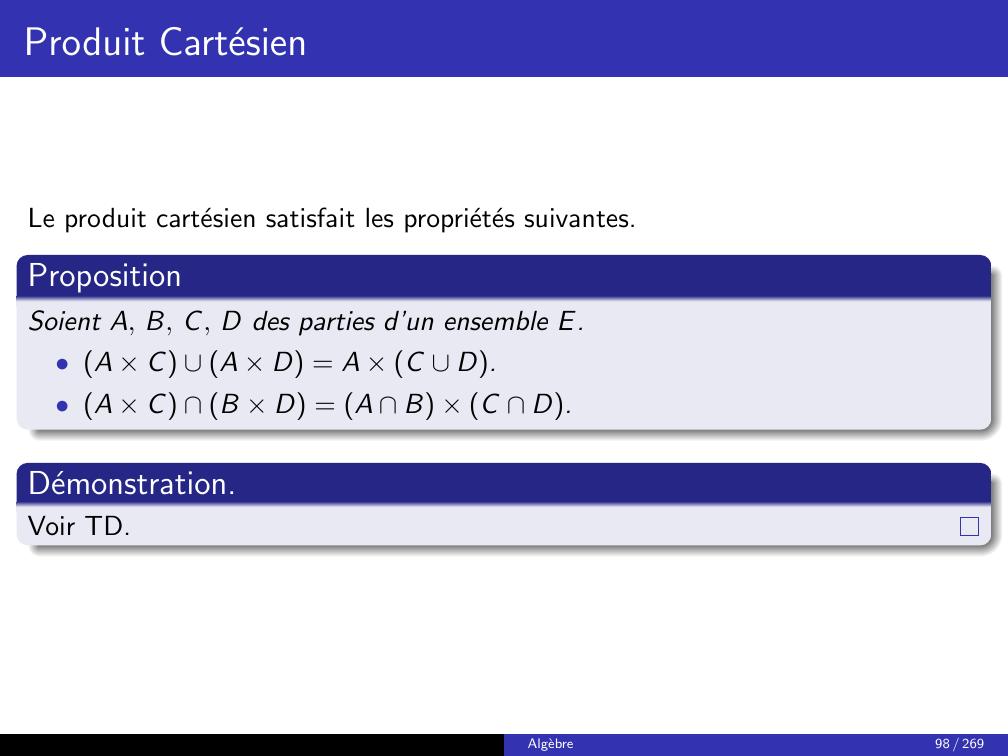
Page 105 : Produit CartesienLe produit cartesien satisfait les proprietes suivantes.PropositionSoient A, B, C, D des parties d’un ensemble E.• A × C A × D = A × C D.• A × C B × D = A B × C D.Demonstration.Voir TD.Algebre98 / 269

Page 106 : Relations Binaires• Relation d’equivalence :• Classes d’equivalence.• Partition d’un ensemble par une relation d’equivalence.• Relation d’ordre :• Relation d’ordre partiel, totale.• Relation d’ordre stricte.• Minimum, maximum, borne inferieure, borne superieure.Algebre99 / 269

Page 107 : Relations BinairesDeﬁnitionSoient E et F deux ensembles. On appelle relation R de E sur F la donnee d’unepartieR E × F.• La partie R est appele le graphe de la relation R.• On dit qu’un element x E est en relation avec un element y F six, y R.• On exprime cette situation en ecrivant xRy. C’est-a-direxRy ⇐⇒x, y R.Finalement, si E = F la relation R est appelee relation binaire.Algebre100 / 269

Page 108 : Relations BinairesExemple : Soit E = 1, 2, 3, 4 et R la relation binaire sur E dont le graphe estdonne parR = 1, 1, 1, 3, 2, 2, 2, 4, 3, 1, 3, 3, 4, 2, 4, 4.C’est-a-direaRb⇐⇒a, b R.Ainsi, par exemple1R1et1R3,mais1 n’est pas en relation avec 2et1 n’est pas en relation avec 4.Algebre101 / 269

Page 109 : Relations BinairesExemple :• La relation d’inclusion dans l’ensemble des parties de EARB ⇐⇒A B.Ici doncR = A, B PE × PE : A B.• La relation de divisibilite sur les entiers relatifsmRn ⇐⇒mnm divise n.Ici doncR = m, n Z × Z : mn Z.• Sur tout ensemble E, on peut deﬁnir la relation egalitexRy ⇐⇒x = y.Ici doncR = a, b E × E : a = b.• Les relations et sur R, sont aussi des relations binaires.Algebre102 / 269

Page 110 : Relations BinairesRemarque : Parce que le couple x, y n’est pas egal au couple y, x, la relationxRy peut ˆetre vraie sans que la relation yRx le soit. Par exemple, si on considerela relation d’inclusion sur R, nous avons0, 2R0, 2car0, 20, 2,mais 0, 2 n’est pas inclus dans 0, 2, donc0, 2n’est pas en relation avec0, 2.Algebre103 / 269

Page 111 : Relations BinairesEtudions certaines proprietes eventuelles des relations binaires.DeﬁnitionSoit R une relation binaire sur E.• On dit que R est reﬂexive si :x E,xRx• On dit que R est transitive si :x E, y E, z E,xRy et yRz=⇒xRz• On dit que R est symetrique si :x E, y E,xRy =⇒yRx• On dit que R est antisymetrique si :x E, y E,xRy et yRx=⇒x = y.Algebre104 / 269

Page 112 : Relations BinairesRemarque : L’antisymetrie n’est pas le contraire de la symetrie. Par exemple, larelation egalite possede les deux proprietes.Exemples :• Soit E = 1, 2, 3, 4. Alors la relation binaire R sur E dont le graphe estdonne parR = 1, 1, 1, 3, 2, 2, 2, 4, 3, 1, 3, 3, 4, 2, 4, 4,est reﬂexive, symetrique et transitive.• La relation d’egalite ” = ” sur E est reﬂexive, transitive, symetrique etantisymetrique.• La relation d’inclusion sur PE est reﬂexive, transitive etantisymetrique.Algebre105 / 269

Page 113 : Relations BinairesExemples :• La relation sur R est reﬂexive, transitive et antisymetrique. Elle n’est passymetrique car par exemple : 2 5 mais : 5 2.• La relation sur R est transitive et antisymetrique, mais elle n’est nireﬂexive, ni symetrique.• La relation de divisibilite sur Z est reﬂexive et transitive, mais elle n’est pasantisymetrique car par exemple : 5 5 et 55 mais 5 ̸= 5.Algebre106 / 269

Page 114 : Relation d’equivalenceNous allons etudier deux importants types des relations binaires : Les relationsd’equivalence et les relations d’ordre. Commencons par etudier les relationsd’equivalence.DeﬁnitionOn dit qu’une relation binaire R sur E est une relation d’equivalence si R est ala fois reﬂexive, transitive et symetrique.Pour a E, l’ensemble des elements x E en relation avec a est appele la classed’equivalence de a, noteeclaouaoua.C’est-a-direcla = x E : aRx.Exemple : Soit n un entier naturel. La relation sur Z deﬁnie paraRb⇐⇒n divise a best une relation d’equivalence. Si aRb on dit que a et b sont congrus modulo n.Algebre107 / 269

Page 115 : Relation d’equivalenceExemple : Soit E = 1, 2, 3, 4. Nous avons vu que la relation binaire R sur Edont le graphe est donne parR = 1, 1, 1, 3, 2, 2, 2, 4, 3, 1, 3, 3, 4, 2, 4, 4,est reﬂexive, symetrique et transitive. C’est-a-dire, R est une relationd’equivalence. De plus, nous avonscl1=1, 3=cl3,cl2=2, 4=cl4.Algebre108 / 269

Page 116 : Relation d’equivalenceL’ensemble des classes d’equivalence nous donnent une partition de l’ensemble E.Proposition Partition d’un ensemble en classes d’equivalenceSoit R une relation d’equivalence sur un ensemble E. Alors les classesd’equivalences forment une partition de E, c’est-a-dire• toute classe d’equivalence est non vide :x E,clx ̸= ,• deux classes d’equivalence sont soit disjointes soit egales :x, y Etel queclx ̸= clyon aclx cly = ,• la reunion des classes d’equivalence est egale a E :E =xEclx.Algebre109 / 269

Page 117 : Relation d’ordrePassons a etudier les relations d’ordre.DeﬁnitionOn dit qu’une relation binaire R sur E est une relation d’ordre si R est a la foisreﬂexive, transitive et antisymetrique.• Les relations d’ordre sont generalement notees ou ou ou ⪯.• Soit une relation d’ordre sur E, on dit alors que E, est un ensembleordonne.Deﬁnition Ordre total ou ordre partielSoit une relation d’ordre sur E.• Deux elements x et y de E sont dits comparables pour six youy x.• Si deux elements quelconques sont toujours comparables, on dit que estune relation d’ordre total. E est dit totalement ordonne par .• Sinon, on dit que est une relation d’ordre partiel. E est dit partiellementordonne par .Algebre110 / 269

Page 118 : Relation d’ordreExemple :• Sur N, Z, Q et R on a une relation d’ordre total, notee Voir coursd’analyse.• Sur PE, la relationA B ⇐⇒A Bc’est une relation d’ordre partiel sauf si E = ou E = a. En eﬀet, sia E, b E, a et b non comparables.• Sur R2x, y x′, y ′⇐⇒x x′ety y ′est un ordre partiel. Par exemple 1, 2 et 4, 0 non comparables.Algebre111 / 269

Page 119 : Relation d’ordreDeﬁnition Relation stricte associee a une relation d’ordreSoit une relation d’ordre sur E. On deﬁnit alors une nouvelle relation sur E parx, y E,x y⇐⇒x yetx ̸= y.La relation on l’appelle la relation stricte associee a .Exemple : Naturellement, la relation usuelle sur R est la relation stricte de larelation .Attention ! : La relation stricte n’est pas une relation d’ordre car elle n’est pasreﬂexive : On ne peut pas avoirx x et x ̸= x.PropositionLa relation est transitive et antisymetrique.Algebre112 / 269

Page 120 : Relation d’ordreDeﬁnition Majorant - MinorantSoit A une partie d’un ensemble E muni d’une relation d’ordre ⪯.• A est majoree s’il existe M E tel que pour tout x A nous avonsx ⪯M.On dit alors que M est un majorant de A.• A est minoree s’il existe m E tel que pour tout x A nous avonsm ⪯x.On dit alors que m est un minorant de A.• A est bornee lorsque A est a la fois majoree et minoree. C’est-a-dire, s’ilexiste m E et M E tel que pour tout x A nous avonsm ⪯x ⪯M.Algebre113 / 269

Page 121 : Relation d’ordreRemarque : On ne parle jamais du majorant d’une partie majoree de E maisbien toujours d’UN majorant car une telle peut posseder plein. Mˆeme chose adire sur les minorants.Exemple :• L’ensemble 8, 10, 12 est minore par 2 et majore par 120 pour la relation dedivisibilite sur N.• PE est minore par et majore par E pour la relation d’inclusion .• Tout reel inferieur ou egal a 0 est un minorant de l’intervalle 0, 1 par rapporta la relation d’ordre usuelle sur R. Tout reel superieur ou egal a 1 est unmajorant de l’intervalle 0, 1 par rapport a la relation d’ordre usuelle sur R.Algebre114 / 269

Page 122 : Relation d’ordreUn majorant ou minorant de une partie A de E, n’appartient pas necessairement aA. Quand il appartient a l’ensemble on dit :Deﬁnition Maximum - MinimumSoit A une partie d’un ensemble E muni d’une relation d’ordre.• Plus grand element : On appelle plus grand element de A ou maximumde A tout element de A qui majore A. C’est-a-dire,tout majorant de A qui est dans A.• Plus petit element : On appelle plus petit element de A ou minimum deA tout element de A qui minore A. C’est-a-dire,tout minorant de A qui est dans A.Exemple : On travaille dans cette serie d’exemples avec l’ordre usuel sur R.• 0 est le plus petit element de R+ et le plus grand element de R.• 0, 1 ne possede ni plus petit element ni plus grand element.• 0 est le plus petit element de 0, 1, et 1 est le plus grand element de 0, 1.Algebre115 / 269

Page 123 : Relation d’ordreExemple : On travaille dans cette serie d’exemples avec la relation de divisibilite sur N.• L’ensemble 2, 3, 6 possede un plus grand element, c’est 6, mais pas de pluspetit element.• 0 est le plus grand element de N et 1 est son plus petit element.• L’ensemble N \ 0, 1 ne possede ni plus petit element ni plus grand element.Theoreme UniciteSoit une relation d’ordre et A une partie de E. Si A possede un plus grandresp. petit element, celui-ci est UNIQUE. On peut donc l’appeler LE plusgrand resp. petit element de A et le notermax Aresp.min A.Algebre116 / 269

Page 124 : Relation d’ordreL’intervallea, bpour la relation d’ordre usuel n’a pas de plus grand element, pourtant sa borne b estquelque chose de cet ordre mais quoi ? Comment decrire conceptuellement ce reel quin’est pas dans a, b mais qui n’est pas n’importe qui pour a, b?Ce qui rend le majorant b si particulier pour a, b, c’est qu’il est le meilleur majorantqu’on pouvait esperer :LE PLUS PETIT POSSIBLE.Nous allons donc le donner un nom au plus petit majorant et au plus grand minorant.DeﬁnitionSoit A une partie de un ensemble E muni d’une relation d’ordre.Si l’ensemble des minorants de A admet un plus grand element, on l’appelle borneinferieure de A et on le noteinf A.Si l’ensemble des majorants de A admet un plus petit element, on l’appelle bornesuperieure de A et on le notesup A.Algebre117 / 269

Page 125 : Relation d’ordreRemarque : La diﬀerence essentielle entre les plus grands elements et les bornessuperieures d’une partie A, c’est que les bornes superieures n’appartiennent pasforcement a A.Exemple : Avec l’ordre usuel sur R, les intervalles a, b, a, b, a, b et a, b onta pour borne inferieur et b pour borne superieur.Theoreme Lien entre les notions de plus grand/petit element etborne superieure/inferieureSoit une relation d’ordre et A une partie de E. Si A possede un plus grandresp. petit element, alors A possede une borne superieure resp. inferieure et :supA = maxAresp. infA = minA.Exemple : Avec l’ordre usuel sur R on a :infa, b = mina, b = aetsupa, b = maxa, b = b.Algebre118 / 269

Page 126 : ApplicationsDeﬁnition ApplicationSoient E et F deux ensembles. Une application f de E vers F est le moyend’associer, a chaque element x de E un unique element y de F. Plusformellement, on appelle application ou fonction de E dans F toute relationdont le graphe Γ E × F est tel que :x E, !y F,x, y Γ.On notey = f x,et on dit que y = f x est l’image de x par f . E est l’ensemble de depart de fet F est l’ensemble d’arrivee de f . On notef : E →Fx 7→y = f x.Si y est un element de F, on dit que x est un antecedent de y par f lorsquey = f x.Algebre119 / 269

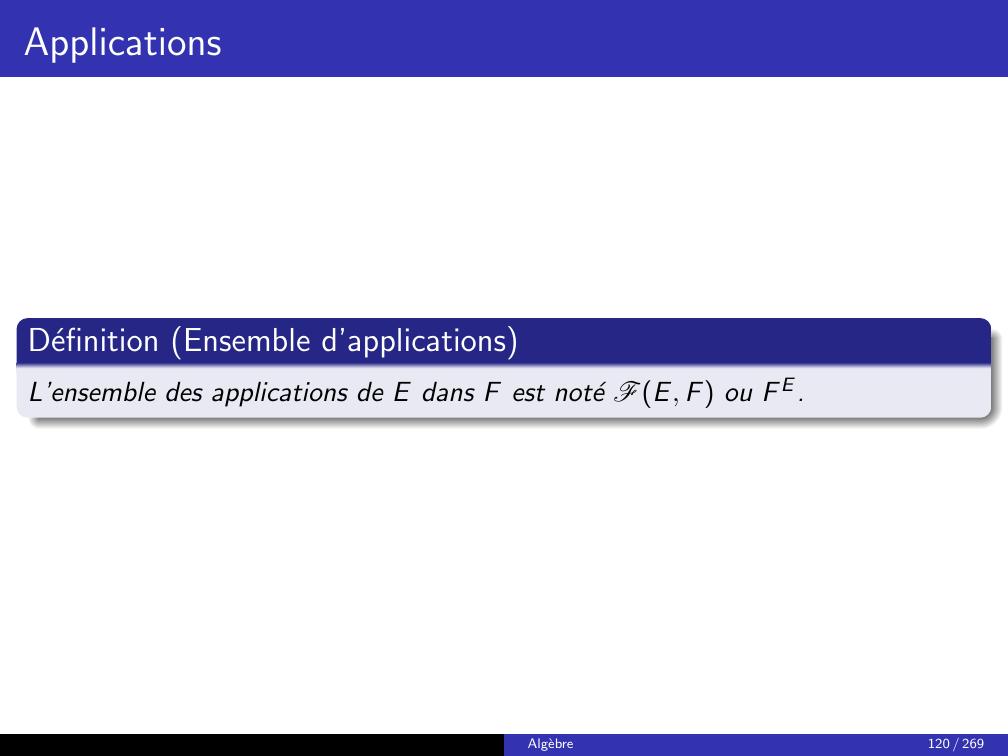
Page 127 : ApplicationsDeﬁnition Ensemble d’applicationsL’ensemble des applications de E dans F est note FE, F ou F E.Algebre120 / 269

Page 128 : ApplicationsExemples :• Application identite : On appelle application identite d’un ensemble E, eton note IdE, l’application de E dans E deﬁnie parIdE : E →Ex 7→x.• Application constante : Une application f : E →F est dite constante s’ilexiste α F tel que x E, f x = α. C’est-a-diref : E →Fx 7→α.• Fonction indicatrice d’une partie d’un ensemble : Soit E un ensemble etA une partie de E. On appelle fonction indicatrice de A et on note 1A lafonction de E dans 0, 1 deﬁnie par :1A : E →0, 1x 7→1Ax = 1si x A,0si x /A.Algebre121 / 269

Page 129 : ApplicationsExemple :• Famille d’elements : Soit E un ensemble et I un ensemble le plus souventﬁni ou denombrable, generalementI = 1, · · · , nouI = NouI = Z.On appelle famille d’elements de E indexee par I toute application de I dansEf : I →Ei 7→f iOn notef i = xiE.On represente un telle famille parxiiI.Remarque : Une suite numerique est une famille d’elements de R indexee par N :unnN.Algebre122 / 269

Page 130 : ApplicationsRemarque : Une fonction est deﬁnie par des couples. Si l’ensemble des couplesest modiﬁe, on n’a pas le mˆeme graphe et on ne deﬁnit plus la mˆeme fonction :f :R→Rx7→x2etg :0, 2→Rx7→x2ne sont pas les mˆemes fonctions.Deﬁnition Egalite entre fonctionsDeux applications f et g sont egales si :• elles ont le mˆeme ensemble de depart E et le mˆeme ensemble d’arrivee, et• si pour tout x E, on af x = gx.Algebre123 / 269

Page 131 : Image directe, Image reciproqueDeﬁnition Image directe d’une partie, image d’une applicationSoit f : E →F une application.• Pour toute partie A de E, on appelle image directe de A par f , noteef A, l’ensemble :f A=y F : a A, y = f a=f a : a A.• L’image de E tout entier est simplement appelee l’image de f et est noteegeneralementImfplutˆot que f E.Algebre124 / 269

Page 132 : Image directe, Image reciproqueExemple :• L’image de R par la fonctionx 7→x2est R+. L’image de 0, 3 par cette mˆeme fonction est 0, 9.• Considerons la fonctionx 7→sin x.Alors :• l’image deπZ := · · · , 2π , π , 0 , π , 2π , · · · par la fonction sinus est le singleton 0.• l’image de 0, π par la fonction sinus est 0, 1.• l’image de π/2, π/2 par la fonction sinus est 1, 1.Algebre125 / 269

Page 133 : Image directe, Image reciproqueDeﬁnition Expression a valeurs dans · · ·Soient f : E →F une application et B une partie de F. On dit que f est avaleurs dans B si toute valeur de f est element de B, i.e. six E, f x B,ou encore siImf B.Remarque : En general, Imf est plus petit que FImfF.Exemple : Les fonctionsR→Rx7→x2etexp :0, 2→Rx7→expx.sont deux fonctions a valeurs dans R+.Algebre126 / 269

Page 134 : Image directe, Image reciproqueEtudions comme l’image directe se comporte par rapport a certaines operationssur les ensembles.PropositionSoit f : E →F. Soit A et B deux parties quelconques de E. On a•A B =⇒f A f B.•f A B = f A f B.•f A B f A f B.•f = etf a = f a.Demonstration.Voir TD.Algebre127 / 269

Page 135 : Image directe, Image reciproqueAttention : Notons que nous avons seulementf A B f A f B.En eﬀet, f A B et f A f B ne sont en general pas egaux, comme l’on peutvoir dans le diagramme :×××××××BAAlgebre128 / 269

Page 136 : Image directe, Image reciproqueDeﬁnition Image reciproque d’une partieSoient f : E →F une application et B une partie de F.L’image reciproque de B par f , notee f 1B est l’ensemble des elements de Edont l’image est dans B :f 1B = x E, f x B.C’est la partie de E formee par les antecedents des elements de B.Remarque :• On peut ecrirex f 1B⇐⇒f x B.• On af 1 = etf 1F = E.Pour tout b Ff 1b = x E : f x = b.Par consequent, si b /Imf on a f 1b = .Algebre129 / 269

Page 137 : Image directe, Image reciproqueExemples :• L’image reciproque de R+ par la fonction exponentielle est R tout entier :exp1 R+ = R.• L’image reciproque de 9, 25 par la fonction carree est :f 1 9, 25 = 5, 3 3, 5.• L’image reciproque de 0 par la fonction sinus estsin1 0 = πZ = kπ : k Z.L’image reciproque de 4, 6 par le mˆeme fonction est :sin1 4, 6 = .Algebre130 / 269

Page 138 : Image directe, Image reciproqueEtudions maintenant comme l’image reciproque se comporte par rapport acertaines operations sur les ensembles.PropositionSoit f : E →F. Soit A F et B F. On a•f 1A B = f 1A f 1B.•f 1A B = f 1A f 1B.•f 1Ac =f 1Ac .Demonstration.Voir TD.Algebre131 / 269

Page 139 : Operations sur les applicationsIntroduisons certaines operations qui vont nous permettre de fabriquer denouvelles applications.Deﬁnition CompositionSoient E, F et G trois ensembles, f une application de E dans F et g uneapplication de F dans G. La composee de f par g est l’application de E dans G,notee g ◦f et deﬁnie pour tout x E parg ◦f x = gf x.c’est-a-direg ◦f : Ef→Fg→Gx 7→f x 7→gf x.Remarque : La composition, en general, n’est possible que dans un seul sens, etquand elle est possible dans les deux, on n’a aucune raison d’avoir :f ◦g = g ◦f .Algebre132 / 269

Page 140 : Operations sur les applicationsLa composition satisfait les proprietes suivantes.PropositionSoient E, F, G, H des ensembles.• Neutralite de l’identite : Pour tout f FE, F, on a : f ◦IdE = f :f ◦IdE : EIdE→Ef→Fx 7→x 7→f x.• Neutralite de l’identite : Pour tout f FE, F, on a : IdF ◦f = f :IdF ◦f : Ef→FIdF→Fx 7→f x 7→f x.• La composition est associative : f FE, F, g FF, G,h FG, H, on a :h ◦g ◦f = h ◦g ◦f .Algebre133 / 269

Page 141 : Operations sur les applicationsDemonstration.Montrons que la composition est associative :h ◦g ◦f = h ◦g ◦f .Pour tout x E on ah ◦g ◦f x = hg ◦f x= hgf x= h ◦gf x=h ◦g ◦fx.Ainsi, h ◦g ◦f = h ◦g ◦f .Algebre134 / 269

Page 142 : Operations sur les applicationsSoit f FE, F. On peut aussi creer de nouvelles applications en ne modiﬁantque l’ensemble de depart ou l’ensemble d’arrivee de f .DeﬁnitionSoit A une partie de E.• Soit f : E →F une application. On appelle restriction de f a A l’applicationnoteef A : A →Fdeﬁnie parx A,f Ax = f x.• Soit f : A →F une application. On appelle prolongement de f a E touteapplication g de E dans F telle que :x A,f x = gx.C’est-a-dire f est la restriction de g a A gA = f .Algebre135 / 269

Page 143 : Operations sur les applicationsRemarque :• Restreindre/prolonger une application, c’est diminuer/augmenter la taille deson ensemble de deﬁnition.• Parce que il existe en general beaucoup de prolongements d’une applicationdonnee, on parle d’un prolongement et non du prolongement. Par exemple, sif est l’identite de R+ :IdR+ : R+ →R+x 7→x,elle possede une inﬁnite de prolongements a R tout entier, parmi lesquels• L’application identite de R.• L’application valeur absolue de R.• L’applicationh : R →Rx 7→12x + x.Notons que h est identiquement nulle sur Ri.e. hx = 0 pour tout x 0.Algebre136 / 269

Page 144 : Injections-Surjections-BijectionsDeﬁnition InjectionSoit f : E →F une application. On dit que f est injective sur E ou que c’est uneinjection sur E si :x E, x′ E,f x = f x′=⇒x = x′.Autrement dit, f est injective si toute element y de F possede au plus unantecedent par f .Algebre137 / 269

Page 145 : Injections-Surjections-BijectionsExemples :• La application identite d’un ensemble E, est injective.• Soit a R×. Alors toute application aﬃne sur R de la forme :f x = ax + best injective.• L’application f : R →R deﬁnie parf x = x3est injective.• L’application exponentielle f x = ex, x R, est injective.Algebre138 / 269

Page 146 : Injections-Surjections-BijectionsRemarques• Une deﬁnition equivalente de l’injectivite estx E, x′ E,x ̸= x′=⇒f x ̸= f x′.Notons que la proposition precedente est la contraposition dex E, x′ E,f x = f x′=⇒x = x′.• Le changement de l’ensemble de depart d’une application peut modiﬁer lapropriete d’ˆetre injective. Par exemple :• La fonction carre n’est pas injective sur R, mais elle l’est sur R+.• La restriction de cos : R →R a l’intervalle 0, π est injective.Algebre139 / 269

Page 147 : Injections-Surjections-BijectionsEtudions certaines proprietes des fonctions injectives.PropositionOn considere deux applications f : E →F et g : F →G.• Si f et g sont injectives, alors g ◦f est injective.• Si g ◦f est injective, alors f est injective.Demonstration.• Soient x, y E. Supposons g ◦f x = g ◦f y. Nous voulons montrer que :x = y. Orgf x = gf y=⇒zg injectivef x = f y=⇒zf injectivex = y.• Soient x, y E. Supposons f x = f y. Nous voulons montrer que : x = y.Orf x = f y=⇒g ◦f x = g ◦f y=⇒zg◦f injectivex = y.Algebre140 / 269

Page 148 : Injections-Surjections-BijectionsDeﬁnition SurjectionSoit f : E →F une application. On dit que f est une application surjective de E sur Fou que c’est une surjection de E sur F si :y F,x E,y = f x.Cela revient a dire que :Imf = F.Autrement dit, f est surjective de E sur F si et seulement si tout element de F possedeau moins un antecedent dans E par f .Exemples :• L’application · : Z →N deﬁnie parn 7→nest surjective.• L’application f : R3 →R2 deﬁnie parx, y, z 7→x, yest surjective.Algebre141 / 269

Page 149 : Injections-Surjections-Bijections.Remarques :• Pour montrer qu’une application f : E →F est surjective, on se donne unelement quelconque y de F et on montre qu’il a au moins un antecedentdans E, c’est-a-dire on montre qu’il existe x E, avecf x = y.• Toute application est surjective de son ensemble de deﬁnition sur son image.• Le changement de l’ensembles d’arrivee d’une application peut modiﬁer lapropriete d’ˆetre surjective. Par exemple :• L’application f de R dans R+ deﬁnie par f x = x2 est surjective.• L’application f de R dans R deﬁnie par f x = x2 n’est pas surjective.Algebre142 / 269

Page 150 : Injections-Surjections-BijectionsEtudions certaines proprietes des fonctions surjectives.PropositionOn considere deux applications f : E →F et g : F →G.• Si f et g sont surjectives, alors g ◦f est surjective.• Si g ◦f est surjective, alors g est surjective.Demonstration.• Montrons que g ◦f est surjective. Soit y G. Nous voulons montrer qu’ilexiste x E tel que y = g ◦f x. Or g est surjective, donc il exist t F tel quey = gt.Mais f est aussi surjective, donc : t = f x pour un certain x E. Finalement,comme voulu :y = gt = gf x = g ◦f x.Algebre143 / 269

Page 151 : Injections-Surjections-BijectionsDemonstration.• Montrons que g est surjective. Soit y G. Nous voulons montrer qu’il existex F tel que y = gx. Or g ◦f est surjective, donc :y = g ◦f tpour un certain t E. Il suﬃt des lors de poser :x = f t pour avoir y = gx.Algebre144 / 269

Page 152 : Injections-Surjections-BijectionsDeﬁnition BijectionSoit f : E →F une application. On dit que f est une application bijective ouencore une bijection siy F,!x E,y = f x.Autrement dit, f est bijective de E sur F si et seulement si tout element de Fpossede un et un seul antecedent dans E par f .PropositionSoit f une application d’un ensemble E dans un ensemble F. Alorsf est bijective⇐⇒f est injective et surjectiveRemarque : Pour montrer qu’une application f : E →F est bijective, on pourraraisonner en deux etapes en montrant l’injectivite et la surjectivite de f .Algebre145 / 269

Page 153 : Injections-Surjections-BijectionsExemples :• Soit m R×. Alors toute application aﬃne de la formex 7→mx + nest bijective.• L’applicationx 7→x3est bijective.• On sait que l’applicationf : R →Rx 7→x2n’est ni injective, ni surjective. Or si on restreint l’ensemble de depart de f a R+, eton modiﬁe l’ensemble d’arrivee de R a R+, on obtient que la fonctiong : R+ →R+x 7→x2est bijective. Le changement de l’ensembles de depart et d’arrivee d’uneapplication peut modiﬁer la propriete d’ˆetre bijective.Algebre146 / 269

Page 154 : Injections-Surjections-BijectionsDeﬁnition Bijection ReciproqueSoit f : E →F une application. On appelle reciproque de f toute applicationg : F →E pour laquelleg ◦f = IdEetf ◦g = IdF.Remarque : Les identites : x E, g ◦f x = x et y F, f ◦gy = yexpriment l’idee que g defait le travail que f opere et vice versa.TheoremeSoit f : E →F une application. Alorsf est bijective de E sur F si et seulement si f possede une reciproque.Une telle reciproque est alors unique, appelee la reciproque de f et notee f 1.Pour tous x E et y F on af 1y = x⇐⇒y = f x.Algebre147 / 269

Page 155 : Injections-Surjections-BijectionsRemarque : Si f : E →F est une application bijective. Alors son applicationreciproque f 1 est l’unique application de F dans E, qui a tout element de Fassocie son unique antecedent par f . C’est-a-diref 1 : F→Ey7→f 1y = l’unique antecedent de y par f .Exemples :• L’application IdE est bijective de E sur E de reciproque elle-mˆeme. En eﬀetIdE ◦IdE = IdE.• Soient a Ret b R. La fonctionx 7→ax + best bijective. Pour trouver sa reciproque, notons quey = ax + b⇐⇒y ba= x.Par consequent, la reciproque de ax + b est la fonction deﬁnie pary 7→y ba.Algebre148 / 269

Page 156 : Injections-Surjections-BijectionsEtudions certaines proprietes des fonctions bijectives.PropositionOn considere deux applications f : E →F et g : F →G.• Si g ◦f est bijective, alors f est injective et g est surjective.• Si f et g sont bijectives, alors g ◦f est bijective et on ag ◦f 1 = f 1 ◦g 1.• Si f est une bijection de E dans F, alors sa bijection reciproque f 1 est aussibijective et :f 11 = f .Algebre149 / 269

Page 157 : Injections-Surjections-BijectionsEn pratique, comment montrer concretement qu’une application f : E →F est bijective ? Letableau suivant, resume la marche a suivre.PrioriteCe qu’on faitCe qu’on obtient1Si on connaˆıt spontanement une expression expli-cite de f 1, on appelle g la fonction en questionet on veriﬁe simplement que :g ◦f = IdEetf ◦g = IdF .Bijectivite + Reciproque2Si on ne connaˆıt pas spontanement f 1, on peutessayer d’en trouver une expression explicite vial’equivalence :y = f x⇐⇒x = f 1y.Bijectivite + Reciproque3Si on ne se sent pas capable de trouver une ex-pression explicite de f 1, on montre en deuxtemps que f est a la fois injective et surjective.BijectiveAlgebre150 / 269

Page 158 : Injections-Surjections-BijectionsSoit f une application de E sur F. C’est important de ne pas confondrel’application reciproque avec l’image reciproquef 1 : PF →PEqui existe mˆeme lorsque f n’est pas bijective. Quand l’application est bijective,nous avons la relation suivante entre l’image reciproque de f et l’image directe def 1.PropositionSoit f une bijection de E sur F et B une partie de F. Alorsf 1B = f 1Bou• f 1B a gauche correspond a l’image reciproque de B par f .• f 1B a droite correspond a l’image directe de B par f 1.Algebre151 / 269

Page 159 : Les Nombres ComplexesIntroduction :• L’equationx + 2 = 1n’as pas de solution dans N, mais elle en a dans Z, un ensemble plus grandque N .• L’equation3x = 1n’as pas de solution dans Z, mais elle en a dans Q.• L’equationx2 = 1n’a pas de solution dans R.On va donc construire un ensemble plus grand que R dans lequel cette equationpossede des solutions. On appellera cet ensemble C :l’ensemble des nombres complexes.Algebre152 / 269

Page 160 : Les Nombres ComplexesOn deﬁnit un element particulier de C, note i qui n’est pas reel, tel quei2 = 1.L’equation x2 + 1 = 0 possede alors 2 solutionsx2 + 1 = 0⇐⇒x2 i2 = 0⇐⇒x ix + i = 0⇐⇒x = ±i.Donnons la deﬁnition de l’ensemble des nombres complexes.DeﬁnitionOn appelle ensemble des nombres complexes et on note C, l’ensemble desnombres de la formea + ibou a et b sont des reels,et ou i est un element qui veriﬁei2 = 1.Algebre153 / 269

Page 161 : Les Nombres ComplexesEtudions quelques proprietes de l’ensemble des nombres complexes.PropositionSoit z C. Alors il existe un unique couple a, b R2 tel quez = a + ib.Demonstration.En eﬀet, si a, b et a′, b′ sont tels quea + ib = z = a′ + ib′=⇒a a′ = ib′ b.En elevant au carre, on obtienta a′2 = b′ b2=⇒a = a′ et b = b′.Algebre154 / 269

Page 162 : Les Nombres ComplexesLa proposition precedente nous amene a deﬁnir.DeﬁnitionSoit z = a + ib C. On dit que z a pour ecriture algebrique a + ib et on deﬁnit :• a sa partie reelle qu’on noteraRez = a,• b sa partie imaginaire qu’on noteraImz = b.Remarques :• Les reels sont exactement les nombres complexes de partie imaginaire nulle,c’est-a-direR = z C : Imz = 0 = a + 0i : a R C.• Un nombre complexe de partie reelle nul est appele un imaginaire pur. L’ensembledes imaginaires pures sera note iR. C’est-a-direiR = z C : Rez = 0 = 0 + ib : b R C.Algebre155 / 269

Page 163 : Les Nombres ComplexesDeﬁnition Egalite entre nombres complexesDeux nombres complexesz = a + bietz′ = a′ + ib′sont egaux si et seulement si ils ont mˆeme partie reelle et mˆeme partieimaginaire :a + ib = a′ + ib′⇐⇒ a = a′b = b′.En resume :UNE egalite de nombres complexes = DEUX egalites de nombres reelsAlgebre156 / 269

Page 164 : Les Nombres ComplexesL’ensemble C est muni de deux operations : d’addition et de multiplication quigeneralisent celles que nous connaissons sur R.Deﬁnition Addition sur CPour tousz = a + ib Cetz′ = a′ + ib′ C,on deﬁnitz + z′ = a + a′ + ib + b′.Ce qui signiﬁe queRez + z′ = Rez + Rez′Imz + z′ = Imz + Imz′.Algebre157 / 269

Page 165 : Les Nombres ComplexesDeﬁnition Multiplication sur CPour tousz = a + ib Cetz′ = a′ + ib′ C,on deﬁnitz · z′ = aa′ bb′ + i ab′ + a′b. .Ce qui signiﬁe queRezz′ = RezRez′ ImzImz′Imzz′ = RezImz′ + ImzRez′.Algebre158 / 269

Page 166 : Les Nombres ComplexesRemarque :• En general :Rezz′ ̸= RezRez′etImzz′ ̸= ImzImz′• En particulier :Rez2 ̸= Rez2etImz2 ̸= Imz2.Deﬁnition QuotientEnﬁn, pour tout z = x + iy C× on a1z =1x + iy = x iyx2 + y 2 .Algebre159 / 269

Page 167 : Les Nombres ComplexesDonnons un point de vu geometrique a la deﬁnition des nombres complexes.PropositionL’applicationf : R2 →Ca, b 7→z = a + ibrealise une bijection de R2 sur C.Interpretation geometrique de C : Si l’on a ﬁxe un repere permettant dedecrire les points du plan par deux coordonnees cartesiennes, alors la bijectionf : a, b 7→z = a + ib,nous permet d’identiﬁer tout nombre complexe z a un point du plan.Algebre160 / 269

Page 168 : Les Nombres ComplexesEn eﬀet, si z est un nombre complexe et si z = a + ib est son ecriture sous formealgebrique, alors le couple a, b R2 fournit un moyen de representer z par unpoint du plan : on represente z par le pointMz d’abscisse a et d’ordonnee b.Reciproquement, si M est un point du plan et si a, b est le couple de nombresreels donnant son abscisse et son ordonnee dans le repere donne, alors le nombrecomplexez = a + ib est appele l’aﬃxe de M.Graphiquement nous avons :Algebre161 / 269

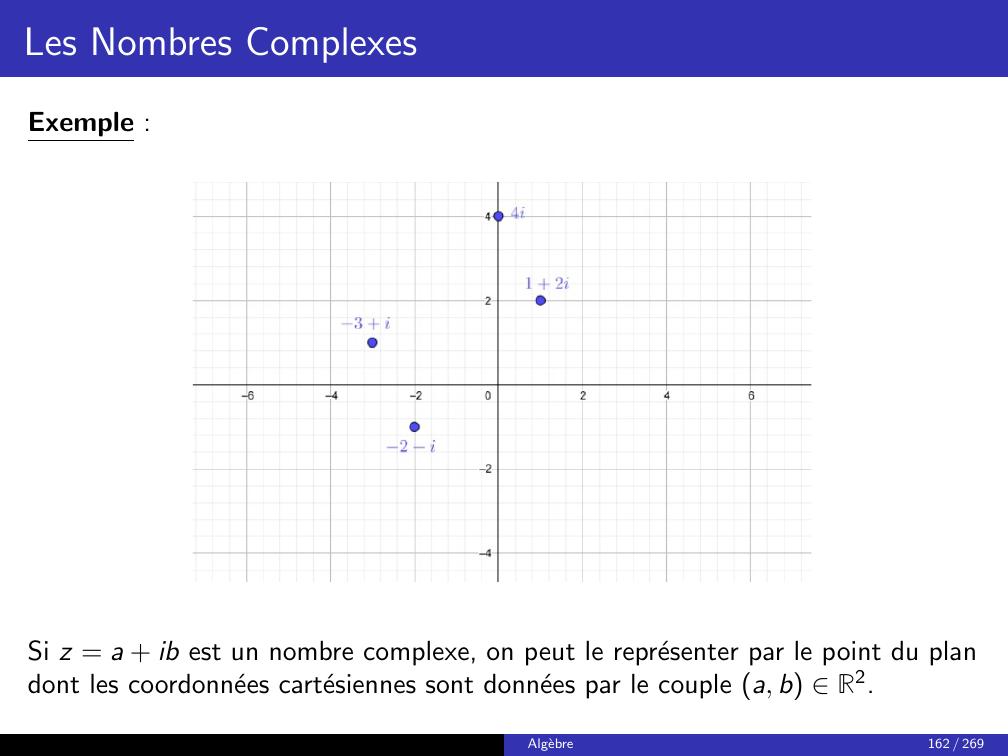
Page 169 : Les Nombres ComplexesExemple :Si z = a + ib est un nombre complexe, on peut le representer par le point du plandont les coordonnees cartesiennes sont donnees par le couple a, b R2.Algebre162 / 269

Page 170 : Les Nombres ComplexesL’addition des nombres complexes admet une interpretation geometriquesimple : si z1 et z2 sont deux nombres complexes et si l’on note O, M1, M2 lespoints du plan d’aﬃxes respectifs 0, z1 et z2, alors le point d’aﬃxe z1 + z2 setrouve au quatrieme sommet du parallelogramme dont les autres sommets sont O,M1 et M2.Algebre163 / 269

Page 171 : Les Nombres ComplexesA tout nombre complexe on peut attacher deux notions importants.Deﬁnition ConjugueSoit z = x + iy C. On appelle conjugue de z le nombre complexe z, deﬁni parz = x iyi.e.z = Rez iImz.Remarque : Notons que z est l’aﬃxe du vecteur du plan de coordonnees x, y :Algebre164 / 269

Page 172 : Les Nombres ComplexesDeﬁnition ModuleSoit z = x + iy C. On appelle module de z le nombre reel positif note z etdeﬁni parz =px2 + y 2i.e.z =qRe2z + Im2zRemarque : Le module z est egal a la norme du vecteur d’aﬃxe z :Algebre165 / 269

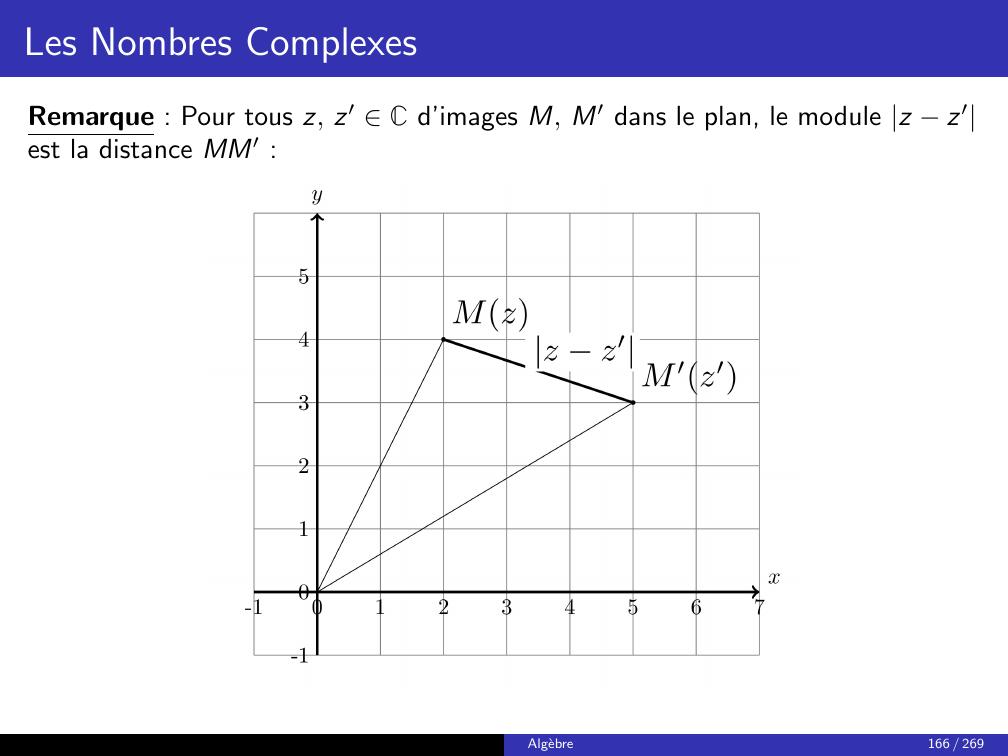
Page 173 : Les Nombres ComplexesRemarque : Pour tous z, z′ C d’images M, M′ dans le plan, le module z z′est la distance MM′ :Algebre166 / 269

Page 174 : Les Nombres ComplexesIl en decoule que pour tout R 0, nous avons :• Le cercle de centre a C et rayon R estz C : z a = R.• Le disque ouvert de centre a C et rayon R estz C : z a R.• Le disque ferme de centre a C et rayon R estz C : z a R.Algebre167 / 269

Page 175 : Les Nombres ComplexesEtudions quelques proprietes du conjuge d’un nombre complexe.PropositionSoit z C. Alors•z = z.•Rez = z + z2.•Imz = z z2i.•z R⇐⇒z = z.•z iR⇐⇒z = z.Algebre168 / 269

Page 176 : Les Nombres ComplexesEtudions comme le conjuge se comporte par rapport a la somme et le produit decomplexes.PropositionPour tous z, z′ C, nous avonsz + z′=z + z′z · z′=z · z′.En particulier, si z′ ̸= 0, alors zz′=zz′ ,et pour tout α Rαz = αz..Algebre169 / 269

Page 177 : Les Nombres ComplexesDonnons maintenant certaines proprietes du module.PropositionSoient z, z′ C.Proprietes algebriques :• z = z• zz′ = z z′, et si z′ ̸= 0 alors zz′ = zz′.Proprietes geometriques :• z = 0 ⇐⇒z = 0.• Rez zetImz z.Algebre170 / 269

Page 178 : Les Nombres ComplexesRemarques :• Pour tout z C nous avonszz=Re2z + Im2z=z2.• L’inverse de z = x + iy C× se calcule donc grˆace a la formulezz = z2.En eﬀetzz = z2=⇒1z =zz2 = x iyx2 + y 2 .Algebre171 / 269

Page 179 : Les Nombres ComplexesEtudions comme le module se comporte par rapport a la somme et la diﬀerence.PropositionSoient z, z′ C.Inegalite triangulaire :z + z′ z + z′.Inegalite triangulaire generalisee 1 :z z′ z + z′ z + z′.Inegalite triangulaire generalisee 2 :z z′ z z′ z + z′.Algebre172 / 269

Page 180 : Nombres complexes de module 1Passons a etudier un important sous-ensemble de C : l’ensemble de nombrescomplexes de module 1.DeﬁnitionOn appelle cercle trigonometrique et on note U l’ensemble des nombrescomplexes de module 1 :U = z C : z = 1.Remarque : Geometriquement, U est le circle de centre 0 et rayon 1. En eﬀet,x + iy U⇐⇒z =px2 + y 2 = 1⇐⇒x2 + y 2 = 1.Nous allons exprimer les elements du cercle trigonometrique a l’aide des fonctionscosinus et sinus. Pour cela deﬁnissons.DeﬁnitionSoit θ R, on appelle exponetielle iθ le nombre complexe deﬁni pareiθ = cos θ + i sin θ.Algebre173 / 269

Page 181 : Nombres complexes de module 1Remarques : Notons que pour tout θ R on a :•eiθ = cosθ + i sin θ =qcos2θ + sin2θ = 1.C’est-a-dire, θ R, eiθ U.• Nous savons que tout point du cercle de centre 0 et de rayon 1 a des coordonneesde la forme cosθ, sinθ, θ R. En eﬀet, nous avonsAinsi, comme pour tout z = x + iy U, nous avons x2 + y 2 = 1, nous pouvonsecrirecosθ = xetsinθ = y=⇒z = cosθ + i sinθ = eiθ.Algebre174 / 269

Page 182 : Nombres complexes de module 1Les remarques precedentes nous permettent d’enoncer le resultat suivant.Theoreme• Pour tout z Cz U⇐⇒θ R, z = eiθ.En resumeU = eiθ, θ R.• Pour tous θ R, θ′ R on aeiθ = eiθ′⇐⇒ cosθ = cosθ′sinθ = sinθ′⇐⇒θ = θ′mod 2π.Algebre175 / 269

Page 183 : Nombres complexes de module 1Etudions quelques proprietes de l’exponentielle iθ.TheoremeSoient θ, θ′ R et n N.• Conjugaison :eiθ = eiθ = 1eiθ• Formule d’Euler :cosθ = eiθ + eiθ2etsinθ = eiθ eiθ2i.• Transformation des sommes en produits :eiθ+θ′ = eiθ · eiθ′.• Formule de De Moivre :cosθ + i sinθn = cosnθ + i sinnθ.Algebre176 / 269

Page 184 : Nombres complexes de module 1Demonstration.• Conjugaison : Pour tout reel θ R, on aeiθ = cosθ + i sinθ = cosθ i sinθ= cosθ + i sinθ= eiθ• Formule d’Euler : Ces formules sont evidentes a partir de la deﬁnition de eiθ.• Transformation des sommes en produits : Soit θ R et θ′ R. Alorseiθ · eiθ′ = cosθ + i sinθcosθ′ + i sinθ′= cosθ cosθ′ sinθ sinθ′ + icosθ sinθ′ + sinθ cosθ′= cosθ + θ′ + i sinθ + θ′= eiθ+θ′.Algebre177 / 269

Page 185 : Nombres complexes de module 1Demonstration.• Formule de De Moivre : Soit θ R. Alors le point precedent nous permet,grˆace a une recurrence simple, de conclureeiθn = einθ =⇒cosθ + i sinθn=eiθn=einθ=cosnθ + i sinnθ.Algebre178 / 269

Page 186 : Applications a la trigonometrieEtudions quelques applications de l’exponentiele iθ a la trigonometrie.Linearisation des puissances de cosinus et sinus : Lineariser une expressionpolynomiale de la formecoskx · sinℓxen sinx et cosx, c’est l’exprimer comme une combinaison lineaire decosx, cos2x, cos3x, · · ·etsinx, sin2x, sin3x, · · ·en supprimant toute puissance et tout produit.Algebre179 / 269

Page 187 : Applications a la trigonometrieDecrivons la methode avec un exemple : Lineariser cos4x sin2x. Onprocede comme suit :1 On utilise les formules d’Euler pour changer cosx et sinx en eix et eix.cos4x sin2x =eix + eix24 eix eix2i22 On developpe completement, avec le binˆome de Newton.cos4x sin2x = 164e4ix + 4e2ix + 6 + 4e2ix + e4ix·e2ix 2 + e2ix= 164e6ix + 2e4ix e2ix 4 e2ix + 2e4ix + e6ix.Algebre180 / 269

Page 188 : Applications a la trigonometrie3 On regroupe les termes deux a deux conjugues pour reconnaˆıtre des cosαxou sinβx grˆace a la formule d’Euler.cos4x sin2x=164e6ix + e6ix+ 2e4ix + e4ixe2ix + e2ix4=132 e6ix + e6ix22e4ix + e4ix2+e2ix + e2ix2+ 2!=132cos6x 2 cos4x + cos2x + 2.Algebre181 / 269

Page 189 : Applications a la trigonometrieTechnique de l’angle moitie : Pour factoriser une expression du typeeix + eiyeteix eiy.On procede comme suit :1. On commence par noter quex = x + y2+ x y2ety = x + y2x y2.2. Donceix + eiy =eix+y2· eixy2+ eix+y2· eixy2= eix+y2eixy2+ eixy2= 2eix+y2cosx y2.De mˆemeeix eiy = eix+y2eixy2eixy2= 2eix+y2i sinx y2.Algebre182 / 269

Page 190 : Applications a la trigonometrieLa technique de l’angle de l’angle moitie nous permet de calculer facilementles expressions suivantes :PropositionPour tous x, y Rcosx + cosy=2 cosx + y2cosx y2cosx cosy=2 sinx + y2sinx y2sinx + siny=2 sinx + y2cosx y2sinx siny=2 cosx + y2sinx y2.Algebre183 / 269

Page 191 : Applications a la trigonometrieExemple : En utilisant quesinx = Imcosx + i sinx = Imeixetsiny = Imcosy + i siny = Imeiy,on deduitsinx + siny = Imeix + eiy=Im2eix+y2cosx y2=2 sinx + y2cosx y2.Algebre184 / 269

Page 192 : Applications a la trigonometrieComme l’on vient de voir dans la proposition precedente, l’une des avantages de laforme exponentielle est qu’elle permet de faire tres facilement des calculs detrigonometrie. Ainsi vous pouvez tres facilement demontrer les formules suivantes.Theoreme1. cosx + y = cosx cosy sinx siny.2. sinx + y = sinx cosy + cosx siny.3. tanx + y =tanx+tany1tanxtany.4. cosx =1tan2 x21+tan2 x2.5. sinx =2 tan2 x21+tan2 x2.6. tanx =2 tan2 x21tan2 x2.Algebre185 / 269

Page 193 : Forme Trigonometrique d’un nombre complexeL’exponentielle iθ nous oﬀre une autre maniere d’exprimer tout nombre complexe.Soit z C avec z ̸= 0. Notons que si on compute le module dezz on obtientzz =z · 1z = z ·1z = z · 1z = zz = 1.Donc pour tout z C avec z ̸= 0, nous avonszz U=⇒θ R,zz = eiθ.Par consequent, tout nombre complexe peut ˆetre ecrit sous la formez = z · eiθ.Algebre186 / 269

Page 194 : Forme Trigonometrique d’un nombre complexeResumons ce que vient d’ˆetre dite dans le theoreme suivant :TheoremeTout nombre complexe non nul peut ˆetre ecrit sous la forme :z = reiθavec r R+ et θ R.Cette forme est dite trigonometrique.• Le reel r est unique car : r = z. En eﬀetz = reiθ = r · eiθ = r.• Mais θ, appele UN argument de z, et note argz, est seulement unique a2π pres. En revanche, il existe un et un seul argument de z dans π, π, etcelui ci est appele l’argument principal de z.• Le couple r, θ est aussi appele UN couple de coordonnees polaires dupoint d’image z.Algebre187 / 269

Page 195 : Forme Trigonometrique d’un nombre complexeRemarques :• Zero n’a pas de forme trigonometrique, donc pas d’arguments. Un peu plusde details, l’egalite0 = 0eiθest veriﬁee par tous les nombres reels θ ; il n’est donc pas raisonnable deparler d’argument du nombre complexe 0 sinon, la coherence imposerait quetout nombre reel soit un argument de 0.• Un nombre complexe non nul admet toujours une inﬁnite d’argumentsdiﬀerents.• Pour tout z C, z′ C, nous avonsz = z′⇐⇒ z = z′argz = argz′mod 2π.Algebre188 / 269

Page 196 : Forme Trigonometrique d’un nombre complexeExemple : Les formes trigonometriques des reels et des imaginaires pur sont :• Cas des reels : Pour tout x R, nous avonsx =xei0si x 0,xeiπsi x 0.• Cas des imaginaires purs : Pour tout y R, nous avonsiy =yei π2si y 0,yei π2si y 0.Algebre189 / 269

Page 197 : Forme Trigonometrique d’un nombre complexeEtudions quelques proprietes des arguments.Proposition Proprietes des argumentsPour tous z C, z′ C, nous avons•argzz′ = argz + argz′mod2π.•argz = argzmod2π.•arg1z= argzmod2π.Algebre190 / 269

Page 198 : Forme Trigonometrique d’un nombre complexeDemonstration.• argzz′ = argz + argz′mod2π : Nous avonszz′ = z · ei argzz′ · ei argz′ = zz′ · eiargz+argz′.D’ou on conclut que argzz′ = argz + argz′mod 2π.• argz = argzmod2π : Nous avonsz = z · ei argz = z · ei argz = z · ei argz = z · ei argz.D’ou on conclut que argz = argzmod 2π.• arg 1z= argzmod2π : Nous avons1z =1z · ei argz = 1z · ei argz.D’ou on conclut que arg 1z= argzmod 2π.Algebre191 / 269

Page 199 : Forme Trigonometrique d’un nombre complexeSoit z C. Nous avons deux fa¸con d’exprimer z :• Forme Algebrique : z = x + iy.• Forme Trigonometrique : z = reiθ.Etudions le lien qui existe entre ces deux ecritures.Theoreme Lien entre la forme algebrique et les formestrigonometriquesSoit z Cdeforme algebrique : z = x + iyet deforme trigonometrique : z = reiθ.1. Forme algebrique en fonction d’une forme trigonometrique :x = r cosθety = r sinθ.2. Forme trigonometrique en fonction d’une forme algebrique :r =px2 + y 2etθ = arctan yxmod 2πsi x 0,arctan yx+ πmod 2πsi x 0.Algebre192 / 269

Page 200 : Equations du second degre a coeﬃcients complexesPassons maintenant a etudier quelques equations polynomiales dans C.Commen¸cons par etudier les equations de degre deux. Notre objectif est demontrer que toute equation de la formeaz2 + bz + c = 0,a C×, b, c Cpossede des solutions sur C.Deﬁnition Racines carrees d’un nombre complexeOn appelle racine carree d’un nombre complexe z tout nombre complexe ωveriﬁantω2 = z.TheoremePour tout z C, l’equation d’inconnu ω C :ω2 = z,possede exactement deux solutions opposees.Algebre193 / 269

Page 201 : Equations du second degre a coeﬃcients complexesDemonstration.On commence par ecrire z sous forme trigonometriquez = reiθ, r R+, θ R.Posonsζ = reiθ2=⇒ζ2 = z.Nous disposons ainsi d’un exemple de racine carree de z, et grˆace a lui, nousallons trouver toutes les solutions de l’equationω2 = z.Algebre194 / 269

Page 202 : Equations du second degre a coeﬃcients complexesDemonstration.Nous avonsω2 = z⇐⇒ω2 = ζ2⇐⇒ω2 ζ2 = 0⇐⇒ω ζω + ζ = 0⇐⇒ω = ζouω = ζ⇐⇒ω = rei θ2ouω = rei θ2⇐⇒ω = rei θ2ouω = rei θ2 +π.On a donc le resultat voulu.Algebre195 / 269

Page 203 : Equations du second degre a coeﬃcients complexesAttention :• x est une notation autorisee si x R+.• z est une notation interdite si z C \ R+.Pourquoi cet interdit ? Parce que nous ne savons pas choisir, tout nombrecomplexe non nul possededeux racines carrees distinctesqui se valent, l’une l’autre. Il n’y a que dans le cas des reels positifs qu’on saitchoisir, car les racines carrees d’un reel positif x sont toutes les deux reelles, l’unepositive, l’autre negative, et on choisit de noter x la premiere.Algebre196 / 269

Page 204 : Equations du second degre a coeﬃcients complexesDe la preuve du theoreme precedent, on sait que si la forme trigonometrique de zestz = reiθ,alors les deux racines carres de z, sontrei θ2etrei θ2 +π.Le probleme c’est que, tres souvent il est tres diﬃcil de determiner la formetrigonometrique d’un complexe. Dans ce cas, pour trouver les racines carres ilnous faut travailler avec l’ecriture algebrique du nombre complexe.Algebre197 / 269

Page 205 : Equations du second degre a coeﬃcients complexesPour determiner l’ecriture algebrique des racines carrees, on procedera commesuit : Decrivons la methode avec un exemple : Calculer les racines carres de24 + 10i.1 On cherche les racines de z = a + ib, sous la formew = x + iy.L’equation w 2 = z donne le systemew 2 = z⇐⇒x2 y 2 + i2xy = a + ib⇐⇒ x2 y 2 = a,2xy = b.en identiﬁant parties reelle et imaginaire. Dans notre exemple :w 2 = 24+10i⇐⇒x2y 2 + i2xy = 24+i10⇐⇒ x2 y 2 = 24,2xy = 10.Algebre198 / 269

Page 206 : Equations du second degre a coeﬃcients complexes2 On pensera systematiquement a ajouter l’equationw2 = z⇐⇒x2 + y 2 =pa2 + b2pour trouver les valeurs de x2 et y 2. Dans notre exemple :w2 = 24 + 10i⇐⇒x2 + y 2 =p242 + 102 = 26.Nous avons donc trois equations :x2 + y 2 = 26,x2 y 2 = 24,2xy = 10.=⇒x2 = 25,y 2 = 1,xy = 5.3 On prend ensuite les racines carrees, en faisant attention aux signes relatifsde x et y, donne par l’equation 2xy = b.Dans notre exemple nous avons donc les solutions :x, y = 5, 1oux, y = 5, 1⇐⇒w = 5+iou w = 5i.Algebre199 / 269

Page 207 : Equations du second degre a coeﬃcients complexesMaintenant que on a montre que tout nombre complexe possede exactement deuxracines carrees, nous pouvons donner la preuve de que toute equation de degre 2possede des solutions dans C.TheoremeSoient a, b et c trois nombres complexes avec a ̸= 0. Alors les solutions del’equation d’inconnu z C :az2 + bz + c = 0sontb + δ2aetb δ2a,ou δ est l’une quelconque des deux racines carrees du discriminant= b2 4ac.Algebre200 / 269

Page 208 : Equations du second degre a coeﬃcients complexesDemonstration.Nous avonsaz2 + bz + c=az2 + ba z + ca=a z + b2a2b2 4ac4a2!.Soit δ l’une de deux racines carres de b2 4ac. Alorsb2 4ac4a2= δ2a2.Ce qui nous permet d’ecrireaz2 + bz + c = a z + b2a2 δ2a2!Algebre201 / 269

Page 209 : Equations du second degre a coeﬃcients complexesDemonstration.Ainsiaz2 + bz + c=a z + b2a2 δ2a2!x2 y 2 = x + yx y=az + b2a+δ2a·z + b2aδ2a=az b δ2a·z b + δ2a.Les racines de az2 + bz + c sont doncb δ2aetb + δ2aAlgebre202 / 269

Page 210 : Equations du second degre a coeﬃcients complexesEn lien avec ce qui precede, la relation triviale :z xz y=z2 x + yz + xynous permet de calculer x et y quand on connaˆıt leur somme x + y et leur produitxy.Theoreme Systemes somme-produitSoient b, c C.Les solutions du systeme somme-produit d’inconnues x, y C x + y = bxy = csont les deux racines du polynˆome z2 bz + c eventuellement egales.Remarque : La somme des solutions de az2 + bz + c vaut ba et leur produit ca.Algebre203 / 269

Page 211 : Racine n-iemeNous avons decrit les racines carrees de tout complexe non nul z. Faisons le mˆeme avecles racines de degre n. Pour tout z C et n N×, nous allons donc etudier l’equation :ζn = z.Commen¸cons avec le cas z = 1.Deﬁnition Racines n-iemes de l’uniteSoit n N. On appelle racines n-iemes de l’unite tout nombre complexe ζ tel que1 = ζn.On note Un l’ensemble de racines n-iemes de l’unite.Le resultat suivant nous donne une description de l’ensemble de racines n-iemes del’unite.TheoremeSoit n N. Alors il existe exactement n racines n-iemes de l’unite, qui sontUn =ne2ikπn:0 k n 1o.Algebre204 / 269

Page 212 : Racine n-iemeDemonstration.Soit ζ C×. Posonsr = ζet notons θ l’unique argument de ζ dans l’intervalle 0, 2π. Par identiﬁcation de formestrigonometriques, on deduitζn = 1⇐⇒r n · einθ = 1 · ei·0⇐⇒r n = 1etnθ = 0mod 2π⇐⇒zr0r = 1etk Z, nθ = 2kπ⇐⇒r = 1etk Z, θ = 2kπ/n⇐⇒zθ0,2πr = 1etk Z, 0 k n 1, θ = 2kπ/n.Ainsi, ζ est une racine n-ieme de l’unite si et seulement sik Z, 0 k n 1, tel que ζ = e2ikπn.Algebre205 / 269

Page 213 : Racine n-iemeDemonstration.Ceci nous fait bien un total de n racines distinctes, car les nombres0, 2πn , 4πn , 6πn , · · · , 2n 1πnsont distincts et elements de 0, 2π, donc les nombres complexes1, e2iπn , e4iπn , e6iπn , · · · , e2n1iπnsont distincts aussi.Algebre206 / 269

Page 214 : Racines n-iemeLes racines de l’unite satisfont la propriete suivante.PropositionSoit n un entier naturel superieur ou egal a 2. La somme des racines n-ieme de l’unite estegale e 0. Autrement dit, sot ζ une racine n-ieme de l’unite diﬀerente de 1, alors1 + ζ + ζ2 + · · · + ζn1 = 0.Un exemple important, est celui de l’ensemble des racines cubiques de l’unite.Deﬁnition Le nombre jOn note j la racine cubique de l’unitej = e2iπ3= 12 + i32 .Quelques relations a connaˆıtrej3 = 1,j = j2,1 + j + j2 = 0,et pour tout z Cz2 + z + 1 = z jz j .Algebre207 / 269

Page 215 : Racines n-iemeVisualisation geometrique des racines de la unite : Soit n 3. Les elementsdans Un deﬁnissent les sommets d’un polygone regulier a n cˆotes.Algebre208 / 269

Page 216 : Racines n-iemeEtudions maintenant les racines n-ieme de tout nombre complexe non nul.Deﬁnition Racines n-iemesSoit n N× et z C non nul. On appelle racine n-ieme de z tout nombrecomplexe ζ tel quez = ζn.L’ensemble de racines n-iemes de z sont decrit dans le resultat suivant.TheoremeSoit n N×.1. La seule racine n-ieme de 0 est 0. En eﬀet, ζn = 0 ⇐⇒ζ = 0.2. Tout nombre complexe z = reiθ Cavec r 0 et θ R possedeexactement n racines n-iemes, a savoir :nr · eiθn + 2ikπn0 k n 1Algebre209 / 269

Page 217 : Racines n-iemeDemonstration.Soit z = reiθ Cavec r 0 et θ R. Posonsζ =nreiθn=⇒ζn = z.Nous disposons ainsi d’un exemple de racine n-eme de z, et grˆace a lui, nous allons lestrouver toutes. Pour tout ω C :ωn = z⇐⇒ωn = ζn⇐⇒ωζn= 1⇐⇒k Z, 0 k n 1, tel que ωζ = e2ikπn⇐⇒k Z, 0 k n 1, tel que ω = ζ · e2ikπn .Ainsi, ωn = z si et seulement sik Z, 0 k n 1, tel que ω =nr · eiθn + 2ikπn .Ce qui montre le resultat.Algebre210 / 269

Page 218 : Exponentielle complexeNous avons deﬁni la fonction exponentielle sur les nombres complexes de la formeiθ, θ R. Etendons sa deﬁnition a tout nombre complexe.DeﬁnitionPour tout z C, on appelle exponentielle complexe de z le nombre complexedeﬁni sous forme trigonometriqueez = eRez · eiImz.En d’autres termesez = eRezetarg ez = Imzmod 2π.Algebre211 / 269

Page 219 : Exponentielle complexeDonnons quelques proprietes de la fonction exponentielle.Proposition1. Periodicite : L’exponentielle complexe est 2iπ-periodique, i.e. pour toutz Cez = ez′⇐⇒z = z′mod 2iπ.2. Transformation des sommes en produits : Pour tous z C, z′ Cnous avonsez+z′ = ez · ez′.Remarque : Faites attention au i dans l’equationez = ez′⇐⇒z = z′ mod 2iπ.Algebre212 / 269

Page 220 : Exponentielle complexeDemonstration.1. Periodicite : Simple identiﬁcation de formes trigonometriques :ez = ez′⇐⇒eRez · eiImz = eRez′ · eiImz′⇐⇒eRez = eRez′eteiImz = eiImz′⇐⇒Rez = Rez′etImz = Imz′mod 2π⇐⇒z = z′mod 2iπ.2. Transformation des sommes en produits : Nous avonsez+z′=eRez+z′ · eiImz+z′=eRez+Rez′ · eiImz+iImz′=eRez · eRez′ · eiImz · eiImz′=eRez · eiImz′ · eRez′ · eiImz=ez · ez′.Algebre213 / 269

Page 221 : Une derniere remarque geometriqueFinissons cet chapitre avec quelques remarques supplementaires sur la geometriedu plan complexe.• L’addition de deux nombres complexes s’interprete geometriquement entermes de translation : En eﬀet soit u C. Alors la applicationtu : C →Cz 7→z + u.correspond geometriquement a la translation de vecteur ⃗u.Algebre214 / 269

Page 222 : Une derniere remarque geometrique• La applicationSO : C →Cz 7→z.correspond, geometriquement, a la symetrie de centre O.• La applicationSx : C →Cz 7→z.correspond, geometriquement, a la symetrie d’axe Ox.• La applicationSy : C →Cz 7→z.correspond, geometriquement, a la symetrie d’axe Oy.Algebre215 / 269

Page 223 : Une derniere remarque geometriqueLe produit de deux nombres complexes s’interprete geometriquement en termesd’homothetie et de rotation. En eﬀet :• Soit λ R. Alors la applicationHλ : C →Cz 7→λz.correspond, geometriquement, a l’homothetie de centre O et de rapport λ.• Soit θ R. Alors la applicationRθ : C →Cz 7→eiθz.correspond, geometriquement, a la rotation de centre O et d’angle θ.• Soit ω = ρeiθ. Alors la applicationHRω : C →Cz 7→ρeiθz.correspond, geometriquement, a la composee d’une rotation de centre O et d’angleθ avec une homothetie de centre O et de rapport ρ.Algebre216 / 269

Page 224 : Polynˆomes• Polynˆomes• Deﬁnition.• Operations sur les polynˆomes.• Degre d’un polynˆome.• Divisibilite dans l’ensemble des polynˆomes.• Racines d’un polynˆome• Evaluation polynˆomiale• Racines d’un polynˆome• Decomposition en facteurs irreductiblesAlgebre217 / 269

Page 225 : PolynˆomesNote : Dans ce chapitre nous travaillerons a la fois sur R et sur C. Aﬁn d’allegerl’ecriture, nous utiliserons la lettre K pour designer R ou C. Ainsi une propriete ouune deﬁnition qui est valable a la fois sur R et sur C sera enoncee sur K.Deﬁnition ScalaireOn appelle scalaire un element de K.Algebre218 / 269

Page 226 : PolynˆomesDeﬁnition PolynˆomeOn appelle polynˆome P d’indeterminee X a coeﬃcients dans K touteexpression de la formePX=a0 + a1X + a2X 2 + · · · + anX n=nXk=0akX k.ou• n N, et• a0, a1 , · · · , an sont des elements de K. On les appelle les coeﬃcients dupolynˆome P.L’ensemble des polynˆomes a coeﬃcients dans K est note KX.Remarque : X N’EST PAS UN NOMBRE ! L’objet X est un objetmathematique bien precis que l’on appelle indeterminee. Ce n’est ni une valeur niune variable.Algebre219 / 269

Page 227 : PolynˆomesDonnons quelques exemples de polynˆomes.DeﬁnitionOn appelle :• Polynˆome constant :Tout polynˆome de la forme PX = a0 avec a0 K.• Polynˆome unite : Le polynˆome PX = 1.• Polynˆome nul : Le polynˆome PX = 0.• Monˆome : Tout polynˆome de la formePX = akX k, ak K.Algebre220 / 269

Page 228 : PolynˆomesTheoreme Egalite entre polynˆomesDeux polynˆomes sont egaux si et seulement si leurs coeﬃcients sont egaux.C’est-a-direnXk=0akX k =mXk=0bkX k⇐⇒m = n et ak = bk, k N, 0 k n.En particulier, un polynˆome est nul si et seulement si tous ses coeﬃcients sontnuls.Remarque : Notons que, siP =nXk=0akX k,alors pour tout m n, on convient d’ecrireP =mXk=0akX k,en posant ak = 0 pour k = n + 1, n + 2, · · · , m.Algebre221 / 269

Page 229 : PolynˆomesSur l’ensemble de polynˆomes nous pouvons deﬁnir une addition et une multiplication.Deﬁnition Addition-MultiplicationSoientPX =nXk=0akX ketQX =mXk=0bkX kdeux polynˆomes a coeﬃcients dans K.• Somme : On deﬁnit le polynome P + Q parP + QX =maxm,nXk=0ak + bkX k.en convenant que ak = 0 si k n et bk = 0 si k m.• Produit : On deﬁnit le polynome P · Q parP · QX =m+nXk=0ckX kouck =kXi=0aibki.en convenant que ak = 0 si k n et bk = 0 si k m.Algebre222 / 269

Page 230 : PolynˆomesDeﬁnition Multiplication par un scalaireSoitPX =nXk=0akX kun polynˆome a coeﬃcients dans K et λ K.• Multiplication par λ : On deﬁnit le polynome λP parλPX =nXk=0λakX k.Algebre223 / 269

Page 231 : PolynˆomesExemple : Considerons les polynˆomesPX = 1 2X X 3etQX = 1 + X 2.AlorsP + QX=2 2X + X 2 X 3.P · QX=1 2X + X 2 3X 3 X 5.λ K, λPx=λ 2λX λX 3.Algebre224 / 269

Page 232 : PolynˆomesSur l’ensemble de pˆolynomes nous pouvons deﬁnir aussi la composition.Deﬁnition CompositionSoientPX =nXk=0akX ketQX =mXk=0bkX kdeux polynˆomes a coeﬃcients dans K.• Composee de deux polynˆomes : On deﬁnit le polynˆome compose P ◦Q parP ◦QX =nXk=0akQXk.Exemple :1 + X 2 ◦2 + X=1 + 2 + X2 = 5 4X + X 2.2 + X ◦1 + X 2=2 + X 2 + 1 = 1 + X 2.1 + X + X 2 ◦1 + X 3=1 + X 3 + 1 + X 3 + 12 = 3 + 3X 3 + X 6.Algebre225 / 269

Page 233 : PolynˆomesEtudions quelques proprietes de l’addition :TheoremeL’addition dans KX est :• associative : Pour tout polynˆome P, Q, R KX, nous avonsP + Q + R = P + Q + R;• commutative : Pour tout polynˆome P, Q KX, nous avonsP + Q = Q + P;• admet pour element neutre le polynˆome nul : Pour tout polynˆomeP KX, nous avons0 + P = P + 0 = P.Demonstration.A vous de veriﬁer.Algebre226 / 269

Page 234 : PolynˆomesEtudions quelques proprietes du produit :TheoremeLe produit dans KX est :• associative : Pour tout polynˆome P, Q, R KXP · Q · R = P · Q · R;• commutative : Pour tout polynˆome P, Q KXP · Q = Q · P;• admet pour element neutre le polynˆome unite : Pour tout polynˆomeP KX1 · P = P · 1 = P.Demonstration.A vous de veriﬁer.Algebre227 / 269

Page 235 : Degre d’un polynˆomeAttache a chaque polynˆome on a l’important notion de degre.Deﬁnition Degre d’un polynˆomeSoitP =nXk=0akX kun polynˆome non nul de KX. On appelle degre du polynˆome P le plus grandentier k tel queak ̸= 0.On note cet entier degP et on dit que :• ak est le coeﬃcient dominant de P. Autrement dit, le coeﬃcientdominant, est le coeﬃcient du monˆome de plus haut degre de PX.• P est unitaire ou normalise si son coeﬃcient dominant est egal a 1.Remarque : Par convention, le polynˆome nul est de degre :deg0 = .Algebre228 / 269

Page 236 : Degre d’un polynˆomeExemple :• X 1515 1 est un polynome unitaire, de degre 1515.• 3X 5 + 2X 4 2x + 1 est un polynome de degre 5 , de coeﬃcient dominant 3.• 5 + 17X + 30X 4 + 6X 7 est un polynome de degre 7, de coeﬃcient dominant6.Le degre d’un polynˆome satisfait les proprietes suivants.TheoremeSoient PX et QX deux polynˆomes a coeﬃcients dans K. Alors• degP + Q maxdegP; degQ.• degP · Q = degP + degQ.• Pour tout λ K, degλP = degP.• Si degQ 1, degP ◦Q = degP · degQ.Algebre229 / 269

Page 237 : Degre d’un polynˆomeDemonstration.SoientPX =nXk=0akX ketQX =mXk=0bkX kavec an ̸= 0 et bm ̸= 0. Alorsdeg P = netdeg Q = mon veriﬁera sans diﬃculte que toutes ses proprietes restent vrais dans le cas oul’un des 2 polynomes est nul.• degP + Q maxdegP, degQ : Pour tout k maxm, n, on aak = bk = 0=⇒ak + bk = 0.Ainsi degP + Q maxdegP, degQ.Algebre230 / 269

Page 238 : Degre d’un polynˆomeDemonstration.• degP · Q = degP + degQ : Le terme de plus haut degre de P · Q estan · bmX n+m.Ainsi degP · Q = m + n.• Si degQ 1, degP ◦Q = degP · degQ : Supposons degQ 1. On a pardeﬁnitionP ◦QX = a0 + a1QX + · · · + anQXn.Maintenant, le point precedent nous permet de conclure que pour tout 0 k n,on adegQk = k degQ.Ainsi, le terme de plus haut degre de P ◦Q est anQXn. D’ou on conclutdegP ◦Q = deganQXn = n · degQ = degP · degQ.Algebre231 / 269

Page 239 : Degre d’un polynˆomeExemple ou degP + Q maxdeg P, deg Q : SoitP = X 3 X + 2etQ = X 3 + X 2.AlorsP + QX = X 2 X + 2 =⇒degP + Q=23 = maxdeg P, deg Q.Remarque : Si degP ̸= degQ, alorsdegP + Q = maxdegP, degQ.Algebre232 / 269

Page 240 : Degre d’un polynˆomeEn utilisant les proprietes du degre, on peut facilement montrer la propositionsuivant.PropositionLe produit de deux polynomes non nuls est non nul. Autrement dit :P, Q KX,P · Q = 0 =⇒P = 0ouQ = 0.Demonstration.P · Q = 0=⇒deg P + deg Q = degP · Q = =⇒deg P = oudeg Q = =⇒P = 0 ou Q = 0.Algebre233 / 269

Page 241 : Derivation de PolynˆomesUne autre operation que on peut deﬁnir sur l’ensemble des polynomes, c’est laderivation.Deﬁnition Polynˆome deriveSoitP =nXk=0akX kun polynˆome dans KX. On appelle derivee formelle du polynˆome P, lepolynˆome P′deﬁni parP′X = 0si degP 0Pnk=1 kakX k1 = a1 + 2a2X + · · · + nanX n1si degP 0.On deﬁnit par iteration les polynˆomes derives successifs de P parP0=PPk=Pk1′pour tout k 1.Algebre234 / 269

Page 242 : Derivation de PolynˆomesExemple : SoitP = 5X 3 + X 2 7X + 3.Alors les derivees succesives de P sont :P0X=5X 3 + X 2 7X + 3P1X=15X 2 + 2X 7P2X=30X + 2P3X=30PkX=0,k 4.Etudions quelques proprietes de la derivation.PropositionSoit P un polynˆome dans KX. Alors, si degP 1, on adegP′ = degP 1.Demonstration.Cela vient tout simplement de la deﬁnition de la derivee. A vous de veriﬁer.Algebre235 / 269

Page 243 : Derivation de PolynˆomesNous avons aussi le resultat suivant.TheoremeSoient PX et QX deux polynˆomes a coeﬃcients dans K.• On a P′ = 0 ⇐⇒P est constant.• P + Q′ = P′ + Q′.• Pour tout λ K, λP′ = λP′.• P · Q′ = P′ · Q + P · Q′.• P ◦Q′ = Q′ · P′ ◦Q.Demonstration.Cela vient aussi tout simplement des deﬁnitions des sommes et produits. A vousde veriﬁer.Algebre236 / 269

Page 244 : Derivation de PolynˆomesUn raissonement par recurrence, nous permet de traduire le theoreme precedentau cas de derivees d’ordre superieur.TheoremeSoient PX et QX deux polynˆomes a coeﬃcients dans K.• Si degP = n, alorsPk = 0pour tout k n.• Pour tout λ, µ K et n N, nous avonsλP + µQk = λPk + µQk.• Formule de Leibniz : Pour tout n N, nous avonsP · Qn =nXk=0nkPkQnk.Algebre237 / 269

Page 245 : Divisibilite dans KXL’ensemble des polynˆomes KX dispose des proprietes similaires de celles del’ensemble des entiers relatif. Sur KX on peut parler de la notion de divisibilite.Deﬁnition DivisibiliteSoient A, B KX. On dit que A divise B ou que B est un multiple de A, s’ilexiste Q KX, tel queB = A · Q.Si A divise B on noteAB.Le polynˆome A est appele diviseur de B et B un multiple de A.Algebre238 / 269

Page 246 : Divisibilite dans KXRemarques :• Un polynˆome PX non nul est divisible par les polynˆomes λ et λPX avecλ K. En eﬀet, pour tout λ K, nous avonsPX = λ · λ1PXetPX = λPX · λ1.• Reciproquement, un polynˆome de degre 0 i.e. polynˆome constant et non nuldivise tous les polynˆomes. En eﬀet, pour tout λ Ket pour toutPX KX, nous avonsPX = λ · λ1PX.• Tout polynˆome divise le polynˆome nul. En eﬀet, pour tout PX KX,nous avons0 = PX · 0.Algebre239 / 269

Page 247 : Divisibilite dans KXEtudions quelques proprietes de la division.PropositionSoit A, B, C et D des polynˆomes dans KX. On a alors :•DA et DB=⇒DP · A + Q · B,P, Q KX.•AB et CD=⇒A · CB · D.•k N,AB=⇒AkBk.Demonstration.A vous de veriﬁer.Algebre240 / 269

Page 248 : Divisibilite dans KXPropositionSoient A, B KX deux polynˆomes non nuls. Alors :AB et BA⇐⇒λ K,A = λBOn dit alors que A et B sont des polynˆomes associes.Demonstration.• ⇐=: Immediat• =⇒: Si AB et BA, alors il existe C, D KX tels queB = A · CetA = B · D.Ainsideg B = deg A + deg C deg Aetdeg A = deg B + deg D deg B.Algebre241 / 269

Page 249 : Divisibilite dans KXDemonstration.D’ou on conclutdeg A = deg B=⇒deg D = deg C = 0.Par consequent, D est un polynome constante et non nul. C’est-a-direD = λ KetA = λB.Algebre242 / 269

Page 250 : Divisibilite dans KXPropositionSoient PX et QX deux polynˆomes a coeﬃcients dans K. AlorsP · Q = 1si et seulement si P et Q sont des constantes inverses l’une de l’autre.Demonstration.• ⇐=: Immediat.• =⇒: Si P · Q = 1, alors0 = degP · Q = degP + degQ=⇒degP = degQ = 0.D’ou on conclut queP = λetQ = λ′.Or λ · λ′ = 1. Ce qui implique λ′ = λ1.Algebre243 / 269

Page 251 : Divisibilite dans KXRemarque : Cela veut dire qu’un polynˆome non nul n’est pas forcementinversible. Les seuls polynˆomes inversibles sont les constantes non nulles.Une autre propriete partage entre l’ensemble des polynˆomes et l’ensemble desentiers relatif, est la division euclidienne.Theoreme Division euclidienneSoient A, B KX tels que B ̸= 0. Alors, il existe un unique couple depolynˆomes Q, R KX2 tel que :A = BQ + R,degR degB.Les polynˆomes Q et R seront alors appeles le quotient et le reste dans la divisioneuclidienne de A par B.Algebre244 / 269

Page 252 : Divisibilite dans KXExemple : Faisons la division euclidienne de A = 2X 4 X 3 2X 2 + 3X 1 parB = X 2 X + 1. Notons que on pose une division de polynˆomes comme on poseune division euclidienne de deux entiers. En eﬀet2X 4-X 3-2X 2+3X-1X 2 X + 1-2X 4-2X 3+2X 22X 2+X -3X 3-4X 2+3X-1-X 3-X 2+X-3X 2+2X-1--3X 2+3X-3-X+2Alors on trouveQ = 2X 2 + X 3 QuotientetR = X + 2 Reste.On n’oublie pas de veriﬁer qu’eﬀectivement A = BQ + R.Algebre245 / 269

Page 253 : Divisibilite dans KXPropositionSoient A, B KX. On aA divise B ⇐⇒le reste de la division euclidienne de A par B est nul.Demonstration.• =⇒: Si AB, alors il existe Q tel que B = AQ. Alors le couple Q, 0satisfait la deﬁnition de la division euclidienne. Par unicite du reste de ladivision euclidienne pour les polynˆomes, on en deduit que ce reste est nul.• ⇐= : Si le reste de la division euclidienne de A par B est nul, on obtient qu’ilexiste Q KX tel queB = AQ + 0 = AQ.Donc on a bien AB.Algebre246 / 269

Page 254 : Evaluation polynomialeDeﬁnition Fonction polynomialeSoit P = Pnk=0 akX k KX et λ K. Alors on deﬁnitPλ =nXk=0akλkon evalue P en λ.La fonctionK→Kx7→Px,est appelee fonction polynomiale associee au polynome P.Algebre247 / 269

Page 255 : Evaluation polynomialeL’evaluation polynomiale nous permet d’exprimer les coeﬃcients d’un polynˆome al’aide des derivees succesives.Theoreme Formule de Taylor en 0Pour tout polynˆome P = Pnk=0 akX k KX de degre n N, on aPX = P0 + P10X + P202!X 2 + · · · + Pn0n!X nCe qui revient aPX =nXk=0Pk0k!X k.C’est-a-direak = Pk0k!.Algebre248 / 269

Page 256 : Evaluation polynomialeNous pouvons generaliser la formule de Taylor a tout a K.Theoreme Formule de Taylor en a KPour tout polynˆome P KX de degre n N et a K, nous avons :PX = Pa + P1aX a + P2a2!X a2 + · · · + Pnan!X anCe qui revient aPX =nXk=0Pkak!X ak.Algebre249 / 269

Page 257 : Racines d’un polynˆomeEtudions les points ou un polynˆome s’annule.Deﬁnition RacinesSoit P KX. On dit que a K est une racine ou un zero de P siPa = 0.Remarques :• Tout polynˆome de degre 1 a une racine : la racine deaX + bestba .En eﬀeta ·ba+ b = 0.• L’existence de racines depend de K : par exemple X 2 + 1 n’a pas de racinedans R, mais il a les racines +i et i dans C.Algebre250 / 269

Page 258 : Racines d’un polynˆomeDonnons une characterization des racines d’un polynˆome.PropositionSoit α K et P KX. Alorsα est racine de P⇐⇒X αP.Demonstration.On raissone par double implication :• ⇐= : Supposons que X αP, alors il existe Q KX tel queP = X αQX.AinsiPα = α αQα = 0.Algebre251 / 269

Page 259 : Racines d’un polynˆomeDemonstration.• =⇒: Supposons que α soit racine de P, et ecrivons la division euclidienne deP par X α :il existe Q, R KX tels que :PX = X αQX + RX,degR degX a = 1.Ainsi, degR 0 et RX = r K. On evalue alors l’egalite precedente enα :0 = Pα = α αQα + r = r=⇒r = 0.Par consequent, PX = X αQX et X α divise P.Algebre252 / 269

Page 260 : Racines d’un polynˆomeExemple : Considerons le polynˆome P = X 3 X + 6. On voit que 2 est racinede P :23 + 2 + 6 = 0Par la proposition precedente, P se factorise par X + 2. Pour obtenir safactorisation, on peut :• soit ecrire P = X + 2aX 2 + bX + c, developper :aX 3 + 2a + bX 2 + 2b + cX + 2c=PX=X 3 X + 6et proceder par identiﬁcation des coeﬃcients1 = a;0 = 2a + b;1 = 2b + c;6 = 2c• soit faire la division euclidienne de P par X + 2 : le quotient correspond al’autre facteur de la factorisation.Algebre253 / 269

Page 261 : Racines d’un polynˆomeDeﬁnition Ordre de multipliciteSoit PX KX un polynˆome non nul et α K. On dit que α est une racined’ordre m ou de multiplicite m de P si :• P est divisible par X αm, et• P n’est pas divisible par X αm+1.Remarque : Puisque X αm divise PX nous avons m degP. Donc1 m degP.Algebre254 / 269

Page 262 : Racines d’un polynˆomeDonnons une caracterisation de l’ordre de multiplicite a l’aide de la derivation.PropositionSoient P KX, α K et m N. On a l’equivalence entre :• X αm divise P,• Pα = P′α = · · · = Pm1α = 0.Si l’une de ces conditions est satisfaite, on dit alors que α est racine de P demultiplicite au moins m.Demonstration.C’est une consequence directe de la formule de Taylor. A vous de veriﬁer.Exemple : Considerons P = X 5 7X 4 + 19X 3 25X2 + 16X 4. On peutveriﬁer queP1 = P′1 = P′′1 = 0.Donc 1 est racine de P de multiplicite au moins 3. AinsiX 13diviseX 5 7X 4 + 19X 3 25X 2 + 16X 4.Algebre255 / 269

Page 263 : Racines d’un polynˆomeComme corollaire du resultat precedent on a :TheoremeSoient P KX, α K et m N. Alors α est une racine de multiplicite m dePX si et seulement siPα = P′α = · · · = Pm1α = 0etPmα ̸= 0.Demonstration.Cela decoule tout simplement de la deﬁnition de la multiplicite d’une racine et dela proposition precedente.Vocabulaire :• Lorsque m 2, on parle de racine multiple.• Les racines d’ordre 1, 2, 3 de P sont respectivement appeles racines simples,doubles, triples de P.Algebre256 / 269

Page 264 : Racines d’un polynˆomeExemple : Considerons toujours P = X 5 7X 4 + 19X 3 25X 2 + 16X 4. On aP1 = P′1 = P′′1 = 0etP31 = 6.Donc 1 est racine de P de multiplicite 3 exactement.Etudions le nombre possible de racines d’un polynˆome.PropositionSoit P KX, et α1, α2 · · · , αp, p racines distincts de P. AlorsX α1 · X α2 · · · · · X αpdiviseP.Algebre257 / 269

Page 265 : Racines d’un polynˆomeComme consequence de cette proposition, on obtient les deux theoremes suivants.TheoremeUn polynˆome de degre n N a au plus n racines distinctes.Demonstration.Soit P un polynˆome et supposons que P admette p racines distinctes α1, · · · , αp.D’apres la proposition precedente, il existe alors Q KX tel que :PX = X α1 · · · · · X αpQX.En prenant les degres dans cette egalite, on en deduit quedegP = p + degQet doncp degP = n.Algebre258 / 269

Page 266 : Racines d’un polynˆomeTheoremeLe seul polynˆome qui possede une inﬁnite de racines est le polynˆome nulle.Demonstration.C’est une consequence directe de la proposition precedente : si P est non nul, iln’a qu’un nombre ﬁni de racines.Algebre259 / 269

Page 267 : Racines d’un polynˆomeSi on compte les racines avec leur multiplicite alors on a :TheoremeSoit P KX, et α1, α2, · · · , αp, p racines distincts de P de multipiciterespectives m1, m2, · · · , mp. AlorsX α1m1 · X α2m2 · · · · · X αpmpdiviseP.Comme consequence du theoreme, on a le resultat suivante.CorollaireUn polynˆome de degre n a au plus n racines comptees avec leurs ordres demultiplicite.Algebre260 / 269

Page 268 : Decomposition en facteurs irreductiblesEtudions comme un polynome se decompose en produit de polynˆomes plussimples i.e. de degre inferieurDeﬁnition Polynˆome irreductibleSoit PX KX. On dit que PX est irreductible, s’il satisfait• deg P 1.• les seuls diviseurs de P sont les polynˆomes :λetλPX,avec λ K.C’est-a-dire, les polynˆomes constants non nuls et les polynˆomes associes aPX.Autrement dit, PX est irreductible sur K s’il satisfaitA, B KX, PX = AXBX=⇒degA = 0 oudegB = 0.Algebre261 / 269

Page 269 : Decomposition en facteurs irreductiblesRemarques• Les polynˆomes de degre un sont irreductibles.• Les polynˆomes irreductibles dans KX jouent le rˆole des nombres premiersdans N.Rappelons que tout element de N peut s’ecrire comme un produit de nombrespremiers, de maniere analogue nous pouvons decomposer tout polynome en tantque produit de polynˆomes irreductibles.TheoremeTout polynˆome de KX de degre superieur ou egal a 1, se decompose de maniereunique en produit d’une constante non nulle et de polynˆomes irreductiblesunitaires a l’ordre des facteurs pres.Algebre262 / 269

Page 270 : Decomposition en facteurs irreductiblesEtudions plus en detail la decomposition d’un polynˆome en facteurs irreductibles.Pour cela on deﬁnit.Deﬁnition Polynˆome ScindeOn dit qu’un polynˆome P KX de degre superieur ou egal a 1 est scinde s’ilpeut ˆetre ecrit comme un produit de polynˆomes de degre 1 de KX.Remarque :• Un polynˆome P KX est scinde et irreductible sur K si et seulement sidegP = 1.• Le polynˆome X 2 + 1 est irreductible sur R mais scinde sur C puisqu’il peuts’ecrire :X 2 + 1 = X iX + i.La decomposition d’un polynˆome depend de K. Nous allons donc distinguer lesdecompositions sur CX et sur RX.Algebre263 / 269

Page 271 : Decomposition dans CXTheoreme Theoreme de d’Alembert-GaussTout polynˆome non constant de CX possede au moins une racine dans C.On a la consequence suivante de ce resultat.PropositionTout polynˆome non nul de CX est scinde.Demonstration.Montrons par recurrence la propriete :n N, Pn : tout polynˆome de CX de degre n est scinde.• Initialisation : Si deg P = 1, alors P est scinde par deﬁnition, donc P1 estvraie.Algebre264 / 269

Page 272 : Decomposition dans CXDemonstration.• Heredite : Soit n Net supposons Pn vraie. Soit P de degre n + 1.D’apres le Theoreme de d’Alembert Gauss, P admet au moins une racineα C. Alors X α divise P et il existe Q KX, tel quePX = X αQX.Or degQ = n et par hypothese de recurrence, Q est scinde :Q = λX α1 · · · · · X αn.AinsiP = λX αX α1 · · · · · X αnest scinde, et Pn + 1 est vraie. On conclut par principe de recurrence.Algebre265 / 269

Page 273 : Decomposition dans CXProposition1 Les polynˆomes irreductibles de CX sont les polynˆomes de degre 1.2 Tout polynˆome P de CX se factorise de fa¸con unique a l’ordre pres desfacteurs en produit de polynˆomes irreductibles de CX sous la forme :PX = λX α1m1 · X α2m2 · · · · · X αkmk .Demonstration.1 On a deja vu que les polynˆomes de degre 1 sont irreductibles.Reciproquement, soit P un polynˆome irreductible. Par le Theoreme ded’Alembert Gauss, il existe α tel que Pα = 0. AinsiQ KX,P = X aQ.Comme de plus P est irreductible, on en deduit que Q Ket que deg P = 1.2 Soit P un polynˆome de degre superieur ou egal a 1 de CX. D’apres laproposition precedente, P est scinde sur CX, d’ou l’existence d’une tellefactorisation.Algebre266 / 269

Page 274 : Decomposition dans RXPassons maintenant a la decomposition dans RX. Commen¸cons par introduire leresultat suivant :LemmaSoit PX RX. Si on considere PX comme un polynˆome de CX et queα C \ R est une racine de PX alors α est aussi une racine complexe de PXavec mˆeme multiplicite.Demonstration.Soit PX = Pnk=0 akX k. Supposons α C \ R est une racine de PX. Alors0 = Pα=⇒0 = Pα.Maintenant, puisque les coeﬃcient de P sont reels, nous pouvons ecrire0 = nXk=0akαk!=nXk=0ak · αk =nXk=0akαk = Pα.Donc α est une racine.Algebre267 / 269

Page 275 : Decomposition dans RXA l’aide du lemme precedent nous pouvons donner la decomposition dans RX.Theoreme1. Les polynˆomes irreductibles de RX sont• les polynˆomes de degre 1 ;• les polynˆomes de degre 2 a discriminant strictement negatif.2. Tout polynˆome P de RX se factorise de fa¸con unique a l’ordre pres desfacteurs en produit de polynˆomes irreductibles de RX sous la forme :PX = λ pYk=1X αkmk! qYk=1X 2 + βkX + γknk!.Algebre268 / 269

Page 276 : Somme et produit des racines d’un polynˆomeOn ﬁnit le chapitre avec le resultat suivant.Proposition Somme et produit des racines d’un polynˆome scindeSoit P = Pnk=0 akX k KX un polynˆome scinde, α1, α2 · · · , αn, ses racinesdistinctes ou non. Alorsα1 + α2 + · · · + αn=an1an.α1 · α2 · · · · · αn=1n a0an.Remarque : En particulier, pour n = 2 et PX = c + bX + aX 2, nous avons :α1 + α2=baα1 · α2=caAlgebre269 / 269

PREING1 S1, Algebre1

Le contenu de cet article est la propriété exclusive de son auteur.

Tags tendance