CM Ondes
Evaluation : 3 CC, majoritairement (voire complètement) en question ouvertes.
2 grandes parties :
I. Oscillations
II. Ondes
Un oscillateur est un système physique présentant un comportement périodique en temps autour d’une position d’équilibre stable.
Couplage d’oscillateurs. Limite continue : onde, traduit la propagation d’une perturbation dans l’espace ($\overrightarrow{r}$) et dans le temps ($t$), périodique dans l’espace et dans le temps.
Partie I : Oscillateurs
Chapitre 1 : Oscillateur individuel
I. Oscillateur harmonique
Oscillateur non-amorti et non-forcé.
1. Exemple : Le système masse-ressort
Dans un référentiel galiléen, on considère un ressort idéal horizontal de raideur $k$ et de longueur à vide $l_{0}$.
À l’une des extrémités est placé un point matériel $M$ de masse $m$.
À l’autre extrémité est placé le point $H$ fixe dans ce référentiel.
On ne considère aucun frottement.
On cherche à résoudre l’équation du mouvement.
Rappel : Force exercée par le ressort sur $M$.
\[{\overrightarrow{F}}_{\rightarrow M} = - k \left( l - l_{0} \right){\overrightarrow{u}}_{HM} = - \overrightarrow{\nabla} \left( E_{p} \right)\ \text{où}\ E_{p} = \frac{1}{2}k \left( l - l_{0} \right)^{2} + \text{cte}\] \[{\overrightarrow{F}}_{\rightarrow M} = - k \left( \left\vert x - x_{H} \right\vert - \left\vert x_{0} - x_{H} \right\vert \right)\overrightarrow{u_{x}}\] \[{\overrightarrow{F}}_{M} = - k \left( x - x_{0} \right)\overrightarrow{u_{x}}\]D’après le PFD sur $M\ $projeté sur $(Ox)$.
\[m\ddot{x} = - k \left( x - x_{0} \right)\]Changement de variable : $X = x - x_{0},\ \dot{X} = \dot{x},\ \ddot{X} = \ddot{x}$
\[\Rightarrow \ddot{X} + \frac{k}{m}X = 0\]Equation différentielle aux dérivées ordinaires linéaire d’ordre 2 à coefficients constants sans second membre.
Dérivées ordinaires : pas de dérivées partielles
Equation différentielle linéaire : $\forall n,\frac{d^{n}x}{dt^{n}}\ \text{sont à la puissance 1}$
2. Linéarité et superposition
Une équation est dite linéaire si pour toutes solutions $f$ et $g$ de cette équation, $\alpha f + \beta g$ (avec $\alpha$ et $\beta$ constantes) est aussi solution. Dans ce cas, $\alpha f + \beta g$ est appelée superposition de $f$ et $g$.
$\Rightarrow$ L’ensemble des solutions de l’équation forme un espace vectoriel (EV).
Pour trouver l’ensemble des solutions, on peut chercher une base de cet EV : $ \left\lbrace f_{i} \right\rbrace_{i = 1,\ldots,\dim(EV)}$
On peut alors exprimer la solution générale de l’équation linéaire comme la superposition (ou combinaison linéaire CL) des $f_{i}$.
\[f = \sum_{i}^{\dim(EV)}{\alpha_{i}f_{i}}\ \text{où}\ \left\lbrace \alpha_{i} \right\rbrace = \text{ctes}\]Prenons une équation aux dérivées ordinaires (EDO) d’ordre $n$ de la forme :
\[S(t) + \sum_{i = 0}^{n}{\beta_{i}\frac{d^{i}f}{dt^{i}}} = 0\]Si $\forall t,\ S(t) = 0$, l’équation est homogène et linéaire.
Si $\exists t,\ S(t) \neq 0$, l’équation est inhomogène et non linéaire (au sens de la superposition).
On s’intéresse au cas homogène.
Cas $S(t) = 0\ \forall t$
*Ansatz *: On « tente le coup »
Cherchons les fonctions de base de l’EV des solutions sous la forme :
$\widetilde{f}(t) = e^{rt}\ \text{où}\ r\mathbb{\in C}$ $\rightarrow$ Ansatz
Notation : $\widetilde{f}\ $: fonction complexe.
Solution physique : $f(t)\mathfrak{= Re} \left\lbrack \widetilde{f}(t) \right\rbrack$ (par linéarité).
On injecte l’Ansatz dans l’EDO avec $S(t) = 0$
\[\sum_{i = 0}^{n}{\beta_{i}\frac{d^{i} \left( e^{rt} \right)}{dt^{i}}} = 0\] \[\left( \sum_{i = 0}^{n}{\beta_{i}r^{i}} \right)e^{rt} = 0\ \forall t\] \[\Rightarrow \sum_{i = 0}^{n}{\beta_{i}r^{i}} = 0\ \text{polynôme caractéristique de degré}\ n\ \text{en}\ r\] \[\Rightarrow \ \text{au plus}\ n\ \text{racines distinctes}\]Or la dimension de l’espace vectoriel des solutions d’une EDO d’ordre $n$ est $n\ $:
Si $n$ racines distinctes et les $f$ sont linéairement indépendantes, alors l’ensemble des $\widetilde{f}$ forme la base recherchée.
Si moins de $n$ racines distinctes, alors il faut compléter avec un autre Ansatz.
Solution générale :
\[\widetilde{f}(t) = \sum_{j = 1}^{n}{\widetilde{\alpha_{j}}e^{r_{j}t}}\] \[\text{Solution physique }:f(t)\mathfrak{= Re} \left\lbrack \widetilde{f}(t) \right\rbrack\]- Résolution de l’exemple de la masse attachée au ressort
Ansatz : $\widetilde{X}(t) = e^{rt}$
\[r^{2} + \frac{k}{m} = 0\] \[r^{2} = - \frac{k}{m} = i^{2}\frac{k}{m}\] \[\Rightarrow r_{\pm} = \pm i\sqrt{\frac{k}{m}} = \pm i\omega_{0}\]$ \left\lbrack \omega_{0} \right\rbrack = T^{- 1}$ : pulsation
- Solution générale :
Les fonctions sont bien linéairement indépendantes.
\[X(t) = Re\lbrack\widetilde{X}(t)\rbrack\] \[X(t) = Re \left( \widetilde{\alpha_{+}}e^{i\omega_{0}t} + \widetilde{\alpha_{-}}e^{- i\omega_{0}t} \right)\] \[X(t) = Re \left( \widetilde{\alpha_{+}} \right)\cos \left( \omega_{0}t \right) - Im \left( \widetilde{\alpha_{+}} \right)\sin \left( \omega_{0}t \right) + Re \left( \widetilde{\alpha_{-}} \right)\cos \left( \omega_{0}t \right) + Im \left( \widetilde{\alpha_{-}} \right)\sin \left( \omega_{0}t \right)\] \[X(t) = \left\lbrack Re \left( \widetilde{\alpha_{+}} \right) + Re \left( \widetilde{\alpha_{-}} \right) \right\rbrack\cos \left( \omega_{0}t \right) + \left\lbrack - Im \left( \widetilde{\alpha_{+}} \right) + Im \left( \alpha_{-} \right) \right\rbrack\sin \left( \omega_{0}t \right)\] \[\Rightarrow X(t) = \alpha_{c}\cos \left( \omega_{0}t \right) + \alpha_{s}\sin \left( \omega_{0}t \right),\ \text{où}\ \alpha_{c}\ \text{et}\ \alpha_{s}\ \text{sont des réels}\] \[\dot{X}(t) = \omega_{0} \left\lbrack - \alpha_{c}\sin \left( \omega_{0}t \right) + \alpha_{s}\cos \left( \omega_{0}t \right) \right\rbrack\]$\alpha_{c}$ et $\alpha_{s}$ déterminés par l’état du système $ \left\lbrace X,\dot{X} \right\rbrace$ à $t$ donné.
Exemple : à $t = 0$
$X(t = 0) = \alpha_{c}$, $\dot{X}(t = 0) = \omega_{0}\alpha_{s}$
N.B. :
\[X(t) = \alpha_{c}\cos \left( \omega_{0}t \right) + \alpha_{s}\sin \left( \omega_{0}t \right)\] \[X(t) = \alpha\cos \left( \omega_{0}t + \varphi_{c} \right) = \alpha\sin \left( \omega_{0}t + \varphi_{s} \right)\]Avec :
\[\alpha^{2} = \alpha_{c}^{2} + \alpha_{s}^{2}\] \[\varphi_{c} = \arctan \left( - \frac{\alpha_{s}}{\alpha_{c}} \right)\] \[\varphi_{s} = \arctan \left( \frac{\alpha_{c}}{\alpha_{s}} \right)\]$X(t)$ est une fonction :
- oscillante autour d’un équilibre stable
d’amplitude constante
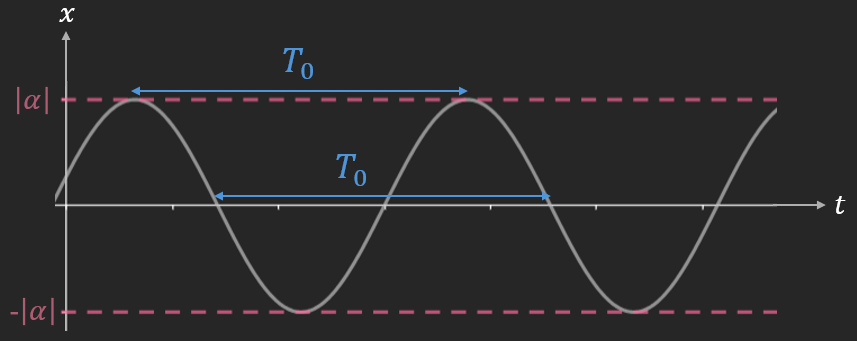
de période $T_{0}\ $: plus courte durée entre deux états identiques du système
Or $\cos\ $est $2\pi$-périodique.
$\omega_{0}T_{0} = 2\pi$
$\omega_{0} = \frac{2\pi}{T_{0}} = \text{pulsation (temporelle)}$
4. Généralisation
On appelle oscillateur harmonique tout système dont la dynamique satisfait à une équation différentielle de la forme :
\[\ddot{q} + \omega_{0}^{2}q = 0\]Avec $q\ $: coordonnée généralisée (n’importe quelle grandeur physique) et $\omega_{0}^{2} \geq 0$
\[\Leftrightarrow \left\lbrace \begin{array}{r} E = \text{cte} \\ E_{p} \propto q^{2} \end{array} \right.\]Les solutions sont des fonctions périodiques d’amplitude constante et de périodicité dépendant uniquement des caractéristiques du système, indépendantes de l’état du système.
Ex : Dans le système masse-ressort,
\[\omega_{0} = \frac{2\pi}{T_{0}} = 2\pi f_{0} = \sqrt{\frac{k}{m}}\]II. Oscillateur amorti non-forcé
On reprend le système masse + ressort horizontal et on ajoute un frottement fluide $\overrightarrow{F} = - \alpha\overrightarrow{v}$, où $\alpha > 0$ et $\overrightarrow{v}$ est la vitesse de $M$ par rapport au fluide.
\[\overrightarrow{F} = - \alpha\dot{x}\overrightarrow{u_{x}}\]D’après le PFD sur $M$ projeté sur $\overrightarrow{u_{x}}\ $:
\[m\ddot{x} = - k \left( x - x_{0} \right) - \alpha\dot{x}\]On pose $X = x - x_{0}$ et on obtient :
\[\ddot{X} + \frac{\alpha}{m}\dot{X} + \frac{k}{m}X = 0\]On note $\frac{k}{m} = \omega_{0}^{2}$ et $\frac{\alpha}{m} = \Gamma$
\[\lbrack\Gamma\rbrack = \left\lbrack \omega_{0} \right\rbrack = T^{- 1}\]Ansatz : $\widetilde{X}(t) = e^{rt}$
\[r^{2} + \Gamma r + \omega_{0}^{2} = 0\] \[r_{\pm} = - \frac{\Gamma}{2} \pm \sqrt{ \left( - \frac{\Gamma}{2} \right)^{2} - \omega_{0}^{2}} = - \frac{\Gamma}{2} \pm \sqrt{\frac{\Gamma^{2}}{4} - \omega_{0}^{2}}\]- Le nombre et la nature des solutions dépend du signe de $\frac{\Gamma^{2}}{4} - \omega_{0}^{2}$
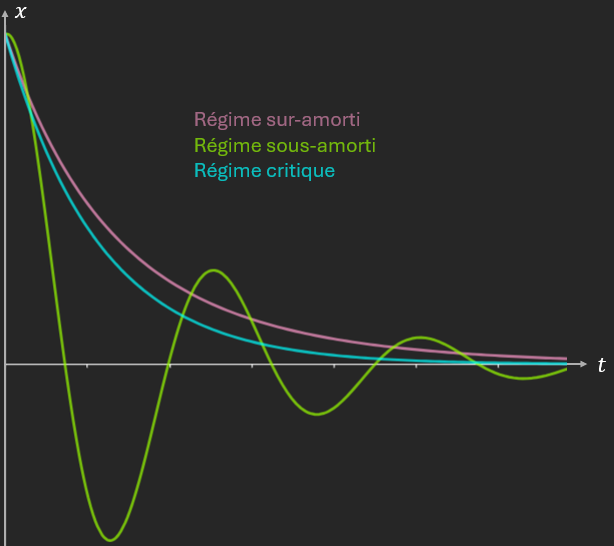
3 régimes :
- $\frac{\Gamma^{2}}{4} - \omega_{0}^{2} > 0 \Rightarrow \frac{\Gamma}{2} > \omega_{0} \geq 0$
$\Rightarrow X(t) = \alpha_{+}e^{r_{+}t} + \alpha_{-}e^{r_{-}t}$ sont deux exponentielles décroissantes, retour à l’équilibre sans osciller. \(X(t) = e^{- \frac{\Gamma}{2}} \left( \alpha_{+}e^{\sqrt{\frac{\Gamma^{2}}{4} - \omega_{0}^{2}}} + \alpha_{-}e^{- \sqrt{\frac{\Gamma^{2}}{4} - \omega_{0}^{2}}} \right)\)
Régime sur-amorti
- $\frac{\Gamma^{2}}{4} - \omega_{0}^{2} < 0 \Rightarrow \omega_{0} > \frac{\Gamma}{2} \geq 0$
Ce $\omega$ est appelé pseudo-pulsation.
\[\widetilde{X}(t) = \widetilde{\alpha_{+}}e^{r_{+}t} + \widetilde{\alpha_{-}}e^{r_{-}t}\] \[X(t) = e^{- \frac{\Gamma}{2}t} \left\lbrack \alpha_{c}\cos(\omega t) + \alpha_{s}\sin(\omega t) \right\rbrack\]$\Rightarrow$ oscillation harmonique avec enveloppe en exponentielle décroissante
Régime sous-amorti
- $\frac{\Gamma^{2}}{4} - \omega_{0}^{2} = 0 \Rightarrow \omega_{0} = \frac{\Gamma}{2}$
Il manque une fonction pour la base de dimension 2 des solutions. Il faut un autre *Ansatz *:
\[X(t) = te^{- \frac{\Gamma}{2}t}\] \[\Rightarrow X(t) = e^{- \frac{\Gamma}{2}t}(\alpha + \beta t)\]Pas d’oscillation, retour à l’équilibre sans osciller.
Régime critique
On peut montrer que c’est le régime qui revient le plus vite à l’équilibre.
III. Oscillateur non-amorti forcé
Traité en TD.
IV. Oscillateur amorti forcé
1. Résolution générale
On reprend l’oscillateur amorti du II. auquel on rajoute une force extérieure de la forme :
\[\overrightarrow{F}(t) = F_{x}(t)\overrightarrow{u_{x}}\]On se place dans un référentiel galiléen. On applique le PFD sur $M\ $:
\[\ddot{X} + \Gamma\dot{X} + \omega_{0}^{2}X = \frac{F_{x}(t)}{m}\ \ (1)\]Solution de $(1)\ $:
Soit $X$ la solution générale de $(1)$.
On cherche d’abord $X_{p}$ une solution particulière de $(1)$ avec second membre $ \left( \frac{F_{x}(t)}{m} \right)$.
Alors $X - X_{p} = X_{h}$ avec $X_{h}$ solution générale de $(1)$ sans second membre, solution de l’équation homogène.
- $X = X_{p} + X_{h}$
Or $X_{h}$ est déjà connue (voir II.)
$X_{h}$ est proportionnel à $e^{- \frac{\Gamma}{2}} \rightarrow_{t \rightarrow + \infty}0$
On a un régime transitoire qui devient un régime permanent en $t \rightarrow + \infty$
\[X \rightarrow X_{p}\]- Ici, on se limite à l’étude du régime permanent avec $F_{x}(t) = F_{0}\cos \left( \omega_{d}t \right) = Re \left\lbrack {\widetilde{F}}_{x}(t) \right\rbrack$
Ansatz : \({\widetilde{X}}_{p} = \widetilde{A}e^{i\omega_{d}t}\) : mouvement oscillant de même pulsation que le forçage.
En replaçant dans $(1)\ $:
\[\left( - \omega_{d}^{2} + i\Gamma\omega_{d} + \omega_{0}^{2} \right)\widetilde{A}e^{i\omega_{d}t} = \frac{F_{0}}{m}e^{i\omega_{d}t}\] \[\Rightarrow \widetilde{A} = \frac{F_{0}}{m \left( - \omega_{d}^{2} + i\Gamma\omega_{d} + \omega_{0}^{2} \right)}\] \[\Rightarrow \widetilde{A} = \frac{F_{0}}{m} \times \frac{1}{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right) + i\Gamma\omega_{d}}\] \[\Rightarrow \widetilde{A} = \frac{F_{0}}{m} \times \frac{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right) - i\Gamma\omega_{d}}{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right)^{2} + \left( \Gamma\omega_{d} \right)^{2}}\] \[\Rightarrow \widetilde{A} = A_{él} - iA_{abs}\] \[\text{Où}\ A_{él}:\ A\ \text{élastique},\ A_{él} = \frac{F_{0}}{m} \times \frac{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right)}{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right)^{2} + \left( \Gamma\omega_{d} \right)^{2}}\] \[\text{Où}\ A_{abs}:\ A\ \text{absorbant},\ A_{él} = \frac{F_{0}}{m} \times \frac{\Gamma\omega_{d}}{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right)^{2} + \left( \Gamma\omega_{d} \right)^{2}}\] \[\Rightarrow {\widetilde{X}}_{p} = \left( A_{él} - iA_{abs} \right)e^{i\omega_{d}t}\] \[\Rightarrow {\widetilde{X}}_{p} = \left\vert \widetilde{A} \right\vert e^{i\theta}e^{i\omega_{d}t}\] \[\text{Avec}\ \left\lbrace \begin{array}{r} \left\vert \widetilde{A} \right\vert = \sqrt{A_{él}^{2} + A_{abs}^{2}} \\ \tan(\theta) = - \frac{A_{abs}}{A_{él}} \end{array} \right\rbrace\] \[\Rightarrow {\widetilde{X}}_{p} = \sqrt{A_{él}^{2} + A_{abs}^{2}}e^{i \left( \omega_{d}t + \theta \right)} = \left\vert {\widetilde{X}}_{p} \right\vert e^{i \left( \omega_{d}t + \theta \right)}\]Déphasage par rapport à $\overrightarrow{F}$ si $\theta \neq 0$
5. Résonnance d’amplitude
Quel est le $\omega_{d}$ tel que l’amplitude du mouvement $ \left\vert {\widetilde{X}}_{p} \right\vert $ soit maximale ?
\[\left\vert {\widetilde{X}}_{p} \right\vert = \sqrt{A_{él}^{2} + A_{abs}^{2}} = \frac{F_{0}}{m} \left( \frac{ \left( \omega_{0}^{2} - \omega_{d}^{2} \right)^{2} + \left( \Gamma\omega_{d} \right)^{2}}{ \left\lbrack \left( \omega_{0}^{2} - \omega_{d}^{2} \right)^{2} + \left( \Gamma\omega_{d} \right)^{2} \right\rbrack^{2}} \right)^{\frac{1}{2}}\]Posons $\Delta \left( \omega_{d} \right) = \left( \omega_{0}^{2} - \omega_{d}^{2} \right) + \left( \Gamma\omega_{d} \right)^{2}$
\[\left\vert {\widetilde{X}}_{p} \right\vert = \frac{F_{0}}{m} \left( \frac{\Delta \left( \omega_{d} \right)}{\Delta^{2} \left( \omega_{d} \right)} \right)^{\frac{1}{2}}\] \[\left\vert {\widetilde{X}}_{p} \right\vert = \frac{F_{0}}{m}\Delta^{- \frac{1}{2}} \left( \omega_{d} \right)\] \[\frac{d \left\vert {\widetilde{X}}_{p} \right\vert }{d\omega_{d}} = \frac{F_{0}}{m} \left( - \frac{1}{2} \right)\frac{d\Delta}{d\omega_{d}}\frac{1}{\Delta^{\frac{3}{2}} \left( \omega_{d} \right)}\] \[\frac{d \left\vert {\widetilde{X}}_{p} \right\vert }{d\omega_{d}} = 0\ \text{si}\ \frac{d\Delta}{d\omega_{d}} = 0\] \[\frac{d\Delta}{d\omega_{d}} = 2 \left( - 2\omega_{d} \right) \left( \omega_{0}^{2} - \omega_{d}^{2} \right) + 2\Gamma^{2}\omega_{d} = 0\] \[\frac{d\Delta}{d\omega_{d}} = 4\omega_{d} \left( \omega_{d}^{2} - \left\lbrack \omega_{0}^{2} - 2 \left( \frac{\Gamma}{2} \right)^{2} \right\rbrack \right)\] \[\Rightarrow \left\lbrace \begin{array}{r} \omega_{d} = 0 \Rightarrow \ \text{forçage n'est pas oscillant} \Rightarrow \ \text{pas gardé} \\ \omega_{d} = \pm \left\lbrack \omega_{0}^{2} - 2 \left( \frac{\Gamma}{2} \right)^{2} \right\rbrack^{\frac{1}{2}} \end{array} \right\rbrace\]$\omega_{d}\mathbb{\in R}$ si $\omega_{0}^{2} \geq 2 \left( \frac{\Gamma}{2} \right)^{2} \Leftrightarrow \omega_{0} \geq \frac{\sqrt{2}}{2}\Gamma$
\[\text{On vérifie que}\ \frac{d^{2} \left\vert {\widetilde{X}}_{p} \right\vert }{d\omega_{d}^{2}} < 0\ \text{pour}\ \omega_{d} = \left\lbrack \omega_{0}^{2} - 2 \left( \frac{\Gamma}{2} \right)^{2} \right\rbrack^{\frac{1}{2}}\]- $ \left\vert {\widetilde{X}}_{p} \right\vert $ est maximal
$\omega_{r}$ est appelé pulsation de résonnance d’amplitude.
\[\left\vert {\widetilde{X}}_{p} \right\vert \left( \omega_{d} = \omega_{r} \right) = \frac{F_{0}}{m} \times \frac{1}{\Gamma \left\lbrack \omega_{0}^{2} - \left( \frac{\Gamma}{2} \right)^{2} \right\rbrack^{\frac{1}{2}}}\]Si $\Gamma \rightarrow 0$, $\omega_{r} \rightarrow \omega_{0}$,
\[\left\vert {\widetilde{X}}_{p} \right\vert \left( \omega_{d} = \omega_{r} \right) \rightarrow + \infty\]Chapitre II : Oscillateurs couplés
Interactions entre oscillateurs
Interactions linéaires dans ce cours
I. Deux oscillateurs couplés : non-amortis et non-forcés
On se place dans un référentiel galiléen.
(Schéma 5)
Remarque : $ \left\lbrace M_{1} + M_{2} \right\rbrace$ est un système isolé
- Soit $I$ le centre d’inertie de $ \left\lbrace M_{1},\ M_{2} \right\rbrace$, alors ${\overrightarrow{a}}_{I} = \overrightarrow{0}$ dans tout référentiel galiléen.
par $3^e$ loi de Newton.
On applique le PFD sur chaque masse, projeté sur $\overrightarrow{u_{x}}\ $:
Sur $M_{1}\ $: $m_{1}\ddot{x_{1}} = k \left( x_{2} - x_{1} - l_{0} \right)\ (1)$
Sur $M_{2}\ $: $m_{2}\ddot{x_{2}} = - k \left( x_{2} - x_{1} - l_{0} \right)\ (2)$
\[(1) \text{ à l'équilibre : } 0 = k \left( {x_{2}}_{eq} - {x_{1}}_{eq} - l_{0} \right)\] \[(2) \text{ à l'équilibre : } 0 = - k \left( {x_{2}}_{eq} - {x_{1}}_{eq} - l_{0} \right)\] \[(1) - (1)_{eq}:m_{1}\ddot{x_{1}} = k \left\lbrack \left( x_{2} - {x_{2}}_{eq} \right) - \left( x_{1} - {x_{1}}_{eq} \right) \right\rbrack\] \[(2) - (2)_{eq}:m_{2}\ddot{x_{2}} = - k \left\lbrack \left( x_{2} - {x_{2}}_{eq} \right) - \left( x_{1} - {x_{1}}_{eq} \right) \right\rbrack\]Soit $X_{1} = x_{1} - {x_{1}}_{eq}$,
$X_{2} = x_{2} - {x_{2}}_{eq}$
\[\left\lbrace \begin{array}{r} m_{1}\ddot{X_{1}} = k \left( X_{2} - X_{1} \right) \\ m_{2}\ddot{X_{2}} = - k \left( X_{2} - X_{1} \right) \end{array} \right\rbrace\] \[\left\lbrace \begin{array}{r} m_{1}\ddot{X_{1}} + k \left( X_{1} - X_{2} \right) = 0 \\ m_{2}\ddot{X_{2}} + k \left( X_{2} - X_{1} \right) = 0 \end{array} \right.\] \[\left\lbrace \begin{array}{r} \ddot{X_{1}} + \frac{k}{m_{1}X_{1}} \left( X_{1} - X_{2} \right) = 0 \\ \ddot{X_{2}} + \frac{k}{m_{2}} \left( X_{2} - X_{1} \right) = 0 \end{array} \right\rbrace\]- $\omega_{1}^{2} = \frac{k}{m_{1}}$, $\omega_{2}^{2} = \frac{k}{m_{2}}$
En notation matricielle :
\[\Leftrightarrow \begin{pmatrix} m_{1} & 0 \\ 0 & m_{2} \end{pmatrix}\ddot{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} + \begin{pmatrix} k & - k \\ - k & k \end{pmatrix}\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\] \[\Leftrightarrow M\ddot{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} + K\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\]$\det M \neq 0$ donc $M$ est inversible.
\[\Rightarrow \ddot{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} + \begin{pmatrix} \omega_{1}^{2} & - \omega_{1}^{2} \\ - \omega_{2}^{2} & \omega_{2}^{2} \end{pmatrix}\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \rightarrow (3)\]Où \(\begin{pmatrix} \omega_{1}^{2} & - \omega_{1}^{2} \\ - \omega_{2}^{2} & \omega_{2}^{2} \end{pmatrix} = M^{- 1}K\)
Résolution du système :
Ansatz : $\widetilde{\begin{pmatrix} X_{1} \ X_{2} \end{pmatrix}} = e^{i\omega t}\begin{pmatrix} A_{1} \ A_{2} \end{pmatrix}$
Mode propre ou normal du système, les deux oscillateurs oscillent avec la même pulsation $\omega$ (mais pas forcément la même amplitude).
$\omega$ est appelé la pulsation propre du système
On injecte l’Ansatz dans $(3)\ $:
\[- \omega^{2}\widetilde{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} + M^{- 1}K\widetilde{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\] \[\Leftrightarrow \left( M^{- 1}K - \omega^{2}I_{2} \right)\widetilde{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}\]Donc $\widetilde{\begin{pmatrix} X_{1} \ X_{2} \end{pmatrix}}$ est vecteur propre $ \left( \overrightarrow{vp} \right)$ de $M^{- 1}K$ de valeur propre $(vp)$ de $\omega^{2}$.
Recherche des $vp\ $:
\[\det \left( M^{- 1}K - \omega^{2}I_{2} \right) = 0\] \[\left\vert \begin{matrix} \omega_{1}^{2} - \omega^{2} & - \omega_{1}^{2} \\ - \omega_{2}^{2} & \omega_{2}^{2} - \omega^{2} \end{matrix} \right\vert = 0\] \[\left( \omega_{1}^{2} - \omega^{2} \right) \left( \omega_{2}^{2} - \omega^{2} \right) - \omega_{1}^{2}\omega_{2}^{2} = 0\] \[\omega_{1}^{2}\omega_{2}^{2} - \left( \omega_{1}^{2} + \omega_{2}^{2} \right)\omega^{2} + \left( \omega^{2} \right)^{2} = \omega_{1}^{2}\omega_{2}^{2}\] \[\omega^{2} \left\lbrack \omega^{2} - \left( \omega_{1}^{2} + \omega_{2}^{2} \right) \right\rbrack = 0\]- Deux solutions :
On a 4 $\omega$ différents : $\pm \omega_{\pm}$
Recherche des $\overrightarrow{vp}\ $:
- $\overrightarrow{vp}_{-}$
- associée à $vp_{-} = \omega_{-}^{2}$
$\Rightarrow$ mouvement à pulsation $\pm \omega_{-} = 0\ $: pas d’oscillation.
$ \left\lbrace M_{1} + M_{2} \right\rbrace$ est bien tel que $\overrightarrow{a_{I}} = \overrightarrow{0}$ dans tout référentiel galiléen.
- $\overrightarrow{vp}_{+}$
- associé à $vp_{+}$
- $= \omega_{+}^{2} = \omega_{1}^{2} + \omega_{2}^{2}$
- Mouvement oscillant à pulsation $\omega_{+} = \sqrt{\omega_{1}^{2} + \omega_{2}^{2}}$ où les masses oscillent en opposition de phase (4) et $ \left\lbrace M_{1} + M_{2} \right\rbrace$ est bien tel que $\overrightarrow{a_{I}} = \overrightarrow{0}$ dans tout référentiel galiléen.
Solution générale :
Combinaison linéaire des modes propres :
\[\widetilde{\begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix}} = \left( {\widetilde{\alpha}}_{+ +}e^{+ i\omega_{+}t} + {\widetilde{\alpha}}_{+ -}e^{- i\omega_{+}t} \right)\widetilde{\begin{pmatrix} {A_{1}}_{+} \\ {A_{2}}_{+} \end{pmatrix}} + \left( {\widetilde{\alpha}}_{- +}e^{i\omega_{-}t} + {\widetilde{\alpha}}_{- -}e^{- i\omega_{-}t} \right)\widetilde{\begin{pmatrix} {A_{1}}_{-} \\ {A_{2}}_{-} \end{pmatrix}}\]Solution physique :
\[\overrightarrow{X} = {Re} \left( \widetilde{\overrightarrow{X}} \right)\]$ \left\lbrace \alpha_{\pm \pm} \right\rbrace$ sont fixés par la connaissance de l’état du système $ \left( \overrightarrow{X},\dot{\overrightarrow{X}} \right)$ à $t$ donné.
V. N oscillateurs couplés
1. Equation du mouvement
Soit 1 chaine de $N$ masses $m$ identiques couplées par $(N + 1)$ ressorts de $\left( k,\ l_{0} \right)$ identiques avec deux murs aux extrémités.
On considère la masse $n $:
\[{\overrightarrow{F}}_{\rightarrow n} = {\overrightarrow{F}}_{n - 1 \rightarrow n} + {\overrightarrow{F}}_{n + 1 \rightarrow n}\]Où \({\overrightarrow{F}}_{n - 1 \rightarrow n} = - k\left( \left\vert x_{n} - x_{n - 1} \right\vert - l_{0} \right)\ \overrightarrow{u_{x}} = - k\left( x_{n} - x_{n - 1} - l_{0} \right)\ \overrightarrow{u_{x}}\)
\[{\overrightarrow{F}}_{n + 1 \rightarrow n} = - k\left( x_{n + 1} - x_{n} - l_{0} \right)\left( - \ \overrightarrow{u_{x}} \right) = - k\left( x_{n} - x_{n + 1} + l_{0} \right)\overrightarrow{u_{x}}\]Dans un référentiel galiléen, d’après le PFD appliqué à la masse $n$ projeté sur $\overrightarrow{u_{x}}\ $:
\[m\ddot{x} = - k\left\lbrack \left( x_{n} - x_{n - 1} \right) - l_{0} + \left( x_{n} - x_{n + 1} \right) + l_{0} \right\rbrack\ (1)\] \[(1)\ \text{à l'équilibre}:\ - k\left\lbrack \left( {x_{n}}_{eq}\ - {x_{n - 1}}_{eq}\ \right) - l_{0} + \left( {x_{n}}_{eq} - {x_{n + 1}}_{eq} \right) + l_{0} \right\rbrack\]Posons \(X_{n} = x_{n} - {x_{n}}_{eq}$. Par $(1) - (1_{eq})\)
\[\ddot{X}(t) + \frac{k}{m}\left\lbrack 2X_{n}(t) - \left( X_{n - 1}(t) + X_{n + 1}(t) \right) \right\rbrack = 0\]Posons $\frac{k}{m} = \omega_{0}^{2}$
\[\left\lbrack \begin{array}{r} \ddot{X}(t) + \omega_{0}^{2}\left\lbrack 2X_{n}(t) - \left( X_{n - 1}(t) + X_{n + 1}(t) \right) \right\rbrack = 0 \\ \forall t,\ X_{0} = X_{N + 1} = 0 \end{array} \right.\]Ecriture matricielle :
\[\ddot{\overrightarrow{X}}(t) + M^{- 1}K\overrightarrow{X}(t) = \overrightarrow{0}\]Où :
\[\overrightarrow{X}(t) = \begin{pmatrix} X_{1}(t) \\ \vdots \\ X_{N}(t) \end{pmatrix}\] \[M = {diag}(m,\ldots,m) = mI_{n} = \begin{pmatrix} m & \ & 0 \\ \ & \ddots & \ \\ 0 & \ & m \end{pmatrix}\]Matrice diagonale $N \times N$
\[M^{- 1} = \frac{1}{m}I_{n} = \begin{pmatrix} \frac{1}{m} & \ & 0 \\ \ & \ddots & \ \\ 0 & \ & \frac{1}{m} \end{pmatrix}\] \[K = k\begin{pmatrix} 2 & - 1 & \ & \ & 0 \\ - 1 & 2 & \ddots & \ & \ \\ \ & \ddots & \ddots & \ddots & \ \\ \ & \ & \ddots & 2 & - 1 \\ 0 & \ & \ & - 1 & 2 \end{pmatrix}\]Matrice symétrique $N \times N$
\[\Rightarrow M^{- 1}K = \omega_{0}^{2}\begin{pmatrix} 2 & - 1 & \ & \ & 0 \\ - 1 & 2 & \ddots & \ & \ \\ \ & \ddots & \ddots & \ddots & \ \\ \ & \ & \ddots & 2 & - 1 \\ 0 & \ & \ & - 1 & 2 \end{pmatrix}\]2. Résolution
Ansatz mode propre : $\forall n,\ \widetilde{X_{n}}(t) = \widetilde{A_{n}}e^{i\omega t}\ (2)$, avec $\omega$ indépendant de $n$.
On injecte $(2)$ dans $(1)$.
\[e^{i\omega t}\left\lbrack - \omega^{2}\widetilde{A_{n}} + \omega_{0}^{2}\left\lbrack 2\widetilde{A_{n}} - \left( \widetilde{A_{n - 1}} + \widetilde{A_{n + 1}} \right) \right\rbrack \right\rbrack = 0\ \forall t\] \[\widetilde{A_{n + 1}} = 2\left( 1 - \frac{\omega^{2}}{2\omega_{0}^{2}} \right)\widetilde{A_{n}} - \widetilde{A_{n - 1}}\] \[A_{0} = A_{N + 1} = 0\] \[\left\lbrack \begin{array}{r} \widetilde{A_{n + 1}} = 2\left( 1 - \frac{\omega^{2}}{2\omega_{0}^{2}} \right)\widetilde{A_{n}} - \widetilde{A_{n - 1}} \\ A_{0} = A_{N + 1} = 0 \end{array} \right. \ \ (3)\]$\widetilde{\overrightarrow{A}} = \begin{pmatrix} \widetilde{A_{1}}
\vdots
\widetilde{A_{N}} \end{pmatrix}$ vecteur propre de $M^{- 1}K$ de valeur propre $\omega$
2^ème^ Ansatz : $\widetilde{A_{n}} = \widetilde{A}e^{in\theta}(4)$ (périodicité spatiale)
Conditions aux bords :
- $A_{0} = {Re}\left( \widetilde{A_{0}} \right) = 0 \Rightarrow \widetilde{A} = iA\ \left( A\mathbb{\in R} \right) \Rightarrow {\widetilde{A}}_{n} = iAe^{in\theta}$
Posons $\alpha = - A$
- $A_{N + 1} = 0$
- Quantification de la période $\theta$
Après injection de $(4)$ dans $(3)\ $:
\[\omega^{2}\widetilde{A}e^{in\theta} = \omega_{0}^{2}\left\lbrack 2 - \left( e^{- i\theta} + e^{i\theta} \right) \right\rbrack\widetilde{A}e^{in\theta}\] \[\omega^{2} = \omega_{0}^{2}\left\lbrack 2 - 2\cos(\theta) \right\rbrack\] \[\omega^{2} = 2\omega_{0}^{2}\left\lbrack 1 - \cos(\theta) \right\rbrack\] \[\omega^{2} = 2\omega_{0}^{2} \times 2\sin^{2}\left( \frac{\theta}{2} \right)\] \[\omega_{p}^{2} = \left\lbrack 2\omega_{0}\sin\left( \frac{\theta_{p}}{2} \right) \right\rbrack^{2}\] \[\omega_{p}^{2} = \left\lbrack 2\omega_{0}\sin\left( \frac{p\pi}{2(N + 1)} \right) \right\rbrack\]Combien de $\omega_{p}^{2}$ différents ?
La fonction $\sin^{2}\ $ est $\pi$-périodique mais à valeurs différentes sur un intervalle $\frac{\pi}{2}$.
\[\Rightarrow 0 \leq \frac{p\pi}{2(N + 1)} < \frac{\pi}{2}\]$\Rightarrow 0 \leq p < N + 1$, or si $p = 0$ alors il n’y a pas d’oscillations
\[\Rightarrow 0 < p < N + 1\]On obtient $N$ valeurs de $p$ pour $N$ valeurs différentes de $\omega_{p}^{2}$
Il y a $N$ modes propres.
Solution générale :
\[{\widetilde{X}}_{n}(t) = \sum_{p = 1}^{+ \infty}{\alpha\sin\left( n\theta_{p} \right)\left( {A_{p}}_{+}e^{+ i\omega_{p}t} + {A_{p}}_{-}e^{- i\omega_{p}t} \right)}\] \[X_{n}(t) = {Re}\left\lbrack {\widetilde{X}}_{n}(t) \right\rbrack\]Rappel/Complément :
\[\widetilde{X_{n}} = \widetilde{A_{n}}e^{i\omega t}\] \[\widetilde{A_{n}} = \widetilde{A}e^{in\theta},\ \ A_{n} = \alpha\sin(n\theta)\] \[\theta_{p} = \frac{p\pi}{N + 1}\]Autre notation :
$\widetilde{A_{n}} = \widetilde{A}e^{ikna}$ ($k$ est analogue de $\omega$ dans l’espace : ne pas confondre avec la raideur des ressorts)
Et $a = {x_{n}}{éq} - x{(n - 1)_{eq}}$
\[\widetilde{A_{n}} = \widetilde{A}e^{ik\left( {x_{n}}_{éq} - {x_{0}}_{eq} \right)}\] \[A_{n} = \alpha\sin(kna)\] \[\theta_{p} = k_{p}a,\ \ k_{p} = \frac{p\pi}{(N + 1)a} = \frac{p\pi}{L}\] \[\omega_{p}^{2} = 4\omega_{0}^{2}\sin^{2}\left( \frac{\theta_{p}}{2} \right) = 4\omega_{0}^{2}\sin^{2}\left( \frac{p\pi}{N + 1} \right) = 4\omega_{0}^{2}\sin^{2}\left( k_{p}\frac{a}{2} \right)\]Solution générale :
\[{\widetilde{X}}_{n}(t) = \sum_{p = 1}^{+ \infty}{\alpha\sin\left( n\theta_{p} \right)\left( {A_{p}}_{+}e^{+ i\omega_{p}t} + {A_{p}}_{-}e^{- i\omega_{p}t} \right)}\] \[{\widetilde{X}}_{n}(t) = \sum_{p = 1}^{+ \infty}{\alpha\sin\left( nk_{p}nq \right)\left( {A_{p}}_{+}e^{+ i\omega_{p}t} + {A_{p}}_{-}e^{- i\omega_{p}t} \right)}\]Partie II : Ondes
Chapitre 1 : Ondes scalaires à une dimension
Onde scalaire : grandeur qui va « onduler » est un scalaire
Exemple d’onde scalaire : perturbation sur une corde
S’oppose aux ondes vectorielles (ex : onde électromagnétique)
I. Etablissement de l’équation d’onde
1. Limite continue des N oscillateurs couplés
\[a \rightarrow 0\] \[m \rightarrow 0\] \[N \rightarrow + \infty\] \[\text{tel que}\ \left\lbrack \begin{array}{r} m_{tot} = cte \\ L_{tot} = L = cte \end{array} \right.\]Lien entre discret et continu :
$X_{n}(t) \leftrightarrow X(x,t)$ (avec $x_{n} = na$)
\[X_{n + 1}(t) \leftrightarrow X\left( x_{n + 1} = (n + 1)a,t \right)\]On réalise un DL à l’ordre 2 en $a$ autour de $x_{n} = na$
\[X_{n + 1}(t) \leftrightarrow X\left( x_{n},t \right) + \frac{\partial X}{\partial x}\left. \ \right\vert _{x_{n}} \times a + \frac{1}{2}\frac{\partial^{2}X}{\partial x^{2}}\left. \ \right\vert _{x_{n}}a^{2}\] \[\ddot{X_{n}}(t) \leftrightarrow \frac{\partial^{2}X}{\partial t^{2}}\left. \ \right\vert _{x_{n}}\]$\Rightarrow$ Dans le PFD :
Discret :
\[{\ddot{X}}_{n}(t) + \omega_{0}^{2}\left\lbrack 2X_{n}(t) - \left\lbrack X_{n - 1}(t) + X_{n + 1}(t) \right\rbrack \right\rbrack = 0\]Continu :
\[\frac{\partial^{2}X}{\partial t^{2}}\left. \ \right\vert _{x_{n}} + \omega_{0}^{2}\left\lbrack 2X\left( x_{n},t \right) - \left\lbrack X_{x_{n},t} - \frac{\partial X}{\partial x}\left. \ \right\vert _{x_{n}}a + \frac{1}{2}\frac{\partial^{2}X}{\partial x^{2}}\left. \ \right\vert _{x_{n}}a^{2} + X_{x_{n},t} + \frac{\partial X}{\partial x}\left. \ \right\vert _{x_{n}}a + \frac{1}{2}\frac{\partial^{2}X}{\partial x^{2}}\left. \ \right\vert _{x_{n}}a^{2} \right\rbrack \right\rbrack = 0\] \[\Rightarrow \frac{\partial^{2}X}{\partial t^{2}}\left. \ \right\vert _{x_{n}} - \omega_{0}^{2}a^{2}\frac{\partial^{2}X}{\partial x^{2}}\left. \ \right\vert _{x_{n}} = 0;\ \ \forall x_{n},t\] \[\frac{\partial^{2}X}{\partial t^{2}}(x,t) - \omega_{0}^{2}a^{2}\frac{\partial^{2}X}{\partial x}(x,t) = 0\]- Equation d’onde, équation de d’Alembert
Où :
\[\left\lbrack \omega_{0}a \right\rbrack = LT^{- 1}\] \[\text{On pose}\ c = \left( \frac{\frac{\partial^{2}X}{\partial t^{2}}}{\frac{\partial^{2}X}{\partial x}} \right)^{\frac{1}{2}} = \frac{\omega_{p}}{k_{p}} = \omega_{0}a\ \ \forall p\]NB : Ici, cette onde est longitudinale. La direction d’oscillation est égale à la direction de propagation.
On a la même équation pour une onde transversale (direction d’oscillation perpendiculaire à la direction de propagation).
2. Pourquoi « équation d’onde » ?
\[\text{Soit}\ \left( \frac{\partial^{2}}{\partial t^{2}} - c^{2}\frac{\partial^{2}}{\partial x^{2}} \right)\psi(x,t) = 0\] \[\left( \frac{\partial}{\partial t} - c\frac{\partial}{\partial x} \right)\left( \frac{\partial}{\partial t} + c\frac{\partial}{\partial x} \right)\psi(x,t) = 0\]On réalise un changement de variable :
\[\left( \text{on pose arbitrairement}\ t_{0} = 0,\ x_{0} = 0 \right)\] \[\left\lbrack \begin{array}{r} \xi = t - \frac{x}{c}\ \\ \eta = t + \frac{x}{c} \end{array} \right.\] \[\Leftrightarrow \left\lbrack \begin{array}{r} t = \frac{1}{2}(\eta + \xi) \\ x = \frac{c}{2}(\eta - \xi) \end{array} \right.\] \[\Rightarrow \left\lbrack \begin{array}{r} \frac{\partial}{\partial\xi} = \frac{\partial}{\partial t}\frac{\partial t}{\partial\xi} + \frac{\partial}{\partial x}\frac{\partial x}{\partial\xi} = \frac{1}{2}\left( \frac{\partial}{\partial t} - c\frac{\partial}{\partial x} \right) \\ \frac{\partial}{\partial\eta} = \frac{1}{2}\left( \frac{\partial}{\partial t} + \frac{\partial}{\partial x} \right) \end{array} \right.\] \[\Rightarrow 4\frac{\partial^{2}\psi(\xi,\eta)}{\partial\xi\partial\eta} = 0\] \[\Rightarrow \psi(\xi,\eta) = \psi_{1}(\xi) + \psi_{2}(\eta)\] \[\Rightarrow \psi(x,t) = \psi_{1}\left( t - \frac{x}{c} \right) + \psi_{2}\left( t + \frac{x}{c} \right)\]Interprétation physique :
$\psi_{1}\left( t - \frac{x}{c} \right)$ / $\psi_{2}\left( t + \frac{x}{c} \right)\ $:
varie au cours du temps à $x$ donné.
varie selon $x$ à $t$ donné.
Est constante pour $t - \frac{x}{c}$ / $t + \frac{x}{c} = cte$
$c = \pm \frac{dx}{dt}\left( = \omega_{0}a \right)$
Toute valeur de $\psi_{1}$, $\psi_{2}$ se propage à $c$ vers $x$ croissants/décroissants.
C’est une onde.
Alors :
$\psi_{1}\text{/}\psi_{2}$ sont appelées ondes :
Planes : $\forall(x,t),\ \psi = \text{cte}$ dans tout plan perpendiculaire à la direction de propagation.
Progressives : propagation selon $x$ et $t$
De vitesse de propagation : $c$
3. Linéarité et superposition
a. Cas général
On considère une EDP linéaire en $x$ et $t$ d’ordre $N$
\[\sum_{j = 0}^{N}{\sum_{n = 0}^{j}{\widetilde{\alpha_{jn}}\frac{\partial^{j - n}}{\partial t^{j - n}}\frac{\partial^{n}}{\partial x^{n}}\widetilde{\psi}(x,t)}} = 0\]Ex : Pour $n = 2$
\[\alpha_{00}\widetilde{\psi}(x,t) + \alpha_{10}\frac{\partial\widetilde{\psi}}{\partial t} + \alpha_{11}\frac{\partial\widetilde{\psi}}{\partial x} + \alpha_{20}\frac{\partial^{2}\widetilde{\psi}}{\partial t^{2}} + \alpha_{21}\frac{\partial^{2}\widetilde{\psi}}{\partial t\partial x} + \alpha_{22}\frac{\partial^{2}\widetilde{\psi}}{\partial x^{2}} = 0\]Linéaire $\Rightarrow$ toute CL de solutions est solution.
$\Rightarrow$ On cherche une base de l’espace vectoriel des solutions.
Ansatz :
\[{\widetilde{\psi}}^{\pm}(x,t) = e^{\pm i(\omega t - kx)}\]Où $k$ est la norme du vecteur d’onde.
On injecte dans l’EDP :
\[\sum_{j = 0}^{N}{\sum_{n = 0}^{j}{\widetilde{\alpha_{jn}}( \pm i\omega)^{j - n}( \mp ik)^{n}{\widetilde{\psi}}^{\pm}(x,t)}} = 0\] \[{\widetilde{\psi}}^{\pm}(x,t)\left\lbrack \sum_{j = 0}^{N}{\sum_{n = 0}^{j}{\widetilde{\alpha_{jn}}( \pm i\omega)^{j - n}( \mp ik)^{n}}} \right\rbrack = 0\] \[\left\lbrack \sum_{j = 0}^{N}{\sum_{n = 0}^{j}{\widetilde{\alpha_{jn}}( \pm i\omega)^{j - n}( \mp ik)^{n}}} \right\rbrack\ \text{est un polynôme d'ordre}\ N\ \text{en}\ \omega\ \text{ou}\ k = 0\]$\Rightarrow N$ racines $\begin{matrix} \omega
k \end{matrix}$ en fonction de $\begin{matrix} k
\omega \end{matrix}\ $: $\left\lbrack \omega_{l}(k) \right\rbrack _{1 \leq l \leq n}$
Toute relation $\omega = f(k)$ s’appelle une relation de dispersion. Il y a donc $N$ relations de dispersion.
b. Cas de l’équation d’onde
\[\frac{\partial^{2}}{\partial t^{2}}\widetilde{\psi}(x,t) - c^{2}\frac{\partial^{2}}{\partial x^{2}}\widetilde{\psi}(x,t) = 0\] \[- \omega^{2} + c^{2}k^{2} = 0\] \[\Rightarrow \omega^{2} = (ck)^{2} \Rightarrow \omega_{l = \begin{matrix} 1 \\ 2 \end{matrix}}(k) \pm ck\] \[{\widetilde{\psi}}_{k}(x,t) = {\widetilde{\alpha_{1}}}^{\pm}e^{\pm i\left\lbrack \omega_{1}(k)t - kx \right\rbrack} + {\widetilde{\alpha_{2}}}^{\pm}e^{\pm i\left\lbrack \omega_{2}(k)t - lx \right\rbrack}\] \[{\widetilde{\psi}}_{k}(x,t) = {\widetilde{\alpha_{1}}}^{\pm}e^{\pm i\lbrack ct - kx\rbrack} + {\widetilde{\alpha_{2}}}^{\pm}e^{\mp i\lbrack ct + lx\rbrack}\]Soit $\phi_{1}$ et $\phi_{2}$ les phases
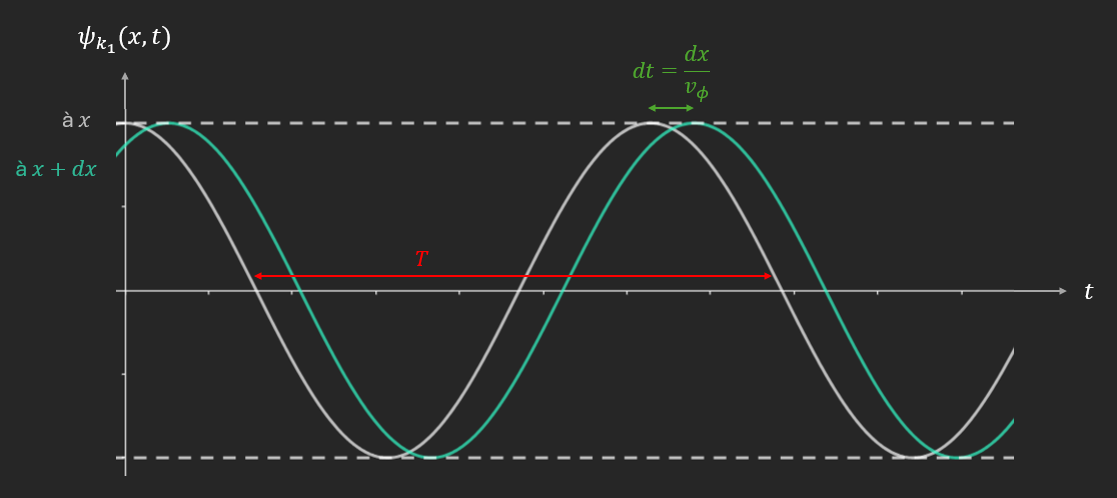
\[{\widetilde{\psi}}_{k}(x,t) = {\widetilde{\alpha_{1}}}^{\pm}e^{\pm i\phi_{1}(x,t)} + {\widetilde{\alpha_{2}}}^{\pm}e^{\pm i\phi_{2}(x,t)}\] \[{\widetilde{\psi}}_{k}(x,t) = { { \widetilde{ \psi } }_{k}}_{1}^{\pm}(ct - x) + {\widetilde{\psi}}_{k_{2}}^{\pm}(ct + x)\]Propagation d’un point de l’onde :
\[{ { \widetilde{ \psi } }_{k}}_{l}^{\pm} = \text{cte} \Rightarrow \phi_{l} = \text{cte} = ct \mp x \Rightarrow \frac{dx}{dt} = \pm c = v_{\phi}:\ \text{vitesse de phase}\] \[= \frac{\omega_{l}(k)}{k}\]\({\widetilde{\psi}}_{k_{1}}:x\) croissants
\({\widetilde{\psi}}_{k_{2}}:x\) décroissants
${\psi_{k}}_{l}$ est périodique dans le temps et dans l’espace.
\[\forall x,t\ \left\lbrack \begin{array}{r} { { \widetilde{ \psi } }_{k}}_{l}(x,t) = { { \widetilde{ \psi } }_{k}}_{l}(x,t + T) \Rightarrow \left\vert \omega_{l}(k) \right\vert = \frac{2\pi}{T_{l}(k)} = 2\pi\nu_{l}(k) \\ { { \widetilde{ \psi } }_{k}}_{l}(x,t) = { { \widetilde{ \psi } }_{k}}_{l}(x + \lambda,t) \Rightarrow k = \frac{2\pi}{\lambda(k)} = 2\pi\sigma \end{array} \right.\]Pulsation, longueur d’onde, fréquence
\[\Rightarrow v_{\phi} = \pm c = \frac{\omega_{l}(k)}{k} = \pm \frac{\lambda}{T_{l}(k)}\]Exemple :
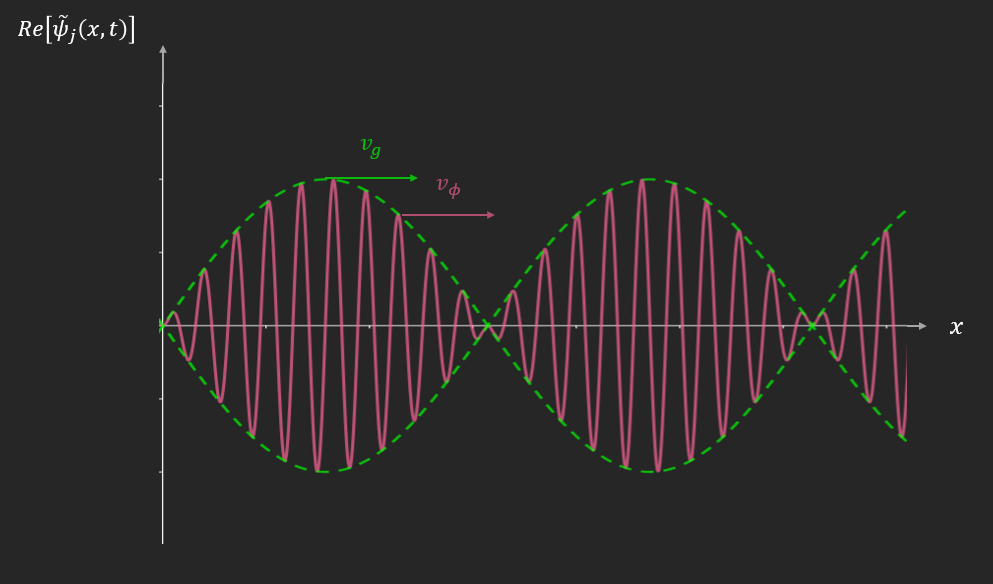
La vitesse de phase $v_{\phi}$ caractérise la vitesse de propagation d’une onde plane progressive (OPP) avec $k$ et les $\omega_{j}(k)$ correspondants.
Que se passe-t-il si on prend l’onde résultante de la combinaison linéaire de plusieurs OPP avec des valeurs de $k$ différentes ?
Exemple :
On prend un intervalle de $k$ voisins d’une valeur appelée $k_{0}$ à un intervalle $\Delta k \rightarrow 0$ près.
On regarde un $\omega_{j}(k)$ donné.
Onde totale obtenue est :
\[{\widetilde{\psi}}_{j}(x,t) = \int_{k_{0} - \Delta k}^{k_{0} + \Delta k}{\widetilde{\alpha_{\pm k}}e^{\pm i\left\lbrack \omega_{j}(k)t - kx \right\rbrack}dk}\]$\widetilde{a_{\pm k}}$ est une densité d’amplitude d’OPP par unité de $k$.
- \[\text{Si}\ \Delta k \rightarrow 0,\ \ \omega_{j}(k) \approx \omega_{j}\left( k_{0} \right) + \frac{d\omega_{j}}{dk}\left. \ \right\vert _{k_{0}}\left( k - k_{0} \right)\]
- \[k = k_{0} + \left( k - k_{0} \right)\]
$e^{\pm i\left( \omega_{j}\left( k_{0} \right)t - k_{0}x \right)}$ est une OPP qui se propage à $v_{\phi} = \frac{\omega_{j}\left( k_{0} \right)}{k_{0}}$.
\[= e^{\pm ik_{0}\left\lbrack \frac{\omega_{j}\left( k_{0} \right)}{k_{0}}t - x \right\rbrack}\]\(e^{\pm i\left( k - k_{0} \right)\left\lbrack \frac{d\omega_{j}}{dk}\left. \ \right\vert _{k_{0}}t - x \right\rbrack}\) est une OPP qui se propage à \(v_{g} = \frac{d\omega_{j}}{dk}\left. \ \right\vert _{k_{0}}\)
$v_{g}$ est appelée « vitesse de groupe ».
${\widetilde{\psi}}_{j}(x,t)$ définit un paquet d’onde.
Exemple :
Remarque :
Si $v_{\phi} = v_{g}$, alors le milieu de propagation est dit « non-dispersif ». $\Rightarrow \omega_{j}(k) \propto k$
Si $v_{\phi} \neq v_{g}$, alors le milieu de propagation est dit « dispersif ».
Remarque :
On peut montrer que l’énergie transportée par une onde (ou la probabilité transportée par une fonction d’onde) se déplace à $v_{g}$.
La relativité restreinte impose donc $v_{g} \leq c:$ vitesse de la lumière dans le vide.
Mais on peut avoir $v_{\phi} > c$ (ne transporte pas de signal physique).
VI. EDP (cas de l’équation d’onde) et conditions au bord
Tout comme les EDO, les EDP ont besoin de conditions aux bords (ou conditions limites) pour avoir une solution complètement définie.
Exemple :
Partie 1 : Oscillations : EDO d’ordre 2 en $t$ $\Rightarrow$ deux conditions aux bords en $t$. (exemple : $\psi\left( t = t_{0} \right);\dot{\psi} = \left( t = t_{0} \right)$).
Partie 2 : Onde : EDP d’ordre 2 en $x$ et $t$ $\Rightarrow$ 4 conditions aux bords : 2 en $x$ et 2 en $t$.
Conditions aux bords en espace : (ici en $x$ à 1 dimension).
Soit $\psi(x,t)$ une onde définie sur $\lbrack a,b\rbrack$ ($a$ et $b$ peuvent être finis ou infinis).
Différents types de conditions au bord possibles :
Conditions de Dirichlet : $\psi(a,t) = \alpha(t)$ et $\psi(b,t) = \beta(t)$
Conditions de Neumann : $\frac{\partial\psi}{\partial x}(a,t) = \gamma(t)$ et $\frac{\partial\psi}{\partial x}(b,t) = \delta(t)$
Mélange des deux
Conditions aux bords en temps :
\[\psi\left( x,t_{0} \right) = f(x),\ \ \frac{\partial\psi}{\partial t}\left( x,t_{0} \right) = g(x)\]4. En espace fini
(Segment si $d = 1$).
a. Conditions aux bords en espace homogène
Pas de source d’oscillation aux bords.
\[\forall t,\left\lbrack \begin{array}{r} \widetilde{\psi}(x = a,t) = 0 \\ \widetilde{\psi}(x = b,t) = 0 \end{array} \right.\] \[\forall x,\left\lbrack \begin{array}{r} \widetilde{\psi}(x,t = 0) = f(x) \\ \frac{\partial\widetilde{\psi}}{\partial t}(x,t = 0) = g(x) \end{array} \right.\] \[\text{Où}\ \widetilde{\psi}(x,t) = {\widetilde{\psi}}_{k}(x,t) = \sum_{j = 1}^{N}{ { \widetilde{ \alpha } }_{j}^{\pm}{\widetilde{\psi}}_{j,k}^{\pm}(x,t)}\]Pour $N = 2$, d’après l’équation d’onde :
\[\widetilde{\psi}(x,t) = {\widetilde{\alpha}}_{1}^{+}e^{i(\omega t - kx)} + {\widetilde{\alpha}}_{1}^{-}e^{- i(\omega t - kx)} + {\widetilde{\alpha}}_{2}^{+}e^{i( - \omega t - kx)} + {\widetilde{\alpha}}_{2}^{-}e^{- i( - \omega t - kx)}\]Où $\omega_{1}(k) = - \omega_{2}(k) = ck = \omega$
- Normalement, on retrouve les mêmes résultats en appliquant les contraintes à la partie réelle de $\psi$
- Conditions aux bords dans l’espace
En $x = a$, $\forall t,$
\[0 = e^{i\omega t}\left( {\widetilde{\alpha}}_{1}^{+}e^{- ika} + {\widetilde{\alpha}}_{2}^{-}e^{ika} \right) + e^{- i\omega t}\left( {\widetilde{\alpha}}_{1}^{-}e^{ika} + {\widetilde{\alpha}}_{2}^{+}e^{- ika} \right)\] \[- e^{2i\omega t} = \frac{ { \widetilde{ \alpha } }_{1}^{-}e^{ika} + {\widetilde{\alpha}}_{2}^{+}e^{- ika}}{ { \widetilde{ \alpha } }_{1}^{+}e^{- ika} + {\widetilde{\alpha}}_{2}^{-}e^{ika}}\]Or $- e^{2i\omega t}$ est dépendant du temps, alors que le membre de droite est indépendant du temps.
Donc \({\widetilde{\alpha}}_{1}^{-}e^{ika} + {\widetilde{\alpha}}_{2}^{+}e^{- ika} = {\widetilde{\alpha}}_{1}^{+}e^{- ika} + {\widetilde{\alpha}}_{2}^{-}e^{ika} = 0\)
\[\Rightarrow \left\lbrack \begin{array}{r} {\widetilde{\alpha}}_{1}^{-} = - {\widetilde{\alpha}}_{2}^{+}e^{- 2ika} \\ {\widetilde{\alpha}}_{2}^{-} = - {\widetilde{\alpha}}_{1}^{+}e^{- 2ika} \end{array} \right.\] \[\Rightarrow \widetilde{\psi}(x,t) = {\widetilde{\alpha}}_{1}^{+}e^{i(\omega t - kx)} - {\widetilde{\alpha}}_{2}^{+}e^{- i(\omega t - kx + 2ka)} + {\widetilde{\alpha}}_{2}^{+}e^{i( - \omega t - kx)} - {\widetilde{\alpha}}_{1}^{+}e^{- i( - \omega t - kx + 2ka)}\] \[\widetilde{\psi}(x,t) = \left( {\widetilde{\alpha}}_{1}^{+}e^{i\omega t} + {\widetilde{\alpha}}_{2}^{+}e^{- i\omega t} \right)\left\lbrack e^{- ikx} - e^{ik(x - 2a)} \right\rbrack\]Posons \({\widetilde{\beta}}_{i}^{+} = {\widetilde{\alpha}}_{i}^{+}e^{- ika}\)
\[\widetilde{\psi}(x,t) = \left( {\widetilde{\beta}}_{1}^{+}e^{i\omega t} + {\widetilde{\beta}}_{2}^{+}e^{- i\omega t} \right)\left\lbrack e^{- ik(x - a)} - e^{ik(x - a)} \right\rbrack = \left( {\widetilde{\beta}}_{1}^{+}e^{i\omega t} + {\widetilde{\beta}}_{2}^{+}e^{- i\omega t} \right)( - 2i\sin\left( k(x - a) \right)\]Posons \({\widetilde{\gamma}}_{i}^{+} = - 2i{\widetilde{\beta}}_{i}^{+}\)
\[\widetilde{\psi}(x,t) = \left( {\widetilde{\gamma}}_{1}^{+}e^{i\omega t} + {\widetilde{\gamma}}_{2}^{+}e^{- i\omega t} \right)\sin\left( k(x - a) \right)\] \[\Rightarrow \psi(x,t) = {Re}\left( \widetilde{\psi}(x,t) \right) = F(t)G(x)\]$\Rightarrow$ découplage entre l’espace et le temps
$\Rightarrow \psi$ est une onde stationnaire.
En $x = b$, $\forall t,$
\[0 = \left( {\widetilde{\gamma}}_{1}^{+}e^{i\omega t} + {\widetilde{\gamma}}_{2}^{+}e^{- i\omega t} \right)\sin\left\lbrack k(b - a) \right\rbrack\] \[\Rightarrow \sin\left\lbrack k(b - a) \right\rbrack = 0\] \[\Rightarrow k = \frac{p\pi}{b - a}\ \text{où}\ p \in \mathbb{N}^{*}\]$\Rightarrow$ quantification des valeurs de $k$, donc de $\omega$
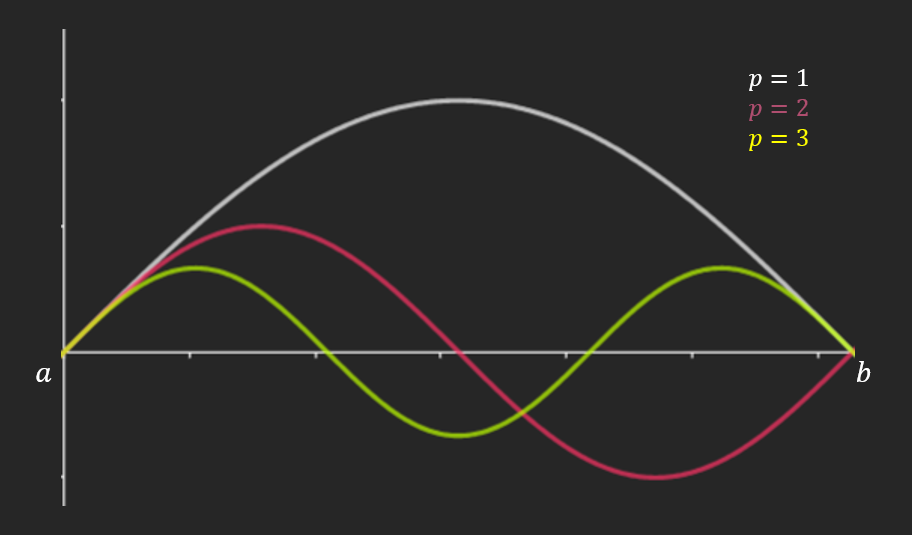
\[\omega_{p} = ck_{p},\ \ \lambda_{p} = \frac{2\pi}{k_{p}}\] \[\omega_{p} = \frac{cp\pi}{b - a} = p\omega_{1}\ \text{où}\ \omega_{1}\ \text{est la pulsation du mode fondamental}\]Où $p$ est le numéro du mode d’oscillation, du mode propre.
Mode propre :
\[{\widetilde{\psi}}_{p}(x,t) = \left( {\widetilde{\gamma}}_{1}^{+}e^{i\omega_{p}t} + {\widetilde{\gamma}}_{2}^{+}e^{- i\omega_{p}t} \right)\sin\left\lbrack k_{p}(x - a) \right\rbrack\]On pose \(A_{p}^{+} = {\widetilde{\gamma}}_{1}^{+}\) et \(A_{p}^{-} = {\widetilde{\gamma}}_{2}^{+}\)
\[{\widetilde{\psi}}_{p}(x,t) = \left( A_{p}^{+}e^{i\omega_{p}t} + A_{p}^{-}e^{- i\omega_{p}t} \right)\sin\left\lbrack k_{p}(x - a) \right\rbrack\]Solution générale : combinaison linéaire des modes propres
\[\widetilde{\psi}(x,t) = \sum_{p = 1}^{+ \infty}{ { \widetilde{ \psi } }_{p}(x,t)}\] \[\psi(x,t) = \sum_{p = 1}^{+ \infty}{\left\lbrack A_{p,c}\cos\left( \omega_{p}t \right) + A_{p,s}\sin\left( \omega_{p}t \right) \right\rbrack\sin\left\lbrack k_{p}(x - a) \right\rbrack}\]$\Rightarrow$ série de Fourier
- Conditions aux bords en temps
Avec $k_{p} = \frac{p\pi}{b - a}$
Propriété :
\[\int_{a}^{b}{\sin\left\lbrack \left( \frac{p\pi}{b - a} \right)(x - a) \right\rbrack\sin\left\lbrack \left( \frac{q\pi}{b - a} \right)(x - a) \right\rbrack dx} = \frac{b - a}{2}\delta_{pq}\]Où $\delta_{pq} = \left\lbrack \begin{array}{r} 1\ \text{si}\ p = q
0\ \text{sinon} \end{array} \right. $ est le delta de Kronecker (avec $p$ et $q$ entiers).
$\Rightarrow$ en $\psi\ $:
\[\int_{a}^{b}{\sin\left\lbrack \left( \frac{q\pi}{b - a} \right)(x - a) \right\rbrack f(x)dx} = \int_{a}^{b}{\sin\left\lbrack \left( \frac{q\pi}{b - a} \right)(x - a) \right\rbrack\sum_{p = 1}^{+ \infty}{\left( {\widetilde{A}}_{p}^{+} - {\widetilde{A}}_{p}^{-} \right)\sin\left\lbrack \left( \frac{p\pi}{b - a} \right)(x - a) \right\rbrack}dx} = = \sum_{p = 1}^{+ \infty}{\int_{a}^{b}{\sin\left\lbrack \left( \frac{q\pi}{b - a} \right)(x - a) \right\rbrack\sin\left\lbrack \left( \frac{p\pi}{b - a} \right)(x - a) \right\rbrack\left( {\widetilde{A}}_{p}^{+} + {\widetilde{A}}_{p}^{-} \right)dx}} = \frac{b - a}{2}\left( {\widetilde{A}}_{q}^{+} + {\widetilde{A}}_{q}^{-} \right)\]$\Rightarrow$ en $\frac{\partial\widetilde{\psi}}{dt}$
\[\int_{a}^{b}{\sin\left\lbrack \left( \frac{q\pi}{b - a} \right)(x - a) \right\rbrack g(x)dx} = \frac{b - a}{2}i\omega_{q}\left( {\widetilde{A}}_{q}^{+} - {\widetilde{A}}_{q}^{-} \right)\]\(\Rightarrow {\widetilde{A}}_{q}^{+}$ et ${\widetilde{A}}_{q}^{-}\) $\forall q$
b. Avec source au(x) bord(s)
$\rightarrow$ non traité
5. En milieu demi-infini
($=$ demi-droite)
a. 1 milieu demi-infini
Exemple : Schéma
Exemple :
Corde attachée à une extrémité et libre à l’autre extrémité
On a vu :
\[\widetilde{\psi}(x,t) = {\widetilde{\psi}}_{-}(ct - x) + {\widetilde{\psi}}_{+}(ct + x)\]Propagation vers les $x$
\[\left\lbrack \begin{array}{r} \text{croissants} \\ \text{décroissants} \end{array} \right.\]à
\[\left \vert \overrightarrow{v_{\phi}} \right \vert = c\] \[\widetilde{\psi}(x,t) = {\widetilde{\alpha}}_{-}e^{ik(ct - x)} + {\widetilde{\alpha}}_{+}e^{ik(ct + x)} = {\widetilde{\alpha}}_{-}e^{i(\omega t - kx)} + {\widetilde{\alpha}}_{+}e^{i(\omega t + kx)}\]Avec $c = \frac{\omega}{k}$
- Condition au bord d’espace
${\widetilde{\alpha}}_{-}e^{i(\omega t - kx)}$ est l’onde incidente
$- {\widetilde{\alpha}}_{-}e^{i(\omega t + kx)}$ est l’onde réfléchir
On pose \({\widetilde{\alpha}}_{i} = {\widetilde{\alpha}}_{r}\) et \({\widetilde{\alpha}}_{r} = - {\widetilde{\alpha}}_{i}\)
\[\widetilde{\psi}(x,t) = {\widetilde{\alpha}}_{-}e^{i(\omega t - kx)} - {\widetilde{\alpha}}_{-}e^{i(\omega t + kx)} = {\widetilde{\alpha}}_{-}e^{i\omega t}\left( e^{- ikx} - e^{ikx} \right)\] \[\Rightarrow \psi(x,t) = {Re}\left( \widetilde{\psi}(x,y) \right) = f(t)g(x)\]$\Rightarrow$ onde stationnaire
Remarque :
Si on avait une condition sur $\frac{\partial\psi}{\partial x}$ au lieu de $\psi$, exemple \(\frac{\partial\psi}{\partial x}(x = 0,t) \Rightarrow {\widetilde{\alpha}}_{-} = {\widetilde{\alpha}}_{+}\)
- On définit le coefficient de réflexion en amplitude
Si $r > 0$, on parle de réflexion molle
Si $r < 0$, on parle de réflexion dure
Ici, dans le première exemple, $r = - 1 \Rightarrow$ réflexion dure
Dans le deuxième exemple, $r = 1 \Rightarrow$ réflexion molle.
NB :
On pourra définir plus loin le coefficient de transmission en amplitude
Ne pas confondre coefficients de réflexion/transmission en amplitude et coefficients de réflexion en transmission et en intensité/énergie ($R$ et $T$, voir physique moderne).
b. Interface de deux milieux demi-infinis
Milieu 1 : $\rbrack - \infty,\ 0\lbrack$
Milieu 2 : $\rbrack 0, + \infty\lbrack$
Voir schéma
Exemple : Deux cordes attachées entre elles en $x = 0$
On excite la corde 1 en $x \rightarrow - \infty$
Région 1 :
\[{\widetilde{\psi}}_{1}(x,t) = {\widetilde{\alpha}}_{i}e^{ik_{1}\left( c_{1}t - x \right)} + {\widetilde{\alpha}}_{r}e^{ik_{1}\left( c_{1}t + x \right)} = {\widetilde{\alpha}}_{1}e^{i\left( \omega_{1}t - k_{1}t \right)} + {\widetilde{\alpha}}_{2}e^{i\left( \omega_{1}t + k_{1}x \right)}\]Région 2 :
\({\widetilde{\psi}}_{2}(x,t) = {\widetilde{\alpha}}_{t}e^{i\left( \omega_{2}t - kx \right)} + 0\) (pas d’onde qui se propage vers les $x$ décroissants).
\[c_{1} = \frac{\omega_{1}}{k_{1}},\ c_{2} = \frac{\omega_{2}}{k_{2}}\]- Condition au bord en espace
$\psi$ est continue à l’interface : toujours valable
Et donc $\frac{\partial^{n}\psi}{\partial t^{n}}$ sont continues
\(\forall t\), =\(\frac{\partial{\widetilde{\psi}}_{1}}{\partial x}\left( x = 0_{-},t \right) = \frac{\partial{\widetilde{\psi}}_{2}}{\partial x}\left( x = 0_{+},t \right)\ (2)\) uniquement si
\[\left\lbrack \begin{array}{r} \left \vert \overrightarrow{T_{r}} \right \vert = \left \vert \overrightarrow{T_{z}} \right \vert \ \text{où}\ \overrightarrow{T}\ \text{est la force de tension} \\ \text{interface de masse}\ \overrightarrow{dm} \rightarrow 0 \end{array} \right.\] \[(1) \Rightarrow \left( {\widetilde{\alpha}}_{i} + {\widetilde{\alpha}}_{n} \right)e^{i\omega_{1}t} = {\widetilde{\alpha}}_{t}e^{i\omega_{2}t}\] \[\frac{ { \widetilde{ \alpha } }_{i} + {\widetilde{\alpha}}_{n}}{ { \widetilde{ \alpha } }_{t}} = e^{i\left( \omega_{2} - \omega_{1} \right)t}\]Indépendant du temps = dépendant du temps
- Soit \(\omega_{1} = \omega_{2} \Rightarrow {\widetilde{\alpha}}_{t} = 0 = {\widetilde{\alpha}}_{i} + {\widetilde{\alpha}}_{n}\)
Pas de transmission, réflexion pure
- Soit \(\omega_{1} = \omega_{2}(3) \Rightarrow {\widetilde{\alpha}}_{t} = {\widetilde{\alpha}}_{i} + {\widetilde{\alpha}}_{r}(4)\)
On étudie le second cas
\[(2) \Rightarrow i\left( - k_{1}{\widetilde{\alpha}}_{i} + k_{1}{\widetilde{\alpha}}_{r} \right) = - ik_{2}{\widetilde{\alpha}}_{t}\] \[\Rightarrow {\widetilde{\alpha}}_{i} - {\widetilde{\alpha}}_{r} = \frac{k_{2}}{k_{1}}{\widetilde{\alpha}}_{t} = \frac{c_{1}}{c_{2}}{\widetilde{\alpha}}_{t}(5)\] \[(4) + (5) \Rightarrow {\widetilde{\alpha}}_{t} = \left( \frac{2c_{2}}{c_{1} + c_{2}} \right){\widetilde{\alpha}}_{i}\ (6)\] \[(6)\ \text{dans}\ (5) \Rightarrow {\widetilde{\alpha}}_{r} = \left( \frac{c_{2} - c_{1}}{c_{1} + c_{2}} \right){\widetilde{\alpha}}_{i}\]$\Rightarrow$ coefficient en amplitude
\[r = \frac{\alpha_{r}}{\alpha_{i}} = \frac{c_{2} - c_{1}}{c_{1} + c_{2}} > 0\ \text{ssi}\ c_{2} > c_{1}\] \[t = \frac{\alpha_{t}}{\alpha_{i}} = \frac{2c_{2}}{c_{1} + c_{2}}\ \text{toujours} \geq 0\]- Cas particuliers
Si $c_{1} = c_{2}$, alors $\left\lbrack \begin{array}{r} r = 0
t = 1 \end{array} \right. $, cohérent car même milieu ou pas d’interface.
Si $c_{2} = 0$, alors $\left\lbrack \begin{array}{r} r = - 1
t = 0 \end{array} \right. $
Coefficient en intensité/énergie :
On peut montrer que $R = \frac{c_{1}}{c_{1}}\left\vert \frac{\alpha_{r}}{\alpha_{i}} \right\vert ^{2} = \left\vert \frac{\alpha_{r}}{\alpha_{i}} \right\vert ^{2} = r^{2}$
\[T = \frac{c_{1}}{c_{2}}\left\vert \frac{\alpha_{t}}{\alpha_{i}} \right\vert ^{2} = \frac{c_{1}}{c_{2}}t^{2}\]Avec $R + T = 1$ (si absence de « dissipation »).
Ici,
\[R + T = \frac{\left( c_{2} - c_{1} \right)^{2} + \frac{c_{1}}{c_{2}}\left( 2c_{2} \right)^{2}}{\left( c_{1} + c_{2} \right)^{2}} = \frac{\left( c_{1} + c_{2} \right)^{2}}{\left( c_{1} + c_{2} \right)^{2}} = 1\]Chapitre 2 : Ondes vectorielles à une
dimension
Ici, à une dimension signifie que l’espace de propagation est à une dimension.
- Jusqu’à présent, la grandeur oscillante était un scalaire : on parlait d’ondes scalaires.
Dans ce chapitre, la grandeur oscillante est un vecteur : on parle d’onde vectorielle.
- Etude du cas important des ondes électromagnétiques (la lumière).
Dans ce cas, la grandeur oscillante est le champ électromagnétique $\left\lbrack \overrightarrow{E},\overrightarrow{B} \right\rbrack $
Ces ondes peuvent se propager dans le vide, à la différence des ondes mécaniques qui font osciller un milieu de propagation.
I. Equation d’onde pour le champ électromagnétique
Dans un référentiel galiléen, dans un milieu homogène et isotrope (ex : le vide)
(Milieu homogène : même propriétés en tout point de l’espace, isotrope : même propriétés en toute direction de l’espace).
Le vide est associé à $\left( \varepsilon_{0},\mu_{0} \right)$.
Equations de Maxwell :
Maxwell-Thomson : ${div}\left( \overrightarrow{B} \right) = 0\ (MT)$
Maxwell-Faraday : $\overrightarrow{rot}\left( \overrightarrow{E} \right) = - \frac{\partial\overrightarrow{B}}{\partial t}\ (MF)$
Maxwell-Gauss : ${div}\left( \overrightarrow{E} \right) = \frac{\rho}{\varepsilon_{0}}(MG)$ où $\rho$ est la densité volumique de charge
Maxwell-Ampère : $\overrightarrow{rot}\left( \overrightarrow{B} \right) = \mu_{0}\left( \overrightarrow{j} + \varepsilon_{0}\frac{\partial\overrightarrow{E}}{\partial t} \right)\ (MA)$ où $\overrightarrow{j}$ est la densité surfacique de courant
Pour $\overrightarrow{E}$
($\overrightarrow{\Delta}$ est le laplacien vectoriel, correspondant à une dérivée seconde par rapport à l’espace)
\[\Leftrightarrow \frac{1}{\varepsilon_{0}}\overrightarrow{grad}\rho - \overrightarrow{\Delta}\overrightarrow{E} = - \mu_{0}\frac{\partial\overrightarrow{j}}{\partial t} - \mu_{0}\varepsilon_{0}\frac{\partial^{2}\overrightarrow{E}}{\partial t^{2}}\] \[\mu_{0}\varepsilon_{0}\frac{\partial^{2}\overrightarrow{E}}{\partial t^{2}} - \overrightarrow{\Delta}\overrightarrow{E} = - \frac{1}{\varepsilon_{0}}\overrightarrow{grad}\rho - \mu_{0}\frac{\partial\overrightarrow{j}}{\partial t}\] \[\frac{1}{c^{2}}\frac{\partial^{2}\overrightarrow{E}}{\partial t^{2}} - \overrightarrow{\Delta}\overrightarrow{E} = - \frac{1}{\varepsilon_{0}}\overrightarrow{grad}\rho - \mu_{0}\frac{\partial\overrightarrow{j}}{\partial t}\]Où $c = \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}} \approx 3 \times 10^{8}\ ms^{- 1}$
- Equation d’onde pour $\overrightarrow{E}$ dans le vide
- Pour $\overrightarrow{B}$
- Equation d’onde pour $\overrightarrow{B}$ dans le vide
N.B. : Si $\rho = 0$ et $\overrightarrow{j} = 0$
\[\Rightarrow \left\lbrack \begin{array}{r} \frac{1}{c^{2}}\frac{\partial^{2}\overrightarrow{E}}{\partial t^{2}} - \overrightarrow{\Delta}\overrightarrow{E} = \overrightarrow{0} \\ \frac{1}{c^{2}}\frac{\partial^{2}\overrightarrow{B}}{\partial t^{2}} - \overrightarrow{\Delta}\overrightarrow{B} = \overrightarrow{0} \end{array} \right. \ (2)\]Forme identique aux équations d’ondes vues précédemment.
Par exemple, pour une propagation à une dimension (selon $x$), on a :
\[\left\lbrack \begin{array}{r} \frac{1}{c^{2}}\frac{\partial^{2}\overrightarrow{E}}{\partial t^{2}} - \frac{\partial^{2}\overrightarrow{E}}{\partial x^{2}} = \overrightarrow{0} \\ \text{idem pour}\ \overrightarrow{B} \end{array} \right.\]Même dans les régions avec absence de charge/de courant, il peut exister des ondes électromagnétiques à cause du couplage $\left\lbrack \overrightarrow{E},\ \overrightarrow{B} \right\rbrack $.
Ansatz sur la solution de $(2)\ $:
\[Ⓒ(\overrightarrow{E}\left( \overrightarrow{r},t \right) = \widetilde{\overrightarrow{E_{0}}}e^{i\left( \omega t - \overrightarrow{k}\overrightarrow{r} \right)}@\overrightarrow{B}\left( \overrightarrow{r},t \right) = \overrightarrow{B_{0}}e^{i\left( \omega t - \overrightarrow{k}\overrightarrow{r} \right)}\]Où $\overrightarrow{k}$ est le vecteur d’onde : $\overrightarrow{k} = \left \vert \overrightarrow{k} \right \vert \overrightarrow{u}$ où $\overrightarrow{u}$ est le vecteur unitaire des directions et sens de propagation de l’onde.
Exemple : Propagation à une dimension selon $x$
\[\overrightarrow{k} = \left \vert \overrightarrow{k} \right \vert \overrightarrow{u_{x}} = k\overrightarrow{u_{x}}\]Et $\overrightarrow{r} = x\overrightarrow{u_{x}} + y\overrightarrow{u_{y}} + z\overrightarrow{u_{z}}$
\[\Rightarrow \overrightarrow{k}. overrightarrow{r} = kx\]Remarque : On obtient une onde plane.
Injection de l’Ansatz dans $(2)\ :$
\[\left\lbrack \frac{1}{c^{2}}\left( - \omega^{2} \right) + k^{2} \right\rbrack\left\lbrack \begin{array}{r} \overrightarrow{E}\left( \overrightarrow{r},t \right) \\ \overrightarrow{B}\left( \overrightarrow{R},t \right) \end{array} \right. = \overrightarrow{0}\]On obtient la relation de dispersion : $\omega = \pm ck$
VII. Direction et orientation du champ électromagnétique dans l’onde électromagnétique
\[\widetilde{\overrightarrow{E}}\left( \overrightarrow{r},t \right) = \widetilde{\overrightarrow{E_{0}}}e^{i\left( \omega t - \overrightarrow{k}\overrightarrow{r} \right)}\] \[\widetilde{\overrightarrow{B}}\left( \overrightarrow{r},t \right) = \widetilde{\overrightarrow{B_{0}}}e^{i\left( \omega t - \overrightarrow{k}\overrightarrow{r} \right)}\] \[\overrightarrow{E}\left( \overrightarrow{r},t \right) = {Re}\left\lbrack \widetilde{\overrightarrow{E}}\left( \overrightarrow{r},t \right) \right\rbrack\] \[\overrightarrow{B}\left( \overrightarrow{r},t \right) = {Re}\left\lbrack \widetilde{\overrightarrow{B}}\left( \overrightarrow{r},t \right) \right\rbrack\]1. L’onde électromagnétique est transversale
Exemple pour des idées :
Propagation selon $+ \overrightarrow{u_{x}}$
\[\overrightarrow{k} = \left\Vert \overrightarrow{k} \right\Vert \overrightarrow{u_{x}} = k\overrightarrow{u_{x}}\] \[\widetilde{\overrightarrow{E}}(x,t) = \widetilde{\overrightarrow{E_{0}}}e^{i(\omega t - kx)}\] \[\widetilde{\overrightarrow{B}}(x,t) = \widetilde{\overrightarrow{B_{0}}}e^{i(\omega t - kx)}\] \[\widetilde{\overrightarrow{E_{0}}} = \widetilde{E_{0x}}\overrightarrow{u_{x}} + \widetilde{E_{0y}}\overrightarrow{u_{y}} + \widetilde{E_{0z}}\overrightarrow{u_{z}}\] \[\widetilde{\overrightarrow{B_{0}}} = \widetilde{B_{0x}}\overrightarrow{u_{x}} + \widetilde{B_{0y}}\overrightarrow{u_{y}} + \widetilde{B_{0z}}\overrightarrow{u_{z}}\]- Maxwell-Faraday
En coordonnées cartésiennes,
\[\overrightarrow{rot}\left( \overrightarrow{E} \right) = \overrightarrow{u_{x}} \land \frac{\partial}{\partial x}\left( \widetilde{E_{x}}\overrightarrow{u_{x}} + \widetilde{E_{y}}\overrightarrow{u_{y}} + \overrightarrow{E_{z}}\overrightarrow{u_{z}} \right) + \overrightarrow{u_{y}} \land \frac{\partial}{\partial y}\left( \widetilde{E_{x}}\overrightarrow{u_{x}} + \widetilde{E_{y}}\overrightarrow{u_{y}} + \overrightarrow{E_{z}}\overrightarrow{u_{z}} \right) + \overrightarrow{u_{z}} \land \frac{\partial}{\partial z}\left( \widetilde{E_{x}}\overrightarrow{u_{x}} + \widetilde{E_{y}}\overrightarrow{u_{y}} + \overrightarrow{E_{z}}\overrightarrow{u_{z}} \right)\] \[\overrightarrow{rot}\left( \overrightarrow{E} \right) = \begin{pmatrix} \frac{\partial\widetilde{E_{y}}}{\partial y} - \frac{\partial\widetilde{E_{y}}}{\partial z} \\ \frac{\partial\widetilde{E_{x}}}{\partial z} - \frac{\partial\widetilde{E_{z}}}{\partial x} \\ \frac{\partial\widetilde{E_{y}}}{\partial x} - \frac{\partial\widetilde{E_{x}}}{\partial y} \end{pmatrix} = \begin{pmatrix} 0 \\ ik\widetilde{E_{z}} \\ - ik\widetilde{E_{y}} \end{pmatrix} = - i\begin{pmatrix} k \\ 0 \\ 0 \end{pmatrix} \land \begin{pmatrix} \widetilde{E_{x}} \\ \widetilde{E_{y}} \\ \widetilde{E_{z}} \end{pmatrix} = - i\overrightarrow{k} \land \widetilde{\overrightarrow{E}}\] \[\Rightarrow - i\overrightarrow{k} \land \overrightarrow{E} = - i\omega\widetilde{\overrightarrow{B}}\] \[\Rightarrow \widetilde{\overrightarrow{B}} = \frac{\overrightarrow{k} \land \widetilde{\overrightarrow{E}}}{\omega}\ \text{avec}\ \left\Vert \frac{\overrightarrow{k}}{\omega} \right\Vert = \frac{1}{c}\] \[\Rightarrow \left\lbrack \begin{array}{r} \overrightarrow{B}\bot\overrightarrow{k}\ \text{et}\ \widetilde{\overrightarrow{E}} \\ \left\Vert \overrightarrow{B} \right\Vert \neq \left\Vert \overrightarrow{E} \right\Vert \ \text{à priori} \end{array} \right.\]- Maxwell-Gauss
$\Rightarrow \left( \overrightarrow{E},\overrightarrow{B} \right)$ oscille dans le plan $\bot\overrightarrow{k} \Rightarrow$ l’onde électromagnétique est transversale. Elle oscille perpendiculairement à la direction de propagation (?)
$\left( \overrightarrow{k};\overrightarrow{E};\overrightarrow{B} \right)$ forment un trièdre direct.
2. Polarisation
Polarisation : Direction de $\overrightarrow{E}\left( \overrightarrow{r},t \right)$
Peut être une fonction de l’espace $\overrightarrow{r}$ et du temps $t$.
On garde la propagation selon $+ \overrightarrow{u_{x}}$
\[\widetilde{\overrightarrow{E}}(x,t) = \widetilde{\overrightarrow{E_{0}}}e^{i(\omega t - kx)}\]Où $\widetilde{\overrightarrow{E_{0}}} = \widetilde{E_{0y}}\overrightarrow{u_{y}} + \widetilde{E_{0z}}\overrightarrow{u_{z}} = \widetilde{\overrightarrow{b}}e^{i\alpha} = \left( \overrightarrow{b_{1}} + i\overrightarrow{b_{2}} \right)e^{i\alpha}$
\[{\widetilde{\overrightarrow{E_{0}}}}^{2} = \left\vert {\widetilde{\overrightarrow{E_{0}}}}^{2} \right\vert e^{2i\alpha} = \left( \overrightarrow{b_{1}} + i\overrightarrow{b_{2}} \right)^{2}e^{2i\alpha} = \left( \left\Vert \overrightarrow{b_{1}} \right\Vert ^{2} - \left\Vert \overrightarrow{b_{2}} \right\Vert ^{2} + 2i\overrightarrow{b_{1}}\overrightarrow{b_{2}} \right)e^{2i\alpha}\]Or $\left\vert {\widetilde{\overrightarrow{E_{0}}}}^{2} \right\vert \mathbb{\in R}$ donc $\left( \left\Vert \overrightarrow{b_{1}} \right\Vert ^{2} - \left\Vert \overrightarrow{b_{2}} \right\Vert ^{2} + 2i\overrightarrow{b_{1}}\overrightarrow{b_{2}} \right)\mathbb{\in R}$
\[\Rightarrow \overrightarrow{b_{1}}\overrightarrow{b_{2}} = \overrightarrow{0} \Rightarrow \overrightarrow{b_{1}}\bot\overrightarrow{b_{2}}\]Ici on peut choisir par exemple $\overrightarrow{b_{1}} = b_{1}\overrightarrow{u_{y}}$ et $\overrightarrow{b_{2}} = b_{2}\overrightarrow{u_{z}}$
\[\Rightarrow \overrightarrow{E}(x,t) = {Re}\left\lbrack \widetilde{\overrightarrow{E}}(x,t) \right\rbrack = \left\lbrack \begin{array}{r} E_{x} = 0 \\ E_{y} = b_{1}\cos(\omega t - kx + \alpha) \\ E_{z} = - b_{2}\sin(\omega t - kx + \alpha) \end{array} \right.\] \[\Rightarrow \forall(x,t),\ \begin{bmatrix} \frac{E_{y}(x,t)}{b_{1}} \end{bmatrix}^{2} + \left\lbrack \frac{E_{z}(x,t)}{b_{2}} \right\rbrack^{2} = 1\]$\Rightarrow$ équation d’une ellipse.
A $x$ donné, $\overrightarrow{E}$ décrit une ellipse au cours du plan $(yz)$
A $x$ donné, $\overrightarrow{B}$ décrit une ellipse au cours du plan $(yz)$ en étant $\bot$ à $\overrightarrow{E}$
A $t$ donné, $\overrightarrow{E}$ (et $\overrightarrow{B}$) décrit une hélice ellipsoïdale autour de l’axe $x$.
$\Rightarrow$ On parle de polarisation elliptique (cas général)
Cas particuliers
- $b_{1} = b_{2} \Rightarrow$ trajectoire circulaire
$\Rightarrow$ polarisation circulaire
- $b_{1} = 0$ ou $b_{2} = 0$ $\Rightarrow \overrightarrow{E}$ oscille sur une seule direction (droite)
$\Rightarrow$ polarisation rectiligne