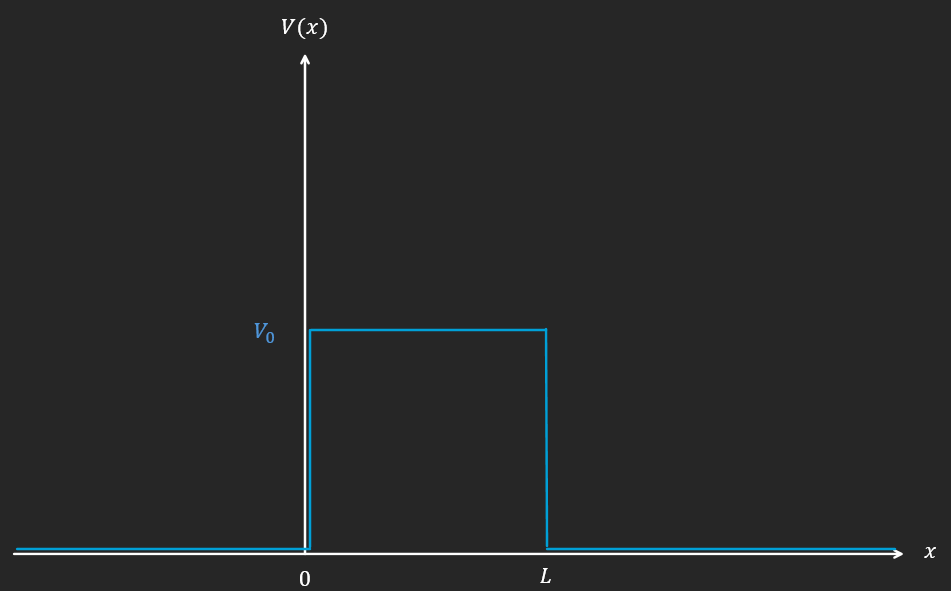CM Introduction Physique Moderne

La physique quantique : ça sert à quoi ?

• Par exemple, expliquer le rayonnement des corps noirs (selon la température)

• Chat de Schrödinger

• Semi-conducteurs

Chapitre 1 : Quanta de lumière

I. Description ondulatoire de la lumière

a. Diffraction et interférences

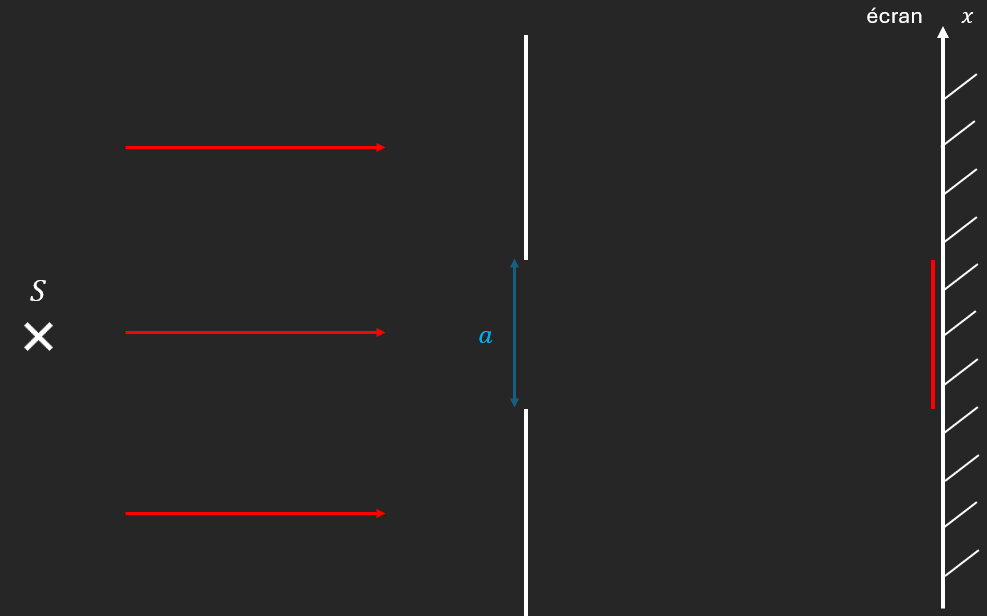
On considère un faisceau de rayons parallèles entre eux et perpendiculaires à la surface.

Soit $\lambda$ la longueur d’onde, $S$ la source de lumière à l’infini, $a$ la taille de l’ouverture.

Cas n°1 : $\lambda \ll a$

On observe une tâche lumineuse de la taille de l’ouverture.

Cas n°2 : $\lambda\ \sim\ a$

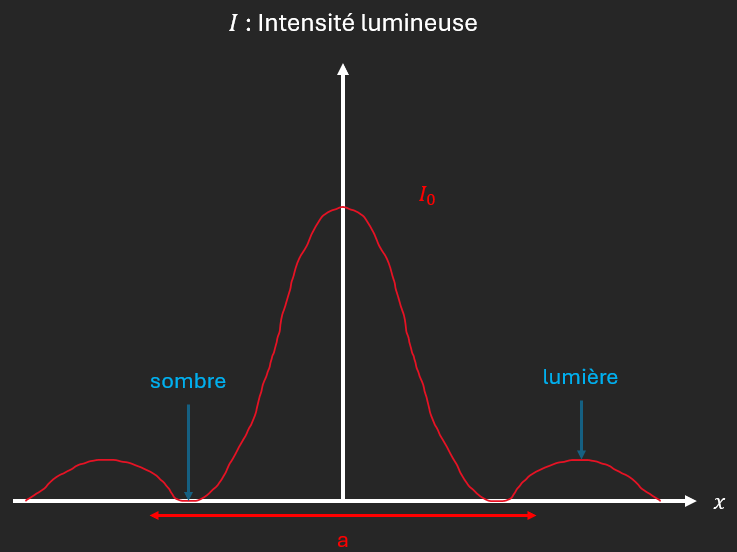
On obtient de la lumière même en dehors de la forme de l’ouverture.

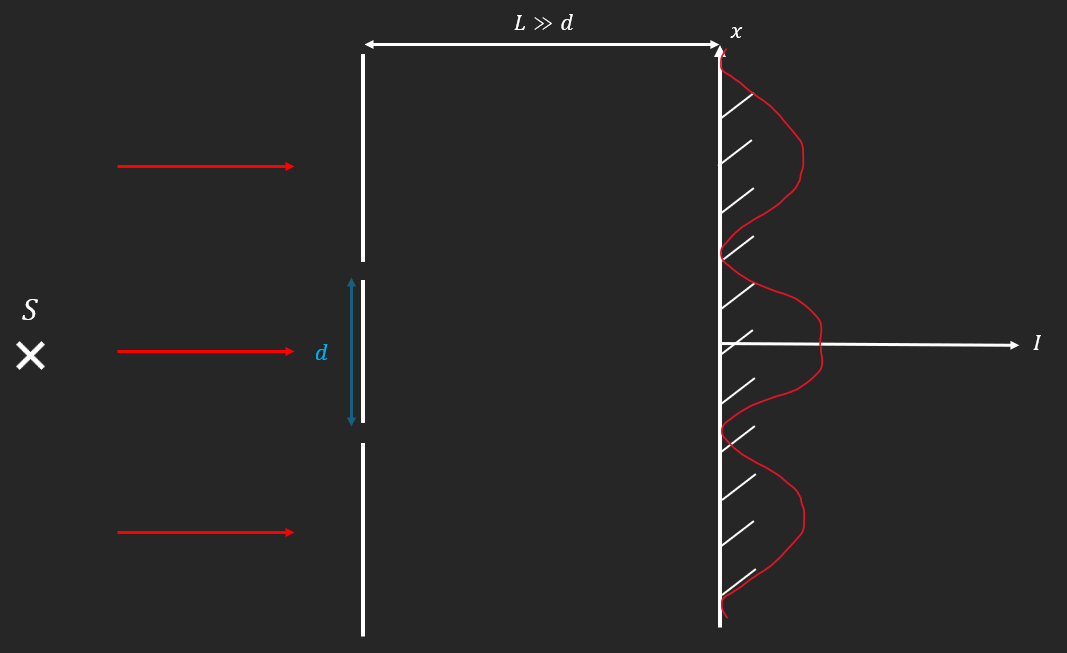
On considère, dans le cas n°2, deux ouvertures de taille $a\sim\lambda$, séparées d’une distance $d$ négligeable devant la distance $L$ entre la surface et l’écran.

b. Diffraction et interférences

Equations de Maxwell dans le vide :

\[div\ \overrightarrow{E} = 0,\ \ div\ \overrightarrow{B} = 0,\ \ \overrightarrow{rot}\ \overrightarrow{B} = \varepsilon_{0}\mu_{0}\frac{\partial\overrightarrow{E}}{\partial t},\ \ \overrightarrow{rot}\ \overrightarrow{E} = - \frac{\partial\overrightarrow{B}}{\partial t}\] \[\overrightarrow{E} = E_{x}\overrightarrow{e_{x}} + E_{y}\overrightarrow{e_{y}} + E_{z}\overrightarrow{e_{z}}\] \[\overrightarrow{B} = B_{x}\overrightarrow{e_{x}} + B_{y}\overrightarrow{e_{y}} + B_{z}\overrightarrow{e_{z}}\]

Hypothèse : On exprime $\overrightarrow{E}$ et $\overrightarrow{B}$ comme fonctions de $x$ et $t\ $:

\[rot\ \overrightarrow{E} = - \frac{\partial E_{z}}{\partial x}\overrightarrow{e_{y}} + \frac{\partial E_{y}}{\partial x}\overrightarrow{e_{z}} = - \frac{\partial\overrightarrow{B}}{\partial t}\] \[\Rightarrow \left\lbrace \begin{array}{r} \frac{\partial B_{x}}{\partial t} = 0 \\ \frac{\partial B_{y}}{\partial t} = \frac{\partial E_{z}}{\partial x}(1) \\ - \frac{\partial B_{z}}{\partial t} = \frac{\partial E_{y}}{\partial x}(2) \end{array} \right\rbrace\] \[div\ \overrightarrow{E} = \frac{\partial E_{x}}{\partial x} = 0 \Rightarrow E_{x}(t) = cte\] \[div\ \overrightarrow{B} = \frac{\partial B_{x}}{\partial x} = 0 \Rightarrow B_{x}(t) = cte\] \[rot\ \overrightarrow{B} = - \frac{\partial B_{z}}{\partial x}\overrightarrow{e_{y}} + \frac{\partial B_{y}}{\partial x}\overrightarrow{e_{z}} = \varepsilon_{0}\mu_{0}\frac{\partial\overrightarrow{E}}{\partial t}\] \[\Rightarrow \left\lbrace \begin{array}{r} \frac{\partial E_{x}}{\partial t} = 0 \\ \frac{\partial E_{y}}{\partial t} = - \frac{1}{\varepsilon_{0}\mu_{0}}\frac{\partial B_{z}}{\partial x} \\ \frac{\partial E_{z}}{\partial t} = \frac{1}{\varepsilon_{0}\mu_{0}}\frac{\partial B_{y}}{\partial x}(4) \end{array}(3) \right\rbrace\] \[\frac{\partial}{\partial t}\ \text{pour}\ (3):\] \[\Rightarrow \frac{\partial^{2}E_{y}}{\partial t^{2}} = - \frac{1}{\varepsilon_{0}\mu_{0}}\frac{\partial^{2}B_{z}}{\partial x\partial t}\] \[\frac{\partial^{2}E_{y}}{\partial t^{2}} = - \frac{1}{\varepsilon_{0}\mu_{0}}\frac{\partial}{\partial x}\left( - \frac{\partial E_{y}}{\partial x} \right)\] \[\frac{\partial^{2}E_{y}}{\partial t^{2}} = \frac{1}{\varepsilon_{0}\mu_{0}}\frac{\partial^{2}E_{y}}{\partial x^{2}}\] \[\frac{\partial^{2}E_{y}}{\partial t^{2}} - c^{2}\frac{\partial^{2}E_{y}}{\partial x^{2}} = 0\ \text{où}\ c^{2} = \frac{1}{\varepsilon_{0}\mu_{0}}\]

Idem pour $B_{z}$

Cette équation est une équation d’onde.

Les solutions de cette équation sont de la forme :

$E_{y}(x,t) = E_{0}\cos(\omega t - kx)$ où

$\omega = 2\pi\nu$ où $\omega$ désigne la pulsation et $\nu$ la fréquence.

\[k = \frac{2\pi}{\lambda}\ \text{ο}\text{ù}\ k\ \text{désigne le nombre d'ondes,}\ \lambda\ \text{la longueur d'onde}\]

On a : $c = \lambda\nu$

• Pour deux sources de lumières identiques :

\[E_{1} = E_{0}\cos(\omega t - kx)\] \[E_{2} = E_{0}\cos(\omega t - kx)\]

Champ électrique total :

\[E = E_{1} + E_{2} = 2E_{0}\cos(\omega t - kx) = 2E_{1}\]

• Interférences constructives

• Pour source 2 allumée avec un retard $\tau = \frac{1}{2\nu}$

\[E_{1} = E_{0}\cos(\omega t - kx)\] \[E_{2} = E_{0}\cos\left( \omega(t + \tau) - kx \right)\]

\(= E_{0}\cos\left( \omega t - kx + \frac{\omega}{2\nu} \right)\) \(= E_{0}\cos\left( \omega t - kx + \frac{\omega}{2\nu} + \pi \right)\) \(= - E_{0}\cos(\omega t - kx)\)

$\Rightarrow E_{1} + E_{2} = 0$.

• Interférences destructives

\[S_{1}:E_{1} = E_{0}\cos(\omega t - kx)\] \[S_{2}:E_{2} = E_{0}\cos\left( \omega t - k(x + \delta) \right)\] \[\sin(\theta) = \frac{\delta}{d} \approx \theta \Rightarrow \delta = \theta d\] \[E_{2} = E_{0}\cos\lbrack\omega t - kx - k\theta d\rbrack = E_{0}\cos\left\lbrack \omega t - kx - \frac{2\pi\theta\delta}{\lambda} \right\rbrack\]

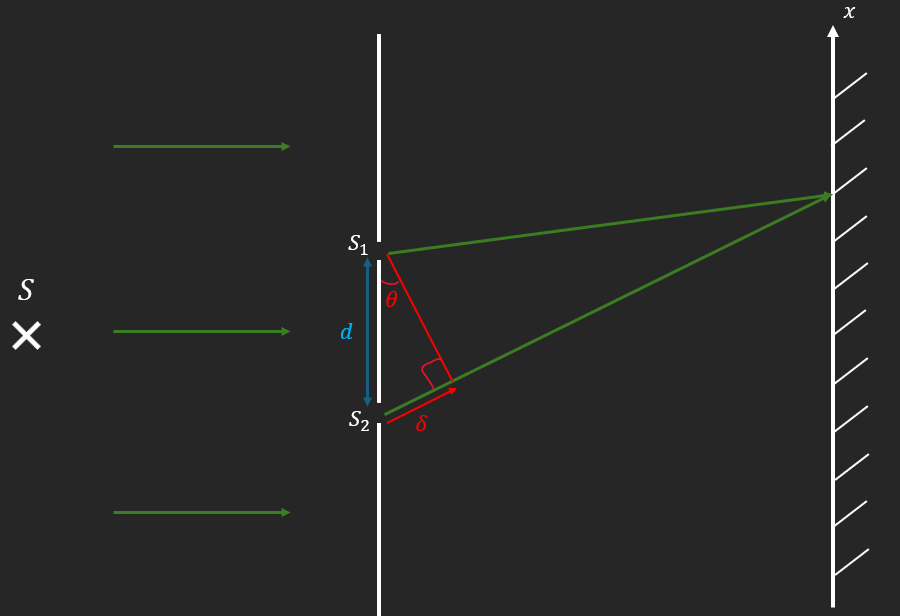
Interférences constructives :

\[\frac{2\pi\theta d}{\lambda} = 2n\pi\ \left( n\mathbb{\in N} \right) \Leftrightarrow \theta d = n\lambda\]

Interférences destructives :

\[\frac{2\pi\theta d}{\lambda} = (2n + 1)\pi\ \left( n\mathbb{\in N} \right) \Leftrightarrow \theta d = \left( n + \frac{1}{2} \right)\lambda\]

II. Insuffisance du modèle ondulatoire

a. Effet photoélectrique

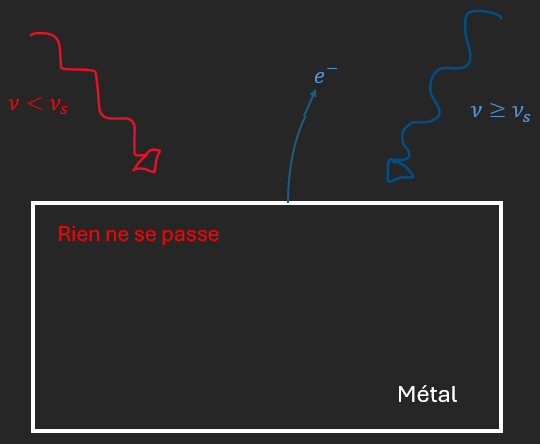
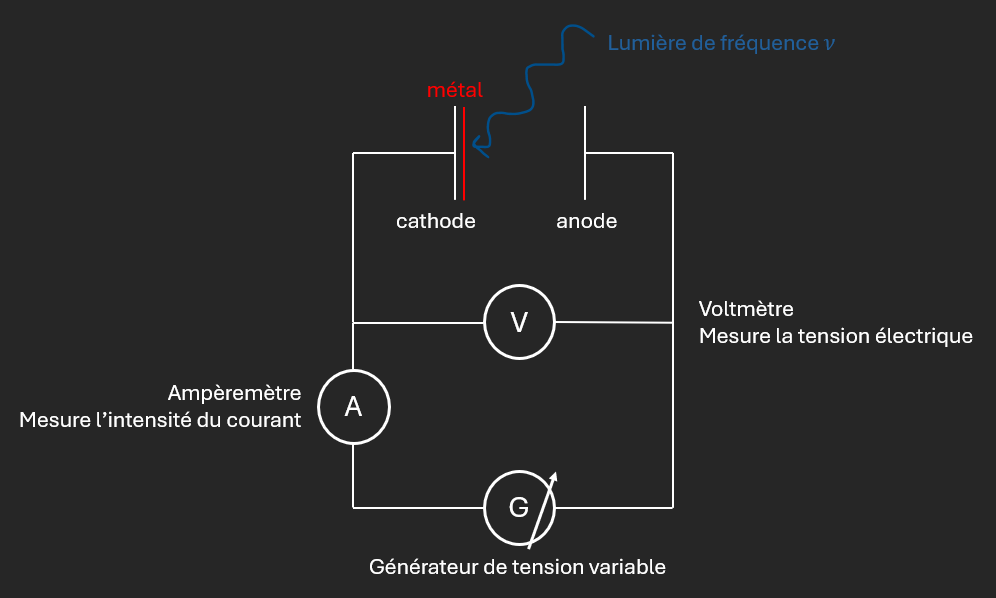
On considère un morceau de métal (dans le vide) éclairé avec une lumière monochromatique (1 seule $\lambda/\nu$).

On observe qu’au-dessus d’une fréquence $\nu_{s}$, la lumière arrache des électrons au métal.

Si $\nu \geq \nu_{s} \Longrightarrow$ électron arraché

$\Longrightarrow$ courant électrique

Si $\nu < \nu_{s} \Longrightarrow$ pas d’électron arraché,

Pas de courant électrique

Si la tension fournie par le générateur est positive $(V > 0)$, le passage des électrons cathode $\rightarrow$ anode est facilité.

Si $V < 0\ $: le circuit s’oppose au passage des électrons.

Remarque : L’intensité $i$ du courant est proportionnelle au nombre d’électrons qui circulent.

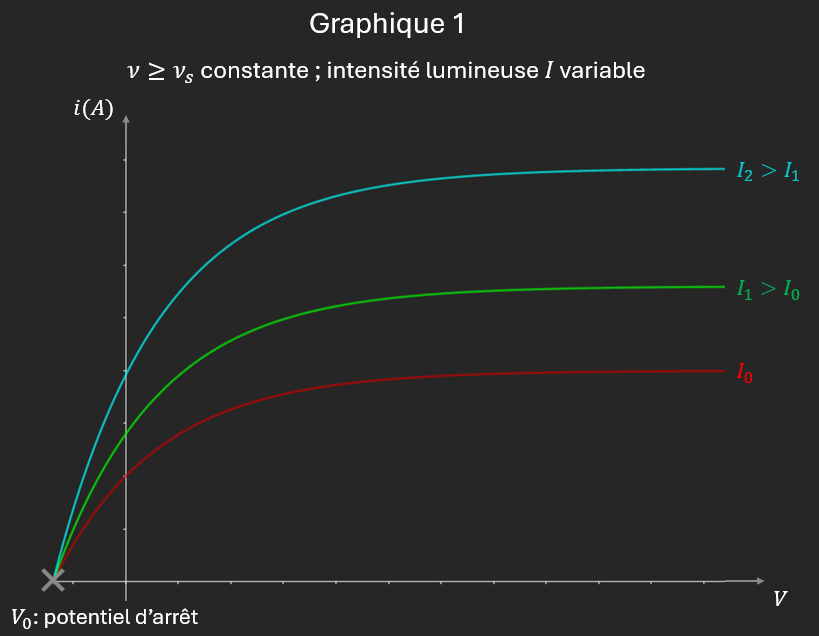
D’après le graphique 1 :

• L’énergie des électrons arrachés est indépendante de l’intensité de la source lumineuse

• $i$ est proportionnel à $I$ $\Leftrightarrow$ le nombre d’électrons arrachés est proportionnel à $I$

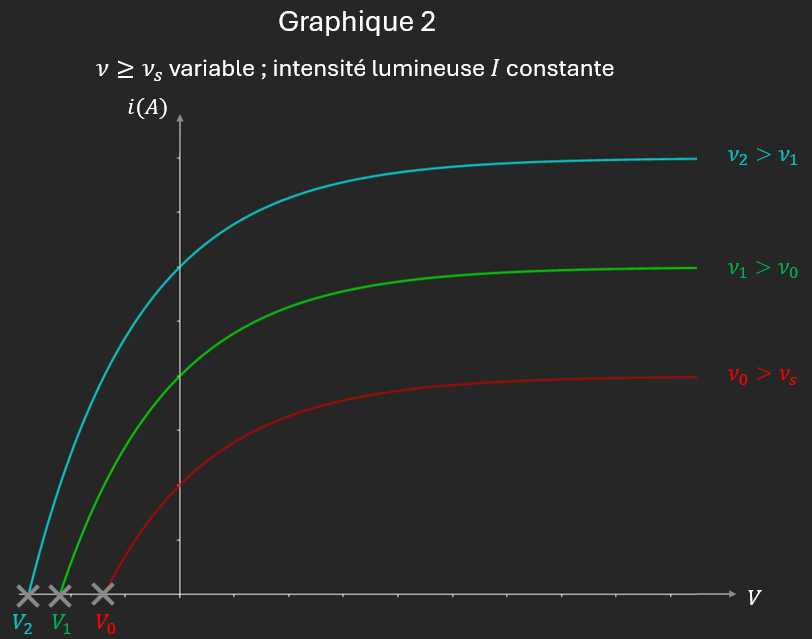
D’après le graphique 2 :

• Le nombre d’électrons arrachés est proportionnel à la fréquence $\nu$

• L’énergie des électrons arrachés est proportionnelle à $\nu\ $: le potentiel d’arrêt $V_{0}$ est proportionnel à $\nu$

Remarques :

• L’effet s’observe quel que soit l’intensité de la lumière si $\nu \geq \nu_{s}$

• Les électrons sont arrachés en quelques nanosecondes

Conservation de l’énergie des électrons :

Si $\nu \geq \nu_{s}\ $:

Les seuls électrons qui arrivent sur l’anode sont ceux qui vérifient :

\[E_{c} > e\vert V\vert\]

Si $V = V_{0}$, par conservation de l’énergie :

\[\Delta E_{m} = 0 \Leftrightarrow \Delta E_{c} + \Delta E_{p} = 0\] \[\left( 0 - \frac{1}{2}mv_{0}^{2} \right) + \left( 0 - eV_{0} \right) = 0\]

$\frac{1}{2}mv_{0}^{2} = - eV_{0}$ où $e = 1.6 \times 10^{- 19}C$

$V_{0}$ est indépendant de l’intensité de $I$. $V_{0}$ diminue lorsque $\nu$ augmente.

c. Interprétation dans le cadre du modèle ondulatoire

Dans le modèle ondulatoire, on s’attend à ce que :

• les électrons soient arrachés $\forall\nu$ (pas de fréquence seuil)

• les électrons soient arrachés pour $I$ donnée en une durée $\tau$ donnée $\pm$ longue.

• l’électron soit arraché après quelques secondes

• en contradiction avec l’observation

d. Nouvelle interprétation

Hypothèse de Planck, reprise par Einstein :

l’énergie de la lumière est proportionnelle à la fréquence : $E = h\nu$

Relation de Planck-Einstein.

\[\text{Or}\ \nu = \frac{\omega}{2\pi} \Longrightarrow E = \frac{h\omega}{2\pi} = \hslash\omega\] \[c = \lambda\nu \Rightarrow \nu = \frac{c}{\lambda} \Rightarrow E = \frac{hc}{\lambda}\]

Bilan d’énergie :

\[E_{\text{photon}} = W + \frac{1}{2}mv^{2}\]

Où $W$ est le travail d’extraction dépendant du métal

\[h\nu = W + \frac{1}{2}mv^{2}\]

Si $\nu = \nu_{s}$, $E_{c} = \frac{1}{2}mv^{2} = 0$ (l’énergie fournie est minimale)

\[W = h\nu_{s}\]

Si $\nu > \nu_{s}$, $E_{c} > 0\ $:

\[h\nu = W + \frac{1}{2}mv^{2}\] \[h\nu = h\nu_{s} + \frac{1}{2}mv^{2}\] \[\frac{1}{2}mv^{2} = h\left( \nu - \nu_{s} \right)\] \[- eV_{0} = h\left( \nu - \nu_{s} \right)\] \[- V_{0} = \frac{h}{c}\left( \nu - \nu_{s} \right) \rightarrow \ \text{expérience de Milikan} \Rightarrow \ \text{détermination de}\ h\]

Attention : Ici, $V_{0} < 0$

On peut montrer, via la relativité restreinte, que $m_{\text{photon}} = 0$

III. La lumière : particule, onde, les deux ou aucun des deux ?

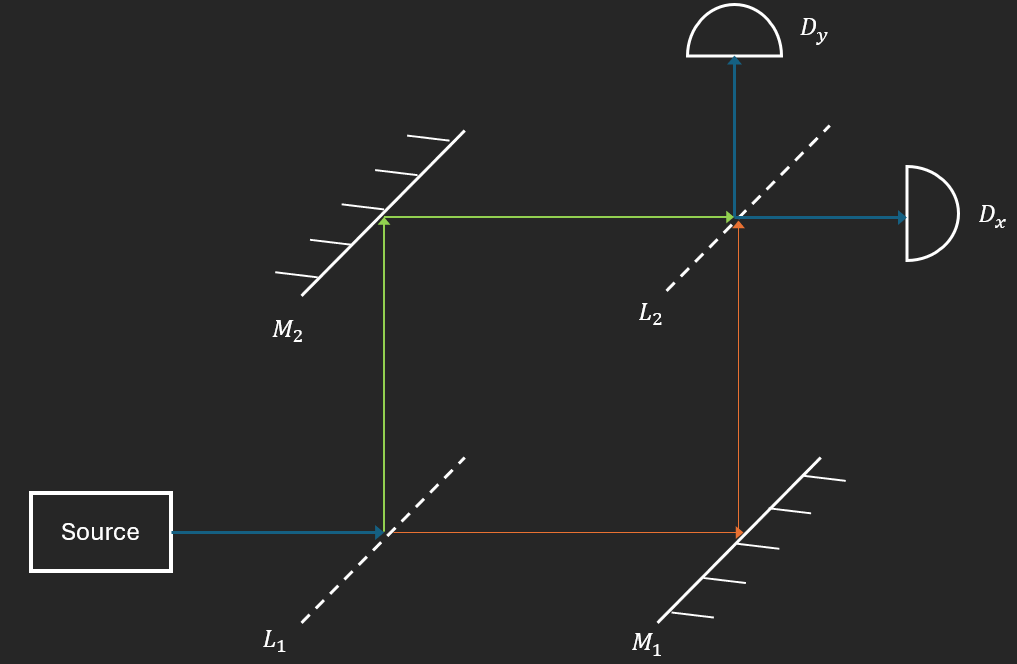
a. Interféromètre de Mach-Zehnder

On considère une source de lumière monochromatique.

$L_{1}$ et $L_{2}$ sont des lames séparatrices, réfléchissent 50% de la lumière et transmettent les 50% restants

$M_{1}$ et $M_{2}$ sont des miroirs parfaits

$D_{x}$ et $D_{y}$ sont des détecteurs de lumière.

On a $L_{1}M_{1} = L_{1}M_{2} = L_{2}M_{1} = L_{2}M_{2}$

Arrivée en $D_{x}$ si $T_{1} \rightarrow R \rightarrow R_{2}$ ou $R_{1} \rightarrow R \rightarrow T_{2}$

Arrivée en $D_{y}$ si $T_{1} \rightarrow R \rightarrow T_{2}$ ou $R_{1} \rightarrow R \rightarrow R_{2}$ $\Rightarrow$ pas le même nombre de réflexions.

Soit $I$ l’intensité de la lumière. $I$ est proportionnelle à $\vert E\vert ^{2}$ où $E$ est l’amplitude du champ électrique.

e. Analyse en termes d’onde

Lors d’une réflexion, l’amplitude $Ε$ est multipliée par $e^{\frac{i\pi}{2}}$

En $L_{1}\ $: Transmission $\Longrightarrow$ aucune modification du champ électrique

Réflexion sur $\overrightarrow{E}$.

Idem en $L_{2}$

En $M_{1}$ et $M_{2}\ $: réflexion uniquement

En $D_{x}$, 2 réflexions et 1 transmission $\Rightarrow \overrightarrow{E}$ est inchangé

En $D_{y}$, nombre de réflexions différent $\Rightarrow \overrightarrow{E} = \overrightarrow{0}$

Remarque :

Il ne faut pas raisonner sur l’intensité $I$, car pas d’interférence mais sur $\overrightarrow{E}$. $I \propto \left \vert \overrightarrow{E} \right \vert $

f. Analyse en termes de photons

Raisonnement naïf :

$D_{x}$ si $T_{1}RR_{2}$ ou $R_{1}RT_{2}$

$D_{y}$ si $R_{1}RR_{2}$ ou $T_{1}RT_{2}$

Probabilité d’une réflexion sur $L_{1}$ ou $L_{2}\ $: $p_{1} = \frac{1}{2}$. Idem pour transmission

Arrivée en $D_{x}\ $:

Probabilité $P_{x}$ d’arriver en $D_{x}\ $:

\[P_{x} = p_{1} \times p_{1} + p_{1} \times p_{1} = \frac{1}{2}\]

Arrivée en $D_{y}\ $:

Idem : $P_{y} = \frac{1}{2}$

$\Longrightarrow$ Pour le raisonnement naïf, la lumière arrive en $D_{x}$ et $D_{y}$.

g. Conclusion

Si le chemin emprunté par le photon n’est pas connu, on observe des interférences. Or, ceci est en contradiction avec une théorie purement corpusculaire classique.

Si le chemin est connu, il n’y a plus d’interférences. Le modèle ondulatoire n’est plus pertinent.

Le photon n’est ni une onde ni une particule.

Conséquences :

• Le photon n’est ni une onde ni une particule mais un nouvel objet physique qui pourra avoir des propriétés corpusculaires ou ondulatoires selon l’expérience. On parle de quanton.

(ex : ornithorynque n’est ni une taupe ni un canard).

• Pour les ondes, le raisonnement sur $\overrightarrow{E}$ fonctionne

La lumière est détectée en $D_{x}$ uniquement, probabilité de détection en $D_{x} = 1$.

Or, en termes de particule, $P_{x} = \frac{1}{2}$

La probabilité observée est $1 \neq \frac{1}{4} + \frac{1}{4} = \frac{1}{2}$

$\Rightarrow$ la somme de probabilité n’est pas pertinente.

Le raisonnement par probabilité ne permet pas d’expliquer les interférences.

Ondes : $I$, $\overrightarrow{E}$

Corpuscules : $p$, ?

Nécessité d’introduire une nouvelle quantité.

Chapitre 2 : Ondes de matière

Matière $\Rightarrow$ $m \neq 0$. $\neq$ photon.

I. Hypothèse de Louis de Broglie

Louis de « Breuille »

De Broglie associe une onde aux particules :

$\psi\left( \overrightarrow{r},t \right) = \psi_{0}\exp\left\lbrack i\left( \omega t - \overrightarrow{k}\overrightarrow{r} \right) \right\rbrack$ Onde plane monochromatique.

Il reprend l’hypothèse de Planck-Einstein : $E = \hslash\omega$ où $\hslash = \frac{h}{2\pi}$

Il utilise le résultat d’Einstein dans la relativité restreinte : la grandeur

\[\left( \frac{E}{c} \right)^{2} - {\overrightarrow{p}}^{2}\ \text{est invariante par changement de référentiel galiléen}\]

De Broglie montre que $\overrightarrow{p} = \hslash\overrightarrow{k}$

Où $\overrightarrow{p}$ est la quantité de mouvement et $\overrightarrow{k}$ est le vecteur d’onde.

Conséquence :

On peut associer une quantité de mouvement à la lumière, ce qui est impossible en physique classique car $\overrightarrow{p} = \overrightarrow{0}$.

Conséquence 2 :

On peut associer des propriétés ondulatoires ($\lambda$ et $f$) aux particules :

\[f = \frac{\omega}{2\pi},\ \ \lambda = \frac{2\pi}{\left \vert \overrightarrow{k} \right \vert }\]

Longueur d’onde $\lambda_{dB} = \frac{2\pi}{\left \vert \overrightarrow{k} \right \vert }$ associée aux particules : longueur d’onde de de Broglie.

De plus, $\overrightarrow{p} = \hslash\overrightarrow{k}$, $\left \vert \overrightarrow{p} \right \vert = \hslash\left \vert \overrightarrow{k} \right \vert $.

\[mv = \hslash\frac{2\pi}{\lambda_{dB}}\] \[\lambda_{dB} = \frac{2\pi\hslash}{mv}\] \[\lambda_{dB} = \frac{h}{mv}\]

II. Confirmation expérimentale

En 1927, expériences de Davisson et Germer.

Quelle taille de « fente » ? On observe des interférences si la longueur d’onde est de l’ordre de la taille des fentes.

Estimons $\lambda_{dB}$ d’un électron de vitesse $v \approx 7 \times 10^{4}\ m.s^{- 1} \ll c$

\[\lambda_{dB} \approx \frac{7 \times 10^{- 34}}{9 \times 10^{- 31} \times 7 \times 10^{4}} = \frac{1}{9}10^{- 7} \approx 10^{- 8}m\]

III. Deux postulats de la mécanique quantique

Un système quantique (particule, …) possède un ensemble de propriétés (position, vitesse, spin) qui constitue l’état du système.

1^er^ postulat

L’état d’un système quantique est entièrement défini par sa fonction d’onde $\psi\left( \overrightarrow{r},t \right)$. L’ensemble de ces fonctions d’ondes appartiennent à un espace vectoriel (de Hilbert).

• Les fonctions d’ondes sont des vecteurs de cet espace.

• On peut faire des CL de vecteurs, donc des CL de fonctions d’onde et d’états

Ex : Pour le chat de Schrödinger, son état serait la somme d’une fonction d’onde « vivant » et d’une fonction d’onde « mort ».

En mécanique quantique, un système peut être dans une CL d’états.

2^e^ postulat

Lors d’un processus de mesure/détection, l’état d’un système quantique passe d’un état initial à un état final.

Au passage de l’état initial à l’état final, on associe une amplitude de probabilité $\mathbb{\in C}$.

La probabilité de passer d’un état à l’autre est donné par $\left\vert \text{amplitude de probabilité} \right\vert ^{2}$.

Dans le cas d’une particule de masse $m \neq 0$

• Si on ne s’intéresse qu’au « déplacement » de la particule, l’état initial est la position initiale ${\overrightarrow{r}}{1}$ et l’état final est la position finale ${\overrightarrow{r}}{2}$.

• $\psi\left( \overrightarrow{r},t \right)$ est l’amplitude de probabilité pour que la particule soit en $\overrightarrow{r}$.

• $\left\vert \psi\left( \overrightarrow{r},t \right) \right\vert ^{2}$ est la distribution des positions de la particule dans l’espace

Complément :

Complément 2 :

En mécanique quantique :

\[P\left( r_{0} \leq r \leq r_{1} \right) = \int_{M_{0}}^{M_{1}}{\left\vert \psi\left( \overrightarrow{r},t \right) \right\vert ^{2}dxdydz}\] \[P = \int_{\begin{array}{r} \text{espace} \\ \text{accessible} \end{array}}^{}{\left\vert \psi\left( \overrightarrow{r},t \right) \right\vert ^{2}dV}\]

Dimension de $\psi$

\[\left\lbrack \text{proba} \right\rbrack = \left\lbrack \int_{}^{}{\vert \varphi\vert ^{2}dV} \right\rbrack\] \[1 = \left\lbrack \vert \psi\vert ^{2} \right\rbrack\lbrack dV\rbrack\] \[\left\lbrack \vert \psi\vert ^{2} \right\rbrack = \frac{1}{L^{3}} \Rightarrow \lbrack\psi\rbrack = \frac{1}{L^{\frac{3}{2}}}\]

Si la particule se déplace dans l’espace 3D

Ex : Fonction d’onde d’un électron autour du noyau d’un atome d’hydrogène

Si l’espace disponible est en 1D, $\lbrack\psi\rbrack = \frac{1}{L^{\frac{1}{2}}}$

On peut utiliser les fonctions d’onde pour expliquer le modèle de l’atome de Bohr.

$\vert \psi\vert ^{2}$ est lié à la probabilité de présence.

\[P = \int_{}^{}{\vert \psi\vert ^{2}dV}\] \[P = \int_{\text{tout le volume disponible}}^{}{\vert \psi\vert ^{2}dV} = 1\]

Limite de la solution de de Broglie :

En 1D, avec $\psi(x,t) = \cos(\omega t - kx)$

\[\int_{- \infty}^{+ \infty}{\vert \psi\vert ^{2}dx} = \int_{- \infty}^{+ \infty}{\cos^{2}(\omega t - kx)dx} \neq 1\]

• L’onde plane monochromatique n’est pas une solution physique possible

Autre exemple de solution non physique :

\[\left\vert \psi(x,t) \right\vert = e^{kx - \omega t}\]

Si la particule se propage dans tout l’espace,

\[\int_{- \infty}^{+ \infty}{e^{2kx}e^{- 2\omega t}dx} = e^{- 2\omega t}\int_{- \infty}^{+ \infty}e^{2kx} \rightarrow + \infty\]

IV. Paquet d’ondes

a. Motivation

Certaines fonctions d’onde comme l’onde plane ne sont pas normalisables à 1.

• Interprétation probabiliste impossible

h. Superposition d’un nombre infini d’ondes

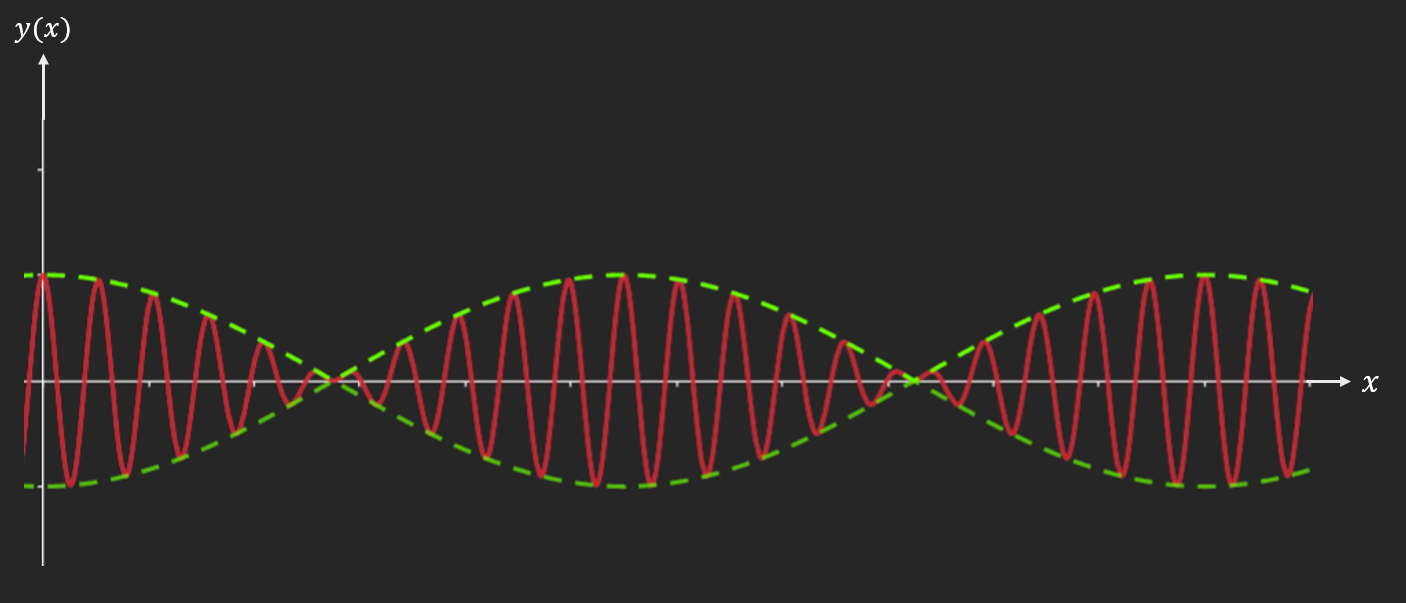
\[y_{1}(x) = A\cos\left( k_{1}x \right) = A\cos\left( \frac{2\pi x}{\lambda_{1}} \right)\] \[y_{2}(x) = A\cos\left( k_{2}x \right) = A\cos\left( \frac{2\pi x}{\lambda_{2}} \right)\] \[y(x) = y_{1}(x) + y_{2}(x) = A\left\lbrack \cos\left( \frac{2\pi x}{\lambda_{1}} \right) + \cos\left( \frac{2\pi x}{\lambda_{2}} \right) \right\rbrack\] \[y^{'}(x) = - A\left\lbrack \frac{2\pi}{\lambda_{1}}\sin\left( \frac{2\pi x}{\lambda_{1}} \right) + \frac{2\pi}{\lambda_{2}}\sin\left( \frac{2\pi x}{\lambda_{2}} \right) \right\rbrack\] \[\frac{1}{\lambda_{1}}\sin\left( \frac{2\pi x}{\lambda_{1}} \right) = - \frac{1}{\lambda_{2}}\sin\left( \frac{2\pi x}{\lambda_{2}} \right)\] \[\cos p + \cos q = 2\cos\left( \frac{p + q}{2} \right)\cos\left( \frac{p - q}{2} \right)\] \[y(x) = 2A\cos\left\lbrack \pi x\left( \frac{1}{\lambda_{1}} + \frac{1}{\lambda_{2}} \right) \right\rbrack\cos\left\lbrack \pi x\left( \frac{1}{\lambda_{1}} - \frac{1}{\lambda_{2}} \right) \right\rbrack\] \[y(x) = 2A\cos\left( \pi x\frac{\lambda_{1} + \lambda_{2}}{\lambda_{1}\lambda_{2}} \right)\cos\left( \pi x\frac{\lambda_{2} - \lambda_{1}}{\lambda_{1}\lambda_{2}} \right)\] \[\lambda_{m} ≔ \frac{\lambda_{1} + \lambda_{2}}{2}\ \text{et}\ \delta\lambda = \frac{\lambda_{2} - \lambda_{1}}{2}\] \[y(x) = 2A\cos\left\lbrack \frac{2\pi x\lambda_{m}}{\lambda_{1}\lambda_{2}} \right\rbrack\cos\left\lbrack \frac{2\pi x\delta\lambda}{\lambda_{1}\lambda_{2}} \right\rbrack\] \[\lambda_{m} \gg \delta\lambda\]

Limites :

• Toujours pas physique car oscillations d’amplitude (enveloppe)

• La particule ne serait pas localisée

• Probabilité totale $\neq 1$

i. Combinaison « infinie » d’ondes

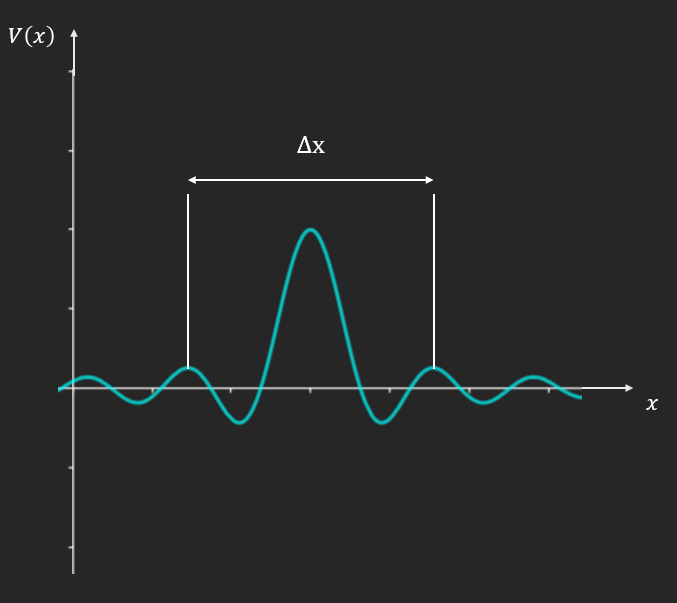
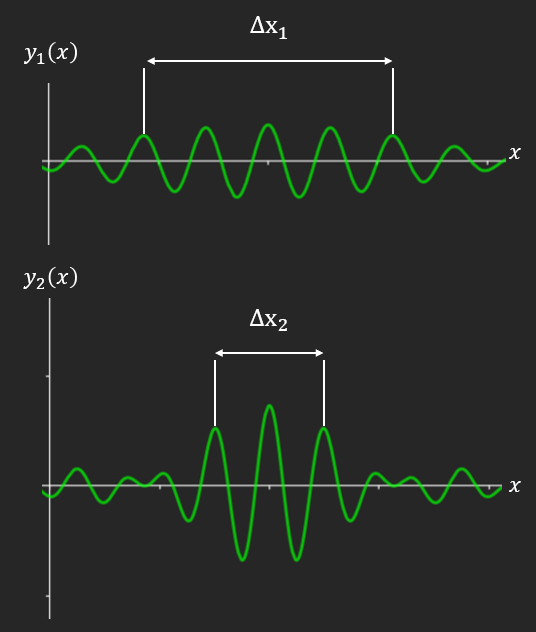
Forme d’un paquet d’ondes

Pas de répétition d’enveloppe : localisation dans un certain intervalle.

II. Relation d’indétermination

a. Ondes classiques

En dehors de $\left\lbrack x_{\min},x_{\max} \right\rbrack$, le paquet d’ondes est significativement moins « intense »/haut.

$\Delta x = x_{\max} - x_{\min}\ $: extension/taille typique du paquet d’ondes.

Ce paquet d’ondes a été obtenu en faisant une somme continue d’ondes de la forme $\cos(kx)$ où $k = \frac{2\pi}{\lambda}$ avec $k \in \left\lbrack k_{\min},k_{\max} \right\rbrack$.

$\Delta k = k_{\max} - k_{\min}\ $: largeur du spectre

Relation d’indétermination : $\Delta x\Delta k \geq 2\pi$

Pour avoir $\Delta x$ très petit, alors $\Delta k$ doit être très grand.

Si le paquet d’ondes est obtenu en faisant varier $k$ sur un petit intervalle, le paquet d’ondes résultant sera très étendu.

\[\Delta x_{1} > \Delta x_{2}\] \[\Delta x_{1}\Delta k_{1} \geq 2\pi\] \[\Delta x_{2}\Delta k_{2} \geq 2\pi\] \[\Delta k_{1} < \Delta k_{2}\]

b. Inégalités d’Heisenberg

Ne pas confonde avec le principe d’incertitude d’Heisenberg.

Pour une particule se déplaçant en 1d selon l’axe $(Ox)$ et de quantité de mouvement (impulsion) $p_{x} = p$.

\[\Delta x\Delta p \geq \frac{\hslash}{2}\]

Relation position-impulsion.

Cohérent avec les ondes classiques : $\overrightarrow{p} = \hslash\overrightarrow{k}$

Si un système quantique a une énergie comprise entre $E_{\min}$ et $E_{\max}$, et une durée de vie dans cet état comprise entre $t_{\min}$et $t_{\max}\ $:

\[\Delta E\Delta t \geq \frac{\hslash}{2}\]

Inégalité énergie-temps.

Où $\Delta E = E_{\max} - E_{\min},\ \Delta t = t_{\max} - t_{\min}$

Origine de la relation énergie-temps :

$\overrightarrow{p} = \hslash\overrightarrow{k} \Rightarrow \left\vert \overrightarrow{p} \right\vert = \hslash\left\vert \overrightarrow{k} \right\vert $, $p = \hslash k = \frac{h}{\lambda}$

Quantité de mouvement $\sim\frac{h}{\text{extension spatiale}}$

\[E = \hslash\omega = h\nu = \frac{h}{T},\ T:\text{période}\] \[\text{énergie}\ \sim\frac{h}{\text{extension temporelle}}\]

c. Conséquences simples

Si on connait parfaitement la position de la particule $\Delta x \rightarrow 0 \Rightarrow_{\text{Heisenberg}}\Delta p \rightarrow + \infty$

$\Rightarrow$ la quantité de mouvement est inconnue.

Si $E$ est parfaitement connue, la durée de vie dans l’état d’énergie $E$ est inconnue.

d. Lien avec la fonction d’onde

$\vert \psi\vert ^{2}(x,t)\ $: distribution des positions de la particule à l’instant $t\ $:

$\left\langle x \right\rangle\ $: position moyenne de la particule

$\left\langle x^{2} \right\rangle\ $: moyenne du carré de la particule

$\Delta x = \sqrt{\left\langle (x - \left\langle x \right\rangle)² \right\rangle} = \sqrt{\left\langle x^{2} \right\rangle - \left\langle x \right\rangle^{2}}\ $: écart-type

Supplément :

\[\left\langle x \right\rangle = \int_{\text{espace accessible}}^{}{x\left\vert \psi(x,t) \right\vert ^{2}dx}\] \[\left\langle x^{2} \right\rangle = \int_{\text{espace accessible}}^{}{x^{2}\left\vert \psi(x,t) \right\vert ^{2}dx}\]

e. Application

Système : Particule de masse $m$ contrainte à rester sur un segment de longueur $L$.

Sur le segment, son énergie potentielle est nulle : la particule est libre.

\[E = E_{c} = \frac{1}{2}mv^{2}\] \[p = mv\] \[E = \frac{p^{2}}{2m}\]

But : montrer que l’énergie minimale de la particule est différente de 0.

\[(\Delta p)^{2} = \left\langle p^{2} \right\rangle - \left\langle p \right\rangle^{2}\]

Or $\left\langle p^{2} \right\rangle \geq \left\langle p \right\rangle^{2}$

Donc $(\Delta p)^{2} \leq \left\langle p^{2} \right\rangle$

\[E = \frac{p^{2}}{2m} \Rightarrow \left\langle E \right\rangle = \frac{1}{2m}\left\langle p^{2} \right\rangle \geq \frac{(\Delta p)^{2}}{2m}\] \[\Delta x\Delta p \geq \frac{\hslash}{2}\] \[(\Delta x)^{2} = \left\langle x^{2} \right\rangle - \left\langle x \right\rangle^{2}\] \[\left\langle x \right\rangle = \int_{0}^{L}{x\left\vert \psi(x,t) \right\vert ^{2}dx}\]

On suppose que $\left\vert \psi(x,t) \right\vert ^{2}$ est uniforme $\left\vert \psi(x,t) \right\vert ^{2}\sim\frac{1}{L}$

\[\left\langle x \right\rangle\ \sim\ \frac{1}{L}\int_{0}^{L}{xdx} = \frac{L}{2}\] \[\left\langle x^{2} \right\rangle\ \sim\frac{1}{L}\int_{0}^{L}{x^{2}dx} = \frac{L^{2}}{3}\] \[(\Delta x)^{2}\ \sim\frac{L^{2}}{3} - \frac{L^{2}}{4} = \frac{L^{2}}{12} \Rightarrow \Delta x\ \sim\frac{L}{\sqrt{12}}\] \[\left\langle E \right\rangle \geq \frac{(\Delta p)^{2}}{2m}\] \[\Delta p \geq \frac{\hslash}{2\Delta x} = \frac{\hslash\sqrt{12}}{2L}\] \[\left\langle E \right\rangle \geq \frac{(\Delta p)^{2}}{2m} \geq \frac{12}{2m}\frac{\hslash^{2}}{L^{2}} = \frac{6\hslash^{2}}{mL^{2}}\] \[\left\langle E \right\rangle \geq \frac{6\hslash^{2}}{mL^{2}}\]

L’énergie moyenne de la particule est non-nulle. La particule est nécessairement en mouvement.

Chapitre 3 : Equation de Schrödinger

I. Equation générale

Evolution de la fonction d’onde $\psi\left( \overrightarrow{r},t \right)$ associée à un système quantique de masse $m \neq 0$ (ne s’applique pas à la lumière) d’énergie potentielle $V\left( \overrightarrow{r},t \right)$.

On dit souvent que la particule évolue dans un potentiel $V\left( \overrightarrow{r},t \right)$

\[i\hslash\frac{\partial\psi}{\partial t}\left( \overrightarrow{r},t \right) = - \frac{\hslash^{2}}{2m}\Delta\psi\left( \overrightarrow{r},t \right) + V\left( \overrightarrow{r},t \right)\psi\left( \overrightarrow{r},t \right)\]

$\Delta\ $: laplacien. En coordonnées cartésiennes :

\[\Delta\psi = \frac{\partial^{2}\psi}{\partial x^{2}} + \frac{\partial^{2}\psi}{\partial y^{2}} + \frac{\partial^{2}\psi}{\partial z^{2}}\]

VIII. Equation de Schrödinger : situations particulières

• Pour un système isolé :

• Energie totale conservée

• Energie invariante par translation dans le temps $\Rightarrow$ fonction ne dépend que de $\overrightarrow{r}$

• $V\left( \overrightarrow{r} \right)$

• Pour une particule libre $\Rightarrow$ pas d’énergie potentielle

• $V\left( \overrightarrow{r},t \right) = 0$

\[i\hslash\frac{\partial\psi}{\partial t} = - \frac{\hslash^{2}}{2m}\Delta\psi\]

• Pour un système isolé ne pouvant se déplacer que selon un axe/une direction $Ox\ $: $\psi\left( \overrightarrow{r},t \right) = \psi(x,t)$

\[i\hslash\frac{\partial\psi}{\partial t} = - \frac{\hslash^{2}}{2m}\frac{\partial^{2}\psi}{\partial x^{2}}(x,t) + V(x,t)\psi(x,t)\]

• Pour un système isolé (1d) dans un potentiel constant : $V(x,t) = V_{0} = cte$

\[i\hslash\frac{\partial\psi}{\partial t} = - \frac{\hslash^{2}}{2m}\frac{\partial^{2}\psi}{\partial x^{2}}(x,t) + V_{0}\psi(x,t)\]

[Les ondes planes sont-elles solutions de l’équation pour une particule ?]{.underline}

\[\psi(x,t) = \psi_{0}e^{i(kx - \omega t)}\] \[\frac{\partial\psi}{\partial t}(x,t) = - i\omega\psi_{0}e^{i(kx - \omega t)}\] \[\frac{\partial^{2}\psi}{\partial x^{2}}(x,t) = - k^{2}\psi_{0}e^{i(kx - \omega t)}\] \[i\hslash\frac{\partial\psi}{\partial t} = \hslash\omega\psi_{0}e^{i(kx - \omega t)} = \hslash\omega\psi(x,t) = E\psi(x,t)\ \text{(Plank-Einstein)}\] \[- \frac{\hslash^{2}}{2m}\frac{\partial^{2}\psi}{\partial x^{2}} = \frac{\hslash^{2}k^{2}}{2m}\psi(x,t) = \frac{p^{2}}{2m}\psi(x,t) = \frac{m^{2}v^{2}}{2m}\psi(x,t) = E\psi(x,t)\ \text{(de Broglie)}\]

Les ondes planes sont solutions de Sch. mais pas physiquement acceptable can non normalisable.

IX. Etats stationnaires

Etat stationnaire : état de la particule d’énergie constante $\Leftrightarrow$ l’énergie est indépendante du temps.

$\Rightarrow$ densité de probabilité indépendante du temps

\[\left\vert \psi(x,t) \right\vert ^{2} = f(x)\]

Rappel :

Si $z = a + ib$, $a,b\mathbb{\in R}$, $\overline{z} = a - ib$

\[\vert z\vert ^{2} = a^{2} + b^{2} = \left\vert \overline{z} \right\vert ^{2}\]

Ici $\left\vert \psi(x,t) \right\vert ^{2} = f(x) \Longleftrightarrow \psi(x,t) = f(x)e^{ig(t)}$ puisque $\left\vert e^{ig(t)} \right\vert ^{2} = 1$

On injecte $\psi(x,t) = f(x)e^{ig(t)}$ dans Sch.

\[i\hslash\left\lbrack i\dot{g}(t)f(x)e^{ig(t)} \right\rbrack = - \frac{\hslash^{2}}{2m}\frac{d^{2}f}{dx^{2}}e^{ig(t)}\] \[- \hslash\dot{g}(t)f(x) = - \frac{\hslash^{2}}{2m}\frac{d^{2}f}{dx^{2}}\] \[\frac{dg}{dt} = \frac{\hslash}{2m}\frac{d^{2}f}{dx^{2}}\]

$\Rightarrow$ les deux termes doivent être constants : $K = cte$

\[\frac{dg}{dt} = K \Rightarrow g(t) = Kt\]

On prend $K = \omega$ car $\lbrack K\rbrack = T^{- 1}$ et cohérent avec les ondes planes

Etat stationnaire :

\[\psi(x,t) = \phi(x)e^{- i\omega t}\]

Or $E = \hslash\omega$

\[\psi(x,t) = \phi(x)e^{- \frac{iEt}{\hslash}}\]

On a bien $\left\vert \psi(x,t) \right\vert ^{2}$ indépendante du temps.

$\phi(x)\ $: partie spatiale d’un état stationnaire

• Equation de Schrödinger indépendante du temps/stationnaire

\[i\hslash\frac{\partial\psi}{\partial t} = - \frac{\hslash^{2}}{2m}\frac{\partial^{2}\psi}{\partial x^{22}} + V(x)\psi(x,t)\]

On injecte un état stationnaire.

\[i\hslash\left( - \frac{iE}{\hslash} \right)\phi(x)e^{- \frac{iEt}{\hslash}} = - \frac{\hslash^{2}}{2m}\frac{d^{2}\phi(x)}{dx^{2}}e^{- \frac{iEt}{\hslash}} + V(x)\psi(x)\] \[E\phi(x)e^{- \frac{iEt}{\hslash}} = - \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx}e^{- \frac{iEt}{\hslash}} + V(x)\phi(x)e^{- \frac{iEt}{\hslash}}\] \[E\phi(x) = - \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} + V(x)\phi(x)\] \[- \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} + V(x)\phi(x) = E\phi(x)\ \rightarrow Sch2\]

Sch2 : équation de Schrödinger indépendante du temps

X. Condition que doit vérifier $\phi(x)$

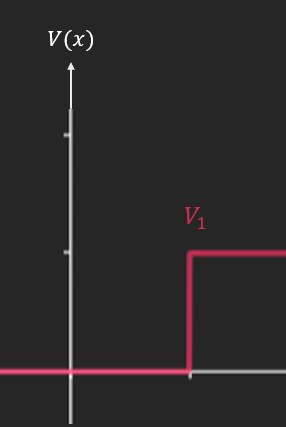
On se place dans le cas d’un potentiel constant par morceaux.

Soit $V_{0}$ non-infini.

\[V(x) = \left\lbrace \begin{array}{r} V_{0}\ \text{sur}\ \lbrack - a,a\rbrack \\ V_{1}\ \text{sur}\ \lbrack a,b\rbrack \end{array} \right.\]

Si $V_{1} \neq \infty$ on doit avoir $\phi(x)$ continu en $x = a$ et $\frac{d\phi}{dx}$ continu en $x = a$.

Si $V_{1} \rightarrow + \infty$, on doit avoir $\phi(a) = 0$ et $\phi^{‘}(a) = 0$

Complément :

Schéma 23

• Condition que doit vérifier $\frac{d\phi}{dx}\left( x = x_{0} \right)\ $?

\[\frac{d^{2}\phi}{dx^{2}}\left( x_{0} \right) = \frac{\phi^{'}\left( x_{0} + \varepsilon \right) - \phi^{'}\left( x_{0} - \varepsilon \right)}{2\varepsilon}\] \[- \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} + V(x)\phi(x) = E\phi(x)\] \[\Rightarrow - \frac{\hslash^{2}}{2m}\frac{\phi^{'}\left( x_{0} + \varepsilon \right) - \phi^{'}\left( x_{0} - \varepsilon \right)}{2\varepsilon} = \left\lbrack E - V\left( x_{0} \right) \right\rbrack\phi\left( x_{0} \right)\]

La différence $E - V\left( x_{0} \right)$ est finie si discontinuité de $V(x)$ finie en $x_{0} \Rightarrow \frac{d\phi}{dx}$ continue.

• Condition que doit vérifier $\phi\left( x_{0} \right)\ $?

$\phi$ intégrable $\Rightarrow$ $\phi\left( x_{0} \right)$ continue

Bilan :

Si $V(x)$ est discontinue en $x_{0}\ $:

• $\phi$ doit être continue en $x_{0}$

• $\frac{d\phi}{dx}$ continue en $x_{0}$ si discontinuité finie

XI. Exemples de potentiels

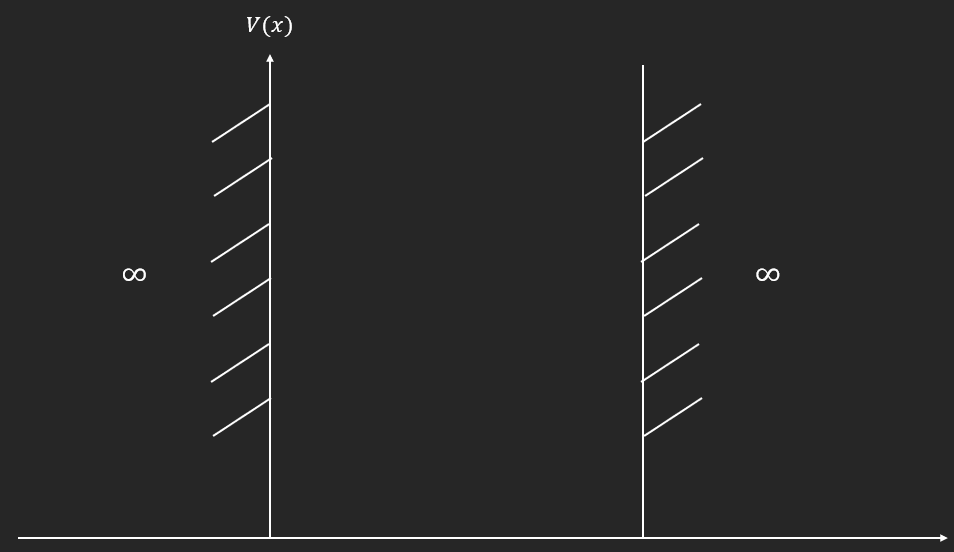
• Puits infini

Ex : corde qui vibre et les extrémités sont fixées.

• Boite quantique

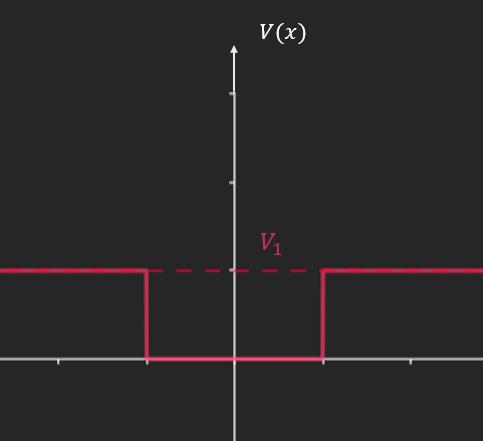
• Puits fini

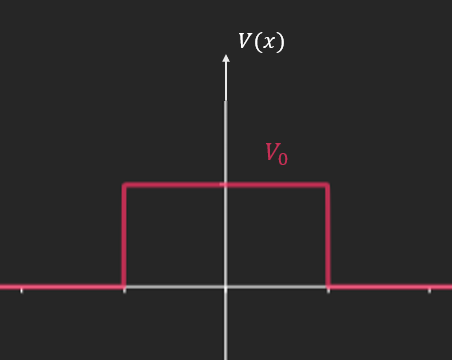
• Barrière de potentiel

• Radioactivité α, effet tunnel

• Marche de potentiel

• Oscillation harmonique (non constant par morceaux)

XII. Puits de potentiel de profondeur infinie

\[V(x) = \left\lbrace \begin{array}{r} 0\ \text{si}\ x \in \lbrack 0,L\rbrack \\ \infty\ \text{sinon} \end{array} \right.\]

But : résoudre Schrödinger indépendant du temps $t$ sur $\lbrack 0,L\rbrack$

a. Etats stationnaires

\[- \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} + V(x)\phi(x) = E\phi(x)\] \[- \frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} = E\phi(x)\ \text{sur}\ \lbrack 0,L\rbrack\] \[\frac{\hslash^{2}}{2m}\frac{d^{2}\phi}{dx^{2}} + E\phi(x) = 0\] \[\frac{d^{2}\phi}{dx^{2}} + \frac{2mE}{\hslash^{2}}\phi(x) = 0\]

(similaire à un oscillateur harmonique)

\[\left\lbrack \frac{d^{2}\phi}{dx^{2}} \right\rbrack = \frac{\lbrack\phi\rbrack}{L^{2}} = \left\lbrack \frac{2mE}{\hslash^{2}} \right\rbrack\lbrack\phi\rbrack\] \[k^{2} = \frac{2mE}{\hslash^{2}} \geq 0\ \text{car}\ E = E_{c}\] \[\frac{d^{2}\phi}{dx^{2}} + k^{2}\phi(x) = 0\]

Solutions :

\[\phi(x) = C\cos(kx) + S\sin(kx)\]

Conditions aux bords :

\[\phi(0) = \phi(L) = 0\] \[\phi(0) = C \Rightarrow C = 0\] \[\phi(L) = S\sin(kL) = 0\] \[\Rightarrow \sin(kL) = 0\]

$\Rightarrow k_{n}L = n\pi$ avec $n \in \mathbb{N}^{*}$

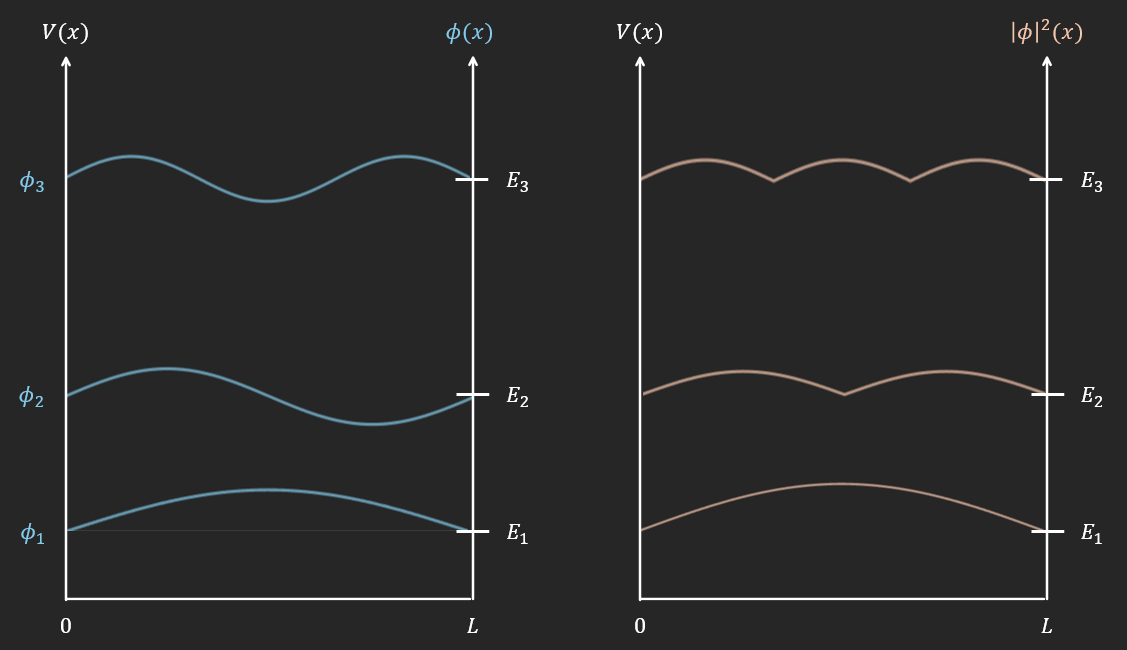
\[k_{n} = \frac{n\pi}{L}\] \[\phi(x) = S\sin\left( k_{n}x \right)\ \text{avec}\ k_{n} = \frac{n\pi}{L},\ n \in \mathbb{N}^{*}\]

Interprétation probabiliste/Born :

\[\int_{0}^{L}{\left\vert \phi(x) \right\vert ^{2}dx} = 1\] \[S^{2}\int_{0}^{L}{\sin^{2}\left( k_{n}x \right)dx} = 1\] \[\text{Or}\sin^{2}\left( k_{n}x \right) = \frac{1}{2} - \frac{1}{2}\cos\left( 2k_{n}x \right)\] \[S^{2}\int_{0}^{L}{\frac{1}{2}dx} - \frac{S^{2}}{2}\int_{0}^{L}{\cos\left( 2k_{n}x \right)dx} = 1\] \[\frac{S^{2}L}{2} - \frac{S^{2}}{2}\int_{0}^{L}{\cos\left\lbrack \frac{2n\pi}{L}x \right\rbrack dx} = 1\] \[\frac{S^{2}L}{2} = 1 \Rightarrow S = \sqrt{\frac{2}{L}}\] \[\phi(x) = \sqrt{\frac{2}{L}}\sin\left( k_{n}x \right)\ \text{avec}\ k_{n} = \frac{n\pi}{L},\ n \in \mathbb{N}^{*}\]

• Energie de la particule

\[k_{n}\ = \frac{\sqrt{2mE}}{\hslash}\] \[\Rightarrow E_{n} = \frac{\hslash^{2}k_{n}^{2}}{2m}\] \[E_{n} = \frac{1}{2m}\left( \frac{n\hslash p}{L} \right)^{2},\ n \in \mathbb{N}^{*}\] \[E_{n} = \frac{1}{2m}\left( \frac{\hslash\pi}{L} \right)^{2}n^{2},\ n \in \mathbb{N}^{*}\] \[E_{n} \geq E_{1} = \frac{\hslash^{2}\pi^{2}}{2mL^{2}} > 0\]

Energie minimale de la particule $E_{1} = \frac{\hslash^{2}\pi^{2}}{2mL^{2}}$ cohérente avec Heisenberg.

Etats stationnaires :

\[\psi(x,t) = \sqrt{\frac{2}{L}}\sin\left( k_{n}x \right)e^{- \frac{iE_{n}t}{\hslash}}\] \[k_{n} = \frac{n\pi}{L},\ E_{n} = \frac{1}{2m}\left( \frac{\hslash\pi}{L} \right)^{2}n^{2},\ n \in \mathbb{N}^{*}\]

Longueur d’onde de de Broglie :

\[\lambda_{n} = \frac{2\pi}{k_{n}} = \frac{2\pi}{n\pi}L = \frac{2L}{n}\]

j. Comparaison avec une particule classique

Une particule classique peut avoir une énergie nulle.

La probabilité de présence d’une telle particule est uniforme.

\[\left\vert \phi_{\text{classique}} \right\vert ^{2} = \text{cte} = \frac{1}{L}\]

k. Etat non stationnaire

Etat initial quelconque :

\[\psi(x,0) = \frac{4}{\sqrt{5L}}\sin^{3}\left( \frac{\pi x}{L} \right) = \frac{4}{\sqrt{5L}}\left\lbrack \frac{3}{4}\sin\left( \frac{\pi x}{L} \right) - \frac{1}{4}\sin\left( \frac{3\pi x}{L} \right) \right\rbrack\] \[\text{Or}\ \phi_{1}(x) = \sqrt{\frac{2}{L}}\sin\left( \frac{\pi x}{L} \right)\] \[\phi_{3}(x) = \sqrt{\frac{2}{L}}\sin\left( \frac{3\pi x}{L} \right)\] \[\psi(x,0) = \frac{4}{\sqrt{5L}}\sqrt{\frac{L}{2}}\left\lbrack \frac{3}{4}\phi_{1}(x) - \frac{1}{4}\phi_{3}(x) \right\rbrack\] \[\psi(x,0) = \frac{3}{\sqrt{10}}\phi_{1}(x) - \frac{1}{\sqrt{10}}\phi_{3}(x)\] \[\psi(x,0) = \frac{4}{\sqrt{5L}}\sin^{3}\left( \frac{\pi x}{L} \right) = \frac{3}{\sqrt{10}}\phi_{1}(x) - \frac{1}{\sqrt{10}}\phi_{3}(x)\] \[\psi(x,t) = \frac{3}{\sqrt{10}}\phi_{1}(x)e^{- \frac{iE_{1}t}{\hslash}} - \frac{1}{\sqrt{10}}\phi_{3}(x)e^{- \frac{iE_{3}t}{\hslash}}\]

Remarque :

\[\left\vert \psi(x,t) \right\vert ^{2} \neq \frac{9}{10}\left\vert \phi_{1}(x) \right\vert ^{2} + \frac{1}{10}\left\vert \phi_{3}(x) \right\vert ^{2}\]

$\Rightarrow$ phénomène d’interférence

l. Vérification d’Heisenberg

But : $\Delta x\Delta p \geq \frac{\hslash}{2}\ ?$

• $\left\langle x \right\rangle$

\[\left\langle x \right\rangle = \int_{0}^{L}{x\left\vert \phi(x) \right\vert ^{2}dx}\] \[\left\langle x \right\rangle = \frac{2}{L}\int_{0}^{L}{\frac{x\sin(n\pi x)}{L}dx}\] \[\left\langle x \right\rangle = \frac{2}{L}\left( \int_{0}^{L}{\frac{x}{2}dx} - \int_{0}^{L}{x\cos\left( \frac{2n\pi x}{L} \right)dx} \right)\] \[\left\langle x \right\rangle = \frac{L}{2} - \frac{2}{L}\int_{0}^{L}{x\cos\left( \frac{2n\pi x}{L} \right)dx} = \frac{L}{2}\] \[\left\langle x \right\rangle = \frac{L}{2}\]

• $\left\langle x^{2} \right\rangle$

\[\left\langle x^{2} \right\rangle = \frac{2}{L}\int_{0}^{L}{x^{2}\sin^{2}\left( \frac{n\pi x}{L} \right)dx}\] \[\left\langle x^{2} \right\rangle = \frac{2}{L}\int_{0}^{L}{\frac{x^{2}}{2}dx} - \frac{2}{L}\int_{0}^{L}{x^{2}\cos\left( \frac{2n\pi x}{L} \right)dx}\] \[\left\langle x^{2} \right\rangle = \frac{L^{2}}{3} - \frac{2}{L}\int_{0}^{L}{x^{2}\cos\left( \frac{2n\pi x}{L} \right)dx}\] \[\left\langle x^{2} \right\rangle = \frac{L^{2}}{3}\left\lbrack 1 - \frac{3}{2n^{2}\pi^{2}} \right\rbrack\ \text{dépend de}\ n\] \[(\Delta x)^{2} = \left\langle x^{2} \right\rangle - \left\langle x \right\rangle^{2} = \frac{L^{2}}{3}\left\lbrack 1 - \frac{3}{2n^{2}\pi^{2}} \right\rbrack - \frac{L^{2}}{4} = L^{2}\left( \frac{1}{12} - \frac{1}{8n^{2}\pi^{2}} \right)\] \[\frac{L}{\sqrt{12}} < \Delta x \leq L^{2}\left( \frac{1}{12} - \frac{1}{8n^{2}\pi^{2}} \right)\]

• $\left\langle p \right\rangle$ et $\left\langle p^{2} \right\rangle$

\[p = - i\hslash\frac{d}{dx}\] \[\left\langle p \right\rangle = \int_{0}^{L}{\overline{\phi}(x)\left\lbrack p\phi(x) \right\rbrack dx}\ \left( \text{où}\ \overline{\phi}\ \text{est le complexe conjugué} \right)\] \[\left\langle p \right\rangle = \int_{0}^{L}{\phi(x)\left\lbrack p\phi(x) \right\rbrack dx} = \int_{0}^{L}{\phi(x)\left\lbrack - i\hslash\frac{d\phi(x)}{dx} \right\rbrack dx} = \int_{0}^{L}{\sqrt{\frac{2}{L}}\sin\left( \frac{n\pi x}{L} \right)\left\lbrack - i\hslash\sqrt{\frac{2}{L}}\frac{n\pi}{L}\cos\left( \frac{n\pi x}{L} \right) \right\rbrack dx}\] \[= - \frac{2i\hslash}{L} \times \frac{n\pi}{L}\int_{0}^{L}{\sin\left( \frac{n\pi x}{L} \right)\cos\left( \frac{n\pi x}{L} \right)dx}\] \[= - \frac{2i\hslash n\pi}{L^{2}}\int_{0}^{L}{\frac{1}{2}\sin\left( \frac{2n\pi x}{L} \right)dx}\] \[= 0\] \[\left\langle p \right\rangle = 0\]

Autre méthode :

\[\left\langle p \right\rangle = - i\hslash\int_{0}^{L}{\frac{\phi(x)d\phi(x)}{dx}dx} = - \frac{i\hslash}{2}\int_{0}^{L}{d\phi^{2}} = - \frac{i\hslash}{2}\left\lbrack \phi^{2} \right\rbrack_{0}^{L} = - \frac{i\hslash}{2} \times \frac{2}{L}\left\lbrack \sin\left( \frac{n\pi x}{L} \right) \right\rbrack_{0}^{L} = 0\] \[\left\langle p^{2} \right\rangle = \int_{0}^{L}{\phi(x)\left\lbrack p^{2}\phi(x) \right\rbrack dx} = \int_{0}^{L}{\phi(x)\left\lbrack - \hslash^{2}\frac{d^{2}}{dx^{2}}\phi(x) \right\rbrack dx} = - \hslash^{2}\int_{0}^{L}{\sqrt{\frac{2}{L}}\sin\left( \frac{n\pi x}{L} \right)\sqrt{\frac{2}{L}}\left\lbrack {- \left( \frac{n\pi}{L} \right)}^{2}\sin\left( \frac{n\pi x}{L} \right) \right\rbrack dx}\] \[\left\langle p^{2} \right\rangle = \frac{2\hslash^{2}}{L}\left( \frac{n\pi}{L} \right)^{2}\int_{0}^{L}{\sin^{2}\left( \frac{n\pi x}{L} \right)dx}\] \[\left\langle p^{2} \right\rangle = \frac{2\hslash^{2}}{L}\left( \frac{n\pi}{L} \right)^{2}\left\lbrace \int_{0}^{L}{\frac{1}{2}dx} - \frac{1}{2}\int_{0}^{L}{\cos\left( \frac{2n\pi x}{L} \right)dx} \right\rbrace\] \[\left\langle p^{2} \right\rangle = \frac{2\hslash^{2}}{L}\left( \frac{n\pi}{L} \right)^{2}\left\lbrace \frac{1}{2} - 0 \right\rbrace\] \[\left\langle p^{2} \right\rangle = \left( \frac{n\pi\hslash}{L} \right)^{2}\] \[(\Delta p)^{2} = \left\langle p^{2} \right\rangle - \left\langle p \right\rangle^{2} = \left\langle p^{2} \right\rangle = \left( \frac{n\pi\hslash}{L} \right)^{2}\]

Vérification :

\[\Delta x\Delta p = \sqrt{L^{2}\left( \frac{1}{12} - \frac{1}{8n^{2}\pi^{2}} \right)} \times \frac{n\pi\hslash}{L}\] \[\Delta x\Delta p = n\pi\hslash\sqrt{\frac{1}{12} - \frac{1}{8n^{2}\pi^{2}}}\] \[\Delta x\Delta p = \hslash\sqrt{\frac{n^{2}\pi^{2}}{12} - \frac{1}{8}} \geq \hslash\sqrt{\frac{\pi^{2}}{12} - \frac{1}{8}} = \hslash \times \frac{1}{2}\sqrt{\frac{\pi^{2} - 3}{6}}\]

On a donc bien $\Delta x\Delta p \geq \frac{\hslash}{2}$

m. Comparaison avec une particule classique

Toutes les positions sont équiprobables

$\Longrightarrow$ distribution de probabilité uniforme :

\[\rho(x) = K \in \mathbb{R}_{+}^{*}\] \[\rho(x)\ \text{vérifie}\ \int_{0}^{L}{\rho(x)dx} = 1\] \[\Leftrightarrow \int_{0}^{L}{Kdx} = 1\] \[\Leftrightarrow KL = 1\] \[\Rightarrow K = \frac{1}{L}\] \[\rho(x) = \frac{1}{L}\]

• Position moyenne $\left\langle x \right\rangle_{cl}$

\[\left\langle x \right\rangle_{cl} = \int_{0}^{L}{x\rho(x)dx} = \frac{1}{L}\int_{0}^{L}{xdx}\] \[\left\langle x \right\rangle_{cl} = \frac{L}{2} = \left\langle x \right\rangle\ \text{pour la particule classique dans un puits infini de potentiel}\] \[\left\langle x^{2} \right\rangle_{cl} = \int_{0}^{L}{x^{2}\rho(x)dx} = \frac{1}{L}\int_{0}^{L}{x^{2}dx} = \frac{L^{2}}{3}\]

Remarque :

\[\left\langle x^{2} \right\rangle = \frac{L^{2}}{3}\left( 1 - \frac{3}{2n^{2}\pi^{2}} \right) \rightarrow_{n \rightarrow + \infty}\frac{L^{2}}{3} = \left\langle x^{2} \right\rangle_{cl}\]

$\left\langle p \right\rangle = 0$ car les déplacements à $v > 0$ et $v < 0$ sont équiprobables.

XIII. Applications

a. « Quantum dot »

Electron enfermé dans une boite.

\[E_{n} = \frac{1}{2m}\ \left( \frac{\hslash\pi}{L} \right)^{2}n^{2}\]

$E_{n + 1} - E_{n} = E_{\gamma}\ $: énergie du photon émis

\[E_{n + 1} - E_{n} = \frac{1}{2m}\ \left( \frac{\hslash\pi}{L} \right)^{2}\left\lbrack (n + 1)^{2} - n^{2} \right\rbrack = \frac{1}{2m}\ \left( \frac{\hslash\pi}{L} \right)^{2}(2n + 1)\] \[E_{\gamma} = \frac{1}{2m}\ \left( \frac{\hslash\pi}{L} \right)^{2}(2n + 1) = \frac{hc}{\lambda_{y}} = \frac{2\pi\hslash c}{\lambda_{y}}\ \text{où}\ \lambda_{\gamma}:\ \text{longueur d'onde lumineuse émise}\] \[\lambda_{\gamma} = \frac{4\pi m\hslash c}{(2n + 1)}\left( \frac{L}{\hslash\pi} \right)^{2}\] \[\lambda_{\gamma} = \frac{4}{2n + 1}\frac{mcL^{2}}{\hslash\pi} = 8\frac{mcL^{2}}{(2n + 1)h}\]

Application : Source de lumière de $\lambda$ très précise.

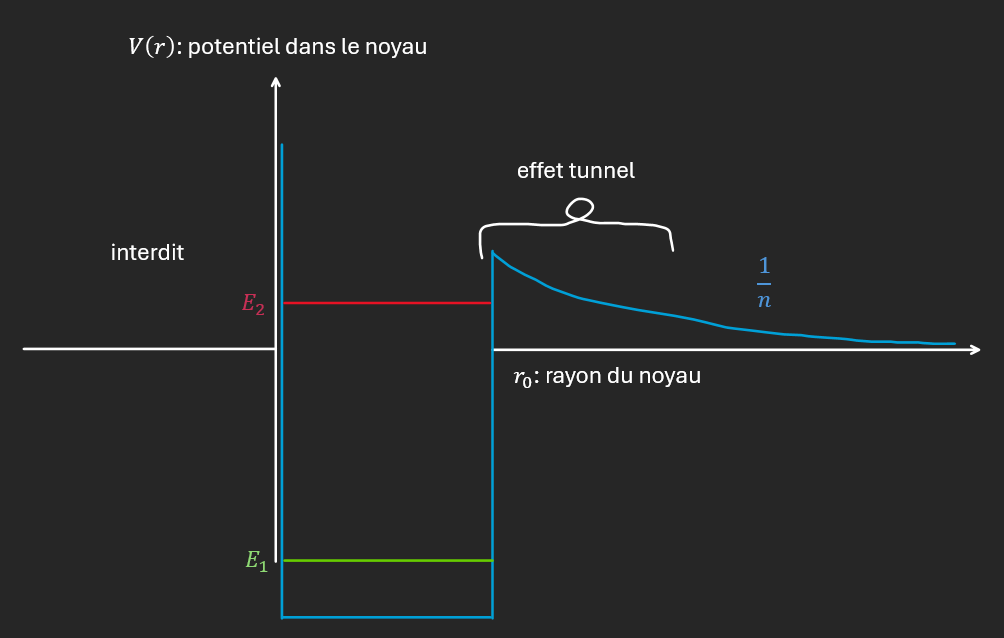
n. Barrière de potentiel

\[V(x) = \left\lbrace \begin{array}{r} 0\ \text{si}\ x < 0 \\ V_{0}\ \text{si}\ x \in \lbrack 0,L\rbrack \\ 0\ \text{si}\ x > L \end{array} \right.\]

Classiquement : s

• Si $E \geq V_{0}$ une particule provenant de $- \infty$ repart en $+ \infty$

• Si $E < V_{0}\ $: s’il provient de $- \infty$ repart en $- \infty$

Quantiquement :

• Si $E \geq V_{0}$, similaire au cas classique

• Si $E < V_{0}$, la probabilité que la particule provenant de $- \infty$ aille en $x > L$ est $\neq 0$

$\Rightarrow$ effet tunnel

• Radioactivité $\alpha$

Emission de noyau d’hélium.

Il existe des forces qui « lient » les protons entre eux car Coulomb prédit une répulsion pour des mêmes charges.

Si $E$ est suffisante mais inférieure à $V\left( r_{0} \right) \Rightarrow$ la probabilité que la particule sorte par effet tunnel est $\neq 0$