Cours 01 Generalite Lumiere
Télécharger le Cours 01 Generalite Lumiere en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Page 1 : Cycle Préparatoire Généralités GENERALITES SUR LA LUMIERE Bibliographie du cours Chapitres 1 à 6: LLLeeesss NNNooouuuvvveeeaaauuuxxx PPPrrréééccciiisss BBBrrréééaaalll ::: PPPhhhyyysssiiiqqquuueee Optique MPSI-PCSI-PTSI P. BRENDERS, M.SAUZEIX Bréal Editions Réf. 209.0345 OOOppptttiiiqqquuueee ::: FFFooonnndddeeemmmeeennntttsss eeettt aaappppppllliiicccaaatttiiiooonnnsss Premiers cycles - Licence José-Philippe PEREZ MASSON Sciences DUNOD 7ème édition HHH PPPrrrééépppaaa ::: NNNooouuuvvveeeaaauuu PPPrrrooogggrrraaammmmmmeee Optique 1ière année MPSI – PCSI – PTSI Jean-Marie BREBEC, Thierry DESMARAIS, Marc MENETRIER, Bruno NOËL, Régine NOËL, Claude Orsini Hachette Supérieur
Page 2 : Cycle Préparatoire Généralités 21. Approche physique de la lumière et de ses interactions avec notre environnement L'observation courante nous montre que la lumière est émise par la matière filament d'ampoule électrique, gaz chauffé dans les flammes ou excité dans des tubes de type néon …, qu'elle se propage à travers un milieu air, eau, verre … jusqu'aux récepteurs œil, plaque photographique, cellule CCD dans les caméras numériques où elle se manifeste par son action. 1.1 Les sources de lumière Certaines sources de lumière transforment une énergie de type électrique, chimique ou thermique en énergie lumineuse. Ces sources sont dites primaires car elles sont à l'origine de cette transformation comme dans le cas de l'ampoule électrique ou du soleil. D'autres sources sont dites secondaires ou objets éclairés car elles ne font que réémettre la lumière qu'elles reçoivent comme dans le cas de la Lune ou des planètes qui sont des objets éclairés par le soleil. Les sources lumineuses sont toujours étendues. Par contre, une source peut être considérée comme ponctuelle si nous regardons son action, à l'aide d'un récepteur corps dont certaines propriétés varient quand il reçoit de la lumière, en des points situés très loin de la source la distance entre la source et le récepteur est très supérieure à la dimension transversale de la source. 1.2 Les milieux de propagation Entre la source et le récepteur, la lumière se propage dans des milieux différents : transparents, translucides ou opaques à la lumière. La lumière se propage aussi dans le vide.
Page 3 : Cycle Préparatoire Généralités 31.3 Les récepteurs de lumière Enfin, les récepteurs transforment l'énergie lumineuse reçue en une énergie de type électrique, chimique ou thermique. La lumière assure donc le transport d'énergie depuis la source vers le récepteur. Si nous plaçons un corps entre l'œil et un objet lumineux, ce corps est dit : • Transparent s'il n'altère pas la visibilité de l'objet lumineux : c'est le cas du verre. • Translucide s'il altère la visibilité de l'objet : c'est le cas du verre dépoli. • Opaque si l'on ne peut voir l'objet au travers : c'est le cas du bois, du métal. Un corps opaque peut être : • Opaque absorbant si l'énergie lumineuse reçue est totalement transformée en une autre énergie thermique par exemple : c'est le cas des matériaux de couleur noire. • Opaque diffusant s'il réémet la lumière dans toutes les directions. Il peut éventuellement absorber une partie de la lumière. C'est le cas le plus général. • Opaque réfléchissant si la lumière est renvoyée dans une direction particulière : c'est la cas des miroirs. La lumière véhicule information et énergie sans déplacement de matière, depuis une source vers un récepteur, au travers d'un milieu qui peut être le vide.
Page 4 : Cycle Préparatoire Généralités 42. Approche historique de la lumière et de ses modèles physiques 2.0 Historique ANTIQUITÉ -3000 à 477, arrivée des francs : notion de rayons lumineux, loi de la réflexion et l'idée que la lumière suit le chemin qui a le temps de parcours minimum germe. ARCHIMÈDE 287 à 212 av JC : a-t-il incendié la flotte romaine devant Syracuse ? Il s'agit sans doute d'une légende car il est très difficile de renvoyer de la lumière à l'aide de miroirs sur une cible mouvante. CLAUDE PTOLÉMÉE 90-168 : mathématicien, astronome, géographe grec d'Alexandrie. On lui doit un traité d'optique et des tables de mesure concernant la réfraction. ALHAZEN 965-1039 : physicien arabe, comprend le premier que l’œil n'émet pas de rayons venant scruter'' les objets mais que ceux-ci, éclairés par des sources, sont à l'origine de rayons lumineux rectilignes. Mise au point expérimentale en Italie des verres correcteurs pour la vue 1285 et d'une lunette d'approche 1590. 1609 - GALILÉE 1564-1642 : physicien et astronome italien. On lui doit la lunette astronomique avec laquelle il découvre les satellites de Jupiter, les anneaux de Saturne, les taches et la rotation du Soleil. La cours de Rome le dénonce comme hérétique et il doit abjurer devant l'inquisition 1633. 1611 - KEPLER 1571-1630 : astronome allemand. Son ouvrage "Dioptrique'' dans lequel il expose le principe d'une lunette à deux lentilles convergentes, publié en 1611, est l'ouvrage d'optique le plus important publié avant "l'Optique'' de Newton. Découvre le mouvement elliptique des planètes autour du Soleil. A la même époque, construction du premier microscope. 1621 - SNELL VAN ROYEN 1580-1626 : astronome et mathématicien hollandais. Découvre la loi de la réfraction. 1637 – René DESCARTES 1596-1650 : philosophe et scientifique français. Formalise les lois de la réflexion et réfraction. Publication d'un ouvrage "Dioptrique''. Le problème de stigmatisme est posé et Descartes donne une théorie de l'arc-en-ciel mais ignore la complexité de la lumière blanche, il ne peut pas expliquer la coloration de l'arc-en-ciel. 1657 - Pierre de FERMAT 1601-1665 : astronome et mathématicien français. Il justifie les lois de l'optique géométrique dans le cadre d'un formalisme variationnel. Il introduit la notion de chemin optique qui permet d'énoncer le Principe de Fermat selon lequel la lumière met un temps minimal pour aller d'un point à l'autre. 1665 - l'anglais Robert HOOKE 1635-1703 puis le hollandais Christian Huygens 1629-1695 postulent la nature ondulatoire de la lumière, idée contre laquelle s'élève l'anglais Isaac NEWTON. Pour ce dernier, la lumière ne peut être que corpusculaire. Francesco Maria GRIMALDI 1618- 1663, physicien jésuite italien, met en évidence un nouveau phénomène lumineux qu'il nomme diffraction publié après sa mort. 1666 - NEWTON 1642-1727 : mathématicien, physicien et astronome anglais. A l'aide d'un écran percé d'un trou, suivi d'un prisme, il découvre, en projetant la lumière sur le mur opposé qu'elle se compose d'une infinité de couleurs. 1672 - NEWTON 1642-1727 : construction du premier télescope. 1676 – ROENER 1644-1710 : astronome danois. Première mesure de la vitesse de la lumière à l'observatoire de Paris. 1704 - NEWTON : publication d'un traité d'optique dans lequel il explique la complexité de la lumière blanche. Celle-ci serait formée de corpuscules : grains de nature imprécise lancés à toute vitesse par l'émetteur. Il explique ainsi la coloration de l'arc-en-ciel. 1802 - YOUNG 1773-1829 : médecin et physicien anglais. Effectue la première mesure de longueur d'onde à partir de ses célèbres fentes. Il découvre aussi l'accommodation du cristallin et les interférences lumineuses. A la même époque, MALUS 1775-1812, FRESNEL 1788-1827 et ARAGO 1786-1853 étudient la polarisation de la lumière. Fresnel suppose que la lumière est propagée par le mouvement vibratoire d'un milieu hypothétique, l'éther. Aucun renseignement n'est donné sur ce milieu. Diverses mesures de la vitesse de la lumière sont réalisées par les français Hippolyte FIZEAU 1819-1896 en 1849 ou Léon FOUCAULT 1819-1868 en 1850. 1870 - MAXWELL 1831-1879 : physicien écossais. Elabore une théorie permettant d'unifier l'optique et les phénomènes électromagnétiques. Dans sa théorie électromagnétiques, les ondes lumineuses visibles ou invisibles sont constituées d'un champ électrique perpendiculaire à un champ magnétique avec des intensités variant périodiquement dans l'espace et dans le temps. Désormais, la lumière est considérée comme une onde électromagnétique se propageant à la vitesse de 3.108 m.s-1. 1905 - EINSTEIN 1879-1955 : physicien allemand. Explore la notion de photon pour interpréter l'effet photoélectrique. Des corps convenablement illuminés expulse des photons. Or il faut fournir énormément d'énergie à un atome pour lui arracher des électrons. Par ailleurs cette extraction se fait sur des niveaux d'énergie discontinus. L'apport énergétique de la lumière se fait sous forme corpusculaire notion de photons. L'extraction étant obligatoirement continue si la lumière était uniquement de nature ondulatoire. Grâce à l'apport de la mécanique ondulatoire, Louis DE BROGLIE 1892-1987, en 1924, a concilié les deux aspects : corpusculaire et ondulatoire.
Page 5 : Cycle Préparatoire Généralités 5On doit à l'époque contemporaine de nombreux perfectionnements en optique instrumentale. L'introduction de la transformée de Fourier a permis de mieux comprendre le rôle de l'optique physique dans la formation des images, les méthodes informatiques permettant d'effectuer des tracés systématiques de rayons et d'introduire des méthodes mathématiques très puissantes dans le traitement des images ex : Hubble. L'invention du laser Light Amplification by Stimulated Emission of Radiation 1960, de l'holographie imaginée en 1949 par Dennis GABOR 1900-1979, n'a donné des résultats satisfaisants qu'en 1960 grâce aux lasers qui fournissent une lumière cohérente, l'utilisation de fibres optiques 400 000 communications téléphoniques en même temps sur la même fibre, 5Gbits/s sont quelques uns des aspects de l'optique moderne. 2.1 Modèles corpusculaire et ondulatoire A la fin du 17ième siècle, Newton supposait une nature corpusculaire de la lumière : une source de lumière émettait des particules très légères ou grains de lumière qui se propageaient en ligne droite dans le vide ou dans l'air en définissant les rayons lumineux. Cette théorie permit de bâtir l'optique géométrique. Mais, dès le début du 19ième siècle, cette conception fut abandonnée pour la théorie ondulatoire. Les travaux de Fresnel sur les interférences et la diffraction permirent d'assimiler la lumière à une onde sinusoïdale analogie avec les ondes acoustiques. Ainsi, deux rayons lumineux atteignant simultanément un même point, peuvent conduirent à l'obscurité interférences destructives si les ondes sont en opposition de phase. Vers la fin du 19ième siècle, Maxwell détermina la nature de l'onde en développant la théorie électromagnétique. Au début du 20ième siècle, la théorie quantique de la lumière développée par Einstein remit la nature corpusculaire en compétition avec la nature ondulatoire. Seule cette théorie permettait de comprendre le échanges d'énergie entre matière et rayonnement comme dans l'effet photoélectrique, sous la forme de quanta, en introduisant les photons, porteurs de quantum d'énergie. La conciliation de ces deux théories fut réalisée par Louis de Broglie en 1924. Ces deux théories ne s'opposent pas mais se complètent : la lumière a une nature duale ; les ondes ont une signification "statistique" : l'intensité de l'onde mesure la probabilité de présence des photons.
Page 6 : Cycle Préparatoire Généralités 62.2 Modèle ondulatoire : ondes électromagnétiques 2.2.1 Onde électromagnétique polarisée rectilignement Le champ électromagnétique est défini par le couple champ électrique E et champ magnétique B en tout point Mx,y,z d'un repère d'espace, à l'instant t. Une onde électromagnétique représente un champ électromagnétique à variations spatiales et temporelles simultanées. L'onde électromagnétique est dite plane lorsque l'état de l'onde est le même, à un instant donné t, en tout point d'un plan, appelé plan d'onde. Par exemple, pour l'onde t,xB,t,xE, tout plan parallèle à yOz, tel que x reste constant, constitue un plan d'onde. L'onde électromagnétique est dite polarisée rectilignement lorsque les champ E et B gardent une direction fixe, en tout point de l'espace et à tout instant t. Par exemple, t,xf.EE0= et t,xg.BB0= 00BetE étant des champs uniformes 2.2.2 Onde progressive monochromatique dans le vide a Préliminaires Une onde progressive est le résultat d'un signal périodique entretenu vibreur, produit par exemple en un point O du milieu. Une onde progressive sinusoïdale correspond à une perturbation produite en O de la forme : tcosas0tOϕω= Avec a : amplitude, ω : pulsation, ϕ0 : phase à l'origine Pour un point M distant de xOM =, la perturbation arrive avec le retard cx , où c représente la vitesse de propagation célérité du signal. On déduit aisément que la vibration en M à l'instant t est partie de O à l'instant cxt . cxtcosasss0cxtOt,xtMϕω===
Page 7 : Cycle Préparatoire Généralités 7b Double périodicité d'une onde monochromatique progressive Une onde progressive est dite monochromatique dans le cas où les champs sont des fonctions sinusoïdales de la quantité cxt , de forme : tcosEcxtcosEt,xE000ϕω=ϕω= De pulsation ω, liée à la période T ou à la fréquence ν de l'onde par : πν=π=ω2T2 T constitue la période temporelle de l'onde : c'est celle de la source. De phase ϕ, à l'abscisse x : 00xcT2xcϕ+π=ϕ+ω=ϕ avec ϕ0, phase à l'origine en x = 0 d'amplitude vectorielle 0E onde polarisée rectilignement Considérons un point M d'abscisse x = constante et observons sa vibration au cours du temps. Lorsque t augmente de ν= 1T, en remplaçant t par t + T dans l'expression de t,xE, la phase augmente de 2π radians. Tt,xEt,xE+= A un instant t figé, observons les états de vibration de l'ensemble des points autour de M. On constate que lorsqu'on se déplace du point M d'une distance ν=λc , en remplaçant x par x + λ, dans l'expression de t,xE, la phase augmente de 2π radians. t,xEt,xEλ+= La période spatiale λ est la plus petite distance qui sépare deux points du milieu de propagation qui ont le même état vibratoire
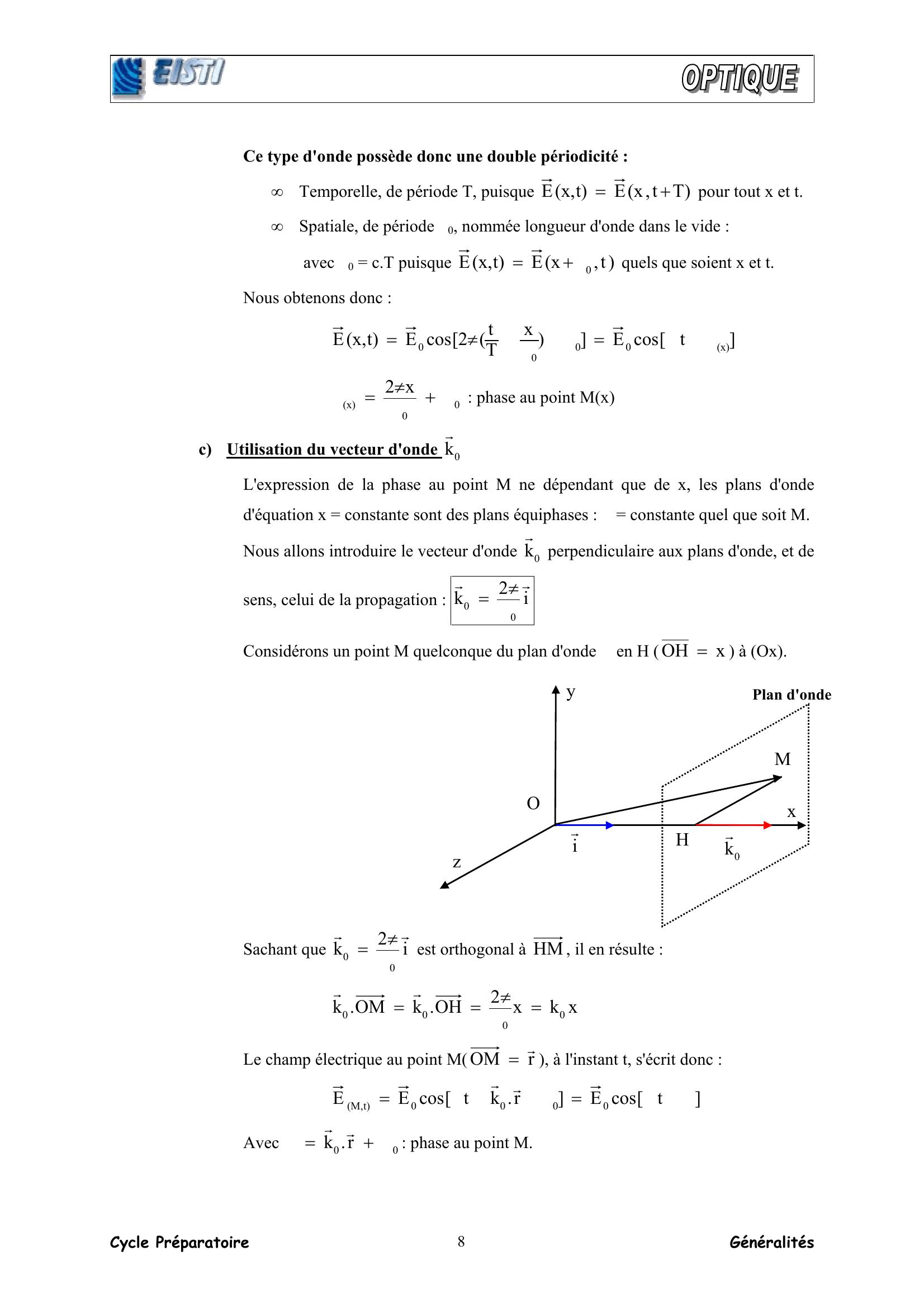
Page 8 : Cycle Préparatoire Généralités 8Ce type d'onde possède donc une double périodicité : • Temporelle, de période T, puisque Tt,xEt,xE+= pour tout x et t. • Spatiale, de période λ0, nommée longueur d'onde dans le vide : avec λ0 = c.T puisque t,xEt,xE0λ+= quels que soient x et t. Nous obtenons donc : tcosExTt2cosEt,xEx0000ϕω=ϕλπ= 00xx2ϕ+λπ=ϕ : phase au point Mx c Utilisation du vecteur d'onde 0kr L'expression de la phase au point M ne dépendant que de x, les plans d'onde d'équation x = constante sont des plans équiphases : ϕ = constante quel que soit M. Nous allons introduire le vecteur d'onde 0kr perpendiculaire aux plans d'onde, et de sens, celui de la propagation : i2k00rrλπ= Considérons un point M quelconque du plan d'onde en H xOH = à Ox. Sachant que i2k00rrλπ= est orthogonal à HM , il en résulte : xkx2OH.kOM.k0000=λπ==rr Le champ électrique au point MrOMr=, à l'instant t, s'écrit donc : tcosEr.ktcosEE0000t,Mϕω=ϕω=rr Avec 00 r.kϕ+=ϕrr: phase au point M. y H M O x z ir0krPlan d'onde
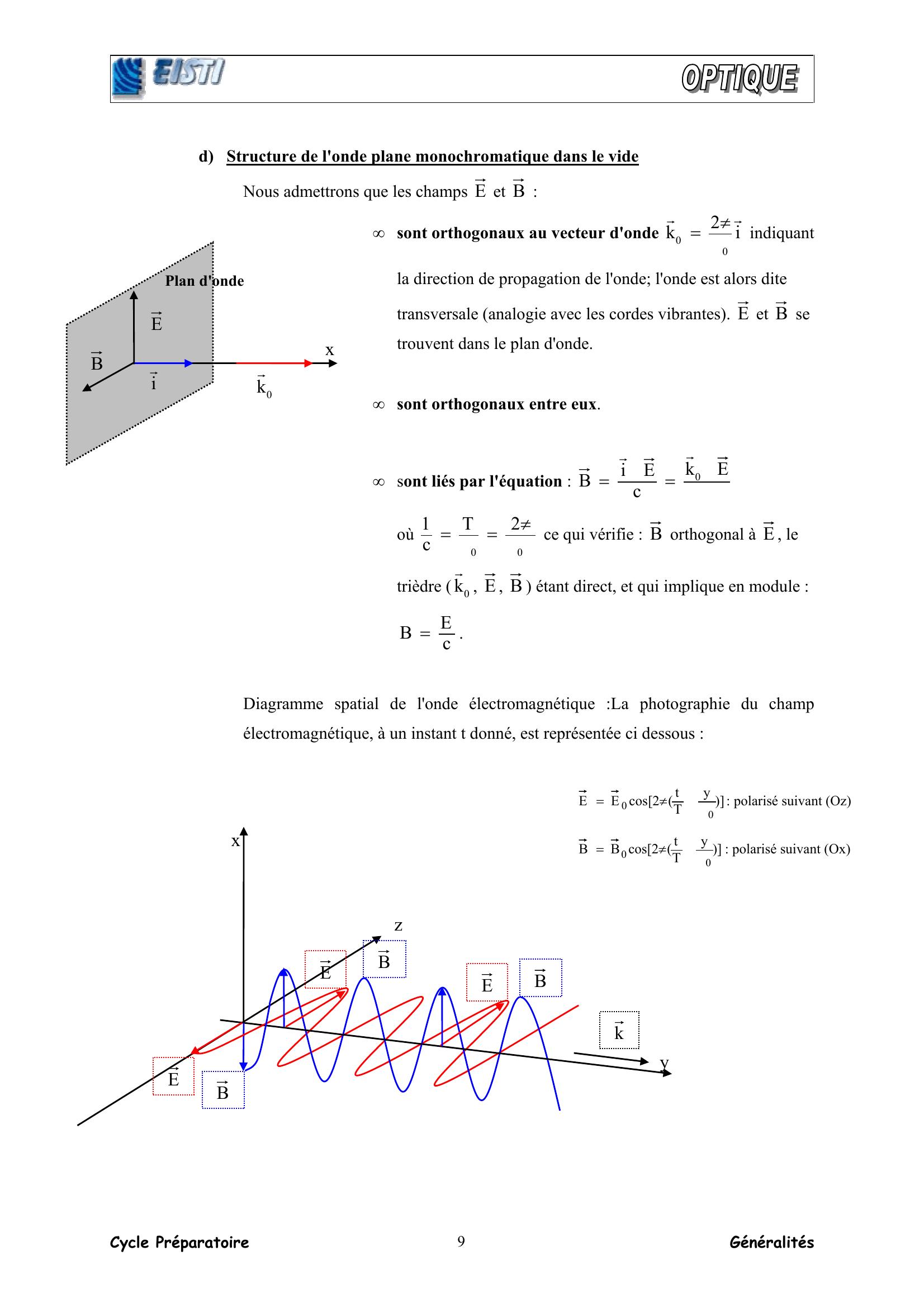
Page 9 : Cycle Préparatoire Généralités 9d Structure de l'onde plane monochromatique dans le vide Nous admettrons que les champs E et B : • sont orthogonaux au vecteur d'onde i2k00rrλπ= indiquant la direction de propagation de l'onde; l'onde est alors dite transversale analogie avec les cordes vibrantes. E et B se trouvent dans le plan d'onde. • sont orthogonaux entre eux. • sont liés par l'équation : ω==EkcEiB0rr où ωλπ=λ=002Tc1 ce qui vérifie : B orthogonal à E , le trièdre 0kr, E , B étant direct, et qui implique en module : cEB =. Diagramme spatial de l'onde électromagnétique :La photographie du champ électromagnétique, à un instant t donné, est représentée ci dessous : yTt2cosEE00λπ=: polarisé suivant Oz yTt2cosBB00λπ=: polarisé suivant Ox Ex Bir0krPlan d'onde x y z BBBEEEk
Page 10 : Cycle Préparatoire Généralités 10e Propriétés de l'onde lumineuse en conclusion Dans le cas du vide, nous pouvons écrire théorie de Maxwell que ces champs électriques et magnétiques se déplacent avec la célérité c telle que : 001cµε= Où c est la célérité de l'onde électromagnétique dans le vide, ε0 et µ0 des constantes fondamentales de valeurs : ε0 = 8,854187817.10-12 F/m µ0 = 4π.10-7 H/m Ce qui donne : c = 2,99792458.108 m/s La célérité de la lumière dans le vide est : • indépendante de la fréquence de l'onde lumineuse • indépendante du référentiel galiléen d'étude l'onde lumineuse réelle est souvent quelconque. Fort heureusement, cette onde peut être décrite comme une superposition d'ondes planes progressives sinusoïdales monochromatiques. En première lecture, nous admettons que le champ électrique associé à une onde lumineuse monochromatique de fréquence ν, se propageant dans le vide selon l'axe Oz, est transversal et peut se mettre sous la forme suivante : vzt2cosEt,zEmMπν= Pour une radiation électromagnétique monochromatique considérée dans le vide, nous obtenons la longueur d'onde associée par la relation : ν==λcT.c
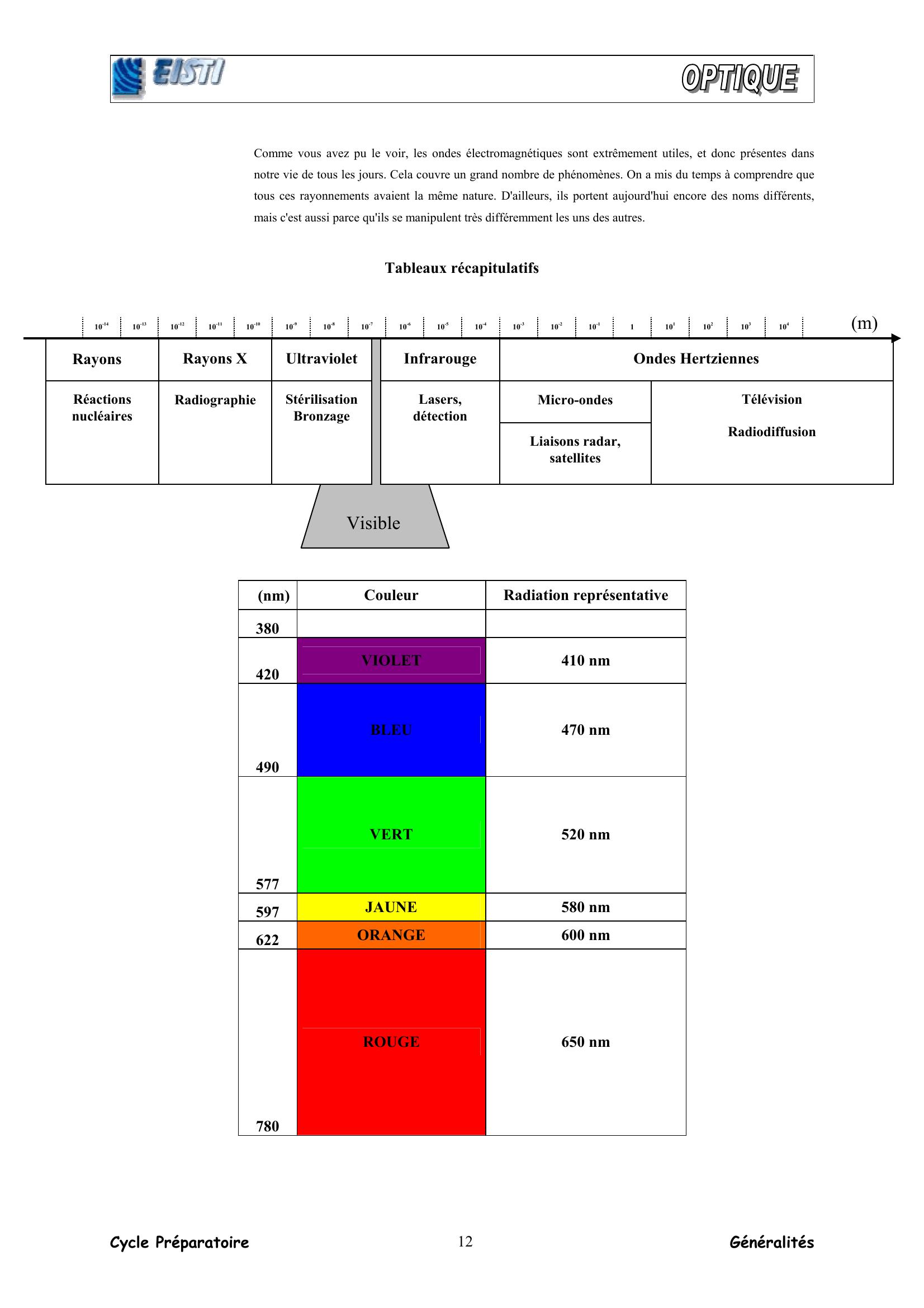
Page 11 : Cycle Préparatoire Généralités 11f Spectre électromagnétique de la lumière Ondes radio, micro-ondes, rayons X, infra-rouge, lumière, tout ces noms désignent en fait le même phénomène : Les ondes électromagnétiques. Un champ électromagnétique nous entoure en permanence, de la même manière que l'air nous entoure. Et les ondes électromagnétiques sont des perturbations du champ électromagnétique, comme le son est une perturbation de la pression de l'air. Ces perturbations - en un mot, ces ondes - se déplacent à la vitesse de la lumière, soit environ 300 000 kilomètres par seconde. Les ondes électromagnétiques, comme n'importe quelle onde, sont caractérisées par leur longueur d'onde, et leur fréquence. La lumière visible n'est qu'un cas particulier d'onde électromagnétique. Il en existe bien d'autre types, mais on ne les appelle pas "lumière", même si c'en est. Chaque type de rayonnement est caractérisé par une gamme de fréquence. Ici sont présentés tous les rayonnements électromagnétique, en partant de ceux qui ont les plus faibles fréquences : c'est ce qu'on appelle le spectre électromagnétique. Les plus basses fréquences sont les ondes radio. Sur terre, elles sont produites par les antennes : les mouvements des électrons dans les antennes produisent ces ondes radio. Les antennes de toits font l'inverse : les ondes produisent des mouvements d'électrons, c'est à dire du courant électrique, dans les antennes réceptrices. C'est ce courant qui est amplifié et transmis aux postes de radio ou de télévision, qui les transforme en son ou en image. Les micro-ondes ont une fréquence un peu plus élevée. Les fours micro-ondes utilisent une fréquence très particulière, pour chauffer les aliments en fait, il s'agit d'une fréquence qui fait vibrer les molécules d'eau, donc qui les chauffe. Les téléphones portables ont souvent tendance à utiliser des fréquences proches, ce qui a provoqué certaines inquiétudes. Mais un téléphone a une puissance mille fois plus petite qu'un four. A des fréquences encore un peu plus élevée, on trouve les infra-rouges. Ils sont situés, comme leur nom l'indique, juste sous la couleur rouge dans le domaine des fréquences. Ils sont surtout émis par les objets chauds comme notre corps, par exemple. Puis on trouve la lumière visible : les rayonnements de plus basse fréquence sont rouges. Ceux de plus haute fréquence sont bleus et violets. On peut manipuler cette lumière grâce à des instruments d'optique : lentilles, prismes, etc. C'est bien parce que cette lumière est facile à manipuler, que nous pouvons la voir. L'œil est juste un instrument d'optique perfectionné. Il ne saisit donc qu'une gamme réduite du spectre électromagnétique. La lumière visible commence à transporter pas mal d'énergie, car sa fréquence est assez grande. D'ailleurs, les plantes utilisent cette lumière pour en tirer leur énergie. Au delà du violet, on trouve les ultra-violets, à des fréquences plus élevées. On ne les voit pas, mais on peut sentir leurs effets coups de soleil.... C'est aussi la lumière noire. Au dessus encore, les fréquences sont importantes, et cela signifie que la lumière transporte beaucoup d'énergie. Tellement, que cela peut provoquer des brûlures, ou des dégâts. De plus, une onde électromagnétique de haute fréquence est capable de traverser la matière. Cela peut être utile, mais cela signifie aussi que si elle fait des dégâts, ils sont internes. Les ultra-violet sont déjà dangereux, car ils ne sont pas arrêtés par les couches superficielles de la peau, comme la lumière visible. Il y a plus énergétique encore : les rayons X, par exemple. Ils sont dangereux à haute dose, mais tellement pratiques ! En fait, ils traversent sans problème le corps, mais pas complètement. Ils traversent moins bien les os - on les utilise donc en radiographie. Enfin, les plus énergétiques de tous sont les rayons gamma. C'est aussi de la lumière, mais tellement énergétique qu'ils sont très dangereux - ils peuvent causer de graves dégâts aux êtres vivants. Par contre, et ça peut être un problème, rien ne les arrête, ou presque : ils sont capables de traverser un coffre fort ! Du coup, cela signifie aussi que, bien que dangereux, ils ont plutôt tendance à traverser le corps humain qu'à s'y arrêter. Ils sont essentiellement produits par les réactions nucléaires.
Page 12 : Cycle Préparatoire Généralités 12Comme vous avez pu le voir, les ondes électromagnétiques sont extrêmement utiles, et donc présentes dans notre vie de tous les jours. Cela couvre un grand nombre de phénomènes. On a mis du temps à comprendre que tous ces rayonnements avaient la même nature. D'ailleurs, ils portent aujourd'hui encore des noms différents, mais c'est aussi parce qu'ils se manipulent très différemment les uns des autres. Tableaux récapitulatifs λλλλ nmCouleur Radiation représentative 380 420 VIOLET 410 nm 490 BLEU 470 nm 577 VERT 520 nm 597 JAUNE 580 nm 622 ORANGE 600 nm 780 ROUGE 650 nm 10-1410-1310-12 10-1110-1010-910-810-710-610-510-410-310-210-11101102103104λmOndes Hertziennes Télévision Radiodiffusion Infrarouge UltravioletRayons X Rayons γγγγ Micro-ondes Lasers, détection StérilisationBronzage Réactions nucléaires RadiographieVisibleLiaisons radar, satellites
Page 13 : Cycle Préparatoire Généralités 132.3 Propagation de la lumière dans les milieux matériels transparents La célérité de la lumière dépend donc de la nature du milieu de propagation et de la fréquence de l'onde. Les hypothèses sur l'onde lumineuse et le milieu où elle se propage sont les suivantes : • Le milieu est linéaire, homogène, isotrope et transparent. • L'onde qui se propage est une onde plane Pour donner corps à ces termes, un bon verre optique est : • Homogène s'il ne contient pas de bulles de gaz emprisonnées ou si son indice optique ne varie pas localement • Isotrope s'il n'est pas biréfringent il n'y a pas de phénomène de double réfraction, c'est à dire que l'on obtient une seule image du même objet • Transparent s'il n'est pas fortement dispersif Concernant la propagation dans un milieu transparent : • Si l'onde est monochromatique, on redéfinira ses paramètres sauf la fréquence • Si l'onde est polychromatique, on observera le caractère dispersif du milieu Dans la suite, selon l'usage, les milieux seront qualifiés de transparents pour résumer leurs propriétés précitées. 2.3.1 Propagation d'une onde lumineuse monochromatique dans un milieu transparent On appelle indice de réfraction n d'un milieu le rapport de la célérité c d'une onde lumineuse monochromatique dans le vide à sa célérité v dans le milieu considéré. On a donc : vcn = ou encore ncv =
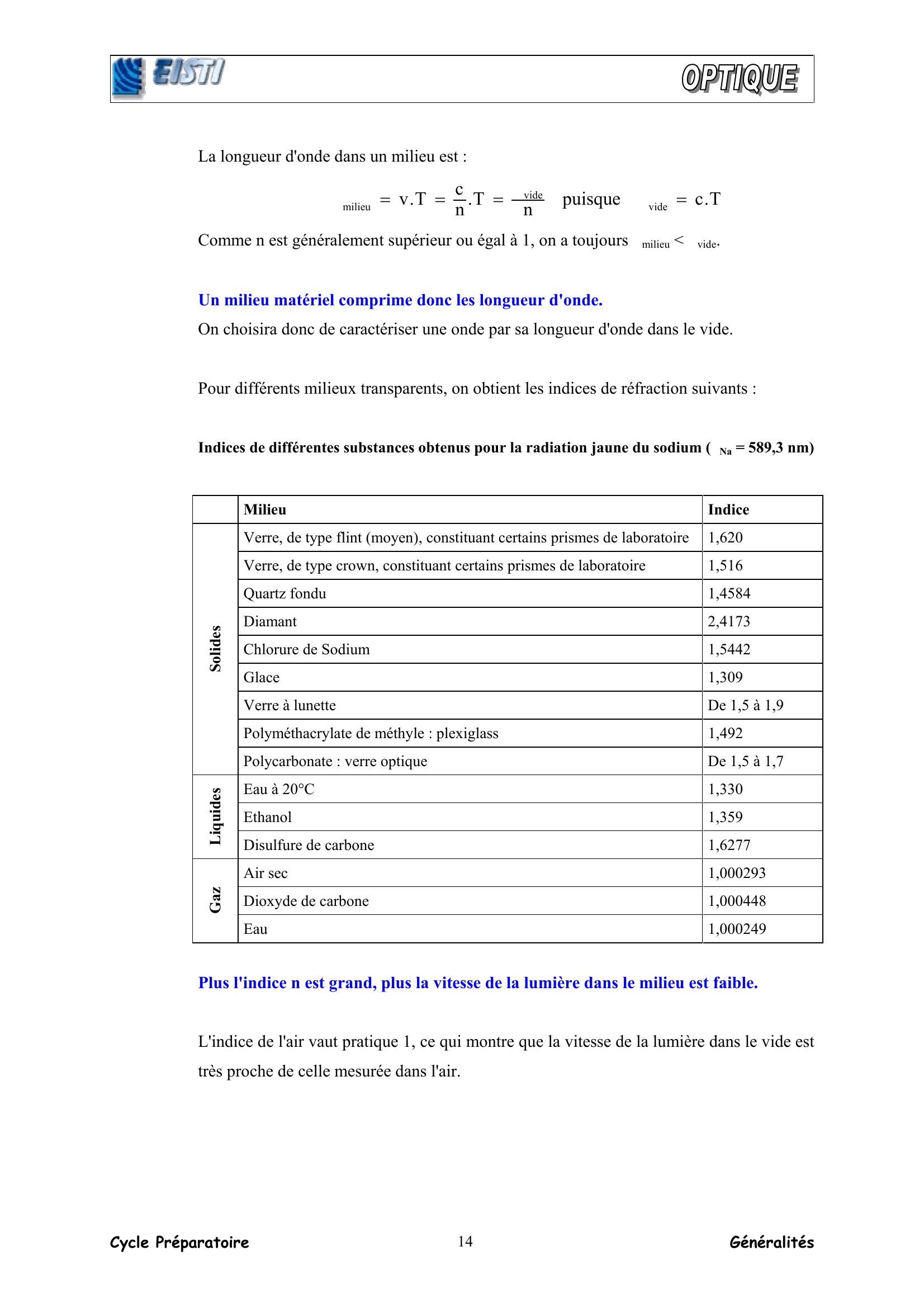
Page 14 : Cycle Préparatoire Généralités 14La longueur d'onde dans un milieu est : T.cpuisquenT.ncT.vvidevidemilieu=λλ===λ Comme n est généralement supérieur ou égal à 1, on a toujours λmilieu λvide. Un milieu matériel comprime donc les longueur d'onde. On choisira donc de caractériser une onde par sa longueur d'onde dans le vide. Pour différents milieux transparents, on obtient les indices de réfraction suivants : Indices de différentes substances obtenus pour la radiation jaune du sodium λλλλNa = 589,3 nm Milieu Indice Verre, de type flint moyen, constituant certains prismes de laboratoire 1,620 Verre, de type crown, constituant certains prismes de laboratoire 1,516 Quartz fondu 1,4584 Diamant 2,4173 Chlorure de Sodium 1,5442 Glace 1,309 Verre à lunette De 1,5 à 1,9 Polyméthacrylate de méthyle : plexiglass 1,492 Solides Polycarbonate : verre optique De 1,5 à 1,7 Eau à 20°C 1,330 Ethanol 1,359 Liquides Disulfure de carbone 1,6277 Air sec 1,000293 Dioxyde de carbone 1,000448 Gaz Eau 1,000249 Plus l'indice n est grand, plus la vitesse de la lumière dans le milieu est faible. L'indice de l'air vaut pratique 1, ce qui montre que la vitesse de la lumière dans le vide est très proche de celle mesurée dans l'air.
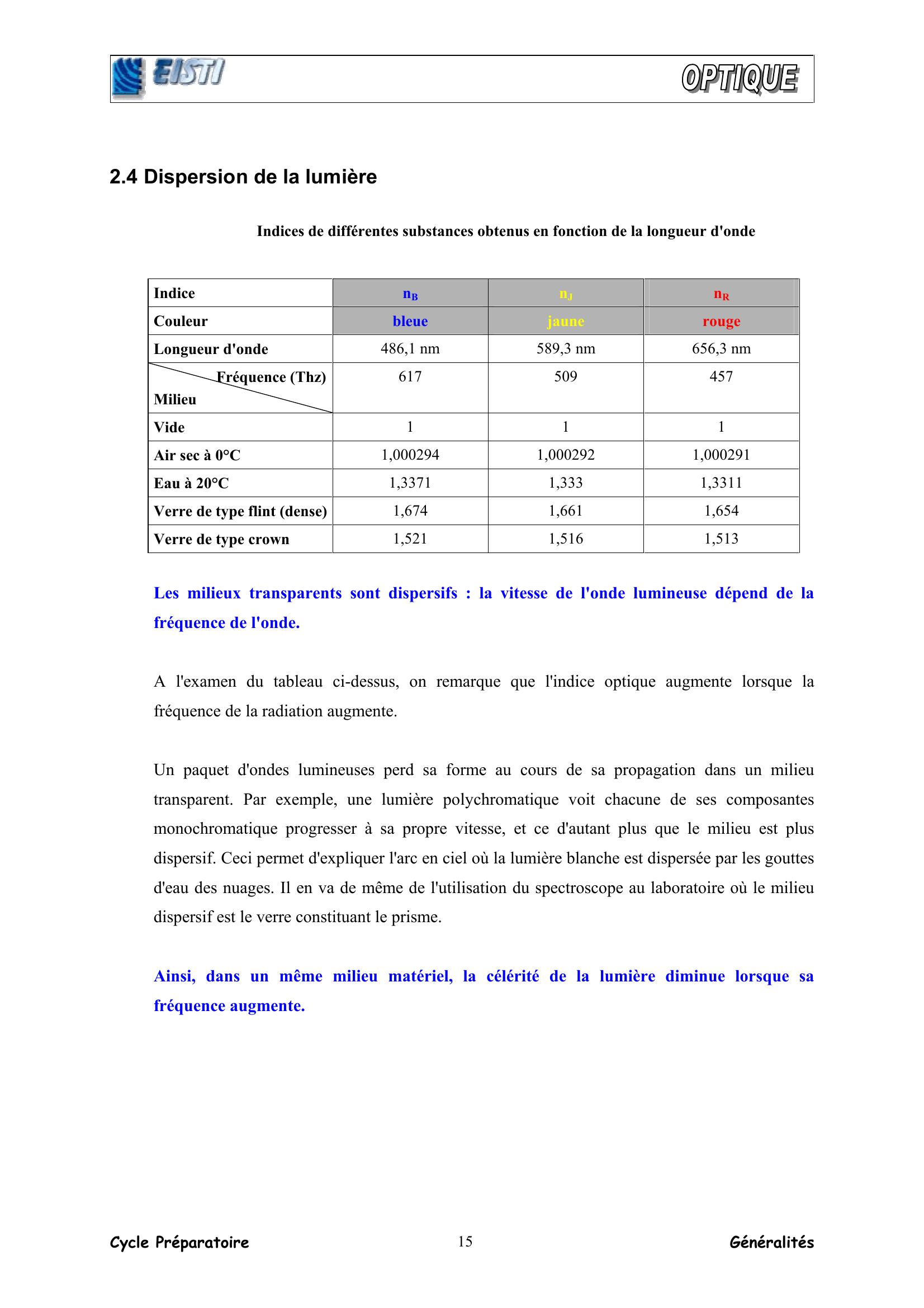
Page 15 : Cycle Préparatoire Généralités 152.4 Dispersion de la lumière Indices de différentes substances obtenus en fonction de la longueur d'onde Indice nB nJ nR Couleur bleue jaune rouge Longueur d'onde 486,1 nm 589,3 nm 656,3 nm Fréquence ThzMilieu 617 509 457 Vide 1 1 1 Air sec à 0°C 1,000294 1,000292 1,000291 Eau à 20°C 1,3371 1,333 1,3311 Verre de type flint dense1,674 1,661 1,654 Verre de type crown 1,521 1,516 1,513 Les milieux transparents sont dispersifs : la vitesse de l'onde lumineuse dépend de la fréquence de l'onde. A l'examen du tableau ci-dessus, on remarque que l'indice optique augmente lorsque la fréquence de la radiation augmente. Un paquet d'ondes lumineuses perd sa forme au cours de sa propagation dans un milieu transparent. Par exemple, une lumière polychromatique voit chacune de ses composantes monochromatique progresser à sa propre vitesse, et ce d'autant plus que le milieu est plus dispersif. Ceci permet d'expliquer l'arc en ciel où la lumière blanche est dispersée par les gouttes d'eau des nuages. Il en va de même de l'utilisation du spectroscope au laboratoire où le milieu dispersif est le verre constituant le prisme. Ainsi, dans un même milieu matériel, la célérité de la lumière diminue lorsque sa fréquence augmente.
Page 16 : Cycle Préparatoire Généralités 162.4.1 Loi de CAUCHY Pour les verres d'optique, dans le visible, Cauchy a établi la relation nl suivante : 2BAnλ+=λ, où A et B sont des constantes positives L'indice d'un verre optique est d'autant plus faible que la longueur d'onde est grande. 2.4.2 Nombre d'Abbe Cette question de la dispersion est particulièrement importante pour les verres de vue et les verres utilisés dans les laboratoires. Aussi, un critère numérique est associé à une matière transparente afin de savoir si elle est fortement dispersive ou pas ; c'est le nombre d'Abbe η défini comme suit : CFDnn1n=η où nD, nF et nC sont les notations conventionnelles des indices de la substance pour les longueurs d'onde suivantes : λD = λJ = 589,3 nm pour la radiation jaune λF = λB = 486,1 nm pour la radiation bleue, λC = λR = 656,3 nm pour la radiation rouge. Nombre d'Abbe de différentes substances Milieu Nombre d'Abbe Verre, de type flint 33 Verre, de type crown 64 Verre à lunette indice 1,523 59 Verre à lunette indice 1,8 35 Polycarbonate : verre optique organique 32 Eau à 20°C 55 Air sec à 0°C 97 Le nombre d'Abbe caractérise le pouvoir dispersif d'une substance; plus ce nombre est élevé, moins le milieu est dispersif.
Page 17 : Cycle Préparatoire Généralités 17On remarque que l'air et l'eau sont des milieux peu dispersifs; nous pouvons donc négliger la dispersion dans ces milieux lorsque la lumière les traverse. La forte dispersion du verre flint fait qu'on les utilise dans le verre cristal qui, de ce fait, a un bel éclat.
Page 18 : Cycle Préparatoire Généralités 183. Ce qu'il faut retenir La lumière dans le vide La célérité des ondes électromagnétiques est une constante universelle : c = 299 792 458 m/s. Une onde lumineuse progressive monochromatique ayant une direction de propagation privilégiée ou onde plane progressive monochromatique est: • Transversale • De période temporelle ν= 1T égale à celle de la source lumineuse • De période spatiale, ou de longueur d'onde λ = c.T La célérité de la lumière est indépendante de la fréquence de l'onde Le domaine des radiations visibles par l'œil est compris entre les longueurs d'onde 400 nm et 800 nm, respectivement de fréquence 750 THz à 375 THz La lumière dans les milieux transparents La fréquence de la radiation est la même que dans le vide et elle est indépendante du milieu de propagation L'onde lumineuse se propage à une vitesse v plus faible que dans le vide La longueur d'onde s'écrit λ = v.T Pour une radiation monochromatique, l'indice de réfraction du milieu est vcn = nvidemilieuλ=λ ; un milieu matériel comprime les longueurs d'onde l'indice de réfraction de l'air est quasiment égal à 1 Dans les milieux dits dispersifs, la vitesse de l'onde dépend de la fréquence de l'onde. L'indice du milieu dépend alors de la longueur d'onde Les verres optiques sont dispersifs et vérifient la loi de Cauchy Le nombre d'Abbe caractérise la dispersion d'une substance