Cours 02 Opitique Geometrique
Télécharger le Cours 02 Opitique Geometrique en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Page 1 : Cycle Préparatoire Optique géométrique 21 OPTIQUE GEOMETRIQUE L'Optique Géométrique repose sur la notion du rayon lumineux. Notation pour le cours qui suit : MHTI : Milieu Homogène, Transparent il n'existe pas d'absorption et Isotrope.
Page 2 : Cycle Préparatoire Optique géométrique 221. Propagation rectiligne dans un MHTI et Rayon lumineux 1.1 Expérience préliminaire Dans une salle obscure, on observe le mince pinceau, de couleur rouge émit par un laser à gaz par exemple. La présence de poussière en suspension dans la salle permet de visualiser le trajet suivi par le rayonnement On constate que le pinceau lumineux se propage de manière rectiligne. 1.2 Hypothèse fondamentale de l'Optique Géométrique On peut reproduire l'expérience précédente en changeant de source de lumière ou de milieu, on aboutit toujours au même résultat. La lumière se propage rectilignement dans un MHTI écran Laserdiaphragme peu lumineux tache centrale
Page 3 : Cycle Préparatoire Optique géométrique 231.3 Approximation de l'Optique Géométrique Question : Peut on isoler un rayon lumineux ? On place devant le rayonnement directif d'un laser, un diaphragme à ouverture circulaire de rayon r réglable. Pour une valeur de r, supérieure au mm, la propagation rectiligne du pinceau lumineux est bien vérifiée; il existe une tache lumineuse de petite dimension, d'éclairement pratiquement uniforme sur l'écran. On diminue r progressivement. Lorsque r devient inférieur à quelques µm, la lumière se répartit essentiellement et de manière non uniforme sur un disque tache lumineuse centrale dont le rayon est supérieur à celui du diaphragme. On vient de mettre en évidence le phénomène de diffraction de la lumière, qui représente un écart à la loi de propagation rectiligne en MHTI et qui se manifeste quand la dimension de l'ouverture du diaphragme est comparable à la longueur d'onde du rayonnement. La loi de propagation rectiligne est une loi limite dans le cas de longueur d'ondes faibles devant les dimensions des diaphragmes limitant les faisceaux lumineux des systèmes optiques. 1.4 Notion de rayon lumineux Nous nous placerons dans des conditions où la lumière se propage en ligne droite comme le ferait un ensemble de particules matérielles les photons libres. Les trajectoires de ces particules constituent les rayons lumineux. La notion de rayon lumineux est illustrée par un pinceau lumineux cylindrique obtenu avec un petit diaphragme mais r λλλλ. Par conséquent, le rayon lumineux caractérise le transport "rectiligne" de l'énergie lumineuse dans un MHTI.
Page 4 : Cycle Préparatoire Optique géométrique 241.5 Interprétation de l'hypothèse fondamentale de l'Optique Géométrique 1.5.1 Définition du chemin optique Dans un milieu où l'indice n varie continûment cas le plus général, le chemin optique AB est défini par : =CdnABl dℓ : trajet géométrique élémentaire sur la courbe C entre A et B Il en résulte que : • Pour un MHTI : AB = n.ℓ avec ℓ : chemin géométrique parcouru par la lumière entre A et B • Pour une succession de MHTI : AB = iiin l 1.5.2 Sens physique Sachant que : vcn = ABBABA.cdtcdvcABτ===l Ainsi, le chemin optique représente la distance que franchit la lumière dans le vide milieu de référence, dans le même temps ττττAB qu'elle met à parcourir AB dans un milieu quelconque. A M M' nMdℓ CB
Page 5 : Cycle Préparatoire Optique géométrique 251.5.3 Propagation rectiligne dans un MHTI Dans un MHTI, la lumière décrit un segment de droite AB, ce qui se traduit par : AB = n.AB cABAB =τ minimal Donc, le chemin effectivement suivi par la lumière, dans un MHTI, correspond au trajet minimal cette propriété est connue sous le nom de Principe de Fermat. A nB
Page 6 : Cycle Préparatoire Optique géométrique 262. Loi de la réflexion : 1ière loi de Descartes 2.1 Mise en évidence expérimentale On dispose un miroir plan M au centre d'un disque gradué. A l'aide d'une source délivrant un mince pinceau lumineux laser par exemple, on éclaire M suivant SI. On repère le rayon "lumineux" IR au moyen du disque gradué. En faisant tourner le miroir autour de I variation de l'angle d'incidence "i", on constate que le rayon réfléchi IR reste toujours symétrique du rayon incident SI, par rapport à la normale IN. De plus on vérifie que SI, IN et IR sont coplanaires. 2.2 Enoncé Soit un rayon lumineux, issu de S, parvenant au point I d'un miroir plan parfaitement réfléchissant. SourceI S i' i N R miroir mobile disque gradué miroir plan i' i I R N S
Page 7 : Cycle Préparatoire Optique géométrique 27La direction du rayon réfléchi IR est donnée par la première loi de Descartes : • Le rayon IR appartient au plan d'incidence, défini par le rayon incident SI et la normale IN au miroir • L'angle de réflexion est égal à l'angle d'incidence : i' = i Remarques : Dans le cas d'une surface réfléchissante non plane, nous pouvons appliquer la loi de Descartes en considérant le plan tangent au point de contact I qui se comporte comme un miroir plan. La première loi de Descartes s'exprime également par la relation vectorielle : Nkuu12rrr+= k : constante avec 1ur , 2ur et N , unitaires suivant SI, IR et IN En effet, T.NkuT.u12rrrrr+= Tr vecteur unitaire du miroir plan conduit à : sini' = sini d'où i' = i miroir plan i' i I R N S 1ur2urTrNr
Page 8 : Cycle Préparatoire Optique géométrique 282.3 Justification L'œil d'un observateur, en B, regarde une source fixe ponctuelle A, à travers un miroir plan. 1. A l'aide de la notion de trajet minimal de la lumière, déterminer graphiquement le point I où le rayon lumineux issu de A atteint le miroir et se réfléchit suivant IB. 2. En déduire la relation entre les angles d'incidence et de réflexion. Le chemin optique AB = AI + IB = n.AI + IB du trajet effectivement suivi par la lumière doit être minimal. En introduisant le point A', symétrique de A par rapport au miroir, nous devons obtenir : AI + IB = A'I + IB : minimal, ce qui se traduit dans le cas "A'IB : segment de droite". Par conséquent, le point I cherché correspond à l'intersection de A'B avec le miroir plan. Par raison de symétrie, on retrouve l'égalité entre i et i'. oeil I B A miroir n source fixe A' oeil I B A miroir n i i i' i' N
Page 9 : Cycle Préparatoire Optique géométrique 292.4 Conséquences 2.4.1 Loi du retour inverse de la lumière Le trajet SIR, suivi par la lumière, est indépendant du sens de parcours les rayons SI et IR étant symétriques par rapport à la normale IN 2.4.2 Notions d'objet réel et d'image virtuelle Soit un rayon incident, issu d'un point objet "réel" A et parvenant au point I d'un miroir plan M. Le rayon réfléchi IR semble provenir du point A' symétrique de A par rapport à M; A' représente l'image dite "virtuelle" de A, à travers le miroir plan. 2.4.3 Rotation d'un miroir plan Lorsqu'un miroir plan M tourne d'un angle α, le rayon réfléchi IR, associé au rayon incident SI, est dévié de 2 α. IR est symétrique de IS par rapport à la normale IN qui vient de tourner de l'angle α I B A M A'N M0 M αααα 2α2α2α2α S R I règle graduée
Page 10 : Cycle Préparatoire Optique géométrique 30Cette propriété est employée dans certains appareils de mesure, pour mesurer l'angle de rotation α d'un système mécanique mobile autour d'un axe fixe. Dans cette méthode dite "de Poggendorf", un miroir M, solidaire du système mécanique tournant, réfléchit le rayon lumineux émis par une source S. La position du spot R, sur une règle graduée distante de D du point I, permet d'évaluer α : Dx2tan=α
Page 11 : Cycle Préparatoire Optique géométrique 313. Loi de la réfraction : 2ième loi de Descartes 3.1 Aspect expérimental Une source monochromatique S éclaire un demi-cylindre en verre d'indice n de l'ordre de 1,5, disposé au centre d'un disque gradué. Suivant la position du demi-cylindre, on peut observer : • soit un changement de direction du rayon incident SI à la surface de séparation air-verre, c'est à dire une "réfraction" de ce rayon lumineux • soit une réflexion du rayon incident, passage verre air, pour i1 θ, avec θ, angle limite de l'ordre de 42° 3.2 Enoncé Un dioptre plan désigne une surface plane séparant deux MHTI d'indices différents n1 et n2. N i1 I N i1 I i2 Source S disque gradué
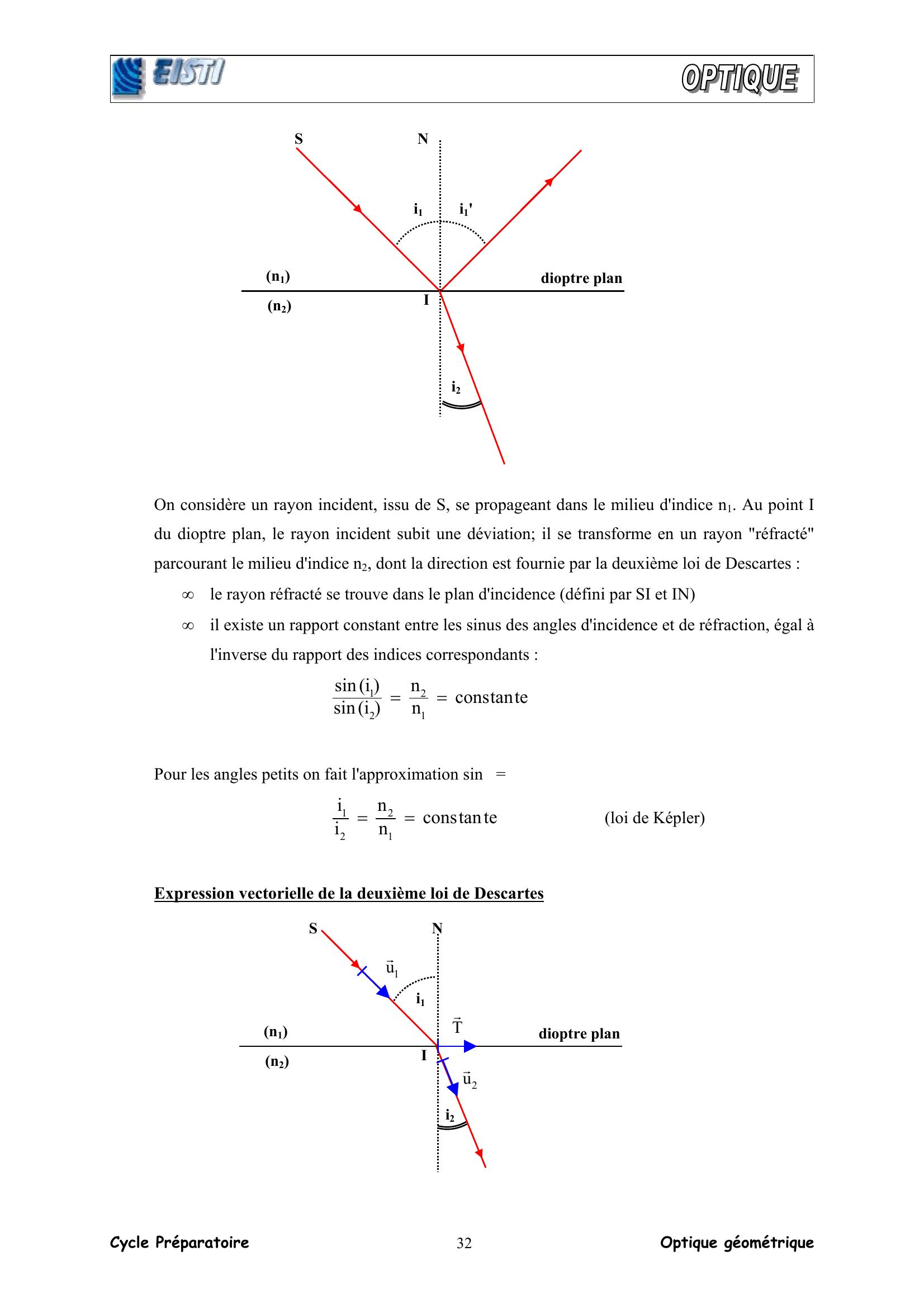
Page 12 : Cycle Préparatoire Optique géométrique 32 On considère un rayon incident, issu de S, se propageant dans le milieu d'indice n1. Au point I du dioptre plan, le rayon incident subit une déviation; il se transforme en un rayon "réfracté" parcourant le milieu d'indice n2, dont la direction est fournie par la deuxième loi de Descartes : • le rayon réfracté se trouve dans le plan d'incidence défini par SI et IN • il existe un rapport constant entre les sinus des angles d'incidence et de réfraction, égal à l'inverse du rapport des indices correspondants : tetanconsnnisinisin1221== Pour les angles petits on fait l'approximation sinθ = θ tetanconsnnii1221== loi de Képler Expression vectorielle de la deuxième loi de Descartes i1' i1 I N S i2 n1 dioptre plan n2 i1 I N S i2 n1 dioptre plan n2 1ur2urTr
Page 13 : Cycle Préparatoire Optique géométrique 33La relation n1.sini1 = n2.sini2 se met sous la forme : T.u.nT.u.n2211rr= avec 1ur , 2ur et T , unitaires C'est à dire : 0T.u.nu.n2211=rr quel que soit Tr sur le dioptre plan Il en résulte que : N.ku.nu.n2211=rr k étant une constante et N le vecteur unitaire normal au dioptre plan. Remarque Si le dioptre n'est pas plan, on doit faire intervenir le plan tangent au point I. 3.3 Construction de Huygens et interprétation 3.3.1 Construction de Huygens La construction de Huygens nous permet de déterminer la direction du rayon réfracté sans employer de rapporteur. Après avoir tracé deux demi-cercles concentriques de centre I et de rayon n1 et n2, nous repérons l'intersection M1 du rayon incident avec C1. Etant donné que n1.sini1 = n2.sini2 = IH, IM2 indique la direction du rayon réfracté M1M2 parallèle à IN. n2 n1 i1 n2 i2 C2 C1 S N H M1 M2 I n1 n2
Page 14 : Cycle Préparatoire Optique géométrique 343.3.2 Interprétation Le phénomène de réfraction résulte du fait que la lumière se propage à des vitesses différentes dans les deux milieux considérés : 2121vvisinisin= Principe d'Huygens avec 2112vvnn= Le changement de direction du rayon lumineux correspond à un chemin optique et à une durée du trajet minimal, entre deux points donnés A et B des milieux n1 et n2. 3.4 Conséquences : réfraction limite – réflexion totale 3.4.1 Préliminaires Comme pour le miroir plan, la loi du retour inverse de la lumière est valable; la deuxième loi de Descartes étant symétrique, relativement aux indices 1 et 2, il suffit d'inverser ces indices pour le vérifier. Si n2 n1, le milieu 2 est dit "plus réfringent" que le milieu 1, sinon il est "moins réfringent". Puisque isin.nnisin1212 =, le milieu 2 supposé plus réfringent, rapproche le rayon lumineux de la normale i2 i1. i1 I N S i2 I n1 n2 n2 n1
Page 15 : Cycle Préparatoire Optique géométrique 353.4.2 Passage d'un MHTI 1 vers un MHTI 2 plus réfringent : réfraction limite Par hypothèse, n2 n1 ; Le tableau de variation de i1 et i2, associé à isin.nnisin1212 =, se présente ainsi : i1 0 2π i2 21m2nnarcsini= 0 En conclusion, lors d'un passage d'un milieu d'indice 1 vers un milieu d'indice 2 plus réfringent, les rayons réfractés sont tous situés à l'intérieur d'une cône de réfraction, de demi-angle au sommet : l'angle i2m, appelé angle de réfraction limite et égal à : 21m2nnarcsini= 3.4.2 Passage d'un MHTI 1 vers un MHTI 2 moins réfringent : réflexion totale D'après le principe du retour inverse de la lumière, nous pouvons effectuer une permutation des indices 1 et 2 du tableau précédent : i1 0 12m1nnarcsini=θ= i2 2π 0 n2 n1i2m n1 I
Page 16 : Cycle Préparatoire Optique géométrique 36Il en résulte que le passage d'un milieu d'indice 1 vers un milieu d'indice 2 moins réfringent se manifeste par une réflexion totale du rayon incident sur le dioptre plan dans le cas où : 121nnarcsini=θ Prismes à réflexion totale Ils sont placés dans certains systèmes optiques afin de provoquer une déviation de 2π ou de π d'un rayon lumineux ; leur indice n doit satisfaire à : n1arcsin4iπ= réflexion totale : substance du prisme verre par exemple air, ce qui conduit à : n121 c'est à dire : 414,12n= I ππππ/4ππππ/4ππππ/4n1 i1 = θθθθ n2 n1N1 I S ππππ/4
Page 17 : Cycle Préparatoire Optique géométrique 37Guides de lumière Le phénomène de conduction de la lumière peut se produire dans des dispositifs variés, à l'aide d'une réflexion totale sur les parois. Quelques guides de lumière : • une veine de liquide coloré fontaine lumineuse • un tube en matière souple permettant d'observer et de photographier des cavités humaines peu accessibles bronches … : principe de l'endoscopie • les fibres optiques dont l'emploi se généralise dans le domaine des télécommunication notamment
Page 18 : Cycle Préparatoire Optique géométrique 384. Application des lois de Descartes : Prisme 4.1 Définitions • Le prisme est un MHTI limité par deux dioptres plans non parallèles. • L'angle du dièdre, noté A, est appelé angle du prisme 60° en général • Le prisme possède un plan de symétrie passant par l'arête du prisme triangle O1,O,O2 isocèle. • En pratique, le matériau utilisé est le verre dont l'indice varie entre 1,5 et 1,8 suivant la longueur de l'onde lumineuse 4.2 Ondes monochromatiques, étude de la déviation 4.2.1 Marche d'un rayon – Lois du prisme Soit un rayon incident parvenant sur le prisme d'indice n et d'angle A au point I. On constate que le rayon émergent est toujours dévié vars la base du prisme La déviation entre le rayon incident et le rayon émergent est notée D A O nO1O2Plan de symétrie
Page 19 : Cycle Préparatoire Optique géométrique 39 On va établir les relations entre les différents paramètres n, i, A, r, r', i' et D : • Loi de Descartes le milieu extérieur est l'air d'indice 1 sini = n.sini' 1 sini' = n.sinr' 2 • On écrit que la somme des angles est égale à π dans les triangles IJI' et IKI' les normales IN et I'N' se coupent en K : r + r' + π – A = π triangle IKI' 3 i – r + i' – r' + π – D = π triangle IJI' 4 d'où r + r' = A 5 D = i + i' – A • Dans le cas de petits angles, les relations 1, 2 et 4 se transforment en : i = n.r i' = n.r' et D = n – 1.A Conditions sur l'angle A du prisme pour qu'il y ait émergence du rayon : On rappelle que r' ilim ; la relation 5 nous indique que la plus petite valeur de r' correspond à la plus grande valeur de r, soit l'angle limite ilim. On a donc aussi A – ilim r'. La double inégalité A – ilim r' ilim nous montre qu'il ne peut y avoir émergence que si A 2ilim. 4.2.2 Etude de la déviation en lumière monochromatique Préliminaires La déviation D d'un rayon lumineux par un prisme dépend de trois paramètres : 1. l'angle d'incidence i 2. l'angle du prisme A 3. l'indice du prisme n N' N i' D I' A J I r' i r A K S n
Page 20 : Cycle Préparatoire Optique géométrique 40Donc, D = fi, A, n La variation de D avec A présente peu d'intérêt; l'angle A d'un prisme est, en général, fixé à 60°. Influence de l'angle d'incidence Par hypothèse, A et n sont fixés tandis que i est variable; exprimons n,AdiDd La différentiation des lois du prisme conduit à : drrcosndiicos= 'dr'rcosn'di'icos= dr + dr' = 0 dD = di + di' D'où rcosndiicos'icos'rcosndi'dr'icos'rcosndidDdr=+= Nous aboutissons à : rcosicos'icos'rcos1diDdn,A= On étudie à présent, le sens de variation de D avec i. Supposons : 0diDdn,A Ce qui se traduit par : icos.'rcosrcos.'icos C'est à dire : icos.'rcosrcos.'icos2222 En tenant compte des lois de Descartes, il vient : rsinn1.'rsin1rsin1.'rsinn1isin2222'isin22224342143421
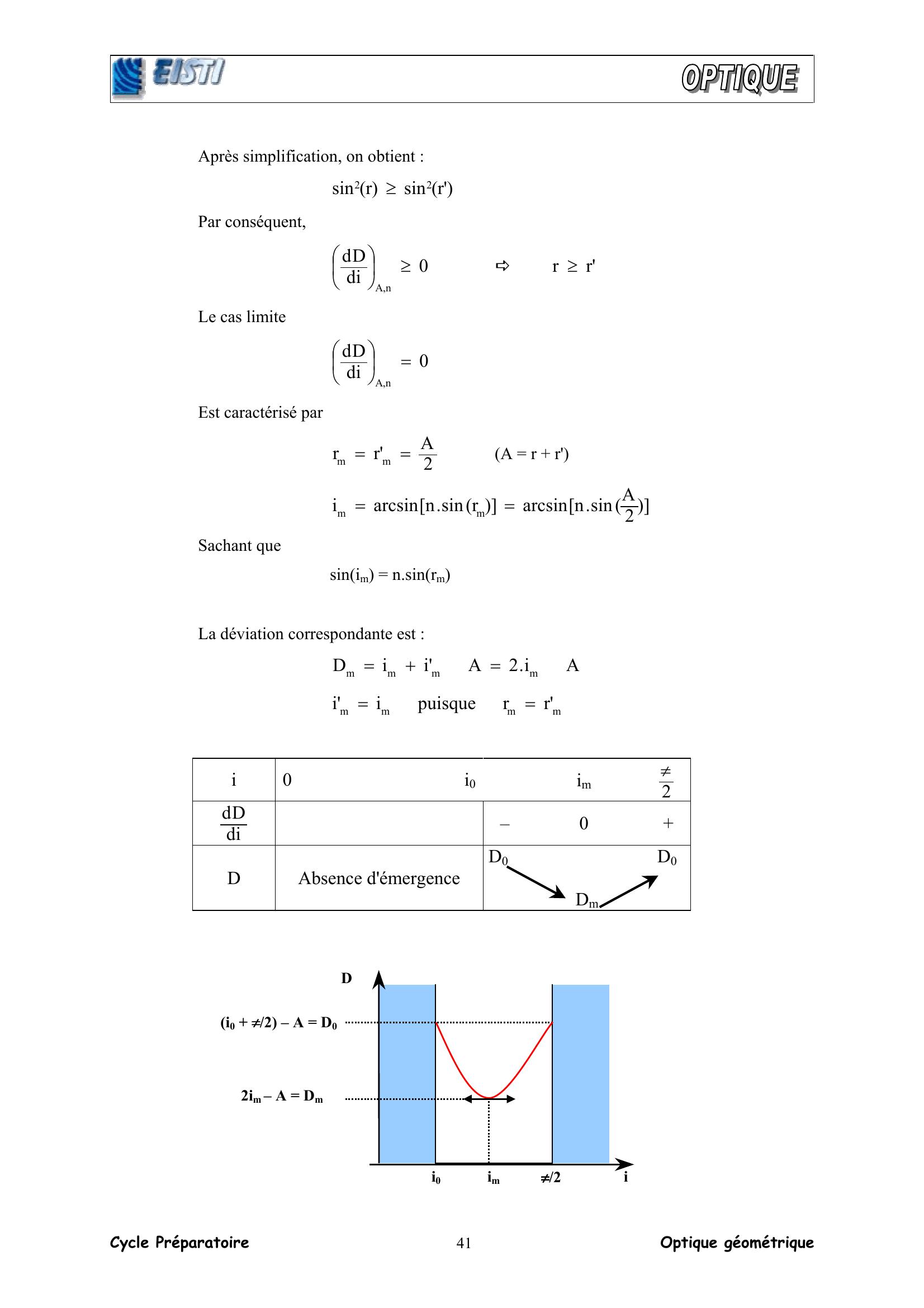
Page 21 : Cycle Préparatoire Optique géométrique 41Après simplification, on obtient : 'rsinrsin22 Par conséquent, 0diDdn,A 'rr Le cas limite 0diDdn,A= Est caractérisé par 2A'rrmm== A = r + r' 2Asin.narcsinrsin.narcsinimm== Sachant que sinim = n.sinrm La déviation correspondante est : Ai.2A'iiDmmmm=+= mmmm'rrpuisquei'i== i 0 i0 im 2π diDd – 0 + D Absence d'émergence D0 D0 Dm i0 + ππππ/2 – A = D0ππππ/2 im i0 i 2im – A = Dm D
Page 22 : Cycle Préparatoire Optique géométrique 42 En conclusion, la déviation d'un prisme, d'angle A constant, éclairé en lumière monochromatique, est minimale lorsque : 2A'rrmm== 2Asin.narcsin'iimm== Ce qui se manifeste par : • un faisceau émergent symétrique du faisceau incident par rapport au plan de symétrie du prisme • un rayon II' parallèle à la base Dm = 2.im – A et sinim = n.sinrm d'où 2Asin2ADsinnm += Ainsi l'indice nλ du prisme pour une radiation de longueur d'onde λ se déduit des mesures de A et Dm. NA/2I'I N'A/2O1NN'O I'2i0 i0 O2I'1I
Page 23 : Cycle Préparatoire Optique géométrique 434.3 Ondes polychromatiques, étude de la dispersion 4.3.1 Dispersion du rayon incident Considérons un rayon polychromatique lumière blanche parvenant au point I du prisme sous l'incidence i On constate, à la sortie du prisme, que la lumière incidente est décomposée en toutes ses radiations monochromatiques constituant le "spectre" de la lumière blanche. On observe que le rayon incident est d'autant plus élevé que sa longueur d'onde est plus faible. Dviolet Djaune Drouge λλλλv = 0,4 µµµµm λλλλv = 0,56 µµµµm λλλλv = 0,8 µµµµm On peut montrer expérimentalement que l'indice nλ varie avec la longueur d'onde, suivant la loi dite de Cauchy : 221CCnλ+=λ C1 et C2 étant des constantes caractérisant la substance du prisme. N I i nλλλλ lumière blanche violet jaune rouge A
Page 24 : Cycle Préparatoire Optique géométrique 44Par exemple, pour certaines variétés de verre, on a : 20102,0619,1nλ+=λ λ en µm Cette loi expérimentale permet d'interpréter que D est une fonction décroissante de λ. En effet, i étant fixé : λ n r r' = A – r i' nisinrsin= 'rsin.n'isin= Et donc, D = i + i' – A cas général Remarque : Dans le cas de petits angles, nous avons établi que D = n – 1.A; on retrouve que la déviation est, comme n, une fonction décroissante de λ. 4.3.2 Efficacité dispersive du prisme Nous nous intéressons à l'influence de la longueur d'onde sur la déviation par un prisme d'un rayon incident polychromatique, i et A étant fixés. Par définition, i,AdDdλ désigne l'efficacité dispersive du prisme, notée eλ. Etant donné que : D = i + i' – A Il en résulte que : A,iA,id'iddDdeλ=λ=λ En général, le prisme est réglé au minimum de déviation pour une radiation λ du spectre et on étudie la déviation subie par une raie voisine λ + dλ.
Page 25 : Cycle Préparatoire Optique géométrique 45Citons l'exemple du doublet jaune d'une lampe à vapeur de sodium : λ1 = 0,5890 µm λ1 = 0,5896 µm Dans ce cas, on peut exprimer eλ en dérivant directement la relation 2ADsin2Asin.nm += caractérisant le minimum de déviation pour λ1 sinim = n.sinrm. L'incidence reste fixée réglage effectué à im pour λ1. La déviation Dm associée à λ1 devient Dm + dDm pour λ2 = λ1 + d λ; A,immmdDd.2ADcos21dnd.2Asinλ+=λ Ce qui conduit à : λ+=λ=λdnd.2ADcos2Asin2dDdemA,imm
Page 26 : Cycle Préparatoire Optique géométrique 465. Ce qu'il faut retenir Le cadre de l'optique géométrique est celui où la longueur d'onde de la lumière est petite devant les dimensions caractéristiques du système où la lumière se propage. L'optique géométrique repose sur la notion de rayon lumineux. Ces rayons lumineux sont indépendants, se propagent en ligne droite dans un milieu homogène, et suivant au retour le même chemin qu'à l'aller. Dans le cadre de l'optique géométrique, la trajectoire du rayon lumineux est entièrement déterminée par la géométrie du milieu. -------------------------------------------------------------------------------------------- Un dioptre est une surface de séparation entre deux milieux transparents d'indices optiques différents. Un miroir est une surface qui réfléchit pratiquement toute la lumière qu'elle reçoit. -------------------------------------------------------------------------------------------- Lorsqu'un rayon lumineux aborde la surface d'un dioptre ou d'un miroir, il donne généralement naissance à : • un rayon réfléchi • un rayon transmis réfracté dans le cas d'un dioptre • un rayon réfléchi uniquement dans le cas d'un miroir Pour un miroir, • le rayon réfléchi est dans le plan d'incidence • l'angle de réflexion est égal à l'angle d'incidence Pour un dioptre, • le rayon réfracté est dans le plan d'incidence • l'angle de réflexion est égal à l'angle d'incidence • l'angle d'incidence et l'angle réfracté vérifient la relation n1.sini1 = n2.sini2 • Les lois de Képler sont une forme approchée des lois de Snell & Descartes lorsque les angles sont petits -------------------------------------------------------------------------------------------- Pour un prisme d'angle au sommet A, s'il existe un rayon réfracté par la deuxième face, la déviation D, entre le rayon incident sous l'angle i et le rayon transmis sous l'angle i', se met sous la forme : D = i + i' – A Pour les petits angles, on a D = n – 1.A Au minimum de déviation Dm, on a : 2ADsin2Asin.nm +=
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26