Cours 03 Stigmatisme
Télécharger le Cours 03 Stigmatisme en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
Page 1 : Cycle Préparatoire Stigmatisme 47 STIGMATISME FORMATION DES IMAGES PAR UN SYSTEME OPTIQUE
Page 2 : Cycle Préparatoire Stigmatisme 481. Notion d'Image La notion d'image est liée à l'observation visuelle à des fins d'information. Par l'intermédiaire de la lumière, l'œil reçoit sur la rétine des informations qu'il transmet au cerveau sous forme de signaux électriques. A partir d'interactions neurobiologiques complexes, où interfèrent les notions propres à chaque individu, notamment la notion d'apprentissage, le cerveau interprète cette observation comme une image. Il s'agit évidemment d'une image mentale, qui ne ressemble en rien à l'image au sens classique, perçue comme une duplication reconnaissable de ce qui génère l'information lumineuse reçue et que nous appelons habituellement l'objet. Nous pouvons nous convaincre de la nature mentale de l'image en constatant qu'en fermant les yeux, nous continuons à voir cette image mentale, et que d'autres images, comme celles de nos rêves, n'ont pas de support objet palpable. La représentation de la vision qui consiste à comparer l'œil à un appareil photographique, et le cerveau à lecteur d'images rétiniennes passif est donc erroné. Les illusions d'optique en sont l'expression la plus évidente exemple ci dessous. Le cerveau, par l'intermédiaire de l'image mentale nous indique que les deux flèches n'ont pas la même longueur alors que le décimètre nous montre que oui. Nous mettons ici en évidence le fait que la perception visuelle utilise l'interprétation active des données. L'image est le résultat d'une synthèse d'informations multiples réalisée par le cerveau. La vision humaine a ses limites physiques, surtout liées à l'œil : impossible de voir des détails très petits, proches ou lointains par exemple, ce qui fait que nous utilisons des systèmes optiques microscope, lunette qui vont donner de ces détails des images optiques ressemblantes et plus riches d'information qu'en vision directe. Nous retrouvons ici la notion classique d'image optique. Dans la suite, nous ne nous intéresserons qu'à cette image optique que nous nommerons simplement "image". L'image optique, ou image, est la reproduction que donne un système optique d'un objet lumineux.
Page 3 : Cycle Préparatoire Stigmatisme 492. Notion de Point Objet et de Point Image en référence à un système optique 2.1 Système Optique Un système optique S est un ensemble de milieux homogènes et transparents séparés par des dioptres ou par des miroirs. Un système optique est dit : Dioptrique : s'il ne comporte que des dioptres Catoptrique : s'il ne comporte que des miroirs Catadioptrique : s'il comporte des dioptres et au moins un miroir Dans la suite de ce chapitre, sauf indication contraire, le système optique S désignera un système dioptrique. Les milieux d'entrée et de sortie baignant les deux faces sont supposés homogènes de sorte que les rayons lumineux s'y propagent en ligne droite. Les indices des milieux d'entrée et de sortie sont supposés égaux, ce qui est généralement le cas. Convention d'orientation de l'espace Nous choisissons comme sens positif le sens réel de parcours de la lumière figure 2 que nous dirigeons conventionnellement de la gauche vers la droite du dessin. Les angles sont orientés dans le sens trigonométrique. Σe Σs Lumière IncidenteS +Figure 2
Page 4 : Cycle Préparatoire Stigmatisme 502.2 Rayon Incident et Rayon Emergent – Face d'Entrée et Face de Sortie du Système Optique Un rayon incident est un rayon qui se dirige vers S, dans le sens de la propagation de la lumière. Un rayon émergent est un rayon qui s'éloigne de S, dans le sens de propagation de la lumière. Un système optique est limité par une face d'entrée Σe située du côté des rayons incidents et par une face de sortie Σs située du côté des rayons émergents 2.3 Point Objet Réel ou Virtuel – Point Image Réel ou Virtuel Considérons un système optique représenté sommairement par ses deux faces . Le système étant supposé dioptrique, un faisceau lumineux incident pénètre par la face d'entrée et ressort par sa face de sortie. Si le faisceau incident est un cône de sommet A, le point A est un point objet pour le système optique. Deux cas peuvent se présenter, le faisceau conique peut être : Divergent : dans ce cas, le point objet A est dit réel figure 3 Convergent : dans ce cas, le point objet A est dit virtuel figure 4 Le point objet réel émet des rayons lumineux alors que le point objet virtuel n'en émet pas ; il est le point de convergence des rayons Σe Σs S + A Figure 3 Σe Σs S +A Figure 4
Page 5 : Cycle Préparatoire Stigmatisme 51Dans ce dernier cas figure 4, nous comprenons que le faisceau incident ne peut converger en A puisque le système S modifie le parcours de ces rayons dès la face d'entrée. Pour indiquer la virtualité de ce parcours de la lumière dans le système optique S et la virtualité de A, on trace en pointillés le prolongement des rayons incidents dans le système optique S. Le point A est un point OBJET pour le système s'il se trouve à l'intersection de rayons lumineux INCIDENTS sur le système ou à l'intersection de leurs prolongements. Remarque : Le point objet est donc une notion idéale puisque le point source dans la réalité est toujours une étendue spatiale. Cependant, cette notion de source étendue est liée au récepteur qui observe le point source. Ainsi, l'œil peut séparer deux points écartés d'au moins trois minutes d'angle. L'ensemble des points sources vus sous un angle inférieur à 3' sera donc considéré comme un point objet. Si le faisceau émergent est un cône de sommet A', le point A' est un point image pour le système optique. Deux cas peuvent se présenter, le faisceau conique émergent peut être : Divergent : dans ce cas, le point image A' est dit virtuel figure 5 Convergent : dans ce cas, le point image A' est dit réel figure 6 Là aussi, le point A' ne peut en pratique émettre les rayons émergents tracés dans la figure 5 : il s'agit d'un point virtuel. Le point A' est un point IMAGE pour le système s'il se trouve à l'intersection de rayons lumineux EMERGENTS du système ou à l'intersection de leurs prolongements. Σe Σs S +A' Figure 6 Figure 5 Σe Σs S +A'
Page 6 : Cycle Préparatoire Stigmatisme 522.4 Objet et Image Un objet est un ensemble étendu de points objets. Une image est un ensemble étendu de points images. 2.5 Espace Objet – Espace Image Le sens de propagation de la lumière définissant "un avant" et "un après" du système optique, un objet réel est situé avant la face d'entrée du système et une image réelle est située après la face de sortie du système. De même, un objet virtuel est situé après la face d'entrée du système et une image virtuelle est située avant la face de sortie du système. Figure 7 Σe Σs S +Espace Objet Réel Espace Image Réelle Espace Image Virtuelle Espace Objet Virtuel
Page 7 : Cycle Préparatoire Stigmatisme 533. Stigmatisme Rigoureux 3.1 Stigmatisme Rigoureux – Points Conjugués Si nous utilisons ou fabriquons des systèmes optiques, c'est pour obtenir des images ressemblantes aux objets observés ou projetés. Pour étudier le fonctionnement optique de ces systèmes, nous utilisons la notion fondamentale d'image d'un objet lumineux. Ces images se forment habituellement sur une surface écran, négatif photographique, rétine, …. Nous souhaitons de plus que ces images soient nettes, c'est à dire que le système optique donne un point image de tout point objet d'un domaine à trois dimensions Nous introduisons donc pour chaque point objet A une correspondance avec un point image, correspondance réalisée par le système optique S, que l'on peut traduire par l'idéogramme suivant : A S A' A' est par définition l'image de A donnée par S Un système optique S est dit rigoureusement stigmatique pour un point objet A réel ou virtuel et le point A' correspondant réel ou virtuel si tous les rayons incidents passant par A émergent du système optique en passant par le point image A'. En appliquant la loi de retour inverse de la lumière, nous obtenons : A' S A, ce qui montre que A et A' forment un couple de points conjugués pour le système optique S rigoureusement stigmatique. 3.2 Que voit l'œil ? Pour ce qui est de la notion d'image optique classique précédemment définie, l'œil est lui même un système optique. En ce sens, il donne une image de chaque point, objet ou image, qui lui envoie de la lumière. Par contre, la vision de l'image, au sens plus complet défini précédemment, relève de l'œil et du cerveau qui est accoutumé à la propagation rectiligne. Le système visuel perçoit la lumière reçue comme venant en ligne droite : l'image est toujours interprétée comme située au point d'intersection des rayons reçus par l'œil. Ceci est notamment à l'origine de la notion de mirage schématisée en figure 8.
Page 8 : Cycle Préparatoire Stigmatisme 54 Mirage inférieur dans un milieu stratifié. Le parcours de la lumière depuis le point objet A se courbe du côté des indices de l'air chauffé le plus fortement. Le système visuel interprète la lumière reçue comme vérifiant le principe de propagation rectiligne ; il "voit" la lumière reçue comme venant de A', image de A, dans la direction OA' et observe le palmier dans le sol, la tête en bas. Après analyse de cette image, et son rejet par le cerveau, vu son caractère impossible, elle est qualifiée d'illusion, de mirage. Remarque : Nous noterons en pointillés un trajet qui n'est pas réellement emprunté par la lumière mais qui correspond à une démarche mentale du cerveau qui utilise systématiquement la propagation rectiligne de la lumière pour interpréter les images. Pour Pamela, dans la direction OA', il y a un palmier. 3.3 Miroir Plan : Système Optique Rigoureusement Stigmatique Le miroir va nous permettre de donner corps à la notion de stigmatisme rigoureux et servira de support pour introduire plusieurs notions importantes concernant les systèmes optiques. O Air chaud A Sol chaud A' Air froid Figure 8
Page 9 : Cycle Préparatoire Stigmatisme 55 Le miroir donne d'un point objet A, une image A' symétrique de A par rapport au plan du miroir. En conséquence, pour obtenir le rayon émergent figure 10 correspondant à un rayon incident issu de A, en un point I quelconque du miroir, il suffit de tracer le symétrique A' de A puis le rayon IK ayant la droite A'I pour support. Dans le cas du système optique miroir plan, tout rayon incident passant par le point objet A se réfléchit en passant par le point image A' symétrique de A par rapport au plan du miroir. Ainsi, tout point objet possède une image rigoureusement stigmatique. Le miroir plan est le seul système rigoureusement stigmatique pour tout point de l'espace objet. Figure 9 i' M i N I H A' A K
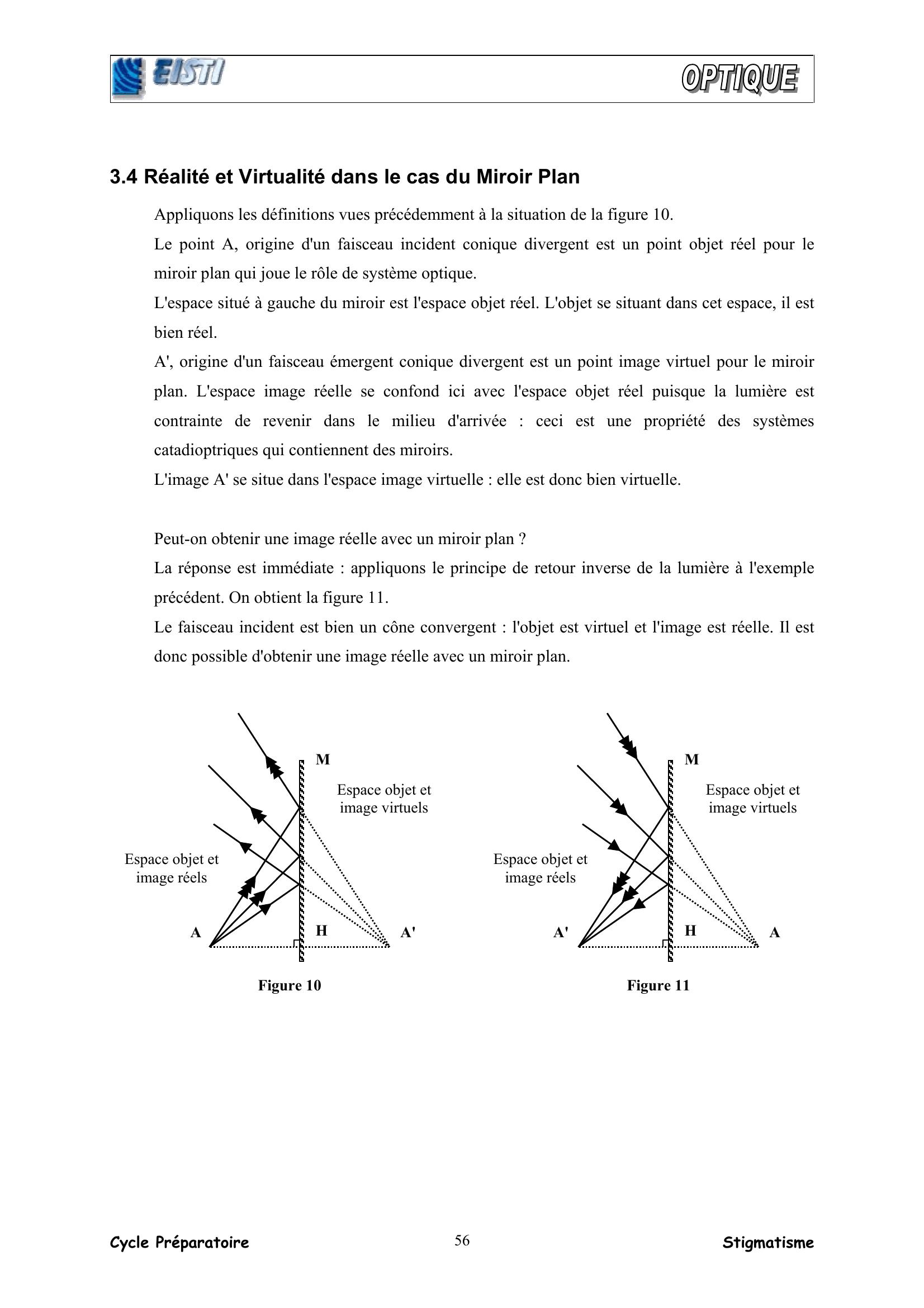
Page 10 : Cycle Préparatoire Stigmatisme 563.4 Réalité et Virtualité dans le cas du Miroir Plan Appliquons les définitions vues précédemment à la situation de la figure 10. Le point A, origine d'un faisceau incident conique divergent est un point objet réel pour le miroir plan qui joue le rôle de système optique. L'espace situé à gauche du miroir est l'espace objet réel. L'objet se situant dans cet espace, il est bien réel. A', origine d'un faisceau émergent conique divergent est un point image virtuel pour le miroir plan. L'espace image réelle se confond ici avec l'espace objet réel puisque la lumière est contrainte de revenir dans le milieu d'arrivée : ceci est une propriété des systèmes catadioptriques qui contiennent des miroirs. L'image A' se situe dans l'espace image virtuelle : elle est donc bien virtuelle. Peut-on obtenir une image réelle avec un miroir plan ? La réponse est immédiate : appliquons le principe de retour inverse de la lumière à l'exemple précédent. On obtient la figure 11. Le faisceau incident est bien un cône convergent : l'objet est virtuel et l'image est réelle. Il est donc possible d'obtenir une image réelle avec un miroir plan. Figure 10MHA'AEspace objet et image virtuelsEspace objet et image réels Figure 11MHAA'Espace objet et image virtuelsEspace objet et image réels
Page 11 : Cycle Préparatoire Stigmatisme 573.5 Construction d'une Image Dans le cas où il y a stigmatisme rigoureux, pour les deux points A et A', si l'on souhaite déterminer A' en connaissant A, ou le contraire, deux rayons provenant de A suffisent pour déterminer le point image A' qui se trouve à l'intersection des rayons émergents correspondants du système optique 3.6 Image d'un Objet Etendu dans un Miroir Plan Chaque point objet donne un point image par symétrie par rapport au miroir. L'opération géométrique qui donne l'image d'un objet étendu dans un miroir plan est donc une symétrie par rapport au plan du miroir. L'objet et son image dans un miroir ne sont généralement pas superposables : l'objet est dit chiral. 3.7 Relation de Conjugaison Dans le cas où il y a stigmatisme rigoureux, l'image d'un point objet est unique. Il existe donc une relation de conjugaison algébrique qui lie la position d'un point objet et de son image. Dans le cas du miroir plan, cette relation de conjugaison s'écrit : 'HAHA= ou H est le projeté orthogonal de A sur le miroir plan.
Page 12 : Cycle Préparatoire Stigmatisme 583.8 Grandissement Transversal Soit un objet de direction AB perpendiculaire à la normale au miroir, passant par le point objet A : cet objet est dit transverse et son image est aussi tranverse. Le grandissement transversal γγγγ, pour le point B, est le rapport algébrique entre la valeur algébrique du segment image transversal et celle du segment objet transversal conjugué. BA'B'A=γ D'une manière générale, lorsque γ 0, alors AB et 'B'A sont de même sens, l'image est dite droite. Si γ 0, alors AB et 'B'A sont de sens opposés, l'image est dite renversée. L'algébrisation usuelle de l'espace repose sur le sens de propagation de la lumière et sur le sens trigonométrique figure 12. Dans le cas du miroir plan, A'B' étant le symétrique de AB par rapport au miroir, alors : AB = 'B'A et γ = 1. L'image transversale donnée par un miroir est toujours droite Figure 12MHA'ABB'+++
Page 13 : Cycle Préparatoire Stigmatisme 593.8 Grandissement Axial γγγγa Soit un objet AB porté par une normale au miroir et A'B' son image donnée par le miroir plan, elle même axiale figure 13 Le grandissement axial γγγγa, pour le point B, est le rapport algébrique entre la valeur algébrique du segment image axial et celle du segment objet axial. Dans le cas du miroir plan, γa = -1, l'image axiale est toujours renversée, en raison des propriétés de symétrie. Figure 13MHA'ABB'+++
Page 14 : Cycle Préparatoire Stigmatisme 604. Les Systèmes Centrés Un système optique centré est un système qui possède un axe de symétrie de révolution appelé axe optique appelé aussi axe principal. Exemple : Le miroir parabolique est un système centré. En effet, ce système est engendré par la rotation autour d'un axe d'une courbe plane qui est un morceau de parabole représentée dans le plan de la feuille. Dans la suite, nous ne considèrerons que des systèmes optiquement centrés dioptre plan, miroir plan. Le prisme est un des rares cas de système optique non centré. Figure 14
Page 15 : Cycle Préparatoire Stigmatisme 615. Aplanétisme Rigoureux Dans le cas d'un système centré pour lequel il existe un couple de points A et A' de son axe optique rigoureusement stigmatiques, si B est un point voisin de A dans un plan transverse, le système est dit rigoureusement aplanétique pour les points A et A' si l'image B' au voisinage de A' est quasiment exempte de défauts, notamment des aberrations sphériques et de coma ces défauts sont définis plus bas dans ce chapitre
Page 16 : Cycle Préparatoire Stigmatisme 626. Stigmatisme Approché A part le cas du miroir plan, il n'existe pas de système optique rigoureusement stigmatique. Au mieux le sont-ils pour quelques points de leurs espaces objet et image. Ainsi, dans le cas des miroirs utilisés en astronomie, la forme de la surface qui reçoit la lumière est un paraboloïde. Pour un rayon incident , par exemple en un point I de la surface, en ce point nous traçons la tangente à la parabole, puis la normale à la surface et enfin, nous appliquons la loi de Snell & Descartes de la réflexion : i = i'. Pour un point B à l'infini, qui envoie des rayons parallèles sur le miroir, nous constatons que tous les rayons issus de B convergent vers un même point F. Il y a donc stigmatisme rigoureux pour les points B et F. Le stigmatisme rigoureux du couple de points F ; B est utilisé dans les phares de voiture l'ampoule est placée au point F et les rayons émis sortent du phare sous forme d'un faisceau cylindrique de rayons. A présent, on cherche l'image d'un point A différent de F de l'axe situé à une distance finie du miroir. L'image de A devrait se trouver sur l'axe puisque le rayon qui suit l'axe revient sur lui même étant donné que l'angle d'incidence sur la surface du miroir est alors nul. Cependant, en traçant plusieurs rayons réfléchis, nous obtenons autant d'images que de rayons incidents, puis réfléchis, considérés deux à deux. Le miroir n'est donc pas rigoureusement stigmatique pour un point objet situé à distance finie. Fort heureusement, il est inutile que les systèmes optiques respectent le stigmatisme rigoureux et cela pour deux raisons : • D'une part, le récepteur de l'image œil, négatif, capteur CCD, … a une résolution limitée. Ainsi, pour l'œil, les cônes récepteurs sur la partie de la rétine la plus sensible ont un écartement de l'ordre de 3 µm ; pour le négatif photographique, le grain le plus petit susceptible de réagir à la lumière est de l'ordre de 4 µm, et cette dimension est de 7 µm pour les photorécepteur de capteurs CCD. Il est donc nécessaire de créer des systèmes optiques qui forment des points images de dimensions un peu inférieures à la taille du récepteur utilisé. • D'autre part, la lumière étant de nature ondulatoire, la diffraction par les ouvertures du système formera d'un point objet une tache de diffraction image sur le récepteur.
Page 17 : Cycle Préparatoire Stigmatisme 63 En conclusion, le stigmatisme rigoureux ne s'impose pas pour un instrument d'optique. Un système optique est dit stigmatique approché pour un couple de points A et A' si les rayons issus du point objet A convergent, après traversée du système optique, dans un volume de petites dimensions autour du point A'. Dans le cas habituel, où le récepteur est une surface, un négatif photographique par exemple, pour qu'il y ait stigmatisme approché, il faut que les rayons convergent sur une surface finie du récepteur adaptée à la dimension des photorécepteurs contenus dans le récepteur. La notion de stigmatisme approché d'un système optique est donc lié à la nature du récepteur. Inutile donc d'utiliser un négatif à grains très fins avec un objectif photographique de mauvaise qualité, c'est à dire un objectif non stigmatique approché.
Page 18 : Cycle Préparatoire Stigmatisme 647. Les Conditions de Gauss 7.1 Mise en Evidence des Conditions de Gauss Considérons un système optique lentille bi-convexe voir ci dessous, placé dans l'air et éclairé par un point source A appartenant à l'axe optique. Cette lentille en verre d'indice n est limitée par deux portions de sphère S1 et S2 dont nous voyons la trace sous forme d'un ménisque dans le plan de figure. Chaque sphère a un rayon que l'on appelle rayon de courbure de la surface. Nous traçons le parcours de chaque rayon en appliquant les lois de l'optique géométrique : les milieux sont supposés homogènes, la lumière s'y propage en ligne droite ; à chaque changement de milieu, nous utilisons les lois de Snell & Descartes pour la réfraction. L'image A' de A doit se trouver sur l'axe optique de la lentille matérialisé en trait mixte sur la figure. En effet, un rayon lumineux qui suit l'axe n'est pas dévié puisque l'angle d'incidence sur les dioptres est alors nul. Nous observons que les rayons éloignés de l'axe, appelés rayons marginaux, qui font avec l'axe des angles importants, convergent les premiers près de la lentille, en des points différents selon les rayons considérés. Ce système optique ne vérifie pas les conditions de stigmatisme rigoureux car l'image d'un point n'est pas un point mais une tache circulaire dont l'aspect, sur un écran perpendiculaire au plan de la figure, dépend de la position le long de l'axe optique.
Page 19 : Cycle Préparatoire Stigmatisme 65 Nous voyons que les rayons peu éloignés de l'axe et peu inclinés sur l'axe, appelés rayons paraxiaux ou rayons centraux, convergent dans un volume fini proche d'un point A' pour y former sur un écran une tache circulaire avec une concentration de lumière au centre de ce cercle. AS1 air air L Lentille en verre S2 n + Zone de l'espace où convergent les rayons proches de l'axe A'Figure 15
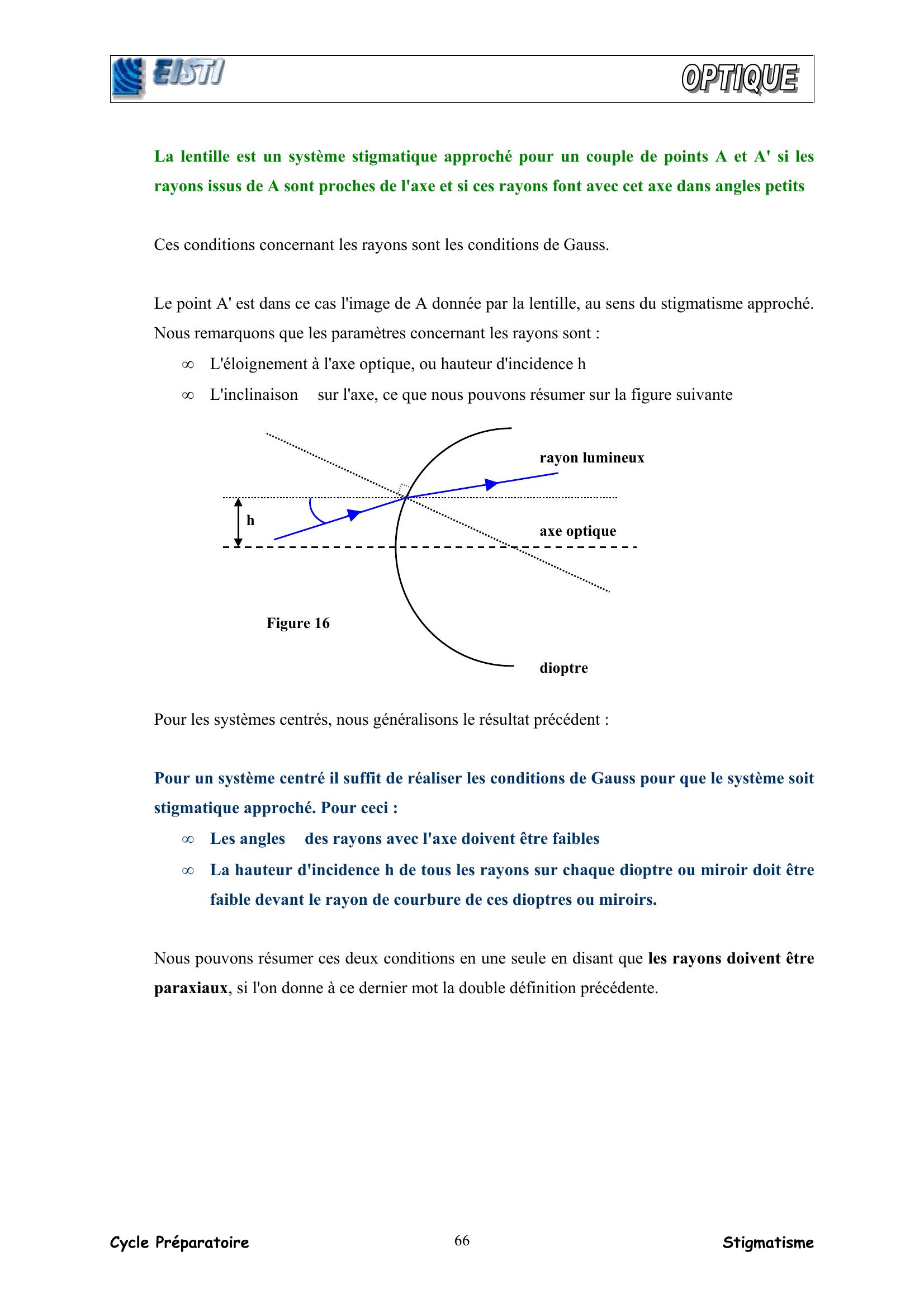
Page 20 : Cycle Préparatoire Stigmatisme 66La lentille est un système stigmatique approché pour un couple de points A et A' si les rayons issus de A sont proches de l'axe et si ces rayons font avec cet axe dans angles petits Ces conditions concernant les rayons sont les conditions de Gauss. Le point A' est dans ce cas l'image de A donnée par la lentille, au sens du stigmatisme approché. Nous remarquons que les paramètres concernant les rayons sont : • L'éloignement à l'axe optique, ou hauteur d'incidence h • L'inclinaison α sur l'axe, ce que nous pouvons résumer sur la figure suivante Pour les systèmes centrés, nous généralisons le résultat précédent : Pour un système centré il suffit de réaliser les conditions de Gauss pour que le système soit stigmatique approché. Pour ceci : • Les angles αααα des rayons avec l'axe doivent être faibles • La hauteur d'incidence h de tous les rayons sur chaque dioptre ou miroir doit être faible devant le rayon de courbure de ces dioptres ou miroirs. Nous pouvons résumer ces deux conditions en une seule en disant que les rayons doivent être paraxiaux, si l'on donne à ce dernier mot la double définition précédente. αααα dioptre axe optique rayon lumineux h Figure 16
Page 21 : Cycle Préparatoire Stigmatisme 677.2 Conséquences des Conditions de Gauss 7.2.1 Approximations trigonométriques Les angles étant supposés petits, nous pourrons accepter les développements limités des fonctions trigonométriques et utiliser des relations approchées : xxsin 2x1xcos2 xxtan et au premier ordre, 1xcos 7.2.2 Aplanétisme approché Dans les conditions de Gauss, un point voisin de l'axe dans un plan transverse vérifie aussi les conditions de stigmatisme approché ce qui fait que l'aplanétisme est toujours vérifié. L'image d'un plan transverse, ou plan de front, est un plan de front. Les plans de front objet et image sont conjugués. 7.2.3 Relation de Conjugaison La conjugaison des points objet A et image A' appartenant à l'axe, ainsi que celle des plans de front associés, en raison du stigmatisme et de l'aplanétisme approchés, se traduit par une relation algébrique appelée relation de conjugaison.
Page 22 : Cycle Préparatoire Stigmatisme 687.2.4 Construction des images Dans les conditions de Gauss, pour construire l'image d'un objet AB situé dans le plan de front, A étant un point fixe de l'axe optique, remarquons que la direction AB et l'axe optique définissent un plan méridien du système centré. Le système étant de révolution, ce plan contient la normale au point d'incidence. Conformément aux lois de Snell & Descartes, deux rayons issus de B et appartenant à ce plan méridien se propagent dans ce plan et leur intersection donne le point image B'. L'image A'B' est donc dans ce plan méridien. Pour obtenir l'image A'B' d'un objet AB situé dans un plan de front, A étant un point de l'axe optique, il suffit de tracer dans le plan méridien contenant AB, deux rayons issus de B, et d'obtenir leur intersection B' à la sortie du système. Le point A' s'obtient ensuite sur l'axe en utilisant la correspondance de plan de front à plan de front, c'est à dire en abaissant la perpendiculaire depuis B' sur l'axe optique. 7.2.5 Grandissement transversal et grandissement angulaire BAL1 α'ααB'A'L3 L2 α'+ Figure 17
Page 23 : Cycle Préparatoire Stigmatisme 69Grandissement transversal La définition du grandissement transversal reste la même que précédemment : BA'B'A=γ Qui ne dépend que du plan de front objet ou image. Le grandissement transversal n'est pas une caractéristique fixe du système optique. Il dépend de la position de l'objet et donc de la position de l'image. • Grandissement angulaire Les angles sont orientés, le grandissement angulaire g est le rapport entre l'angle que fait le rayon émergent avec 'axe optique et l'angle que fait le rayon incident avec ce même axe. αα='g Le grandissement angulaire est aussi le rapport entre l'angle d'ouverture α' d'un pinceau émergent passant par B' et l'angle d'ouverture du pinceau incident correspondant passant par B, alors, αα='g 7.2.6 Foyers • Foyer objet d'un système optique S Le foyer objet F d'un système optique a pour conjugué le point image A' réel à l'infini. • Foyer image d'un système optique S Le foyer image F' d'un système optique est le conjugué du point objet A réel à l'infini. Le point objet A étant à l'infini, il envoie sur S un faisceau cylindrique qui est transformé par le système en un faisceau conique. Le sommet de ce cône est le foyer image F' qui peut être réel ou virtuel.
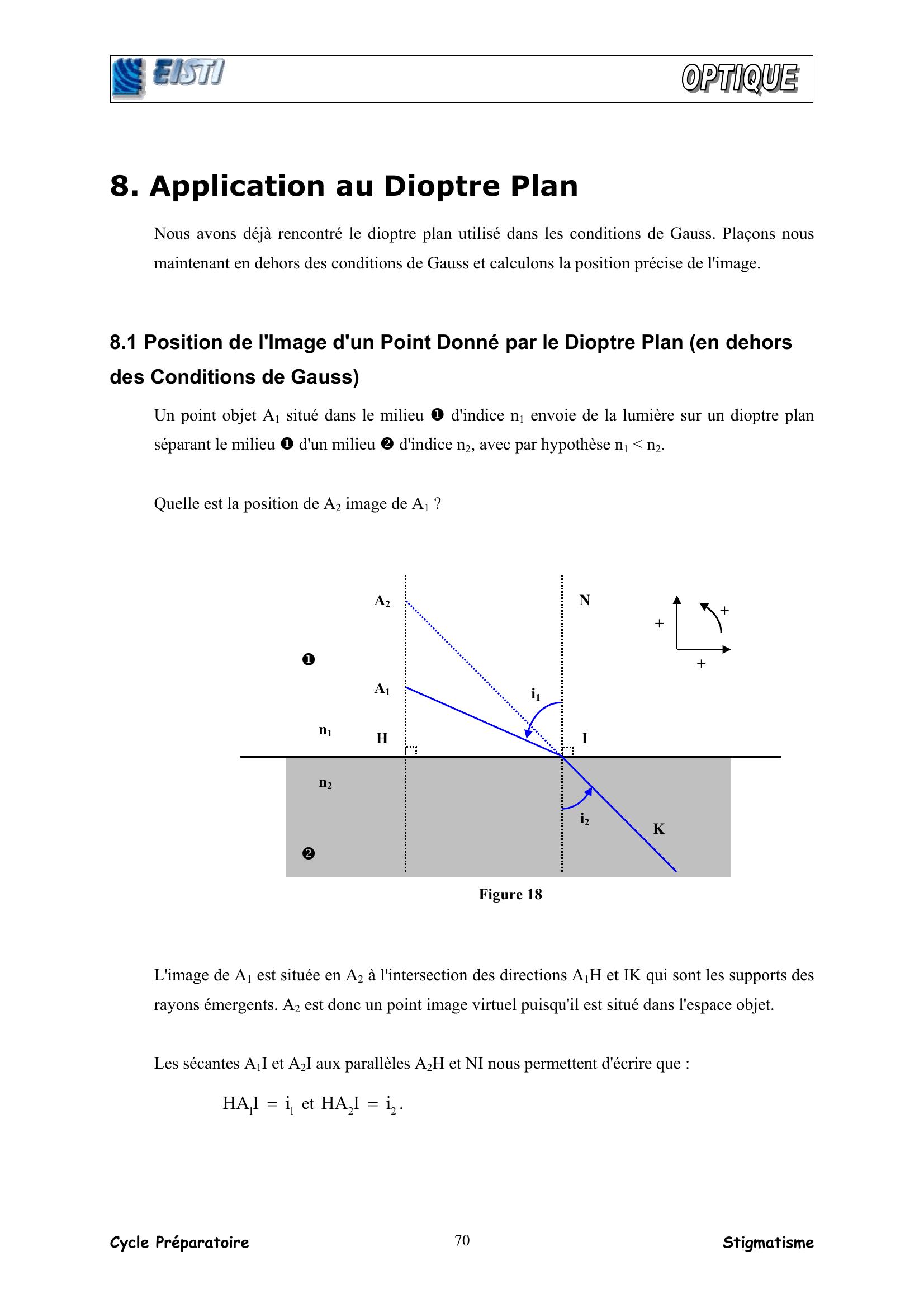
Page 24 : Cycle Préparatoire Stigmatisme 708. Application au Dioptre Plan Nous avons déjà rencontré le dioptre plan utilisé dans les conditions de Gauss. Plaçons nous maintenant en dehors des conditions de Gauss et calculons la position précise de l'image. 8.1 Position de l'Image d'un Point Donné par le Dioptre Plan en dehors des Conditions de Gauss Un point objet A1 situé dans le milieu d'indice n1 envoie de la lumière sur un dioptre plan séparant le milieu d'un milieu d'indice n2, avec par hypothèse n1 n2. Quelle est la position de A2 image de A1 ? L'image de A1 est située en A2 à l'intersection des directions A1H et IK qui sont les supports des rayons émergents. A2 est donc un point image virtuel puisqu'il est situé dans l'espace objet. Les sécantes A1I et A2I aux parallèles A2H et NI nous permettent d'écrire que : 11iIHA= et 22iIHA=. +++NHn1A1A2i2i1n2I KFigure 18
Page 25 : Cycle Préparatoire Stigmatisme 71En écrivant l'expression algébrique de la tangente des angles i1 et i2 dans les triangles A2HI et A1HI, nous obtenons : itan.HAitan.HAHI2211== et donc itanitanHAHA2112 = Exprimons 2HA en fonction de i1 qui est la donnée du problème. icosicosnnHAicosicosisinisinHAHA12121122112== puisque isinnisinn2211= or : isinnn1isin1icos12221222== ce qui donne la relation de conjugaison : icosisinnn1nnHAHA1122211212= Equation 8.1.1 La position de A2 dépend donc de l'angle d'incidence i1. Chaque rayon provenant de A1 et interceptant le dioptre plan donne une image A2 de A1 située sur HA1 différente de celles données par des rayons arrivant sous d'autres incidences. Il n'y a donc pas dans ce cas stigmatisme rigoureux. L'image d'un point quelconque n'est pas un point.
Page 26 : Cycle Préparatoire Stigmatisme 728.2 Points Particuliers Assurant le Stigmatisme Rigoureux du Dioptre Plan Il y a stigmatisme rigoureux si 2HA ne dépend pas de l'angle d'incidence i1, ce qui est le cas si : 0HA1 = 0HA 2 = Le point objet et son image sont alors sur le dioptre plan. ±→1HA ±→2HA Le point objet et son image sont à l'infini. Seul le second cas a un intérêt certain : le système est alors dit afocal et tout faisceau cylindrique incident émerge comme un faisceau cylindrique intérêt pour travailler en lumière parallèle avec un prisme. 8.3 Stigmatisme Approché du Dioptre Plan Si l'angle i1 est petit, nous pouvons dire que : cosi1 1 et sini1 0 L'équation 8.1.1 devient donc : 1212nnHAHA→ Plus rigoureusement, si i1 est petit, nous pouvons utiliser les développements limités de sini1 et cosi1. Le point H étant le projeté du point A1 sur le dioptre plan, si les rayons font un petit angle avec la droite HA1, qui est aussi l'axe optique du dioptre plan, le dioptre plan fournit une image A2 stigmatique approchée du point A1. La relation de conjugaison s'écrit alors : 1212nnHAHA= Si l'objet est réel comme sur la figure précédente, l'image est virtuelle. Si l'objet est virtuel, l'image est réelle. En conclusion, si les conditions de Gauss sont vérifiées pour le dioptre plan, alors le dioptre plan est stigmatique et il existe une relation de conjugaison simple de point objet à point image qui ne dépend pas de l'angle d'incidence des rayons issus du point objet.
Page 27 : Cycle Préparatoire Stigmatisme 739. Aberrations des Systèmes Optiques 9.1 Introduction Dans le cas général, les images obtenues ne sont pas parfaites car : • Il n'y a pas de stigmatisme rigoureux • La diffraction donne d'un point objet une tache de diffraction • Les dioptres traversés par la lumière polychromatique la dispersent • Dans les systèmes réels, des rayons peuvent être très inclinés sur l'axe ou éloignés de l'axe On désigne sous le nom d'aberration les défauts des images dus à la dispersion et aux écarts à l'optique de Gauss On distingue deux catégories d'aberrations • Les aberrations dues à la dispersion, ou aberrations chromatiques, • Les aberrations en lumière monochromatique dues aux termes négligés dans le cas de l'optique paraxiale cf relation de conjugaison du dioptre plan, que l'on appelle aberrations géométriques. Dans les cas des aberrations géométriques, on distingue l'aberration sphérique, l'aberration de coma, l'astigmatisme, la courbure de champ et la distorsion. 9.2 Aberration Chromatique Cette aberration concerne les systèmes optiques transparents traversés par une lumière polychromatique comme la lumière blanche par exemple. Puisque l'angle de déviation aux changements de milieu x dépend de l'indice, donc de la longueur d'onde, il y a dispersion de la lumière. Ainsi, nous savons que la déviation d'un rayon lumineux due à un prisme est plus importante pour les radiations bleues que pour les radiations rouges. Un objet éclairé en lumière blanche, placé devant une lentille, donne donc une image différente pour chaque longueur d'onde ; chaque image a une position et une grandeur différente. Il y a donc chromatisme de position, ou chromatisme axial et chromatisme de grandissement. Pour corriger cette aberration et fabriquer des lentilles achromatiques convergentes, on accole à des lentilles convergentes taillées dans des verres crown peu dispersifs, des lentilles divergentes en verre flint très dispersifs.
Page 28 : Cycle Préparatoire Stigmatisme 749.3 Aberrations Géométriques 9.3.1 Aberration de Sphéricité Au paragraphe 7.1 mise en évidence des conditions de Gauss, nous avons mis en évidence l'aberration de sphéricité d'une lentille en montrant que les rayons réfractés par les bords de la lentilles, les rayons marginaux, coupent l'axe optique en des points plus rapprochés de la lentille que les rayons paraxiaux ne le sont. Il y a perte de stigmatisme, même approché. Cette aberration qui n'est pas propre aux seules lentilles , est liée à la hauteur d'incidence des rayons et donc à la dimension du diaphragme ou du système optique. C'est donc une aberration due à l'ouverture du système. Il y a accumulation de lumière sur une surface de révolution appelée caustique, en forme de pointe de flèche. La trace de cette caustique est marquée en pointillée dans le plan de la figure suivante. Pour corriger cette aberration, nous pouvons fermer le diaphragme, tant que la diminution d'intensité lumineuse n'est pas préjudiciable à l'image, ou fabriquer des lentilles dont la forme de la surface compense ces aberrations trop coûteux. Dans la pratique, on préfère associer une lentille divergente à la lentille convergente, qui a le même comportement pour ce qui est des rayons paraxiaux et marginaux, en combinant les rayons de courbure et les indices des verres pour que les aberrations des deux lentilles se compensent. 9.3.2 Aberration de coma L'aberration de coma est observée dans le cas de faisceaux inclinés sur l'axe optique de systèmes optiques tels que les lentilles ou les miroirs sphériques de grande ouverture. On observe encore une caustique. Dans ce cas, le point image a la forme d'une queue de comète, d'où le nom donné à cette aberration. En effet, les rayons marginaux convergent de manière dissymétrique ce qui donne une tache allongée. Figure 19 +++
Page 29 : Cycle Préparatoire Stigmatisme 75L'aberration de coma se traduit par une perte de netteté et de contraste. On peut là encore limiter cette aberration en fermant le diaphragme. 9.3.3 L'astigmatisme L'astigmatisme est un défaut de l'image qui concerne un point éloigné de l'axe optique, même pour des systèmes très diaphragmés. On observe alors un point image allongé verticalement ou horizontalement si l'on déplace un écran pour recueillir l'image. Si l'on prend un objet plan tel une croix, on ne peut jamais obtenir au même endroit une image nette du trait vertical et du trait horizontal. On sait construire des objets anastigmats qui corrigent partiellement ce défaut, par association de lentilles. Le champ de netteté ne dépasse pas les 50°. Ce défaut affecte souvent l'œil. Dans ce cas, il est dû à la forme non sphérique de la cornée et il affecte la vision des points sur l'axe. Il est corrigé par des verres anastigmats. 9.3.4 La courbure de champ Ce défaut est lié au précédent mais il peut exister même si l'astigmatisme est corrigé. Dans le cas de la lentille, l'image d'un objet transverse se forme sur une surface courbe dont la concavité est tournée vers la lentille. Cette aberration donne des bords d'image flous. La courbure des lentilles est à l'origine de ce défaut que l'on peut corriger en associant plusieurs lentilles d'indices différents, ou en diaphragmant. 9.3.5 La distorsion Cette aberration concerne de grands objets transverses et elle n'affecte pas l'image d'un point au sens du stigmatisme approché. Le défaut porte sur la position de cette image, que l'on trouve à un autre emplacement que ce que prévoit l'optique paraxiale. La distorsion varie avec la position du point objet et l'emplacement du diaphragme. Dans cette expérimentation, à l'aide d'une lentille mince convergente, nous formons l'image d'un quadrillage sur un écran situé dans le plan conjugué de l'objet. Plaçons un diaphragme au plus près de la lentille. Nous observons sur l'écran une figure semblable à la figure 20a car les conditions sont celles de Gauss, l'image est ressemblante à l'objet.
Page 30 : Cycle Préparatoire Stigmatisme 76Si nous éloignons le diaphragme de la lentille, en le gardant entre l'objet et la lentille, nous obtenons une image en forme de barillet et nous constatons que le grandissement transversal est plus faible au bord du champ qu'au centre figure 20b. Si le diaphragme est éloigné, tout en restant entre la lentille et l'image, nous obtenons une image en forme de coussinet et nous constatons que le grandissement transversal est plus important au bord du champ qu'au centre. figure 20c. Ces deux dernières observations ont dues au parcours des rayons marginaux. Ce défaut est difficile à corriger totalement. La plupart des systèmes optiques travaillent hors de conditions de Gauss car elles sont trp restrictives intensité lumineuse, ouverture, inclinaison. En conséquence, la complexité des systèmes optiques résulte de la correction des aberrations mais il est rare que toutes les aberrations géométriques puissent être corrigées en même temps. Objet et Image paraxiale Barillet Coussinet Figure 20a Figure 20c Figure 20b
Page 31 : Cycle Préparatoire Stigmatisme 7710. Ce qu'il faut retenir Lorsqu'un rayon issu d'un point A passe par un point image unique A' après avoir traversé l'instrument, on dit que le système est stigmatique. De même, lorsqu'un objet placé dans un plan perpendiculaire à l'axe de l'instrument donne une image également perpendiculaire à cet axe, le système correspondant est dit aplanétique. Pour que le stigmatisme soit vérifié, il faut se placer dans l'approximation de Gauss : • faisceaux peu ouverts pinceaux • angles d'incidences petits Une image est virtuelle si elle est formée par l'intersection des prolongements de rayons physiques. Elle ne peut pas être obtenue sur un écran cas d'une image vue à travers une lame à faces parallèles et le miroir plan. Au contraire, une image est réelle si elle est formée par l'intersection de rayons physiques issus de l'objet A. Elle peut être obtenue sur un écran cas d'une image donnée par un projecteur de diapositives. Un objet est réel s'il existe physiquement lampe, soleil, …. Si le système étudié est précédé d'un autre système optique, on peut dans certains cas constituer un objet virtuel. On peut distinguer trois types de systèmes optiques : • les systèmes dioptriques qui sont constitués de dioptres transparents dans lesquels un rayon ne peut subir que des réfractions • les systèmes catadioptriques qui contiennent au moins un miroir, un rayon incident pouvant subir des réfractions et des réflexions • les systèmes catoptriques qui ne contiennent que des surfaces réfléchissantes La nature de l'image formée par un système optique est liée à sa position dans l'espace. On peut diviser l'espace en deux régions, l'espace réel et l'espace virtuel : • Pour un système dioptrique, l'espace "image virtuelle" est en avant et l'espace "image réelle" est en arrière • Pour un système catadioptrique, l'espace "image virtuelle" est en arrière, l'espace "image réelle" est en avant • Dans les deux cas, l'espace "objet réel" est en avant et l'espace "objet virtuel" est en arrière Le miroir plan Rigoureusement stigmatique, l'image A' est symétrique de A par rapport au plan du miroir avec : • 'HAHA=, où H est le projeté orthogonal de A sur le miroir • Le grandissement transversal est égal à +1, le grandissement axial est égal à –1 Le dioptre plan Rigoureusement stigmatique lorsque l'objet est à l'infini, ou bien lorsque l'objet est sur le dioptre. Dans le cas du stigmatisme approché, les positions de l'objet A1, de l'image A2 et du projeté orthogonal H de A1 sur la surface du dioptre sont données par la relation de conjugaison : 2211nHAnHA=, n1 est l'indice du milieu où se situe l'objet et n2 l'indice du milieu où la lumière est réfractée
Page 32 : Cycle Préparatoire Stigmatisme 7811. Mise en Oeuvre Méthode générale permettant de déterminer l'image d'un objet donnée par le dioptre plan. • Vérifier les conditions nécessaires à la formation d'une image : ce sont les conditions de Gauss. Il faut donc considérer des rayons lumineux émis par l'objet et peu inclinés sur la normale au dioptre • Construire géométriquement l'image de l'objet sachant qu'en pratique on est obligé de tracer des rayons lumineux avec un angle suffisamment grand afin de garantir la lisibilité de la figure • Appliquer la relation de conjugaison pour déterminer par exemple la position de l'image. -------------------------------------------------------------------------------------------- Application Un insecte vole à 20 cm au dessus de la surface de l'eau et passe à la verticale d'un poisson situé à 1 m sous la surface de l'eau. A quelle distance le poisson situe-t-il l'insecte lors de son passage à la verticale ? -------------------------------------------------------------------------------------------- Solution Il faut se placer dans le cadre des conditions de Gauss. Dans cette situation, cela revient à considérer l'insecte à la verticale de l'œil du poisson. Pour simplifier, on assimile l'insecte à un objet ponctuel A On détermine géométriquement la position de l'image A' de A à travers le dioptre plan formé par la surface de l'eau en utilisant la loi de Snell & Descartes de la réfraction. La position A' peut être obtenue en utilisant la relation de conjugaison : 21n'HAnHA = avec ici n1 = 1,00 ; n2 = 1,33 et HA = 20,0 cm Le poisson voit donc l'insecte à une distance de 126,6 cm. Dans ce type d'exercice, même si le calcul direct est possible, il est vivement recommandé de déterminer qualitativement dans un premier temps la position de l'image de l'objet. +Hn1AA'i2i1n2I
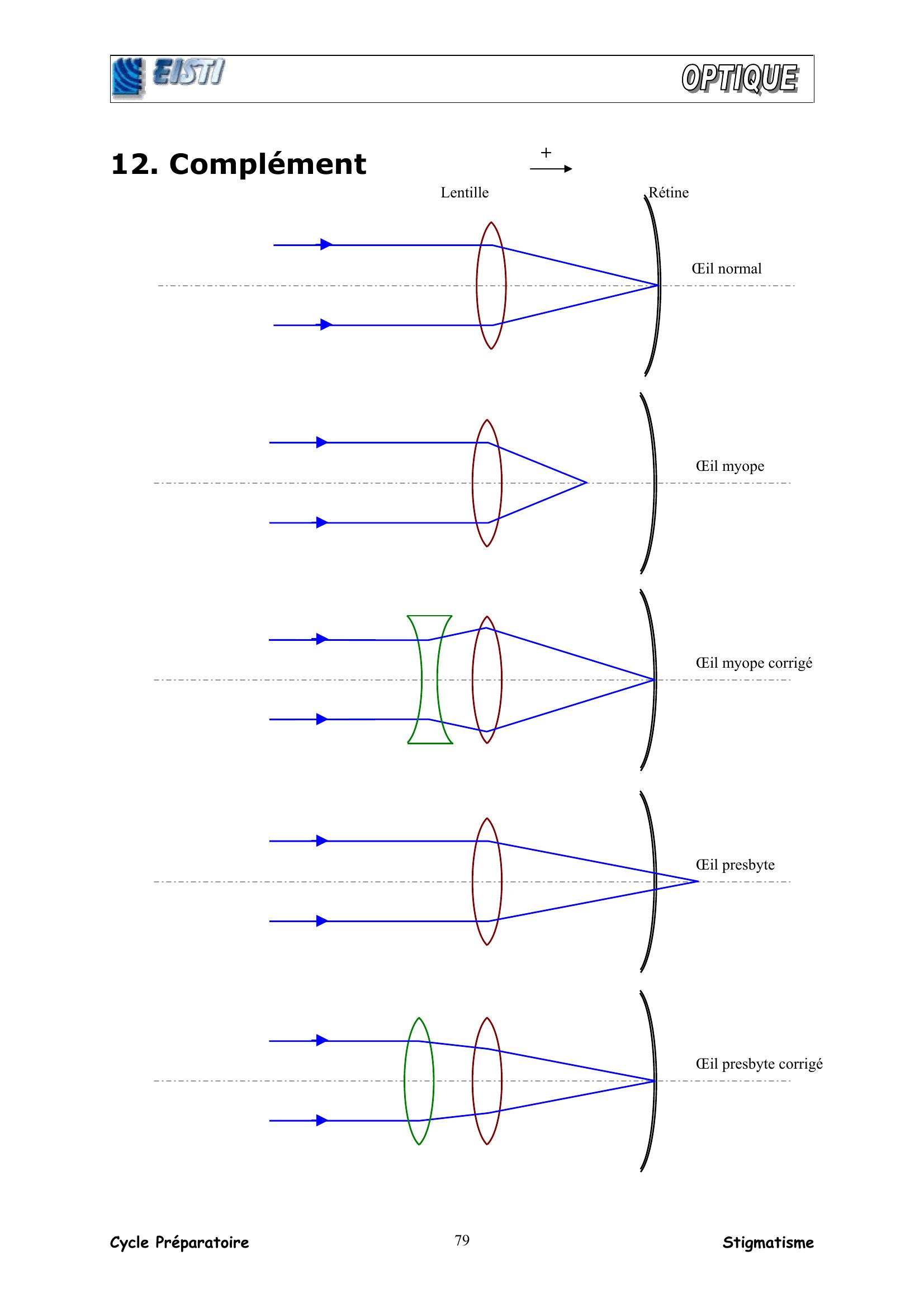
Page 33 : Cycle Préparatoire Stigmatisme 7912. Complément Œil normal Lentille Rétine + Œil myope Œil presbyte Œil presbyte corrigé Œil myope corrigé
Page 34 : Cycle Préparatoire Stigmatisme 80
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34