Cours 05 Lentilles

Télécharger le Cours 05 Lentilles en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

Page 1 : Cycle Préparatoire Lentilles Minces 103 LENTILLES MINCES SPHERIQUES

Page 2 : Cycle Préparatoire Lentilles Minces 1041. Lentilles Sphériques 1.1 Lentilles réelles C1, C2 centres des dioptres sphériques R1, R2 rayons des dioptres sphériques e épaisseur de la lentille Une lentille sphérique est un milieu transparent homogène et isotrope limité par deux dioptres sphériques de centres C1 et C2 ou un dioptre sphérique et un dioptre plan. L'axe de révolution de cette lentille est son axe optique. Dans tout le chapitre on supposera que la lentille est plongée dans un même milieu à son entrée et à sa sortie. air verre S2 S1 C2 R2 e air verre e R1 S2 C1 S1 air R1 C1 Trace de la sphère dans le plan de coupe Axe de symétrie Dioptre sphérique dans le plan de coupeTrace du plan dans le plan de Dioptre dans le plan de coupe

Page 3 : Cycle Préparatoire Lentilles Minces 105Il existe deux catégories de lentilles : 1. Les lentilles convergentes : le rayon lumineux émergent est dévié vers l'axe optique comme le montre la Figure 1. 2. Les lentilles divergentes : le rayon lumineux émergent s'écarte de l'axe optique comme le montre la Figure 2. Il existe trois types de lentilles convergentes dont les représentations en coupe sont données en Figure 3. Les bords de chaque lentille sont minces par rapport à son épaisseur au centre. On rencontre trois types de lentilles divergentes dont les représentations en coupe sont données en Figure 4. Les bords de chaque lentille sont épais par rapport à leur épaisseur au centre. verre air n = 1,5 air Axe optique Figure 1 verre air n = 1,5 air Axe optique Figure 2 Figure 3 Figure 4 biconvexe ménisque convergent plan convexebiconcave ménisque divergent plan concaveAxe optique

Page 4 : Cycle Préparatoire Lentilles Minces 106Propriété d'un point particulier, appelé centre optique de la lentille sphérique réelle, noté O. • Ce point est situé entre S1 et S2 pour une lentille biconvexe. • Tout rayon dont le trajet intérieur à la lentille passe par le centre optique, ressort de la lentille parallèlement à la direction du rayon incident. 1.2 Approximation de la lentille mince sphérique Une lentille sphérique est dite mince si son épaisseur e est très petite devant les rayons de courbure R1 et R2 des dioptres délimitant la lentille. 2121RRe;Re;Re On emploie ici des valeurs absolues du fait que les rayons de courbure soient des grandeurs algébriques. 01,0RRe21 Les symboles pour les deux types de lentilles minces sont données par la Figure 6. air C1 Figure 5 S1 S2 O air C2 D Verre 1,5 Lentille mince convergente Figure 6 Axe optique O O Lentille mince convergente

Page 5 : Cycle Préparatoire Lentilles Minces 1072. Algébrisation – Espace objet et image Comme nous l'avons vu dans les chapitres précédents, les relations de conjugaison sont algébriques. Une convention existe, qui fixe le sens positif : ce sens est celui de la lumière incidente. Traditionnellement, en optique, les figures sont faites avec la lumière progressant de la gauche vers la droite. Espaces objet et image Sens positif de la lumière Figure 7 Axe optique O O + I J B Sens positif de la lumière Figure 8 +Espace image réelle Espace objet réel Espace objet virtuel Espace image virtuelle

Page 6 : Cycle Préparatoire Lentilles Minces 1083. Stigmatisme et aplanétisme On admettra les conclusions suivantes : Une lentille sphérique peut être considérée stigmatique et aplanétique au sens du stigmatisme et de l'aplanétisme approchés : • Si les rayons sont parallèles à l'axe et peu éloignés de l'axe. • Si les rayons sont peu inclinés sur l'axe optique. Ces conditions du stigmatisme et de l'aplanétisme approchés sont les conditions de Gauss. Dans la suite, tous les systèmes optiques à base de lentilles que nous envisagerons seront utilisés dans les conditions de Gauss on négligera entre autres les effets dus à la diffraction introduite par la monture de la lentille.

Page 7 : Cycle Préparatoire Lentilles Minces 1094. Propriétés des lentilles minces 4.1 Centre optique d'une lentille mince Si la lentille représentée en Figure 5 peut être considérée comme mince, alors les sommets S1 et S2 qui délimitent le dioptre sont confondus avec le centre optique O. Le décalage latéral D est alors nul. Tout rayon lumineux passant par le centre optique O d'une lentille mince n'est pas dévié. Le point O est donc à l'intersection de l'axe optique 4.2 Foyers, plans focaux, distances focales Le foyer principal image F' est le point de l'axe optique dont l'objet est à l'infini sur l'axe Sens positif de la lumière Figure 9 Axe optique O +Figure 10 Sens positif de la lumière O O F' est virtuel F' ππππ'F' ππππ'F' est réel +

Page 8 : Cycle Préparatoire Lentilles Minces 110Le foyer principal objet F est le point objet de l'axe optique dont l'image est à l'infini sur l'axe. Lorsque le milieu optique possède le même indice de chaque côté de la lentille, F et F' sont symétrique par rapport au centre optique. Sauf mention contraire, il en sera ainsi pour toute la suite du programme. Le plan perpendiculaire à l'axe optique en F est appelé plan focal objet plan ππππ. Le plan perpendiculaire à l'axe optique en F' est appelé plan focal image plan ππππ'. Un faisceau de rayons parallèles issus de l'espace objet, inclinés sur l'axe optique, donne un faisceau émergent de rayons dont les supports se croisent en un point image ΦΦΦΦ' du plan focal image. ΦΦΦΦ' est obtenu par intersection du plan focal image et du rayon non dévié, parallèle au faisceau incident et passant par le centre optique. Sens positif de la lumière Figure 11 O O F ππππ F ππππ Pour une lentille convergente, F est un objet réel Pour une lentille divergente, F est un objet virtuel+Figure 12 Sens positif de la lumière O O F' ππππ'Pour une lentille convergentePour une lentille divergente+ ΦΦΦΦ' F' ππππ'ΦΦΦΦ' αααα αααα

Page 9 : Cycle Préparatoire Lentilles Minces 111 L'image d'un point ΦΦΦΦ, appartenant au plan focal objet et situé hors de l'axe optique, est rejeté à l'infini dans la direction du support passant par ΦΦΦΦ et O. Les mesures algébriques OF et 'OF sont appelées respectivement distance focale objet et distance focale image de la lentille. On note OFf =; 'OF'f = et on a la relation f = – f', lorsque le milieu est le même des deux côtés de la lentille. Pour une lentille convergente : f' 0 c'est à dire f 0 Pour une lentille divergente : f' 0 c'est à dire f 0 La distance focale s'exprime en mètre m. Attention, il s'agit d'une grandeur algébrique. 4.3 Vergence La vergence V d'une lentille est l'inverse de la distance focale image. 'f1V = La vergence s'exprime de dioptrie δ avec 1 δ = 1 m-1 Une lentille de vergence de – 5 δ est divergente et sa distance focale image vaut – 0,2 m Figure 13 Sens positif de la lumière O O F ππππ Pour une lentille convergentePour une lentille divergente+ ΦΦΦΦ F ππππ ΦΦΦΦ αααα αααα

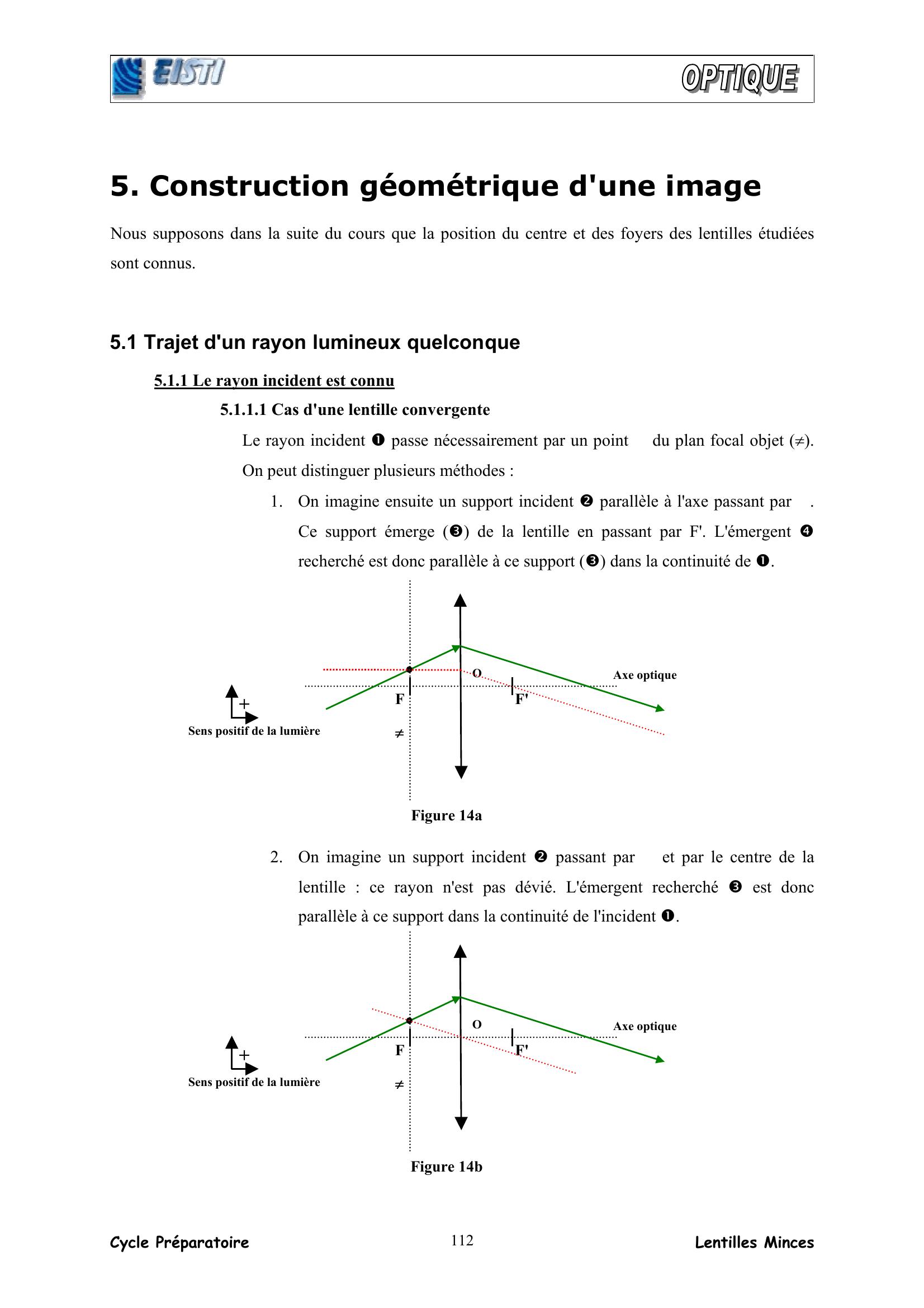
Page 10 : Cycle Préparatoire Lentilles Minces 1125. Construction géométrique d'une image Nous supposons dans la suite du cours que la position du centre et des foyers des lentilles étudiées sont connus. 5.1 Trajet d'un rayon lumineux quelconque 5.1.1 Le rayon incident est connu 5.1.1.1 Cas d'une lentille convergente Le rayon incident passe nécessairement par un point Φ du plan focal objet π. On peut distinguer plusieurs méthodes : 1. On imagine ensuite un support incident parallèle à l'axe passant par Φ. Ce support émerge de la lentille en passant par F'. L'émergent recherché est donc parallèle à ce support dans la continuité de . 2. On imagine un support incident passant par Φ et par le centre de la lentille : ce rayon n'est pas dévié. L'émergent recherché est donc parallèle à ce support dans la continuité de l'incident . Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ Figure 14a ππππ Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ Figure 14b ππππ

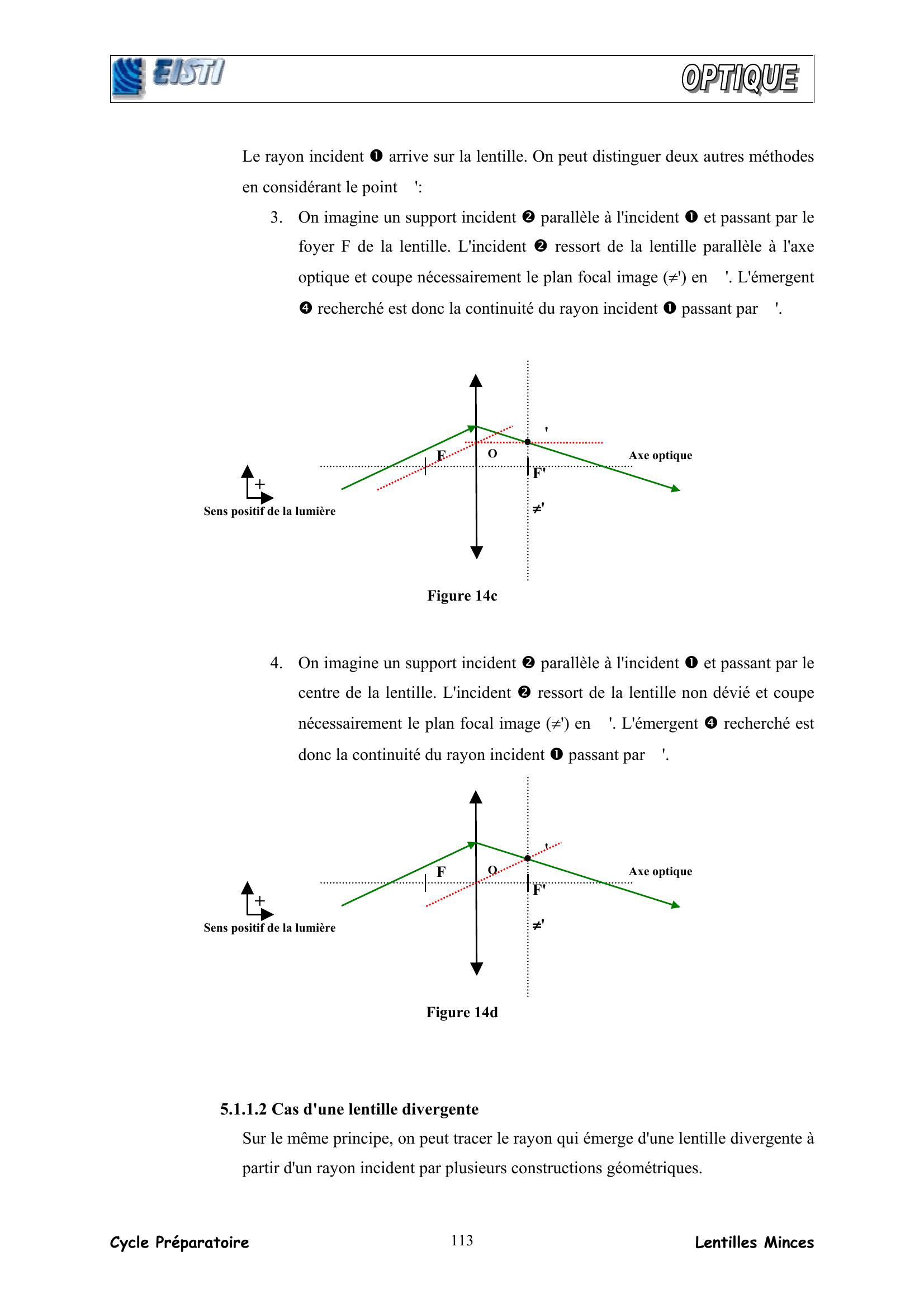
Page 11 : Cycle Préparatoire Lentilles Minces 113Le rayon incident arrive sur la lentille. On peut distinguer deux autres méthodes en considérant le point Φ': 3. On imagine un support incident parallèle à l'incident et passant par le foyer F de la lentille. L'incident ressort de la lentille parallèle à l'axe optique et coupe nécessairement le plan focal image π' en Φ'. L'émergent recherché est donc la continuité du rayon incident passant par Φ'. 4. On imagine un support incident parallèle à l'incident et passant par le centre de la lentille. L'incident ressort de la lentille non dévié et coupe nécessairement le plan focal image π' en Φ'. L'émergent recherché est donc la continuité du rayon incident passant par Φ'. 5.1.1.2 Cas d'une lentille divergente Sur le même principe, on peut tracer le rayon qui émerge d'une lentille divergente à partir d'un rayon incident par plusieurs constructions géométriques. Sens positif de la lumière Axe optique O +F ππππ' F' ΦΦΦΦ' Figure 14c Sens positif de la lumière Axe optique O +F ππππ' F' ΦΦΦΦ' Figure 14d

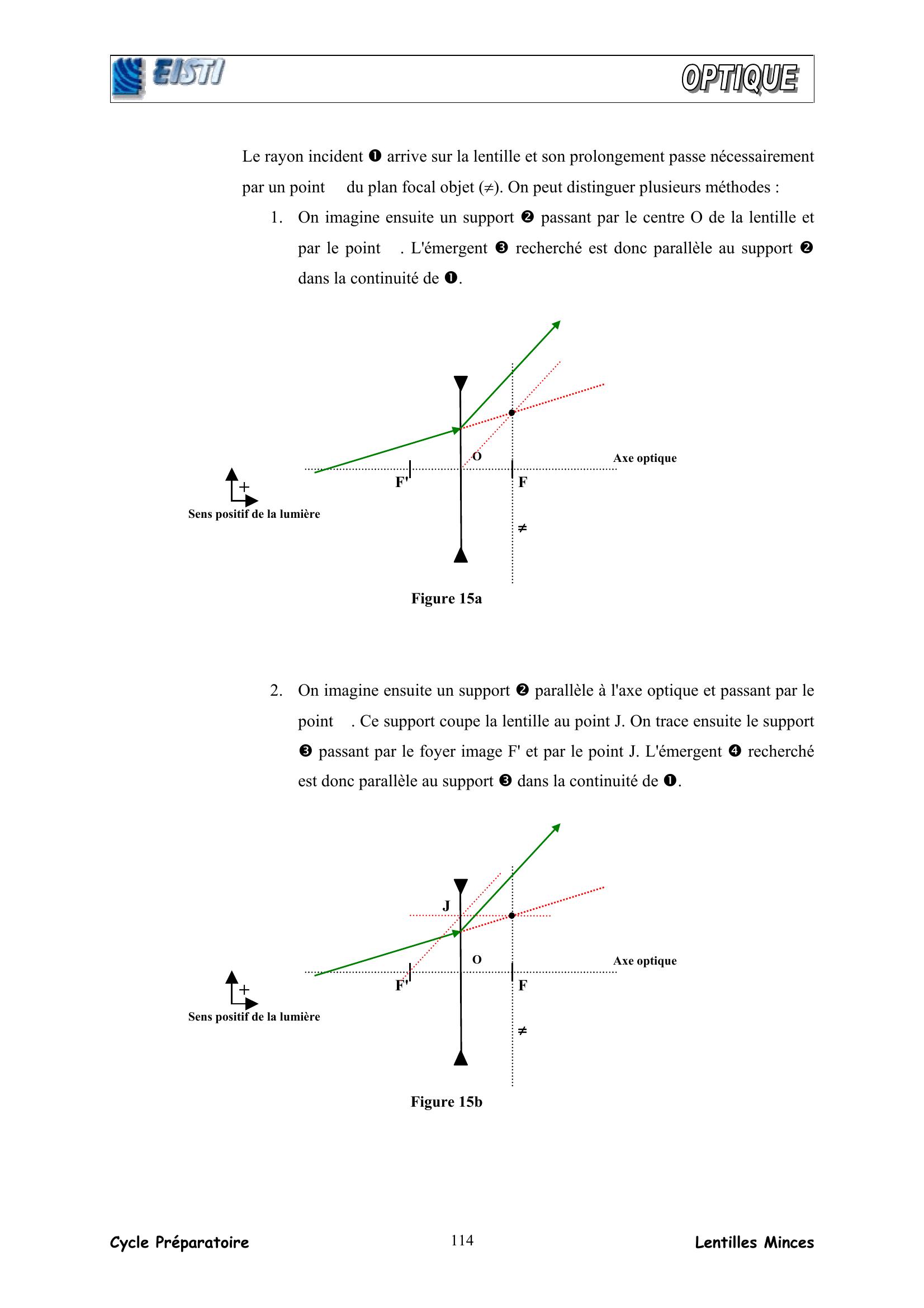
Page 12 : Cycle Préparatoire Lentilles Minces 114Le rayon incident arrive sur la lentille et son prolongement passe nécessairement par un point Φ du plan focal objet π. On peut distinguer plusieurs méthodes : 1. On imagine ensuite un support passant par le centre O de la lentille et par le point Φ. L'émergent recherché est donc parallèle au support dans la continuité de . 2. On imagine ensuite un support parallèle à l'axe optique et passant par le point Φ. Ce support coupe la lentille au point J. On trace ensuite le support passant par le foyer image F' et par le point J. L'émergent recherché est donc parallèle au support dans la continuité de . Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ Figure 15a ππππ Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ Figure 15b ππππ J

Page 13 : Cycle Préparatoire Lentilles Minces 115Le rayon incident arrive sur la lentille. On peut distinguer deux autres méthodes en considérant le point Φ': 3. On imagine ensuite un support incident parallèle au rayon incident et passant par le centre de la lentille. Ce support non dévié coupe le plan focal image au point Φ'. L'émergent recherché est alors tracé dans la continuité de et passant par le point Φ'. 4. On imagine un support incident parallèle au rayon incident et passant par le foyer objet F de la lentille. Ce support coupe la lentille au point J. On trace ensuite le support passant par le point J et parallèle à l'axe optique. Ce support coupe nécessairement le plan focal image au point Φ'. L'émergent recherché est alors tracé dans la continuité de et passant par le point Φ'. Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ' Figure 15c ππππ' Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ' Figure 15d ππππ' J

Page 14 : Cycle Préparatoire Lentilles Minces 1165.1.2 Le rayon émergent est connu 5.1.2.1 Cas d'une lentille convergente 1. On trace un rayon parallèle au rayon émergent connu passant par le foyer image F' de la lentille. On en déduit alors un rayon incident parallèle à l'axe optique et coupant le plan focal objet π en Φ. Le rayon incident recherché passe alors par le point Φ et se trouve prolongé par le rayon émergent . 2. On trace un rayon parallèle au rayon émergent connu passant par le centre O de la lentille. Ce rayon non dévié coupe nécessairement le plan focal objet en Φ. Le rayon incident recherché passe alors par le point Φ et se trouve prolongé par le rayon émergent . Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ Figure 16a Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ Figure 16b

Page 15 : Cycle Préparatoire Lentilles Minces 1173. Le rayon émergent , connu, coupe forcément le plan focal image π' en Φ'. On imagine un support parallèle à l'axe optique, passant par le point Φ' et coupant la lentille en un point J. Ce rayon émergent est donc issu d'un rayon incident passant par le foyer F de la lentille. L'incient recherché est alors parallèle au rayon incident et est finalement continué par le rayon émergent . 4. Le rayon émergent , connu, coupe forcément le plan focal image π' en Φ'. On imagine un support passant par le point Φ' et coupant la lentille en son centre optique O. Ce rayon émergent est donc issu d'un rayon incident non dévié. L'incident recherché est alors parallèle au rayon incident et est finalement continué par le rayon émergent . Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ' Figure 16c Sens positif de la lumière Axe optique O +F F' ΦΦΦΦ' Figure 16d

Page 16 : Cycle Préparatoire Lentilles Minces 118 5.1.2.2 Cas d'une lentille divergente 1. On trace un support , parallèle au rayon émergent connu, passant par le centre optique de la lentille. Ce rayon coupe le plan focal objet π en Φ. On trace alors le rayon joignant le point Φ au point d'émergence de sur la lentille. L'incident recherché est donc le rayon prolongé par le support . 2. On trace un support , parallèle au rayon émergent connu, passant par le foyer image F' de la lentille. Ce rayon coupe la lentille au point J. On trace alors le rayon parallèle à l'axe optique, passant par le point J. Le rayon coupe alors le plan focal objet π en Φ. On trace alors le rayon joignant le point Φ au point d'émergence de sur la lentille. L'incident recherché est donc le rayon prolongé par le support . Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ Figure 17a Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ Figure 17b

Page 17 : Cycle Préparatoire Lentilles Minces 1193. On prolonge le rayon émergent connu jusqu'au point d'intersection Φ' avec le plan focal image π'. On imagine ensuite un support passant par le centre O de la lentille et le point Φ'. L'incident recherché est alors parallèle au rayon et est continué par . 4. On prolonge le rayon émergent connu jusqu'au point d'intersection Φ' avec le plan focal image π'. On imagine ensuite un support parallèle à l'axe optique, passant par le point Φ'. Ce support coupe la lentille au point J. On trace un support reliant le point J au foyer objet F de la lentille Ce support est donc nécessairement le prolongement d'un rayon incident . L'incident recherché est alors parallèle au rayon et est continué par . Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ' Figure 17c Sens positif de la lumière Axe optique O +F' F ΦΦΦΦ' Figure 17d

Page 18 : Cycle Préparatoire Lentilles Minces 1205.2 Image d'un objet perpendiculaire à l'axe optique Nous souhaitons déterminer l'image A'B' d'un objet AB, perpendiculaire à l'axe optique d'une lentille convergente. Nous construisons dans un premier temps l'image A' de A en utilisant un rayon incident quelconque passant par A. Sens positif de la lumière Axe optique O +A F A' F' ΦΦΦΦ' Figure 19 Figure 18 Sens positif de la lumière Axe optique O +A B F F'

Page 19 : Cycle Préparatoire Lentilles Minces 121Pour construire l'image de B, deux des trois rayons particuliers suivants sont suffisants : Celui qui passe par le centre de la lentille et qui n'est pas dévié, Celui qui passe par F et qui ressort parallèle à l'axe optique, Celui qui arrive sur la lentille parallèle à l'axe optique et qui émerge en passant par F'. Finalement on obtient : On peut s'affranchir du calcul de l'image A' de l'objet A du fait du caractère aplanétique conditions de Gauss de la lentille. Pour trouver A', il suffit alors de projeter B' sur l'axe optique. Sens positif de la lumière Axe optique O +B F B' F' Figure 20 Figure 21 Sens positif de la lumière Axe optique O +A B F B' F' A'

Page 20 : Cycle Préparatoire Lentilles Minces 1226. Relations de conjugaison et de grandissement On considère ici le cas d'une lentille convergente, mais les résultats restent valables dans le cas d'une lentille divergente. 6.1 Avec origine au centre Descartes Les triangles OAB et OA'B' sont des triangles semblables dans lesquels nous pouvons appliquer le théorème de Thalès ce qui nous conduit immédiatement à l'expression du grandissement transversal γ : OA'OAAB'B'A==γ 1 D'autre part : AB'B'AOI'B'AO'F'A'F== 2 Car les triangles F'OI et F'A'B' sont aussi semblables. De plus, O'F'OA1O'F'OAO'FO'F'A'F+=+= 3 Les égalités 1, 2 et 3 donnent donc : O'F'OA1OA'OA+= Figure 22 Sens positif de la lumière Axe optique O +A B F B' F' I J A'

Page 21 : Cycle Préparatoire Lentilles Minces 123Et en divisant les deux membres de cette égalité par 'OA nous obtenons : 'OF1'OA1OA1= Enfin, OF1'OF1OA1'OA1== Cette relation de conjugaison fait intervenir le centre optique : c'est la relation de Descartes. Application : Dans une expérience d'optique, l'image d'un objet virtuel est formé à l'aide d'une lentille divergente de distance focale cm20'f=. L'objet est à 25 cm de la lentille. Calculer la distance entre la lentille et l'image en précisant sa nature. Solution : Appliquons la relation de conjugaison précédente. Ainsi, 'OA = 100 cm. 'OA 0 donc A' est dans l'espace objet, c'est à dire avant la lentille : l'image est virtuelle et renversée. 6.2 Avec origine aux foyers Newton Nous allons montrer que le grossissement transversal peut s'exprimer en fonction de FA ou 'A'F, puis en déduire une relation de conjugaison liant FA et 'A'F. La relation 2 fournit immédiatement une expression du grandissement qui fait intervenir le foyer image de la lentille : AB'B'AOI'B'AO'F'A'F== 2 'f'A'F'OF'A'FO'F'A'FAB'B'A====γ Cherchons alors une relation qui contienne FA ; en remarquant que les triangles FOJ et FAB sont semblables, on peut écrire : FA'fFAFOABOJAB'B'A====γ

Page 22 : Cycle Préparatoire Lentilles Minces 124Par conséquent : FA'f'f'A'F==γ Cette dernière égalité fournit également la relation de conjugaison cherchée : 'f.f'f'A'F.FA2 == Cette relation de conjugaison fait intervenir les foyers de la lentille : c'est la relation de Newton. Application : La distance minimale dm de vision nette d'un œil sans défaut est égale à 25 cm. Un individu ayant cette faculté place son œil au foyer image d'une loupe de vergence = 25 δ et observe un insecte. A quelle distance de la loupe se trouve l'insecte si l'image est nette et se forme au plus près de l'œil ? Solution : Commencer par effectuer une construction géométrique en utilisant le fait que l'image formée par une loupe est nécessairement virtuelle et agrandie L'insecte représenté par AB se situe entre le foyer objet et le centre de la lentille en avant. 'A'F = dm f' = 251 m = 4 cm On applique le théorème de Newton : FA = 0,64 cm D'où : OA = 3,36 cm L'insecte représenté par AB doit donc être placé à 3,36 cm en avant de la lentille. Remarque : Les formules de conjugaison ne sont utilisables que pour des points objets ou image situés exclusivement sur l'axe optique.

Page 23 : Cycle Préparatoire Lentilles Minces 1257. Association de lentilles minces Nous nous limiterons au cas où les lentilles ont même axe optique. Lorsque les lentilles sont accolées, on considère que les centres optiques O1 et O2 sont confondus. Lorsque les lentilles ne sont pas accolées, on considère d, la distance constante séparant O1 et O2. 7.1 Lentilles accolées Un objet AB a une image A1B1 au travers de la première lentille L1. A1B1 est un objet pour la lentille L2 qui en donne l'image A2B2. A2B2 est aussi l'image de AB à travers l'ensemble des deux lentilles. 2L1LAAA21→→ On peut écrire les relations de Descartes pour chacune des deux lentilles : Lentille L1 11'f1OA1OA1= et OAOAABBA1111==γ Lentille L2 212'f1OA1OA1= et 1211222OAOABABA==γ D'où : 212'f1'f1OA1OA1+= et OAOAABBA22221==γγ L'ensemble des deux lentilles accolées est donc équivalent à une lentille unique L de distance focale f' telle que : 'f1'f1'f1OA1OA1212=+=

Page 24 : Cycle Préparatoire Lentilles Minces 1267.2 Lentilles non accolées On va déterminer la position du foyer image F' de cet ensemble de deux lentilles, non accolées. A la sortie de L1, le rayon lumineux passe par F'1, foyer image de L1. En utilisant par exemple le point Φ2, on construit le rayon sortant de L2 dont l'intersection avec l'axe optique définit le foyer image F' de l'ensemble du système optique. F' est donc le conjugué de F'1 pour la lentille L2. On peut également déterminer la position de ce foyer image F' par un calcul algébrique en appliquant la relation de Newton pour la lentille L2 : 22212'f'F'F.'FF= Avec 1211122212'fd'f'FOOOOF'FF+=++= Ainsi : 2122'2'f'fd'f'FF= 4 Les paramètres d, f'1 et f'2 étant connus, la relation 4 permet donc de trouver la position du foyer image du doublet de lentilles. Cas particulier : Si le foyer image de la lentille d'entrée est confondu avec le foyer objet de la lentille de sortie, tout rayon incident parallèle à l'axe optique ressort du doublet parallèlement à l'axe optique. De même, l'image d'un faisceau parallèle incident sur le système optique est un faisceau émergent parallèle : le système optique est dit afocal. Sens positif de la lumière Axe optique d + O1L2 F1 F' F'1L1 ππππ2O2F2 F'2ΦΦΦΦ2

Page 25 : Cycle Préparatoire Lentilles Minces 1278. Aberration chromatique d'une lentille Uniquement pour les lentilles non pour les miroirs. 8.1 Mise en évidence Pour illustrer ce point du cours, on considère une lentille mince supposée sans aberration géométrique et éclairée par une source lumineuse blanche donc non monochromatique. On note ici l'aberration chromatique transversale principale δT à titre indicatif. On observe que selon la longueur d'onde de la radiation lumineuse traversant la lentille, le point de convergence foyer image ne se situe pas à la même position sur l'axe optique. On fait apparaître les foyers F'F radiation bleue et F'C radiation rouge correspondant à deux longueurs d'onde de référence du spectre visible La distance δL séparant ces deux foyers est appelée aberration chromatique longitudinale principale. En notant f'C, f'F et f'D les distances focales images associées respectivement aux radiations C, F et D définies au chapitre I et le nombre d'Abbe η, on montre que : η==δDFCL'f'f'f Plus le nombre d'Abbe est élevé, plus l'aberration chromatique longitudinale est petite. F' F'F F'C Axe optique δδδδL2 δ2 δ2 δ2 δT

Page 26 : Cycle Préparatoire Lentilles Minces 1288.2 Correction de l'aberration En pratique, l'aberration chromatique peut être réduite voire même supprimée par combinaison de lentilles de nature et de matériaux différents afin de réaliser ce que l'on nomme un système achromatique. Dans le cas particulier où les deux lentilles L1 et L2 sont accolées nous savons que les distances focales f'C, f'F et f'D pour les raies C, D et F de l'association vérifient : C2C1C'f1'f1'f1+= 1 et F2F1F'f1'f1'f1+= 2 Nous trouvons après simplifications : D22D112D2F2C22D1F1C12DFC'f1'f1'f'f'f'f'f'f'f'f'fη+η=+= Cette dernière relation montre qu'il est possible d'annuler ou au moins fortement atténuer l'aberration longitudinale. Pour annule l'aberration longitudinale, il faut que : 0'f1'f1D22D11=η+η 3 Le nombre d'Abbe des verres transparents constituant les deux lentilles étant toujours positif, il suffit de choisir une lentille divergente et l'autre convergente puisque leurs distance focales sont de signe contraire. Ainsi, la quantité 2211'f1'f1η+η peut être nulle. Application : On souhaite élaborer à l'aide de deux lentilles accolées L1 et L2, une lentille achromatique, de vergence égale à une dioptrie. L1 est réalisée à l'aie d'un verre de type flint η1 = 33 et L2 avec un verre de type crown η2 = 64. Comment choisir les deux lentilles ? Solution : Il y a deux inconnues, f'1 et f'2, il faut donc poser deux équations : 0'f641'f33121=+ et 1'f1'f121=+ La résolution numérique conduit à : f'1 = 94 cm et f'2 = 48,5 cm. L1 est donc divergente et L2 convergente.

Page 27 : Cycle Préparatoire Lentilles Minces 1299. Ce qu'il faut retenir Axe optique, centre optique, espaces image ou objet, foyers objets ou images, plans focaux, distances focales f et f' mètre m et vergence V dioptrie δδδδ 'OF'f = représente la distance focale image algébrique m. 'f1V = Relation de conjugaison et de grandissement Origine au centre optique 'OF1OA1'OA1= OA'OAAB'B'A==γ Origine au foyer 2'f'f.f'OF.OF'A'F.FA=== 'f'A'FFAfAB'B'A===γ Nature des foyers Les foyers sont symétriques par rapport au centre optique et sont : Réels pour une lentille convergente, Virtuels pour une lentilles divergente.

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27