DS 2021 2022 GM Correction
Télécharger le DS 2021 2022 GM Correction en pdf
Page 1 : ING1-GM EXAMEN DE DATA EXPLORATION 2021-2022 2h Examen papier 2 feuilles R/V manuscrites autorisées Calculatrice autorisée Exercice 1 On a interrogé une partie des élèves d’un collège pour connaitre la distance qu’ils doivent parcourir pour se rendre à l’établissement scolaire et qui représente la variable X regroupée selon trois catégories courte, moyenne et longue i.e. distance domicile/collège. On s’intéresse de plus à la variable Y qui représente le niveau scolaire de l’élève. L’objectif est d’étudier l’éventuel impact de la distance domicile/collège sur les résultats. On obtient ainsi le tableau suivant : FaibleMoyenneElevéCourte232579Moyenne838555Longue10221271 Préciser les variables étudiées ainsi que leur type. Quelle est la population étudiée ? Quelle est la taille de l’échantillon ? Les deux variables sont : la distance parcourue par l’élève pour se rendre à l’établissement scolaire X et son niveau scolaire Y. Les deux variables sont qualitatives. La taille de l’échantillon est : 500 élèves. 2 Etablir le tableau complet des effectifs observés en ajoutant les effectifs marginaux. FaibleMoyenneElevéTotalCourte232579127Moyenne838555223Longue1022127150Total2081311615003 Calculer le tableau des fréquences observées. FaibleMoyenneElevéTotalCourte0.0460.050.1580.254Moyenne0.1660.170.110.446Longue0.2040.0420.0540.3Total0.4160.2620.32214 Donner le tableau des profils lignes. FaibleMoyenneElevéTotalCourte0.18110.1960.6221Moyenne0.3720.3810.2461Longue0.680.140.181 5 Comparer le tableau de profils lignes avec le profil moyen ligne. Que pouvez-vous en conclure sur le lien entre les deux variables ? Justifiez votre réponse. Il faut comparer les lignes de tableau des profils lignes avec le profil moyen ligne suivant : 0.4160.2620.322
Page 2 : On peut remarquer que les profils lignes s'écartent du profil moyen ligne. Par exemple toutes distances confondues, on constate qu’il y a 41,6 d’élève ayant un niveau faible. Or pour les distances courtes, ce pourcentage tombe à 18,11 ,et a contrario, pour les distances longues, il augmente à 68. Ce qui nous laisse conclure que les deux variables sont liées. Conclusion à confirmer avec le test de X². 6 Quelle est la probabilité que : a un élève parcourt une distance longue ? 0.3 b un élève qui parcourt une longue distance ait un niveau faible ? 0.68 Tableau des profils lignes c un élève ait un niveau faible et parcourt une distance moyenne ? 83/208 = 0.39 0.166 Tableau des fréquences 7 En supposant que les deux variables sont indépendantes, calculer l’effectif théorique des élèves de niveau faible et qui parcourent une distance courte. Détailler vos calculs. L’effectif théorique est : 208127/500 = 52.832 8 La distance du chi-deux entre le tableau des effectifs observés et celui des effectifs théoriques est 114.74. Peut-on conclure que les variables sont liées ? Voici le tableau de seuils de décision d.d.l.4 5 6 7 8 9 10 15 Seuil 9.4911.07512.5914.0715.5116.9218.3124.99 Le d.d.l est : 3-13-1=4 donc le seuil est 9.49.. X²=114.74 9.49 alors les variables sont fortement liées. Attention, les résultats de ce test ne sont valables que si les effectifs théoriques sont 5 ce qui doit être le cas car tous les effectifs marginaux sont élevés Exercice 2 Le tableau ci-après présente une partie des offres locatives de 31 appartements rennais proposés sur le site leboncoin.fr au 02/01/2017. A- Modèle de prévision du loyer en fonction de la surface En premier temps, on s’intéresse à étudier la relation entre le loyer Y de ces appartements et leur surface X. Avec le logiciel R nous avons obtenu ce résultat : 1 Donner une estimation du coefficient de corrélation entre le loyer et la surface d’un appartement. Est-ce que la surface joue un rôle sur le prix de location des appartements ? Considérez-vous ce rôle comme important ? Le coefficient de détermination est 0.5808, alors le coefficient de corrélation est ±0.762, les variables sont donc fortement corrélées entre elles. Logiquement, on peut dire que le coefficient de corrélation est 0.762 et pas -0.762 car les deux variables Surface et Prix de location sont souvent corrélé de sens positive. 2 Proposer un modèle permettant de donner la relation entre le loyer des appartements et leur surface. X : Surface Y : Loyer
Page 3 : Y=7.282 X+244.296+ ε ou bien Y^ Loyer = 7.282Surface+244.296+ ε 3 Donner le coefficient de détermination. Interpréter. R²=0.5808, alors 58 de la variabilité des loyers est expliqué par la droite de régression. 4 Un ami qui est en location à Rennes dans un appartement de 30 m² m’affirme qu’il paye un loyer de 410 euros. Si je cherche à louer sur Rennes un appartement de même surface : a Calculer la valeur prédite du prix de location. Pour Surface X=30 m², la valeur de Loyer prédite par le modèle est : 7.28230+244.296=462.756 b Calculer en détaillant la valeur du résidu dans ce cas. Résidu = Vrai valeur – Valeur prédite = 410-462.756=-52.756 B- Etude du lien entre le loyer et le quartier On souhaite maintenant savoir si la localisation de l’appartement a un impact sur son loyer. Pour cela on transforme la variable quantitative Loyer en une variable qualitative LoyerB avec 3 modalités suivant les seuils suivants : LoyerBFaibleLoyer 500Modéré500 Loyer 600ElevéLoyer 6001 Quelle méthode statistique pouvez-vous mettre en place pour déterminer si les deux variables, LoyerB et Quartier, sont liées ? Test d’indépendance de Khi-deux. 2 Supposons que suite à cette méthode vous avez conclu que les variables sont liées. Vous souhaitez maintenant étudier plus précisément le lien entre les modalités. Pour cela, on effectue une AFC. a Que représente le pourcentage affiché sur les axes ? L’axe 1 représente 58.68 du Khi-deux. L’axe 2 représente 41.32 du Khi-deux. 100 de la distance du chi-deux est expliquée alors par le plan principal b Expliquez pourquoi la somme des deux axes fait exactement 100.
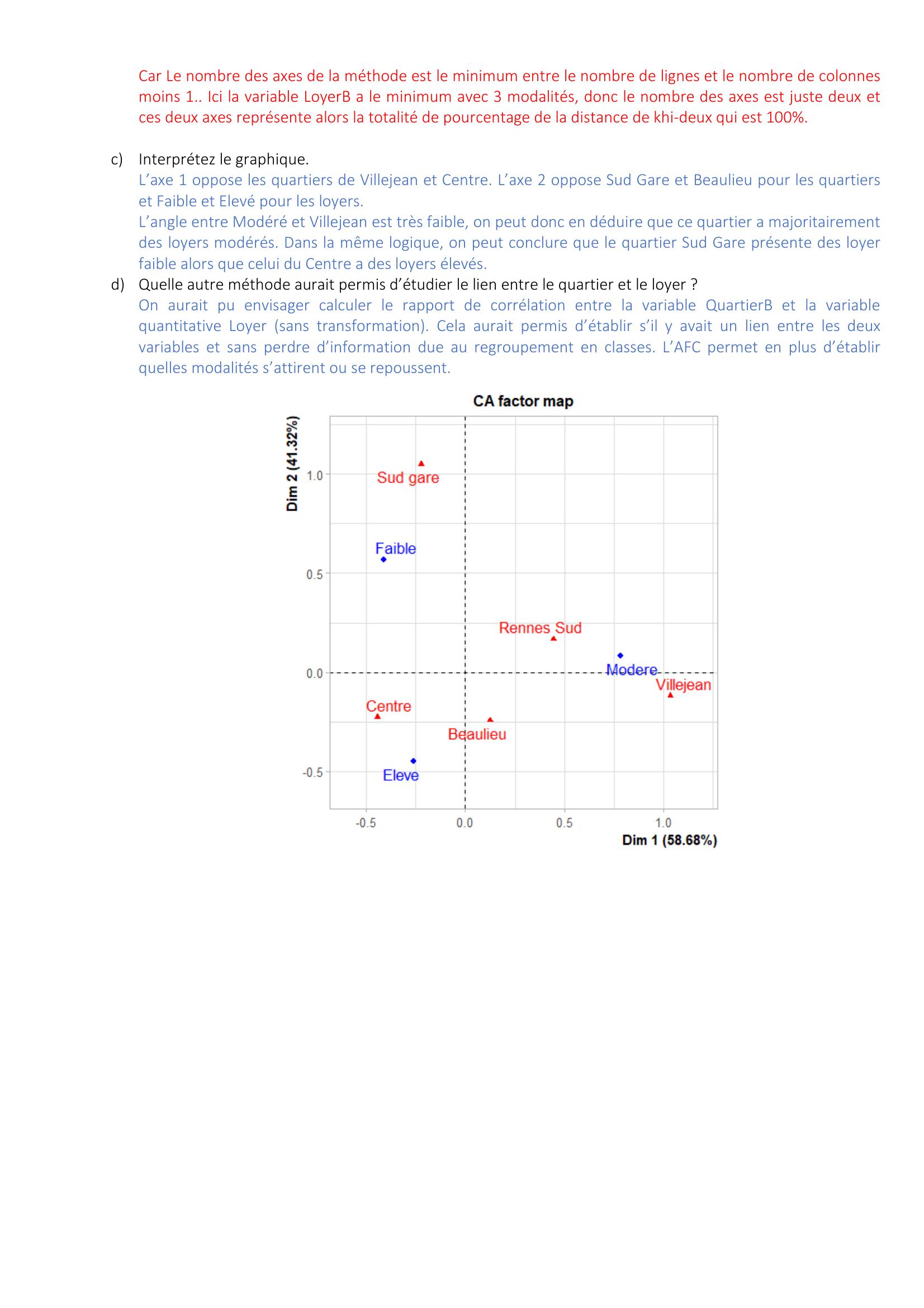
Page 4 : Car Le nombre des axes de la méthode est le minimum entre le nombre de lignes et le nombre de colonnes moins 1.. Ici la variable LoyerB a le minimum avec 3 modalités, donc le nombre des axes est juste deux et ces deux axes représente alors la totalité de pourcentage de la distance de khi-deux qui est 100. c Interprétez le graphique. L’axe 1 oppose les quartiers de Villejean et Centre. L’axe 2 oppose Sud Gare et Beaulieu pour les quartiers et Faible et Elevé pour les loyers. L’angle entre Modéré et Villejean est très faible, on peut donc en déduire que ce quartier a majoritairement des loyers modérés. Dans la même logique, on peut conclure que le quartier Sud Gare présente des loyer faible alors que celui du Centre a des loyers élevés. d Quelle autre méthode aurait permis d’étudier le lien entre le quartier et le loyer ? On aurait pu envisager calculer le rapport de corrélation entre la variable QuartierB et la variable quantitative Loyer sans transformation. Cela aurait permis d’établir s’il y avait un lien entre les deux variables et sans perdre d’information due au regroupement en classes. L’AFC permet en plus d’établir quelles modalités s’attirent ou se repoussent.