DS 2023 2024 GI
Télécharger le DS 2023 2024 GI en pdf
Page 1 : ExamenData Exploration - ING1 GIDate : 22 décembre 20232 feuilles R/V manuscrites autorisées, Calculatrice autoriséeDurée : 2hNombre de pages : 6Il sera tenu compte de la qualité de la rédaction et de la précision desjustifications.Exercice 1Le jeu des données Airbnb se compose d’informations publiques sur les annonces et les mesures Airbnbà New York. Les données ouvertes Airbnb de la ville de New York 2019 comprennent des informationssur environ 28590 logements Airbnb dans la ville et sont mises à la disposition du public par le gou-vernement de la ville de New York pour promouvoir la transparence et la compréhension de l’impactdes locations sur la ville. Dans la suite, on prendra que les 500 premiers logements et voici un extrait :IdNeighbourhoodLatitudeLongitudeRoom typePriceMinimum nightNumber of reviewsAvailability2539Brooklyn40.64747-73.9724Private room12551493242595Manahattan40.15792-73.5896Entire home2253451943647Brooklyn40.76489-73.965Shared room53152149...........................1. Préciser les variables étudiées, donner leur type et un moyen de les représenter graphiquement2. Quelle est la population étudiée ? Quelle est la taille de l’échantillon ?A- Analyse Univariée : Étude de la variable prix en dollarsLe logiciel R nous fournit les résultats suivants :quantile Airbnbprice0255075100338512518620001. Donner et interpréter les quartiles.2. Calculer l’écart inter-quartiles et l’étendue.3. La moyenne de prix par nuit est de 152.3. Comment interprétez-vous la différence entre lamoyenne et la médiane ?4. Parmi les indicateurs numériques calculés avant, lesquels sont des indicateurs de dispersion etlesquels sont des indicateurs de positions ?5. Voici le Boxplot boite à moustache pour la variable ‘prix’.1
Page 2 : a Calculer les extrémités des moustaches.b Y a-t-il des valeurs aberrantes ? Justifier votre réponse.B- Analyse Bivariée : Etude entre Prix et Neighbourhood arrondissementLa ville de New York compte 5 arrondissements neighbourhood. On s’intéresse maintenant à étudierle lien entre les deux variables arrondissements et le prix des locations dans ces arrondissements. Lelogiciel R nous fournit les résultats suivants : model - lm priceas.factorneighbourhood,data=Airbnb anovamodelAnalysis of Variance TableResponse: priceDfSum SqMean SqF value PrFas.factorneighbourhood68 1253070184281.1695 0.1819Residuals431 6791083157571. Donner la variance inter groupes et la variance intra groupes. En déduire la variation totale.2. Calculer le rapport de corrélation et interpréter cette valeur.C- Analyse Bivariée : Etude entre Room-Type type de chambre et NeighbourhoodarrondissementOn donne le tableau de contingenceEntire home/aptPrivate roomShared roomBronx340Brooklyn139980Manhattan139864Queens10120Staten Island0501. Etablir le tableau complet des effectifs observés en ajoutant les effectifs marginaux.2. Calculer et interpréter les valeurs suivantes n·1, f5·, f·2.3. Donner le tableau de profils colonnes. Comparer le tableau de profils colonnes avec le profilmoyen colonne. Que pouvez-vous prédire sur le lien entre ces deux variables ?On donne le tableau des effectifs théoriques2
Page 3 : Entire home/aptPrivate roomShared roomBronx4.0742.870.056Brooklyn137.93497.17?Manhattan133.27893.891.832Queens12.8049.020.176Staten Island2.910?0.044. Compléter les valeurs manquantes dans le tableau des effectifs théoriques, en détaillant lescalculs.5. Le calcul de la distance du khi-deux nous donne la valeur 15.139. Expliquer comment cettedistance est calculée.6. Y a-t-il un lien entre l’arrondissement et le type de chambre ? Justifiez votre réponse.d.d.l.4567891015Seuil9.4911.07512.5914.0715.5116.9218.3124.997. Faites vous confiance à ce résultat ? Justifiez votre réponse.D- Classification des appartements en fonction de leur prix, latitude et longitudeOn s’intéresse à une classification des appartements à partir de leur prix, latitude et longitude. Avecle logiciel R, on obtient les résultats suivants : kmean - kmeansAirbnbclus, centers=5printkmeanK-means clustering with 5 clusters of sizes 170, 15, 98, 121, 96Cluster means:latitudelongitudeprice10.09793711 -0.57990510.19903322 -0.34840931 -0.55111683.733524431.615389480.6041057 -0.24378884 -0.577245550.8876835 -0.38054485 -1.04046485 -0.6225150 -0.2073050Within cluster sum of squares by cluster:1 121.4429143.039589.2709170.924195.5637betweenSS / totalSS =58.6 Available components:1 "cluster""centers""totss""withinss""tot.withinss"6 "betweenss""size""iter""ifault"1. Quelle méthode a été utilisée pour effectuer cette classification ?2. Calculer l’inertie intra-classes.3. Donner le pourcentage d’inertie expliqué par les classes.4. Calculer l’inertie inter-classes.5. Déduire l’inertie totale.6. Proposer une autre méthode de classification et donner la différence entre les deux méthodes.3
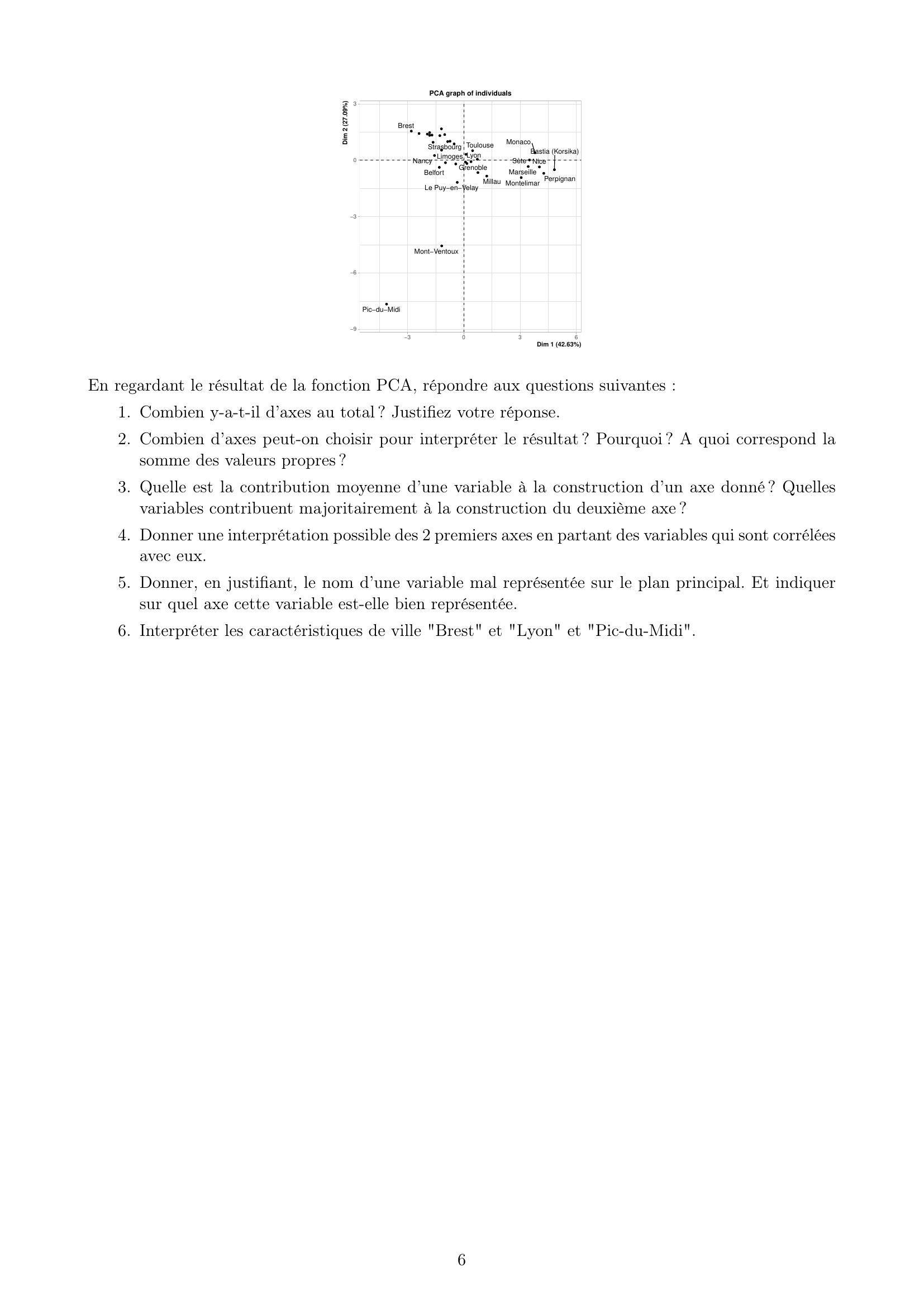
Page 4 : 7. On donne les affectations des 30 premiers appartements ainsi que l’arrondissement de ces ap-partements :kmean.cluster Airbnb.neighbourhoodgroup15Brooklyn21Manhattan33Manhattan45Brooklyn53Manhattan61Manhattan74Brooklyn81Manhattan93Manhattan101Manhattan113Manhattan121Manhattan135Brooklyn143Manhattan151Manhattan164Brooklyn175Brooklyn185Brooklyn195Brooklyn203Manhattan215Brooklyn223Manhattan231Manhattan243Manhattan253Manhattan264Brooklyn271Manhattan284Brooklyn292Manhattan305BrooklynPeut-on considérer que les clusters correspondent aux 5 arrondissements ? Justifier votre réponse.Exercice 2On considère data : Climfrance.txt. Ces données se composent de 36 lignes observations et 11 co-lonnes caractéristiques/variables. Les caractéristiques sont : l’altitude, la latitude, la longitude, latempérature annuelle moyenne, la température annuelle maximale, la température annuelle minimale,l’humidité relative, les précipitations annuelles moyennes, les précipitations maximales en 24 heures,le nombre de jours de pluie et le nombre d’heures d’ensoleillement par an.clim = read.table"Climfrance.txt", header = T, sep = ";", dec = "."install.packages"FactoMineR"libraryFactoMineRres.PCA.clim - PCAclimheadres.PCA.climeigeigenvaluepercentage of variancecumulative percentage of variancecomp 14.698556442.71414942.71415comp 22.942702026.75183769.465994
Page 5 : comp 31.340164712.18331681.64930comp 40.78153007.10481888.75412comp 50.55140825.01280293.76692comp 60.23853312.16848395.93540 res.PCA.climvarcontrib,1:4Dim.1Dim.2Dim.3Dim.4altitude2.84792993 27.3803710.17885911.15421895lat9.97555726 10.4212594.71061161.84063577lon6.020508552.025628 17.3696828 36.95051294tmean10.14368290 15.8695711.80207560.07607592tmax7.13248282 12.4612420.1501642 14.19652610tmin9.22985599 11.5264182.45170418.83405789relhumidity11.699895496.9932223.09854833.20138110pmean0.016800454.448227 56.76721949.42186140pmax24h12.575351763.4766648.37291412.68703808rainydays16.590682091.3386144.89838724.76582364sunshinehperyrs 13.767252774.0587850.1998335 16.87186820 res.PCA.climvarcos2,1:4Dim.1Dim.2Dim.3Dim.4altitude0.1335494714 0.81604125 0.002265643 0.009432545lat0.4677890372 0.31059394 0.059670231 0.015042103lon0.2823228641 0.06037157 0.220025144 0.301968164tmean0.4756730411 0.47297476 0.022827241 0.000621710tmax0.3344672570 0.37139335 0.001902159 0.116017305tmin0.4328204769 0.34353196 0.031056211 0.072193971relhumidity0.5486493340 0.20842513 0.039249913 0.026162429pmean0.0007878324 0.13257442 0.719081386 0.076997637pmax24h0.5897025642 0.10361807 0.106061328 0.021959099rainydays0.7779955548 0.03989588 0.062048822 0.038947416sunshinehperyrs 0.6455950031 0.12096755 0.002531330 0.137880821plotres.PCA.clim, choix="var"plotres.PCA.clim, choix="ind"5
Page 6 : MarseilleNiceBastia KorsikaPerpignanMonacoMontelimarSèteBrestStrasbourg ToulouseLyonNancyGrenobleLimogesMillauBelfortLe PuyenVelayMontVentouxPicduMidi963033036Dim 1 42.63Dim 2 27.09PCA graph of individualsEn regardant le résultat de la fonction PCA, répondre aux questions suivantes :1. Combien y-a-t-il d’axes au total ? Justifiez votre réponse.2. Combien d’axes peut-on choisir pour interpréter le résultat ? Pourquoi ? A quoi correspond lasomme des valeurs propres ?3. Quelle est la contribution moyenne d’une variable à la construction d’un axe donné ? Quellesvariables contribuent majoritairement à la construction du deuxième axe ?4. Donner une interprétation possible des 2 premiers axes en partant des variables qui sont corréléesavec eux.5. Donner, en justifiant, le nom d’une variable mal représentée sur le plan principal. Et indiquersur quel axe cette variable est-elle bien représentée.6. Interpréter les caractéristiques de ville "Brest" et "Lyon" et "Pic-du-Midi".6