DS 2024 2025 GIMA
Télécharger le DS 2024 2025 GIMA en pdf
Page 1 : CY-Tech – Département Mathématiques ING1 GIA-GMA – Examen Data Exploration 2024-2025 Durée 2h00 - 2 feuilles R/V autorisées manuscrits ou non - Calculatrice autorisée Il n’y a qu’une façon d’échouer, c’est d’abandonner avant d’avoir réussi !! Le jeu de données Animaux.csv contient des informations sur 50 animaux. Nous nous intéressons aux variables suivantes : - Type de régime alimentaire : Le type d'alimentation de l'animal : Carnivore, Herbivore, Omnivore, Insectivore. - Poids : Le poids moyen de l'animal en kilogrammes. - Taille : La taille moyenne de l'animal, mesurée en mètres. - Espérance de vie : L'âge moyen auquel un animal peut vivre dans la nature en année. - Vitesse maximale : La vitesse maximale à laquelle l'animal peut se déplacer, mesurée en kilomètre par heure. - Nombre de petits par an : Le nombre moyen de petits qu'un animal produit chaque année. - Longévité en captivité : L'espérance de vie moyenne de l'animal en année. - Consommation quotidienne : La quantité de nourriture que l'animal consomme en kilogramme par jour. - Habitat principal : L'endroit où l'animal vit naturellement : Savane, Désert, Océan… - Statut de conservation : L'état de conservation de l'espèce, selon les critères de la Liste rouge de l'Union Internationale pour la Conservation de la Nature UICN. Espèce en danger, Vulnérable, Non menacée. A- Analyse Univariée On commence à étudier la variable Espérance de vie. Le logiciel R nous fournit les résultats suivants : summaryDatasetEspérance de vie Min. 1st Qu. Median Mean 3rd Qu. Max. 7.0 12.00 21.00 25.94 40.00 100.00 1- Quelle est la population étudiée ? Quelle est la taille de l'échantillon ? 2- Préciser la nature de cette variable ainsi qu'un moyen de la représenter graphiquement. 3- Donner et interpréter les quartiles. 4- Calculer l'écart inter-quartiles et l'étendue. 5- Calculer et interpréter les extrémités m et M du Boxplot. 6- Donner la moyenne de la variable Esperance de vie. Comment interprétez-vous la différence entre la moyenne et la médiane ? 7- Parmi tous les indicateurs numériques calculés avant, lesquels sont des indicateurs de dispersion et lesquels sont des indicateurs de positions ? 8- Y a-t-il des valeurs aberrantes ? Justifier votre réponse.
Page 2 : B- Analyse Bivariée 1- Étude sur le lien entre Poids de l’animal et son vitesse maximale. Nous examinons en particulier les informations concernant le poids X et la vitesse maximale Y de sept animaux. Les données sont présentées dans le tableau suivant : Animal Poids Vitesse max Pélican 5 30 Paon 5 15 Loup 50 60 Koala 15 30 Lynx 25 80 Chien 50 55 Chouette 0.5 15 On a les résultats suivants : 𝑋𝑖7i=1= 150.5, 𝑌𝑖7i=1= 285, 𝑋𝑖7i=1𝑌𝑖=8432.5, Xi27i=1 = 5900.25, Yi27i=1 = 15275. 1- Calculer et interpréter le coefficient de corrélation entre les deux Variables X et Y. 2- Donner le modèle de régression linéaire de Y en fonction de X. 3- Calculer et interpréter le coefficient de détermination. 4- La vitesse d’un animal de 5 kg peut aller jusqu’à 25 km/h. a- Estimer la vitesse du Panda roux qui pèse en moyenne 5 kg. b- Calculer l’erreur de l’estimation. 2- Étude sur lien entre l’espérance de vie de l’animal et son régime alimentaire. Maintenant, on s’intéresse à étudier le lien entre l’espérance de vie de l’animal et son régime alimentaire. Pour la suite, nous allons tenir compte de tous les animaux présents dans le jeu de données Animaux.csv. Le logiciel R nous fournit les résultats suivants : Modele-lmDatasetEspérance de vie as.factorDatasetType de régime alimentaire anovaModele Analysis of Variance Table Response: DatasetEspérance de vie Df Sum Sq Mean Sq F value PrF as.factorDatasetType de régime alimentaire 3 1549.1 516.37 1.4258 0.2474 Residuals 46 16659.7 362.17 1- Calculer les variances inter-groupes, intra-groupes. 2- Déduire la variance totale. 3- Calculer et interpréter le rapport de corrélation.
Page 3 : 3- Étude sur le lien entre le type de régime alimentaire de l’animal et son statut de conservation. On s’intéresse à étudier le lien entre le type de régime alimentaire de l’animal et son statut de conservation. On donne le tableau de contingence suivant : Carnivore Herbivore Insectivore Omnivore Espèce en danger 2 4 1 0 Non menacée 20 12 0 6 Vulnérable 0 3 0 2 1- Donner les effectifs marginaux pour chacune de deux variables. 2- Donner le tableau des fréquences observées. 3- Calculer et interpréter les valeurs suivantes f33, f3/3, n.3 et f3. 4- Donner le tableau de profils lignes. 5- Donner le profil moyen colonne et le profil moyen ligne. 6- Comparer le tableau de profils lignes avec le profil moyen ligne et prédire le lien entre les deux variables. On donne le tableau des effectifs théoriques : 7- Calculer les valeurs t22 et t33 dans le tableau des effectifs théoriques, en détaillant les calculs. 8- Le calcul de la distance de Khi-deux nous donne la valeur de 14.01023. Expliquer comment cette distance est calculée. 9- Y a-t-il un lien entre le type de régime alimentaire de l’animal et son Statut de conservation? Justifier votre réponse en réalisant un test statistique convenable. 10- Faites-vous confiance à ce résultat? Justifier votre réponse? Voici la table des seuils de la loi du Khi-deux : d.d.l 1 2 3 4 5 6 7 8 9 10 Seuil 3.84 5.99 7.82 9.49 11.075 12.59 14.07 15.51 16.92 18.31 C- Analyse Multivariée Nous cherchons maintenant à établir le lien entre toutes les variables quantitatives présentes dans le jeu de données Animaux.csv, à l'aide d'une analyse en composantes principales. Les résultats obtenus par le logiciel R sont présentés en annexe. 1- Quel est le but de réaliser un ACP. 2- Pourquoi faut-il centrer et réduire les variables avant de réaliser un ACP? Carnivore Herbivore Insectivore Omnivore Espèce en danger 3.08 2.66 0.14 1.12 Non menacée 16.72 t22 0.76 6.08 Vulnérable 2.2 1.90 t33 0.8
Page 4 : 3- Combien y-a-t-il de points dans le nuage de points. En quelle dimension ces points sont-ils représentés? 4- Définir l’inertie totale, puis donner sa valeur. 5- Combien d’axes faut-il retenir pour avoir une bonne représentation? Justifier. 6- Donner les deux valeurs manquantes dans le tableau en justifiant vos calculs. 7- Donner la contribution moyenne de chaque variable ainsi que de chaque observation. 8- Est-ce que toutes les variables sont bien représenté dans le plan de dimension 2? Justifier. 9- Interpréter le graphe des variables. 10- Bonus L’observation 44 représente la baleine bleue. Comment pouvez-vous qualifiez cet animal? La plus belle réussite c'est de ne pas lâcher prise. Bon courage !
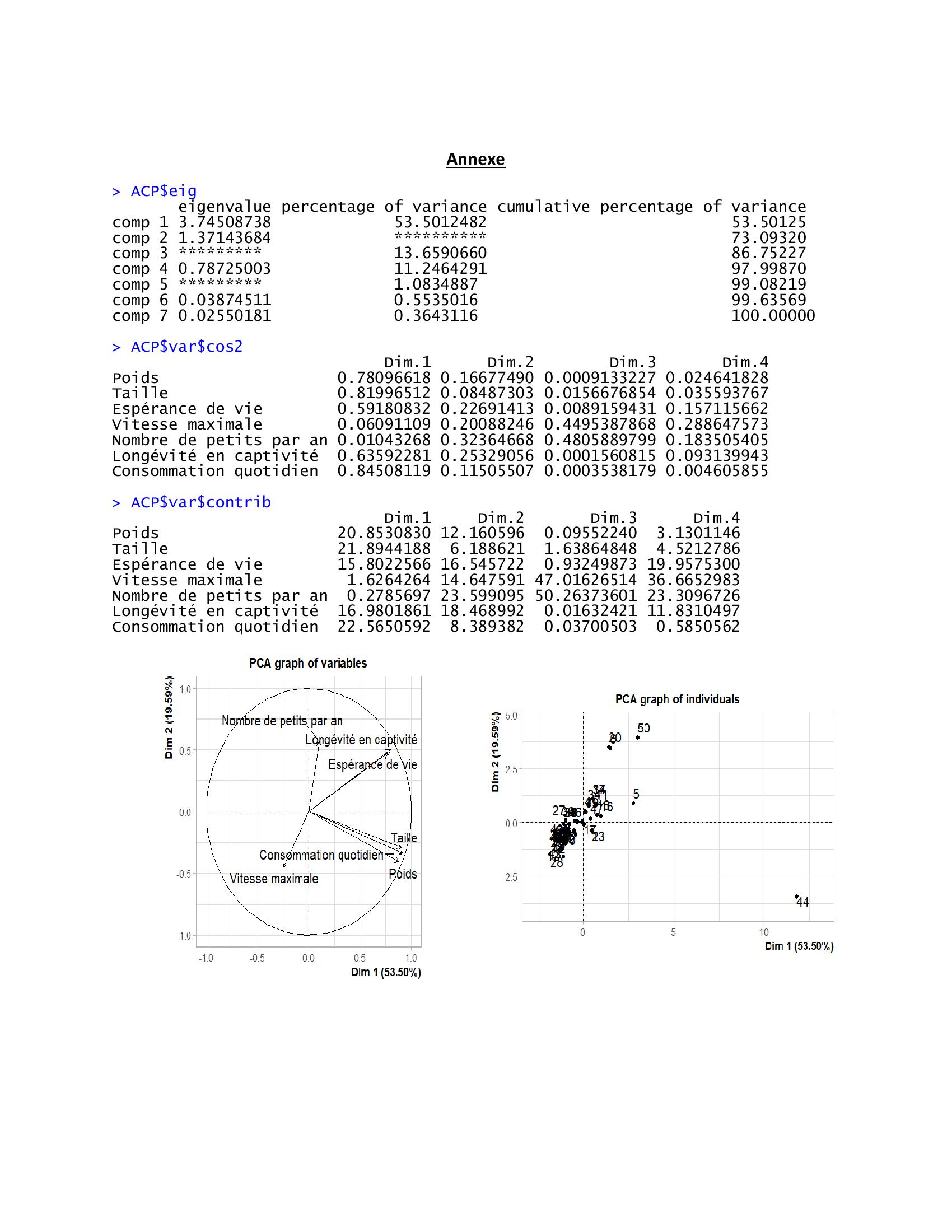
Page 5 : Annexe ACPeig eigenvalue percentage of variance cumulative percentage of variance comp 1 3.74508738 53.5012482 53.50125 comp 2 1.37143684 73.09320 comp 3 13.6590660 86.75227 comp 4 0.78725003 11.2464291 97.99870 comp 5 1.0834887 99.08219 comp 6 0.03874511 0.5535016 99.63569 comp 7 0.02550181 0.3643116 100.00000 ACPvarcos2 Dim.1 Dim.2 Dim.3 Dim.4 Poids 0.78096618 0.16677490 0.0009133227 0.024641828 Taille 0.81996512 0.08487303 0.0156676854 0.035593767 Espérance de vie 0.59180832 0.22691413 0.0089159431 0.157115662 Vitesse maximale 0.06091109 0.20088246 0.4495387868 0.288647573 Nombre de petits par an 0.01043268 0.32364668 0.4805889799 0.183505405 Longévité en captivité 0.63592281 0.25329056 0.0001560815 0.093139943 Consommation quotidien 0.84508119 0.11505507 0.0003538179 0.004605855 ACPvarcontrib Dim.1 Dim.2 Dim.3 Dim.4 Poids 20.8530830 12.160596 0.09552240 3.1301146 Taille 21.8944188 6.188621 1.63864848 4.5212786 Espérance de vie 15.8022566 16.545722 0.93249873 19.9575300 Vitesse maximale 1.6264264 14.647591 47.01626514 36.6652983 Nombre de petits par an 0.2785697 23.599095 50.26373601 23.3096726 Longévité en captivité 16.9801861 18.468992 0.01632421 11.8310497 Consommation quotidien 22.5650592 8.389382 0.03700503 0.5850562