DS 2024 2025 GIMA
Télécharger le DS 2024 2025 GIMA en pdf
Page 1 : 2024/2025Département MathématiquesIng1-GIA et Ing1-GMAProbabilités & SimulationRattrapage - mars 2025◁Consignes ▷Durée : 120 mn▶Autorisé : Trois feuilles A4 recto-verso manuscrites. Calculatrices.▶Non autorisé : Tout autre document et tous les supports électroniques smart-phone, tablette,ordinateur,....- L’épreuve est composée de 4 exercices indépendants.- La table de la loi normale standard y est jointe.◁Sujet de l’épreuve ▷▶On notera :• v.a.r. pour variable aléatoire réelle.• v.a.r.d. pour variable aléatoire réelle discrète.• v.a.r.a.c. pour variable aléatoire réelle absolument continue.• f.m.p. pour fonction de masse de probabilité.• f.d.p. pour fonction de densité de probabilité.• f.r. pour fonction de répartition.Exercice 1.xx ptsLa quantité de pain en centaines de kilos qu’un boulanger vend en une journée est une v.a.r.a.c. Xde f.d.p. f donnée parfx =axsi 0 x 3a6 xsi 3 x 60sinonOù a est un réel.1a Montrer que a = 19.b Tracer l’allure de la courbe représentative de f.2a Déterminer F, la fonction de répartition de X.b Tracer l’allure de la courbe représentative de F.3 En faisant usage de F, calculer la probabilité des événements suivants :a A = "le boulanger vend en une journée, plus de 300 kilos de pain".b B = "le boulanger vend en une journée, entre 100 et 300 kilos de pain".4 Déterminer la médiane de X, c’est-à-dire le réel m telle que PX m = 1/2.5 Calculer EX, l’espérance de X.1
Page 2 : Exercice 2.xx ptsPour toute v.a.r.a.c. suivant une loi normale standard, on notera φ sa f.d.p. et Φ sa f.r..Soit X une v.a.r. qui suit une loi normale standard, i.e. X N0, 1. Soit x R+ ; prouver que :a PX x = PX x ;b PX x = 2PX x ;c PX x = 2PX x 1Exercice 3.xx ptsPour toute v.a.r.a.c. suivant une loi normale standard, on notera φ sa f.d.p. et Φ sa f.r..Soit Z une v.a.r. distribuée selon une loi Nµ, σ2, avec µ = 1 et σ = 2.1 Calculer les probabilités suivantes :a PZ 0 ;b PZ 12 ;c PZ 1 42 Résoudre les équations en x suivantes :a PZ x = 0.5 ;b P2x Z 1 2x = 0.98 ;c PZ x = 0.2Exercice 4.xx ptsSoit X une v.a.r.a.c. suivant une loi uniforme sur a, b, avec a b. On note µ son espérance et σ sonécart-type.1a Donner la valeur de µ et la valeur de σ, en fonction de a et b.b Démontrer que µ σ a et que µ + σ b.c Calculer PX µ σ, µ + σ.2 On suppose maintenant que 0 a b. Soit Y = X2, une nouvelle v.a.r..a Donner FX, la fonction de répartition de X.b Déterminer FY la fonction de répartition de Yc Justifier que Y est une v.a.r.a.c.. Montrer que la fonction fY ci-après est une f.d.p de Y .fY y =0si y a212b aysi a2 y b20si b2 yd Calculer EY , l’espérance de Y .2
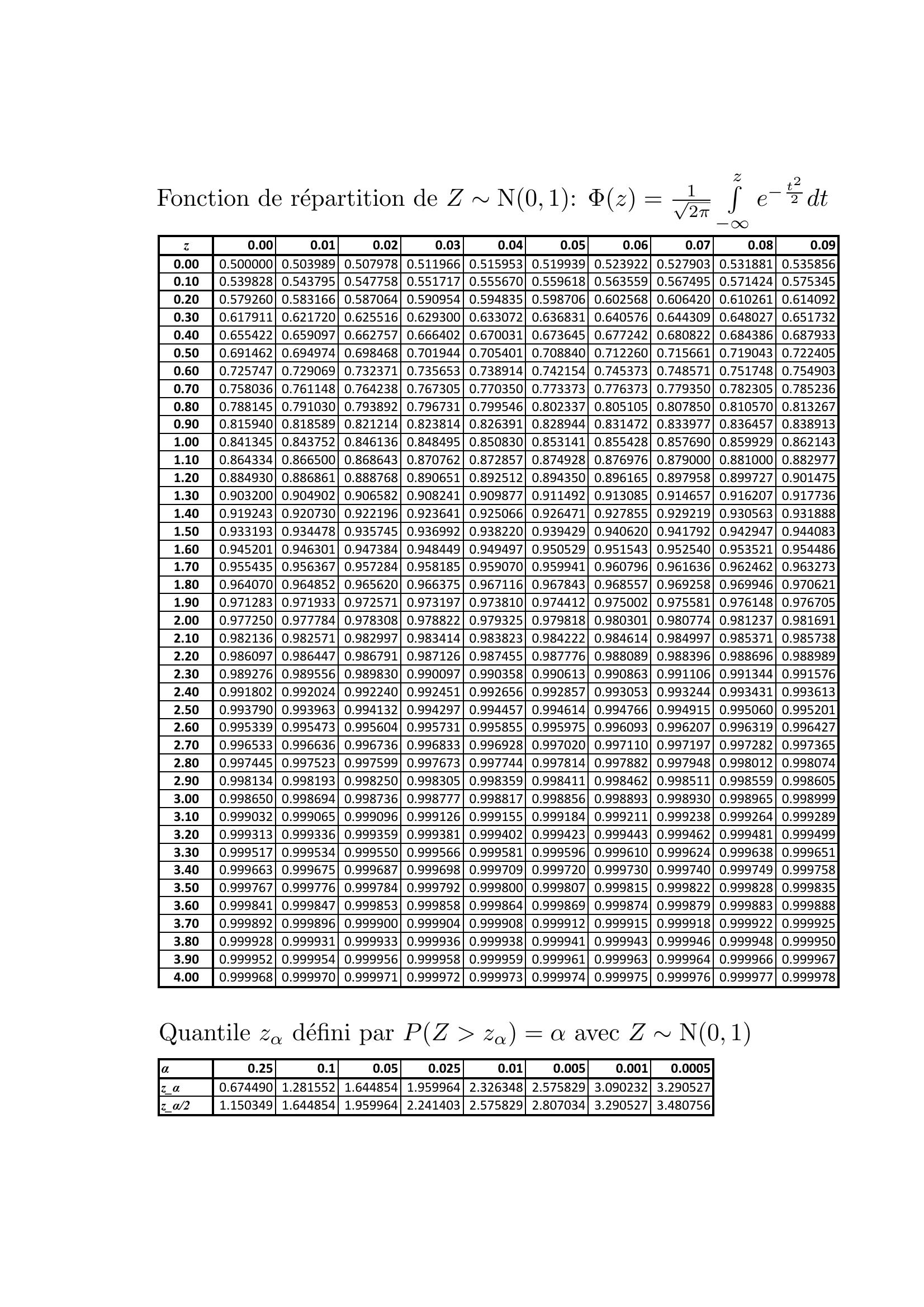
Page 3 : z0.000.010.020.030.040.050.060.070.080.090.000.500000 0.503989 0.507978 0.511966 0.515953 0.519939 0.523922 0.527903 0.531881 0.5358560.100.539828 0.543795 0.547758 0.551717 0.555670 0.559618 0.563559 0.567495 0.571424 0.5753450.200.579260 0.583166 0.587064 0.590954 0.594835 0.598706 0.602568 0.606420 0.610261 0.6140920.300.617911 0.621720 0.625516 0.629300 0.633072 0.636831 0.640576 0.644309 0.648027 0.6517320.400.655422 0.659097 0.662757 0.666402 0.670031 0.673645 0.677242 0.680822 0.684386 0.6879330.500.691462 0.694974 0.698468 0.701944 0.705401 0.708840 0.712260 0.715661 0.719043 0.7224050.600.725747 0.729069 0.732371 0.735653 0.738914 0.742154 0.745373 0.748571 0.751748 0.7549030.700.758036 0.761148 0.764238 0.767305 0.770350 0.773373 0.776373 0.779350 0.782305 0.7852360.800.788145 0.791030 0.793892 0.796731 0.799546 0.802337 0.805105 0.807850 0.810570 0.8132670.900.815940 0.818589 0.821214 0.823814 0.826391 0.828944 0.831472 0.833977 0.836457 0.8389131.000.841345 0.843752 0.846136 0.848495 0.850830 0.853141 0.855428 0.857690 0.859929 0.8621431.100.864334 0.866500 0.868643 0.870762 0.872857 0.874928 0.876976 0.879000 0.881000 0.8829771.200.884930 0.886861 0.888768 0.890651 0.892512 0.894350 0.896165 0.897958 0.899727 0.9014751.300.903200 0.904902 0.906582 0.908241 0.909877 0.911492 0.913085 0.914657 0.916207 0.9177361.400.919243 0.920730 0.922196 0.923641 0.925066 0.926471 0.927855 0.929219 0.930563 0.9318881.500.933193 0.934478 0.935745 0.936992 0.938220 0.939429 0.940620 0.941792 0.942947 0.9440831.600.945201 0.946301 0.947384 0.948449 0.949497 0.950529 0.951543 0.952540 0.953521 0.9544861.700.955435 0.956367 0.957284 0.958185 0.959070 0.959941 0.960796 0.961636 0.962462 0.9632731.800.964070 0.964852 0.965620 0.966375 0.967116 0.967843 0.968557 0.969258 0.969946 0.9706211.900.971283 0.971933 0.972571 0.973197 0.973810 0.974412 0.975002 0.975581 0.976148 0.9767052.000.977250 0.977784 0.978308 0.978822 0.979325 0.979818 0.980301 0.980774 0.981237 0.9816912.100.982136 0.982571 0.982997 0.983414 0.983823 0.984222 0.984614 0.984997 0.985371 0.9857382.200.986097 0.986447 0.986791 0.987126 0.987455 0.987776 0.988089 0.988396 0.988696 0.9889892.300.989276 0.989556 0.989830 0.990097 0.990358 0.990613 0.990863 0.991106 0.991344 0.9915762.400.991802 0.992024 0.992240 0.992451 0.992656 0.992857 0.993053 0.993244 0.993431 0.9936132.500.993790 0.993963 0.994132 0.994297 0.994457 0.994614 0.994766 0.994915 0.995060 0.9952012.600.995339 0.995473 0.995604 0.995731 0.995855 0.995975 0.996093 0.996207 0.996319 0.9964272.700.996533 0.996636 0.996736 0.996833 0.996928 0.997020 0.997110 0.997197 0.997282 0.9973652.800.997445 0.997523 0.997599 0.997673 0.997744 0.997814 0.997882 0.997948 0.998012 0.9980742.900.998134 0.998193 0.998250 0.998305 0.998359 0.998411 0.998462 0.998511 0.998559 0.9986053.000.998650 0.998694 0.998736 0.998777 0.998817 0.998856 0.998893 0.998930 0.998965 0.9989993.100.999032 0.999065 0.999096 0.999126 0.999155 0.999184 0.999211 0.999238 0.999264 0.9992893.200.999313 0.999336 0.999359 0.999381 0.999402 0.999423 0.999443 0.999462 0.999481 0.9994993.300.999517 0.999534 0.999550 0.999566 0.999581 0.999596 0.999610 0.999624 0.999638 0.9996513.400.999663 0.999675 0.999687 0.999698 0.999709 0.999720 0.999730 0.999740 0.999749 0.9997583.500.999767 0.999776 0.999784 0.999792 0.999800 0.999807 0.999815 0.999822 0.999828 0.9998353.600.999841 0.999847 0.999853 0.999858 0.999864 0.999869 0.999874 0.999879 0.999883 0.9998883.700.999892 0.999896 0.999900 0.999904 0.999908 0.999912 0.999915 0.999918 0.999922 0.9999253.800.999928 0.999931 0.999933 0.999936 0.999938 0.999941 0.999943 0.999946 0.999948 0.9999503.900.999952 0.999954 0.999956 0.999958 0.999959 0.999961 0.999963 0.999964 0.999966 0.9999674.000.999968 0.999970 0.999971 0.999972 0.999973 0.999974 0.999975 0.999976 0.999977 0.999978α0.250.10.050.0250.010.0050.0010.0005zα 0.674490 1.281552 1.644854 1.959964 2.326348 2.575829 3.090232 3.290527zα/2 1.150349 1.644854 1.959964 2.241403 2.575829 2.807034 3.290527 3.480756Fonction de repartition de Z ⇠N0, 1: Φz =1p2⇡zR1et22 dtQuantile z↵defini par PZ z↵ = ↵avec Z ⇠N0, 1