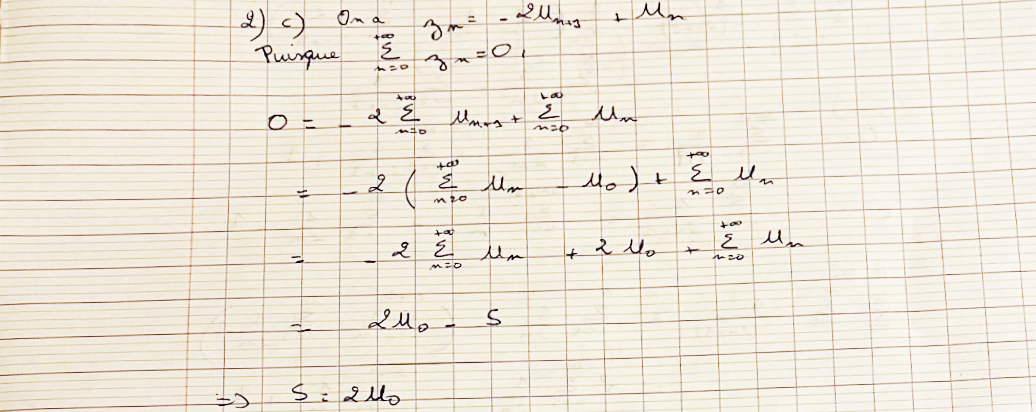DS1 2018 2019 Correction
La correction contient des erreurs qui ont été corrigées sur le site (bas de page) mais pas sur le pdf.
Télécharger le DS1 2018 2019 Correction en pdf
Page 1 : SérieEISTI-Deuxième annéeCorrection du DS1 - Octobre 2018Exercice 1.1. Si la suite unnN tend vers 0, alors la sérieXn0un converge.La proposition est fausse.Un contre exemple : Soit unnNla suite dénie pour tout n Npar un = 1n, on a lasuite unnNconverge vers 0 mais la sérieXn11n diverge : il s'agit de la série de Riemann avecα = 1 1.2. Si la sérieXn0un diverge, alors la sérieXn0u2n diverge. La proposition est fausse.Un contre exemple : Soit unnNla suite dénie pour tout n N, par un = 1n, on a lasérie de terme général un diverge série de Riemann avec α = 1 1, mais la série de termegénéral u2n converge la série de Riemann avec α = 2 1.3. Si la sérieXn0un diverge, alors la suite unnN ne tend pas vers 0. La proposition est fausse.Un contre exemple : Soit unnNla suite dénie pour tout n Npar un = 1n, on a lasuite unnNconverge vers 0 et la sérieXn11n diverge série de Riemmann avec α = 1 1.4. Si la sérieXn0un converge, alors la sérieXn0u2n converge. La proposition est vraie. Preuve :La suite unnN converge vers 0, car la série de terme général un converge, donc u2n =+oun.On peut déduire qu'à partir d'un certain rang n0 N, que 0 u2n un.La sérieXn0un converge, donc d'après le théorème de majoration appliqué aux séries à termespositifs la sérieXn0u2n converge.Exercice 2.1. Le terme génaral de la sérieXn0un converge vers 1 ̸= 0, donc la sérieXn0un diverge.2. La suite vnnN est à valeurs positives. On applique la règle de Cauchy, on avn1n=2n + 5 42n + 5n=1 +42n + 5n=en ln142n+5 On a n ln142n+5 +42n+5, par suitelimn→+n ln142n+5 = 2, d'oulimn→+vn1n = e2 1.Ce qui implique la convergence de la série de terme général vn.1/4
Page 2 : SérieEISTI-Deuxième année3. Pour tout entier naturel n, le terme wn = n!33n!.3n est postif. On applique la règle de d'Alembert :wn+1wn=n + 1!3n!33n!3n + 1!3n+13n=3.n + 133n + 33n + 23n + 1=n + 123n + 23n + 1limn→+wn+1wn= 19 1, d'après la règle de D'Alembert la série de terme général wn converge.Exercice 31. La suite unnN est à valeurs positives. On applique la règle de nαun pour montrer la conver-gence de la sérieXn0un. On alimn→+n2un =limn→+n2n+1enln3 = 0 croissance comparée.On a prouvé l'existence d'un α = 2 1 telle que n2un tend vers 0, d'ou la convergence deXn0un.2. On note S la valeur de la série+Xn=0un. On a13S=+Xn=0n + 13n+1=+Xn=1n3n=+Xn=1n + 13n+Xn=113n=S u0 1311 13=S 32On a alors 1 13S = 32 par suite S = 94.2/4
Page 3 : SérieEISTI-Deuxième annéeExercice 4.1. 1.a Le développement limité à l'ordre 2 de wn estwn=ln n + 1n2 un+1un!=ln n + 1n2 n + 1n + 3!=2 ln1 + 1n + lnn1 + 1nlnn1 + 3n=3 ln1 + 1n + lnn1 + 1nln1 + 3n=3 1n 121n2 + o 1n2 3n 129n2 + o 1n2 =3n2 + o 1n2 On déduit alors l'équivalence wn+3n2 . D'après le critère de Riemann la sérieXn11n2converge α = 2 1, donc la sérieXn13n2 converge, de plus wnnN et 1n2 nNsont àvaleurs positives, en appliquant le théorème des équivalences, la sérieXn0wn converge.b On a la sérieXn0wn =Xn0vn+1 vn est une série téléscopique convergente d'après lapremière question, la suite vnnNest donc convergente. Soit ℓsa limite.c En tulisant la relation vn = lnn2un, on déduit que un = evnn2 . la suite vnnNconvergevers ℓ, donc la suite evnnNconverge vers L = eℓ. D'ou l'équivalence un +Ln2 .2. a A l'aide de l'équivalence un +Ln2 , on alimn→+nun =limn→+Ln = 0.b Soit SN =NXn=1zn =NXn=0n + 1un+1 nun = N + 1uN+1 car il s'agit d'une série télésco-pique.D'après la question précédentelimn→+NXn=0zn =limn→+SN =limN→+nun = 0.c On note S la valeur de la série+Xn=0un. On commence par montrer que zn = 2un+1 + un.3/4
Page 4 : SérieEISTI-Deuxième annéeEn eet, on azn=n + 1un+1 nun=n + 1un+1 n + 1un + un=n + 11 n + 3n + 1un+1 + un=n + 1 2n + 1un+1 + un=2un+1 + unPuisque+Xn=0zn = 0, on a0=2+Xn=0un+1 ++Xn=0un=2S u0 + S=u0 SOn déduit alors que S = u0.4/4