DS1 2019 2020
Télécharger le DS1 2019 2020 en pdf
Page 1 : Cycle préparatoire 2ème annéeDevoir surveillé 1K. Fayad, K. Guezguez, J.-M. Masereel, R. NuadiMatière : AlgèbreDate : Vendredi 18 octobre 2019Appareils électroniques et documents interditsDurée : 2 heuresNombre de pages : 3Il sera tenu compte de la qualité de la rédaction et de la précision des justifications.Le sujet comporte six exercices. L’ordre dans lequel ceux-ci sont traités n’est pas imposé. La page 3 est àrendre.Exercice 1. 3 points1. En interprétant P par « je pars », Q par « tu restes » et R par « il n’y a personne », traduire les formuleslogiques suivantes en langage naturel = en français :P nonQ ⇒R;nonP Q ⇒nonR.2. Les deux propositions précédentes sont-elles équivalentes? Justifier.Exercice 2. 4 points1. Montrer que, pour tout entier naturel non nul n,nXk=11kk = 1n2n + 1 14.2. Soit n un entier naturel non nul. Montrer quepn2 + 1 n’est pas un entier.Exercice 3. 2 pointsSoit A,B,C des parties d’un ensemble E . Montrer queA \ B \ C = A \ B C .Exercice 4. 2 pointsOn considére les deux propositions suivantes :P1 : x R,y R,y 2 x.P2 : x R,y R,z R, x = y + z 2.1. Exprimer à l’aide de quantificateurs la négation des propositions P1 et P2.2. Les assertions P1 et P2 sont-elles vraies ou fausses? Justifier.- 1 / 3 -
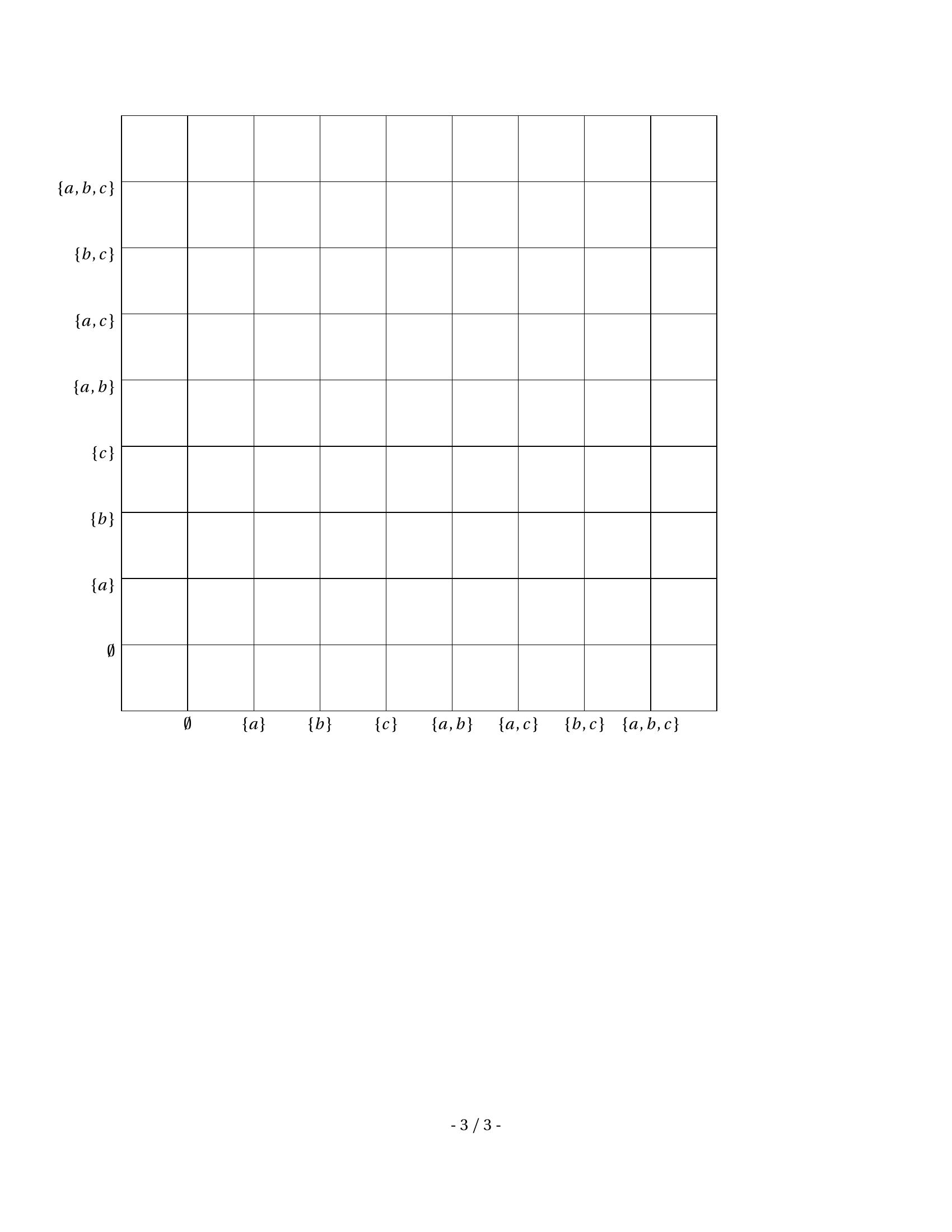
Page 2 : Exercice 5. 4.5 pointsOn définit dans Z la relation en posant, pour tout couple x; y Z2 :x y ⇔k N, y = k x.1. Montrer que la relation est une relation d’ordre dans Z.On considére dans la suite que Z est ordonné par la relation .2. Cette relation d’ordre est-elle totale? Justifier.3. Dans l’ensemble Z, on considére A = 2,3,6.a Si possible, donner un majorant et un minorant de A. Justifier.b Si possible, donner le plus petit élément et le plus grand élément de A. Justifier.Exercice 6. 9 pointsSoir E un ensemble et A une partie de E . Soit R la relation définie sur PE par :X RY ⇔X A = Y A1. Montrer que R est une relation d’équivalence.2. On pose dans cette question E = a;b ;c et A = a;b .a Quel est le cardinal de PE ?b Pour chaque X et Y deux parties de E , si X RY , placer sur le repère voir la page 3 le point decoordonnées X ,Y .c Comment lire sur le graphe que la relation R est symétrique, réflexive?d Pour toute partie B de E déterminer C l B, la classe d’équivalence de B pour la relation R.e Donner une partition de E à l’aide des classes d’équivalence de R.- 2 / 3 -
Page 3 : ;ab c a,b a,c b,c a,b,c ;ab c a,b a,c b,c a,b,c - 3 / 3 -