DS1 2022 2023 Correction Analyse2-DS PREING1 S2

Correction proposée par Mathis S. La plupart des résultats ont été vérifiés via des outils informatiques mais des erreurs peuvent s’être glissées.

Voir le Sujet DS1 2022 2023

Exercice 1 :

1.

\[\text{Soit }w\ \text{la fonction définie par }w(x) = x^{2} + 4x + \frac{1}{x - 1}\] \[\text{Alors }w^{'}(x) = 2x + 4 - \frac{1}{(x - 1)^{2}}\] \[f^{'}(x) = w^{'}(x)\cos\left( w(x) \right) = \left( 2x + 4 - \frac{1}{(x - 1)^{2}} \right)\cos\left( x^{2} + 4x + \frac{1}{x - 1} \right)\] \[\forall x\mathbb{\in R\backslash}\text{\{}1\},\ f'(x) = \left( 2x + 4 - \frac{1}{(x - 1)^{2}} \right)\cos\left( x^{2} + 4x + \frac{1}{x - 1} \right)\]

2.

\[\text{Soient }u\ \text{et}\ v\ \text{deux fonctions définies par }u(x) = 2x^{2} + 1\ \text{et }v(x) = x^{2} + 3\] \[\text{Alors }u^{'}(x) = 4x\ \text{et }v^{'}(x) = 2x\] \[g^{'}(x) = \frac{\left( u^{'}v - uv^{'} \right)(x)}{v(x)^{2}}\] \[= \frac{4x\left( x^{2} + 3 \right) - 2x\left( 2x^{2} + 1 \right)}{\left( x^{2} + 3 \right)^{2}}\] \[= \frac{4x^{3} + 12x - 4x^{3} - 2x}{\left( x^{2} + 3 \right)^{2}} = \frac{10x}{\left( x^{2} + 3 \right)^{2}}\] \[\forall x\mathbb{\in R,\ }g^{'}(x) = \frac{10x}{\left( x^{2} + 3 \right)^{2}}\]

Exercice 2 :

1.

\[g(x) = \frac{x^{2} - 4}{x + 1}\] \[g^{'}(x) = \frac{2x(x + 1) - (x^{2} - 4)}{(x + 1)^{2}} = \frac{2x^{2} + 2x - x^{2} + 4}{(x + 1)^{2}} = \frac{x^{2} + 2x + 4}{(x + 1)^{2}}\] \[g^{''}(x) = \frac{(2x + 2)(x + 1)^{2} - \left( x^{2} + 2x + 4 \right)2(x + 1)}{(x + 1)^{4}}\] \[= \frac{(2x + 2)(x + 1) - 2\left( x^{2} + 2x + 4 \right)}{(x + 1)^{3}}\] \[= \frac{2x^{2} + 2x + 2x + 2 - 2x^{2} - 4x - 8}{(x + 1)^{3}}\] \[= - \frac{6}{(x + 1)^{3}}\] \[g^{''}(x - 1) = - \frac{6}{x^{3}} = 3( - 1)^{3}\left( \frac{2!}{x^{3}} \right)\]

• \[\text{Montrons par récurrence que }\forall n \geq 2,\ g^{(n)}(x - 1) = 3( - 1)^{n + 1}\left( \frac{n!}{x^{n + 1}} \right),\]

\[\text{soit }g^{(n)}(x) = 3( - 1)^{n + 1}\left( \frac{n!}{(x + 1)^{n + 1}} \right)\] \[\text{Soit }P(n):g^{(n)}(x - 1) = 3( - 1)^{n + 1}\left( \frac{n!}{x^{n + 1}} \right)\]

• Nous venons de montrer que $P(2)$ est vraie. Montrons maintenant que $P(n) \Rightarrow P(n + 1)$

\[g^{(n + 1)}(x - 1)\] \[= \left( g^{(n)}(x - 1) \right)^{'}\] \[= \left( 3( - 1)^{n + 1}\left( \frac{n!}{x^{n + 1}} \right) \right)^{'}\] \[= \left( 3( - 1)^{n + 1}\ n!x^{- n - 1} \right)^{'}\] \[g^{(n + 1)}(x - 1) = 3 \times n!( - 1)^{n + 1} \times \left( - (n + 1) \right)x^{- n - 2}\] \[g^{(n + 1)}(x - 1) = 3( - 1)^{n + 2}\frac{n!(n + 1)}{x^{n + 2}} = 3( - 1)^{n + 2}\frac{(n + 1)!}{x^{n + 2}}\]

• Conclusion :

\[g^{'}(x) = \frac{x^{2} + 2x + 4}{(x + 1)^{2}}\] \[\forall n \geq 2,\ g^{(n)}(x) = 3( - 1)^{n + 1}\left( \frac{n!}{(x + 1)^{n + 1}} \right)\]

Autre méthode : Fractions partielles

• \(\text{On admet qu'il existe trois réels }A,B,C\ \text{tels que }g(x) = \frac{A}{x + 1} + Bx + C\)

\[g(x) = \frac{A + Bx(x + 1) + C(x + 1)}{x + 1}\] \[= \frac{A + Bx^{2} + (B + C)x + C}{x + 1}\]

• Par identification, on trouve $B = 1,\ C = - 1,\ A = - 3$

\[g(x) = - \frac{3}{x + 1} + x - 1\]

• Il est aisé de calculer les dérivées $n$-ièmes de cette fonction.

2.

\[\lim_{x \rightarrow 0}\frac{1 + \ln(x + 1) - e^{x}}{1 - \cos(x)}\] \[\text{Nous avons }\lim_{x \rightarrow 0}\left( 1 + \ln(x + 1) - e^{x} \right) = 1 - \ln(1) - e^{1} = 0\] \[\lim_{x \rightarrow 0}\left( 1 - \cos(x) \right) = 1 - \cos(0) = 0\]

• Les fonctions $x \rightarrow \left( 1 + \ln(x + 1) - e^{x} \right)$ et $x \rightarrow \left( 1 - \cos(x) \right)$ sont dérivables au voisinage de 0 et le dénominateur ne s’annule pas au voisinage de 0, nous pouvons donc appliquer le théorème de l’Hôpital.

\[\lim_{x \rightarrow 0}\frac{1 + \ln(x + 1) - e^{x}}{1 - \cos(x)} = \lim_{x \rightarrow 0}\frac{\frac{1}{x + 1} - e^{x}}{\sin(x)}\] \[\text{Nous avons }\lim_{x \rightarrow 0}\left( \frac{1}{x + 1} - e^{x} \right) = \lim_{x \rightarrow 0}{\sin(x)} = 0\]

• Le numérateur et le dénominateur sont dérivables au voisinage de 0 et $\sin(x)$ ne s’annule pas au voisinage de 0, nous pouvons donc appliquer le théorème de l’Hôpital.

\[\lim_{x \rightarrow 0}\frac{1 + \ln(x + 1) - e^{x}}{1 - \cos(x)}\] \[= \lim_{x \rightarrow 0}\frac{\frac{1}{x + 1} - e^{x}}{\sin(x)}\] \[= \lim_{x \rightarrow 0}\frac{- \frac{1}{(x + 1)^{2}} - e^{x}}{\cos(x)} = - 2\] \[\lim_{x \rightarrow 0}\frac{1 + \ln(x + 1) - e^{x}}{1 - \cos(x)} = - 2\]

Exercice 3 :

1.

\[f\ \text{est sous la forme}\frac{u}{v}\ \text{ avec }u(x) = e^{x}\text{ et }v(x) = x^{e}\] \[u^{'}(x) = e^{x}\ \text{et }v^{'}(x) = ex^{e - 1} = \frac{ex^{e}}{x}\] \[f^{'} = \frac{u^{'}v - uv^{'}}{v^{2}}\] \[\forall x \in \mathbb{R}_{+}^{*}, f^{'}(x)= \frac{e^{x}x^{e} - ex^{e - 1}e^{x}}{\left( x^{e} \right)^{2}}\] \[= \frac{e^{x}}{x^{e}} - \left( \frac{e}{x} \right)\left( \frac{e^{x}}{x^{e}} \right)\] \[= f(x) - \left( \frac{e}{x} \right)f(x)\] \[f^{'}(x) = \left( 1 - \frac{e}{x} \right)f(x) = \left( \frac{x - e}{x} \right) \cdot f(x)\] \[\text{Ainsi }f\text{ vérifie }x \cdot f(x) = (x - e) \cdot f(x)\text{ pour tout }x > 0\]

2.

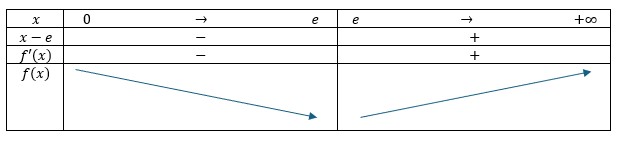
• Dressons le tableau de variations de $f$, sachant que $f$ est strictement positive sur $\rbrack 0, + \infty\lbrack$

3.

• D’après le tableau de variations précédent, $f$ admet un minimum en $e$

\[\text{La valeur de ce minimum est }f(e) = \frac{e^{e}}{e^{e}} = 1\]

Exercice 4 :

1.

• \(f\ \text{est continue sur }\mathbb{R\ }\text{si et seulement si }f(0) = \lim_{x \rightarrow 0^{+}}{f(x)}\)

• Alors, $c = 1$

2.

• $f$ est dérivable sur $\mathbb{R}^{*}$

\[f^{'}(x) = \Biggl \{ \begin{matrix} 2ax + b\ \text{si }x < 0 \\ \cos(x) - \sin(x)\text{ si }x > 0 \end{matrix}\]

• \(f^{'} \text{est définie et continue en 0 si }\lim_{x \rightarrow 0^{-}}{f^{'}(x)} = \lim_{x \rightarrow 0^{+}}{f^{'}(x)}\ \text{soit}\ b = 1\)

• Alors $f^{‘}(0) = 1$

3.

• $f^{‘}$ est dérivable sur $\mathbb{R}^{*}$

\[f^{'}(x) = \Biggl \{ \begin{matrix} 2a\ \text{si }x < 0 \\ - \sin(x) - \cos(x)\text{ si }x > 0 \end{matrix}\] \[f^{''}\text{est définie et continue en 0 si }\lim_{x \rightarrow 0^{-}}{f^{''}(x)} = \lim_{x \rightarrow 0^{+}}{f^{''}(x)}\] \[\text{Alors }2a = - 1\ \text{soit }a = - \frac{1}{2}\] \[\text{Alors } f^{''}(0) = - 1\]

4.

\[f^{''} \text{ est dérivable sur } \mathbb{R}^{*}\] \[f^{(3)}(x) = \Biggl \{ \begin{matrix} 0\ \text{si }x < 0 \\ \sin(x) - \cos(x)\text{ si }x > 0 \end{matrix}\] \[f^{(3)}\text{ est définie et continue en 0 si }\lim_{x \rightarrow 0^{-}}{f^{(3)}(x)} = \lim_{x \rightarrow 0^{+}}{f^{(3)}(x)}\] \[\text{Or }\lim_{x \rightarrow 0^{-}}{f^{(3)}(x)} = 0\ \text{et }\lim_{x \rightarrow 0^{+}}{f^{(3)}(x)} = - 1\]

• Donc $f^{(3)}(x)$ n’est pas définie en 0, $f^{(3)}(x)$ n’est pas continue sur $\mathbb{R}$

5.

• $f$ est deux fois dérivable sur $\mathbb{R}$ et $f^{‘’}$ est continue sur $\mathbb{R}$, $f$ est donc de classe $C^{2}$

• $f$ n’est pas trois fois dérivable sur $\mathbb{R}$ donc $f$ n’est pas de classe $C^{3}$

Exercice 5 :

1.

• Si $f$ est dérivable sur $\lbrack a,b\rbrack,\ b > a$, alors, d’après le théorème des accroissements finis,

\[\exists c \in \rbrack a,b\lbrack,\ f^{'}(c) = \frac{f(b) - f(a)}{b - a}\]

2.

\[f^{'}(z) = - \frac{1}{z^{2}}\]

• D’après le théorème des accroissements finis appliqué à la fonction $f$ sur $\lbrack x,x + 1\rbrack$,

\[\exists c \in \rbrack x,x + 1\lbrack,\ f^{'}(c) = \frac{f(x + 1) - f(x)}{x + 1 - x}\] \[\exists c \in \rbrack x,x + 1\lbrack,\ - \frac{1}{c^{2}} = \frac{1}{x + 1} - \frac{1}{x}\]

• On a $x < c < x + 1$

\[\Leftrightarrow x^{2} < c^{2} < (x + 1)^{2}\] \[\Leftrightarrow \frac{1}{x^{2}} > \frac{1}{c^{2}} > \frac{1}{(x + 1)^{2}}\] \[\Leftrightarrow - \frac{1}{x^{2}} < - \frac{1}{c^{2}} < - \frac{1}{(x + 1)^{2}}\] \[\Leftrightarrow - \frac{1}{x^{2}} < \frac{1}{x + 1} - \frac{1}{x} < - \frac{1}{(x + 1)^{2}}\]

3.

\[\lim_{x \rightarrow 0^{+}}\left( \frac{1}{x + 1} - \frac{1}{x} \right) = - \infty\] \[\lim_{X \rightarrow - \infty}{\exp(X)} = 0\]

• Donc $\lim_{x \rightarrow 0^{+}}{\exp\left( \frac{1}{x + 1} - \frac{1}{x} \right)} = 0$

N.B. : Ce résultat ne découle pas de l’inégalité précédente