DS1 2023 2024 Correction
Télécharger le DS1 2023 2024 Correction en pdf
Page 1 : Préing 2 : DS 1 sujet 1 d’Analyse dans RnL’usage de tout appareil électronique est interdit.Date : Lundi 13 Novembre 2023Aucun document n’est autorisé.Durée : 1hLe barème est donné à titre indicatif.Nombre de pages : 1 page rectoIl sera tenu compte de la qualité de la rédaction et de la précision des justifications. Lesujet comporte 4 exercices. L’ordre dans lequel ceux-ci sont traités n’est pas imposé.♣♣♣Exercice 1 : Questions de cours/TD 4.5 pointsSoit E, · un espace vectoriel normé quelconque. Soit r 0 et a un point quelconque de E.Montrer que la boule fermée de centre a et de rayon r, Ba, r, est un fermé.Correction :On doit donc étudier si le complémentaire de Ba, r est un ouvert. On commence par intro-duire, en un point X quelconque de CEBa, r, la boule ouverte BX, r′ = X ar. CommeX CEBa, r, X a r et donc r′ = X ar 0.Vérifions maintenant que BX, r′ = X ar CEBa, r :Soit Y BX, r′ = X ar un point quelconque de BX, r′ = X ar. AlorsX a= X Y + Y aX Y + Y a⇐⇒Y aX Y X a⇐⇒Y a X ar X a⇐⇒Y a rOn voit donc que Y est bien extérieur à Ba, r, donc Y CEBa, r. Comme cela est vrai pourn’importe quel Y BX, r′ = X ar, cela signifie que BX, r′ = X ar CEBa, r.Donc CEBa, r est un ouvert et donc Ba, r est un fermé.0.5 point si l’étudiant indique que Ba, r est fermé si et seulement si CEBa, r ouvert.1 point si c’est le bon rayon de boule r′ qui est donné.1 point si il est justifié que r′ 0.1 point si il est correctement démontré que Y a r.1 point pour conclure correctement à partir du point précédent.1
Page 2 : Exercice 2 : 2 normes sur R2 9 pointsSoit les deux applications suivantes définies sur R2N1x, y = 3x + y + x + yetN2x, y = 12x + y1. Montrer que N1 et N2 sont des normes sur R2. 4.5 points2. Que signifie que les normes N1 et N2 sont équivalentes ? 1 point3. Ces normes sont-elles équivalentes ? 0.5 point4. Tracer la sphère associée à la norme N1 de centre 0, 0 et de rayon r = 1. 3 pointsCorrection :1. Pour N1 :a Soit N1x, y = 0. Alors3x + y + x + y = 0 ⇐⇒3x + y = 0x + y = 0⇐⇒2x = 0y = x⇐⇒x = 0y = 0Finalement N1x, y = 0 =⇒x = y = 0.1 point si et seulement si toutes les étapes précédentes sont présentes.0 s’il n’y a pas le système d’équation.b Soit x, y R2 et λ R. Alors calculons la norme de λx, λy :Nλx, λy = λ3x + y + λx + y = λ3x + y + x + y = λNx, y0.5 point.c Considérons maintenant x, y et x′, y′. Et introduisons le vecteurx, y + x′ + y′ = x + x′, y + y′1Et calculons maintenant sa normeN1x + x′, y + y′ = 3x + 3x′ + y + y′ + x + x′ + y + y′ 3x + y + 3x′ + y′ + x + y + x′ + y′Nx, y + Nx′, y′1 point.Finalement N1 est une norme sur R2.Pour N2 :a N2x, y = 0 =⇒x = y = 00.5 point2
Page 3 : b Soit x, y R2 et λ R. Alors calculons la norme de λx, λy :N2λx, λy = 12λx + λy = λ12x + y= λN2x, y0.5 pointc Considérons maintenant x, y et x′, y′. Et introduisons le vecteurx, y + x′ + y′ = x + x′, y + y′2Et calculons maintenant sa normeN2x + x′, y + y′ = 12x + x′ + y + y′ 12x + y + 12x′ + y′ = N2x, y + N2x′, y′1 pointDonc N2 est bien une norme.2. N1 et N2 sont des normes équivalentes sur R2 si et seulement siα, β 0 / X R2, αN1X N2X βN1X1 point s’il n’y a aucune ambiguité.0.5 point pour la moindre ambiguité.0 point pour la moindre erreur.3. Ces normes sont nécessairement équivalentes puisque R2 est un espace de dimension 2. Oron sait que sur un espace vectoriel de dimension finie, toutes les normes sont équivalentes.0.5 point.0 s’il n’y a pas de justification ou que la justification est fausse ou partiellement fausse.4. On souhaite maintenant trouver la sphère de rayon 1 et de centre 0, 0 associée à la normeN1. Par définition, la sphère S 0, 0, r = 1 est donnée parS0, 0, r = 1=x, y R2/N1x, y = 1Ainsi, la sphère est obtenue en résolvant l’équation3x + y + x + y = 130.5 point si l’équation précédente et/ou S 0, 0, r = 1 sont correctement écrits.Cas 1 :Partons du principe que3x + y 0x + y 0⇐⇒y 3xy xAlors l’équation 3 devient3x + y + x + y = 1 ⇐⇒4x + 2y = 1 ⇐⇒y = 12 2x0.5 point3
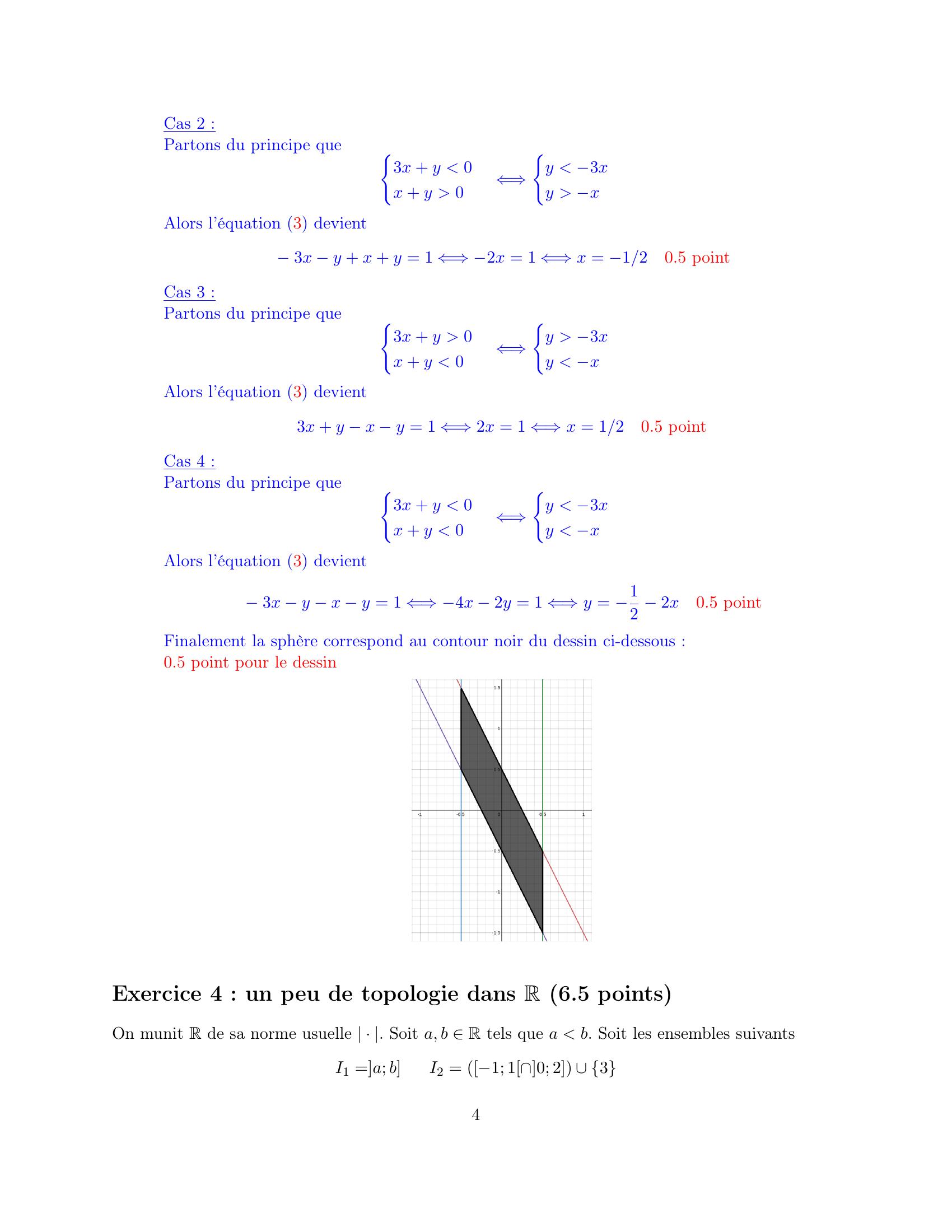
Page 4 : Cas 2 :Partons du principe que3x + y 0x + y 0⇐⇒y 3xy xAlors l’équation 3 devient3x y + x + y = 1 ⇐⇒2x = 1 ⇐⇒x = 1/20.5 pointCas 3 :Partons du principe que3x + y 0x + y 0⇐⇒y 3xy xAlors l’équation 3 devient3x + y x y = 1 ⇐⇒2x = 1 ⇐⇒x = 1/20.5 pointCas 4 :Partons du principe que3x + y 0x + y 0⇐⇒y 3xy xAlors l’équation 3 devient3x y x y = 1 ⇐⇒4x 2y = 1 ⇐⇒y = 12 2x0.5 pointFinalement la sphère correspond au contour noir du dessin ci-dessous :0.5 point pour le dessinExercice 4 : un peu de topologie dans R 6.5 pointsOn munit R de sa norme usuelle · . Soit a, b R tels que a b. Soit les ensembles suivantsI1 =a; bI2 = 1; 10; 2 34
Page 5 : 1. Déterminer si les ensembles précédents sont ouverts, fermés, ou aucun des deux en passantsoit en utilisant directement les définitions soit en utilisant les suites d’éléments de R. 2.5 pointsOn commence par I1 :Fermé ? exemple de méthodeSoit la suite un = a + 1n. Alorsa + 1n b ⇐⇒n 1b aPosons n0 le plus petit entier tel que n0 1/b a. Ainsin n0, un I1Orlimn→un = a /I1donc I1 n’est pas un fermé.0.5 point, s’il est précisé qu’à partir d’un certain rang, un est une suite d’élément de I1.0.25, si c’est juste mais que ce n’est pas précisé.Seule autre méthode acceptée :prendre le complémentaire de I1 dans R et montrer qu’en a aucune boule ne peut êtreincluse dans le complémentaire.Ouvert ? exemple de méthodeNous allons cette fois-ci utiliser les boules. Il semble y avoir un problème en b.Soit r 0. Soit Bb, r =br; b+r la boule ouverte centrée en b et de rayon r. Considéronsalors y = b + r2 Bb, r. Or clairement r 0, y b. Donc r 0, y /I1. Donc r 0,Bb, r ̸I1. Donc I1 n’est pas un ouvert.0.5 point si c’est bien fait r 0.Seule autre méthode acceptée :On prend le complémentaire dans R de I1 et on montre grâce aux suites que ce complémen-taire n’est pas un fermé.On poursuit avec I2 :I2 =0; 130.5 point5
Page 6 : Fermé ? exemple de méthodeClairement il y a un problème en 0 et en 1.Soit un = 1n. Alorsn 2, un I2Orlimn→un = 0 /I2et finalement I2 n’est pas fermé.0.5 point, s’il est précisé qu’à partir d’un certain rang, un est une suite d’élément de I2.0.25, si c’est juste mais que ce n’est pas précisé.Seule autre méthode acceptée :prendre le complémentaire de I2 dans R et montrer qu’en 0 aucune boule ne peut êtreincluse dans le complémentaire.Ouvert ? exemple de méthodeOn va utiliser cette fois-ci les boules ouvertes.Soit r 0. Soit B3, r =3r; 3+r la boule ouverte centrée en 3 et de rayon r. Considéronsalors y = 3 + r2 Bb, r. Or clairement r 0, y 3. Donc r 0, y /I2. Donc r 0,B3, r ̸I2. Donc I2 n’est pas un ouvert.0.5 point si c’est bien fait r 0.Seule autre méthode acceptée :On prend le complémentaire dans R de I2 et on montre grâce aux suites que ce complémen-taire n’est pas un fermé.2. Déterminer l’intérieur de I1 et l’adhérent de I2 par la méthode de votre choix. 4 pointsOn commence par I1 :Intérieur de ˚I1 :Etape 1 0.5 point : proposons un candidat sur la base du fait que l’intérieur de I1 estle plus grand ouvert contenu dans I1. Ainsi, posonsC =a, bEtape 2 0.5 point : Nous devons vérifier que C est bien un ouvert et que C I1.6
Page 7 : C =a, b= Ba + b2, r = b a2Donc C est bien un ouvert car il s’agit d’une boule ouverte.De plus I1 = C b ce qui implique que C I1.D’après le TD, on sait alors que C ˚I1.Etape 3 1 point : Nous devons maintenant vérifier que ˚I1 C.˚I1 C ⇐⇒x I1\C, r 0, Bx, r ̸I1Ici I1\C = b.Soit r 0 et soit Bb, r =b r; b + r la boule centrée en b et de rayon r. Considé-rons alors y = b + r2 Bb, r. Or, r 0, y b donc y /I1. Ainsi r 0, Bb, r ̸I1 eton a donc ˚I1 C.Finalement : ˚I1 = C =a, b.Détermination de I2 :De la même façon il faut proposer un candidat C = 0; 1 3 0.5 point.Puis on vérifie que I2 C et que C est un fermé. On sait alors que I2 C 0.5 point.Il ne reste plus qu’à montrer que C I2 ce qui est équivalent àx C\I2, r 0, Bx, r I2 ̸= où dit autrement que tous les points de C\I2 appartiennent bien à I2.Or ici C\I2 = 0 1. On peut par exemple introduire les suitesun = 1nvn = 1 1nIl existe pour chacune des suites un rang à partir duquel tous les éléments de la suite appar-tiennent à I2. Orlimn→+un = 0limn→+vn = 1Donc 1 et 2 appartiennent à I2. 1 pointOn a donc I2 = C = 0; 1 3.7
Page 8 : 0.5 si ˚I1 est donné sans justificatif ou que le reste de la démonstration est faux.0.5 si I2 est donné sans justificatif ou que le reste de la démonstration est faux.8