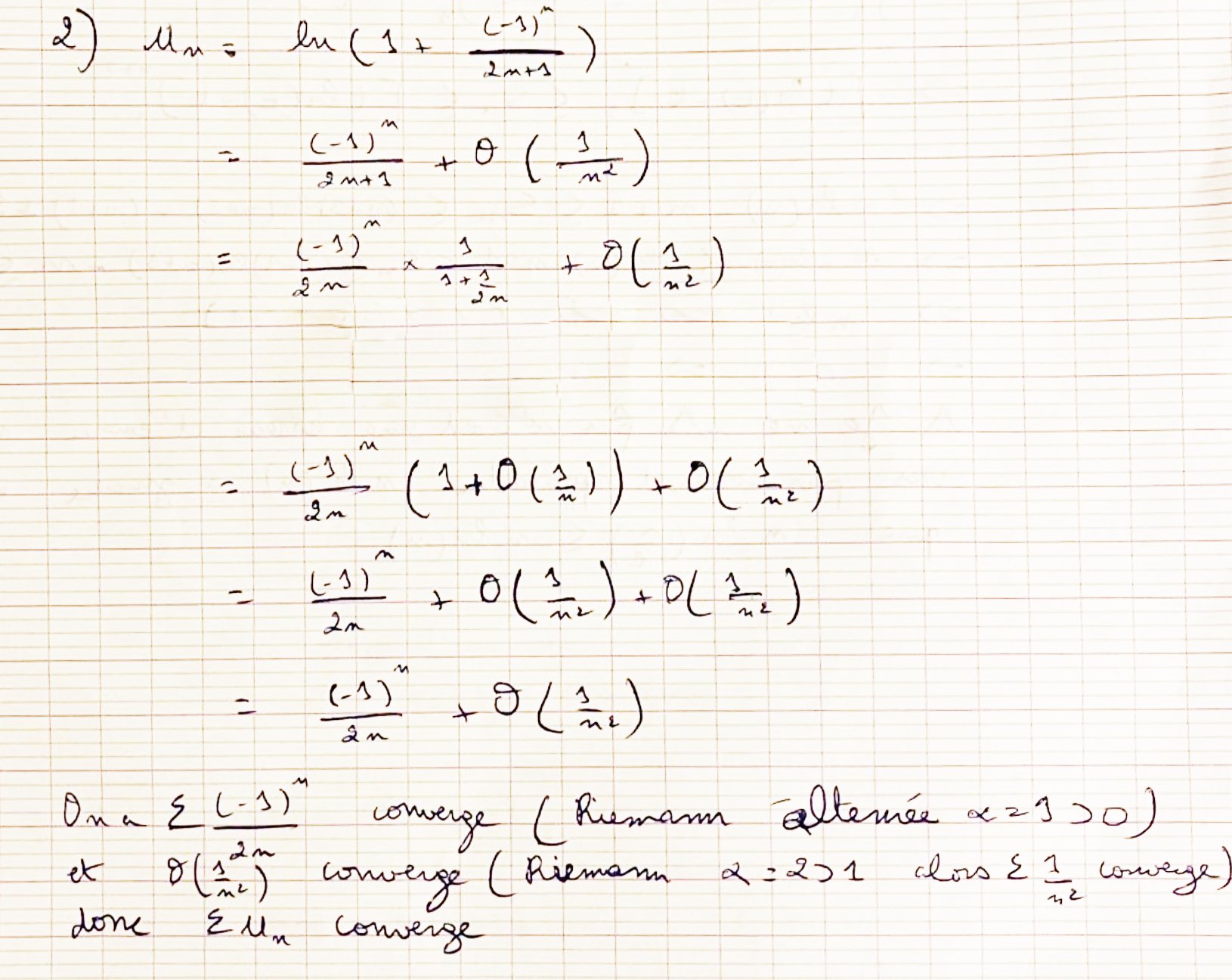DS1 2023 2024 V1 Correction Series-DS PREING2 S1

Écrit par Hiba M.

complétée par Maïssa T.

Vérifiée et complétée par Rayane M. et Mathis S.

Exercices : 1 2 3 4

Exercice 1 :

Exercice 2 :

Exercice 3 :

Exercice 4 :

\[u_{k} ≔ \ln(k)\ \text{et}\ S_{n} ≔ \sum_{k = 1}^{n}u_{k}\]

1.

Montrer que $\forall n \in \mathbb{N}^{*},\int_{1}^{n}{\ln(t)dt} \leq S_{n} \leq \int_{1}^{n + 1}{\ln(t)dt}$

\[\forall x \in \lbrack k;k + 1\rbrack,k \geq 1\] \[\ln(k) \leq \ln(x)\] \[\ln(k) \leq \int_{k}^{k + 1}{\ln(t)dt}\]

Par somme de 1 à $n$

\[\sum_{k = 1}^{n}{\ln(k)} \leq \int_{1}^{n + 1}{\ln(t)dt}\] \[S_{n} \leq \int_{1}^{n + 1}{\ln(t)dt}\] \[\forall x \in \lbrack k;k + 1\rbrack,k \geq 2\] \[\ln(x - 1) \leq \ln(k)\] \[\int_{k}^{k + 1}{\ln(t - 1)dt} \leq \ln(k)\] \[\int_{k - 1}^{k}{\ln(t)dt} \leq \ln(k)\]

Par somme de 2 à $n$,

\[\int_{1}^{n}{\ln(t)dt} \leq \sum_{k = 2}^{n}{\ln(k)} = S_{n}\ \text{car}\ u_{1} = 0\] \[\int_{1}^{n}{\ln(t)dt} \leq S_{n} \leq \int_{1}^{n + 1}{\ln(t)dt}\]

2.

\[\int_{}^{}{\ln(t)dt} = \int_{}^{}{1 \times \ln(t)dt}\] \[u^{'}(t) = 1,\ u(t) = t\] \[v(t) = \ln(t),\ v^{'}(t) = \frac{1}{t}\] \[\int_{}^{}{u^{'}v} = uv - \int_{}^{}{uv^{'}}\ \text{(intégration par parties)}\] \[\int_{}^{}{\ln(t)dt} = t\ln(t) - \int_{}^{}1 = t\ln(t) - t + C\] \[\int_{1}^{n}{\ln(t)dt} = \left\lbrack t\ln(t) - t \right\rbrack_{1}^{n} = n\ln(n) - n + 1 = n\left( \ln(n) - 1 \right) + 1\] \[\int_{1}^{n + 1}{\ln(t)dt} = \left\lbrack t\ln(t) - t \right\rbrack_{1}^{n + 1} = (n + 1)\ln(n + 1) - (n + 1) + 1 = (n + 1)\ln(n + 1) - n\] \[n\left( \ln(n) - 1 \right) + 1 \leq S_{n} \leq (n + 1)\ln(n + 1) - n \leq (n + 1)\ln(n + 1)\] \[n\left( \ln(n) - 1 \right) + 1 \leq S_{n} \leq (n + 1)\ln(n + 1)\] \[n\left( \ln(n) - 1 \right) \leq n\left( \ln(n) - 1 \right) + 1 \leq S_{n} \leq (n + 1)\ln(n + 1)\] \[n\left( \ln(n) - 1 \right) \leq S_{n} \leq (n + 1)\ln(n + 1)\]

On ne peut pas aller plus loin a cause d’une erreur dans l’énoncé.

Pages : Exercices : 1 2 3 4