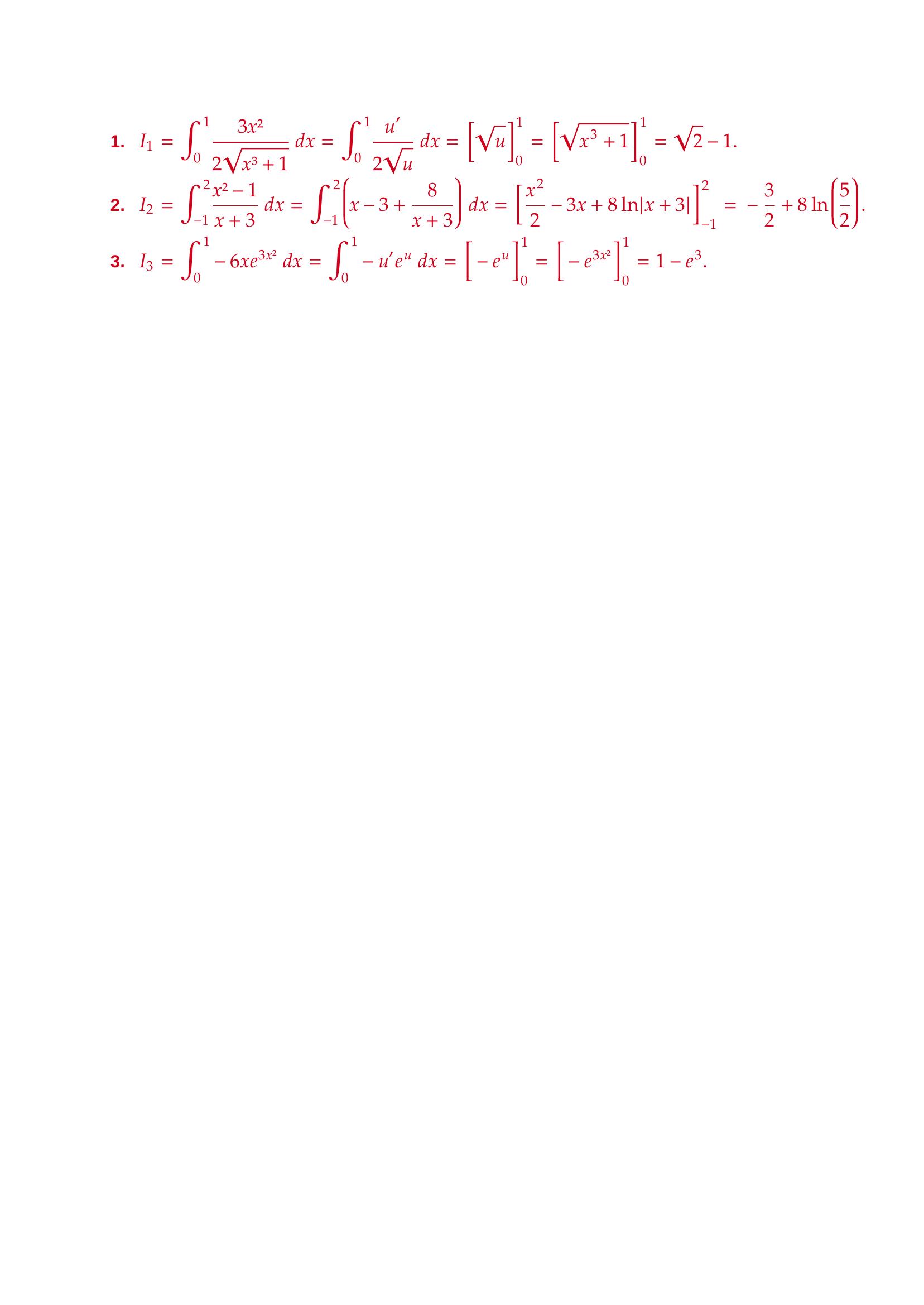DS2 2020 2021 V2
Télécharger le DS2 2020 2021 V2 en pdf
Page 1 : Proposition DS 61. Exercice 1 :Déterminer un équivalent simple des suites ou des fonctions suivantes : 1. Déterminer un équivalent simple de la suite : u =.nn³ + nn + 4ln2. Déterminer un équivalent simple de la fonction , au voisinage de f x = 𝜋xsinxa = 1.3. Montrer la relation d'équivalence suivante au voisinage de : 0 xx + 1ex0xCorrection : 1. n + n =n1 +=n+1 += 3n +1 +ln3ln31n2ln3ln1n2ln ln1n2⟹u =nn³ + nn + 4ln3nnln 2. = 1 ⟹ 1.limx1→xx 1Si on pose , on peut écrire : x = 1 + h.𝜋x =𝜋1 + h=𝜋+ 𝜋h = -𝜋h- 𝜋hsinsin sinsin 0Finalement : f x =- 𝜋x - 1 𝜋xsinx13. Il y avait encore une erreur dans l'énoncé : l'équivalent devait être demandé en +et non pas en .0===== exx+1exxx + 1exxxeex1+xln1+xxln eexx 1+ln1x1+xxln eexx +x1+ln ln1x1+xxln x1+-1lnOr : x1 +- 1 x+ o- 1o 1⟹x1 +- 1 = 0ln1x=+1x1x=+ limx+→ln1x.⟹= 1limx+→xx+1exxD'où le résultat : xx + 1ex+x1x
Page 2 : Au voisinage de , on pourrait dire :0=x + 1xxxeex1+xlnxxln .x1 + x =xx = 0 ⟹= 1 ⟹x + 1 xlimx0→+lnlimx0→+ln limx0→+x + 1xxxx 0x2. Exercice 2 :Calculer les développements limités suivants :1. à l'ordre au voisinage de .g x =1 + 2x1 ln1 - x202. à l'ordre au voisinage de .g x =2 1 - 3xxcos 203. à l'ordre au voisinage de .g x = xe3 x31Correction : 1. = 1 - x 1 +-x --x+ o x 1 -x -x + o x.1 - x13 =0131922 =01319221 + 2x2x -+ o x 2x - 2x + o x.ln =0 2x222 =022g x =1 + 2x2x - 2x + o x1 -x -x + o x1 ln1 - x =022131922g x 2x -x + o x.1 =083222. .⟹ 1 -x + o xxcos =01422 1 + u + u + o u⟹ 1 + 3x + 9x + o x.1 - u =0221 - 3x =0221 -x + o x1 + 3x + 9x + o x1 - 3xxcos =014222g x 1 + 3x +x + o x.2 =0354223. Au voisinage de , on fait le changement de variable : .1x = 1 + h ⟺h = x - 1g x = xe = 1 + h e= 1 + h e e= f h3 x 1+h 1 h3 x 1 -x + o x.cos =01222 1 +u -u + o u.1 + u =0121822112333
Page 3 : f he 1 + h1 + h +++ o h3 =0 h22h633f he 1 + 2h +++ o h3 =03h222h333g xe 1 + 2 x - 1 +++ ox - 13 =13 x - 1222 x - 1333g xe + 2e x - 1 +++ ox - 13 =13e x - 1222e x - 13333. Exercice 3 :On considère la fonction , définie sur , par :fI =- 1, + .f x = x +1 + x ln1. Montrer que réalise une bijection de vers .fIR2. Déterminer le de , et montrer que , réciproque de , possède également DL 02 ff-1fun . DL 02 3. Le de sera noté : DL 02 f-1fxa + a x + a x² + o x² .-1 =0012 Justifier que l'on a forcément : .a = 004. A l'aide de légalité : et de l'unicité des montrer que et f fx = x-1 DLa =112.a =21165. En déduire l'équation de la tangente à en et la position de la courbe par rapport f-10à cette tangente.Correction : 1. est définie et dérivable sur et f : x ↦x +1 + xlnIf x = 1 + 0.' 11 + x est strictement croissante sur . Elle réalise donc une bijection de vers .fIIf I et f x = - limx-1→+ f x = + ⟹f I = R.limx+→ 2. est de classe sur , elle possède donc des à tout ordre. En particulier. fCIDL0n f x = x +1 + xx + x -+ o x² 2x -+ o x² . ln =0x²2 =0x²2 ne s'annule pas sur , donc est de classe sur . Elle possède donc des à f'If-1CRDL0n tout ordre.3. et et donc : fxa + a x + a x² + o x²-1 =0012 f 0 = 0 ⟹f0 = 0 -1 a = 0.0
Page 4 : Le de s'écrit donc : DL 02 f-1fxa x + a x² + o x² .-1 =012 4. On sait que : que et que fxa x + a x² + o x²-1 =012 f x 2x -+ o x² =0x²2 .f x = 0limx0→ On en déduit, puisque , que : f fx = x-1 2 a x + a x² -a x + a x²+ o x²x + o x² 1212 122 =0 ⟺2a x + 2a x -+ o x²x + o x²122a x²221 =0 ⟺2a x + 2a -x + o x²x + o x²12a2212 =0 L'unicité des implique : .DL⟺a =112a ==2a4211165. On a établi que : .fxx +x² + o x²-1 =012116 On en déduit que la tangente en de a pour équation : .0f-1y =x12La position de la courbe est déterminée par le signe du terme : .x² ⩾0116Donc la courbe est au dessus de cette tangente au voisinage de . 04. Exercice 4 :Calculer les intégrales suivantes :1. I =dx.1103x²2x³ + 12. I =dx.22-1x² - 1x + 3Indication : Penser à une décomposition en éléments simples.3. I =- 6xedx.3103x²Correction : 2a = 112a -= 02a221
Page 5 : 1. I =dx =dx ===- 1.1103x²2x³ + 110u2'uu10x + 131022. I =dx =x - 3 +dx =- 3x + 8x + 3= -+ 8.22-1x² - 1x + 32-18x + 3x22ln2-132ln 523. I =- 6xedx =- u e dx =- e=- e= 1 - e .3103x²10' uu103x²103