DS2 2021 2022
Télécharger le DS2 2021 2022 en pdf
Page 1 : Préing 1Devoir Surveillé 2Algèbre IDate: Mardi 7 Decembre 2021L’usage de tout appareil électronique est interditDurée: 1h30Nombre de pages: 2Il sera tenu compte de la qualité de la rédaction et de la précision des justifications.Le sujet comporte 5 exercices. L’ordre dans lequel ceux-ci sont traités n’est pas imposé.Exercice 1Dans N, on définit une relation en posantm ⪯n⇐⇒k N, n = km.1. Montrer que ⪯est une relation d’ordre sur N.• Reflexive: Pour tout n N, nous avonsn = 1·n=⇒n ⪯n.• Antisymetrie: Pour tout m,n N, nous avonsm = nk, k Netn = k′m, k′ N=⇒m = kk′m=⇒kk′ = 1=⇒k = k′ = 1=⇒m = n.Doncm ⪯netn ⪯m=⇒m = n.• Transitive: Pour tout m,n,p N, nous avonsm = nk, k Netp = k′m, k′ N=⇒p = kk′n.Doncn ⪯metm ⪯p=⇒n ⪯p.L’ordre ⪯est-il total?Non, par exemple, entre 2 et 3 il n’y a pas de relation.On considère dans la suite de l’exercice que l’ensemble Nest ordonné par la relation ⪯.1
Page 2 : 2. L’ensemble Npossède-t-il un plus grand élément?L’ensembleNon. Par l’absurde, supposons donc que Nadmette un plus grand élément noté M alorsk N,kM = k · M=⇒M ⪯2M.Ce qui signifie que kM est plus grand au sens de ⪯ que M ce qui est contradictoire puisque M est leplus grand élémént, donc il n’y a pas de plus grand élément.Npossède-t-il un plus petit élément?Oui, 1. En effet, pour tout n N, nous avons n = 1·n. Donc pour tout n N, 1 ⪯n.3. Soit E = 3,4,5,30.L’ensemble E ordonné par la relation ⪯possède-t-il un plus grand élément?Non. En effet, 3,4 et 5 sont premiers entre eux, aucune d’entre eux ne peut donc pas être le plus grandélémént. De plus 4 ne divise pas 30, donc 30 n’est peut pas non plus être le plus grand élémént.L’ensemble E ordonné par la relation ⪯possède-t-il un petit élément?Non. En effet, 3,4 et 5 sont premiers entre eux, aucune d’entre eux ne peut donc pas être le plus petitélémént. De plus 3 ⪯30 et 5 ⪯30, donc 30 n’est peut pas non plus être le plus petit élémént.Exercice 2On définit sur R la relationxRy⇐⇒x2 y2 = x y.1. Montrer que R est une relation d’équivalence.Tout d’abord, notons quexRy⇐⇒x2 y2 = x y⇐⇒x2 x = y2 y.Ainsi• Reflexive: Pour tout x R, nous avonsx2 x = x2 x=⇒xRx.• Symetrique: Pour tout x, y R, nous avonsx2 x = y2 y=⇒y2 y = x2 x.DoncxRy=⇒yRx.2
Page 3 : • Transitive: Pour tout x, y,z R, nous avonsx2 x = y2 yety2 y = z2 z =⇒x2 x = z2 z.DoncxRyetyRz=⇒xRz.2. Déterminer la classe d’équivalence d’un élément x de R.Combien y-a-t-il d’éléments dans cette classe?Soit x R, alorsx=y R : xRy=y R :x2 x = y2 y=y R :x2 y2 x y = 0=y R :x yx + yx y = 0=y R :x yx + y 1 = 0=y R :y = xouy = 1x.Ainsi, la classe de x est constituée de deux éléments, sauf six = 1x⇐⇒x = 12.Dans ce cas, la classe est donnée par© 12ª.Exercice 3Soient E et F deux ensembles et f : E →F l’application de E dans F définie parf x = 1+ x+1x2.1. On suppose que E = F = R.a Étant donné un réel x0, comparer f x0 et f x0.La fonction f est-elle injective ?Soit x0 R. Alorsf x0 = 1x0+1x02 = 1x0+1+ x02= 1+ x0+1x02= f x0.Ainsi, pour tout x0 R, nous avons f x0 = f x0. La application est donc paire. Ce qui im-plique que l’application f n’est pas injective.3
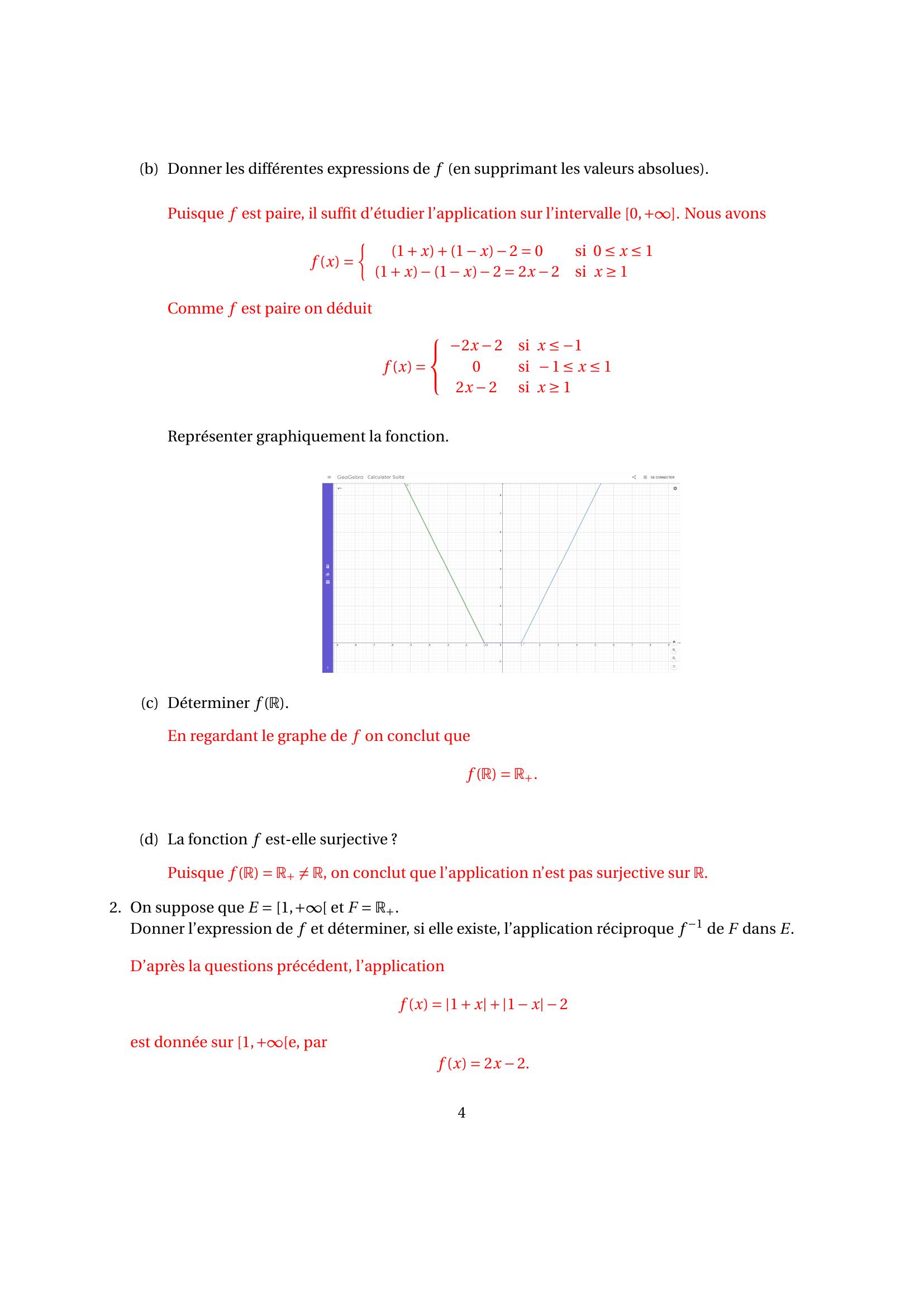
Page 4 : b Donner les différentes expressions de f en supprimant les valeurs absolues.Puisque f est paire, il suffit d’étudier l’application sur l’intervalle 0,+. Nous avonsf x =½1+ x+1x2 = 0si 0 x 11+ x1x2 = 2x 2si x 1Comme f est paire on déduitf x =2x 2si x 10si 1 x 12x 2si x 1Représenter graphiquement la fonction.c Déterminer f R.En regardant le graphe de f on conclut quef R = R+.d La fonction f est-elle surjective ?Puisque f R = R+ ̸= R, on conclut que l’application n’est pas surjective sur R.2. On suppose que E = 1,+ et F = R+.Donner l’expression de f et déterminer, si elle existe, l’application réciproque f 1 de F dans E.D’après la questions précédent, l’applicationf x = 1+ x+1x2est donnée sur 1,+e, parf x = 2x 2.4
Page 5 : De plus, pour tout y R+, nous avonsy = 2x 2⇐⇒y +22= x.Ce qui nous permet de conclure que pour tout y R+, y possède un unique antécédent donné pary +22.Par conséquent, f est bijective. Elle dispose donc d’une application réciproque, qui est donnée parg : R+→1,+y7→y +22.Exercice 4Soient E,F deux ensembles et f : E →F une application.Démontrer pour tout A E et tout B F, l’équivalence:f AB ̸= ;⇐⇒A f 1B ̸= ;.On raissone par double implication. Supposonsf AB ̸= ;=⇒y F,y f AB=⇒y F,y f Aety B=⇒x A,y = f xetf x B=⇒x A,x f 1B=⇒x E,x A f 1B=⇒A f 1B ̸= ;.De mêmeA f 1B ̸= ;=⇒x E,x A f 1B=⇒x E,x Aetx f 1B=⇒x E,x Aetf x B=⇒x E,f x f Aetf x B=⇒f x f AB=⇒f AB ̸= ;.Exercice 55
Page 6 : 1. Mettre sous forme algébrique les nombres suivants4+5i2+2i 45i22i;1+i8.Nous avons4+5i2+2i 45i22i=4+5i2+2i 4+5i2+2i=2iImµ4+5i2+2i¶.Or4+5i2+2i = 4+5i22i8= 18 18+2i.Donc4+5i2+2i 45i22i=2iImµ4+5i2+2i¶=2iµ28¶= i2.Nous avons1+i =p2eiπ4=⇒1+i8 = p28ei8π4 = 24ei2π = 16.2. Donner le module et un argument des nombres complexes suivants6;11i;i +p3;11i .• module6 = 6 et arg6 = π.• module11i = 11 et arg11i = π2 .• modulep3+i = 2 et argp3+i = π6 .• module¡ 11i¢=1p2 et arg¡ 11i¢= π4 .6