DS2 2023 2024 V2
Télécharger le DS2 2023 2024 V2 en pdf
Page 1 : Préing 2 : DS 2 sujet 0 d’Analyse dans RnL’usage d’appareil électronique est interdit.Date : Lundi 11 Décembre 2023 à 10h15Aucun document n’est autorisé.Durée : 1hLe barème est donné à titre indicatif.Nombre de pages : 1 page recto versoIl sera tenu compte de la qualité de la rédaction et de la précision des justifications. Lesujet comporte 3 exercices. L’ordre dans lequel ceux-ci sont traités n’est pas imposé.♣♣♣Exercice 1 : limite, continuité, différentiabilité et classe C1. 11.5pointsSoit l’application f définie parfx, y =x2 sin1x2+y2si x, y ̸= 0, 00sinon1. Montrer que f est continue sur R2. 1.5 points2. Sur quels domaines f est-elle de classe C1 ? 6.5 points3. Sur quels domaines f est-elle différentiable et le cas échéant, quelle est sa différentielle ?3.5 points1. Montrons que f est continue sur R2.Sur R2\0, 0 : 0.5 point1/px2 + y2 est continue sur R2\0, 0 car le dénominateur ne s’annule jamais sur cetensemble et que x2 + y2 est positif. On déduit de cela que sin1/px2 + y2 est continuesur R2\0, 0 comme composée de fonctions continues. Finalement, x2 sin1/px2 + y2 estcontinue sur R2\0, 0 comme produit de fonctions continues.En 0, 0 : 1 pointOn afx, y =x2 sin 1px2 + y2! x2→x,y→0,0 0donclimx,y→0,0 fx, y = 0 = f0, 0Finalement f est continue sur R2.1
Page 2 : 2. Etudions les dérivées partielles premières de f :En 0, 0 :fx0,0= limt→0ft, 0 f0, 0t= limt→01t × t2 sin 1t= 01 pointfx0,0= limt→0f0, t f0, 0t= 01 pointEn x, y ̸= 0, 0 :fxx,y= 2x sin 1px2 + y2!x3x2 + y23/2 cos 1px2 + y2!1 pointfyx,y= yx2x2 + y23/2 cos 1px2 + y2!1 pointAinsi, les applications dérivées partielles premières de f sont données sur R2 parfxx,y=2x sin1x2+y2x3x2+y23/2 cos1x2+y2si x, y ̸= 0, 00sinonfyx,y=yx2x2+y23/2 cos1x2+y2si x, y ̸= 0, 00sinonContinuité des dérivées partielles premières sur R2\0, 0 : 1 pointComme précédemment 1/px2 + y2 est continue sur R2\0, 0 car x2 + y2 est strictementpositif. De ce fait cos1/px2 + y2 et sin1/px2 + y2 sont continues comme composéesde fonctions continues. De plus x3/x2 + y23/2 et yx2/x2 + y23/2 sont continues commefractions rationnelles dont le dénominateur ne s’annule jamais. Finalement les deux dérivéespartielles sont conitnues sur R2\0, 0.Continuité des dérivées partielles premières en 0, 0 : 1.5 pointPosons, pour simplifier les notationshx, y = fyx,yPassons en coordonnées polaires˜hρ, θ = ρ3 cos2θ sinθρ3 cos1ρ= cos2θ sinθ cos1ρqui n’est clairement pas défini quand ρ tend vers 0. Ainsi f n’est pas C1 en 0, 0.2
Page 3 : 3. Etudions maintenant si f est différentiable.Sur R2\0, 0 :Comme f est C1 sur cet ensemble alors f y est différentiable. 0.5 pointDe plus la différentielle est alors donnée parDx,yfh1, h2 = h1"2x sin 1px2 + y2!x3x2 + y23/2 cos 1px2 + y2! h2"yx2x2 + y23/2 cos 1px2 + y2! 0.5 pointEn 0, 0 :D’après le cours, f est différentiable en 0, 0 si et seulement silimh1,h2→0,01ph21 + h22"fh1, h2 f0, 0 h1fx0,0h2fy0,0= 00.5 pointnotons alorsϵh1, h2 =1ph21 + h22"fh1, h2 f0, 0 h1fx0,0h2fy0,0Dans notre cas, on aϵh1, h2 =1ph21 + h22h21 sin 1px2 + y2!0.5 pointPassons alors en coordonnées polaires˜ϵρ, θ = ρ cos2θ sin1ρ→rho→0 01 pointdonc f est différentiable en 0, 0.La différentielle est alors donnée parD0,0fh1, h2 = 00.5 pointExercice 2 : Continuité 4 pointsSoit la fonction définie parfx, y =xy2si y x4yx+y2siy x et x, y ̸= 0, 00si x, y = 0, 03
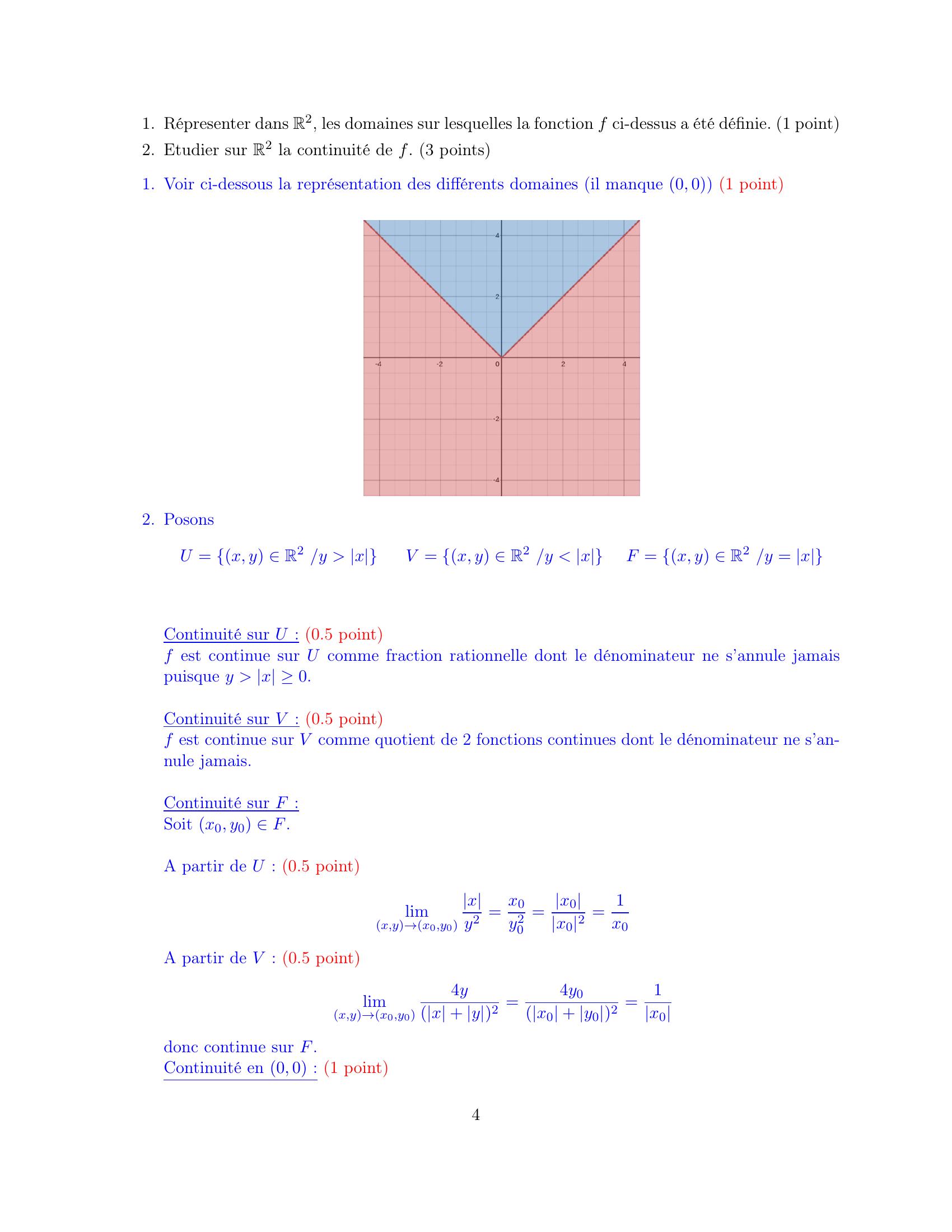
Page 4 : 1. Répresenter dans R2, les domaines sur lesquelles la fonction f ci-dessus a été définie. 1 point2. Etudier sur R2 la continuité de f. 3 points1. Voir ci-dessous la représentation des différents domaines il manque 0, 0 1 point2. PosonsU = x, y R2 /y xV = x, y R2 /y xF = x, y R2 /y = xContinuité sur U : 0.5 pointf est continue sur U comme fraction rationnelle dont le dénominateur ne s’annule jamaispuisque y x 0.Continuité sur V : 0.5 pointf est continue sur V comme quotient de 2 fonctions continues dont le dénominateur ne s’an-nule jamais.Continuité sur F :Soit x0, y0 F.A partir de U : 0.5 pointlimx,y→x0,y0xy2 = x0y20= x0x02 = 1x0A partir de V : 0.5 pointlimx,y→x0,y04yx + y2 =4y0x0 + y02 =1x0donc continue sur F.Continuité en 0, 0 : 1 point4
Page 5 : Prenons yy 0. Alorsf0, y = 4yy2 = 4y →y→0 donc f n’est pas continue en 0, 0.Finalement f est continue sur R2\0, 0.Exercice 3 : continuité bis 4.5 pointsDéterminer sur R2, la continuité des fonctions suivantes 1 point + 1.5 points + 2 pointsf1x, y =xy3x2 + y2f2x, y = x2 + y2x + yf3x, y =y3x12+y2si x, y ̸= 1, 00si x, y = 1, 0Soit fx, y =xy3x2+y2 :Pour R2\0, 0 : 0.5 pointLa fonction est clairement continue comme fraction rationnelle dont le dénominateur ne s’annulejamais.En 0, 0 : 0.5 pointf1x, y = xyy2x2 + y2 xy→x,y→0,0 0donc la fonction est continue en 0, 0 et sa limite est 0.Finalement la fonction est continue sur R2.Soit fx, y x2+y2x+y :Pour R2\0, 0 : 0.5 pointLa fonction est clairement continue comme quotient de deux fonctions continues dont le dénomina-teur ne s’annule jamais.En 0, 0 : 1 pointPassons en polaire˜f2ρ, θ =ρ2ρ cosθ + sinθ =ρ cosθ + sinθorθ R, cosθ + sinθ 0d’où l’on déduit que˜f2ρ, θ →ρ→0 05
Page 6 : et finalement f2 est continue en 0, 0 et sa limite vaut 0.Soitf3x, y =y3x12+y2si x, y ̸= 1, 00si x, y = 1, 0Pour R2\1, 0 : 0.5 pointLa fonction est clairement continue comme fraction rationnelle dont le dénominateur ne s’annulejamais.En 0, 0 : 1.5 pointPassons en polaire en posantx = 1 + ρ cosθy = ρ sinθAlors˜f3ρ, θ =ρ3 sin3θρ2cos2θ + sin2θ = ρ sin3θ →ρ→0 0donc la fonction est continue en 1, 0 et sa limite vaut 0.6