DS2 2024 2025 V1 Correction
Télécharger le DS2 2024 2025 V1 Correction en pdf
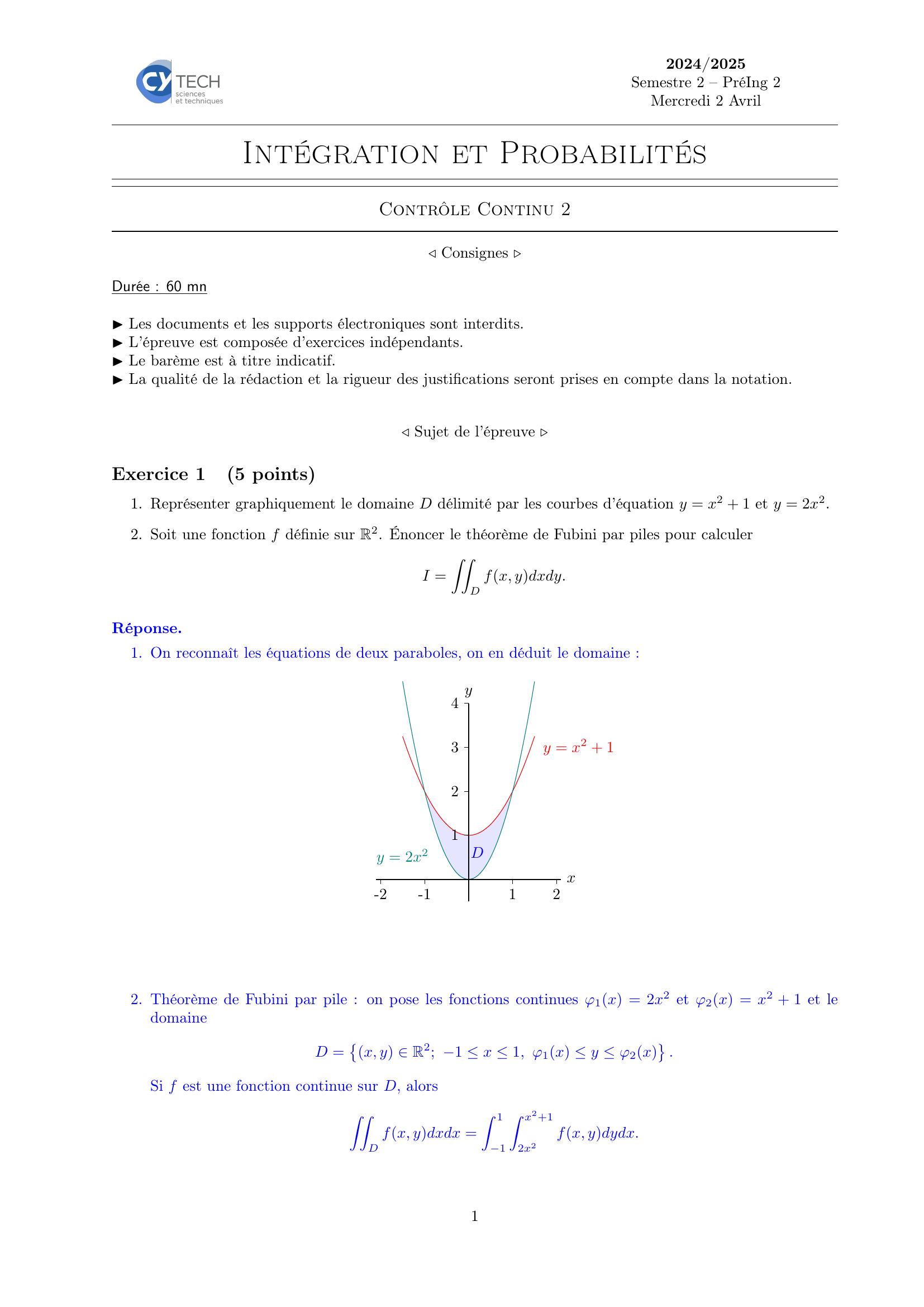
Page 1 : 2024/2025Semestre 2 – PréIng 2Mercredi 2 AvrilIntégration et ProbabilitésContrôle Continu 2◁Consignes ▷Durée : 60 mn▶Les documents et les supports électroniques sont interdits.▶L’épreuve est composée d’exercices indépendants.▶Le barème est à titre indicatif.▶La qualité de la rédaction et la rigueur des justifications seront prises en compte dans la notation.◁Sujet de l’épreuve ▷Exercice 15 points1. Représenter graphiquement le domaine D délimité par les courbes d’équation y = x2 + 1 et y = 2x2.2. Soit une fonction f définie sur R2. Énoncer le théorème de Fubini par piles pour calculerI =ZZDfx, ydxdy.Réponse.1. On reconnaît les équations de deux paraboles, on en déduit le domaine :xy-2-1121234y = x2 + 1y = 2x2D2. Théorème de Fubini par pile : on pose les fonctions continues φ1x = 2x2 et φ2x = x2 + 1 et ledomaineD =x, y R2; 1 x 1, φ1x y φ2x.Si f est une fonction continue sur D, alorsZZDfx, ydxdx =Z 11Z x2+12x2fx, ydydx.1
Page 2 : Exercice 28 pointsSoit l’application F définie parFx =ZRlnt2 + x1 + t2dt.1. Montrer que F est définie sur R+.2. Montrer que F C0R+.3. Montrer que F C1R+ et calculer sa dérivée.4. La fonction F admet-elle un minimum sur R+?Réponse.1. Montrer que F est bien définie sur R+. Soit la fonction f définie par ft, x = lnt2+x1+t2. Onpose les domainesA = R+ et I = R.On remarque que pour x = 0, la fonction t 7→ft, 0 admet une singularité en 0, ce qui n’est pas le cassi x 0.• Si x 0, alors la fonction t →ft, x est continue sur R. On vérifie le comportement en +:ft, x t→+lnt2t2donc t32 ft, x→t→+0. Puisque la fonction t 7→ft, x est paire en t, on a la même limite en .Ainsi, par le critère de Riemann avec α = 32 1, l’intégraleRI ft, xdt est convergente.• Si x = 0, on a ft, 0 = lnt21+t2 . Cette fonction est continue sur R+ et sur R. De plus, puisqu’elleest paire, on peut se limiter à l’étude sur R+. En +, on utilise le même argument que lorsquex 0. En 0, on aft, 0 t→0+ lnt2,donc t12 ft, 0→t→0+ 0. Par le critère de Riemann en 0, avec α = 12 1, l’intégraleZR+ft, 0dtest convergente.On a donc montré que pour tout x R+, l’intégraleRI ft, xdt est convergente, donc F est bien définiesur R+.2. Cette question est plus difficile que la question 3. Il vaut mieux montrer d’abord la question 3, puismontrer que la fonction F est continue en 0. Cette question n’est donc que très peu prise en comptedans le barème. On donne ici la démonstration de la continuité de F sur R+ dans un premier temps,puis on montrer ensuite la continuité de F en 0.Pour montrer la continuité de F sur R+, on utilise le théorème de continuité sous le signe intégrale. Onremarque que pour la domination, on ne pourra pas borner uniformément en x la fonction lnt2 + xlorsque x →+. On va donc se restreindre à un intervalle ϵ, A. Ainsi, si x ϵ, A, on a t2 + x t2 + ϵ ϵ, et la fonction y14 lny est continue sur ϵ, + et tend vers 0 par croissance comparée en+. Elle est donc bornée par une constante K qui dépend de ϵ sur ϵ; +, et on ax ϵ; A, ft, x =t2 + x14 lnt2 + xt2 + x1411 + t2 Kt21 + t24 +x1 + t2414⩽K11 + t23 +A1 + t24 14⩽K 1 + A141 + t234 .1On utilisera cette fonction pour la domination. On applique le théorème sur ϵ, A:a Continuité : soit t I. L’application x 7→ft, x est continue sur ϵ, A.b Continuité : soit x ϵ, A. L’application t 7→ft, x est continue sur R.2
Page 3 : c Domination : pour tout t, x I × ϵ, A, on aft, x ⩽K 1 + A141 + t234 ,qui est une fonction indépendante de x et intégrable sur R.D’après le théorème, F est continue sur ϵ, A. Puisque ce résultat est vrai pour tout 0 ϵ A, on endéduit que F est continue sur R+.Montrons à présent que F est continue en 0. On se restreint à un intervalle en x, par exemple 0; 1, eton montre la continuité de F sur cet intervalle. Par parité, on va séparer Fx = Fx + F+x oùFx =Z 0ft, xdt et F+x =Z +0ft, xdt.On va utiliser le théorème de convergence dominée sur F+, le résultat est identique sur F. On séparel’intervalle en deux I1 =0; 11; +.• Sur 0; 1, on a t2 + x 0; 2. On remarque que la fonction y 7→y14 lny est continue sur 0; 2 etprolongeable par continuité en 0, elle est donc bornée par une constante K1. Ainsi on ax 0; 1, t 0; 1, ft, x =t2 + x14 lnt2 + x1t2 + x14 1 + t2 ⩽K1t12 .• Sur 1; +, on a de nouveau t2 + x 1, donc on peut réutiliser l’argument 1 avec K2 = Kx 0; 1, t J =1; +, ft, x ⩽lnt2 + xt2 + x14t2 + x141 + t2 ⩽K22141 + t234 .On définit donc la fonction utile pour la dominationφt = K1t12 10;1 + K2214 1 + t234 11;+.On applique le théorème de convergence dominée sur 0; +.a Soit t 0; +. On définit lt = lnt21+t2 , et on a limx→0+ ft, x = lt.b Pour tout x 0; 1, la fonction t 7→ft, x est continue sur R+.c La fonction lt est continue sur R+.d Pour la domination, on at, x R+×0; 1, ft, x ⩽φt.Ainsi, la fonction l est intégrable sur R+ et limx→0+ F+x =R +0lnt1+t2 dt. La fonction F+ est donccontinue sur 0; 1. En procédant de même avec F, on montre que Fest aussi continue sur 0; 1.Ainsi, F est continue sur 0; 1.3. Pour montrer que F est C1 sur R+, on utilise le théorème de dérivation sous le signe intégrale. Onconsid‘ere l’intervalle ϵ; +. On aa Pour tout t R, la fonction x 7→ft, x est C1 sur ϵ; + et on addxft, x =1t2 + x11 + t2 .b Intégrabilité : on a déjà montré à la première question que pour tout x R+, la fonctiont 7→ft, x est intégrable sur R.c Pour tout x R+, la fonction t 7→ddxft, x est continue sur R.d Domination :t, x R × ϵ; +,ddxft, x ⩽1ϵ11 + t2qui est intégrable et indépendante de x.3
Page 4 : Par application du théorème, la fonction F est C1 sur R+ etF ′x =ZR1t2 + x11 + t2 dt.4. Puisque pour tout x 0 on a F ′x 0, la fonction F est strictement croissante sur R+. Par continuitésur R+, la fonction F atteint son minimum en 0.Exercice 37 pointsDans un plan muni d’un repère orthonormé, on considère le domaineΩ=x, y R2; x 0, x2 + y2 1.1. Représenter graphiquement le domaine Ω.2. Soit la fonction fx, y = expx2 y2. CalculerZZΩfx, y dxdy.Réponse.1. On reconnaît un demi-cerclexy-11-11y =px2 + 1D2. On peut appliquer le changement de variable en polaire. On pose l’application φ : r, θ 7→r cosθ, r sinθ.φ est un C1 difféomorphisme de 0; 1×π2 ; π2 sur D =nx, y R2; 1 y 1, 0 x p1 y2o.Pour un changement de variable en polaire on a Jacφ = r. Ainsi, puisque l’application f est continuesur D, on aZZDfx, ydxdy =Z 1r=0Zπ2π2er2rdθdret puisque l’intégrande est à variables séparéesZZDfx, ydxdy =Zπ2π2dθZ 10rer2dr = π12 er210= π21 e1.4