DS2 2024 2025 V2 Correction
Télécharger le DS2 2024 2025 V2 Correction en pdf
Page 1 : 2024/2025Semestre 2 – PréIng 2Mercredi 2 AvrilIntégration et ProbabilitésContrôle Continu 2◁Consignes ▷Durée : 60 mn▶Les documents et les supports électroniques sont interdits.▶L’épreuve est composée d’exercices indépendants.▶Le barème est à titre indicatif.▶La qualité de la rédaction et la rigueur des justifications seront prises en compte dans la notation.◁Sujet de l’épreuve ▷Exercice 15 points1. Représenter graphiquement le domaine D délimité par les courbes d’équation y2 = x1 et x2 +y2 = 4.2. Soit une fonction f définie sur R2. Énoncer le théorème de Fubini par tranches pour calculerI =ZZDfx, ydxdy.Réponse.1. On reconnaît l’équation d’une parabole x = y2 + 1 et d’un cercle de centre 0, 0 et de rayon 2 :x2 + y2 = 4, on en déduit le domaine :xy-2-1123-2-112x = y2 + 1x2 + y2 = 4D2. Théorème de Fubini par tranche : Soient c, d R tels que c d, et ψ1, ψ2 deux fonctions continuespar morceaux sur c, d telles que y c, d, ψ1y ψ2y.Soient D le domaineD = x, y R2 : c y d, ψ1y x ψ2yet f : R2 →R une fonction continue sur D. AlorsZZDf =Z dc Z ψ2yψ1yfx, y dx!dy.1
Page 2 : Exercice 28 pointsOn rappelle que la fonction sinus cardinal, définie sur R parsincy = sinyyest continue sur R et bornée, en valeur absolue, par une constante positive K.Soit la fonctionFx =Z +0et sinxttdt.1. Montrer que F est de classe C1 sur R et déterminer F ′x.2. À l’aide d’intégrations par parties, montrer queF ′x = 1 x2F ′x.3. En déduire une expression explicite de F ′ en fonction de x, puis de F on pourra s’aider de la valeurde F0.Réponse.1. On veut utiliser le théorème de convergence dominée pour la dérivabilité i.e. le théorème de dérivationsous le signe intégrale. On note f : t, x 7→et sinxttet on vérifie les hypothèses du théorème :• Pour tout t 0, + fixé, la fonction x 7→ft, x est C1 sur R car le sinus est C1 sur R.• Pour tout x R fixé on at R+ :ft, x =xet sinxtxt Kxetavec K un majorant du sinus cardinal. La fonction t 7→Kxet est intégrable sur 0, + commemultiple de t 7→et intégrale généralisée de référence. Par le théorème de majoration pour lesintégrales généralisées on en déduit que la fonction t 7→ft, x est intégrable sur R+.• Pour tout t, x R+ × R, fxt, x = et costx. Pour tout x R fixé, t 7→fxt, x est biencontinue sur 0, + comme produit de fonctions continues.• On pose ψ : t 7→et. La fonction ψ est intégrable sur 0, + intégrale généralisée de référenceet on at, x R+ × R,fxt, x ψtcar le cosinus est borné par 1 en valeur absolue.Les quatre hypothèses du théorème sont vérifiées et on peut donc conclure que F est C1 sur R etx R,F ′x =Z +0et cosxt dt.2. Soit x R fixé. On va procéder à deux intégrations par parties sur l’intégrale généralisée F ′x. Onsait que l’intégrale converge par la question 1, de plus :limt→0 et cosxt = 1,limt→+et cosxt = 0donc on peut appliquer le théorème d’intégration par partie dans le cas d’intégrales convergentes et onobtientF ′x =et cosxt+0Z +0etx sinxt dt = 1 xZ +0et sinxt dt.On procède maintenant à une deuxième intégration par parties, on sait que l’intégrale converge et quelimt→0 et sintx = 0,limt→+et sintx = 02
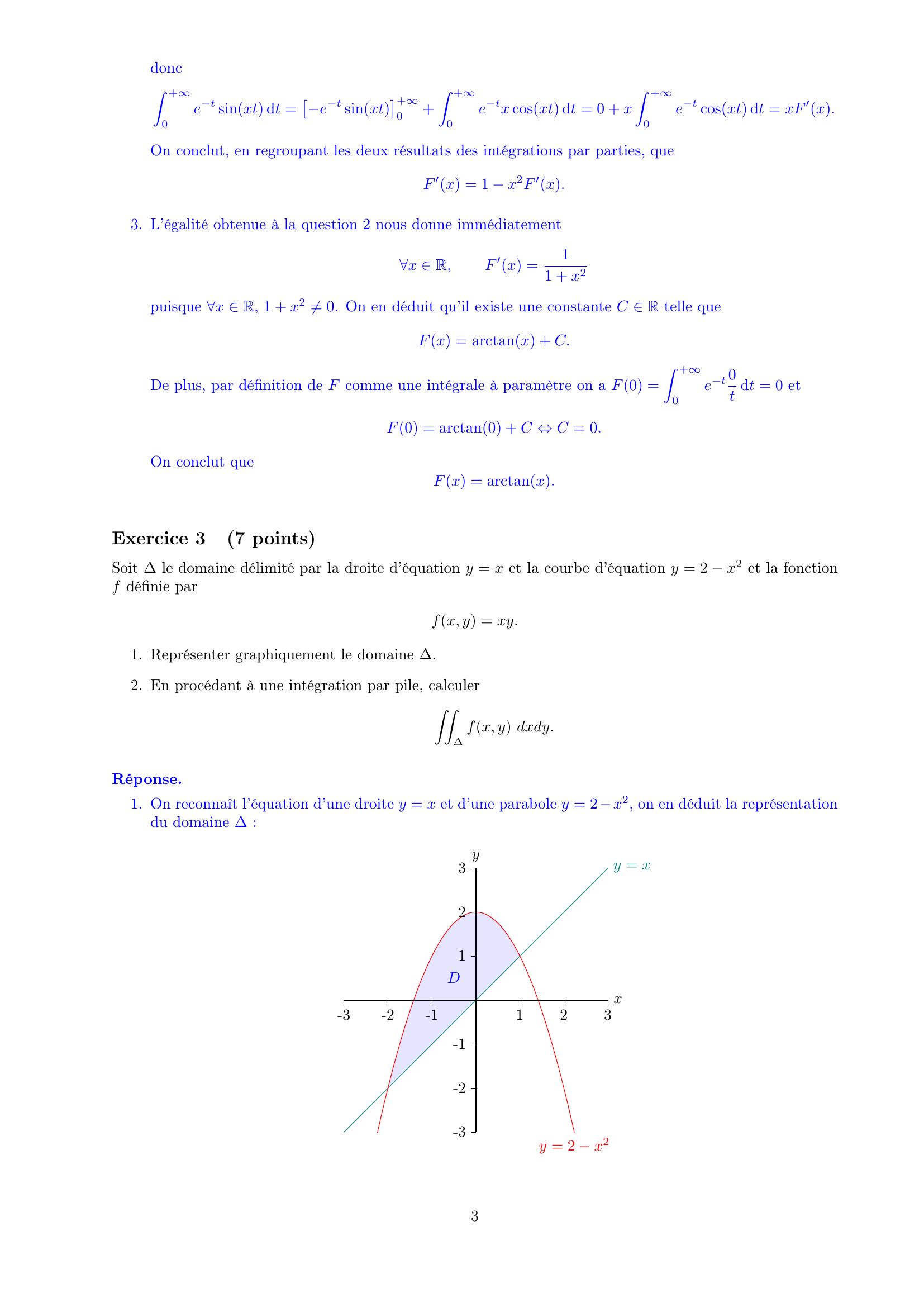
Page 3 : doncZ +0et sinxt dt =et sinxt+0+Z +0etx cosxt dt = 0 + xZ +0et cosxt dt = xF ′x.On conclut, en regroupant les deux résultats des intégrations par parties, queF ′x = 1 x2F ′x.3. L’égalité obtenue à la question 2 nous donne immédiatementx R,F ′x =11 + x2puisque x R, 1 + x2 ̸= 0. On en déduit qu’il existe une constante C R telle queFx = arctanx + C.De plus, par définition de F comme une intégrale à paramètre on a F0 =Z +0et 0t dt = 0 etF0 = arctan0 + C ⇔C = 0.On conclut queFx = arctanx.Exercice 37 pointsSoit le domaine délimité par la droite d’équation y = x et la courbe d’équation y = 2 x2 et la fonctionf définie parfx, y = xy.1. Représenter graphiquement le domaine .2. En procédant à une intégration par pile, calculerZZfx, y dxdy.Réponse.1. On reconnaît l’équation d’une droite y = x et d’une parabole y = 2x2, on en déduit la représentationdu domaine :y = xy = 2 x2xy-3-2-1123-3-2-1123D3
Page 4 : 2. Le domaine peut être décrit par := x, y R2 : x y et y 2 x2.En particulier, pour que les deux conditions puissent être remplies simultanément il faut que x 2x2donc être entre les deux racines du polynôme x2 + x 2 = x 1x + 2. On peut donc réécrire ledomaine sous la forme adaptée à l’intégration par piles := x, y R2 : 2 x 1, x y 2 x2Les fonctions φ1 : x 7→x et φ2 : x 7→2 x2 sont continues sur 2, 1 et la fonction f : x, y 7→xy estcontinue sur R2 car polynomiale donc en particulier sur . On peut donc appliquer le théorème deFubini par piles pour calculer :ZZf =Z 12 Z 2x2xxy dy!dx=Z 12xy222x2xdx=Z 12x22 x22 x2dx= 12Z 12x5 5x3 + 4x dx= 12x66 5x44+ 2x212= 1216 54 + 2 646 + 5 × 1642 × 4= 98.4