Feuille Cours0 Rappel

Télécharger le Feuille Cours0 Rappel en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

Page 1 : Table des matières1Suites et récurrence21.1Généralités. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21.1.1Définitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21.1.2Sens de variation des suites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21.1.3Suites majorées, minorées, bornées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31.2Suites Arithmétiques et Suite Géométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31.2.1Suites arithmétiques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .31.2.2Suites géométriques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41.3Raisonnement par récurrence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .41.4Convergence - Divergences de suites. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .71.4.1Définitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .71.4.2Propriétés sur les limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .81.4.3Théorèmes de comparaisons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .92Fonctions92.1Limite d’une fonction au voisinage de l’infini. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .92.1.1Limite finie - Asymptote horizontale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .92.1.2Limite infinie - Asymptote Oblique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .102.2Limite d’une fonction en un réel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .102.2.1Limite infinie - Asymptote verticale. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .102.2.2Limite finie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .112.3Limites de référence. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .112.4Opérations Algébriques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .122.4.1Cas général . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .122.4.2Cas particuliers des formes indéterminées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .132.5Théorème de comparaison . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .142.6Limite d’une fonction composée en a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .153Continuité d’une fonction163.1Définition et premières propriétés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .163.2Continuité et opérations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .163.3Le théorème des valeurs intermédiaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .164Dérivation174.1Généralités. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .174.2Opérations algébriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .184.3Formules de calculs des dérivées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .184.4Dérivée d’une fonction composée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .194.5Lien entre fonction et dérivée . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .195Fonctions Sinus et Cosinus195.1Rappel : Repérage sur le cercle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .195.1.1Définitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .195.1.2Position des angles remarquables sur le cercle trigonométrique. . . . . . . . . . . . . . . . . . . . . . .215.2Définition de sinus et cosinus. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .215.3Formules Trigonométriques. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .215.4Fonctions Trigonométriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .225.4.1Définitions. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .225.4.2Propriété. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .225.4.3Représentation graphique des fonctions trigonométriques . . . . . . . . . . . . . . . . . . . . . . . . . .23

Page 2 : 1Suites et récurrence1.1Généralités1.1.1DéfinitionsDéfinition 1.1. Une suite numérique u est une fonction à valeur dans R telle que :Il existe un entier naturel n0 tel que l’ensemble de définition de u est l’ensemble des entiers n n0.Remarque 1.1. On nomme souvent les suites en utilisant les lettres u et pour écrire les images des entiers un, on écritde préférence un. On peut donc alors noter les suitesunnn0Le terme initial de la suite est le terme un0.Le terme général de la suite est un.L’entier n est appellé indice du terme un.Exemple 1.1. exemples de suitesNomDéfinitionTerme initialDeuxièmeTroisièmeunn0n N, un = 2n + 1.u0 = 1u1 = 3u2 = 5hnn0n N, hn = 2n.h0 = 2h1 = 4h2 = 8knn0n N, kn = 1 12n.k0 = 0k1 = 12 = 0.5k2 = 34 = 0.75vnn1n N, vn = 1n.v1 = 1v2 = 12 = 0.5v3 = 13 0.3333wnn0w0 = 4 et n N, wn+1 = 12wn + 1w0 = 3w1 = 52 = 2.5w2 = 94 = 2.25tnn0n N, tn = 2nt0 = 1t1 = 2t2 = 4snn0s0 = 3 et n N, sn+1 = 12sn.s0 = 3s1 = 32 = 1.5s2 = 34 = 0.75Remarque 1.2. Une suite peut être définie :1. Soit à partir d’une formule en fonction de n, comme les fonctions suites un, hn, vn de l’exemple 1.12. Soit à partir d’une formule en fonction d’un ou plusieurs termes précédents et éventuellement de n, comme les suiteswn, sn de l’exemple 1.1Dans le premier cas, on peut calculer n’importe quel terme de la suite rapidement, dans le second cas, il faut calculer tousles termes intermédiaires.1.1.2Sens de variation des suitesDéfinition 1.2. suite monotoneUne suite unn0 croissante est telle que pour tout n N, un+1 un.Une suite unn0 décroissante est telle que pour tout n N, un+1 un.Une suite est monotone si elle est croissante ou si elle est décroissante.Remarque 1.3. La suite est strictement croissante ou décroissante lorsque l’inégalité est stricte.Exemple 1.2. Les suites un, hn, kn sont croissantes, les suites vn, wn sont décroissantes, les suitestn, sn ne sont ni croissantes, ni décroissantes.Propriété 1.1. Soit une suite unnN définie de façon explicite : n N, un = fn.Si la fonction f est croissante sur 0; + la suite est croissante, si la fonction f est décroissante sur 0; +, lasuite est décroissante.

Page 3 : On dispose donc de plusieurs méthodes pour étudier le sens de variation d’une suite :— étudier le signe de la différence un+1 un— pour une suite à termes strictement positifs, étudier un+1unà 1.— si la suite est du type un+1 = fn, on peut étudier le sens de variation de f, puis en déduire celui de la suite maispas dans le cas où un+1 = fun la suite wn de l’exemple 1.1 est un contre-exemple.Remarque 1.4. Pour démontrer qu’une suite est croissante, il faut démontrer que pour tout n, un+1 un. Il ne suffit pasde constater que les premiers termes sont en ordre croissant.Par contre pour démontrer qu’une suite n’est pas croissante il suffit de trouver deux termes en ordre décroissant.1.1.3Suites majorées, minorées, bornéesDéfinition 1.3. suites majorées, minorées, bornées• Par définition, une suite unn0 majorée est telle qu’il existe un réel M tel que pour tout entier naturel n,un M• Par définition, une suite un minorée est telle qu’il existe un réel m tel que pour tout entier naturel n,m un.• Par définition, une suite bornée est majorée et minorée.Exemple 1.3. On se réfère aux suites de l’exemple 1.11. La suite sn est majorée par 1 et 0.2. La suite un n’est pas majorée.3. La suite kn et majorée par 1 et minorée par 0, elle est donc bornée.Exercice 1.1. Défi: Soit la suite un définie par un = 1 + 12 + 13 + 14 + . . . + 1n. Est-elle bornée ?on pourra programmer le calcul des termes successifs pour tester.1.2Suites Arithmétiques et Suite Géométriques1.2.1Suites arithmétiquesDéfinition 1.4. Une suite unn0 est dite “arithmétique” lorsqu’il existe un réel r tels que pour tout entiernaturel n un+1 = un + r relation de récurrence.Le réel r s’appelle la raison de la suite arithmétique.u0+ru1+ru2+ru3+rRemarque: Montrer qu’une suite est arithmétique revient à montrer que un+1un est constant “common difference sequence”Propriété 1.2. terme général Si unn0 est une suite arithmétique de raison r alorspour tout entier naturel n, un = u0 + nr ←formule du terme de rang n en fonction de nPlus généralement, pour tout entier naturel k, un = uk + n krPropriété 1.3. Une suite unn0 est arithmétique si et seulement si elle est définie par un = an + b.La raison de la suite un est a. Le premier terme u0 = b.Propriété 1.4. Soit une suite arithmétique unnN.La somme de Sn = u0 + u1 + u2 + . . . + un =nXi=0ui = n + 12u0 + un.D’une façon générale, soit m et p deux entiers tels que m p, la somme des termes consécutifs des termes deum à up est le produit de la moyenne des deux termes extrêmes um et up et du nombre de termes.

Page 4 : Propriété 1.5. sens de variationSoit un réel a. Soit unn0 une suite arithmétique de raison a.Si a 0, la suite est strictement croissante.Si a = 0 la suite est constante.Si a 0, la suite est strictement décroissante.1.2.2Suites géométriquesDéfinition 1.5. Une suite unn0 est dite “géométrique” lorsque il existe un entier naturel n0 et un réel q telsque pour tout entier naturel n, un+1 = qun relation de récurrence.Le réel q s’appelle la “raison” de la suite géométrique.u0×qu1×qu2×qu3×qRemarque: Lorsque l’on est assuré que les termes sont non nuls, montrer qu’une suite est géométrique revient à montrer queun+1/un est constant “common ratio sequence”Propriété 1.6. terme général Si unn0 est une suite géométrique de raison q alorspour tout entier naturel n, un = u0qn ←formule du terme de rang n en fonction de nPlus généralement, pour tout entier naturel k , un = ukqnk .Propriété 1.7. admiseSoit une suite géométique de raison q ̸= 1, vnnN.La somme de Sn = v0 + v1 + v2 + . . . + vn =nXi=0vi = v01 qn+11 q.Remarque 1.5. Pour deux entiers n et p tels que p n,Sn = vp + vp+1 + vp+2 + . . . + vn =nXi=pvi = vp1 qnp+11 q.Propriété 1.8. sens de variationSoit un réel q non nul. Soit unn0 une suite géométrique de raison q.Si q 1, si u0 0, la suite est strictement croissante, si u0 0 la suite est strictement croissante.Si 0 q 1, si u0 0 la suite est strictement décroissante, si u0 0 la suite est strictement décroissante.Si q 0, la suite n’est pas monotone.Exemple 1.4. En se référant à l’exemple 1.1La suite hn est géométrique et croissante car le premier terme est positif et la raison q = 2 1.Les suites tn et sn sont géométriques mais ni croissantes, ni décroissantes car leurs raisons, respectivement-2 et 12 sont négatives.1.3Raisonnement par récurrencePropriété 1.9. Récurrence simple.Soit P une propriété portant sur les entiers naturels.Soit n0 un entier naturel.On suppose que Pn0 est vraie.On suppose également que pour tout entier n n0 , si Pn est vraie, alors Pn + 1 est vraie.cela revient à dire que l’implication Pn ⇒Pn + 1 est vraieAlors pour tout entier n n0, la proposition Pn est vraie.

Page 5 : Voici comment doit se faire un raisonnement par récurrence et comment il doit être rédigé :1. On énonce clairement la propriété P étudiée.2. On vérifie que la propriété P est vraie pour n0 Initialisation3. On se donne un entier n n0 quelconque et on suppose que Pn est vraie Hypothèse de récurrence.On démontre alors que Pn + 1 est vraie Hérédité4. On conclut en annonçant que, par récurrence, la propriété est vraie pour tout entier n n0.Remarque 1.6. Il faut voir le principe de récurrence comme une échelle que l’on essaye de monter :Si l’on est capable de poser le pied sur le premier barreau et que l’on est capable de passer d’un barreau au suivant, alors onest capable de monter l’échelle en entier. Si l’une des deux conditions manque, alors nous ne pouvons pas monter l’échelle.D’où l’importance de vérifier l’initialisation ET l’hérédité.Exemple 1.5. Démontrer par récurrence que pour tout N N, on a l’égalité 1 + 2 + 3 + + n = nn + 121. Soit Pn la propriété définie sur Npar 1 + 2 + 3 + + n = nn + 122. Nous avons 1 = 11 + 12, donc P1 est vraie.3. Soit un entier n Ntel Pn est vraie. Démontrons alors que Pn + 1 est vraie aussi. Nous devonsdonc montrer que1 + 2 + 3 + · · · + n + n + 1 = n + 1n + 22Nous avons supposé que Pn est vrai, donc on peut écrire :1 + 2 + · · · + n + n + 1 = 1 + 2 + · · · + n + n + 1= nn + 12+ n + 1= nn + 1 + 2n + 12= n + 1n + 22Donc l’implication Pn ⇒Pn + 1 est vraie.4. Nous avons donc montré par récurrence que pour tout entier n N, 1 + 2 + 3 + · · · + n = nn + 12Une erreur classique est d’oublier l’initialisation. L’exemple suivant est un exemple de cette erreur classique.

Page 6 : Exemple 1.6 FAUX !. Démontrer par récurrence que pour tout n N, on a l’égalité fausse 1+2+3++n =n2 + n + 121. Soit Pn la propriété définie sur N: 1 + 2 + 3 + + n = n2 + n + 122. L’élève oublie l’initialisation.3. Soit un entier n Ntel Pn est vraie. Démontrons alors que Pn + 1 est vraie aussi. Nous devonsdonc montrer que1 + 2 + 3 + + n + n + 1 = n + 12 + n + 1 + 12La fraction est égale à n + 12 + n + 1 + 12= n2 + 3n + 32.De plus1 + 2 + · · · + n + n + 1 = 1 + 2 + · · · + n + n + 1= n2 + n + 12+ n + 1= n2 + n + 1 + 2n + 22= n2 + 3n + 32= n + 12 + n + 1 + 12Donc l’implication Pn ⇒Pn + 1 est vrai.4. Nous avons donc montré par récurrence que pour tout entier n N, 1 + 2 + 3 + + N = n2 + n + 12Vous l’aurez compris, il y a une erreur. Un calcul simple permet de montrer que P1 est fausse puisqu’ellestipule que 1 = 32. Le premier barreau étant cassé, nous ne pouvons pas monter à l’échelle.Remarque 1.7. Pour montrer une propriété universelle , c’est à dire montrer que tous les éléments d’un ensemble ontcette propriété, on prend un élément quelconque de l’ensemble et on démontre qu’il a la propriété.On utilise souvent une rédaction du type “Soit....”.Exemple 1.7. Par exemple :« Pour tout quadrilatère, le quadrilatère non croisé formé par les milieux des segments est un parallélogramme.»Soit un quadrilatère quelconque, nommons les sommets ABCD et les milieux I, J, K et L respectivement deAB, BC,CD et DA.D’après la propriété de la droite des milieux dans ABC, →IJ = 12→AC. De meme →LK = 12→AC donc →IJ = →AC.Donc IJKL est un parallélogramme.Conclusion «Pour tout quadrilatère, le quadrilatère non croisé formé par les milieux des segments est unparallélogramme.»Exemple 1.8. Autre exemple :« La somme de 3 entiers consécutifs est un multiple de 3.»"pour tout 3 entiers consécutifs, etc..."Soit trois entiers consécutifs quelconques.On note n le plus petit des trois. La somme est alors n + n + 1 + n + 2 = 3n + 3 = 3n + 1 donc est unmultiple de 3.D’où la propriété annoncée.Remarque 1.8. Pour montrer P ⇒Q que faut-il montrer ?

Page 7 : Table de vérité de l’implicationPQP ⇒QVVVVFFFVVFFVDonc si P est faux, l’implication est toujours vraie un P faux peut donner n’importe : quoi Q vraie et Q faux conviennent.Pour montrer l’implication, il suffit de montrer qu’elle n’est pas fausse, cela n’arrive que dans un seul cas : quand P est vraieet Q est faux. Donc on va vérifier que «si P est vraie, Q est vraie aussi».Donc pour montrer P ⇒Q on rédige :«Supposons P vraie, montrons Q vraie.»Exemple 1.9. Si n est impair alors n2 est impair.Supposons n pair, n = 2 × p + 1 avec p N. Donc n2 = 22p2 + 2p + 1 donc n2 est impair.L’implication est donc vraie.Exercice 1.2. Démontrer une formuleSoit la suite unnN définie par :u0 = 2 et n N, un+1 = 3un 5.Démontrer par récurrence que n N, un = 125 3nRemarque 1.9. Penser à utiliser la calculatrice application suite pour vérifier que la formule est correcteSolutionPour tout n N soit la propriété Pn : un = 125 3n• 125 30 = 125 1 = 2 = u0 donc P0 est vraie.Vérification au premier rang• Soit n N. On suppose que Pn est vraie. C’est à dire un = 125 3n.On veut montrer que pour tout n, si Pn est vraie, on a Pn + 1 vraie. On choisit donc un n quelconque, on supposeque Pn est vraie et on va essayer de montrer que Pn + 1 est vraie. Puisque n était quelconque, on a bien démontréque pour tout n, si Pn est vraie, Pn + 1 est vraie.On veut montrer que Pn + 1 est vraie, c’est à dire un+1 = 125 3n+1 On a un+1 = 3un 5 = 3125 3n5= 152 3n+125 = 52 3n+12Donc Pn + 1 est vraie.• Donc par récurrence, pour tout entier naturel n, un = 125 3n.1.4Convergence - Divergences de suites1.4.1DéfinitionsDéfinition 1.6. Une suite numérique admet le réel l comme limite lorsque pour tout intervalle ouvert quicontient l, il existe un entier n0 tel que pour tous les entiers n n0, un appartient à I.Cela revient, en écriture symbolique, à :ϵ R 0, n0, n N, n n0, un l ϵ; l + ϵ

Page 8 : Définition 1.7. Une suite numérique admet pour limite +respectivement lorsque pour tout intervalleouvert I de la forme a; + de la forme ; a, il existe un entier n0 tel que pour tous les entiers n n0,un appartient à I.Cela revient, en écriture symbolique, à :a R, n0, n N, n n0, un a; +Définition 1.8. Par définition,Une suite convergente admet une limite finie.Une suite divergente est une suite qui n’est pas convergente.Remarque:Il y a deux suites de type convergentes :— Les suites monotones. Dans l’exemple 1.1 : kn, vn, wn ou 1nnN— Les suites qui ne sont pas monotones. Dans l’exemple 1.1 : sn ou12nnNIl y a deux types de suites divergentes :— les suites qui ont pour limite +ou . Dans l’exemple 1.1 : un, hn ou nnN— les suites qui n’ont pas de limite. Dans l’exemple 1.1 : tn ou 2nnNUNE LIMITEPAS DE LIMITEFINIEINFINIECONVERGENTEDIVERGENTE1.4.2Propriétés sur les limitesPropriété 1.10. Si une suite admet une limite finie ou infinie, alors celle-ci est unique.Remarque 1.10. Une suite convergente n’est pas nécessairement monotone. Par exemple12n.Propriété 1.11. Si une suite est croissante et admet pour limite l, alors tous les termes de la suite sont inférieursou égaux à l.Théorème 1.1. Convergence des suites monotones bornéesToute suite monotone et bornée converge.Autrement dit :• Si un est une suite croissante et majorée alors elle converge.• Si un est une suite décroissante et minorée alors elle converge.Propriété 1.12. Soit f une fonction continue sur un intervalle I de R à valeur dans I et soit un une suite telleque u0 I et n N, un+1 = fun.Si un converge vers une limite l alors l vérifie l’équation l = flThéorème 1.2. Divergence des suites monotones non bornéesSi un est une suite croissante et non majorée alorslimn→+un = +.Si un est une suite décroissante et non minorée alorslimn→+un = .

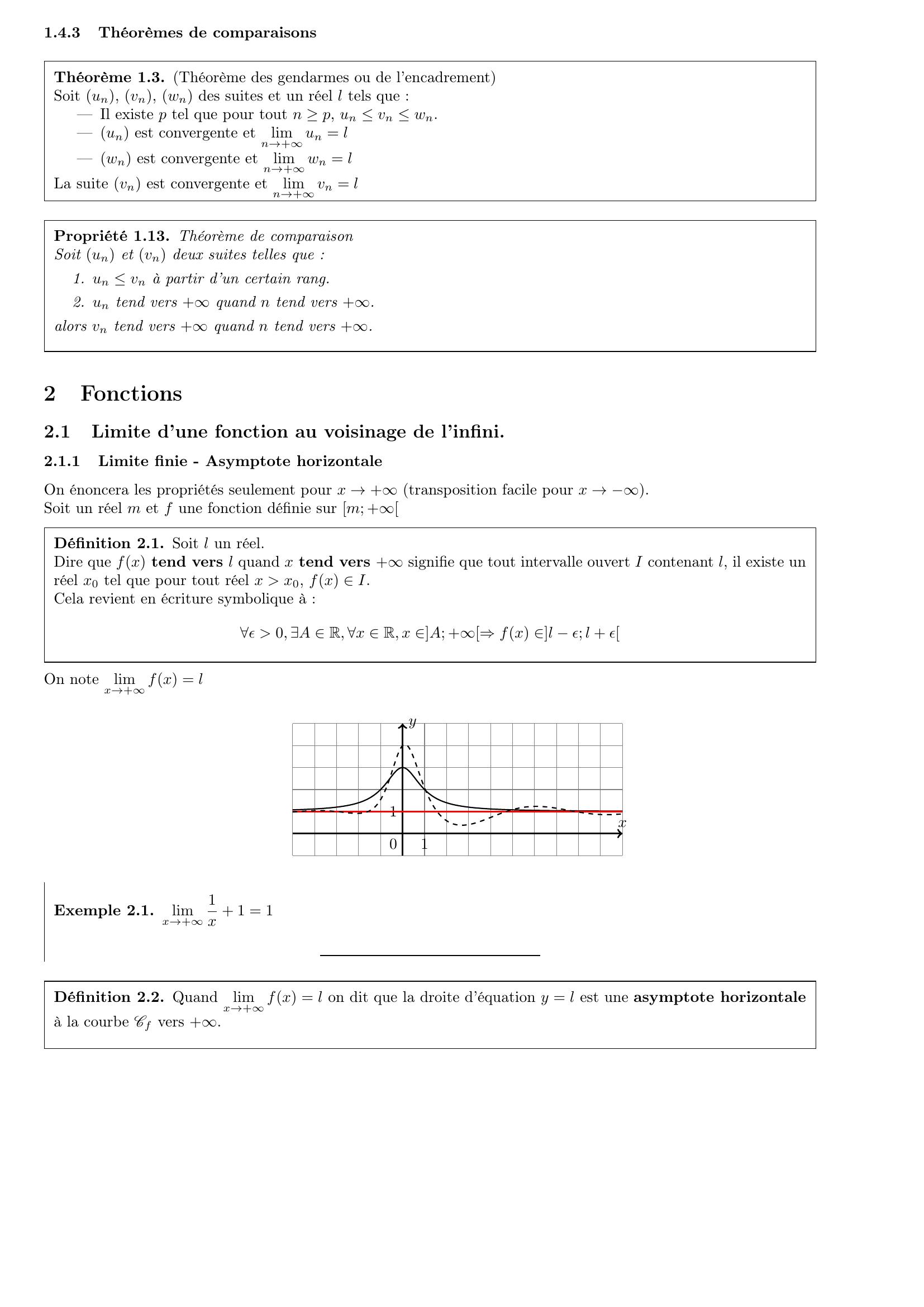
Page 9 : 1.4.3Théorèmes de comparaisonsThéorème 1.3. Théorème des gendarmes ou de l’encadrementSoit un, vn, wn des suites et un réel l tels que :— Il existe p tel que pour tout n p, un vn wn.— un est convergente etlimn→+un = l— wn est convergente etlimn→+wn = lLa suite vn est convergente etlimn→+vn = lPropriété 1.13. Théorème de comparaisonSoit un et vn deux suites telles que :1. un vn à partir d’un certain rang.2. un tend vers +quand n tend vers +.alors vn tend vers +quand n tend vers +.2Fonctions2.1Limite d’une fonction au voisinage de l’infini.2.1.1Limite finie - Asymptote horizontaleOn énoncera les propriétés seulement pour x →+transposition facile pour x →.Soit un réel m et f une fonction définie sur m; +Définition 2.1. Soit l un réel.Dire que fx tend vers l quand x tend vers +signifie que tout intervalle ouvert I contenant l, il existe unréel x0 tel que pour tout réel x x0, fx I.Cela revient en écriture symbolique à :ϵ 0, A R, x R, x A; +⇒fx l ϵ; l + ϵOn notelimx→+fx = lxy110Exemple 2.1.limx→+1x + 1 = 1Définition 2.2. Quandlimx→+fx = l on dit que la droite d’équation y = l est une asymptote horizontaleà la courbe Cf vers +.

Page 10 : 2.1.2Limite infinie - Asymptote ObliqueDéfinition 2.3. Dire que fx tend vers +quand x tend vers +signifie que pour tout réel M, , il existeun réel x0 tel que pour tout réel x x0, fx ACela revient en écriture symbolique à :M R, A R/x R, x A; +⇒fx M; +Dire que fx tend vers quand x tend vers +signifie que pour tout réel M, il existe un réel x0 tel quepour tout réel x x0, fx A.Cela revient en écriture symbolique à :M R, A R/x R, x A; +⇒fx ; Mxy110Exemple 2.2.limx→+x22 = +Définition 2.4. Soit a et b deux réels , a non nul. Quandlimx→+fx ax + b = 0 on dit que la droited’équation y = ax + b est une asymptote oblique à la courbe Cf vers +.Remarque 2.1. Attention : toute courbe représentative d’une fonction “définie” en +n’admet pas nécessairement uneasymptote : la parabole fonction carréxy110Exemple 2.3. Soit f définie sur R \ 3 par fx = x2 3x + 1x 3, on écrit fx = ax + b +cx 3 ; on trouvefx = x +1x 3. Commelimx→+fx x =limx→+1x 3 = 0 et égalementlimx→fx x =limx→1x 3 = 0la droite d’équation y = x est une asymptote oblique à la courbe Cf2.2Limite d’une fonction en un réel2.2.1Limite infinie - Asymptote verticaleSoit un réel a. Soit un intervalle I de R tel que a I. Soit f une fonction définie sur I en excluant éventuellement le point a.

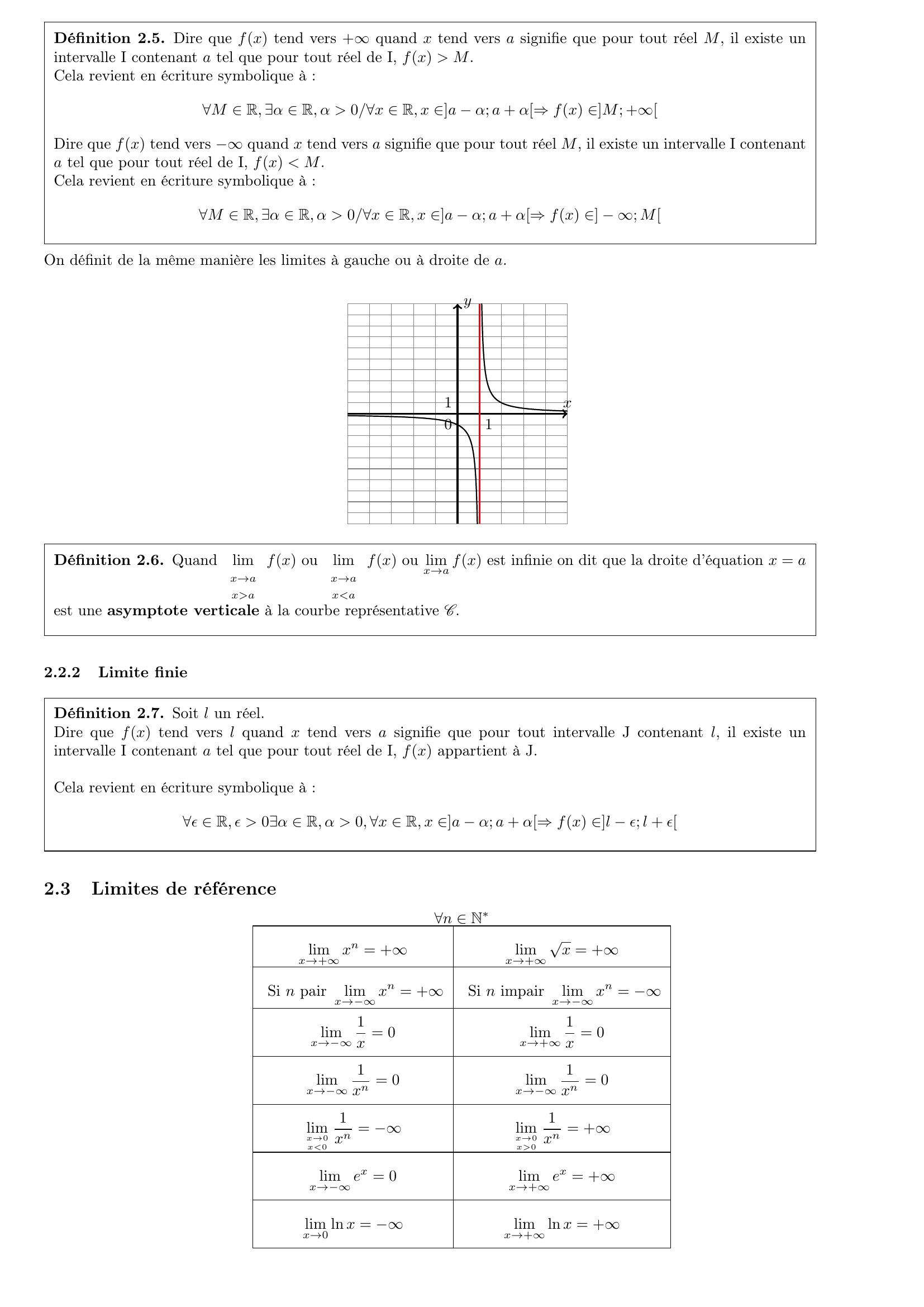
Page 11 : Définition 2.5. Dire que fx tend vers +quand x tend vers a signifie que pour tout réel M, il existe unintervalle I contenant a tel que pour tout réel de I, fx M.Cela revient en écriture symbolique à :M R, α R, α 0/x R, x a α; a + α⇒fx M; +Dire que fx tend vers quand x tend vers a signifie que pour tout réel M, il existe un intervalle I contenanta tel que pour tout réel de I, fx M.Cela revient en écriture symbolique à :M R, α R, α 0/x R, x a α; a + α⇒fx ; MOn définit de la même manière les limites à gauche ou à droite de a.xy110Définition 2.6. Quandlimx→axafx oulimx→axafx ou limx→a fx est infinie on dit que la droite d’équation x = aest une asymptote verticale à la courbe représentative C.2.2.2Limite finieDéfinition 2.7. Soit l un réel.Dire que fx tend vers l quand x tend vers a signifie que pour tout intervalle J contenant l, il existe unintervalle I contenant a tel que pour tout réel de I, fx appartient à J.Cela revient en écriture symbolique à :ϵ R, ϵ 0α R, α 0, x R, x a α; a + α⇒fx l ϵ; l + ϵ2.3Limites de référencen Nlimx→+xn = +limx→+x = +Si n pairlimx→xn = +Si n impairlimx→xn = limx→1x = 0limx→+1x = 0limx→1xn = 0limx→1xn = 0limx→0x01xn = limx→0x01xn = +limx→ex = 0limx→+ex = +limx→0 ln x = limx→+ln x = +

Page 12 : 2.4Opérations Algébriques2.4.1Cas généralLes théorèmes qui suivent, présentés sous forme de tableaux, permettent de connaître les limites des fonctions f + g, fg,fglorsque l’on connaît celle de f et celle de g.Les limites des fonctions f et g sont prises soit en +soit en , soit en un réel a.l et l′ sont des nombres réels. Les cases barrées signalent les cas ou il n’y a pas de conclusion en général, on dit qu’il s’agit deformes indéterminées. Dans tous les autres cas, les résultats, que nous admettrons, sont intuitifs et faciles à retenir.Limite d’une sommeSi f a pour limitelll++et si g a pour limitel′++alors f + g a pour limitel + l′++?Limite d’un produitsi f a pour limitell 0l 0l 0l 0++0et si g a pour limitel′++++ou alors fg a pour limitell′++++?Limite d’un quotientCas où la limite d’un dénominateur g n’est pas nulle.si f a pour limitell++ou + et si g a pour limitel′ ̸= 0ou + l′ 0l′ 0l′ 0l′ 0ou + alors fg a pour limitell′0++?

Page 13 : Cas où la limite d’un dénominateur g est nulle.si f a pour limitel 0 ou + l 0 ou + l 0 ou l 0 ou 0et si g a pour limite0 en restant0 en restant0 en restant0 en restant0positivenégativepositivenégativealors fg a pour limite++?Etude des limites de ABBAm 00m 0+FI000FIl 0+ml0ml0sgnsgnFIsgnsgnl 0ml0ml++FI000FIsgn signifie qu’il faut étudier le signe avant de conclure.FI signifie forme indéterminée : il faut écrire l’expressiondifféremment pour pouvoir conclure.2.4.2Cas particuliers des formes indéterminéesLes cas de formes indéterminées nécessiteront une étude particulière chaque fois qu’ils se présenteront. Ces cas sont au nombrede quatre :"" , "0 × " , "" , "00"Méthodes Comment lever une forme indéterminée :Dans les exercices qui suivent on admettra l’existence d’une limite.Le cas “ ”• On peut factoriser le numérateur et le dénominateur par le terme le plus “influent”.Exemple 2.4. Déterminer les limites si elles existent des expressions suivantes :1 2xx 5 en +.On a x R, 1 2xx 5 =x 1x 2x1 5x =1x 21 5x.Donc la limite est -21 x31 + 2x2 en +.On a x R, 1 x31 + 2x2 =x31 1x3x2 1x2 + 2 = x1 1x31x2 + 2donc la limite est +Propriété 2.1. Soit une fonction polynôme P de monôme de plus haut degré axna réels non nul, n un entiernaturelP admet en +respectivement en une limite qui est égale à la limite de axn.

Page 14 : Propriété 2.2. Soient R une fonction rationnelle d’ensemble de définition D et deux polynômes P et Q tels quex D, Rx = PxQx.Sachant que P et Q admettent pour monômes de plus haut degré respectivement axn et bxm a, b réels non nuls,n, m deux entiers naturels.R admet en +et une limite qui est égale à la limite de la fonction rationnelle axnbxm .Remarque: Cette propriété ne s’applique qu’à un quotient de polynômes.Le cas ""• On peut factoriser par le terme le plus “influent”• Pour les expressions avec radicaux, on peut utiliser l’expression conjuguée voir Section 4Exemple 2.5. 3x5 2x4 + x8 en .3x5 2x4 + x8 = x8 3x3 2 1x4 + 1Le cas “ 00”• Lorsqu’on prend la limite en a on peut factoriser x a au numérateur et dénominateur, puis simplifier.• Pour les expressions avec des radicaux, on peut utiliser l’expression conjuguée voir Section 4Exemple 2.6. x2 2x + 1x2 1en 1.x2 2x + 1x2 1=x 12x + 1x 1 = x 1x + 1.x2 x2x + 2 en 1.x2 2x + 1x2 1=x 122x 1 = x2.2.5Théorème de comparaisonl et l′ désignent deux réels. a est un réel ou +ou .Théorème 2.1. théorème de comparaison Soit f et g deux fonctions telles que pour tout x assez proche dea, fx gx.Si limx→a fx = l et limx→a gx = l′ alors l l′.Théorème 2.2. Soit f et g deux fonctions telles que pour tout x assez proche de a, fx gx.Si limx→a fx = +alors limx→a gx = +.Si limx→a gx = alors limx→a fx = .Exemple 2.7.limx→+x cos x x3On a x R+, x cos x x3 x x3. Donc commelimx→+x x3 = ,limx→+x cos x x3 = Théorème 2.3. Théorème des gendarmesSoit f, g et h trois fonctions telles que pour tout x assez proche de a, fx gx hx.Si f et h admettent une limite en a égale à l alors g admet une limite en a et limx→a gx = l.Remarque 2.2. Ce théorème est souvent utiliser avec des limites utilisant des fonctions trigonométrique sin, cos et tan

Page 15 : 2.6Limite d’une fonction composée en aDéfinition 2.8. Soit I et J deux intervalles.Soit g une fonction définie sur J et u une fonction définie sur I telles quepour tout x de I, ux appartient à l’intervalle J.La fonction f définie pour tout élément de I par f : x 7→gux est appelée "composée" de u suivi de g.Cela correspond au “montage” : xu→ux = Ug→gU = guxRemarque 2.3. On la note g ◦u.On considère les fonctions g et u telles que leur composée existe guThéorème 2.4. a, b c sont des réels ou bien ils désignent +ou .Si limx→a ux = b et que limU→b gU = c alors limx→a gux = cExemple 2.8. On veut déterminerlimx→+r1x + 4On décompose xu→1x + 4 = Ug→U =r1x + 4On calcule les limiteslimx→+1x + 4 = 4 et limU→4U = 2d’où par compositionlimx→+r1x + 4 = 2Formes indéterminées avec radicauxOn utilise la propriété suivante :Propriété 2.3. Pour tout x R+,x2 = x et pour tout x R,x2 = xDéterminer les limites si elles existent des expressions suivantes.•x2x2 + 2en +et .Si x positif,x2x2 + 2=x2x r1 + 2x! =x r1 + 2x! donc la limite en +est +Si x négatif,x2x2 + 2=x2x r1 + 2x! = x r1 + 2x! donc la limite en est +•px2 + 1 2x en +•x x en .•x + 1 x en +.•p4x2 + 1 2x en +px2 + 2 2x + 3 en +et en .px2 + 2 x en +.x + xx 1en 1.limx→+p4x2 + 3x + 1 2x = 34Propriété 2.4. Quelques limites à connaîtrelimx→0sin xx= 1limx→0ex 1x= 1limx→0lnx + 1x= 1

Page 16 : 3Continuité d’une fonction3.1Définition et premières propriétésDéfinition 3.1. Soit a un réel, soit une fonction f définie sur un intervalle I contenant a.• f est continue en a quand limx→a fx = fa• f est continue sur un intervalle I lorsque f est continue pour tout a de I.Remarque 3.1. Lorsque la courbe représentative de f se trace sans lever le crayon ne présente pas de saut f est continuesur I.3.2Continuité et opérationsPropriété 3.1. admiseLes fonctions de référence sont continues sur chaque intervalle de leur ensemble de définition.Les sommes, produits, quotients ou composées des fonctions continues sont continues sur chaque intervalle deleur ensemble de définition.En particulier, les fonctions polynômes et les fonctions rationnelles sont continues sur chaque intervalle de leurensemble de définition.3.3Le théorème des valeurs intermédiairesxykxykxykFonctions continue monotoneFonction continueFonction discontinueThéorème 3.1. Théorème des valeurs intermédiairesSoit f une fonction définie et continue sur un intervalle a; b.Pour tout réel k compris entre fa et fb, il existe au moins un réel c compris entre a et b tel que fc = k.Remarque 3.2. Ce théorème peut être démontré à l’aide des suites adjacentes.Propriété 3.2. image d’un intervalle par une fonction continueSoit f un fonction définie et continue sur un intervalle a; b.L’image d’un intervalle est un intervalle.Théorème 3.2. Soit f une fonction continue et strictement monotone sur a; b.Pour tout réel k compris entre fa et fb, l’équation fx = k admet une solution unique dans a; b il existeun unique réel c dans a; b tel que fc = k.

Page 17 : xacbvar. de x 7→ffakfbxacbvar. de x 7→ffakfbFonctions croissanteFonctions décroissanteRemarque 3.3. Extension du théorème : on admet que ces théorèmes restent vrais pour tout type d’intervalle fini ou infini,ouvert ou semi-ouvert en remplaçant les images par les limites.Exemple 3.1. Soit fx = x3 12x définie sur R. Son tableau de variations est donné ci-dessous.x22+Variations de fx16-16+Déterminer le nombre de solutions de fx = 1 ; de fx = kpour k 16 une solution ;k = 16 deux solutions ;pour 16 k 16 trois solutions ;pour k = 16 deux solutions ;pour 16 k une solution ;4Dérivation4.1GénéralitésDéfinition 4.1. Soit une fonction f définie sur un intervalle contenant a.On dit que f dérivable en a quand le taux de variation fx fax aadmet une limite en a. Le nombre dérivéeest la limite de ce taux et est noté f ′af ′a = limx→afx fax aou bienf ′a = limh→0fa + h fahExemple 4.1. Démontrer que la fonction inverse est dérivable en 2.Propriété 4.1. Le nombre dérivé f ′a est le coefficient directeur de la tangente.L’équation de cette tangente est doncy = f ′ax a + faExemple 4.2. Déterminer l’équation de la tangente à la courbe représentative de la fonction inverse au pointd’abscisse 2.Définition 4.2. Une fonction f est dérivable sur un intervalle I lorsqu’elle est dérivable en tout point de I.Dans ce cas on appelle dérivé la fonction x 7→f ′x

Page 18 : Exemple 4.3. Soit la fonction f : x 7→x2 + 2x 3. Déterminer f ′x et f ′′x4.2Opérations algébriquesThéorème 4.1. Soit u et v deux fonctions dérivables sur un intervalle I et k un réel.Les fonctions u + v, ku et uv sont dérivables sur I.Si v ne s’annule pas sur I alors les fonctions 1v et uv sont dérivables sur I.On a alors :u + v′ = u′ + v′uv′ = u′v + uv′ et ku′ = ku′uv′= u′v uv′v2et1v′= v′v24.3Formules de calculs des dérivéesTableau des fonctions dérivées pour lesfonctions de référenceFonction fDfFonction f ′D′ffx = kRf ′x = 0Rfx = xRf ′x = 1Rfx = x2Rf ′x = 2xRfx = xn n NRf ′x = nxn1Rfx = xn n ZRf ′x = nxn1Rfx = 1xRf ′x = 1x2Rfx = xR+f ′x =12xR+fx = sinxRf ′x = cosxRfx = cosxRf ′x = sinxRfx = exRf ′x = exRfx = lnxR+f ′x = 1xR+Tableau de dérivation des fonctions composéesSoit u une fonction définie et dérivable sur un intervalle IFonction fconditionsd’existencede fFonction f ′conditionsd’existencede f ′f = u2f ′ = 2uu′fx = un n Nf ′x = nun1u′f = 1uux ̸= 0f ′ = u′u2ux ̸= 0f = un n Zux ̸= 0f ′ = nun1u′ux ̸= 0f = uux 0f ′ =u′2uux 0f = sinuf ′ = cosuu′f = cosuf ′ = sinuu′f = euf ′ = euu′f = ln uf ′ = u′uPropriété 4.2. Toute fonction polynôme est dérivable sur R.Toute fonction rationnelle est dérivable sur tout intervalle de son ensemble de définition.Remarque 4.1. Chacune de ces formules se démontre en déterminant la limite du taux de variation en x. Voir par exemplela démonstration de la formule pour la fonction sinus.

Page 19 : 4.4Dérivée d’une fonction composéeThéorème 4.2. admis Soit u une fonction dérivable sur un intervalle I et g une fonction dérivable en toutréel ux avec x I.Alors la fonction f : x 7→gux est dérivable sur I et, pour tout x de If ′x = g′uxu′xPropriété 4.3. Soit a et b deux réels, soit f une fonction définie sur un intervalle I, soit J un intervalle tel quex J, ax + b I. La fonction g : x 7→fax + b est dérivable etg′x = af ′ax + b4.5Lien entre fonction et dérivéeSoit f une fonction dérivable sur un intervalle I.Théorème 4.3. Signe de la dérivée et sens de variations de la fonction• f est constante sur I si et seulement si f ′ est nulle sur I.• Si f ′ est strictement positive sur I, à l’exception d’un nombre fini de réels où elle s’annule alors f est strictementcroissante sur I.• Si f ′ est strictement négative sur I, à l’exception d’un nombre fini de réels où elle s’annule alors f eststrictement décroissante sur I.Théorème 4.4. Zéro de la dérivée et extremum local de la fonction• Si f admet un extremum local en a alors f ′a = 0• Si f ′ s’annule en a en changeant de signe alors f admet un extremum local en a.Propriété 4.4. Toute fonction dont la dérivée est nulle sur un intervalle est constante.5Fonctions Sinus et Cosinus5.1Rappel : Repérage sur le cercle5.1.1DéfinitionsSoit un repère O,→i ,→j .Soit I le point de coordonnées 1,0.Soit D la droite passant par I parallèle à l’axe des ordonnées, munie du repèreI,→j .Soit C le cercle de centre O et de rayon 1.A tout réel x, on associe le point N d’abscisse x sur la droite D.Lorsque l’on “enroule” la droite sur le cercle dans le sens inverse des aiguillesd’une montre, le point N coïncide avec un point M situé sur le cercle C .On a donc défini un repère sur le cercle C dont l’origine est I. L’abscisse d’unpoint dans ce repère est appelée abscisse curviligne.MN→i→jOIJCDDéfinition 5.1. Le cercle C de centre O, de rayon 1 muni d’un tel repère est appelé le cercle trigonométrique.

Page 20 : Propriété 5.1. Tout point du cercle est reperé de manière unique par un réel compris dans l’intervalle π; πou dans tout intervalle d’amplitude 2π.Remarque 5.1. Un point du cercle peut être repéré avec une infinité de réels : si un point M du cercle est associé au réelx, il est aussi associé à l’ensemble des réels de la forme x + 2kπ où k est entier.Exemple 5.1. Le point associé au réel π4 est aussi associé aux réels 9π4 ,17π4 ,7π4 .Définition 5.2.Le radian est la mesure de l’angle du secteur d’un cercle tel quela longueur de l’arc est égale au rayon.On note un angle en radian «1 rad» ou «1» sans unité.1111 radRemarque 5.2. Sur le cercle trigonométrique, la longueur de l’arc et la mesure de l’angle en radian coïncident.Remarque 5.3. Un angle de mesure 360° degrés correspond à un angle de mesure 2π radians puisque le périmètre d’uncercle de rayon 1 est 2π.Propriété 5.2. Les mesures des angles en degrés et les mesures des angles en radians sont proportionnellesavec un facteur de proportionnalité deπ180.Angle exprimé en degré ⇒en radian : multiplier parπ180.Angle exprimé en radian ⇒en degré : multiplier par 180π .Remarque 5.4. Intérêt des radians.Si l’on souhaite calculer la longueur d’un arc de cercle correspondant à un secteur de 86 degrés. On construit le tableau deproportionnalité suivant :360862πRlOn en déduit que l = 2π36086R or α = 2π36086 est la mesure de l’angle en radian donc l = αR.Correspondance Degrés - Radiansdegrés030456090180radians0π6π4π3π2π

Page 21 : 5.1.2Position des angles remarquables sur le cercle trigonométrique.Iπ2π3π20 ou 2ππ6π32π35π67π64π35π311π6π43π45π47π4Iπ2ππ20 ou 2π5π62π3π3π6π6π32π35π63π4π4π43π4Exercice 5.1. Placer sur le cercle trigonométrique les angles suivants :5π, 5π2 , 11π3 , 11π4 , 13π4 , 13π6 , 5π3 , 534π, 99π25.2Définition de sinus et cosinusDéfinition 5.3. A tout réel x, on associe le point M repéré par x surle cercle trigonométrique.L’abscisse de ce point dans le repère O,→i ,→j est appelé cosinus de xnoté cosx, l’ordonnée de ce point est appelé sinus de x noté sinx.On peut donc définir deux fonctions : x 7→cosx, y 7→sinx.Remarque: Pour 0 x π2 , les fonctions cosinus et sinus correspondent auxnotions rencontrées en troisième.JJ’AHOMcos αsin αtan αPropriété 5.3. Quelques valeurs des sinus et cosinus.x0π6π4π3π2πcosx13222120-1sinx0122232105.3Formules TrigonométriquesPropriété 5.4. Les fonctions sinus et cosinus sont telles que pour tout réel x,cos2x + sin2x = 1Cette relation est connue sous le nom de "relation fondamentale de la trigonométrie".

Page 22 : Propriété 5.5. Pour tout réel xcos x + 2π = cos xsin x + 2π = sin xcos x + π = cos xsin x + π = sin xcos x = cos xsinx = sin xcos π x = cos xsin π x = sin xcosπ2 x= sin xsinπ2 x= cos xcosπ2 + x= sin xsinπ2 + x= cos x5.4Fonctions Trigonométriques5.4.1DéfinitionsDéfinition 5.4. A tout réel x, on peut associer le sinus de x en radian. La fonction correspondante s’appelle lafonction sinus et est notée sin.Définition 5.5. A tout réel x, on peut associer le cosinus de x en radian. La fonction correspondante s’appellela fonction cosinus et est notée cos.5.4.2PropriétéDéfinition 5.6. RappelSoit un réel T. Une fonction f définie sur R est périodique, s’il existe un réel T tel que pour tout x de R,fx + T = fx.La période T d’une fonction périodique est le plus petit réel non nul qui vérifie la propriété.T = minT R, x R, fx + T = fxPropriété 5.6. Fonction cosinus— La fonction cosinus est paire.— La fonction cosinus x 7→cosx est une fonction périodique de période 2π.— Pour tout réel x, 1 cosx 1.xy110π2π2ππ2π2π3π23π2Propriété 5.7. Fonction sinus— La fonction sinus est impaire.— La fonction sinus x 7→sinx est une fonction périodique de période 2π.— Pour tout réel x, 1 sinx 1.

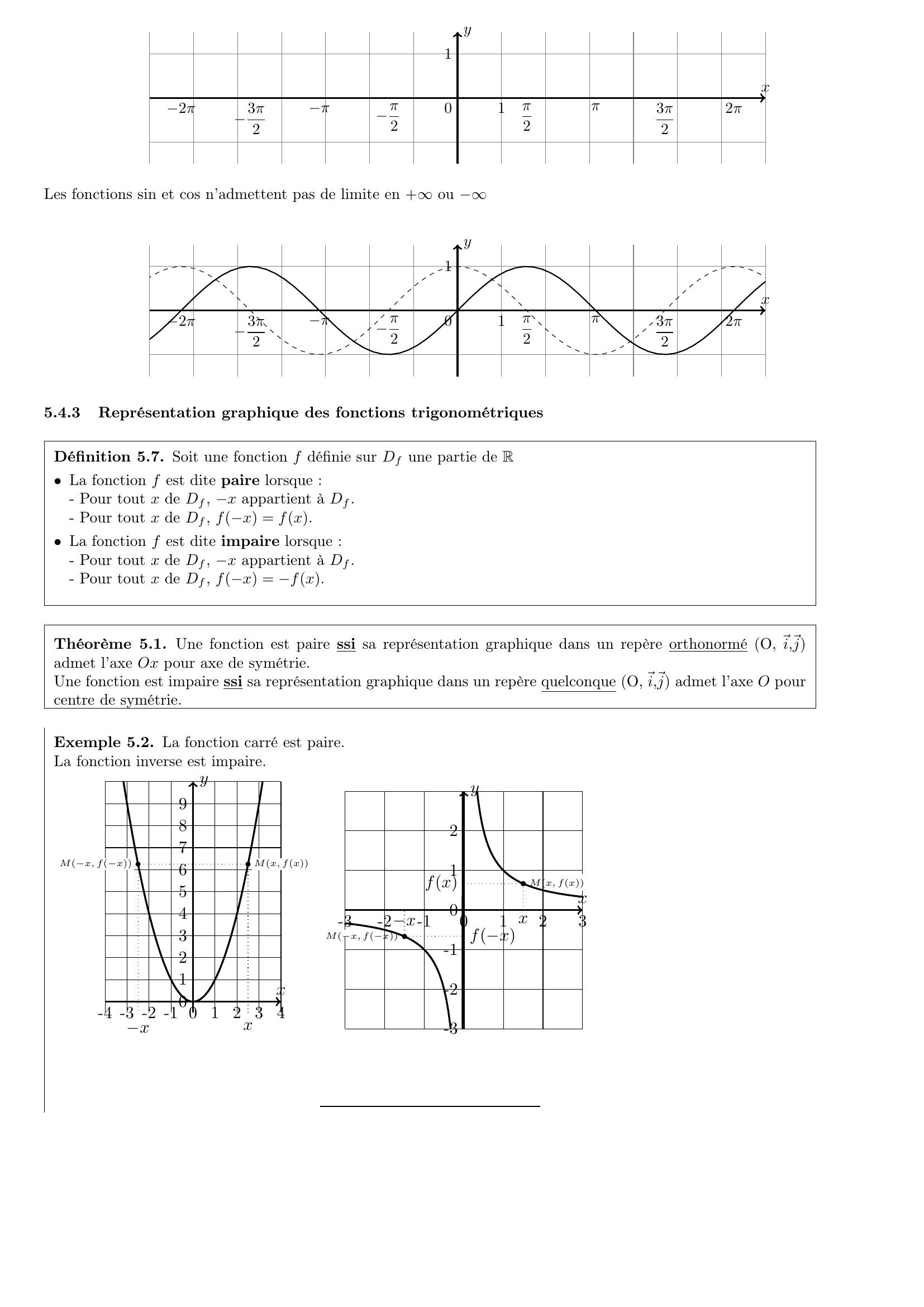
Page 23 : xy110π2π2ππ2π2π3π23π2Les fonctions sin et cos n’admettent pas de limite en +ou xy110π2π2ππ2π2π3π23π25.4.3Représentation graphique des fonctions trigonométriquesDéfinition 5.7. Soit une fonction f définie sur Df une partie de R• La fonction f est dite paire lorsque :- Pour tout x de Df, x appartient à Df.- Pour tout x de Df, fx = fx.• La fonction f est dite impaire lorsque :- Pour tout x de Df, x appartient à Df.- Pour tout x de Df, fx = fx.Théorème 5.1. Une fonction est paire ssi sa représentation graphique dans un repère orthonormé O, ⃗i,⃗jadmet l’axe Ox pour axe de symétrie.Une fonction est impaire ssi sa représentation graphique dans un repère quelconque O,⃗i,⃗j admet l’axe O pourcentre de symétrie.Exemple 5.2. La fonction carré est paire.La fonction inverse est impaire.xy-4 -3 -2 -1 0 1 2 3 40123456789Mx, fxMx, fxxxxy-3-2-10123-3-2-1012Mx, fxMx, fxfxfxxx

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23