Feuille Cours

Posté le 07/02/2025

Chargé de TD/CM : E. Masnada.

120 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127

Page 1 : Analyse dans RnElian Masnada1,211 septembre 20201. J’encourage les élèves à me faire part de leurs remarques par emailà l’adresse elian.masnada@cyu.fr aﬁn de m’aider à améliorer ce cours.2. En partie inspiré du polycopié de Jean-Michel Masereel.

Page 2 : 2

Page 3 : Table des matières1Introduction et objectifs du cours52Espace Vectoriel Normé92.1Objectifs du chapitre . . . . . . . . . . . . . . . . . . . . . . .92.2Eléments de topologie dans Rn. . . . . . . . . . . . . . . . .102.2.1Norme & Distance . . . . . . . . . . . . . . . . . . . .102.2.2Boule ouverte, Boule Fermée et Sphère . . . . . . . . .192.2.3Voisinage. . . . . . . . . . . . . . . . . . . . . . . . .222.2.4Ouvert, Fermé. . . . . . . . . . . . . . . . . . . . . .252.2.5Intérieur et adhérent . . . . . . . . . . . . . . . . . . .322.2.6Méthodologies. . . . . . . . . . . . . . . . . . . . . .362.3Suites d’éléments d’un EVN . . . . . . . . . . . . . . . . . . .372.3.1Rappels . . . . . . . . . . . . . . . . . . . . . . . . . .372.3.2Généralisation et Généralités. . . . . . . . . . . . . .382.3.3Suites Convergentes. . . . . . . . . . . . . . . . . . .402.3.4Valeur d’adhérence et point d’adhérent . . . . . . . . .442.3.5Suites de Cauchy . . . . . . . . . . . . . . . . . . . . .482.3.6Compacité . . . . . . . . . . . . . . . . . . . . . . . . .503Limite et Continuité d’applications553.1Objectifs du chapitre . . . . . . . . . . . . . . . . . . . . . . .553.2Limite, Continuité. . . . . . . . . . . . . . . . . . . . . . . .573.2.1Méthodologie . . . . . . . . . . . . . . . . . . . . . . .663.3Continuité uniforme. . . . . . . . . . . . . . . . . . . . . . .703.4Topologie et fonctions continues . . . . . . . . . . . . . . . . .724Calcul diﬀérentiel du 1er ordre754.1Objectifs du chapitre . . . . . . . . . . . . . . . . . . . . . . .754.2Dérivée partielle. . . . . . . . . . . . . . . . . . . . . . . . .763

Page 4 : 4TABLE DES MATIÈRES4.3Fonctions diﬀérentiables sur un ouvert . . . . . . . . . . . . .804.3.1Généralités. . . . . . . . . . . . . . . . . . . . . . . .804.3.2Fonction de classe C1 . . . . . . . . . . . . . . . . . . .884.3.3Composition et changement de variables . . . . . . . .934.3.4Matrice de Jacobi, gradient et inégalité des accroisse-ments ﬁnis . . . . . . . . . . . . . . . . . . . . . . . . .974.4EDP du 1er ordre et C1-diﬀéomorphisme . . . . . . . . . . . . 1024.4.1Généralités. . . . . . . . . . . . . . . . . . . . . . . . 1024.4.2C1-diﬀéomorphisme et changement de variables . . . . 1034.4.3Résolution des EDPs par changement de variables. . 1075Calcul diﬀérentiel d’ordre supérieur1115.1Objectifs du chapitre . . . . . . . . . . . . . . . . . . . . . . . 1115.2Diﬀérentiation d’ordre supérieur ou égal à 2 . . . . . . . . . . 1125.3Systèmes d’EDPs du 1er ordre. . . . . . . . . . . . . . . . . 1155.4EDPs d’ordre 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 1185.5Extremums de fonctions à valeurs dans R. . . . . . . . . . . 1215.5.1Cas des fonctions de R dans R. . . . . . . . . . . . . 1215.5.2Cas des fonctions de Rn dans R . . . . . . . . . . . . . 122

Page 5 : Chapitre 1Introduction et objectifs ducoursEn Analyse 1ère année, vous avez très longuement étudié l’ensemble desréels et les fonctions de R dans R. Malheureusement, que ce soit en phy-sique, en économie, en ﬁnance ou encore en sciences sociales, la descriptiondes phénomènes, issus de ces domaines, fait souvent appel à des fonctionsplus complexes : des fonctions de Rn dans Rp où n, p N tels que, aumoins, soit n soit p soit un entier supérieur à 1, c’est à dire des fonctionsvectorielles si n 1 de plusieurs variables si p 1. Par exemple, en ther-modynamique, la description de l’énergie interne U d’un système se fait parl’intermédiaire de la température et de la pression. Ainsi, il faut introduire lafonction UT, P de R+ ×R+ dans R pour étudier l’évolution de ce système.Il s’agit d’une fonction sclaire à 2 variables. De même en électromagnétisme,la connaissance d’un système passe par la donnée des champs vectoriels ⃗E et⃗B qui sont, tous deux, des applications de R3 dans R3, en toute généralité. Ilfaut donc mieux appréhender des espaces de plus grandes dimensions que Rcomme Rn et les fonctions de plusieurs variables. Ainsi, l’objectif du coursd’Analyse dans Rn est d’étendre tous les concepts que vous avez étudiés enAnalyse 1ère année aﬁn de pouvoir manipuler des fonctions de plusieurs va-riables, capitales dans un grand nombre de domaines.Rappelons ici les principales notions que vous avez abordées en 1ère an-née et qui seront généralisées dans ce cours d’Analyse dans Rn :1. Tout d’abord la topologie de base ouvert, fermé, compact,... qui vousa été introduite dans R et qui sera donc étendu en toute généralité à5

Page 6 : 6CHAPITRE 1. INTRODUCTION ET OBJECTIFS DU COURSdes espaces vectoriels normés et en particulier à Rn. On déﬁnira danscette partie les notionsa de norme et de distanceb d’espace vectoriel norméc de boule ouverte et de boule ferméed d’ouvert, de fermé et de compacte et enﬁn, d’intérieur et d’adhérentCette partie nous permettra d’introduire rigoureusement tous les conceptsqui suivent.2. Nous allons généraliser les notions associées aux suites d’élémentsde R. Nous introduirons en eﬀet dans ce cours des suites d’élémentsd’espaces vectoriels normés, aﬁn de déﬁnir, dans ce cadre, les notionsa de convergenceb de suites extraites et de valeurs d’adhérencec de suite de Cauchyd et enﬁn, d’espace complet et de Banach3. les notions de limite, de continuité, de dérivée et de dérivabilité pourles fonctions de R dans R. Encore une fois tout cela sera étenduaux applications déﬁnies sur un espace vectoriel normé quelconqueà valeurs dans un autre espace vectoriel normé quelconque. Ainsi,nous introduirons les notionsa de limiteb de continuité et de continuité uniformec de dérivées partielles d’ordre 1 et d’ordre supérieurd de diﬀérentiabilitée de classe Ck4. et enﬁn nous généraliserons les équations diﬀérentielles qui sont deséquations fonctionnelles dont l’inconnue est une fonction de R dansR en introduisant les équations aux dérivées partielles équationsfonctionnelles dont l’inconnue est une fonction de Rn dans Rp. Vous

Page 7 : 7avez déjà rencontré ce type d’équations en physique comme en élec-tromagnétisme avec l’équation de Gauss par exempleExx, y, zx+ Eyx, y, zy+ Ezx, y, zz= ρϵ0oùx signiﬁe dérivée partielle par rapport x. Il s’agit ici d’une "équa-tion diﬀérentielle" portant sur une fonction de R3 dans R3.

Page 8 : 8CHAPITRE 1. INTRODUCTION ET OBJECTIFS DU COURS

Page 9 : Chapitre 2Espace Vectoriel Normé2.1Objectifs du chapitreLe but de ce cours étant d’apprendre à manipuler les fonctions de plusieursvariables typiquement des fonctions de Rp dans Rn mais plus généralementd’un espace vectoriel quelconque à un autre, nous devons tout d’abord nouspencher sur la structure même des espaces vectoriels. En eﬀet, lorsque dansla suite du cours, nous allons manipuler des fonctions de plusieurs vairables,nous devrons manipuler des limites à la fois pour déﬁnir la notion de conti-nuité et la notion de dérivées partielles. Or, vous savez que pour une fonctionf de R dans R, l est la limite en a R si et seulement siϵ 0, η 0 / x a η =⇒fx l ϵ2.1xa se comprend intuitivement comme la distance entre x et a. De même,fx l est la distance entre fx et l. Pour généraliser cela au cas d’unefonction f allant d’un espace vectoriel quelconque à un autre, il faudra doncgénéraliser 2.1 ce qui nécessitera de déﬁnir la notion de distance et denorme dans un espace vectoriel.De plus, nous verrons que les propriétés que nous allons déﬁnir sur les fonc-tions de plusieurs variables nécessitent que les ensembles sur lesquels lesfonctions sont déﬁnies remplissent certaines conditions topologiques commeouvert, fermé, compact...Et enﬁn, nous déﬁnirons des suites d’éléments d’espace vectoriel qui serontutilisés dans le chapitre suivant pour caractériser la limite et à la continuitéde fonctions de plusieurs variables.9

Page 10 : 10CHAPITRE 2. ESPACE VECTORIEL NORMÉMots clefs :Topologie : norme et distance, espace vectoriel normé, boule ouverte etboule fermée, ouvert, fermé et compact, intérieur et d’adhérentSuites : convergence, suites extraites et de valeurs d’adhérence, suite deCauchy, espace complet et de Banach2.2Eléments de topologie dans Rn2.2.1Norme & DistanceDéﬁnition 1 : normeSoit E un espace vectoriel. Soit ·une application de E dans R. ·estune norme sur E, si, et seulement si, l’application vériﬁe les 3 propriétéssuivantes1. x E, x= 0 =⇒x = 0Eséparation2. x E, λ R, λx= λ xabsolue homogénéité3. x, y E, x + yx+ yinégalité triangulaireOn dira alors que E, · est un espace vectoriel normé EVN.Remarque 1 :On peut combiner les deux premières propriétés de la déﬁnition pour montrerque x = 0E =⇒x= 0. En eﬀet0E= 0 × 0E= 0 × 0E= 0Remarque 2 :la norme du vecteur x E représente évidemment la taille du vec-teur x, mais comme nous allons le montrer par la suite, il peut exis-ter sur un espace vectoriel donné, plusieurs normes. Vous connaissezdéjà une norme dans le cas des vecteurs appartenant à R3 : soit ⃗X = x, y, zalors ⃗X =px2 + y2 + z2

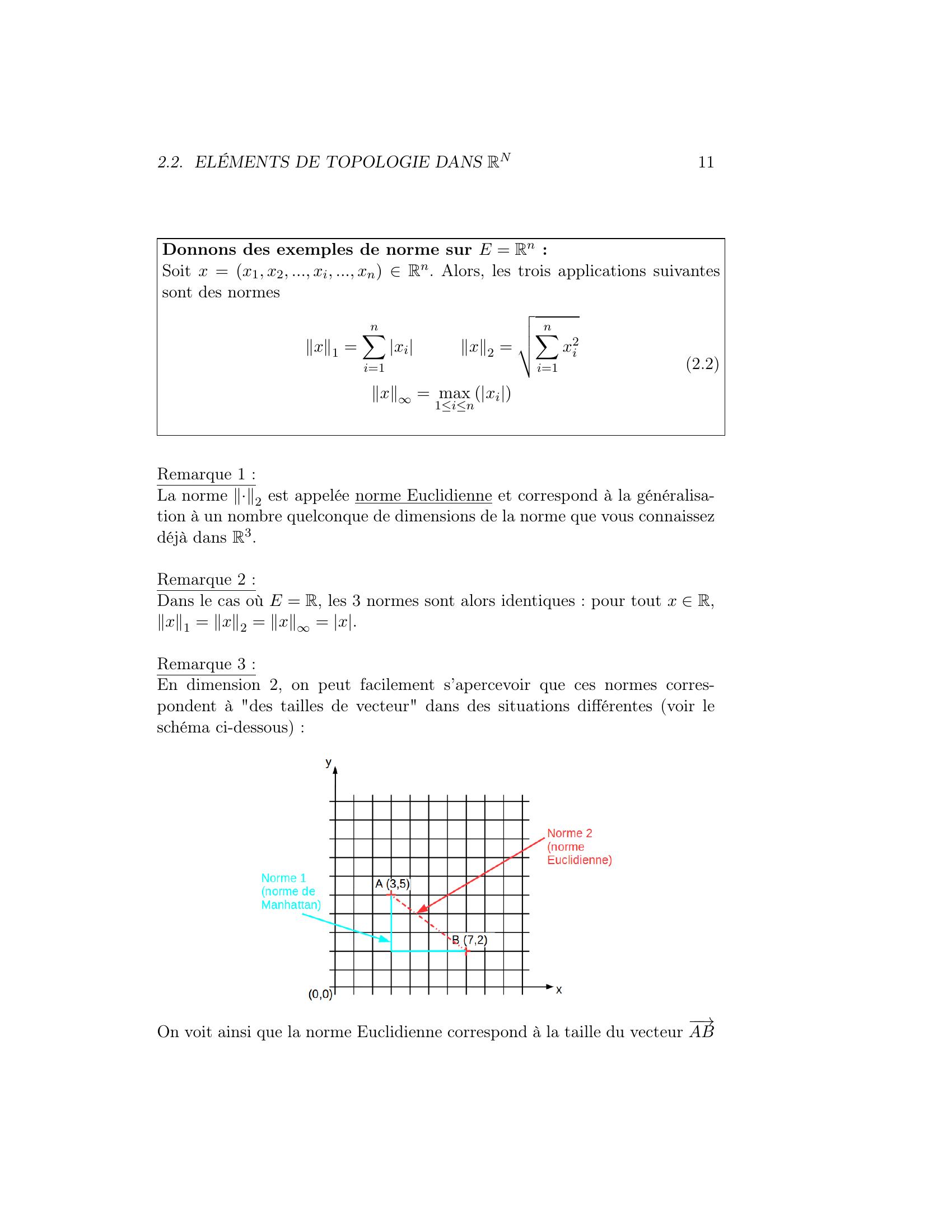
Page 11 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN11Donnons des exemples de norme sur E = Rn :Soit x = x1, x2, ..., xi, ..., xn Rn. Alors, les trois applications suivantessont des normesx1 =nXi=1xix2 =vuutnXi=1x2ix= max1inxi2.2Remarque 1 :La norme ·2 est appelée norme Euclidienne et correspond à la généralisa-tion à un nombre quelconque de dimensions de la norme que vous connaissezdéjà dans R3.Remarque 2 :Dans le cas où E = R, les 3 normes sont alors identiques : pour tout x R,x1 = x2 = x= x.Remarque 3 :En dimension 2, on peut facilement s’apercevoir que ces normes corres-pondent à "des tailles de vecteur" dans des situations diﬀérentes voir leschéma ci-dessous :On voit ainsi que la norme Euclidienne correspond à la taille du vecteur →AB

Page 12 : 12CHAPITRE 2. ESPACE VECTORIEL NORMÉà vol d’oiseau tandis que la norme 1 correspond à la taille du vecteur →AB ensuivant le quadrillage 1.Remarque 4 :Montrons par exemple que ·1 est bien une norme sur Rn. Pour cela, nousdevons vériﬁer les trois points de la déﬁnition 1 :1. Vériﬁcation de la 1ère propriété :x1 = 0 =⇒i, xi = 0. On voit donc que x1 = 0 =⇒x = 0E.2. Vériﬁcation de la 2ème propriétés :Soit x = x1, x2, ..., xn et λ R. On a donc λx = λx1, λx2, ..., λxn.Alorsλx1 =nXi=1λxi = λnXi=1xi = λ x13. Vériﬁcation de la 3ème propriétés :Soient x = x1, x2, ..., xn et y = y1, y2, ..., yn. Alors x + y = x1 +y1, ..., xn + yn. Doncx + y1 =nXi=1xi + yi nXi=1xi + yi = x1 + y1Finalement ·1 est bien une norme. Les deux autres normes seront étudiéesen TD.Donnons des exemples de norme sur E = C0, 1, R, où E corres-pond alors à l’espace des fonctions continues sur 0, 1 dans R. Soit fune fonction appartenant à E. Alors les trois normes les plus souvent utiliséessontf1 =Z 10fxdxf2 =sZ 10f2xdxf= sup0x1fx2.31. Aux USA, on appelle aussi la norme 2, la norme de Manhattan. En eﬀet, on voitque cette norme correspond à la distance même si nous n’avons pas encore déterminé lelien entre norme et distance que l’on doit parcourir entre deux points dans une ville trèsquadrillée comme Manhattan.

Page 13 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN13Exemple :L’application suivante est-elle une norme ?N:R2→Rx, y7→Nx, y = 4x + 7yPour répondre à cette question, nous devons vériﬁer si N vériﬁe les troispropriétés de la déﬁnition 1. Commençons par la première.Si Nx, y = 0 alors 4x + 7y = 0 ⇐⇒x = 74y. On déduit doncque la 1ère propriété n’est pas vériﬁée puisque Nx, y = 0 n’implique pasx = 0, y = 0. Finalement N n’est pas une norme.Quelques propriétés des normesPropriété 1 : PositivitéLa norme est déﬁnie positive : x, x0.démonstration :x E, 0 = 0E= x xx+ x= 2 x. Donc x0.Propriété 2 :Pour la norme euclidienne : x, y E, x + y= x+ y⇐⇒x = λyavec λ R.Démonstration : Admis car cela fera l’objet d’une démonstration dans lecours d’algèbre bilinéaire.Remarque :Cela n’est pas le cas pour d’autres normes les normes qui ne sont pas issuesd’un produit scalaire comme vous le verrez dans le cours d’algèbre bilinéaire.Illustrons cela sur l’EVN R2, ·. Considérons alors X et Y tels queX = 1, 1Y = 1, 0=⇒X + Y = 2, 1

Page 14 : 14CHAPITRE 2. ESPACE VECTORIEL NORMÉOn a doncx + y= max2, 1 = 2x= y= 1on voit doncx + y= x+ yalors que λ R, X ̸= λY .Propriété 3 : 2nd inégalité triangulairex, y E, ·, x y xy2.4démonstration :x, yx= x y + yx y+ y=⇒x yxyy= y x + xy x+ x=⇒x yyx2.5On voit donc quex ymaxyx, xy = xyDéﬁnition 2 : normes équivalentesSoit E un espace vectoriel muni de deux normes ·a et ·b. Alors,on dit que ·a est équivalent à ·b si, et seulement si, il existe α, β 0tels quex E, α xa xb β xaCette équivalence est bien une relation d’ordre :— Réﬂexivité :·a est équivalent à ·a. En eﬀet,x E, xa xa xa

Page 15 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN15— Symétrie :Si ·a est équivalent à ·b alors ·b est équivalent à ·a.démonstration :Considérons que ·a est équivalent à ·b. Cela signiﬁe queα, β 0 / x E, α xa xb β xad’après l’inégalité de gauche comme α 0 :xa 1α xb2.6d’après l’inégalité de droite comme β 0 :1β xb xa2.7On a doncx E, 1β xb xa 1α xbet donc ·b est équivalent à ·a— Transitif :Si ·a équivalent à ·b1Si ·b équivalent à ·c2Alors ·a équivalent à ·c3Démonstration :D’après 1 : α, β 0 / x E, α xa xb β xaD’après 2 : η, γ 0 / x E, η xb xc γ xbde ces deux expressions, on déduitxc γ xb γβ xaxc η xb ηα xaDoncηα xa xc γβ xaFinalement ·a est équivalent à ·c.

Page 16 : 16CHAPITRE 2. ESPACE VECTORIEL NORMÉThéorème 1 : Equivalence des normesSoit E un espace vectoriel de dimension ﬁnie. Alors, toutes les normes surE sont équivalentes.Démonstration : admis.De manière très intuitive, vous savez que l’on peut grâce à la norme déﬁnir ladistance entre deux points. On se propose ici de déﬁnir ce qu’est une distanceDéﬁnition 3 : DistanceSoit X un ensemble quelconque. L’application d, de X × X →R+,est une distance sur X, si et seulement si, elle vériﬁe :1. X, Y X2, dX, Y = 0 ⇐⇒X = Y2. X, Y X2, dX, Y = dY, X3. X, Y, Z X3, dX, Y dX, Z + dZ, Y Remarque : en réalité les propriétés demandées sont triviales :1. La seule façon pour que la distance entre deux points soit nulle est queles deux points soient confondus.2. La distance est symétrique. La distance entre X et Y est la même que ladistance entre Y et X.3.dX, Y dX, Z + dZ, Y : si je passe par un autre point Z pour aller deX à Y , au mieux je ne réduis pas la distance au pire je fais un détour.

Page 17 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN17Propriété 4 : positivité de la distanceLa distance est une application déﬁnie positive : X, Y X2, dX, Y 0.Démonstration :X, Y X2, dX, X dX, Y + dY, X0 2dX, Y 0 dX, Y Propriété 5 : Distance associée à une normeSoit E, · un EVN. Alors, on appelle distance associée à la norme·, l’application d déﬁnie pard:E × E→R+X, Y7→dX, Y = X Y Vériﬁons qu’il s’agit bien d’une distance. Pour cela, on doit contrôler quecette application respecte bien les trois propriétés introduites dans la déﬁni-tion de la distance :1. Si X = Y alors dX, Y = X Y = 0E= 0Si dX, Y = 0, alors X Y = 0, ce qui implique que X = Y .2. dX, Y = X Y = Y X= 1 Y X= dY, X3. dX, Y = X Y = X Z + Z Y X Z+ Z Y et ﬁnalement dX, Y dX, Z + dY, Z.Propriété 6 :Soient E, · un EVN et d la distance associée à la norme ·. Alors, dvériﬁeX, Y E, λ R,dλX, λY = λdX, Y

Page 18 : 18CHAPITRE 2. ESPACE VECTORIEL NORMÉDémonstration :dλX, λY = λX λY = λ X Y = λdX, Y C’est cette propriété 6 que nous utiliserons pour montrer qu’une distancen’est pas associée à aucune norme.Exemples de distance :— Considérons l’EVN R2, ·2. Alors, l’applicationd:R2 × R2→R+X, Y 7→dX, Y = X Y 2 =px1 y12 + x2 y22avec X = x1, x2 et Y = y1, y2, est bien une distance.— Soit E un espace vectoriel quelconque. Alors l’application suivanteest une distanced0:E × E→R+X, Y 7→d0X, Y =0si X = Y1si X ̸= YVériﬁons qu’il s’agit bien d’une distance.a Si X = Y alors d0X, Y = 0 par construction.Si d0X, Y = 0 alors X = Y .b d0 est trivialement symétrique.c vériﬁons si X, Y, Z, dX, Y dX, Z + dY, Z ?Si X = Y = Z,alors 0 0 + 0 donc OKSi X = Y ̸= Z,alors 0 1 + 1 donc OKSi X = Z ̸= Y ,alors 1 0 + 1 donc OKSi X ̸= Y = Z,alors 1 1 + 0 donc OKSi tous diﬀérents, alors 1 1 + 1 donc OK

Page 19 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN19Mais clairement, cette distance n’est pas associée à une norme. Eneﬀet, prenons X ̸= Y et λ = 3. Alorsd03X, 3Y = 1 puisque 3X ̸= 3Ydonc d03X, 3Y ̸= 3d0X, Y .2.2.2Boule ouverte, Boule Fermée et SphèreDéﬁnition 4 : Boule ouverte, Boule fermée et SphèreSoit E, · un EVN. a E, r 0, on déﬁnit :1. la boule ouverte de centre a et de rayon r, comme l’ensemble despoints vériﬁantsBa, r = x E / x a r2. la boule fermée de centre a et de rayon r, comme l’ensemble des pointsvériﬁantsBa, r = x E / x ar3. la sphère de centre a et de rayon r, comme l’ensemble des pointsvériﬁantsSa, r = x E / x a= rOn remarque alors que Ba, r = Ba, r Sa, rLa forme des boules et de la sphère dépend entièrement de lanorme choisie. Pour illustrer cela, nous allons déterminer les boules fer-mées de centre 0, 0 et de rayon 1 des EVN suivants : R2, ·1, R2, ·2et R2, ·.1. Cas R2, ·1 :Soit X = x, y R2. Alors X 0, 01 = x+y. Nous allons toutd’abord chercher la sphère, c’est-à-dire l’ensemble des points x, y deR2 tels que x + y = 1.Si x 0, y 0, alors X1 = 1 ⇐⇒x + y = 1 ⇐⇒y = 1 x.Si x 0, y 0, alors X1 = 1 ⇐⇒x y = 1 ⇐⇒y = x 1.

Page 20 : 20CHAPITRE 2. ESPACE VECTORIEL NORMÉSi x 0, y 0, alors X1 = 1 ⇐⇒x + y = 1 ⇐⇒y = 1 + x.Si x 0, y 0, alors X1 = 1 ⇐⇒x y = 1 ⇐⇒y = 1 x.Donc la sphère correspond à un losange centré en 0 et la boule ferméepour la norme 1 est donnée par2. Cas R2, ·2 :Soit X = x, y R2. Déterminons la sphère de centre 0, 0 et derayon 1, c’est-à-dire l’ensemble des points vériﬁantsX 0, 02 = X2 =px2 + y2ceci correspond à un cercle de rayon 1. Ainsi la boule fermée pour lanorme 2 est donnée par3. Cas R2, · :En exercice, vériﬁer que la boule fermée de rayon 1 et centrée en 0, 0pour la norme est donnée par

Page 21 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN21Propriété 7 :Soit E, · un EVN. Alors, r, r′ 0 et a E :r r′ ⇐⇒Ba, r Ba, r′r r′ ⇐⇒Ba, r Ba, r′Démonstration : On étudie ici seulement la boule ouverte.=⇒: On ar r′x0 Ba, r=⇒x0 a r r′Finalement x0 Ba, r′.⇐= :Ba, r Ba, r′ =⇒il existe yBa, r′/Ba, rtel que r y a r′

Page 22 : 22CHAPITRE 2. ESPACE VECTORIEL NORMÉ2.2.3VoisinageDéﬁnition 5 : VoisinageSoit E, · un EVN. Soient a E et Vune partie de E. On ditque V est un voisinage de a, si, et seulement si, V contient au moins uneboule ouverte centrée en a et de rayon r 0.Formulation mathématique :V voisinage de a ⇐⇒r 0 /Ba, r VOn note Va l’ensemble des voisinages de a.Aﬁn de mieux comprendre le concept, donnons un petit exemple de voisi-nage :Pour cela, considérons R2, ·2. On cherche à savoir si l’ensemble V caca-huète sur le schéma est bien un voisinage du point a = 1, 1.La réponse est oui puisqu’il existe au moins une boule ouverte, de centre a,contenue dans V . À ce stade, nous pourrions nous demander si la notion devoisinage dépend de la norme choisie ou dit autrement est-ce qu’un ensemblepeut être un voisinage d’un point pour une norme donnée et ne pas l’êtrepour une autre norme.

Page 23 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN23Propriété 8 :Soit E un EVN de dimension ﬁnie, muni de plusieurs normes. Soienta E et V une partie de E. Alors le fait que V soit voisinage ou non de ane dépend pas de la norme choisie.Démonstration :La démonstration de cette propriété sera discutée en TD.Propriété 9 :a est toujours un élément de ses voisinages V Va, a V Démonstration :V Va, r 0 tel que Ba, r V . Or a Ba, r puisque a a=0E r. Donc a V puisque a Ba, r et Ba, r V .Propriété 10 :Toute réunion de voisinages de a est un voisinage de a.Démonstration :Soit ViiI une famille de voisinage de a. On pose V = iIVi l’union devoisinage de a. i I, ri 0 tel que Ba, r Vi V . Donc, il existe biendes boules ouvertes centrées en a entièrement contenues dans V . Donc V estun voisinage de a.Propriété 11 :Toute intersection ﬁnie de voisinage de a est un voisinage de a.Démonstration :Rappel : r r′ ⇐⇒Ba, r Ba, r′.

Page 24 : 24CHAPITRE 2. ESPACE VECTORIEL NORMÉSoit ViiI une famille ﬁnie de voisinage de a. On pose V = iIVi l’in-tersection de voisinages de a. Posons r = miniI ri où ri est le rayon de laboule ouverte contenue dans Vi. Comme pour tout i, ri 0, on a évidem-ment r 0. Donc i, Ba, r Ba, ri et ﬁnalement Ba, r V . V estbien un voisinage de a puisqu’il contient une boule ouverte.Remarque : WARNINGMontrons que si l’on considère une intersection inﬁnie de voisinage alors cen’est pas nécessairement un voisinage. Pour cela, considérons l’EVN R, · et la famille des voisinages de 0, Vi = 1n, 1n. On voit donc queV = i=1Vi = 0. Or aucune boule ouverte ne peut être contenue dansV = 0 et ﬁnalement V n’est pas un voisinage.Propriété 12 :Toute boule fermée ou ouverte de rayon r et de centre a est un voisi-nage de a.Démonstration : Trivial.Déﬁnition 6 : Espace séparéSoit E un ensemble quelconque. On dit que E est séparé si, et seule-ment si, a, b E, si a ̸= b, alorsVa Va, Vb Vb tels que Va Vb = Il est en réalité très diﬃcile de se représenter un ensemble non séparé.Propriété 13 : EVN séparéTout EVN est un espace séparé.

Page 25 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN25Démonstration :Aﬁn de faire la démonstration, nous allons nous appuyer sur la représentationsur R de la propriété précédente.Soit a, b E tels que a ̸= b. Introduisons les deux voisinages suivantsVa = Ba, b a2Vb = Bb, b a2Vériﬁons que Va Vb = . Pour cela, imaginons x Va Vb. On a donc,puisque x appartient aux deux boulesx a b a2etx b b a2On peut alors utiliser l’inégalité triangulairea b= a x + x ba x+ x b a bce qui est incohérent. Ainsi, il n’existe pas x appartenant aux deux bouleset donc les deux voisinages sont disjoints.2.2.4Ouvert, FerméDéﬁnition 7 : OuvertSoit E, · un EVN et U une partie de E. Alors U est un ouvert,si, et seulement si, il existe pour chaque point de U un voisinage contenudans U.Formulation mathématique :U ouvert ⇐⇒x U, r 0 tel que Ba, r URemarque importante : r peut évidemment dépendre de x. Plus on se rap-proche des bords de U est plus r doit être petit. Voir le schéma ci-dessous.

Page 26 : 26CHAPITRE 2. ESPACE VECTORIEL NORMÉDans la suite, sur les schémas, les ouverts seront représentés par un contouren pointillé.Comme lorsque l’on a introduit la notion de voisinage, nous nous sommesdemandés si cette notion dépendait de la norme choisie, nous pouvons icinous poser la même question, à savoir : est-ce que la notion d’ouvert dépendde la norme choisie.Propriété 14 :Soit E un EVN de dimension ﬁnie muni de plusieurs normes. Soit Uune partie de E. Alors le fait que U soit un ouvert ou non ne dépend pas duchoix de la norme.Démonstration :La démonstration de cette propriété sera discutée en TD.Propriété 15 :Soit E, · un EVN. Alors et E sont des ouverts.Démonstration :À ce stade, le fait que soit un ouvert est conventionnel.

Page 27 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN27E ouvert : trivial.Propriété 16 :Une boule ouverte est un ouvert.Démonstration :Pour démontrer qu’une boule ouverte est un ouvert, nous allons nous guideravec la représentation dans R2, ·2 d’une boule ouverte mais nous allonstout de même faire une démonstration générale.Soit la boule ouverte Ba, r. Guider par le schéma ci-dessus, on introduitla boule ouverte centrée en un point X quelconque appartenant à Ba, r :BX, r′ = r X a. Comme le montre le schéma, on voit que dans R2,BX, r′ Ba, r. Il suﬃt maintenant de montrer que cela reste vrai pourE, · quelconque et pour tout X Ba, r.Etape 0 : Vériﬁons que BX, r′ Ba, r pour E, ·.Soit Y BX, r′. On peut alors écrireY X + X aY X+ X aY a r X a+ X aY ar

Page 28 : 28CHAPITRE 2. ESPACE VECTORIEL NORMÉDonc BX, r′ Ba, r.Etape 1 : Vériﬁons que BX, r′ Ba, r pour tout X.Or pour X BX, r′, r′ 0 puisque r′ = r X aet X a r.Donc X Ba, r, BX, r′ Ba, r.Finalement la boule ouverte est un ouvert.Propriété 17 :Une union quelconque d’ouverts est un ouvert.Démonstration :Soit UiiI une famille quelconque d’ouverts. On note U = iIUi l’union.Soit x U. Alors i tel que x Ui. Or Ui est un ouvert donc il existe ri 0tel que Bx, ri Ui U. Or ce raisonnement peut-être fait pour tout xdonc U est un ouvert.Propriété 18 :Toute intersection ﬁnie d’ouverts est un ouvert.Démonstration :Soit Ui1in une famille ﬁnie d’ouverts. On note U = iUi l’intersectionde ces ouverts.Soit x U ⇐⇒x U1comme U1 est un ouvert, U1 est un voisinage de xx U2comme U2 est un ouvert, U2 est un voisinage de x...x Uncomme Un est un ouvert, Un est un voisinage de xDonc x appartient à une intersection ﬁnie de voisinage de x qui est donc unvoisinage de x. Donc pour tout x U, U est un voisinage de x donc U estun ouvert.

Page 29 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN29Corollaire des propriétés précédentes :Soient E = R et a, b R tel que a b. Alors, les intervalles suivants sontdes ouverts , ba, ba, +Démonstration :— a, b= Ba+b2 , ba2 . Or une boule ouverte est un ouvert donc a, b estun ouvert.— , b= αbα, b union inﬁnie d’ouverts donc ouvert.— a, = αaa, α union inﬁnie d’ouverts donc ouvert.Déﬁnition 8 : FerméSoit E, · un EVN et F une partie de E. Alors F est un fermé si,et seulement si, CEF complémentaire de F dans E est un ouvert.Propriété 19 :Soit E, · un EVN, alors et E sont des fermés.Donc E et sont à la fois des ouverts et des fermés voir prop. 15.Démonstration :— Pour : CE= E qui est un ouvert donc est un fermé.— Pour E : CEE = qui est un ouvert d’après la propriété 15 doncE est un fermé.Propriété 20 :Une boule fermée est un fermé.

Page 30 : 30CHAPITRE 2. ESPACE VECTORIEL NORMÉDémonstration :Aﬁn de faire la démonstration, on va s’aider du schéma ci-dessous valabledans R2, ·2. On doit donc étudier si le complémentaire de Ba, r estun ouvert. On commence par introduire en suivant le schéma suivant, enun point X quelconque de CEBa, r, la boule ouverte BX, X ar.Commençons par montrer que cette boule est bien incluse dans CEBa, rpuis on montrera que cela est vrai pour tout X CEBa, r.Etape 0 : Vériﬁons que BX, X ar CEBa, rSoit Y BX, X ar. AlorsX a= X Y + Y aX Y + Y a⇐⇒Y aX Y X a⇐⇒Y a X ar X a⇐⇒Y a rOn voit donc que Y est bien extérieur à Ba, r, donc Y CEBa, r.Etape 1 : Or X, X ar 0 et donc CEBa, r est un ouvert etdonc Ba, r est un fermé.

Page 31 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN31Propriété 21 :Toute intersection de fermés est un fermé.Démonstration :Rappel : CEiUi = iCEUi.On sait que si UiiI est une famille d’ouverts alors :1. U = iUi est un ouvert propriété 17.2. CEUiiI est une famille de fermés puisque le complémentaire deCEUi est Ui qui est un ouvert.Puisque U est un ouvert, CEU est un fermé et puisque, pour tout i, Ui estun ouvert, CEUi est un fermé. OrCEU = CEiUi = iCEUiDonc l’intersection de fermés est fermé.Propriété 22 :Toute union ﬁnie de fermés est un fermé.Démonstration :Même chose que précédemment. En passant au complémentaire c’est immé-diat.Corollaire :Soient E = R et a, b R tel que a b. Alors, les intervalles suivants sontdes fermés , ba, ba, +Démonstration :— a, b = Ba+b2 , ba2 . Or une boule fermée est un fermé donc a, b estun fermé.

Page 32 : 32CHAPITRE 2. ESPACE VECTORIEL NORMÉ— trivial.— trivial.2.2.5Intérieur et adhérentDéﬁnition 9 : IntérieurSoit E, · un EVN. Soient A E et a E. On dit que a est in-térieur à A si, et seulement si, A est un voisinage de a. On appelle Intérieurde A, que l’on note ˚A, l’ensemble des points intérieurs à A.Formulation mathématiquex ˚A ⇐⇒r 0 / Bx, r Ax ˚A ⇐⇒U A / U ouvert et x UPropriété 23 :Soit E, · un EVN. Soient AE et˚A l’intérieur de A. Alors˚A A.Démonstration :x ˚A ⇐⇒r 0 / Bx, r A donc x A donc ˚A A.Propriété 24 :Soit E, · un EVN. Soient A E et ˚A l’intérieur de A. Alors ˚Aest le plus grand ouvert contenu dans A.Démonstration :— Montrons tout d’abord que tout ouvert U inclus dans A est inclusdans ˚ASoit U A un ouvert. Alorsx U, r 0 / Bx, r U A donc x ˚A

Page 33 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN33Soit UiiI une famille quelconque d’ouverts tels que Ui A. Alorspuisque iUi est également un ouvert contenu dans A alors iUi ˚A— Il faut maintenant montrer que ˚A iUiSoit x ˚A tel que x n’appartient à aucun ouvert U A alors x /˚A.Donc ˚A iUiFinalement, on voit que ˚A = iUi où l’union porte sur tous les ouverts inclusdans A. Donc ﬁnalement ˚A est le plus grand des ouverts contenu dans A.Propriété 25 :Soit E, · un EVN. Soient A et B deux parties de E. Alors1. A ouvert ⇐⇒˚A = A2. ˚˚A = ˚A3. Si A B alors ˚A ˚BDémonstration :1. a Si A est un ouvert alors le plus grand ouvert contenu dans A estA lui-même. Donc ˚A = A.b Si ˚A = A alors A est un ouvert puisque ˚A est un ouvert.2. ˚A est un ouvert. Donc le plus grand ouvert contenu dans ˚A est ˚A.Finalement ˚˚A = ˚A.3. Soit x ˚A ⇐⇒r 0 / Bx, r A B donc x ˚B. Finalement˚A ˚B.Quelques exemples :— Dans R :˚a, b =˚a, b =˚a, b =˚a, b =a, b— Dans Rn :˚Ba, r = Ba, r˚Ba, r = Ba, r

Page 34 : 34CHAPITRE 2. ESPACE VECTORIEL NORMÉDéﬁnition 10 :Soit E, · un EVN. Soient A E et a E. On dit que a estadhérent à A si, et seulement si, tout voisinage de a rencontre A. On appellel’adhérent de A, noté A, l’ensemble des points adhérents à A.Formulation mathématique :x A ⇐⇒r 0, Bx, r A ̸= Propriété 26 :Soit E, · un EVN. Soit A une partie de E. Alors A ADémonstration :x A, r 0, Bx, r A ̸= puisque x A et x Bx, r. Donc x Aet ﬁnalement A A.Propriété 27 :Soit E, · un EVN. Soit A une partie de E. Alors A est un ferméDémonstration :Pour cela étudions CEA : si c’est un ouvert alors A est un fermé.x A ⇐⇒r 0 / Bx, r A ̸= .Donc pour x CEA, r 0 tel que Bx, r A = sinon x serait unélément de A. Donc, r 0 /Bx, r CEA. On voit donc que CEA est unouvert. Finalement A est un fermé.Propriété 28 :A est le plus petit fermé contenant A.

Page 35 : 2.2. ELÉMENTS DE TOPOLOGIE DANS RN35Démonstration :Démonstration remise à plus tard.Propriété 29 :1. A fermé ⇐⇒A = A2. A = A3. Si A B alors A BDémonstration :1. a Si A = A alors comme A est un fermé alors A est un fermé.b Si A est un fermé alors le plus petit fermé qui contient A est A.Donc A = A2. Soit A l’adhérent de A. Donc A est un fermé. Donc le plus petit fermécontenant A est A. Finalement A = A.3. Soit a A et V un voisinage de a. On a donc que A V ̸= . Orcomme A B, on a AV BV , il vient que BV ̸= . Finalementa B.Déﬁnition 11 :Soit E, · un EVN. Soit A une partie E. On appelle frontière deA, noté Fra ou A, l’ensemble :A = A\˚AQuelques exemples :Soit la boule fermée Ba, r alorsBa, r = Ba, ret˚Ba, r = Ba, rDoncBa, r = Ba, r\Ba, r = Sa, r

Page 36 : 36CHAPITRE 2. ESPACE VECTORIEL NORMÉPropriété 30 :1. A = A A2. ˚A = A\ADémonstration :Démonstration remise à plus tard.2.2.6MéthodologiesMontrer qu’un ensemble A n’est pas ouvert :Le plus simple est de trouver au moins un point qui se trouve sur la frontièrede l’ensemble tel que quelque soit la taille de la boule ouverte, une partiede la boule soit en dehors de A.Montrer qu’un ensemble A n’est pas fermé :Le plus simple est de montrer que le complémentaire de cet ensemble n’estpas ouvert. Pour cela, il suﬃt d’appliquer la méthode précédente au complé-mentaire de A.Trouver l’adhérent de A : démonstration dans le TD3Il est relativement facile d’avoir une idée intuitive de ce qu’est A connaissantA. En eﬀet, A est le plus petit fermé contenant A. Dans la suite, nous allonsappeler B l’ensemble que nous considérons comme le candidat pour être A.Etape 1 : Vériﬁer que B est un fermé.Etape 2 : Vériﬁer que A B.Si les deux conditions précédentes sont bien remplies, alors on sait que pourx CEB, on a r 0 / Bx, r A = . On est alors sûr qu’il n’y a pasde points extérieurs à B qui appartient à A. Ceci revient à dire que B n’estpas trop petit.Toutefois, à ce stade, on sait seulement que A B mais on ne sait passi B est trop grand on doit vériﬁer que B A.Etape 3 : Il faut maintenant vériﬁer que B n’est pas trop grand B tropgrand si, et seulement si, x B\A tel que r 0, Bx, r A = .

Page 37 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN37On doit vériﬁer que pour x B\A :r 0, Bx, r A ̸= alors A = B. Sinon il faut supprimer les points qui ne vériﬁent pas cettecondition.Trouver l’intérieur de A : démonstration dans le TD3Comme précédemment, il est plutôt facile d’avoir une intuition de ce qu’est˚A puisqu’il s’agit du plus grand ouvert contenu dans A. Notons B ce candi-dat. AlorsEtape 1 : Vériﬁer que B est un ouvertEtape 2 : Vériﬁer que B ASi les deux conditions précédentes sont remplies, alors x B, r 0 telque Bx, r A, ce qui revient à vériﬁer que B n’est pas trop grand : B ˚A.Toutefois, à ce stade, on sait que B n’est pas trop grand mais il reste àvériﬁer que B n’est pas trop petit ˚A B.Etape 3 : On doit vériﬁer que pour x A\B alors :r 0, Bx, r ̸ASi c’est le cas alors ˚A = B. Sinon, B est trop petit.2.3Suites d’éléments d’un EVN2.3.1RappelsEn première année, vous avez étudié ce qu’est une suite d’éléments de R. Lebut étant dans cette partie de chapitre, d’étendre au cas de suites d’élémentsd’un EVN quelconque, commençons par rappeler ce que vous connaissez déjà.Rappel 1 : Suite d’éléments de RUne suite d’éléments de R est une application de N dans R. Si x estune suite d’éléments de R de terme général xn, on notera la suite xnnN

Page 38 : 38CHAPITRE 2. ESPACE VECTORIEL NORMÉComme exemples de telles suites, nous pouvons considérerN→Rn7→xn = 2.3nou encoreN→Rn7→xn = 1nRappel 2 : Suite d’éléments de R qui convergeLa suite xnnN d’éléments de R converge vers lR si, et seule-ment si, elle vériﬁe le critère suivant :ϵ 0, N N / n N, xn l ϵOn note alors limn→xn = l cette limite.Nous n’allons pas rentrer plus en détail mais vous avez aussi vu que la limite,si elle existe, est unique. Je renvoie à votre cours de 1ère année pour plus dedétails sachant que nous allons généraliser ces déﬁnitions et résultats dansce cette partie.2.3.2Généralisation et GénéralitésDéﬁnition 12 : Suite d’éléments d’un EVNSoit E un espace vectoriel normé. Une suite d’éléments de E est uneapplication de N dans E. Si x est une suite de E de terme général xn, onnotera la suite xnnNQuelques exemples :— si E = R, on retombe sur le cas étudié en première année :N→Rn7→xn = 2.3n

Page 39 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN39— si E = R3 cas étudié en analyse dans Rn :N→R3n7→1n; 2n + 3; 32nDéﬁnition 13 : Suite bornéeSoit E, · un EVN. La suite xnnN de E est dite bornée si, etseulement si, la suite numérique réelle xnnN est bornée, c’est-à-dire si,et seulement siM 0 / n N, xnMAttention, il est capital de noter que M est indépendant de n.Quelques exemples :— Soit E, · = R, · :Considérons la suiteN→Rn7→xn = 1/nAlorsxn=1n = 1ndonc n N, xn1 et la suite est bornée.— Soit E, · = R3, ·2 :Considérons la suiteN→R3n7→xn = 2n, 3n, 1/nAlorsxn2 =r4n2 + 9n2 + 1n2→n→++donc xn n’est pas borné.

Page 40 : 40CHAPITRE 2. ESPACE VECTORIEL NORMÉ2.3.3Suites ConvergentesDéﬁnition 14 : Suite convergenteSoit E, · un EVN. Soit l E. La suite xnnN d’éléments de Econverge vers l si, et seulement si, elle vériﬁe l’une des 3 propriétés équiva-lentes suivantes1. ϵ 0, N N / n N, xn l ϵ.2. ϵ 0, N N / n N, xn Bl, ϵ.3. V Vl, N N / n N, xn V .Les 3 formulations sont parfaitement équivalentes puisquexn l ϵ ⇐⇒xn Bl, ϵDonc 1. et 2. sont équivalents. De plusV Vl ⇐⇒ϵ 0 / Bl, ϵ VdoncV Vl ⇐⇒ϵ 0 on considère Bl, ϵd’où l’on déduit que 2. et 3. sont équivalents.Propriété 31 : Unicité de la limiteSoit E, · un EVN. Si une suite d’éléments de E, notée xnnN,converge alors elle admet une limite unique l. On note alors cette limitelimn→xn = l2.8Démonstration :Soit xnnN une suite d’éléments de E, ·. Par hypothèse, posons l1, l2 E tels que l1 ̸= l2, vers lesquels xn converge. On a donc, d’après la déﬁnitionde la convergence :Vl1 Vl1, N1 N / n N1, xn Vl1Vl2 Vl1, N2 N / n N2, xn Vl2

Page 41 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN41Or un EVN est séparé donc comme l1 ̸= l2, V1 Vl1 et V2 Vl2 telsque V1 V2 ̸= . On a donc, en posant N = maxN1, N2 :n N,xn V1xn V2,or V1 V2 = donc absurdeet ﬁnalement l1 = l2.Propriété 32 :Soit E, · un EVN. Soient xnnN et ynnN deux suites d’éléments deE, convergentes vers l, l′ E respectivement. On a alors1.limn→xn = l =⇒limn→xn= l2.limn→xn = 0E ⇐⇒limn→xn= 03.limn→xn + λyn = l + λl′Remarque : faisons une petite remarque avant de démontrer les propriétésprécédentes. Quelle est la signiﬁcation delimn→xn= lLa suite xnest une suite d’éléments de N dans R+ puisque la norme ·est une application de E dans R+. Ainsi, on a, d’après le Rappel 2 en notantque lR+ :limn→xn= l⇐⇒ϵ 0, N N / n N, xnl ϵDémonstration :1. Si limn→xn = l alorsϵ 0, N N / n N, xn l ϵor d’après la 2nd inégalité triangulaire, n N, xnl xn l, on a doncϵ 0, N N / n N, xnl xn l ϵ

Page 42 : 42CHAPITRE 2. ESPACE VECTORIEL NORMÉdonclimn→xn= lRemarque :Mais attention, la réciproque est trivialement fausse.Pour voir cela, nous pouvons considérer la suite d’éléments de l’espacevectoriel normé R, · suivante :xn = 1nAlors trivialement xn= 1, n N. Ainsi limn→xn= 1 alorsmême que la suite xn n’admet aucune limite.2. C’est immédiat. En eﬀet,limn→xn = 0E⇐⇒ϵ 0, N N / n N, xn ϵlimn→xn= 0⇐⇒ϵ 0, N N / n N, xn ϵC’est donc totalement équivalent.3. On aϵ 0, N N / n N, xn l ϵϵ′ 0, N′ N / n N′, yn l ϵ′or d’après l’inégalité triangulairexn + λyn l + λl′ xn l+ λyn l′donc en posant ϵ′′ = ϵ + λϵ′, on obtientϵ′′ 0, N′′ = maxN, N′ N / n N′′,xn + λyn l + λl′ ϵ′′donc limn→xn + λyn = l + λl′

Page 43 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN43Propriété 33 :Soit E = Rp, ·. On notexnnN =x1n nN, x2n nN , ... , xpn nNune suite d’éléments de Rp où lesxinnN sont des suites d’éléments de Ndans R. Alorslimn→xn = l1, l2, ..., lp avec li = limn→xinDémonstration :li = limn→xin ⇐⇒ϵi 0, Ni N / n Ni, xin li ϵiPosons N = maxN1, ..., Np et ϵ = Ppi=1 ϵi. Soit e1, e2, ..., ep une basenormée, pour la norme choisie, de Rp. Alorsxn l1, l2, ..., lp=x1n l1e1 + ... + xpn lpepx1n l1e1 +x2n l2e2 + ... +xpn l1epx1n l1 e1+ x2n l2 e2+ ... + xpn lp epXϵi = ϵExemple :Soit la suiteN→R2n7→xn = 1 1n, 1n2 Alorslimn→xn =limn→1 1n, limn→1n2= 1, 0Donc la suite xnnN converge vers le vecteur l = 1, 0.

Page 44 : 44CHAPITRE 2. ESPACE VECTORIEL NORMÉ2.3.4Valeur d’adhérence et point d’adhérentDéﬁnition : Suite extraite, RappelSoit E, · un EVN. Soit xnnN une suite d’éléments de E. Soit φune application strictement croissante de N →N. On appelle alors suiteextraite de xnnN ou sous-suite extraite la suite ynnN déﬁnie paryn = xφnUne suite extraite d’une suite, est simplement une suite dont on choisit leséléments mais cette séléction se fait forcément en augmentant le rang deséléments qui sont sélectionnés. Ainsi on peut, par exemple, pour construirela suite extraite yn, sélectionner la suite xn pour n = 1, puis 2, puis 20 puis21... et ainsi de suite. Mais on ne peut pas choisir n = 1, puis 2, puis 20 puis18 car alors la fonction φ ne serait pas strictement croissante.Considérons par exemple la suiteN→R2n7→xn =1n, 1n2On peut par exemple extraire de cette suite, tous les éléments n pairs de lasuite, conduisant ainsi à la suite extraiteN→R2n7→yn = x2n =1,12n2Propriété 35 : convergence des suites extraites d’une suite convergenteSoit E, · un EVN. Soit xnnN une suite de E qui converge versl E. Alors toute suite extraite converge également vers l.Démonstration :— Tout d’abord, comme φ est une fonction strictement croissante den N, on a évidemment, n N, φn n. Montrons-le par récur-rence.

Page 45 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN45rang 0 : φ0 0 donc OKhérédité : vériﬁons que si la propriété est vraie au rang n alors elleest vraie au rang n+1. Vériﬁons donc que l’on a bien φn+1 n+1.Par hypothèse : φn n. Or φ est strictement croissante doncφn + 1 φn. Puisque φn n, on déduit que φn + 1 φn n. D’où l’on déduit que φn + 1 n + 1. CQFD.— Montrons maintenant que toute suite extraite de xnnN qui convergevers l, converge aussi vers l.xnnN CV vers l ⇐⇒ϵ 0, N N / n N, xn l ϵor n, φn n doncϵ 0, N N / φn n N,xφn l ϵdonc ﬁnalement limn→xφn = l.Déﬁnition 14 : Valeur d’adhérence d’une suiteSoit E, · un EVN. Soit l E. Soit xnnN une suite d’élémentsde E. Soit a E. Alors, on dit que a est valeur d’adhérence de la suitexnnN, si, et seulement si, l’une des propriétés équivalentes suivantes estvériﬁés1. Il existe une suite extraite de xnnN qui converge vers a.2. ϵ 0, l’ensemble n N, xn a ϵ est inﬁni.3. V Va, l’ensemble n N, xn V est inﬁni.Exemple :Soit la suitexnnN:N→Rn7→x2n = 1x2n+1 = 1

Page 46 : 46CHAPITRE 2. ESPACE VECTORIEL NORMÉ- Alors, il existe une suite extraite, la suite des n paires, qui converge vers 1.Donc 1 est valeur d’adhérence de la suite xnnN.- Il existe une autre suite extraite, la suite des n impaires, qui convergevers 1.On voit donc que la suite des xn = 1n est bornée car xn= 1, a deuxvaleurs d’adhérence 1 et 1 mais malgré tout est non convergente.Propriété 36 :Soit E, · un EVN. Soit xnnN une suite d’éléments de E. SixnnN converge vers l E, alors l est l’unique valeur d’adhérence dexnnN.Démonstration :— l est valeur d’adhérence de xnnN car il suﬃt de prendre commesuite extraite, la suite elle-même φ : n →n.— Or d’après la propriété 35, toute suite extraite de la suite xnnNconvergera également vers l.Attention : la réciproque est fausse. Une suite peut n’avoir qu’une valeurd’adhérence est être non convergente. Exemple :n N,x2n = 2nx2n+1 = 11 est valeur d’adhérence de la suite, tandis que la suite diverge.Propriété 37 :Soit E, · un EVN. Soient A E et a E. Alors, les 3 proposi-tions suivantes sont équivalentes :1. a est adhérent à A.2. il existe une suite xnnN d’éléments de A dont a est une valeurd’adhérence.3. il existe une suite xnnN d’éléments de A qui converge vers a.

Page 47 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN47Démonstration :— 1 =⇒3 : soit a un point adhérent à A. Alors, n NBa, 1nA ̸= Soit xn A Ba, 1/n. Alors puisque xn Ba, 1/n, on axn a 1n donclimn→xn = a2.9— 3 =⇒1 : Soit xnnN une suite d’éléments de A qui converge vers a.Soit V un voisinage de a. Alors, N N tel que n N, xn V . Orxn A puisque xnnN est une suite d’éléments de A. On conclutdonc que xn A V donc A V ̸= . On peut faire ce raisonnementpour tout V Va. Donc a A.— 2 =⇒3 : On choisit alors comme suite extraite de xnnN la suitequi converge vers a.— 3 =⇒2 : Comme la suite xnnN de A converge vers a alors a estl’unique valeur d’adhérence de xnnNFinalement 1 ⇐⇒2 ⇐⇒3.Propriété 38 :Soit E, · un EVN. Soient A E et a E. Alors1. A est l’ensemble des valeurs d’adhérence des suites d’éléments de A,ou dit autrement, l’ensemble des limites de toutes les suites conver-gentes d’éléments de A.2. A est fermé si, et seulement si, toute suite d’éléments de A quiconverge admet une limite dans A.Démonstration :1. a A ⇐⇒il existe une suite d’éléments de A qui converge vers Apropriété 37.Donc A est l’ensemble des limites des suites de A.

Page 48 : 48CHAPITRE 2. ESPACE VECTORIEL NORMÉ2. =⇒: Si A fermé alors A = A. Or A est l’ensemble des limites des suitesdes éléments de A. Donc si A fermé, l’ensemble des suites convergentesde A converge dans A.⇐= : la réciproque est tout aussi évidente.2.3.5Suites de CauchyDéﬁnition 15 : Suite de CauchySoit E, · un EVN. Soit xnnN une suite d’éléments de E. AlorsxnnN est une suite de Cauchy si et seulement siϵ 0, N N / n N, p N, xp xn ϵAvant de discuter de l’intérêt du concept de suite de Cauchy, nous allonsmontrer quelques propriétés.Propriété 39 :1. Toute suite convergente est de Cauchy2. Toute suite de Cauchy est bornéeDémonstration :1. Soit xnnN une suite convergente vers l. Alorsϵ1 0, N N / n N, xn l ϵ1Or, xn, xpxn xp= xn l + l xpxn l+ xp lDonc, n, p N, on axn xp 2ϵ1et ﬁnalementϵ = 2ϵ1 0, N N / n, p N, xp xn ϵ

Page 49 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN492. Démonstration remise à plus tard.Propriété 40 :Si une suite de Cauchy admet une valeur d’adhérence, alors elle convergevers sa valeur d’adhérence.Démonstration :Soit E, · un EVN. Soit xnnN une suite de Cauchy d’éléments de E.Soit a une valeur d’adhérence de la suite. Alors :Soit ϵ 0. Il existe Nc N tel que pour tout n Nc, et p Nc, onait xn xp ϵ/2. Soit xφnnN une suite extraite qui converge vers a.Alors il existe N1 N tel que pour tout n N1, on aitxφn a ϵ/2.On note N = maxNc, N1. Pour tout n N, on a φn n N Nc.D’oùxn axn xφn +xφn a ϵNous venons de montrer queϵ 0, N N/ n N, xn a ϵDonc la suite converge vers la valeur d’adhérence a.Il est important de discuter du contenu mathématique des suites de Cauchy.La déﬁnition stipule que les termes d’une suite de Cauchy se rapproche in-éxorablement à partir d’un certain rang. Intuitivement, cela implique qu’unesuite de Cauchy converge. Toutefois, et il est capital de le comprendre, unesuite de Cauchy ne converge pas nécessairement dans le même espace quel’espace dans lequel la suite est déﬁnie.Pour le comprendre, étudions la suite suivante suite de Héronxn+1 =xn +2xn2avec x0 = 2Commençons par remarquer que tous les termes de la suite sont évidemmentdes rationnels.

Page 50 : 50CHAPITRE 2. ESPACE VECTORIEL NORMÉEnsuite, on peut déterminer le point de convergence de cette suite. Pourcela, on voit que, n N, xn 0. De plusx2n+1 2 =x2n + 22xn22 = x4n + 22 + 2 × 2x2n4x2n2 =x2n 22xn20d’où l’on déduit que n N, xn 2. De plus, n Nxn+1 xn = x2n + 22xnxn = 2 x2n2xnor puisque xn 2, on a 2 x2n 0, ce qui implique que xn+1 xn. Doncla suite est décroissante et positive ce qui implique qu’elle converge rappeldu cours de préING 1. Donc puisque la limite existe, notons la l. On a doncl = l + 2l2=⇒l =2car la suite est positiveDonc, alors que la suite de Héron est une suite déﬁnie sur l’espace des ration-nels Q, elle converge vers un irrationnel. Ainsi, il est intéressant de distinguerles espaces tels que toute suite de Cauchy déﬁnie dessus, y converge, des es-paces où les suites de Cauchy ne convergent pas mais convergent tout demême en dehors. Ainsi :Déﬁnition 16 : Espace complet, Espace de Banach1. Un espace métrique c’est-à-dire un espace muni d’une distance estdit complet si, et seulement si, toute suite de Cauchy déﬁnie sur cetespace y converge.2. Un espace vectoriel normé complet est appelé un espace de BanachCe type d’espace jouera un rôle central en analyse fonctionnelle cursus GM,Math-ϕ.2.3.6CompacitéThéorème 1 : de Bolzano-WeierstrassToute suite bornée d’un espace vectoriel de dimension ﬁnie possèdeune suite extraite convergente.

Page 51 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN51Démonstration : Admis.Déﬁnition 17 : CompacitéSoit E, · un EVN. Soit A E. On dit que A est compact dansE si et seulement si toute suite de A admet une suite extraite convergentedans A.Exemple :R est un ensemble non compact. En eﬀet, considérons la suiteunnN:N→Rn7→un = ncette suite ne converge pas et aucune suite extraite d’elle ne converge. Doncil existe au moins une suite de R dont aucune suite extraite ne converge dansR. Finalement R n’est pas compact.Propriété 41 :Soit E, · un EVN de dimension ﬁnie. Alors1. compact ⇐⇒fermé et borné2. l’ensemble vide est compact.3. toute partie fermée d’un compact de E est compacteDémonstration :1. a Montrons tout d’abord que : compact =⇒fermé et borné.compact =⇒fermé : A compact donc de toute suite xn, on peutextraire une suite xφn qui converge vers l A. Or, si la suitexn converge, elle converge nécessairement vers l. Donc toute suiteconvergente d’éléments de A converge dans A =⇒fermé carac-térisation séquentielle des fermés.

Page 52 : 52CHAPITRE 2. ESPACE VECTORIEL NORMÉcompact =⇒borné : Pour cela prenons la contraposénon borné =⇒non compactSi l’ensemble A n’est pas borné, alors on peut prendre une suitetelle que n N, xnn. D’où, pour toute suite extraite xφn,nous avons n φn xφn. On en déduit donc que toute suiteextraite de xnnN diverge et donc A n’est pas compact.Finalement, compact =⇒borné, fermé.b Montrons maintenant que borné, fermé =⇒compact :Soit A un ensemble borné d’un espace vectoriel normé de dimen-sion ﬁnie. Alors toute suite de A est bornée. D’après le théorèmede Bolzano-Weiestrass, toute suite de A admet donc une suite ex-traite qui converge. Or A est fermé donc A = A donc toute suiteextraite converge bien dans A.2. l’ensemble vide est fermé et borné donc c’est un compact.3. A compact =⇒A fermé et borné. Soit B A un fermé. Alors B estégalement borné puisque A borné. Donc B est un compact.Remarque : en dimension inﬁnie la propriété 1. devientcompact =⇒borné et fermé mais la réciproque devient faussePropriété 42 :Tout compact d’un espace vectoriel normé est complet.Démonstration :Rappel pour la démonstration :1. complet : toute suite de Cauchy d’éléments de A converge dans A.2. toute suite convergente est de Cauchy3. toute suite de Cauchy ayant une valeur d’adhérence converge

Page 53 : 2.3. SUITES D’ÉLÉMENTS D’UN EVN53A est un compact donc toute suite xn d’éléments de A admet une suite ex-traite xφn qui converge dans A. Or si xn est une suite de Cauchy, alorselle admet une valeur d’adhérence dans A et converge donc vers cette valeurd’adhérence =⇒toute suite de Cauchy de A converge dans A donc A com-plet.Propriété 43 :Soient E, ·E et F, ·F deux EVN. Soient A E et BFdeux compacts. Alors A × B est un compact de E × F.Démonstration remise à plus tard.

Page 54 : 54CHAPITRE 2. ESPACE VECTORIEL NORMÉ

Page 55 : Chapitre 3Limite et Continuitéd’applications3.1Objectifs du chapitreLe but de ce chapitre est de généraliser les notions de limite de fonctions etde continuité que vous avez étudiées en préING 1 pour les fonctions de Rdans R fonctions d’une variable aux fonctions de Rp dans Rn où p, n N,fonction de plusieurs variables.Rappels de préING 1 :— Soit f une fonction de D R →R. Alors la limite l de f quand xtend vers a estϵ, α 0, x D, x a α =⇒fx l ϵce que l’on note :limx→a fx = l— Si a appartient au domaine de déﬁnition de la fonction alorslimx→a fx = fapuisque ϵ 0, fa l ϵ.Dit autrement, si fa n’aboutit pas une forme indéterminée 0/0,0 × , /ou encore alorslimx→a fx = fa55

Page 56 : 56CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSS’il y a une forme indeterminée, alors il faut la lever pour trouver lalimite. Par exemplelimx→0x3x2 x = 00Forme indeterminéeAlorslimx→0x3x2 x = limx→0x3xx 1 = limx→0x2x 1 = 0— Pour qu’une fonction f : R →R soit continue en a, il faut et il suﬃtquelimx→afx = limx→a+ fx = faexemple : Soit la fonction de Heaviside que vous avez rencontrédans le cours d’Automatiquef:R→Rx7→fx =1si x 00si x 0dont une représentation est donnée sur la ﬁgure suivanteClairement, cette fonction n’admet pas de limite en 0.Nous allons donc généraliser ces remarques et plus encore... aux cas desfonctions de Rp →Rn fonctions de plusieurs variables comme par exempleles fonctions suivantesf:R2→Rx, y7→fx, y =xyx2+y2ou encoreg:R2→R2x, y7→gx, y =x2+y21x;sinx2+siny2x2+y2On peut alors se demander : quelle est la limite de f et g au point 1, 2 ?Sont-elles continues en 0, 0 ?Nous verrons que les notions de topologie introduites au chapitre précédentsont capitales : norme, voisinage, ouvert, fermé, borné.

Page 57 : 3.2. LIMITE, CONTINUITÉ573.2Limite, ContinuitéNous devons commencer par généraliser la notion de limite des fonctions deR →R au cas des fonctions d’un EVN quelconque dans un autre EVN.Déﬁnition 1 : limite d’une fonction en un pointSoient E, ·E et F, ·F , deux EVN. Soit A E. Soit f une ap-plication de A dans F. Soient a A et l F. On dit que f admet une limitel lorsque x tend vers a, si et seulement si, l’une des propriétés équivalentessuivantes est vériﬁée1. ϵ 0, η 0, x A, x aE η =⇒fx lF ϵ2. ϵ 0, η 0, x A, x BEa, η =⇒fx BF l, ϵ3. VF Vl, VE VEa, x A, x VE =⇒fx VF 4. VF Vl, VE VEa, fVE A VFRemarques :— ϵ est la précision à laquelle on connait la valeur prise par fx. Ainsi,on ﬁxe la précision ϵ. Alors, il existe η tel que pour tout x se trouvantà une distance inférieure à η possède une image par f à une distancede l inférieure à la précision ϵ.

Page 58 : 58CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSSi ϵ tend vers 0 alors η doit tendre vers 0.— Si f est déﬁnie en a, alors la limite est fa.Exemple :f:R2→Rx, y7→fx, y =xyx2+y2Alors en a = 1, 1 on a fa = f1, 1 = 12 qui est donc la limite def en a.Mais en a = 0, 0, on voit que l’on obtient une forme indeterminéedu type 0/0. Il faut alors lever l’indetermination. On étudiera dans lasuite de ce chapitre des techniques pour cela lorsque la fonction est àplusieurs variables comme c’est le cas ici.Propriété 1 : unicité de la limiteSoient E, ·E et F, ·F , deux EVN. Soit A E. Soit f une ap-plication de A dans F. Soit a A. Si f admet une limite l F en a alorselle est unique.On note alors cette limitelimx→a fx = lDémonstration :Supposons que f possède deux limites l et l′ telles que l ̸= l′. Posons alorsϵ = 13 l l′F 0. Alors, il existe η, η′ 0 tels quex A, x aE η =⇒fx lF ϵx A, x aE η′ =⇒fx l′F ϵ′Prenons x aE minη, η′. On a alorsfx l ϵetfx l′ ϵ′Donc3ϵ =l l′F =l fx + fx l′F l fxF +fx l′F 2ϵ

Page 59 : 3.2. LIMITE, CONTINUITÉ59ce qui est absurde. Donc l = l′.Exemple :Reprenons l’exemple de fonction précédentf:R2→Rx, y7→fx, y =xyx2+y2Dont la représentation graphique est la suivanteEtudions la limite de cette fonction en a = 0, 0. Pour cela, nous allonspasser en coordonnées polaires

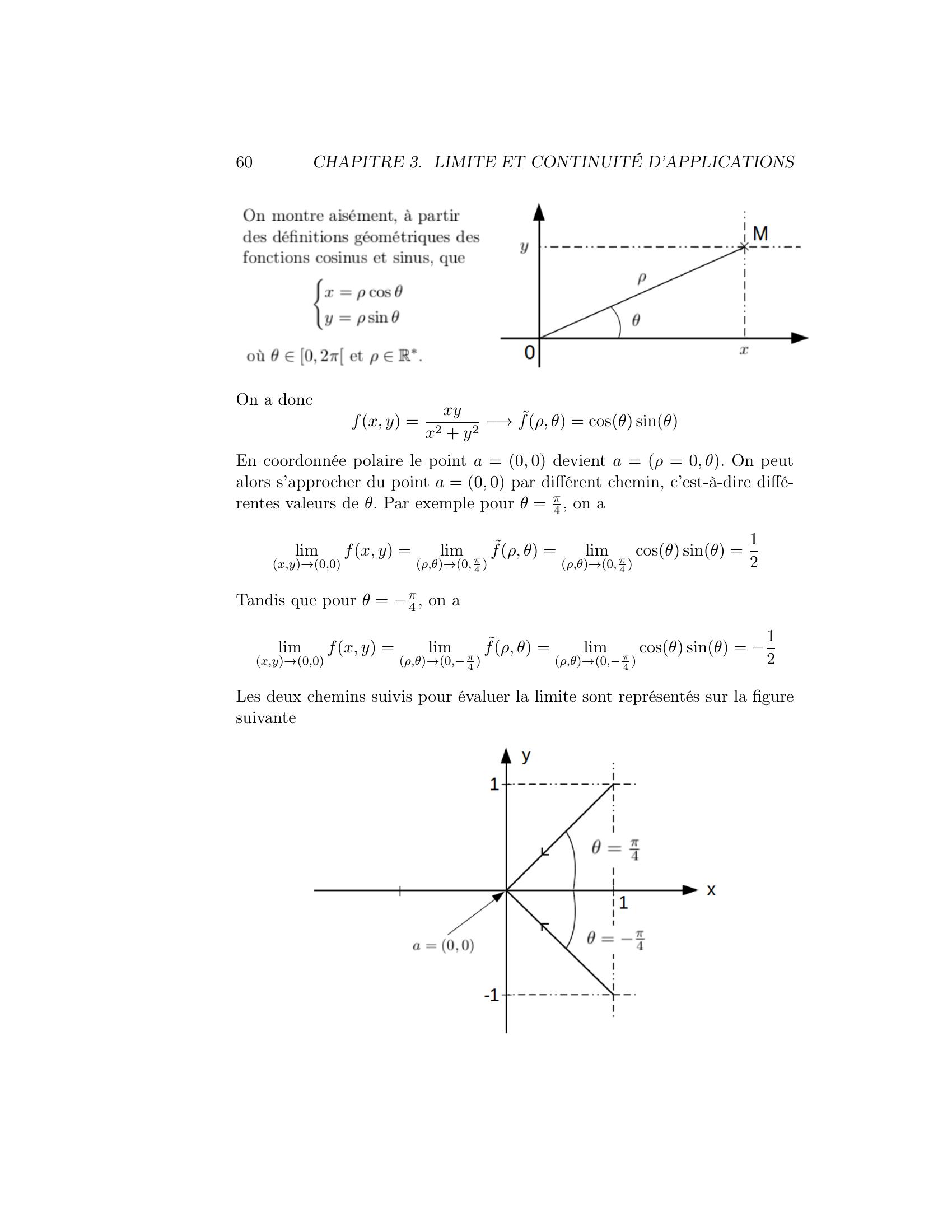
Page 60 : 60CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSOn a doncfx, y =xyx2 + y2 →˜fρ, θ = cosθ sinθEn coordonnée polaire le point a = 0, 0 devient a = ρ = 0, θ. On peutalors s’approcher du point a = 0, 0 par diﬀérent chemin, c’est-à-dire diﬀé-rentes valeurs de θ. Par exemple pour θ = π4 , on alimx,y→0,0 fx, y =limρ,θ→0, π4 ˜fρ, θ =limρ,θ→0, π4 cosθ sinθ = 12Tandis que pour θ = π4 , on alimx,y→0,0 fx, y =limρ,θ→0,π4 ˜fρ, θ =limρ,θ→0,π4 cosθ sinθ = 12Les deux chemins suivis pour évaluer la limite sont représentés sur la ﬁguresuivante

Page 61 : 3.2. LIMITE, CONTINUITÉ61Finalement commelimρ,θ→0, π4 ˜fρ, θ ̸=limρ,θ→0,π4 ˜fρ, θla fonction f n’admet pas de limite en a = 0, 0.Remarque :Sur cette exemple, on peut voir une diﬀérence fondamentale entre le cas desfonctions de R dans R et celui des fonctions de Rp dans Rn. En eﬀet, dansle premier cas, évaluer la limite en un point a quelconque revient seulementà s’approcher par deux chemins : par les x plus grands que a et les x pluspetits que a. Mais dans le second cas, il existe en fait une inﬁnité de cheminspar lesquels on peut s’approcher de a.et pour que la limite existe, il faut que tous les chemins par lesquels on peuts’approcher de a donne les mêmes limites.Propriété 2 :Changer les normes ·E et ·F par des normes équivalentes ne change pasle fait que la limite existe ou non. Si de plus elle existe, elle reste inchangée.Démonstration :Soit E et F deux EVN munis tous les deux de deux normes équivalentes.Pour E les deux normes équivalentes sont ·1,E et ·2,E. Il existe donc

Page 62 : 62CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSα, β 0 tels que x Eα x2,E x1,E β x2,EDe même, pour F les deux normes équivalentes sont ·1,F et ·2,F . Il existedonc γ, δ 0 tels que y Fγ y2,F y1,F δ y2,FSoit f une fonction allant de E dans F qui admet une limite l F en a Eselon les normes ·1,E et ·1,F . Doncϵ 0, η 0 / x E, x a1,E η =⇒fx l1,F ϵPosons maintenant ϵ = ϵ′/δ et η′ = η/α. Alorsx a1,E η =⇒α x a2,E x a1,E η =⇒x a2,E ηα = η′De mêmefx l1,F ϵ =⇒γ fx l2,F fx l1,F ϵ =⇒fx l2,F ϵγ = ϵ′Doncϵ′ = ϵγ , η′ = ηα / x E, x a2,E η′ =⇒fx l2,F ϵ′Propriété 3 :Soient E, ·E et F, ·F deux EVN et AE. Soient f et gdeux applications de A dand F, a A et l F. Silimx→a fx = l1etlimx→a gx = l2Alorslimx→a fx + λgx = l1 + λl2pour λ RDémonstration :Par hypothèse, on alimx→a fx = l1 ⇐⇒ϵ 0, η 0, x E, x aE η =⇒fx l1F ϵlimx→a gx = l2 ⇐⇒ϵ′ 0, η′ 0, x E, x aE η′ =⇒fx l2F ϵ′

Page 63 : 3.2. LIMITE, CONTINUITÉ63Calculons maintenant fx + λgx l1 + λl2Ffx + λgx l1 + λl2F fx l1F + λ gx l2FFinalement, en posant ϵ′′ = ϵ + λϵ′ et η′′ = minη, η′ϵ′′ 0, η′′ 0, x aE η′′ =⇒fx + λgx l1 + λl2F ϵ′′Propriété 4 :Soient E, ·E et F, ·F deux EVN. Soit F R et A E. Soient f etg deux applications de A →F. Soit a A. f et g sont telles quelimx→a fx = l1 et limx→a gx = l2avec l1, l2 R. Alors1. limx→a fxgx = l1l22. Si l2 ̸= 0, limx→a fx/gx = l1/l2Démonstration : laissée en exercicePropriété 5 :Soient E = Rn et F = Rp. Alors une application f de E →F ad-met l = l1, l2, ..., lp comme limite lorsque x tend vers a E si, etseulement si, pour tout entier J1; pK, la ième "application composante"fi : E →R de f admet li pour limite quand x tend vers a.Démonstration : laissé en exerciceExemple :Soit l’applicationf:R2→R2x, y7→fx, y =xy2x2+y2 ;xyx2+y2Etudions la limite en a = 0, 0 de cette fonction. D’après la propriété pré-

Page 64 : 64CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONScédente, il suﬃt d’étudier la limite de chacune des applications composantesf1:R2→Rx, y7→f1x, y =xy2x2+y2f2:R2→Rx, y7→f2x, y =xyx2+y2Même si nous avons déjà vu que f2 n’admet pas de limite en 0, 0, ce quiest suﬃsant pour dire que f n’admet pas de limite en ce point, étudions f1.Nous allons une fois de plus utiliser les coordonnées polaires. Posons doncx = ρ cos θy = ρ sin θAlorslimx,y→0,0xy2x2 + y2 =limρ,θ→0,θρ3 cos θ sin2 θρ2= 0pour θDonc la fonction composante f1 admet bien une limite en 0, 0.Déﬁnition 2 : Application continueSoient E, ·E et F, ·F , deux EVN. Soient A E, f une appli-cation de A →F et a A. On dit que f est continue en a si, etseulement si, f admet une limite en a. La fonction f est dite disconti-nue en a si, et seulement si, f n’est pas continue en a. La fonction estdite continue sur l’ensemble A si, et seulement si, elle est continue en toutpoint de A. On note CA, F l’ensemble des fonctions continues de A dans F.La continuité en un point quelconque a consiste donc à étudier si quelquesoit le chemin par lequel on s’approche de a, la fonction tend vers la mêmevaleur. Il s’agit également de la déﬁnition de la continuité en un point dansle cas d’une fonction de R →R. Mais dans le cas des fonctions de R →Ron ne peut s’approcher que de deux façon du point : soit par les x plus grandsoit par les x plus petit. La situation est beaucoup plus complexe dans lecas générale d’une fonction de Rp →Rn puisqu’il y a alors une inﬁnitéde façon de s’approcher du point a avec p 1 un entier. Par exemple, sip = 2 et a = 0, 0, alors on peut s’approcher par tous les chemins du plans’approchant de l’origine.

Page 65 : 3.2. LIMITE, CONTINUITÉ65Théorème 1 : Caractérisation séquentielle de la limiteSoient E, ·E et F, ·F , deux EVN. Soient A E, f une appli-cation de A →F et a A. Alors f admet une limite l F quand x tendvers a si, et seulement si, pour toute suite xnnN d’éléments de A quiconverge vers a, la suitefxnnN converge vers l.Démonstration : AdmisCorollaire : Caractérisation séquentielle de la continuitéSoient E, ·E et F, ·F , deux EVN. Soient A E, f une appli-cation de A →F et a A. Alors f est continue en a si, et seulementsi, pour toute suite xnnN d’éléments de A qui converge vers a, la suitefxnnN converge vers fa.Exemple :Soit la fonctionf:R2→Rx, y7→fx, y =xyx2+y2si x, y ̸= 0, 00si x, y = 0, 0

Page 66 : 66CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSPrenons par exemple un = 1n, 1n alors clairementlimn→un = 0, 0. Orfun = n2/2n2 = 1/2. Donc limn→fun =12 ̸= f0, 0 = 0. Donc lafonction n’est pas continue en 0, 0.3.2.1MéthodologieNous résumons ici les méthodes à notre disposition pour la recherche de limited’une fonction de R2 dans R en a = x0, y0. On cherche donc à déterminerlimx,y→x0,y0 fx, yEtape 1 :On calcule fx0, y0 et si on n’obtient pas une forme indeterminée 0 × ,/, 0/0, ,..., alorslimx,y→x0,y0 fx, y = fx0, y0Si on obtient une forme indeterminée, alors il faut lever l’indétermination etpour cela, vous devez passer à l’Etape 2.Etape 2 :Il y a dans cette deuxième étape plusieurs possibilités. Mais quelle que soit laméthode, l’objectif est de montrer : i soit que tous les chemins qui tendentvers a aboutissent à la même valeur et alors la fonction est continue en a etprend cette valeur ii soit il existe au moins deux chemins qui tendent versa mais qui n’aboutissent pas à la même valeur de f et dans ce cas la fonctionn’a pas de limite en a. Pour cela :1. On peut passer en coordonnées polaires notamment si le dénomina-teur si prête bien par exemple de la forme x x02 + y y02. Onpose alorsx = x0 + ρ cosθy = y0 + ρ sinθpermettant d’introduire la fonction ˜fρ, θ = fx, y. On a alorslimx,y→x0,y0 fx, y =limρ,θ→0,θ˜fρ, θSi le résultat ne dépend pas de θ alors la fonction f admet une limitedonnée parlimρ,θ→0,θ˜fρ, θ. Cela correspond au cas où la valeur de

Page 67 : 3.2. LIMITE, CONTINUITÉ67f ne dépend pas du chemin qui tend vers a. Si le résultat dépend deθ alors la fonction n’admet pas de limite en a car selon le chemin parlequel on tend vers a c’est-à-dire selon la valeur de θ, la valeur def est diﬀérente.2. Si la fonction n’a pas la bonne forme pour passer en coordonnées po-laires, on calcule explicitement la valeur de f pour diﬀérents cheminsd’approche du point a = x0, y0. Pour cela, on a deux méthodesa Caractérisation séquentielle :Nous savons que si un est une suite d’éléments de N dans R2 tellequelimn→un = x0, y0alors si f est continue, on alimx,y→x0,y0 fx, y = limn→funOn calcule alors cette limite pour diﬀérents chemins, c’est-à-direpour diﬀérentes suites un.b Caractérisation cartésienne :On exprime les diﬀérents chemins par leur expression cartésiennequi sont de la forme x, αx par exemple où α est une applica-tion de R dans R.Si deux chemins donnent des valeurs diﬀérentes, quelle que soit laméthode, alors la fonction f n’a pas de limite en a.Si, par contre, tous les chemins donnent la même valeur, alors cettevaleur, notée lc, est un bon candidat pour être la limite de la fonction.On passe alors à l’étape 3.3. Il ne reste plus qu’à calculer fx, y lc. Si cette quantité tend vers0 pour x, y tend vers x0, y0 alors :— Si fx, y lc→x,y→x0,y0 0, alorslimx,y→x0,y0 fx, y = lc— Sinon, la fonction n’admet aucune limite en x0, y0

Page 68 : 68CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSExemple 1 :Soit la fonction f1x, y = xy/x2 + y2 dont on cherche la limite en 0, 0.Clairement f10, 0 = 0/0 est une forme indeterminée.

Page 69 : 3.2. LIMITE, CONTINUITÉ69Exemple 2 :Soit la fonction f2x, y = 1+x3/x2+y2 dont on cherche la limite en 0, 0.Clairement f20, 0 = 0/0 est une forme indeterminée.On ne peut pas conclure à partir des deux dernières méthodes. En eﬀet,ce n’est pas parce que les deux chemins choisis donnent 1 que cela signiﬁeque la fonction est continue. Pour conclure avec ces deux méthodes, on doitmaintenant étudier fx, y lc où lc = 1.fx, y lc = fx, y 1 =x3x2 + y2 =x2x2 + y2 x x→x,y→0,0 0ﬁnalement, avec les 3 méthodes, on aboutit bien àlimx,y→0,0 f2x, y = 1

Page 70 : 70CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONS3.3Continuité uniformeDéﬁnition 2 : Continuité uniformeSoient E, ·E et F, ·F , deux EVN. Soient A E, f une appli-cation de A →F et a A. On dit que f est uniformément continue sur Asi, et seulement si,ϵ 0, η 0, a A, x A,x aE η =⇒fx faF ϵOn rappelle que la continuité classique celle de la section précédente surl’ensemble A s’écrita A, ϵ 0, η 0, x A,x aE η =⇒fx faF ϵLa diﬀérence entre la continuité uniforme sur l’ensemble A et la continuitésur l’ensemble A provient donc du fait que dans la continuité uniforme η estindépendant du point a A considéré ; d’où le nom de continuité uniforme.Propriété 6 :Toute application uniformément continue est continue.Démonstration :C’est trivial. Soit f une application de A E dans F. Alors f est uniformé-ment continue sur A si, et seulement siϵ 0, η 0, a A, x A,x aE η =⇒fx faF ϵqui implique évidemment la continuitéa A, ϵ 0, η 0, x A,x aE η =⇒fx faF ϵ

Page 71 : 3.3. CONTINUITÉ UNIFORME71Déﬁnition 3 : Application lipschitzienneSoient E, ·E et F, ·F , deux EVN. Une application f : E →F estdite lipschitzienne si, et seulement siκ 0, x E, y E, fx fyF κ x yEOn dit alors que f est κ-lipschitzienne de E dans F.Remarque : en dimension ﬁnie, le caractère lipschitzien d’une applicationne dépend pas des normes utilisées, par contre la valeur de κ, elle, en dé-pend.Propriété 7 :Toute application lipschitzienne est uniformément continue.Démonstration :Soient E, ·E et F, ·F deux EVN et f une application κ-lipschitziennede E dans F.1. Si κ = 0 alors f est une fonction constante. Donc pour tout a Eet x E, fx faF = 0 ϵ. On conclut donc que f estuniformément continue.2. Si κ ̸= 0, alors posons η = ϵ/κ 0. Soit a E et x E tels quex aE η. Alors fx faF κ x aE κη = ϵ. Onvient donc de montrer queϵ 0, η 0, a E, x E,x aE η =⇒fx faF ϵdonc f est uniformément continue.Propriété 8 :Soit E, ·E un EVN. Alors l’application ·Eest 1-lipschitziennede E dans R, · .

Page 72 : 72CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONSDémonstration :f est donc ici l’application ·E. Il suﬃt donc de montrer queκ 0, x E, y E, xE yE κ x yEavec κ = 1. Or d’après la 2nd inégalité triangulaire, x, y E, on a xE yE x yE. CQFD.Théorème 2 : théorème de HeineToute application continue sur un compact y est uniformément conti-nueDémonstration :Raisonnons par l’absurde. Soit f une application continue et non uniformé-ment continue sur un compact. Alorsϵ0 0, η 0, x, y A2 / x yE η ET fx fyF ϵ0Ainsi, en posant pour n N, ηn = 2n, nous avonsxn, yn A2 / xn ynE 2n ET fx fyF ϵ0Or A est un compact. Donc, il existe une suite extraite xφnnN convergentevers x A. Orxφn yφn 2φn 2n, ce qui implique que yφnconverge également vers x. Ainsi, f étant continue, fxφn et fyφnconvergent vers fx d’oùfxφn fyφnF →0or c’est absurde puisque cela doit être supérieur à ϵ0.3.4Topologie et fonctions continuesAﬁn de déterminer si un ensemble est un ouvert, un fermé ou un com-pact, il est également possible d’utiliser les fonctions continues à travers lesdeux théorèmes suivants

Page 73 : 3.4. TOPOLOGIE ET FONCTIONS CONTINUES73Théorème 3 : Images réciproques d’ouverts, de fermés1. L’image réciproque d’un ouvert par une application continue est unouvert.2. L’image réciproque d’un fermé par une application continue est unfermé.Démonstration :Soit f une application continue de E, ·E dans F, ·F . Commençonspar rappeler que f est continue en a et de plus fa = l, si, et seulement sielle vériﬁe :VF Vl, VE VEa, x A, x VE =⇒fx VF 1. Soit VF un ouvert de F. Soit x f1VF : alors évidemment fx VF . Or VF est un ouvert, c’est donc un voisinage de fx. Par conti-nuité :VE VEx / x VE, fx VFDonc VE f1VF . Comme VE est un voisinage de x, cela signiﬁedonc que f1VF l’est aussi. Comme cette démonstration reste vraiepour tout fx VF , on conclue que f1VF est bien un ouvert.

Page 74 : 74CHAPITRE 3. LIMITE ET CONTINUITÉ D’APPLICATIONS2. Soit A un fermé de F. Alorsx CEf1A ⇐⇒fx ̸A ⇐⇒fx CF A ⇐⇒x f1CF Ad’où l’on déduit que CEf1A = f1CF A. Comme A est un ferméde F, CF A est un ouvert de F. Donc compte-tenu de 1., f1CF A estun ouvert de E. Donc CEf1A est un ouvert puisque CEf1A =f1CF A. Finalement CECEf1A = f1A est un fermé.Théorème 4 : Image directe d’un compactSoient E, ·E et F, ·F deux EVN. Soit f une application continuede E dans F, alors l’image direct d’un compact de E par f est un compactde F.Démonstration :Soit A un compact de E et f une application continue sur A. Si bnnNest une suite d’éléments de fA, alors pour n N, an A telle quebn = fan. A étant compact, il existe une suite extraite aφn conver-gente vers a A. Or f est continue donc bφn = faφn convergevers fa fA. Donc fA est un compact.

Page 75 : Chapitre 4Calcul diﬀérentiel du 1er ordre4.1Objectifs du chapitreL’objectif de ce chapitre est de généraliser des notions que vous avez étudiédans le cas des applications de R dans R et/ou de vous introduire rigoureu-sement des concepts que vous avez déjà utilisé en physique :1. dérivée première →dérivée partiel du premier ordre :En fait, vous avez déjà calculé en éléctromagnétisme et en thermody-namique des dérivées partielles. Considérons, par exemple, la fonctionsuivantef:R2→R3x, y7→fx, y =x + y, x2 y2, x2yAlorsfxx,y= 1, 2x, 2xyfyx,y= 1, 2y, x2La première expression est obtenue en dérivant par rapport à x enﬁxant y ou dit autrement, en considérant y comme une constante,tandis que la seconde expression est obtenue en dérivant par rapportà y en ﬁxant x.75

Page 76 : 76CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREOn introduira également la notion de gradient d’un champ scalaireque vous avez étudié en mécanique ⃗F = ⃗V ou encore en électro-magnétisme. Considérons, par exemple, la fonction :f:R2→Rx, y7→fx, y = x2 + xyAlors⃗f = fxx,y, fyx,y= y + 2x, x2. diﬀérentiabilité : il s’agit d’une notion que vous connaissez pour lesfonctions de R dans R. Nous allons l’étendre au cas de fonctions de Rpdans Rn. On introduira alors les notions de diﬀérentielles, de classeC1.3. Nous généraliserons la notion d’équation diﬀérentielle d’ordre 1 enintroduisons les équations aux dérivées partielles du 1er ordre4.2Dérivée partielleDéﬁnition 1 : Dérivée partielleSoit U un ouvert de Rp. Soient a Rp et f une application de Udans F où F est un EVN. Soit e1, e2, ..., ep la base canonique de Rp. Ondit dit que f admet une dérivée partielle première en a par rapport à lajème variable si, et seulement si, l’applicationφj =Dj →Ft 7→fa + tejest dérivable en 0 avec Dj = t R / a + tej U. On a alors :fxja= φ′j0 = limt→0fa + tej fatRemarque : la notationfxja signiﬁe que l’on calcule la dérivée de f parrapport à la jème variable au point a ou que l’on évalue cette dérivée au

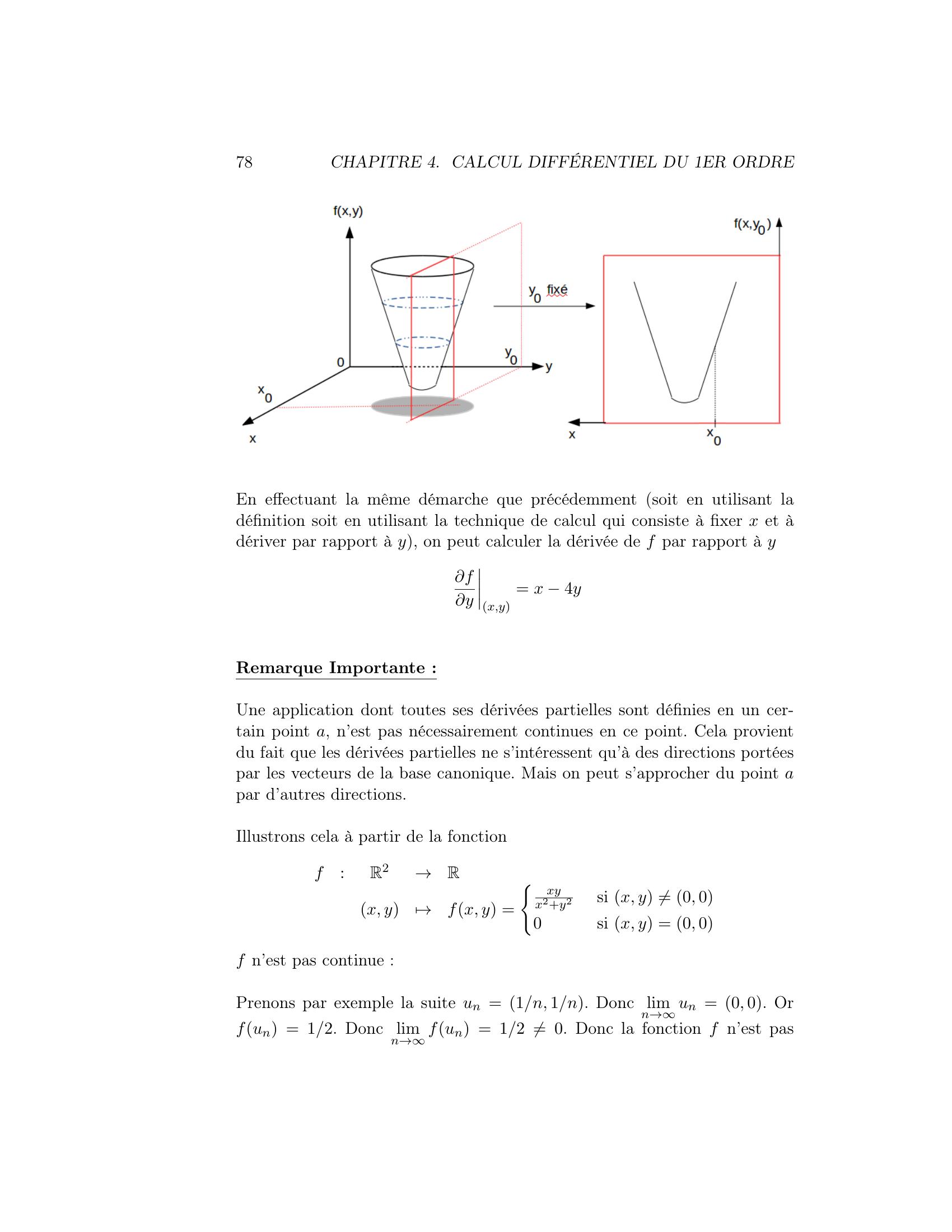
Page 77 : 4.2. DÉRIVÉE PARTIELLE77point a. Il s’agit d’une notation plutôt utilisée par les physiciens. Les ma-thématiciens préfèrent utiliser la notationfxj a ou encore faxjExemple : Soit f l’application suivantef:R2→Rx, y7→fx, y = 3x2 + xy 2y2Déterminons les dérivées partielles d’ordre 1 en fonction de x et y en toutpoint x, y.fxx,y= limt→0fx, y + t, 0fx, yt= limt→0fx + t, yfx, yt= limt→03x + t2 + x + ty 2y2 3x2 xy + 2y2t= limt→03t2 + 6xt + tyt= limt→03t + 6x + y= 6x + yCe qui est bien équivalent à ﬁxer y et à dériver par rapport à x :fxx,y= 6x + ySigniﬁcation graphique :Discutons du sens de fxx0,y0. Pour cela, nous avons schématiquement re-présenté une fonction de R2 dans R sur la ﬁgure suivante. Alors la dérivéepartielle de f par rapport à x au point x0, y0 revient à calculer la dérivéepar rapport à x au point x0 de la fonction fx, y0. Graphiquement, celasigniﬁe que l’on commence par prendre l’intersection du plan parallèle à xOzsitué en y = y0 avec la courbe fx, y. Cela permet d’obtenir fx, y0. Il nereste plus qu’à calculer la dérivée en x0 de cette fonction fx, y0.

Page 78 : 78CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREEn eﬀectuant la même démarche que précédemment soit en utilisant ladéﬁnition soit en utilisant la technique de calcul qui consiste à ﬁxer x et àdériver par rapport à y, on peut calculer la dérivée de f par rapport à yfyx,y= x 4yRemarque Importante :Une application dont toutes ses dérivées partielles sont déﬁnies en un cer-tain point a, n’est pas nécessairement continues en ce point. Cela provientdu fait que les dérivées partielles ne s’intéressent qu’à des directions portéespar les vecteurs de la base canonique. Mais on peut s’approcher du point apar d’autres directions.Illustrons cela à partir de la fonctionf:R2→Rx, y7→fx, y =xyx2+y2si x, y ̸= 0, 00si x, y = 0, 0f n’est pas continue :Prenons par exemple la suite un = 1/n, 1/n. Donc limn→un = 0, 0. Orfun = 1/2. Donc limn→fun = 1/2 ̸= 0. Donc la fonction f n’est pas

Page 79 : 4.2. DÉRIVÉE PARTIELLE79continue en 0.Les dérivées sont déﬁnies :fx0,0= limt→0ft, 0 f0, 0t= 0fy0,0= limt→0f0, t f0, 0t= 0Donc les dérivées partielles existent alors que la fonction n’est pas continue,cela vient du fait que la dérivée n’est déﬁnie que dans les directions x et yalors qu’il y a une inﬁnité de façons de s’approcher du point 0, 0.Propriété 1 :Soit U un ouvert de Rp. Soit f une application de U →Rn. f admetune dérivée première par rapport à la jème variable j J1; pK si, etseulement si, pour i J1; nK,fixja est déﬁnie. Dans ce cas, on afxja= f1xja; f2xja; ... ; fnxja!Démonstation :Soit f une application de U Rp dans Rn. Alors en toute généralité cetteapplication peut s’écriref:U Rp→Rnx1, ..., xp7→fx1, ..., xp =f1x1, ..., xp ; ... ; fnx1, ..., xpoù les fi, pour i J1; pK, sont les applications composantes qui vont de Rpdans R.Alors, étudions la dérivée par rapport à xj variable portée par le vecteur

Page 80 : 80CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREcanonique ej. On doit donc calculer la dérivée au point a Ufxja= limt→0fa + tej fat= limt→0 f1a + tej f1at; ... ; fna + tej fnat!Or comme nous l’avons vu au chapitre précédent Propriété 5 du chapitre"Limite et Applications Continues", on afxja= limt→0fa + tej fat= limt→0f1a + tej f1at; ... ; limt→0fna + tej fnat!= f1xja; f2xja; ... ; fnxja!4.3Fonctions diﬀérentiables sur un ouvert4.3.1GénéralitésDéﬁnition 2 : Fonction diﬀérentiableSoit U un ouvert de Rp, ·p. Soit a U. Soit f une application deU dans F, ·F . Soit U0 l’ensemble déﬁnie parU0 = h Rp / a + h UOn dit que f est diﬀérentiable en a si, et seulement si, il existe uneapplication linéaire l de Rp dans F et une application ϵ de U0 dans Ftelles que :1.limh→0Rp ϵh = 0F2. h U0, fa + h = fa + lh + hp ϵhLe second point est le développement limité à l’ordre 1 de f en a. On ditque f est diﬀérentiable sur U si, et seulement si, f est diﬀérentiable en toutpoint de U.

Page 81 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT81Théorème 1 : diﬀérentielleSoit U un ouvert de E = Rp, ·E. Soit a U. Soit f une applica-tion de U dans F, ·F . Si f est diﬀérentiable en a alors l’application l estunique. Cette application est appelé diﬀérentielle de f en a et est notée Daf.Démonstration :On rappelle que U est un ouvert de Rp et F un EVN. Soit f une applicationde U dans F. Soit U0 = h Rp / a + h U où a Rp.Postulons que f possède 2 diﬀérentielles l1 et l2 en a. On a donch U0, fa + h = fa + l1 + hE ϵ1haveclimh→0E ϵ1h = 0Feth U0, fa + h = fa + l2 + hE ϵ1haveclimh→0E ϵ2h = 0Falors h U0, on a0F = l1h l2h + hEϵ1h ϵ2het enﬁn dernier rappel, comme U est un ouvert, r 0 / Ba, r U.Etape 1 : Etude de l1h l2h dans la boule ouverte B0E, r.→Si h0 B0E, r alors x0 = a + h0 Ba, r U et h0 U0.démo :h0 B0E, r ⇐⇒h0E ralorsx0 aE r =⇒h0E rsi x0 = a + h0orBa, r Udoncx0 Ba, r Uet ﬁnalement puisque x0 = a + h0 U alors h0 U0.

Page 82 : 82CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRE→Montrons que pour t 0, 1, th0 U0 :démo :On a h0E r. Donc pour t 0, 1a + th0 aE = th0E = t h0E rDonc a + th0 Ba, r U donc a + th0 U donc th0 U0.→Donc pour t 0, 1 :0F = l1th0 l2th0 + th0pϵ1th0 ϵ2th0Par linéarité de l1 et l2, on a0F = tl1h0 l2h0+ t h0Eϵ1th0 ϵ2th0Pour t ̸= 0, on peut simpliﬁer par t0F = l1h0 l2h0 + h0Eϵ1th0 ϵ2th0orlimt→0 th0 = 0E =⇒limt→0 ϵ1th0 = limt→0 ϵ2th0 = 0FDonc pour h0 B0E, r, on a0F = l1h0 l2h0Donc sur B0E, r, les fonctions l1 et l2 sont identiques.Etape 2 : Généralisation du résultat sur E = Rp.Soit h E.→Si h = 0E alors h B0E, r donc l1 = l2 compte tenu de l’étape 1.→Si h ̸= 0E. On pose˜h = r2hhEd’où l’on déduit que˜hE = r2 rh = 2 hEr˜h

Page 83 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT83On voit donc que ˜h B0E, r.l1˜h = l2˜h ⇐⇒l1 r2hhE!= l2 r2hhE!Par linéarité de l1 et l2, on obtient alorsl1h = l2hPropriété 2 :Toute application linéaire φ de Rp dans un EVN quelconque Festdiﬀérentiable et pour a Rp, Daφ = φDémonstration :φ est linéaire. Donc, a, h Rp, on aφa + h = φa + φh + 0Fon a donc juste à poser que Daφ = φ et ϵh = 0F .Propriété 3 :Soit U un ouvert de Rp. Soit a U et f une application de U →F.Si f est diﬀérentiable en a, alors, ses dérivées partielles premières parrapport à toutes ses variables sont déﬁnies en a et sa diﬀérentielle en cepoint est donnée parDaf:Rp→Fh = h1, ..., hp7→Dafh = Ppi=1 hifxjaDémonstration :f est diﬀérentiable par hypothèse. Etudions tout d’abord les dérivéesj J1; pK :fxja= limt→0fa + tej fat

Page 84 : 84CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREOr f est diﬀérentiable. Il existe donc une diﬀérentielle Daf telle quefa + tej = fa + Daftej + tejϵtejDoncfxja= limt→0Daftej + tejϵtejt= limt→0Dafej + ejϵtejdoncfxja= DafejPrenons donch = h1, h2, ..., hp =pXi=1hieiAlors par linéarité de Daf on aDafh = DafpXi=1hiei =pXi=1hiDafeiDafh =pXi=1hifxja

Page 85 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT85Remarque :l’expression Dafh=Ppi=1 hifxja doit normalement vous rappelerquelque chose... de la physique... plus précisément de la thermodynamique.Soit U l’énergie interne d’un système. U dépend de la température et duvolume par exemple =⇒UT, V . La diﬀérentielle de U au pointT0, V0 estalors donnée pardUT0, V0 = UTT0,V0dT + UVT0,V0dV4.1L’expression précédente est strictement identique à l’expression Dafh =Ppi=1 hifxja. Pour voir cela, il suﬃt de poser les notations suivantesU→fT, V →x1, x2T0, V0→adU→DafdT, dV →h = h1, h2En TD, nous utiliserons la physique et plus particulièrement le calcul d’in-certitude aﬁn d’obtenir une vision intuitive de ce qu’est une diﬀérentielle.Nous montrerons ainsi que la diﬀerentielle Dafh correspond à la variationde la fonction f au point a lorsque l’on se déplace du vecteur h à partir dupoint a ceci est d’autant plus juste que h tend vers 0E. Ceci est d’ailleurscomplètement contenu dans l’expression utilisée dans la déﬁnition d’une dif-férentielle déﬁnition 2h U0, fa + h = fa + Dafh + hE ϵhavec limh→0 ϵh = 0FDans le cas de l’expression 4.1, l’interprétation se formule de la façonsuivante : il s’agit de la variation d’énergie interne U lorsque la températurepasse de T0 à T0 + dT et le volume passe de V0 à V0 + dV et ceci estd’autant plus juste que dT et dV sont proches de 0.

Page 86 : 86CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREPropriété 4 :Soit U un ouvert de Rp. Soit a U. Soit F, ·F un EVN. Soit fune application de U →F. Alors si f est diﬀérentiable en a, alors f estcontinue en a.Démonstation :On rappelle que f diﬀérentiable en a signiﬁe queh = h1, ..., hp U0 avec U0 = h Rp / a + h Uon afa + h = fa +pXj=1hjfxja+ hE ϵhEn prenant la norme de l’expression précédente, on obtientfa + h faF =pXj=1hjfxja+ hE ϵhFpXj=1hjfxjaF+ hE ϵhFpXj=1hjfxja + hE ϵhFOr les termes de droite tendent vers 0 lorsque h tend vers 0E puisque ϵhtend vers 0F et que les termesfxja sont bien déﬁnies car f est diﬀérentiable.Donc ﬁnalementlimh→0E fa + h = face qui montre puisque h est quelconque dans la limite précédente que f estcontinue en a.

Page 87 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT87On peut maintenant se demander comment savoir si une application estdiﬀérentiable c’est-à-dire si elle admet une diﬀérentielle dont l’expressionest donnée dans la propriété précédente ? Nous allons répondre ici à cettequestion dans le cas particulier d’une application de R2 dans un EVN quel-conque.Théorème 2 : Diﬀérentiabilité sur R2Soit U un ouvert de R2. Soit x, y U. Soit F, ·F un EVN. Etenﬁn, soit f une application de U dans F. Alors f est diﬀérentiable enx, y, si, et seulement silimh1,h2→0,01h1, h2 fx+h1, y+h2fx, yh1fxx,yh2fyx,y!= 0FOù la norme utilisée n’a pas d’inﬂuence sur le résultat ﬁnal.Démonstration :— Commençons par montrer que si f diﬀérentiable alors elle vériﬁe l’ex-pression précédente :Si f est diﬀérentiable au point x, y alors il existe Dx,yfh1, h2donnée parDx,yfh1, h2 = h1fxx,y+ h2fyx,ytelle quefx+h1, y+h2 = fx, y+h1fxx,y+h2fyx,y+h1, h2ϵh1, h2aveclimh1,h2→0,0 ϵh1, h2 = 0F . Donclimh1,h2→0,01h1, h2 fx + h1, y + h2fx, y h1fxx,yh2fyx,y!=limh1,h2→0,0 ϵh1, h2 = 0F

Page 88 : 88CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRE— Montrons maintenant que si f vériﬁe l’expression précédente alors fest diﬀérentiable :Par hypothèse, on a donclimh1,h2→0,01h1, h2 fx+h1, y+h2fx, yh1fxx,yh2fyx,y!= 0Fposons doncϵh1, h2 =1h1, h2 fx+h1, y+h2fx, yh1fxx,yh2fyx,y!4.2qui a bien la propriété quelimh1,h2→0,0 ϵh1, h2 = 0FEt il ne reste plus qu’à réarranger les termes dans l’expression 4.2fx+h1, y+h2= fx, y+h1fxx,y+h2fyx,y+h1, h2ϵh1, h2qui est bien la déﬁnition d’une diﬀérentielle.4.3.2Fonction de classe C1Déninition 3 : Fonction de classe C1Soit U un ouvert de Rp. Soit F, ·F un EVN. Soit f une applica-tion de U dans F. Alors f est dite de classe C1 sur U si, et seulementsi, toutes les fonctions dérivées partielles premières de f sont déﬁnies etcontinues en tout point a U. On note C1U, F l’ensemble des applicationsde U dans F de classe C1 sur U.

Page 89 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT89Commençons par donner un exemple de fonction qui est de classe C1.Propriété 5 :Toute application φ linéaire de Rp dans F est de classe C1 sur Rp.Démonstration :Soit ei la base canonique de Rp. Alors, si a Rp :φxia= limt→0φa + tei φt= limt→0 φa + tei at= φeiDonc pour tout i J1, pK, les dérivées partielles sont déﬁnies.De plus, la fonctionφxi:Rp→Fa7→φxia = φeiest clairement continue et même constante sur Rp.Donc φ est de classe C1 sur Rp.L’intérêt d’introduire cette notion provient du théorème suivant :Théorème 3 :Soit U un ouvert de E=Rp. Soit F, ·F un EVN. Soit f uneapplication de U dans F. Si f est de classe C1 sur U, alors1. f est diﬀérentiable sur U.2. f est continue sur U.Démonstration :1. Admis2. Si f est C1 alors f est diﬀérentiable sur U. Comme f est diﬀérentiablesur U alors f est continue sur U propriété 4.

Page 90 : 90CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRELe lien entre diﬀérentiabilité, classe C1, continuité de f et existence des dé-rivées premières de f peut être résumé par le schéma suivantAttention :1. si f est C1 en a, alors par déﬁnition de ce qu’est la classe C1 lesdérivées premières, en a, sont déﬁnies et continues.2. si f n’est que diﬀérentiable en a alors les dérivées premières sontdéﬁnies mais pas continuesIllustration :Soit la fonctionf:U R2→Rx, y7→fx, y =x2 + y2 sin1x2+y2si x, y ̸= 0, 00si x, y = 0, 0→f1 est continue sur R2.En eﬀet, si x, y = 0, 0 alorsfx, y =x2 + y2 sin 1px2 + y2! x2 + y2 →0donclimx,y→0,0 fx, y = 0→Etudions maintenant la diﬀérentiabilité :Une fonction de R2 →R est diﬀérentiable, en x, y, si, et seulement si :

Page 91 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT91limh1,h2→0,01h1, h2 fx+h1, y+h2fx, yh1fxx,yh2fyx,y!= 0FVériﬁons que cette fonction est diﬀérentiable en 0, 0. Pour cela calculonstout d’abord les dérivées partiellesfx0,0= limt→0ft, 0 f0, 0t= limt→01tt2 sin 1t 0= limt→0 t sin 1t = 0 = fy0,0Alorslimh1,h2→0,01ph21 + h22 h21 + h22 sin1ph21 + h22!=qh21 + h22 sin1ph21 + h22qui tend vers 0. Donc f est diﬀérentiable en 0, 0.→Mais les dérivées ne sont pas continue en 0, 0 :Pour cela calculons la dérivée par rapport à x en x, y quelconquefxx,y= 2x sin 1px2 + y2!xx2 + y23/2 cos 1px2 + y2!Donc la dérivée première par rapport à x est donnéefxx,y=2x sin1x2+y2xx2+y23/2 cos1x2+y2si x, y ̸= 0, 00si x, y = 0, 0Or, en prenant un = 1/n, 0, alorsfxun= 2n sinn 1nn23/2 cosn= sin nnn2 cosnqui ne converge pas et donc qui ne converge pas vers 0. Donc la fonctionn’est pas C1. De plus, on peut voir, sur cet exemple, que f est continue en

Page 92 : 92CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRE0, 0, les dérivées partielles premières en 0, 0 existent mais elles ne sontpas continues.Dans la suite, la structure algébrique des fonctions C1 va nous être très utilepour l’étude des C1-diﬀéomorphisme changement de variables et la résolu-tion des équations aux dérivées partielles. Nous allons donc la préciser ici :Théorème 4 :Soit U un ouvert de Rp. Soit F un EVN quelconque. L’ensemble C1U, Fest un sous espace vectoriel des fonctions continues de U dans F, c’est-à-direde CU, F.Démonstration :1. La fonction nulle est le 0 de l’espace vectoriel CU, F. Or la fonctionnulle a pour dérivées partielles la fonction nulle. Donc la fonctionnulle a ses dérivées partielles continues. Finallement la fonction nulleapprtient à C1U, F.2. De plus pour λ R, f, g C1U, F, f +λg est également de classeC1 sur U car la somme de fonctions continues et continues et de mêmepour la dérivée laissé en exercice. Donc f + λg C1U, FThéorème 5 :Soit Uun ouvert de Rp. Soit Fun EVN quelconque. Alors, pourf, g C1U, F, f × g C1U, F.Démonstration : exercice.

Page 93 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT93Théorème 6 :Soit U un ouvert de Rp et f une application de classe C1 de U dansRq. Soit V un ouvert de Rq et g une application de classe C1 de V dans Rn.Si fU V , alors g ◦f est de classe C1 sur U.Démonstration : Admis.4.3.3Composition et changement de variablesNous allons maintenant introduire deux propriétés qui nous seront capitalesaﬁn de résoudre les équations aux dérivées partielles.Propriété 6 :Soit f:Rn →R une fonction de classe C1 sur un ouvert U. Soientu1, u2, ..., un, n fonctions de classe C1 sur un intervalle I R telles quepour t I,u1t ; u2t ; ...; untU.Alors la fonctiong:I→Rt7→gt = fu1t ; u2t ; ...; untest de classe C1 sur I et de plus, t Ig′t = u′1t fx1u1t,...,unt+ ... + u′nt fxnu1t,...,untRemarque :La formule précédente est l’analogue de la formule g ◦f′ = g′ ◦f × f′.Démonstration :Nous allons faire la démonstration pour une application f de R2 dans R.

Page 94 : 94CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREAinsi, nous pouvons écrire les développements limités à l’ordre 1 des fonc-tions f, u1 et u2 en un point quelconque t0 et x0, y0u1t0 + h = u1t0 + hu′1t0 + hϵ1hu2t0 + h = u2t0 + hu′2t0 + hϵ1hfx0 + h1, y0 + h2 = fx0, y0 + h1fxx0,y0+ h2fyx0,y0+ h1, h2ϵ3h1, h2De plusu′1t0 h + hϵ1h ; u′2t0 h + hϵ2h = hu′1t0 + ϵ1h ; u′2t0 + ϵ2hdonc lorsque t tend vers 0, la norme précédente tend également vers 0. Onpeut donc poserh1 = u′1t0h + hϵ1hh2 = u′2t0h + hϵ2hpuisque h1, h2doit tendre vers 0. On peut maintenant écriregt0 + h = fu1t0 + h ; u2t0 + h= fu1t0 + u′1t0h + hϵ1h ; u2t0 + u′2t0h + hϵ2hBig= fu1t0 + h1 ; u2t0 + h2On peut maintenant utiliser le développement à l’ordre 1 de la fonction f :gt0 + h = fu1t0, v1t0+ h1fxu1t0,u2t0+ h2fyu1t0,u2t0+ h1, h2ϵ3h1, h2Ce qui conduit àgt0 + h = gt0 + h u′1t0 fxu1t0,u2t0+ u′2t0 fyu1t0,u2t0!+ h ϵ1h fxu1t0,u2t0+ ϵ2h fyu1t0,u2t0!+ h h1, h2ϵ3h1, h2Posons maintenantϵh = ϵ1h fxu1t0,u2t0+ ϵ2h fyu1t0,u2t0+ h h1, h2ϵ3h1, h2

Page 95 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT95qui tend bien vers 0 quand h tend vers 0. Finalementgt0+h = gt0+h u′1t0 fxu1t0,u2t0+ u′2t0 fyu1t0,u2t0!+hϵhOn peut donc conclure, puisque le deuxième terme du développement limitéd’ordre 1 est la dérivée g′t0g′t0 = u′1t0 fxu1t0,u2t0+ u′2t0 fyu1t0,u2t0Propriété 7 :Soient U et V deux ouverts de R2. Soit f une application de U dansR. Soient g1 et g2 deux applications de V dans R. f, g1 et g2 sont C1 sur leurdomaine de déﬁnition respectif. Pour u, v V ,g1u, v, g2u, vU.Alors la fonctionh:V→Ru, v7→hu, v = fg1u, v ; g2u, vest de classe C1 sur V et de plus, u, v Vhuu,v = fxg1u,v,g2u,vg1uu,v + fyg1u,v,g2u,vg2uu,vhvu,v = fxg1u,v,g2u,vg1vu,v + fyg1u,v,g2u,vg2vu,vDémonstration :Nous n’allons montrer ici que la première égalité, la seconde se démontrantstrictement de la même façon. Pour la première égalité, on cherche à exprimerhuu,ven fonction des dérivées de g1 et g2. Or, prendre la dérivée partielle de h parrapport à u revient à étudier la variation de h en fonction de u lorsque v est

Page 96 : 96CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREﬁxé. Introduisons donc les fonctionsgv1u = g1u, vgv2u = g2u, vEtudions maintenant la fonction H déﬁnie par Hu = hu, v = fgv1u ; gv2u.La fonction H est C1 pour tout u puisque f, g1 et g2 sont C1. De plus, d’aprèsla propriété 6H′u = fxgv1u,gv2ugv1′u + fygv1u,gv2ugv2′uorgv1′u = g1uu,vgv2′u = g2uu,vet ﬁnalementhuu,v= fxg1u,v,g2u,vg1uu,v+ fyg1u,v,g2u,vg2uu,vRemarque :Posons, dans la propriété 7, gu, v =g1u, v, g2u, vqui est une fonctionC1 sur V . Alors : hu, v = f ◦gu, v où f est la fonction : x, y 7→fx, y.On voit donc que la propriété 7 permet en fait de calculer les dérivées par-tielles de h par rapport à u ou v qui sont les variables naturelles de hconnaissant les dérivées partielles de f par rapport à x et y qui sont lesvariables naturelles de f. Nous verrons que cela nous sera particulièrementutile pour résoudre des équations aux dérivées partielles par changement devariables qui est la seule méthode que nous verrons cette année pour lesrésoudre. Pour illustrer ce qui vient d’être dit, considérons par exemple lafonction f déﬁnie sur R2 parf:R2→Rx, y7→fx, y = 2x2y + y2 + xEt, proposons d’introduire les fonctions suivantes qui jouent le rôle de g1 etg2xu, v = u + vyu, v = u v

Page 97 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT97On peut alors introduire la fonction h déﬁnie par hu, v = fxu, v, yu, vet calculer les dérivées de cette fonction h par rapport à u et v en utilisantles dérivées de f par rapport à x.huu,v = fxx,yxuu,v + fyx,yyuu,vhvu,v = fxx,yxvu,v + fyx,yyvu,vce qui donne, en faisant le calcul explicitement huu,v = 4xy + 1 × 1 + 2x2 + 2y × 1hvu,v = 4xy + 1 × 1 + 2x2 + 2y × 1or x = u + v et y = u v, donc huu,v = 6u2 2v2 + 2u 2v + 4uv + 1hvu,v = 2u2 6v2 + 1 2u + 2v 4uv4.3On peut vériﬁer le résultat précédent, en faisant le calcul explicite de lafonction hu, v, ainsi en utilisant que hu, v = fxu, v, yu, vavecxu, v = u + v et yu, v = u v, on obtienthu, v = 2u + v2u v + u v2 + u + v= 2u3 2v3 + 2u2v 2v2u + u2 + v2 2uv + u + vpuis en calculant explicitement huu,v et hvu,v on réobtient bien les expres-sions 4.3.4.3.4Matrice de Jacobi, gradient et inégalité des accroisse-ments ﬁnisNous allons ici introduire la notion de matrice de Jacobi, nous verrons quedans les changements de variables, elle joue un rôle primordial suite de cecours et "cours d’intégration & probabilité" du second semestre. La matricede Jacobi nous permettra ensuite d’introduire un opérateur que vous avezdéjà rencontré en physique : le gradient. Enﬁn, nous relirons le gradient àl’inégalité des accroissements ﬁnis.

Page 98 : 98CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREDéﬁnition 4 : Matrice de JacobiSoit U un ouvert de Rp, a U et f une application, diﬀérentiable ena, de U dans Rn. On déﬁnit la matrice de Jacobi ou matrice jacobiennede f en a, notée Jfa, la matrice à n lignes et p colonnes de Dfarelativement aux bases canoniques de Rn et Rp, c’est-à-dire la matriceJfa = fixja=f1x1a...f1xpa...fnx1a...fnxpaSi n = p, on appelle jacobien de f en a, le déterminant de la matrice Jfade f en a.Introduisons maintenant le gradient :Déﬁnition 5 : GradientSoit U un ouvert de Rp, a U et f une application, diﬀérentiable ena, de U dans R. On déﬁnit alors le gradient de f en a, noté⃗gradfa ou⃗af, par⃗af =tJfa =fx1a.fxpaPropriété 8 : gradient et diﬀérentielleSoit U un ouvert de Rp et f une application, diﬀérentiable en a U,de U dans R. Alorsa, h U2, Dafh = ⃗af · hoù ⃗af · h est le produit scalaire entre les deux vecteurs.Démonstration :

Page 99 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT99⃗af · h = fx1a; ... ;fxpa· h1 ; ... ; hp =pXi=1hifxiaPropriété 9 : interprétation du gradientLe gradient d’une fonction f, de Rn dans R, est un vecteur perpendi-culaire aux directions où f est constante et pointant dans la direction où lavariation de f est maximale de plus grande pente. La norme du gradientest d’autant plus grande qu’au point où il est calculé, la variation de f estgrande.Démonstration :Soit f une application de U dans R où U est un ouvert de Rn. Soit a unpoint de Rn.1. Considérons le point pt = a + tv où t R et v Rn telle quept U et v · ⃗af = 0 le vecteur v est donc orthogonal au vecteurgradient de f en a. Alors d’après la propriété 6ddtfptt=0= ⃗af · p′t = 0 = ⃗af · v = 0On voit donc que si l’on se déplace orthogonalement à ⃗af alors fest constante. La réciproque se démontre par le même raisonnement.2. Considérons maintenant le point pt = a + t⃗fa où t R. Alorsd’après la propriété 6ddtfptt=0= ⃗af · p′t = 0 = ⃗af · ⃗af =⃗af2 0On voit donc que plus la norme du gradient de f en a est grande etplus la variation de f est grande.3. Considérons le point pt = a + tv où t R et v Rn telle quev= 1. Alors d’après la propriété 6ddtfptt=0= ⃗af · v

Page 100 : 100CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREce produit scalaire est maximum si, et seulement si v est colinéaire etdans le même sens que ⃗af. Donc ⃗af indique la direction de plusgrande penteNous allons maintenant généralisé le théorème des accroissements ﬁnis quevous avez étudié dans le case des fonctions de R dans R.Théorème 7 : inégalité des accroissements ﬁnisSoit U un ouvert de Rp et f une application de U dans R de classe C1 sur U.Soit a et b deux points de U tels que a, b = 1 λa + λb/λ 0, 1 U.Si il existe un réel M tel quex a, b,⃗xf1 =pXj=1fxjx Malorsfb fa M b a1Démonstration : remise à plus tard.Déﬁnition 6 : Partie convexeSoit E un espace vectoriel quelconque. Une partie C de E est diteconvexe si, et seulement six, y C2, λ 0, 1, 1 λx + λy CCela signiﬁe qu’un ensemble C est convexe si, et seulement si, tout segmentjoignant toute paire de points de C est contenu dans C. Pour illustrer cela,nous avons représenté dans la ﬁgure suivante une ellipse qui est un espaceconvexe de R2 et une cacahuète qui n’est clairement pas convexe puisqu’ilexiste au moins deux points représentés sur la ﬁgure tels que le segmentde droite n’appartienne pas entièrement à l’espace le segment extérieur àl’espace est représenté en rouge.

Page 101 : 4.3. FONCTIONS DIFFÉRENTIABLES SUR UN OUVERT101Propriété 10 :Soit U un ouvert convexe de Rp et f une application de U dans Rde classe C1 sur U. Si il existe un réel M tel que pour tout point a U on a⃗xf1 =pXj=1fxjx Malors f est M-lipschitzienne sur U.Démonstration :Il suﬃt d’appliquer le théorème des accroissements ﬁnis à toutes les pairesde points de U. On a donca, b U, fb fa M b a1ce qui est la déﬁnition d’une application M-lipschitzienne.Propriété 11 : fonction constanteSoit U un ouvert convexe de Rp et f une application de U dans Rde classe C1 sur U. Alors f est constante sur U si, et seulement si, ⃗af estnul pour tout a U, c’est-à-direj J1, pK, a U, fxja= 0alors f est M-lipschitzienne sur U.

Page 102 : 102CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREDémonstration :f constante ⇐⇒f 0-lipschitzienne4.4EDP du 1er ordre et C1-diﬀéomorphisme4.4.1GénéralitésUne équation aux dérivées partielles est une généralisation des équations dif-férentielles. En eﬀet :une equation diﬀérentiellel’inconnue d’une équation diﬀest une équation liant une→est une fonction ne dépendantfonction à ses dérivéesque d’une unique variable.alors que :une equation aux dérivées partiellesl’inconnue d’une équation auxest une équation liant une fonction→dérivées partielles est uneà ses dérivées partiellesfonction de plusieurs variable.On considérera dans la suite de cette section des équations aux dérivéespartielles de la formeFfx, fy , f, x, y= 0où la fonction f inconnue est une fonction de R2 dans R. Ce type d’équationaux dérivées partielles est appelé équations aux dérivées partielles du 1erordre car, elle fait intervenir au plus des dérivées partielles d’ordre 1.Considérons tout d’abord la plus simple des EDPs du 1er ordre

Page 103 : 4.4. EDP DU 1ER ORDRE ET C1-DIFFÉOMORPHISME103Théorème 8 :Soit g: R2 →R une application continue sur un ouvert U R2.Les solutions de classe C1 sur U de l’EDPfxx,y= gx, y4.4sont de la formefx, y = Ky +Zgx, ydxoùRgx, ydx est une primitive quelconque de g par rapport à la variablex. K est une fonction quelconque de R dans R de classe C1 sur un ouvert deR correspondant à la projection de U sur l’axe Oy.Démonstration : trivialMalheureusement, la vie physique, ﬁnance, biologie, climatologie,... n’estpas aussi simple que l’EDP précédente. Dans la suite, on cherchera des so-lutions à des EDP du 1er ordre un peu plus complexe. Pour cela, on seraamené à eﬀectuer des changements de variables aﬁn de ramener l’EDP étu-diée à une EDP de la forme 4.4. Nous allons donc commencer par déﬁnirles conditions sous-lesquelles une application peut être considérée comme unchangement de variables.4.4.2C1-diﬀéomorphisme et changement de variablesDéﬁnition 7 : C1-diﬀéomorphismeSoient U un ouvert de Rp et Vun ouvert de Rn. Une application φde U dans V est un C1-diﬀéomorphisme de U dans V , si, et seulement si,les propriétés suivantes sont vériﬁées1. φ est de classe C1 sur U.2. φ réalise une bijection de U dans V .3. φ1 est de classe C1 sur V .Quel est l’intérêt d’introduire le concept de C1-diﬀéomorphisme ?

Page 104 : 104CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREPour la résolution des EDPs du 1er ordre, les changements de variablesdoivent être des C1-diﬀéomorphismes. En eﬀet, pour s’en persuader, consi-dérons une EDP portant sur la fonction inconnue f. Soit φ une fonctionpermettant un changement de variables directe 1, pour un changement devariables indirect le raisonnement est strictement identique. Ainsi f devienth = f ◦φ. Alors1. Si φ est C1 alors h est C1 par composition de fonctions C1 et h peutdonc être solution d’une EDP du 1er ordre.2. Si φ est une bijection, cela permet de passer des nouvelles variablesaux anciennes et inversement ce qui est nécessaire pour pouvoir eﬀec-tuer légalement le changement de variables.3. Si φ1 est C1 alors f = h ◦φ1 et f est bien C1.Il existe un cas très simple pour lequel on est en mesure de dire immé-diatement qu’il s’agit bien d’un C1-diﬀéomorphisme :Propriété 12 :Si φ est une application linéaire bijective de Rp dans Rn, alors p = net φ est un C1-diﬀéomorphisme.Démonstration :Une application linéaire est une bijection si et seulement si n = p voir votrecours de préING 1 d’algèbre linéaire. De plus, comme φ est linéaire, on saitqu’il s’agit d’une application C1. Or φ1 est aussi une application linéaireet donc est C1. Finalement l’application linéaire est un C1-diﬀéomorphisme.1. Nous déﬁnirons par la suite ce que l’on entend par changement de variables directou indirect

Page 105 : 4.4. EDP DU 1ER ORDRE ET C1-DIFFÉOMORPHISME105Propriété 13 : caractérisation rapide d’un C1-diﬀéomorphismeSoit U un ouvert de Rp et V un ouvert de Rn. Si l’application φ deU dans V vériﬁe les 3 prorpiétés suivantes1. φ est de classe C1 sur U2. φ réalise une bijection de U dans V3. pour tout point a de U, Daφ est une application linéaire bijective deRp dans Rn.alors p = n et φ est un C1-diﬀéomorphisme de U sur V .Démonstration : Admis.Propriété 14 :Soient U un ouvert de Rp et a U. Soit φ une application de Udans Rn. Si le jacobien associé à l’application φ, en a, est non nul alors Daφest une application linéaire bijective en a.Démonstration :Soient U et V deux ouverts de Rp et Rq. Soit φ une application de U dansV . Soit ψ une application de V dans Rn. Soient a U et b = φa V .Alors1. Daφh1 = Jφah1 et Dbψh2 = Jψbh2 où h1 est un vecteur de Rpet h2 un vecteur de Rq.2. Daψ ◦φ = Dφaψ ◦Daφ et donc Jψ◦φa = JψφaJφaDonc, si detJφa ̸= 0 cela signiﬁe que la matrice Jφa est inversible. Orjustement si on considère que ψ = φ1 alors Jφ1◦φa = Id = Jφ1φaJφaet donc Dφa est inversible et l’inverse est donné par l’inverse de la matriceJφa.Exemple :Soit U et V les deux ensembles déﬁnis parU = R+×0, 2π×0, πV = R3\R+ × 0 × R

Page 106 : 106CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDREet l’applicationf:U→Vρ, θ, φ7→fρ, θ, φ = ρ sin θ sin φ, ρ sin θ sin φ, ρ cos φ= f1, f2, f3alors f est bien un C1-diﬀéomorphisme. En eﬀet1. f est C1 sur U car toutes les applications composantes le sont.2. f est une bijection de U dans V puisque3. montrons maintenant que Daf pour tout a U est bijective. Pourcela déterminons le jacobienJfa =f1ρaf1θaf1φaf2ρaf2θaf2φaf3ρaf3θaf3φa=cos θ sin φρ sin θ sin φρ cos θ cos φsin θ sin φρ cos θ sin φρ sin θ cos φcos φ0ρ sin φet donc Jfa = ρ2 sin φ ̸= 0 pour tout a U.

Page 107 : 4.4. EDP DU 1ER ORDRE ET C1-DIFFÉOMORPHISME1074.4.3Résolution des EDPs par changement de variablesLe tableau suivant résume intégralement la démarche que nous utiliseronspour résoudre les EDPs du 1er ordre où la fonction inconnue f va de R2 dansR.On a séparé en deux types de changement de variables : les changements devariables directs et indirects mais nous verrons qu’il n’est pas nécessaire defaire cette distinction.Exemple : Aﬁn d’illustrer la méthode de résolution des EDPs, cherchonsla solution sur R2 de l’équation :2 fxx,yfyx,y= x2y4.5en utilisant le changement de variablesu, v = x, x + 2y

Page 108 : 108CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRECommençons par identiﬁer la fonction ϕf:R2→R2x, y7→ϕx, y =ux, y, vx, y= x, x + 2yIl faut tout d’abord montrer que ϕ est bien un C1-diﬀéomorphisme. Commeϕ est une application linéaire, il suﬃt de montrer que c’est une bijection deR2 dans R2.u = xv = x + 2y⇐⇒x = uv = u + 2y⇐⇒x = uy = v u/2il s’agit donc bien d’une bijection et ﬁnalement ϕ est bien un C1-diﬀéomorphisme.Utilisons maintenant ϕ aﬁn d’introduire une nouvelle fonction g déﬁnie parfx, y = g ◦ϕx, y = gux, y, vx, y⇐⇒f = g ◦ϕil s’agit donc d’un changement de variable indirect. De plus, on agu, v = f ◦ϕ1x, y ⇐⇒g = f ◦ϕ1Comme f et ϕ sont C1 sur R2 par stabilité de la propriété C1 par composi-tion, g est également C1 sur R2.On peut maintenant, grâce à la propriété 7, exprimer les dérivées partiellesde f en fonction de celle de gfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donnefxx,y = guu,v + gvu,vfyx,y = 2 gvu,vOn injecte maintenant ces expressions dans l’EDP que l’on cherche à résoudre2 guu,v= x2y = u2 × v u2

Page 109 : 4.4. EDP DU 1ER ORDRE ET C1-DIFFÉOMORPHISME109On doit donc résoudre l’EDPguu,v= 14u2v u3On peut facilement résoudre cette EDP en utilisant le théorème 8gu, v = u3v12 u416 + Kvoù K est une fonction quelconque, C1 sur R.Or f = g ◦ϕ, doncfx, y = gx, x + 2y = x3x + 2y12x416 + Kx + 2yqui est donc solution de l’EDP 4.5.

Page 110 : 110CHAPITRE 4. CALCUL DIFFÉRENTIEL DU 1ER ORDRE

Page 111 : Chapitre 5Calcul diﬀérentiel d’ordresupérieur5.1Objectifs du chapitreDans le chapitre précédent, nous avons appris à résoudre les équations auxdérivées partielles du 1er ordre qui font donc intervenir des dérivées par-tielles du 1er ordre. Nous allons, dans ce chapitre, nous intéresser aux EDPsfaisant intervenir des dérivées partielles d’ordres supérieurs.De plus, nous nous intéresserons à la résolution de systèmes d’EDPs du1er ordre dont la résolution nécessite de manipuler des dérivées partiellesd’ordre 2.Et enﬁn, nous développerons une méthode aﬁn d’étudier les extremums defonctions allant de R2 à R.111

Page 112 : 112CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEUR5.2Diﬀérentiation d’ordre supérieur ou égal à 2Déﬁnition 1 : Dérivées partielles d’ordre supérieurSoient U un ouvert de Rp, f une application de U dans Rn et a U. Soientk Net i1, i2, .., ik J1, pKk un k-uplet d’entiers.On dit que f admet une dérivée partielle kème en a par rapport auxvariables numéro i1, ..., ik si, et seulement si— f admet une dérivée k 1ème par rapport aux variables numéroi1, i2, ..., ik1 sur un voisinage de a.— cette dérivée partielle k 1ème admet, elle-même, une dérivée par-tielle première en a par rapport à la variable kème.Dans ce cas, cette dernière dérivée est appelée la dérivée partielle kème en apar rapport aux variables numéro i1, i2, ..., ik. On note cette dérivéekfxik...xi2xi1aNous venons d’introduire de manière très complexe et très formelle la notionde dérivée partielle d’ordre supérieur à 1 comme par exemple2fx2a2fxya3fxyzaExemple : Soit fx, y, z = xy2z3. Alors3fxyzx,y,z=2xyx,y,zfzx,y,z= 23xy2z2xyx,y,z= xx,y,z3xy2z2yx,y,z= 6xyz2xx,y,z= 6yz2Notons que l’on peut montrer que3fxyzx,y,z=3fyxzx,y,z=3fzyxx,y,z= ...ainsi, pour cette fonction, l’ordre dans lequel on eﬀectue les dérivées par-tielles n’a aucune inﬂuence sur le résultat. Nous y reviendrons par la suite.

Page 113 : 5.2. DIFFÉRENTIATION D’ORDRE SUPÉRIEUR OU ÉGAL À 2113Déﬁnition 2 : fonction de classe Ck, CSoit U un ouvert de Rp. Soit f une application de U dans Rn. L’ap-plication f est dite de classe Ck sur U, si, et seulement si, toutes ses dérivéespartielles d’ordre k existent et sont continues sur U. L’application f est ditede classe Csi, et seulement si, pour tout k N, elle est Ck.Propriété 1 :Soit U un ouvert de Rp. Soit f une application de U dans Rn. f estCk sur U. Alors toutes les dérivées partielles d’ordre inférieur ou égal à ksont déﬁnies et continues.Démonstration : Admis.La structure algébrique de l’espace CkU, F espace des fonctions Ck surU Rp est la même que celle de l’espace C1U, F introduit au chapitreprécédent théorème 4, 5 et 6 du chapitre précédent. Nous n’allons rappelerici que la stabilité par compositionThéorème 1 : stabilité de Ck par compositionSoit U un ouvert de Rp et f une application Ck de U dans Rq. SoitV un ouvert de Rq et g une application de classe Ck de V dans Rn. SifU V , alors g ◦f est de classe Ck sur U.Démonstration : Admis.

Page 114 : 114CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEURThéorème 2 :Soit U un ouvert de Rp et f une application Ck de U dans Rn. On aéquivalence entre1. la fonction f est de classe Ck.2. les fonctions coordonnées de f dans la base Rn sont de classe Ck.Démonstration : évident.Théorème 3 : théorème de SchwarzSoit U un ouvert de Rp et f une application C1 de U dans Rq. Soita U et i, j J1, pK2. Si2fxjxi et2fxixj sont déﬁnies et continues en aalors2fxjxia=2fxixjaDémonstration : Admis.Exemple : cas où il n’y a pas égalité.Soit la fonctionfx, y =xyx2y2x2+y2si x, y ̸= 0, 00si x, y = 0, 0Calculons les dérivées partielles du 1er ordre en 0, 0fx0,0 = limt→0ft,0f0,0t= 0fy0,0 = limt→0f0,tf0,0t= 0Calculons maintenant les dérivées partielles du 1er ordre en un point x, y ̸=0, 0fxx,y = y4x2y2+x4y4x2+y22fy0,0 = x4x2y2x4+y4x2+y22

Page 115 : 5.3. SYSTÈMES D’EDPS DU 1ER ORDRE115Les fonctions dérivées partielles premières sont doncfxx,y=y4x2y2+x4y4x2+y22si x, y = 0, 00si x, y ̸= 0, 0fxx,y=x4x2y2x4+y4x2+y22si x, y = 0, 00si x, y ̸= 0, 0Or en passant aux coordonnées polaires, il est facile de montrer que ces deuxapplications sont continues.Etudions maintenant les dérivées secondes croiséesxfyyfxxfy0,0= limt→01t fyt,0fy0,0= limt→0t5t5 = 1yfx0,0= limt→01t fx0,tfx0,0= limt→0 t5t5 = 1on voit donc quexfy0,0̸= yfx0,0ce qui signiﬁe que les dérivées secondes ne sont pas continues.Nous avons ici introduit les déﬁnitions et théorèmes nécessaires à la réso-lution d’EDPs d’ordre supérieur à 1 ou alors de systèmes d’EDPs du 1erordre. Nous allons donc maintenant étudier ces deux problèmes.5.3Systèmes d’EDPs du 1er ordreOn cherche ici à résoudre le système d’équations aux dérivées partiellesfxx,y = gx, yfyx,y = hx, yoù f, g et h sont C1.

Page 116 : 116CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEURPour résoudre ce système, nous utiliserons la démarche suivanteEtape 1 :On vériﬁe quegyx,y= hxx,yEn eﬀet, si g et h sont C1 alors gx, gy, hx et hy sont continues. Donc2fx2 = gx ;2fy2 = hy;2fxy = hxet2fyx = gysont continues. On déduit donc cela que f est C2. Donc f vériﬁe le théorèmede Schwarz2fxy = 2fyxd’où l’on peut écriregy = hxEtape 2 :On résoud l’une des deux équations aux dérivées partielles. Résolvons parexemple la première :fx, y = Gx, y + K1yoù G est une primtive selon x de g et K1 est une fonction quelconque C2.Etape 3 :On dérive maintenant par l’autre variable ici y la solution obtenue à l’étape2. Puis on injecte cette dérivée dans l’équation aux dérivées partielles qui n’apas encore été utilisée.=⇒équation sur K1Etape 4 :On résoud l’équation obtenue à l’étape 3.Etape 5 :On écrit alors la solution obtenue à l’étape 2 et l’étape 4

Page 117 : 5.3. SYSTÈMES D’EDPS DU 1ER ORDRE117Exemple :On cherche à résoudre, sur R2, le système d’équations aux dérivées partiellesfxx,y = x + 1 cosx + y + sinx + y sin x = gx, yfyx,y = x + 1 cosx + y = hx, yEtape 1 :On vériﬁe quegyx,y= hxx,yalorsgy = x + 1 sinx + y + cosx + y = hxdonc, il est possible de trouver des solutions à ce système d’équations.Etape 2 :On intégre par rapport à y la seconde EDP car elle est plus simple à inté-grer. On obtient alorsfx, y = x + 1 sinx + y + K1xoù K1 est une fonction C2 sur R.Etape 3 :On dérive maintenant l’expression précédente par rapport à x l’autre va-riablefxx,y= sinx + y + x + 1 cosx + y + K1xOn injecte cette expression dans l’EDP qui n’a pas encore été utiliséesinx+y+x+1 cosx+y+ K1x = x+1 cosx+y+sinx+ysin xet ﬁnalementK1x = sin x

Page 118 : 118CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEUREtape 4 :On intègre maintenant l’équation précédenteK1x = cosx + Coù C R est une constante d’intégration.Etape 5 :On peut maintenant écrire la solutionfx, y = x + 1 sinx + y + K1x= x + 1 sinx + y + cosx + Cavec C R.5.4EDPs d’ordre 2Nous allons maintenant résoudre des EDPs d’ordre 2. La démarche sera lamême que pour les EDPs d’ordre 1 : il s’agira d’utiliser des changementsde variables pour ramener l’EDP considérée à une EDP dont on connaît lasolution.Théorème 4 :Soit U un ouvert de R2. Les solutions de classe C2 de l’équation 2fx2 = 0sont de la formefx, y = xGy + Hyoù G et H sont des fonctions C2 sur la projection de U sur l’axe Oy.Démonstration : il suﬃt d’intégrer deux fois en utilisant le théorème d’inté-gration des EDP du chapitre précédent.

Page 119 : 5.4. EDPS D’ORDRE 2119Théorème 5 :Soit U un ouvert de R2. Les solutions de classe C2 de l’équation2fxy = 0sont de la formefx, y = Gx + Hyoù G et H sont des fonctions C2 sur la projection de U sur l’axe Ox et 0yrespectivement.Démonstration : tout autant trivial.Comme pour les EDPs d’ordre 1, un changement de variables ne sera li-cite que si il s’agit d’un C2-diﬀéomorphisme :Déﬁnition 3 : C2-diﬀéomorphismeSoient U un ouvert de Rp et Vun ouvert de Rn. Une application φde U dans V est un C2-diﬀéomorphisme de U dans V , si, et seulement si,les propriétés suivantes sont vériﬁées1. φ est de classe C2 sur U.2. φ réalise une bijection de U dans V .3. φ1 est de classe C2 sur V .Exemple de résolution d’une EDP du 2nd ordre :Trouver les applications f de R2 →R de classe C2 sur R2 solutions dex, t R2,2fx2x,t1c22fT 2x,t= 0en utilisant le changement de variable X, Y = x + ct, x ct.Commençons par identiﬁer l’application changement de variables :φ:R2→R2x, t7→X, Y = φx, t = x + ct, x ctCommençons par vériﬁer qu’il s’agit bien d’un C2-diﬀéomorphisme. φ réaliseclairement une bijection de R2 dans R2 car kerφ = 0R2. De plus φ est clai-rement C2 car chaque application composante est C2. Il en va de même de

Page 120 : 120CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEURφ1. Donc φ est un C2-diﬀéomorphisme.On peut alors introduire la fonction g déﬁnie parf = g◦φ ⇐⇒fx, y = g◦φx, y = g◦φx, y = gx+ct, xct = gX, Y Donc g = f ◦φ1. Or la stabilité par composition de la propriété C2, lafonction g est bien C2 puisque φ1 et f le sont.On peut maintenant exprimer les dérivées partielles de f en fonction desdérivées partielles de g.fxx,t =gXX,YXxx,t + gYX,YYxx,tftx,t =gXX,YXtx,t + gYX,YYtx,tce qui donnefxx,y =gXX,Y + gYX,Yftx,y = c gXX,Y c gYX,Yen eﬀectuant le même développement pour les dérivées secondes, on obtient2fx2x,t =2gX2X,Y + 2gY 2X,Y + 22gXYX,Y2ft2x,t = c2 2gX2X,Y + c2 2gY 2X,Y 2c22gXYX,YInjectons maintenant ces dérivées partielles dans l’EDP que l’on cherche àrésoudre, aﬁn d’obtenir2gX2X,Y= 0or cette EDP a pour solutiongX, Y = hY + kXoù h et k sont des fonctions quelconques C2 sur R. Il ne reste plus qu’à serappeler que f = g ◦φ doncfx, t = g ◦φx, t = gx + ct, x ct = hx ct + kx + ct

Page 121 : 5.5. EXTREMUMS DE FONCTIONS À VALEURS DANS R1215.5Extremums de fonctions à valeurs dans R5.5.1Cas des fonctions de R dans RCommençons, avant de discuter de la recherche des extremums des fonctionsde plusieurs variables, par rappeler le cas simple des fonctions d’une seulevariable. Soit f une fonction C2 de A R dans R. Alors on sait qu’unecondition nécessaire pour que le point a ˚A soit un extremum est quef′a = 0 tangente horizontale. Toutefois, ce critère n’est pas suﬃsammentrestrictif. En eﬀet, c’est le signe de la dérivée seconde qui permet de concluresur la nature du point a.Le cas de gauche correspond à un minimum, celui du centre à un maximumet enﬁn celui de droite à un méplat ni un maximum ni un minimum. Dansle dernier cas, la dérivée seconde change de signe au point a.

Page 122 : 122CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEUR5.5.2Cas des fonctions de Rn dans RDéﬁnition 4 : maximum local ou strict, minimum local ou strictSoit A une partie de Rp, a˚A et f une fonction de A dans R. Alors :1. f admet un minimum local en a, si, et seulement si, il existe unvoisinage V A de a tel quex V, fx fa2. f admet un minimum strict en a, si, et seulement si, il existe unvoisinage V A de a tel quex V \a, fx fa3. f admet un maximum local en a, si, et seulement si, il existe unvoisinage V A de a tel quex V, fx fa4. f admet un maximum strict en a, si, et seulement si, il existe unvoisinage V A de a tel quex V \a, fx faOn appelle, de manière générique, les maximums et les minimums des extre-mums.Déﬁnition 5 : extremum globalSoient A une partie de Rp, a ˚A et f une application de A dans R. Alors :1. f admet un minimum global en a, si, et seulement six A, fx fa2. f admet un maximum global en a, si, et seulement six A, fx fa

Page 123 : 5.5. EXTREMUMS DE FONCTIONS À VALEURS DANS R123Déﬁnition 7 : point critiqueSoient U un ouvert de Rp, a U et f une application de U dans R.On dit que a est un point critique de f, si, et seulement si, toutes les déri-vées partielles premières de f en a sont déﬁnies et égales à 0, c’est-à-dire, si,et seulement si, le gradient de f en a est déﬁni et nul :⃗af = 0RpPropriété 2 :Soient U un ouvert de Rp, a U et f une application de U dans R.Si f admet un extremum local en a et que toutes les dérivées partielles def en a sont déﬁnies, alors a est un point critique de f.Démonstration :Nous allons faire la démonstration dans le cas où a est un minimum local.Il existe alors r 0 tel que Ba, r U et pour x Ba, r, fx fa.Soit e1, e2, ..., ep une base de Rp. Soit i J1, pK. Nous avons alorsfxia= limh→0fa + hei fahOr si h r ce qui est le cas à partir d’un moment puisque h tend vers 0,nous avons a + hei Ba, r et donc fa + hei fa 0. D’oùlimh→0+fa + hei fah0limh→0fa + hei fah0d’où une limite nulle. Comme cela est vrai pour tout i J1, pK, ⃗af = 0Rp.Comme dans le cas des fonctions de R dans R, la connaissance des points cri-tiques n’est pas suﬃsante pour connaitre leur nature minimum, maximumou aucun des deux. Et comme dans le cas des fonctions de R dans R, il fautétudier les dérivées du second ordre pour conclure.

Page 124 : 124CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEURPropriété 3 : Développement limité d’ordre 2Soient U un ouvert de Rp, · et f une application de U dans R declasse C2 sur U. Soient a U et U0 = h Rp/a + h U. Alors, il existeune application ϵ : U0 →R telle quelimh→0Rp ϵh = 0 eth = h1, ..., hp U0,fa + h = fa +pXj=1hjfxja+ 12pXi=1pXj=1hihj2fxixja+ h2 ϵhCette relation est appelée développement limité de f à l’ordre 2 en a.Démonstration : admis.Théorème 6 : Condition suﬃsante d’ordre 2Soient U un ouvert de Rp, · et f une application de U dans R declasse C2 sur U. Soit a un point critique de f. On introduit la fonction QQ:Rp→Rh = h1, ..., hp7→Qh = Ppi=1Ppj=1 hihj2fxixjaS’il existe un voisinage de 0Rp sur lequel1. Q est positive et ne s’annule qu’en h = 0, alors f admet un minimumlocal strict en a2. Q est négative et ne s’annule qu’en h = 0, alors f admet un maximumlocal strict en a.Si pour tout voisinage de 0Rp, Q admet des valeurs positives et négatives,alors f n’admet pas d’extremum local en a.Démonstration :Pour h suﬃsamment petit, ⃗a+hf 0Rp puisque a est un point critique.

Page 125 : 5.5. EXTREMUMS DE FONCTIONS À VALEURS DANS R125Doncfa + h fa pXi=1pXj=1hihj2fxixja= QhSi Q est positif alors fa + h fa donc minimum.Si Q est négatif alors fa + h fa donc maximum.Aﬁn de systématiser l’étude précédente, on peut introduire la matrice hes-sienneDéﬁnition 8 : Matrice hessienneSoient U un ouvert de Rp, · et f une application de U dans R declasse C2 sur U. Soit a U un point critique de f. On déﬁnit alors lamatrice hessienne de f en a, notée Hfa, parHfa =2fx21a...2fx1xpa.........2fxpx1a...2fx2paOn introduit alors, pour les fonctions de R2 dans R les notations de MongeDéﬁnition 9 : Notations de MongeSoient U un ouvert de R2 et f une application de U dans R de classe C2sur U. Soit a U un point critique de f. On déﬁnit alors les notations deMonge commer = 2fx2as =2fxya=2fyxat = 2fy2aalors avec ces notationsHfa =rsst

Page 126 : 126CHAPITRE 5. CALCUL DIFFÉRENTIEL D’ORDRE SUPÉRIEURThéorème 7 : Condition suﬃsante d’ordre 2Soient U un ouvert de R2 et f une application de U dans R de classe C2 surU. Soit a un point critique de f. Alors1. Si detHfa= rt s2 0 :a si r 0, alors f admet un minimum local strict en a.b si r 0, alors f admet un maximum local strict en a.2. Si detHfa= rt s2 0, alors f n’a pas d’extremum local en a.Dans ce cas, a est appelé point-col, ou point-selle de f.3. Si detHfa= rt s2 = 0, alors on ne peut pas conclure sans faireune étude locale poussée.Démonstration :distribuée en cours.

Page 127 : 5.5. EXTREMUMS DE FONCTIONS À VALEURS DANS R127Finalement, la détermination des extremas d’une fonction de R2 dans Rs’eﬀectue par la méthode générale et systèmatique suivante :

PREING2 S1, Analyse-dans-RN

PREING2 S1 Analyse-dans-RN 2022/2023 E. Masnada Feuille Cours

Le contenu de cet article est la propriété exclusive de son auteur.

Tags tendance