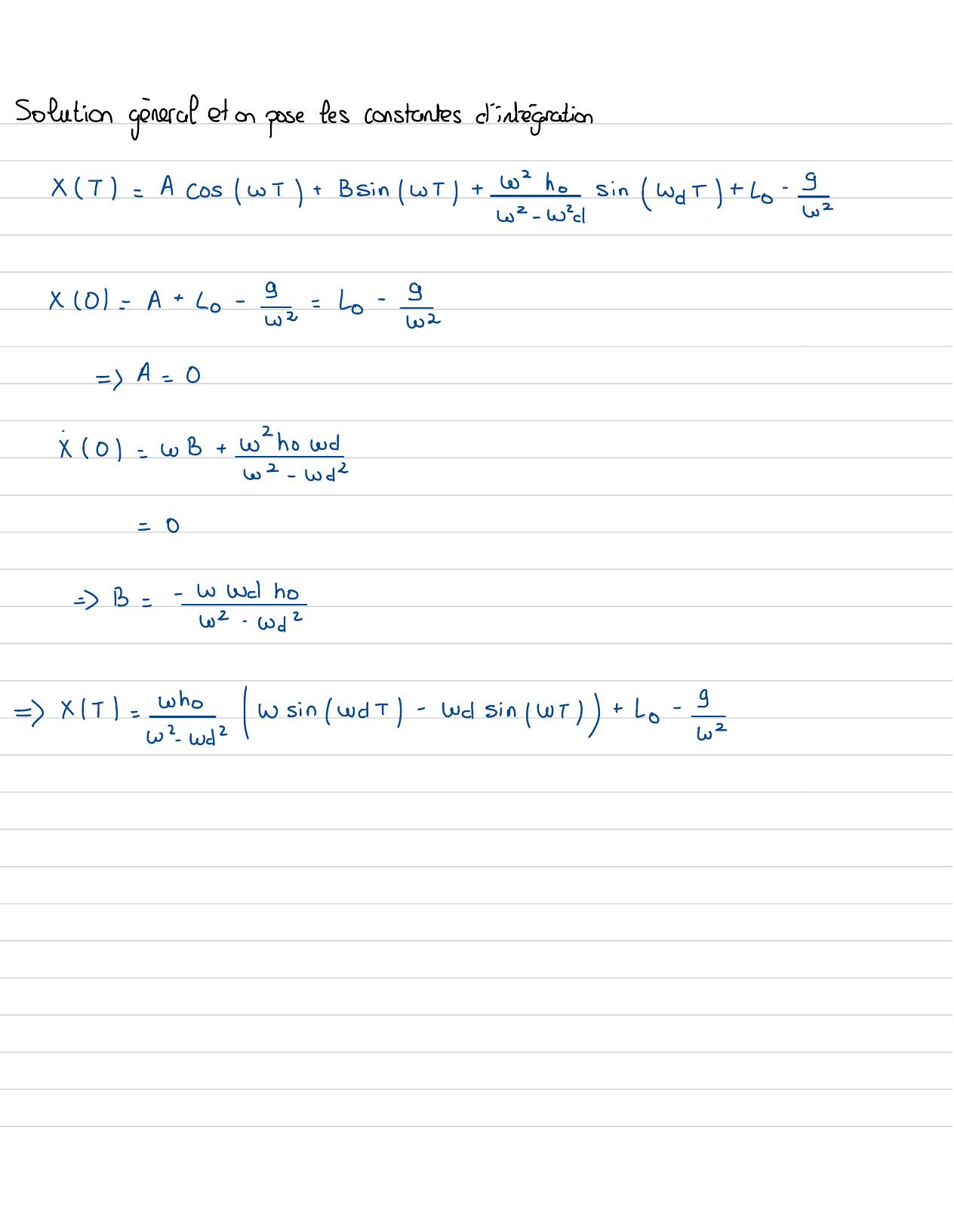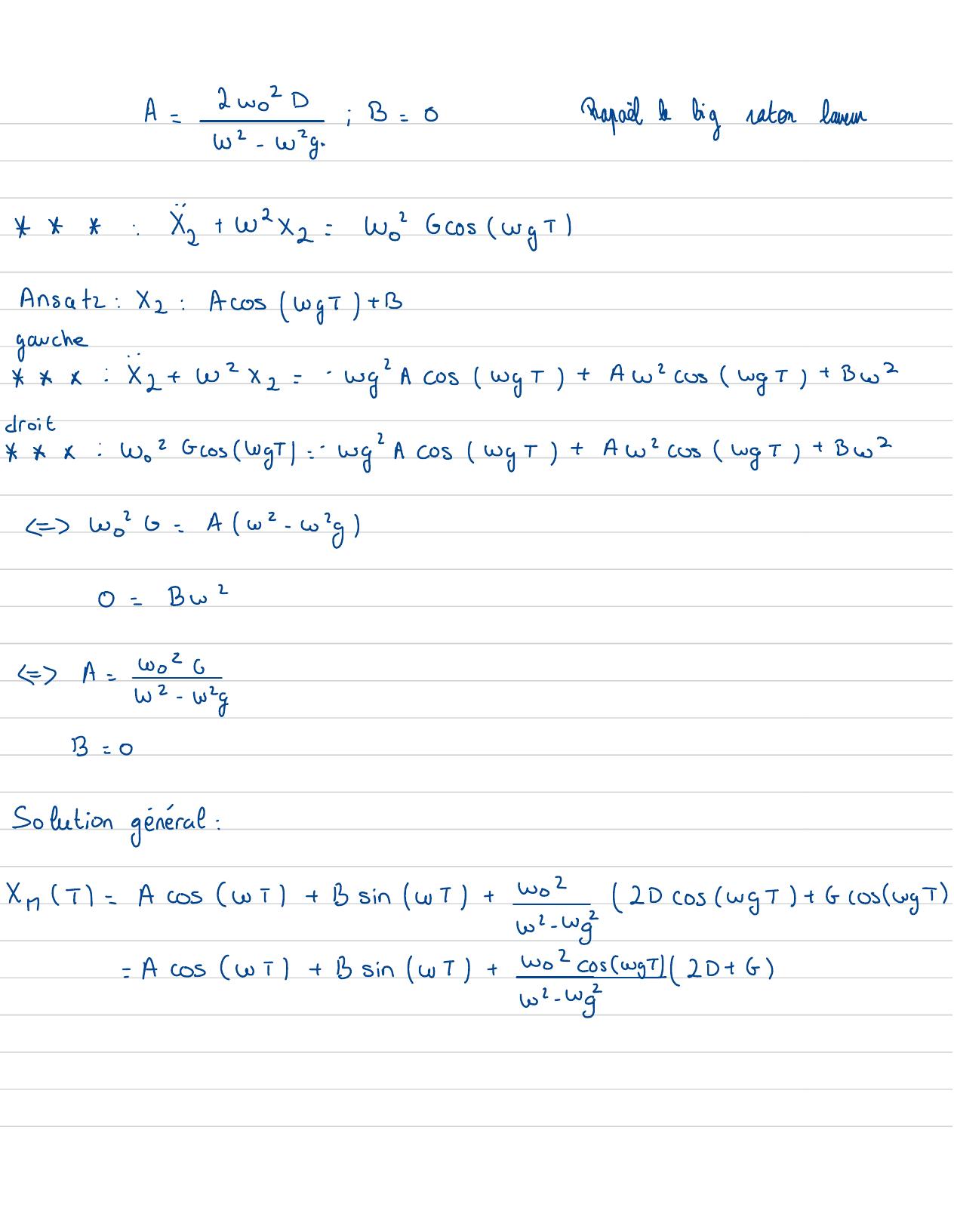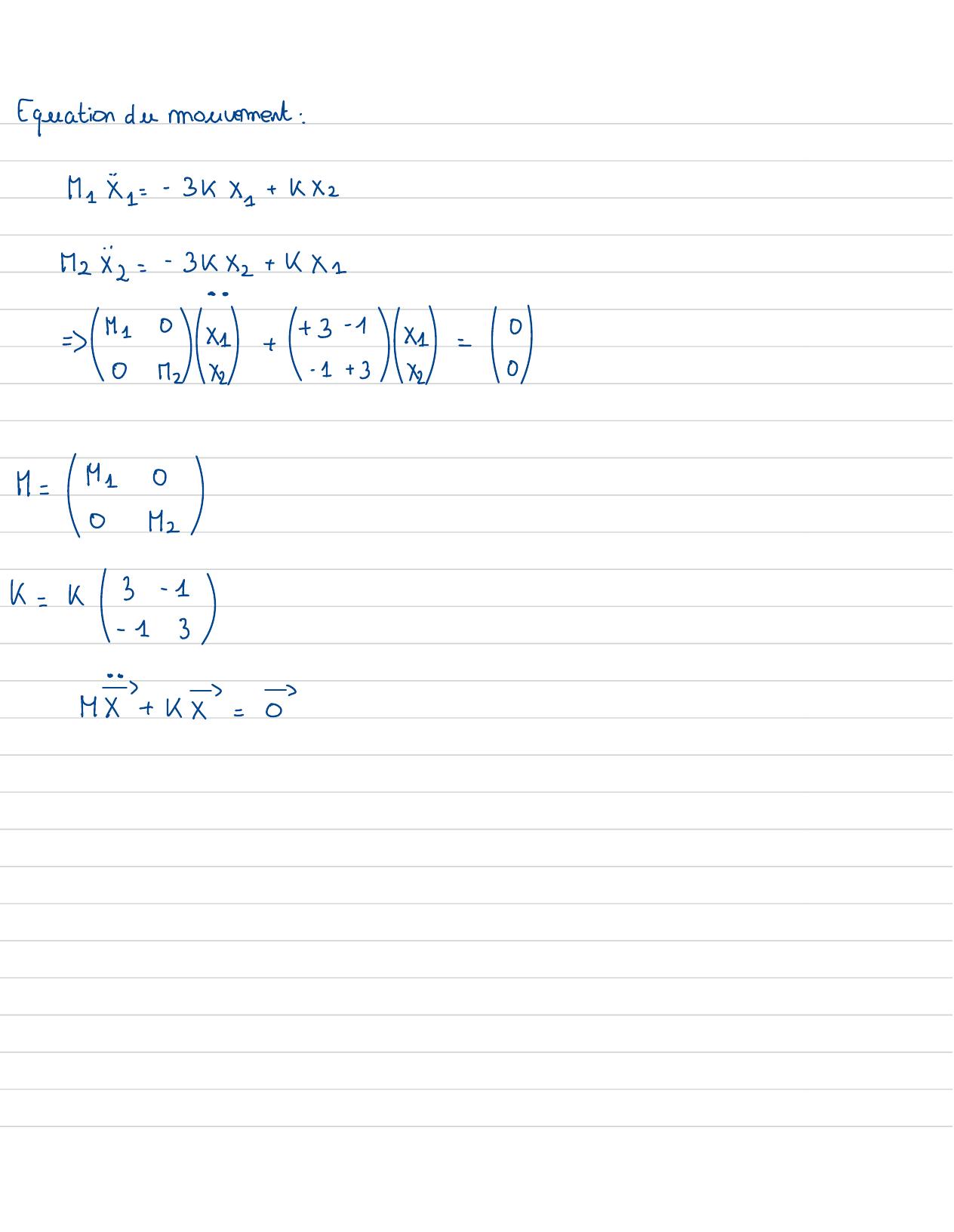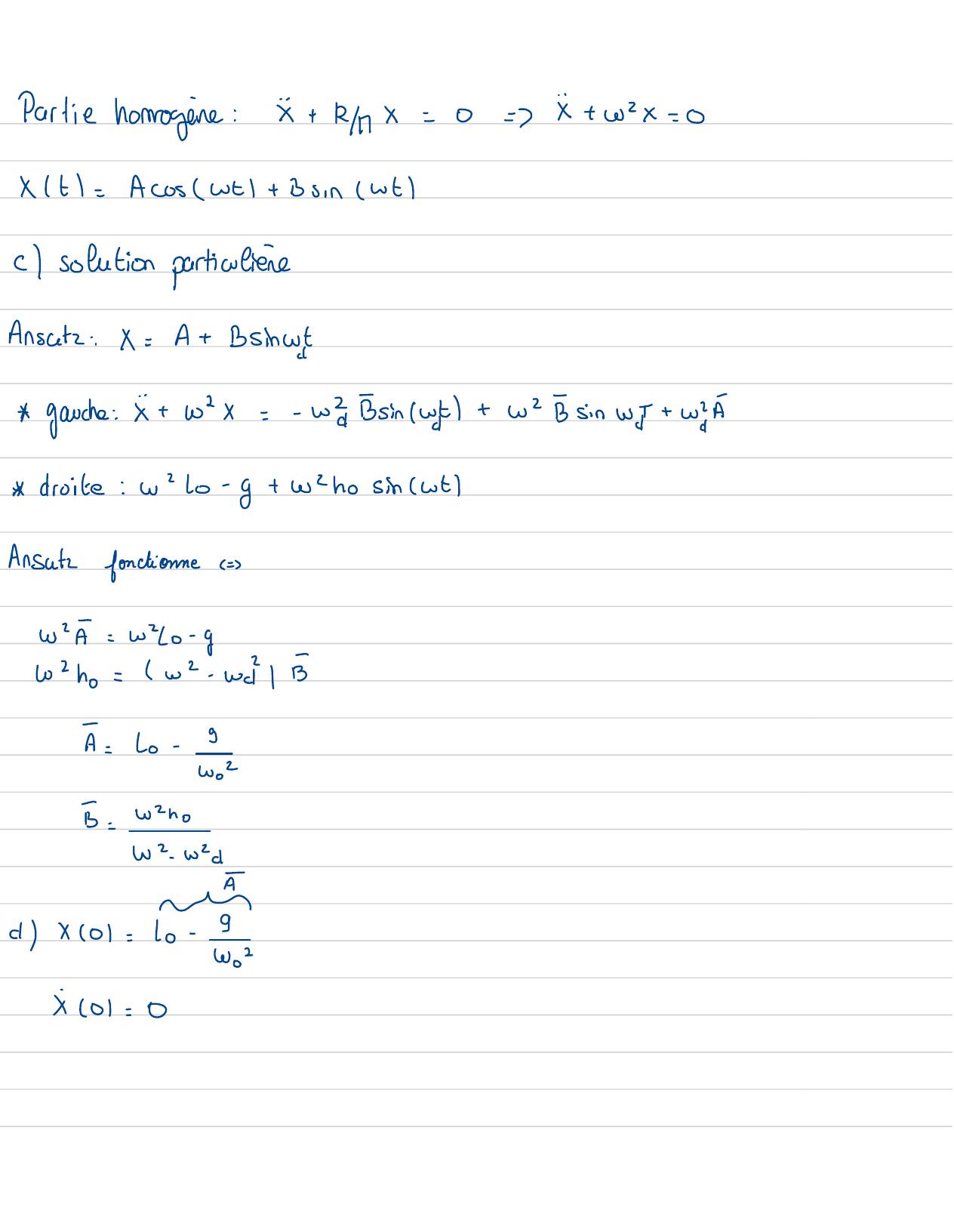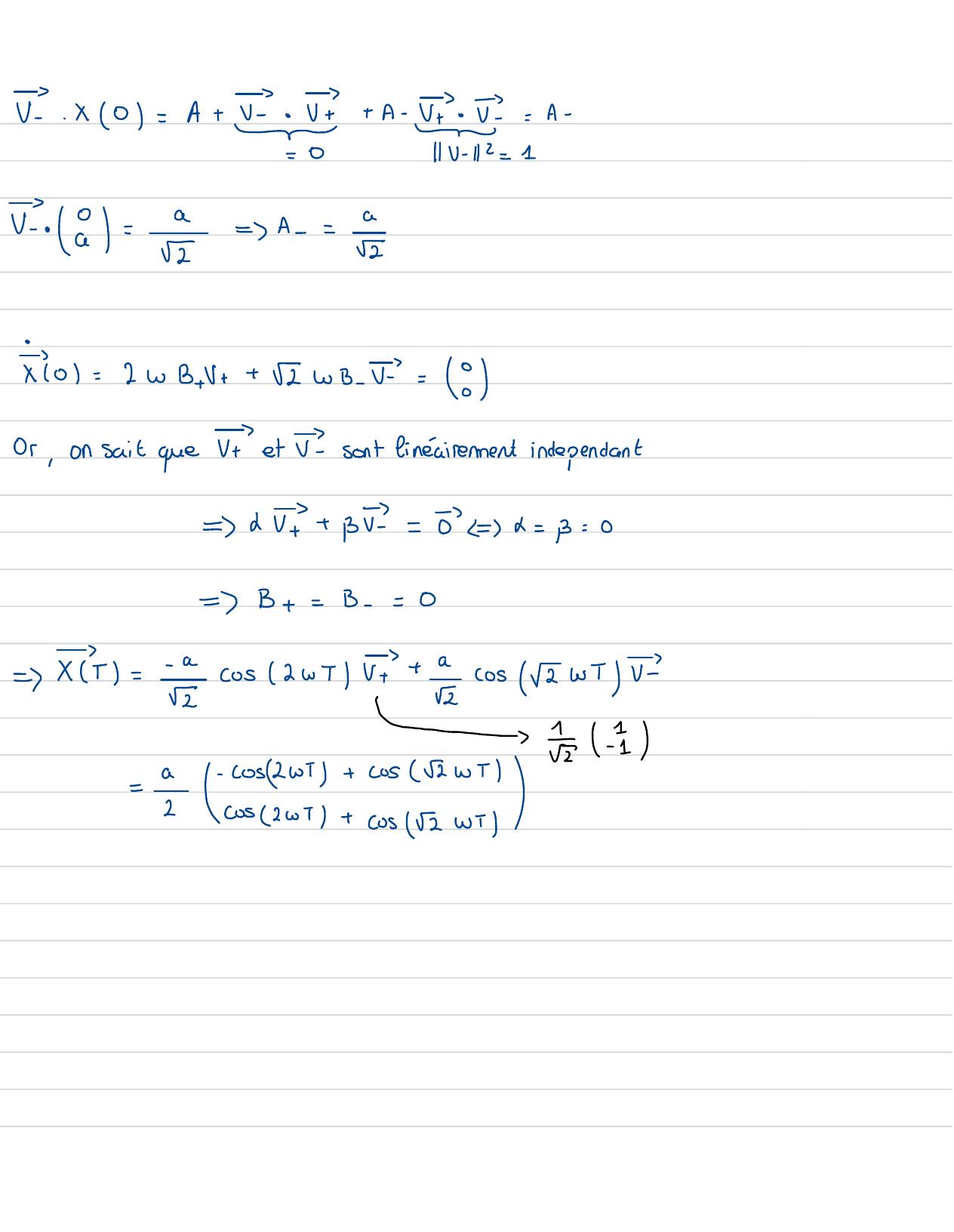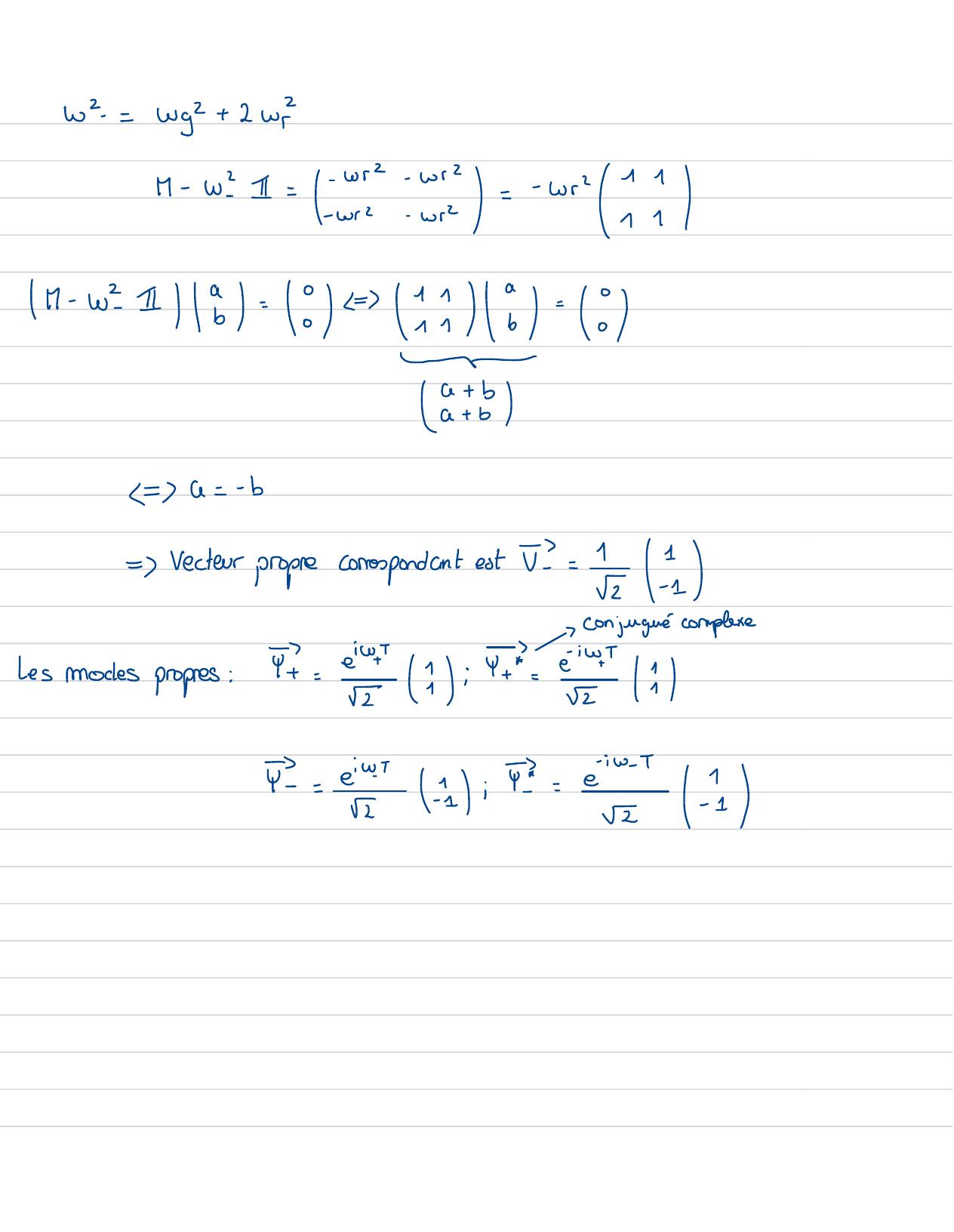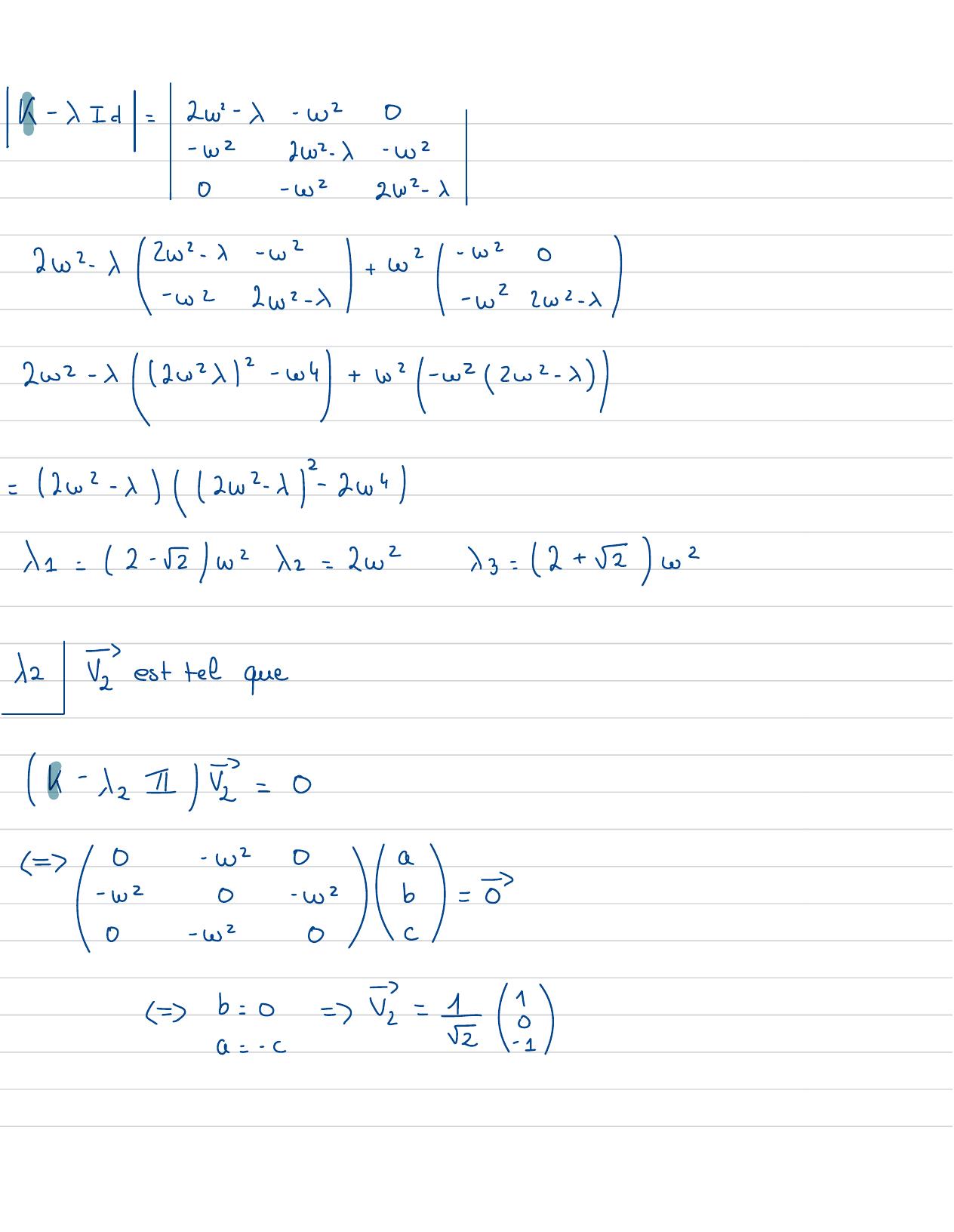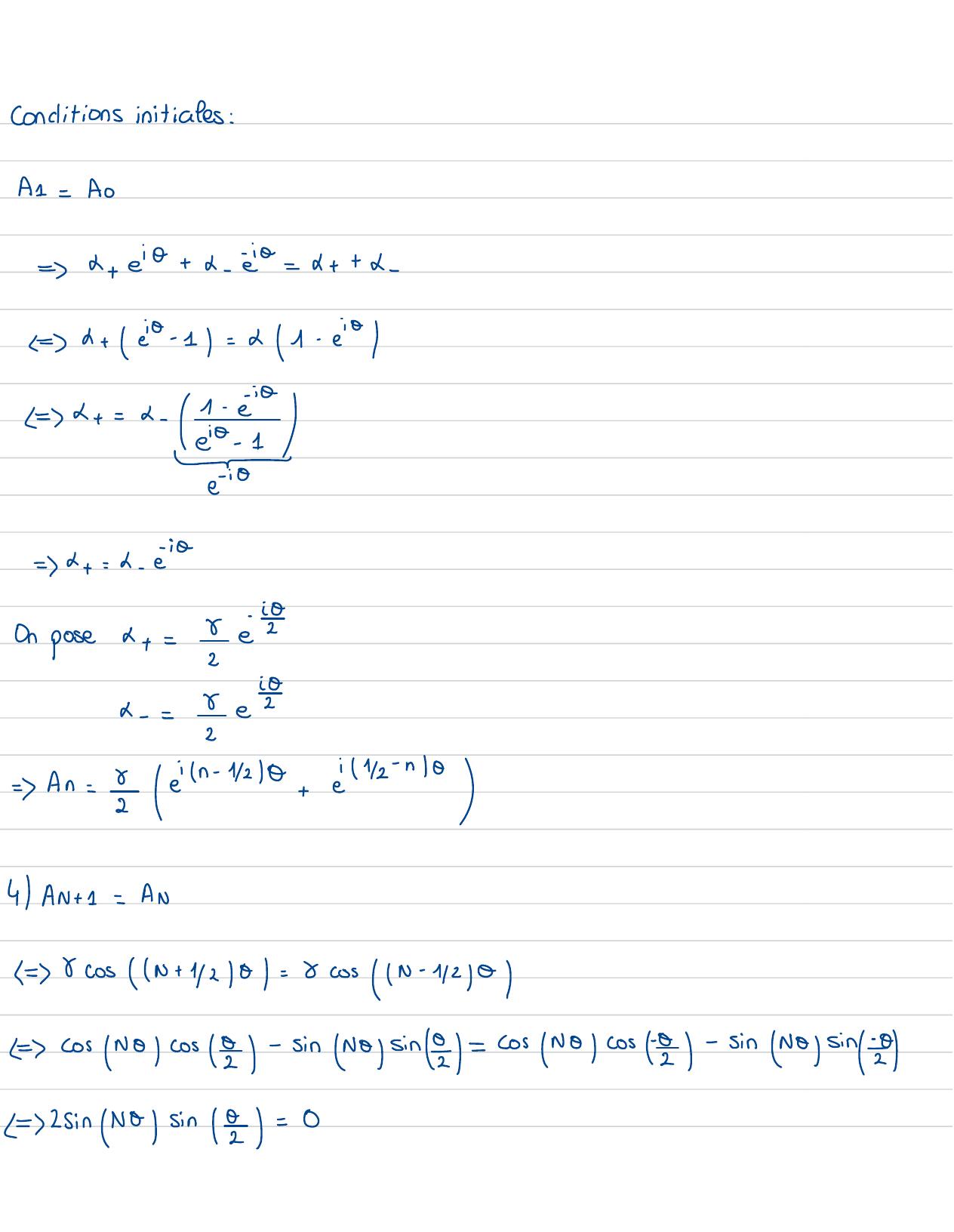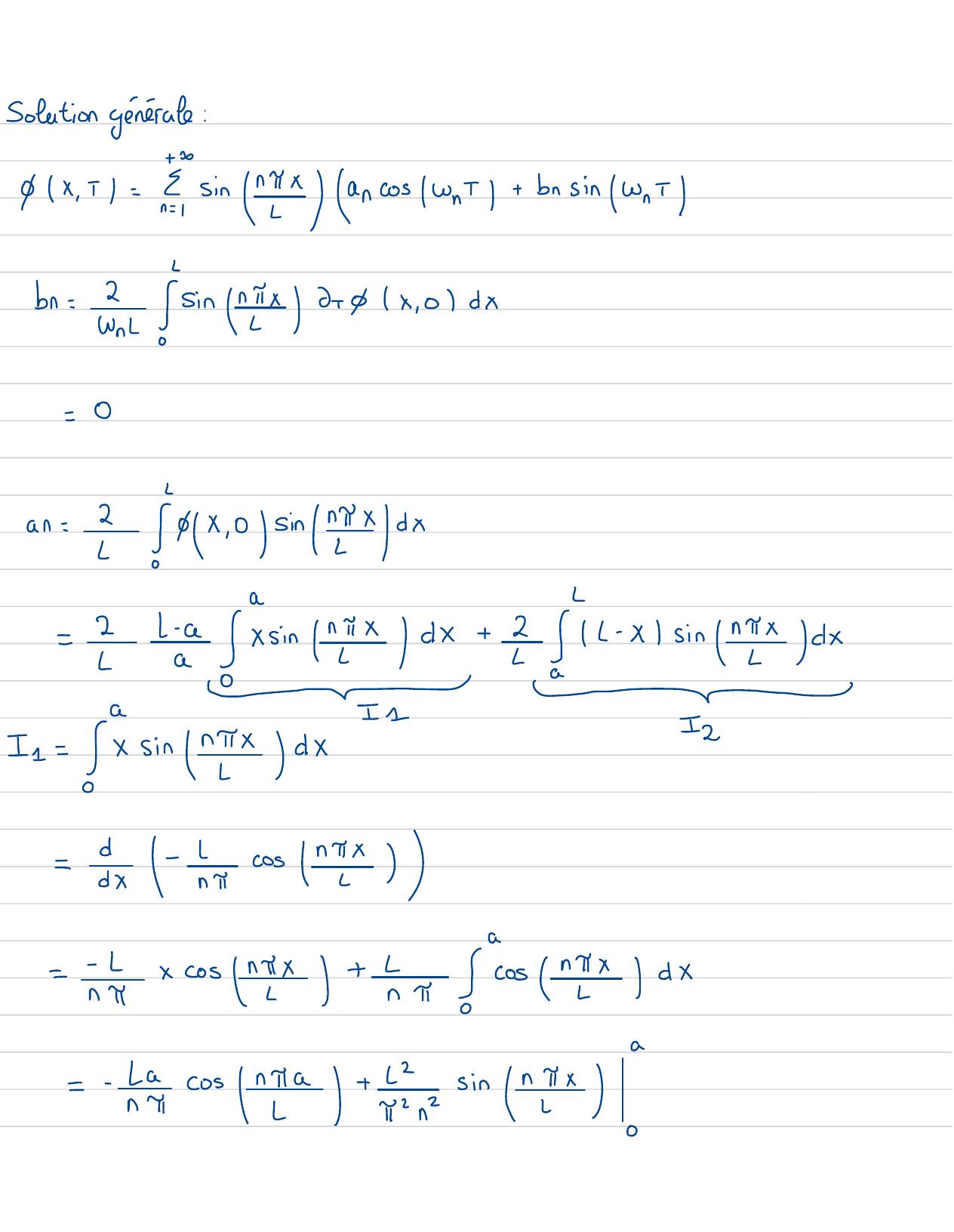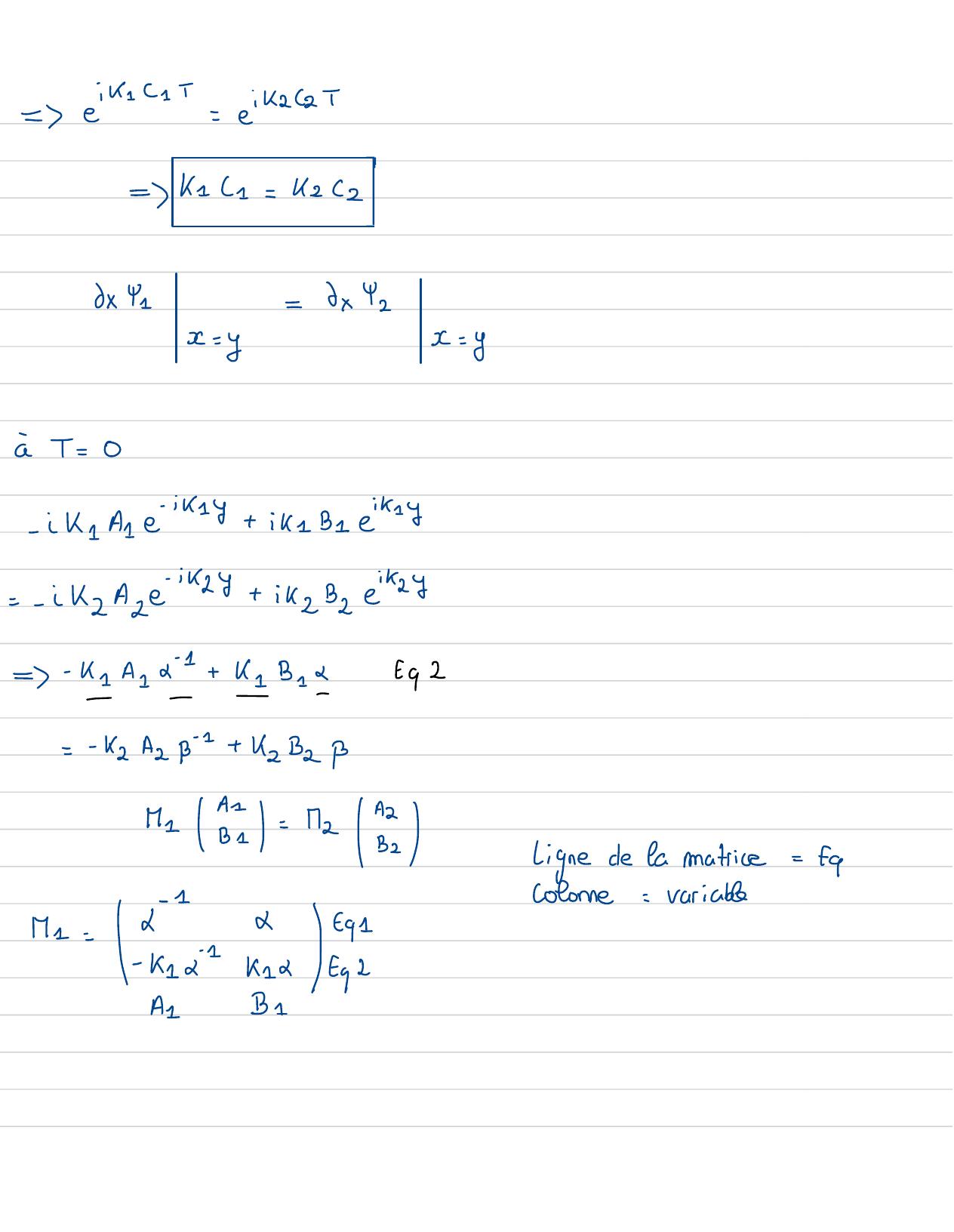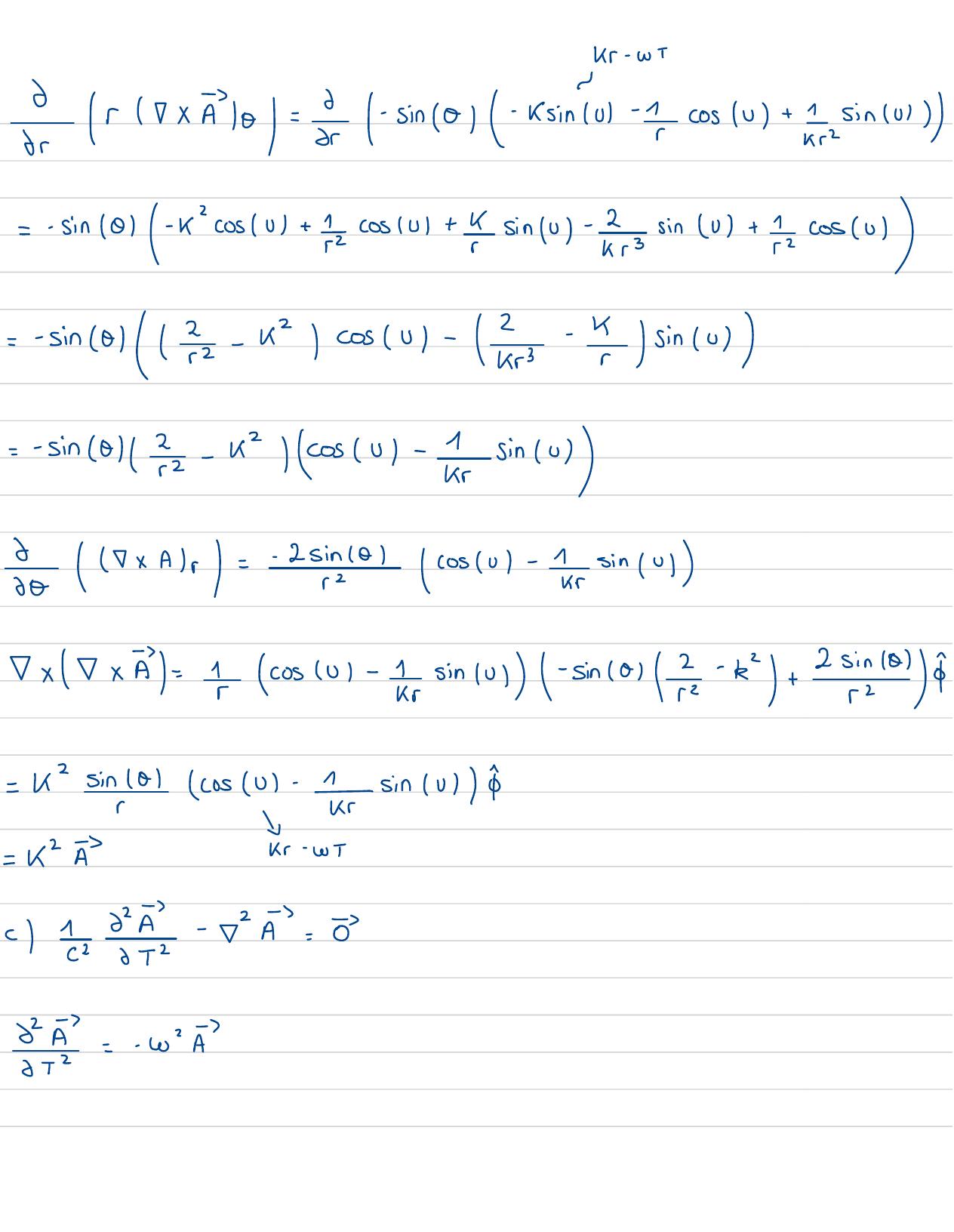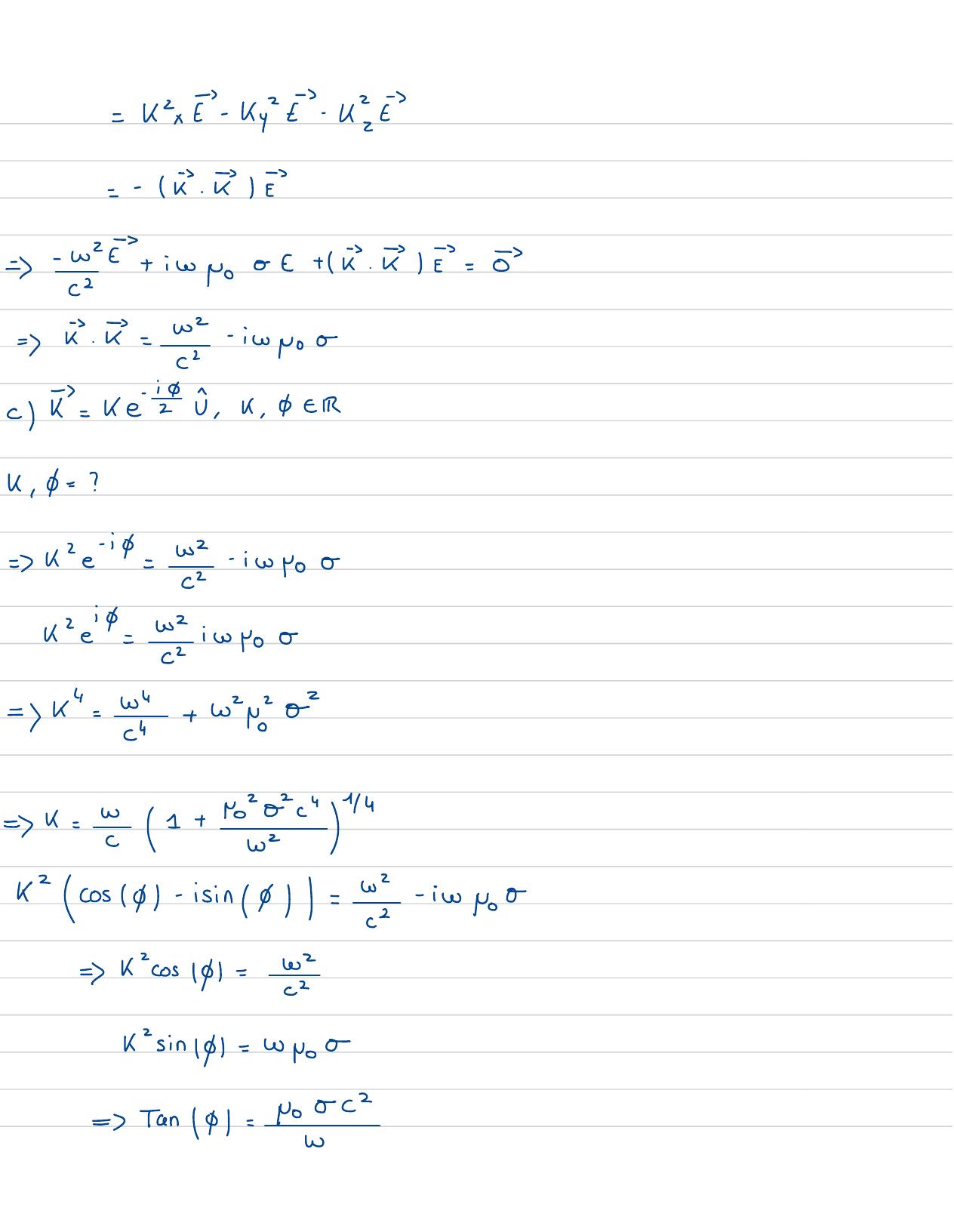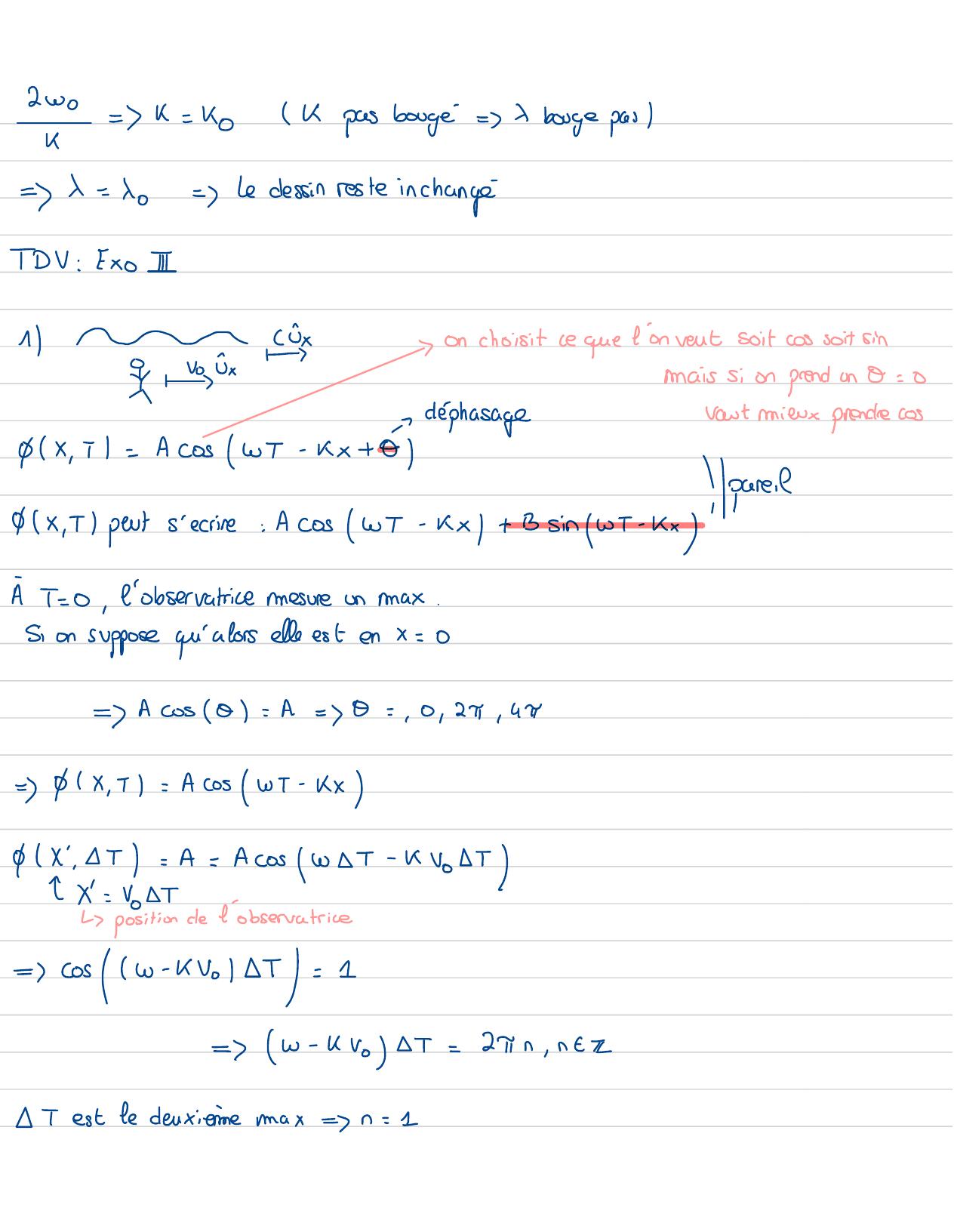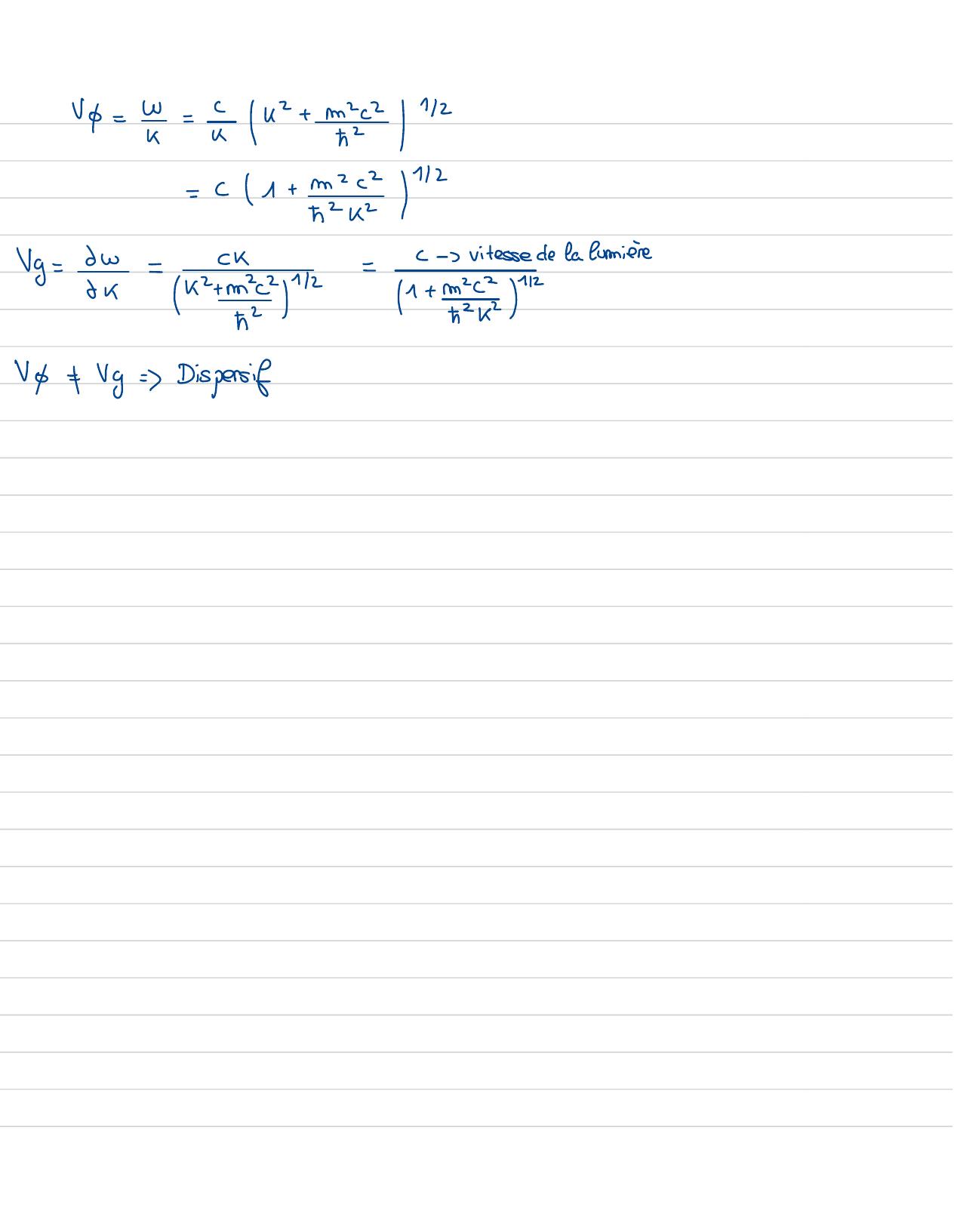TD Correction
Télécharger le TD Correction en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
Page 1 : OndesTD 2022-2023
Page 2 : -------------Uz33k , 07Z3k , 0a DescenteTente jusqu'à ie que la masses'arrête: la force du ressort compenseexactementta force gravitationelleona:fg= Mgz-recteur de longueurqui pointe dans la directionoùZ augmentefi=K /Lo-z/Yzon verifielesorientations: fgpointevershebas vfin" pointeverste haut LovE to basE LloV
Page 3 : A l'équilibre: Inforauassort=MgUz+ k1- z5z=z= 0+ Mba- Equation du mouvement- zzZeme loi de Newton: f= Mâ= MzIlMg+ K/Lo-z//Vz=ME= Mg+ KLo-kz E+ kz=g+⑭tequationda mouvementb-Résoudre Le probleme de Cauchyi. eRésoudre l'equationsiz 10= Lo , EC01=0On pose w= K/M E+ wiz= g+ 40= E+w2m+ 440=0xt
Page 4 : i= =- wz9+ 4 =me=constante i+ w=01cOscillateur harmonique simple!=XT= AcoswT+B sinrT/=zT= AcoswT+ BsinnT +/1+ 0Onaz10= 10=A+ 19+ Lo=A=-M=0=0=- WAsin 0+ Bwcos/0een01concB=0=ET= 20+ 491-coswiavecw:rc frequence?Pulsation:w=/Mfréquence:we-1k/M2π2la fréquencere depend pasde g.
Page 5 : dLa longueur moyenne:= la periode =2=24K/Mz = 2star= 1+/1- coswitll dY=0 +3dT-Icoslwa↓W--0-Il!III-1FT= IL=z=10+Mgkc'est la longueur trouvéeen al !
Page 6 : LCalness- radians/secondesfrequence angulaire= pulsation w=1CT tempsx 9 mcapacité1= i D↓1iI2:c=I3+"/1 DinductancesAmpene=1= Pein ==1=w=WarLLLCblnessloi des maiffes: U+ V,=0I1potentiel electriqueUL= LdTQI1 Uc=COr le systeme est fermé = ICT=1= 0courant est due a la dechargede condensateur
Page 7 : Loi des maiffes: I+ Qc=0= + ac=0 8+9=0mer22IW==+ 1,8=0= E Ic Ifrequence angulaire1LCPériode: 2= 25 LMasse-Lc-Ykaa-Ec energie conducteur= 1IinductanceElenergie inductancel=I-iEp energie potentielle= & 10-222Mx2Ecin/cinétique: IMU2, V= X=1Ec -Ep,aro -XEl-Ecin,0=- x
Page 8 : bw /frequencel de la conservationde l'energief + 0 += 18+ 18=estedETT= 208+200dT=0 d'apres la loi des maifles=19+ Lce qui garantie que l'energie est conservelracinedeguartet 021+ 0= 0car l'energie est consenialtoutveoscillateur harmonique:X+ m2 x=01W=LCEquation du mouvement↓conservation de l'energiefxT0=2 T010+ TfT01= I SfITdTTo2 methodes :Force Brutafe!1.Trouve les solutions des équations du mouvement
Page 9 : Méthode"ingenieur"uav=Mv- vidtTo + IEL /T0=1SdI S 4894a+ 90= 08+ poTo↳Lo-L98 Tot jägtfT=-3- fa22Tr④Tol& Tolme= 0T+ Y9T+ 2- 9/T08/To=0To+ YTo + Isecliol: =as==etTo2CEc!Ww= 1iw2= I=Ec /Tol1xx= 0estle point d'equilibrealw= !Toutd'abordon cherche les equations de mouvement
Page 10 : équations de mounementFressort: K/20-21xFino= Frax= 01- kxxforce ressort de GaucheFins= ERpx= 01- 2kxxStot=-3kxx+", ebeucestà é'équilibreZeime Loi de Newton: Frot= Ma=MYx=My=-3kX= i+ 3kX=0Mw3Kwi =w=Mbl Six=V forsquex= 0quelle est l'amplitude de l'oscillationdu bloc ?Suppose qu'aT =0, X=0=x 101=VxT= Acoswi+Bsin wTTrois methodespour trouver l'amplitucleT= AcoswT+ = AeiNT+BeiNTA=A2+ B2A=/Al
Page 11 : Acoswi+B sin WT=X 101:A=Oconditions initialesconditions initialesSx 0= Bu=VV=B=eAmplitude:Al+ B2-IV-VMW3kMontrer que:1.Sin /8+ 0:sin 0cos 0+cos /01Sin /072.cos /0+ 4=cos 01cos 8- sin 01 Sin 0Ci10+ 41=cos10+ 4+ isin /0+ Ilsoit =cos 01+ isin 101 /cos 41+ isin /41= cos 01cos - sin 0sin 4 / +i/cos0lsin4+ sin /0/cus 0Reei 10 +41= cos0+ 4=cos0 cos4- sin 10/sin 0ImeiC0 +41=sin 10 +01=cos 01 sin 4+ sin 0cos 82
Page 12 : 3.cos 301=4 cos /0- 3cos 0leig= /COS 01+ isin 101=cos" 01-cosOlsin 0- 2 sin 0 cos 01 + i- sin 0+ cost 01 sin0+ 2 sin /O Co0=cos0cos 01-3 sin /0+isin 8-sinal+3cos01Ree: 0=cos30=cos0 10s" 01- 31-cos"01=4cos 0- 3 cos 0Ime:1=sin /301=isin 0 /sin 101+ 3 1-sin 01rcos"0-- 4 sin 01+3 sin 0
Page 13 : X1..........vihThT1= hosin /WITIa Equation du morverment de La masseTrouver La forceon utilise l'énergieFressort= 1 /Lo -x+ b 2Egravité= MgXf=-I tornexsur lamasse=1k26- x+ b- 1+ Mg/xf=-grdu si l'énergie=Ux- kx-Mg- k1+ hcinétiquene dependpas de la position= f= Ma= MYxenergie potentielle ne=Mi=- kx- 1Mg- k+ hdepend pasde la vitesse=x+ 4x= 4nt- g- 4,0
Page 14 : bSolution générale de la partie hommogenePartie homogène:Tout les terres qui ne dependent pas de X=0i + kx=0MweW2=X T=A cos 25+ Bsin NTc Solution particulièrede l'équationAnsatz /supposition éclairée:XT=A sin W4T1+ Bg: x+ wX=- wIA sin WdTl +AwsinWdT+ Bu: W2nT-lg -wo= whosinwaTl-lg-wogauchedroit y= A en eE Alw"- wa= whoBu=- g-w20A=whowa-wiB= Lod X101=Lo-=x 0= 0
Page 15 : Solution general et on pose les constantes d'intégrationxT= Acoswi+ Bsin/wT +22 hosin WDT+Lo-em- wicx 01=A+ Lo-2=Lo-9w=A=0X 0= wB+whoad22- Wa-0=B=-wwdno22-God=xT= w /WsinwdT -wdsinwil +Lo-e
Page 16 : seccest-a Equation pour PIt1 ?Loi des maiffesUc+ U+ UR=0uc =quandc ex3r= I= LI= PdiffdeEUR=RI= RQpotentiela+ 0+ R8=0=Ö+i+ I ,Q=0équation du mouvement
Page 17 : i+ /X+ woX=0SURLb 00=Po,01= 0a-CaSSOMS- armortiSolution générale:q T= eAcoswil+ BsinwiIwh=Wy94Ansatz: AedTPT=A edT8 T1=dAedT: /T1=Aed2+ 16+ wo Ae=0--4woL== Ir - w22ic
Page 18 : Sous-armorti:Imd +02Wor I0, 0=A=Po0 T=-20x+ ef-1- wAsinwi+ wBcoswilj 0=--2001+wB=0B= 20b- cas critiquec=-2=2- womes= wo= 0Acon remplacepard①T= e2A+ BTAeT =AeReld: Imm d2①5= eRed A ei FmC' BéFrksiganemarche pas 9 TI= A Ted
Page 19 : 0 01=A= 00: /T=- 29T+ Béc00=- 29+ B=0=B =290-29151= 901++-cas sur-amortiest grandpas d'oscillationW-a=- 2= 2- wLER=2wosursors-cas critiquecosh x: etex①T= e IT Ae+ BeWT2sinhx=ex- éx=é / Acoshwil +B sinhlwill200=A+ B= Po· T=- 29T+e- 4 /wAeWT-wBewT
Page 20 : 0 0=- 290+ wA- B=0A+ B=Po1A- B=022we=1+ 2:A= ⑲1+ w2=1-2:B= ⑲1- w2Revision:x+ rix+ wo X=0transformeren plde polynome⑦on remplace notreX par eX= AeTx=2x, i= 2xexponentielle clone jamais= 062+c+ wo/X= 0=42 + x+ w2=0=d=-1=2- wo2-ensiw foon est pas critiquewfautvoirsile discriminantsiwFo, on a deux solution&+, -est +ou--Sit surarmortisi-sousamorti
Page 21 : Solution générale:XIT= Ae+ Bed- TProbleme: Six += &-, ilnousen immanque uneXIT= ATeTOscillation: Im =1 +ocassous amorti:Im 61 FOcas surarmorti:Im 61=0cas critique:↓+=↓-! TR2k.nM-!"--XolT1= GcoswgtNoCT= DcosWgT
Page 22 : Equation du mouvement :Forces:E= kx/xn + XaEs=- 2küxxn- xxfor= kxxG+ 2xD-3xn= 1xxxy+ 3kx=x0+ 2xDMurWoPartie horrogene: /3woxi=0in + Lewhb Solution générale:Xt1 : A cos wt+ B sin wtlRappel:x+ w2x= S1t+ S2tsol général:xT=X01T1 +X, 5+ X2 5
Page 23 : Xo-sol général partie hormogeneX1 Sol particulièreavecS, - 0XSol particulièreavecs- 021No+ wXo=0 x1+ W2X1= 2wo XeX2+w2Xc= Woxo Solution générale:Xolt=Acos wtl+ B sin wtSolution particulière:x,+ wX,=2wo DcoswgTAnsatz:X : AcoswgT +BgaucheAxi+ wX,=- AwcosNgT +weAcoSwgT+ Budroit: 2 Wo DCOSWgT=-ANY cosIWgT+ weAcoSwgT+ Bu=2 WD= Aw2 -wig0=Bu2
Page 24 : A=2woD:B=0Rapaëlbe bigratonlaverw2-wg. A:X2+ W2X2:WoGCosWgTAnsatz:X2:Acos WgT +Bgarche.+ 20X2=- wg"AcosWyT+ AwIcoswgT+ Bu A:XdroitA:Wo" GosWgT1: -Wg"ACOS WyT+ AwIcosWgT+ BuEWo"G:A w2-wig0=Bw2EA=wo Gwa-wig13= 0Solution général:Xi T1=Acos wil+ BsinwT +wo22DcoswgT+6coslwgTwh- wig=Acos wil+ BsinwT+wo2coswg2D+ 6wh- wig
Page 25 : cXn 101=0,XpC01=0solution:Xp 101: As=A=- 0xy01=+ Bw= 0=B=0=Xy 5= 4coswgT -coswi
Page 26 : TD 3:2k⑳xk2k-intumMe ↳↳"XI-X 2a Equation du mouvement+Tenseurs Ket MTenseur d'ordrenTenseur d'urdren- 17i.Tenseur d'ordre0 scataireIbeoce=7-2kx, -kX, -xcxIbloc=- 2kx2+ kx =- x21x
Page 27 : Equation de mouvement :M1x1=- 3kX1+ kx2M2x2=- 3kX2+ KX 18= M10X1++ 3-1x1-00M2X2-1+ 3X20M=M100M2k=k3- 1-13MY + kx=0
Page 28 : TD 1: Ex 2 :CI-&ILC-on ventles combiner pouravoirne expressionavec les mirmesunités quew11D2w= +3L=1T72w=1Cc: I T"1 12TD 2:Pb 1:1MX=ht= hosinwtYultalf=- kx- n- 0Vxfg=- Myfor=- kx+ h- 0Ux- MgUx= MxUxMi=- 2x+ kn+ klo- Rg= x+Ex=ht+0- g
Page 29 : Partie homogène:x+ RAX=0=x+ w2x= 0x t=AcosWEl+ Bsin wtlc solution particulièreAnsatz:X=A+ Bsihwtch gauche:X+ wix=- wBsinw,t+w2sin wir+ wdroite: wilo-g+who sinwtlAnsutzfonctionne=WA= wo- gco2h=w2- wal BA=Lo-3wo-B=wInoW ? WdEedXC01=Lo-IWox 01= 0
Page 30 : Ansatzsolution générale esolution générale:XIT= A + BsinwdT+ Acoswt+ BshwtX 01= A=A+ AA=0x 01= Bwa+Bw=0B=-wd5↳=XT=A+ B sinwali-sin /Wais+D
Page 31 : a Equationdu mouvementsons forme matricielleSolutionuneprecedemment1592+ 12 i= 10seneKM3 Utiliserles ruleurspropresbe TAKpour trouver h pulsations propresdusystemeEquation de mouvement: i+ Mr= 8
Page 32 : pulsations propres:W, telles que= I'ew soitsolationdes equationsdu morrement= weiNT + keiwT ==L Nk-22= 8matrice identitéAlgebre finéaire: Tro estune valeur proprede MetAest levecteur proprecorrespondantValeur propre:X estvaleur proprede TAK↳=det 1-7K- x1=0ex=4 - s-SXmatrice inversedeKOn pose WI =W2"= Fic=x=Swe- A-wi- 3w,- x11= 3w- x3w-- x- wwX- 3w+ wix+ 8wwe
Page 33 : =XI= Ew+ wisE2-32 winIw" +9w 2" -14 We wIpulsations propres:WI=1 Iw=x +aux-On supposemaintenant queM1=M2=17=W1= Wz=W2 Trouver lesvecteurs propres de Tit correspondantàx+etx-1 ==wi+ wi= = 9w!+ gw2-14ww"= 3w= =79+ 9- 14/04/12=3w= =4wix= 3w= 12w2= B= 1wVecteurpropre:= 5telque M-1KE= D=M- 1 k=302- 22a= w23a- b-23r2b- a+ 3b
Page 34 : x += 422w2-"= 4w-8=3a- b= 4a=a=- b- a+ 3b=4b=7b=- a= VI=1==1-= 2w= w233= 2w5I=3a- b= 2a=a=b- a+ 3b= 2bb=a= T =EIv=SiVestun vecteur propre, alors XV C'estaussi / x-K. Typiquement,or choisitlesrecteurspropres pour que HIVl= 1.Onaurait per choisir== i= 12 1= 1+ 1=2
Page 35 : Solution générale:,pulsation propres =/AjcoswT+B; sin W; Tl!- recteur propre correspondantIdimension de=xAcos2wT+B+ sin2wT ++↑AcoswT+B sinwillv-pulsations propres: w= bu2am2 whW1= 2w,wz= I'wa xi01= a, xi01=Donner La solution particulièredu systemex301=A+ V+ A - V!= a1↑/E-2iVI. x 0=A+ VI . VI+ A- V . VI=A +emen11 V + 1 2=1=1- x=0vi. a= 2=A+ =
Page 36 : V?. x 0=A+ v. V+ A- V . v=A---emen=0110 - 112= 1Vi . a= 2=A-=CI↑01=2wB+ ++ kwB - v-= 8Or,on sait que VI et VIsont linéairement independant= av+ B= 8= B=0=B+=B-=0= XIT=cos2wTIV+ +cos 2wT U =EUn-E - accostes ete
Page 37 : a Equation dumouvement d'un penduleEnergie?X 4=L sin 4L-y -L-↑x=Lcos4XL-y14= cos4=y= L1- cos4⑧i=L Sin 414Energie potentielle: Ep= Mgy= MgL1 -cos4&
Page 38 : Energie cinétique : cassin 4= 4e=ETOT= MgL/1-cos41+ R iEnergieestconservée =1for=050Tor= 1gLYsin4+ ML25= M ? sinP+ i=0=Soit Y= 0on+ Ssin /P= a Equation du mouvementsous quellesconditions- oscillation. harmonique ?i+ w= Y=0SiY1, Sin Y=Y =i+Y=0=oscillateur harmoniquearecw=1, T= 4= 25
Page 39 : bPar les mènes arguments qu'en al,on aX 1= sin41, 1= L1-cosY=X2= sinY2, Yz= L1- csYza3--!I-longueur du ressortSYz2 =yz- y1+ a+ xz- x 1 123=IL cosY=-Lcos4211+ a+LsinsYMaissi P 1 1 1, 42 1,Sin 4. =Y1, sin 42=Yzcos4= 1 - 41, cosYz= 1- Y=2 la re ESi Y1 1, Y2 1 ,=- a= Yz- YzbPour utiliser ta2eme Loide Newton, on introductte paramètres,la longueurde l'arc de cercle parcouru par te pendule."Fi=Si= L4:
Page 40 : Equation de Mouvement15:= MLii=p=-64:Ep↳SiYi=Mi: =- 1:p= ER- Eg:Eg: Mg71+ MgYz=AgL1 -cosY1+ Rg1 -cos4241 1, 42 1=Mgr /4+ 422ER= Y- a= /42- 4 = =Ep= 44 Y- 412+ ngh42+ YzYrep= k224- 4- 2+ rgt41-412= k2241- Yz+ RgLY1rep= k224- 4+ 2+ rigtY26422k22 41- 42+ RgLY2
Page 41 : Ona:MLi==- Ge= MLi==-k41-Y-RgLYn41+ + 2/4 =- 242=0==Y1+ wr+ wigY1- wiz= 0même arguments:↑2+ wr +wiYz- w== 0Sous forme matricielle:= equation du mouvement:+wigtwo-wi-wiLawiY =pulsationpropressont telles que=A "eiwT estsolutiondes equationsdumouvementavec At oi. e: soit une valeur proprede-identité det witwr-wr"- wiI=0-WrWg+ w?= wg+ 22- wi- w=0=wg+ wr- -2- wrWY+ wi -+ w2r= W = wigau wig+2wr
Page 42 : les pulsationspropres:Wt=WI=WgW -=wi + zwIModes propres:solutionde la formeP = Y Fi/WI pulsation propresOn doit trouver Ivecteur propre de La matricewig +wi-wiqui correspondàw-WrWg+ w?Pour une matriceM, Vestun vecteur proprede Valeur propre x 1- 1 = =0WI= Lg"/M-wg1=Wr2-wr-Wr wi=Wi-1-11In-wig 115== -8a= b=levecpropreest V= = i
Page 43 : w2=Wg2+ 2 wrn- wiI= 2=-w ?? 11- 22 15: 18 -by- 181=G=- b=vecteur proprecorrespondantest VI= I Econjugué complexe↳Les modes propres:↑I: e 2 :4 +=e 1= ew 2: = e 1
Page 44 : Retour DS:Moyenne:10 , 2-Max: 19 , 5Min:OErreurs: Definir nos variablesDirectionTD4:04aL0, g=0-Mf =- UMXnUx1 n+ /+ k= 0pythagoreI= x= , x2 , x3x- S mB -·AtXn-xn-1Xn+ 1aIn---
Page 45 : S-=A-c02a0=B - 10f -= E= 2Xn- xn - 1+ a=f=- derivee de l'energie:-Ott -xdXnf=- mXn-Xn-1 /Ux+= A+02a=B+ 3 102f+= E+= 2Xn- Xn - 1+ ab= f=- derivée de l'energie:-Ott +xdXnf=- rXn-Xn+= /UxI-fror= F+ F++ fs= k2Xn- Xn- 1- Xn+/x- UMXnxn=1, 2, 3 ,Xo=Xy=0
Page 46 : Zeie loide NewtonOna enleverlesxmasseMin=- k /2xn-Xn-1- Xn+ 1- WMxn sculaire nombre+ Wxn+2xn- Xn- 1- Xn+ 1=0Ma+ 94+ Eauscule- ex31S= 6-matrice identitéM: T-3x3x1X2X 3k=k2-10St-M- 12-1We--w20- 12X3-n=2car pasde X1x2+ 2x+- x1+ 2x- xy= 0n=3 Dgiexg+ 2x +- x2+2x,- xy= 02 V,recteurs propres?Valeurs propres:1 tel quedet K-x Id=0
Page 47 : k-xId=2w- 1- wo-w202.1- 22I0-222w2X I202x "cix " wax202- x 1202x12-w4+ 2- -2 / 2w2- x=2w2- x2w2x1-2w"11= 2 -Ew2x2= 2w2x3= 2+ 2 co2de Iest telquek- x I=01= 0-w20a-w0-2b=0-220C-1=b=0==62 EG=- C- 1
Page 48 : de IIest telquek- 11 I=01= I-10a-12-Ab=0- 1ICnormeBunaltipletee=b= Ea =a=C1= 11-2-Eb= Icb=a/1= 1+ 52+ 12=4IsVest telqueE= 2, 15= 1+ 2+ 1= 4-k- xI=0ve= YvVe= 11V1= 1. 4= 1LIl1= E-10a-1--1b=0-1- IC-b= xa=xa= c, Vz= 7-Ea=-Xc1
Page 49 : 3t= filTI E=mi+ rf+ wifi=0M+ Sx+ k=0·.matrice identité--Vivecteur proprede K↳fiMVi+ fift?+ f. kVi=0Imeune 7ViEriX i Vi + 0+ difi =+ 5+ xifi=0mi=1,i=01, wi=Di1O0411- 5000coefficientsde frottement pournos3 masses001i=1 I=r02000020012 /+-0I21Eq mouvement:fr2+ 4+ + 5+ xf=0
Page 50 : koefficientde B=7f=07=f=constante=2j+ 0f+ x15=0=f=0=Non!L'Ansatzne fonctionne pas!Vecteur proprescommuns=- K= /K
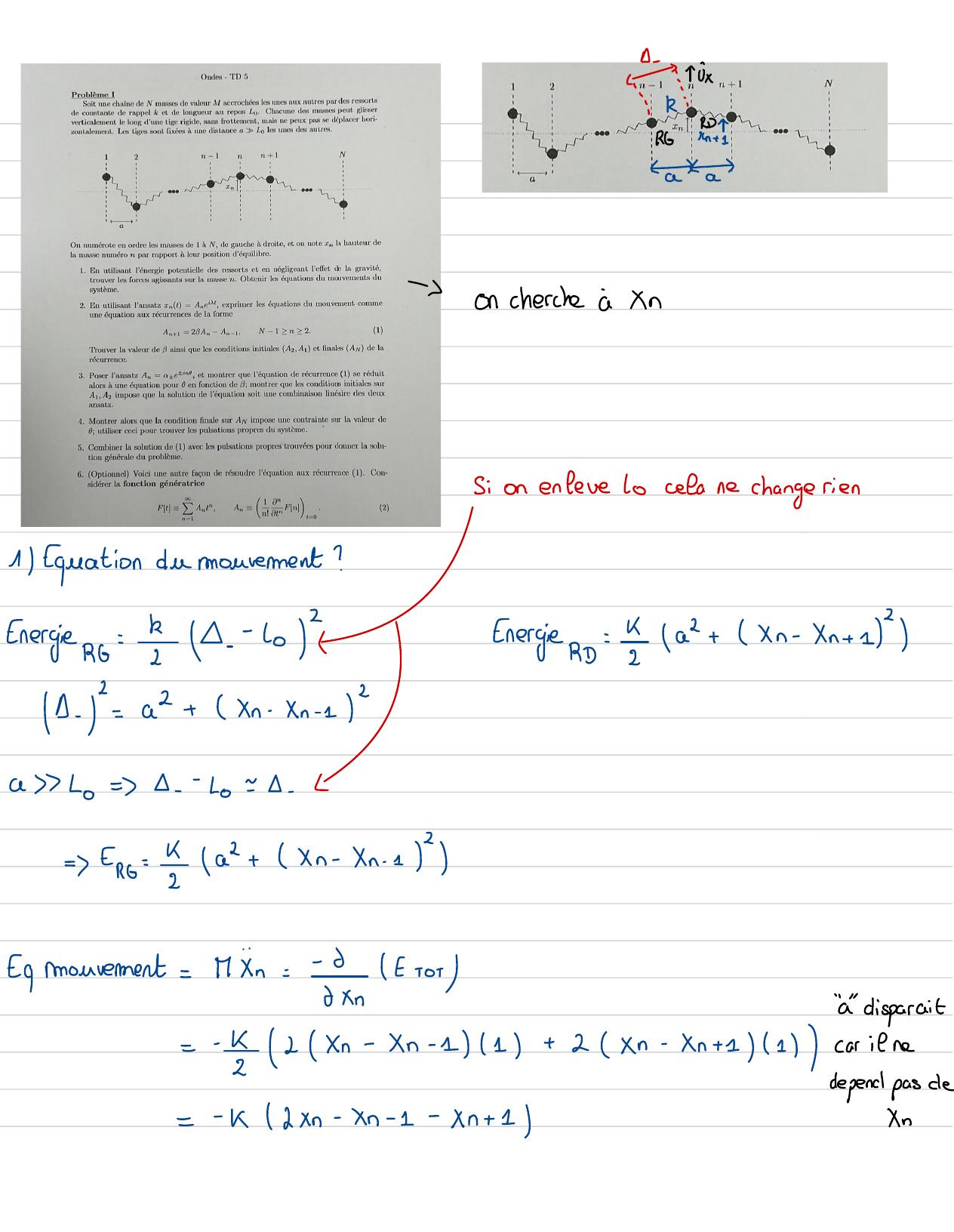
Page 51 : A -1 Ux."RRD-RGn + 1ta-oncherche àXnSion enfere locelane change rien1 Equation du mouvement ?Energie:E-- 101Energies=a+ Xn- Xn + 1B-= a+Xn-Xn -1axL=--=- L=Fro=a+ Xn - Xn- 1Epimouvement=MAn=n/t Toi"à disparait=2Xn- xn- 11+ 2Xn- xn +1 1carienedepend pas de=k2xn- xn- 1- xn+ 1Xn
Page 52 : =Xn+ w2/2Xn -Xn-1-Xn + 1=0w2=kMn= 11+ w2/2X =- Yo- X2=0Mais l'equationdu mouvementde X1est:X1+ w2X=- Xz=0=Xo=x =l'equationde mouvementde Xest:XN + 2Xw-YN=0= Xn+1= XnN2Xn= AneixTque:Antz=2 BAn-An-1B= ?,An= ?,Ao=?"Solution :Eq: in+ w22Xn -Xn -1- Xn +1=0Xo=X1,XN + 1=XN- x AneixT+c2 2 An-An-1-Antr/eixT=o5 W2 An+1= /202- x /An-w"An-1= An+ 1= 2 1- x2 /An-An-kAo=A 1, AN+1= AnLu
Page 53 : 3An= deindon poseAn= deinOLeil+ 10=2 peind- Geik-a= e=2B- éio=B=ei +:=cos 01= BL·non poseAn= 2 eO-iln-110in + 110= 2en - dede0=2B-ei020a=B=2=cos01= BDeuxAnsatz produisent les minnes valeur pour p en fanction de &donc'est linecombinaison fineaire des 2=An=d+ einO+ déine
Page 54 : conditions initiales :A 1=Ao=d+ ei0+ 1- ei0=&++ ↓- -+ 20- 1= 21- ei0/+= be=&+= d- éi0i OOn posex+=↳e2iOesx-=5=An=&ein-1/218+ el42-n10I4AN+1=AN= Wcos IN +12/01= 2 cosN-1210= CosN0/cos2- Sin No/sin= cos/No/cost2- sin Noysin/ &=2Sin N0/sin 2=0
Page 55 : =sin NO=0=Or= Y, rtkPulsations propres:XB=1-2=cos 0= r= 2w20r= busin 184= Dsin 185Solution générate?Modes propresXn: AneixT=Xrn= cosn -1/Or :ArtX4wsintOr =Xnt= arXn pr Xn↓r , BrtCConstantes arbitraires
Page 56 : 6 Montrer que fT1=Antest une fonction rationnettede TSolution:An+1=2An-An-1=Anta T=2AnT-An-1 T"An+ 1 T= 2Ant- " An-1 Tn= 1n= 1--+=T -An+1=TEAn- 1 T-1n= 1on poser=n+ 1,S=n- 1T- 1+ 8AsTS3Ar=2+T-TS= 0EneufT- ATfT+ Ao=+ 1 fT- A 1=2fT- TfT+ TAoT+ 1- 2fT= TAo+ A1= fT=TA0+ A 1T+1- 2BT16fTAn=n !ThT= 0
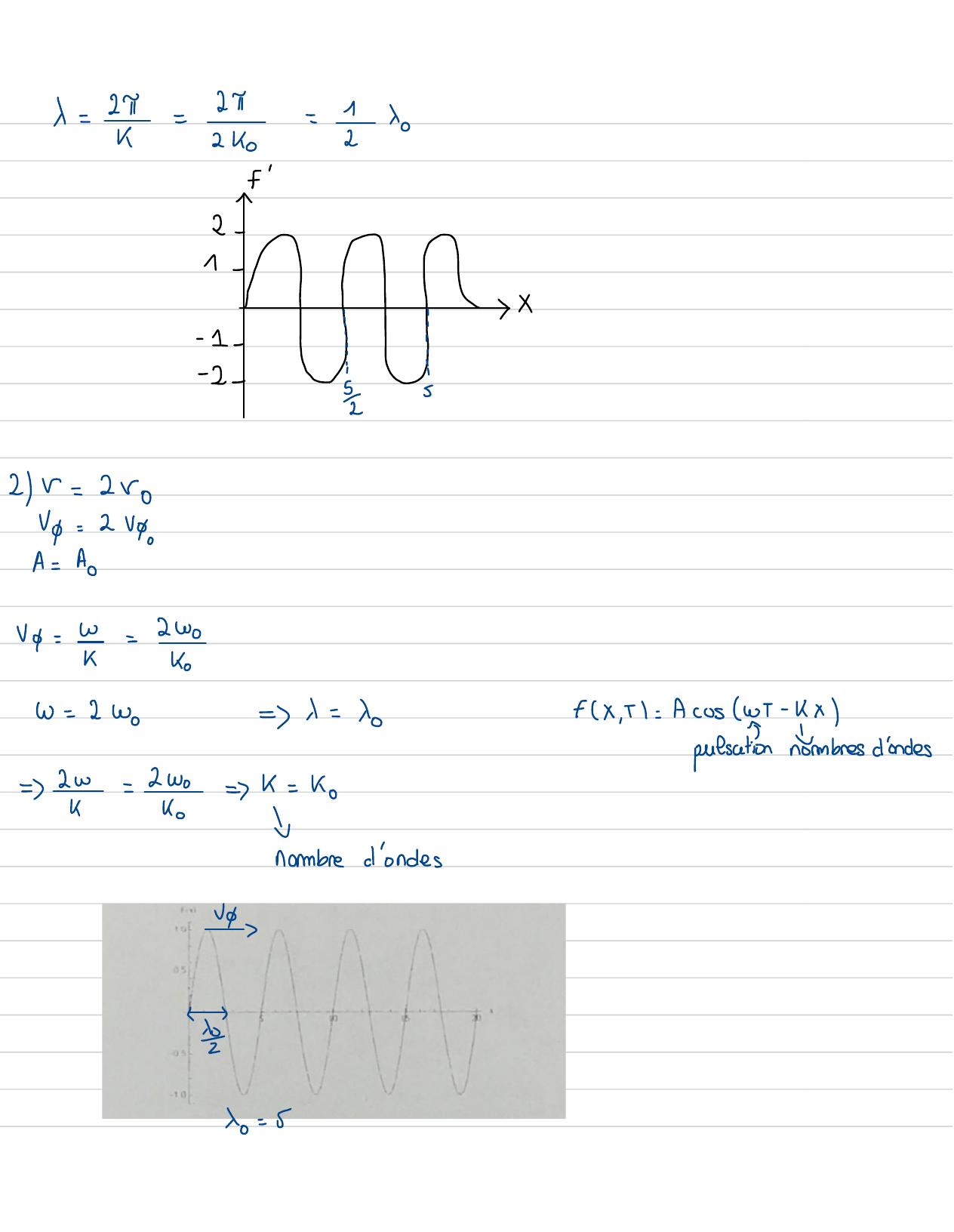
Page 57 : An B Polynome de Chebyshev10+soisWderni- éon eur d'onde1 A est doublée est doubléeVo est constanteA=1=A=1x 2=2doublee5= 2↓fréquence initialeVp= V.vitesse de phase initialeX=?double frequence = doublepulsation.vg= Yx=2π Vwok-ko=2=woko=Y=Ko=k=2ky
Page 58 : 1=2π-2 T-1xoK2 ko2if2-1-::X2 r= 2woV=2 VoA =ApVq= Y=2 wokoW=2 Wo=↓=dofx,51= Acos wi- kxIApulsationnombres d'ondes=2w= 2w=k= kotnombred'ondes·Yo= 5
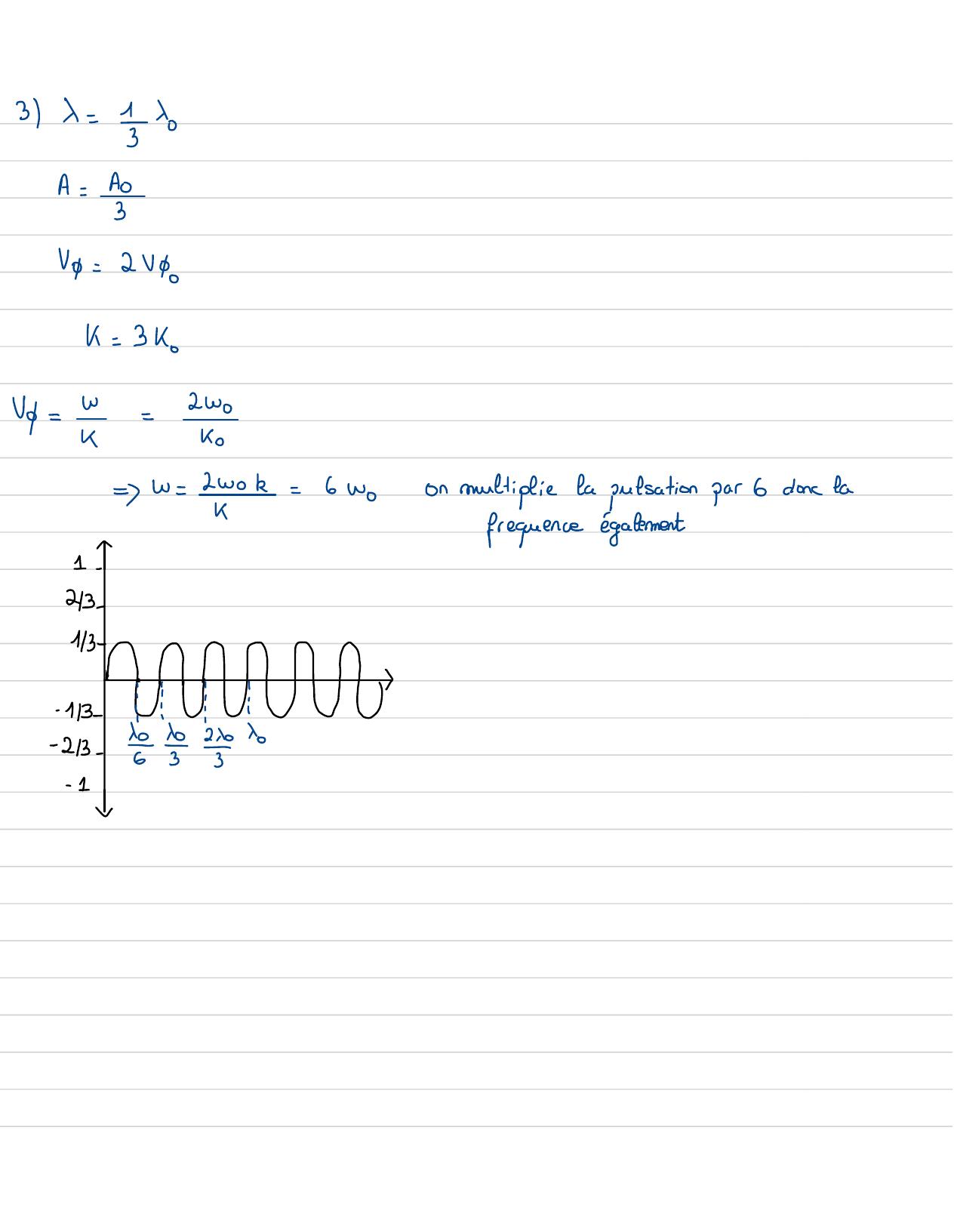
Page 59 : 3X= =A=Ar3Vp=2 VPok= 3ko2woVp= Y=ko=w=2wok=Gwoon multipliela pulsation par 6donc lak-frequence également1213-113 u--113mili-213- 555+
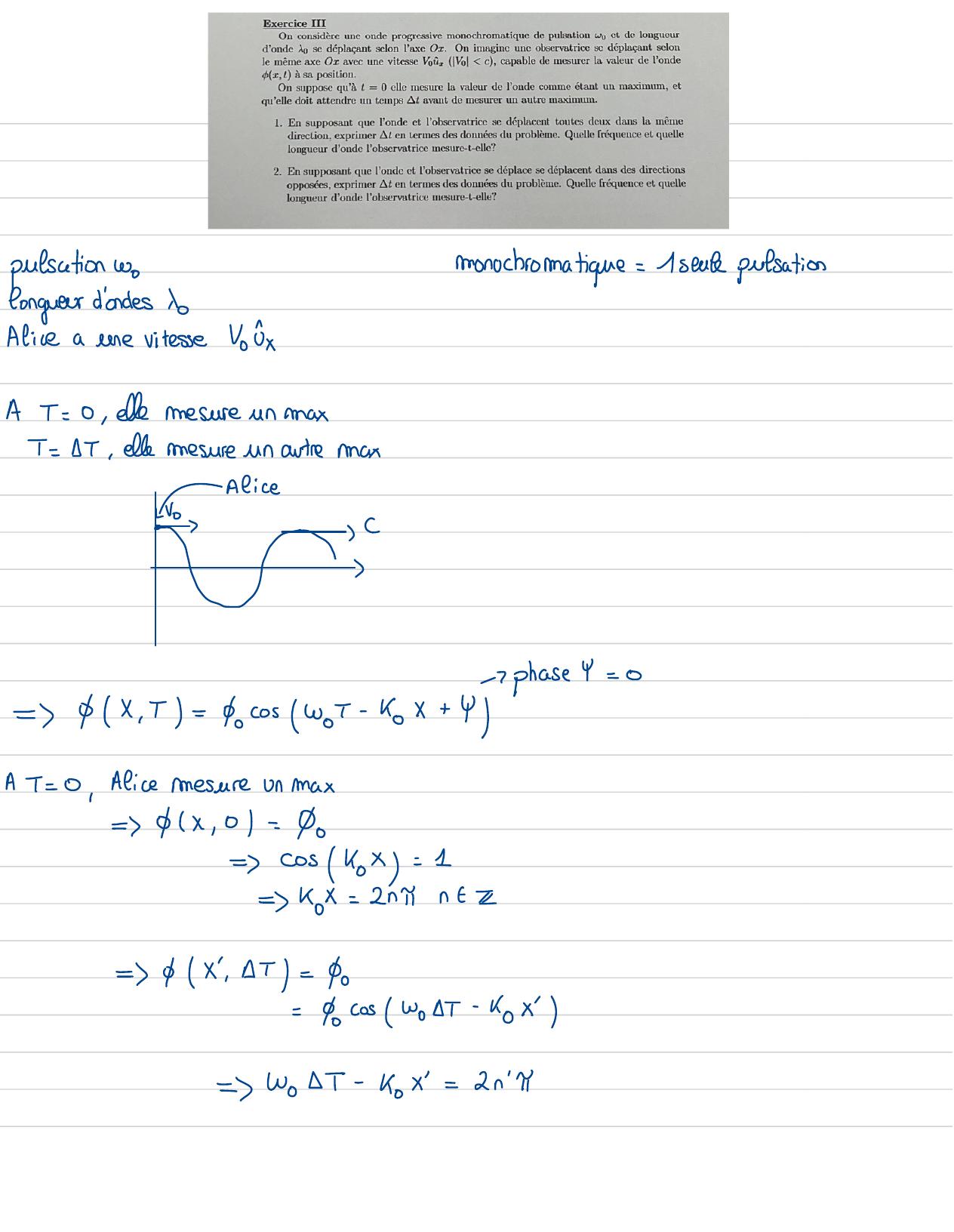
Page 60 : sulsation womonochromatique=1 sente pulsationICongueur d'ondes DoAlicea eine vitesse VoxAT=0 , ellemesure un maxT = IT, elle mesure un autremaxAlicewo⑧2↳- PhaseY= 0=yX , T= PocosWor -kox+ YA T = 0,Alice mesureun max=PX , 01= =coskox= 1=Kox= 2nYnt E=4X , BT=0= cos Wo T-kox=WoT-kox=2 n'
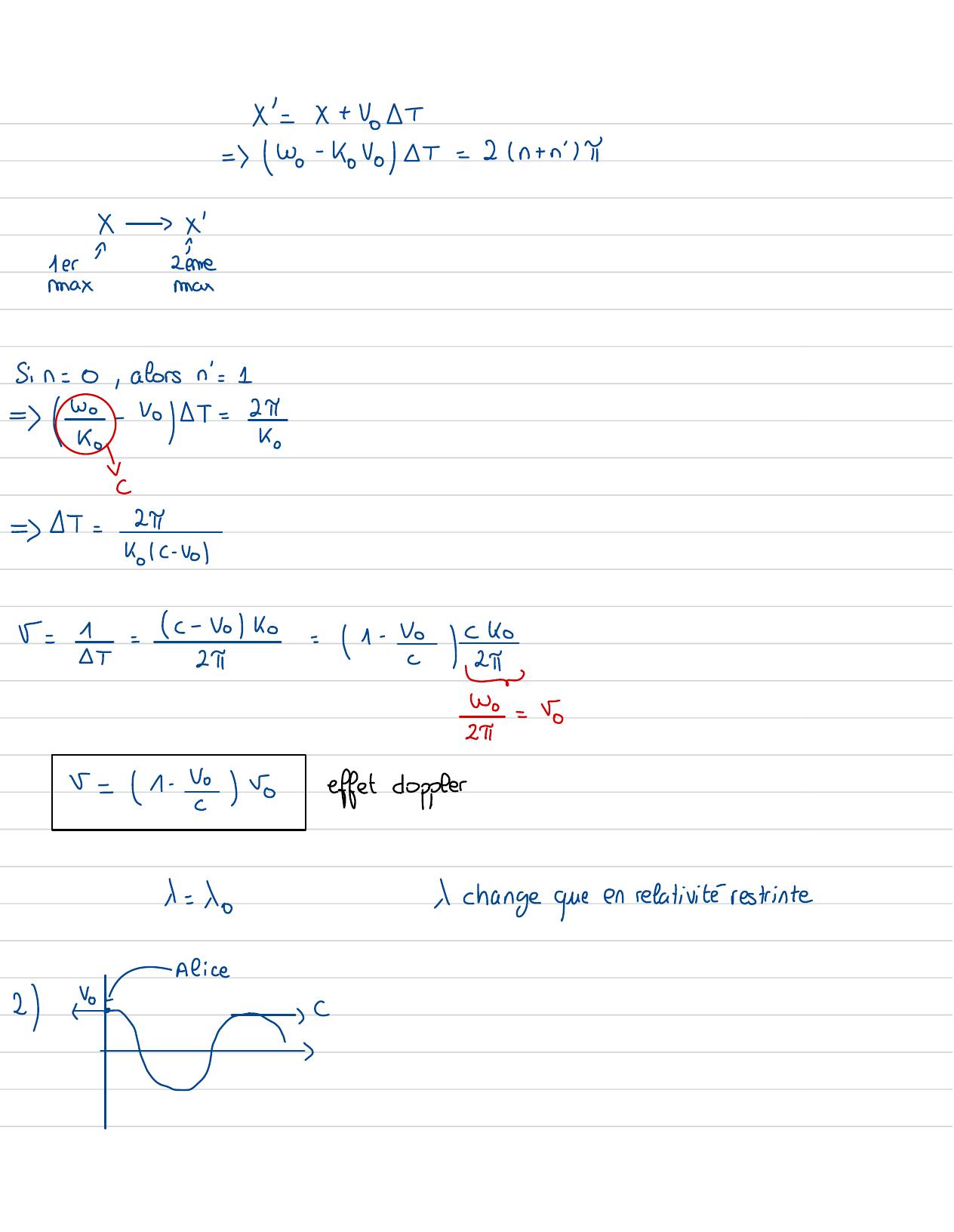
Page 61 : X=x+ VoT=Wo -KoVoT=2 n+n'sh/x'2fereinemaxmaxSin= o, alorsn'= 1= 2- vT=2πKo↓C=T=24KIC-volr =1=c- volko= /e-/T2πe=Vov= 1- Y Toeffet dopplerd= do↓change queen relativité restrinteAlice2↳VoL⑧Ex:
Page 62 : qX , 01==cos KoxPosons alorsX=0à T=0Maxen T =T①X,T1= Po=P. cosWo T-kox'x=- VoT= coswo +Ko VolT= 1=wo+ koV/T = 2=T= rottros=retvosr= i= c+ vol=+ /r= 1+ Yteffet doppler
Page 63 : 1=dorelativité galiléenne les dimensions ne changent pasTD6ad6tyx , t+ 2p2t6ex ,t+3yx , t=0J6tRelation de dispersion:on pose ppc . t=A e"lwi-kxon cherche wK tel quec'estune solution de l'equation6,=- w20, a =- 42,6 + x0= why= 2002+ 2PWK-WK2&:02 + 0=622- 2BWK +242=0=w=2pk=4p2k2- 42k222
Page 64 : W=kB1aEXB2-25Relation de dispersionIVitesse de phase: Vow =B= 12- 25--k2-2icicar 2presationsVitesse de groupe: dérivéede lapulsation par rapporta KIVg= de= = 1B- cr= Vy=Dispersif ?In milienest dispersif s:UpF VgIciVp=Vg=milieu non-dispersifb610-5": G=0,onpose&= Ael1WT-keel64 4= iw"y=wiq:=, q= 1- ik4y= k"=w"- k"y=0=w"= k"&=w=k,- k,ik,- ikRelation de dispersion
Page 65 : Vp= Y=1,- 1, i,- i=V= Vgvg= 4=1,- 1, i,- i=non dispersifcb=p+ a2xq=0,on posep= A eilwT-kson remplace- w+ ck"=0=w=1dk4=1 kdRelation de dispersionVp= w==kXVgE==2k&= 2vgF=Dispersif0a -24+ mep=06x2On pose &=A e" WT- kx=- w+ 42+ m?0=WI= Ick2+ mRelation de dispersionVpF=w IIc1+ m2x2kk 22Vgt= Iw- IC1+ m2x2=Ug=k+ m2x2- k==C-2k 22
Page 66 : =Vg=== =sim Fo, le milieuest dispersifsim=0, le milieu estnon dispersifRemarque:1 . V=1+ m221=74k 2422. m2c2= 42k1- 492Vg2=↳k= mcVgc: quantité de mouvement relativiste pour une1- Vg2Particulede masser et de Vitesse VgIEn mécanique quantique , tikquantite de mouvemente48- 220=0;on pose y: AeWT-kiw+ 2k=0=iw=-k=W = intRelation de dispersionVo= Y=i2kVg= r= 2iak=2 va=Dispersif
Page 67 : ↓tension↓module de Young6dT62-YS242T2-44c↑↳Yox"4= 0↓densitéEre transversale de la cordeCinéïque de masse1on pose o= AeiWi-xx=- w+ ak- bk"=0=w= ak2- bk"Relationde dispersionVo= 2=Yak2- bk4==a- bk2=Vg=Vgt= but== 2w2ak- 4bk3bk-2bk2+ Vydispersi
Page 68 : 2On commence par trouver les modespropresi. esolutions de la formePk= reiwT- kx+ SeilwT+Yx- eiwTräik+seik-= wkOn cherchetel queo respecte les conditionsauxbords:p 0 , 51= P2 , 51=09k0 , 51= eiWTr+ s=0= r=- S&k 12, 51= eiNTreikL+ Sei= 02ikL=r=- Ser=r=e2ik=1=7kn= 1n+ 1=Pr= eiWnTseikne-Seine /=LiseWnTsinknxla solution généraleest mineSomme arbitrairede modes propres :=yx , t=SinganeiWnT+breiwnt-In cos WnT+ BnSinWnTSAVOIRPAR DLaserie de fourierAn=? /x. 01 sinn4x/¢X0
Page 69 : 3 pX , 01= E1Wn B sin n=Br= 2+/x, 0+ sinxdxp= 2 /Ancoswi+ Bnsin will4Le piano:↑X , 0=06+ 0x , 01= 3 a An, Br=?An= 3X ,olsinn4x/dx=0Br= Zon !x , 01singnex / ex= je singex ax
Page 70 : =- zu icosnate -cosnaLWnEx 1=Br =E sinacosPa+ 2= cosna- sinnyadb Application musicale de la dépendanceen a ?Wn pulsationentendueBr -Volorme du Sona=4=Br=sin 4=0Wn-1est présent, mais paslunB=0 il faut frappersurLongueur
Page 71 : ca= 2, quelssontles harmoniques presents Wnt0Donner/X , 51Br=j 2sin/IOsin est pair1sin= 2k+ 1harmoniques:W2K+1,K=0,1 , 2qx , 5=-21" sinXxSinWaktT9 Yx, 01=x a02x2 aI L- XaXkL6 + yx, 0=0a coefficientsan et bu?
Page 72 : Solution générale:-x . 51=sinx ancoswnT+basinwnibr= w !sin x6 -x, 0dx=0an= 20x,0/sin/n x/dx=3!Ysin/x/ax+ /Y- xsinx/dxa- eIn =sinxdxI1I2- xi cosnix - =4xcosn4x+ 4!cosn4x/dX=-cos/na+ fünzsin nx
Page 73 : In=cos/ + n sin, alIz= /ic-x xexindix cosnix=4/- x/cos/4xa in cosnex ax=n -alcos/nya- Insin nyx- calcos n a+En singaok= eiwT/Aneikx+BKeiRXconditions auxbordsicern T=In=sin /Exek= 4p0 , T=0solution generale:- 4 and .51= 0-2ikLAk=- Bre
Page 74 : an= 31 =+Fz=3 -al cosjuray- me laal Singual +alcos/ -ne Sinnal=3 latesina= ansin a=anb Sia=↳, e=?an= eSin=Sing= E=↳SesE=h2=, 2 modeI- 1sinon
Page 75 : TD7PD I .densite-TI62Px, t-62PIX , T=0Uf8 t 22x2t↓pression atmosphériqueIindice adiabatique1 Relationde dispersion ?vo= Vg?WIK= relation de dispersionon pose PIX, T= Po eilWT-kxI-w2p , t+ k2X, 5=0Uf=k2=w29592=W2=WPKRelation de dispersionf
Page 76 : V0= Y= 4+2Vg= j= P+ 2= vo=Non dispersig2 P2 , T= P0 , 5=0Modespropres?In=sin /4x/ eiWn- CLun=Vokn= n2424222in=km-n-RLongueur d'onde maximale:22
Page 77 : TD 7PbI↓pPX. 5-24X, 5=0e6x21/c1. Relationde dispersionVo ?, Vg=?Solution:PIX, 5= PoeilwT- xx62CX, 5=- w2Px, T65262PX, 5=- 42 PX, Tox2Eg:- w2px, T+ 42pX, 5= 0aeO=22= ckRelation de dispersionw=2k=C k
Page 78 : V=Y=C=VoVg= Y=c=VgV=Vg= non dispersif2 P, T=P10 , 5=0Modes propres?Wr= CkOn posePx, T= eNT/Are+ BreikxP 10, 51= eWrTAr+ Br=0=Ak+ Bx=0=Ar=- BxPL , T= 0=eiWkT Are+ Brei=Ar=- Bre2ik
Page 79 : -= ézik- 12k1=2n π/e--1n=kn =↳,nt E=Modes propres:Wn= nRx , T= eiwTsingnYx/ISin 0=cio -ea↓pas oblige de temettre2icar les modes propressont définie àun multiple scalaire petComme espace vectoriel ,Ux ou X çanechange rien3P0 , T= Posin/WoT, NoF pulsations propresSolution générale?Solution générale=solution générale homogène+ solution particulièreAnsatz=PX, T=Sin Wor-koX AP0 , 5= Asin/Lko/ Sin Wor=Posin Wor=A =nikollPIL, T=A sin WoTsin 10=0
Page 80 : 122I62P226521-jx2=0!=- woPX , Tj=- koPX, 5PIX ,Test solution particulière si :Wo= ck.Solution générale:PX, T= PosinWoTsinCkoK-x+ AeNTsinnYY Sinkotne ITrouver l'Ansatz ?PX , 51= AsinWoT -Kox +BsinWor +koxP10 , 51= Asin /WoT+ BsinwoT=A+ B sin /Worl
Page 81 : cos Wor sin koL +SinWoTcoskoL-PI , T1= AsinWoT -KoL+ BsinWor +KoLlen- cosWor/sinKoL+ cosroL/Sin WoT=cosWoT-AsinkoL+ BsinkoL+ sin/WoT/ AcosoL +BcosKoll=0=B=0doncAnsatzne functione pas
Page 82 : I ↳xypx= 2x, yic2224- 2224=0RYx , T=A - eikr25- x+ Breik2 T+ xx YI Azeikz C25- x+ Breikz 2T+ xx, 2↑C-aEn utilisant lesrelation de continuitéobteniruneeqM = B= 4252relation de continuité:Y y, T= 42 y, TeikecTA = e418+B1 ei / B IVraipour tout IIeik=eik A = e28+B1 e27 I2iT= 0Ar+ B= Az'+ Bapr
Page 83 : = eik= eikaceT-trecel6xY1=6xYzx= yx= ya T =0-ik1A1e 1+ ik1Bey-- ikzAje28+ ikzBze"2y=- 41A1+ B =692=k2Azp+ kzB2 PM EE=42 Lignede la matrice= facolonne=variableMe=IL-1K12IA1B1
Page 84 : - 1M1=BEq111 Eq22KaAzB221 I ?? = ac-x" âCalculer MIMa- G=Ir a1BMitr: In se t rap=Exka+ k2KSB-YBk1-k2& Bak= 1+ k2=I-1+ k2/k1&B1- k2/k2p1- k21B1+ 42m
Page 85 : 3y=0,B2=0I: E= ?= x=n22y=0== B= 1AzE= = - inte0Ar=1+ EA2, k= 2k== E=Az= 2B == 21- 4A2= c+c1- ==B1=2- 1A =22+ 1
Page 86 : TD 8:UenE=Sin /Olcosr-will-Singhr-wist,a divE= ? , rotationnel E=?divE==+ +GAz52-ExcI· EParArtrsncalasincasAa+ Irsincas---&A 4
Page 87 : =0---roT A=XA-niaalApsin Callr- 1IrA48-rina2sinialcoscal/cossul sinra-coscal-" /cosUS -sincultricEn eb. E,xx =1= !merrotationnelA= cure. E1=0f=Güx+ Gfy +-0--13.A=usincal 0 +&x1 r 8rsin0& P=⑧+rxA10 -jo xYr8
Page 88 : Kr-WI28rx = 0=-sincos-KsinTos -cosul +Esinvis=- sin 0 -k"cosv +1 cos 1rl+Ysin V -rsinr+ I coSr--sincol22- 42 / cosrs- /Ers-sincos-- sin 0 22- 42 /cOSW- Isincus& xAr= -25cOlcosrl- ISin Colxxl==cosOl- Isin col-sincos- R+ 2 sinca= K2sincalcosr- -sin u Irt-K2Kr- wTE -=65t=- w"E
Page 89 : k- -E=7. Al-xx Eme= 0=221- wil-1- KES=k2- w2EI-2en122= cr"-O,Eo , No , ff= 051 ==+ Po-= 8al Montrer Que:16 T26 Ti.=0ii=. B=0-ix-=- ↓B-Tliv=x=No+ Not
Page 90 : xx =1=x- 55= Ix 5+ /No+ o= Pos- por -- =E-x1x ElIwa= 0Nodo=1= NocoEn+ No22b M0si E = jelwT-est solution siE -w- in w:vecteur d'oncle:directionde propagationde l'ondeE: PolarisationproduitscalaireX. E=0divergence de E= &Et6 tt↓Ee5462-D'apres Maxwell:. t=0
Page 91 : -E= Y+ 64+6tzcomposanteenxdeK. Ux62-E, -ikxeiwt -. + E , -ikyeilwt-+Ez -ikz eilwT--E= ikE=0car.=0=K. E0↳Champs magnétiquee· eilT- -B--xt=- 656 Trotationel E=- ik x E=- eilwT-- iw Bo---Eproduit vectorieldextBo=kx EswJE= iwE↓I2-6 E652=- wencartesien2- 222222222222E-ttM52X62 Y522I---Laplacion:. 2-x42 i
Page 92 : =kE - kyE- K2E=-EE=- w2 -+iwpoo+ la. E =c2-=a. k= w2-icopo o-2c= ke 2,k , deik , d=?= ke-id= w- iwkeidw iw24=k"=c+ wa2=k= Y1+ Ya244w↑2cos14- isin / =2- iwNoo=k2coS4=wh22k2 sin l= wNoo22=Tan /P=No O↳
Page 93 : TD 5- 6 - 7Isauf exo 1 TD5+ question chap4 et 5orcos101= E=rowcjoNoch1A savoir :-Equation d'onde :2 I: oRelation de dispersion: wk↑= deilwT- kx↳-=vers fa droite=vers ta gauchew= pulsationK:nombre d'oncle: AmplitudeDirection: Iv sikOSolution générale:d= fx- cT+ gx+ cTf, g deux fonctions arbitraires
Page 94 : =fik- wi+ gikx+ wiW=CKondesen milieu finie ,avecdes bords& 0, T1= hT0 2 , T1= 515I derichletI ona la dérivéede La fonctionaux bords /Neumann6x P0 , 5= h'IT6x42 , T=51TPrincipe de superposition=x, T , P2x , +1&1a , T=h, T, 42a, T= hzT9.+ Ya. 5=h =5+ hzT=solution generale= solution homogène + solution particulièredr= eiwTareik+ bre"/9ka, T=Pxb , T=0
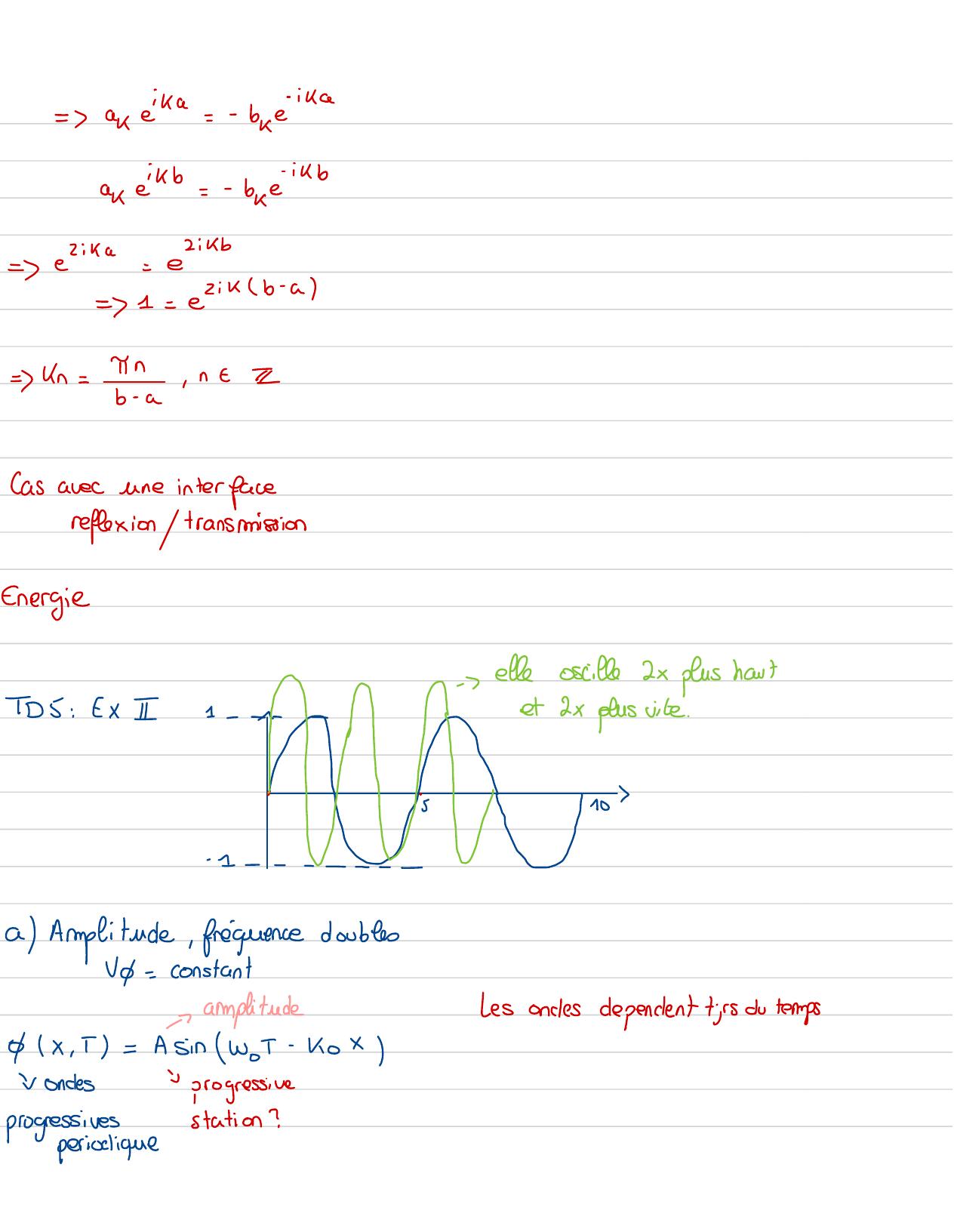
Page 95 : -ika=apeika- beKap eikb=breikb2ikb=elika=e=== exikb- a=Yn= Y, neECasavecune interfacereflexiontransmissionEnergieTD5 : ExI= ---elle gilleslus La teeNWinWN---------a Amplitude, frequence doublesV=constant-T amplitudeLesondes dependent tjrs du temps& x , 5=A sin WoT -kox ↓Ondes↓progressiveprogressivesstation ?periodique
Page 96 : Dans lacasoul'onde est stationnaire:onde:sin Wotsin /kox↓l'ondeso deplace pas, elle faitque oscilleprogressive= ellese deplaceVitessede phase ?:- pulsation nombrederadian panniste tengs, erni dans fonde wo -1s, Ko: 1/mVy= wVg= Dw:Vitesse de groupe-Nefrequence= Vo=woI pulsation/252π-7 nouvellecondeon a doubliep'x, T=A'sin wi- kxWcar on a double la frequence u-A!2A-= 240= 2=wo↓ondouble2π=w=2woVo= Y=szwo-k
Page 97 : =k=2kowo=vitessede phase InitiateKo2wo= Y:vitessede phase finale6=2 Asin 2woT-2kox/A= 1Wo= ?2ko=-Do=longueur d'oncle:24= 5Hkodistanceou l'onde revient à sonpoint de départ1= 0=25↓nouvelle longueur d'andedivisée par2 carKo était x2.2 W=2 Vo, Vg=2 Vp , 0Az= AV= 20=w=2woVy= Y=2 w
Page 98 : 2w0 =K= KoKpas borge=bouge pasK=↳= do=Le dessin reste inchangeTDU: Exo iecx↳on choisitce que l'on ventsoitcos soit sinroxmais sion prendun &= 0gx , T1= AcoswT- kx +Y dephasagerout mieux proncre cosYoure.9,I0X , 5 peuts'ecrive: AcosWT- kx+ B sinwT- kxA T= 0, l'observatricemesureun max.Sion suppose qu'alors elle estenx=0=Acos0= A= 0=,0 , 2π, 4π=Px , T= Acoswi- kxG X:T= A= AcoswT- kVoiI↑X psiti de l'observatrice↳= cosw-kvol 5=1=w-kvoT=2πn, neETest le deuxiememax=n= 1
Page 99 : =T= 2vo-nombrefrequence? Wi=MaxUnitéde temps=1=2r- vo=c- vo Y/x=21- 2= r1- YL'esse de L'onde /=VIWi=4TC-vitessede phaseC= -voT= x-C-vitesseLaquellese déplace l'ondea- Vovitesse i laquelleso déplace l'oberatricedoncvitesse de l'unde=c- Vo
Page 100 : es er 79=On remplaceVo -- Vo=Wi= 1+ 1= xTDEx0 1:Relation de dispersition, vitesse de Phasewiklvitesse de grouped Klein-Gordon1624 -+ m4=0c2652on suppose que p= eilwT -xx-w2p+ 42+ mes=00 =O=w= c2k+ m2c"-2=w= ck2+ me
Page 101 : Up= Y= ik+ mi12=c1+ MaiCK=vitesse de la lumièreVg= I=2mini-1+ m2c 112+242kVp+ Vg= Dispersif
Page 102 : &T=iw6x=ik1 0-AewT- xx-on remplace, if faut culauferles derivie524=- wd22 =- k42"xy= k"p= wrp+a- 45"y=04T8=3- w2+T42-Ys " "=044 5445mereAB=W=Ak- BK" Relation de dispersionune relation de dispersion C'estune relation qui refie wetk
Page 103 : vitesse de phase: V= YV= AkY- BK42vo= a- bk2/12Vitesse de groupe:dérivéedew par rapport à Kvg= r= iAr2- Bx" /12=IAr2- Bx"-11272AK-YBKY/1-A-BK2112 /A- 2k=A-2BK= VgV4DispersifcarVg F VYon verifie:Vg=Vg2-bx2VoSib= 0=Vg= Vy don pas dispers.I=Vp-bu2voDispersif b0
Page 104 : 2 P X , T =ancoswnt+BusinLonTsinnex:ouvertbord ouvert, fixes:↑10, 51= 41 , T=0corde: soit libre ou fixestuyau: soit ferméou ouvertbord fermé: 6x4 0, T1=0= 6x4 , T↓revoir celle laOn poseikx↑x,T= = eilwT -kx+ reilwT+kx= einTreikx+re90, 51= eiwTre+ rz=0=+1+ 12=0=yr 1=- 1pld,T= ent/reikkein=0rarik+ ren -0=E=- rzelik=- rz=2k= 2nnt1
Page 105 : iOe=cos01+isin 101=1cos 0= 1=0=0 , 24, 44...2n, ntI=kn =π↑1=-52iWT- ikn XiknXPrX , T= reS- e+eI-2isin =Zirzeiwntsinn4x=lesmodespropresbase de l'espace des solutionssonton:eiwn Tin /SiSep +2- abx"-b2 /4=0-pérateur lineceeInfinie: endomorphismeRodes propres vecteurpopec eefinie:MatriceIIvecteur propres de valpres
Page 106 : constantes modes propres-=4x , T=gnx, -combinaison finéaire demodespropres-angn+1 an An=0-aneiwntsinn4x+ aneiWentsin-n4xS-Wn- icon T-Esin aneiwt- ceI-lan-an/coswat +iman/sinwaieanBr-Esin44x//ancoswnT +BusingwnT3an=?4 x , 0= =ensingt
Page 107 : 4Yx , 0=0,6 + 4X , 01= -0 siacx2a+ 2E-aLn, Br =man= 2/ 4x, 0/sinrx/dx=0Br= En!/. 2sin dXex1,sia- bx = ,/Pfxdx =b- afafonctioncontinue--Bu-v sinaG Applicationmusicale?Les harmoniqueslessonsproduitsLe valume"de lapulsationwn, estprop à01+/4n/2=sin=0, westabsente !
Page 108 : TD7:Pr I1 2 p-22p=0c26 T26x22 P10, T= P12, T1=0Rodes propreson posePIX , T=ent Laei+ beon imposetesconditionsaux bords=PnX, T= eiWnT sin n /4 Ix , 51= -Prix , ilan=sinxancoswaT +BusinweilPl0, T1=Po sin /WoTlwon'est pasune pulsationpropreCon=&Cw= ckk=πL
Page 109 : ↑x , 51=!Isolgénéral inhomogène=sol gen homogene+ sol particulione inhorogenePX, 51=Asin wor/Sin k-x1SinkLP10, T=Asin WoT=A=loPX, T= PosinWoT sink2-xsinkL6219-- WohP22C Tc222p2x2=- k2pC'estunesolution si-wo+k=0=k=woCSolution générale:↑x, 5= Posinworsin -xsinanx,
Page 110 :
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110