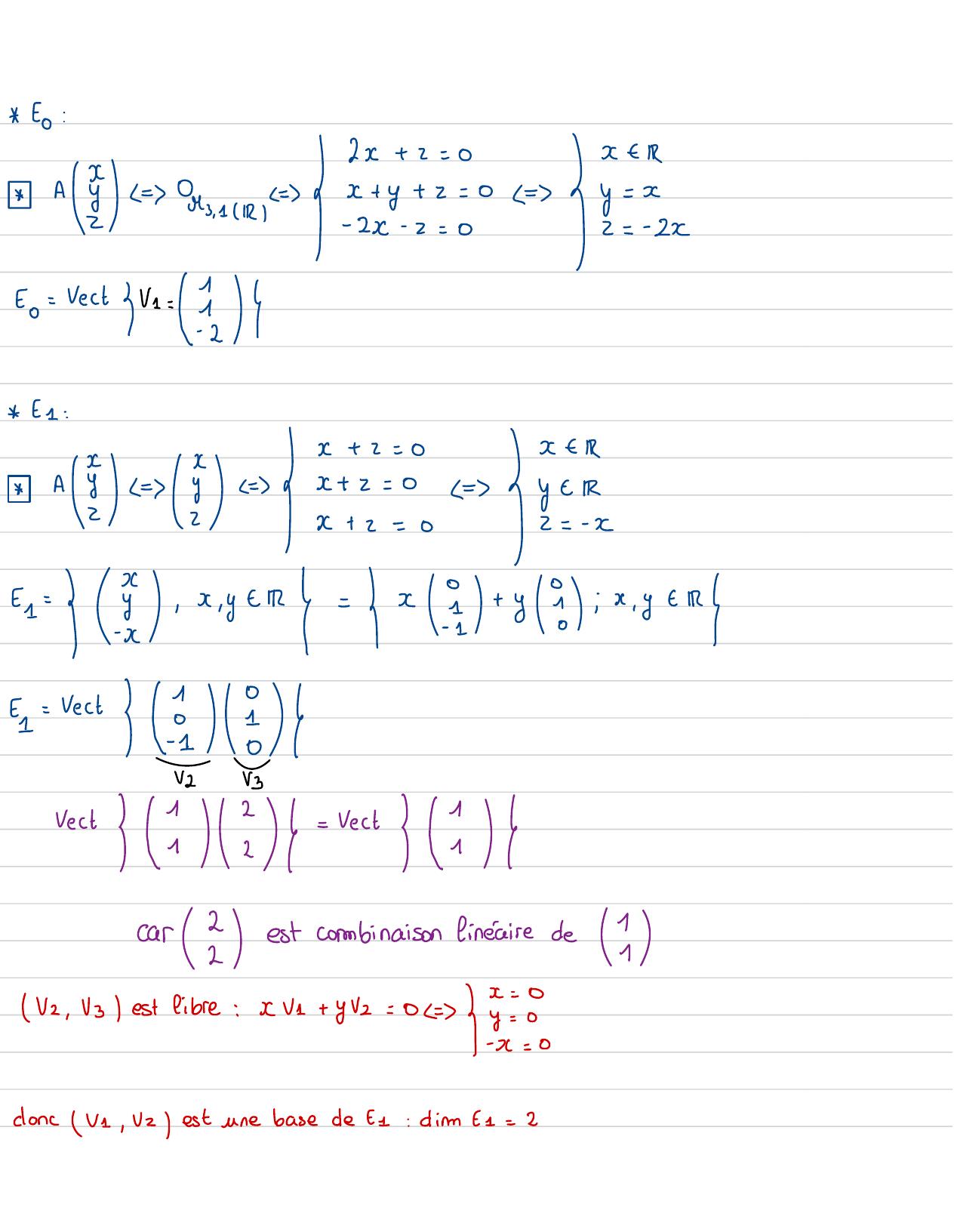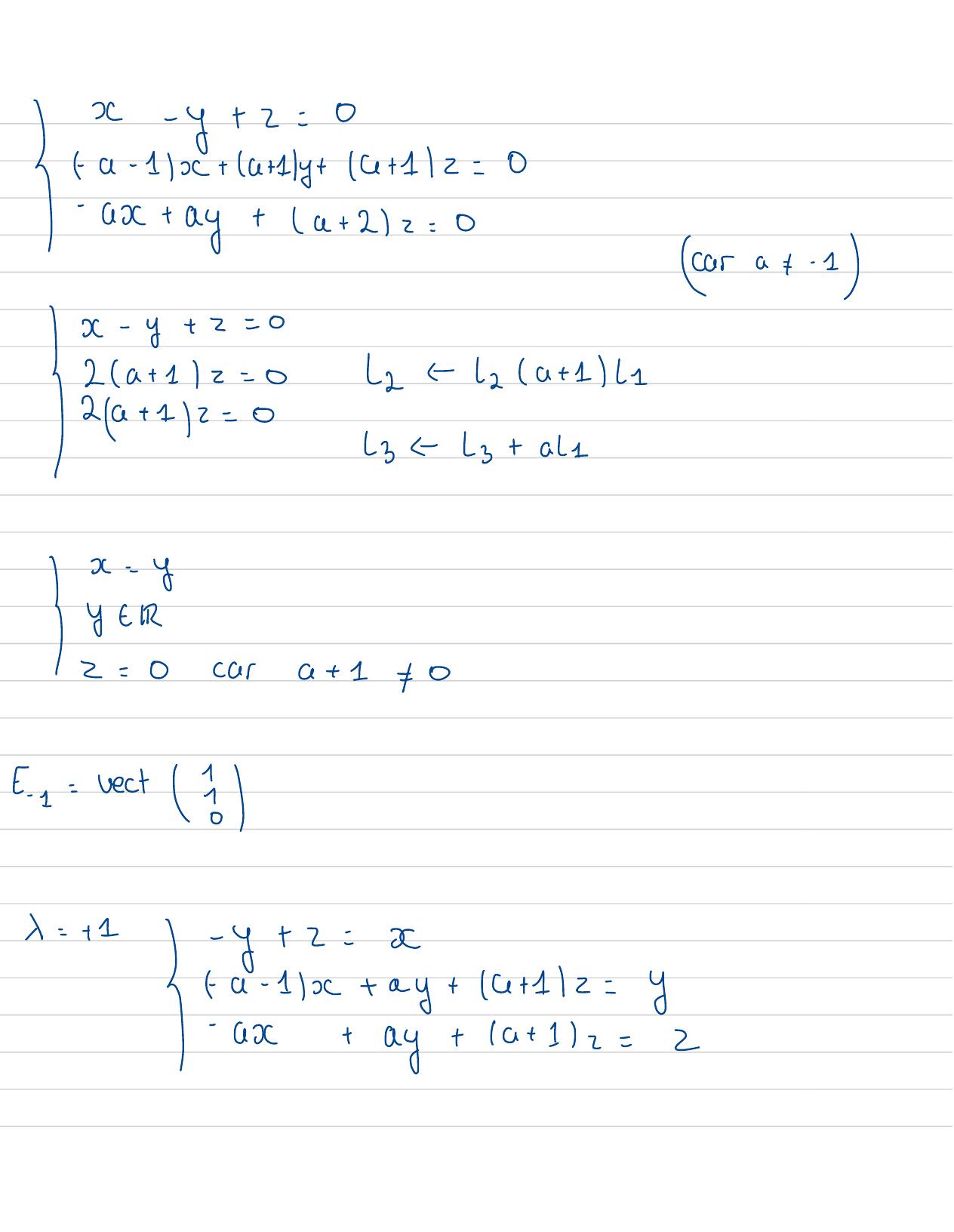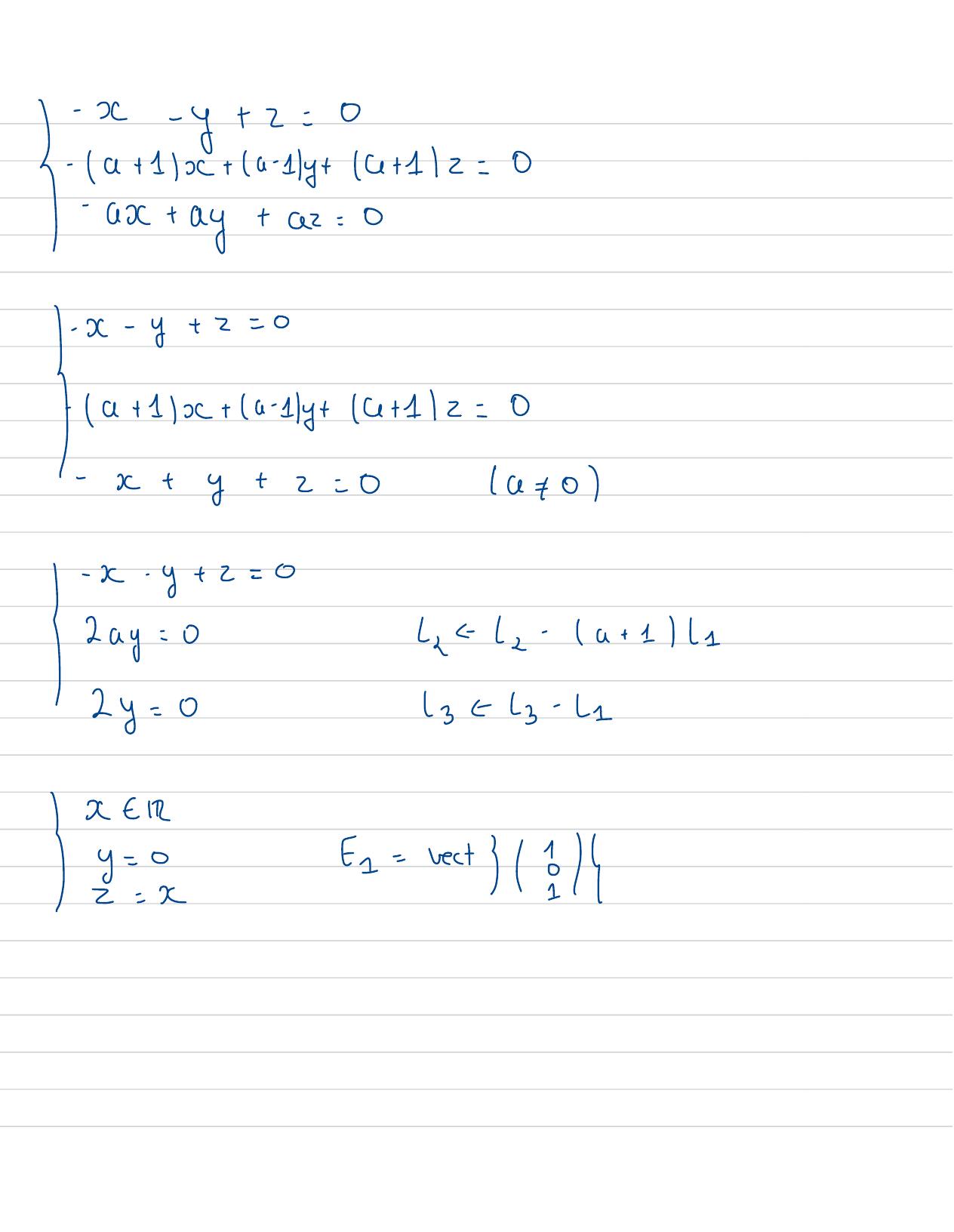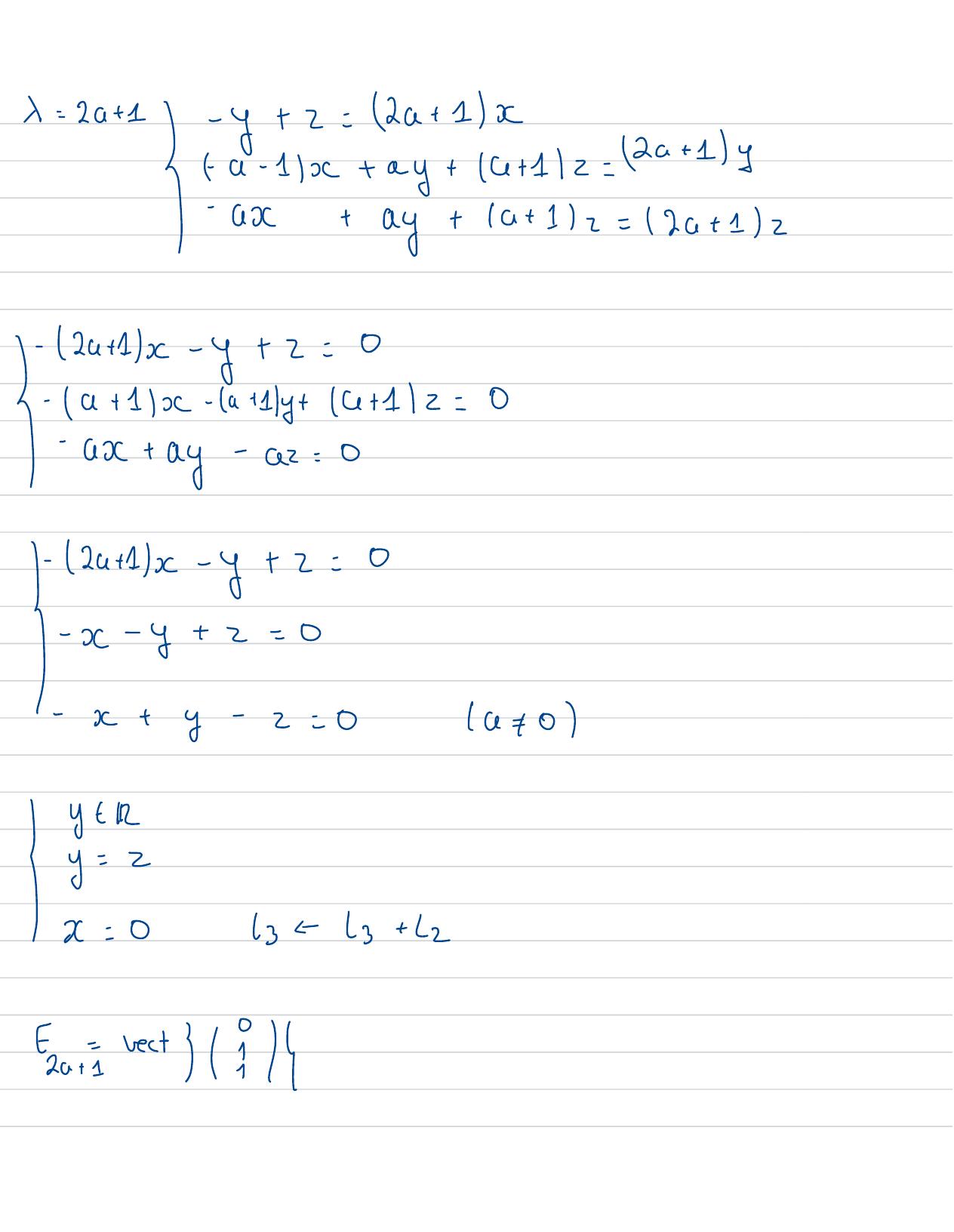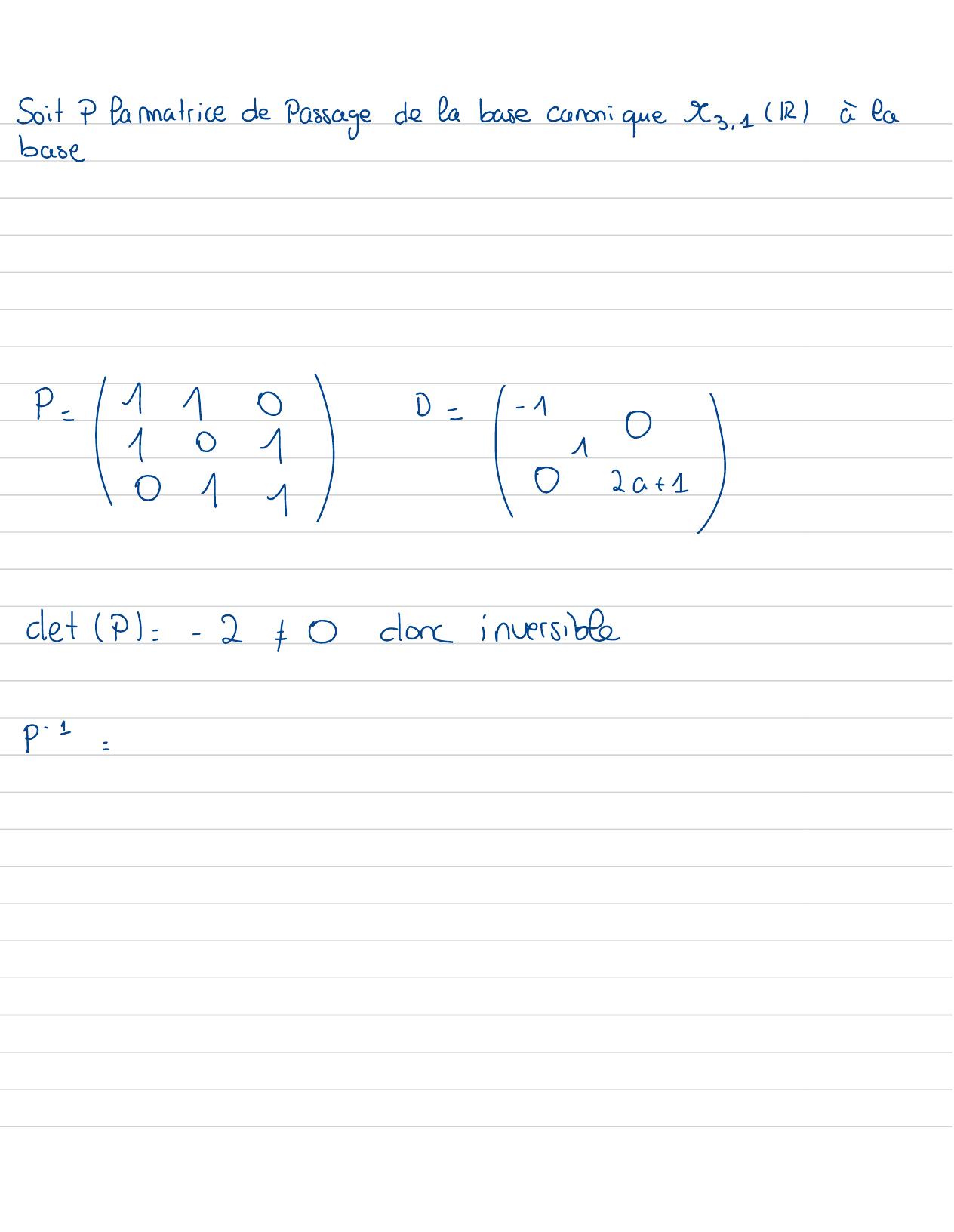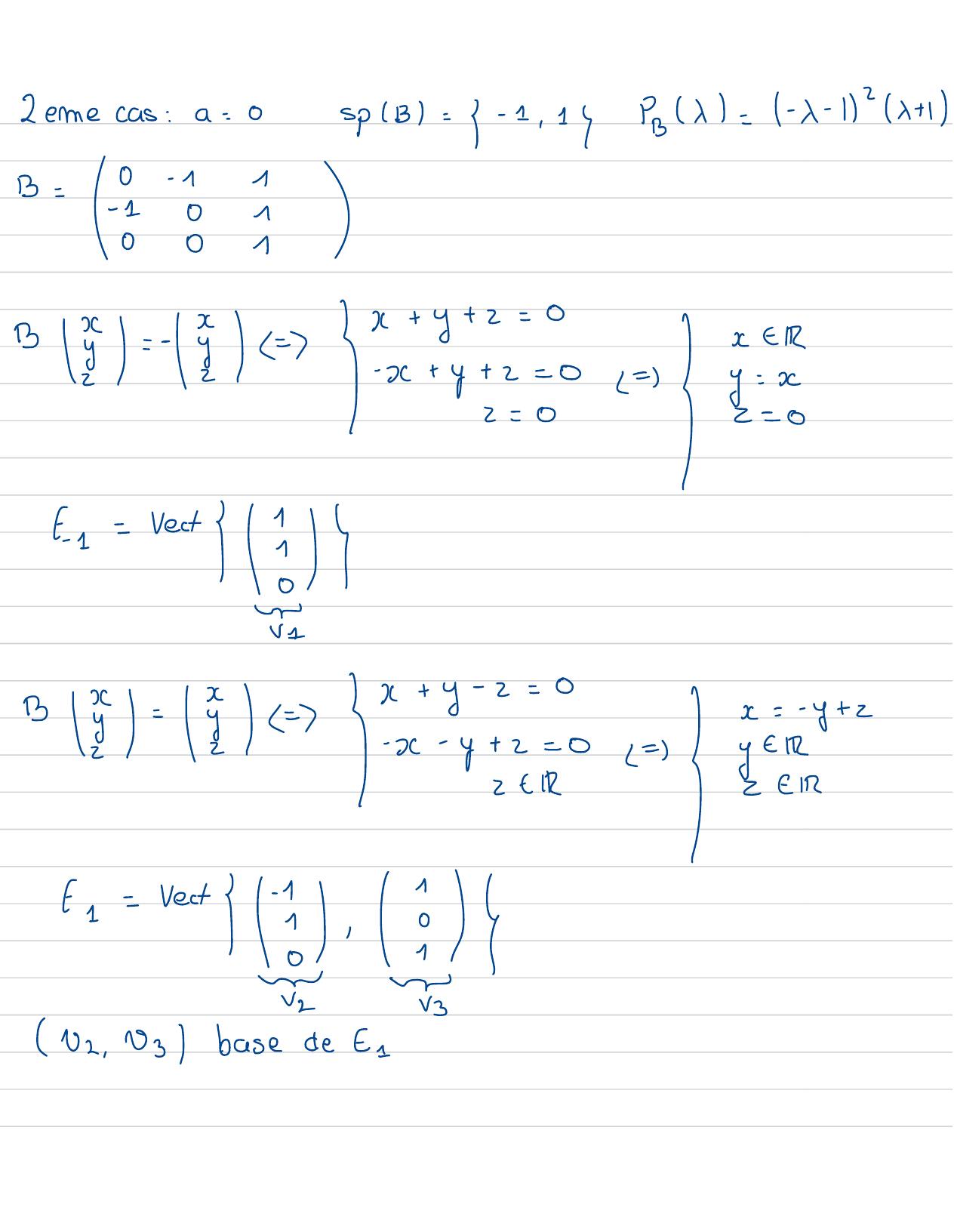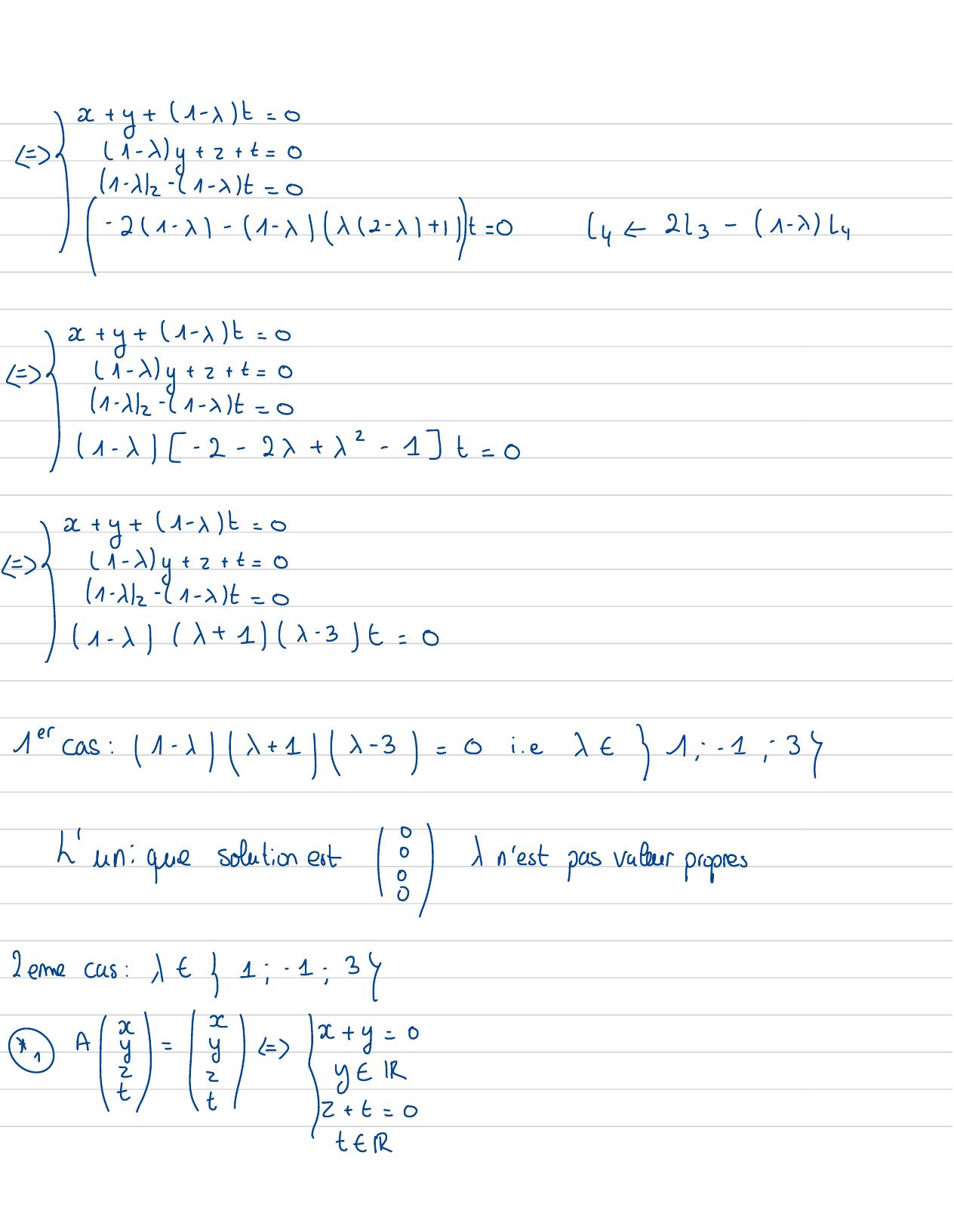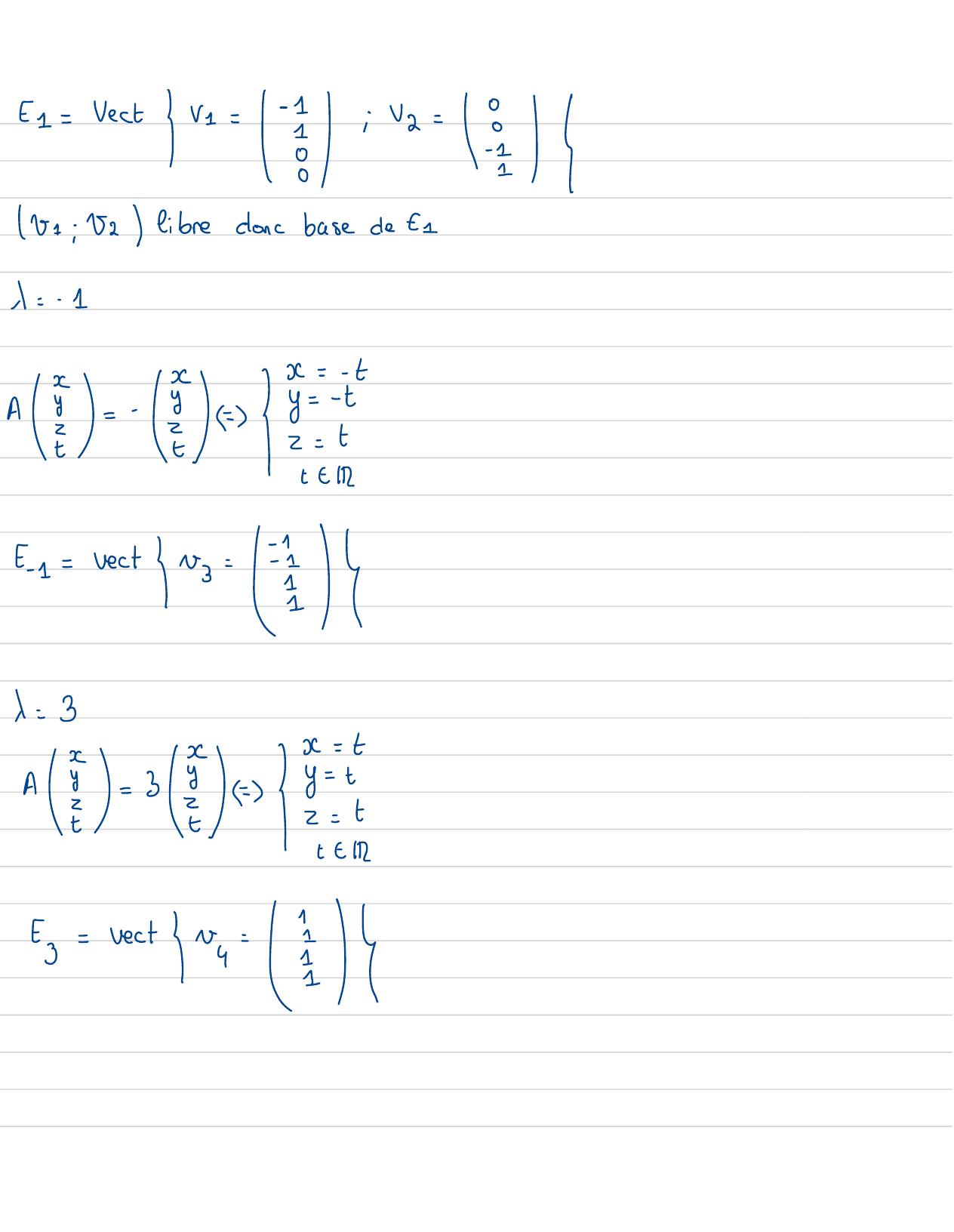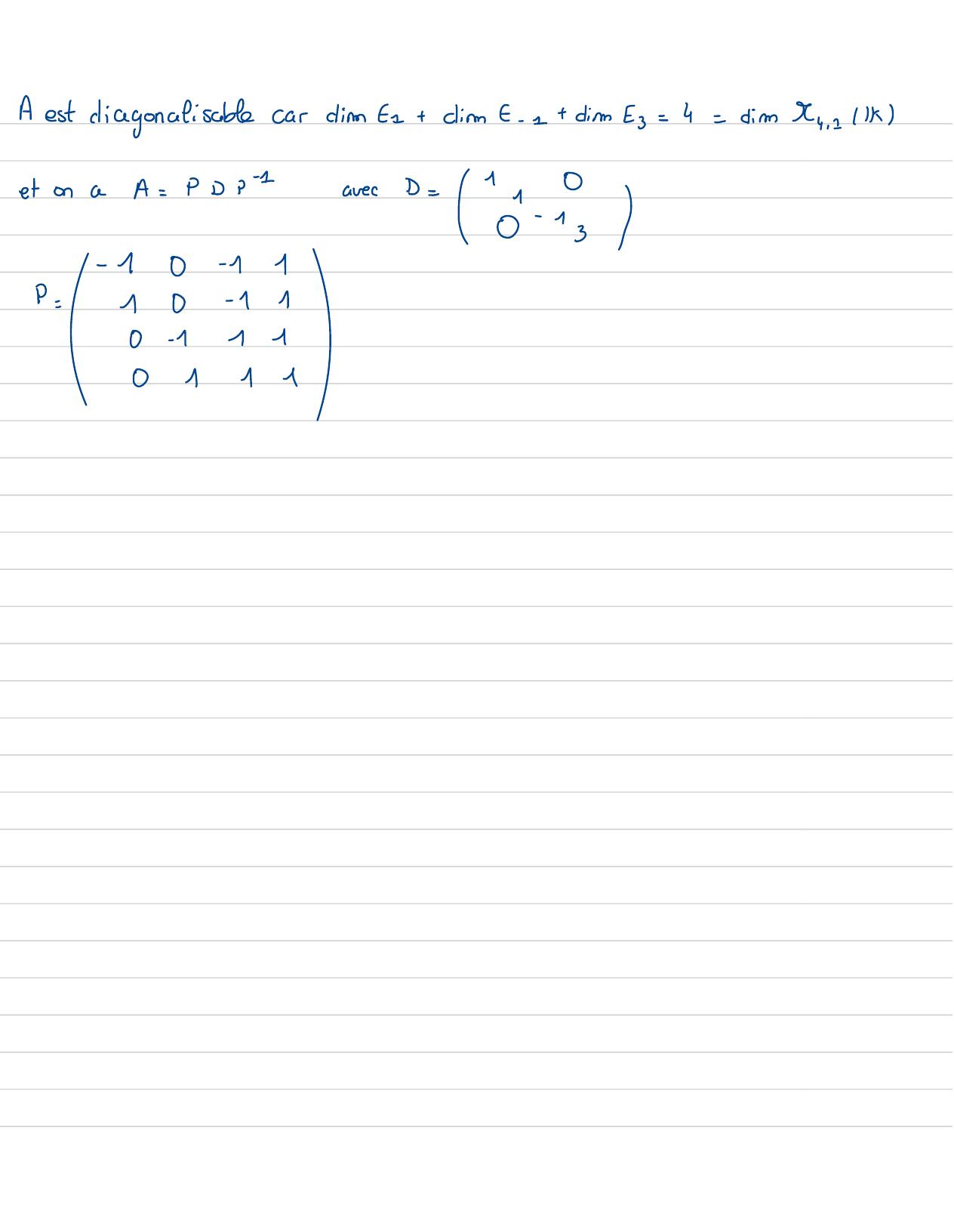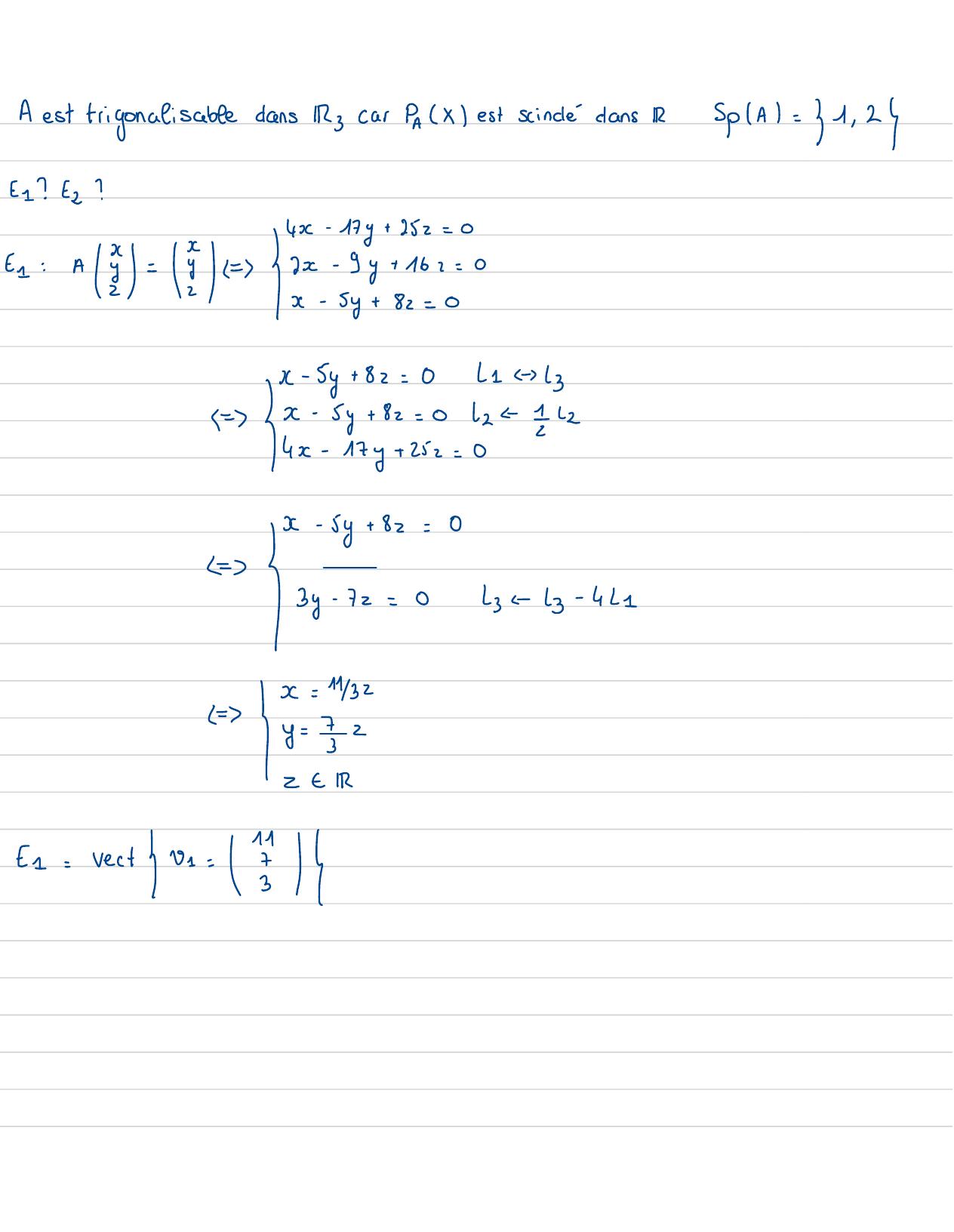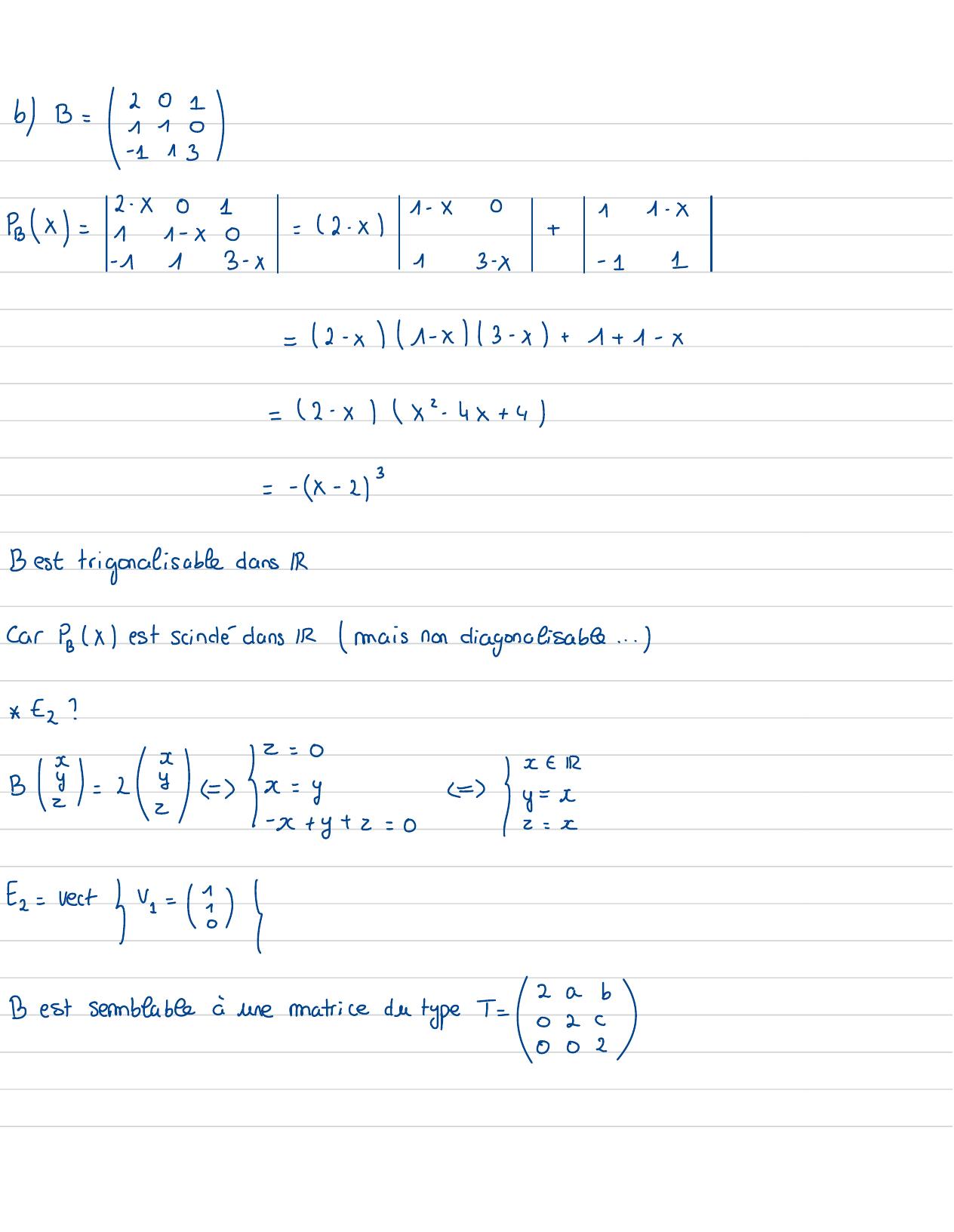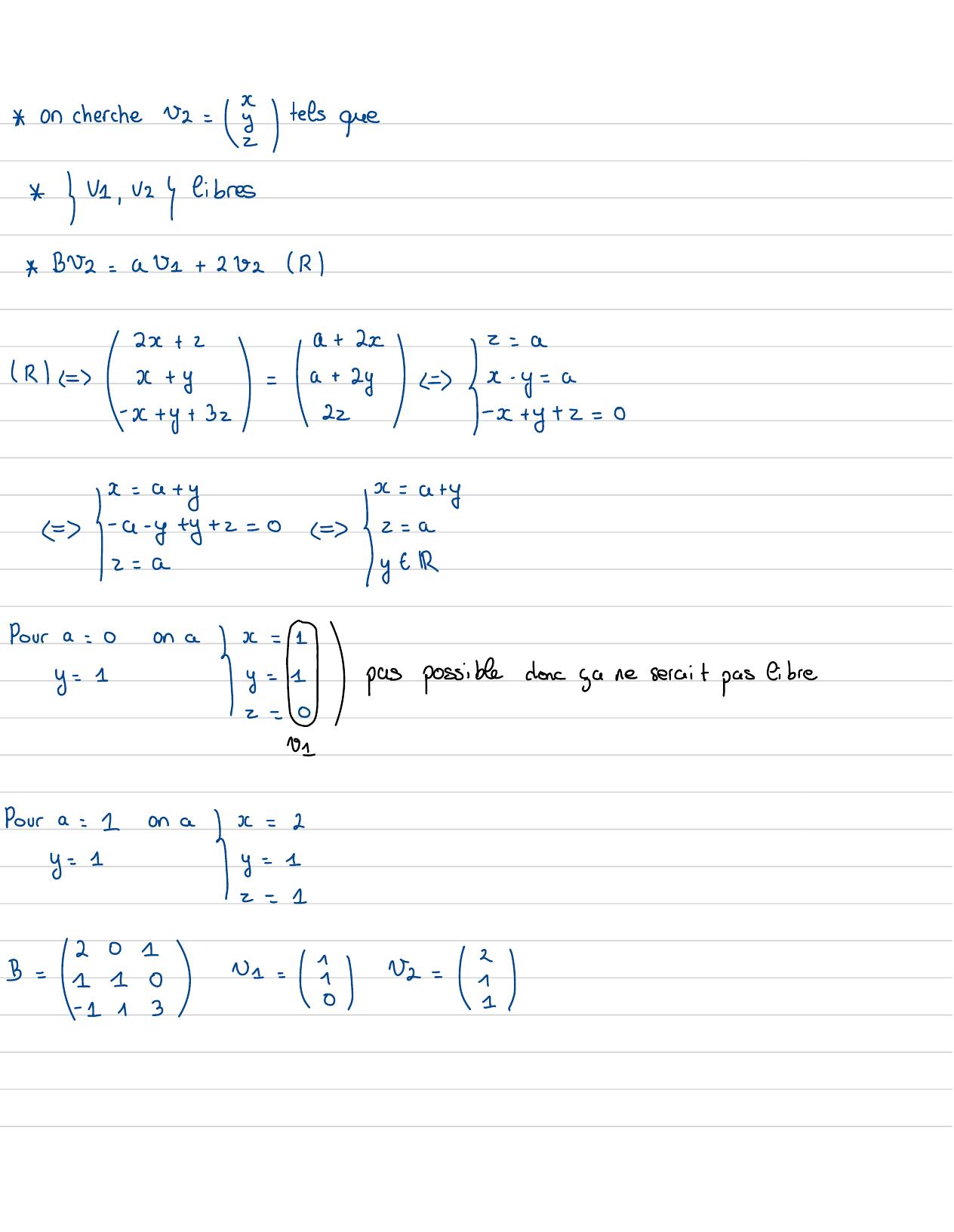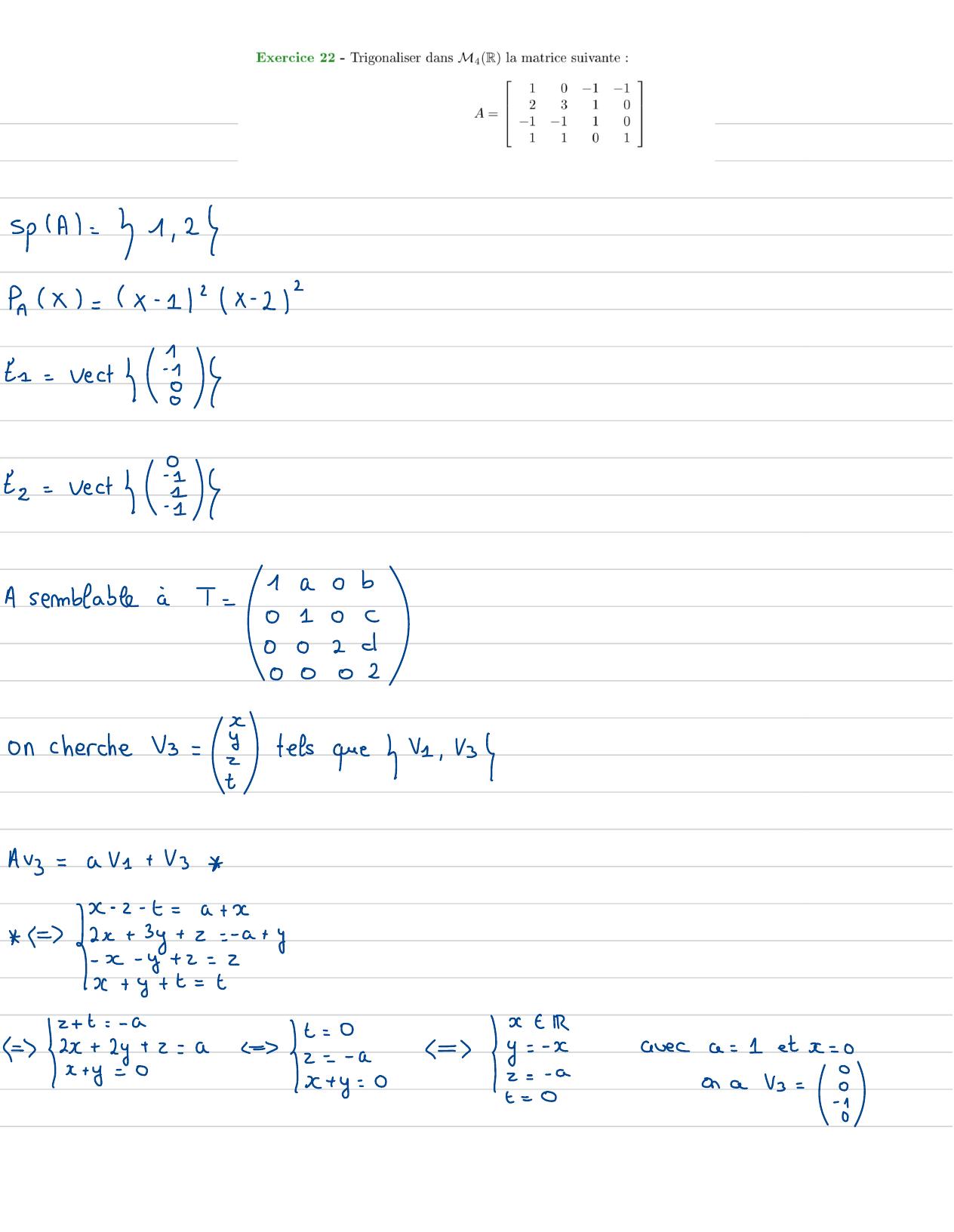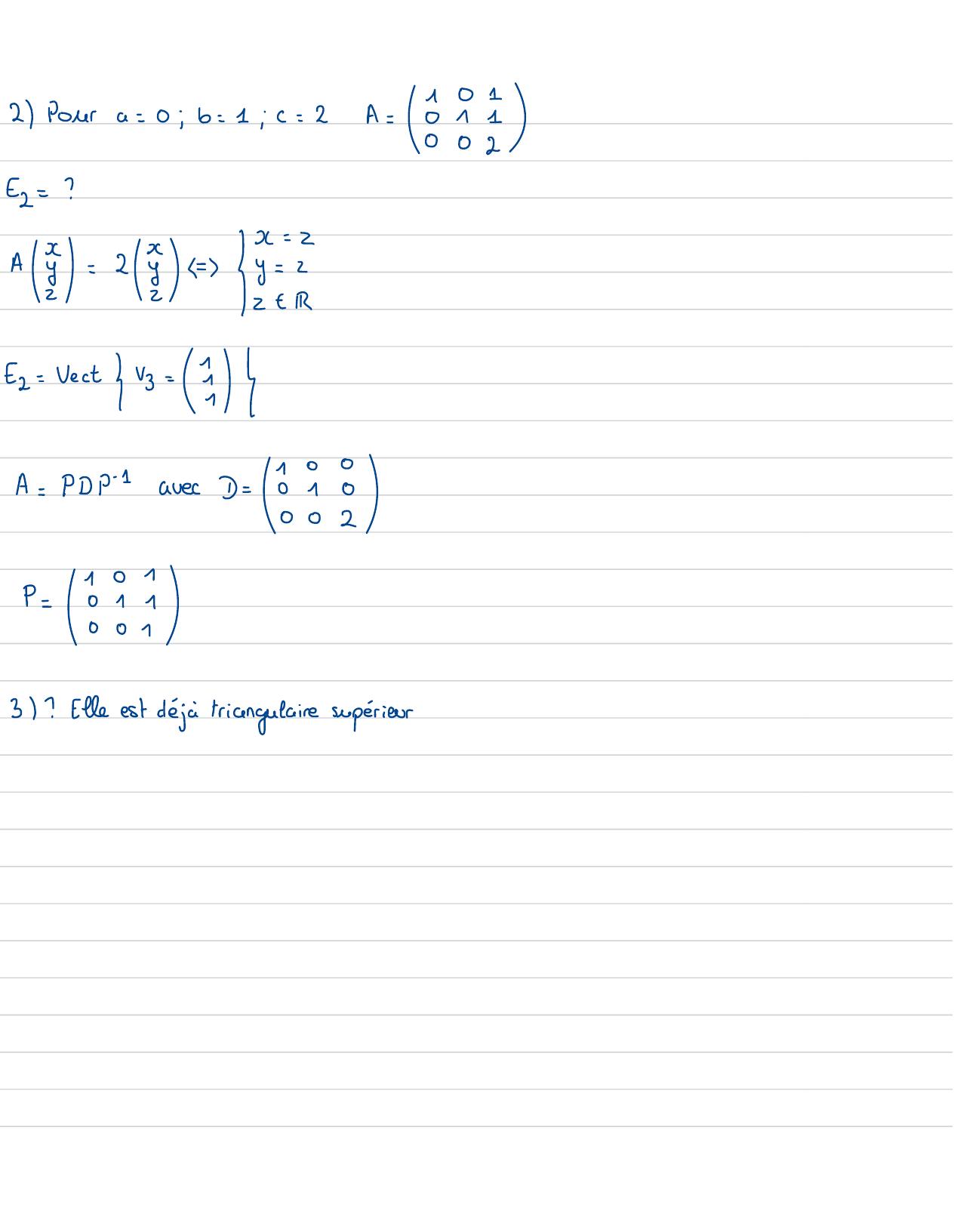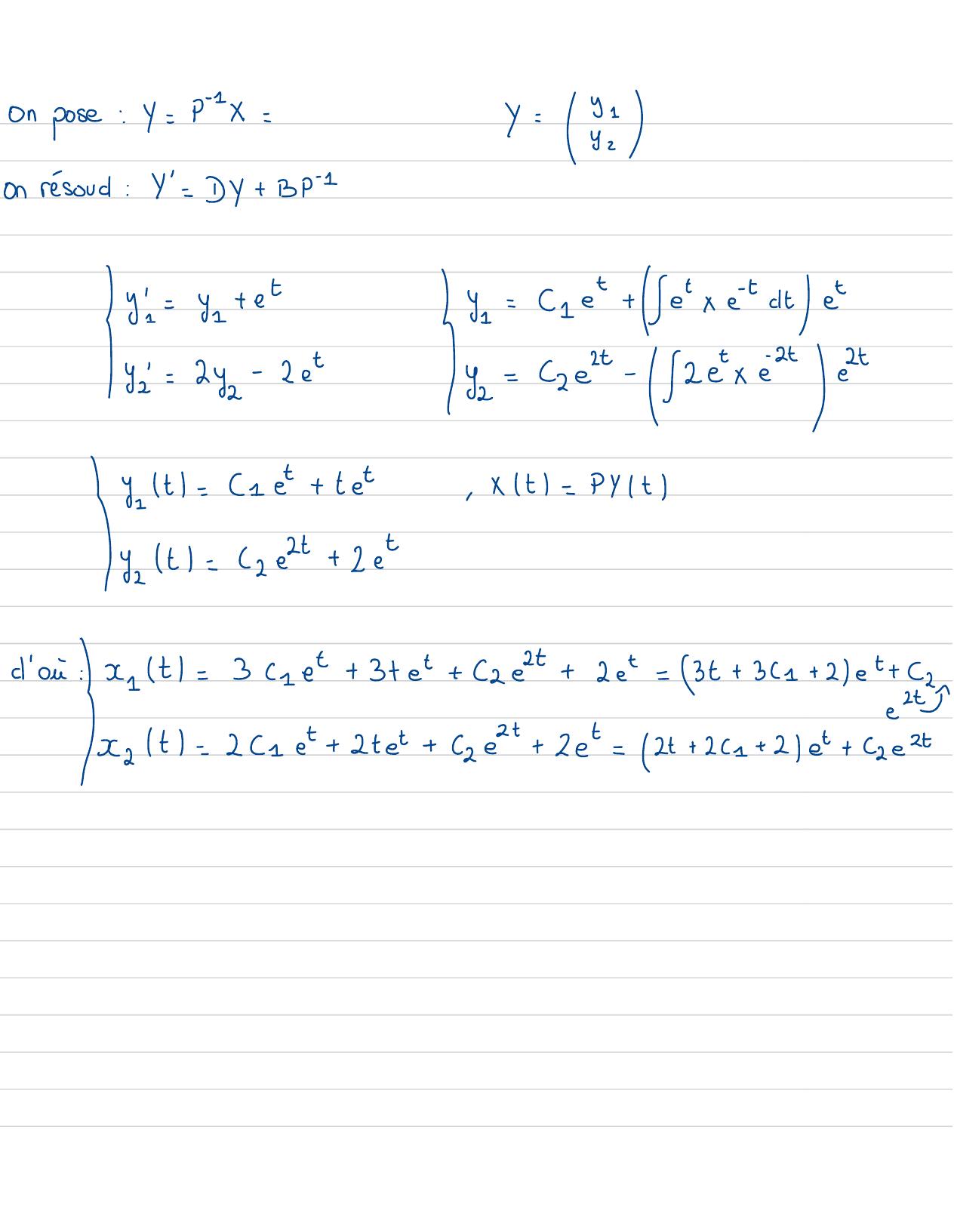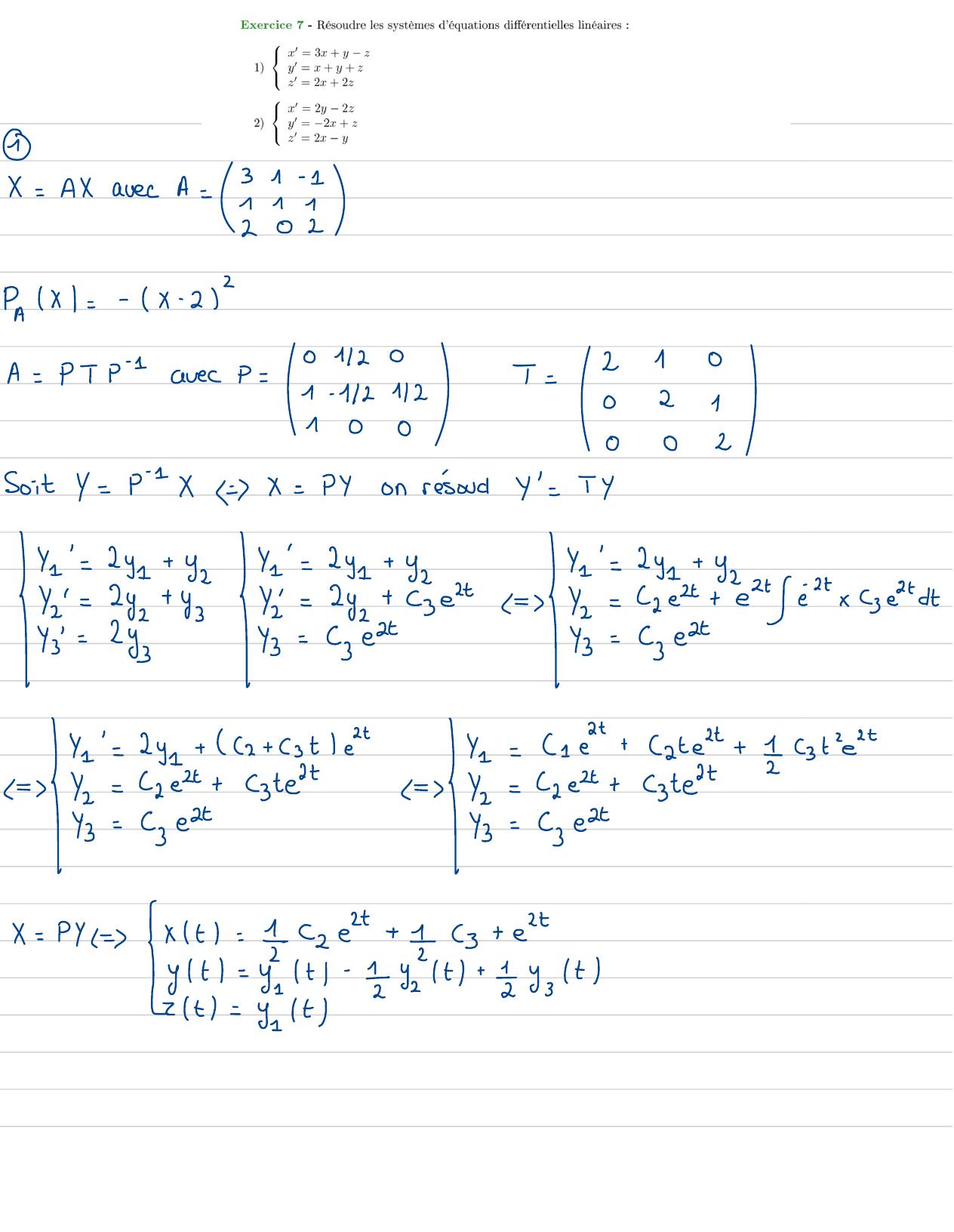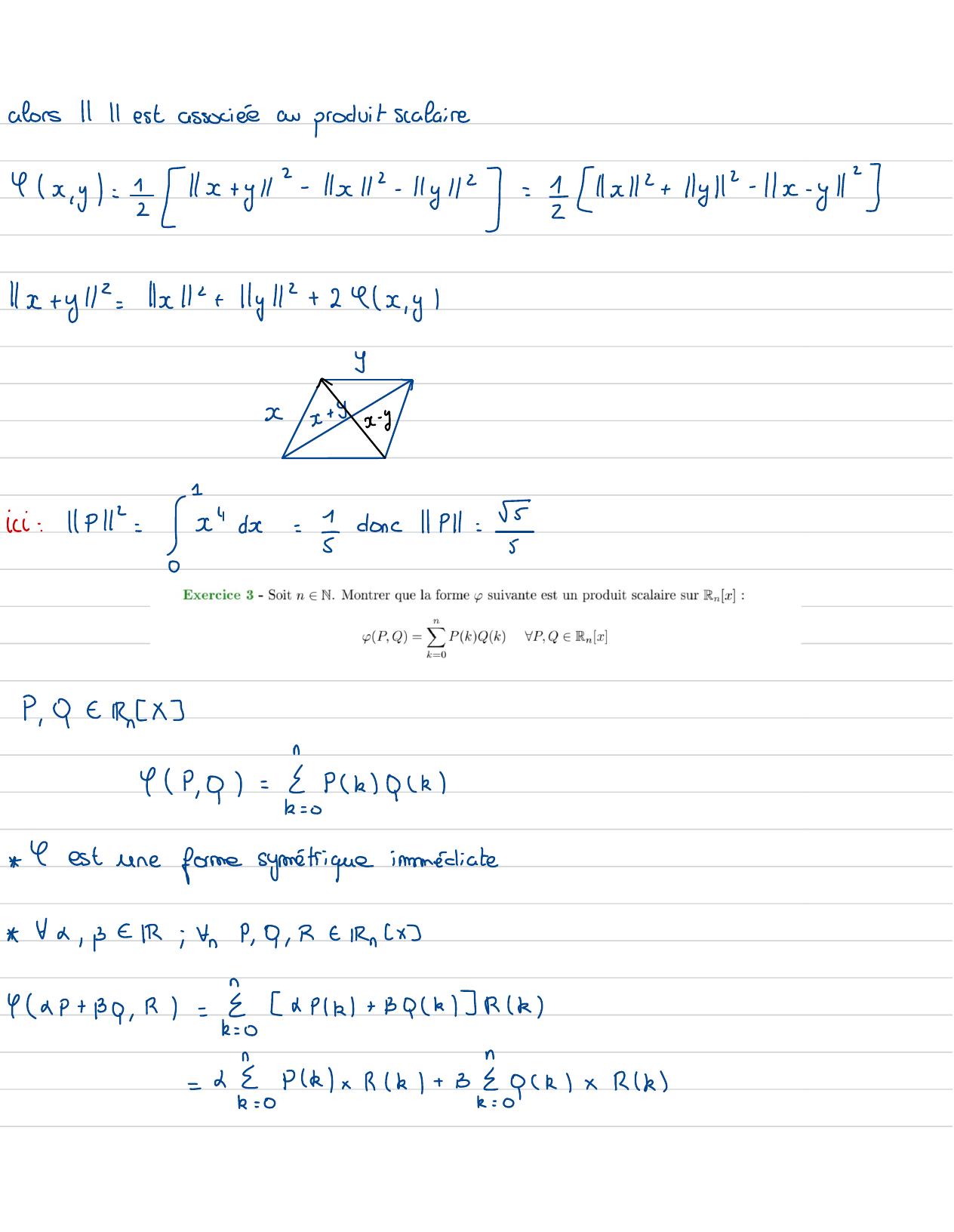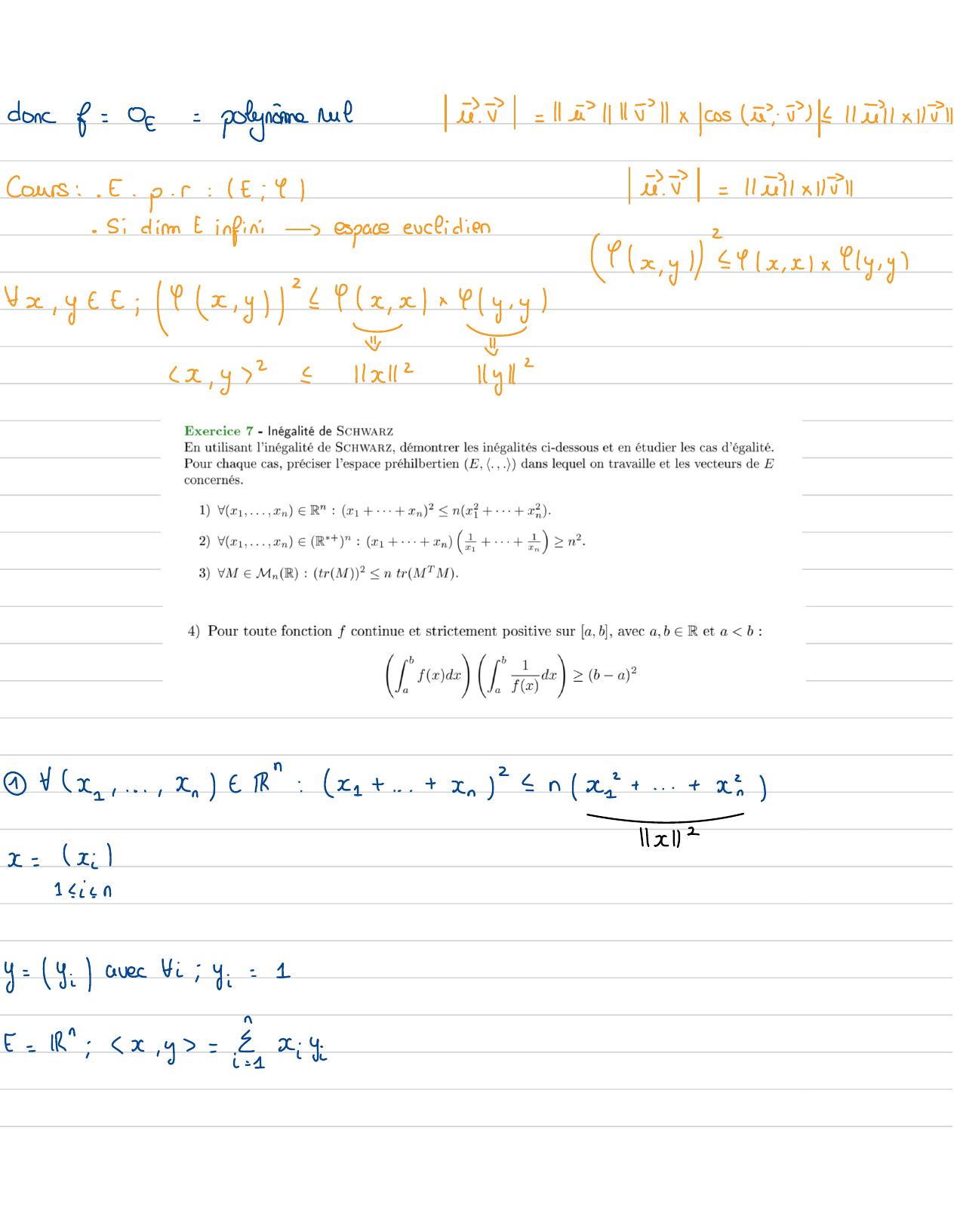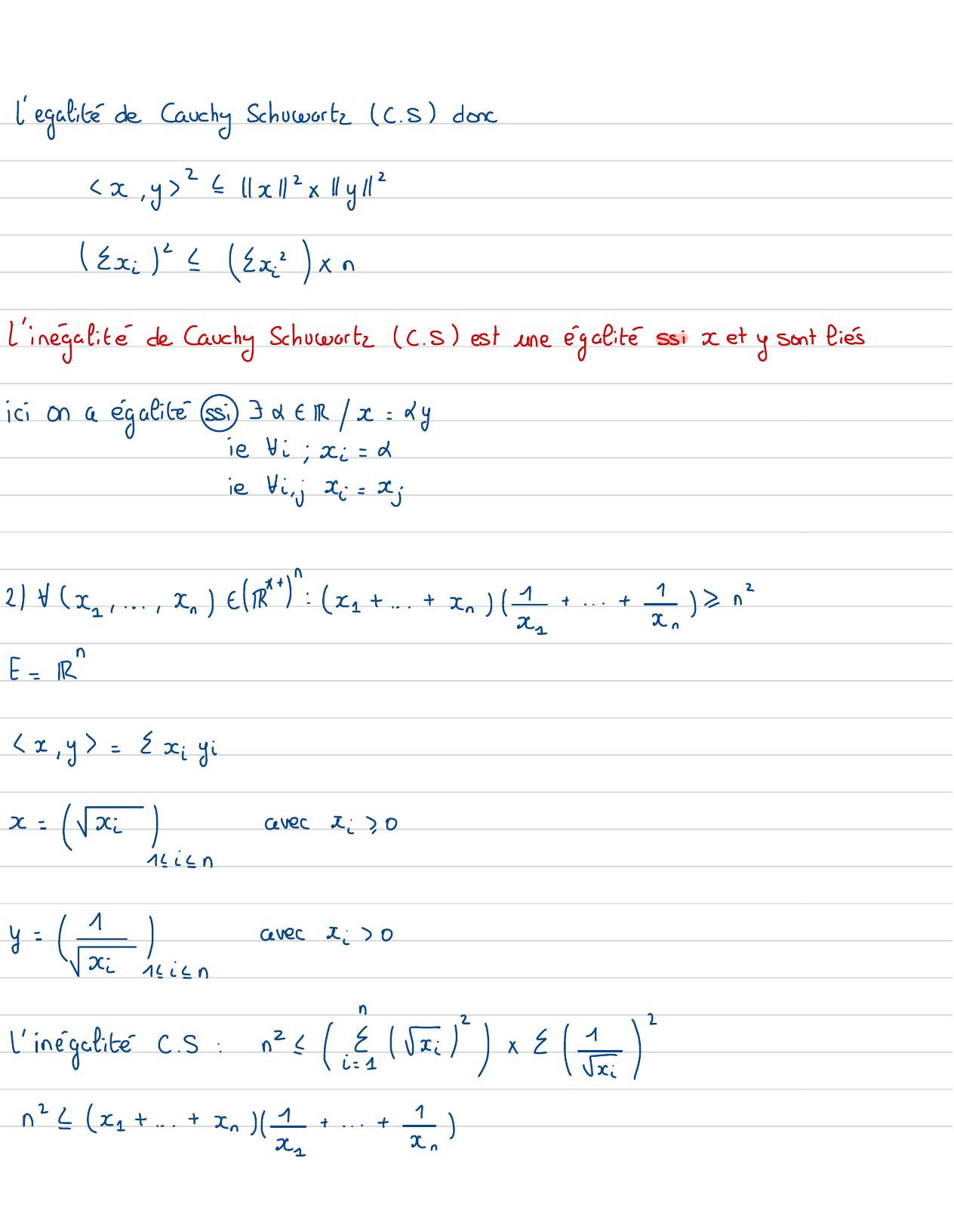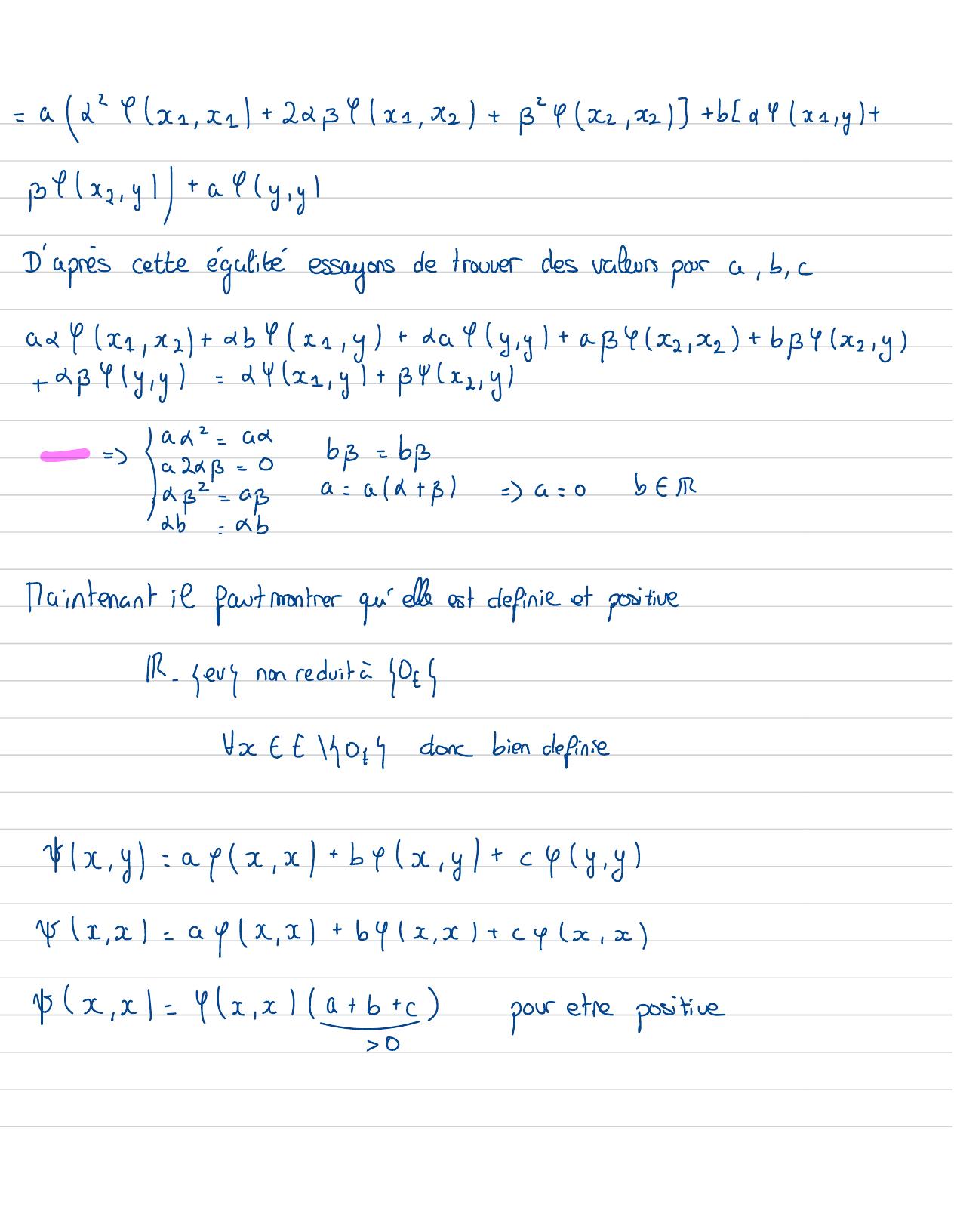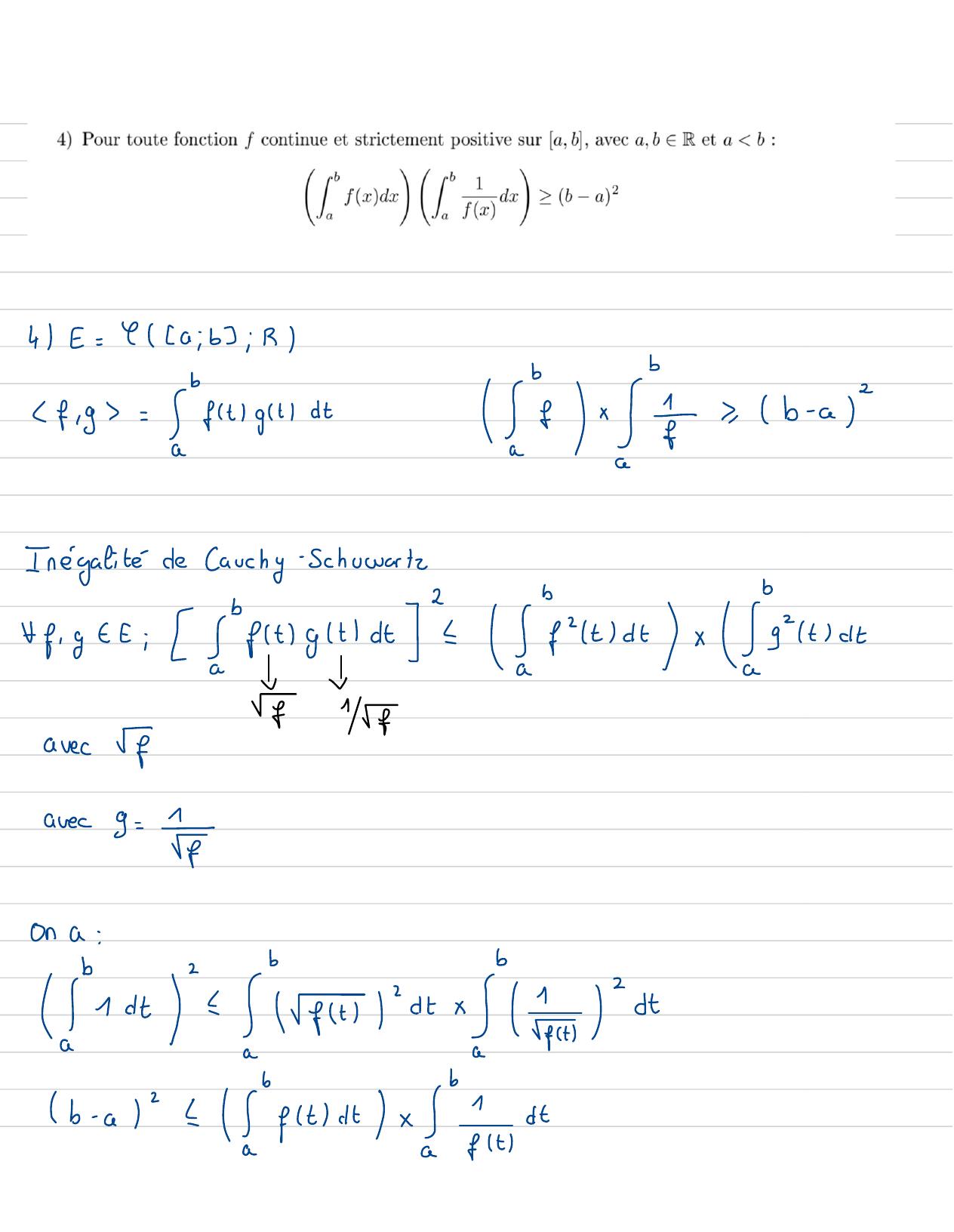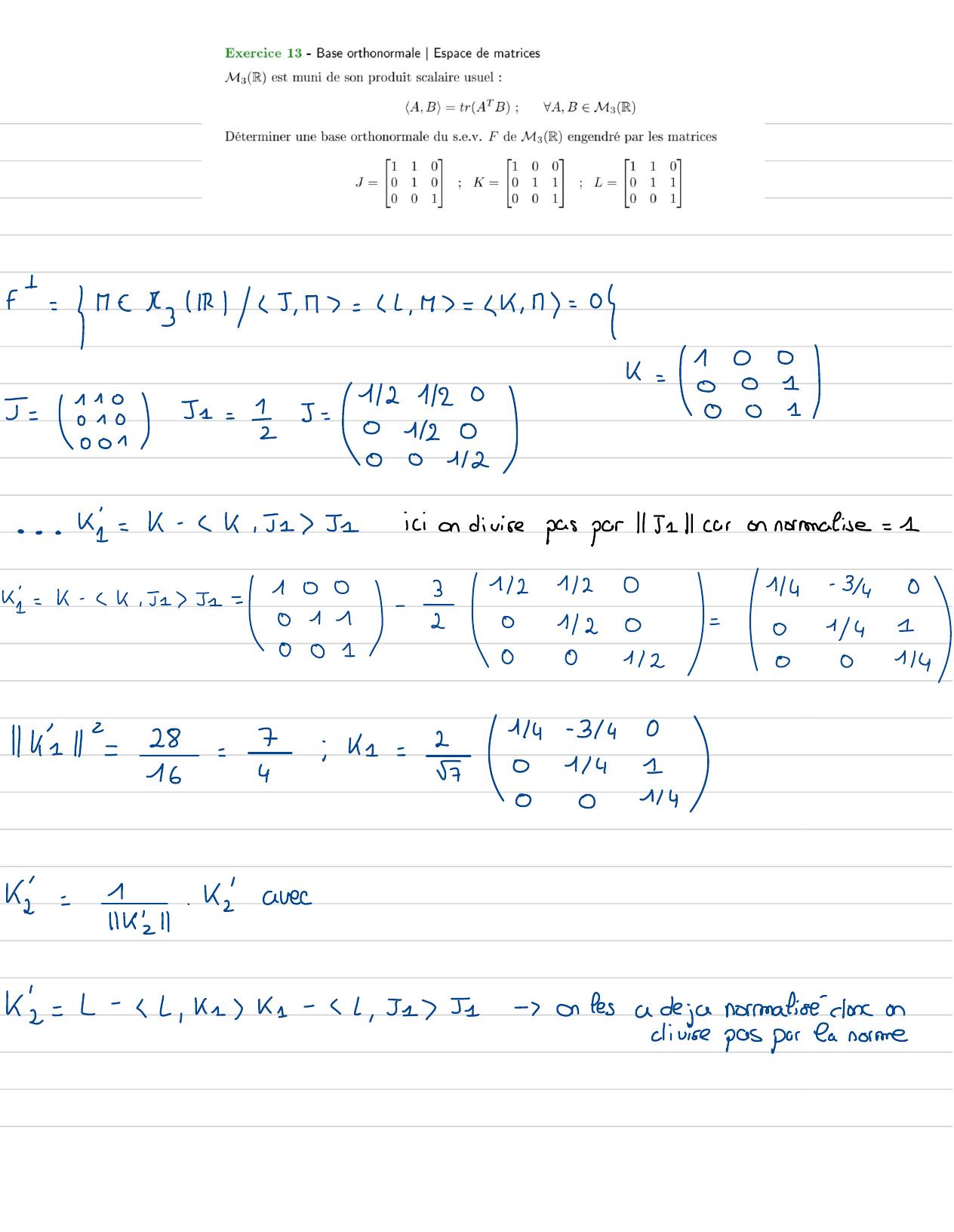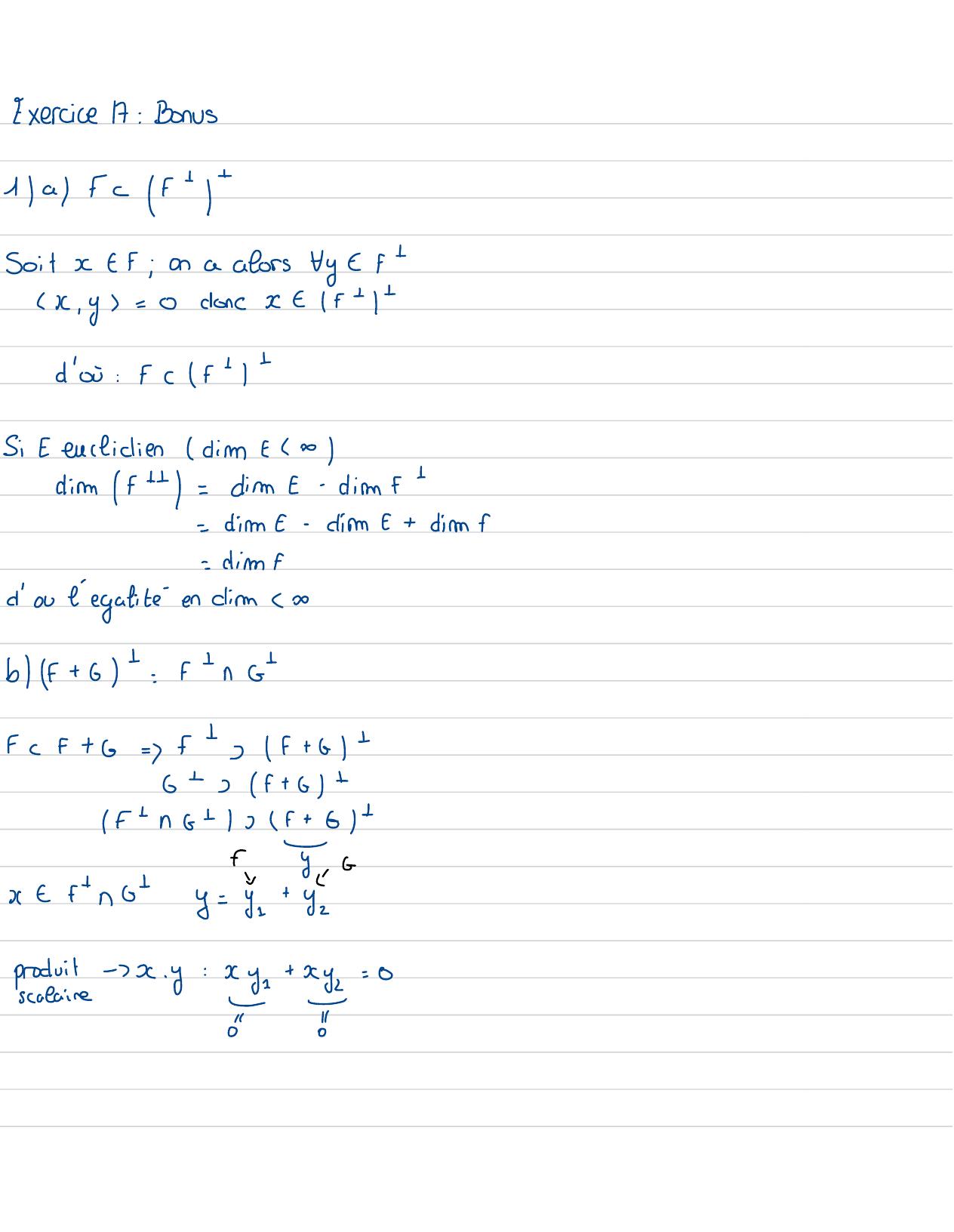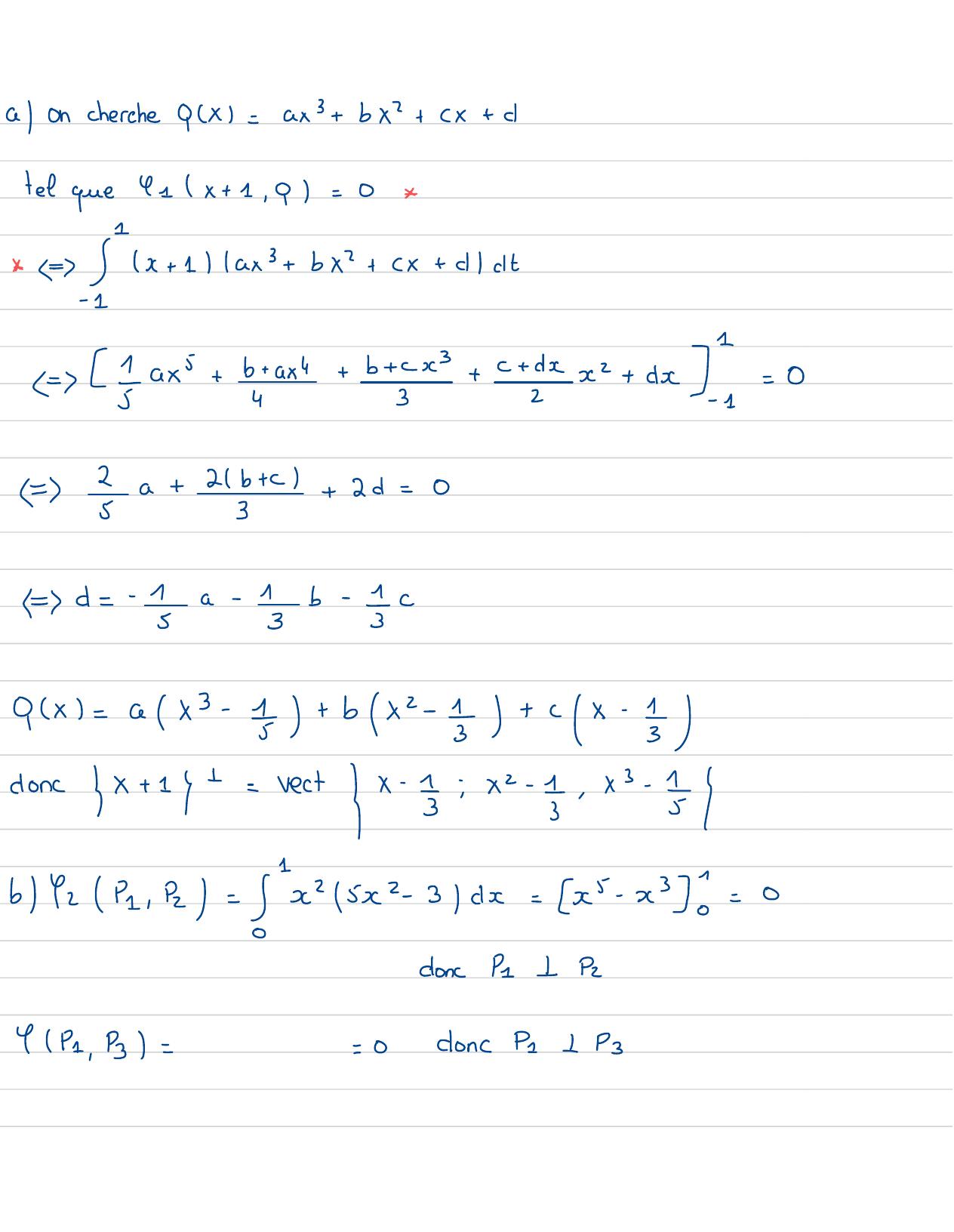TD Correction

Télécharger le TD Correction en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141

Page 1 : Algebre BilinéaireTD 2022 -2023

Page 2 : chercher les elements propres:-valeurs propres-vecteurs propresa =On cherche/CIR tel que:5x,; xz F 02tel que fx,; x2= xx ,, x 2f- 3x2, x1=X- 3x2 , x- 3x2 , x=1 - xx =, xxEEx1- xxz=0==-Exterie7= xx,+ 3x2=0 2I1- xx21= E 03+xYx2=2- x =3+x2=0carXERROn a donc=3==0Exz=0f n'a pasde valeurs propres dansR

Page 3 : 2 DansK= EC =- xx2=03+ xx=0 Si3+ x20ie x =15or== xz=0n'estpasune valeur propresix4= 15le systemese recit à:x =- xx=0x1= xx2↓estvaleur propredont tesous espacepropre 1ex= 3: c es= recthEEfig= rect fir= rect"

Page 4 : on admet qu'elle est linewineApplication linéaire dans IRR-Rux1= baii1 SoitA GIKI,...,nx'z=Esin=fz1, z2=X21 , 22= X21, xzz==21- xz= 0rE4 x 2 =-22= 02=21- xz412- 1122= 02 s2- x1tercas: x- 1+0iex- = 1Ona 22=2 1=0X n'est pas une vallur propreLeiecas:X- = 1le systemese réduità21= x22Conclusion: fa2 valeurs propresx=1 : =x= 2e k= rectE

Page 5 : x = 1 : ex22k= rectElBaby= xfx , y= y,x symmetrie· M'lb, al2 Soit &EK222 , 0, 523=X21 , 22, 23= X21, Xzz , xzzd222= x21222- x21=0=I.s= Ix 22=0523- x23= 0E1 2 1- 222=0122=045- xzz=0X= 5;2 se k322=0=722=0puis==0Sest valeur propre5: vect0

Page 6 : 1F5 :23=0↓=0:22 EIR2z=22=00 est valeurpropreto= rect8↓=0i21= 2z= zz=0↓n'est pas valeurproprefz1....., zn= 21 , 22 ......, nanf 2 = ..., zn= xz ..., zn12=Fr - k1 ; nk2p= 12kE nän E, En= +me41, nB1- k2= 01e cas: Ik= 41, nD:2 m=0danscecasx= kdanscecas Firk;on a -ilzi=0donc2i= 0me0

Page 7 : doncx= bestune valeur propreet tr= rectbiennelM18=538diagonalisabledans tabasejj? ... ncanoniqueest valeur propre de fIm+0 fx= bufu- xu =Ker f-xid 304=718 -xid /a= 8Zeimecas: FRE 41, ni: 2=0;x n'est pas valeur propre↓- R= 0 iex = kR foiseIR= fof of... of-sif inversible: f-1f- k= f- 7,k-valeur propre Ker f-id = 3004↳identitéf= f- = fft f1

Page 8 : 1 O valeur proprede fI u +-04, fu=0 .=0= Ju+ 0 i rKerf= Kerf F GOGY5 festnon injective= fest nonbijectivedimension finie2 fo get goyout mome valeurs propresSoitx - spfog; 5x+ 0,if0gr= brvaleur propredonc gf0gu1= xgagfyu= xga908gx= xgx1er cas: gnDe :est mine valeur propre de gofassocié au vecteur propregu.zeie cas: gu=0+alors f gu= Dudonne: f02= DreOz=Aud'au&= 0car n+02

Page 9 : PE Pdonc:fognon injectivegofnon injectiveP =Oestvaleur proprede gofdonc sp/fog sp 908 spf0gAc B cA signifieA= Bdonc spf0g= sp9083 Xt spf= XhEN ,x- sp/8/icicen'est pas puissance multiplicationmais compositionx espf =5u + 0 ifu= xe=7u + 0i fu= xfa= xuRécurrence=5u+ 0; fx= xfa= xuLf=id, =1estbienmine valeur propre de fo=icsigal= DeH. Ralors fil= fx= xkfx=xedoncestune valeur propre associé à m.

Page 10 : 4finversible: Application fineaire bijectivesi me application fineaine est bijectiveSça fonction recipro que est bijectiveaussia- Soit x- sp/f:5 esF oftel que fu= brdou f - fa= xf-+ur= xf- 1a-ce quil fallaitdemontreror fest bijectivedoncO n'est pas valeur propre defie XF0dou ffa= 4 x=x= rdonc 1= xest une valeurpropreassociéeb↓testvaleur propre def-1donc1-7 /4 deff-1= f-kQuand bijectiveX01- kf- kpour reciproqueKnx: dimensionnespacevectorielde dimension=n+ 11x: dimension quelconqueBase,infinie1, xjx ...-, xespace lectoriel infinie

Page 11 : A=Avf2= f1PAX=detA. XI1:-x"EpolynomeI2- x= 12- x- 2=- x1- xcaracteristique=Xx- 1onsiAt M2 /IKPAX=det A-xIn11-19X+1- 11- trA+...+ det APaX=x 2-trCAl. x+ det Aformule pour matrice carréde degre2, A connaitreSpA=Les racinesdu polynomes caracteristiquesclans te corspK.1sosespace propreMme K=tax.... afo= x-Mn=k, AX=0. x= 04↑Ocles rets↓Mr, 1x= 4Les deux racinesdeAx= 0=2x+ zy=0y=- xpolynome caracteristiqueI Ix+ z=0to= vect-14L'ensembledes matricescolores-1IAx=X 2x+ zy= x1= -x+ y=0= x= yI Ix+ z= yIx+ y= 0

Page 12 : == vect/ElLa matriceest diagonalisableCas général:A-CMnA:A2=AA FOnA est-elle diagonalisable ?1 valeur propre possiblede A ?1- spA= 5 x - Mn. 1 1k ,X+ OrM= 1Ax= XXdoncAx= DAX= & XA X=Ax=xXdonc /X= XX12- xX=0done 1-x=0carX =0Ainsi:Les valeurs possibledeX Sont0 et 1: spA30 , 14 Ax=0? Y'a-t-ildes solutionsautre que 8

Page 13 : x-2Mn, 1 /kA 2x=AX=AAX- x=0watoujoursdans KerAlcarson image est o=Ax-x-KerA=X-AXEKer AlOn a doncX=X- Ax+ AXunweKerAlIrm AlAXenEo1Ax=AXAAX= AXWerecteurde Valeur 1AfOndonc 5K;AX=Odanscecas:A AX= Ax= AXA x=0donc 1est valeur propre associeàAX.Montrons queKer A+ImA=Mn, 1 1Montre que ke sommeest directona déjàKerA+ Im A=Mn,IkSixKer Al n Irm /AlAlorsAX=0X = IrmA=5 X ;X=AXAx= Ax= =X

Page 14 : finalementMn.= K=Ker A+ Irm AlSiA f On: KerA + 40Soit=dinn Ker Ale =...esunebase de KerAp ,...enunebase deImm Ale.. p....enunebase deMme IkDans cettebase la matricede l'endomorphisme, associé àA s'écritOpPn- PA=......0P ........ 1qui est diagonale - Im AOn-PInpX= AxAx=Ax= Ax =Xsion estdansImsont image est lui-mêmeEn effectsiXe Irm CALX= Ax'Ax=A 2x=XLorsque l'onanun projecteur=KerAl+ FrmA= Mme Kaforsc'estforcement diagonalisable.

Page 15 : trace d'unematrice=Sommede la diagonale1 Pfx=x- 0x+ 1= x+ 1Dans Ipas de valeur propreDansD: spAl= - i, il Ay=-iyc -y=- ix= 40= y- ixx=-iy2 := vecti3 oncherche lsous espace propre associé à i y=-ix y=- ix A8=: 8:4 y=- ix:= vecti3Remarque:Al": iproduit scataire= 0donc recteur orthogonaux- 900

Page 16 : Toutes valeurspropreà unsurs espacepropre qui à ne infinité de vecteurspropres.Dansunematricecarré de degren, dansKonva pouvoir trigonalise la matricetoute matriceest trigonalisableDansD,si spA= d -... nle determinant= produitdes racinesIxi=cet A1trAB= trBAles/LtrAxPp-1Pp- 1=AtrA=2X ;y.......nracine0exercice:tr 1=a+b=7+ 8doncb=11· detA1=4b- 2a=7x 844- 56d'oua =-- 62

Page 17 : Exercice pourDS1 f-2E?montrer une applicationest linéairea- t- onPERRzx: fP-ReX ?P = Ax+ Bx+ 2fP=2x+ 1Ax+ Bx+ c- x2- 12Ax+ b=Ax+ 2Bx2+ 2cx+ Ax + Bx + c-2Ax3 -bx2+ 2Ax+B= Bx2+ 2x+2Ax+ Ax2+ Bx+ c+B=A+ Bxz+ 2A+ B+ 2Cx+ B+ cfPeRzX linéaritéC,= K; P , GEEfxp+ Ba=2x+ 12p+ Bp- x2- =ap+ Bal= c2x+ 1P+ B2x+ 110- cx2- 1p1- Bx2- 110= afp+ Bfa- Lineaireconclusion: f- &E

Page 18 : 21B= 1, x, x"1f1=2x+1fx= x2+x+ 1fx2= x+ 2x110Mizf=A=212011Remarque:On a Ve que fAX+ BX+C=A+ B x+2A+ B+ 22X+ B+c=Ax+ B'x+ cCC=B+ c= c+ b+ 0af:B1↳B=2A+ B+ ICAA1A+ B=0+ b+ aCbal10les valeurs propres d'un endomorphisme122sont les mene valeurs propresde Despace011associéLa matriceA s'obtient aforsdirectementC1↳33 spIf?1- x10PAX= det A -xIz=21- x2011-XIC2

Page 19 : 1- X10=01- x2I11- C3X-111-Xdet C1 , C.... nPAx= X- 1- 11001 - X2det AC1,2. ... n11- XinPpx= X- 10.. - ....Oi1- x1- x2121+ 2in:1- x21AC1↓2=-x- 111- x2=-X- 11-x- 2221- X=x- 1- 1- x3- xPAX=-X- 1x+ 1x- 3SpA=G- 1; 1; 344 AAy= -Cette =-2x+ y= 0x+ y+ z= 0Ex+ y+ z= 0= E y+ 2z= 0y+ 2z= 0-y- 2z= 0

Page 20 : x+ y+ z= 0E y+28 aEen21== vect -2x tIR Ay==c 12= y= E2,2= 0 Gy+z=z2=-xE= vect. Ay= 3 Y= CetteE-2x+ y= 0Ex- y+z= 0=x- y+ z=0=y- 2z=0yy- 2z=0- y+ 2z= 0x=2231G= vect1 I2At M, K eta3 valeurs propres distincts3 Valeurs propres et degre3doncAest diagonalisable= diagonalisable3 Valeurs propres et degre 5=pas diagonalisable

Page 21 : SoitP =111etD=-100- 202D1D1- 11003A 2 1=- 21--1+ 0e 2 t 03=100on a alorsA= PDP oiD= PA Ap'ici P= I1- 11-202111on a alors par récurrence:A= PDp=D=1- 1 "001&0031fP= p5 ? PfOfet be R , fP= /PieP= x P

Page 22 : Sidfo etdoP= n1cas impossiblecar dop=n- 1etdo XP=nSix= 0fP=0 P=0P=este· est l'unique valeur propreet to = polynôme constantde 1RX3EClassedes fonctions infiniment derivableà l'infiniider avec -= 3R, 115 g FO2et XER, fg= AgSquation diffg= xg=fx=k. e ER, best valeur propre: sp8= REx= vectx 1e"D81= g128= xfy= ayfa= keHsolutionsde cette equa diff fx= e

Page 23 : F Pet: FxtiRfP= xPX+ 1x- 3P= x+ xP18 cas: doP=n 12erecas:P constant1P=C=StefP=xP x+ x/xc=0c·Sic=0:P=0n'estpas Vecteur propre/·Si c Fo : legalitén'estpas possibleUn polynômeconstantne peut pas êtreune valeurpropre1er cas:Pron constanti. edop= n, 1dop'=bopdoncon peutrien conclureon cherchetoterme dominantnotesanx"le termedominantdepavecan0·Le terredominantdex+ 1X-3P' est: nanxCeluideX+ xPest:anx+ 1

Page 24 : x + 1x- 3P=x+ xp=Man= an= n-1/an=0=R= 1cloneP=ax+baveca +0Itraitedans leLeine casfP= xP=ax+ 1X- 3= x+ xax+ bx+ 1X- 3=x+ xx+ 2- X estune racinedu polynomme x+1X-31deracines- 1 et 3doneX=1oux=- 3x= 1· fp= P X+ 1x- 3=x + 1x+ 2 =- 3 b=- 3adoncPX= ax-3a= aX- 31= aX- 3:a- R=rectx-3

Page 25 : 1 =- 3· fp=- 34 X+ 1x- 3=x - 31x+ 2= b= 1b= aadoncPX= ax+ 1a= ax+ 16.= ax+a;aR=ax+ 1;a- R=vectx+1A - MnKtelle queFitk1 ; n: sain= 1Ic .....n1 ElkSoitx= " eMme IKOn ventmontier que1 est valeur propreABli=Finx BasAx= X= Fit 1, nAX1 := Ximatrice colonne

Page 26 : = Fi-21,nidinx= XiEn choisissantX=?i. e Fi, Xi= 1on a Fi; AimXm= 2 Aik= 1=Xidoncestun vecteur proprede Aassociéà la valeur propre 1= 1.Rappel:Matrice est diagonalisablesi elleest diagonaleon supposeAnon diagonale- Montrer queA n'est pas diagonalisable=sizi:IP inversibleA= PDPAavecD=x IdoncA= PXIP-1= pp7XI= x Iimpossiblecarnon diagonale

Page 27 : 1Fn-DV;9n+= 2xn+ yn=Xn+1=AxnEIn +1=6n+ 24navec x=Y" etA=29CalculdeA"?· Diagonalisation:PAX=det A-XIz=bet2- x112- X=12- x1- 1= 1- xx- 3Sp= 1, 34diagonalisablecar2 valeurs propreset effe est dedegré 2A8= Y=4,!2- y=- x

Page 28 : 1= vectk= - AY=333E3 E2x+ y= 3xx+ 2y= 3y y=xE= vectr=ISoitPfa matrice de passagede labasecanoniquedeM2. = IRàfabase V1 , Velp = Idet =2Yet1ona alorsp=1--1211:A= adet A=ad- bcISidet Al =OA=1d- Cdet Al-baona alors:A=PDP-10iD= 83onaafors:A= PDp-1Al=111101- 12-1103411

Page 29 : Al= 1n-11+3- 1+ 3422- 1+ 341+ 34de l'égalité: Xn-DV:Xn+1= AXnOn a par recurrence: An:A"NoEn effet: Axo= Ic Yo=NoYoh pour= 0 SiXn= A Xo Hypothèse de recurrencealorsXn+1= AXn= Ax AXo= A "No,ce qui achèveXn= 11+ 34- 1+ 3Co=34x0+ y0+ xo-202- 1+ 31+ 3Yo23410+ y0- x0Yo2-n= 23"x+ y+ x0- 20donz :4En=3"x+ 70- xot y

Page 30 : A=201111-20- 1 SpIAl!on faitavec la deuxiemecolonnePAx=2- xO1=-0x 2- 1x+ 1- x2- x1-ox2 - x111- X1- 2- 1- X11-20- 1- X=x-1x- 2X+ 1+ 2=- XX- 1X- 1=- XX- 112spA= 0, 14

Page 31 : to:2x+2=0 Ay OMs. 1 CIRIx+ y+n= 0ecI-2x- 2= 0=Eto=rectGre= ↳1 :x+2=0x E Rx+2= 0L=y E R A2== Y13x+2=D2=-x1=!,x ,yt= x+ y8ix,yen== vect88V2V3rect2G= vecti2carest combinaison finéairede11V2 , V3 / est libre:xV1+ y= 0= -donc VI, V2est une basede t1: dim +1 = 2

Page 32 : finalement dir to+ dim Er= 3et Ad'ordre 3doncAest diagonalisablesoitla matrice de passagede la base canoniqueà la base VI , V2 , ve11DonaaforsA= PDP-1P =A01-2-10000avec D-010001inversion de P11010⑧A01010-2-100011212-1111010D33+ 2210-11-1100102011101000-11-1103=3+ 1201101112 =12- 13Tdet=- 11x- 1 x 1

Page 33 : 11010⑧⑧- 10- 20-100111111010001020112-12001111I3- 10-120111L1- 12111-=P- 1pour la diagonalisationon cherche la matriceP, Pf et D , des que c'est faiton a montré la diagonalisationbl Ax, y, z El;XXEkx- xy+ z= 0By= xy=x = xy= a8EEx- xy+ z= 01 = 7 Ey- xz=012 11y- xz= 0zc3- x1

Page 34 : x- xy+ z= 01 = 7 1- x=0- x2+ xx=12= 0zz- x = 112x- xy+ z= 0Eri- in· Six40, -55 :YLa sentesolutionest8qui ne peut-être valeur propre· Six40, -55 :Y· x=02=-xB 3= 8Ec= rectIx=2dememeEz= Vecty2 y=-222 CIR=2= vectY ? !

Page 35 : ona alorsA= PDPI- 111avecP =O-22111000↓C=O-2000 IC11- 5511- x- 5511 - x-5C=- 53-3Pcx=det C- x13=-53- x- 3- 53- x5335-33 - x5-3PcX=11- x3- x12+75+ 75- 25/3- x- 911-x- 25/3- x=11- x3- x2+ 591- 99=11- x9- 6x+ x+ 59x- 99=- x3+ 17x2- 16xExemple:polynome degre 3= x- x+ 17x- 16c +racinePx=2x3+ 5x2- 6x- 1= xx- 1- x+ 16=x- 12x+ bx+ 11Iracine↑les deuxeviclenteextremitesPcx= xx- 1- x+ 16dePNSpC= 30 ; 1 : 1673 valeurs propres distinctes2degre: by - 2x: b-2xdoncC est diagonalisable1- bx= 1- b xSousespaces propres:AX-x= 8A- xI Xpolynôme caractéristiquede degren:son coefficientest -1"

Page 36 : X=011x- 5y+ 52=011x- 5y+ 52= 0c=Y= 0= I- 5x+ zy- 32= 0= I8y- z= 02=2+ 512511Z5x- 3y+ 32=0ZE IR313+ 22mer1x=0signifie que notre systeme ests Bide rang 2 et non 3Icar y'a une équationqui sauteGo= 22z EM= rect?= VrX= 110x- 5y+ 52=02x-y+z= 0c==c I- 5x+ 2y- 32= 0= I- je+ 2y- 32= 0Z5x- 3y+ 22=05x- 3y+ 22=02x- y+z=0= I- y- 1z= 0252+ 512-y-z= 03=13+ 22= -Y aI-1==z zem= rect == 02

Page 37 : X=1611x-xy52= 16xN- j32x- jy+ 52=0x+y-z= 0c=y=16 I- 5x- 13y- 32= 0= I- jec- By- 32= 0ZZ5x- 3y- 132=05x- by- 132=0J+ y- z=0= I-0y- 82= 02 =2+ 321-8y-82= 03=23 - 521IC = 22= Ici=152 zER: rect :E-I-152A: PBp-1=2 matrices sembables même enclomorphismonedansdeux bases differentesdiagonaliser/trigonaliser:Trouver une matrice qui fuiest semblableSoitP=I IonaalorsC: PDPFonD= PC P111↳matrice diagonaleor j'a les valeurs propre000D=o1D0016

Page 38 : 2aA=-1aaPAx=- 1- x- x1-x00 -aPAx= x1- 1001SpA=G- 1 ;0 ; 1=A est diagonalisablea0fez=ae1X= 00⑧"I-x+ ay+ az= 000 A=0 -az= 0fen=ben02=0bIayy=- Ento= rectWI=IX= 1-2x+ ay+ a= 0x=0 Ay= Y= I2EIREd-y- an=0 Yif= rectfa= v

Page 39 : X=- 1ay+ az=0x t IRy- az=0I=8 Ay= -= I22=0EEc= recty8= BSoit Planatrice de passagede La base canoniqueà labase !W1 ;2: WeltoE1E - 1a01ona alorsA= PDPFD=0 IP=1- Ce0⑧01000- 1Une matrice etsu transposéeont fa même base.Inversible= 10

Page 40 : 1 A savoir: FMeMnIdet 1=det MYPAd=det A- x In=detA-xInY=det AT- XInl"↳matrice diagonaledoncsa transposéeest elle mene= det AT- XIn=P+xA et AToutmeme polynome caracteristiqueet donc même valeurs propres: SpAl= SpLAT·A et AT n'ont pas necessairement les mêmes vecteursprogresA non diagonateA=12dans tabase canonique en : enx= SpAl0 1Aucunechance d'etre diagonaliAez= e1;e1est vecteurpropreassociéà b= 1-sableAT=MDAT-M=21+ 2e+21A= PxIp- 1= pp- 1 XI21212= XIen'est pas vecteur propre de A

Page 41 : 20- SpA 5 x t Mn. e 1k:x = 0Mne 1ktel queAx= 85x =0; Ax=0= kerA + 307=Aestnon inversible3 Déjà fait ex492Sinon: Montrons que spAB1= SpBA 1Soit- SpCABI alors X = 0;ABX= XXdoneBABX= xBXIcion peut pas dire valeur propre. Il faut montrer I oyyMer cas : BXFO , danscecasest valeur propredeBAassocié au vecteurBXdoncx E sp/BACommecas: BX=0, l'égalitéABX= XXdoncDX=00quisD=0Car x+0O est ruheur propre deAB AB estnon inversiblevia q2nonclet= 0=cet AB= 0= det BA=0E BAestnon inversibledonc0 est valeur proprede BADans tous les cas I est valeur propre de BA

Page 42 : =spAB spBA spABdoncspBA= spABl4Par recerrence sur REN: Initialisation: Ax= IX=X=YXHérédite :supposonsque A= XXalorsAX=&AX= x Xce quiachèvela récurrence: NREN; x valeur proprede Alassociéeau mennevecteur propre.5 detA =OdoncA est inversibledoncO n'estpas valeur propre de Axt spA=5 X + 0 :AX= XX=I X FO;A FAX= A xx= 5x+0iX= xA- =Xon peutdiviser parA carA estun réal 0=5x+0 :A+ x= YXcarx = 0donc 1= = G SpA↓est valur proprede A 1· Soit REI:sik c'estOk!Viap4· SikL0:- R0donc via 944est valeur propre de Art-Ri . e:1est valeur proprede Ak.

Page 43 : 1 f est fineairecar;FA; Be MnIRIFa , be IKfaA+ bB=aA+ bBT=aA++bB-=GAT+ bB= afA+ bfBdonc f- 2 Mn 112 Sixe Spf afors7AE MnCIRI;A=OnfAl =DAi. e:A T=xA= AT= xA-=A=xAt=A= x2 Acar A T=xA=X2 - 11A=On=D- 1=0car AfOn=X=- 10 x= 1Les valeurs propres def possibles sont-1et 1i. e: spfc-1: 143n= 1 f= Idr BSa senl valeur propre est 1associea toutes matrices non mullesn= 2f= MzRM2Rababca↳c c 1 f= -= b=c

Page 44 : 1 est valeur propre de fii= a03+ b88....1= ab,a, b, de = vect58: : :: 18: 2 fa=-= Es 98IIb=- C-1 est valeur propre de fE==0b, beR:Vect 8IIRemarque:dirmt1+ dim E-1= dirn MzIRdone f est diagonalisable4 M, 2 1fA= AlAT= A c=A symétrique↑est valeur propreet fr =matrice symétrique de Mn- G+Gax01+ 2+ 3 + ..+n=nn+ 1nn+ 1-n= ntqui est dedimensionnn+12

Page 45 : 2fA=-AEAT=- A/ definitiond'unematriceantisymetrique l-1est valeur propre defet t-1= imatrice antisymétriqueden IRS4qui est dedimensionnin-12Remarque: FA-RnIRA=A+ AT+ 1A- ATsymetriqueantisymétriquedonc MnIRestlasommedes sous-espacesdes matrices symétriques etantisymétriques et cettesummeest directe.61 AV==6V-124Xvecteur proprede A= MnIRassociéan vecteur propreX=Vecteur propre de Alan même vecteur propre Xse provie par récurrence

Page 46 : Exercice:Soit At Mn1kon donnePAX=- x+ 6 x2- 1 x+ 61Que diredeA!21Mq I BMCI / B= A- "+-l Tracex"....+ detA1 At Ms1kPAx=-x+ 6x2- 1x + 6PAIN=cet A- xInP 01=cet AdetA=PA 0=+ 6=0Aest inversibleTraced'unematrice:c'est La sommedesracines complexesTravedeA=6Diagonalisable ?PA 1=0PAx= x- 1- x+ bx2- 6Terre de degré 2 : b+ x2=b+ 1 x2onadonb+1=6doncb= 5PAx= x- 1- x+ 5x2- 6=-x- 1x- 2X- 3

Page 47 : spAl= 1 , 2 , 34A diagonalisablecar elle a3 valeurs propresdistinctes.Elleestsemblable âD= 88 IDeux matrices sontsemblablessiA5 uneimmatricePinversibletelle que A=PDP-1SoitB=P/82/SalorsB2= P82P-2=Pep- == APx=det B- xIg=- x- 11- a- 1a -xa + 1-aaa+ 1- xC1-I- x- 1- 11=x- 1 !1- x- 1G-xa+ 1a-xa+10aa + 1- x0a+ 1- x

Page 48 : x- 1ax1= x+ 1+-112- 12- L1a+10a+ 1-xa0a+ 1- x0a+ 1- xPpx=- x+ 1a+ 1- xaCeG+ 1- x=- x+ 1a+ 1-x- a=x+ 1a+ 1- x- aa+ 1- x+ aPyx=- x+ 11- x2a+ 1- xSpAl= - 1; 1; 2a+1Mercas:2a+ 17- 1et2a+ 1= 1i. ea+7- 1; 0Best diagonalisablecar elleavaleurs propres- y+ z=-xa- 1x+ ay+ x+1/2=- yX=- 1I-ax+ay+a+ 12=- 2

Page 49 : Ix- y+ z=0a- 1x+ a+1/y+4+1/2=0-ax+ay+a+ 2z=0ara+- 1x- y+ z=02a+ 11z=02=2a+ 11I 2+ 12=0L3-Lz+ aL1I y2=0cara+ 10=1= vect5x=+ x- y+ z=xa- 1x+ ay+ x+1/2=yI-ax+ay+a+ 12=2

Page 50 : I-x- y+ z=0-a+ 11x+ a-1/y+ x+12=0-ax+ay+az=0I-x- y+ z=0-a+ 11x+ a-1/y+ x+12=0-x+y+z=0a+ 0-x- y+z= 0I2 ay=04 = -a+ 112y=0z- 21I EIRIy=0E==ve+ 382= x

Page 51 : X= 2a+ 1- y+ z= 2a+ 1xIfa- 1x+ ay+4+1/z= 2a+1y- ax+ay+a+ 12= 12+ 12-24 +1/x- y+ 2=0-a+ 1x- a+1y+ x+12=0I- ax+ay-xz=0-2x+1x- y+ z=0I- x- y+z=0- x+y-z= 0a+ 0y t Ry=zIx= 01323+ 12Far=rest314

Page 52 : Soit Pfarmatrice de Passagede Labase canonique Mu. 1 IRà labaseP= 589= I-0S02a+ 1detP=- 2= 0doncinversiblep- 1=

Page 53 : Zeimecas:a=0spB=G- 1, 14PBx=- x- 14 x+ 1B=0- 110I ox+ y+ z=0I EIRB3= 2 -2= 0 =I2=0-x+ y+ 2= 0y= x=e= vect-1- +-=0Ix=-y+ z-x- y !20= yEIR2 GIRxe=vect5: suz. Vel basede

Page 54 : finalement Best diagonalisablecar dirta+ dim t.1= 3etona:B= & = 88-I 1Sa=1...elleestaussi diagonalisable11 14x+z+t=xxx+ y + 1 - xt=0A2=- 2= Iy+z+ t= xy1= I1- xy+z+ t=0x+ y+ z=xZx+ y+ 1- xz= 0x+ y+ b=xt1- xx+z+ +=0x+ y+ 1 - xt=0EbI =Lzt13- 21-1-xy+ z+ x2-xt=0y=Ly- 1- x1x+ y+ 1 - xt=0Eb1- xy+z+ t=01-x2- 1- xt= 0I 22+ x2- x+ 1/t=0y Ly+ 12

Page 55 : x+ y+ 1 - xt=0Eb1- xy+z+ t=01-x2- 1- xt= 0I I-2x1- x- 11- xx1- x1 + 11+=0y=2- 1- x4=I 1- x- 2- 2x+ x2- 17t= 0x+ y+ 1 - xt=0EI 1- xx+1x- 3t=018 as: 1- xx+ 1x-3= 0i. ex- 1 i- 1 ; 3L'uniquesolation est 88↓n'est pas valeur propresCeme as:1 - 1 :- 1 : 37A2= 3= x+ y=0It IR2+ t=0tEIR

Page 56 : =2= vectr= 5: r= E151; 2 libredoncbasede 211=- 1A 2=- 2 = /Et=== vetvx= E1= 3ai= 3i=== vet-,= E

Page 57 : Aest diagonalisablecardim ta+ dirn t-1+ dinn ty=4=dinn M4 . = 1ketonaA=PDS1avecD=y- 1S-10-11P=10- 110-1110111

Page 58 : A= 92PAx= x2- x+ 1= 0 - 2x+ 1= x- 12pas diagonabledonc pas diagonalisablecar qu'une seule valeur propre= 1A semblableâ1 aa !01spA= 1A-x+ y= 0y= xEx= VectE=1=Ven fonction deLabase canoniqueV1=21+ e2Soit 02= 5Vz, W2/est unebasede2IRAus= unpremierrecteur deLabasecanoniqueAV2= AN1+ BU2IV1, 02 1 est une basede2. IR

Page 59 : Exprimons: Au 1et Awzen fonction de N1et2AN1=U1a+ b= 0AU2= aN1+ bOz = Ia=-1= Ia=-1b=1AV2 =- 01+ v2Avr= 1T=1- 1II0=et P=48v= 6A=PT P 1

Page 60 : Ppx=detB- XIz1=1- X0⑧D- X10- 12- x=1- x- x1-12- X=1- x- 2x+ x+ 1=- x- 1X- 112=- x-1B est trigonalisablecar PilXspB= 1estscindé dans IRspB= xBriest pas diagonalisablecarsinon:B= PDPFD= XI3= PAIP-1Isce quiest faux=0 +:2= i=-8+2=0L I yin=-I-y+ z=02= y== rectv== e+v= i

Page 61 : &Ve, V2est libreimmédiat doncestunebaseB est trigonalisableet semblableà unematricede ta forme =18= 1VeVeVeBV3=xV1+ yVa+zVx⑧SoitV3=01IVI,V2. Ve Yestunebase deMo. - IcarP=est inversiblecardetP= 10it fant que la matricedepassagesoit inversible /pour MyExprimons:B enfonction de U1,2,3B=E IBe=av1+ boz+ w ! !I b+ 1=2L=a= 0etb= 1Ainsi:B03=02+ UbfinalementB=PT p 1avecP=100etT =10010118001

Page 62 : 5-1725A=3=BPfx= detA -XIz=5- X-17252- 9- x161-59- X1- 59- X--2- 9- X1611- 135 - X-17251-59- X- -01- x- 2+ 2X↳- 2- 2108- 5x- x2+ 14x- 20y cby- 5-x11- x- 2+ 2xPAx=-8 -5x- x2+ 14x-20factorisation trinome: ax, /x-x=- 1- x- x+ 14x- 20+ 211- x8- 5x=X- 1- x2+ 14x- 20+ 2/8- 5x=x- 1- x+ 4x- 4= x- 1- x- 4x+ 4=- x- -X- 22

Page 63 : A est trigonalisabledans Iscar PAXestscincle'dansRSpA=1 , 2Es? Es ?4x- 17y+ 252=0=1:A3= 2 = I2x- 9y+ 162=0x- 5y+82=0x -5y+ 82=017/3\= x- 5y+ 82= 012- 12I 4x- 17y+ 252=0x- jy+ 82=0L= I by- 72=0z=by- 421L= I·ete= rect0- =1

Page 64 : 4x- 17y+ 252= 2x2: A2=2 2x- 9y+ 16= 2yx- 5y+82=222x- 17y+ 252=01= I2x- 1y+ 162= 0x- jy+ 62=0 2,5y+ 62=0I-Ily+ 162=0- sy+ 92=0= I32szu2 t IREI2=rectv= =21A est semblableàunematrice du typeT=10aRemarque:on peut prendrea= 0grâcean cours02b002SoitUs=8

Page 65 : IVz, V2, Volesteinebase de Maiz IRP= 3DMa+ 3b+ 2=5AV=GW1+ bN2 +28 = 7a+ 2b=2I ba+ b= 1I=ma+ 3b+ 2= 50k !=a=0Ib= 1finalement:Ava=52+2 Eset on a:A=PT P- 1avec1131⑧P =720etT = =I310

Page 66 : bB= et-1Pix=2.x01=2. x1- x01 1- x11- x0I-113- x1-x- 11=2- x1- x3- x+1+ 1- x=2- xx2- 4x+ 4=x- 23Best trigonalisable dans IRCar PXest scindé dans 1maisnon diagonalisable... Ez ?= y c eB 3= 2=Et +2= 0I5= vectr= 8Best semblableà unematrice du type T=2ab88

Page 67 : on cherchev2= 2 tels que V1, vey libres BU2=aU1 +202R2x+2a+ 2xRx+ y-a+ 2y ya-x+ y+ 3222I -x+ y+ z=0x=a+y=- G- y+y+ z=0LL=2= aIzI yt RPoura=E 0on a =pas possibledonc çane serait pas libre01Poura=1on ax=2y=1E = I201B=1v== 3 v= E10- 113

Page 68 : Soit Ub= 8: = ,2,s yest une base de3. 1 1CarP =8estinversible puisque detP= -10011T =2 132002Ib+ 22= 1LE=B03=bU1+ 82+ 03=b+ 2=0=c+ 2=3finalementBO3=-=+2+2bEn conclusion:B=PTp- 121- 1120avec T=etP =0211002! 1

Page 69 : a , b - R ,aF 1:Mn+ 1=aUn+ bUnI Un+ 1=Un11"=Un et Un en fonction de n... puisconvergenceVn estconstante: Une N ;Un= NodoncUn+1=a Un+bWn Suite arithetico geometriquelo=ol1= alo+ boM2= alo+ ba+ 1VoMy= aMo+ aba+1/N+bro= avo+ ba2+ a+ 1toMontrons que parrecurrence que: Fnt I:Un= avo+ b1-a xtoa+ 11- a Vraipourn=0SupposonsqueUn=a"No+bx 1toalors Untz=a. Un+ b= aVo+abx1-av+ bts1 - aUn+1= al+Vo+ bWsax1+ 1= avo+ broxa- al++1- a1- a= a +Us+ b51- an+11 - 0

Page 70 : Ce quiachève farecurrence:Un+1=aUn+ ba + 1Fre NiUn=aUUo+ b.1-aL=ax+ b1- a -Un+1 -d= aUn- dUn+ 1aUnUn+1=3Un-42=34- 4-T=2=2Un=Un-2=3x Vo IUn=2+3 VoUnbSoit W r=ona aforsUnabWnt1= AUnavecA=01Un+1Unin=AUn +1Unona alors parrecurrence immédiate: Un= A"No: No =/ !A=aab+ b01spA= a; 1a= 1doncAest diagonalisable

Page 71 : es l1erecteurde La base canoniqueestVp:Ae1=21-a= vectezAy ya- 21x+ by= 0 x=a!1Y0=0Sy - Rex= vectvc= a IA= PDP 1avecP=1- bID=a00a - 101I a= 1donc inversiblea- 1bp- 1=01RMpuis: A= PDp-1avecD-O001puis: Un= AVopuis:Un let Unen fonction den

Page 72 : spAl= 4 1, 2Px= x- 1"x- 212Er= rectEz= rect31a0bA semblableàT =010C0020 ·on cherche Vi=&telsque Ve, ve2tAvz=aV1+ V3x- 2- t=a+ x 2x+ 3y+z=- a+ yI - x- y+ z=2x+ y+ t= tt= 0=z= aL=E x+ y=0= y=eaveca= 1 et x= 02=-Gx+ y-00On aVe=⑧- ↓

Page 73 : Soit Up=8010O0&VA, Va, Vo, Up / est une basede My, 1 IRcarP =- 10- 11est inversible0-11000-10puisque detP=1 +0AV=bU1+ cu+ dV2 +204b-0b=0- b- d+ 2=31= =c=0I- c+d=1 Ib==1-d=1finalementA= PT P- 11100avecT-0100002-10002

Page 74 : 1c1A=01bSic=1=1 seute valeur propredonc A= identité00C·1est uneconditionnécessaire,suffisante ?· Px= x- =12c- xIay+z=0bz= 0A=i =I -12=0ici C= 1done on pent diviser parC-1 pour avoirz98.ISi a Fo;ona:t21= rect8IIdir 21= 172Ane seraitpas diagonalisableOn a donca= 0A=Yy etIEx= vectre=8v= 2dansce casA est diagonalisablecar dirEc=1et donedim 3 = M3 , 1 diagonalisabledimensionorcre

Page 75 : 2 Polera=0;b= 1ic=2A= EEz =?x= 2A= 2Y I Einfz= vectB==,4A= PDp-1avec1= 19800P =8 e3 ? Elle est dejä triangulaire supérieur

Page 76 : 1det Fz- A=det112- 14=3- 11411216donc I2-Aest inversibleet ona /Iz-A=161214314122X= Ax+ BX- AX=B=Iz- AX= BX= Iz- A- 2BX = 161214B X= 2314123a- Un+ 1=xn+ 1-X=AXn+ B- Xonsoustraitmembreà membreet on=AUn+ X+ B- xCi=AUn+ Ax+ B- X①Xn + 1= AXn+ Ben0CarAx+ B= X②X=AX +BUn+ 1= AUn=0-2=Xn+1- x= AXn-xUn+1=A Uni. eUn+1=AUn

Page 77 : b- Par récurrence:AVo= I. Vo=VoS:Un=A"Uo alorsUntl= AUn= A Voce qui achère la récurrence2 Diagonalisationde A3/40A=PDp- =D=01/4P =1- 111A= PDp- 1A=1E" E"112 1- 11A= 2 ! - d-deUn= Avo- 8un== 5- Ero+ 2- lVoon obtient E un= = y- Ero+ 2- lVo

Page 78 : on a: firm Un=0n-D04 Xn=Un+ Xdonc hin=Xi. e Xn converge X1-sint1A=-20cost-sintcos It0PpX=det A-XIg=- X1-sint- 1-Xcostsinctcost-X=x- xcost-1-1cost-sinHl1- Xcost-Xsint- XSin t cost=xx2 -cos't -x+costsint -sinCtcost +SintIX=- x3+ xcos+- x+ SinCt X=x+ cos+ 1+ sit/X- x=- xY

Page 79 : spA= 0A n'est pas diagonalisablecar si elle l'était A= POyP= OsAbsurde2 B= fen: fes: esbase canonique0es==flez=/ifleg=A. fleg= sin1cost- SinIt0Mif"eg, fez, ez=sinctcosCHoinversiblecar det= 1 to101doncBestune base deE3T=Mp: f=Mi: f3es ; fey: fescomposante f"Cez=1, 0. 0MisSfeg! fle secomposante fez=0, 1, 0cost0010fez= Afez=ASin t-0d'oiT=010D0000-Prx=0= 0

Page 80 : 1dofP= Max doP, dox+1P'Indonc fPt1nxLinearité: fdP+ 4= 2p+ p- x+1ap+ 0= 2P- x+ 1Pj+ p- x+ 1q= dfP+ f4donc fe L1Rnx3SoitA= MBfB= Xix"" ...., x,fi- 0;nB : fx4=xP- kx+ 1xk-+=kxk- 1+ 1- k xR1- n⑧00A=- D2- R⑧0Ai........spAl= 1- 4, ke 40, nB0"/0·.......spAl= k- n, ke 41,n+Bfan+ 1= dimRnCxvateurs propres distinctsetestdonc diagonalisableSi Pestaste: fP=PdonPest valeur proprepour 1

Page 81 : A=0immon1/m0me1/m2 1/m0PqX= det/A -XIz=- Xmro1/m- xme1/m2 Mim-X=X- Xm iHimim+ i2Hom-x=- x+ 1 2x- 21 m- x1/m2- X1/mArmSpA= - 1: 2x+ My+ m2z= 0-1:A Y=- y=I1 x+ y+ M2= 0+ my+m22=0my, z EIR1m2x+ my+ z= 0f - == vectk=/ ir=-m↳Ve , V2basede E-1

Page 82 : 2:AY= 2 Y= rect4 V=M I22Ona finalement:A= PDP-1- m- n2m 2- 100avec P =10meetD-0-100A1002A= PDp-1D= diag -1":-1": 20pointducours :Systemelinéaire homogène: xIt=at xxt+ 1slt= ce/actt= ceAstAltl=/at dtequa diff 1 ordreavecsecond membrex'lt= atxxt+ btXt= xt+ xt: xton chercheunesolutionde la forme: xt= tet

Page 83 : xt= cteAt+ ctxateAtalt xcteAt+ bItY=alt xxt+ btx t Solution= C'teAct= bt= Ct= bte Atc1t= bte Ast Itpuisxt= bteAlt dt/eAtxt=x+ t+ xtSaltdt+SbIteAltdt / eAtsolution: xt=cemeCH-t1= 2+y xlt= 2xt+ eI yt=cet, 2- Ron resoud:x't= 2xt+ c et

Page 84 : - primitive integrale c'est avecles bornes /Itxt= 2et+ et xe2 dtC=Get- 1 etfinalement to systemea poursolution:xt=- 5 et+ cetC1 , 22 - Ry t=C etRemarque:le systeme s'écritx1 t=A. xtx t=xtytA= 21-imatrice diagonale = valeurs propresont2 et- 1A est diagonalisable: spA =-1: 2xt= 2x+ y+ 3c1 etbi!=2x+y+ 33t-22=- y +Wittevaleurs propres:2, -1, 1

Page 85 : ylt=- y+ cetyt= Cet+ cet xet dt ét-t=Ge+ 2etbteon résord:x't= 2xt+ ce+cetx't= Axt+ BtX: t= AxXot+ BtItct= ze2+ et+ etéteX-Xol= AX-XoxIt= Cett -Iet- 1esolutionparticuliere metro et enverification: xt=2 zett- Cet+cet· 2xt+ yt+ 3e= 2e2t- 7e -et+ ét+ 1et+ 3e= 2zet- =cet+ détx= 4x- 2y3 I x t=A. xtxt=xty1= x+ yytA=4- 211

Page 86 : PAx=4- x1- x+ 2=4- 4x- x+ x2+ 2= x2- 5x+ 6=X- 2X- 3SpA= 2, 3A est diagonalisableA=PDP1avecP -12D =20A103Pointcours:X'It= Ax1t+ Bsi Aest diagonalisablext=PDp- 1 Xt+ Bt=P- 1 x1=xp- + x+p- + BtSon multipliepar P-zsi BIt= 0Pserta rien =Y= Dy+p-1 Btavecy=P-1 XSi BIt=Onxt4= DYapoursolution :CeX=PYC2 exzt: AntEn2

Page 87 : Solutionexo 93:Xt=12Cett-Cet+ 2zet3t112eCet+ 2esti. e=xt= et+ 22etyt= 1e2+ 2est1x=- x+ 3x+ et= X=Ax+ i3avecX=xtytx2=- 2x1+ 4x2A=-13B=et-240A est diagonalisable siA=PDP-1P =31D=102102p- 1=1-1-23

Page 88 : on pose:Y= P X=y=Y =on résord: V= Dy+ Bp =yc=y =+ etIIIy =1 et+exedtet32= 24z-2etY= Get- /2exectety = t=1 et+ tet,Xt= PytI Y2t= 2e2t+ 2etd'on :t=3cet+ 3+ et+ 2e2+2e t= 3t+ 31+ 2et+ Cxe2tIxt= 21 et+ 2 tet+ Cett+ 2et= 2t+ 21+ 2/et+ cre2t

Page 89 : X= AxarecA: PoEIIPpx=2- x- 1210- 5- X7= xx+ 14-22- xspA= 30:- 110x- 5y+ 72=0 2x- y+2z=0A2= 02= 2x- y+ 2=0E-22=0Ly =3- 2214x- 2y+ 2z=0-32=02712-521jatto=rectadir to=ordre de multiplicitede eAest non diagonalisableA trigonalisablecar PAXI est scindeEs: A 3=-Et 3x 2y ! 22- 8= 2x-+4x- 2y+ 32=02y-2=0z = 313- 41bi= rt ! El

Page 90 : on utilise gaA estsemblableàmine imatricede TypeT =0cbT =:00C00C00-100VeVaVbasesoit v= /81DEAvyimage du vecteur 3= Av1+ BU2=+=E- ab2=7 I !a+ 2b=102a=4a= 2SoitP =-111T =-102120200040000on pose: y=P- 1 X =X=PY-ty= Ty yi=- 31+ 243=y1=1 e+ 23yi=443Iys =0I 3=5ax t= at xxt+ btxt= eSaltdt+ eatxéatxbtdtxt=Ceat+ extx/eatxbItdtSibIt=b XIt=ceat-

Page 91 : ⑪31- 1X=AXavecA=111202PpX=- X- 212A= PT PAavecP =01120T =2101- 112112021100002SoitY=P X EX=PYon resordY'=TY/- 241+ y2y== 241+ y2/Ce1= Yz= je2 +S-2x edtI=Ce =2 etI2tCettyz=C, e2t22II 2yzeneIY1- et+ ate+teet1= Yz= je2 += Yz= 22 e2 +yz=C, e2tX= Py= xt= 22 et+ E Cy+ etEyt= y=t- =yt+ zygt2t= y1t

Page 92 : A= matrice A②X= AXavecA-02- 2e= EAlarA-201n, on !2- 10A=PDP -1e= DE DU000non !- =A=PDP- 1D =0-32000bie=Px0p 1e es.Résultat: Six 1...psoient lesvaleurs propres réels↑r=4p= BricomplexesLes solutionssont combinaisons fineaire desfonctions: exit11:1P· eltlestet etsontBatSuiteexo:xt=A =+Az cos3t + As sin13tex+ BiIyt=B1+ B2cos3t+ Bysin 3tescosB1+sinA2t=1+ 2c0s3t+ 3 sin 3tBon utiliseles relationsde départdu systemepourreduirele nombre deconstanteà3210010A =-213+ BB=03023⑧002000-binome de Neuton function siles matrice commuteet =? A=A

Page 93 : 2-on s'arreteâ2cara partir de 3= 0A=on/B" CI-e= : =- 8fx, y=x, y,+ 3y,+ 3yz- cxyyM 14: I10⑧0I010000I0000 .

Page 94 : -isomorpheensemble forme bilinéaire symétriquematriceEn dimension finie: SnR +AnR=MnIR: fr-MnI:M= n+ idim:na + 1+ nn-1=dim n222+n=- i2symétriqueantisymétriqueDeux ensembles isormorphes= its sont pareiln+ 1exemple:Rnx=IRPreuve:Soit f2z exE ; -bilineairecarstable par finearite-symétriqueposons: fx,y= I fx, y+ fy, xetfz:y= 1, y- fy, x -antisymétrique-bilineainebifineairef1-22sext ; R et fa-22,a2xt ; Retonaf= f1+ fzOn adonc: 22 E xE: 1R1:22, s ExE; R+ 22, a txt ; R-S-Aunicité:f= fat fz- F- 91=22- 12tun-f= 9192S=A== 0Idonc&1= 91et82= 92SA

Page 95 : supposons quef= f=+ 72=9 1+ 92avec &: IIforme bifineaire symmetriqueet f:92forme bifineaire antisymmetriqueona alors&:==92- faf1- 91est symétrique I8=-9==92 -f=0 22ext, 1fz-92est antisymétriqueie fi= 91 et f2= 92CCL:La sommeest directe

Page 96 : ①n= 2; +x, y=x , y =- 2x2yde la base canonique4= 2Yest symétriquecar M/41 C'estY n'est pas positivecar- 2estupde M1Y/ est -20②A= M4 :A=1- 10S0- 1-2- 10-2I n'est ni symétriqueni antisymétriquecarAne l'est pas③B= MY : B=108 S0-300- 1trique donc 4 C'est· Best syme· I n'est pas définie positivecarspA= 71 : -3 : -17...- 30. . .④c= M4ic=0- 1- 2Squand tr echanges 2 colonnes10- 3dans un determinant sont230déterminant est l'opposéeCest antisymétriquedonc4 C'est

Page 97 : 1918 =6fxedoncI n'est pasune formesur = e M: /car par exemple:Y exp=xé"de=ex= +inappee": mol!2 == Rx+Soit PERCX:Placle " di -R?firmx ex=03- 30firm Px e42=0donc;5 A, tel queA=Place-1=Place"e /2!-1dx= - 2e x12= 2

Page 98 : 6- /2 dconverge doncPlace"d converge =Pé"vergedoncestmine forme sart Fa, B- Riy48+ By= im48x+ Bgx/=-dfig x....=x Yf+Bx +gProduit scalaire:forme bilinéaire symetrique de finie positiveE=IRPformabilinéaire: fx ,y= 2 Gij sise;fx,y= =- 2x31- 2y2+ x2yz+ x2+ x3y+ Y3 Yestune forme bilineairecarde La forme9 x ,1=jandjac ya 2 Y est symétrique immédiat:fy, x1= 31- 2y2/x =- 2x2+y,x+ y+ yx2+ xz= fx , y

Page 99 : 2 fx-R: Yx ,= x- 2x2+ x+ x+ xg2, 0yx, x= 0=x1- 2x2=0Yest définie= 7x1= xz= xz= 0Jositive et↓I1= 0I est donc produitscalaireE=1Rx918, 91= 10xd· Yestune forme symétrique sur E· Fa ,R;P, aiR- t424+ 30 ; R=- px+ B0kRx de- .../PxRxx+ BxRxd= 2YP, R+!BY9, R. Yest bilinéairecar linéaireà la première composanteet symetrique

Page 100 : Rappel:Sigest continue et, 0Sur a , b alors 8 , 0Sigcontinue etg=0alors f=0ic:FREIRx; P:=/Px/d,0et YP. P=0 Pxdx=0=fxt0; 1Px32= 0= Xx0; 1Px= 0Le sent polynome quian racineestte polynome nutleIciPestun polynome ayantune infinitéde racines doncP est le polynômenafte.finalementtestune forme bilineaire symetrique positiveetestdoncunproduit scalaireSoit Pc=calculer11P11?=siYestun produit scalaire ser:Ilsell=elixN:E IR+· Nx=0= 7x= 0IlIlest unenoriasur t· Nxx= X. Nx· Nx+ y ! Nx+ NyReciproquemment: SillIl est une norme. Verifiantfx, y -E,1x+y+ 11x- y= 2x2+ 1y2identité du paraftelogramme"

Page 101 : alorsIIIlestassociéeau produit scalairefx,y= =x+ y12- 111"- 1y112=Ill"+ Hy12-11-yll"11x+ y112= 1+ 1y2+ 24x, yI7xx+yx- yici:11P1: c"d= Idonc/P11:p, 0E RnXf4, 0= Pkqm ↳est une forme symétrique immédiate&, BERR; YnP, 0 , R tiRnCxyap+ Ba , R= 2xP1k+ B0kRk= 23Pkx Rk+ BRx Rk

Page 102 : -deP, a+ BY0 : RPIRnCx3;YP, 9= EPRI"0· P, P=0=PIRIS=0 +Re40inD ; Pk=0PERnX etPaawmoins+ 1racinesdoncP=0.R polynime rotte finalementtestune forme bilineaire symetrique positiveetestdoncunproduit scalaire Testune forme bilineaire symmetrique immediatâ demontrer 12418, 81= f1- +dt030e8, 81= 0 ft1- tdt=0=t-- 1, 13 ft1- t=0car 0 et continue

Page 103 : =f t - j- 1, 1ft= 0donc ft- -1, 17 ; ft=0 carf estcontinuesur -1: 1CCL: Yest un produit scalaireonmontreTestune forme bilineaire symmetriquesur t bili neaire positivea, BER; Xf, g, b---28+ Bg; d= 2f101+ bg01/ xh0+ ft +pgl/x ht9128+ Bgih= fl01h10 + gthitldt+ Bglochlol+ Hxh'd=aff , h+ BYg , h fg:418. 81= +!2+13-30918 .f1=0= f103=0 et. 18 +1 'dt=0=f01=0; Xt ft=0= f01=0 effconstante=&= be

Page 104 : donc &=0= polyniment= 1 11/01/x /cos vis =11l xIIllCours :· J. p. r: It : 41i!=111 x Ill· Si di E infinic espace euclidienx ,y 4x , x1x4y , yfx, ytiyx, y" -fx , x+ 4-↓x,yIlsIlIyI1 fx-...., n tM": x =+...+ xn= nx+...+ xhIl call2x=xi1 idy=Y : /avec Fi; yi=1==R" :xx,y==0: Y:

Page 105 : l'égalité de Cauchy SchwartzC. Sdoncx, y2=1x12x /y121x: dxxnl'inégalitéde Cauchy SchwartzC. Sestune égalité siet ysont liesiciona égalité si52EIRx: Lyin fi ; := dinFi ,jCCj= xj2 Fx...., n e: xe +...+ xl? annE= IRx, y=Ex: yix= xikiznavec:, 08= 7 kiznavec:0l'inégalitéC. S:ni= ri" /: nex +...+ xnl- an

Page 106 : ↑x,y= aYx, x+ bx, y+ cyy,ysymétrie:Yx , y= Yy, xfx,ytt=Fx, yt: a- cfx, x- yy,y= 0Si a- cFoalorsFx , yt; fx, x= 4y,y= 410 , 0=0impossibledonca=cYx, y= afx, x+ b4x , y+ a4y, yyy+00, y=0+0+ a4y,y↑p. S=Y0 ,y=0=bya. y, y=0=a= 0

Page 107 : finalement↑x,y= byx , y↑est positive:FactPx, x 0x FOE=b. Yx, x0=b0car Yx , 0d'orYx, y= bYx , y etb 0Reciproquemment:si Px ,y= bY x ,yavecb 0on verifieaiserment que Yestun Produit scalaire.

Page 108 : Exercice faità la maisonExercice 6:condition pourmontierun produit scalaire:formabilineaire symetrique / definiesur -positifverifierfa symétriewx , y= afx, x+ bfx, y+ cyy, y=YWy , x= afy, y+ byy, x+ cyx, x↳:a=cb=bcarYestun produit scalairedonc je peuxinverser yet sdonc symétrique-developperLinearité , vérifieryxx+ xz, y= 24xy+ ByxyC , BeiRyxx+ 3x2, y= a4xx=+ pxy, dx1+ 3x+ byxx=+ 3x2 , y+cyy , y= aayx1, x1+ 24x1, x2+ Bxyx,e+2 yx2 ,x-+ ba4x1, y+ Byx1 , y+ afy,y

Page 109 : = aafx = , x+ 22 , Yx1, xz+ Byx2, xz+bayx = , y +pfx, y+ afy, yD'aprèscette égalitéessayonsde trouverdes Valeurs poura, b, cad4x1 , x2+ abyx =, y+ dafy , y+ ayx2, xz+ byxz,y+ &BYy , y= dYx, y+ Byx , yat=ad= azp=0by= b=Ba= a+ B=a=0beiMaintenant it faut montrer qu'elleest definie et positiveIR- gerynon reduit à 02fx- - 14044doncbien definiewx , y= afx, x+ bfx, y+ cyy, y↑x, x= ayx , x+ byx , x+ cyx, xvx, x= 4x, xa+ b+ cpour etre positive0

Page 110 : conpor conclusion; pour quepsoitunproduit scalaireetora=cetoneaditions necessaires esiffisantes sant:a , c=0et bi03 E= MnRA , B=trace ATBinégalitéde Cauchy schwartzStrace ATB1 2trace ATAlxtraceBTBavecA:IdetB= Aona: trace M"trace Frmx trace PTTi. e-Extrace n'nona égalité siHet Imsont liesi. e5x t R:M=2 In

Page 111 : 4E= Ya ; b ; Rf ,g= ftgtdt1:b-aInégalité de Cauchy-Schuwarteffigee: ftigitdt t x agitatv- YfavecIavec9= 1fort!4 fi laatb- a =ftd x it

Page 112 : Norme surN:E1R+x: Nx=11 x11· Nx= 0= x=0Nxx=1x1. NxNx + y=Nx+ Ny2sicicet un produit scataire sur -Nx=2x ,xestunenormesur -1:Unenorme sur - n'est pas necessairement associeàun produit scalairei. en'est pas necessairementeuclidienneet on a : Nest euclidienne si elle verifie l'identité du parallelogramme11x+y1l+ 11x- y2= 2x2+ 1/y11211x+y2=k112+ 11y12+ 2 x , y 11x+y2kell2+ 1y12- 2 x , y on a alorsdans cecas:x,y=z 11x+ y2- 1 12-1y112ouvoircours

Page 113 : 11x 111=x 11+ 1x21 a- fx= xixtiR: 1x,0et 11x ==0 x 11+ kxz=0=x1= x=0= x1=x2=0x=0R2 2FXEIR;Fx= x =, x2 tIR211xx11= 1xx = ; xx2 1 1=xx2+ Xx2=x+ 1xz 3fx ,yRix=x ,, xy= 7=17z

Page 114 : 11x+ y1= x+y=1+ xz+ yz= x =+ y=+ xz+ yzConclusion:11Il1est unenorme sur 12IIIsella+Hyle11x+ y1= x+ y-Tabl11x1== x 11+ 211x+ y+ 1x-y2= 2x2+ 1ySoitx=1, 0x+ y= 1, 1y=0 , 1x- y=1, 111x +y112+ 11x-y12=8l'identitédu parallélogrammen'est pas verifice211x 112+ 1y112=4doncII IIIn'est pas unenorme euclidienneA, B= trace ATBI- A2 matrices-A Bli-s Ak : Bri=an: Pri-

Page 115 : n=2=zaki bki=a = 1bx+ a,242+ a, q4ba2a-x, y=x = 31+ x272II. Il estfa normeassociéeàce produit scalaire.A , B7:trace /A T , BI=trace ABCarAT= A-trace = I=0donc At B2 A+- trogorlede ytt, quelques soitA , y. e=ytf, xEA ,y, x= 07sous espacede Eetona: rect Al+= GAYtAYT= B -2 R tel que;A, B= 0

Page 116 : SoitB= =A , BT= trace ATB1=traceAB= trace â "A , B= 07= xa+ b+ c+ d=0=b=- a- b- cB= ,- -bc= a8-2+ b8-2+ iiII-EEEsiffaut qu'il soitrefinalement ayt= reattz, En; te4· Ez, t, Ez Yest fibre carat+ bz+ ctz=02=-b= 02I=a= b= c=0finalement c'est minebase de Aqui estde dimensionsRemarquesAcB= A BytAAst= Ag+' A

Page 117 : 114fig= ftgtdt· ff , g=e g, f evident· Ff:gE ;X2, B-CIRth-2E978+gih= Yfth1t +gtxhtdtIcorligtear finerie en1= d. Yf , h+ BYg, h· 418 , f1= 0!-f"tdt= 0 At; ft= 0car fest " et,01 Vt. ft=0

Page 118 : 2 Soitn , meDV ffrm, frm=Yos25nt/x cosTmt dt6cospxcos g=eP+ e iPXei4+ é 9 =e+4l+4 e-42+e-i- 4elfrm. gen= 2 ! si n+mit +cos an-mt at1n+mto=2n+Sin 2Tn+mitEssern-mstdt=4os2 +n-mtdtorthogonal:produitscalaire= oorthonormal:Il+ norme= 1Sintimei. en-mo7 frm : fin= = 2Fcn-mSi 25n-mst=0Ifn/ neest orthogonale

Page 119 : sin= mYfnifn= zdt =11full=ffnifr=== 2+ 1La farmille n'est pas orthonormale· gr= VI frAn,infrY 9n : 9m= Ykfr : frm=24fn: frm=011 gall= 1152fall=Ellfnll= Ex I= 1Ignest orthonormate& tIN

Page 120 : fi= j9i j 3j= 4x0=0et i, 2i= -1+ 1+ 1+ 1= 1oncherche:En=a , b,c, d tel que E1 ,..., En orthonormalei. e-i. 2: fi1, 3 34, di= 0et 112411= 1a+ b+ c+ b= 0a+ b+ c+ b= 0=a= d Ea- b+c- d=0=-2b- 2d=0b=-dIa+ b- c- d=0L I-2- 2d=0Ic=- cdEIRdoncE,- rectEEie34= 1 /119411=4a2=2a115411=1 a= 1a=2

Page 121 : finalementEx= 21i- 1 i- 1 ; 1 =24 =1i- 1i- 1 : 1cours:VI.....nlibrele1 , ..., en orthogonaleel= FEllWArect de1 ...., en=vect 1 , ...,UnS-2Ce...piep+ 1ez= Uc- Piep+ 1=p+ 1- x = e- de e....peppu=Fjpif faut que leproduit scalaire=oep+ 1. ej= 0=p+ 1. ej- djllejll2dj= Pp+ 1. ejIlejl

Page 122 : on l redressepour qu'il soitcolinéaireorthogonalité:---V2I-on enlevecette composanteVe,.., Vn7E↳141 ,-. ., qnq=/ Vell.V=x91=91= V142=Va- x 1410= 41: 82- x = 114111" =11=V2. 4142=02-Tv2, d11421124 ,=02-V2, 413. 4111 421124z: By - 20: 923. 42-53, 413. 41formule générale:Pp+r:Up +2- Epiz: PremSi normalisenormaliser:rendre fa norie= 1

Page 123 : 44 + ==Vp+ 1 +x : piP1P2fr = p4r4p + 2= 0on partde La base 1,X, X2deRe x3=Pr.p+ 1+ /R /14/12xx=- ak. Up+ 111 a K 11 2Pr=1Won chercheP2= /- X-P= Prtel que X ; Pr=ficc =P2=X- X; P=P111 P= 112-= 1P= x- I1PI= " x- =dx= 3x- =3= E11P211= 25on cherchePs tel queP=x 2- xr· Pa-X , P =PeIl P1112x : P= x3- Exdx=1121R1= x- =1= 25x- 11= 2 14=450=Yws

Page 124 : x2, P1= IP3=x2- x+- 5Pz= x2- x+ 5Une base orthogonalede Rex est1: x-Ei x- x+!Exercive 12 bis:dans MeR. Determiner favec== rect5= = 8= ==f+=M- Mz1/kAef ;A, x= 0++=M- +R/5 , 4= x, 1= 0i= ii5 , M= Trace+ = trace-+- bd=-I , M= Trace= i" = trace/câte25+a=

Page 125 : finalement:s+= 2- +R:25 s=IEc=GId=- c- 2b4= a- cra, b t IR+ += vectr-2-2:r=81 l 99l=a+ b+ c+ dDeterminer une base 1 def-k -= E-2 k1= k :11k11=3 R1=R- TR,k = k =Il k1112R == 18 -2- 32-2= =2- 43Une baseorthonormaledef-est15 = =: sâs -s

Page 126 : f+=M- Mz1/5 , 4= x, 1= k , n= 0II5= 88851= 25= 220 Ik= !· .=K- 7 k, 51 51iciondivisepas par /ITall caron normatise= 111121/201/4-3/40ki=k- xk, 5151=ISI1/20-01/418e00112001/4Il =Il=28-7ik==214- 3/40164E01/41001/4/ra=Tr21. Isareak2=L- x, k1k1- , 51351-onfesa de ja normalisedononclivise pas par la norme

Page 127 : - II·E-E S3/70I3/7k2= 3=3=-17- 177kz= 2. kaE= t !asignifie que⑪E= 1+ 22②Ent taE1= VectGU1, UzyGWe, Uzybase de Encar libreEz= VectV, vayGUI, veybase de Eccar libre

Page 128 : Det U1, Uz, V1, V2=1010-200⑧10- 1010- 1001010 101010- 10 10- 1Det U1, Uz, V1, V2= 20-10=20- 10101200-10- 110-1S2 =12+ 23=4x 2=- 4+0U1, Un, V1, Vaestminebase de4, = IREIdonct=G 1+ 22a- t- on1+ Ez !f+ 2 u= ivz+ v=ivzon a immédiatement Fi, j =1 , 2yWi, Vi= 0donc t= 21Ez

Page 129 : 2 GUn, U2, V1, Ve orthogonaleviace qu'ilprecede etU1, Uz= V1 , V2=02 énoncés supplementaireExercice 16: E : espaceeuclidien, dimension finieissue d'un produitscalaire- estun espace deEMontrer que: f+ ft =-If=EExercice 17 : E : / espaceeuclidien, dimension finieissue d'un produitscalairefet 62 sous-espace de -Montrer que: a -f= fb- f+ 6t= f+ nat-fnzt= f++ 6

Page 130 : es....enx=Sec ; ei= torjarso sarfExercice 16:ei= x;quandei. ei= 1carorthonormeSoit ez...., epyunebase orthonormale defet x-- soit z=x-; eialors FR- 4 1 ; pB2, 2: 7= x, ek- Ph= xk- xk=0conc2 eftPex=2t2e, eidonct= f+ f+-i= 1Eft-Efde plas fnf+= 0donc t=-+ ftExercice 17 :a-ft+=· Xxf+; tytf; x , y=0donc fcf

Page 131 : Exercice17: Bonus1afcf+ -SoitEf;on a alors ty eftx, y=0doncElf+ 1d'o: fcf+ 1 tSizeustidiendim =0dirmft= dire-dirft- dirt-dire+ dirf-dinnfd'ou l'égalitéen dir 3bf+ 6+=++ natfc f+ 6=f+ yf+ 2+6+ f+ 6+f+ n+ 137f+ 6t-yG-xeftnsty= y=+ yzproduit-x. y: c+etescolaire

Page 132 : f++ a+ cf na+fe fSi /Post 1/unsous espacedoncstablepar l'additionf++ 2+ cf na+dirf+ 6= dirf+ dir G-dirf nGExercice15 :E= Er+Er=E=E1++ Ezt ==+nec=0AmontrerSoitEtat n+fyt ;y=y1+ Yzy, Etix , y= x, yz+ x, yz=0car et fi+ et x t Estdonexec+= 074

Page 133 : ↳dirm Ent+ din Ezt=dimE-dir En+ dime-dirm tz-dir- -dimE-dir Ez+dim E- dir Es=clime tdonc tr①Est= t21e= e10, z f. g = tgtdtH= f=E: f0= 0a Hestun hyperplannoyau d'une forme linéaire4:E RI9f= f0est une formelinéaire sur EKer T: Hquiest doncun hyperplanbl Ht =Soit: f C Halors Fg -H; , g = tgtd=0ht= tft;h0=0donchtHf-H+= f , =0=+ft dt=0=ft-20 ; 1: t ft2=0cart - t ft2 est continueet c, 0Sur 20; 1

Page 134 : =Vt-30, 1 flt=0, f continue surC0 ; 13donet =C0 , 13ft=0finalementH+= 02fcf+ t=endimension finie.H+=02=E=AcarHest un hyperplande fde co dimensionn-1- H=E6= 0==G= HtHGA+ tExercice 16:Bonus10 /E , , /euclidienfunsousespace /ft=to2 Application:e= e10 , 23 fiy= yt1gtdt-= rect1 , xprojete orthogonale decsarf:P, 92

Page 135 : Idée:· Pfx-fdonc Pfx=ax+b, a, btR-projeté· x-P, x - s+= 31jx+rectAt= Atonadonc x- P, x; 1= x - Pfx ; x=0Exercice18:Bonus6+= xt, kytG,xx, y= 06= rect1, 1 , 2, 02 , 1 , 1,x6+= x, y, z, teR", x+ y+ 2= 0et2x+ y+ z- t=0 Ex+ x+ y+ z- t=0-= 0Ix+ y+ z= 0Ix- t=0 -yst= vectv=1, 0,- 1, 1, v=0. 1.- 1, 0IPour f:onchoisit2 vecteurs

Page 136 : Soitve= /1,- 1, 2 , 1 etv= 1 , 2, 3,- kf= X= x, y, n,teR" , x , v=x , v2=0 IdonzUn f+etUzE ftdonc rest U1,Uzycff= GUxiVz g+= frectu=,val+vect Al↓donc ft= rectU1 , Unendimension finie Att=rect AExercice 19:a Dans 13 X munitdu produit scalaire& P, a =actactdtdeterminerx+14 tbDansIRe Xon donneP==X2:P2= 5 x 2-3, 43=4 x-3Montrer que P11P2etP11Psendedrirex"+pour92 4, 0:PI9dS

Page 137 : aoncherche PX=ax+ bx2+cx+ dtel que41x+ 1, 9=0 x+ 1ax+ bx+cx+ dtjax+ b+ ax4+b+ xx3+c + xxx+ dx1=032a+ 2b+c+2d=0d=- fa- 1b-c0x= ax3- 7+ bx2- 5+ cx- 5doncx+ 1+= rectX-5: x-1, x- EbY92 , Pn= xc2xx2- 3dx= x- x3=0doncP1↓P2-91, P3==0doncP11P3

Page 138 : finalementP2: Psycx24--SOUS espacerectP2 : By xY+Pz et P,sont librecar dedimensiondonc P2; Psest mne basederectP2: P3quiestde dir 2Ix+= rectP2, P3donc x2y += dimRz X-1=2x=x+ 2y- zExercice 20:Résoudre y'=2x+ 4y- 222=- x- 2y+ zx= Axava= 22=2Attention coff,clominantPAX= detA- Ic=1- x2- 124- x-2-1-21-x=2- x+ 6Px= 0=1=0aux=6spA= 30 , 67

Page 139 : to? A= 8 =x+ 2y- z= 0x+ 2y-z=0=72=x+ 2y-x- 2y+z=0xEIR , y ERRto= rectv= , 02= 2Uroreibebase de tox= Al? = b= /-= = -5-x- 2y-z=0t=-ee=estorect r:DIIA estdiagonalisablecur dirto+ dir Es=3dir Ma . IRA=PDp"avecD= IIIS888iP= EX=PDpXpX= Dpx

Page 140 : px= DPXIY-DYPosons:Y=P'Xx= Ax=Y= DyYj=8Iyj= 633-21C2CA, Cz, C3ER=cettx+= 1+ dzebty= P"x X= P4 Iyt=z+ 23e6t2t=1+2cz- zebtAutreexo :Xt=vo+ Netv1+ WeltraavecUxvecteur propreassocié à x0= 2== Ev= i

Page 141 :

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141