TD Correction

Posté le 08/02/2025

Chargé de TD/CM : E. Masnada.

135 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154

Page 1 : Correction des TDs d’analyse dansRnElian Masnada.25 novembre 2020J’encourage les élèves à me faire part de leurs remarques par email àl’adresse elian.masnada@cyu.fr aﬁn de m’aider à améliorer ce corrigé.1

Page 2 : TD1 1 : Normes, distances et boulesExercice 1 : Normes de RnSoit E = Rn. Pour x = x1, ..., xn Rn, on posex1 =nXi=1xix2 =vuutnXi=1x2ix= max1inxi1. Démontrer que ·1, ·2 et ·sont des normes.Indication : pour ·2, on utilisera l’inégalité de Schwarz admise ici ⟨uv⟩ u2 v2où ⟨uv⟩= Pni=1 uivi avec u = u1, ..., un et v = v1, ..., vn.2. Démontrer que pour a, b 0 :a + b a +b.3. Généralisation : montrer quea1, ..., an 0,vuutnXi=1ai nXi=1ai4. En déduire que pour x, x2 x15. Démontrer quex, xx2 x1 n x6. Les 3 normes sont-elles équivalentes ?7. Représenter, pour R2, la boule fermée unité Ba = 0, 0, r = 1pour chacune de ces normes.1. Petite précision car il est toujours important de rendre à César ce qui est à César :tout au long du document, lorsque la correction est en rouge vif alors elle a été rédigé parmes soins, lorsque la correction est en bordeaux alors il s’agit d’une correction rédigée parles soins de M. Masereel c’est le cas pour 5 exercices ou parties d’exercice.2

Page 3 : Réponses :1. Démontrons que ces trois applications sont bien des normes. Pour celail faut montrer que chacune de ces applications vériﬁe les 3 propriétéssuivantesa x Rn, x= 0 =⇒x = 0Rnb x Rn et λ R, λx= λ xc x Rn et y Rn, x + yx+ yPour la norme ·1 :a Si x1 = 0 alors Pni=1 xi = 0 =⇒i, xi = 0ﬁnalement x1 = 0 =⇒x = 0, 0, ..., 0 = 0Rnb Soit λ R et x = x1, ..., xn Rn, alors λx = λx1, ..., λxn.ﬁnalement :λx1 = Pni=1 λxi = Pni=1 λ xi = λ Pni=1 xi = λ x1c Soit x = x1, ..., xn Rn et y = y1, ..., yn Rn.Alors x + y = x1 + y1, ..., xn + ynx + y1 = Pni=1 xi + yi. Or i, xi + yi xi + yi. Ainsix + y1 = Pni=1 xi + yi Pni=1 xi + Pni=1 yi = x1 + y1Pour la norme ·2 :a Si x2 = 0 alorsqPni=1 x2i = 0 =⇒i, xi = 0ﬁnalement x2 = 0 =⇒x = 0, 0, ..., 0 = 0Rnb Soit λ R et x = x1, ..., xn Rn, alors λx = λx1, ..., λxn.ﬁnalement :λx2 =pPni=1λxi2 =qλ2 Pni=1 x2i = λqPni=1 x2i = λ x2c Soit x = x1, ..., xn Rn et y = y1, ..., yn Rn.Alors x + y = x1 + y1, ..., xn + yn. On a alors :x + y22 =nXi=1xi + yi2 =nXi=1x2i + y2i + xiyi3

Page 4 : Or d’après l’énoncé, nous avons l’indication : Pni=1 xiyi qPni=1 x2iqPni=1 y2iAinsi :x + y22 =nXi=1x2i + y2i + 2xiyi nXi=1x2i +nXi=1y2i + 2nXi=1xiyinXi=1x2i +nXi=1y2i + 2vuutnXi=1x2ivuutnXi=1y2i = x22 + y22 + 2 x2 y2d’où l’on déduit x + y22 x2 + y22. Or puisque ·2 estclairement une application déﬁnie positive, on peut prendre laracine carrée de l’inégalité précédente sans changer le sens de l’in-égalité. Ainsix + y2 x2 + y2Pour la norme ·:a Si x= 0 alors max1inxi = 0 =⇒i, xi = 0ﬁnalement x= 0 =⇒x = 0, 0, ..., 0 = 0Rnb Soit λ R et x = x1, ..., xn Rn, alors λx = λx1, ..., λxn.ﬁnalement :λx= max1inλxi = λ max1inxi = λ xc Soit x = x1, ..., xn Rn et y = y1, ..., yn Rn.Alors x + y = x1 + y1, ..., xn + yn. On a alors :i, xi + yi xi + yi max1inxi + max1inyiComme c’est vrai pour tout i, c’est notamment vrai pour la valeurde i tel que xi + yi soit maximal. Ainsimax1inxi + yi max1inxi + max1inyiet ﬁnalement x + yx+ y.Donc les 3 applications sont bien des normes.2. Montrons quea + b a +b pour a, b 0 :4

Page 5 : Puisque 2ab 0, on a évidemment0 a + b a + b + 2ab = a +b2On peut alors prendre la racine carrée de l’expression précédente pourainsi obtenir le résultat demandé.3. généralisons maintenant l’expression précédente. Pour cela, on re-marque que0 nXi=1ai nXi=1ai + 2nXijaiaj = nXi=1ai2on prend alors la racine carrée pour obtenir le résultat demandé, àsavoirvuutnXi=1ai nXi=1ai4. Démontrons que x, x2 x1 :On veut donc démontrervuutnXi=1x2i nXi=1xior, i, xi =qx2i . On a donc d’après la question précédente enposant ai = x2i vuutnXi=1x2i nXi=1qx2i =nXi=1xiCQFD5. On veut démontrer que x, xx2 x1 n xOn a déjà démontré l’inégalité intérieure à la question précédente.Commençons par montrer que xx2, c’est-à-dire que :max1inxi qPni=1 x2i5

Page 6 : Or ceci est trivial car x2=max1inxi2et doncx22 =nXi=1x2i = x2+ αoù α est positif. Donc ﬁnalement, x, xx2Montrons maintenant que x1 n x:c’est encore une fois trivial. En eﬀet : i, xi max1inxi, ce quiimplique quePni=1 xi n max1inxi, et ﬁnalement x1 n xOn a bien x, xx2 x1 n x6. On nous demande maintenant si les 3 normes sont équivalentes. Il ya 2 façons de répondre à celaa La façon la plus simple de répondre est de voir que comme on a icides normes déﬁnies sur un espace de dimension ﬁnie dimensionn alors les normes sont équivalentes.b Mais on peut aussi utiliser la réponse à la question 5. En eﬀet, decette question, on déduit que les normes 2 et sont équivalenteset que les normes 1 et sont équivalentes. Donc par transitivitéles normes 2 et 1 sont équivalentes.7. Ces boules ont été faites en cours. Du coup, cela peut être fait enautonomie par les élèves.Exercice 2 : Norme sur RnSoit E = Rn. Soit a1, a2, ..., an R. Soit N une application de E →Rdéﬁnit parx = x1, ..., xn Rn, Nx = a1x1 + a2x2 + ... + anxnDonner une condition nécessaire et suﬃsante sur les ak pour que N soit unenorme sur Rn ?6

Page 7 : Réponses : Il faut montrer sous quelles conditions N vériﬁe les 3 propriétéssuivantes1. x Rn, Nx = 0 =⇒x = 0Rn2. x Rn et λ R, Nλx = λNx3. x Rn et y Rn, Nx + y Nx + Ny1. Imaginons qu’il existe j tel que aj = 0. Pour ﬁxer les idées, disonsque j = 2. Alors tout vecteur de la forme X = 0, x2, 0, ..., 0 avecx2 R conduit à NX = 0, ce qui contredit la première propriété.On voit donc qu’il faut que i, ai ̸= 0.Mais il faut de plus que tous les ai soit strictement positif. En ef-fet, il faut qu’ils soient de même signe pour assurer que Nx = 0 =⇒x = 0Rn et positif de façon à ce que l’application soit déﬁnie positive.Ainsi, la première propriété implique quei, ai 02. Soit λ R et x = x1, ..., xn Rn. AlorsNλx = a1λx1+...+anλxn = λa1x1+...+anλxn = λNx3. Soit x = x1, ..., xn Rn et y = y1, ..., yn Rn. AlorsNx + y = a1x1 + y1 + ... + anxn + yn a1x1 + a1y1 + ... + anxn + anynNx + y Nx + NyFinalement N est une norme ssii, ai 0Exercice 3 : Norme sur l’espace des matrices carréesSoit a MnR. Pour a, on déﬁnit les deux applicationsN1 : MnR →Ra →N1a = max1innXj=1aij7

Page 8 : etN2 : MnR →Ra →N2a =pTrtaa1. Montrer que ces deux applications sont des normes.2. Sont-elles équivalentes ?Réponses :1. Il va falloir montrer que N1 et N2 vériﬁent bien les 3 conditions sui-vantesa a MnR, Na = 0 =⇒x = 0MnRb a MnR et λ R, Nλa = λNac a MnR et b MnR, Na + b Na + NbPour N1 :a Soit a MnR tel que N1a = 0. Alors max1in Pnj=1 aij= 0ce qui implique que i, j aij = 0 et ﬁnalement a = 0MnR qui estla matrice nulle.b Soit a MnR et λ R, alors pour tout i, j, aij →λaij. AinsiN1λa = max1in Pnj=1 λaij= λ max1in Pnj=1 aij= λN1ac Soit a MnR et b MnR, alors i, j :aij + bij aij + bijEn sommant sur toute la lignenXj=1aij+bij nXj=1aij+nXj=1bij max1innXj=1aij+ max1innXj=1bij= N1a+N1bOn peut maintenant prendre le max de l’ensemble de l’expressionprécédente ce qui ne change rien à droite puisque le max du maxest égal au max. On obtient alors N1a + b N1a + N1b.8

Page 9 : Pour N2 :Il faut tout d’abord trouver l’expression de cette application. Pourrappel :baij =nXkbikakjOr si b = ta, on a bik = aki, ce qui impliquetaaij =nXkakiakjEt ﬁnalementTrtaa =nXi nXkakiaki!=nXi,ka2kiDonca MnR, N2a =vuutnXi,ka2kia Soit a MnR tel que N2a = 0. AlorsqPni,k a2ki = 0 ce quiimplique que i, j aij = 0 et ﬁnalement a = 0MnR qui est lamatrice nulle.b Soit a MnR et λ R, alors pour tout i, j, aij →λaij. AinsiN2λa =qPi,kλaki2 =qλ2 Pi,kaki2 = λN2ac Soit a MnR et b MnR, alors i, j :aij + bij2 a2ij + b2ij + 2aijbijOr pour α, β R, on a αβ 12α2 + β2. Ainsi, en posantα = aij/N2a et β = bij/N2b, on aaijbijN2aN2b 12h aijN2a2+ bijN2b2 i9

Page 10 : En eﬀectuant une somme sur tous les éléments, on obtientXi,jaijbijN2aN2b 12Xi,jh aijN2a2+ bijN2b2 i121N2aXi,jaij2 +1N2bXi,jbij2= 1AinsiXi,jaijbij N2aN2bRevenons maintenant à l’inégalité triangulaire :N22 a + b =Xi,jaij + bij2 Xi,jaij2 +Xi,jbij2 + 2Xi,jaijbijN22 a + N22 b + 2N2aN2b = N2a + N2b2Comme l’application N2 est déﬁnie positive, on peut prendre laracine carrée de cette expression, conduisant ainsi à l’inégalitétriangulaireN2a + b N2a + N2b2. Puisque l’espace est de dimension ﬁnie et que N1 et N2 sont desnormes alors ces normes sont équivalentes.Exercice 4 : Norme sur l’espace des fonctions continues sur0, 1Soit E l’ensemble des fonctions continues sur 0, 1 →R. On déﬁnit lesapplications suivantes f E :f1 =Z 10fxdxf2 =sZ 10f2xdxf= supx0,1fx1. Montrer que ·1 et ·sont des normes on admettra que ·2 estbien une norme.2. Ces trois normes sont-elles équivalentes ?3. Déduire que E n’est pas un espace de dimension ﬁnie.Réponses :10

Page 11 : 1. On doit vériﬁer que ces 3 applications vériﬁenta f E, f= 0 =⇒f = 0b f E et λ R, λf= λ fc f E et g E, f + gf+ gPour ·1a Si f1 = 0 alors f1 =R 10 fxdx = 0 ce qui implique évidem-ment f = 0b Soit f E et λ R,λf1 =R 10 λfxdx = λR 10 fxdx = λ f1c Soit f, g E,f + g1 =Z 10fx+gxdx Z 10fxdx+Z 10gxdx = f1+g1puisque x 0, 1, fx + gx fx + gx.Pour ·a Si f= 0 alors f= supx0,1fx ce qui implique évidem-ment f = 0b Soit f E et λ R,λf= supx0,1λfx = λ supx0,1fx = λ fc Soit f, g E, alors pour tout x 0, 1fx + gx fx + gxor évidemment pour tout x 0, 1fx supx0,1fxgx supx0,1gxDonc : x 0, 1fx + gx fx + gx supx0,1fx + supx0,1gx11

Page 12 : Il ne reste plus qu’à passer au sup :supx0,1fx + gx supx0,1fx + supx0,1gxconduisant à l’inégalité triangulaire voulue.2. On cherche à savoir si ces 3 normes sont équivalentes. Par exemple,pour les normes ·1 et ·2, cela revient à dire qu’il existe 4 réelsstrictement positifs a, b, c et d tels que pour toute fonction f continuepar morceaux sur 0, 1, on aia f1 f2 b f1c f2 f1 d f2Pour qu’il n’y ai pas équivalence, il suﬃt que l’on trouve une famillede fonction f telle que a, b, c ou d tendent vers 0 ou l’inﬁni. Il suﬃtdonc d’étudier le rapport f1 / f2 ou f2 / f1 tendent vers 0ou l’inﬁni. Ici, nous allons déﬁnir la famille de fonctionsfn :0, 1 →Rx →xnOn a alors pour tout n Nfn1 =1n+1fn2 =12n+1fn= 1Conduisant donc, lorsque n tend vers l’inﬁni, àfn2fn1 →fnfn1 →fnfn2 →Les normes ne sont donc pas équivalentes3. Comme les normes ne sont pas équivalentes, l’espace est de dimensioninﬁnie.12

Page 13 : Exercice 5 : Norme sur R2Soient a, b 0. On pose pour X = x, y R2NX = Nx, y =pa2x2 + b2y21. Montrer que Nx, y = NX, avec X = x, y R2, est une normesur R2. utiliser l’inégalité de Schwarz donnée dans l’exercice 1 de ceTD2. Dessiner la boule fermée unité Ba = 0, 0, r = 1cette questionest à traiter si la notion de boule a déjà été déﬁnie en cours.3. Trouver le plus grand réel q et le plus petit réel p tels queq ·1 N p ·2Réponses :1. Démontrons que cette application est bien une norme. Pour cela ilfaut montrer qu’elle vériﬁe les 3 propriétés suivantesa X R2, NX = 0 =⇒X = 0, 0b X R2 et λ R, NX = λNXc X1 R2 et X2 R2, NX1 + X2 NX1 + NX2Donca Soit NX = 0, alorspa2x2 + b2y2 = 0 où X = x, y. Orcomme a et b sont strictement positifs, x = y = 0. FinalementX = 0, 0.b Soit X = x, y R2 et λ R, alorsNλX =pa2λ2x2 + b2λ2y2 = λpa2x2 + b2y2 = λNXc Soit X1 = x1, y1 R2 et X2 = x2, y2 R2. Alors X1 + X2 =x1 + x2, y1 + y2 et doncN2X1 + X2 = a2x1 + x22 + b2y1 + y22= a2x21 + a2x22 + 2a2x1x2 + b2y21 + b2y22 + 2b2y1y2= a2x21 + a2x22 + b2y21 + b2y22 + 2ax1ax2 + by1by213

Page 14 : Utilisons maintenant Cauchy-Schwarz sur w1 = ax1, by1 et w2 =ax2, by2. Alorsax1ax2 + by1by2 qa2x21 + b2y21qa2x22 + b2y22FinalementN2X1 + X2 a2x21 + a2x22 + b2y21 + b2y22 + 2qa2x21 + b2y21qa2x22 + b2y22qa2x21 + b2y21 +qa2x22 + b2y222NX1 + NX22Or l’application N est déﬁnie positive permettant donc de prendrela racine carrée de l’expression précédente. AinsiNX1 + X2 NX1 + NX22. La boule fermée unité est donné par NX 1 avec X = x, y. Ona doncpa2x2 + b2y2 1En élevant au carré, on obtient que le contour de la boule est donnépar a2x2 + b2y2 = 1 ce qui correspond à une ellipse de demi-axes 1/aet 1/b.3.Exercice 6 : Norme sur l’espace des polynômesSoit n un entier naturel non nul et E = RnX espace des polynômes dedegré n. On déﬁnit·: E →RP →P=supkJ0,nKP k0où P k est la dérivée kème de P, etN : E →RP →NP = supxRPx1 + xn14

Page 15 : 1. Montrer que N est bien déﬁnie.2. Montrer que ces deux applications sont des normes.3. Montrer qu’il existe C 0 tel queP E, PCNpRéponses :1. Commençons par vériﬁer que l’application NP = supxRPx1+xn estbien déﬁnie. Clairement pour x R, 1 + xn ̸= 0. Le problèmese trouve donc éventuellement en ±. Pour investiguer cela, notonsPx = Pnk=0 akxk, alorsPx1 + xn =nXk=0akxk1 + xn = anxn1 + xn +n1Xk=0akxk1 + xnLa somme tend clairement vers 0 quand x tend vers ±et le premiertend vers an. Il s’ensuit que NP est bornée sur R.2. Nous devons maintenant montrer que ces applications sont des normes.Pour ·:a Soit Pn= 0 alors supkJ0,nKP k0 = 0. Notons Pnx = Pnk=0 akxkce polynome. Alors P kn= k!ak pour tout k J0, nK. Ainsi,supkJ0,nKP k0 = 0 implique k, ak = 0 et donc Pn = 0.b Soit λ un réel et Pn un polynome. Alors λP kn= λk!ak. Finale-mentλPn=supkJ0,nKλP k0 =supkJ0,nKλk!ak = λ Pnc Soit Pn et Qn deux polynômes de degré n. Alorsk J0, nK, P + Qk0 P k0 + Qk0ork J0, nK, P k0 supkJ0,nKP k0k J0, nK, Qk0 supkJ0,nKQk015

Page 16 : ﬁnalementk J0, nK, P+Qk0 P k0+Qk0 supkJ0,nKP k0+ supkJ0,nKQk0et en prenant le sup de cette expression, on retrouve bien l’inégalitétriangulaire.Pour N :a trivialb trivialc La démonstration est très exactement de même nature que pourla norme précédente. Ainsi, pour x RP + Qx1 + xnPx1 + xn + Qx1 + xnorx R,Px1 + xn supxRPx1 + xnx R,Qx1 + xn supxRQx1 + xnﬁnalementP + Qx1 + xnPx1 + xn + Qx1 + xn supxRPx1 + xn + supxRQx1 + xnen prenant le sup de cette expression, alors on retombe sur l’in-égalité triangulaire.3. L’espace est de dimension ﬁnie. Les deux normes sont donc équiva-lentes. Ainsi, il existe a et b deux réels strictement positifs tels queP, aNp PbNpIl suﬃt alors de poser C = b. CQFD16

Page 17 : Exercice 7 : "3ème inégalité triangulaire"Soit E, · un espace vectoriel normé. Montrer que pour x, y E, on ax+ yx y+ x + yRéponses :1 x + y + x y= 2x= 2 xx + y+ x y2 y + x + y x= 2y= 2 yx + y+ x yIl suﬃt maintenant de faire 1+2x+ yx y+ x + yExercice 8 : Autre normeSoit l’application N de R2 →R qui à tout x, y R2 associe Nx, y =4x + y.1. N est-elle une norme ?2. Dessiner la boule fermée de centre 0, 0 et de rayon 1. Quelles sontses symétries ?3. En toute généralité quelle est la symétrie d’une boule fermée.Réponses : A rédiger plus tard car l’exercice est vraiment trivial.Exercice 9 : A propos des distancesDans cet exercice on déﬁnit des applications di de R × R →R. Dans lasuite x, y R.d1 : x, y →d1x, y = x y2d2 : x, y →d2x, y =px yd3 : x, y →d3x, y = x2 y2d4 : x, y →d4x, y = x 2yd5 : x, y →d5x, y =x y1 + x yd6 : x, y →d6x, y = x3 y317

Page 18 : Ces applications sont-elles des distances ? Sont-elles associées à des normes ?Réponses :Rappel 1 :Pour savoir si une application d de E2 dans R est une distance, il faut qued vériﬁe les 3 propriétés suivantes1. X, Y E2, dX, Y = 0 ⇐⇒X = Y2. X, Y E2, dX, Y = dY, X3. X, Y, Z E3, dX, Y dX, Z + dZ, Y Dans notre cas, E = R.Rappel 2 :On rappelle également que si une distance d sur E2 est associée à la norme·sur E, alors1. X, Y E2, dX, Y = X Y 2. Si d est associée à une norme alors λ R et X, Y E2,dλX, λY = λdX, Y 3. Si d est associée à une norme alors dX, 0 doit vériﬁer les propriétésd’une norme.1. On considère d1 = x y2 où x, y R.a Si x = y alors d1x, x = x x2 = 0Si d1x, y = 0 alors x y2 = 0 ce qui implique x = y.b Vériﬁons la symétrie.d1x, y = x y2 = 1y x2 = y x2 = d1y, xc soit x, y, z R3. Alorsx y2 = x z + z y2 = x z2 + z y2 + 2x zz yor si l’inégalité triangulaire est vraie, on devrait également avoirx y2 x z2 + z y2Il suﬃt donc de montrer qu’il existe x, y, z tels que 2xzzy 0 pour montrer que l’inégalité n’est pas vériﬁer. Prenons x = 3,z = 2 et y = 1, conduisant à 2x zz y = 1donc d1 n’est pas une distance puisqu’elle ne vériﬁe pas la dernièrepropriété.18

Page 19 : 2. On considère d2 =px y où x, y R.a Si x = y alors d2x, x =px x = 0Si d2x, y = 0 alorspx y = 0 ce qui implique x = y.b Vériﬁons la symétrie.d2x, y =px y =py x = d2y, xc soit x, y, z R3. On a évidemmentx y x z + y zPrenons la racine carrée de cette expression ce qui n’aﬀecte pasle signe de l’inégalitépx y px z + y zor pour tout a, b réels positifs, on aa + b a +b cara+b a+b+2ab = a+b2 et il ne reste plus qu’à prendrela racine carrée de cette expression. Ainsipx y px z + y z px z +py zqui est bien l’inégalité triangulaire.donc d2 est bien une distance. Vériﬁons si elle dérive ou non d’unenorme. Pour cela, on va vériﬁer si d2x, 0 =px a ou non les pro-priétés d’une norme.Evidemment si d2x, 0 =px = 0 alors x = 0 donc la premièrepropriété est vériﬁée.Soit λ et x deux réels quelconques. Alors d2λx, 0 =pλx =pλpxqui ne vériﬁe pas la deuxième propriété. Donc d2 n’est pas associée àune norme.3. Soit d3x, y = x2 y2. Si d3x, y = 0 alors x2 y2 = 0 doncx2 = y2. Ainsi, x = 1 et y = 1 conduisent à d3x, y = 0 alors quex ̸= y. Donc d3 n’est pas une distance.4. Soit d4x, y = x 2y. Donc pour tout couple x, y tel que x = 2yd4x, y = 0 alors que x ̸= y. Donc d4 n’est pas une distance.5. Soit d5x, y =xy1+xy.19

Page 20 : a Si x = y alors d5x, x =xx1+xx = 0Si d5x, y = 0 alors x y = 0 ce qui implique x = y.b Clairement, grâce à la valeur absolue, d5 est symétrique : d5x, y =d5y, x.c Montrons tout d’abord que pour tout a, b, c réels strictement po-sitifs, on aa b + c =⇒a1 + a b1 + b +c1 + cPour cela, calculons explicitementa1 + a+b1 + b+c1 + c = 2bc + abc + b + c a1 + a1 + b1 + c = b + c + a + bca + 21 + a1 + b1 + c 0Or, on ax y x z + y zon peut alors utiliser l’expression démontrée précédemment oùa = x y, b = x z et c = y zx y1 + x y x z1 + x z +y z1 + y zoù on reconnait donc d5x, y d5x, z + d5y, z.Encore une fois, cette distance n’est pas issue d’une norme car d5λx, λy ̸=λd5x, y ou encore parce que d5λx, 0 ̸= λd5x, 0.6. Laissée en exercice. C’est bien une distance mais elle n’est pas issued’une norme.20

Page 21 : TD2 : Ouverts et fermésExercice 1 : Normes équivalentes et notions d’ouvert et ferméSoit E un espace vectoriel muni de deux normes équivalentes ·1 et ·2.1. Soit B·1a, r = x E/ x a1 r. Montrer qu’il existe r′ telqueB·1a, r B·2a, r′où B·2a, r′ = x E/ x a2 r′.2. Soit B·2a, r′′ = x E/ x a2 r′′. Montrer qu’il existe r′′′tel queB·2a, r′′ B·1a, r′′′où B·1a, r′′′ = x E/ x a1 r′′′.3. En déduire qu’un ouvert de E, ·1 est un ouvert de E, ·2 etréciproquement.4. Même question pour les fermées.Réponses :1. Les deux normes étant équivalentes, nous savons qu’il existe α et βdes réels strictement positifs tels que pour tout x, a E2α x a1 x a2 β x a1Alorsx0 B·1a, r ⇐⇒x0 a1 r21

Page 22 : Doncα x0 a1 x0 a2 β x0 a1 βrAinsi x0 appartient à une boule ouverte de la norme 2 et de rayon βrx0 B·2a, βrComme cela est vrai pour tout x0 B·1a, r, ﬁnalement, on déduitqueB·1a, r B·2a, r′avec r′ = βr2. Il s’agit ici de faire le même raisonnement. Les deux normes étantéquivalentes, nous savons qu’il existe α et β des réels strictementpositifs les mêmes qu’à la question précédente tels que pour toutx, a E21β x a2 x a1 1α x a2Alorsx0 B·2a, r′′ ⇐⇒x0 a2 r′′Donc1β x0 a2 x0 a1 1α x0 a2 r′′αAinsi x0 appartient à une boule ouverte de la norme 1 et de rayonr′′/αx0 B·1a, r′′α Comme cela est vrai pour tout x0 B·2a, r′′, ﬁnalement, on déduitqueB·2a, r′′ B·1a, r′′′avec r′′′ = r′′α3. Soit A E un sous ensemble. AlorsA ouvert selon ·1 ⇐⇒x A, R 0 / B·1x, R AOr compte-tenu de la question 2, nous savons queB·2x, αR B·1x, R A22

Page 23 : puisque R = r′′/α, r′′ = αR.Donc A est un ouvert selon la norme ·2.À l’inverse :A ouvert selon ·2 ⇐⇒x A, R 0 / B·2x, R AOr compte-tenu de la question 1, nous savons queB·1x, Rβ B·2x, R Apuisque R = βr, r = Rβ .Donc A est un ouvert selon la norme ·1.4. Si F est un fermé pour la norme ·1 alors CEF est un ouvert selonla norme ·1. Or si CEF est un ouvert pour ·1, d’après 3, CEFest aussi un ouvert pour la norme ·2 et ﬁnalement F est un fermépour la norme ·2.Conclusion de l’exercice : Les notions d’ouvert et de fermé ne dépendentpas de la norme choisie dans les espaces de dimension ﬁnie puisque toutesles normes y sont équivalentes.Exercice 2 :Soit E, · un espace vectoriel normé.1. Montrer qu’une boule fermée n’est pas un ouvert.2. Montrer qu’une boule ouverte n’est pas un fermé.Réponses :1. Commençons par illustrer les choses dans R2, · voir ﬁgure ci-dessous23

Page 24 : On note Ba, r la boule fermé de rayon r et de centre a. On considèreun point x se trouvant sur le bord de cette boule et la boule ouverteBx, ϵ, c’est-à-dire, la boule ouverte de centre x et de rayon ϵ 0. Lebut va être de montrer en toute généralité, il y aura toujours un pointy appartenant à Bx, ϵ pour ϵ 0 extérieur à Ba, r conduisantdonc au fait que Ba, r n’est pas un ouvert. Pour cela le point y estchoisi tel que les vecteurs yx et xa sont colinéaires, ainsi, il existeλ 0 tel quey x = λx aDe plus le point y est choisi à mi-chemin entre x et le bord de la bouleBx, ϵ. On a donc y x= ϵ2, d’où l’on tirey x= λ x a=⇒λ = y xx a= ϵ2rDoncy = x + ϵ2rx a ⇐⇒y a =1 + ϵ2rx aOn peut maintenant prendre la norme de cette expressiony a=1 + ϵ2rx aor ϵ 0 donc y a x a. Finalement y /Ba, r pour tout ϵet donc aucune boule ouverte centrée en x n’est entièrement contenudans Ba, r qui n’est donc pas un ouvert.2. On se demande maintenant si une boule ouverte est un fermé. NotonsBa, r la boule ouverte de centre a et de rayon r de l’ensemble E.Pour déterminer si Ba, r est un fermé, il suﬃt d’étudier le complé-mentaire CEBa, r. Si CEBa, r est un ouvert alors Ba, r est unfermé sinon, ce n’est pas un fermé. Illustrons cela dans R2.24

Page 25 : On va démontrer que le point y est toujours extérieur à CEBa, r.Pour cela le point y est choisi tel que les vecteurs y x et x a sontcolinéaires, ainsi, il existe λ 0 tel quey x = λx aDe plus y est choisi à mi-chemin entre x est le bord de Bx, ϵ. On adonc y x= ϵ2, d’où l’on tirey x= λ x a=⇒λ = y xx a= ϵ2rDoncy = x ϵ2rx a ⇐⇒y a =1 ϵ2rx aOn peut maintenant prendre la norme de cette expressiony a=1 ϵ2rx aor ϵ 0 donc y a r. Finalement y /CEBa, r pour tout ϵet donc aucune boule ouverte centrée en x n’est entièrement contenudans CEBa, r qui n’est donc pas un ouvert. Donc Ba, r n’est pasfermé.Exercice 3 :Déterminer si les ensembles suivants sont des ouverts, des fermés, les deuxou aucun des deux.1. A = 0, 12. C = 0, +25

Page 26 : 3. D =0, 124. E = N5. F = x, y R2/ x2 + y2 46. G = x, y R2/ x2 + y2 27. H = x, y R2/ 0 x 1 18. I = x, y R2/ x 1 et y 19. J = x, y R2/ 0 y x et 0 x 3Réponses :1. On considère A = 0, 1.Ouvert ?Il semble y avoir un problème en 0. Prenons la norme · de toutefaçon, nous avons vu que le choix de la norme n’impacte pas la notiond’ouvert en dimension ﬁnie et considérons la boule ouverte centréeen 0 et de rayon quelconque r 0 : B0, r = r, rPrenons y = r/2. Alors y 0= y 0 = r/2 r, donc y B0, r. Mais r 0, y /A. Donc, r 0, B0, r ̸A et ﬁnalementA n’est pas un ouvert.Fermé ?A est un fermé, si son complémentaire CRA = , 01, estun ouvert.On voit qu’il y a un problème potentiel en 1. Pour cela,on considère la boule ouverte centrée en 1 et de rayon quelconquer 0 : B0, r =1 r, 1 + r. Prenons y = 1 r/2. Alors y 1=y 1 = r/2 r, donc y B1, r. Mais pour r →r0 0, y /CRA.Donc, B0, r ̸CRA et ﬁnalement A n’est pas un fermé.2. Soit C = 0, 26

Page 27 : Ouvert ?Le problème ne peut-être qu’en 0. C’est très exactement la même dé-monstration que pour A. Considérons la boule ouverte centrée en 0et de rayon quelconque r 0 : B0, r = r, r. Prenons y = r/2.Alors y 0= y 0 = r/2 r, donc y B0, r. Mais r 0,y /C. Donc, r 0, B0, r ̸C et ﬁnalement C n’est pas un ouvert.Fermé ?Si CRC = , 0 est un ouvert alors C est un fermé, sinon, ce n’estpas un fermé. Il y a plusieurs façons de traiter celaa Faire appel au cours : dans le cours, nous avons vu qu’un ensemblede la forme , a, avec a un réel, est un ouvert. Donc C est unfermé.b Utiliser une union inﬁni d’ouverts : on sait en eﬀet qu’une unioninﬁnie d’ouvert est un ouvert. De plus, pour tout a, b R2, a, best un ouvert. Or CRC = a0a, 0. Donc CRC est un ouvert etC un fermé.c Démonstration brutale : le problème ne peut être qu’en 0.On introduit la boule Bx, r = x/2 = Bx, x/2 =32x, 12x.Pour x CRC ; r = x/2 0 et Bx, r CRC puisque, y Bx, r, y 12x CRC. Donc CRC est un ouvert ce qui impliqueque C est un fermé.3. D =0, 12Ouvert ?Clairement il y a un problème en 2. Prenons par exemple la bouleB2, r =2 r, 2 + r avec r 0. Alors le point y = 2 + r2, qui ap-partient à B2, r n’appartient pas à D quelque soit r 0. Donc Dn’est pas un ouvert.Fermé ?Si CRD =, 01, 22, est un ouvert alors D est un fermé. En27

Page 28 : 0, il y a clairement un problème. Pour cela, il suﬃt de prendre la bouleouverte B0, r = r, r avec r 0. Considérons le point y = r/2qui appartient clairement à B0, r. Or, pour r →r0 0, y /CRD, doncB0, r ̸CRD donc D n’est pas un ouvert. Finalement D n’est pasun fermé.4. E = NOuvert ?E = 0 1 2 .... Nous avons déjà vu qu’un singleton n’estpas un ouvert. Donc E n’est pas un ouvert.Fermé ?CR =0, 11, 22, 3..., qui est une union inﬁnie d’ouverts donc unouvert. Finalement N est un fermé.5. Soit F =x, y R2 / x2 + y2 4. On reconnait ici B·20, 2 quiest une boule ouverte. Or nous avons vu qu’une boule ouverte est unouvert et pas un fermé.6. Soit G =x, y R2 / x2 + y2 2. On reconnait ici B·20,2qui est une boule fermée. Or nous avons vu qu’une boule fermée estun fermé et pas un ouvert.7. Soit H =x, y R2 / 0 x 1 1.Ouvert ? Commençons par représenter l’ensemble.Il y a alors plusieurs façons de résoudre ce problèmea Compte tenu des symétries et des invariances l’ensemble est in-variant par translation selon y, on peut étudier ce problème dans28

Page 29 : R. Ainsi, si 0, 11, 2 est un ouvert alors H est un ouvert. Orc’est bien un ouvert comme une union de deux ouverts. Donc Hest un ouvert.b On peut également utiliser un pavage de cet ensemble par lesboules ouvertes de la norme inﬁnie. En eﬀet, rappelez vous queB0, r est un carré de côté 2r et centré en 0. Ainsi, on peutmontrer queH = nZBa = 12, n2 , 12Ba = 32, n2 , 12Or une union inﬁnie d’ouverts est un ouvert donc H est un ouvert.Fermé ?On représente ci-dessous CR2HIl y a encore plusieurs façons de résoudre ce problèmea Compte tenu des symétries et des invariances l’ensemble est in-variant par translation selon y, on peut étudier ce problème dansR. Ainsi, si , 0 2, est un ouvert alors H est un fermé.Toutefois, nous savons que , 0 2, n’est pas un ouvertà cause de 0 et 2 même démonstration que ce qui a été fait pourles premiers ensembles.b On peut également faire la démonstration directement. Prenonsle point I = 0, 0 et regardons si r 0 / B2I, r CR2H.Prenons J = r/2, 0. Comme J I2 =r2 r, y B2I, r.Alors pour r →r0 0, J /CR2H. Finalement CR2H n’est pas unouvert donc H n’est un fermé.29

Page 30 : 8. I =x, y R2 / x 1 et y 1.Ouvert ? Commençons par représenter l’ensemble.Considérons le point i = 0, 1 I. Considérons la boule B2i, r avecr 0. Alors y = 0, 1 + r2 B2i, r. Or pour r →r0 0, y /I donc In’est pas un ouvert.Fermé ?On représente ci-dessous le complémentaire de IMême principe de démontration en utilisant par exemple le pointi = 1, 0.9. J = x, y R2/ 0 y x et 0 x 3Ouvert ?Ci-dessous est représenté l’ensemble J.30

Page 31 : On considère le point I = 2, 0. Prenons B2I, r. r 0 et I′ =2, r/2, I′ B2I, r. Or r 0, I′ /J. Donc J n’est pas unouvert.Fermé ?C’est bien un fermé.Exercice 4 : Ensemble ouvert et majoréSoit A un ouvert majoré de R, · . Montrer que A ne contient pas sonmajorant.Réponse :Méthode 1 : pour les moins matheuxSoit E un ensemble majoré alors, M R+, tel que pour tout x E,xM. On dit que M est le majorant de E. Ici, A R. Donc il existe Mtel que pour tout x de R : x M ⇐⇒M x M ⇐⇒x M, M.Or A est un ouvert de R et est donc de la forme A =α, β, avec α et β deuxréels. Il faut donc que A s’écrive A = M, M et donc A ne contient pas saborne supérieure M.Méthode 2 :Soit M la borne supérieure de A. Si M A, alors en tant qu’ouvert, A estun voisinage de M. Donc il existe α 0 tel que BM, α A, c’est-à-direM α; M + αA. Ce qui implique que M + α A. Or M était censé êtrela borne supérieure de A, d’où une contradiction. Donc A ne contient pas saborne supérieure.Exercice 5 : Somme d’ensemblesSoit A R et B R. On introduit l’ensembleA + B = x R / a, b A × B, x = a + b31

Page 32 : 1. Montrer que si A ou B est ouvert alors A + B est ouvert.2. La réciproque est-elle vraie ?Réponses :1. Supposons A un ouvert et B quelconque. Soit x = a + b A + B.Puisque A est un ouvert, il est un voisinage de a. Donc il existeϵ 0 tel que a ϵ, a + ϵA. Soit y x ϵ, x + ϵ. Nous avonsa+bϵ = xϵ y x+ϵ = a+b+ϵ. D’où y b aϵ, a+ϵA.D’où en posant a′ = y b A, nous avons bien y = a′ + b A + B.Donc x ϵ, x + ϵA + B et A + B est un ouvert.2. La réciproque est fausse. Soit A =0, 1 2, 3 et B =1, 2 3, 4.Ils sont tous les deux ouverts et pourtant A + B =1, 7 est bien unouvert.Exercice 6 : Produit cartésienSoit E, ·E et F, ·F deux espaces vectoriels normés. On note ·E×Fl’application déﬁnie sur E × F parx, yE×F = max xE , yF 1. Montrer que ·E×F est une norme.2. Montrer que si A E et B F sont des ouverts alors A × B est unouvert.3. Montrer que si A E et B F sont des fermés alors A × B est unfermé.Réponses :1. Il faut montrer que l’application ·E×F vériﬁe les 3 propriétés sui-vantesa x, yE×F = 0 =⇒x, y = 0E, 0F b λx, yE×F = λ x, yE×Fc x1, y1 + x2, y2E×F x1, y1E×F + x2, y2E×FDémonstration :32

Page 33 : a Soit x, yE×F = 0, alors maxxE , yF = 0 ce qui impliquexE = yF = 0 et donc x, y = 0E, 0F , puisque ·E et ·Fsont des normes.b λx, yE×F = max λxE , λyF = max λ xE , λ yF =λ x, yE×Fc On cherche à déterminerx1, y1 + x2, y2E×F =x1 + x2, y1, y2E×F = maxx1 + x2E , y1 + y2F .Orx1 + x2E x1E + x2E maxx1E , y1F + maxx2E , y2F y1 + y2F y1F + y2F maxx1E , y1F + maxx2E , y2F On voit donc quemaxx1 + x2E , y1 + y2F maxx1E , y1F +maxx2E , y2F .Finalementx1, y1 + x2, y2E×F x1, y1E×F + x2, y2E×F2. Soit x, y A × B. Il existe r1 0 et r2 0 tels que Bx, r1 Aet By, r2 B. Posons r = minr1, r2. Soit z, t Bx, y, r. Ona ...33

Page 34 : TD3 : Intérieur et AdhérenceExercice 1 :Soit E, · un espace vectoriel normé. Soient A et B deux ensembles telsqueA B E et B fermé1. Montrer alors que pour x CEBr 0 / Bx, r A = 2. Peut-on alors avoir A = B et si oui sous quelles conditions ?Réponses :1. On aB fermé ⇐⇒CEB ouvert ⇐⇒x CEB, r 0 / Bx, r CEBDonc, r 0 tel que Bx, rB = . Or A B, donc Bx, rA = .Finalementx CEB, r 0 / Bx, r A = .34

Page 35 : 2. Pour rappel :x A ⇐⇒r 0, Bx, r A ̸= D’après la question 1, on a montré que A B. Mais B peut êtretrop grand. Ainsi, B A si et seulementx B\A, on a :r 0, Bx, r A ̸= Et on a alors B = A.Exercice 2 :Soit E, · un espace vectoriel normé. Soient A et B deux ensembles telsqueB A E et B ouvert1. Montrer alors que pour x Br 0 / Bx, r A2. Peut-on alors avoir◦A = B et si oui sous quelles conditions ?Réponses :1. On aB ouvert ⇐⇒x B, r 0 / Bx, r BOr B A, doncx B, x A et r 0 / Bx, r B ADoncx B, r 0 / Bx, r A2. Pour rappel :x ◦A ⇐⇒r 0 / Bx, r ACompte tenu de la question précédente, on sait que B ◦A. Mais Bpeut être trop petit. Finalement◦A = B ssi x A\B, r 0, Bx, r ̸A◦A ̸= B ssi x A\B, r 0, Bx, r A35

Page 36 : Exercice 3 :Soit E, · un espace vectoriel normé. Déterminer l’intérieur et l’adhérentde1. l’ensemble A qui est la boule fermée de rayon r et de centre a2. l’ensemble A qui est la boule ouverte de rayon r et de centre aRéponses :1. Déterminons A et◦A :A :Comme la boule fermée est un fermé alors A = A◦A :On cherche le plus grand ouvert contenu dans A. Prenons commecandidat C = Ba, r c’est-à-dire, la boule ouverte de centre a et derayon r. Alors clairement :C est un ouvertC A1Compte tenu de l’exercice 2, on sait alors que C ◦A. On doit main-tenant montrer que◦A C. Or ceci est le cas si et seulement six A\C, r 0, Bx, r ̸Aet on aura alors◦A = C.On aA\C = Ba, r\Ba, r = Sa, rSoit x Sa, r. Soit Bx, ϵ la boule ouverte de centre x et de rayonϵ. On déﬁnit le point y sur la droite liant a et x. Voir ﬁgure ci-dessous.36

Page 37 : On a alors y x = λx a. De plus on choisit y a mi-chemin entrex et le bord de Bx, ϵ. On déduit de cela quey x= ϵ2 = λ x ace qui conduit à λ = λ =ϵ2r. On a doncy x = ϵ2rx ace qui permet d’écrirey a = 1 + ϵ2rx aPrenons maintenant la norme de l’expression précédentey a= 1 + ϵ2r x a= 1 + ϵ2r × ror ϵ 0 doncy a rFinalement, ϵ 0, y /A donc Bx, ϵ ̸A. On a donc bien◦A = C.2. Déterminons A et◦A :◦A :Comme la boule ouverte est un ouvert alors◦A = AA :On cherche le plus petit fermé contenant A. Prenons comme candidatC = Ba, r. Alors clairement :C est un ferméA C237

Page 38 : Compte tenu de l’exercice 1, on sait alors que A C. On doit main-tenant montrer que C A. Or ceci est le cas si et seulement six C\A, r 0, Bx, r A ̸= On aC\A = Ba, r\Ba, r = Sa, rSoit x Sa, r. Soit Bx, ϵ la boule ouverte de centre x et de rayonϵ. On déﬁnit le point y sur la droite liant a et x. Voir ﬁgure ci-dessous.On a alors y x = λa x. De plus on choisit y a mi-chemin entrex et le bord de Bx, ϵ. On déduit de cela quey x= ϵ2 = λ a xce qui conduit à λ = λ =ϵ2r. On a doncy x = ϵ2ra xce qui permet d’écrirey a = 1 ϵ2rx aPrenons maintenant la norme de l’expression précédentey a= 1 ϵ2r x a=1 ϵ2r × ror ϵ 0 doncy a rFinalement, ϵ 0, y a r donc Bx, ϵ A ̸= et A = C.38

Page 39 : Exercice 4 :Soit E, · un espace vectoriel normé. Soient A et B deux ensembles de E.Montrer que1. A B = A B2. A B A B3.˚⌢A B =◦A ◦B4.◦A ◦B ˚⌢A BRéponses :1. Montrons que A B = A B :A A BB A B=⇒A A BB A B=⇒A B A BOr A B est un fermé puisque A et B sont des fermés. Ceci impliquequeA B = A BDe plusA AB B=⇒A B A B =⇒A B A B = A BFinalement, puisque A B A B et A B A B, on aA B = A B2. Montrons que A B A BA B AA B B=⇒A B AA B B=⇒A B A B3. Montrons˚⌢A B =◦A ◦B :A B AA B B=⇒˚⌢A B ◦A˚⌢A B ◦B=⇒˚⌢A B ◦A ◦B39

Page 40 : or◦A ◦B est un ouvert puisque◦A et◦B sont des ouverts, donc˚⌢◦A ◦B =◦A ◦B4. Laissée en exercice.Exercice 5 :Déterminer l’adhérent et l’intérieur des ensembles donnés dans l’exercice 3du TD2.Réponses :1. Soit A = 0, 1a Détermination de◦A :On sait que l’intérieur de A est le plus grand ouvert contenu dansA. Proposons donc C =0, 1. Comme C est un ouvert contenudans A alors on sait que C ◦A. Il reste à savoir si◦A C. Pourcela vériﬁons que pour x A\C, r 0, Bx, r ̸A. Ici A\C =0. Or clairement toute boule centrée en 0 ne sera pas contenudans A. En eﬀet, considérons r 0 la boule B0, r = r, r.Prenons le point y = r2 B0, r. Donc r 0, y 0 ce quiimplique y /A. Finalement r 0, Bx, r ̸A et donc◦A = C.b Détermination de A :On sait que A est le plus petit fermé contenant A. Prenons donccomme candidat C = 0, 1. Or C est un fermé et A est contenudans C, on sait donc A C. Il faut donc vériﬁer que C A,c’est-à-dire que x C\Ar 0, Bx, r A ̸= Ici C\A = 1. Soit B1, r =1 r, 1 + r la boule centrée en 1de rayon r 0. Prenons y = 1 r2 B1, r. On déduit doncr 0, y 1 ce qui implique que y A et donc B1, r A ̸= .Finalement A = C.2. Soit C = 0, +40

Page 41 : a Détermination de◦C :On sait que l’intérieur de C est le plus grand ouvert contenu dansC. Proposons donc ˜C =0, +. Comme ˜C est un ouvert contenudans C alors on sait que ˜C ◦C. Il reste à savoir si◦C ˜C. Pourcela vériﬁons que pour x C\ ˜C, r 0, Bx, r ̸C. Ici C\ ˜C =0. Or clairement toute boule centrée en 0 ne sera pas contenudans C. En eﬀet, considérons r 0 la boule B0, r = r, r.Prenons le point y = r2 B0, r. Donc r 0, y 0 ce quiimplique y /C. Finalement r 0, Bx, r ̸C et donc◦C = ˜C.b Détermination de C :C = C car C est un fermé.3. Soit D =0, 12a Détermination de◦C :On sait que l’intérieur de D est le plus grand ouvert contenu dansD. Proposons donc C =0, 1. Comme C est un ouvert contenudans D alors on sait que C ◦D. Il reste à savoir si◦D C.Pour cela vériﬁons que pour x D\C, r 0, Bx, r ̸D. IciD\C = 2. Or clairement toute boule centrée en 2 ne sera pascontenu dans D. En eﬀet, considérons r 0 la boule B2, r =2 r, 2 + r. Prenons le point y = 2 + r2 B2, r. Donc r 0,y 2 ce qui implique y /D. Finalement r 0, Bx, r ̸D etdonc◦D = C.b Détermination de D :Méthode 1 :On sait que D est le plus petit fermé contenant D. Prenons donccomme candidat C = 0, 1 2. Or C est un fermé union dedeux fermés et D est contenu dans C, on sait donc D C. Ilfaut donc vériﬁer que C D, c’est-à-dire que x C\Dr 0, Bx, r D ̸= Ici C\D = 0 1. Soit B1, r =1 r, 1 + r la boule centréeen 1 de rayon r 0. Alors r 0, B1, r D ̸= . De même en0. Finalement D = C.41

Page 42 : Méthode 2 :D’après l’exercice précédent, on sait que A B = A B. En po-sant A =0, 1 et B = 2, on a A = 0, 1 et B = 2 et doncD = 0, 1 24. Soit E = N :◦E = et E = E.5. Soit F = x, y R2/ x2 + y2 4 :On sait que F = B·20, 2. F est donc une boule ouverte et commeon l’a montré en toute généralité pour une boule ouverte :◦F = F et F = B·20, 2.6. Soit G = x, y R2/ x2 + y2 2On sait que G = B·20,2. G est donc une boule fermée et commeon l’a montré en toute généralité pour une boule fermée :◦G = B·20,2 et G = G.7. Soit H = x, y R2/ 0 x 1 1On a vu que H est un ouvert donc◦H = H.Pour l’adhérent, nous prenons le candidatC = x, y R2/ 0 x 1 1 = x, y R2/ 0 x 2Clairement C est un fermé et H C donc H C. Mais C peutêtre trop grand. On doit donc vériﬁer quex C\H = x, y R2/ x = 0 ou x = 1 ou x = 2, r 0,Bx, r H ̸= . Or ceci est trivialement vrai. Donc H = C.8. Soit I = x, y R2/ x 1 et y 1I = x, y R2/ x 1 et y 1◦I = x, y R2/ x 1 et y 142

Page 43 : 9. Soit J = x, y R2/ 0 y x et 0 x 3J est un fermé. Donc J = J.◦J = x, y R2/ 0 y x et 0 x 343

Page 44 : TD4 : SuitesExercice 1 :Donner un exemple de suite complexe zn = xn + iyn n’ayant aucune valeurd’adhérence dans C mais telle que les suite xn et yn en aient dans R.Réponses :Introduisons les deux suites suivantesxn =x2n = 0x2n+1 = fnet yny2n = gnx2n+1 = 0avec fn et gn deux fonctions strictement croissantes de N dans R. Doncfn et gn ont chacune 0 comme valeur d’adhérence. Toutefoiszn =z2n = ignz2n+1 = fnn’a aucune valeur d’adhérence, puisque fn et gn sont strictement crois-santes.Rappel : l est une valeur d’adhérence ssi, φ telle queϵ 0, N N / n N,xφn l ϵoù φ est une fonction strictement croissante de N dans N.Exercice 2 :Soit un et vn deux suites réelles telles que un vn converge vers 0. Montrerque un et vn ont les mêmes valeurs d’adhérences.Réponses :Posons zn = un vn. Comme zn tend vers 0 quand n tend vers l’inﬁni, 0 estla seule valeur d’adhérence de zn.Alors, soit l une valeur d’adhérence de un. Il existe donc φ:N →Nstrictement croissante telle que uφn converge vers l. Mais zφn converge44

Page 45 : vers 0 car 0 est la seule valeur d’adhérence de zn puisque zn converge vers 0.Donczφn = uφn vφnlimn→zφn = 0 =limn→uφn limn→vφn = l limn→vφnet puisquelimn→uφn = l0 = l limn→vφn ⇐⇒limn→vφn = lEn eﬀectuant le même raisonnement sur vφn, on obtiendrait le même résul-tat. Finalement un et vn ont les mêmes valeurs d’adhérences.Exercice 3 :Donner des exemples de suites ayant :1. aucune valeur d’adhérence.2. une unique valeur d’adhérence.3. deux valeurs d’adhérence.4. trois valeurs d’adhérence.5. une unique valeur d’adhérence mais la suite ne converge pas.Réponses :1. La suite déﬁnie parxn:N→R2n7→2n, 1nn’a aucune valeur d’adhérence.2. La suite déﬁnie parxn:N→R2n7→x2n = 0x2n+1 = na une unique valeur d’adhérence.3. La suite un = 1n a deux valeurs d’adhérence, à savoir 1 et 1.45

Page 46 : 4. La suitex2n = 1nx2n+1 = 3a 3 valeurs d’adhérence, à savoir 3, 1 et 1. En eﬀet :x0 = 1, x1 = 3, x2 = 1, x3 = 3, x4 = 1, x5 = 3, x6 = 1,...5. voir la réponse à la question 2.Exercice 4 :Déterminer si les ensembles suivants sont des ouverts, des fermés, les deuxou aucun des deux. Déterminer également leur adhérence.1. A = 0, 12. C = 0, +3. D =0, 124. E = N5. H = x, y R2/ 0 x 1 1 que fermé6. I = x, y R2/ x 1 et y 17. J = x, y R2/ 0 y x et 0 x 3 que ouvertRéponses :1. Nous devons déterminer, en utilisant les suites, si A = 0, 1 est unfermé, un ouvert ainsi que son adhérent.a Fermé ?A est un fermé si et seulement si toute suite convergente de Aconverge dans A. Or si on prend la suite xn = 1 1n, n N,alors xn A maislimn→xn = 1 /A. Donc A n’est pas un fermé.b Ouvert ?A est un ouvert si et seulement si CRA = , 01, + estun fermé. Or CRA est un fermé si et seulement si toute suiteconvergente de CRA converge dans CRA. Or si on prend la suiteyn = 1n, n N, alors yn CRA maislimn→yn = 0 /CRA.Donc CRA n’est pas un fermé, donc A n’est pas un ouvert.46

Page 47 : c Adhérent ?L’adhérence de A est l’ensemble des points vers lesquels les suitesconvergentes de A convergent. On a alorsSoit 0 xn 1 =⇒0 x 1 donc A 0, 1l’implication ci-dessus correspond au passage à la limite.Il faut maintenant vériﬁer que 0, 1 A. On sait que A A.Intéressons nous donc à A\A = 1. Or il existe bien une suited’éléments de A = 0, 1 qui converge vers 1, à savoir xn = 1 1n,n N.2. Nous devons déterminer, en utilisant les suites, si C = 0, + est unfermé, un ouvert ainsi que son adhérent.a Fermé ?C est un fermé si et seulement si toute suite convergente de Cconverge dans C.0 xn =⇒0 x donc x 0, +donc C est un fermé.b Ouvert ?C est un ouvert si et seulement si CRC = , 0 est un fermé.Or CRC est un fermé si et seulement si toute suite convergentede CRC converge dans CRC. Or si on prend la suite yn = 1n,n N, alors yn CRC maislimn→yn = 0 /CRC. Donc CRCn’est pas un fermé, donc C n’est pas un ouvert.c Adhérent ?C est un fermé donc C = C.3. Nous devons déterminer, en utilisant les suites, si D =0, 12 estun fermé, un ouvert ainsi que son adhérent.a Fermé ?D est un fermé si et seulement si toute suite convergente de Dconverge dans D. Or si on prend la suite xn = 1n, n 1, alorsxn D maislimn→xn = 0 /D. Donc D n’est pas un fermé.47

Page 48 : b Ouvert ?D est un ouvert si et seulement si CRD =, 01, 22, +est un fermé. Or CRD est un fermé si et seulement si toute suiteconvergente de CRD converge dans CRD. Or si on prend la suiteyn = 2 1n, n N, alors yn CRD maislimn→yn = 2 /CRD.Donc CRD n’est pas un fermé, donc D n’est pas un ouvert.c Adhérent ?L’adhérence de D est l’ensemble des points vers lesquels les suitesconvergentes de D convergent. On a alorsSoit 0 xn 1 =⇒0 x 1Soit xn = 2 =⇒x = 2les implications ci-dessus correspondent au passage à la limite.donc D 0, 1 2.Vériﬁons maintenant que 0, 1 2 D. Or D D. Intéressonsnous donc à D\D = 0 1. Or il existe bien une suite d’élé-ments de D = 0, 12 qui converge vers 1, à savoir xn = 11n,n N. De même pour 0, à savoir la suite xn = 1n, n N.4. Laissée en exercice car du même type que les trois questions précé-dentes.5. Nous devons déterminer, en utilisant les suites, si H = x, y R2/ 0 x 1 1 est un fermé, un ouvert ainsi que son adhérent.Fermé ?H est un fermé si et seulement si toute suite convergente de Hconverge dans H. Or si on prend la suite xn = 1n, 0, n N,alors xn H maislimn→xn = 0, 0 /H. Donc H n’est pas un fermé.6. Nous devons déterminer, en utilisant les suites, si I = x, y R2/ x 1 et y 1 est un fermé, un ouvert ainsi que son adhérent.a Fermé ?I est un fermé si et seulement si toute suite convergente de Iconverge dans I. Or si on prend la suite un = 1 1n, 0, n N,48

Page 49 : alors un I mais limn→un = 1, 0 /I. Donc I n’est pas un fermé.b Ouvert ?I est un ouvert si et seulement si CR2I est un fermé. Or CR2I est unfermé si et seulement si toute suite convergente de CR2I convergedans CR2I. Or si on prend la suite un = 0, 1 1n, n N, alorsun CR2I maislimn→un = 0, 1 /CR2I. Donc CR2I n’est pasun fermé, donc I n’est pas un ouvert.c Adhérent ?L’adhérence de I est l’ensemble des points vers lesquels les suitesconvergentes de I convergent. On a alorsSoit1 xn 11 yn 1=⇒1 x 11 y 1l’implication ci-dessus correspond au passage à la limite.Donc toute suite xn, yn converge dansC = x, y R2 / 1 x 1 et 1 y 1.Donc I C.Etudions maintenant C\I aﬁn de vériﬁer que C I. AlorsC\I = A B où A =x, y R2 / x = 1, 1 y 1et B =x, y R2 / x = +1, 1 y 1Prenons maintenant y 1, 1, alors un = 1 + 1n, y I etlimn→un = 1, 0 C\I. On peut faire la même étude pour B.Ainsi I = C.49

Page 50 : TD5 : Limites et ContinuitésExercice 1 :1. Montrer que si x et y sont des réels alors 2xy x2 + y22. Soit f l’application de A = R2\0, 0 dans R déﬁnie parfx, y = 3x2 + xypx2 + y2a Montrer que pour tout x, y A, on a :fx, y 72 x, y2 avec 72 x, y2 =px2 + y2b En déduire que f admet une limite en 0, 0.Réponses :1. Montrons que 2xy x2 + y2 :Pour cela, remarquons0 x y2 = x2 + y2 2xyce qui conduit à2xy x2 + y22. On considère maintenant la fonctionfx, y = 3x2 + xypx2 + y2a Montrons que fx, y 4 x, y2 où x, y2 =px2 + y2.fx, y =3x2px2 + y2 +xypx2 + y2orx2 x2 + y2 = x, y2trivialpx2 + y2 = x, y22trivialxy 12x2 + y2 = 12 x, y22d’après la question 150

Page 51 : qui injecté dans l’expression précédente donnefx, y 3 x, y22x, y2+ x, y222 x, y2= 72 x, y2b D’après la question précédentefx, y 72 x, y2 = 72px2 + y2→x,y→0,0 0donc cette expression tend vers 0 quelque soit la façon dont x ety tendent vers 0. On déduit donc quelimx,y→0,0 fx, y = 0Exercice 2 :Etudier les limites en 0, 0 des fonctions suivantes1. fx, y = x + y sin1x2+y2 2. fx, y =1xy3. fx, y = x2y2x2+y24. fx, y = x2+xy+y2x2+y25. fx, y =x2yx2+y26. fx, y =x2y2x2+y27. fx, y = x3y8. fx, y = x+3yx2y29. fx, y = x2+y2x+y10. fx, y =xyx2+y211. fx, y =sinxyx2+y212. fx, y = xy13. fx, y =x2+y21xsinx ,sinx2+siny2x2+y2Réponses :51

Page 52 : 1. Soit fx, y = x+y sin1x2+y2 . La présence du sinus doit nous inciterà prendre la valeur absoluefx, y x + y→x,y→0,0 0On déduit donc quelimx,y→0,0 fx, y = 02. Soit fx, y =1xy. On a plusieurs méthodes.Méthode 1 : en cartésienPrenons le chemin x+, 0 alorslimx,0→0+,0 fx, y =limx,0→0,01x = +Tandis que le chemin 0, y+ aboutit àlim0,y→0,0 fx, y =lim0,y→0,0+ 1y = Ainsi, fx, y n’admet pas de limite en 0, 0.Méthode 2 : caractérisation séquentiellePrenons la suite un = 1n, 0 qui tant bien vers 0, 0 quand n tendvers l’inﬁni ce chemin correspond en cartésien au chemin x, 0 alorslimn→fun =limn→n = +Tandis que la suite vn = 0, 1n qui tant bien vers 0, 0 quand ntend vers l’inﬁni ce chemin correspond en cartésien au chemin 0, ydonnelimn→fvn =limn→n = Ainsi, fx, y n’admet pas de limite en 0, 0.Méthode 3 : coordonnées polairesOn pose maintenantx = ρ cosθy = ρ sinθ52

Page 53 : Ainsifx, y →˜fρ, θ =1ρcosθ sinθclairement, on voit sur cette expression que le résultat dépend de θ etque de plus il peut tendre vers l’inﬁni. Prenons par exemple le cheminρ →0, θ = 0 qui correspond au chemin cartésien x+, 0, on alorslimρ,θ=0→0+,0˜fρ, θ =limρ,θ=0→0+,01ρ = +et prenons le chemin ρ →0, θ = π2 qui correspond au chemincartésien 0, x+, on alorslimρ,θ= π2 →0+, π2 ˜fρ, θ =limρ,θ= π2 →0+, π2 1ρ = et encore une fois, on constate bien que f n’admet pas de limite en0, 0.3. Soit fx, y = x2y2x2+y2 . Il y a encore plusieurs méthodes.Méthode 1 : en cartésienCommençons par essayer d’évaluer la fonction en calculant par exempleles limites de fx, 0 = 1 et f0, y = 1. Ce qui implique quelimx,0→0+,0 fx, 0 =limx,0→0+,0 1 = 1lim0,y→0,0+ f0, y =lim0,y→0,0+ 1 = 1donc f n’admet pas de limite en 0, 0.Méthode 2 : caractérisation séquentiellePrenons la suite un = 1n, 0 qui tant bien vers 0, 0 quand n tendvers l’inﬁni ce chemin correspond en cartésien au chemin x+, 0alorslimn→fun =limn→1 = 1Tandis que la suite vn = 0, 1n qui tant bien vers 0, 0 quand n tendvers l’inﬁni ce chemin correspond en cartésien au chemin 0, y+donnelimn→fvn =limn→1 = 153

Page 54 : Ainsi, fx, y n’admet pas de limite en 0, 0.Méthode 3 : coordonnées polairesOn pose maintenantx = ρ cosθy = ρ sinθAinsifx, y →˜fρ, θ = ρ2cos2θ sin2θρ2= cos2θclairement, on voit sur cette expression que le résultat dépend de θ etque donc f n’admet pas de limite en 0, 0. Prenons par exemple lechemin ρ →0, θ = 0 qui correspond au chemin cartésien x+, 0,on alorslimρ,θ=0→0+,0˜fρ, θ =limρ,θ=0→0+,0 1 = 1et prenons le chemin ρ →0, θ = π2 qui correspond au chemincartésien 0, x+, on alorslimρ,θ= π2 →0+, π2 ˜fρ, θ =limρ,θ= π2 →0+, π2 1 = 1et encore une fois, on constate bien que f n’admet pas de limite en0, 0.4. Soit fx, y = x2+xy+y2x2+y2. Comme précédemment, nous pouvons utili-ser les 3 méthodes.Méthode 1 : en cartésienCommençons par essayer d’évaluer la fonction en calculant par exempleles limites de fx, 0 = 1 et fx, x = 32. Ce qui implique quelimx,0→0+,0 fx, 0 =limx,0→0+,0 1 = 1limx,x→0+,0+ fx, x =limx,x→0+,0+32 = 32donc f n’admet pas de limite en 0, 0.Méthode 2 : caractérisation séquentielle54

Page 55 : Prenons la suite un = 1n, 0 qui tant bien vers 0, 0 quand n tendvers l’inﬁni ce chemin correspond en cartésien au chemin x+, 0alorslimn→fun =limn→1 = 1Tandis que la suite vn = 1n, 1n qui tant bien vers 0, 0 quand n tendvers l’inﬁni ce chemin correspond en cartésien au chemin x+, x+donnelimn→fvn =limn→32 = 32Ainsi, fx, y n’admet pas de limite en 0, 0.Méthode 3 : coordonnées polairesOn pose maintenantx = ρ cosθy = ρ sinθAinsifx, y →˜fρ, θ = 1 + cosθ sinθclairement, on voit sur cette expression que le résultat dépend de θ etque donc f n’admet pas de limite en 0, 0. Prenons par exemple lechemin ρ →0, θ = 0 qui correspond au chemin cartésien x+, 0,on alorslimρ,θ=0→0+,0˜fρ, θ =limρ,θ=0→0+,01 + cosθ sinθ= 1et prenons le chemin ρ →0, θ = π4 qui correspond au chemincartésien x+, x+, on alorslimρ,θ= π4 →0+, π4 ˜fρ, θ =limρ,θ= π4 →0+, π4 1 + cosθ sinθ= 32et encore une fois, on constate bien que f n’admet pas de limite en0, 0.5. Soit fx, y =x2yx2+y2 .Méthode 1 : À tatonsCommençons par évaluer la fonction sur quelques chemins ici je me55

Page 56 : limite aux chemins cartésiens mais vous pouvez encore une fois utili-ser les deux autres méthodes. Par exemple fx, x = x2, fx, 0 = 0et f0, x = 0. Ainsilimx,x→0+,0+ fx, x =limx,0→0+,0 fx, 0 =lim0,y→0,0+ fx, 0 = 0À ce stade, nous ne pouvons pas conclure que 0 est la limite de f en0, 0 mais c’est un bon candidat. Cherchons donc à déterminerfx, y 0si cette quantité tend vers 0 quand x, y tend vers 0, 0 alors la limitede la fonction en 0, 0 sera 0. Alorsfx, y 0 = fx, y = yx × xx2 + y2or comme nous l’avons vu dans l’exercice 1xy 12x2 + y2ce qui permet d’écrirefx, y = yx × xx2 + y2x2→x,y→0,0 0donc ﬁnalement la limite de la fonction f en 0, 0 est 0.Méthode 2 : coordonnées polaires On peut également directement pas-ser en coordonnées polaires en posantx = ρ cosθy = ρ sinθAinsifx, y →˜fρ, θ = ρ cos2θ sinθet clairement, θ, ˜f tend vers 0 quand ρ tend vers 0 et ﬁnalementlimx,y→0,0 fx, y = 056

Page 57 : 6. Soit fx, y =x2y2x2+y2 .Il s’agit de faire très exactement la même chose que précédemment.Donc cette question est laissée en exercice.7. Soit fx, y = x3yOn peut encore utiliser les diﬀérentes méthodes précédentes. Maisnous allons nous contenter ici des coordonnées polaires. Ainsi en po-santx = ρ cosθy = ρ sinθAinsifx, y →˜fρ, θ = ρ2 cos3θsinθMais en réalité, il est très diﬃcile de conclure de cette façon. Mais onsent que ca peut ne pas converger si le dénominateur converge tropvite vers 0.Méthode 2 : en cartésienEssayer d’évaluer la fonction en calculant par exemple les limites def0, y = 0 et fx, x3 = 1. Ce qui implique quelim0,y→0,0+ f0, y =lim0,y→0,0+ 0 = 0limx,x3→0+,0+ fx, x3 =limx,x3→0+,0+ 1 = 1donc f n’admet pas de limite en 0, 0.Méthode 3 : caractérisation séquentielleLaissée en exercice mais il suﬃt de poser un = 0, 1n et vn = 1n, 1n3 .8. Soit fx, y = x+3yx2y2 .Pas de limite en 0, 0. En cartésien, il suﬃt de prendre les chemins0, x et 0, x et en polaire de prendre θ = π/2 et θ = π/4.9. Soit fx, y = x2+y2x+y.On sent que cette fonction à des bonnes chances de converger car le57

Page 58 : numérateur convergera plus vite vers 0 que le dénominateur.Méthode 1 : Par exemple fx, x = x = fx, 0 = 0 et f0, y = y.Ainsilimx,x→0+,0+ fx, x =limx,0→0+,0 fx, 0 =lim0,y→0,0+ f0, y = 0À ce stade, nous ne pouvons pas conclure que 0 est la limite de f en0, 0 mais c’est un bon candidat. Cherchons donc à déterminerfx, y 0Ainsifx, y = x2 + y2x + yor x + y2 = x2 + y2 + 2xy x2 + y2. Doncfx, y = x2 + y2x + y x + y2x + y= x + y→x,y→0,0 0limx,y→0,0 fx, y = 0Méthode 2 : en coordonnées polairesOn peut également directement passer en coordonnées polaires enposantx = ρ cosθy = ρ sinθAinsifx, y →˜fρ, θ =ρ cosθ + sinθOr θ, le dénominateur ne s’annule jamais, donclimρ,θ→0,θ˜fρ, θ = 0 =limx,y→0,0 fx, y10. Soit fx, y =xyx2+y2 .Il y a encore plusieurs méthodes. Ici, on en traitera qu’une :fx, y =xypx2 + y2 x2 + y22px2 + y2 = 12px2 + y258

Page 59 : qui tend bien vers 0 lorsque x, y tend vers 0, 011. Soit fx, y =sinxyx2+y2 .Puisque x R, sinx x, on afx, y =sinxypx2 + y2 xypx2 + y2 x2 + y22px2 + y2 = 12px2 + y2qui tend bien vers 0 quand x, y tend vers 0, 0. Donc f a pour limite0 quand x, y tend vers 0, 0.12. Soit fx, y = xyOn peut ré-écrire f de la façon suivantefx, y = ey lnxAlors f 1n, 0 = 1 et f 1n,1lnn = 1e. Ainsi, f n’admet pas de limiteen 0, 0.13. Soit fx, y =x2+y21xsinx ,sinx2+siny2x2+y2.Exercice 3 :Soit f la fonction déﬁnie sur R2 parfx, y = 12x2 + y2 1pour x2 + y2 112x2pour x2 + y2 1Montrer que f est continue.Réponses :59

Page 60 : On doit vériﬁer que la fonction f est continue dans les régions A et B maisaussi à l’interface entre les deux régions. On doit donc vériﬁer qu’en toutpoint x, y la fonction admet une limite et notamment que sur le cercled’équation x2 + y2 = 1, la limite est la même que l’on prenne l’expression12x2 + y2 1 ou 12x2.Région A : l’expression 12x2 admet bien une limite en tout point x, ytel que x2 + y2 1. Donc la fonction est continue sur la région A.Région B : l’expression 12x2 + y2 1 admet bien une limite en tout pointx, y tel que x2 + y2 1. Donc la fonction est continue sur la région B.A l’interface A/B : soit x0, y0 un point du cercle vériﬁant donc x20 +y20 = 1.limx,y→x0,y0 12x2 = 12x20limx,y→x0,y012x2 + y2 1 = 12x20 + y20 1 = 12x20La fonction f est donc continue sur R2.Exercice 4 :1. On considère la fonction f1 déﬁnie parf1 : R × R→Rx, y →1 + x2 + y2ysinyDéterminer si f1 admet une limite en 0, 0.2. On note D = x, y R2/x2 y2 ̸= 0. On considère la fonctionf2 : D →Rx, y →1 + x + yx2 y2Déterminer si f2 admet une limite en 0, 0.Réponses :60

Page 61 : 1.limx,y→0,0 f1x, y =limx,y→0,01 + x2 + y2×limx,y→0,0sinyy= 1×1 = 1donc f1 est continue en 0, 0.2.limx,0→0,0 f2x, y =limx,0→0,01 + xx2= lim0,y→0,0 f2x, y =lim0,y→0,01 + yy2 = donc f2 n’est pas continue en 0, 0.Exercice 5 :La fonction suivante est-elle continue ?fx, y = 2x2 + y2 1pour x2 + y2 1x2pour x2 + y2 1Réponse :Laissée en exercice la fonction est continue.Exercice 6 :On considère la fonction f déﬁnie parfx, y = yx2 ey/x2pour x ̸= 00pour x = 01. Soit λ un réel et Aλ = x, λx/x R. On note fλ la restriction def à Aλ. Calculer la limite de fλ en 0, 0.2. Soit B = x, x2/x R. On note g la restriction de f à B. Calculerla limite de g en 0, 0.3. Que peut-on dire de la continuité de f en 0, 0.Réponses :61

Page 62 : 1. On cherche à calculer la limite de f pour les points de la forme x, λx.fx, λx = λx exp λx0d’où l’on déduit par croissance comparéelimx→0λx expλx= 0Donc la limite de fλ en 0, 0 est bien 0 et la fonction est continue ence point.2.fx, x2 = x2x2 expx2x2 = 1e, x ̸= 0et vaut 0 pour x = 0. Donc g n’est pas continue en 0, 0.3. L’exercice est très intéressant. En eﬀet, d’après la question 1, quelquesoit la façon dont on s’approche de 0, 0 selon une droite alors onaboutit à la même limite ici 0. Toutefois, d’après la question 2, onvoit que si l’on s’approche par une parabole alors on obtient une autrelimite. Ainsi la fonction n’a pas de limite en 0, 0.Exercice 7 :Pour chacune des fonctions, étudier sa continuité en 0, 0.62

Page 63 : Réponses :1. Passons en coordonnées polaires. Ainsi˜fρ, θ =cos2θ + sin2θ= 1donc la fonction n’est pas continue en 0, 0.2.fx, y = x3 + y3x2 + y2 x3 + y3x2 + y2= xx2 + yy2x2 + y2= xx2x2 + y2 +yy2x2 + y2puisquey2x2+y2 1 etx2x2+y2 1fx, y x + yqui tend bien vers 0 quand x, y tend vers 0, 0. Donc la limite de fen 0, 0 est 0 et ﬁnalement f est continue en 0, 0.3. fx, x = e4 ̸= 0 donc la fonction n’est pas continue en 0, 0.63

Page 64 : TD6 7 : Limites, Continuités et CompacitéExercice 1 :Les fonctions suivantes sont-elles prolongeables en 0, 0 sur leur domaine dedéﬁnition D ?1. D = x, y R2/xy 0, fx, y = 1cosxyy2. D = x, y R2/x ̸= y, fx, y = cosxcosyxy3. D = x, y R2/x ̸= ±y, fx, y = sinx2+siny2x2y24. D = R2\0, 0, fx, y =xy2x2+y4Réponses :1. Considérons la suite un = xn, yn tel que xn et yn tendent vers 0quand n tend vers l’inﬁni et aussi tel que xnyn 0. Alorsfun = 1 cosxnynyn1 1 xnyn22yn= xnyn2yn = xn2→xn,yn→0 0l’équivalence est prise pour xnyn →0. Ainsi la fonction admetbien une limite en 0, 0. Donc f est prolongeable par continuité en0, 0 en posant f0, 0 = 0.2. On va même montrer qu’elle est prolongeable en tout point de laforme a, a avec a R. Pour cela, on introduit deux suites xn et yntelles quexn ̸= yn et xn, yn →n→a, aOrx, y R2, cosx sinx = 2 sinx + y2sinx y2Doncfxn, yn = cosxn cosynxn yn=1xn yn2 sinxn + yn2sinxn yn2= 2 sinxn + yn2 sin xnyn2xnyn2× 1264

Page 65 : et comme z R, sinzztend vers 1 quand z tend vers 0, on afxn, yn = sinxn + yn2→n→sinaDonc f est prolongeable par continuité en a, a en posantfa, a = sina.3. Clairement, cette fonction n’est pas prolongeable pour voir cela, ilsuﬃt de prendre les chemins fx, 0 et f0, y. En eﬀetfx, 0 = sinx2x2→x→0 1f0, y = siny2y2→y→0 14. Pas prolongeable. En eﬀetfx, x =x3x2 + x4 =xx2 + 1 →x→0 0fy2, y =y4y4 + y4 →y→012Exercice 2 :Etudier les limites en 0, 0 des fonctions suivantes1. fx, y = x+2yx2y22. fx, y =xyxyRéponses :1. Clairement la fonction n’a pas de limite en 0, 0. En eﬀetfx, 0 = 1x →x→0 ±2. Laissée en exercice.65

Page 66 : Exercice 3 :Soit E, · un espace vectoriel normé. Montrer que l’application · est1-lipschitzienne de E, · dans R, · .Réponses :Rappel :L’application N de E, ·E dans F, ·F est 1-lipschitzienne si et seule-ment six, y E, Nx NyF x yE3Ici : l’application ·E est de E dans R ce qui signiﬁe que ·F = · . Eninjectant cela dans 3, on obtientx, y E, xE yE x yEor cette expression est vraie puisqu’il s’agit de la 2ème inégalité triangulaire.CQFDExercice 4 :Soit E = C00, 1, R muni de · 1 déﬁnie parf1 =Z 10ftdtEtudier la continuité de la forme linéaire φ de E dans R déﬁnie parφf =Z 10tftdtRéponses :Montrons que φ est continue sur E.φf =Z 10tftdt Z 10tftdtOr t 0, 1, tft ft. Doncφf =Z 10tftdt Z 10tftdt Z 10ftdt f1φ est donc 1-lipschitzienne et donc continue.66

Page 67 : Exercice 5 :1. Rappeler la déﬁnition de la continuité uniforme.2. Quelle est la négation de la continuité uniforme.3. Soit a, b deux réels positifs tels que a b. Montrer que la fonctionfx = x2 est uniformément continue sur a, b.4. Montrer que la fonction fx = x2 n’est pas uniformément continuesur R.5. Montrer que la fonction fx = 1/x n’est pas uniformément continuesur 0, 1.6. Montrer que la fonction lnx n’est pas uniformément continue surR+.Réponses :1. Soit f une application de E, ·E dans F, ·F . Alors f est uni-formément continue sur A E si et seulement siϵ 0, x, y A2, η 0 / x yE η =⇒fx fyF ϵ2. f n’est pas uniformément continue sur A si et seulement siϵ 0, x, y A2, / η 0, x yE η =⇒fx fyF ϵ3. Soient a et b deux réels positifs tels que a b. Montrons que la fonc-tion fx = x2 est uniformément continue sur a, b.a Démonstration 1 :On voit clairement sur la ﬁgure ci-dessous que si ϵ est ﬁxé alors ηdépend du point x.67

Page 68 : On peut même écrire que η et ϵ sont liés par la dérivée de f. Eneﬀet, si ϵ et η sont suﬃsamment petit alors on peut utiliser latangente de la fonction en x0 voir ﬁgure ci-dessousAlorsfx = f′x0x x0 + fx0fx fx0 = f′x0 × x x0ϵ = f′x0ηOn voit donc que pour ϵ 0, si on ﬁxe ϵ, lorsque x →a, ηaugmente puisque f′x diminue. Or, on cherche η indépendantde x, y a, b. Prenons donc le plus petit η qui correspond au casx = b.On ﬁxe alors ϵ. On prend η =ϵf′b =ϵ2b.alors x y η = ϵ2b ⇐⇒2bx 2by ϵ68

Page 69 : orx, y a, b, x2 y2 2bx yen eﬀet :x, y a, b, x + y 2bet en multipliant par x y, on obtientx, y a, b, x y × x + y = x2 y2 2bx yon déduit donc quex, y a, b, x2 y2 2bx y ϵFinalementϵ 0, x, y a, b2, η = ϵ2b / xy η =⇒fxfy ϵet donc la fonction est bien uniformément continue.Rq : nous avons, se faisant, démontré que la fonction est en fait2b-lipschitzienne ce qui fera l’objet des démo 2 et 3. En eﬀetnous avons montré quex, y a, b, x2 y2 2bx yb Démonstration 2 :On va maintenant montrer que la fonction est κ-lipschitzienne sura, b. On cherche donc x, y a, b, fx fy κx y, cequi dans notre cas s’écrit x2 y2 κx y. Prenons κ = 2b enfait c’est la démo 3 qui justiﬁera cela. Alorsx, y a, b, x + y 2bEn multipliant par x y, on obtientx + y × x y = x2 y2 2bx yOn a donc bienx, y a, b, fx fy 2bx ydonc fx = x2 est 2b-lipschitzienne et donc uniformément conti-nue sur a, b.69

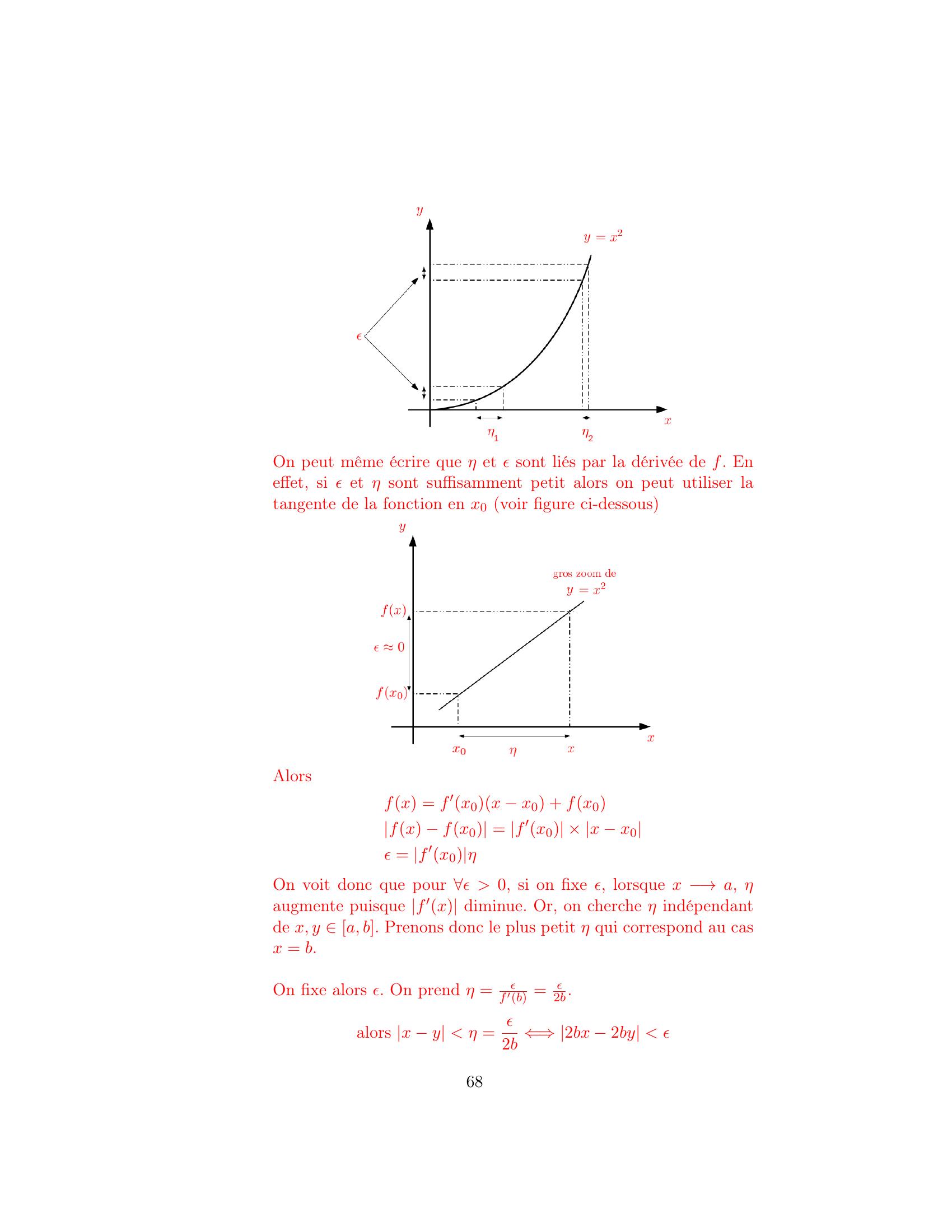
Page 70 : c Démonstration 3 : fausse démo...c’est plus une intuitionMontrons maintenant qu’une fonction dérivable, à dérivée bornéeest alors lipschitzienne. La fonction fx = x2 est dérivable sura, b. La dérivée est même bornée sur cet ensemble.x a, b, f′x M, avec M RDonc limx→yfx fyx y M, x, y a, bDonc intuitivement, on peut imaginer quex, y a, b, fx fy Mx yDonc, de tout ce que l’on vient de dire, on comprend que la déri-vée joue un rôle crucial. En eﬀet, plus la dérivée est grande en 1point et plus pour une précision donnée ϵ, le η doit être petit puisqueϵ = f′xη, donc si f′ →alors η →0 et il ne peut pas y avoirde convergence uniforme.4. On voit que la dérivée n’est pas bornée lorsque x →, il y a doncun problème en l’inﬁni. Prenons les deux suites xn = n et yn = n+ 1n.Alorslimn→yn xn = 0 orlimn→fyn fxn = 2Donc bien que les points x et y tendent vers l’inﬁni et l’un vers l’autre,la distance de leur image reste supérieure à 0.5. Encore une fois en 0, la dérivée n’est pas bornée. Si il y a un problème,le problème est donc en ce point. Prenons xn = 1n et yn =12n. Alorslimn→yn xn = 0 orlimn→fyn fxn = Donc bien que les points x et y tendent vers 0 et l’un vers l’autre , ladistance de leur image reste supérieure à 0.70

Page 71 : 6. Problème en 0 car la dérivée n’est pas bornée. Il suﬃt de prendreencore une fois xn = 1n et yn =12n. Alorslimn→yn xn = 0 orlimn→fyn fxn = ln 2Donc bien que les points x et y tendent vers 0 et l’un vers l’autre , ladistance de leur image reste supérieure à 0.Exercice 6 :Soit E, · un espace vectoriel normé. Soit l’application f : E →E déﬁnieparfx =xmax1, x1. Dessiner le graphe de f pour R, · .2. Montrer que f est bornée sur E.3. Montrer que f est continue sur E.4. Montrer que f est 2-lipschitzienne sur E.Réponses :1. Pour représenter ce graphe, commençons par remarquer queSi x 1 alors fx = xSi x 1 alors fx =1si x 11 si x 1donc71

Page 72 : 2. Montrons en toute généralité que f est bornée.Si x1, fx = x, donc fx= x1.Si x 1, alors fx =xxd’où l’on déduit que fx= 1.Donc x E, 0 fx1.3. Si x 1 alors fx = x, donc fx= x 1donc f est continue sur ce sous-ensemble.Si x 1 alors fx =xx, donc fx= x 1donc f est continue sur ce sous-ensemble.Si x= 1 :Si on vient de x tel que x 1 alors fx = x lorsque x= 1.Si on vient de x tel que x 1 alors fx = x lorsque x= 1.Finalement f est continue sur E.4. Montrons que f est 2-lipschitzienne :a Soit x1 et y1. Alorsfx fy= x yOn a donc bien trivialementfx fy= x y2 x yb Soit x1 et y 1. Alorsfx fy=x yy = x × yyyx × yy= x × yx + x yxy1 + x yxy1+ x y472

Page 73 : Orxy1+ x y= xy1 + x y= xy1 + x ycar y 15En injectant 5 dans 4, on obtientfx fyxy1 + x yy1 + x yyx+ x ycar x1yx + x y2 x yoù la dernière transformation s’est faite à l’aide de la 2ème inéga-lité triangulaire yx x yLe cas y1 et x 1 est parfaitement symétrique à celui-ci.c Dernier cas :x 1 et y 1 :fx fy=xxxx =x yy xxy= x yy y+ y yy xxyx y yxy+yyxxyx yx+ yxxor comme x 1, on afx fyx y+ yxx y+ x y= 2 x yoù nous avons utilisé, pour passer de la ligne 1 à la ligne 2, la 2èmeinégalité triangulaire.Bilan : f est bien 2-lipschitzienne.73

Page 74 : Exercice 7 :Pour chaque sous-ensemble suivant, indiquer si il s’agit de compact ou non.1. A1 = x, y R2/x2 + y4 = 12. A2 = x, y R2/x2 + y5 = 13. A3 = x, y R2/x2 + xy + y2 14. A4 = x, y R2/x2 + 8xy + y2 15. A5 = x, y R2/y2 = x1 2xRéponses :1. On considère l’ensemble A1 = x, y R2/x2 + y4 = 1a Soit l’application f de R2 dans R déﬁnie par fx, y = x2 + y4. fest continue sur R2. On voit donc que A1 = f11. Donc A1est l’antécédant d’un fermé par une application continue, donc A1est un fermé.b x2 + y4 = 1 =⇒x2 1 et y2 1 =⇒x 1 et y 1.d’où l’on déduit que x, y A1, x, y1. Donc A1 estborné.Finalement A1 est un fermé borné donc un compact.2. On considère l’ensemble A2 = x, y R2/x2 + y5 = 1a Soit l’application f de R2 dans R déﬁnie par fx, y = x2 + y5. fest continue sur R2. On voit donc que A2 = f11. Donc A2est l’antécédant d’un fermé par une application continue, donc A2est un fermé.b Nous avons x 0, x,51 x2 A2. Puisque x peut êtrearbitrairement grand, A2 n’est pas borné.Finalement A2 est un fermé, non borné, donc A2 n’est pas un com-pact.74

Page 75 : 3. On considère l’ensemble A3 = x, y R2/x2 + xy + y2 1a Soit l’application f de R2 dans R déﬁnie par fx, y = x2+xy+y2.f est continue sur R2. On voit donc que A3 = f1, 1. DoncA3 est l’antécédant d’un fermé par une application continue, doncA3 est un fermé.bFinalement A3 est un fermé, borné, donc A3 est un compact.4. On considère l’ensemble A4 = x, y R2/x2 + 8xy + y2 1x R, x, x A4puisque si x, x alors x2 8x2 + x2 = 6x2 1.Or x, x= x qui est arbitrairement grand. Donc A4 n’estpas borné donc A4 n’est pas un compact.5. On considère l’ensemble A5 = x, y R2/y2 = x1 2xa Soit l’application f de R2 dans R déﬁnie par fx, y = y2 x1 2x. f est continue sur R2. On voit donc que A5 = f10. DoncA5 est l’antécédant d’un fermé par une application continue, doncA5 est un fermé.b x, y A5 =⇒x1 2x 0 =⇒x 0, 12. On a donc0 x 12 =⇒12 x 2x2 12d’où l’on déduit que y 12. Finalement :x, y A5 =⇒x2 + y2 34 =⇒x, y22 34.Donc A5 est borné.Enﬁn, A5 est un fermé borné donc un compact.75

Page 76 : Exercice 8 :Soit K un compact non vide d’un espace vectoriel normé E et f : K →Ktelle quex, y K2, x ̸= y =⇒fx fy x y1. Montrer que f possède au plus un point ﬁxe.2. Justiﬁer qu’il existe c K tel quex K, fx x fc c3. En déduire que f admet un point ﬁxe.Réponses :1. On rappelle que z est un point ﬁxe si et seulement si fz = z.Supposons maintenant que f possède deux points ﬁxes tels que x ̸= y.L’hypothèse sur f donnefx fy x yce qui est absurde si fx = x et fy = y.2. On introduit la fonction δ:x 7→fx xdéﬁnie sur K. Lafonction δ est continue sur le compact K, elle admet donc un minimumen un point c K et alorsx K, δx δc3. Par l’absurde, si fc ̸= c alorsδfc=ffcfc fc c= δcce qui contredit la minimalité de c. Ainsi fc = c et c est le seulpoint ﬁxe de f.76

Page 77 : TD8 : Fonctions de plusieurs variablesExercice 1 :Calculer les dérivées partielles premières des fonctions suivantes :1. fx, y = ex cosy2. fx, y = x2 + y2 cosxy3. fx, y =p1 + x2y2Réponses :Il est totalement clair que chacune des applications dérivées partielles existespour les deux premières parce qu’elles sont le produit de fonctions dérivablespartout et la troisième car le terme 1 + x2y2 ne s’annule jamais.1. On considère la fonction fx, y = ex cosyMéthode 1 : bourrin et à n’utiliser que dans certains casOn déﬁnit l’applicationφx:R→Rt7→φxt = fx, y + t1, 0= fx + t, y= exet cosyEtudions maintenant la dérivée en t = 0 de φxt. Alorsφ′x0 = limt→0φxt φx0t= limt→0exet cosy ex cosyt= limt→0 ex cosyet 1tor quand t →0, et 1 + t. Doncfxx,y= φ′x0 = ex cosyEn introduisant φyt = fx, y + t0, 1et en faisant le mêmedéveloppement, on obtientfyx,y= φ′y0 = ex siny77

Page 78 : Méthode 2 : calcul directOn peut aussi faire le calcul directement, comme fait pendant voscours de physique, à savoir :La dérivée partielle de f par rapport à x, s’obtient en considérant quey est ﬁxe et en dérivant l’expression par rapport à x.La dérivée partielle de f par rapport à y, s’obtient en considérant quex est ﬁxe et en dérivant l’expression par rapport à y.Ainsi, en faisant le calcul de cette façon, on obtient directementfyx,y= ex cosyfyx,y= ex siny2. Soit la fonction fx, y = x2 + y2 cosxy. Alors en utilisant ladeuxième méthode, on trouve directementfyx,y= 2x cosxyyx2+y2 sinxyfyx,y= 2y cosxyxx2+y2 sinxy3. Soit la fonction fx, y =p1 + x2y2. Alors en utilisant la deuxièmeméthode, on trouve directementfyx,y=xy2p1 + x2y2fyx,y=x2yp1 + x2y2Exercice 2 : Calculs bêtes et méchantsSoit un gaz de molécules. Ce gaz, de volume V , de température T et soumisà la pression P, contient n moles.1. On commence par décrire ce gaz par la loi des gaz parfait : PV = nRToù R est la constance des gaz parfaits. Montrer alors quePVVTTP = 1T PTVT = nR2. Une meilleur approximation des gaz a été proposé à la ﬁn du 19ièmesiècle par Van Der WaalsP + n2aV 2V nb= nRToù a, b sont deux constantes positives. Calculer TP et PV .78

Page 79 : Réponses :1. Calculons séparément toutes les dérivées intervenant dans les expres-sions précédentesPVVTTPPTalorsPV = VnRTV= nRTV 2VT = TnRTP= nRPTP = PPVnR= VnRPT = TnRTV= nRVIl ne reste plus qu’à eﬀectuer les calculsPVVTTP = nRTV 2× nRP × VnR = nRTPV= 1etT PTVT = T × nRV× nRP= nRT × nRPV= nR2. On considère maintenant l’équation de van der Waals dont on chercheà calculerTPPValorsTP = P 1nR ×P + n2aV 2× V nb= V nbnRpour le second calcul, on doit manipuler un peu plus l’équation devan der Waals pour exprimer P en fonction des autres variables.P =nRTV nb n2aV 279

Page 80 : ﬁnalementPV = V nRTV nb n2aV 2= nRTV nb2 + 2n2aV 3Exercice 3 :Calculer toutes les dérivées partielles d’ordre 1 sans se préoccuper de leurdomaine de déﬁnitionRéponses :80

Page 81 : 81

Page 82 : Exercice 4 :Soient f et g deux fonctions d’une variable réele à valeurs dans R et dérivablessur R. Pour chacune des fonctions de deux variables Fi suivantes, déterminerles dérivées partielles en fonction des dérivées f′ et g′1. F1x, y = fx + gy2. F2x, y = fxgy3. F3x, y = fxgyRéponses :1. Sans diﬃcultéF1xx,y= f′xetF1yx,y= g′y2. Sans diﬃcultéF2xx,y= f′xgyetF2yx,y= fxg′y3. C’est simplement un peu plus techniqueF3xx,y= f′xgyetF3yx,y= fxg′yg2y82

Page 83 : Exercice 5 :Soit f la fonction de R2 dans R déﬁnie parfx, y =xyx+y,si x, y ̸= 0, 0.0,sinon.61. Justiﬁer que f est continue sur R2. Etudier les dérivées partielles de f en 0, 0.Réponses :1. Pour R2\0, 0 la fonction est trivialement continue comme fractionrationnelle dont le dénominateur ne s’annule jamais.En 0, 0 la situation est très diﬀérente puisque le dénominateur s’an-nule. Compte tenu de la fonction, f ne peut être continue en 0, 0 siet seulement silimx,y→0,0 fx, y = 0ce qui est vrai si et seulement sifx, y 0→x,y→x,y 0Orfx, y 0 = x × yx + y x→x,y→x,y 0CQFD2. Etudions maintenant les dérivées partielles premières de f en 0, 0.Or dans ce cas, comme il y a une discontinuité dans la déﬁnition de fau point où l’on veut savoir si la fonction est dérivable ou non, noussommes obligés de passer par la déﬁnition. Ainsifxx,y= limt→0f0, 0 + t1, 0f0, 0tOr f0, 0 + t1, 0= f0, 0 = 0 et doncfx0,0= limt→0f0, 0 + t1, 0f0, 0t= 083

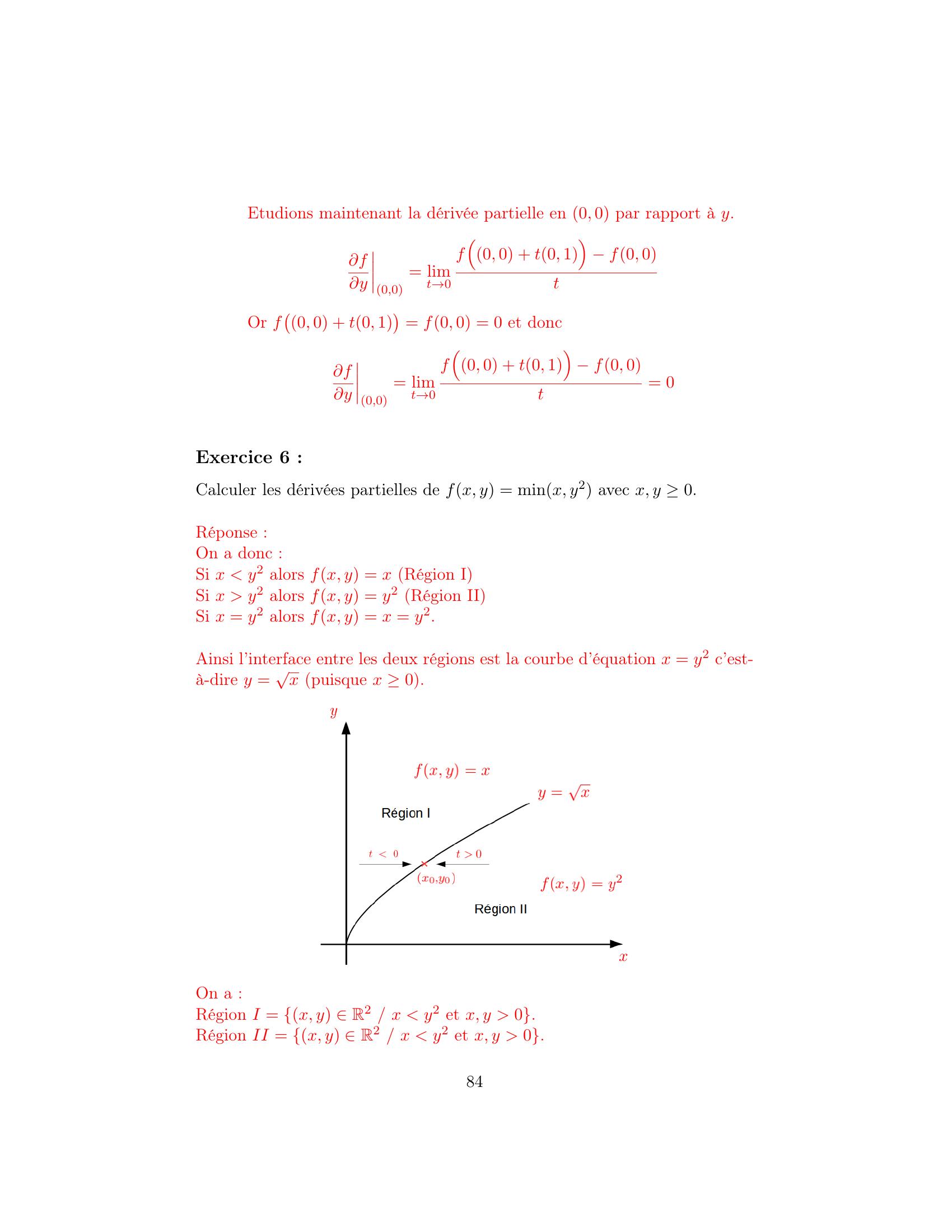
Page 84 : Etudions maintenant la dérivée partielle en 0, 0 par rapport à y.fy0,0= limt→0f0, 0 + t0, 1f0, 0tOr f0, 0 + t0, 1= f0, 0 = 0 et doncfy0,0= limt→0f0, 0 + t0, 1f0, 0t= 0Exercice 6 :Calculer les dérivées partielles de fx, y = minx, y2 avec x, y 0.Réponse :On a donc :Si x y2 alors fx, y = x Région ISi x y2 alors fx, y = y2 Région IISi x = y2 alors fx, y = x = y2.Ainsi l’interface entre les deux régions est la courbe d’équation x = y2 c’est-à-dire y = x puisque x 0.On a :Région I = x, y R2 / x y2 et x, y 0.Région II = x, y R2 / x y2 et x, y 0.84

Page 85 : Interface= x, y R2 / x = y2 et y 0.Soit x, y I alors fx, y = x et on afxx,yI= 1fyx,yI= 0Soit x, y II alors fx, y = y2 et on afxx,yII= 0fyx,yII= 2yOn doit maintenant se poser la question à l’interface, c’est-à-dire pour y =x. Pour cela considérons un point x0, y0 appartenant à l’interface, c’est-à-dire, tel que x0 0 et y0 = x0. Alorsfxx0,y0= limt→0fx0 + t, y0 fx0, y0tdonc pour t 0, il faut prendre fx, y = x tandis que pour t 0,fx, y = y2. AlorsPour t 0 :fxx0,y0= limt→0+fx0 + t, y0 fx0, y0t= limt→0+y20 y20t= 0Pour t 0 :fxx0,y0= limt→0fx0 + t, y0 fx0, y0t= limt→0x0 + t x0t= 1Ainsi la dérivée première selon x n’est pas déﬁnie sur la courbe y = x ̸= 0.Il en va de même pour la dérivée première par rapport y.Exercice 7 :Etudier la continuité des fonctions suivantes ainsi que l’existence et la conti-nuité de leurs dérivées partielles premières1.f1x, y =x+y2x2+y2 ,si x, y ̸= 0, 0.0,sinon.785

Page 86 : 2.f2x, y =x2 + y2 sin1x2+y2 ,si x, y ̸= 0, 0.0,sinon.83.f3x, y =x sin yy sin xx2+y2,si x, y ̸= 0, 0.0,sinon.9Réponses :1. Etudions f1 :a Continuité de f1 :x, y R2\0, 0 la fonction est continue comme fraction ration-nelle dont le dénominateur ne s’annule jamais. On doit maintenantétudier ce qu’il en est en 0, 0 puisque le dénominateur s’annule.Compte tenu de la fonction, f1 ne peut être continue en 0, 0 siet seulement silimx,y→0,0 f1x, y = 0Pour cela, passons en coordonnées polaires en posant x = ρ cosθet y = ρ sinθ. Alors˜f1ρ, θ =cosθ + sinθ2Donc la valeur de ˜f1 dépend de θ et f1 n’est pas continue en 0, 0.b Etudions maintenant les dérivées premières.x, y R2\0, 0 alorsf1xx,y= 2yy2 x2x2 + y22f1yx,y= 2xy2 x2x2 + y22En 0, 0, nous devons utiliser la déﬁnition des dérivées partiellesf1x0,0= limt→0f1t, 0 f10, 0t= limt→01tt2t2 0= limt→01t = ±Donc la dérivée partielle selon x n’est pas continue en 0, 0. Jevous laisse faire le travaille pour la dérivée partielle selon y.86

Page 87 : Finalement f1 n’est continue sur R2 et évidemment pas C1 sur R2.Toutefois la fonction est C1 sur R2\0, 0.2. Etudions f2 :a Continuité de f2 :x, y R2\0, 0 la fonction est continue. On doit maintenantétudier ce qu’il en est en 0, 0 puisque le dénominateur s’annule etqu’on a alors une forme indéterminée. Compte tenu de la fonction,f2 ne peut être continue en 0, 0 si et seulement silimx,y→0,0 f2x, y = 0Etudions donc f2x, y 0f2x, y = x2 + y2sin 1px2 + y2! x2 + y2→x,y→0,0 0Donc f2 est continue en 0, 0.Finalement f2 est continue sur R2.b Etudions maintenant les dérivées premières.x, y R2\0, 0 alorsf2xx,y= 2x sin 1px2 + y2!xpx2 + y2 cos 1px2 + y2!f2yx,y= 2y sin 1px2 + y2!ypx2 + y2 cos 1px2 + y2!En 0, 0, nous devons utiliser la déﬁnition des dérivées partiellesf2x0,0= limt→0f2t, 0 f20, 0t= limt→01tt2 sin 1t0= limt→0 t sin 1t= 0On montre de la même façon quef2y0,0= 087

Page 88 : Ainsi, on af2x:R2→Rx, y7→2x sin1x2+y2xx2+y2 cos1x2+y20etf2y:R2→Rx, y7→2y sin1x2+y2yx2+y2 cos1x2+y20Montrons maintenant que ces deux applications ne sont pas conti-nues.Pour f2x :Soit un = 1n, 0 alors un tend vers 0, 0 quand n tend vers l’inﬁni.Orf2xun= 2n sinn cosnqui n’a pas de limite quand n tend vers l’inﬁni. Donc f2x n’est pascontinue en 0, 0.Pour f2y :Soit un = 0, 1n alors un tend vers 0, 0 quand n tend vers l’inﬁni.Orf2yun= 2n sinn cosnqui n’a pas de limite quand n tend vers l’inﬁni. Donc f2y n’est pascontinue en 0, 0.Finalement f2 est continue sur R2 mais elle n’est pas C1 sur R2.Par contre f2 est C1 sur R2\0, 0.3. Etudions f3 :a Continuité de f3 :x, y R2\0, 0 la fonction est continue car le dénominateur88

Page 89 : ne s’annule jamais. On doit maintenant étudier ce qu’il en est en0, 0 puisque le dénominateur s’annule et qu’on a alors une formeindéterminée. Compte tenu de la fonction, f3 ne peut être continueen 0, 0 si et seulement silimx,y→0,0 f3x, y = 0Pour étudier cela, nous allons eﬀectuer un développement limité.Ainsif3x, y =1x2 + y2xy y36 + y4ϵ1yyx x36 + x4ϵ2x= x3y xy3 + 6xy4ϵ1y 6yx4ϵ2x6x2 + y2=xy6x2 + y2x2 y2 + 6y3ϵ1y 6x3ϵ2xavec ϵ1 qui tend vers 0 quand x tend vers 0 et ϵ2 qui tend vers 0quand y tend vers 0. Alorsf3x, y =xy6x2 + y2 ×x2 y2 + 6y3ϵ1y 6x3ϵ2xx2 + y22 × 6x2 + y2 ×x2 y2 + 6y3ϵ1y 6x3ϵ2x112 ×x2 + y2 + 6y3ϵ1y + 6x3ϵ2x→x,y→0,0 0Donc f3 est continue en 0, 0 car on a aussi f0, 0 = 0.Finalement f3 est continue sur R2.b Etudions maintenant les dérivées premières.x, y R2\0, 0 alorsf3xx,y= siny y cosxx2 + y22xx siny y sinxx2 + y22f3yx,y= x cosy sinxx2 + y22yx siny y sinxx2 + y22En 0, 0, nous devons utiliser la déﬁnition des dérivées partiellesf3x0,0= limt→0f3t, 0 f30, 0t= 089

Page 90 : On montre de la même façon quef3y0,0= 0Ainsi, on af3x:R2→Rx, y7→sinyy cosxx2+y22xx sinyy sinxx2+y220etf3y:R2→Rx, y7→x cosysinxx2+y22yx sinyy sinxx2+y220Montrons maintenant que f3x est une application continue. Pourcela, on va étudier séparément les deux termes qui composentl’expression de f3x .siny y cosxx2 + y2=y y36 + y4ϵ1y y1 x22 + x3ϵ2xx2 + y2= y y26 + x22 + y3ϵ1y + x3ϵ2xx2 + y2!Alorssiny y cosxx2 + y2 y16 + 12 + yϵ1y + xϵ2x→x,y→0,0 0En faisant une étude similaire sur le 2nd terme, on obtient aussique le second terme tend vers 0 quand x, y tend vers 0. Doncﬁnalement f3x tend vers 0 quand x, y tend vers 0. Finalementf3x est continue sur R2.Il en va de même pour f3y .Finalement f3 est C1 sur R2.90

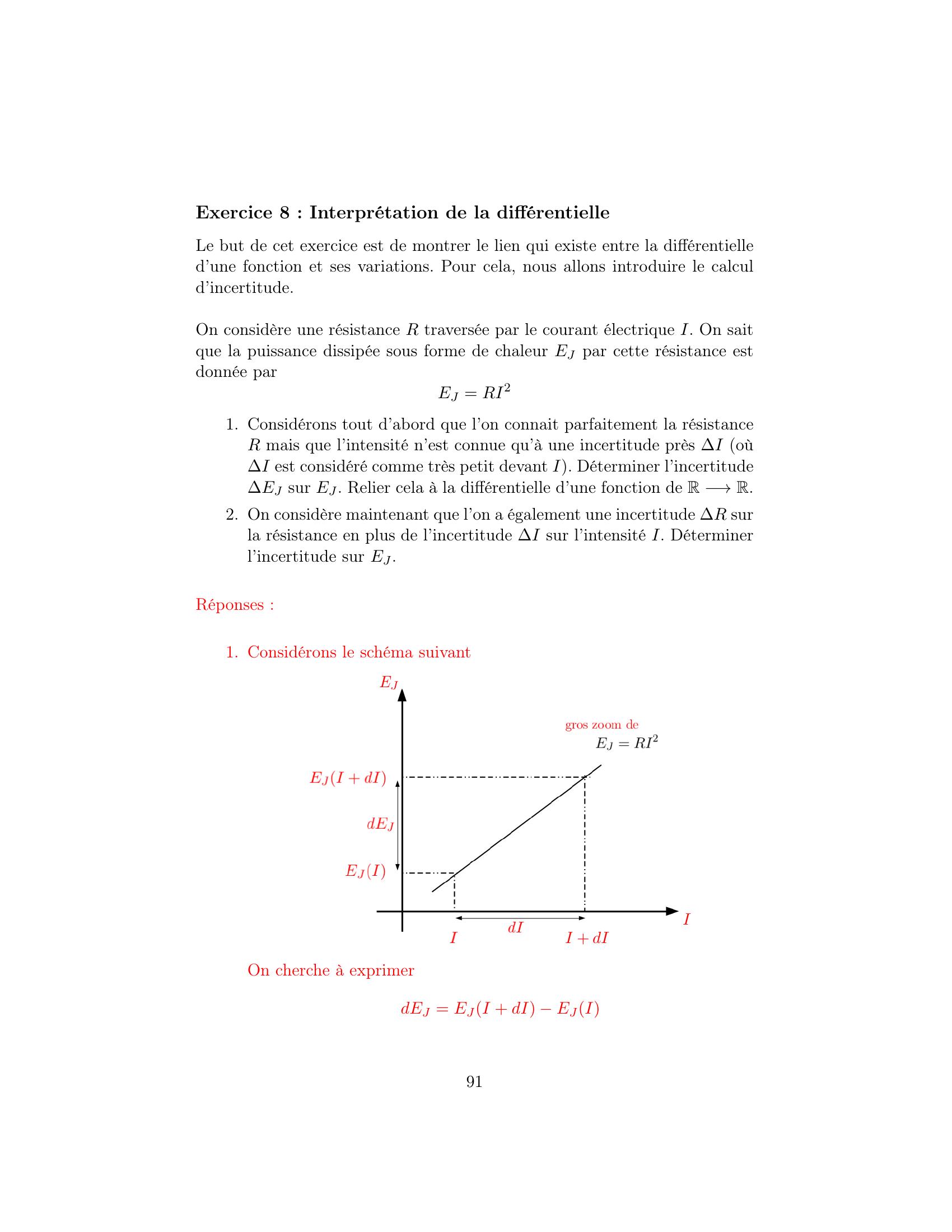
Page 91 : Exercice 8 : Interprétation de la diﬀérentielleLe but de cet exercice est de montrer le lien qui existe entre la diﬀérentielled’une fonction et ses variations. Pour cela, nous allons introduire le calculd’incertitude.On considère une résistance R traversée par le courant électrique I. On saitque la puissance dissipée sous forme de chaleur EJ par cette résistance estdonnée parEJ = RI21. Considérons tout d’abord que l’on connait parfaitement la résistanceR mais que l’intensité n’est connue qu’à une incertitude près I oùI est considéré comme très petit devant I. Déterminer l’incertitudeEJ sur EJ. Relier cela à la diﬀérentielle d’une fonction de R →R.2. On considère maintenant que l’on a également une incertitude R surla résistance en plus de l’incertitude I sur l’intensité I. Déterminerl’incertitude sur EJ.Réponses :1. Considérons le schéma suivantOn cherche à exprimerdEJ = EJI + dI EJI91

Page 92 : OrEJI + dI = RI + dI2 = RI2 + 2RIdI + RdI2 RI2 + 2RIdIL’approximation vient du fait que dI1 et donc dI2 0. On obtientainsidEJ 2RIdI = E′JIdIoù E′JI est la dérivée de EJ prise en I.On voit donc que si on a une incertitude dI sur l’intensité I alorsl’incertitude sur la puissance dissipée est donnée pardEJ = 2RIdI = E′JdI2. On se pose maintenant la même question sauf que cette fois-ci, nousavons une incertitude à la fois sur R et sur I. On a alorsdEJ = dEIJ+ dERJoù dEIJet dERJsont respectivement l’incertitude sur EJ dû à l’in-certitude sur I et à l’incertitude sur R. On a alorsdEIJ= 2IRdI = EJII,RdIetdEPJ= I2dR = EJRI,RdRFinalement on adEJ = EJRI,RdR + EJII,RdIOn reconnait ici la diﬀérentielle vu en cours. Ce qui signiﬁe que ladiﬀérentielle au point I, R permet de connaître la variation de lafonction EJ lorsque la variable I devient I + dI et la variable Rdevient R + dR.92

Page 93 : Exercice 9 :1. Soit a un réel non nul. Etudier la diﬀérentiabilité au point a, 0 dela fonction f déﬁnie sur R2\0, 0 parfx, y =x2yx2 + y102. Discuter selon la valeur du réel α de la diﬀérentiabilité au point 0, 0degx, y = xαyx2+y,si x, y ̸= 0, 0.0,sinon.11Réponses :1. f est diﬀérentiable en a, 0 si et seulement silimh1,h2→0,01h1, h22"fa + h1, h2 fa, 0 h1fxa,0h2fya,0= 0fxa,0= 2xyx2 + y 2x3yx2 + y2a,0= 0fya,0= limk→0fa, k fa, 0ka,0= limk→0a2ka2 + kka,0= 1 car a ̸= 0alorsϵh1, h2 =limh1,h2→0,01ph21 + h22ha + h12h2a + h12 + h2 0 h1 × 0 h2 × 1iϵh1, h2 =limh1,h2→0,0h2h2a + h12 + h21ph21 + h22ϵh1, h2 ph21 + h22a + h12 + h2→x,y→0,0 0Donc f est diﬀérentiable en a, 0, et la diﬀérentielle est donnée parDa,0fh1, h2 = h2.2.93

Page 94 : Exercice 10 :Étudier la continuité et la diﬀérentiabilité puis calculer le gradient lorsqu’ilexiste des fonctions suivantes94

Page 95 : 95

Page 96 : 96

Page 97 : 97

Page 98 : 98

Page 99 : TD9 10 :Exercice 1 :1. Soit f : R2 →R une application C1 sur R2. On pose g : R →Rdéﬁnie par gt = f2t, 1+t2. Exprimer g′t en fonction des dérivéespartielles de f.2. Soit fx, y = xy une fonction dépendant des variables x et y qui sontparamétrées par t :xt = costyt = sint12Détemriner g′t où gt = fxt, ytexplicitement puis en utili-sant la relation donnée dans la Prop D1 du cours.3. Soit x1, ..., xn, h1, ..., hn R2n, f C1Rn, R et t R. On posealorsgt = fx1 + th1, ..., xn + thn13Calculer g′tRéponses :1. Introduisons les deux applications de R dans R suivantes :u1t = 2tu2t = 1 + t2qui sont clairement chacune C1 sur R. Alors d’après le cours, la fonc-tion g = f ◦u1, u2 est elle-même C1 sur R et sa dérivée est donnéeparg′t = fxu1t,u2t u′1t + fyu1t,u2t u′2t= 2 fx2t,1+t2 + 2t fy2t,1+t299

Page 100 : 2. Posons les fonctions ui de R dans R suivantesu1t = x1 + h1tu2t = x2 + h2t...unt = xn + hntqui sont C1 sur R. Alors la fonction g = f ◦u1, u2, ..., un est elle-même C1 sur R. Alorsg′t =nXi=1hifxiu1t,u2t,...,untExercice 2 :Soit f une application diﬀérentiable de R2 dans R. Soit la fonction g déﬁniepargu, v = fu2 + v2, uv141. Justiﬁer que g est diﬀérentiable.2. Exprimer les dérivées partielles de g par rapport à u et v en fonctiondes dérivées partielles de f par rapport à x et y.Réponses :1. Compte tenu de l’expression de g, on a g = f ◦φ où φ est la fonctiondéﬁnie parφ:R2→R2u, v7→g1u, v, g2u, v= u2 + v2, uvLa fonction φ est trivialement diﬀérentiable sur R2 car elle est C1 surR2 puisque les applications g1 et g2 sont trivialement C1 sur R2. Donc,puisque f et φ sont diﬀérentiable sur R2, g est diﬀérentiable sur R2par stabilité de la propriété de diﬀérentiabilité par composition.100

Page 101 : 2. On a doncguu,v= fxg1u,v,g2u,vg1uu,v + fyg1u,v,g2u,vg2uu,vgvu,v= fxg1u,v,g2u,vg1vu,v + fyg1u,v,g2u,vg2vu,valorsguu,v= 2u fxu2+v2,uv + v fyu2+v2,uvgvu,v= 2v fxu2+v2,uv + u fyu2+v2,uvExercice 3 :Soit f : x, y →fx, y diﬀérentiable et g : ρ, θ →fρ cosθ, ρ sinθ.1. Justiﬁer que g est diﬀérentiable.2. Exprimer les dérivées partielles de g en fonction de celles de f.3. En déduire les dérivées partielles de f en fonction de celles de g.4. Vériﬁer les résultats des deux questions précédentes sur la fonctionfx, y = x2 + y2 + x.Réponses :1. On a comme dans l’exercice précédent g = f ◦φ où φ est déﬁnie parφ:R2→R2ρ, θ7→x, y = ρ cosθ, ρ sinθOr φ est clairement C1 sur R2 et donc diﬀérentiable sur R2. Par hypo-thèse, il en va de même pour f. Donc g est diﬀérentiable par stabilitéde cette propriété par composition.2. On a doncgρρ,θ= fxx,yxρρ,θ + fyx,yyρρ,θgθρ,θ= fxx,yxθρ,θ + fyx,yyθρ,θ101

Page 102 : ce qui donnegρρ,θ= cosθ fxx,y + sinθ fyx,ygθρ,θ= ρ sinθ fxx,y + ρ cosθ fyx,yOn peut alors remarquergρρ,θgθρ,θ=cosθsinθρ sinθρ cosθfxx,yfyx,y3. Il suﬃt d’inverser la matrice précédentefxx,yfyx,y= 1ρρ cosθsinθρ sinθcosθgρρ,θgθρ,θ4. Soit fx, y = x2 + y2 + x. On souhaite calculer les dérivées de g. Ona alors 2 méthodes :Méthode 1 : méthode directe.on sait que gρ, θ = ρ2 + ρ cosθ. Alorsgρρ,θ = 2ρ + cosθgθρ,θ = ρ sinθMéthode 2 : en utilisant les questions précédentes.gρρ,θ= cosθ fxx,y + sinθ fyx,y = cosθ2ρ cosθ + 1+ sinθ2ρ sinθ= 2ρ + cosθgθρ,θ= ρ sinθ fxx,y + ρ cosθ fyx,y = ρ sinθ102

Page 103 : Exercice 4 :Soit f : R2 →R diﬀérentiable. On suppose que pour t R, x, y R2fx + t, y + t = fx, y15Montrer que x, y R2fxx,y+ fyx,y= 0Réponse :Posons gt = fx+t, y+t = fu1t, u2t où l’on a introduit les fonctionsu1t = x + tu2t = y + tqui sont C1 sur R. Alors u′1t = 1 = u′2t. On a doncg′t = fxu1t,u2t u′1t + fyu1t,u2t u′2t= fxx+t,y+t + fyx+t,y+tor dans notre cas g′t =ddtfx, y = 0. Il suﬃt alors de prendre t = 0,conduisant donc àfxx,y+ fyx,y= 0Exercice 5 :Soit f : R2 →R diﬀérentiable. On suppose que pour t R, x, y R2fxt, yt = fx, y16Montrer que x, y R2xfxx,y+ y fyx,y= 017Réponse :103

Page 104 : Introduisons la fonction gt = fxt, yt = fu1t, u2t où l’on a introduitles fonctionsu1t = xtu2t = ytqui sont C1 sur R. Alors u′1t = x et u′2t = y. On a doncg′t = fxu1t,u2t u′1t + fyu1t,u2t u′2t= x fxxt,yt + y fyxt,ytor dans notre cas g′t =ddtfx, y = 0. Il suﬃt alors de prendre t = 1,conduisant donc àx fxx,y+ y fyx,y= 0Exercice 6 :On considère l’application f de R2 dans R2 déﬁnie parfx, y =xp1 + y2 + yp1 + x2; x +p1 + x2y +p1 + y2181. Montrer que f est de classe C1 sur R2.2. Calculer le jacobien de f en tout point x, y R2. Qu’en déduit-onpour f ?Réponses :1. Les applications composantes sont C1 comme produit et composée defonctions de classe C1 sur R2 puisque 1 + x2 et 1 + y2 ne s’annulentjamais.2. Calculons maintenant les dérivées premières en posantf1x, y = xp1 + y2+yp1 + x2etf2x, y = x+p1 + x2y+p1 + y2etf1x, y = xuy + yuxf2x, y =x + uxy + uy= xy + uxuy + f1x, y104

Page 105 : où u est l’application déﬁnie par ut =t2 + 1 conduisant à u′t =tut.Alors pour f1 :f1xx,y = uy + yxux = f2x,yf1x,yuxf1yx,y =xyuy + ux = f2x,yf1x,yuytandis que pour f2 :f2xx,y = y + xuyux + f1xx,y = f2x,yuxf2yx,y = x + uxyuy + f1yx,y = f2x,yuyon obtient doncJfx, y =f1xx,yf1yx,yf2xx,yf2yx,y= f2x,yf1x,yuxf2x,yf1x,yuyf2x,yuxf2x,yuy!le jacobien déterminant de la matrice précédente est ainsi égal à 0.On déduit donc que f n’est pas un C1-diﬀéomorphisme.Exercice 7 :Soit f une fonction de R2 dans R admettant des dérivées partielles en toutpoint, θ un réel et g : R2 →R2 la fonction déﬁnie pargx, y =x cosθy sinθ ; x sinθ+y cosθ=ux, y ; vx, y191. Montrer que la fonction F = f ◦g admet des dérivées partielles entout point.2. Calculer Fx et Fy en a, b R2 en fonction des dérivées partiellesde f.Réponses :1. F = f ◦g. Or f admet des dérivées partielles en tout point et de plusu et v sont clairement C1 sur R2. Donc F admet des dérivées partiellesen tout point.105

Page 106 : 2. Nous allons maintenant calculer les dérivées partielles de F en x =a, y = b en fonction des dérivées partielles de f. Or on rappelle queF = f ◦g ⇐⇒Fx, y = f ◦gx, y = f ◦gx, y = fux, y, vx, yDonc les "variables naturelles" de F sont x et y tandis que celle de fsont u et v.Fxa,b = fuua,b,va,buxa,b + fvua,b,va,bvxa,bFya,b = fuua,b,va,buya,b + fvua,b,va,bvya,boùua, b = a cosθ b sinθva, b = a sinθ b cosθFinalementFxa,b = fuua,b,va,b cosθ + fvua,b,va,b sinθFya,b = fuua,b,va,b sinθ + fvua,b,va,b cosθExercice 8 :On cherche toutes les fonctions f de R2 dans R, C1 sur R2, telles queE : x, y R2, fxx,y+ 2x fyx,y= 020On considère l’application ϕ qui associe à u, v R2 ϕu, v = u, v + u2.1. Montrer que ϕ est bijective de classe C1 sur R2.2. Montrer que ϕ1 est de classe C1 sur R2.3. Que peut-on en déduire pour ϕ ?4. On introduit maintenant la fonction déﬁnie par g = f ◦ϕa Montrer que g est de classe C1 sur R2.106

Page 107 : b Montrer que f est solution de E si et seulement siguu,v= 0215. En déduire que fx, y = hy x2, où h est C1 sur R, est solutionde E.Réponses :1. Clairement ϕ est C1 sur R2. Montrons maintenant que ϕ est bijective.Soit u, v R2, alorsϕu, v = x, y ⇐⇒x = uy = v + u2⇐⇒u = xv = y x2Donc ϕ est bijective.2. Compte tenu de l’expression trouvée à la question précédente, on voitclairement que ϕ1 est C1 sur R2.3. On déduit donc que ϕ est un C1-diﬀéomorphisme de R2 dans R2.4. a On rappelle que ϕ est C1 sur R2 et de plus par hypothèse f estC1 sur R2. Donc par stabilité de la propriété C1 par composition,g = f ◦ϕ est C1 sur R2.b Calculons les dérivées partielles de g qui a pour variable u et v.Alorsguu,v = fxxu,v,yu,vxuu,v + fyxu,v,yu,vyuu,vgvu,v = fxxu,v,yu,vxvu,v + fyxu,v,yu,vyvu,vNous n’allons considérer que la première dérivéeguu,v = fxxu,v,yu,v + 2u fyxu,v,yu,v107

Page 108 : or, puisque x = u, on aguu,v = fxxu,v,yu,v + 2x fyxu,v,yu,vOn voit donc quesolution de E =⇒guu,v = 05. D’après la question précédente f vériﬁe E si et seulement g = f ◦ϕvériﬁeguu,v = 0. Orguu,v = 0 ⇐⇒gu, v = hv où h est C1sur R. Ainsifx, y = g ◦ϕ1x, y = gx, y x2 = hy x2Exercice 9 :Résoudre les équations aux dérivées partielles du premier ordre suivantesd’inconnue f : U →R à l’aide du changement de variables fourni1. U = R+ × R ; xfx + y fy = 0 ; changement de variables : u, v =x, y/x.2. U = R+ × R ; xfx + y fy =px4 + y4 ; changement de variables :u, v = y/x, x2 + y2.3. U = R+ × R ; xfx y fy = xy2 ; changement de variables : u, v =x, yx.4. U = R+ × R ; xfx + y fy = af ; a R ; changement de variables :coordonnées polaires.Réponses :108

Page 109 : 109

Page 110 : Exercice 10 :Soit f: Rn →R une application. Dire si les aﬃrmations suivantes sontvraies ou faussesRéponses :1. vrai4. faux7. vrai10. faux2. vrai5. faux8. vrai11. faux3. vrai6. faux9. faux12. faux110

Page 111 : Exercice 11 :On cherche toutes les fonctions de g de R2 dans R vériﬁant, x, y R2gxx,ygyx,y= aoù a est un réel.1. Soit f la fonction déﬁnie sur R2 par fu, v = gu+v2 , vu2. En utili-sant le théorème de composition, montrer quefuu,v= a22. Intégrer cette équation pour en déduire l’expression de f.3. En déduire les solutions de l’équation initiale.Réponses :1. Cela revient à avoir posé le changement de variables suivantϕ:R2→R2u, v7→x, y = ϕu, v =u+v2 , vu2clairement ϕ est C1 sur R2. On axy= 12 1111 uvor on peut facilement inverser cette matrice, ce qui conduit àuv= 1111 xyOn a donc u = x y et v = x + y. Ainsi ϕ est bijectif et de plus ϕ1est également C1 sur R2. Donc ϕ est un C1-diﬀéomorphisme. Il s’agitdonc d’un changement de variable légal. On ag = f ◦ϕ1 ⇐⇒gx, y =f ◦ϕ1x, y = fϕ1x, yf = g ◦ϕ⇐⇒fu, v =g ◦ϕx, y = gϕu, v111

Page 112 : On peut alors calculer la dérivée partielle de f par rapport à ufuu,v = gxxu,v,yu,vxuu,v+ gyxu,v,yu,vyuu,v= 12gxxu,v,yu,v 12gyxu,v,yu,v = a22. On peut maintenant intégrer cette équationfu, v = a2u + hvavec h qui est une fonction C1 sur R.3. On peut facilement obtenir g puisque g = f ◦ϕ1 où ϕ1x, y =x y, x + y. On a alorsgx, y = fx y, x + y = a2x y + hx + yExercice 12 :Déterminer toutes les fonctions f de R2 dans R vériﬁant les équations sui-vantes1. x, y R2, 2 fxx,y fyx,y = 0Indication : On utilisera le changement de variables u = x + y etv = x + 2y.2. x, y R2, x fxx,y + y fyx,y =px2 + y2 sur V = x, y R2/x 0Indication : On passera en coordonnées polaires.Réponses :1. On nous propose le changement de variablesu = x + yv = x + 2y112

Page 113 : Introduisons donc la fonction changement de variables ϕ suivanteϕ:R2→R2x, y7→u, v = ϕx, y =x + y, x + 2yOn peut alors introduire la fonction g qui est telle quef = g ◦ϕ ⇐⇒fx, y = g ◦ϕx, y = gϕx, y = gx + y, x + 2yJe vous laisse vériﬁer que ϕ est un C1-diﬀéomorphisme de R2 dans R2c’est-à-dire que c’est une bijection de R2 dans R2, C1 sur R2 et telleque ϕ1 est C1 sur R2fxx,y = guux,y,vx,yuxx,y + gvux,y,vx,yvxx,yfyx,y = guux,y,vx,yuyx,y + gvux,y,vx,yvyx,yce qui conduit àfxx,y = guux,y,vx,y + gvux,y,vx,yfyx,y = guux,y,vx,y + 2 gvux,y,vx,yalors2 fxx,yfyx,y= guux,y,vx,yd’où l’on déduit que0 = guux,y,vx,ypuisque2 fxx,yfyx,y= 0On peut maintenant résoudre l’équation aux dérivées partielles sur gd’où l’on tiregu, v = hv113

Page 114 : où h est une fonction C1 sur R. Or f = g ◦ϕ c’est-à-direfx, y = g ◦ϕx, y = gux, y, vx, y= gx + y, x + 2yﬁnalement, on déduit quefx, y = hx + 2yoù h est une fonction C1 sur R quelconque.2. On introduit la fonction changement de variable suivanteϕ:U = R+× π2 , π2 →V = R+ × Rr, θ7→x, y = ϕr, θ =r cosθ, r sinθϕ est clairement C1 sur U dans V . Montrons maintenant que ϕ estbijective. Pour cela, rappelons que l’on ax = r cosθy = r sinθor x2 + y2 = r2 or puisque r 0 :x2 + y2 = r2 ⇐⇒r =px2 + y2De plus comme x ̸= 0, on peut calculer y/x d’où l’on obtientyx = sinθcosθ = tanθor comme θ π2 , π2 , on peut écrireyx = tanθ ⇐⇒θ = Arctanyxainsix = r cosθy = r sinθ⇐⇒r =px2 + y2θ = Arctan yxoù x, y U et r, θ V et il s’agit bien d’une bijection.114

Page 115 : Vériﬁons maintenant que ϕ1 est C1 sur V = R+ × R. Pour cela,calculons les diﬀérentes dérivées partiellesrx =xpx2 + y2 = cosθry =ypx2 + y2 = sinθθx = Arctan′ yx×yx′=11 + y2x2× yx2 = yx2 + y2 = sinθrθx = Arctan′ yx×yx′=11 + y2x2× 1x =xx2 + y2 = cosθrToutes les dérivées premières sont bien déﬁnies x, y V et doncϕ1 est bien C1 sur V .Finalement ϕ est un C1-diﬀéomorphisme de U dans V .Utilisons maintenant ce changement de variable aﬁn de déterminerles dérivées partielles de f en fonction des dérivées partielles de g.fxx,y = grr,θrxx,y + gθr,θθxx,yfyx,y = grr,θryx,y + gθr,θθyx,yCe qui donne, compte-tenu des expressions des dérivées partiellesfxx,y = cosθ grr,θ sinθrgθr,θfyx,y = sinθ grr,θ + cosθrgθr,θon peut maintenant calculer x fxx,y + y fyx,y en utilisant lesrelations précédentesr = x fxx,y+ y fyx,y= r grr,θ115

Page 116 : on déduit donc puisque r ̸= 0grr,θ= 1cette équation peut facilement s’intégrer pour obtenirgr, θ = r + hθoù h est C1 sur π2 , π2 . Org = f ◦ϕ ⇐⇒gρ, θ = f ◦ϕr, θ = fr cosθ, r sinθc’est-à-diref = g◦ϕ1 ⇐⇒fx, y = g◦ϕ1x, y = gpx2 + y2, Arctany/xet ﬁnalement la solution de l’EDP est donnée parx, y V, fx, y =px2 + y2 + h Arctany/xoù h est une application C1 sur π2 , π2 .Exercice 13 :Résoudre sur R2 les équations aux dérivées partielles suivantesRéponses :1. On nous propose le changement de variables suivantϕ:R2→R2x, y7→u, v = ϕx, y = 2x + y, 3x + y116

Page 117 : Je vous laisse vériﬁer que cette application est bien un C1-diﬀéomorphismede R2 dans R2. on a alorsf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gu, v = g2x+y, 3x+y22On peut alors exprimer les dérivées partielles de f en fonction desdérivées partielles de g :fxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yqui donnefxx,y = 2 guu,v + 3 gvu,vfyx,y = guu,v + gvu,vAlorsfxx,y 3 fyx,y = 0 ⇐⇒guu,v = 0Cette dernière EDP est facilement intégrable et conduit àgu, v = hvoù h est C1 sur R. Or, d’après 23, on afx, y = h3x + yAinsi, x, y R2, la solution à l’EDP donnée estfx, y = h3x + yoù h est C1 sur R.2. On nous propose le changement de variables suivantϕ:R2→R2x, y7→u, v = ϕx, y = x, y x117

Page 118 : Je vous laisse vériﬁer que cette application est bien un C1-diﬀéomorphismede R2 dans R2. on a alorsf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gu, v = g2x+y, 3x+y23On peut alors exprimer les dérivées partielles de f en fonction desdérivées partielles de g :fxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yqui donnefxx,y = guu,v gvu,vfyx,y = gvu,vAlorsfxx,y + fyx,y = fx, y ⇐⇒guu,v = gu, vCette dernière équation est équivalente à une équation diﬀérentiellequi a pour solutiongu, v = Cveuoù C est C1 sur R. Or, d’après 23, on afx, y = Cy xexAinsi, x, y R2, la solution à l’EDP donnée estfx, y = Cy xexoù h est C1 sur R.118

Page 119 : TD11 12 :Exercice 1 :Déterminer les fonctions f solutions des systèmes suivants1.fx = xy2fy = x2y242.fx =xx2+y2fy =yx2+y2253.fx =xx2+y2fy = yx2+y226Réponses :1. Résolution du système d’EDP :Etape 1 : vériﬁons que2fxy =2fyx.2fxyx,y =xfyx,y=xyx2 = 2xy2fyxx,y =yfxx,y=yxy2 = 2xyainsi, on sait qu’il existe bien une solution à ce système d’EDP.Etape 2 : intégration de l’une des deux équations. Ici on va intégrerfx = xy2. Alorsfx, y = 12x2y2 + Kyoù K est C2 sur R.Etape 3 : dérivation par l’autre variable de la solution précédente.fy = y12x2y2 + Ky= x2y + Kyy119

Page 120 : or, on sait, compte tenu de la deuxième EDP du système d’EDPs,fy = yx2, d’où l’on déduit quefy = y12x2y2 + Ky= x2y + Kyy= x2ydonc, on obtient l’équation diﬀérentielle suivanteKyy= 0Etape 4 : intégration de l’équation diﬀérentielle précédenteKy = Cavec C REtape 5 : écriture de la solution.La solution est donc donnée parfx, y = 12x2y2 + Cavec C R2. Résolution du système d’EDP :Etape 1 : vériﬁons que2fxy =2fyx.2fxyx,y =xfyx,y=xyx2+y2= y xhx2 + y212i= xyx2+y2322fyxx,y =yfxx,y=yxx2+y2= x xhx2 + y212i= xyx2+y232ainsi, on sait qu’il existe bien une solution à ce système d’EDP.Etape 2 : intégration de l’une des deux équations. Ici on va intégrerfx =xx2+y2 . Alorsfx, y =px2 + y2 + Kyoù K est C2 sur R.Etape 3 : dérivation par l’autre variable de la solution précédente.fy = ypx2 + y2 + Ky=ypx2 + y2 + Kyy120

Page 121 : or, on sait, compte tenu de la deuxième EDP du système d’EDPs,fy =yx2+y2 , d’où l’on déduit quefy = ypx2 + y2 + Ky=ypx2 + y2 + Kyy=ypx2 + y2donc, on obtient l’équation diﬀérentielle suivanteKyy= 0Etape 4 : intégration de l’équation diﬀérentielle précédenteKy = Cavec C REtape 5 : écriture de la solution.La solution est donc donnée parfx, y =px2 + y2 + Cavec C R3. Résolution du système d’EDP :Etape 1 : vériﬁons si2fxy =2fyx.2fxyx,y =xyx2+y2=2xyx2+y222fyxx,y =xxx2+y2= 2xyx2+y22ainsi, il n’existe pas de solution C2 à ce système d’EDP.Exercice 2 :Pour toutes les fonctions suivantes, calculer l’expression de toutes les dérivéessecondes en précisant les domaines d’existance1. fx, y = x2y + xy2. fx, y = sinx + y + cosx y3. fx, y =x2 + y23/2121

Page 122 : 4. fx, y = cos25x + 2y5. fx, y = x2x + y6. fx, y = cosxyRéponses :1. Pour les dérivées 1ères :fxx,y = 2xy + yfyx,y = x2 +x2yelles sont déﬁnies sur R × R+.Pour les dérivées secondes :2fx2x,y = 2y2fyxx,y = 2x +12y2fxyx,y = 2x +12y2fy2x,y = x4y32elles sont déﬁnies sur R × R+.2. Pour les dérivées 1ères :fxx,y = cosx + y sinx yfyx,y = cosx + y + sinx yelles sont déﬁnies sur R × R.Pour les dérivées secondes :2fx2x,y = sinx + y cosx y2fyxx,y = sinx + y + cosx y2fxyx,y = sinx + y + cosx y2fy2x,y = sinx + y cosx y122

Page 123 : elles sont déﬁnies sur R × R.3. Pour les dérivées 1ères :fxx,y = 3xpx2 + y2fyx,y = 3ypx2 + y2elles sont déﬁnies sur R × R.Pour les dérivées secondes :2fx2x,y = 3px2 + y2 +3x22x2+y22fyxx,y =3xy2x2+y22fxyx,y =3xy2x2+y22fy2x,y = 3px2 + y2 +3y22x2+y2elles sont déﬁnies sur R2\0, 0.4. Pour les dérivées 1ères :fxx,y = 10 sin5x + 2y cos5x + 2fyx,y = 4 sin5x + 2y cos5x + 2yelles sont déﬁnies sur R × R.Pour les dérivées secondes :2fx2x,y = 50 cos25x + 2y + 50 sin25x + 2y2fyxx,y = 20 cos5x + 2y + 20 sin5x + 2y2fxyx,y = 20 cos5x + 2y + 20 sin5x + 2y2fy2x,y = 8 cos25x + 2y + 8 sin25x + 2yelles sont déﬁnies sur R2.123

Page 124 : 5. Pour les dérivées 1ères :fxx,y = 2xx + y + x2fyx,y = x2elles sont déﬁnies sur R × R.Pour les dérivées secondes :2fx2x,y = 6x + 2y2fyxx,y = 2x2fxyx,y = 2x2fy2x,y = 0elles sont déﬁnies sur R2.6. Pour les dérivées 1ères :fxx,y = y sinxyfyx,y = x sinxyelles sont déﬁnies sur R × R.Pour les dérivées secondes :2fx2x,y = y2 cosxy2fyxx,y = sinxy xy cosxy2fxyx,y = sinxy xy cosxy2fy2x,y = x2 cosxyelles sont déﬁnies sur R2.124

Page 125 : Exercice 3 :Pour chaque fonction déterminer la dérivée partielle indiquée1.3fx3 : fx, y = x2y4 + 2x4y2.3fx2y : fx, y = exy23.3fzyx : fx, y, z = x5 + 4x4y4z3 + yz24.3fyzy : fx, y, z = exyz5.3fxyz : ux, y, z = lnx + 2y2 + 3z2Réponses :1.fxx,y= 2xy4+8x3y ;2fx2x,y= 2y4+24x2y ;3fx3x,y= 48xy2.fyx,y=2yxexy2;2fxyx,y= 2yexy2 + 2y3xexy23fx2yx,y= 4y3exy2 + 2y5xexy23.fxx,y=5x4 + 16x3y4z3;2fyxx,y= 64x3y3z33fzyxx,y= 192x3y3z24.fyx,y=xzexyz;2fzyx,y= x + x2yzexyz3fyzyx,y= x2z2 + xyzexyz125

Page 126 : 5.uzx,y=6zx + 2y2 + 3z2;2uyzx,y= 24yzx + 2y2 + 3z223uxyzx,y=48yzx + 2y2 + 3z23Exercice 4 :Vériﬁer le théorème de Schwarz sur les fonctions suivantes1. fx, y = x5y4 3x2y3 + 2x22. fx, y = sin2x cosyRéponses :1.fxx,y = 5x4y4 6xy3 + 4xfyx,y = 4x5y3 9x2y22fyxx,y = 20x4y3 18xy22fxyx,y = 20x4y3 18xy2On a donc bien2fyxx,y =2fxyx,y.2.fxx,y = 2 sinx cosx cosyfyx,y = sin2x siny2fyxx,y = 2 sinx cosx siny2fxyx,y = 2 sinx cosx sinyOn a donc bien2fyxx,y =2fxyx,y.126

Page 127 : Exercice 5 :Soit f une application de classe C2 sur un ouvert U R2 à valeurs réelles.On déﬁnit le laplacien de f comme étant l’application déﬁnie sur U parfx, y = 2fx2 + 2fy227Déterminer le laplacien de chacune des fonctions suivantes1. U = R2 : fx, y = x2 y22. U = R2 : fx, y = x2 + y23. U = R2\0, 0 : fx, y = lnpx2 + y24. U = R2\0, 0 : fx, y =xx2+y2Réponses :1.fxx,y= 2x2fx2x,y= 2fyx,y= 2y2fy2x,y= 2ainsi f = 02.fxx,y= 2x2fx2x,y= 2fyx,y= 2y2fy2x,y= 2ainsi f = 43.fxx,y=xx2 + y22fx2x,y=y2 x2x2 + y22fyx,y=yx2 + y22fy2x,y=x2 y2x2 + y22127

Page 128 : ainsi f = 04.fxx,y=y2 x2x2 + y222fx2x,y= 2x3 6xy2x2 + y23fyx,y= 2xyx2 + y222fy2x,y= 2x3 + 6xy2x2 + y23ainsi f = 0Exercice 6 :Soit f la fonction déﬁnie sur R2 parfx, y =xy3x2+y2 ,si x, y ̸= 0, 0.0,sinon.281. Montrer que f est C1 sur R22. Montrer que2fxy et2fyx sont déﬁnies en 0, 0 mais n’ont pas mêmevaleur.3. Que peut-on en déduire ?Réponses :1. Pour montrer que f est C1 sur R2, il faut et il suﬃt que les dérivéespremières soient continues sur R2.Sur x, y ̸= 0, 0 :Les dérivées premières sont données parfxx,y̸=0,0= y3x2 + y2 2x2y3x2 + y22= y5 x2y3x2 + y22fyx,y̸=0,0= 3y2xx2 + y2 2xy4x2 + y22= 3x3y2 + xy4x2 + y22Les dérivées sont clairement continues x, y ̸= 0, 0.128

Page 129 : Sur x, y = 0, 0 :On calcule ici les dérivées premières en 0, 0 en utilisant la déﬁnitionfxx,y̸=0,0= limt→0ft, 0 f0, 0t= 0fyx,y̸=0,0= limt→0f0, t f0, 0t= 0RésuméAinsi, les applications dérivées premières sont données parfx:R2→R2x, y7→fx = y5x2y3x2+y22si x, y ̸= 0, 00si x, y = 0, 0fy:R2→R2x, y7→fx =3x3y2+xy4x2+y22si x, y ̸= 0, 00si x, y = 0, 0Continuité :Il faut maintenant vériﬁer que ces deux applications sont bien conti-nues en 0, 0 car elles le sont clairement en dehors.Commençons par fx. Pour cela, passons en coordonnées polaires enposant x = ρ cosθ et y = ρ sinθ :˜fx = ρ sin3θsin2θ cos2θ→ρ→0 0ainsi, on a bienlimx,y→0,0fx = 0 = fx0,0donc fx est continue sur R2. De la même façon, fy est continue surR2. Finalement, f est C1 sur R2.2. Etudions maintenant les dérivées secondes croisées en 0, 0. Alorsxfy0,0= limt→01t"fyt,0fy0,0= 0yfx0,0= limt→01t"fx0,tfx0,0= limt→01t × t5t4 = 1129

Page 130 : 3. Donc, les dérivées secondes croisées ne sont pas égales en 0, 0, ce quiimplique que soit2fxy, soit2fyx, soit les deux, ne sont pas continuesen 0, 0 et donc f n’est pas C1 sur R2.Exercice 7 :1. Soit f la fonction déﬁnie sur R2 parfx, y =y4x2+y2 ,si x, y ̸= 0, 0.0,sinon.29a Montrer que f est C1 en 0, 0b Montrer que2fxy et2fyx sont déﬁnies en 0, 0 et ont même va-leur.c Que peut-on en déduire ?2. Mêmes questions pourfx, y = xy2x+y,si x + y ̸= 0.0,sinon.30Réponses :1. a Montrons que f est C1 sur R2. Pour cela, nous allons montrer queles dérivées premières sont continues sur R2.Etude des dérivées sur R2\0, 0 :fxx,y̸=0,0= 2xy4x2 + y22fyx,y̸=0,0= 4y3x2 + 2y5x2 + y22Clairement, ses dérivées premières sont continues pour x, y ̸=0, 0.130

Page 131 : Etude des dérivées en 0, 0 :fxx,y̸=0,0= limt→0ft, 0 f0, 0t= 0fyx,y̸=0,0= limt→0f0, t f0, 0t= limt→0 t3 = 0RésuméAinsi, les applications dérivées premières sont données parfx:R2→R2x, y7→fx =2xy4x2+y22si x, y ̸= 0, 00si x, y = 0, 0fy:R2→R2x, y7→fx =4y3x2+2y5x2+y22si x, y ̸= 0, 00si x, y = 0, 0Continuité :Il faut maintenant vériﬁer que ces deux applications sont biencontinues en 0, 0 car elles le sont clairement en dehors. Pourcela, passons en coordonnées polaires en posant x = ρ cosθ ety = ρ sinθ :˜fx = 2ρ cosθ sin4θ →ρ→0 0ainsi, on a bienlimx,y→0,0fx = 0 = fx0,0donc fx est continue sur R2. De la même façon, fy est continuesur R2. Finalement, f est C1 sur R2.131

Page 132 : b Montrons maintenant que les dérivées secondes croisées ont bienmême valeur en 0, 0.xfy0,0= limt→01t"fyt,0fy0,0= 0yfx0,0= limt→01t"fx0,tfx0,0= 0Les dérivées croisées ont donc bien même valeur en 0, 0. Tou-tefois, cela ne permet pas de conclure qu’elles sont continues en0, 0.c On ne peut pas conclure que les dérivées secondes croisées sontcontinues. Pour voir cela, calculons tout d’abord la dérivées se-conde croisée pour x, y ̸= 0, 0.fxyx,y̸=0,0=fyxx,y̸=0,0= 8x3y3x2 + y23ainsify:R2→R2x, y7→fxy =8x3y3x2+y23si x, y ̸= 0, 00si x, y = 0, 0orfxyx,x= 8x62x23 = 1 ̸= 0ainsi la dérivée seconde croisée n’est pas continue en 0, 0 et doncf n’est pas C2 sur R2.2. laissée en exercice.Exercice 8 :Déterminer la classe exacte des applications suivantes1.fx, y =x2y22x2+y2 ,si x, y ̸= 0, 0.0,sinon.31132

Page 133 : 2.fx, y =xy2x2+yx22 ,si x, y ̸= 0, 0.0,sinon.323.fx, y =ex21ey21x2+y2,si x, y ̸= 0, 0.0,sinon.33Réponses :1. Etudions la 1ère fonction. Soit U1 = R\0, 0. La fonction f estde classe Csur U1 car fraction rationnelle dont le dénominateur nes’annule pas. Mais évidemment, il va falloir étudier les choses en 0, 0.Continuité en 0, 0 :Etudions fx, y f0, 0 = fx, y. Si cette quantité tend vers 0alorslimx,y→0,0 fx, y = 0 = f0, 0et la fonction sera continue. Alorsfx, y =x4 + y4 2x2y2x2 + y2 x2x2 + y2 x2 + 2x2y2x2 + y2 +y2x2 + y2 y2x2 + 2y2 + y2→x,y→0,0 0donc f est continue en 0, 0 et donc sur R2.Etude des dérivées premières :Régardons si f est C1.Commencons par calculer les dérivées partielles sur U1fxx,yU1= 4xx2 y2x2 + y22xx2 y22x2 + y22= 2xx2 y2x2 + 3y2x2 + y22fyx,yU1= 2y5 + 4x2y3 6x4yx2 + y22= 2yx2 y23x2 + y2x2 + y22Les dérivées partielles premières sont clairement continues sur U1.Mais il faut aussi étudier les dérivées partielles premières en 0, 0.133

Page 134 : Dérivées partielles en 0, 0 :fx0,0= limt→0ft, 0 f0, 0t= limt→01t × t4t2 = 0fy0,0= limt→0f0, t f0, 0t= limt→0 t = 0On déduit donc quefx0,0= 0fy0,0= 0Il faut donc maintenant étudier la continuité des fonctions dérivéespartielles premières sur R2fy:R2→R2x, y7→fx =2xx2y2x2+3y2x2+y22si x, y ̸= 0, 00si x, y = 0, 0etfy:R2→R2x, y7→fy =2yx2y23x2+y2x2+y22si x, y ̸= 0, 00si x, y = 0, 0dans les deux cas, on peut passer en coordonnées polaires en posantx = ρ cosθ et y = ρ sinθ pour étudier la continuité des dérivéespartielles premières en 0, 0 :˜fxx,y= 2ρ cosθcos2θ sin2θ cos2θ + 3 sin2θ→x,y→0,0 0˜fyx,y= 2ρ sinθcos2θ sin2θ 3 cos2θ + sin2θ→x,y→0,0 0Finalementlimx,y→0,0fxx,y= 0 = fx0,0limx,y→0,0fyx,y= 0 = fy0,0134

Page 135 : Donc les dérivées partielles premières sont continues en 0, 0 et doncsur R2.Etudions maintenant les dérivées secondes :Pour cela, calculons les dérivées partielles croisées. Pour x, y U1,on a2fxyx,yU1=fyxx,yU1= 8xyx2 y22x2 + y238xyx2 + y2Faisons maintenant l’étude en 0, 02fxy0,0= limt→01t"fyt,0fy0,0= 02fyx0,0= limt→01t"fx0,tfx0,0= 0Ainsi, la fonction dérivée partielle seconde croisée est donnée par2fyx:R2→R2x, y7→2fyxx,y =8xyx2y22x2+y238xyx2+y2si x, y ̸= 0, 00si x, y = 0, 0Or2fyxx,x= 4→x,x→0,0 0 ̸=2fyx0,0Donc la fonction dérivée partielle seconde croisée n’est pas continuesur R2 et ﬁnalement f n’est pas C2.2. Etudions la 2ème fonction. Soit U1 = R\0, 0. La fonction f estde classe Csur U1 car fraction rationnelle dont le dénominateur nes’annule pas. Mais évidemment, il va falloir étudier les choses en 0, 0.Continuité en 0, 0 :Pour cela, commençons par modiﬁer l’expression de ffx, y =xy2x2 + y x22 =xy2x2 + y2 + x4 2yx2135

Page 136 : Passons maintenant en coordonnées polaires en posant x = ρ cosθet y = ρ sinθ˜fx, y =ρ3 cosθ sin2θρ2 + ρ cosθ4 2ρ3 sinθ cos2θ=ρ cosθ sinθ1 + ρ ρ cos4θ 2 cos2θ sinθor clairement, puisque θ, ρρ cos4θ 2 cos2θ sinθ→ρ→0 0, doncθ, ˜fx, y →ρ→0 0et ﬁnalementlimx,y→0,0 fx, y = 0 = f0, 0et donc f est continue en 0, 0 et donc sur R2.Etude des dérivées premières :Régardons si f est C1.Commencons par calculer les dérivées partielles sur U1fxx,yU1=y2x2 + y x22 xy2 2x 4xy x2x2 + y x222fyx,yU1=2xyx2 + y x22 2xy2 y x2x2 + y x222Les dérivées partielles premières sont clairement continues sur U1.Mais il faut aussi étudier les dérivées partielles premières en 0, 0.Dérivées partielles en 0, 0 :fx0,0= limt→0ft, 0 f0, 0t= limt→01t × t4t2 = 0fy0,0= limt→0f0, t f0, 0t= limt→0 t = 0On déduit donc quefx0,0= 0fy0,0= 0136

Page 137 : Il faut donc maintenant étudier la continuité des fonctions dérivéespartielles premières sur R2fy:R2→R2x, y7→fx =y2x2+yx22 xy22x4xyx2x2+yx222si x, y ̸= 0, 00si x, y = 0, 0etfy:R2→R2x, y7→fy =2xyx2+yx22 2xy2yx2x2+yx222si x, y ̸= 0, 00si x, y = 0, 0Or, on afx0,y= 1 →y→0 1 ̸= 0 = fx0,0Donc la dérivée partielle première par rapport à x n’est pas continueen 0, 0 et donc f n’est pas C1 sur R2.3. Etudions la dernière fonction. Soit U1 = R\0, 0. La fonction f estde classe Csur U1 car fraction rationnelle dont le dénominateur nes’annule pas. Mais évidemment, il va falloir étudier les choses en 0, 0.Continuité en 0, 0 :Alorsfx, y = ex2 1ey2 1x2 + y2= ex2 1x2x2y2x2 + y2ey2 1y2→x,y→0,0 0donc f est continue en 0, 0 et donc sur R2.Etude des dérivées premières :Régardons si f est C1.Commencons par calculer les dérivées partielles sur U1fxx,yU1=2xex2 ey2 1x2 + y22xex2 1 ey2 1x2 + y22fyx,yU1=2yey2 ex2 1x2 + y22yex2 1 ey2 1x2 + y22137

Page 138 : Les dérivées partielles premières sont clairement continues sur U1.Mais il faut aussi étudier les dérivées partielles premières en 0, 0.Dérivées partielles en 0, 0 :fx0,0= limt→0ft, 0 f0, 0t= 0fy0,0= limt→0f0, t f0, 0t= 0On déduit donc quefx0,0= 0fy0,0= 0Il faut donc maintenant étudier la continuité des fonctions dérivéespartielles premières sur R2fx:R2→R2x, y7→fx =2xex2ey21x2+y22xex21ey21x2+y22si x, y ̸= 0, 00si x, y = 0, 0etfy:R2→R2x, y7→fy =2yey2ex21x2+y22yex21ey21x2+y22si x, y ̸= 0, 00si x, y = 0, 0Etudions la continuité de la dérivée partielle première par rapport àx en 0, 0 :fxx,yfx0,0 2xex2 ey2 1x2 + y2+ 2xex2 1 ×ey2 1x2 + y222 xy2x2 + y2 ex2ey2 1y2+ 2x3y2x2 + y22ex2 1x2ey2 1y2→x,y→0,0 0138

Page 139 : Il en va de même pour la dérivée première par rapport à y.Finalementlimx,y→0,0fxx,y= 0 = fx0,0limx,y→0,0fyx,y= 0 = fy0,0Donc les dérivées partielles premières sont continues en 0, 0 et doncsur R2.Etudions maintenant les dérivées secondes :Pour cela, calculons les dérivées partielles croisées. Pour x, y U1,on a2fxyx,yU1=4xyx2 + y2 ex2+y2 ex2 1ey2x2 + y2ey2 1ex2x2 + y2+ 2ex2 1ey2 1x2 + y22!=fyxx,yU1Or, on a2fxyx,x= 2e2x2 ex2 ex2 1x2+ 12 ex2 1x2!2→x→0 12fxy0,y= 0 →y→0 0Donc la fonction dérivée partielle seconde croisée n’est pas continuesur R2 et ﬁnalement f n’est pas C2 sur R2.Exercice 9 :Résoudre les EDP du second d’ordre d’inconnue f : U →R de classe C2 àl’aide du changement de variables fourni1. U = R2 : 2fx2 2fy2 = 0 ; u, v = x + y, x y2. U = R+ × R : x2 2fx2 + 2xy 2fxy + y2 2fy2 = 0 ; u, v = x, y/x3. U = R+ × R+ : x2 2fx2 y2 2fy2 xfx + y fy = 0 ; u, v = xy, y/x139

Page 140 : 4. U = R+ ×R+ : x2 2fx2 y2 2fy2 +xfx y fy = 0 ; u, v = lnx, lny5. U = R+ × R : 2fx2 4x2 2fy2 1xfx = 0 ; u, v = x2 y, x2 + y6. U = R2 : 2fx2 2 2fxy + 2fy2 = 0 ; u, v = x, x + y7. U = R+ × R+ : x2 2fx2 y2 2fy2 = 0 ; u, v = xy, x/yRéponses :1. Résolution de l’EDPU = R2 : 2fx2 2fy2 = 0 ; u, v = x + y, x yEtape 1 : le changement de variable ϕ identiﬁcation de ϕ et vériﬁca-tion que ϕ est bien C2ϕ:U = R × R→Ux, y7→u, v = ϕx, y = x + y, x yRegardons maintenant que ϕ est bien un C2 diﬀéomorphisme de Udans U :a ϕ est clairement C2 de U dans U car les deux fonctions compo-santes sont C2 de U dans U.b Montrons que ϕ est bien une bijection de U dans U :u = x + yv = x y⇐⇒x = u yv = u 2y⇐⇒x = 12u + vy = 12u vDonc ϕ est l’application bijective de U dans U déﬁnie par ϕ1u, v =12u + v, 12u v.c ϕ1 est bien C2 de U dans U.Finalement ϕ est bien un C2-diﬀéomorphisme de U dans U.Etape 2 : introduction de la fonction gOn introduit donc la fonction g déﬁnie parf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gx+y, xy= gu, v140

Page 141 : Et, on a donc g = f ◦ϕ1. Or, compte-tenu du fait que f est ϕ1 sontC2 de U dans U, on voit que g est C2 de U dans U par composition.Etape 3 : Dérivées de fPuisque g est C2 de U dans U, on peut exprimer les dérivées partiellesde f en fonction des dérivées partielles de g. On a alorsfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donne, étant données les expressions de u et vfxx,y = guu,v + gvu,vfyx,y = guu,v gvu,vNous pouvons maintenant calculer les dérivées secondes :2fx2 = xfx= xgu + gv= u + v gu + gv2fx2 = 2gu2 + 2gv2 + 2 2guvet ﬁnalement :2fy2 = yfy= ygu gv= u v gu + gv2fy2 = 2gu2 + 2gv2 2 2guvEtape 4 : expression de l’EDP en fonction de g.Nous pouvons maintenant injecter les expressions des dérivées se-condes de f dans l’EDP aﬁn d’obtenir une EDP sur g qui sera,normalement, beaucoup plus simple2gu2 + 2gv2 + 2 2guv 2gu2 2gv2 + 2 2guv = 0141

Page 142 : avec les nombreuses simpliﬁcations de l’expression précédente, nousobtenons2guv = 0Cette EDP a pour solutionu, v U, gu, v = hv + kvavec h et k deux applications C2 de R dans R.Etape 5 : retour à la fonction f.On rappelle que f = g ◦ϕ. Donc la solution de l’EDP initiale estx, y U, fx, y = g x + y, x y = h x y + k x + yavec h et k deux applications C2 de R dans R.2. Résolution de l’EDPU = R+ × R : x2 2fx2 + 2xy 2fxy + y2 2fy2 = 0 ; u, v = x, y/xEtape 1 : le changement de variable ϕ identiﬁcation de ϕ et vériﬁca-tion que ϕ est bien C2ϕ:U = R+ × R→Ux, y7→u, v = ϕx, y =x, yxRegardons maintenant que ϕ est bien un C2 diﬀéomorphisme de Udans U :a ϕ est clairement C2 de U dans U car les deux fonctions compo-santes sont C2 de U dans U.b Montrons que ϕ est bien une bijection de U dans U :u = xv = yx⇐⇒x = uy = vx⇐⇒x = uy = uvDonc ϕ est l’application bijective de U dans U déﬁnie par ϕ1u, v =u, uv.142

Page 143 : c ϕ1 est bien C2 de U dans U.Finalement ϕ est bien un C2-diﬀéomorphisme de U dans U.Etape 2 : introduction de la fonction gOn introduit donc la fonction g déﬁnie parf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gx, yx= gu, vEt, on a donc g = f ◦ϕ1. Or, compte-tenu du fait que f est ϕ1 sontC2 de U dans U, on voit que g est C2 de U dans U par composition.Etape 3 : Dérivées de fPuisque g est C2 de U dans U, on peut exprimer les dérivées partiellesde f en fonction des dérivées partielles de g. On a alorsfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donne, étant données les expressions de u et vfxx,y = guu,v yx2gvu,vfyx,y = 1xgvu,vNous pouvons maintenant calculer les dérivées secondes :2fx2 = xfx= xgu yx2gv= xgux yx2 gv yx2xgv2fx2 = u yx2v gu+ 2yx3gv yx2 u yx2v gv2fx2 = 2gu2 yx22guv + 2 yx3gv yx22guv + y2x42gv22fx2 = 2gu2 2 yx22guv + 2 yx3gv + y2x42gv2143

Page 144 : Calculons maintenant la dérivée seconde croisée :2fxy = yfx= ygu yx2gv= yguy yx2 gv yx2ygv2fxy = 1xvgu1x2gv yx2 × 1xvgv2fxy = 1x2guv 1x2gv yx32gv2et ﬁnalement :2fy2 = yfy= y1x gv + 1xygv = 1x × 1xvgv= 1x22gv2Etape 4 : expression de l’EDP en fonction de g.Nous pouvons maintenant injecter les expressions des dérivées se-condes de f dans l’EDP aﬁn d’obtenir une EDP sur g qui sera,normalement, beaucoup plus simplex2 2gu2 2y 2guv+2yxgv+y2x22gv2 +2y 2guv2yxgv2y2x22gv2 +y2x22gv2 = 0avec les nombreuses simpliﬁcations de l’expression précédente, nousobtenonsx2 2gu2 = 0or x = u donc u2 2gu2 = 0, et comme u R+, cette équation estéquivalente à2gu2 = 034Cette EDP a pour solutionu, v U, gu, v = uhv + kvavec h et k deux applications C2 de R dans R.Etape 5 : retour à la fonction f.On rappelle que f = g ◦ϕ. Donc la solution de l’EDP initiale estx, y U, fx, y = gx, yx= xhyx+ kyxavec h et k deux applications C2 de R dans R.144

Page 145 : 3. Résolution de l’EDPU = R+×R+ : x2 2fx2 y2 2fy2 xfx +yfy = 0 ; u, v = xy, y/xEtape 1 : le changement de variable ϕ identiﬁcation de ϕ et vériﬁca-tion que ϕ est bien C2ϕ:U = R+ × R+→Ux, y7→u, v = ϕx, y =xy, yxRegardons maintenant que ϕ est bien un C2 diﬀéomorphisme de Udans U :a ϕ est clairement C2 de U dans U car les deux fonctions compo-santes sont C2 de U dans U.b Montrons que ϕ est bien une bijection de U dans U :u = xyv = yx⇐⇒u = xyy = vx⇐⇒u = x2vy = vx⇐⇒x2 = uvy = vxor on sait que x R+ doncx2 = uvy = vx⇐⇒x = p uvy = uvDonc ϕ est l’application bijective de U dans U déﬁnie par ϕ1u, v =puv , uv.c ϕ1 est bien C2 de U dans U.Finalement ϕ est bien un C2-diﬀéomorphisme de U dans U.Etape 2 : introduction de la fonction gOn introduit donc la fonction g déﬁnie parf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gxy, yx= gu, vEt, on a donc g = f ◦ϕ1. Or, compte-tenu du fait que f est ϕ1 sontC2 de U dans U, on voit que g est C2 de U dans U par composition.145

Page 146 : Etape 3 : Dérivées de fPuisque g est C2 de U dans U, on peut exprimer les dérivées partiellesde f en fonction des dérivées partielles de g. On a alorsfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donne, étant données les expressions de u et vfxx,y = y guu,v yx2gvu,vfyx,y = x guu,v + 1xgvu,vNous pouvons maintenant calculer les dérivées secondes qui inter-viennent dans l’EDP :2fx2 = xfx= xy gu yx2gv= y xgux yx2 gv yx2xgv2fx2 = yy u yx2v gu+ 2yx3gv yx2y u yx2v gv2fx2 = y2 2gu2 y2x22guv + 2 yx3gv y2x22guv + y2x42gv22fx2 = y2 2gu2 2y2x22guv + 2 yx3gv + y2x42gv2et ﬁnalement, calculons la dernière dérivée manquante :2fy2 = yfy= yxgu + 1xgv= x ygu + 1xygv2fy2 = xx u + 1xv gu + 1xx u + 1xv gv2fy2 = x2 2gu2 + 2 2guv + 1x22gv2Etape 4 : expression de l’EDP en fonction de g.146

Page 147 : Nous pouvons maintenant injecter les expressions des dérivées se-condes et premières de f dans l’EDP aﬁn d’obtenir une EDP surg qui sera, normalement, beaucoup plus simple4y2 2guv + 4yxgv = 0 ⇐⇒uv 2guv = vgvor v R+ doncu 2guv = gvIntroduisons maintenant la fonction h = gv. On a alors l’équationsuivantehu, v u huu,v= 0que l’on va résoudre comme une équation diﬀérentielle ordinaire puisquecette équation ne fait intervenir que la variable u. Pour cela, nous al-lons écrire de manière très impropre l’équation précédente de la façonsuivantehu udhdu = 0 ⇐⇒duu = dhh ⇐⇒lnh = lnu + coù c R pour l’instant. A noter que la première équivalence se justiﬁecar u ̸= 0 et par le théorème de Cauchy-Lipschitz h ̸= 0. En prenantensuite l’exponentielle de cette expression, on obtient ﬁnalementhu = cuToutefois la fonction dépend normalement aussi de v. On peut ra-jouter cette dépendance, en introduisant cv au lieu de R où c estune application C2 sur R+. Alors la solution de l’EDP sur h est de laformehu, v = cvuOr h = gv, doncgu, v = Cvu + Duoù C est la primitive de c et D est C2 de R+ dans R+.Etape 5 : retour à la fonction f.On rappelle que f = g ◦ϕ. Donc la solution de l’EDP initiale estx, y U, fx, y = gxy, yx= xy × Cyx+ Dxy147

Page 148 : 4. Résolution de l’EDPU = R+×R+ : x2 2fx2 y2 2fy2 +xfxyfy = 0 ; u, v = lnx, lnyEtape 1 : le changement de variable ϕ identiﬁcation de ϕ et vériﬁca-tion que ϕ est bien C2ϕ:U = R+ × R+→R2x, y7→u, v = ϕx, y = lnx, lnyRegardons maintenant que ϕ est bien un C2-diﬀéomorphisme de Udans R2 :a ϕ est clairement C2 de U dans R2 car les deux fonctions compo-santes sont C2 de U dans R2.b Montrons que ϕ est bien une bijection de U dans R2 :u = lnxv = lny⇐⇒x = euy = evDonc ϕ est l’application bijective de U dans U déﬁnie par ϕ1u, v =eu, ev.c ϕ1 est bien C2 de R2 dans U.Finalement ϕ est bien un C2-diﬀéomorphisme de U dans R2.Etape 2 : introduction de la fonction gOn introduit donc la fonction g déﬁnie parf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= glnx, lny= gu, vEt, on a donc g = f ◦ϕ1. Or, compte-tenu du fait que f et ϕ1 sontC2 de U dans R2, on voit que g est C2 de R2 dans U par composition.Etape 3 : Dérivées de fPuisque g est C2 de R2 dans U, on peut exprimer les dérivées partielles148

Page 149 : de f en fonction des dérivées partielles de g. On a alorsfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donne, étant données les expressions de u et vfxx,y = 1xguu,vfyx,y = 1ygvu,vNous pouvons maintenant calculer les dérivées secondes qui inter-viennent dans l’EDP :2fx2 = xfx= x1xgu= 1x2gu + 1x22gu2et ﬁnalement, calculons la dernière dérivée manquante :2fy2 = yfy= y1ygv= 1y2gv + 1y22gv2Etape 4 : expression de l’EDP en fonction de g.Nous pouvons maintenant injecter les expressions des dérivées se-condes et premières de f dans l’EDP aﬁn d’obtenir une EDP surg qui sera, normalement, beaucoup plus simple2gu2 = 2gv2Nous allons introduire un nouveau changement de variable :ψ:R2→R2u, v7→s, t = ψu, v = u + v, u vOn introduit alors la fonction h déﬁnie comme g = h ◦ψ. Alorsguu,v = hss,tsuu,v + hts,ttuu,vgvu,v = hss,tsvu,v + hts,ttvu,v149

Page 150 : ce qui donne, étant données les expressions de u et vguu,v = hsu,v + htu,vgvu,v = hsu,v htu,vJe vous laisse montrer que les dérivées secondes qui interviennent dansl’EDP sont données par2gu2u,v = 2hs2u,v + 2ht2u,v + 2 2hstu,v2gv2u,v = 2hs2u,v + 2ht2u,v 2 2hstu,vAlors l’EDP sur g implique sur h :2hst = 0qui a pour solutionhs, t = Kt + LsOn a doncgu, v = Ku v + Lu + vEt ﬁnalementfx, y = K lnx lny+L lnx + lny = Klnxy+L lnxy5. Résolution de l’EDPU = R+ × R : 2fx2 4x2 2fy2 1xfx = 0 ; u, v = x2 y, x2 + yEtape 1 : le changement de variable ϕ identiﬁcation de ϕ et vériﬁca-tion que ϕ est bien C2ϕ:U = R+ × R→R2x, y7→u, v = ϕx, y =x2 y, x2 + yRegardons maintenant que ϕ est bien un C2 diﬀéomorphisme de Udans R2 :150

Page 151 : a ϕ est clairement C2 de U dans R2 car les deux fonctions compo-santes sont C2 de U dans R2.b Montrons que ϕ est bien une bijection de U dans U :u = x2 yv = x2 + y⇐⇒u + v = 2x2 0v = x2 + y⇐⇒x2 = u+v2v = x2 + y⇐⇒x =qu+v2car x R+y = v x2 = vu2Donc ϕ est l’application bijective de U dans R2 déﬁnie par ϕ1u, v =pu + v/2, v u/2.c ϕ1 est bien C2 de R2 dans U. En eﬀet : u + v = 2x2 0 puisquex R+ pour le vériﬁer vous pouvez aussi calculer explicitementles dérivées partielles premières et secondes.Finalement ϕ est bien un C2-diﬀéomorphisme de U dans R2.Etape 2 : introduction de la fonction gOn introduit donc la fonction g déﬁnie parf = g◦ϕ ⇐⇒fx, y = g◦ϕx, y = gϕx, y= gx2y, x2+y= gu, vEt, on a donc g = f ◦ϕ1. Or, compte-tenu du fait que f est ϕ1 sontC2 de U dans U, on voit que g est C2 de U dans U par composition.Etape 3 : Dérivées de fPuisque g est C2 de U dans U, on peut exprimer les dérivées partiellesde f en fonction des dérivées partielles de g. On a alorsfxx,y = guu,vuxx,y + gvu,vvxx,yfyx,y = guu,vuyx,y + gvu,vvyx,yce qui donne, étant données les expressions de u et vfxx,y = 2x guu,v + 2x gvu,vfyx,y = gvu,v + gvu,v151

Page 152 : Nous pouvons maintenant calculer les dérivées secondes :2fx2 = xfx= x2xgu + 2xgv= 2gu + 2x xgu+ 2gv + 2x xgv2fx2 = 2gu + 2gv + 2x2x u + 2x v gu+ 2x2x u + 2x v gv2fx2 = 2gu + 2gv + 4x2 2gu2 + 4x2 2guv + 4x2 2guv + 4x2 2gv22fx2 = 2gu + 2gv + 4x2 2gu2 + 8x2 2guv + 4x2 2gv2et ﬁnalement :2fy2 = yfy=v + gv gv + gv= 2gu2 2 2guv + 2gv2Etape 4 : expression de l’EDP en fonction de g.Nous pouvons maintenant injecter les expressions des dérivées se-condes de f dans l’EDP aﬁn d’obtenir une EDP sur g qui sera,normalement, beaucoup plus simple16x2 2guv = 0 ⇐⇒16u + v22guv = 0or comme u + v 0, on a ﬁnalement2guv = 0Cette EDP a pour solutionu, v R2, gu, v = Lv + Kuavec L et K deux applications C2 de R dans R.Etape 5 : retour à la fonction f.On rappelle que f = g ◦ϕ. Donc la solution de l’EDP initiale estx, y U, fx, y = gx2 + y, x2 y= Lx2 + y + Kx2 yavec L et K deux applications C2 de R dans R.152

Page 153 : 6.7.Exercice 10 :Déterminer les points critiques et les extrema des fonctions f : R2 →Rsuivantes153

Page 154 : 1. fx, y = x2 + xy + y2 3x 6y2. fx, y = x2 + 2y2 2xy 2y + 53. fx, y = x3 + y34. fx, y = x y2 + x + y35. fx, y = x3 + y3 3xy6. fx, y = xln2x + y2sur le demi-plan 0Exercice 11 :Déterminer les extrema locaux et globaux des applications suivantes.Exercice 12 :154

PREING2 S1, Analyse-dans-RN

Le contenu de cet article est la propriété exclusive de son auteur.

Tags tendance