TD0 Rappels Correction
Télécharger le TD0 Rappels Correction en pdf
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85
Page 1 : Analyse 1 - Premier semestre 2023 - 2024CY TechTD AnalyseInegalites, Sigma et Fonctions Trigonometriques.Analyse
Page 2 : Exercice 1Montrer les inegalites suivantes.1. x 0, +, x + 1x 2.Solution : On commence par noter quex 0, +, x 12 0=⇒x 0, +, x2 2x + 1 0=⇒x 0, +, x2 + 1 2x=⇒z× 1xx 0, +,x + 1x 2.2. x R, y R, xy 12x2 + y 2.Solution : Comme pour la question precedente, on commence parremarquer quex R, y R, 0 x y2=⇒x R, y R, 0 x2 2xy + y 2=⇒x R, y R, 2xy x2 + y 2=⇒x R, y R, xy 12x2 + y 2.Analyse
Page 3 : Exercice 13. x R, y R, z R, x2 + y 2 + z2 xy + yz + zx.Solution : D’apres le point 2., pour tout x R, pour tout y R, pourtout z R, on axy12x2 + y 2xz12x2 + z2yz12y 2 + z2.En additionnant les trois inegalites, on obtientxy + yz + zx12x2 + y 2+ 12x2 + z2+ 12y 2 + z2x2 + y 2 + z2.Analyse
Page 4 : Exercice 14. Demontrer que :x R,0 x2 + 2x + 4x2 + 2x + 2 3.Solution : Commen¸cons par montrer que x2+2x+4x2+2x+2 0. Pour celaetudions le signe du numerateur et celui du denominateur. Pour ledenominateur, le discriminant est= b2 4ac = 4 4 · 1 · 2 = 4.Le denominateur n’a pas de racine et garde donc partout le signe de a,c-a-d pour tout x R, nous avonsx2 + 2x + 2 0.De mˆeme, le discriminant du numerateur est donne par= 4 4 · 1 · 4 = 12alors pour tout x R, nous avonsx2 + 2x + 4 0.Analyse
Page 5 : Exercice 1D’ou on obtient que le rapport est strictement positif :0 x2 + 2x + 4x2 + 2x + 2.Deuxieme methode : Notons quex2 + 2x + 4=x + 12 + 3 3 0x2 + 2x + 2=x + 12 + 1 1 0.Si on prend le quotient entre la premiere et la deuxieme inequation, onconclutx2 + 2x + 4x2 + 2x + 2 0.Analyse
Page 6 : Exercice 1Pour montrer la deuxieme inegalite, il suffit de noter que pour toutx R, nous avonsx2 + 2x + 4x2 + 2x + 2 3⇐⇒x2 + 2x + 4 3x2 + 2x + 2⇐⇒x2 + 2x + 4 3x2 + 6x + 6⇐⇒0 2x2 + 4x + 2⇐⇒0 2x2 + 2x + 1 = 2x + 12.La derniere proposition etant vraie, la premiere l’est egalement.Analyse
Page 7 : Exercice 1Deuxieme methode : Pour montrerx2 + 2x + 4x2 + 2x + 2 3On passe tout a gauche et on essaie de montrer que l’expression est negative :x2 + 2x + 4x2 + 2x + 2 3=x2 + 2x + 4x2 + 2x + 2 3x2 + 2x + 2x2 + 2x + 2=x2 + 2x + 4 3x2 + 2x + 2x2 + 2x + 2=x2 + 2x + 4 3x2 6x 6x2 + 2x + 2=2x2 4x 2x2 + 2x + 2 .Il ne nous reste qu’a determiner le signe du numerateur := 42 422 = 16 16 = 0Donc le numerateur garde le mˆeme signe, celui de a = 2 0. Par consequentle numerateur est negatif, et le rapport est negatif egalement.Analyse
Page 8 : Exercice 1Ainsix2 + 2x + 4x2 + 2x + 2 3 0=⇒x2 + 2x + 4x2 + 2x + 2 3.Analyse
Page 9 : A faire chez soi - Exercice 21. Demontrer que x R, y R, xy x+y22 .Solution : Mˆeme idee, on commence par noter quex R, y R, 0 x y2=⇒x R, y R, 0 x2 2xy + y 2=⇒x R, y R, 2xy x2 + y 2=⇒x R, y R, 4xy x2 + 2xy + y 2=⇒x R, y R, 4xy x + y2=⇒x R, y R, xy x + y24=⇒x R, y R, xy x + y22.Analyse
Page 10 : A faire chez soi - Exercice 22. Soit f : R →R, definie pour tout x R parx 7→x2 + 2x + 2x2 + 2x + 3.Sans etudier les variations de f , trouver le minimum de f sur R.Solution : Pour trouver le minimum de f on commence par noter quex2 + 2x + 3 = x + 12 + 2 2.D’ou12 1x2 + 2x + 3.Maintenantx2 + 2x + 2x2 + 2x + 3=x2 + 2x + 3 1x2 + 2x + 3=x2 + 2x + 3x2 + 2x + 3 1x2 + 2x + 3=1 1x2 + 2x + 31 12 = 12.Analyse
Page 11 : A faire chez soi - Exercice 2Ainsi, pour tout x R nous avonsf x 12.1Notons de plus quef 1 = 12.Le minimum de f est donc 12.Analyse
Page 12 : A faire chez soi - Exercice 3Soient x, y, z trois reels tels que :0 a x b,d y c 0,0 e z f .Determiner un encadrement de :4x 2ySolution : En multipliant par 4 l’inegalite 0 a x b, on obtient0 4a 4x 4b,et en multipliant par 2 l’inegalite d y c 0, on conclut0 2c 2y 2d.Finalement, en additionnant les deux inegalites, on deduit4a 2c 4x 2y 4b 2d.Analyse
Page 13 : A faire chez soi - Exercice 3Determiner un encadrement de :x yz.Solution : On a0 a x b,2et en multipliant par 1 l’inegalite d y c 0, on obtient0 c y d.3En additionant l’inegalite 2 avec l’inegalite 3, on deduit0 a c x y b d.4Maintenat,0 e z f .Donc0 1f 1z 1e .5Finalement, en multipliant l’inegalite 4 avec l’inegalite 5 on conclut0 a cfx yzb de.Analyse
Page 14 : A faire chez soi - Exercice 3Remarque :1 x 3et2 y 1n’implique pas que2 xy 3.Analyse
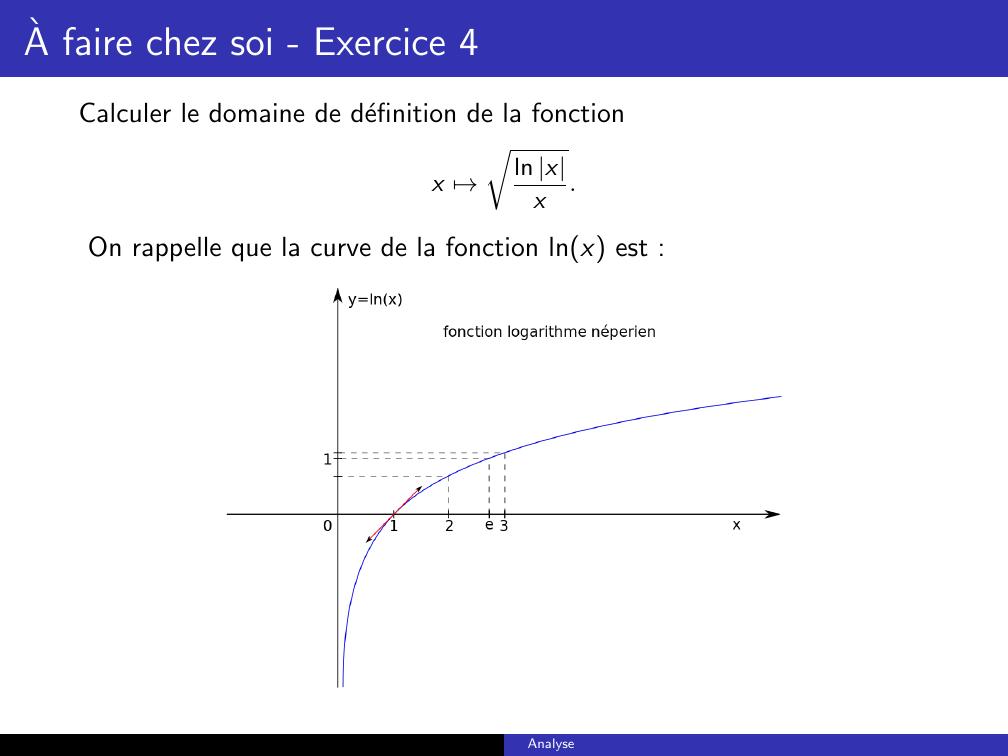
Page 15 : A faire chez soi - Exercice 4Calculer le domaine de definition de la fonctionx 7→rln xx.On rappelle que la curve de la fonction lnx est :Analyse
Page 16 : A faire chez soi - Exercice 4Solution : La fonctionx 7→ln x est bien definie si et seulement si x ̸= 0.x 7→1x est bien definie si et seulement si x ̸= 0.D’ou on conclut que la fonctionx 7→ln xxa par domaine de definition, l’ensemble R \ 0. En suite, commex 7→x,a par domaine de definition R+, on deduit querln xxest bien definie⇐⇒lnxx0.Analyse
Page 17 : A faire chez soi - Exercice 4On rappelle queln x 0si et seulement six 1.DoncPour tout x 1lnxx0.Pour tout 0 x 1lnxx0.Pour tout 1 x 0lnxx0.Pour tout x 1lnxx0.Analyse
Page 18 : A faire chez soi - Exercice 4Par consequent le domaine de definition deqln xxest1, 0 1, +.Analyse
Page 19 : Exercice 5Soient a et x des nombres reels. Supposons que a est non nul et que l’on ax a a.Montrer que x est non nul et que x est de mˆeme signe que a.Solution : En utilisant la definition de la valeur absolue, l’inequationx a a, peut ˆetre reecrit sous la formea x a a.6On a deux cas a etudier :Si a 0, alors l’inegalite 6 devienta x a a.D’ou0 x 2a=⇒x est non nul et positif mˆeme signe que a.Si a 0, alors l’inegalite 6 devienta x a a.D’ou2a x 0=⇒x est non nul et negatif mˆeme signe que a.Analyse
Page 20 : Exercice 6Resoudre dans R les inequations suivantes :x + 1 0.1Solution : En utilisant la definition de la valeur absolue, l’inequationx + 1 0.1, peut ˆetre reecrit sous la forme0.1 x + 1 0.1,ce qui est equivalent a1.1 = 0.1 1 x 0.1 1 = 0.9.Par consequentx + 1 0.1⇐⇒1.1 x 0.9.L’inequation a donc par ensemble solution, l’intervalle 1.1, 0.9.Analyse
Page 21 : Exercice 6x 2 10Solution : On a deux cas a etudier :• Si x 2 0, c’est-a-dire si x 2, alors l’inegalite x 2 10 devientx 2 10=⇒x 12.C’est-a-dire, dans l’intervalle 2, +, l’inequation a par ensemble solutionl’intervalle12, +.• Si x 2 0, c’est-a-dire si x 2, alors l’inegalite x 2 10 devientx 2 10⇐⇒x + 2 10⇐⇒x 8⇐⇒x 8.C’est-a-dire, dans l’intervalle , 2 l’inequation a par ensemblesolution, l’intervalle , 8.L’inequation a donc par ensemble solution, l’ensemble , 8 12, +.Analyse
Page 22 : Exercice 6x x + 1Solution : En utilisant la definition de la valeur absolue, l’inequationx x + 1 peut ˆetre reecrit sous la formex + 1 x x + 1.7On a donc deux cas a etudier• Si x 1, alors l’inegalite 7 devientx 1 x x + 1d’ou on obtient1 2x 2x + 1· 12=⇒12 x x + 12 =⇒12 x.C’est-a-dire, dans l’intervalle 1, +, l’inequation a par ensemblesolution l’intervalle 1/2, +.• Si x 1, alors x 1 0 et x + 1 0. Doncx x + 1=⇒x x 1=⇒0 1.Contradiction ! ! Par consequent, sur l’intervalle , 1 l’inequationn’a pas de solution.Analyse
Page 23 : Exercice 6L’inequation a donc par ensemble solution, l’intervalle12 , +.Autre methode pour resoudre :x x + 1Nous avonsx x + 1⇐⇒x2 x + 12⇐⇒x2 x2 + 2x + 1⇐⇒0 2x + 1⇐⇒12 x.Analyse
Page 24 : Exercice 62x 1 x 1.Nous allons utiliser une methode differente a celle de l’exercice precedent.Pour cela rappelons :Pour tout x 0 :x a⇐⇒x2 a2eta 0.Pour tous x 0, a 0 :x a⇐⇒x2 a2.Pour tous x R, a R :x2 a2⇐⇒x a.Analyse
Page 25 : Exercice 6Solution : On a2x 1 x 1⇐⇒2x 12 x 12⇐⇒4x2 4x + 1 x2 2x + 1⇐⇒3x2 2x 0⇐⇒x · 3x 2 0⇐⇒3x ·x 23 0⇐⇒x ·x 23 0⇐⇒0 xetx 23⇐⇒0 x 23.Analyse
Page 26 : Exercice 6L’inequation a donc par ensemble solution, l’intervalle0 , 23.Analyse
Page 27 : Exercice 6x + 3 1 2Solution : En utilisant la definition de la valeur absolue, l’inequationx + 3 1 2 peut ˆetre reecrit sous la forme2 x + 3 1 2Ce qui est equivalent a1 x + 3 3,et comme x + 3 est toujours positif, la derniere inequation est equivalent a0 x + 3 3.D’ou on deduit0 x + 3 3⇐⇒3 x + 3 3⇐⇒6 x 0.Par consequent, l’inequation a par ensemble solution l’intervalle6, 0.Analyse
Page 28 : Exercice 6x 1x + 2 3Solution : On a deux cas a etudier :Si x 2, alorsx 1x + 2 3 ⇐⇒x 1 3x + 6⇐⇒7 2x⇐⇒72 x.Mais on ne peut pas avoir en mˆeme temps 72 x et x 2. Parconsequent, sur l’intervalle 2, + l’inequation n’a pas de solution.Si x 2, alorsx 1x + 2 3 ⇐⇒x 1 3x + 6⇐⇒7 2x⇐⇒72 x.Analyse
Page 29 : Exercice 6L’inequation a donc par ensemble solution, l’intervalle72 , 2.Autre methode : On ax 1x + 2 3⇐⇒x 1x + 2 3 0⇐⇒2x 7x + 20.Par consequent, l’inequation precedente est vraie si et seulement si lenumerateur et le denominateur ont le mˆeme signe ou si le numerateurest zero. En faisant un tableau de signe on obtientValeurs de x-7/2-2+2x 7+--x + 2--+2x7x+2-+-L’inequation a donc par ensemble solution, l’intervalle72 , 2.Analyse
Page 30 : Exercice 6x 3 2x + 1 4Solution : On commence par noter que, pour que l’inequation soit bien definie,il fautx 3 0⇐⇒x 3, et2x + 1 0⇐⇒x 12.L’inequation est donc bien definie si et seulent si x 3. Maintenant, pourx 3, on a4 x=⇒x 4 2x=⇒0 x 3 2x + 1,d’ou on conclut en prenant la racine carreex 3 2x + 1,ce qui est equivalent ax 3 2x + 1 0.Par consequent, pour tout x 3 on ax 3 2x + 1 0 4.L’inequation a donc par ensemble solution, l’intervalle3, +.Analyse
Page 31 : Exercice 6px2 2x + 3 x 1.Solution : On cherche a resoudre :x2 2x + 3 x 1. On separe leprobleme en trois cas :• Si x 1, alors x 1 0 maispx2 2x + 3est toujours un reel positif. Par consequent, sur l’intervalle , 1l’inequation n’a pas de solution.• Si x = 1, on obtientp12 2 · 1 + 3 =2 0.Donc, x = 1 n’est pas une solution de l’inequation.• Si x 1, on peut ecrirepx2 2x + 3 x 1⇐⇒x2 2x + 3 x 12⇐⇒x2 2x + 3 x2 2x + 1⇐⇒3 1.Contradiction ! Par consequent, sur l’intervalle 1, + l’inequation n’apas de solution.Analyse
Page 32 : Exercice 7Calculer la valeur de :1nXi=12Solution : On anXi=12 = 2 nXi=11!= 21 + 1 + 1 + · · · + 1zn fois= 2n2nYi=13Solution : On anYi=13 = 3 · 3 · 3 ·· · ·· 3zn fois!= 3n.Analyse
Page 33 : Exercice 7nXk=12ak+1 3ak + ak1Solution : Notons que2ak+1 3ak + ak1=2ak+1 2ak ak + ak1=2ak+1 ak ak ak1.Ce qui nous permet d’ecrirenXk=12ak+1 3ak + ak1=nXk=12ak+1 ak ak ak1=2nXk=1ak+1 ak nXk=1ak ak1.MaintenantnXk=1ak+1 aketnXk=1ak ak1sont de sommes telescopiques.Analyse
Page 34 : Exercice 7Par consequentnXk=1ak+1 ak=an+1 a1nXk=1ak ak1=an a0.D’ou on obtientnXk=12ak+1 3ak + ak1=2nXk=1ak+1 ak nXk=1ak ak1=2an+1 a1 an a0=2an+1 an 2a1 + a0.Analyse
Page 35 : Exercice 7nXk=1k.Solution : Notons quenXk=1k = 1 + 2 + 3 + · · · + n 1 + n+nXk=1k = n + n 1 + · · · + 3 + 2 + 12nXk=1k = n + 1 + n + 1 + · · · + n + 1zn foisPar consequent2nXk=1k = nn + 1.Analyse
Page 36 : Exercice 7d’ou on conclutnXk=1k = nn + 12.Analyse
Page 37 : Exercice 7nXk=232k.Solution : On commence par rappeler la valeur de la somme geometrique. Pourtout a R avec a ̸= 1, on anXk=0ak = 1 an+11 a.Pour demontrer cette formule il suffit de noternXk=0ak=1 + a + a2 + · · · + an1 + ana ·nXk=0ak=a + a2 + · · · + an + an+1nXk=0ak a ·nXk=0ak=1 an+1Analyse
Page 38 : Exercice 7Par consequent1 a ·nXk=0ak =nXk=0ak a ·nXk=0ak = 1 an+1AinsinXk=0ak = 1 an+11 a.MaintenantnXk=232k =nXk=29k=nXk=09k 1 + 9=1 9n+11 910=9n+1 18808= 9n+1 928= 929n1 18.Analyse
Page 39 : Exercice 7En remarquant quek + 12 k2 = 2k + 1,montrer que :n1Xk=02k + 1 = n2 =nXk=12k 1.Solution : En effet on ak + 12 k2 = k2 + 2k + 1 k2 = 2k + 1.Ce qui nous permet d’ecriren1Xk=02k + 1=n1Xk=0k + 12 k2zsomme telescopique de terme ak=k2=an a0=n2 02=n2.Analyse
Page 40 : Exercice 7Notons aussi quek2 k 12 = k2 k2 2k + 1 = 2k 1.Par consequentnXk=12k 1=nXk=1k2 k 12zsomme telescopique de terme ak=k12=an+1 a1=n + 1 12 1 12=n2.Analyse
Page 41 : Exercice 7Autre maniere pour montrer quen1Xk=02k + 1 =nXk=12k 1.Utilisons le changement d’indice k′ = k + 1. Alorsk = 0=⇒k′ = 1etk = n 1=⇒k′ = n,et on peut ecriren1Xk=02k + 1 =nXk′=12k′ 1 + 1 =nXk′=12k′ 1.Analyse
Page 42 : Exercice 7Montrer quenXk=0k + 13 nXk=0k3 = 3nXk=1k2 + n + 13n + 22.En deduire Pnk=0 k2.Solution : On commence par noter quenXk=0k + 13 nXk=0k3 =nXk=0k + 13 k3=nXk=0k3 + 3k2 + 3k + 1 k3=nXk=03k2 + 3k + 1= 3nXk=0k2 + 3nXk=0k +nXk=01.Analyse
Page 43 : Exercice 7MaintenantnXk=01 = n + 1et d’apres l’Exercice 7 Question 4 on saitnXk=0k = nn + 12.Par consequentnXk=0k + 13 nXk=0k3 = 3nXk=0k2 + 3nXk=0k +nXk=01= 3nXk=0k2 + 3nn + 12+ n + 1= 3nXk=0k2 + 3nn + 1 + 2n + 12= 3nXk=0k2 + n + 13n + 22.Analyse
Page 44 : Exercice 7D’autre partnXk=0k + 13 nXk=0k3 =nXk=0k + 13 k3zsomme telescopique de terme ak=k3= n + 13 03= n + 13.Ce qui nous permet de conclure quen + 13=3nXk=1k2 + n + 13n + 22D’ou on deduit l’egalitenXk=0k2=2n + 13 n + 13n + 26.Analyse
Page 45 : Exercice 7Finalement,2n + 13 n + 13n + 26= n + 12n + 12 3n + 26= n + 12n2 + 4n + 2 3n + 26= n + 12n2 + n6= nn + 12n + 16.et on conclutnXk=1k2 = nn + 12n + 16.Analyse
Page 46 : Exercice 8Calculer les sommes suivantes :nXk=15knk;n1Xk=03knk;nXk=0knk.Solution :nXk=15knk= nXk=1nk5k +n050!n050= nXk=0nk5k!n050= nXk=0nk5k!1= nXk=0nk5k · 1nk!1=5 + 1n 1 = 6n 1.Analyse
Page 47 : Exercice 8n1Xk=03knk= n1Xk=0nk3k +nn3n!nn3n= nXk=0nk3k!nn3n= nXk=0nk3k!3n= nXk=0nk3k · 1nk!3n=3 + 1n 3n=2n 3n.Analyse
Page 48 : Exercice 8•nXk=0knk=nXk=1knk=nXk=1k · n!k!n k!=nXk=1n!k 1!n k!Utilisons le changement d’indice k′ = k 1. Alorsk = 1=⇒k′ = 0etk = n=⇒k′ = n 1,et on peut ecrirenXk=1n!k 1!n k!=n1Xk′=0n!k′!n 1 k′!=n ·n1Xk′=0n 1!k′!n 1 k′!Analyse
Page 49 : Exercice 8AinsinXk=0knk=nn1Xk′=0n 1!k′!n 1 k′!=n ·n1Xk′=0n 1k′=n ·n1Xk′=0n 1k′1k′ · 1n1k′=n · 1 + 1n1=n · 2n1.Analyse
Page 50 : Exercice 9Ecrire a l’aide de factorielles les expressions suivantes :nYk=1k2;n1Yk=3k;nYk=22k + 1.Solution :nYk=1k2 = nYk=1k!2= n!2.n1Yk=3k =11 · 2 ·n1Yk=1k = n 1!2Analyse
Page 51 : Exercice 9nYk=22k + 1= 2n+1Yk=5k!· nYk=32k!1= 2n+1Yk=5k!· nYk=3k!1· nYk=32!1= 11 · 2 · 3 · 4 ·2n+1Yk=1k!· 11 · 2nYk=1k!1·12n+13=2n + 1!4!·n!21·12n2=2n + 1!12 · 2n2n!Analyse
Page 52 : Exercice 10Calculer les produits suivants :nYk=03k;nYk=2kk + 2.Solution :nYk=03k = 3 · 32 · 33 · · · 3n = 31+2+3+···+n = 3Pnk=1 k = 3nn+12.nYk=2kk + 2 =Qnk=2 kQnk=2 k + 2Maintenant, le changement d’indice k′ = k + 2, nous permet d’ecrirenYk=2k + 2=zk=2, k=n =⇒k′=4, k′=n+2n+2Yk′=4k′ =n+2Yk=4k.Analyse
Page 53 : Exercice 10AinsiQnk=2 kQnk=2 k + 2 =Qnk=2 kQn+2k=4 k=2 · 3 · Qnk=4 kn + 1n + 2 · Qnk=4 k =6n + 1n + 2.Par consequentnYk=2kk + 2 =6n + 1n + 2.Analyse
Page 54 : Pour aller plus loin - Exercice 11Soit p N× et n N× tels que p n. Montrer que np + 1!= pp!+ p + 1p!+ · · · + n 1p!.Solution : On commence par rappeler la definition du coefficients binomial :pour toute couple d’entiers 0 k n on appelle coefficients binomial lenombre nk!=n!k!n k!.Le nombrenkse lit : k parmi n. Le coefficient binomial satisfait la proprietesuivant, appellee Formule de Pascal : pour tous entiers n et k tels que0 k n on a nk + 1!= n 1k + 1!+ n 1k!.Analyse
Page 55 : Pour aller plus loin - Exercice 11nk + 1=n 1k + 1+n 1k.Preuve : n 1k + 1!+ n 1k!=n 1!k + 1!n 2 k! +n 1!k!n 1 k!= n 1!1k + 1!n 2 k! +1k!n 1 k!Maintenantk + 1! = k!k + 1etn 1 k! = n 2 k!n 1 k.Donc1k + 1!n 2 k! =n 1 kk + 1!n 2 k!n 1 k =n 1 kk + 1!n 1 k!1k!n 1 k! =k + 1k!k + 1n 1 k! =k + 1k + 1!n 1 k!.Analyse
Page 56 : Pour aller plus loin - Exercice 11D’ou on conclut n 1k + 1!+ n 1k!= n 1!1k + 1!n 2 k! +1k + 1!n 1 k!= n 1!n 1 kk + 1!n 1 k! +k + 1k + 1!n 1 k!= n 1! n 1 k + k + 1k + 1!n 1 k!= n 1!nk + 1!n 1 k!=n 1!nk + 1!n 1 k!=n!k + 1!n 1 k!= nk + 1!.Analyse
Page 57 : Pour aller plus loin - Exercice 11En utilisant la formule de Pascal, on peut ecrire np + 1!= n 1p + 1!+ n 1p! n 1p + 1!= n 2p + 1!+ n 2p! n 2p + 1!= n 3p + 1!+ n 3p!......... p + 3p + 1!= p + 2p + 1!+ p + 2p! p + 2p + 1!= p + 1p + 1!+ p + 1p!= pp!+ p + 1p!.Analyse
Page 58 : Pour aller plus loin - Exercice 11Ce qui nous permet de conclure np + 1!= n 1p + 1!z+ n 1p!= n 2p + 1!z+ n 2p!+ n 1p!= n 3p + 1!+ n 3p!+ n 2p!+ n 1p!.........= p + 2p + 1!z+ p + 2p!+ · · · + n 3p!+ n 2p!+ n 1p!= pp!+ p + 1p!+ p + 2p!+ · · · + n 3p!+ n 2p!+ n 1p!.Analyse
Page 59 : Pour aller plus loin - Exercice 11Deuxieme methode : Montrons l’egalitePn : np + 1!= pp!+ p + 1p!+ · · · + n 1p!en utilisant un raisonnement par recurrence sur n 2.Initialisation : Pour n = 2, necessairement p = 1 et on a np + 1!= 22!= 1 pp!= 11!= 1Les deux sont egaux, donc P1 est vraie.Analyse
Page 60 : Pour aller plus loin - Exercice 11Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire np + 1!= pp!+ p + 1p!+ · · · + n 1p!.Montrons que Pn + 1 est vraie, autrement dit, montrons n + 1p + 1!= pp!+ p + 1p!+ · · · + np!.Partons du membre de droite pp!+ · · · + n 1p!+ np!= pp!+ · · · + n 1p!!+ np!= np + 1!+ np!d’apres l’hypothese de recurrence.Analyse
Page 61 : Exercice 7Maintenant, a l’aide de la formule de Pascale, nous pouvons ecrirenp + 1+np=n + 1p + 1Ainsipp+p + 1p+ · · · +n 1p+np=np + 1+np=n + 1p + 1Donc la propriete est vraie pour n + 1. Fin de la recurrence. Parconsequent Pn =⇒Pn + 1, et on conclut que pour tout entiernaturel n on anp + 1=pp+p + 1p+ · · · +n 1p.Analyse
Page 62 : Exercice 12Demontrer les formules suivantes :sinx + siny = 2 sinx + y2cosx y2cosx cosy = 2 sinx y2sinx + y2Rappelons certaines proprietes des fonction sinus et cosinus :sinx + 2π = sinxcosx + 2π = cosxsinx = sinxcosx = cosxsin2x + cos2x = 1Analyse
Page 63 : Exercice 12Formules d’addition :sinx + y = sin x cos y + cos x sin ysinx y = sin x cos y cos x sin ycosx + y = cos x cos y sin x sin ycosx y = cos x cos y + sin x sin y.Pour x = y, ces relations s’appellent formules de duplicationsin2x = 2 sin x cos xcos2x = cos2 x sin2 x = 2 cos2 x 1 = 1 2 sin2 x.A partir de ces formules ou en regardant le cercle trigonometrique onpeut deduiresinx + π = sinxetsinx π = sinx.sinx + π/2 = cosxetsinx π/2 = cosx.cosx + π = cosxetcosx π = cosx.cosx + π/2 = sinxetcosx + π/2 = sinx.Analyse
Page 64 : Exercice 12sinx + siny = 2 sinx + y2cosx y2Solution : On commence par noter quex = x + y2+ x y2ety = x + y2x y2.En utilisant ces egalites on peut ecriresinx = sinx + y2+ x y2= sinx + y2cosx y2+ cosx + y2sinx y2De maniere similairesiny = sinx + y2x y2= sinx + y2cosx y2cosx + y2sinx y2En additionant les deux egalites, on obtientsinx + siny = 2 sinx + y2cosx y2.Analyse
Page 65 : Exercice 12Methode 2 : En utilisant directement les formules de produit. En effet :sinx + y2cosx y2=12sinx + y2+ x y2+ sinx + y2x y2=12 sinx + siny .Ainsisinx + siny = 2 sinx + y2cosx y2.Analyse
Page 66 : Exercice 12Montrons la deuxieme egalite :cosx cosy = 2 sinx y2sinx + y2.Pour cela, on commence par noter que pour tout x R, on asinx + π2= sinx cosπ2+ cosx sinπ2= cosx.Identite qui nous permet aussi d’ecrirecosy = siny + π2,et en utilisant que sinus est une fonction impaire, on deduitcosy = siny π2.Par consequentcosx cosy = sinx + π2+ siny π2.Maintenant, en utilisant l’exercice precedent, on obtientcosx cosy = 2 sinx y2cosx + y2+ π2Analyse
Page 67 : Exercice 12Finalementcosx + y2+ π2=cosx + y2cosπ2sinx + y2sinπ2=sinx + y2.d’ou on conclutcosx cosy=2 sinx y2cosx + y2+ π2=2 sinx y2sinx + y2.Analyse
Page 68 : Exercice 12Methode 2 : En utilisant directement les formules de produit. En effet :sinx y2sinx + y2=12cosx + y2x y2cosx + y2+ x y2=12 cosy cosx .Ainsicosx cosy = 2 sinx y2sinx + y2.Analyse
Page 69 : Exercice 12Demontrer la formule suivantetanx + y = tanx + tany1 tanx tanySolution : En utilisant la definition de la tangente, on peut ecriretanx + tany1 tanx tany =sinxcosx + sinycosy1 sinxcosxsinycosy=sinx cosy+cosx sinycosx cosycosx cosysinx sinycosx cosy= sinx cosy + cosx sinycosx cosy sinx siny= sinx + ycosx + y= tanx + yAnalyse
Page 70 : Exercice 12Autre Methode :tanx + y = sinx + ycosx + y= sinx cosy + cosx sinycosx cosy sinx siny=cosx cosysinx cosycosx cosy + cosx sinycosx cosycosx cosy1 sinx sinycosx cosy=cosx cosysinxcosx + sinycosycosx cosy1 sinx sinycosx cosy=sinxcosx + sinycosy1 sinx sinycosx cosy= tanx + tany1 tanx tany.Analyse
Page 71 : Exercice 12Soitt = tanx2.Demontrer les formules suivantes1 t21 + t2 = cosx.2t1 + t2 = sinx.Analyse
Page 72 : Exercice 12Solution : Montrons la premiere identite. On compute1 t21 + t2 = 1 tan2 x21 + tan2 x2=1 sin2 x2cos2 x21 +sin2 x2cos2 x2=cos2 x2sin2 x2cos2 x2cos2 x2+sin2 x2cos2 x2= cos2 x2sin2 x2cos2 x2+ sin2 x2= cos2 x2sin2 x2= cosx2 + x2= cosx.Analyse
Page 73 : Exercice 12Montrons la deuxieme egalite. On compute2t1 + t2 =2 tan x21 + tan2 x2 =2sin x2cos x21 +sin2 x2cos2 x2=2sin x2cos x2cos2 x2+sin2 x2cos2 x2=2sin x2cos x21cos2 x2= 2 sinx2cosx2= sinx2 + x2= sinx.Analyse
Page 74 : Exercice 13Calculercos π12,sin π12ettan π12.Rappelons quelques valeurs remarquables du sinus, du cosinus et de latangenteAnalyse
Page 75 : Exercice 13Solution : On commence par noter queπ12 = π4 π6 .Alorscos π12 = cosπ4 π6= cos π4 cos π6 + sin π4 sin π6=22 ·32 +22 · 12=64 +24=6 +24.Analyse
Page 76 : Exercice 13etsin π12 = sinπ4 π6= sin π4 cos π6 cos π4 sin π6=22 ·32 22 · 12=64 24=6 24.Finalementtan π12 = sin π12cos π12=6 26 +2.Analyse
Page 77 : Exercice 14Resoudre les equations suivantes, d’inconnue x R :sinx + sin2x = 0.Resolution d’equations : Pour tous x, y R on asinx = siny⇐⇒x = y + 2kπoux = π y + 2kπ,avec k Zcosx = cosy⇐⇒x = y + 2kπoux = y + 2kπ,avec k Ztanx = tany⇐⇒x = y + kπ,avec k Z.Analyse
Page 78 : Exercice 14Solution : Pour tout x R, on asinx + sin2x = 0⇐⇒sinx + 2 sinx cosx = 0⇐⇒sinx1 + 2 cosx = 0.Ainsisinx + sin2x = 0⇐⇒sinx = 0 ou 1 + 2 cosx = 0.Maintenantsinx = 0, si et seulement six = kπ,k Z.1 + 2 cosx = 0, si et seulement sicosx = 12.Essayons de trouver x tel que cosx = 12. La table de valeursremarquables nous dit que cos π3= 12, maiscosπ π3= cosπ3= 12 =⇒cos2π3= 1/2.Analyse
Page 79 : Exercice 14D’ou on conclut que 1 + 2 cosx = 0 si et seulement six = 2π3+ 2kπoux = 2π3+ 2kπ.ou de maniere equivalentex = 2π3+ 2kπoux = 4π3+ 2kπ.Finalement, l’ensemble des solutions estS =kπ, 2π3+ 2kπ, 4π3+ 2kπ : k Z.Analyse
Page 80 : Exercice 14Resoudre l’equation suivante, d’inconnue x R :cosx =3 sinx.Solution : Notons que si cosx = 0, alors sinx = ±1, l’equationdonnerait :0 = ±3Ce qui est absurde. On peut donc supposer cosx ̸= 0, ce qui nousautorise a faire la division suivantecosx =3 sinx⇐⇒sinxcosx =13⇐⇒tanx =13⇐⇒tanx = tan π6 .Donc, l’ensemble des solutions estS =nπ6 + kπ :k Zo.Analyse
Page 81 : Exercice 14Autre methode : Nous avonscosx =3 sinx⇐⇒cosx 3 sinx = 0⇐⇒2 12 cosx 32 sinx!= 0⇐⇒12 cosx 32 sinx = 0⇐⇒cos π3 cosx sin π3 sinx = 0⇐⇒cosx + π3= 0⇐⇒cosx + π3= cos π2⇐⇒x + π3 = π2 + 2kπoux + π3 = π2 + 2kπ⇐⇒x = π3 + π2 + 2kπoux = π3 π2 + 2kπ⇐⇒x = π6 + 2kπoux = 5π6 + 2kπ.Analyse
Page 82 : Exercice 14Ainsi, l’ensemble des solutions estS=π6 + 2kπ, 5π6 + 2kπ : k Z=nπ6 + kπ : k Zo.Analyse
Page 83 : Exercice 14Resoudre l’equation suivante, d’inconnue x R :tan2x = 3 tanx.Solution : Pour tout x R avecx ̸= π2 + kπ, k Zetx ̸= π4 + k π2 , k Zon atan2x = 3 tanx⇐⇒2 tanx1 tan2x = 3 tanx⇐⇒2 tanx = 3 tanx1 tan2x⇐⇒tanx2 31 tan2x = 0⇐⇒tanx = 0ou2 31 tan2x = 0⇐⇒tanx = 0outan2x = 13⇐⇒tanx = 0outanx =r13outanx = r13.Analyse
Page 84 : Exercice 14Maintenanttanx = 0 si et seulement si x = kπ, k Z.tanx =q13 si et seulement si x = π6 + kπ, k Z.tanx = q13 si et seulement si x = π6 + kπ, k Z.Par consequent, l’ensemble des solutions estS =nkπ, π6 + kπ, π6 + kπ :k Zo.Analyse
Page 85 : Exercices SupplementairesResoudre les equations suivantes :3x 1 52x + 1etx2 6x + 8x 1 0.Calculer la somme :nXk=1= 3k.Resoudre les equations suivantes :cos2x cosx = 0tanx = 1tanπ4 sinx + 1= 1.Analyse
Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85