TD1 Derivabilite

Posté le 07/02/2025

Chargé de TD/CM : D. Maths.

38 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Page 1 : Cycle Preparatoire - Premiere AnneeAnalyse II - 2021/2022Derivabilite et calculs de deriveesExercice 1 TechDeterminer l’expression de la derivee de chacune des fonctions suivantes :1. f1x = x3x + 12.2. f2x = 3x 24.3. f3x = 2x2 + 1x2 + 3 .4. f4x =3x + 52x + 13.5. f5x =px3 + 2x2 + 1.6. f6x = ex sinx.7. f7x = lnx +px2 + 1.8. f8x =q2x + 5.Solution1. f ′1x = 3x2x + 12 + x3 · 2x + 1 = 3x2 x2 + 2x + 1+ 2x4 + 2x3 = 3x4 + 6x3 + 3x2 + 2x4 + 2x3Donc f ′1x = 5x4 + 8x3 + 3x22. f ′2x = 4 · 3 · 3x 23 = 123x 23Donc f ′2x = 123x 233. f ′3x = 4xx2 + 32x2x2 + 1x2 + 32= 4x3 + 12x 4x3 2xx2 + 32Donc f ′3x =10xx2 + 324. f ′4x = 3 ·3x + 52x + 1′·3x + 52x + 12= 3 ·32x + 1 23x + 52x + 12·3x + 52x + 12= 3 ·6x + 3 6x 102x + 12·3x + 52x + 12= 3 ·72x + 12 3x + 52x + 12Donc f ′4x = 213x + 522x + 135. f ′5x =3x2 + 4x2x3 + 2x2 + 16. f ′6x = x · sin x′ · ex·sin x = sin x + x · cos x · ex·sin xDonc f ′6x = sin x + x · cos x · ex·sin x7. f ′7x =x +x2 + 1′x +x2 + 1=1 +2x2x2+1x +x2 + 1=1x +x2 + 1 x2 + 1 + xx2 + 1!Donc f ′7x =1x2 + 1Exercice 2Etudier la derivabilite sur R des applications suivantes :f : x 7→xx,g : x 7→x1 + x,h : x 7→11 + x.Solution1. On note que x et x sont derivables sur R.Ainsi, leur produit x.x deﬁnit ume fonction derivable sur R.Veriﬁons la derivabilite de f en 0. Pour cela on calcule la limite suivante :limx→0fx f0x 0= limx→0xx 0x 0= limx→0x · xx= limx→0 x = 0On a bien obtenu une limite ﬁnie dans la fonction est derivable.

Page 2 : 2. Les deux fonctions x et 1 + x sont derivables sur R, et de plus 1 + x le denominateur ne s’annule passur Ralors, g le quotient de ces deux fonctoons derivables est une fonction derivable sur R.Il reste donc a veriﬁer la derivabilite de g en 0 :On calcule la limite :limx→0gx g0x 0= limx→0x1 + x 0 = limx0x1 + x · 1x= limx→011 + x = 1Comme cette derniere limite est ﬁnie : on conclut que f est derivable en 0, donc g est derivable sur R.3.h : x →11 + x La fonction 1 + x est derivable sur Ret s’annule pas. Donc h est derivable sur R. Ilreste a veriﬁer si la fonction h est derivable en 0.On etudie le taux de variation :hx h0x 0= limx→011+x 1x 0= 1 1 xx1 + x = xx1 + xLa limite du taux de variation en 0 est soit 1 si x 0, soit -1 si x 0Donc ce taux n’admet pas de limite. On conclut que h n’est pas derivable en 0. h est donc derivable surRmais pas en R .Exercice 3 La fonction x →cos x est-elle derivable en 0 ?Solutioncos x cos0x 0=2 cos2 x21 1x= 2cos2 x21x= 2sin2 x2 x224= 12sin2 x2 x22or limx→0+x2= 0 et limu→0+sin uu= 1 donc par composition limx→0+sin x2 x2= 1Finalement limx→0+cos x cos0x 0= 12Comme le taux de variation a une limite ﬁnie, la fonction est derivable en 0.Exercice 4 ◦Determiner a et b pour que la fonction f deﬁnie ci-dessous de R+ dans R soit derivable sur R+.Soit f : x 7→xsi 0 ⩽x 1x 7→ax2 + bx + csi 1 ⩽xSolutionLa fonction f est la restriction de la fonction sur 0; 1 donc elle est continue et derivable sur 0; 1La fonction f est la restriction d’une fonction polynˆome sur 1; + donc elle est continue et derivable sur1; +On s’interesse donc a la continuite et la derivabilite en 1 :limx→1x = 1 et limx→1 ax2 + bx + c = a + b + c. La fonction f est donc continue en 1 si et seulement si a + b + c = 1La fonction est derivable en 1 et de nombre derivee121 = 12La fonction x 7→ax2 + bx + c est derivable en 1 et de derivee 2a + bLa fonction f est donc derivable en 1 lorsque a + b + c = 1 et 2a + b = 12En utilisant a comme parametre, b = 12 2a et c = 1 a b = 1 a 12 + 2a = 1 + a 12 on a doncax2 + bx + c = ax2 +12 2ax + 1 + a 12ax2 + bx + c = ax 12 + 12x + 1On remarque la partie qui ne depend pas de a assure la continuite et la derivabilite et la partie en a rajouteune fonction dont la fonction et la derivee en 1 valent 0.Exercice 5 TechCalculer les limites suivantes :limx→0e3x+2 e2x,limx→0cos x 1x,limx→1ln2 xx 1,limx→π2expcos x 1x π2.

Page 3 : limx→02 sin x sin 2xx2,limx→0sin xx ,limx→0x sin x1 cos x,limx→0cos2 x 1x.Solution1. limx→0e3x+2 e2x= 3e3×0+2 = 3e2 c’est le nombre derive en 0 de la fonction x 7→e3x+22. limx→0cos x 1x= sin 0 = 0 c’est le nombre derivee en 0 de la fonction cos3. limx→1ln2 xx 1= limx→1ln2 x ln2 1x 1= limx→1 12 x = 1 c’est le nombre derivee en 0 de la fonctionx 7→ln2 x4. limx→π2expcos x 1x π2= limx→π2expcos x expcos xx π2= sin 0 expcos 0 = 0 c’est le nombre derivee en 0 dela fonction x 7→lncos x5. limx→02 sin x sin 2xx2= 2 limx→0sin x1 cos xx2= 2 limx→0sin xx· 1 cos xx= 26. limx→0sin xx = limx→0sin xxx = 07. limx→0x sin x1 cos x = limx→0 sin xx1 cos x = 08. limx→0cos2 x 1x= limx→0cos x 1xcos x + 1 = 0Calculs de derivee n-iemeExercice 6Soit n N, calculer l’expression de la derivee d’ordre n des fonctions f, g, h deﬁnies par :1. f1x = sin x.2. f2x = sin2 x.3. f3x = x2 + 2x + 3ex.4. f4x = x2 cos x.5. f5x = cos3 x.6. f6x = 1x.7. f7x = x2ex8. f8x = xn1 lnx + 1Solution1. On deﬁnit n N, Pn : f n1x = sinx + nπ2• On a f ′x = cos x = sinx + π2 . Donc P1 est vraie.• Soit n N, supposons Pn vraie.f n = sinx + nπ2Donc f n+1 = sinx + nπ2 + π2= sinx + n + 1π2Donc Pn + 1 est veriﬁe.• Donc n N, sinx + nπ22. On a f2x = 1 cos 2x2= 1 sin2x + π2 2On applique la propriete precedente pour imaginer la formule :n N, f n2= 2n1 sin2x + n 1π2 que l’on peut demontrer par recurrence.3. On utilise la formule de LeibniznXk=0nkx2+2x+3kexnk =n0x2+2x+31nex+n12x+21n1ex+n221n2ex= x2 + 2x + 3 2x + 2n + nn 1ex1n= x2 + 21 nx + n2 3n + 3ex1n

Page 4 : 4. On utilise la formule de LeibniznXk=0nkx2kcos xnk =n0x2 cosx + nπ2+n12x cosx + n 1π2+n22 cosx + n 2π2= x2 cosx + nπ2+ 2nx cosx + n 1π2+ nn 1 cosx + n 2π25. hx = cos3x = 14 3 cos x + cos 3xOn peut donc imaginer la formule :n N, f n3= 143 cosx + nπ2 + 3n cos3x + nπ2 que l’on peut demontrer par recurrence.6. f6x On conjecture f n6= 1nn!xn+1On demontre par reccurence : element de preuve :Initialisation :f 06= 100!x0+1okHeredite :On suppose f n6′ = n + 11nn!xn+2= 1n+1n + 1!xn+27. On utilise la formule de LeibniznXk=0nkx2kexnk =n0x2ex +n12xex +n22ex= exx2 + 2nx + nn 18.Exercice 7Soient a un reel, et n, k N. Montrer quex + ank =n!n k!x + ank: si k ⩽n0: si k nSolutionSoit n N. On raisonne par recurrence sur k NOn deﬁnit la proprietek N, Pk : x + ank =n!n k!x + ank: si k ⩽n0: si k nLa propriete est vraie au rank k = 0 carn!n 0!x + an0 = x + an0Supposons qu’elle est vraie au rang k N, alorsx R, x + ank+1 =x + ank′Soit k n alors x + ank+1 = 0′ = 0Sinon x + ank+1 =n!n k!x + ank′Soit k = n, donc x + ann+1 =n!n n!x + ann′= 0Soit k n etx R, x + ank+1 = n kn!n k!x + ank1 =n!n k + 1!x + ank+1.Dans tous les cas, on a obtenu la formule pour k + 1 donc Pk+1 est vraie.Donc n N, Pn est vraie.Exercice 8Soient a et b deux reels et fx = x anx bn.Calculer f n et en deduirenXk=0nk2.Indication : choisir a = b.

Page 5 : SolutionPuisque f est le produit de deux fonctions derivables :gx = x an et hx = x bn on peut utiliser la formule de Leibniz pour calculer f nxf nx =nXk=0 nk· gk · hnkxOn peut montrer par recurrence que gkx =n!n k!x ankDe mˆeme hkx =n!n k!x bnkFinalementf nx =nXk=0 nk·n!n k!x ank · n!k!x bk = n!nXk=0 nk·n!n k!k!x ank · x bkFinalement :f nx = n!nXk=0 nk2· x ank · x bkLorsque a = b, la formule devient :f nx = n!x annXk=0 nk2Pour a = b, fx = x a2n donc f 2nx = 2n!n! x anOn obtient donc la formule 2nn= 2n!n!n! =nXk=0 nk2Exercice 9Determiner le prolongement par continuite en 0 de chacune des fonctions suivantes et determiner si la fonctionobtenue est de classe C1 c’est a dire derivable et a derivee continue.1. f1x = x ln x2. f2x = ex 1x3. f3x =x + 1 1lnx + 14. f4x = x3 sin 1x5. f5x = x sin 1xSolution1. On commence par prolonger f1 par continuite en 0. On calcule la limite :limx→0+x · ln x = limx→0+ 2x · ln xon a limx→0x = 0 et limu→0 u ln u = 0 donc par composition limx→0x ln x = 0.Donc limx→0+x · ln x = 0Ainsi, on peut prolonger f1 por continuite en 0 et on deﬁnit la nouvelle fonction ˜f1 continue en 0 :˜f1x = 0si x = 0x · ln xsi x 0Etudions maintenant la derivabilite de f1.Sur 0; +, x 7→x et x 7→ln x sont derivables sur R, donc leur prodiit x · ln x deﬁnit aussi unefonction derivable sur R+.On examine maintenant la derivabilite de ˜f1 en 0.On calcule la limite :˜f1x ˜f0x 0= limx→0+x · ln xx= limx→0+ln xx = .Cette derniere limite n’est pas ﬁnie donc ˜f1 n’est pas derivable en 0 .

Page 6 : 2. Pour prolonger f2 par continuite en 0 , on commence par calculer la limite :Pour pouvoir la prolonger en 0, il faudrait qu’elle possede une limite ﬁnie en 0.Or :limx→0 f2x = limx→0+ex 1x= limx→0+ex 1xx = 0 car limx→0+ex 1x= 1On peut donc prolonger f2 en 0 : on deﬁnit la fonction ef2 le prolongement de f2 par continuite :˜f2x =0si x = 0ex 1xsi x 0Etudions maintenant la derivabilite de f2.Comme precedemment, sur R+, f2 est derivable comme quotient de fonction derivables.Etudions la derivabilite en 0.On calcule :f2x f20x 0=ex1xx= ex 1xx = ex 1x× 1xDonc : limx→0+f2x f20x 0= limx→0+ex 1x× 1x = +.La limite n’est pas ﬁnie, f2 n’est donc pas derivable en 0.3. f3x =x + 1 1lnx + 1=x + 1 1x·xlnx + 1On ax + 1 1x= gx g0x 0→x→0 g′x en posant g deﬁnie de 1; + dans R par g : x 7→x + 1g est une fonction derivable avec g′x =12x + 1 donc g′0 = 12Donc limx→0x + 1 1x= 12On a aussi lnx + 1x= hx h0x 0en posant h deﬁnie de 1; + dans R par h : x 7→lnx + 1h est une fonction derivable avec h′x =1x + 1 donc h′0 = 12Donc limx→0lnx + 1x=11 + 0 = 1Finalement en eﬀectuant le produit : limx→0x + 1 1lnx + 1= 12Ainsi, on peut prolonger f1 par continuite en 0 et on deﬁnit la nouvelle fonction ˜f1 continue en 0 :˜f3x =0si x = 12x + 1 1lnx + 1si x 0Etudions maintenant la derivabilite de f3.Comme precedemment, sur R+, f3 est derivable comme quotient de fonction derivables.Etudions la derivabilite en 0.On calcule :f3x f30x 0=x + 1 1lnx + 112x=x + 1 1xlnx + 12xlnx + 14. On sait x R, sin x ⩽1 donc f4x x3.D’apres le theoreme des gendarmes, limx→0 f4x = 0.Ainsi, on peut prolonger f4 por continuite en 0 et on deﬁnit la nouvelle fonction ˜f4 continue en 0 :˜f4x =0si x = 0x3 sin 1xsi x 0Etudions maintenant la derivabilite de f4.Comme precedemment, sur R+, f4 est derivable comme quotient de fonction derivables.Etudions la derivabilite en 0.On calcule :f4x f40x 0=x3 sin 1xx= x2 sin 1x

Page 7 : On sait x R, sin x ⩽x donc sin 1x 1x donc f4x f40x 0 x.donc la limite est 0. Donc la fonction f4 est derivable en 0.5. On sait x R, sin x ⩽1 donc donc f5x ⩽x.D’apres le theoreme des gendarmes, limx→0 f5x = 0.Ainsi, on peut prolonger f5 por continuite en 0 et on deﬁnit la nouvelle fonction ˜f5 continue en 0 :˜f5x =0si x = 0x sin 1xsi x 0Etudions maintenant la derivabilite de f4.Comme precedemment, sur R+, f5 est derivable comme quotient de fonction derivables.Etudions la derivabilite en 0.On calcule :f5x f50x 0=x sin 1xx= sin 1xPour tout k N, sin112πk= sin 2πk = 0 et sin112πk + π2= sin2πk + π2= 1Or les suites 12πkket12πk + π2ktendent toutes les deux vers 0 donc la limite du taux de variationn’existe pas. Donc la fonction n’est pas derivable en 0Exercice 10Pour tout x 1, + on pose fx = x lnx x.1. Montrer que f est une bijection de 1, + sur 1, +.2. On pose g = f 1 l’application reciproque de f.Calculer g0 et g′0.Solution1. f est continue sur 1; + comme somme et produit de fonctions continues sur 1; +f est derivable sur 1; + et x 1; +, f ′x = 1 · ln x + x 1x 1 = ln x x 1; +, f ′x 0 donc fest strictement croissante.f etant une fonction continue et strictement croissante, deﬁnie sur un intervalle, elle est injective.On determine f1; + = 1; +.Donc f est une bijection croissante de 1; + dans 1; +.2. g0 = x ⇔0 = fx ⇔x ln x x = 0 ⇔xln x 1 = 0 ⇔x = 0 ou x = eOr 0 /1; +Donc g0 = eLa fonction f ′ ne s’annule pas sur 1; +, la fonction g est derivable sur 1; +, de derivee :g′x =1f ′gx =1ln gxOn a donc g′0 =1ln g0 =1ln e = 1Fonctions de classe CkExercice 11 ◦Soit une fonction f deﬁnie sur R a valeurs dans RSoit f :x 7→ex si x 0x 7→ax2 + bx + c si x ⩽0Determiner a, b, c pour que f soit C2.La fonction f est-elle C3 ?Solutionf est de classe C2 ssi et seulement si les trois conditions suivantes sont veriﬁees :

Page 8 : 1. La fonction est continue donclimx→0+ fx = limx→0fxOr limx→0+ fx = e0 = 1et limx→0fx = a · 02 + b · 0 + c = cDonc c = 12. f est derivable et de derivee continue :limx→0+ f ′x = limx→0f ′xOr limx→0+ f ′x = e0 = 1et limx→0fx = 2a · 02 + b = bDonc b = 13. f est derivable deux fois et de derivee seconde continue donclimx→0+ f ′′x = limx→0f ′′xOr limx→0+ f ′′x = e0 = 1et limx→0f ′′x = 2aDonc a = 12On veriﬁera que la fonctionf :x 7→ex si x 0x 7→12x2 + x + 1 si x ⩽0repond bien a la question.Lorsque l’on derive 3 fois a droite et a gauche, on obtient :Or limx→0+ f ′′′x = e0 = 1et limx→0f ′′′x = 0Donc la fonction obtenue n’est pas C3Exercice 12 ◦La fonction f deﬁnie sur R a valeurs dans R est elle de classe C1 ? Est-elle de classe C2 ? Est-elle de classe C3 ?Soit f :x 7→x si x ⩽0x 7→sin x si x 0SolutionSur Rla fonction est Ccar les restrictions sur Ret R+sont C. On s’interesse donc au voisinage de 0Comme dans l’exercice precedent, on etudie les limites a gauche et a droite :limx→0+ fx = 0 et limx→0fx = 0 donc la fonction est continue.limx→0+ f ′x = 1 et limx→0f ′x = cos0 = 1 donc la fonction est C1limx→0+ f ′′x = 0 et limx→0f ′′x = sin0 = 0 donc la fonction est C2limx→0+ f ′′′x = 0 et limx→0f ′′′x = cos0 = 1 donc la fonction n’est pas C3Grands theoremesExercice 131. Montrer que pour tout x 0, on a :1x + 1 lnx + 1 lnx 1x2. n 1, montrer que :lnn + 1 lnn 1n lnn lnn 13. On poseHn =1n + 1 +1n + 2 + . . . +1n + nMontrer que :ln2n + 1 lnn + 1 Hn ln2n lnn

Page 9 : 4. En deduire que Hn converge et determiner sa limite.5. On poseSn =3nXk=n+11kMontrer que Sn converge et determiner sa limite.Solution1. On utilise le theoreme des accroissements ﬁnis a la fonction f : u 7→lnu sur l’intervalle x; x + 1f est continue sur x; x + 1, f est derivable sur x; x + 1 doncil existe c x; x + 1 tel que fx + 1 fx = f ′cx + 1 1 = f ′cOr x c x + 1 donc1x + 1 ⩽f ′c ⩽1xOn a donc1x + 1 ⩽lnx + 1 ln x ⩽1x2. La derniere inegalite appliquee a gauche pour x = n permet d’obtenir l’inegalite a droite.En rempla¸cant x = n 1 on obtient l’inegalite a gauche.Donclnn + 1 lnn 1n lnn lnn 13. Hn =k=nXk=n+11k + nOn utilise les inegalites precedentes et on obtient :2nXk=n+1lnk + 1 ln k ⩽2nXk=n+11k + n ⩽2nXk=n+1ln k lnk 1On separe les sommes :2nXk=n+1lnk + 1 2nXk=n+1ln k ⩽2nXk=n+11k + n ⩽2nXk=n+1lnk 2nXk=n+1ln k 1On eﬀectue un changement d’indices :2n+1Xk=n+2lnk 2nXk=n+1ln k ⩽2nXk=n+11k + n ⩽2nXk=n+1ln k 2n1Xk=nln kOn simpliﬁe les sommes :ln2n + 1 lnn + 1 ⩽2nXk=n+11k + n ⩽ln2n lnn4. Or ln2n + 1 lnn + 1 = ln2 + ln n + 12n + 1Orlimn→+n + 12n + 1 = 1 donclimn→+ln2n + 1 lnn + 1 = ln 2etlimn→+ln2n lnn + 1 =limn→+ln 2 = ln 2D’apres le theoreme des gendarmes, on aetlimn→+Hn = ln 25. On peut obtenir une inegalite equivalente :3nXk=n+1lnk + 1 ln k ⩽3nXk=n+11k + n ⩽3nXk=n+1ln k lnk 1Doncln3n + 1 lnn + 1 ⩽2nXk=n+11k + n ⩽ln3n lnnIl vient alorslimn→+3nXk=n+11k = ln 3

Page 10 : Exercice 141. Soient a0, . . . , an tels que a0 + a12 + . . . +ann + 1 = 0.Montrer que x 0, 1 tel que a0 + a1x + . . . + anxn = 0.On pourra considerer la fonction fx = a0x + a12 x2 + . . . +ann + 1xn+1.2. Soit P un polynˆome reel ayant n racines reelles distinctes, montrer que P ′ en a au moins n 1.Solution1. On considere la fonction fx = a0x + a12 x2 + · · · +ann + 1xn+1. f est une fonction continue sur 0, 1 etderivable sur 0; 1.On a f0 = a00 + a12 0 + · · · + 0 = 0.et f0 = a01 + a12 1 + · · · + 1 = 0Donc f0 = f1 = 0, par le theoreme de Rolle : il existe un x 0, 1 tel que f ′x = 0.Orf ′x = a0 + a12 · 2x + · · · +ann + 1 · n + 1 · xn = a0 + a1x + · · · + anxnD’ou le resultat.2. Soit α1 α2 α3 . . . αn les racines de P.k J0; n 1K, sur l’intervale αk, αk+1, la fonction polynˆomiale x 7→Px est continue et derivable etfαk = fαk+1 = 0.On peut donc appliquer le theoreme de Rolle donc il existe donc un reel ck αk, αk+1 tel que P ′αk = 0.Donc il y a donc n 1 racines.Exercice 15Soient n N et a, b R et fx = xn + ax + b.1. Montrer que le polynˆome f admet au plus trois racines reelles.2. Si n est pair. Montrer que le polynˆome f admet au plus deux racines reelles.Solution1. Par l’absurde, supposons que P admet 4 racines reelles :x0 x1 x2 x3Dans ce cas n ⩾4— Pour k = 0 ou k = 1 ou k = 2P est continue sur xk; xk+1, derivable sur xk; xk+1 et Pxk = Pxk+1 = 0 car les xk sont desracines de P.On peut appliquer le theoreme de Rolle donc P ′ admet 3 racines, y0, y1, y2 avecx0 y0 x1 y1 x2 y2 x3— Pour k = 0 ou k = 1P ′ est continue sur yk; yk+1, derivable sur yk; yk+1 et P ′yk = P ′yk+1 = 0 car les yk sont desracines de P ′On peut donc appliquer le theoreme de Rolle donc P ′′ admet 2 racines z0, z1 ety0 z0 y1 z1 y2Or fx = xn + ax + b, donc f ′x = nxn1 + a et f ′′x = nn 1xn2Or f ′′x admet une seule racine qui est 0 ce qui est contradictoire avec l’existence de deux racinesdistinctes z0 et z1.2. Si n est pair, alors f ′′x = nn 1xn2 + a avec n 2 pair. Donc f ′ est strictement croissante. f ′x =nxn1 + a avec n 1 impair. Donc limf ′ = et lim+f ′ = +. Or f ′ est continue donc f ′ realise unebijection sur R donc elle ne s’annule qu’une fois en une reel α.f est donc strictement decroissante sur ; α et strictement croissante sur α; +Elle ne peut donc pas s’annuler 3 fois. Elle admet donc au plus 2 racines reelles.

Page 11 : Exercice 16 Extension du theoreme de RolleSoit f une fonction continue et derivable sur a, + et telle que limx→fx = fa.Montrer qu’il existe un element c dans a, + tel que f ′c = 0.SolutionSi f est constante alors f ′ = 0, donc la conclusion est veriﬁee. Sinon, soit b a; +, fb ̸= fa.Alors, par continuite, il existe α dans a; b antecedent de fa + fb2.Comme limx→fx = fa, il existe β b; + antecedent de fa + fb2.On considere l’intervalle α; β. La f est derivable et continue sur α; β avec fα = fβ donc, en appliquantle theoreme de Rolle, il existe c α; β tel que f ′c = 0.Autre methodeUne autre fa¸con d’etendre le theoreme est de considerer la fonction g deﬁnie sur 0; a pargx =f 1x: si x 0fa: si x = 0on a limx→01x = 0 et limx→fx = faDonc limx→0 gx = limx→0+ f 1x= fa = ga donc g est continue en 0.Par composition de la fonction inverse avec la fonction f, g est derivable sur 0; a.on peut donc appliquer le theoreme de Rolle a g donc il existe c 0; a tel que g′c = 0 donc f ′1c1c2 = 0donc f ′1cet 1c est bien le reel de a; + recherche.Exercice 17Dans l’application du theoreme des accroissements ﬁnis a la fonctionfx = αx2 + βx + γsur l’intervalle a, b donner une expression de c a; b en fonction de α, β et γ.Donner une interpretation geometrique.SolutionOn calcule fb fab a= αb2 a2 + βb ab a= αb + a + βOr f ′c = 2αc + β.donc fb fab a= f ′c ⇔c = a + b2ApplicationsExercice 18Considerons les deux courbes C1 et C2 deﬁnie par les equations C1 : y = x2 et C2 : y = 1x1. Determiner les equations des droites tangentes a C1 passant par le point de coordonnees 0, -1.2. Determiner les equations des droites tangentes a C2 de pente -2.3. Demontrer que les courbes de l’equation y = x2 et y = 1x admettent une unique tangente commune.4. Demontrer que les courbes C3 : y =33x et C2 admettent un point commun ou la droite tangente a C2 etla droite tangente a C3 sont orthogonales. Determiner ce point.Deux droites qui ne sont pas paralleles a l’axe des ordonnees sont orthogonale si et seulement si le produitde leur coeﬃcient directeur est -1Solution1. Soit la fonction f : x 7→x2 deﬁnie de R dans R. f est derivable sur R de derivee f ′x = 2x.Soit a un reel. La tangente a la courbe C1 au point d’abscisse a a pour equationy = f ′ax a + fa ⇔y = 2ax a + a2 ⇔y = 2ax a2Cette tangente passe par le point de coordonnees 0 ;-1 si et seulement si 1 = a2 si et seulement sia = 1 ou a = 1Les equations des tangentes sont y = 2x 1 et y = 2x 1

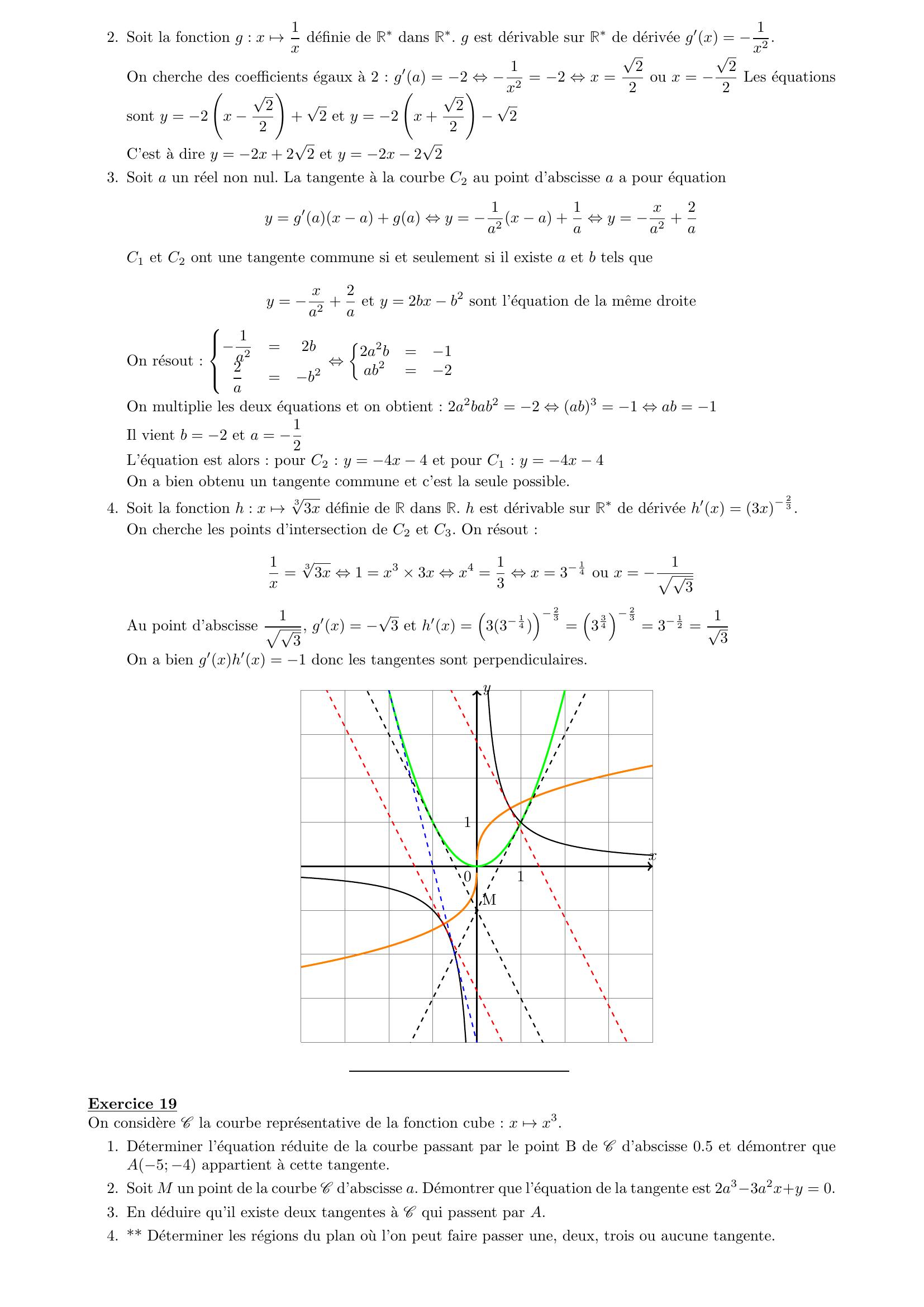
Page 12 : 2. Soit la fonction g : x 7→1x deﬁnie de Rdans R. g est derivable sur Rde derivee g′x = 1x2 .On cherche des coeﬃcients egaux a 2 : g′a = 2 ⇔1x2 = 2 ⇔x =22ou x = 22Les equationssont y = 2 x 22!+2 et y = 2 x +22!2C’est a dire y = 2x + 22 et y = 2x 223. Soit a un reel non nul. La tangente a la courbe C2 au point d’abscisse a a pour equationy = g′ax a + ga ⇔y = 1a2 x a + 1a ⇔y = xa2 + 2aC1 et C2 ont une tangente commune si et seulement si il existe a et b tels quey = xa2 + 2a et y = 2bx b2 sont l’equation de la mˆeme droiteOn resout :1a2=2b2a=b2 ⇔2a2b=1ab2=2On multiplie les deux equations et on obtient : 2a2bab2 = 2 ⇔ab3 = 1 ⇔ab = 1Il vient b = 2 et a = 12L’equation est alors : pour C2 : y = 4x 4 et pour C1 : y = 4x 4On a bien obtenu un tangente commune et c’est la seule possible.4. Soit la fonction h : x 7→33x deﬁnie de R dans R. h est derivable sur Rde derivee h′x = 3x23 .On cherche les points d’intersection de C2 et C3. On resout :1x =33x ⇔1 = x3 × 3x ⇔x4 = 13 ⇔x = 314 ou x = 1p3Au point d’abscisse1p3, g′x = 3 et h′x =3314 23 =33423 = 312 =13On a bien g′xh′x = 1 donc les tangentes sont perpendiculaires.xy110MExercice 19On considere C la courbe representative de la fonction cube : x 7→x3.1. Determiner l’equation reduite de la courbe passant par le point B de C d’abscisse 0.5 et demontrer queA5; 4 appartient a cette tangente.2. Soit M un point de la courbe C d’abscisse a. Demontrer que l’equation de la tangente est 2a33a2x+y = 0.3. En deduire qu’il existe deux tangentes a C qui passent par A.4. Determiner les regions du plan ou l’on peut faire passer une, deux, trois ou aucune tangente.

Page 13 : Solution1. On a f ′0.5 = 32 = 34 f0.5 = 18Donc l’equation de la tangente est y = 34x 12+ 18y = 34x 14On calcule :345 14 = 15 14= 4Donc B appartient a la tangente.2. Ma, a3 donc l’equation de la tangente Ta en a est y = 3a2x a + a3Doncy = 3a2x 2a3B Ta ⇔4 = 3a25 2a3 ⇔2a3 + 15a2 4 = 0On sait que a = 12 est solution de cette equation car on a vu que T 12 contient B.On factorise donc par a 12 ou bien 2a 1.On obtient 2a3 + 15a2 4 = 2a 1a2 + 8a + 4On resout a2 + 8a + 4 = 0 ⇔a + 42 12 = 0a2 = 4 + 23 et a3 = 4 233a22 = 84 483 et 2a32 = 2403 4163a23 = 84 + 483 et 2a33 = 2403 416Les equations des deux autres tangentes sont donc :y = 84 483x 2403 + 416et y = 84 + 483x + 2403 + 416Exercice 20Soient n 2 et f : 0, +→R une fonction deﬁnie parfx = 1 + xn1 + xn1. Montrer que f est derivable sur R+et calculer sa derivee.2. Montrer que f atteint un minimum sur R+. Determiner sa valeur ?3. En deduire les inegalites suivantes :x R+1 + xn 2n1 1 + xn ,x, y R2+y + xn 2n1 yn + xn .Solution1. f est le quotient de deux polynˆomes dont le denominateur ne s’annule par sur R+ donc f est continue etderivable sur R+.f ′x = n1 + xnnxn1 1 + xn n1 + xn11 + x2n= 1 + xnnxn1 1 + xn n1 + xn11 + x2n= n1 + xn1 xn11 + x 1 + xn1 + x2n= n1 + xn1 xn1 + xn 1 xn1 + x2n= n1 + xn1 xn1 + xn 1 xn1 + x2n= n1 + xn1 xn1 11 + x2n

Page 14 : 2. f ′x est du signe de xn1 1. Or la fonction x 7→xn1 1 est strictement croissante sur R doncinjective et 1 est solution de l’equation donc f ′x 0 pour x 0; 1 et f est strictement decroissanteet pour x 1; +, f ′x 0 et f est strictement croissante. Donc f admet un minimum en 1. Orf1 = 22n =12n1Donc x R+, fx ⩾12n1 ⇔1 + xn ⩾1 + xn2n1⇔1 + xn ⩽2n11 + xnor x, y R2+, yx 0 donc1 + yxn⩽2n1 1 +yxnEn multipliant par xn, on obtientx + yn ⩽2n1 xn + ynet cette propriete est vraie pour x = 0 ou y = 0Exercice 21 Tech ◦Calculer le maximum et le minimum des fonctions suivantes :1. f1x = x2 + 5x + 6,x 4, 4.2. f2x = x3 3x2 x + 10,x 0, 3.3. f3x = 2 cos x x,x 0, 4π.Solution1. f1x = x2 + 5x + 6x 4, 4f ′1x = 2x + 5 ⇔x = 525214f4 = 42 + 54 + 6 = 16 20 + 6 = 2f52=522+ 552+ 6 = 25 50 244= 14f4 = 42 + 54 + 6 = 16 + 20 + 6 = 42Donc les extremums sont 42 et -142. f2x = x3 3x2 x + 10x 0, 3f ′2x = 3x2 6x 1= 62 + 4 × 3 × 1 = 48 =432x1 = 3 233/0, 3x2 = 3 + 2333 + 23363 16397

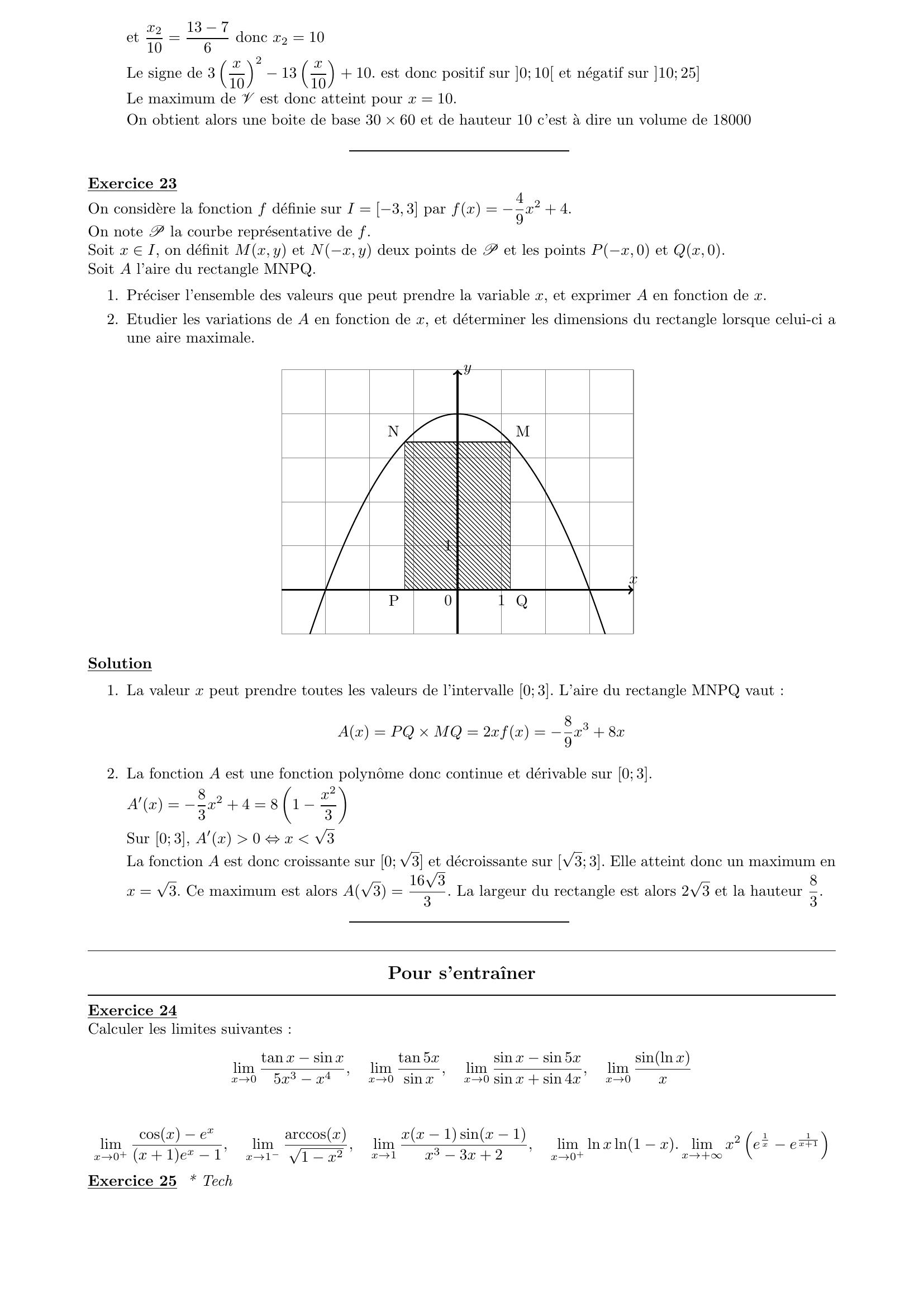
Page 15 : f20 = 0 0 0 + 10 = 10f23 = 33 3x32 3+ 10 = 7f2 3 + 233!= 3 + 233!33 3 + 233!23 + 23310 =63 1639Donc les extremums sont 10 et 63 16393. f3x = 2 cosx xx 0, 4πf ′3x = 2 sinx 1f ′3x ⩾0 ⇐⇒2 sin x 1 ⩾0 ⇐⇒sin x ⩾12 ⇐⇒sin x ⩾sin π6 ⇔x π6 ; 5π613π6 ; 17π6On a donc le tableau de variations suivant :La fonction f3 est donc croissante surπ6 ; 5π6et sur13π6 ; 17π6et decroissante surh0; π6i,5π6 ; 13π6et17π6 ; 4πElle admet donc deux maximums locaux en 5π6 et 17π6f35π6= 2 cos5π65π6 =3 5π6f317π6= 2 cos17π617π6=3 17π6Donc le maximum est3 5π6Exercice 22 ◦On dispose une feuille de carton rectangulaire, de 80 cm de long et 50 cm de large, avec laquelle on veutfabriquer une boite ayant la forme d’un parallelepipede rectangle. Pour cela, on decoupe dans la feuille quatrecarres egaux, aux quatre coins voir la ﬁgure, puis on plie le carton suivant les segments AB, BC, CD, DA.On appelle x la mesure en cm de cˆote de chaque carre decoupe.ABCDx1. Preciser entre quelles valeurs peut varier x pour que la boite soit realisable. On obtiendra un intervalle I.Determiner le volume de la boite obtenue en fonction de x.2. Etudier les variations de la fonction volume sur I, et en deduire la valeur de x qui rend le volume de laboite maximum. Quels sont alors les dimensions et le volume de la boite obtenue ?Solution1. La valeur de x doit ˆetre positive et 2x ne peut pas exceder 50 sinon la boite n’a plus de fond. Doncx 0; 25.L’aire de la base de ce parallelepipede estA = 80 2x50 2xLa hauteur etant x, le volume estV x = x80 2x50 2x2. On developpe V pour ensuite deriver cette fonction polynˆome qui est donc derivable sur I en tant quepolynˆome.V = 4x3 260x2 + 4000xx I, V ′x = 12x2 520x + 4000 = 4003 x10213 x10+ 10On recherche le signe de la fonction polynˆome 3 x10213 x10+ 10.= 132 4310 = 169 120 = 49 = 72Donc x110 = 13 + 76donc x1 = 1003

Page 16 : et x210 = 13 76donc x2 = 10Le signe de 3 x10213 x10+ 10. est donc positif sur 0; 10 et negatif sur 10; 25Le maximum de V est donc atteint pour x = 10.On obtient alors une boite de base 30 × 60 et de hauteur 10 c’est a dire un volume de 18000Exercice 23On considere la fonction f deﬁnie sur I = 3, 3 par fx = 49x2 + 4.On note P la courbe representative de f.Soit x I, on deﬁnit Mx, y et Nx, y deux points de P et les points Px, 0 et Qx, 0.Soit A l’aire du rectangle MNPQ.1. Preciser l’ensemble des valeurs que peut prendre la variable x, et exprimer A en fonction de x.2. Etudier les variations de A en fonction de x, et determiner les dimensions du rectangle lorsque celui-ci aune aire maximale.xy110MNPQSolution1. La valeur x peut prendre toutes les valeurs de l’intervalle 0; 3. L’aire du rectangle MNPQ vaut :Ax = PQ × MQ = 2xfx = 89x3 + 8x2. La fonction A est une fonction polynˆome donc continue et derivable sur 0; 3.A′x = 83x2 + 4 = 81 x23Sur 0; 3, A′x 0 ⇔x 3La fonction A est donc croissante sur 0;3 et decroissante sur 3; 3. Elle atteint donc un maximum enx =3. Ce maximum est alors A3 = 1633. La largeur du rectangle est alors 23 et la hauteur 83.Pour s’entraˆınerExercice 24Calculer les limites suivantes :limx→0tan x sin x5x3 x4,limx→0tan 5xsin x ,limx→0sin x sin 5xsin x + sin 4x,limx→0sinln xxlimx→0+cosx exx + 1ex 1,limx→1arccosx1 x2 ,limx→1xx 1 sinx 1x3 3x + 2,limx→0+ ln x ln1 x.limx→+x2 e1x e1x+1Exercice 25 Tech

Page 17 : Determiner l’expression de la derivee de chacune des fonctions suivantes :f1x = x32 ex2,f2x = sin2x2x2 + 3 ,f3x = sincos3x 22,f4x =2tan2x + 1,f5x = sinx8 + 5x2,f6x = ex sin5x,f7x = ex lnlnlnx,f8x = sinx2cos x2 + x3.Exercice 26Montrer que n Nxne1xn+1= 1n+1xn+2e1x .Solution• On deﬁnit la propriete n N, Pn :xne1xn+1= 1n+1xn+2e1x• Pour n = 0, on a e1x ′ = e1x1x2= 10+1x0+2e1x Donc P0 est vrai.• Soit n N, on suppose Pnxn+1e1xn+2=xxn+1e1xn+2=Xk=0n + 2kxk xne1xn+2k=n + 20xxne1xn+2+n + 21 xne1xn+1on utilise la relation de recurrence := 1n+1x xn+2e1x 1x2n + 2xn+1e1xx2n+4!+ n + 21n+1e1xxn+2= 1n+1e1x x n + 2x2 + n + 2x2xn+4= 1n+1e1x xxn+4 = 1n+2e1x1xn+3Donc Pn+1 est vraie• Donc n N,xne1xn+1= 1n+1e1xxn+2Exercice 27Prolonger par continuite en a et etudier la derivabilte et la continuite de la derivee et si la fonction est declasse C1 ou non de chacune des fonctions suivantes :f1x = e2x 1x,a = 0;f2x = x sinx sin 1x,a = 0f3x = xx2 2x + 1x 1,a = 1;f4x = x2 cos 1x,a = 0f5x = exx ,a = 0.Exercice 28Soit f : R →R une fonction deﬁnie par fx = 0: si x 0e1x: si x 01. Montrer que f est de classe Csur 0, +, et que f nx = e1x Pn 1xou Pn RX.2. Montrer que f est de classe Csur R.Exercice 291. Determiner l’expression de la derivee de la fonction ln x sur R.2. Determiner le plus grand entier n N tel que f est de classe Cn sur R.fx =x3 ln x: si x 00: si x 0Solutiona Soit la fonction gx = ln x. Si x 0, gx = ln x donc g′x = 1xSi x 0, gx = lnx donc g′x =1x × 1 = 1x.Dans tous les cas, g′x = 1xb Pour x 0, fx = x3 lnx.La fonction est Csur R.

Page 18 : i. On a limx→0 x ln x = 0 donc limx→0 x3 ln x = 0. Donc la fonction f est continue en 0 car elle est nullea droite.On a x3 ln x 0x 0= x2 ln x →x→0 0. Donc f est derivable en 0.x R, f ′x = 3x2 lnx + x3 1x = 3x2 lnx + x2On a limx→0 x ln x = 0 donc limx→0 f ′x = 0. Donc la fonction f ′ est continue en 0 car elle est nullea droite.Donc la fonction f est de classe C1.ii. 3x2 ln x 0x 0= 3x ln x →x→0 0 on calcule le taux pour la seulle partie de f ′ qui pourrait poserun probleme. Donc f ′ est derivable en 0.x R, f ′′x = 6x lnx + 5x.On a limx→0 x ln x = 0 donc limx→0 f ′′x = 0. Donc la fonction f ′′ est continue en 0 car elle est nullea droite.Donc la fonction f est de classe C2.iii. 6x ln x 0x 0= 6 ln x →x→0 . Donc f ′′′ n’est pas derivable en 0.La fonction est donc de classe C2 et pas de classe C3. L’entier n est 2Exercice 301. Montrer que, n N,12n + 1 n + 1 n 12n2. On posevn = 8n + 4 8pnn + 1Montrer que :1n + 1 vn 1nEn deduire que vn converge et determiner sa limite.Autres exercicesExercice 31 Injectivite localeSoit f : R →R derivable et a R tel que f ′a ̸= 0.1. Montrer qu’il existe un voisinage V de a tel que x V \a, fx ̸= fa.2. Si f ′ est continue au point a, montrer qu’il existe un voisinage V de a tel que fV soit injective.Exercice 32 Proprietes de parite et de periodiciteSoit f : R →R derivable.1. Que peut-on dire de f ′ si on sait que f est paire ? impaire ? periodique ?2. Que peut-on dire de f si on sait que f ′ est paire ? impaire ? periodique ?3. Montrer que si f ′ est T-periodique et fT ̸= f0, alors f n’a pas de periode on etudiera fnT pourn N.Exercice 33Soit f une fonction de classe Cn sur a, b s’annulant en n + 1 points distincts de a, b.On suppose donc qu’il existe n + 1 elements de a, b, notes : x00 x01 ... x0n , qui veriﬁent :fx00 = fx01 = ... = fx0n = 0.1. Montrer, par recurrence sur k que : pour tout entier k tel que 0 k n, il existe n k + 1 elements dea, b, notes xk0 xk1 ... xknk qui veriﬁent : f kxk0 = f kxk1 = ... = f kxkn = 0.2. Que pouvez vous en deduire concernant l’existence de zeros eventuels de f n sur a, b ?Exercice 34Soit f derivable sur R et qui possede un unique point ﬁxe ω tel que fω = ω. On deﬁnit une suite xnnN parla donnee de x0 et la recurrence xn+1 = fxn.1. Montrer que si f ′ω 1, alors α 0, k R, 0 k 1, x ω α, ω + α,fx fωx ω k.2. En deduire, par recurrence, que si x0 ω α, ω + α, alors : n N,fxn fω knx0 ω.

Page 19 : 3. Conclure quant a la convergence vers w.4. On suppose maintenant que f ′ω 1 et on va montrer que la suite xnnN converge vers w si etseulement si elle est stationnaire i.e. xn = ω a partir d’un certain rang.Montrer que α 0, k 1, x ω α, ω + α,fx fωx ω k.5. Supposons donc, par l’absurde, que : n, xn ̸= ω non stationnaire, et que lim un = ω.a Montrer qu’a partir d’un certain rang N, on aura : xn ω α, ω + α,b En deduire, par recurrence, que : n N, fxnfω knNxN ω et obtenez la contradictionsouhaitee.6. Que dire dans le cas f ′ω = 1 ?On pourra etudier la suite deﬁnie a l’aide de la fonction : fx = x2 + 12, avec x0 = 0 puis avec x0 = 2.Solution1. La fonction f etant derivable sur R, elle est derivable en ω doncϵ 0, α 0, x ω α, fx fωx ωf ′ω ϵOn a pour ϵ = 1 f ′ω2x, x ω α,fx fωx ω fx fωx ωf ′ω + f ′ω 1 f ′ω2+ f ′ω 1 + f ′ω2On pose k = 1 + f ′ω2qui repond a la question.2. D’apres la question precedente,x ω α; ω + α, fx fωx ω k donc fx fω kx ωOn construire un raisonnement par recurrence :On prouve la propriete n N, Pn : fxn fω knx0 ωOn a fx0 fω kx0 ωExercice 35Soit f C2a, b, R telle que fa = f ′a et fb = f ′b. Montrer qu’il existe c a, b tel que f ′′c = f ′c.Classiﬁcation des exercices :Tech : techniques a maˆıtriser. diﬃcile