TD1 Logique et Raisonnement Correction

Télécharger le TD1 Logique et Raisonnement Correction en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93

Page 1 : Algebre-Premier semestre 2023 - 2024CY TechTD AlgebreLogique et Raisonnement.Algebre

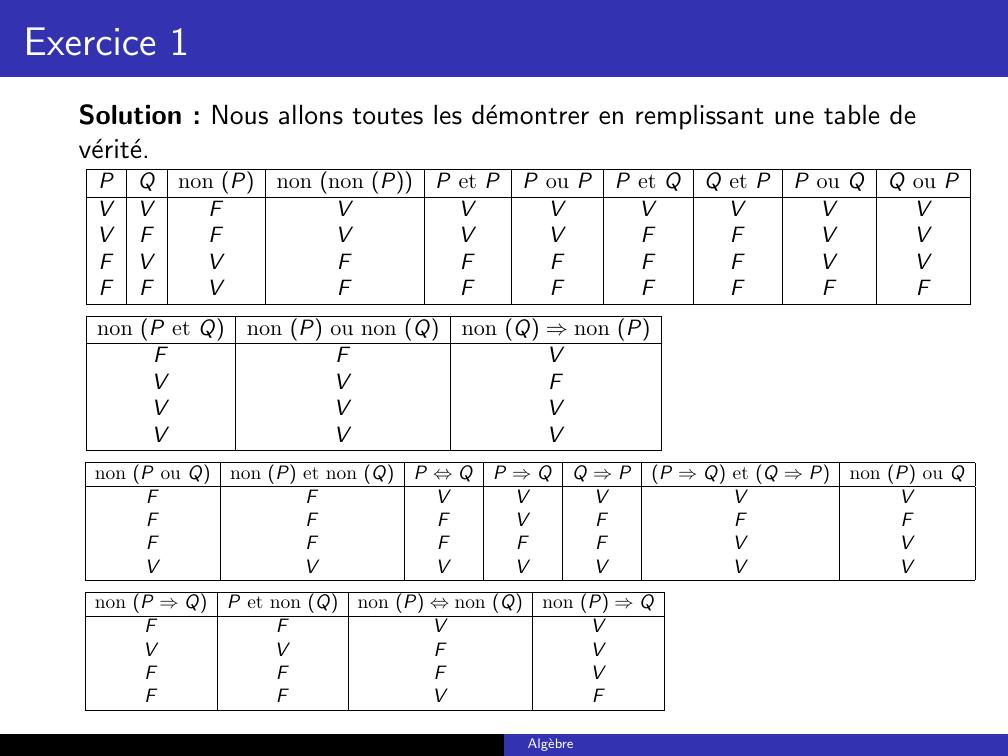
Page 2 : Exercice 1.1Soit P, Q deux propositions. Demontrer les equivalences suivantes enutilisant des tables de verite.1non non P ⇔P2P et P ⇔P3P ou P ⇔P4P et Q ⇔Q et P5P ou Q ⇔Q ou P6non P ou Q ⇔non P et non Q7P ⇒Q ⇔non P ou Q8P ⇔Q ⇔non P ⇔non Q9P ou Q ⇔non P ⇒QAlgebre

Page 3 : Exercice 1Solution : Nous allons toutes les demontrer en remplissant une table deverite.PQnon Pnon non PP et PP ou PP et QQ et PP ou QQ ou PVVFVVVVVVVVFFVVVFFVVFVVFFFFFVVFFVFFFFFFFnon P et Qnon P ou non Qnon Q ⇒non PFFVVVFVVVVVVnon P ou Qnon P et non QP ⇔QP ⇒QQ ⇒PP ⇒Q et Q ⇒Pnon P ou QFFVVVVVFFFVFFFFFFFFVVVVVVVVVnon P ⇒QP et non Qnon P ⇔non Qnon P ⇒QFFVVVVFVFFFVFFVFAlgebre

Page 4 : Exercice 1.1Soit P, Q et R trois propositions. Demontrer les equivalences suivantesen utilisant des tables de verite.1P et Q et R ⇔P et Q et R2P ou Q ou R ⇔P ou Q ou R3P ou Q et R ⇔P ou Q et P ou R4P et Q ou R ⇔P et Q ou P et RAlgebre

Page 5 : Exercice 1.1Solution : Nous allons toutes les demontrer en remplissant une table deverite.PQRQ et RP et Q et RP et QP et Q et RP ou Q ou RVVVVVVVVVVFFFVFVVFVFFFFVVFFFFFFVFVVVFFFVFVFFFFFVFFVFFFFVFFFFFFFFP ou QP ou Q ou RP ou Q et RP ou RVVVVVVVVVVVVVVVVVVVVVVFFFVFVFFFFAlgebre

Page 6 : Exercice 1.1Nous avons aussi :PQRP ou Q et P ou RP et RQ ou RP et Q ou RP et Q ou P et RVVVVVVVVVVFVFVVVVFVVVVVVVFFVFFFFFVVVFVFFFVFFFVFFFFVFFVFFFFFFFFFFAlgebre

Page 7 : Exercice 1.2Soient P, Q et R deux propositions. Les propositionsP ou Q et R etP ou Q et R sont-elles equivalentes ?Solution : Nous allons les comparer en remplissant une table de verite.PQRQ et RP ou Q et RP ou QP ou Q et RVVVVVVVVVFFVVFVFVFVVVVFFFVVFFVVVVVVFVFFFVFFFVFFFFFFFFFFFComme les table de verite sont differents, on conclut que les propositionsP ou Q et R etP ou Q et R ne sont pas equivalents.Algebre

Page 8 : Exercice 1.3Sans utiliser de table de verite mais en utilisant les differentes proprietes dejademontrees, demontrer quenon P =⇒Q⇐⇒P et non QetP ou Q⇐⇒non P =⇒Q .Reponse : D’abordnon P =⇒Q⇐⇒non non P ou Q⇐⇒non non P et non Q⇐⇒P et non Q.En suitenon P =⇒Q⇐⇒non non PouQ⇐⇒P ou Q.Algebre

Page 9 : Exercice 1.4Traduire en toutes lettres les sept propositions suivantes lorsque x designe unindividu, y un film et que Px, y est la propositionL’individu x a vu le film y .On traduit :x : Pour tout individu = tous les individus.y : Pour tout film = tous les films.x : il existe au moins un individu.y : il existe au moins un film.1x, y, Px, yReponse : Tous les individus ont vus tous les films.2x, y, Px, yReponse : Il existe un individu qui a vu tous les films.Algebre

Page 10 : Exercice 1.43y, x, Px, yReponse : Il existe un film qui a ete vu par tous les individus.4x, y, Px, yReponse : Tous les individus ont vu au moins un film.5x, y, Px, yReponse : Il existe un individu qui a vu au moins un film.6y, x, Px, yReponse : Il existe un film qui a ete vu par au moins un individu.Algebre

Page 11 : Exercice 1.47y, x, Px, yReponse : Tous les films ont ete vus par au moins un individu.Algebre

Page 12 : Exercice 1.5Soit I un intervalle non vide de R et f : I →R une fonction definie sur Ia valeurs reelles. Exprimer verbalement la signification des propositionssuivantes :1λ R, x I, f x = λ.Reponse : La fonction f est constante sur I, de valeur λ.2x I, f x = 0 =⇒x = 0.Reponse : Si la fonction f s’annule, alors elle s’annule uniquementen 0, c-a-d, la fonction f s’annule uniquement en 0, ou ne s’annulepas.3y R, x I, f x = y.Reponse : La fonction f est surjective, c’est-a-dire, toutes lesvaleurs de R sont atteintes par f .Algebre

Page 13 : Exercice 1.54x I, y I, f x = f y =⇒x = y.Reponse : La fonction f est injective, c’est-a-dire, f prend au plusune fois chaque valeur.5ϵ 0, y R, α 0, x R, x y α =⇒f xf y ϵ.Reponse : La fonction f est continue en R.6ϵ 0, α 0, x R, y R, x y α =⇒f xf y ϵ.Reponse : La fonction f est uniformement continue.Algebre

Page 14 : Exercice 1.6Soit I un intervalle non vide de R et f : I →R une fonction definie sur Ia valeurs reelles. Exprimer a l’aide de quantificateurs les propositionssuivantes :1f est l’application nulle.Reponse : x I, f x = 0.2f n’est pas l’application nulle.Reponse : x I, f x ̸= 0.3La fonction f s’annule.Reponse : x I, f x = 0.4f ne s’annule pas sur I.Reponse : x I, f x ̸= 0.Algebre

Page 15 : Exercice 1.65f est une fonction constante.Reponse : λ R, x I, f x = λ oux I, y I, f x = f y.6La fonction f n’est pas une fonction constante.Reponse : x I, y I, f x ̸= f y.7La fonction f ne prend jamais deux fois la mˆeme valeur.Reponse : x I, y I, x ̸= y =⇒f x ̸= f y.8La fonction f presente un minimum.Reponse : c I, x I, f x f c.Algebre

Page 16 : Exercice 1.69La fonction f prend des valeurs arbitrairement grandes.Reponse : M R, x I, f x M.10 f est une fonction affine.Reponse : m R, n R, x R, f x = mx + n.Algebre

Page 17 : Exercice 1.7Donner la negation des phrases suivantes1x 3.Reponse : x 3.20 x 2=0 x et x 2.Reponse : x 0 ou x 2.3x R, y R, x + y 0.Reponse : x R, y R, x + y 0.4x R, y R, x + y 0.Reponse : x R, y R, x + y 0.Algebre

Page 18 : Exercice 1.75x R, y R, x + y 0.Reponse : x R, y R, x + y 0.6x R, y R, y 2 x.Reponse : x R, y R, y 2 x.7P et non Q.Reponse : non P ou Qqui est equivalent aP =⇒Q8P et Q et R.Reponse : non P ou non Q ou non R.Algebre

Page 19 : Exercice 1.79P ou Q et R.Reponse : non P et non Q ou non R10 P et Q =⇒R =⇒S.Reponse : Rappelons queP et Q =⇒R =⇒S⇐⇒non P et Q ou R =⇒S.Donc la negation de P et Q =⇒R =⇒S est :nonnon P et Q ou R =⇒S⇐⇒P et Q et non R =⇒S⇐⇒P et Q et non non R ou S⇐⇒P et Q et R et non S⇐⇒P et Q et R et non S.Algebre

Page 20 : Exercice 1.711 Tous les habitants de la rue du Havre qui ont les yeux bleusgagneront au loto et prendront leur retraite avant 50 ans.Reponse : Il existe un habitant de la rue du Havre qui a les yeuxbleus, qui ne gagnera pas au loto ou qui prendra sa retraite apres50 ans.12 Tout triangle rectangle possede un angle droit.Reponse :Il existe un triangle rectangle qui n’a pas d’angle droit.13 Dans toutes les ecuries, tous les chevaux sont noirs.Reponse : Il existe une ecurie dans laquelle il y a au moins uncheval qui n’est pas noire.Algebre

Page 21 : Exercice 1.714 Pour tout entier x, il existe un entier y tel que, pour tout entier z, larelation z x implique la relation z x + 1.Reponse : A l’aide de quantificateurs on peut ecrire :x, y, z,z x =⇒z x + 1.Donc la negation c’est : Il existe un entier x, tel que pour toutentier y, il existe un entier z tel que l’on a a la fois z x etz x + 1.15 ϵ 0, α 0,x 57 α =⇒5x 7 ϵ.Reponse : ϵ 0,α 0,x 57 αet5x 7 ϵ.Algebre

Page 22 : Exercice 1.8Soitf : R →R.Indiquer la difference de sens entre les deux propositions proposees :1. x R, y R, y = f xety R, x R, y = f x.Reponse :Dans le premier cas, chaque reel possede au moins une image, doncla fonction est bien definie sur R.Dans le second tous les reels ont la mˆeme image donc f estconstante.2. y R, x R, y = f xetx R, y R, y = f x.Reponse :Dans le premier cas, toutes les valeurs de R sont atteintes par f fest surjective sur R ;Dans le second cas, il existe un x tel que f x prend toutes lesvaleurs reelles possibles donc le graphe de f est une droiteverticale.Algebre

Page 23 : Exercice 1.83. x R, M R, f x MetM R, x R, f x M.Reponse :Dans le premier cas, f x est toujours plus petit qu’un reel.Dans le second cas, f est majoree par M.Algebre

Page 24 : A faire chez soi - Exercice 1.9Soit f : R →R une fonction. Pour chacune des propositions suivantes,donner graphiquement a main levee un exemple de fonction f NE laverifiant PAS contre-exemple.1M R, x R, f x M2x R, f x 0 ⇒x 03x R, f x 1 ou f x 1Solution : Une courbe qui repond aux trois questions est la courberepresentative de la fonction carre.Algebre

Page 25 : A faire chez soi - Exercice 1.10Soit I un intervalle non vide de R etf : I →Rune fonction a valeurs reelles definie sur I. Exprimer les negations despropositions suivantes :1x I, f x ̸= 0.Reponse : x I, f x = 0.2y R, x I, f x = y.Reponse : y R, x I, f x ̸= y.3M R, x I, f x M.Reponse : M R, x I, f x M.4x I, y I, f x = f y =⇒x = y.Reponse : x I, y I, f x = f y et x ̸= y.Algebre

Page 26 : A faire chez soi - Exercice 1.11Completer les pointilles par le connecteur logique qui s’impose=⇒,⇐=,⇐⇒1x R; x2 = 4 · · · · · · x = 2.Reponse : x R; x2 = 4 ⇐= x = 2.2z C; z = z · · · · · · z RReponse : z C; z = z ⇐⇒z R.3x R; x = π · · · · · · e2ix = 1.Reponse : x R; x = π =⇒e2ix = 1.Algebre

Page 27 : A faire chez soi - Exercice 1.12Les propositions suivantes sont-elles vraies ou fausses ? Justifier.1x R, x 2 ⇒x 32x, y R+2, x y ⇔1x 1y3x R+, x x4n N, Pnk=0 k 100Solution :1Faux, en effet, x R, x 2 et x 3. Il suffit de prendre x = 2.5.Puisque la negation est vraie, la phrase est fausse.2Faux. On prend x 0 y, ainsi, 1x 0 1y . Ce n’est vrai que si onimpose a x et y d’ˆetre de mˆeme signe.3Vrai, il suffit de prendre x = 0.25, x = 0.54Vrai, il suffit de prendre n = 100.Algebre

Page 28 : A faire chez soi - Exercice supplementaireReprendre l’exercice 5 en donnant a chaque fois les negations en toutes lettreset avec les quantificateurs. On commence par noter quenon Px, y = L’individu x n’a pas vu le film y Reponse :1x, y, non Px, y : Il existe un individu qui n’a pas vu au moins unfilm.2x, y, non Px, y : Pour tous les individus, il existe un film qui n’apas ete vu. On peut aussi dire : Pour chaque individu, il existe au moinsun film qu’il n’a pas vu personne n’a vu tous les films.3y, x, non Px, y : Pour tous les films, il existe un individu qui ne l’apas vu Aucun film n’a ete vu par tout le monde.4x, y, non Px, y : Il existe un individu qui n’a vu aucun film.Algebre

Page 29 : A faire chez soi - Exercice supplementaire5x, y, nonPx, y : Aucun individu n’a vu de film.6y, x, non Px, y : Aucun film n’a ete vu7y, x, non Px, y : Il existe un film qui n’a ete vu par aucun individu.Algebre

Page 30 : Exercice 2.11Soit x un irrationnel positif. Montrer que x est irrationnel.2Montrer que2 est un nombre irrationnel.Solution : Voir CM.Algebre

Page 31 : Exercice 2.1Soit x un irrationnel positif. Montrer que x est irrationnel. C’est-a-dire,nous devons montrer : sot x un reel positifSi x est un irrationnel=⇒x est irrationnel.On rappelle quex n’est pas irrationnel⇐⇒x est rationnel.Nous allons montrer la proposition en utilisant un raisonnement parcontraposition.Reponse : Nous devons donc montrer : soit x un reel positif alorsx est rationnel=⇒x est rationnel.Supposons x rationnel. Par definition d’un nombre rationnel, il existep, q Z tel quex = pq=⇒x = p2q2qui est le quotient de deux entiers naturels. Donc x est rationnel.Algebre

Page 32 : Exercice 2.2Demontrer, en raisonnant par l’absurde, que si n N×, alors n2 + 1 n’estpas le carre d’un entier naturel.Reponse : Supposons que n est un entier strictement positif et quen2 + 1 est le carre d’un entier naturel a. Trouvons une contradiction.Par hypothesea2 = n2 + 1.Donc1 = a2 n2 = a na + n.Puisque le produit de ces deux nombre est egal a 1, on concluta + nest different de 0.On a en plusa 0.Par consequent a + n N car a N et n N eta + n n 0.Algebre

Page 33 : Exercice 2.2Le nombre a + n est donc un entier positif. Il s’ensuit, comme 1 est unentier positif, quea nest un entier positif.Maintenant, un produit d’entiers positifs est egal a 1 si et seulement sichacune d’entre eux est egal a 1. On en deduita n = 1eta + n = 1.Par soustraction des deux egalites2n = 0.Puisque n est strictement positif, cela est une contradiction. D’ou onconclut que n2 + 1 n’est pas le carre d’un entier naturel.Algebre

Page 34 : Exercice 2.3Montrer que lorsqu’un reel peut ˆetre ecrit sous la formea + b2,a Z, b Z,alors les entiers a et b sont necessairement uniques.Reponse : Soit r R tel quer = a + b2a Z, b Z.Nous allons montrer que cette ecriture est unique en raisonnant parl’absurde. Supposons donc qu’il existe deux couples distincts d’entiersa, b et a′, b′ tels quer = a + b2etr = a′ + b′2Essayons d’obtenir une contradiction. Pour cela on ecrit0 = r r=a + b2 a′ + b′2=a a′ + b b′2.Algebre

Page 35 : Exercice 2.3On a deux cas a etudierSi b = b′, alors a = a′ ce qui est en contradiction avec la hypotheseque les couples etaient distincts.Si b ̸= b′, on deduit0 = a a′ + b b′2=⇒2 =a′ a Zb b′ Z Q.C’est-a-dire2 est un rationnel. Ce qui est faux, contradiction.Par consequent, lorsqu’un reel peut ˆetre ecrit sous la formea + b2,a Z, b Z,alors les entiers a et b sont necessairement uniques.Algebre

Page 36 : Exercice 2.4Montrer que toute fonction f : R →R s’ecrit de fa¸con unique comme lasomme d’une fonction paire et d’une fonction impaire. Donner cettedecomposition sif x =x + 1x2 + x + 1Preuve : Nous allons raisonner par analyse-synthese.Soit f une fonction de R dans R.• Analyse : Supposons le probleme resolu, c’est-a-dire qu’il existe deuxfonctionsg : R →Reth : R →R,avecgpaireethimpairetelles quex R,f x = gx + hx.1Algebre

Page 37 : Exercice 2.4Comme g est paire et h est impaire on a aussix R,f x = gx + hx = gx hx.2En additionnant et soustrayant les egalites 1 et 2 nous obtenons2gx = f x + f x=⇒gx = f x + f x22hx = f x f x=⇒hx = f x f x2.Ainsi, s’il existe une solution au probleme, alors ce sont necessairementles fonctions g et h ci-dessus.Algebre

Page 38 : Exercice 2.4• Synthese : Nous allons verifier que g et h sont bien solutions duprobleme.On a bien f = g + h. En effetx R,gx + hx = 2f x2= f x.La fonction g est paire. En effetx R,gx = f x + f x2= gx.La fonction h est impaire. En effetx R,hx = f x f x2= hx.Nous avons donc demontre par Analyse-Synthese qu’il existe un uniquecouple g, h avec g paire et h impaire tel que f = g + h.Algebre

Page 39 : Exercice 2.4Finalement, sif x =x + 1x2 + x + 1alorsgx =1x4 + x2 + 1,ethx =x3x4 + x2 + 1.Algebre

Page 40 : A faire chez soi - Exercice 2.5Soit a et b deux reels. Montrer quea2 + b2 = 0=⇒a = b = 0.Solution : Voir CM.Algebre

Page 41 : A faire chez soi - Exercice 2.6Soitf : R →Rune fonction. Montrer quefimpaire=⇒f 0 = 0.On rappelle que une fonction f : R →R est dite impaire si pour toutx R on af x = f x.Nous allons montrer la proposition en utilisant un raisonnement direct.Reponse : Supposons f impaire. Montrons f 0 = 0. Puisque f estimpaire, pour tout x R on af x = f x.En particulier pour x = 0, on obtientf 0 = f 0 = f 0=⇒2f 0 = 0=⇒f 0 = 0.Algebre

Page 42 : A faire chez soi - Exercice 2.7Deux joueurs s’affrontent sur le jeu suivant. Ils disent chacun a leur tour unnombre entre 1 et 7 . Les nombres sont additionnes et des que le cumul desnombres qu’ils ont proposes vaut 100, le jeu est fini. Le joueur qui a atteint 100et a donc parle en dernier gagne. Comment jouer ?Solution : On raisonne par analyse-synthese.Analyse : Nous allons trouver la reponse de maniere naturelle, en partant del’objectif qui est d’atteindre 100 . Si je veux atteindre 100 , il faut que monadversaire ait atteint un nombre entre 93 auquel cas je dirai 7 et 99 auquelcas je dirai 1 . Pour obtenir cela, il suffit que j’atteigne 92 a l’etapeprecedente. Mais pour atteindre 92 a coup sˆur, j ’ ai besoin que mon adversaireait atteint un nombre entre 85 auquel cas je dirai 7 et 91 auquel cas je dirai1. Pour cela, il faudrait que j’atteigne 84 a l’etape precedente. On reproduit leraisonnement et on realise que pour gagner, il suffit que j’arrive a atteindre al’etape precedente 84 8 = 76, donc juste avant 76 8 = 68, et ainsi de suite60, 52, 44, 36, 28, 20, 12 et 4 . On observe ici une suite arithmetique de raison 8 .Algebre

Page 43 : A faire chez soi - Exercice 2.7Synthese : Nous sommes partis du resultat la victoire pour remonter audebut de la partie et voir comment la jouer. Nous pouvons maintenant donnerla strategie gagnante, en respectant les regles du jeu.- Si je commence, je dis 4, puis mon adversaire va porter le cumul a un nombreentre 5 et 11, et je dis le chiffre qu’il faut pour atteindre 12, puis20,28,36,44,52,60,68,74,82, et enfin 100.- Si mon adversaire commence et connait cette strategie, je perdrai. Mais sinon,je peux la rattraper : des que je peux je dis le chiffre me permettant deretomber sur 4 ou 12 ou 20 . . .. Si il commence par 1, 2, 3, 5,6 ou 7, je repondspar 3, 2, 1, 7, 6, 5. S’il commence par 4, je reponds par 1 et attends de voir cequ’il dit. S’il dit 1, 2, 3, 4, 5, ou 6, j’atteins 12 avec 7, 6, 5, 4, 3, 2. Mais s’ilrepond 7, je recommence a dire 1 et attends le tour suivant pour atteindre 20etc. S’il repond tout le temps 7, c’est qu’il avait compris la strategie et je perds.Algebre

Page 44 : A faire chez soi - Exercice 2.8Un vol a ete commis dans un asile. Trois pensionnaires A, B et C sontsuspects. Voici leurs temoignages, chacun formulant trois assertions :A: Je suis innocent. A l’heure du vol, j’etais avec B. C’est C le coupable.B: Je suis innocent. A aussi. A n’etait pas avec moi a l’heure du vol.C: Je suis innocent. B aussi. A a menti trois fois.Vous savez que chaque suspect a au moins menti une fois sur ses troisaffirmations. Qui est le coupable ?Solution : Trois coupables possibles, donc trois cas a etudier on raisonne pardisjonction des cas :A coupable : A et B ne peuvent pas ˆetre ensembles a l’heure du vol puisqu’iln’y a qu’un coupable.Affirmations de A : F, F, FAffirmations de B : V, F, VAffirmations de C : V, V, VOr C est cense mentir au moins une fois, donc A est innocentAlgebre

Page 45 : A faire chez soi - Exercice 2.8B coupable : A et B ne peuvent pas ˆetre ensembles a l’heure du vol puisqu’iln’y a qu’un coupable.Affirmations de A : V, F, FAffirmations de B : F, V, VAffirmations de C : V, V, FLes trois ont menti au moins une fois, donc B est potentiellement le coupable.C coupable :Affirmations de A : V, ?, V . La deuxieme proposition est donc forcement fausse,donc A et B n’etaient pas ensembles.Affirmations de B : V, V, ? . La troisieme proposition est donc forcement fausse,donc A et B etaient ensemble. C’est en contradiction avec ce qui precede.Affirmations de C : F, V, FIl est impossible que A et B mentent au moins une fois. Donc C est innocent.En conclusion, le coupable est B.Algebre

Page 46 : A faire chez soi - Exercice 2.9Thomas, Jules et Yves sont partis contempler des oiseaux. Chacun a vu unoiseau que les deux autres n’ont pas vu. Chaque deux ont vu un oiseau que letroisieme n’a pas vu, et un oiseau a ete vu par les trois.Parmi les oiseaux que Thomas a vus, deux sont jaunes. Pami ceux vus parJules, trois sont jaunes, et pami ceux vus par Yves, quatre sont jaunes.Combien d’oiseaux jaunes ont ete vus au total ? Combien d’oiseaux non jaunesont ete vus au total ?Solution : Nous allons remplir un tableau avec une ligne par individu et autantde colonnes que necessaires pour les oiseaux.abcdefgThomasVXXVVXVJulesXVXVXVVYvesXXVXVVVPuisque que Yves n’a vu que quatre oiseaux et qu’il a vu au moins quatreoiseaux jaunes, on en deduit que tous ses oiseaux sont jaunes, donc c, e, f et gsont jaunes. Thomas n’a vu que deux oiseaux jaunes, donc a et d ne sont pasjaunes. Jules a vu trois oiseaux jaunes, donc b est jaunes. Au final : 5 oiseauxjaunes b, c, e, f, g et 2 non jaunes a et d.Algebre

Page 47 : A faire chez soi - Exercice supplementaireSoit x un reel positif. Montrer queϵ 0, x ϵ=⇒x = 0Nous allons montrer la proposition en utilisant un raisonnement parcontraposition. C’est-a-dire, nous allons montrer : soit x un reel positifx ̸= 0=⇒ϵ 0, x ϵPreuve : Soit x un reel positif. Supposons x ̸= 0. Donc x 0. Enchoisissantϵ = x2,on obtientϵ 0, etx ϵ.Autrement dit, pour tout x 0 existe ϵ 0 tel que ϵ x. Ce qui montrela proposition.Algebre

Page 48 : A faire chez soi - Exercice supplementaireSoit a et b deux reels. Montrer en utilisant deux methodes quea + b 1=⇒a 12oub 12.Solution :Par contraposition. Nous allons donc montrer quea 12etb 12=⇒a + b 1.Cette implication est evidente. En effet, en additionnant les deuxinegalites strictes de gauche on obtient celle de droite.Par disjonction de cas. Deux cas sont possibles :Si a 12, alors on a bien a 12 ou b 12.Si a 12, alors a 12 et 1 a 1 12. Donca + b 1=⇒b 1 a=⇒b 1 12 = 12.et on a bien a 12 ou b 12.Algebre

Page 49 : A faire chez soi - Exercice supplementaireLa somme et le produit d’un nombre rationnel non-nul pour le produitet d’un nombre irrationnel sont des nombres irrationnels.Rappelons que :La somme de deux nombres rationnels est un nombres rationnel. Eneffetpq + p′q′ = pq′ + p′qqq′Q.Le produit de deux nombres rationnels est un nombres rationnel. Eneffetpq · p′q′ = pp′qq′ Q.Nous allons montrer la proposition en raisonant par l’absurde.Algebre

Page 50 : A faire chez soi - Exercice supplementairePreuve : Soit r Q et x ̸Q.Il nous faut montrer quer + x ̸Q.Pour cela, raisonnons par l’absurde et supposons r + x Q. Alors onax = x + r z QrzQzQ.Contradiction ! Par consequent r + x ̸Q. C’est-a-dire r + x estirrationnel.Algebre

Page 51 : A faire chez soi - Exercice supplementaireIl nous faut montrer quer · x ̸Q.Raisonnons par l’absurde et supposons r · x Q. Alors on ax = r · x z Q·1rzQzQ.Contradiction ! Par consequent r · x ̸Q. C’est-a-dire r · x estirrationnel.Algebre

Page 52 : A faire chez soi - Exercice supplementaireUn rectangle a pour aire 170 m2. Montrer que sa longueur est superieurea 13 m.Soit l R×+ la largeur du rectangle et L l, + sa longueur. On doitdonc montrer : l R×+, L l, +on al × L = 170=⇒L 13.Nous allons montrer la proposition en utilisant un raisonnement parcontraposition. C’est-a-dire, nous allons montrer : l R×+,L l, +on aL 13=⇒l × L ̸= 170.Preuve : Supposons L 13. Alors l L 13, c’est-a-direl 13etL 13,et on peut conclure par produit des inegalites quel × L 13 × 13 = 169 170.Algebre

Page 53 : A faire chez soi - Exercice supplementaireDemontrer que si vous rangez n + 1 paires de chaussettes dans n tiroirsdistincts, alors il y a au moins un tiroir contenant au moins deux paires dechaussettes.Preuve : NotonsP = On a range n + 1 chaussettes dans n tiroirs distincts.Q = Il existe un tiroir contenant au moins deux paires de chaussettes.On doit donc montrer queP=⇒Q.Nous allons montrer la proposition en raisonant par l’absurde. C’est-a-dire onsupposePetnon Q,et on essaye d’arriver a une contradictionSupposons donc que on a range n + 1 chaussetes dans n tiroirs distincts, etque chaque tiroir contient au plus une paire de chaussettes. Alors il y aura auplus1 + 1 + · · · + 1 = npaires de chaussettes, ce qui contredit qu’il y en a n + 1. Donc un tiroir doitcontenir au moins deux paires de chaussettes.Algebre

Page 54 : A faire chez soi - Exercice supplementaireDeterminer toutes les fonctionsf : R →Rqui satisfont l’equationx R, f x + xf 1 x = 1 + x.3Preuve : Nous allons raisonner par analyse-synthese.Analyse : Supposons f est solution de l’equation. Posonsy = 1 x=⇒x = 1 y.Alors en rempla¸cant x par 1 y dans 1, on obtientf 1 y + 1 yf y = 2 y.D’ou on peut conclure que, pour tout y Rf 1 y = 1 yf y + 2 y.Algebre

Page 55 : A faire chez soi - Exercice supplementaireAinsi, en posant y = x dans la equation de depart, on conclutf y + y1 yf y + 2 y = 1 + y⇐⇒f y + yf y + y 2f y + 2y y 2 = 1 + y⇐⇒f y1 y + y 2 + 2y y 2 = 1 + y⇐⇒f y1 y + y 2 = 1 y + y 2.Maintenant, comme 1 y + y 2 ̸= 0, on en deduit quey R,f y = 1.Synthese : Nous allons verifier que la fonction constante f = 1 estbien solution du probleme. En effetf x + xf 1 x = 1 + x.L’unique solution de cette equation est donc la fonction constantex 7→f x = 1.Algebre

Page 56 : A faire chez soi - Exercice supplementaireSoit f la fonction definie parf : R →Rx 7→f x = x + 12x 1.Montrer que pour tout y ̸= 12, il existe x ̸= 12 tel que f x = y.Preuve : Nous allons raisonner par analyse-synthese.Analyse : Supposons le probleme resolu, c’est-a-dire qu’on a x tel quef x = y. Alorsx + 12x 1 = y⇐⇒x + 1 = 2x 1y⇐⇒x + 1 = 2xy y⇐⇒y + 1 = 2xy x⇐⇒y + 1 = x2y 1et comme y ̸= 12, on peut ecrirex = y + 12y 1.Ainsi, s’il existe x tel que f x = y, x doit necessairement ˆetre donne par laderniere egalite.Algebre

Page 57 : A faire chez soi - Exercice supplementaireSynthese : Verifions que x est bien solution du probleme. Nous devonsmontrer :x ̸= 12 : Faisons un raisonnement par l’absurde et supposons x = 12. Alors12 = y + 12y 1=⇒2y 1 = 2y + 2=⇒1 = 2.Contradiction ! Par consequent x ̸= 12.f x = y : On computef x = x + 12x 1 =y+12y1 + 12y+12y1 1=y+1+2y12y12y+12y12y1= y + 1 + 2y 12y + 1 2y 1= 3y3 = y.Nous avons donc demontre par Analyse-Synthese que si y ̸= 12, alors il existeun unique reel x R \ 12, tel quef x = y.Algebre

Page 58 : Exercice 2.10Demontrer que pour tout entier naturel non nul n on aPn : n! 2n1.Preuve : On raisonne par recurrence sur n.Initialisation : On a 1! = 1 211. Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire,n! 2n1.Montrons que Pn + 1 est vraie, autrement dit, montrons quen + 1! 2n+11 = 2n.On an + 1! = n + 1 · n!.Ainsi, par hypothese de recurrence, on en deduitn + 1! = n + 1 · n! n + 1 · 2n1.Algebre

Page 59 : Exercice 2.10Maintenant, pour tout n Non an 1=⇒n + 1 2.Par consequentn + 1! = n + 1 · n! n + 1 · 2n1 2 · 2n1 = 2n.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut que pour tout entier naturel n Non an! 2n1.Algebre

Page 60 : Exercice 2.11.aDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k = nn + 12.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k = 1et1 · 1 + 12= 1=⇒1Xk=1k = 11 + 12.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=1k = nn + 12.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k = n + 1n + 1 + 12= n + 1n + 22Algebre

Page 61 : Exercice 2.11.aOn computen+1Xk=1k=nXk=1k+n + 1=zHypothese de Recurrencenn + 12+ n + 1=nn + 1 + 2n + 12=n + 1n + 22.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on conclut pourtout entier naturel n N, l’identitenXk=1k = nn + 12.Algebre

Page 62 : Exercice 2.11.bDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k2 = nn + 12n + 16.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k2 = 12 = 1et11 + 12 · 1 + 16= 1=⇒1Xk=1k2 = 11 + 12 · 1 + 16.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=1k2 = nn + 12n + 16.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k2 = n + 1n + 1 + 12n + 1 + 16= n + 1n + 22n + 36Algebre

Page 63 : Exercice 2.11.bOn computen+1Xk=1k2=nXk=1k2+n + 12=zHypothese de Recurrencenn + 12n + 16+ n + 12=nn + 12n + 1 + 6n + 126=n + 1n2n + 1 + 6n + 16=n + 12n2 + 7n + 66=n + 1n + 22n + 36.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on conclut pourtout entier naturel n Nl’identitenXk=1k2 = nn + 12n + 16.Algebre

Page 64 : Exercice 2.11.cDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k3 = nXk=1k!2.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k3 = 13 = 12 = 1Xk=1k!2.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire,nXk=1k3 = nXk=1k!2.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k3 = n+1Xk=1k!2Algebre

Page 65 : Exercice 2.11.cOn computen+1Xk=1k3=nXk=1k3 + n + 13=zHypothese de Recurrence nXk=1k!2+ n + 13.Maintenant, d’apres l’exercice 2.11.a on peut ecrirenXk=1k = nn + 12d’ou on conclutn+1Xk=1k3 =nn + 122+ n + 13 = n2n + 124+ n + 13= n2n + 12 + 4n + 134= n + 12n2 + 4n + 14= n + 12n2 + 4n + 44= n + 12n + 224Algebre

Page 66 : Exercice 2.11.cMaisn + 12n + 224=n + 1n + 222= n+1Xk=1k!2Doncn+1Xk=1k3 = n+1Xk=1k!2.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut pour tout entier naturel n Nl’identitenXk=1k3 = nXk=1k!2= n2n + 124.Algebre

Page 67 : Exercice 2.12Demontrer que pour tout entier naturel n :Pn :3 divise 4n + 2.Pn :7 divise 32n+1 + 2n+2.Soit un entier a 2 tel que 3 divise a2 a. Demontrer que pourtout entier naturel n 2, 3 divise an a.Pn :17 divise 3 · 52n+1 + 23n+1.Preuve : On raisonne par recurrence sur n.Algebre

Page 68 : Exercice 2.12n N, Pn :3 divise 4n + 2.Initialisation : On a 40 + 2 = 1 + 2 = 3. Donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire4n + 2 est divisible par 3⇐⇒4n + 2 = 3k,k Z.Montrons que Pn + 1 est vraie, autrement dit, montronsk′ Z,4n+1 + 2 = 3k′On a4n+1 + 2 = 4 · 4n + 2= 43k 2 + 2Hypothese de Recurrence= 3 · 4k 8 + 2= 3 · 4k 6 = 34k 2zk′.Algebre

Page 69 : Exercice 2.12C’est-a-dire 4n+1 + 2 est divisible par 3. Fin de la recurrence. Parconsequent Pn =⇒Pn + 1, et on conclut que pour tout entiernaturel n on a3 divise 4n + 2Algebre

Page 70 : Exercice 2.12n N, Pn :7 divise 32n+1 + 2n+2Initialisation : On a 32·0+1 + 20+2 = 3 + 4 = 7. Donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire32n+1 + 2n+2 est divisible par 7⇐⇒32n+1 + 2n+2 = 7k,k Z.Montrons que Pn + 1 est vraie, autrement dit, montronsk′ Z,32n+1+1 + 2n+1+2 = 7k′On a32n+1+1 + 2n+1+2 = 32 · 32n+1 + 2 · 2n+2= 327k 2n+2 + 2 · 2n+2Hypothese de Recurrence= 9 · 7k 9 · 2n+2 + 2 · 2n+2= 7 · 9k 9 22n+2 = 79k 2n+2zk′.Algebre

Page 71 : Exercice 2.12C’est-a-dire 32n+1+1 + 2n+1+2 est divisible par 7. Fin de la recurrence.Par consequent Pn =⇒Pn + 1, et on conclut que pour tout entiernaturel n on a7 divise 32n+1 + 2n+2.Algebre

Page 72 : Exercice 2.12Soit un entier a 2 tel que 3 divise a2 a. Montrer la propriete :n N, Pn : n 2, 3 divise an a.Initialisation : La propriete est vraie au rang 2 d’apres l’enonce.Heredite : Soit n N avec n 2. Supposons Pn vraie, c’est-a-dire3 divise an a.Montrons que Pn + 1 est vraie, autrement dit, montrons3 divise an+1 a.On aan+1 a=an+1 a2 + a2 a=aan a + a2 aOr 3 divise an a par l’hypothese de recurrence et 3 divise a2 a. Donc3 divise la somme. C’est-a-dire : 3 divise an+1 a.Algebre

Page 73 : Exercice 2.12Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on a doncbien la propriete :3 divise an a pour tout entier n 2.Algebre

Page 74 : Exercice 2.12n N, Pn :17 divise 3 · 52n+1 + 23n+1Initialisation : On a 3 · 52·0+1 + 23·0+1 = 3 · 5 + 2 = 17. Donc P0 estvraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire3 · 52n+1 + 23n+1 est divisible par 17⇐⇒3 · 52n+1 + 23n+1 = 17k,k Z.Montrons que Pn + 1 est vraie, autrement dit, montronsk′ Z,3 · 52n+1+1 + 23n+1+1 = 17k′On a3 · 52n+1+1 + 23n+1+1 = 3 · 25 · 52n+1 + 8 · 23n+1= 2517k 23n+1 + 8 · 23n+1 Hypothese de Recurrence= 25 · 17k 25 · 23n+1 + 8 · 23n+1= 17 · 25k 25 823n+1 = 1725k 23n+1zk′.Algebre

Page 75 : Exercice 2.12C’est-a-dire 3 · 52n+1+1 + 23n+1+1 est divisible par 17. Fin de larecurrence. Par consequent Pn =⇒Pn + 1, et on conclut quepour tout entier naturel n on a17 divise 3 · 52n+1 + 23n+1Algebre

Page 76 : Exercice 2.13Soit un la suite reelle determinee par u0 = 2, u1 = 3 et pour toutn N :un+2 = 3un+1 2un.Montrer que pour tout n N : un = 2n + 1.Preuve : On raisonne par recurrence double sur n.Initialisation : On au0 = 2 = 1 + 1 = 20 + 1etu1 = 3 = 2 + 1 = 21 + 1.Donc P0 et P1 sont vrais.Heredite : Soit n N. Supposons Pn et Pn + 1 sont vrais,c’est-a-direun = 2n + 1etun+1 = 2n+1 + 1.Montrons que Pn + 2 est vraie, autrement dit, montrons queun+2 = 2n+2 + 1.Algebre

Page 77 : Exercice 2.13On aun+2 = 3un+1 2un= 32n+1 + 1 22n + 1Hypothese de Recurrence= 3 · 2n+1 + 3 2n+1 2= 3 1 · 2n+1 + 1= 2 · 2n+1 + 1= 2n+2 + 1.Fin de la recurrence. Par consequent Pn et Pn + 1 =⇒Pn + 2,et on conclut que pour tout entier naturel n on aun = 2n + 1.Algebre

Page 78 : A faire chez soi - Exercice 2.14Demontrer par recurrence l’egalite suivanten N, Pn :nXk=11kk + 1k + 2 =nn + 34n + 1n + 2.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=11kk + 1k + 2 =111 + 11 + 2 =11 + 341 + 11 + 2.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=11kk + 1k + 2 =nn + 34n + 1n + 2.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=11kk + 1k + 2 =n + 1n + 1 + 34n + 1 + 1n + 1 + 2 = n + 1n + 44n + 2n + 3.Algebre

Page 79 : A faire chez soi - Exercice 2.14On computen+1Xk=11kk + 1k + 2 = nXk=11kk + 1k + 2!+1n + 1n + 2n + 3=zHypothese de Recurrencenn + 34n + 1n + 2 +1n + 1n + 2n + 3=nn + 324n + 1n + 2n + 3 +44n + 1n + 2n + 3=nn + 32 + 44n + 1n + 2n + 3 =n3 + 6n2 + 9n + 44n + 1n + 2n + 3= n3 + 5n2 + 4n + n2 + 5n + 44n + 1n + 2n + 3= nn2 + 5n + 4 + n2 + 5n + 44n + 1n + 2n + 3=n + 1n2 + 5n + 44n + 1n + 2n + 3 = n + 1n + 1n + 44n + 1n + 2n + 3= n + 1n + 44n + 2n + 3Algebre

Page 80 : A faire chez soi - Exercice 2.14Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut pour tout entier naturel n Nl’identitenXk=11kk + 1k + 2 =nn + 34n + 1n + 2Algebre

Page 81 : A faire chez soi - 2.16Soit un la suite reelle determinee par u0 = 0, u1 = 0, u2 = 2 et pourtout n N :un+3 = 3un+2 3un+1 + un.Montrer que pour tout n N : un = nn 1.Preuve : On raisonne par recurrence triple sur n.Initialisation : On au0 = 0 = 00 1etu1 = 0 = 11 1etu2 = 2 = 22 1.Donc P0, P1 et P2 sont vrais.Heredite : Soit n N. Supposons Pn, Pn + 1 et Pn + 2 sontvrais, c’est-a-direun = nn 1etun+1 = n + 1netun+2 = n + 2n + 1.Montrons que Pn + 3 est vraie, autrement dit, montrons queun+3 = n + 3n + 2.Algebre

Page 82 : A faire chez soi - 2.16On aun+3 = 3un+2 3un+1 + un= 3n + 2n + 1 3n + 1n + nn 1= 3n + 2n + 1 + nn 1 3n + 1= 3n + 2n + 1 + n2n 4= 3n + 2n + 1 2nn + 2= n + 23n + 1 2n= n + 2n + 3.Fin de la recurrence. Par consequentPn, Pn + 1 et Pn + 2 =⇒Pn + 3,et on conclut que pour tout entier naturel n on aun = nn 1.Algebre

Page 83 : A faire chez soi - Exercice supplementaireDemontrer que pour tout entier non nul n on a :nXk=1k · k! = n + 1! 1.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k · k! = 1 · 1! = 1 = 2 1 = 2! 1.Donc P0 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=1k · k! = n + 1! 1.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k · k! = n + 1 + 1! 1 = n + 2! 1.Algebre

Page 84 : A faire chez soi - Exercice supplementaireOn computen+1Xk=1k · k!= nXk=1k · k!!+ n + 1 · n + 1!=zHypothese de Recurrencen + 1! 1 + n + 1 · n + 1!=n + 1!1 + n + 1 1=n + 1!n + 2 1=n + 2! 1.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on conclut pourtout entier naturel n l’identitenXk=1k · k! = n + 1! 1.Algebre

Page 85 : A faire chez soi - Exercice supplementaireSoit un la suite reelle determinee par u0 = 1, u1 = cosθ et pourn 2 :un = 2u1un1 un2.Montrer que pour tout n N : un = cosnθ.Preuve : On raisonne par recurrence double sur n.Initialisation : On au0 = 1 = cos0etu1 = cosθ.Donc P0 et P1 sont vrais.Heredite : Soit n N. Supposons Pn et Pn + 1 sont vrais,c’est-a-direun = cosnθetun+1 = cosn + 1θ.Montrons que Pn + 2 est vraie, autrement dit, montrons queun+2 = 2u1un+1 un cosn + 2θ.Algebre

Page 86 : A faire chez soi - Exercice supplementaireOn aun+2 = 2u1un+1 un= 2 cosθ cosn + 1θ cosnθHypothese de Recurrence= 2 cosθcosnθ cosθ sinnθ sinθ cosnθ= 2 cos2θ cosnθ 2 sinnθ cosθ sinθ cosnθ= cosnθ2 cos2θ 1 sinnθ2 cosθ sinθ= cosnθ cos2θ sinnθ sin2θ= cosnθ + 2θ= cosn + 2θFin de la recurrence. Par consequent Pn et Pn + 1 =⇒Pn + 2,et on conclut que pour tout entier naturel n on aun = cosnθ.Algebre

Page 87 : Pour aller plus loin - Exercice 2.17Demontrer quen N, Pn : a, b R2, n N,a + bn =nXk=0 nk!ankbk.Quelques rappels :Pour toute couple d’entiers 0 k n on appelle coefficient binomial lenombre nk!=n!k!n k!.Le nombrenkse lit : k parmi n. Le coefficient binomial satisfait les proprietessuivants :Pour tout n N on an0= 1 =nn.Rappel : 0 !=1.Formule de Pascal : pour tous entiers n et k tels que 0 k n on a nk + 1!= n 1k + 1!+ n 1k!.Algebre

Page 88 : Pour aller plus loin - Exercice 2.17Pn : a, b R2, n N,a + bn =nXk=0 nk!ankbk.Preuve : On fixe a, b R et on raisonne par recurrence sur n.Initialisation : On aa + b1 = a + b =10ab0 +11a0b =1Xk=01ka1kbk.Donc P1 est vraie.Heredite : Soit n N×. Supposons Pn vraie, c’est-a-direa + bn =nXk=0 nk!ankbk.Montrons que Pn + 1 est vraie, autrement dit, montronsa + bn+1 =n+1Xk=0 n + 1k!an+1kbk.Algebre

Page 89 : Pour aller plus loin - Exercice 2.17On aa + bn+1 = a + ba + bn= a + bnXk=0 nk!ankbkHypothese de Recurrence=nXk=0 nk!an+1kbk +nXk=0 nk!ankbk+1= n0!an+1 + nXk=1 nk!an+1kbk!+ n1Xk=0 nk!ankbk+1!+ nn!bn+1.= an+1 + nXk=1 nk!an+1kbk!+ n1Xk=0 nk!ankbk+1!+ bn+1.Maintenant, en utilisant le changement d’indice l = k + 1 on peut ecriren1Xk=0 nk!ankbk+1 =nXl=1 nl 1!an+1lbl =nXk=1 nk 1!an+1kbk.Algebre

Page 90 : Pour aller plus loin - Exercice 2.17D’ou on concluta + bn+1 = an+1 + nXk=1 nk!an+1kbk!+ nXk=1 nk 1!an+1kbk!+ bn+1Ce qui est equivalent aa + bn+1 = an+1 + nXk=1" nk!+ nk 1!an+1kbk!+ bn+1.Maintenant, la formule de Pascal nous dit nk!+ nk 1!= n + 1k!Ce qui nous permet d’ecrirea + bn+1=an+1 + nXk=1" nk!+ nk 1!an+1kbk!+ bn+1=an+1 + nXk=1 n + 1k!an+1kbk!+ bn+1.Algebre

Page 91 : Pour aller plus loin - Exercice 2.17Ainsia + bn+1=an+1 + nXk=1n + 1kan+1kbk!+ bn+1=n + 10an+1 + nXk=1n + 1kan+1kbk!+n + 1n + 1bn+1=n+1Xk=0n + 1kan+1kbk.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut que pour tout entier n Non aa + bn =nXk=0nkankbk.Algebre

Page 92 : Pour aller plus loin - Exercice 2.18On revient sur la propriete :Tout ensemble fini de N non vide admet un plus grand element.Pour definir N, on peut soit admettre cette propriete et demontrerl’axiome de recurrence, soit admettre l’axiome de recurrence et endeduire cette propriete.Demontrer que si l’on admet l’axiome de recurrence, on peut demontrerla propriete.Reponse : Soit la propriete :n N, Pn : tout ensemble a n element admet un plus grand element.Initialisation : La propriete est vraie au rang 1 : un ensemble a 1element admet un plus grand element : l’unique element de l’ensemble.Algebre

Page 93 : Pour aller plus loin - Exercice 2.18Heredite : Soit n N. On suppose que Pn est vraie hypothese derecurrence.On considere un ensemble A a n + 1 elements. On choisit un element αde A. AlorsA \ αest un ensemble a n elements. D’apres l’hypothese de recurrence il admetun plus grand element β. Nous avons deux cas a etudier :• Si α β alors α est le plus grand element de A.• Sinon, β est le plus grand element de A.Dans tous les cas, A admet un plus grand element donc Pn+1 est vraie.Par consequent, pour tout n N, Pn : tout ensemble a n elementadmet un plus grand element.Algebre

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93