TD1 Logique et Raisonnement Correction

Télécharger le TD1 Logique et Raisonnement Correction en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67

Page 1 : Algebre-Premier semestre 2024 - 2025CY TechTD AlgebreLogique et Raisonnement.Algebre

Page 2 : Exercice 1.1Soit P, Q deux propositions. Demontrer les equivalences suivantes enutilisant des tables de verite.1non non P ⇔P2P et P ⇔P3P ou P ⇔P4P et Q ⇔Q et P5P ou Q ⇔Q ou P6non P ou Q ⇔non P et non Q7P ⇒Q ⇔non P ou Q8P ⇔Q ⇔non P ⇔non Q9P ou Q ⇔non P ⇒QAlgebre

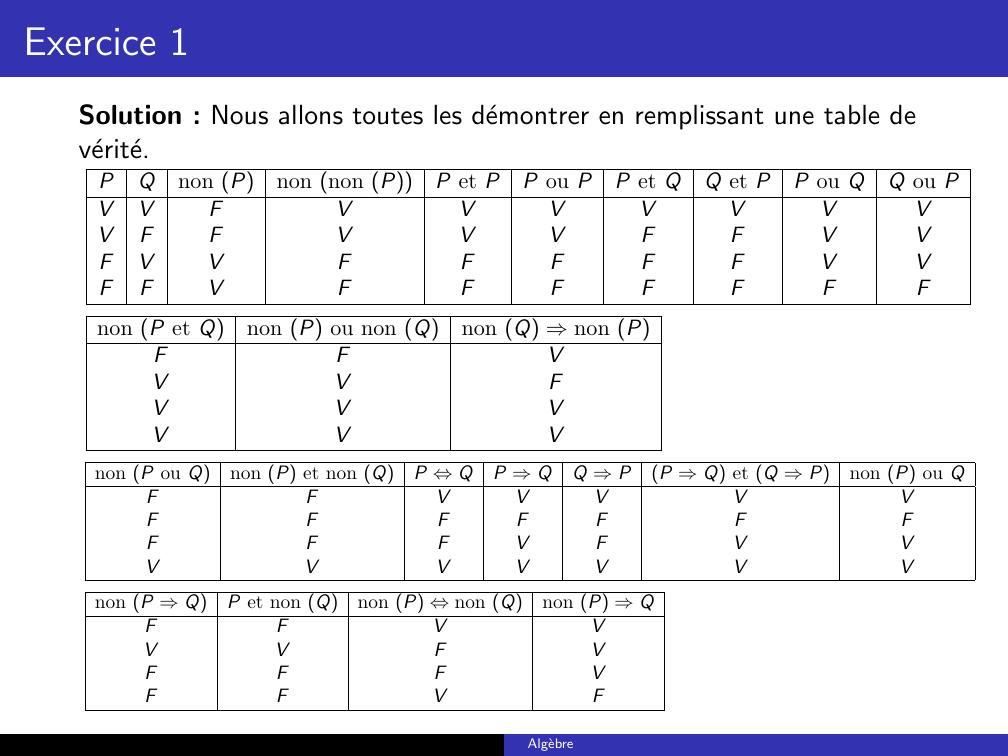
Page 3 : Exercice 1Solution : Nous allons toutes les demontrer en remplissant une table deverite.PQnon Pnon non PP et PP ou PP et QQ et PP ou QQ ou PVVFVVVVVVVVFFVVVFFVVFVVFFFFFVVFFVFFFFFFFnon P et Qnon P ou non Qnon Q ⇒non PFFVVVFVVVVVVnon P ou Qnon P et non QP ⇔QP ⇒QQ ⇒PP ⇒Q et Q ⇒Pnon P ou QFFVVVVVFFFFFFFFFFVFVVVVVVVVVnon P ⇒QP et non Qnon P ⇔non Qnon P ⇒QFFVVVVFVFFFVFFVFAlgebre

Page 4 : Exercice 1.1Soit P, Q et R trois propositions. Demontrer les equivalences suivantesen utilisant des tables de verite.1P et Q et R ⇔P et Q et R2P ou Q ou R ⇔P ou Q ou R3P ou Q et R ⇔P ou Q et P ou R4P et Q ou R ⇔P et Q ou P et RAlgebre

Page 5 : Exercice 1.1Solution : Nous allons toutes les demontrer en remplissant une table deverite.PQRQ et RP et Q et RP et QP et Q et RP ou Q ou RVVVVVVVVVVFFFVFVVFVFFFFVVFFFFFFVFVVVFFFVFVFFFFFVFFVFFFFVFFFFFFFFP ou QP ou Q ou RP ou Q et RP ou RVVVVVVVVVVVVVVVVVVVVVVFFFVFVFFFFAlgebre

Page 6 : Exercice 1.1Nous avons aussi :PQRP ou Q et P ou RP et RQ ou RP et Q ou RP et Q ou P et RVVVVVVVVVVFVFVVVVFVVVVVVVFFVFFFFFVVVFVFFFVFFFVFFFFVFFVFFFFFFFFFFAlgebre

Page 7 : Exercice 1.2Soient P, Q et R deux propositions. Les propositionsP ou Q et R etP ou Q et R sont-elles equivalentes ?Solution : Nous allons les comparer en remplissant une table de verite.PQRQ et RP ou Q et RP ou QP ou Q et RVVVVVVVVVFFVVFVFVFVVVVFFFVVFFVVVVVVFVFFFVFFFVFFFFFFFFFFFComme les table de verite sont differents, on conclut que les propositionsP ou Q et R etP ou Q et R ne sont pas equivalents.Algebre

Page 8 : Exercice 1.3Sans utiliser de table de verite mais en utilisant les differentes proprietes dejademontrees, demontrer quenon P =⇒Q⇐⇒P et non QetP ou Q⇐⇒non P =⇒Q .Reponse : D’abordnon P =⇒Q⇐⇒non non P ou Q⇐⇒non non P et non Q⇐⇒P et non Q.En suitenon P =⇒Q⇐⇒non non PouQ⇐⇒P ou Q.Algebre

Page 9 : Exercice 1.4Traduire en toutes lettres les sept propositions suivantes lorsque x designe unindividu, y un film et que Px, y est la propositionL’individu x a vu le film y .On traduit :x : Pour tout individu = tous les individus.y : Pour tout film = tous les films.x : il existe au moins un individu.y : il existe au moins un film.1x, y, Px, yReponse : Tous les individus ont vus tous les films.2x, y, Px, yReponse : Il existe un individu qui a vu tous les films.Algebre

Page 10 : Exercice 1.43y, x, Px, yReponse : Il existe un film qui a ete vu par tous les individus.4x, y, Px, yReponse : Tous les individus ont vu au moins un film.5x, y, Px, yReponse : Il existe un individu qui a vu au moins un film.6y, x, Px, yReponse : Il existe un film qui a ete vu par au moins un individu.Algebre

Page 11 : Exercice 1.47y, x, Px, yReponse : Tous les films ont ete vus par au moins un individu.Algebre

Page 12 : Exercice 1.5Soit I un intervalle non vide de R et f : I →R une fonction definie sur Ia valeurs reelles. Exprimer verbalement la signification des propositionssuivantes :1λ R, x I, f x = λ.Reponse : La fonction f est constante sur I, de valeur λ.2x I, f x = 0 =⇒x = 0.Reponse : Si la fonction f s’annule, alors elle s’annule uniquementen 0, c-a-d, la fonction f s’annule uniquement en 0, ou ne s’annulepas.3y R, x I, f x = y.Reponse : La fonction f est surjective, c’est-a-dire, toutes lesvaleurs de R sont atteintes par f .Algebre

Page 13 : Exercice 1.54x I, y I, f x = f y =⇒x = y.Reponse : La fonction f est injective, c’est-a-dire, f prend au plusune fois chaque valeur.5ϵ 0, y R, α 0, x R, x y α =⇒f xf y ϵ.Reponse : La fonction f est continue en R.6ϵ 0, α 0, x R, y R, x y α =⇒f xf y ϵ.Reponse : La fonction f est uniformement continue.Algebre

Page 14 : Exercice 1.6Soit I un intervalle non vide de R et f : I →R une fonction definie sur Ia valeurs reelles. Exprimer a l’aide de quantificateurs les propositionssuivantes :1f est l’application nulle.Reponse : x I, f x = 0.2f n’est pas l’application nulle.Reponse : x I, f x ̸= 0.3La fonction f s’annule.Reponse : x I, f x = 0.4f ne s’annule pas sur I.Reponse : x I, f x ̸= 0.Algebre

Page 15 : Exercice 1.65f est une fonction constante.Reponse : λ R, x I, f x = λ oux I, y I, f x = f y.6La fonction f n’est pas une fonction constante.Reponse : x I, y I, f x ̸= f y.7La fonction f ne prend jamais deux fois la mˆeme valeur.Reponse : x I, y I, x ̸= y =⇒f x ̸= f y.8La fonction f presente un minimum.Reponse : c I, x I, f x f c.Algebre

Page 16 : Exercice 1.69La fonction f prend des valeurs arbitrairement grandes.Reponse : M R, x I, f x M.10 f est une fonction affine.Reponse : m R, n R, x R, f x = mx + n.Algebre

Page 17 : Exercice 1.7Donner la negation des phrases suivantes1x 3.Reponse : x 3.20 x 2=0 x et x 2.Reponse : x 0 ou x 2.3x R, y R, x + y 0.Reponse : x R, y R, x + y 0.4x R, y R, x + y 0.Reponse : x R, y R, x + y 0.Algebre

Page 18 : Exercice 1.75x R, y R, x + y 0.Reponse : x R, y R, x + y 0.6x R, y R, y 2 x.Reponse : x R, y R, y 2 x.7P et non Q.Reponse : non P ou Qqui est equivalent aP =⇒Q8P et Q et R.Reponse : non P ou non Q ou non R.Algebre

Page 19 : Exercice 1.79P ou Q et R.Reponse : non P et non Q ou non R10 P et Q =⇒R =⇒S.Reponse : Rappelons queP et Q =⇒R =⇒S⇐⇒non P et Q ou R =⇒S.Donc la negation de P et Q =⇒R =⇒S est :nonnon P et Q ou R =⇒S⇐⇒P et Q et non R =⇒S⇐⇒P et Q et non non R ou S⇐⇒P et Q et R et non S⇐⇒P et Q et R et non S.Algebre

Page 20 : Exercice 1.711 Tous les habitants de la rue du Havre qui ont les yeux bleusgagneront au loto et prendront leur retraite avant 50 ans.Reponse : Il existe un habitant de la rue du Havre qui a les yeuxbleus, qui ne gagnera pas au loto ou qui prendra sa retraite apres50 ans.12 Tout triangle rectangle possede un angle droit.Reponse :Il existe un triangle rectangle qui n’a pas d’angle droit.13 Dans toutes les ecuries, tous les chevaux sont noirs.Reponse : Il existe une ecurie dans laquelle il y a au moins uncheval qui n’est pas noire.Algebre

Page 21 : Exercice 1.714 Pour tout entier x, il existe un entier y tel que, pour tout entier z, larelation z x implique la relation z x + 1.Reponse : A l’aide de quantificateurs on peut ecrire :x, y, z,z x =⇒z x + 1.Donc la negation c’est : Il existe un entier x, tel que pour toutentier y, il existe un entier z tel que l’on a a la fois z x etz x + 1.15 ϵ 0, α 0,x 57 α =⇒5x 7 ϵ.Reponse : ϵ 0,α 0,x 57 αet5x 7 ϵ.Algebre

Page 22 : Exercice 1.8Soitf : R →R.Indiquer la difference de sens entre les deux propositions proposees :1. x R, y R, y = f xety R, x R, y = f x.Reponse :Dans le premier cas, chaque reel possede au moins une image, doncla fonction est bien definie sur R.Dans le second tous les reels ont la mˆeme image donc f estconstante.2. y R, x R, y = f xetx R, y R, y = f x.Reponse :Dans le premier cas, toutes les valeurs de R sont atteintes par f fest surjective sur R ;Dans le second cas, il existe un x tel que f x prend toutes lesvaleurs reelles possibles donc le graphe de f est une droiteverticale.Algebre

Page 23 : Exercice 1.83. x R, M R, f x MetM R, x R, f x M.Reponse :Dans le premier cas, f x est toujours plus petit qu’un reel.Dans le second cas, f est majoree par M.Algebre

Page 24 : A faire chez soi - Exercice 1.9Soit f : R →R une fonction. Pour chacune des propositions suivantes,donner graphiquement a main levee un exemple de fonction f NE laverifiant PAS contre-exemple.1M R, x R, f x M2x R, f x 0 ⇒x 03x R, f x 1 ou f x 1Solution : Une courbe qui repond aux trois questions est la courberepresentative de la fonction carre.Algebre

Page 25 : A faire chez soi - Exercice 1.10Soit I un intervalle non vide de R etf : I →Rune fonction a valeurs reelles definie sur I. Exprimer les negations despropositions suivantes :1x I, f x ̸= 0.Reponse : x I, f x = 0.2y R, x I, f x = y.Reponse : y R, x I, f x ̸= y.3M R, x I, f x M.Reponse : M R, x I, f x M.4x I, y I, f x = f y =⇒x = y.Reponse : x I, y I, f x = f y et x ̸= y.Algebre

Page 26 : A faire chez soi - Exercice 1.11Completer les pointilles par le connecteur logique qui s’impose=⇒,⇐=,⇐⇒1x R; x2 = 4 · · · · · · x = 2.Reponse : x R; x2 = 4 ⇐= x = 2.2z C; z = z · · · · · · z RReponse : z C; z = z ⇐⇒z R.3x R; x = π · · · · · · e2ix = 1.Reponse : x R; x = π =⇒e2ix = 1.Algebre

Page 27 : A faire chez soi - Exercice 1.12Les propositions suivantes sont-elles vraies ou fausses ? Justifier.1x R, x 2 ⇒x 32x, y R+2, x y ⇔1x 1y3x R+, x x4n N, Pnk=0 k 100Solution :1Faux, en effet, x R, x 2 et x 3. Il suffit de prendre x = 2.5.Puisque la negation est vraie, la phrase est fausse.2Faux. On prend x 0 y, ainsi, 1x 0 1y . Ce n’est vrai que si onimpose a x et y d’ˆetre de mˆeme signe.3Vrai, il suffit de prendre x = 0.25, x = 0.54Vrai, il suffit de prendre n = 100.Algebre

Page 28 : A faire chez soi - Exercice supplementaireReprendre l’exercice 5 en donnant a chaque fois les negations en toutes lettreset avec les quantificateurs. On commence par noter quenon Px, y = L’individu x n’a pas vu le film y Reponse :1x, y, non Px, y : Il existe un individu qui n’a pas vu au moins unfilm.2x, y, non Px, y : Pour tous les individus, il existe un film qui n’apas ete vu. On peut aussi dire : Pour chaque individu, il existe au moinsun film qu’il n’a pas vu personne n’a vu tous les films.3y, x, non Px, y : Pour tous les films, il existe un individu qui ne l’apas vu Aucun film n’a ete vu par tout le monde.4x, y, non Px, y : Il existe un individu qui n’a vu aucun film.Algebre

Page 29 : A faire chez soi - Exercice supplementaire5x, y, nonPx, y : Aucun individu n’a vu de film.6y, x, non Px, y : Aucun film n’a ete vu7y, x, non Px, y : Il existe un film qui n’a ete vu par aucun individu.Algebre

Page 30 : Exercice 2.11Soit x un irrationnel positif. Montrer que x est irrationnel.2Montrer que2 est un nombre irrationnel.Solution : Voir CM.Algebre

Page 31 : Exercice 2.1Soit x un irrationnel positif. Montrer que x est irrationnel. C’est-a-dire,nous devons montrer : sot x un reel positifSi x est un irrationnel=⇒x est irrationnel.On rappelle quex n’est pas irrationnel⇐⇒x est rationnel.Nous allons montrer la proposition en utilisant un raisonnement parcontraposition.Reponse : Nous devons donc montrer : soit x un reel positif alorsx est rationnel=⇒x est rationnel.Supposons x rationnel. Par definition d’un nombre rationnel, il existep, q Z tel quex = pq=⇒x = p2q2qui est le quotient de deux entiers naturels. Donc x est rationnel.Algebre

Page 32 : Exercice 2.2Demontrer, en raisonnant par l’absurde, que si n N×, alors n2 + 1 n’estpas le carre d’un entier naturel.Reponse : Supposons que n est un entier strictement positif et quen2 + 1 est le carre d’un entier naturel a. Trouvons une contradiction.Par hypothesea2 = n2 + 1.Donc1 = a2 n2 = a na + n.Puisque le produit de ces deux nombre est egal a 1, on concluta + nest different de 0.On a en plusa 0.Par consequent a + n N car a N et n N eta + n n 0.Algebre

Page 33 : Exercice 2.2Le nombre a + n est donc un entier positif. Il s’ensuit, comme 1 est unentier positif, quea nest un entier positif.Maintenant, un produit d’entiers positifs est egal a 1 si et seulement sichacune d’entre eux est egal a 1. On en deduita n = 1eta + n = 1.Par soustraction des deux egalites2n = 0.Puisque n est strictement positif, cela est une contradiction. D’ou onconclut que n2 + 1 n’est pas le carre d’un entier naturel.Algebre

Page 34 : Exercice 2.3Montrer que lorsqu’un reel peut ˆetre ecrit sous la formea + b2,a Z, b Z,alors les entiers a et b sont necessairement uniques.Reponse : Soit r R tel quer = a + b2a Z, b Z.Nous allons montrer que cette ecriture est unique en raisonnant parl’absurde. Supposons donc qu’il existe deux couples distincts d’entiersa, b et a′, b′ tels quer = a + b2etr = a′ + b′2Essayons d’obtenir une contradiction. Pour cela on ecrit0 = r r=a + b2 a′ + b′2=a a′ + b b′2.Algebre

Page 35 : Exercice 2.3On a deux cas a etudierSi b = b′, alors a = a′ ce qui est en contradiction avec la hypotheseque les couples etaient distincts.Si b ̸= b′, on deduit0 = a a′ + b b′2=⇒2 =a′ a Zb b′ Z Q.C’est-a-dire2 est un rationnel. Ce qui est faux, contradiction.Par consequent, lorsqu’un reel peut ˆetre ecrit sous la formea + b2,a Z, b Z,alors les entiers a et b sont necessairement uniques.Algebre

Page 36 : Exercice 2.4Montrer que toute fonction f : R →R s’ecrit de fa¸con unique comme lasomme d’une fonction paire et d’une fonction impaire. Donner cettedecomposition sif x =x + 1x2 + x + 1Preuve : Nous allons raisonner par analyse-synthese.Soit f une fonction de R dans R.• Analyse : Supposons le probleme resolu, c’est-a-dire qu’il existe deuxfonctionsg : R →Reth : R →R,avecgpaireethimpairetelles quex R,f x = gx + hx.1Algebre

Page 37 : Exercice 2.4Comme g est paire et h est impaire on a aussix R,f x = gx + hx = gx hx.2En additionnant et soustrayant les egalites 1 et 2 nous obtenons2gx = f x + f x=⇒gx = f x + f x22hx = f x f x=⇒hx = f x f x2.Ainsi, s’il existe une solution au probleme, alors ce sont necessairementles fonctions g et h ci-dessus.Algebre

Page 38 : Exercice 2.4• Synthese : Nous allons verifier que g et h sont bien solutions duprobleme.On a bien f = g + h. En effetx R,gx + hx = 2f x2= f x.La fonction g est paire. En effetx R,gx = f x + f x2= gx.La fonction h est impaire. En effetx R,hx = f x f x2= hx.Nous avons donc demontre par Analyse-Synthese qu’il existe un uniquecouple g, h avec g paire et h impaire tel que f = g + h.Algebre

Page 39 : Exercice 2.4Finalement, sif x =x + 1x2 + x + 1alorsgx =1x4 + x2 + 1,ethx =x3x4 + x2 + 1.Algebre

Page 40 : A faire chez soi - Exercice 2.5Soit a et b deux reels. Montrer quea2 + b2 = 0=⇒a = b = 0.Solution : Voir CM.Algebre

Page 41 : A faire chez soi - Exercice 2.6Soitf : R →Rune fonction. Montrer quefimpaire=⇒f 0 = 0.On rappelle que une fonction f : R →R est dite impaire si pour toutx R on af x = f x.Nous allons montrer la proposition en utilisant un raisonnement direct.Reponse : Supposons f impaire. Montrons f 0 = 0. Puisque f estimpaire, pour tout x R on af x = f x.En particulier pour x = 0, on obtientf 0 = f 0 = f 0=⇒2f 0 = 0=⇒f 0 = 0.Algebre

Page 42 : A faire chez soi - Exercice 2.7Deux joueurs s’affrontent sur le jeu suivant. Ils disent chacun a leur tour unnombre entre 1 et 7 . Les nombres sont additionnes et des que le cumul desnombres qu’ils ont proposes vaut 100, le jeu est fini. Le joueur qui a atteint 100et a donc parle en dernier gagne. Comment jouer ?Solution : On raisonne par analyse-synthese.Analyse : Nous allons trouver la reponse de maniere naturelle, en partant del’objectif qui est d’atteindre 100 . Si je veux atteindre 100 , il faut que monadversaire ait atteint un nombre entre 93 auquel cas je dirai 7 et 99 auquelcas je dirai 1 . Pour obtenir cela, il suffit que j’atteigne 92 a l’etapeprecedente. Mais pour atteindre 92 a coup sˆur, j ’ ai besoin que mon adversaireait atteint un nombre entre 85 auquel cas je dirai 7 et 91 auquel cas je dirai1. Pour cela, il faudrait que j’atteigne 84 a l’etape precedente. On reproduit leraisonnement et on realise que pour gagner, il suffit que j’arrive a atteindre al’etape precedente 84 8 = 76, donc juste avant 76 8 = 68, et ainsi de suite60, 52, 44, 36, 28, 20, 12 et 4 . On observe ici une suite arithmetique de raison 8 .Algebre

Page 43 : A faire chez soi - Exercice 2.7Synthese : Nous sommes partis du resultat la victoire pour remonter audebut de la partie et voir comment la jouer. Nous pouvons maintenant donnerla strategie gagnante, en respectant les regles du jeu.- Si je commence, je dis 4, puis mon adversaire va porter le cumul a un nombreentre 5 et 11, et je dis le chiffre qu’il faut pour atteindre 12, puis20,28,36,44,52,60,68,74,82, et enfin 100.- Si mon adversaire commence et connait cette strategie, je perdrai. Mais sinon,je peux la rattraper : des que je peux je dis le chiffre me permettant deretomber sur 4 ou 12 ou 20 . . .. Si il commence par 1, 2, 3, 5,6 ou 7, je repondspar 3, 2, 1, 7, 6, 5. S’il commence par 4, je reponds par 1 et attends de voir cequ’il dit. S’il dit 1, 2, 3, 4, 5, ou 6, j’atteins 12 avec 7, 6, 5, 4, 3, 2. Mais s’ilrepond 7, je recommence a dire 1 et attends le tour suivant pour atteindre 20etc. S’il repond tout le temps 7, c’est qu’il avait compris la strategie et je perds.Algebre

Page 44 : A faire chez soi - Exercice 2.8Un vol a ete commis dans un asile. Trois pensionnaires A, B et C sontsuspects. Voici leurs temoignages, chacun formulant trois assertions :A: Je suis innocent. A l’heure du vol, j’etais avec B. C’est C le coupable.B: Je suis innocent. A aussi. A n’etait pas avec moi a l’heure du vol.C: Je suis innocent. B aussi. A a menti trois fois.Vous savez que chaque suspect a au moins menti une fois sur ses troisaffirmations. Qui est le coupable ?Solution : Trois coupables possibles, donc trois cas a etudier on raisonne pardisjonction des cas :A coupable : A et B ne peuvent pas ˆetre ensembles a l’heure du vol puisqu’iln’y a qu’un coupable.Affirmations de A : F, F, FAffirmations de B : V, F, VAffirmations de C : V, V, VOr C est cense mentir au moins une fois, donc A est innocentAlgebre

Page 45 : A faire chez soi - Exercice 2.8B coupable : A et B ne peuvent pas ˆetre ensembles a l’heure du vol puisqu’iln’y a qu’un coupable.Affirmations de A : V, F, FAffirmations de B : F, V, VAffirmations de C : V, V, FLes trois ont menti au moins une fois, donc B est potentiellement le coupable.C coupable :Affirmations de A : V, ?, V . La deuxieme proposition est donc forcement fausse,donc A et B n’etaient pas ensembles.Affirmations de B : V, V, ? . La troisieme proposition est donc forcement fausse,donc A et B etaient ensemble. C’est en contradiction avec ce qui precede.Affirmations de C : F, V, FIl est impossible que A et B mentent au moins une fois. Donc C est innocent.En conclusion, le coupable est B.Algebre

Page 46 : A faire chez soi - Exercice 2.9Thomas, Jules et Yves sont partis contempler des oiseaux. Chacun a vu unoiseau que les deux autres n’ont pas vu. Chaque deux ont vu un oiseau que letroisieme n’a pas vu, et un oiseau a ete vu par les trois.Parmi les oiseaux que Thomas a vus, deux sont jaunes. Pami ceux vus parJules, trois sont jaunes, et pami ceux vus par Yves, quatre sont jaunes.Combien d’oiseaux jaunes ont ete vus au total ? Combien d’oiseaux non jaunesont ete vus au total ?Solution : Nous allons remplir un tableau avec une ligne par individu et autantde colonnes que necessaires pour les oiseaux.abcdefgThomasVXXVVXVJulesXVXVXVVYvesXXVXVVVPuisque que Yves n’a vu que quatre oiseaux et qu’il a vu au moins quatreoiseaux jaunes, on en deduit que tous ses oiseaux sont jaunes, donc c, e, f et gsont jaunes. Thomas n’a vu que deux oiseaux jaunes, donc a et d ne sont pasjaunes. Jules a vu trois oiseaux jaunes, donc b est jaunes. Au final : 5 oiseauxjaunes b, c, e, f, g et 2 non jaunes a et d.Algebre

Page 47 : A faire chez soi - Exercice supplementaireSoit x un reel positif. Montrer queϵ 0, x ϵ=⇒x = 0Nous allons montrer la proposition en utilisant un raisonnement parcontraposition. C’est-a-dire, nous allons montrer : soit x un reel positifx ̸= 0=⇒ϵ 0, x ϵPreuve : Soit x un reel positif. Supposons x ̸= 0. Donc x 0. Enchoisissantϵ = x2,on obtientϵ 0, etx ϵ.Autrement dit, pour tout x 0 existe ϵ 0 tel que ϵ x. Ce qui montrela proposition.Algebre

Page 48 : A faire chez soi - Exercice supplementaireSoit a et b deux reels. Montrer en utilisant deux methodes quea + b 1=⇒a 12oub 12.Solution :Par contraposition. Nous allons donc montrer quea 12etb 12=⇒a + b 1.Cette implication est evidente. En effet, en additionnant les deuxinegalites strictes de gauche on obtient celle de droite.Par disjonction de cas. Deux cas sont possibles :Si a 12, alors on a bien a 12 ou b 12.Si a 12, alors a 12 et 1 a 1 12. Donca + b 1=⇒b 1 a=⇒b 1 12 = 12.et on a bien a 12 ou b 12.Algebre

Page 49 : A faire chez soi - Exercice supplementaireLa somme et le produit d’un nombre rationnel non-nul pour le produitet d’un nombre irrationnel sont des nombres irrationnels.Rappelons que :La somme de deux nombres rationnels est un nombres rationnel. Eneffetpq + p′q′ = pq′ + p′qqq′Q.Le produit de deux nombres rationnels est un nombres rationnel. Eneffetpq · p′q′ = pp′qq′ Q.Nous allons montrer la proposition en raisonant par l’absurde.Algebre

Page 50 : A faire chez soi - Exercice supplementairePreuve : Soit r Q et x ̸Q.Il nous faut montrer quer + x ̸Q.Pour cela, raisonnons par l’absurde et supposons r + x Q. Alors onax = x + r z QrzQzQ.Contradiction ! Par consequent r + x ̸Q. C’est-a-dire r + x estirrationnel.Algebre

Page 51 : A faire chez soi - Exercice supplementaireIl nous faut montrer quer · x ̸Q.Raisonnons par l’absurde et supposons r · x Q. Alors on ax = r · x z Q·1rzQzQ.Contradiction ! Par consequent r · x ̸Q. C’est-a-dire r · x estirrationnel.Algebre

Page 52 : A faire chez soi - Exercice supplementaireUn rectangle a pour aire 170 m2. Montrer que sa longueur est superieurea 13 m.Soit l R×+ la largeur du rectangle et L l, + sa longueur. On doitdonc montrer : l R×+, L l, +on al × L = 170=⇒L 13.Nous allons montrer la proposition en utilisant un raisonnement parcontraposition. C’est-a-dire, nous allons montrer : l R×+,L l, +on aL 13=⇒l × L ̸= 170.Preuve : Supposons L 13. Alors l L 13, c’est-a-direl 13etL 13,et on peut conclure par produit des inegalites quel × L 13 × 13 = 169 170.Algebre

Page 53 : A faire chez soi - Exercice supplementaireDemontrer que si vous rangez n + 1 paires de chaussettes dans n tiroirsdistincts, alors il y a au moins un tiroir contenant au moins deux paires dechaussettes.Preuve : NotonsP = On a range n + 1 chaussettes dans n tiroirs distincts.Q = Il existe un tiroir contenant au moins deux paires de chaussettes.On doit donc montrer queP=⇒Q.Nous allons montrer la proposition en raisonant par l’absurde. C’est-a-dire onsupposePetnon Q,et on essaye d’arriver a une contradictionSupposons donc que on a range n + 1 chaussetes dans n tiroirs distincts, etque chaque tiroir contient au plus une paire de chaussettes. Alors il y aura auplus1 + 1 + · · · + 1 = npaires de chaussettes, ce qui contredit qu’il y en a n + 1. Donc un tiroir doitcontenir au moins deux paires de chaussettes.Algebre

Page 54 : A faire chez soi - Exercice supplementaireDeterminer toutes les fonctionsf : R →Rqui satisfont l’equationx R, f x + xf 1 x = 1 + x.3Preuve : Nous allons raisonner par analyse-synthese.Analyse : Supposons f est solution de l’equation. Posonsy = 1 x=⇒x = 1 y.Alors en rempla¸cant x par 1 y dans 1, on obtientf 1 y + 1 yf y = 2 y.D’ou on peut conclure que, pour tout y Rf 1 y = 1 yf y + 2 y.Algebre

Page 55 : A faire chez soi - Exercice supplementaireAinsi, en posant y = x dans la equation de depart, on conclutf y + y1 yf y + 2 y = 1 + y⇐⇒f y + yf y + y 2f y + 2y y 2 = 1 + y⇐⇒f y1 y + y 2 + 2y y 2 = 1 + y⇐⇒f y1 y + y 2 = 1 y + y 2.Maintenant, comme 1 y + y 2 ̸= 0, on en deduit quey R,f y = 1.Synthese : Nous allons verifier que la fonction constante f = 1 estbien solution du probleme. En effetf x + xf 1 x = 1 + x.L’unique solution de cette equation est donc la fonction constantex 7→f x = 1.Algebre

Page 56 : A faire chez soi - Exercice supplementaireSoit f la fonction definie parf : R →Rx 7→f x = x + 12x 1.Montrer que pour tout y ̸= 12, il existe x ̸= 12 tel que f x = y.Preuve : Nous allons raisonner par analyse-synthese.Analyse : Supposons le probleme resolu, c’est-a-dire qu’on a x tel quef x = y. Alorsx + 12x 1 = y⇐⇒x + 1 = 2x 1y⇐⇒x + 1 = 2xy y⇐⇒y + 1 = 2xy x⇐⇒y + 1 = x2y 1et comme y ̸= 12, on peut ecrirex = y + 12y 1.Ainsi, s’il existe x tel que f x = y, x doit necessairement ˆetre donne par laderniere egalite.Algebre

Page 57 : A faire chez soi - Exercice supplementaireSynthese : Verifions que x est bien solution du probleme. Nous devonsmontrer :x ̸= 12 : Faisons un raisonnement par l’absurde et supposons x = 12. Alors12 = y + 12y 1=⇒2y 1 = 2y + 2=⇒1 = 2.Contradiction ! Par consequent x ̸= 12.f x = y : On computef x = x + 12x 1 =y+12y1 + 12y+12y1 1=y+1+2y12y12y+12y12y1= y + 1 + 2y 12y + 1 2y 1= 3y3 = y.Nous avons donc demontre par Analyse-Synthese que si y ̸= 12, alors il existeun unique reel x R \ 12, tel quef x = y.Algebre

Page 58 : Exercice 2.10Demontrer que pour tout entier naturel non nul n on aPn : n! 2n1.Preuve : On raisonne par recurrence sur n.Initialisation : On a 1! = 1 211. Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire,n! 2n1.Montrons que Pn + 1 est vraie, autrement dit, montrons quen + 1! 2n+11 = 2n.On an + 1! = n + 1 · n!.Ainsi, par hypothese de recurrence, on en deduitn + 1! = n + 1 · n! n + 1 · 2n1.Algebre

Page 59 : Exercice 2.10Maintenant, pour tout n Non an 1=⇒n + 1 2.Par consequentn + 1! = n + 1 · n! n + 1 · 2n1 2 · 2n1 = 2n.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut que pour tout entier naturel n Non an! 2n1.Algebre

Page 60 : Exercice 2.11.aDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k = nn + 12.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k = 1et1 · 1 + 12= 1=⇒1Xk=1k = 11 + 12.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=1k = nn + 12.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k = n + 1n + 1 + 12= n + 1n + 22Algebre

Page 61 : Exercice 2.11.aOn computen+1Xk=1k=nXk=1k+n + 1=zHypothese de Recurrencenn + 12+ n + 1=nn + 1 + 2n + 12=n + 1n + 22.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on conclut pourtout entier naturel n N, l’identitenXk=1k = nn + 12.Algebre

Page 62 : Exercice 2.11.bDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k2 = nn + 12n + 16.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k2 = 12 = 1et11 + 12 · 1 + 16= 1=⇒1Xk=1k2 = 11 + 12 · 1 + 16.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-direnXk=1k2 = nn + 12n + 16.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k2 = n + 1n + 1 + 12n + 1 + 16= n + 1n + 22n + 36Algebre

Page 63 : Exercice 2.11.bOn computen+1Xk=1k2=nXk=1k2+n + 12=zHypothese de Recurrencenn + 12n + 16+ n + 12=nn + 12n + 1 + 6n + 126=n + 1n2n + 1 + 6n + 16=n + 12n2 + 7n + 66=n + 1n + 22n + 36.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et on conclut pourtout entier naturel n Nl’identitenXk=1k2 = nn + 12n + 16.Algebre

Page 64 : Exercice 2.11.cDemontrer par recurrence l’egalite suivanten N, Pn :nXk=1k3 = nXk=1k!2.Preuve : On raisonne par recurrence sur n.Initialisation : On a1Xk=1k3 = 13 = 12 = 1Xk=1k!2.Donc P1 est vraie.Heredite : Soit n N. Supposons Pn vraie, c’est-a-dire,nXk=1k3 = nXk=1k!2.Montrons que Pn + 1 est vraie, autrement dit, montronsn+1Xk=1k3 = n+1Xk=1k!2Algebre

Page 65 : Exercice 2.11.cOn computen+1Xk=1k3=nXk=1k3 + n + 13=zHypothese de Recurrence nXk=1k!2+ n + 13.Maintenant, d’apres l’exercice 2.11.a on peut ecrirenXk=1k = nn + 12d’ou on conclutn+1Xk=1k3 =nn + 122+ n + 13 = n2n + 124+ n + 13= n2n + 12 + 4n + 134= n + 12n2 + 4n + 14= n + 12n2 + 4n + 44= n + 12n + 224Algebre

Page 66 : Exercice 2.11.cMaisn + 12n + 224=n + 1n + 222= n+1Xk=1k!2Doncn+1Xk=1k3 = n+1Xk=1k!2.Fin de la recurrence. Par consequent Pn =⇒Pn + 1, et onconclut pour tout entier naturel n Nl’identitenXk=1k3 = nXk=1k!2= n2n + 124.Algebre

Page 67 : Exercice 2.12Demontrer que pour tout entier naturel n :Pn :3 divise 4n + 2.Pn :7 divise 32n+1 + 2n+2.Soit un entier a 2 tel que 3 divise a2 a. Demontrer que pourtout entier naturel n 2, 3 divise an a.Pn :17 divise 3 · 52n+1 + 23n+1.Preuve : On raisonne par recurrence sur n.Algebre

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67