TD4 Applications Correction

Télécharger le TD4 Applications Correction en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94

Page 1 : Algebre-Premier semestre 2024 - 2025CY TechTD AlgebreApplications.Algebre

Page 2 : Exercice 1Determiner f R+, f R, f 1, f 1R+, f 1R, f 11pour les fonctions suivantes :1f x = ex2f x = lnx3f x = cosxAlgebre

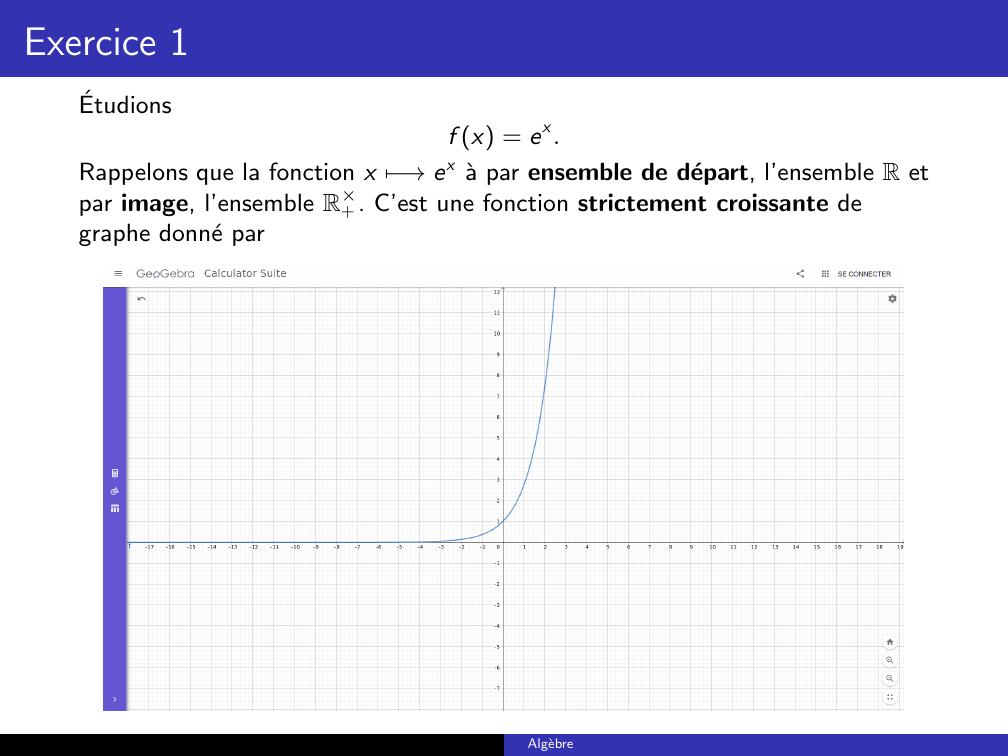
Page 3 : Exercice 1Etudionsf x = ex.Rappelons que la fonction x 7→ex a par ensemble de depart, l’ensemble R etpar image, l’ensemble R×+. C’est une fonction strictement croissante degraphe donne parAlgebre

Page 4 : Exercice 1Ce qui nous permet de concluref R+ = 1, +;f R =0, 1;f 1 = f 1 = e1etf 1R+ = R;f 1R = ;f 11 = Algebre

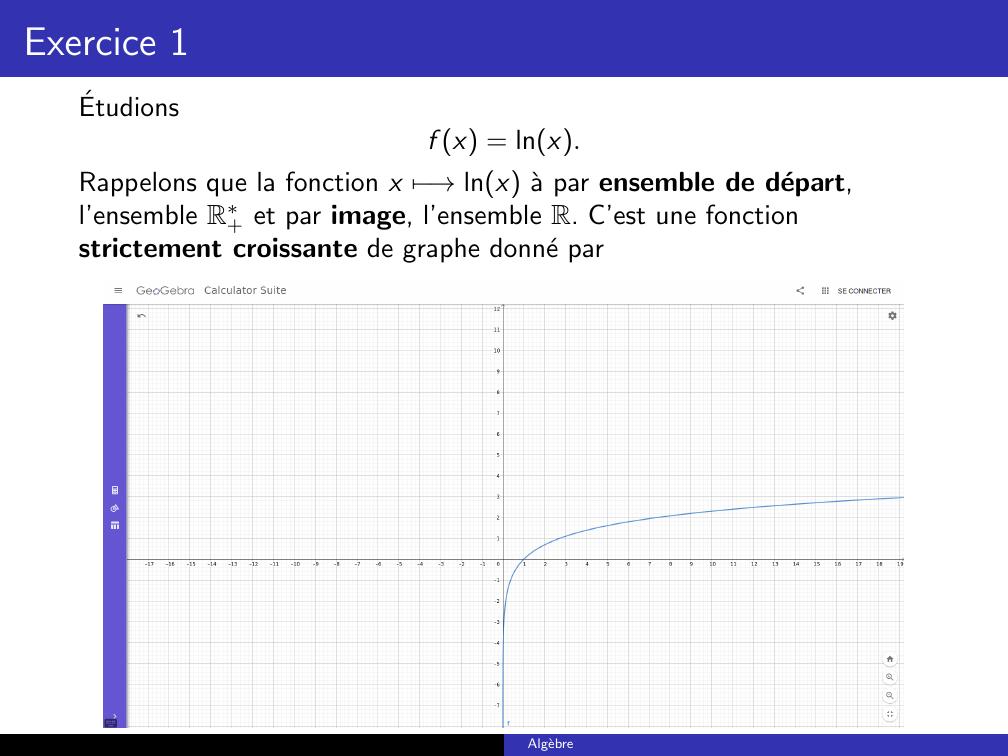
Page 5 : Exercice 1Etudionsf x = lnx.Rappelons que la fonction x 7→lnx a par ensemble de depart,l’ensemble R+ et par image, l’ensemble R. C’est une fonctionstrictement croissante de graphe donne parAlgebre

Page 6 : Exercice 1Ce qui nous permet de concluref R+ = R;f R = ;f 1 = etf 1R+ = 1, +;f 1R =0, 1.Finalement, puisquelne1= 1et ln est une fonction strictement croissant, on conclutf 11 = e1.Algebre

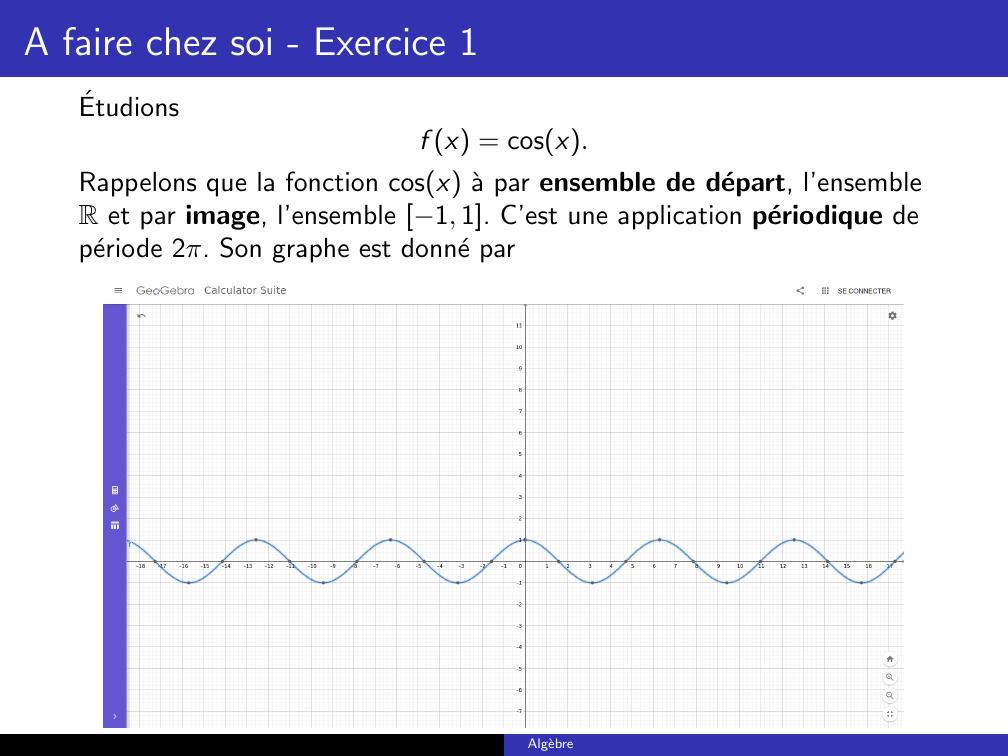
Page 7 : A faire chez soi - Exercice 1Etudionsf x = cosx.Rappelons que la fonction cosx a par ensemble de depart, l’ensembleR et par image, l’ensemble 1, 1. C’est une application periodique deperiode 2π. Son graphe est donne parAlgebre

Page 8 : A faire chez soi - Exercice 1Ce qui nous permet de concluref R+ = 1, 1;f R = 1, 1;f 1 = f 1 = cos1De mˆemef 1R+ =hπ2 , π2i+ 2kπetf 1R =π2 , 3π2+ 2kπetf 11 = π + 2kπ.Algebre

Page 9 : Exercice 2Soit f l’application de R dans R definie par f x = x2.1Determiner les ensembles suivants :f 3; 1;f 2; 1etf 3; 1 2; 1;f 3; 1 2; 1.Les comparer.2Mˆemes questions pour les ensembles :f 1 ; 2;f 11; +etf 1 ; 2 1; +;f 1 ; 2 1; +.Algebre

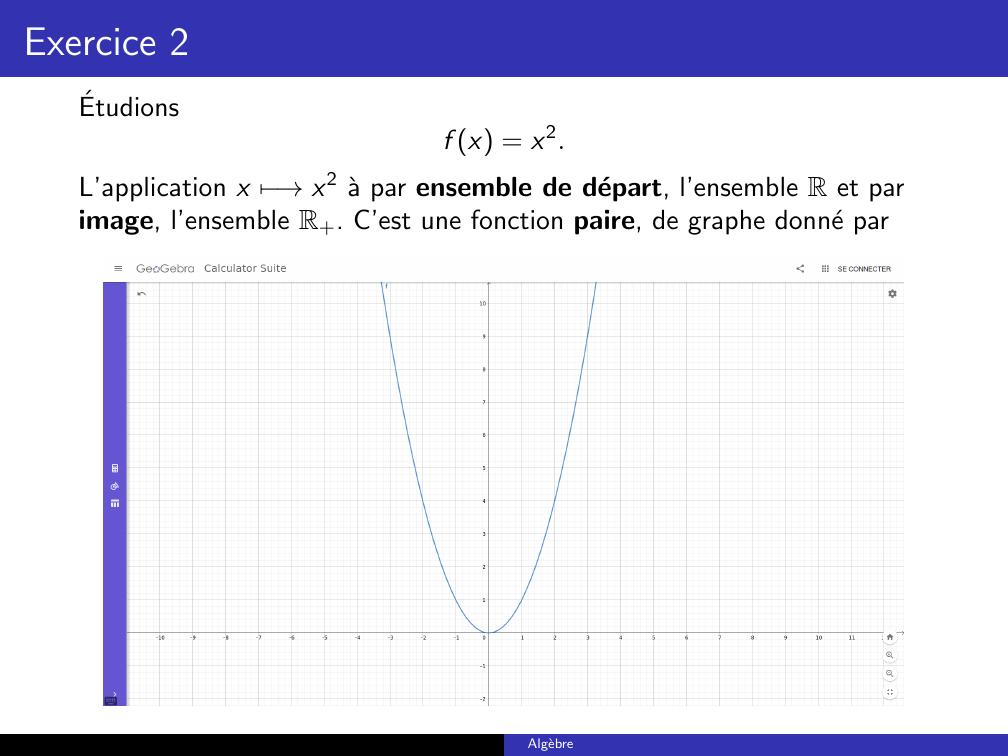
Page 10 : Exercice 2Etudionsf x = x2.L’application x 7→x2 a par ensemble de depart, l’ensemble R et parimage, l’ensemble R+. C’est une fonction paire, de graphe donne parAlgebre

Page 11 : Exercice 2Ce qui nous permet de concluref 3, 1 = 1, 9;f 2, 1 = 0, 4De mˆemef 3, 1 2, 1 = f 3, 1 = 0, 9.Notons quef 3, 1 2, 1=0, 9=1, 9 0, 4=f 3, 1 f 2, 1.Finalementf 3, 1 2, 1 = f 2, 1 = 1, 4.On fait noter quef 3, 1 2, 1=1, 4=1, 9 0, 4=f 3, 1 f 2, 1.Algebre

Page 12 : Exercice 2Maintenantf 1 , 2 = f 10, 2 = 2,2etf 11, + = , 1 1, +.De mˆemef 1 , 2 1, + = f 1R= R= 2,2 , 1 1, += f 1 , 2 f 11, +.Finalementf 1 , 2 1, + = f 11, 2= 2, 1 1,2= 2,2 , 1 1, += f 1 , 2 f 11, +.Algebre

Page 13 : Exercice 3Soit f l’application de R dans R definie parf x = minx2, 3.Determiner les ensembles suivants :f R;f 0, 1;f 1, 2;f 2, +etf 10; 1;f 14; +.Avant de determiner les ensembles, notons que pour tout x R, on aminx2, 3 = x2si3 x 3,3six 3oux 3.Algebre

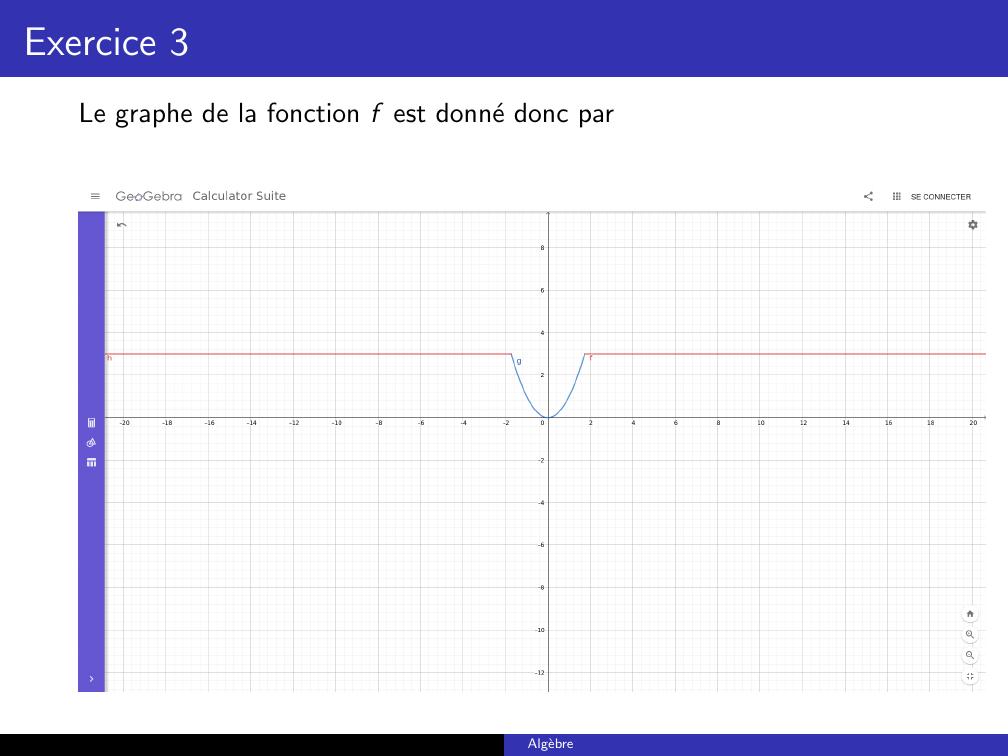
Page 14 : Exercice 3Le graphe de la fonction f est donne donc parAlgebre

Page 15 : Exercice 3En sachant cela, determinons les ensembles demandes. On a :f R = 0, 3;f 0, 1 = 0, 1;f 1, 2 = 1, 3etf 2, + = 3.De mˆemef 10, 1 = 1, 1;f 14; + = .Algebre

Page 16 : Exercice 4Les applications suivantes sont-elles injectives ? surjectives ? bijectives ?1 n 7→n + 1 de N dans N.2 x 7→x+1x1 de R \ 1 dans R.3 x; y 7→1; x y; y de R2 dans R3.4 x; y; z 7→x + y + z; x y z; x de R3 dans R3.5 x; y 7→x + y; xy de R2 dans R2.6 n 7→n + 1 de Z dans Z.7 x; y 7→2y de R2 dans R.8 x; y 7→x; xy y 3 de R2 dans R2.Algebre

Page 17 : Exercice 4Solution :1f : n 7→n + 1de N dans N.Injective : Pour tout couple n N, n′ N, on af n = f n′=⇒n + 1 = n′ + 1=⇒n = n′.Donce f est injective.Surjective : Non car 0 n’a pas d’antecedents. En effet, si f n = 0alors n + 1 = 0. Ce qui implique que n = 1, mais n N. Doncf n ̸= 0 pour tout n N.Algebre

Page 18 : Exercice 42f : x 7→x + 1x 1de R \ 1 dans R.Injective : Pour tout couple x R \ 1, x′ R \ 1 on af x = f x′ =⇒x + 1x 1 = x′ + 1x′ 1 =⇒x + 1x′ 1 = x′ + 1x 1=⇒xx′ x + x′ = xx′ + x x′=⇒x + x′ = x x′=⇒2x = 2x′=⇒x = x′.Donce f est injective.Surjective : Non, car 1 n’a pas d’antecedents. En effet, s’il existex R \ 1 tel que f x = 1, alorsf x = 1=⇒x + 1x 1 = 1=⇒x + 1 = x 1=⇒0 = 2.Contradiction ! Donc 1 n’a pas d’antecedent.Algebre

Page 19 : Exercice 43f : x, y 7→1, x y, yde R2 dans R3.Injective : Pour toute couple x, y R2, x′, y ′ R2, on a1, x y, y = 1, x′ y ′, y ′=⇒x y = x′ y ′ et y = y ′=⇒x = x′ et y = y ′=⇒x, y = x′, y ′.Donce f est injective.Surjective : Non, car tout element de la forme a, b, c avec a ̸= 1n’a pas d’antecedents.Algebre

Page 20 : Exercice 44f : x, y, z 7→x + y + z, x y z, xde R3 dans R3.Injective : Non. En effet, nous avons par example pour toute couplede la forme0, y, y R3 et 0, y ′, y ′ R3,avec y ̸= y ′,l’egalitey y, y + y, 0 = 0, 0, 0 = y ′ y ′, y ′ + y ′, 0.Surjective : Notons d’abord que pour tout a, b, c R3 on ax + y + z, x y z, x = a, b, c⇐⇒x + y + z = a ; x y z = b ; x = c.⇐⇒y + z = a c ; y + z = b c ; x = c.Ainsi, si a c ̸= b c, le systeme ne possede pas de solution,et a, b, c ne possede pas d’antecedents. Donc f n’est passurjective.Algebre

Page 21 : Exercice 4Par exemple, 0, 1, 1 n’a pas d’antecedent. En effet, sif x, y, z = 0, 1, 1 alorsx + y + z, x y z, x = 0, 1, 1.Ceci implique quex = 1;1 + y + z = 0;1 y z = 1=⇒0 = y + z = 1.Ce qui est absurde. Donc 0, 1, 1 n’a pas d’antecedents.Algebre

Page 22 : Exercice 45x, y 7→x + y, xyde R2 dans R2.Injective : Non. En effet, nous avons par example pour toute couplede la forme a, b R2 et b, a R2, l’egalitea + b, a · b = b + a, b · a.Surjective : Notons d’abord que pour tout a, b R2 on ax + y, xy = a, b⇐⇒x + y = a et xy = b⇐⇒y = a x et xa x = b⇐⇒y = a x et x2 ax + b = 0.C’est-a-dire a, b a un antecedent si et seulement si le polynomex2 ax + b possede une racine reel. Ceci implique, par exemple, quel’element 0, 1 ne possede pas d’antecedents. Donce f n’est passurjective.Algebre

Page 23 : Exercice 46f : n 7→n + 1de Z dans Z.Injective : Oui. En effet, pour toute couple n Z, n′ Z on af n = f n′=⇒n + 1 = n′ + 1=⇒n = n′.Surjective : Pour tout n Z, nous avonsn 1 + 1 = n=⇒f n 1 = n 1 + 1 = n.Ceci entraˆıne que pour tout n Z, n 1 est l’unique antecedent den. En particulier, pour tout n Z il existe un UNIQUE antecedent.La fonction f est donc bijective, en particulier surjective.Algebre

Page 24 : Exercice 47f : x, y 7→2yde R2 dans R.Injective : Non. En effet, pour toute couple de la forme x, y R2,x′, y R2 avec x ̸= x′, on af x, y = 2y = f x′, y.Par exemple f 1, 2 = 4 et f 3, 2 = 4, mais 1, 2 ̸= 3, 2.Surjective : Pour tout y R on ay = 2 · y2=⇒x R, fx, y2= 2 · y2 = y.Ceci entraˆıne que pour tout y R il existe au moins un antecedent.Donc f est surjective.Algebre

Page 25 : Exercice 48x; y 7→x; xy y 3de R2 dans R2.Injective : A vous de verifier.Surjective : A vous de verifier.Algebre

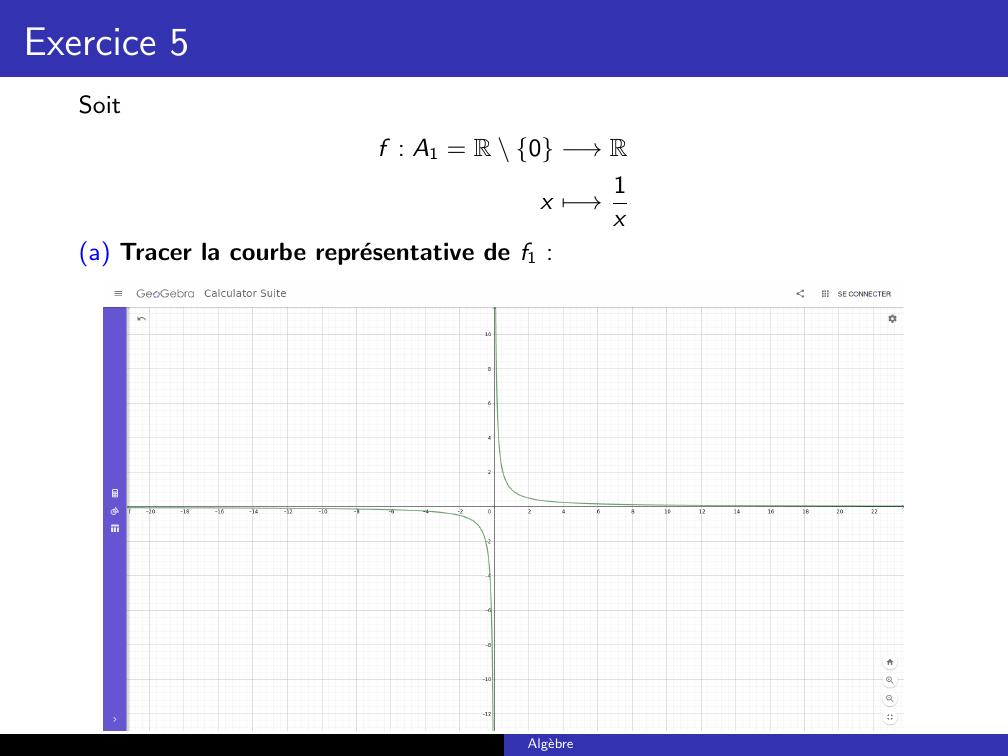
Page 26 : Exercice 5Soitf : A1 = R \ 0 →Rx 7→1xa Tracer la courbe representative de f1 :Algebre

Page 27 : Exercice 5b Dire si f1 est injective, surjective, bijective :Injective : Oui. En, effet pour tout x R \ 0, y R \ 0 nousavonsf1x = f1y⇐⇒1x = 1y=⇒x = y.Surjective : Non. En effet, 0 n’a pas d’antecedents.c Si f1 n’est pas bijective, determiner des ensembles E1 et F1 tels que f1soit une bijection de E1 sur F1 :Solution : Puisque l’image de f1 est R \ 0, il suffit de prendre :E1 = F1 = R \ 0.Algebre

Page 28 : Exercice 5d Determiner les ensembles f1A1, f10; 2, f 11 1, 1.Solution : Nous avonsf1A1 = R \ 0;f10, 2 =12, +et ;f 11 1, 1 = , 1 1, +.Algebre

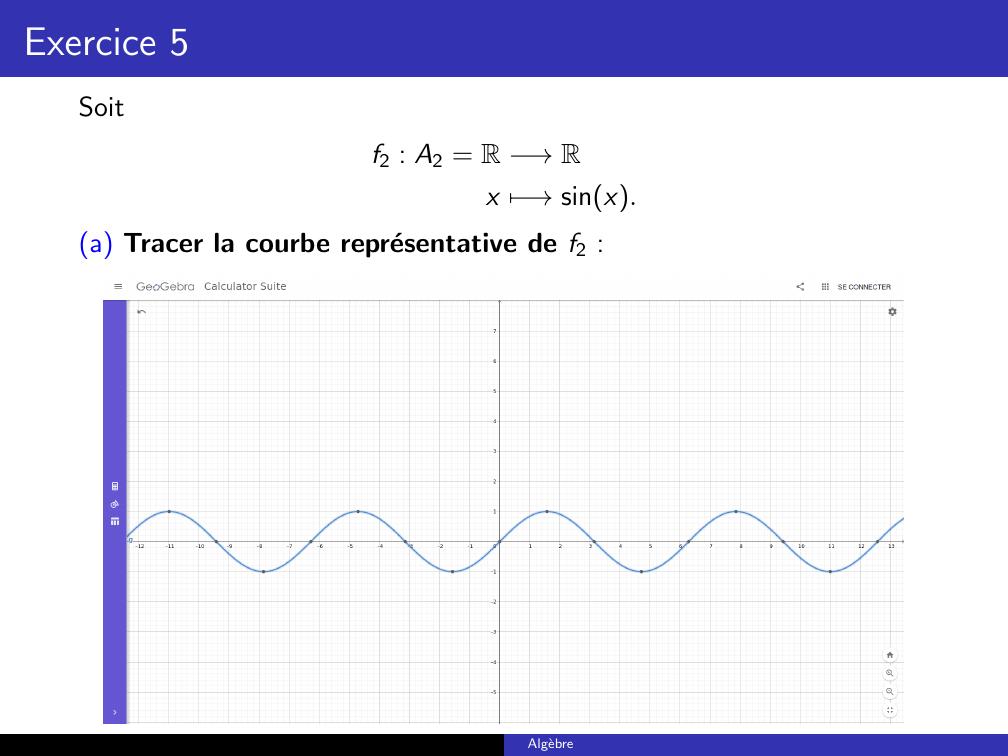
Page 29 : Exercice 5Soitf2 : A2 = R →Rx 7→sinx.a Tracer la courbe representative de f2 :Algebre

Page 30 : Exercice 5b Dire si f2 est injective, surjective, bijective :Injective : Non. En effet, la fonction sinus est une fonctionperiodique de periode 2π.Surjective : Non. En effet, tout reel dans R \ 1, 1 n’a pasd’antecedents.c Si f2 n’est pas bijective, determiner des ensembles E2 et F2 tels que f2soit une bijection de E2 sur F2.Solution : Nous pouvons par exemple prendre :E2 =hπ2 , π2ietF2 = 1, 1.Algebre

Page 31 : Exercice 5d Determiner les ensembles f2A2, f20; 2, f 12 1, 1.Solution : Nous avonsf2A2 = 1, 1;f20, 2 = 0, 1etf 12 1, 1 =iπ2 , π2h+ kπ.Algebre

Page 32 : Exercice 5Determiner l’ensemble de definition et l’expression de chacune des applicationssuivantes :f2 ◦f1etf1 ◦f2.Solution :f2 ◦f1 : Nous avonsf2 ◦f1x = f2f1x = f2 1x= sin 1x.Doncf2 ◦f1 : x 7→sin 1x.Ainsi, l’ensemble de definition de f2 ◦f1 est R \ 0.f1 ◦f2 : Nous avonsf1 ◦f2x = f1f2x = f1 sinx =1sinx.Doncf1 ◦f2 : x 7→1sinx.Puisque sinx = 0 si et seulement si x = kπ, on conclut que l’ensemblede definition de f1 ◦f2 est R \ kπ, k Z.Algebre

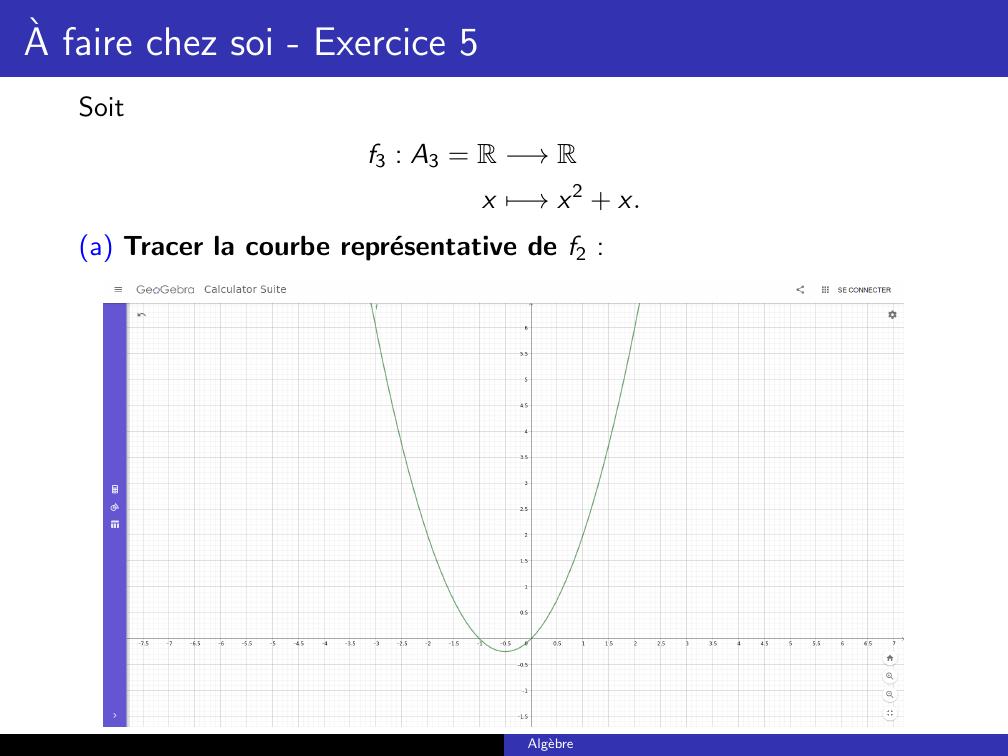
Page 33 : A faire chez soi - Exercice 5Soitf3 : A3 = R →Rx 7→x2 + x.a Tracer la courbe representative de f2 :Algebre

Page 34 : A faire chez soi - Exercice 5b Dire si f3 est injective, surjective, bijective :Injective : Non. En effetf30 = 0 = f31.Surjective : Non. Pour voir cela, notons que l’axe de symetrie de laparabole c’estx = 12.Rappelons que l’axe de symetrie de ax2 + bx + c c’est x = b2a .Ceci implique quex R, f3x f312= 14 12 = 14Par consequent, tout reel plus petit que 14 n’a pas d’antecedents etImx2 + x =14, +.Algebre

Page 35 : A faire chez soi - Exercice 5c Si f3 n’est pas bijective, determiner des ensembles E3 et F3 tels que f3soit une bijection de E3 sur F3.Solution : Puisque l’axe de symetrie de la parabole c’est x = 12 etl’image de f3 c’est14, +, il suffit de prendre :E3 =12, +etF3 =14, +.Algebre

Page 36 : A faire chez soi - Exercice 5d Determiner les ensembles f3R, f30; 2, f 13 1, 1.Solution : Nous avonsf3R =14, +;f30, 2 = 0, 6 .Pour trouver f 13 1, 1, notons quex f 13 1, 1 ⇐⇒f3x 1, 1⇐⇒1 f3x 1⇐⇒1 x2 + x 1.Maintenant1 x2 + x 1si et seulement six 1 52, 1 +52.Par consequentf 13 1, 1 =1 52, 1 +52.Algebre

Page 37 : Exercice 6Soit f : E →F l’application definie parf x = 1 + x + 1 x 2.1 On suppose que E = F = R.1Etant donne un reel x0, comparer f x0 et f x0. La fonction fest-elle injective ?2Donner les differentes expressions de f en supprimant les valeursabsolues. Faire son graphe.3Determiner f R. La fonction f est-elle surjective ?2 On suppose que E = 1, + et F = R+. Donner l’expression de f etdeterminer, si elle existe, l’application reciproque f 1 de F dans E.Algebre

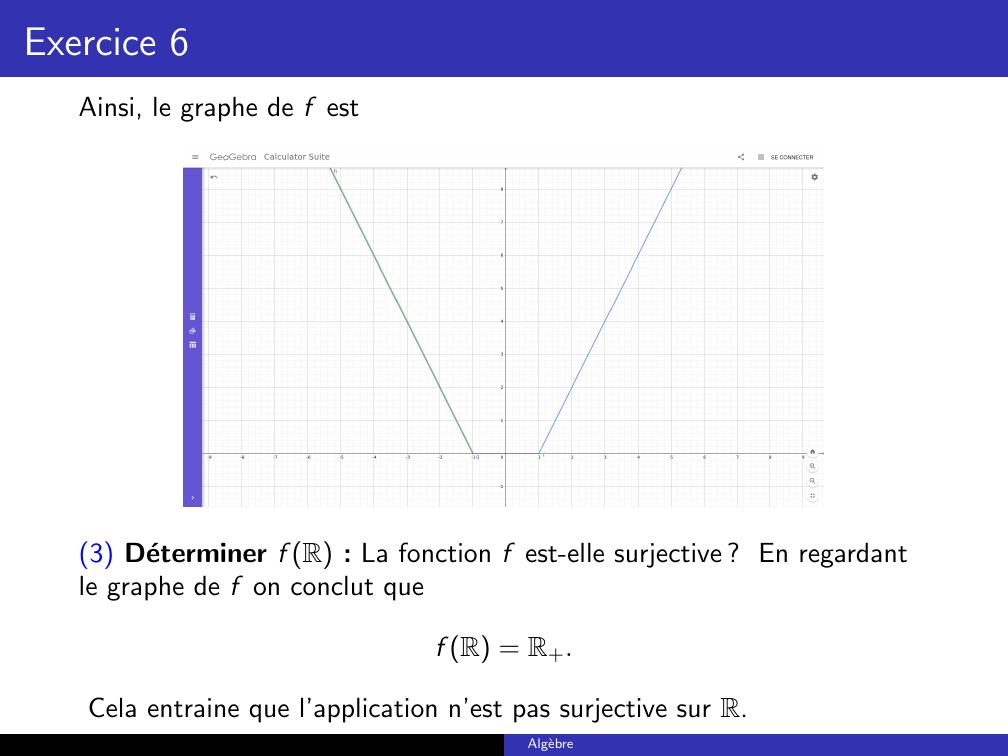
Page 38 : Exercice 6Soit f x = 1 + x + 1 x 2. On suppose que E = F = R.1 Comparer f x0 et f x0 : Soit x0 R. Alorsf x0 = 1 x0 + 1 x0 2 = 1 x0 + 1 + x0 2= 1 + x0 + 1 x0 2 = f x0.Ainsi, pour tout x0 R, nous avons f x0 = f x0. La application est doncpaire. Ce qui implique que l’application f n’est pas injective.2 Donner les differentes expressions de f : Puisque f est paire, il suffitd’etudier l’application sur l’intervalle 0, +. Nous avonsf x =1 + x + 1 x 2 = 0si 0 x 11 + x 1 x 2 = 2x 2si x 1Comme f est paire on deduitf x =2x 2si x 10si1 x 12x 2si x 1Algebre

Page 39 : Exercice 6Ainsi, le graphe de f est3 Determiner f R : La fonction f est-elle surjective ? En regardantle graphe de f on conclut quef R = R+.Cela entraine que l’application n’est pas surjective sur R.Algebre

Page 40 : Exercice 6b Supposons que E = 1, + et F = R+. Donner l’expression de f etdeterminer, si elle existe, l’application reciproque f 1 de F dans E.Solution : D’apres la questions precedent, l’applicationf x = 1 + x + 1 x 2est donnee sur 1, +, parf x = 2x 2.De plus, pour tout y R+, nous avonsy = 2x 2⇐⇒y + 22= x.Ce qui nous permet de conclure que pour tout y R+, y possede un uniqueantecedent donne par y+22 . Par consequent, f est bijective. Elle dispose doncd’une application reciproque, qui est donnee parg : R+→1, +y7→y + 22= unique antecedent de y par f.Algebre

Page 41 : Exercice 7On considere les applicationsf :N→Nn7→f n = 2netg :N→Nn7→gn =n2si n pairnsi n impair1L’application f est-elle injective ? surjective ? bijective ?2Mˆemes questions pour g.3Determiner f ◦g et g ◦f .Solution : Commen¸cons par etudier la fonction n 7→f n = 2n.Injective : Oui. En effet, pour tout couple n N, n′ N nous avonsf n = f n′=⇒2n = 2n′=⇒n = n′.Surjective : Non, car aucune nombre impair a d’antecedents.Bijective : Puisque elle n’est pas surjective, l’application f n’est pasbijective.Algebre

Page 42 : Exercice 7Etudions la fonctiong :N→Nn7→gn =n2si n pairnsi n impairInjective : Non. En effet, il suffit de noter que pour tout n N,nous avonsg2n + 1 = 2n + 1 = 22n + 12= g4n + 2.Surjective : Oui. En effet, pour tout n N, nous avonsn = 2n2=⇒n = g2n.Ceci entraine que tout n N possede un antecedent.Bijective : Puisque elle n’est pas injective, l’application g n’est pasbijective.Algebre

Page 43 : Exercice 7Determinerf ◦getg ◦f .Solution : Pour tout n N, on af ◦gn = f gn = 2gn =nsi n est pair,2nsi n est impair.De mˆeme, pour tout n N, on ag ◦f n = gf n = g2n = n.Algebre

Page 44 : A faire chez soi - Exercice 81Soit f l’application de R dans 1; 1 definie par f x = sinπx.L’application f est-elle injective, surjective, bijective ?2On note g la restriction de f a 12; 12. Montrer que g est uneapplication bijective de 12; 12 sur 1; 1.Solution :1 f x = sinπxInjective : Non. En effet, il suffit de noter quef 0 = sinπ · 0 = sin0 = 0 = sinπ = sinπ · 1 = f 1.Donc l’application f n’est pas injective.Surjective : Oui. En effet, on sait du cours d’analyse que toute valeur de1; 1 est atteinte par la fonction sinus. Par consequent, pour touty 1; 1 il existe x R tel quesinx = y=⇒y = sinπ · xπ= f xπ.C’est-a-dire xπ est un antecedent de y. L’application f est donc surjective.Bijective : Puisque elle n’est pas injective, l’application f n’est pasbijective.Algebre

Page 45 : A faire chez soi - Exercice 82 Soit g la restriction de f a 12, 12. On doit montrer que g est Bijective.Notons que pour tout x 12, 12, l’image gx est definit grˆace a lacompositionx 7→π · x 7→sin π · x = gx.C’est-a-dire que l’application g est la composee de12, 12→π2 , π2x7→π · xetsin :π2 , π2→ 1, 1x7→sinxMaintenantL’application x 7→π · x est bijective.Du cours d’analyse on sait que la application sinus est bijective deπ2 ; π2sur 1; 1, en particulier elle est bijective deπ2 ; π2sur 1; 1.Finalement, du cours on a le resultat suivant : Soit h : E →F et f : F →G.Alorsfethsont bijectives=⇒f ◦hbijective.Puisque g est la composition de deux fonctions bijectives, on conclut que laapplication g est bijective.Algebre

Page 46 : A faire chez soi - Exercice 9Soit f : R \ 2 →R \ 3 l’application definie par 3x+1x2 .1Determiner f 0, 22, 4.2Determiner f 10, 33, 4.3Montrer que f est une bijection et determiner sa reciproque.Algebre

Page 47 : A faire chez soi - Exercice 9Avant de repondre aux differents questions, faissons une etude de l’applicationf : x 7→3x + 1x 2 .On commence par notter que pour tout x R \ 2 nous avons3x + 1x 2 = 3x + 7 6x 2= 3x 6x 2 +7x 2 = 3 +7x 2.Ce qui nous permet de conclurex, y R \ 2, x y=⇒x 2 y 2=⇒1y 2 1x 2=⇒7y 2 7x 2=⇒3 +7y 2 3 +7x 2=⇒3y + 1y 2 3x + 1x 2=⇒f y f x.Ce qui implique que f est une fonction decroissant.Algebre

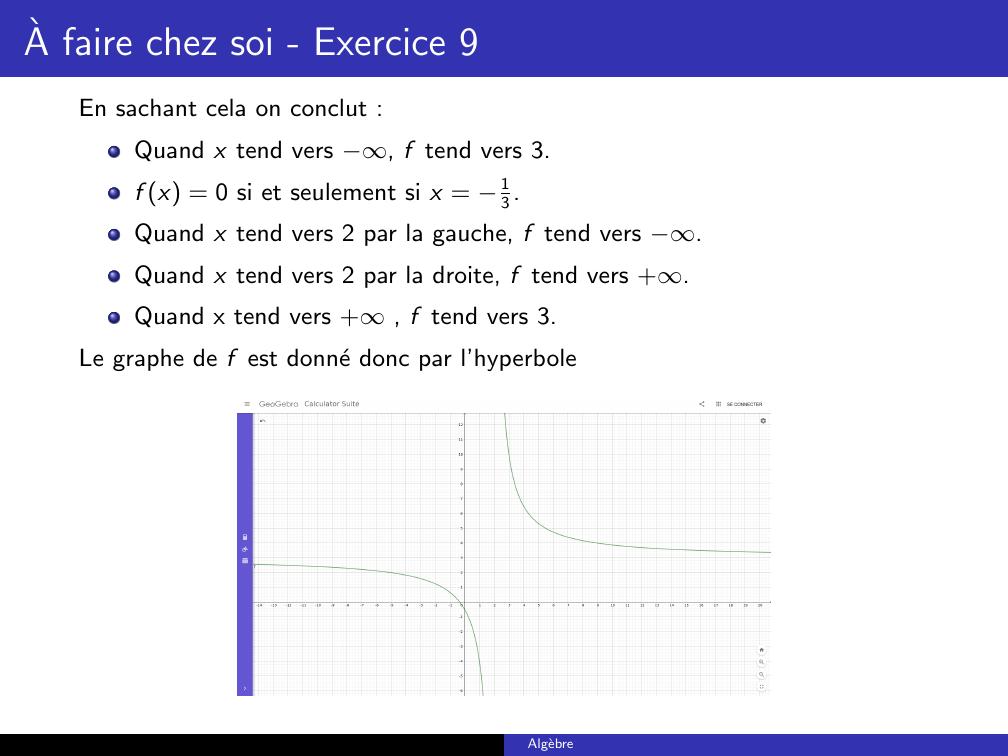
Page 48 : A faire chez soi - Exercice 9En sachant cela on conclut :Quand x tend vers , f tend vers 3.f x = 0 si et seulement si x = 13.Quand x tend vers 2 par la gauche, f tend vers .Quand x tend vers 2 par la droite, f tend vers +.Quand x tend vers +, f tend vers 3.Le graphe de f est donne donc par l’hyperboleAlgebre

Page 49 : A faire chez soi - Exercice 9Avec ceci, nous pouvons facilement repondre au questions.1Determiner f 0, 22, 4 : Puisque f est decroissant, nous avonsf 0, 22, 4 = f 0, 2 f 2, 4=, f 0f 4, +=, 12132 , +.2Determiner f 10, 33, 4 : Nous avonsf 10, 33, 4 = f 10, 3 f 13, 4.Maintenantx f 10, 3⇐⇒0 3x + 1x 2 = 3 +7x 2 0 ⇐⇒x , 13x f 13, 4⇐⇒3 3x + 1x 2 = 3 +7x 2 4 ⇐⇒x 9, +Par consequentf 10, 33, 4 =, 139, + .Algebre

Page 50 : A faire chez soi - Exercice 93Montrer que f est une bijection et determiner sa reciproque :Pour cela notons que pour tout y R \ 3 nous avonsy = 3x + 1x 2⇐⇒xy 2y = 3x + 1⇐⇒xy 3x = 2y + 1⇐⇒x = 2y + 1y 3 .Ce qui nous permet de conclure que pour tout y R \ 3, y possede ununique antecedent donne par x = 2y+1y3 . Par consequent, f est bijective.Elle dispose donc d’une application reciproque, qui par definition estdonnee parg : R \ 3→R \ 2y7→unique antecedent de y par f = 2y + 1y 3 .Algebre

Page 51 : A faire chez soi - Exercice 10On considere l’ensemble des ˆetre humains.1. A chaque individu on lui associe sa mere . Cela definit-il uneapplication ?2. Si oui, est-elle injective, surjective, bijective ?3. Mˆemes questions avec sa sœur .Solution :1. Puisque chaque individu a exactement une mere biologique Unindividu peut ne plus avoir de mere encore vivante. L’operationEnsemble des ˆetre humains →Ensemble des ˆetre humainsIndividu 7→Mere de l’individudefinit bien une application.2. Elle n’est pas injective car deux individus peuvent avoir la mˆememere. Elle n’est pas non plus surjective car tout individu surtout leshommes ne sont pas forcement la mere de quelqu’un.Algebre

Page 52 : A faire chez soi - Exercice 103. Puisque il se peut que un individu ne possede pas de soeur, et s’ilpossede il peut avoir plusieurs, l’operationEnsemble des ˆetre humains →Ensemble des ˆetre humainsIndividu 7→Soeur de l’individune definit pas une application.Algebre

Page 53 : Exercice 11Soit f : E →F une application, A et B deux parties de E, C et D deux partiesde F. Montrer que :a f A B = f A f B.b f A B f A f B.c f 1C D = f 1C f 1D.d f 1C D = f 1C f 1D.e f A f 1C = f A C.Algebre

Page 54 : Exercice 11a Montrerf A B = f A f B.Solution : On raisonne par double inclusion.: Montrons quef A B f A f BSoit y f A B. Alors il existe x A B, tel quey = f x.On a deux possibilites pour x.Si x A, alorsy = f x f A f A f B.Si x B, alorsy = f x f B f A f B.Dans les deux cas, y f A f B. Donc f A B f A f B.Algebre

Page 55 : Exercice 11: Montrons quef A B f A f B.Soit y f A f B. On a deux possibilites pour y.Si y f A, alors il existe x A, tel quey = f x.Orx A A B=⇒y f A B.Si y f B, alors il existe x B, tel quey = f x.Orx B A B=⇒y f A B.Dans les deux cas, y f A B. Donc f A f B f A B.Ainsi f A f B = f A B.Algebre

Page 56 : A faire chez soi - Exercice 11b Montrerf A B f A f B.Solution : Soit y f A B. Alors il existe x A B, tel quey = f x.Orx A B A=⇒y = f x f A,x A B B=⇒y = f x f B.Donc y f A f B. Par consequentf A B f A f B.Algebre

Page 57 : A faire chez soi - Exercice 11c Montrerf 1C D = f 1C f 1D.Solution : On raisonne par double inclusion.: Montrons quef 1C D f 1C f 1D.Soit x f 1C D. Alors f x C D. On a donc deuxpossibilites pour f x.Si f x C, alorsx f 1C f 1C f 1D.Si f x D, alorsx f 1D f 1C f 1D.Dans les deux cas x f 1C f 1D. Doncf 1C D f 1C f 1D.Algebre

Page 58 : A faire chez soi - Exercice 11: Montrons quef 1C D f 1C f 1D.Soit x f 1C f 1D. On a deux possibilites pour x.Si x f 1C, alorsf x C C D=⇒x f 1C D.Si x f 1D, alorsf x D C D=⇒x f 1C D.Dans les deux cas, x f 1C D. Doncf 1C f 1D f 1C D.Ainsif 1C D = f 1C f 1D.Algebre

Page 59 : Exercice 11d Montrerf 1C D = f 1C f 1D.On raisonne par double inclusion.: Montrons quef 1C D f 1C f 1D.Soit x f 1C D, alors f x C D. Orf x C D C=⇒x f 1C,f x C D D=⇒x f 1D.Donc x f 1C f 1D. Ainsif 1C D f 1C f 1D.Algebre

Page 60 : Exercice 11: Montrons quef 1C D f 1C f 1D.Soit x f 1C f 1D. Alorsf x Cetf x D.D’ouf x C D=⇒x f 1C D=⇒f 1C f 1D f 1C DPar consequentf 1C D = f 1C f 1D.Algebre

Page 61 : Exercice 11e Montrerf A f 1C = f A C.Solution : On raisonne par double inclusion.: Montronsf A f 1C f A C.Soit y f A f 1C. Alors il existe x A f 1C, tel quef x = y.Puisque x A, on obtient y = f x f A. De mˆeme, puisquex f 1C, on obtient y = f x C. Ainsiy f A C=⇒f A f 1C f A C.Algebre

Page 62 : Exercice 11: Montronsf A f 1C f A C.Soit y f A C. Puisque y f A, il existe x A tel quef x = y.Comme on a aussi y = f x C,on deduit que x f 1C. Ainsix A f 1C.D’ou on conclut quey = f x f A f 1C=⇒f A C f A f 1C.Par consequentf A C = f A f 1C.Algebre

Page 63 : Exercice 12Soit f : E →F une application, A et B deux parties de E, C et D deuxparties de F. Montrer que :a A f 1f A.b f f 1C = f E C.c f est injective ⇐⇒A E, A = f 1f A.d f est surjective ⇐⇒C F, f f 1C = C.Algebre

Page 64 : Exercice 12a Montrer :A f 1f A.Solution : Soit x A. Alors f x f A, d’ou on conclut quex f 1f A.Algebre

Page 65 : Exercice 12b Montrer :f f 1C = f E C.Solution : On raisonne par double inclusion.: Montronsf f 1C f E C.Soit y f f 1C. Alors existe x f 1C tel quef x = y.Or x f 1C, donc f x C. Ce qui impliquey = f x C.Maintenant, x E d’ou f x f E. Ainsi y C f E. Doncf f 1C f E C.: Montronsf f 1C f E C.Soit y f E C. Alors y f E et y C. Puisque y f E,existe x E tel quey = f x.Algebre

Page 66 : Exercice 12Mais y C, doncy = f x C=⇒x f 1C.C’est-a-direy = f xetx f 1C=⇒y f f 1C.D’ouf f 1C f E CFinalement, puisquef f 1C f E Cetf f 1C f E C.on conclutf f 1C = f E C.Algebre

Page 67 : Exercice 12c Montrer :f est injective⇐⇒A E, A = f 1f A.Solution : On raisonne par double implication.=⇒: Montronsf est injective=⇒A E, A = f 1f A.Il suffit de montrerf 1f A AOn sait deja que A f 1f A. Soit x f 1f A, alorsf x f A.Ainsi existe y A tel que f x = f y. Mais f etant injective, on conclutx = y A=⇒f 1f A A.Par consequentf 1f A = A.Algebre

Page 68 : Exercice 12⇐= : Montronsf est injective⇐=A E, A = f 1f A.Soit x E, y E tel quef x = f y.Montrons x = y. Posons A = x. Alors f A = f x, et d’apresl’hypothese nous pouvons ecriref 1f x = f 1f A = A = x.Ainsiy x=⇒x = y=⇒f est injective .Algebre

Page 69 : Exercice 12d Montrer :f est surjective⇐⇒C F, f f 1C = C.Solution : On raisonne par double implication.=⇒: Montronsf est surjective=⇒C F, f f 1C = C.Il suffit de montrerC f f 1COn sait deja que f f 1C = f E C C. Soit x C. Puisque f estsurjective, existe a E, tel quex = f a.Donc f a C, ce qui implique que a f 1C. D’ou on obtient quex = f a f f 1C=⇒C f f 1CAinsiC = f f 1CAlgebre

Page 70 : Exercice 12⇐= : Montronsf est surjective⇐=C F, f f 1C = C.Soit y F. Posons C = y. Alors d’apres l’hypothese, nous avonsf f 1y = y=⇒f f 1y ̸= =⇒f 1y ̸= .Par consequent, tout y F possede un antecendent. Donc f estsurjective.Algebre

Page 71 : Exercice 13Soient f : E →F et g : F →G deux applications. Montrer lesimplications suivantes :1 g ◦f est surjective =⇒g est surjective.2 g ◦f est injective =⇒f est injective.3 g ◦f est surjective et g est injective =⇒f est surjective.4 g ◦f est injective et f est surjective =⇒g est injective.Algebre

Page 72 : Exercice 131 Montronsg ◦f est surjective=⇒g est surjective.Soit y G. Nous voulons montrer qu’il existe x F tel quey = gx.Or g ◦f est surjective, donc :t E, y = g ◦f t.Il suffit des lors de poser : x = f t, pour avoiry = gx.Ainsi, tout element y G possede un antecedent. Donc g est surjective.Algebre

Page 73 : Exercice 132 Montronsg ◦f est injective=⇒f est injective.Soient x, y E. Supposons f x = f y. Nous voulons montrer que :x = y. Orf x = f y=⇒g ◦f x = g ◦f y=⇒zg◦f injectivex = y.Ainsi, f est injective.Algebre

Page 74 : Exercice 133 Soient f : E →F et g : F →G deux applications. Montronsg ◦f est surjective et g est injective=⇒f est surjective.Soit y F. Alors gy G. Comme g ◦f est surjective, il existe x Etel quegy = g ◦f x=⇒gy = gf x.Or g est injective, doncy = f x.Par consequent, tout y F possede au moins un antecedent.L’application f est donc surjective.Algebre

Page 75 : Exercice 134 Soient f : E →F et g : F →G deux applications. Montronsg ◦f est injective et f est surjective=⇒g est injective.Soient x F et y F, tels quegx = gy.Comme f est surjectivea E, f a = xetb E, f b = y.Ce qui nous permet d’ecriregx = gy=⇒gf a = gf b=⇒zg◦f injectivea = bAinsix = f a = f b = y.D’ou on conclut que g est injective.Algebre

Page 76 : Exercice 14Soit f : E →F, g : F →G, et h : G →E trois applications telles que h ◦g ◦finjective, g ◦f ◦h injective et f ◦h ◦g surjective. Montrer que f , g et h sontbijectives.Solution : D’apres la question 13 points 1 et 2, nous pouvons conclureh ◦g ◦f = h ◦g ◦fest injective=⇒f est injective.Aussif ◦h ◦g = f ◦h ◦g est surjective=⇒fest surjective.Donc f est bijective.De mˆemeg ◦f ◦h = g ◦f ◦h est injective=⇒h est injective.f ◦h ◦g = f ◦h ◦g est surjective=⇒f ◦h est surjective.Ainsi, nous avons f ◦h surjective et f injective. Donc h est surjectived’apres la question 13 3. D’ou on deduit que h est bijective.Algebre

Page 77 : Exercice 14Maintenant, nous avons vu en cours quefethinjectives=⇒f ◦hest injectivePar consequent, f ◦h est injective et surjective. Ce qui nous permet deconclure, d’apres les points 13 3 et 4 :f ◦h ◦gsurjectiveet f ◦h injective=⇒g est surjective.g ◦f ◦h injectiveet f ◦h surjective=⇒g est injective.Ainsi g est bijective.Algebre

Page 78 : Exercice 15Soit f : E →F une application. Montrer l’equivalence suivante :f est bijective⇐⇒A E, f Ac = f AcSolution : On raisonne par double implication. Montronsf est bijective=⇒A E, f Ac = f Ac.Soit A E. Montrons f Ac = f Ac. On raisonne par double inclusion.: Soit y f Ac. Alors existe x Ac = E \ A, tel quey = f x.Si y f A, alors existe x′ A tel que y = f x′. Ainsif x = f x′=⇒zf injectivex = x′.Ce qui est absurde car x Ac et x′ A. Doncy f Ac=⇒f Ac f Ac.Algebre

Page 79 : Exercice 15: Soit y f Ac. f etant surjective, il existe x E tel quey = f x.Si x A, alorsy = f x f A.Ce qui est absurde car y f Ac. Ainsi, x Ac, doncy = f x f Ac=⇒f Ac f Ac .Par consequentf Ac f Ac et f Ac f Ac=⇒f Ac = f Ac.Algebre

Page 80 : Exercice 15Soit f : E →F une application. MontronsA E, f Ac = f Ac=⇒f est bijectiveMontrons f injective : Soit x, y E, tel que x ̸= y. Montrons quef x ̸= f y. Nous avonsx ̸= y=⇒y ̸x=⇒y xc=⇒f y f xc.Or, d’apres l’hypothese, nous avonsf xc = f xc = f xc.Doncf y f xc=⇒f x ̸= f y.Montrons f surjective : Soit A = E. On aImf = f E = f Ecc=zHypothesef E cc = f c = c = F.Ainsi Imf = F. Par consequent, f est surjective.Algebre

Page 81 : A faire chez soi - Exercice 16Soit f : E →F, g : F →G et h : G →H trois applications. Montrerque :g ◦f et h ◦g sont bijectives⇐⇒f , g et h sont bijectivesSolution : On raisonne par double implication :⇐= : Montronsf , g et h sont bijectives=⇒g ◦f et h ◦g sont bijectives.Supposons f , g et h bijectives. Rappelons du cours quegetfbijectives=⇒g ◦fest bijective.De mˆemehetgbijectives=⇒h ◦gest bijective.Ce qui montre la proposition.Algebre

Page 82 : A faire chez soi - Exercice 16=⇒: Montronsg ◦f et h ◦g sont bijectives=⇒f , g et h sont bijectivesD’apres la question 4.10 points 1 et 2, nous avonsh ◦gbijective=⇒h ◦ginjective=⇒ginjective.aussig ◦fbijective=⇒g ◦fsurjective=⇒gsurjective.Donc g est bijective.De mˆemeg ◦fbijective=⇒g ◦finjective=⇒finjective.Nous avons aussig ◦f bijective=⇒g ◦f surjective.De plus, comme g est injective, on obtient d’apres la question 4.10point 3, que f est surjective. Donc f est bijective.Algebre

Page 83 : A faire chez soi - Exercice 16Finalementh ◦gbijective=⇒h ◦gsurjective=⇒h surjective.De plus, comme h ◦g est injective car bijective et g estsurjective on deduit, d’apres la question 4.10 point 4, que h estinjective. Donc h est bijective.Algebre

Page 84 : A faire chez soi - Exercice 17Soit f : E →F une application. Montrer l’implication suivante :f est surjective =⇒pour tout ensemble G et toutes applications g, h : F →G, g ◦f = h ◦f=⇒g = hSolution : Soit G un ensemble. Soientg : F →Geth : F →G.deux applications telles queg ◦f = h ◦f .Montrons que g = h. Soit x F. Puisque f est surjective existe y E tel quex = f y.Org ◦f y = h ◦f y=⇒gf y = hf y=⇒gx = hx.Ainsi pour tout x F on a gx = hx, d’oug = h.Algebre

Page 85 : A faire chez soi - Exercice supplementaireSoitf : E →Fune application. Discuter des affirmations suivantes E et F sont decardinal cardinal = nombre d’elements strictement superieur a 1 :1x E, y F, f x = y.2x E, y F, f x = y.3x E, y F, f x = y.4x E, y F, f x = y.5y F, x E, f x = y.6y F, x E, f x = y.7y F, x E, f x = y.8y F, x E, f x = y.Algebre

Page 86 : A faire chez soi - Exercice supplementaireSolution :1x E, y F, f x = y. Faux. En effet, il suffit que F possedeplus d’un element pour que la proposition soit fausse.2x E, y F, f x = y. Vrai. Ceci decoule de la definition d’uneapplication de E vers F.3x E, y F, f x = y. Faux. En effet, il suffit que F possedeplus d’un element pour que la proposition soit fausse.4x E, y F, f x = y. Vrai. Ceci decoule de la definition d’uneapplication de E vers F.5y F, x E, f x = y. Faux. Cette proposition est equivalent ala premiere proposition.6y F, x E, f x = y. Vrai uniquement si la application estsurjective.7y F, x E, f x = y. Vrai uniquement si la application estconstante.8y F, x E, f x = y. Vrai. Cette proposition est equivalent ala proposition quatre.Algebre

Page 87 : Pour aller plus loin - Exercice 18Soit A, B, C trois parties d’un ensemble E.1Determiner 1A\B en fonction de 1A et 1B.2Determiner 1AB en fonction de 1A et 1B.3Quand est-il vrai que AB C = AB AC ?Avant de repondre a la question, rappelons la definition de l’applicationindicatrice et donnons certaines de ses proprietes. Soit A E, alorsl’application indicatrice de A est1A : E →0, 1x 7→1Ax = 1si x A,0si x /A.D’apres la definition precedent on peut deduire11A = 1B si et seulement si A = B.Et 12A = 1A.21AB = 1A · 1B.31AB = 1A + 1B 1AB41Ac = 1 1A, ou 1 denote la fonction constante egale a 1, i.e. pour toutx E, 1x = 1.Algebre

Page 88 : Pour aller plus loin - Exercice 18Determiner 1A\B en fonction de1Aet1B.Solution : CommeA \ B = A Bc,nous pouvons ecrire1A\B = 1ABc = 1A · 1BcD’apres la propriete 2 de l’indicatrice= 1A · 1 1BD’apres la propriete 4 de l’indicatrice= 1A 1A · 1B= 1A 1AB.Algebre

Page 89 : Pour aller plus loin - Exercice 18Determiner 1AB en fonction de1Aet1B.Solution : CommeAB = A B \ A B,nous pouvons ecrire1AB = 1AB\AB= 1AB 1ABABD’apres la question precedent= 1AB 1ABcar A B A B= 1A + 1B 1AB 1ABD’apres la propriete 3 de l’indicatrice= 1A + 1B 2 · 1AB= 1A + 1B 2 · 1A · 1B.Algebre

Page 90 : Pour aller plus loin - Exercice 18Quand est-il vrai queAB C = AB AC?Solution : PuisqueAB C = AB AC⇐⇒1ABC = 1ABAC,nous allons resoudre cet exercice avec l’aide de l’application indicatrice. Notonsque grˆace a l’exercice 4.1 question 2 nous avons1ABC = 1A + 1BC 2 · 1A · 1BC= 1A + 1B · 1C 2 · 1A · 1B · 1C.De mˆeme, les proprietes de l’application indicatrice nous permetent d’ecrire1ABAC =1AB · 1ACD’apres la propriete 2 de l’indicatrice=1A + 1B 2 · 1A · 1B1A + 1C 2 · 1A · 1C12A = 1A =⇒ =1A + 1A · 1C 2 · 1A · 1C + 1B · 1A + 1B · 1C 2 · 1A · 1B · 1C 2 · 1A · 1B 2 · 1A · 1B · 1C + 4 · 1A · 1B · 1C=1A 1A · 1C 1A · 1B + 1B · 1CAlgebre

Page 91 : Pour aller plus loin - Exercice 18Par consequent1ABC=1ABAC⇐⇒1A + 1B · 1C 2 · 1A · 1B · 1C=1A 1A · 1C 1A · 1B + 1B · 1C⇐⇒0=1A · 1B + 1A · 1C 21A · 1B · 1C⇐⇒0= 1A · 1B + 1C 21B · 1C⇐⇒0= 1A · 1BC = 1ABCCe qui nous permet de conclure queAB C = AB AC ⇐⇒1ABC = 1ABAC⇐⇒0 = 1ABC ⇐⇒A BC = .Donc AB C = AB AC si et seulement si A BC = . Cequi est equivalent a BC Ac.Algebre

Page 92 : Pour aller plus loin - Exercice 19Soitf : C \ 0 →Cz 7→1z + z.1L’application f est-elle injective, surjective, bijective ?2Determiner l’image par f du cercle unite centre 0 et rayon 1.3Determiner l’image reciproque par f de iR.Solution :Injective : Non. En effet, pour tout z C \ 0 nous avonsz = 11z=⇒1z + z = 1z + 11z= 11z+ 1z=⇒f z = f 1z.Surjective : Notons que pour tout a C, il existe z C× tel quef z = a⇐⇒1z + z = a⇐⇒z2 az + 1 = 0.D’ou on conclut que les antecedents de a C par f sont les solutions del’equation z2 az + 1. Puisque toute equation de degree 2 possede des solutiondans C, on deduit que f est surjective.Algebre

Page 93 : Pour aller plus loin - Exercice 19De plus, pour tout a C les antecedent de a par f sonta + δ2eta δ2,ou δ est l’une quelconque des deux racines carrees du discriminant= a2 4.2 Pour determiner l’image par f du cercle unite on rappelle quez U⇐⇒θ π, π, z = eiθ.Maintenant, pour tout θ π, π nous avonsf eiθ = eiθ1 + eiθ=eiθ + eiθ=cosθ + i sinθ + cosθ + i sinθ=cosθ i sinθ + cosθ + i sinθ=2 cos θ.Par consequentf U = 2 cos π, π = 21, 1 = 2, 2.Algebre

Page 94 : Pour aller plus loin - Exercice 193 Determinons l’image reciproque par f de iR. Pour cela, notons que pourtout z C \ 0, nous avons1z = 1z · zz =zz2 =⇒Re1z= Re zz2= Rezz2= Rezz2=⇒Rez + 1z= Rez + Re1z= Rez + Rezz2= Rez ·1 +1z2Ce qui nous permet conclure queRef z = Rez + 1z= 0⇐⇒Rez1 +1z2= 0⇐⇒Rez = 0D’ou on deduit quef 1 iR =z C× : f z iR=z C× : Ref z = 0= z C× : Rez = 0 = iR.Algebre

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94