Post

TD4 Arbres Correction Informatique3 PREING2 S1

Posté Mis à jour
Par Ahmed A. .
17 min de lecture

Télécharger le TD4 Arbres Correction en pdf

Exercices : 1 2 3 4

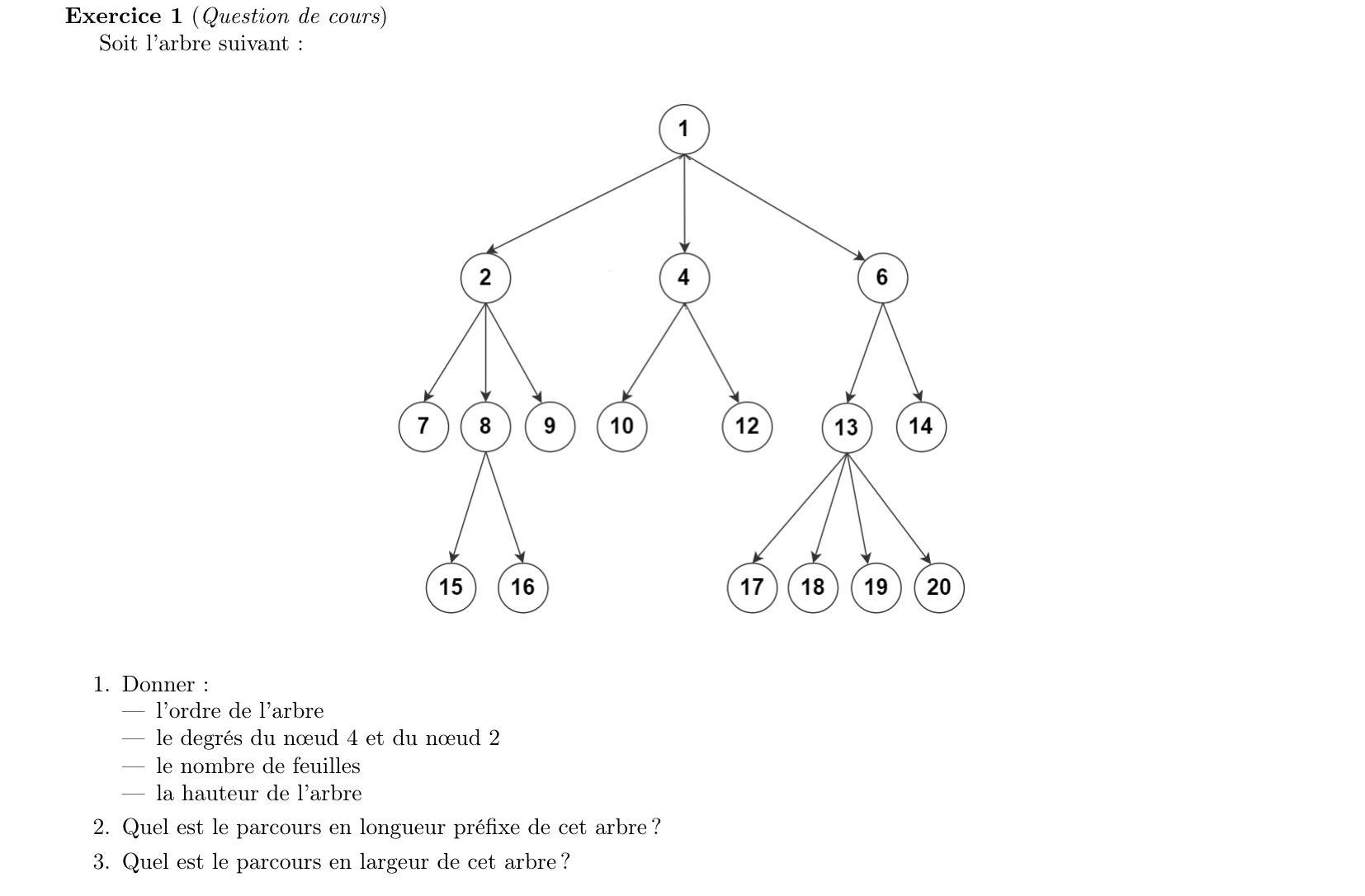
Exercice 1

Télécharger l’exercice exo1.c

exercice 1

  • L’arbre est d’ordre $ 4 $
  • Le degré du noeud $4$ est $2$
  • Le degré du noeud $2$ est $3$
  • il y’a $ 11 $ feuilles
  • l’arbre est de hauteur $3$ (racine de hauteur $0$)
  • Parcour préfixe : $ 1 \rightarrow 2 \rightarrow 7 \rightarrow 8 \rightarrow 15 \rightarrow 16 \rightarrow9 4 \rightarrow 10 \rightarrow 12 \rightarrow 6 \rightarrow 13 \rightarrow 17 \rightarrow 18 \rightarrow 19 \rightarrow 20 \rightarrow 14 $
  • Parcours en largeur : $ 1 \rightarrow 2 \rightarrow 4 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 10 \rightarrow 12 \rightarrow 13 \rightarrow 14 \rightarrow 15 \rightarrow 16 \rightarrow 17 \rightarrow 18 \rightarrow 19 \rightarrow 20 $

Exercice 2

Télécharger l’exercice exo2.c

exercice 2exercice 2

Partie 1 : Construction de l’arbre

  • On définie la structure qui représente un nœud dans l’arbre binaire
1
2
3
4
5
6
7
8
9
10
11

#include <stdio.h>
#include <stdlib.h>
typedef struct arbre_struct
{
    int value;                  // Valeur du nœud
    struct arbre_struct* fg;    // Pointeur vers le fils gauche
    struct arbre_struct* fd;    // Pointeur vers le fils droit
} Arbre;

typedef Arbre* pArbre;
  • On crée la fonction pour créer un nœud d’arbre avec une valeur spécifiée
1
2
3
4
5
6
7
8
9
10
11

pArbre creerArbre(int e) {
    pArbre new = malloc(sizeof(Arbre));
    if (new == NULL) {           // Vérifie si l'allocation mémoire a réussi
        exit(EXIT_FAILURE);
    }
    new->fd = NULL;              // Initialisation du fils droit à NULL
    new->fg = NULL;              // Initialisation du fils gauche à NULL
    new->value = e;              // Assigne la valeur au nœud
    return new;
}
  • On crée la fonction qui vérifie si l’arbre est vide (pointeur nul)
1
2
3
4

int estVide(pArbre a) {
    return a == NULL;
}
  • On crée la fonction qui vérifie si un nœud est une feuille (sans fils)
1
2
3
4
5
6
7

int estFeuille(pArbre a) {
    if (estVide(a)) {            // Erreur si le nœud n'existe pas
        exit(EXIT_FAILURE);
    }
    return a->fg == NULL && a->fd == NULL;
}
  • On crée la fonction qui récupère la valeur d’un nœud, avec vérification d’existence
1
2
3
4
5
6
7

int element(pArbre a) {
    if (estVide(a)) {            // Erreur si le nœud n'existe pas
        exit(EXIT_FAILURE);
    }
    return a->value;
}
  • On crée la fonction qui vérifie si un nœud a un fils gauche
1
2
3
4
5
6
7

int existeFilsGauche(pArbre a) {
    if (estVide(a)) {
        exit(EXIT_FAILURE);
    }
    return a->fg != NULL;
}
  • On crée la fonction qui vérifie si un nœud a un fils droit
1
2
3
4
5
6
7

int existeFilsDroit(pArbre a) {
    if (estVide(a)) {
        exit(EXIT_FAILURE);
    }
    return a->fd != NULL;
}
  • On crée la fonction qui ajoute un fils gauche au nœud spécifié
1
2
3
4
5
6
7
8

int ajouterFilsGauche(pArbre a, int e) {
    if (estVide(a) || existeFilsGauche(a)) {
        return 0;               // Erreur si l'arbre est vide ou à déjà un fils gauche
    }
    a->fg = creerArbre(e);      // Crée et assigne le fils gauche
    return 1;
}
  • On crée la fonction qui ajoute un fils droit au nœud spécifié
1
2
3
4
5
6
7
8

int ajouterFilsDroit(pArbre a, int e) {
    if (estVide(a) || existeFilsDroit(a)) {
        return 0;               // Erreur si l'arbre est vide ou à déjà un fils droit
    }
    a->fd = creerArbre(e);      // Crée et assigne le fils droit
    return 1;
}

Partie 2 : Parcours de l’arbre

  • On crée la fonction qui affiche un nœud
1
2
3
4
5
6
7
8

void traiter(pArbre a) {
    if (estVide(a)) {            // Vérifie si le nœud est vide
        printf("vide\n");
    } else {
        printf("%d\n", a->value);
    }
}
  • On implémente le parcours préfixe (nœud, gauche, droite)
1
2
3
4
5
6
7
8
9
10
11
12

void parcoursPrefixe(pArbre a) {
    traiter(a);                  // Affiche la valeur du nœud actuel
    if (!estVide(a)) {
        if (existeFilsGauche(a)) {
            parcoursPrefixe(a->fg); // Parcours du fils gauche
        }
        if (existeFilsDroit(a)) {
            parcoursPrefixe(a->fd); // Parcours du fils droit
        }
    }
}
  • On implémente le parcours postfixe (gauche, droite, nœud)
1
2
3
4
5
6
7
8
9
10
11
12

void parcoursPostfixe(pArbre a) {
    if (!estVide(a)) {
        if (existeFilsGauche(a)) {
            parcoursPostfixe(a->fg); // Parcours du fils gauche
        }
        if (existeFilsDroit(a)) {
            parcoursPostfixe(a->fd); // Parcours du fils droit
        }
    }
    traiter(a);                 // Affiche la valeur du nœud après ses fils
}
  • On reprend les fonctions et structures du TD2 exo3 en les adaptant aux arbres
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

typedef struct chainon_struct {
    pArbre value;
    struct chainon_struct* next;
} Chainon;

typedef struct file_struct {
    Chainon* tete;              
    Chainon* fin;               
} File;

File* creationFile() {
    File* nouvelleFile = malloc(sizeof(File));
    if (nouvelleFile == NULL) {
        exit(EXIT_FAILURE);
    }
    nouvelleFile->tete = NULL;
    nouvelleFile->fin = NULL;
    return nouvelleFile;
}

Chainon* creationChainon(pArbre a) {
    Chainon* nouveau = malloc(sizeof(Chainon));
    if (nouveau == NULL) {   
        exit(EXIT_FAILURE);
    }
    nouveau->value = a;
    nouveau->next = NULL;
    return nouveau;
}

void enfiler(File* pfile, pArbre a) {
    if (pfile == NULL) {
        exit(EXIT_FAILURE);
    }
    if (pfile->fin == NULL) {   
        pfile->fin = creationChainon(a);
        pfile->tete = pfile->fin;
    } else {
        pfile->fin->next = creationChainon(a);
        pfile->fin = pfile->fin->next;
    }
}

int defiler(File* pfile, pArbre* value) {
    if (pfile == NULL || pfile->tete == NULL) {
        return -1;               
    }
    Chainon* tmp = pfile->tete->next; 
    *value = pfile->tete->value;
    free(pfile->tete);           
    pfile->tete = tmp;           
    if (pfile->tete == NULL) {   
        pfile->fin = NULL;
    }
    return 0;
}
  • On implémente le parcours en largeur de l’arbre
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

void parcoursLargeur(pArbre a) {
    File* f = creationFile();    // Création de la file
    pArbre value;
    enfiler(f, a);               // Enfile la racine
    while (f->tete != NULL) {    // Tant que la file n'est pas vide
        defiler(f, &value);
        traiter(value);          // Affiche le nœud actuel
        if (!estVide(value)) {   // Enfile les fils
            if (existeFilsGauche(value)) {
                enfiler(f, value->fg);
            }
            if (existeFilsDroit(value)) {
                enfiler(f, value->fd);
            }
        }
    }
}

Partie 3 : Modification de l’arbre

  • On crée une fonction qui modifie la valeur de la racine de l’arbre
1
2
3
4
5
6
7
8

pArbre modifierRacine(pArbre a, int e) {
    if (estVide(a)) {
        exit(EXIT_FAILURE);
    }
    a->value = e;  // Met à jour la valeur de la racine
    return a;
}
  • On crée les fonctions de suppression des sous-arbres gauche et droit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

void supprimerFilsDroit(pArbre); //déclaration car utilisée dans supprimerFilsGauche


void supprimerFilsGauche(pArbre a) {
    if (!estVide(a) && existeFilsGauche(a)) { // si l'arbre est vide ou si le fils gauche est vide on ne supprime rien
        supprimerFilsGauche(a->fg); // On supprime le fils gauche du fils gauche
        supprimerFilsDroit(a->fg); // On supprime le fils droit du fils gauche
        free(a->fg); // On libère la mémoire
        a->fg = NULL; // On supprime la reference a la mémoire libérée
    }
}

void supprimerFilsDroit(pArbre a) {
    if (!estVide(a) && existeFilsDroit(a)) { // si l'arbre est vide ou si le fils droit est vide on ne supprime rien
        supprimerFilsGauche(a->fd); // On supprime le fils gauche du fils droit
        supprimerFilsDroit(a->fd); // On supprime le fils droit du fils droit
        free(a->fd); // On libère la mémoire
        a->fd = NULL; // On supprime la reference a la mémoire libérée
    }
}
  • On crée une fonction récursive qui compte le nombre de feuilles
1
2
3
4
5
6
7
8
9
10

int nmbFeuille(pArbre a) {
    if (estVide(a)) {  // si a vide alors l'arbre contient 0 nœuds
        return 0;
    }
    if (estFeuille(a)) { // si a feuille alors l'arbre contient 1 feuille
        return 1;
    }
    return nmbFeuille(a->fg) + nmbFeuille(a->fd); // on compte le nombre de feuille des deux arbres fils
}
  • On calcul de la taille de l’arbre (nombre total de nœuds)
1
2
3
4
5
6
7

int tailleArbre(pArbre a) {
    if (estVide(a)) {
        return 0; // si a vide alors l'arbre contient 0 nœuds
    }
    return 1 + tailleArbre(a->fg) + tailleArbre(a->fd); // si a n'est pas vide alors on compte 1 et ajoute a cela la taille des deux sous arbres
}
  • On calcule de la hauteur de l’arbre
1
2
3
4
5
6
7
8
9
10
11
12
13
14

int max(int a, int b) { // simple fonction max
    return a > b ? a : b; // cette notation remplace le if
}

int hauteur(pArbre a) {
    if (estVide(a)) { // si c'est vide alors on retourn -1
        return -1;
    }
    if (estFeuille(a)) { // si c'est une feuille alors on retourne 0 car on commence a racine = 0 et on doit omettre un étage
        return 0;
    }
    return 1 + max(hauteur(a->fg), hauteur(a->fd)); //On calcule la hauteur max entre les fils et on y ajoute 1
}

la notation a > b ? a : b est équivalente à if (a > b) {return a;} else {return b;}

  • On test dans le main les fonctionnalités de manipulation de l’arbre
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

int main() {
    pArbre arbre1 = creerArbre(1);

    // Construction de l'arbre avec plusieurs nœuds
    ajouterFilsGauche(arbre1, 2);
    ajouterFilsDroit(arbre1, 8);
    ajouterFilsGauche(arbre1->fg, 3);
    ajouterFilsDroit(arbre1->fg, 6);
    ajouterFilsGauche(arbre1->fd, 9);
    ajouterFilsDroit(arbre1->fd, 10);
    ajouterFilsGauche(arbre1->fg->fg, 4);
    ajouterFilsDroit(arbre1->fg->fg, 5);

    // Exécution des parcours et affichage des résultats pour test
    printf("Parcours en largeur :\n");
    parcoursLargeur(arbre1);
    return 0;
}

Exercice 3

Télécharger l’exercice exo3.c

exercice 3

  • On reprend les fonctions de l’exercice 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef struct arbre_struct
{...}Arbre;
typedef Arbre* pArbre;
pArbre creerArbre(int e){...}
int estVide(pArbre a){...}
int estFeuille(pArbre a){...}
int existeFilsGauche(pArbre a){...}
int existeFilsDroit(pArbre a){...}
int ajouterFilsGauche(pArbre a, int e){...}
int ajouterFilsDroit(pArbre a, int e){...}
void traiter(pArbre a){...}
void parcoursPrefixe(pArbre a){...}
  • On crée une fonction qui vérifie si l’arbre est filiforme : chaque nœud a au plus un fils
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

int filiforme1(pArbre a) {
    if (estVide(a) || estFeuille(a)) { // Un arbre vide ou feuille est filiforme
        return 1;
    }
    if (existeFilsGauche(a) && existeFilsDroit(a)) { // Si le nœud a deux fils, il n'est pas filiforme
        return 0;
    }
    // Appel récursif sur les sous-arbres gauche et droit, il faut que les deux sous arbre soit aussi filiforme
    return filiforme1(a->fg) && filiforme1(a->fd);
}

int filiforme2(pArbre a) { // Autre méthode (itérative)
    pArbre tmp = a;
    while (!estVide(tmp) && !estFeuille(tmp)) { // Parcourt jusqu'à atteindre une feuille
        if (existeFilsDroit(tmp) && existeFilsGauche(tmp)) { // Si un nœud a deux fils, il n'est pas filiforme
            return 0;
        } else if (existeFilsDroit(tmp)) { // Avance dans le fils droit
            tmp = tmp->fd;
        } else if (existeFilsGauche(tmp)) { // Avance dans le fils gauche
            tmp = tmp->fg;
        }
    }
    return 1; // Tous les nœuds n'avaient qu'un seul fils ou moins
}
  • On crée une fonction qui vérifie si l’arbre est un “peigne gauche” : chaque nœud n’a qu’un fils gauche
1
2
3
4
5
6
7
8
9
10

int peigne_gauche(pArbre a) {
    if (estVide(a) || estFeuille(a)) { // Un arbre vide ou une feuille est un peigne gauche
        return 1;
    }
    if (existeFilsDroit(a)) { // Si un nœud a un fils droit, il n'est pas un peigne gauche
        return 0;
    }
    return peigne_gauche(a->fg); // Appel récursif sur le fils gauche, peut etre fait aussi de manière itérative
}
  • On crée une fonction qui construit un arbre en “peigne gauche” de hauteur h
1
2
3
4
5
6
7
8
9
10
11

pArbre constrPeigneGauche(int h) {
    pArbre root = creerArbre(rand() % 11); // Crée la racine avec une valeur aléatoire
    pArbre actual = root;
    while (h > 1) { // Ajoute des fils gauches jusqu'à atteindre la hauteur
        ajouterFilsGauche(actual, rand() % 11); // Valeur aléatoire pour chaque nouveau nœud
        actual = actual->fg;
        h--;
    }
    return root;
}
  • On test le tout dans le main
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

int main() {
    srand(time(NULL)); // Initialise le générateur de nombres aléatoires

    // Création d'un arbre pour tester les fonctions
    pArbre arbre1 = creerArbre(1);
    ajouterFilsGauche(arbre1, 2);
    ajouterFilsDroit(arbre1, 8);
    ajouterFilsGauche(arbre1->fg, 3);
    ajouterFilsDroit(arbre1->fg, 6);
    ajouterFilsGauche(arbre1->fd, 9);
    ajouterFilsDroit(arbre1->fd, 10);
    ajouterFilsGauche(arbre1->fg->fg, 4);
    ajouterFilsDroit(arbre1->fg->fg, 5);
    ajouterFilsDroit(arbre1->fg->fd, 7);

    // Test des fonctions sur arbre1
    printf("Arbre 1 est filiforme (méthode récursive) : %d\n", filiforme1(arbre1));
    printf("Arbre 1 est filiforme (méthode itérative) : %d\n", filiforme2(arbre1));
    printf("Arbre 1 est peigne gauche : %d\n", peigne_gauche(arbre1));

    // Création d'un second arbre pour tester
    pArbre arbre2 = creerArbre(1);
    ajouterFilsGauche(arbre2, 3);
    ajouterFilsDroit(arbre2->fg, 6);
    ajouterFilsDroit(arbre2->fg->fd, 6);
    ajouterFilsGauche(arbre2->fg->fd->fd, 3);

    // Test des fonctions sur arbre2
    printf("Arbre 2 est filiforme (méthode récursive) : %d\n", filiforme1(arbre2));
    printf("Arbre 2 est filiforme (méthode itérative) : %d\n", filiforme2(arbre2));
    printf("Arbre 2 est peigne gauche : %d\n", peigne_gauche(arbre2));

    // Création d'un peigne gauche de hauteur 5
    pArbre arbre3 = constrPeigneGauche(5);
    printf("Parcours préfixe de l'arbre 3 (peigne gauche) :\n");
    parcoursPrefixe(arbre3);

    // Test des fonctions sur arbre3
    printf("Arbre 3 est filiforme (méthode récursive) : %d\n", filiforme1(arbre3));
    printf("Arbre 3 est filiforme (méthode itérative) : %d\n", filiforme2(arbre3));
    printf("Arbre 3 est peigne gauche : %d\n", peigne_gauche(arbre3));

    return 0;
}

Exercice 4

Télécharger l’exercice exo4.c

exercice 4exercice 4

  • $5$ $a$ $1$ $+$ $b$ $1$ $+$ $$ $a$ $b$ $+$ $/$ $$

\[\frac{1}{\frac{(8-2)\times(7-4)}{3+6}} = \frac{1}{2}\]
  • On crée et adapte les structure de l’exo1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

#include <stdio.h>
#include <stdlib.h>

typedef enum operations_enum{ // enum pour les operations
    ADD = '+',
    SUB = '-',
    DIV = '/',
    MULT = '*',
    EQ = '='
}Operations;

typedef struct terme_struct
{
    float value; 
    Operations typeTerme;
}Terme;

typedef struct arbre_struct
{
    Terme terme;
    struct arbre_struct* fg;
    struct arbre_struct* fd;
}Arbre;

typedef Arbre* pArbre;

pArbre creerArbre(float e, Operations type){
    pArbre new = malloc(sizeof(Arbre));
    if (new == NULL)
    {       
        exit(EXIT_FAILURE);
    }
    
    new->fd = NULL;
    new->fg = NULL;
    new->terme.value = e;
    new->terme.typeTerme = type;
    return new;
}

int estVide(pArbre a){ // Même que l'exo1
    return a == NULL;
}

int estFeuille(pArbre a){ // Même que l'exo1
    if (estVide(a))
    {
        exit(EXIT_FAILURE);
    }
    return a->fg == NULL && a->fd == NULL;
}

int existeFilsGauche(pArbre a){ // Même que l'exo1
    if (estVide(a))
    {
        exit(EXIT_FAILURE);
    }
    return a->fg != NULL;
}

int existeFilsDroit(pArbre a){ // Même que l'exo1
    if (estVide(a))
    {
        exit(EXIT_FAILURE);
    }
    return a->fd != NULL;
}

int ajouterFilsGauche(pArbre a, float e, Operations type){
    if (estVide(a) || existeFilsGauche(a))
    {
        return 0;
    }
    a->fg = creerArbre(e, type);
    return 1;
}


int ajouterFilsDroit(pArbre a, float e, Operations type){
    if (estVide(a) || existeFilsDroit(a))
    {
        return 0;
    }
    a->fd = creerArbre(e, type);
    return 1;
}
  • On adapte le traitement pour afficher la notation polonaise
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

void traiter(pArbre a) {// On affiche la valeur ou l'opérateur
    if (estVide(a)) {
        printf("vide\n");
    } else {
        // Si le type du nœud est une opération (EQ), on affiche sa valeur
        if (a->terme.typeTerme == EQ) {
            printf("%0.2f\n", a->terme.value);
        } else {
            printf("%c\n", a->terme.typeTerme); // Affiche le type d'opération si ce n'est pas une valeur
        }
    }
}

void parcoursPostfixe(pArbre a) { // Même que l'exo1
    if (!estVide(a)) {
        if (existeFilsGauche(a)) {
            parcoursPostfixe(a->fg); // Parcours du sous-arbre gauche
        }
        if (existeFilsDroit(a)) {
            parcoursPostfixe(a->fd); // Parcours du sous-arbre droit
        }
    }
    traiter(a); // Traite le nœud actuel après avoir traité ses fils
}

void afficherNotationPolonaiseInversee(pArbre a) { // Affiche la notation polonaise inverse (postfixe)
    parcoursPostfixe(a);
}
  • On effectue une opération sur deux nombres en fonction du type d’opération donné
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

float operation(float a, float b, Operations type) {
    switch (type) {
        case MULT:
            return a * b;
        case DIV:
            return a / b;
        case SUB:
            return a - b;
        case ADD:
            return a + b;
        default:
            exit(EXIT_FAILURE); 
    }
}
  • On calcule l’expression stockée dans l’arbre
1
2
3
4
5
6
7
8
9
10
11
12
13

float eval(pArbre a) {
    if (!estVide(a)) {
        if (estFeuille(a)) {
            return a->terme.value; // Si le nœud est une feuille, retourne sa valeur
        } else if (existeFilsDroit(a) && existeFilsGauche(a)) {
            // Calcule les sous-arbres gauche et droit, puis applique l'opération
            return operation(eval(a->fg), eval(a->fd), a->terme.typeTerme);
        }
        exit(EXIT_FAILURE); // Si le nœud a un seul fils, c'est une erreur
    }
    exit(EXIT_FAILURE); // Si l'arbre est vide, c'est une erreur
}
  • On test le tout dans le main
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

int main() {

    // Crée un arbre représentant l'expression $3$ $4$ $−$ $2$ $∗$ $3$ $+$
    pArbre arbre1 = creerArbre(0, ADD);
    ajouterFilsGauche(arbre1, 0, MULT);
    ajouterFilsDroit(arbre1, 3, EQ);

    ajouterFilsGauche(arbre1->fg, 0, SUB);
    ajouterFilsDroit(arbre1->fg, 2, EQ);

    ajouterFilsGauche(arbre1->fg->fg, 3, EQ);
    ajouterFilsDroit(arbre1->fg->fg, 4, EQ);

    printf("Résultat de l'évaluation de arbre1 : %0.2f \n", eval(arbre1));
    printf("Notation polonaise inverse de arbre1 : \n");
    afficherNotationPolonaiseInversee(arbre1);

    // Arbre représentant l'expression de la question 2
    pArbre arbre2 = creerArbre(0, DIV);
    ajouterFilsGauche(arbre2, 1, EQ);

    ajouterFilsDroit(arbre2, 0, DIV);
    ajouterFilsGauche(arbre2->fd, 0, MULT);
    ajouterFilsDroit(arbre2->fd, 0, ADD);

    ajouterFilsGauche(arbre2->fd->fd, 3, EQ);
    ajouterFilsDroit(arbre2->fd->fd, 6, EQ);

    ajouterFilsGauche(arbre2->fd->fg, 0, SUB);
    ajouterFilsDroit(arbre2->fd->fg, 0, SUB);

    ajouterFilsGauche(arbre2->fd->fg->fg, 8, EQ);
    ajouterFilsDroit(arbre2->fd->fg->fg, 2, EQ);

    ajouterFilsGauche(arbre2->fd->fg->fd, 7, EQ);
    ajouterFilsDroit(arbre2->fd->fg->fd, 4, EQ);

    printf("Résultat de l'évaluation de arbre2 : %0.2f \n", eval(arbre2));
    printf("Notation polonaise inverse de arbre2 : \n");
    afficherNotationPolonaiseInversee(arbre2);

    return 0;
}

Exercices : 1 2 3 4

PREING2S1, Informatique3
PREING2S1 Informatique3
Cet article est sous licence BSD 2-Close licence par l'auteur.