TD4 Derivabilite
Télécharger le TD4 Derivabilite en pdf
Page 1 : Departement de MathematiquesPreING1-Analyse2021 - 2022TD 4 - DerivabiliteCalcul de derivee et derivabiliteExercice 1. -Determiner l’expression de la derivee de chacune des fonctions suivantes :f1x = x3x + 12,f2x = 3x 24,f3x = 2x2 + 1x2 + 3 ,f4x =3x + 52x + 13,f5x =px3 + 2x2 + 1,f6x = ex sinx,f7x = lnx +px2 + 1,f8x =q2x + 5.Exercice 2. -Etudier la derivabilite sur R des applications suivantes :f : x 7→xx,g : x 7→x1 + x.Exercice 3. -La fonction x →cos x est-elle derivable en 0 ?Exercice 4. -Determiner a, b R de maniere a ce que la fonction suivante f soit derivable sur R+ :fx =x: si 0 x 1ax2 + bx + 1: si x 1Exercice 5. -Calculer les limites suivantes :limx→0e3x+2 e2x,limx→0cos x 1x,limx→1ln2 xx 1,limx→π2expcos x 1x π2,limx→0sin xx ,limx→0cos2 x 1x.Exercice 6. -Calculer l’expression de la derivee d’ordre n des fonctions definies par :f1x = sin x,f2x = sin2 x,f3x = x2 + 2x + 3ex,f4x = x2 cos x,f5x = cos3 x,f6x = 1x.Exercice 7. -Soient a un reel, et n, k N. Montrer quex + ank =n!n k!x + ank: si k n0: si k n12023-2024
Page 2 : Exercice 8. -Soient a et b deux reels et fx = x anx bn. Calculer f n et quand a = b en deduirenPk=0Cnk 2.Exercice 9. -Pour tout x 1, + on pose fx = x lnx x.1. Montrer que f est une bijection de 1, + sur 1, +.2. On pose g = f 1 l’application reciproque de f. Calculer g0 et g′0.Classe CkExercice 10. -Determiner le prolongement par continuite en 0 de chacune des fonctions suivantes et determiner si lafonction obtenue est de classe C1 :f1x = x ln x,a = 0;f2x = ex 1x ,a = 0f3x =x + 1 1lnx + 1 ,a = 0;f4x = x3 sin 1x,a = 0f5x = x sin 1x,a = 0Exercice 11. -Soit f une fonction reelle a valeurs reellesfx =ex: si x 0ax2 + bx + c: sinonDeterminer a, b, c pour que f soit de classe C2. La fonction f est-elle de classe C3 ?Exercice 12. -Etudier si la fonction suivante est de classe C1, C2 et C3 sur Rfx =x: si x 0sinx: sinonGrands theoremesExercice 13. -1. Montrer que pour tout x 0, on a :1x + 1 lnx + 1 lnx 1x2. n 1, montrer que :lnn + 1 lnn 1n lnn lnn 13. On poseHn =1n + 1 +1n + 2 + ... +1n + nMontrer que :ln2n + 1 lnn + 1 Hn ln2n lnnEn deduire que Hn converge et determiner sa limite.2
Page 3 : Exercice 14. -1. Soient a0, ..., an tels que a0 + a12 + ... +ann+1 = 0, montrer que x 0, 1 tel quea0 + a1x + ... + anxn = 0. Considerer la fonction fx = a0x + a12 x2 + ... +ann+1xn+1 .2. Soit P un polynˆome reel ayant n racines reelles distinctes, montrer que P′ en a au moins n 1.Exercice 15. -Soient n N et a, b R et fx = xn + ax + b.1. Montrer que le polynˆome f admet au plus trois racines reelles.2. Si n est pair. Montrer que le polynˆome f admet au plus deux racines reelles.Exercice 16. - Theoreme de Rolle a l’infiniSoit f une fonction continue et derivable sur a, + et telle que limx→fx = fa. Montrer qu’ilexiste un element c dans a, + tel que f ′c = 0.Exercice 17. -Dans l’application du theoreme des accroissements finis a la fonctionfx = αx2 + βx + γsur l’intervalle a, b preciser le nombre “c” de a, b. Donner une interpretation geometrique.ApplicationsExercice 18. -Calculer les limites suivantes :limx→0tan x sin x5x3 x4,limx→0tan 5xsin x ,limx→0sin x sin 5xsin x + sin 4x,limx→0sinx ln xxlimx→0+cosx exx + 1ex 1,limx→0sin x sin 2xx2,limx→0x sin x1 cos x.Exercice 19. -Soient C1 et C2 deux courbes definies par l’equation y = x2 et y = 1x respectivement.1. Demontrer que les courbes C1 et C2 admettent une unique tangente commune.2. Trouver les droites tangentes a C1 passant par le point 0, 1.3. Trouver les droites tangentes a C2 de la pente 2.Exercice 20. -Soient n 2 et f : 0, +→R une fonction definie parfx = 1 + xn1 + xn1. Montrer que f est derivable sur R+ et calculer sa derivee.2. Montrer que f atteint un minimum sur R+, et on le determine.3. En deduire les inegalites suivantes : Pour tout x R+, on a1 + xn 2n11 + xn,Pour tout x, y R+, on ay + xn 2n1yn + xn.Exercice 21. -Calculer le maximum et le minimum des fonctions suivantes :1. f1x = x2 + 5x + 6,x 4, 4.3
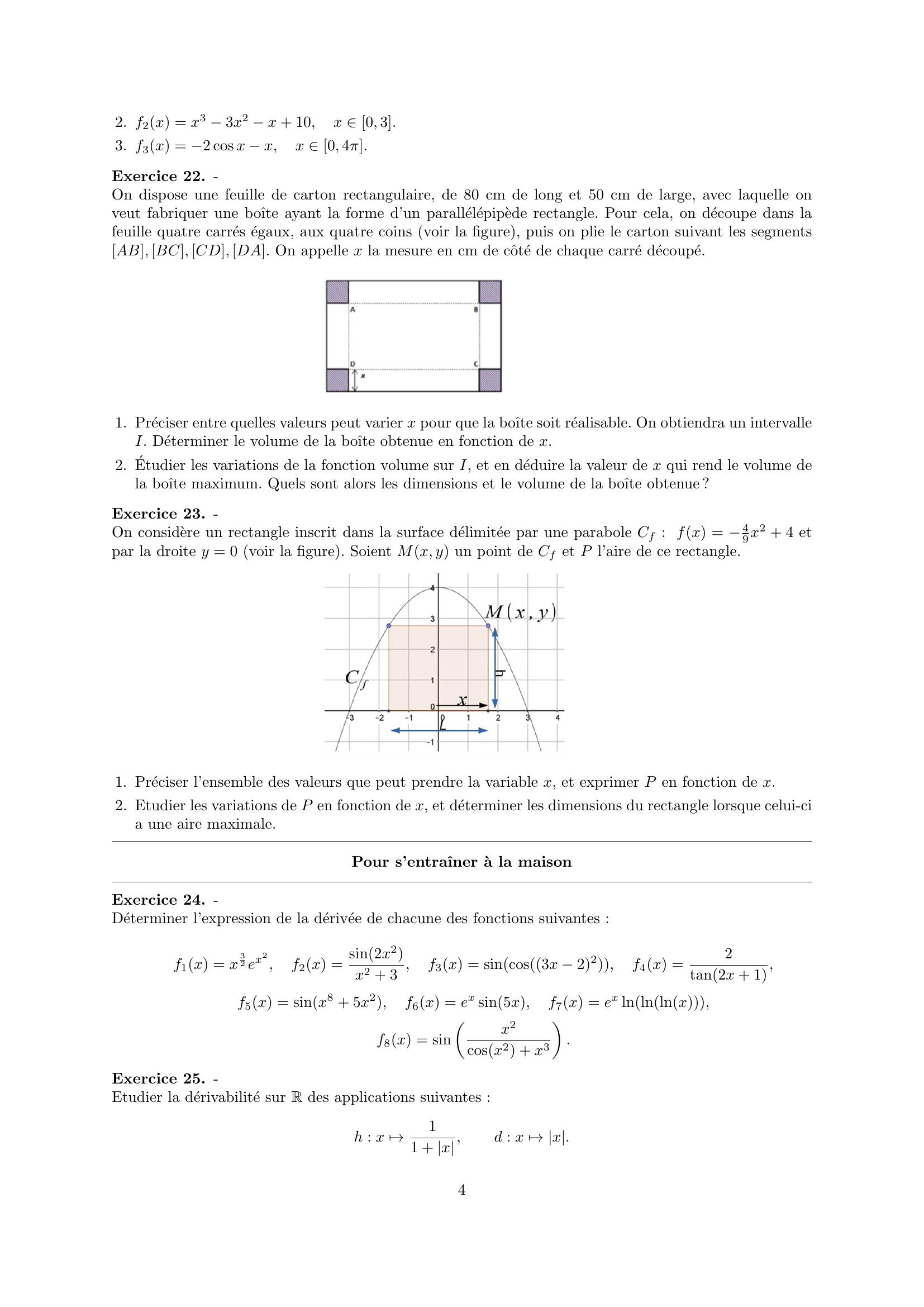
Page 4 : 2. f2x = x3 3x2 x + 10,x 0, 3.3. f3x = 2 cos x x,x 0, 4π.Exercice 22. -On dispose une feuille de carton rectangulaire, de 80 cm de long et 50 cm de large, avec laquelle onveut fabriquer une boˆıte ayant la forme d’un parallelepipede rectangle. Pour cela, on decoupe dans lafeuille quatre carres egaux, aux quatre coins voir la figure, puis on plie le carton suivant les segmentsAB, BC, CD, DA. On appelle x la mesure en cm de cˆote de chaque carre decoupe.1. Preciser entre quelles valeurs peut varier x pour que la boˆıte soit realisable. On obtiendra un intervalleI. Determiner le volume de la boˆıte obtenue en fonction de x.2. Etudier les variations de la fonction volume sur I, et en deduire la valeur de x qui rend le volume dela boˆıte maximum. Quels sont alors les dimensions et le volume de la boˆıte obtenue ?Exercice 23. -On considere un rectangle inscrit dans la surface delimitee par une parabole Cf : fx = 49x2 + 4 etpar la droite y = 0 voir la figure. Soient Mx, y un point de Cf et P l’aire de ce rectangle.1. Preciser l’ensemble des valeurs que peut prendre la variable x, et exprimer P en fonction de x.2. Etudier les variations de P en fonction de x, et determiner les dimensions du rectangle lorsque celui-cia une aire maximale.Pour s’entraˆıner a la maisonExercice 24. -Determiner l’expression de la derivee de chacune des fonctions suivantes :f1x = x32 ex2,f2x = sin2x2x2 + 3 ,f3x = sincos3x 22,f4x =2tan2x + 1,f5x = sinx8 + 5x2,f6x = ex sin5x,f7x = ex lnlnlnx,f8x = sinx2cosx2 + x3.Exercice 25. -Etudier la derivabilite sur R des applications suivantes :h : x 7→11 + x,d : x 7→x.4
Page 5 : Exercice 26. -Calculer l’expression de la derivee d’ordre n des fonctions definies par :f1x = x2ex,f2x = xn1 lnx + 1.Exercice 27. -Soit n N. Montrer quexne1x n+1 = 1n+1xn+2e1x .Exercice 28. -Determiner le prolongement par continuite en a de chacune des fonctions suivantes et determiner si lafonction obtenue est de classe C1 :f1x = e2x 1x2,a = 0;f2x = x sinx sin 1x,a = 0;f5x = exx ,a = 0f3x = xx2 2x + 1x 1,a = 1;f4x = x2 cos 1x,a = 0.Exercice 29. -Soit f : R →R une fonction definie parfx =0: si x 0e1x: sinon1. Montrer que f est de classe Csur 0, +, et que f nx = e1x Pn 1x ou Pn RX.2. Montrer que f est de classe Csur R.Exercice 30. -1. Determiner l’expression de la derivee de la fonction ln x sur R.2. soitfx =x3 ln x: si x 00: sinonSoit f est de classe Ck sur R. Trouver les valeurs possibles de k N.Exercice 31. -Etudier si la fonction suivante est de classe C1 sur Rfx =x2 sin 1x: si x ̸= 00: sinonExercice 32. -1. Montrer que, n N,12n + 1 n + 1 n 12na On posevn = 8n + 4 8pnn + 1b Montrer que :1n + 1 vn 1nEn deduire que vn converge et determiner sa limite.5
Page 6 : Exercice 33. -Calculer les limites suivantes :limx→1arccosx1 x2 ,limx→1xx 1 sinx 1x3 3x + 2,limx→0+ ln x · ln1 x,limx→+x2e1x e1x+1 .Exercice 34. -Soient C1 et C2 deux courbes definies par l’equation y = x22 et y = 1x respectivement.1. Demontrer que les courbes C1 et C2 admettent une unique tangente commune.2. Trouver les droites tangentes a C1 passant par le point 0, 2.3. Trouver les droites tangentes a C2 de la pente 1.4. Demontrer que les courbes C3 : y =33x et C2 admettent un point commun ou la droite tangente aC2 et la droite tangente a C3 sont orthogonales. Trouvez-les.Pour aller plus loin a la maisonExercice 35 Injectivite locale. -Soit f : R →R derivable et a R tel que f ′a ̸= 0.1. Montrer qu’il existe un voisinage V de a tel que x V \ a, fx ̸= fa.2. Si f ′ est continue au point a, montrer qu’il existe un voisinage V de a tel que fV soit injective.Exercice 36 Proprietes de parite et de periodicite. -Soit f : R →R derivable.1. Que peut-on dire de f ′ si on sait que f est paire ? impaire ? periodique ?2. Que peut-on dire de f si on sait que f ′ est paire ? impaire ? periodique ?3. Montrer que si f ′ est T-periodique et fT ̸= f0, alors f n’a pas de periode on etudiera fnTpour n N.Exercice 37. -Soit f une fonction de classe Cn sur a, b s’annulant en n + 1 points distincts de a, b.On suppose donc qu’il existe n + 1 elements de a, b, notes : x00 x01 ... x0n , qui verifient :fx00 = fx01 = ... = fx0n = 0.1. Montrer, par recurrence sur k que : pour tout entier k tel que 0 k n, il existe nk +1 elementsde a, b, notes xk0 xk1 ... xknk qui verifient : f kxk0 = f kxk1 = ... = f kxkn = 0.2. Que pouvez vous en deduire concernant l’existence de zeros eventuels de f n sur a, b ?Exercice 38. -Soit f derivable sur R et qui possede un unique point fixe ω tel que fω = ω. On definit une suitexnnN par la donnee de x0 et la recurrence xn+1 = fxn.1. Montrer que si f ′ω 1, alors α 0, 0 k 1, x ω α, ω + α,fx fωx ω k.2. En deduire, par recurrence, que si x0 ω α, ω + α, alors : n N,fxn fω knx0 ω.3. Conclure quant a la convergence vers w.4. On suppose maintenant que f ′ω 1 et on va montrer que la suite xnnN converge vers w si etseulement si elle est stationnaire i.e. xn = ω a partir d’un certain rang.Montrer que α 0, k 1, x ω α, ω + α,fx fωx ω k.5. Supposons donc, par l’absurde, que : n, xn ̸= ω non stationnaire, et que lim un = ω.a Montrer qu’a partir d’un certain rang N, on aura : xn ω α, ω + α,6
Page 7 : b En deduire, par recurrence, que : n N,fxn fω knNxN ω et obtenez lacontradiction souhaitee.6. Que dire dans le cas f ′ω = 1 ?On pourra etudier la suite definie a l’aide de la fonction : fx = x2 + 12, avec x0 = 0 puis avecx0 = 2.7