TD5 ACP
Page 1 : Data Exploration ING1 Informatique TD5 : Analyse en composantes principales Exercice 1 : Une analyse en composante principale ACP normée a été effectuée sur 50 avions. On a déterminé, pour chacun d’eux, la valeur de 10 variables vitesse de croisière, rayon d’action, consommation, nombre de places, coût de revient du transport par passager et par kilomètre, etc. On considère la représentation de ces variables dans le cercle de corrélation ci- dessous. 1. Quelles sont les variables qui peuvent aider à donner une signification à l’axe 1 ? 2. Quelles sont les variables qui ne doivent pas être interprétées sur cette figure ? 3. Donner 3 groupes de variables qui, au sein d’un même groupe, sont fortement corrélées positivement entre elles. 4. Citer deux variables qui sont peu corrélées entre elles. 5. Citer deux variables qui sont fortement corrélées négativement avec la variable V4. 6. Quel est approximativement le coefficient de corrélation entre la variable V1 et la première composante principale ? 7. Citer une variable dont le coefficient de corrélation avec la deuxième composante principale vaut presque 1. 8. Que peut-on dire sur la corrélation entre les variables V3 et V7 ? 9. Que signifie le coefficient de corrélation entre la première et la deuxième composante principale.
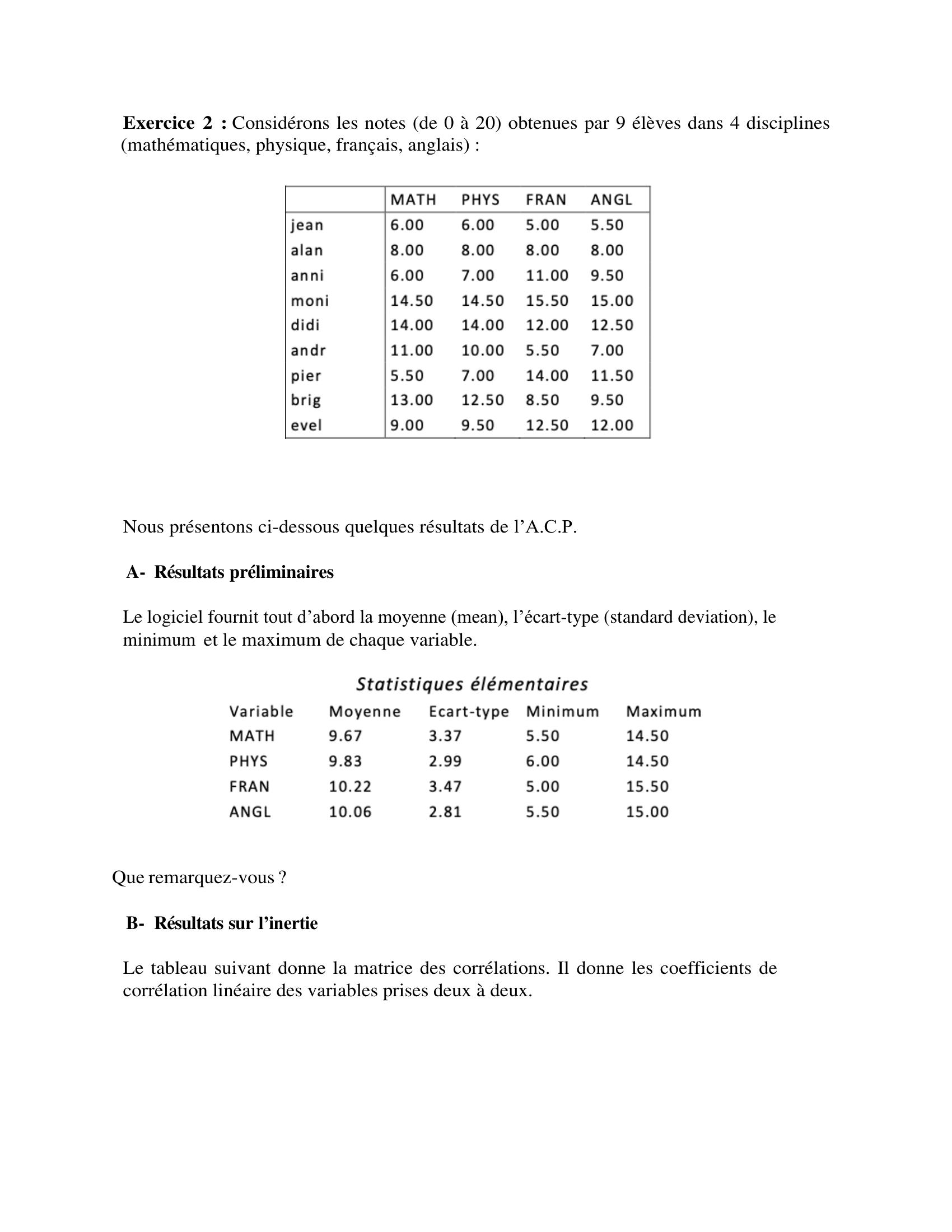
Page 2 : Exercice 2 : Considérons les notes de 0 à 20 obtenues par 9 élèves dans 4 disciplines mathématiques, physique, français, anglais : Nous présentons ci-dessous quelques résultats de l’A.C.P. A- Résultats préliminaires Le logiciel fournit tout d’abord la moyenne mean, l’écart-type standard deviation, le minimum et le maximum de chaque variable. Que remarquez-vous ? B- Résultats sur l’inertie Le tableau suivant donne la matrice des corrélations. Il donne les coefficients de corrélation linéaire des variables prises deux à deux.
Page 3 : Que remarquez-vous ? C- Résultats généraux On donne la matrice de variance-covariance, puis le tableau des valeurs propres et de la variance expliquée. PCT.VAR= pourcentage de variance PCT.CUM=pourcentage cumulé : exemple 28.23/40.3100=70 . a. Quelle est la relation entre λi et la variance de Ci . b. Comment interprétez-vous la relation suivante qui relie la variance des variables initiales Xi avec celle des composantes principales Ci. Var Xi = 4i=1 Var Ci4i=1 D- Résultats sur les variables Le résultat fondamental concernant les variables est le tableau des corrélations
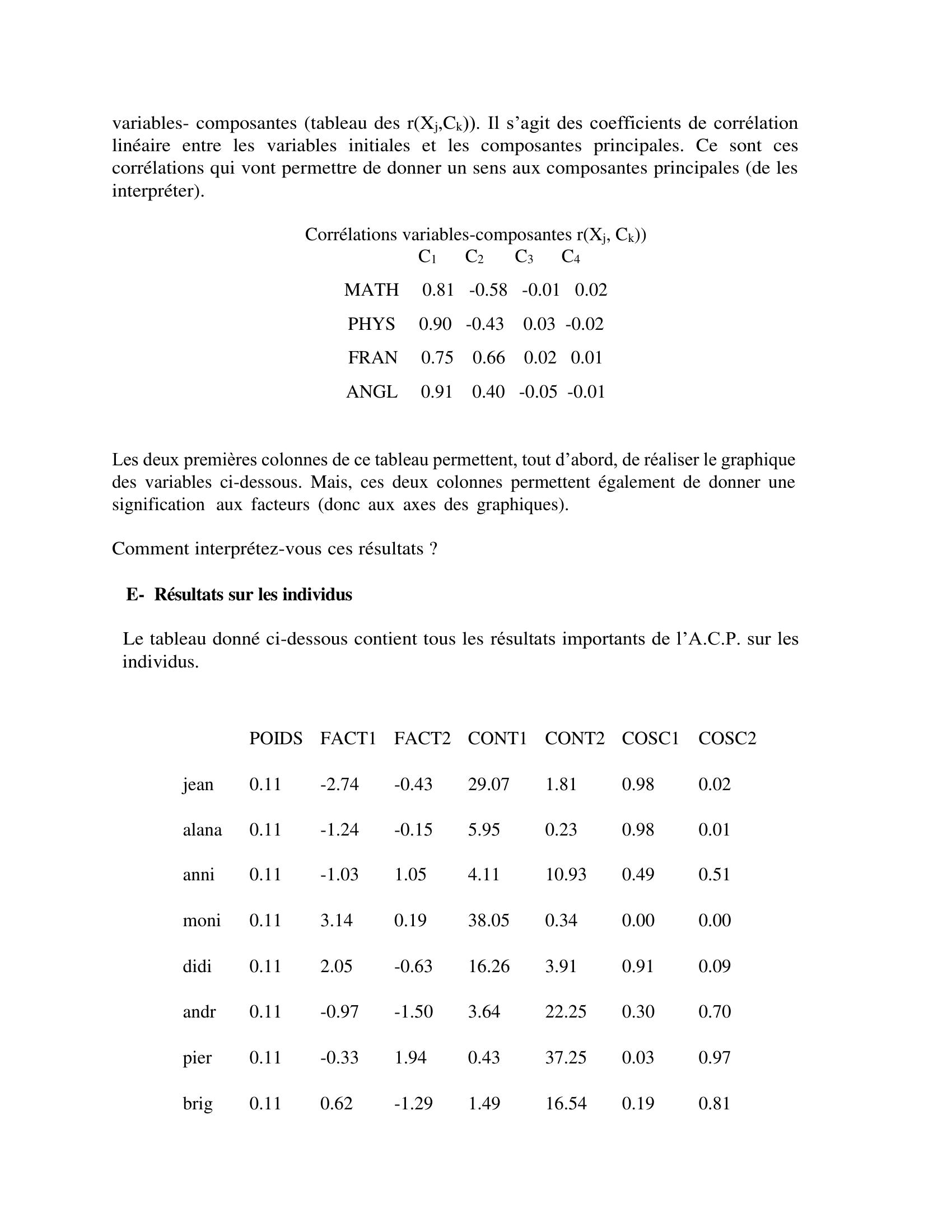
Page 4 : variables- composantes tableau des rXj,Ck. Il s’agit des coefficients de corrélation linéaire entre les variables initiales et les composantes principales. Ce sont ces corrélations qui vont permettre de donner un sens aux composantes principales de les interpréter. Corrélations variables-composantes rXj, Ck C1 C2 C3 C4 MATH 0.81 -0.58 -0.01 0.02 PHYS 0.90 -0.43 0.03 -0.02 FRAN 0.75 0.66 0.02 0.01 ANGL 0.91 0.40 -0.05 -0.01 Les deux premières colonnes de ce tableau permettent, tout d’abord, de réaliser le graphique des variables ci-dessous. Mais, ces deux colonnes permettent également de donner une signification aux facteurs donc aux axes des graphiques. Comment interprétez-vous ces résultats ? E- Résultats sur les individus Le tableau donné ci-dessous contient tous les résultats importants de l’A.C.P. sur les individus. POIDS FACT1 FACT2 CONT1 CONT2 COSC1 COSC2 jean 0.11 -2.74 -0.43 29.07 1.81 0.98 0.02 alana 0.11 -1.24 -0.15 5.95 0.23 0.98 0.01 anni 0.11 -1.03 1.05 4.11 10.93 0.49 0.51 moni 0.11 3.14 0.19 38.05 0.34 0.00 0.00 didi 0.11 2.05 -0.63 16.26 3.91 0.91 0.09 andr 0.11 -0.97 -1.50 3.64 22.25 0.30 0.70 pier 0.11 -0.33 1.94 0.43 37.25 0.03 0.97 brig 0.11 0.62 -1.29 1.49 16.54 0.19 0.81
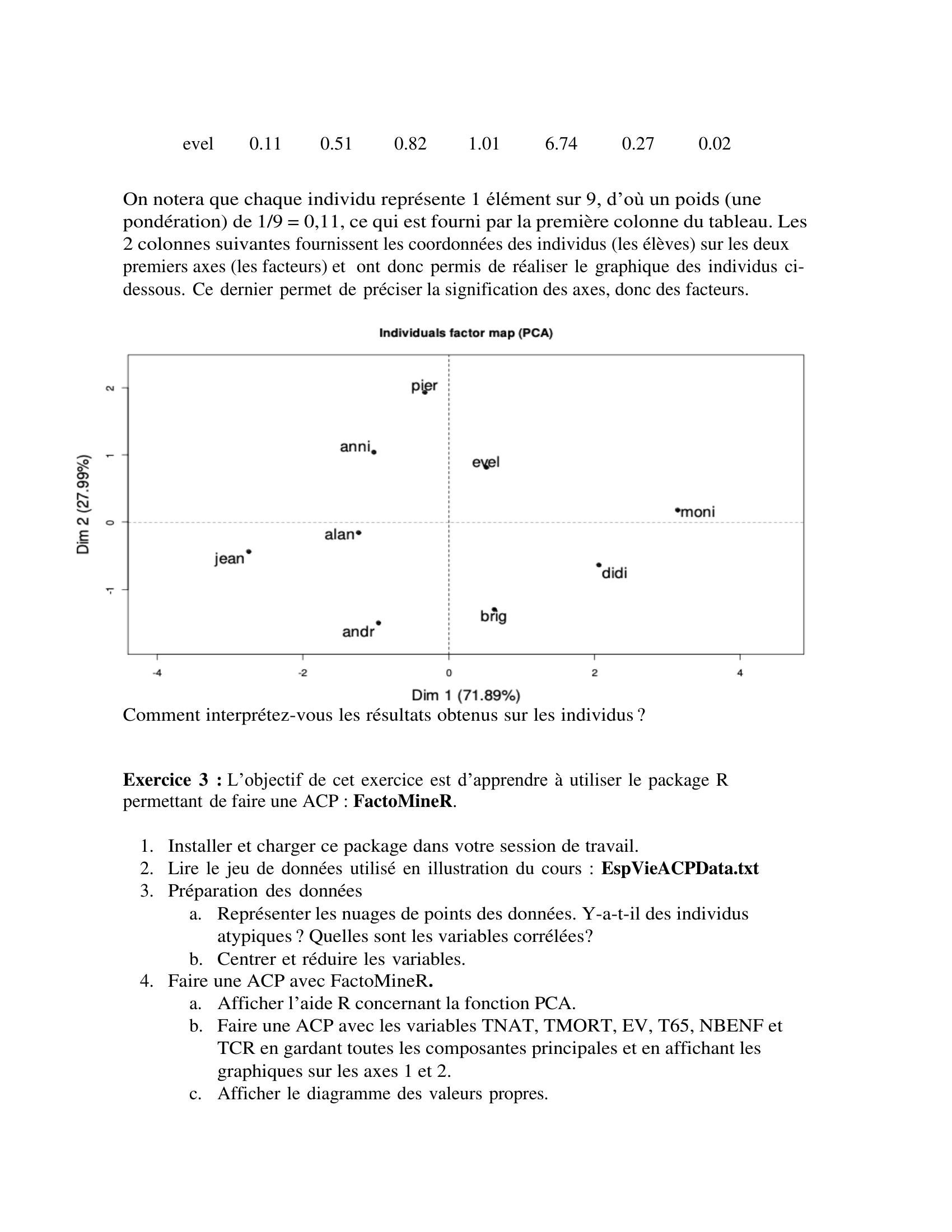
Page 5 : evel 0.11 0.51 0.82 1.01 6.74 0.27 0.02 On notera que chaque individu représente 1 élément sur 9, d’où un poids une pondération de 1/9 = 0,11, ce qui est fourni par la première colonne du tableau. Les 2 colonnes suivantes fournissent les coordonnées des individus les élèves sur les deux premiers axes les facteurs et ont donc permis de réaliser le graphique des individus ci-dessous. Ce dernier permet de préciser la signification des axes, donc des facteurs. Comment interprétez-vous les résultats obtenus sur les individus ? Exercice 3 : L’objectif de cet exercice est d’apprendre à utiliser le package R permettant de faire une ACP : FactoMineR. 1. Installer et charger ce package dans votre session de travail. 2. Lire le jeu de données utilisé en illustration du cours : EspVieACPData.txt 3. Préparation des données a. Représenter les nuages de points des données. Y-a-t-il des individus atypiques ? Quelles sont les variables corrélées? b. Centrer et réduire les variables. 4. Faire une ACP avec FactoMineR. a. Afficher l’aide R concernant la fonction PCA. b. Faire une ACP avec les variables TNAT, TMORT, EV, T65, NBENF et TCR en gardant toutes les composantes principales et en affichant les graphiques sur les axes 1 et 2. c. Afficher le diagramme des valeurs propres.
Page 6 : 5. Résultats concernant les variables : a. Calculer la somme du cos2 de TNAT. b. Sur Quels axes la variable TMORT est-elle bien représentée? c. Quelles variables contribuent à la formation de l’axe 1? 6. Résultats sur les individus : a. Quels axes faut-il afficher pour avoir des informations concernant le Bangladesh? b. Quelle est la contribution moyenne d’un pays à la construction des axes? c. Y-a-t-il des pays qui dépassent très largement cette contribution moyenne? d. Supprimer le pays ayant la plus grande contribution et regarder si cela change la construction des axes. e. Ajouter la variable Continent sur le graphique des individus. 7. Visualisation avec explor. Exercice 4 : Le jeu de données DecathlonData.xls de données contient 41 lignes et 13 colonnes. Les colonnes 1à 12 sont des variables quantitatives : Les dix premières colonnes correspondent aux performances des athlètes pour les dix épreuves du décathlon. Les colonnes 11 et 12 correspondent respectivement au rang et au nombre de points obtenus. La dernière colonne est une variable qualitative correspondant au nom de la compétition Jeu Olympiques de 2004 ou Décastar 2004. Les lignes désignent les athlètes. Nous allons faire une ACP sur les colonnes de 1 à 10. 1. Quel pourcentage de l’inertie totale contiennent les deux premières composantes principales ? Combien faut-il choisir de composantes principales pour avoir plus de 70 de l’inertie totale ? 2. Etude des variables. a. Pourquoi les variables "X100m ","X400m"," X110m.hurdle " et "X1500m" se trouvent-elles à gauche de l’axe des ordonnées? b. Comment interprétez-vous la corrélation entre les variables "X100m" et " long.jump"? c. Peut-on distinguer des groupes de variables? Quelle est la corrélation entre ces groupes ? Comment l’interprétez-vous? d. Quelles variables contribuent majoritairement à la première composante principale, à la deuxième composante principale? Comment pouvez-vous interpréter le plan défini par les deux premières composantes principales? 3. Etude des individus.
Page 7 : a. Comment qualifieriez-vous l’athlète Lorenzo? A votre avis, comment se fait-il qu’il ne soit pas dernier de sa compétition? b. Comment qualifieriez-vous les athlètes suivants : Karpov,Sebrle, Casarsa? Quel est leur classement? c. On ajoute les variables supplémentaires "Rank" et "Points". Ces variables n’entrent pas en compte dans le calcul des composantes principales mais aident à une meilleure compréhension des axes. Que pouvez-vous en conclure? d. Comparer la position de Karpov, Clay,. . . aux jeux olympiques et au décastar. Peut-on en conclure que le niveau des deux compétitions n’est pas le même? Pour répondre à cette question, on ajoute la variable supplémentaire "Compétition". Cette variable est qualitative et est qualifiée de facteur. Deux nouveaux individus représentants un individu moyen pour chaque compétition sont ajoutés au graphique. Que pouvez-vous en conclure?