TD5
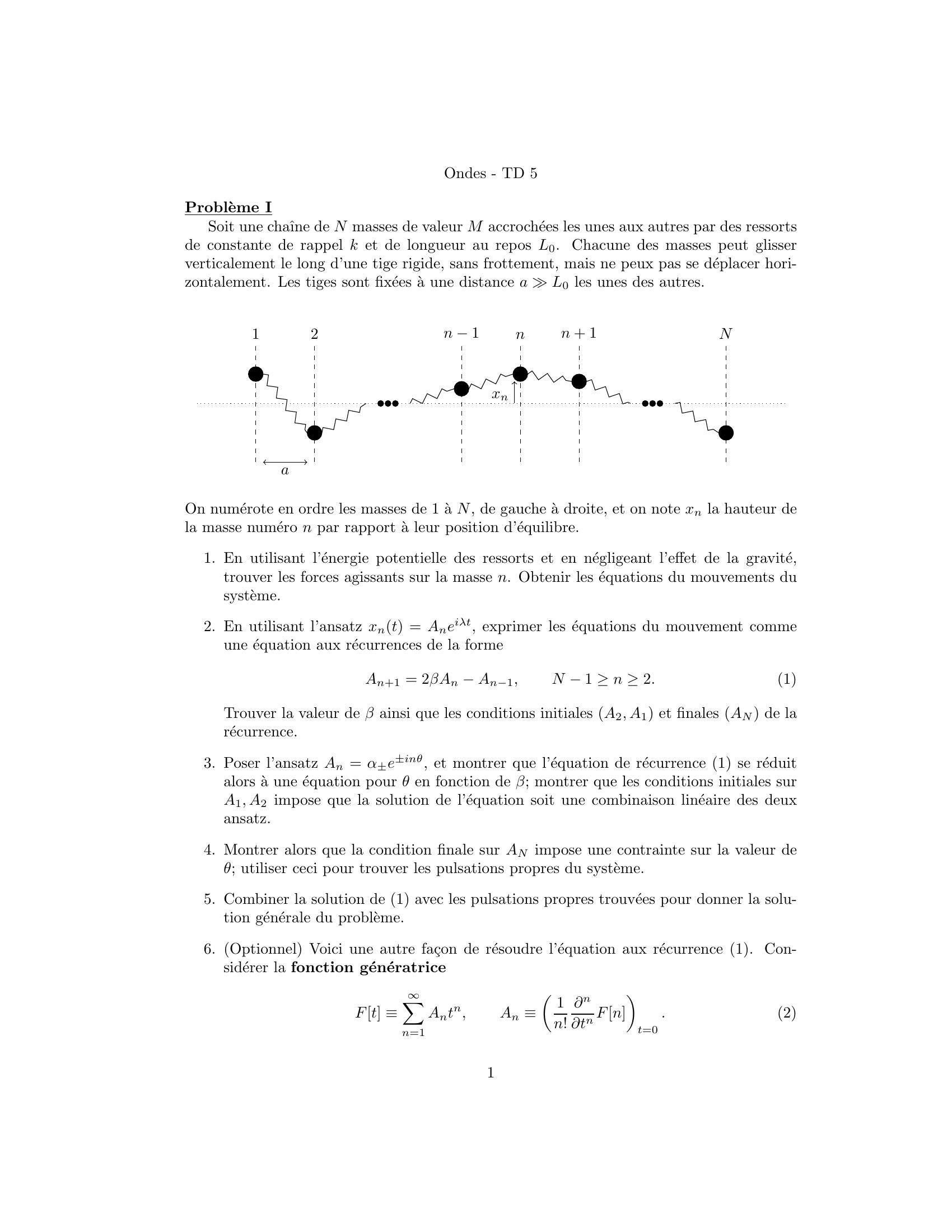
Page 1 : Ondes - TD 5Probleme ISoit une chaˆıne de N masses de valeur M accrochees les unes aux autres par des ressortsde constante de rappel k et de longueur au repos L0. Chacune des masses peut glisserverticalement le long d’une tige rigide, sans frottement, mais ne peux pas se deplacer hori-zontalement. Les tiges sont fixees a une distance a L0 les unes des autres.a12n 1nn + 1NxnOn numerote en ordre les masses de 1 a N, de gauche a droite, et on note xn la hauteur dela masse numero n par rapport a leur position d’equilibre.1. En utilisant l’energie potentielle des ressorts et en negligeant l’effet de la gravite,trouver les forces agissants sur la masse n. Obtenir les equations du mouvements dusysteme.2. En utilisant l’ansatz xnt = Aneiλt, exprimer les equations du mouvement commeune equation aux recurrences de la formeAn+1 = 2βAn An1,N 1 n 2.1Trouver la valeur de β ainsi que les conditions initiales A2, A1 et finales AN de larecurrence.3. Poser l’ansatz An = α±e±inθ, et montrer que l’equation de recurrence 1 se reduitalors a une equation pour θ en fonction de β; montrer que les conditions initiales surA1, A2 impose que la solution de l’equation soit une combinaison lineaire des deuxansatz.4. Montrer alors que la condition finale sur AN impose une contrainte sur la valeur deθ; utiliser ceci pour trouver les pulsations propres du systeme.5. Combiner la solution de 1 avec les pulsations propres trouvees pour donner la solu-tion generale du probleme.6. Optionnel Voici une autre fa¸con de resoudre l’equation aux recurrence 1. Con-siderer la fonction generatriceFt Xn=1Antn,An 1n!ntn Fnt=0.21
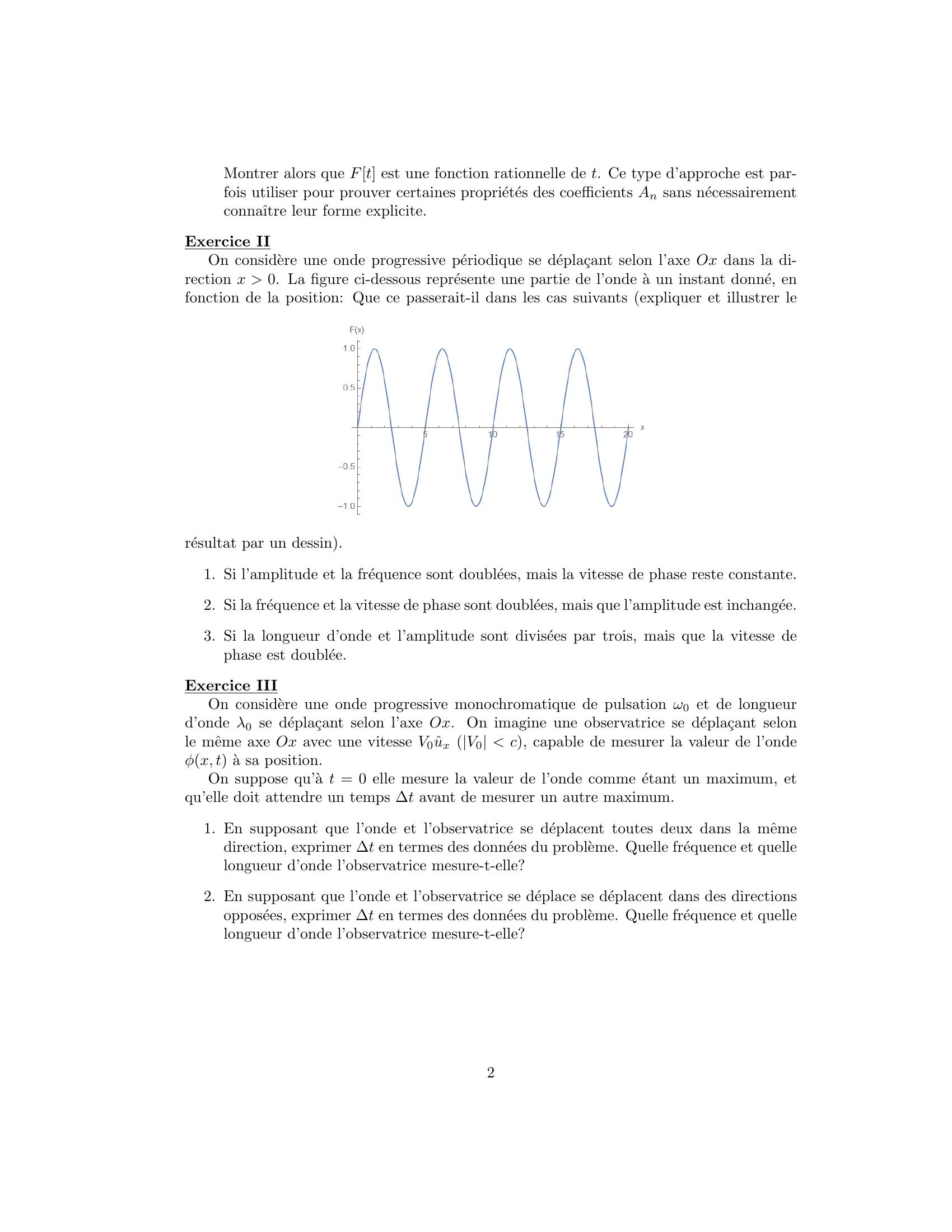
Page 2 : Montrer alors que Ft est une fonction rationnelle de t. Ce type d’approche est par-fois utiliser pour prouver certaines proprietes des coefficients An sans necessairementconnaˆıtre leur forme explicite.Exercice IIOn considere une onde progressive periodique se depla¸cant selon l’axe Ox dans la di-rection x 0. La figure ci-dessous represente une partie de l’onde a un instant donne, enfonction de la position: Que ce passerait-il dans les cas suivants expliquer et illustrer leresultat par un dessin.1. Si l’amplitude et la frequence sont doublees, mais la vitesse de phase reste constante.2. Si la frequence et la vitesse de phase sont doublees, mais que l’amplitude est inchangee.3. Si la longueur d’onde et l’amplitude sont divisees par trois, mais que la vitesse dephase est doublee.Exercice IIIOn considere une onde progressive monochromatique de pulsation ω0 et de longueurd’onde λ0 se depla¸cant selon l’axe Ox. On imagine une observatrice se depla¸cant selonle mˆeme axe Ox avec une vitesse V0ˆux V0 c, capable de mesurer la valeur de l’ondeφx, t a sa position.On suppose qu’a t = 0 elle mesure la valeur de l’onde comme etant un maximum, etqu’elle doit attendre un temps t avant de mesurer un autre maximum.1. En supposant que l’onde et l’observatrice se deplacent toutes deux dans la mˆemedirection, exprimer t en termes des donnees du probleme. Quelle frequence et quellelongueur d’onde l’observatrice mesure-t-elle?2. En supposant que l’onde et l’observatrice se deplace se deplacent dans des directionsopposees, exprimer t en termes des donnees du probleme. Quelle frequence et quellelongueur d’onde l’observatrice mesure-t-elle?2