TD

Posté le 09/02/2025

Chargé de TD/CM : D. Physique.

42 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

Page 1 : Université de Cergy-Pontoise S1-MPI Introduction à la mécanique du point Travaux dirigés 2013/2014

Page 2 :

Page 3 : Universite de Cergy-PontoiseIntroduction a la mecanique du pointS1-MPI 2013-2014Plan du cours1Dimensions, unites, analyse dimensionnelle2Calcul vectoriel : rappels3CinematiquePosition, vitesse, acceleration ; chute libre, mouvement circulaire uniforme, relatif.4DynamiqueLes 3 lois de Newton, referentiels galileens, quelques forces force de gravitation, poids, force decontact solide, force de frottement ﬂuide, tension d’une corde, force de rappel du ressort.5Travail et energieTravail, puissance, energie cinetique et son theoreme, energie potentielle et forces conservatives/nonconservatives, energie mecanique et son theoreme, courbes d’energie potentielle, positions d’equilibreet leurs stabilites.6Systemes de particules, collisionsMouvement du centre de masse quantite de mouvement, energie, choc entre 2 masses ponctuellesconservation de la quantite de mouvement, collisions elastiques/inelastiques.References bibliographiquesListe non exhaustive de livres recommandes pour ce cours.- Halliday, Resnick, Walker : “Physique 1. Mecanique”, Dunod- Hecht : “Physique 1 : Mecanique”, de Boeck- Alonso, Finn : “Physique generale 1”, InterEditions- Giancoli : “Physique generale 1”, De Boeck Universite- Seguin : “Physique : Mecanique”, de Boeck- Gie, Sarmant : “Mecanique 1ere Annee”, Tec et Doc- Perez : “Mecanique : Fondements et applications”, Masson- Levy-Leblonc : “La physique en question : mecanique”, Vuibert- Valentin : “L’univers mecanique”, Hermann...Site web du cours :http ://cpinettes.u-cergy.fr/S1-MecaVous y trouverez :- des resumes du cours- des petites questions pour vous aider a assimiler les notions du cours- des corriges petites questions, partiels, examens- des liens vers des videos illustrant le cours/TD- un formulaire de maths pour la physique

Page 4 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointTD 1 : Unites et dimensionsEx. 1En utilisant les deﬁnitions d’une vitesse moyenne et d’une acceleration moyenne, donner les di-mensions d’une vitesse et d’une acceleration. Deduire la dimension d’une force de la 2eme loi deNewton.Ex. 2Etablir les dimensions d’un travail, d’une puissance et d’une charge electrique. Rappeler leur unitedans le systeme international S.I..Ex. 3Une voiture americaine consomme en moyenne 4 gallons d’essence pour 100 miles. Calculer saconsommation en L / km.1 gallon = 3,785 L et 1 km = 0,621 mile.Ex. 4Sachant que la force de Lorentz s’ecrit F = q vB sin⃗v, ⃗B, en deduire la dimension du champmagnetique B puis son unite dans le systeme S.I.Ex. 5La force de Coulomb ayant comme expression F = qq′/4πϵ0r2, etablir la dimension de la constanteuniverselle ϵ0 puis son unite dans le systeme S.I.Ex. 6Determiner la dimension de la constante R des gaz parfaits ﬁgurant dans l’equation d’etat du gazparfait PV = nRT ou P designe la pression du gaz, V son volume, T sa temperature et n lenombre de moles gazeuses.L’unite de la constante R dans le systeme S.I. est J.mol1.K1 : veriﬁer que cette unite estcompatible avec la dimension trouvee.Ex. 7Veriﬁer l’homogeneite des relations suivantes, sachant que k est la raideur d’un ressort :a x = v0t + 12at2b y =gx22v20 cos2 αc E = 12mR2ω2 + mgR sin θd Ep = 12kx2Ex. 8Trouver, a l’aide d’une analyse dimensionnelle, la formule donnant la poussee d’Archimede, sachantque cette force est fonction du volume du corps immerge V , de la masse volumique ρ du ﬂuide etde l’acceleration de pesanteur g.Aide : on cherchera les valeurs des exposants α, β et γ satisfaisant l’equation PA = C V αρβgγ, Cetant une constante numerique sans dimension.Ex. 9Un pendule simple est un ﬁl sans masse de longueur l au bout duquel est attache un poids demasse m. Soit T la periode des oscillations d’un tel pendule. T peut dependre de g, l, m et θl’angle maximum de deviation par rapport a la verticale. Galilee est le premier a s’ˆetre renducompte experimentalement que la periode ne depend que tres faiblement de θ quand θ est petit.Montrer que dans ce cas la periode T est une fonction de l et g uniquement.Ex. 10On lˆache sans vitesse initiale un objet de masse m d’une hauteur h au-dessus du sol. On veuttrouver par une analyse dimensionnelle une expression de sa vitesse ﬁnale vf en negligeant toutfrottement. Quelles sont les grandeurs pertinentes du probleme? En deduire une expression pourla vitesse vf a l’aide d’une analyse dimensionnelle.

Page 5 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointTD 2 : Vecteurs1Petites Questionsa Si ⃗V = ⃗V1 + ⃗V2, V = ⃗V est-il necessairement plus grand que V1 = ⃗V1, V2 = ⃗V2 ?b La somme de deux vecteurs de normes diﬀerentes peut-elle correspondre a un vecteur nul ?Est-ce possible avec trois vecteurs de normes diﬀerentes ?c Indiquer dans quels cas la somme des vecteurs donnes sur les ﬁgures ne peut avoir uneresultante nulle.abcd Si ⃗a.⃗b = 0 ceci implique que ⃗a et ⃗b sont perpendiculaires. Vrai ou faux ?e Si ⃗a.⃗b = ⃗a.⃗c ceci implique que ⃗b = ⃗c. Vrai ou faux ?2Vol de la moucheUne mouche vole d’un coin d’une chambre de dimensions 5m× 4m × 3m jusqu’au coin oppose surla diagonale du parallelepipede.a Quelle est la norme de son vecteur deplacement ? Choisir un systeme de coordonnees etdonner les composantes dudit vecteur. Le representer graphiquement.b La longueur de la trajectoire de la mouche peut-elle ˆetre inferieure superieure ou egale a lanorme du vecteur deplacement ?c Si la mouche marchait au lieu de voler ; quelle serait la trajectoire la plus courte pour lemˆeme deplacement ?3Sommes et Diﬀerences de VecteursEtant donnes les vecteurs :⃗a=3⃗i 2⃗j + ⃗k⃗b=⃗i 5⃗j + 2⃗k⃗c=3⃗i 4⃗kCalculer : a 5⃗a ; b ⃗a +⃗b ; c 2⃗a +⃗b ⃗c ; d ⃗a ⃗b/⃗c + ⃗c

Page 6 : 4Composantes de vecteursTrouver les composantes cartesiennes des vecteurs suivants et les indiquer sur le diagramme lanorme des vecteurs est indiquee en unites arbitraires. Pour le cas c projeter les vecteurs sur lesaxes x’,y’ indiques sur la ﬁgure :xyθ = π6θ = π6axybθ = 1500αy′x′yx⃗b = 4⃗a = 4⃗a = 3⃗b = 3⃗c = 3⃗a = 4c5Produit Scalairea En utilisant la deﬁnition du produit scalaire de deux vecteurs, calculer les produits scalairesdes vecteurs de base du repere cartesien.b En utilisant la propriete distributive du produit scalaire par rapport a l’addition montrer quesi : ⃗a = ax⃗i + ay⃗j + az⃗k et ⃗b = bx⃗i + by⃗j + bz⃗k, alors : ⃗a.⃗b = axbx + ayby + azbz. En deduirel’expression de a = ⃗ac Trouver l’angle forme par les vecteurs : ⃗a = 3⃗i + 2⃗j ⃗k et ⃗b = ⃗i + 2⃗k.6Et pour terminerUne roue d’un rayon de R = 45cm roule sans glissement d’un demi-tour. On repere le point decontact avec le sol a t = 0 avec la lettre P. Trouver i la norme et ii l’angle par rapport au soldu vecteur deplacement du point P lors de ce deplacement.PP

Page 7 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointTD 3 : Cinematique 1d1Vitesse Moyennea Un joueur de cricket lance une balle a une vitesse de 160 km/h vers le batteur, distant de18,4 m. Quel est le temps de vol de la balle ?b Un pilote de chasse s’exerce au vol en dessous du radar. Il vole horizontalement a une altitudede 35 m et a une vitesse de 1300 km/h. Subitement il rencontre un terrain qui a une pentede 4, 3o. Cette pente est suﬃsamment douce pour ˆetre diﬃcile a detecter. De combien detemps dispose le pilote pour ne pas s’ecraser ?2Vitesse InstantaneeLa position d’une particule, se depla¸cant le long de l’axe x, est donnee par l’equation :x = 9, 75 + 1, 50t3, ou t est mesure en secondes et x en metres. Calculer :a la vitesse moyenne entre t = 2, 00 s et t = 3, 00 sb la vitesse instantanee a t = 2, 00 s, t = 3, 00 s et t = 2, 50 s.c la vitesse lorsque la particule se trouve a mi-chemin entre sa position a t = 2, 00 s et at = 3, 00 sd Tracer le graphe de xt, indiquant graphiquement vos reponses.e Mˆemes questions pour x = 5 + 2t2 a faire a la maison.3Acceleration Constantea Un electron avec une vitesse initiale de v0 = 1, 50×105ms1 rentre dans une region longue de1 cm ou il est accelere electriquement. Il sort avec une vitesse de 5, 70×105ms1. Supposantque l’acceleration est constante, quelle est sa valeur ?b L’ascenseur a l’hˆotel Marriott a un parcours de 190 m le long de l’axe y. Il a une vitessemaximale de 305 m/min et son acceleration et deceleration sont de mˆeme norme : a0 =1, 22ms2.i Quelle distance est parcourue par l’ascenseur dans la phase d’acceleration : repos →vitesse maximale ?ii Combien de temps faut-il pour faire le trajet de 190 m, commen¸cant et terminant aurepos ?iii Tracer les graphes de at, vt et yt.4Chute Librea Un etudiant, content de la ﬁn du cours de mecanique, lance son cartable en l’air verticalementselon l’axe y.i Avec quelle vitesse faut-il le lancer pour qu’il atteigne une altitude maximum de 10 m ?ii Combien de temps passe-t-il en l’air ?iii Tracer les graphes de yt, vt et at, en indiquant sur les deux premiers le momentou le cartable a atteint 10 m.b Une Montgolﬁere monte a une vitesse de 12ms1 et se trouve a 80 m du sol lorsqu’un sac desable est lˆache.i Combien de temps faut-il pour que le sac de sable touche le sol ?ii Avec quelle vitesse touche-t-il le sol ?

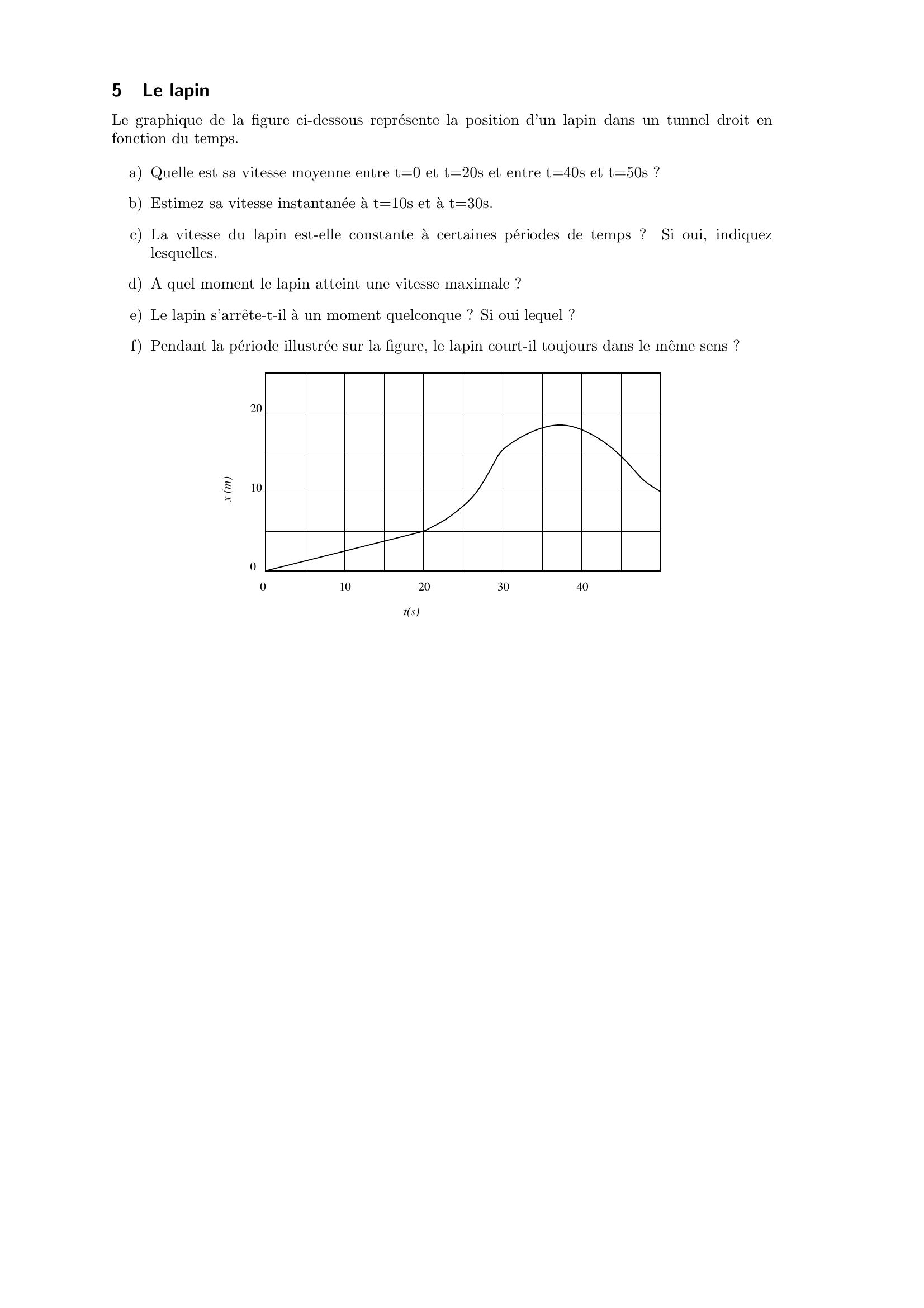
Page 8 : 5Le lapinLe graphique de la ﬁgure ci-dessous represente la position d’un lapin dans un tunnel droit enfonction du temps.a Quelle est sa vitesse moyenne entre t=0 et t=20s et entre t=40s et t=50s ?b Estimez sa vitesse instantanee a t=10s et a t=30s.c La vitesse du lapin est-elle constante a certaines periodes de temps ?Si oui, indiquezlesquelles.d A quel moment le lapin atteint une vitesse maximale ?e Le lapin s’arrˆete-t-il a un moment quelconque ? Si oui lequel ?f Pendant la periode illustree sur la ﬁgure, le lapin court-il toujours dans le mˆeme sens ?010204001020tsx m30

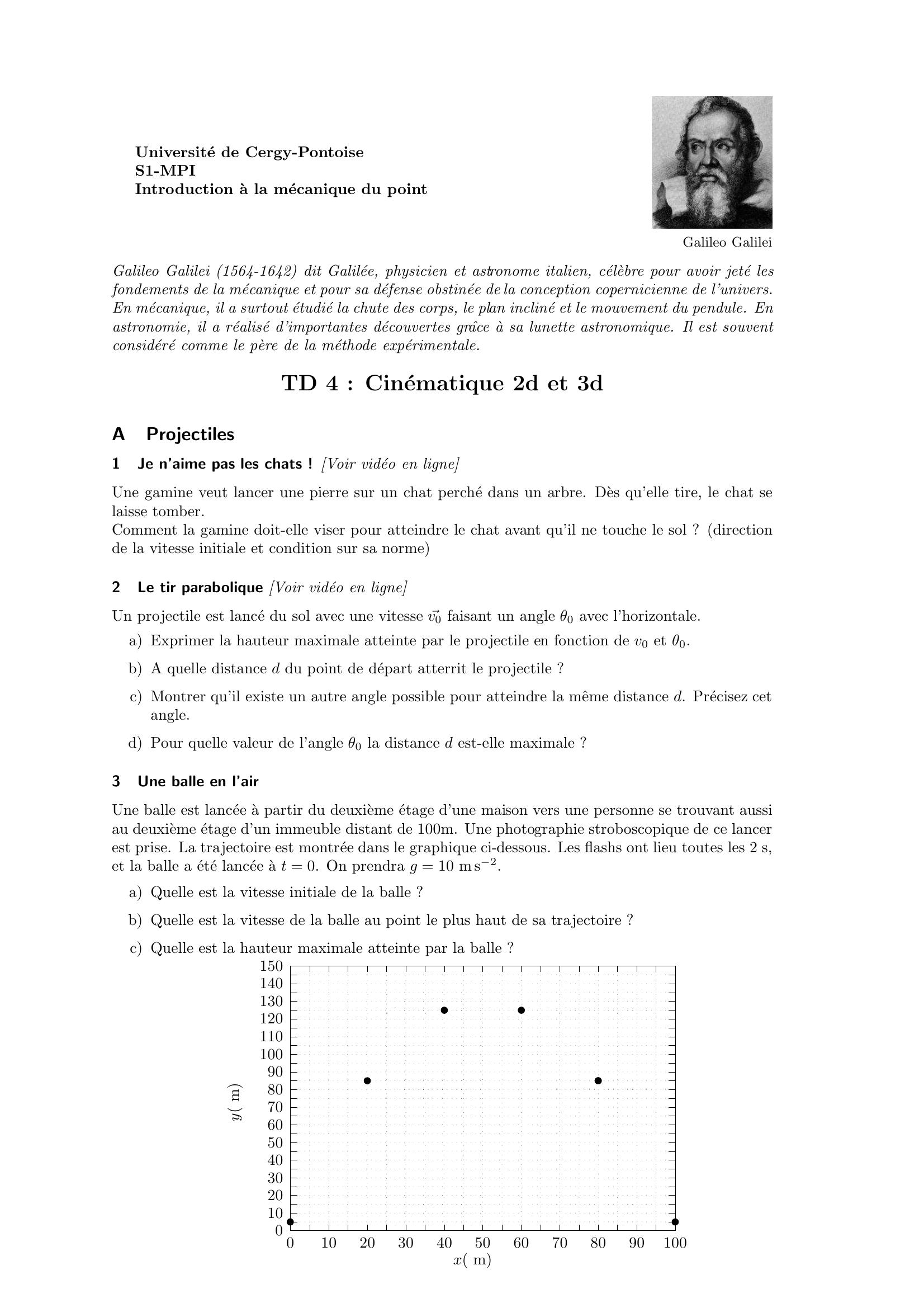
Page 9 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointGalileo GalileiGalileo Galilei 1564-1642 dit Galilee, physicien et astronome italien, celebre pour avoir jete lesfondements de la mecanique et pour sa defense obstinee de la conception copernicienne de l’univers.En mecanique, il a surtout etudie la chute des corps, le plan incline et le mouvement du pendule. Enastronomie, il a realise d’importantes decouvertes grˆace a sa lunette astronomique. Il est souventconsidere comme le pere de la methode experimentale.TD 4 : Cinematique 2d et 3dAProjectiles1Je n’aime pas les chats ! Voir video en ligneUne gamine veut lancer une pierre sur un chat perche dans un arbre. Des qu’elle tire, le chat selaisse tomber.Comment la gamine doit-elle viser pour atteindre le chat avant qu’il ne touche le sol ? directionde la vitesse initiale et condition sur sa norme2Le tir parabolique Voir video en ligneUn projectile est lance du sol avec une vitesse ⃗v0 faisant un angle θ0 avec l’horizontale.a Exprimer la hauteur maximale atteinte par le projectile en fonction de v0 et θ0.b A quelle distance d du point de depart atterrit le projectile ?c Montrer qu’il existe un autre angle possible pour atteindre la mˆeme distance d. Precisez cetangle.d Pour quelle valeur de l’angle θ0 la distance d est-elle maximale ?3Une balle en l’airUne balle est lancee a partir du deuxieme etage d’une maison vers une personne se trouvant aussiau deuxieme etage d’un immeuble distant de 100m. Une photographie stroboscopique de ce lancerest prise. La trajectoire est montree dans le graphique ci-dessous. Les ﬂashs ont lieu toutes les 2 s,et la balle a ete lancee a t = 0. On prendra g = 10 m s2.a Quelle est la vitesse initiale de la balle ?b Quelle est la vitesse de la balle au point le plus haut de sa trajectoire ?c Quelle est la hauteur maximale atteinte par la balle ?01020304050607080901001101201301401500102030405060708090100y mx m

Page 10 : 4Un colis venu des airsUn avion humanitaire vole a une vitesse de 290 km h1 et plonge sur sa cible a un angle de 300 endessous de l’horizontale. Le pilote lˆache un colis a 700 m de sa cible distance au sol.a Quel est le temps de vol du colis ?b Quelle etait l’altitude de l’avion lorsque le colis a ete lˆache ?BMouvement Circulaire Uniforme1Diﬀerents Satellitesa Des satellites de reconnaissance, de prospection ou de surveillance sont parfois lances autourde la Terre sur une orbite circulaire uniforme a 150 km seulement de la Terre.Calculer leur periode de rotation.b Pour les telecommunications, nous avons besoin de satellites geostationnaires, ﬁxes dans leciel. Ces satellites ont une orbite circulaire uniforme dans le plan de l’equateur avec la mˆemeperiode de rotation T que la Terre.Calculer l’altitude des orbites geostationnaires.On donne la masse de la Terre : MT = 6 × 1024 kg, le rayon de la Terre : RT = 6400 km et laconstante de gravitation universelle : G = 6, 67 × 1011 N.m2.kg2.2Le TGVLe TGV a une vitesse moyenne de 216 km h1 en service normal. Si le train prend un virage acette vitesse, et il est precise que les passagers ne doivent pas subir une acceleration centripetesuperieure a 0, 05g :a Quel est le rayon le plus petit pour la courbe ? prendre g = 9, 8 m s2.b A quelle vitesse le train doit-il prendre un virage de rayon 1 km ?3Quelques vitesses de rotationDans le plan xy, un point materiel M eﬀectue un mouvement circulaire uniforme de rayon R = 2m autour de l’origine O, dans le sens inverse des aiguilles d’une montre. La periode du mouvementest T = 12 s. A t = 0, le point est situe en A voir ﬁgure.xyOAxCalculer on fera l’approximation π 3 pour simpliﬁer les A.N. :a la vitesse angulaire.b les coordonnees cartesiennes de M aux instants t1 = 3 s et t2 = 6 s.c le vecteur vitesse moyenne ⃗vm entre t1 et t2.d les vecteurs vitesse ⃗v1 a t1 et ⃗v2 a t2 ,e le vecteur acceleration moyenne ⃗am entre t1 et t2.f les vecteurs acceleration ⃗a1 a t1 et ⃗a2 a t2.

Page 11 : CMouvement relatif1L’escalateur en panneUne personne monte a pieds un escalateur en panne, long de 15 m, en 90 s. Lorsque la personne semet en position stationnaire sur le mˆeme escalateur une fois repare, elle traverse la mˆeme distanceen 60 s.a Combien de temps faut-il pour monter si la personne marche sur l’escalateur qui fonctionne?b Est-ce que ce resultat depend de la longueur de l’escalateur ?2Bateau sur l’eauUn bateau doit traverser un ﬂeuve de largeur L. La vitesse d’ecoulement de l’eau du ﬂeuve parrapport a la terre, ⃗v0, est parallele aux rives et constante. La vitesse ⃗v1 du bateau par rapport al’eau est constante.a Quel doit ˆetre l’angle entre ⃗v0 et ⃗v1 pour que le bateau arrive juste en face du point de departsi ⃗v1 = 2 ⃗v0 ?b En deduire la vitesse du bateau par rapport a la terre.DLe pistonOn considere un systeme articule en A et constitue de deux barres identiques OA et AB assujettiesa rester dans le plan x, y. O est ﬁxe et B glisse le long de l’axe x et l’angle entre OA et l’axe x,ϕ, varie tel que ϕ = ωt. Chaque barre est de longueur 2b.a Determiner l’equation cartesienne de la trajectoire du milieu, M, de AB. Decrire cette tra-jectoire.b Determiner la vitesse et l’acceleration du point M.c Determiner les expressions des coordonnees du point B en fonction du temps.d La vitesse maximale du point B est de 12 m s1 et b = 1 cm. Determiner la vitesse derotation en tour/min du point A dans son mouvement de rotation autour de O.

Page 12 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointIsaac NewtonIsaac Newton 1642 – 1727, physicien et mathematicien anglais. Il a invente le calcul inﬁnitesimalet integral, pose les bases de la mecanique classique avec ses trois lois et decouvert la loi d’attractionuniverselle. Il a aussi realise d’importants travaux en optique. Son ouvrage ”Philosophiæ NaturalisPrincipia Mathematica” paru en 1687 est considere comme une oeuvre majeure dans l’histoire dela science.TD 5 : Les Lois de NewtonAPetites Questions1Le bloc de glaceOn tire un bloc de glace le long d’un sol plan avec deux forces, ⃗F1 et ⃗F2, comme indiquees sur laﬁgure. On peut negliger les forces de frottement entre le bloc de glace et le sol. Les deux forces sontchoisies pour que la vitesse de glissement reste constante. Si l’angle θ est diminue, pour garder lavitesse constante faut-il augmenter, diminuer ou garder constante la norme de la force ⃗F2 ?θ⃗F1⃗F22Chute libre sur la LuneSur la lune le temps de chute verticale d’un objet sur une hauteur h = 1 m est t = 1, 1 s. Endeduire la masse ML de la Lune sachant que son rayon est RL = 1, 75 × 103 km.On donne : G = 6, 67 × 1011 N.m2.kg2.3La masse suspendueUne masse m de 10 kg est suspendue a deux cordes identiques, accrochees au plafond, comme lemontre la ﬁgure. Calculer la tension dans les cordes. On donne α = 300 et β = 600.αβT1T2m

Page 13 : 4Les blocs glissantsOn supposera les frottements negligeables, le ﬁl inextensible et la poulie et le ﬁl de massesnegligeables. Calculer la valeur de m1 pour que ce systeme se deplace : a a vitesse constante.b avec une acceleration vers la gauche de g/2 pour α = π/4.m12mαg5Un pendule coniqueUne bille de masse m est attachee a deux ﬁls inextensibles de longueur L, ﬁxes en A et B telsque AB = L. La bille decrit un mouvement circulaire uniforme dans un plan horizontal avec unevitesse angulaire ω les ﬁls sont tendus.AzωmLLBLa Exprimer la tension de chaque ﬁl en fonction de m, L et ω.b Quelle est la vitesse angulaire minimale pour que les ﬁls restent tendus ?BLois de Newton1Grande Table Sur Une Petite PlaneteIndiquez les forces agissant sur le bloc de masse m de la ﬁgure ci-dessous. Pour chaque force,indiquer clairement les paires de forces action-reaction.mPetite Planete2Blocs en mouvementDeux blocs en contact peuvent glisser sans frottement sur une surface horizontale. Une forceconstante ⃗F s’exerce sur le bloc A, entraˆınant un mouvement d’ensemble des deux blocs, c.f.ﬁgure.FABa La force exercee par B sur A est-elle egale en module a la force exercee par A sur B ?b La force exercee par le bloc A sur le bloc B est-elle egale a ⃗F ?c Reprendre ces questions lorsque les blocs s’immobilisent contre le mur.3Je ne suis pas un ˆaneUn vieux fermier attache son ˆane a son chariot et essaye de le faire avancer. Mais l’ˆane, qui vientde lire les “Principiea Mathematica” de Newton, lui dit : “Il est inutile que j’essaye de faire bougerle chariot. Etant donne que l’action et la reaction sont de mˆeme module mais de sens opposes, lechariot tirera sur moi autant que je tirerai sur lui et aucun de nous n’avancera”.Etant donne votre maˆıtrise des principes de Newton et sachant que vous n’ˆetes pas un ˆane, pourriez-vous convaincre l’ˆane “erudit” de bouger ?

Page 14 : CFrottements1Glissera, glissera pas ?Voir video en ligneUn bloc de masse m est pose sur un plan faisant un angle α avec l’horizontale. On notera µs lecoeﬃcient de frottement statique entre le bloc et le plan. Quel est l’angle α limite pour que le blocse mette en mouvement ?2Bloc frottantUn bloc est tire a l’aide d’une corde avec une force ⃗F, indiquee sur la ﬁgure, qui fait un angle θavec l’horizontale.θ⃗FSi le bloc est au repos et θ augmente, quelles sont les quantites qui augmentent, decroient, ou restentles mˆemes parmia Fx, la composante horizontale de la force ;b fs, la force de frottementstatique ; c N, la force normale; d fs,max, la force de frottement statique maximale.Si, par contre, le bloc est en mouvement, et θ est augmente, est-ce que la force de frottementaugmente, diminue ou reste la mˆeme ?3Attention au freinageUne voiture bloque ses roues. Elle derape sur une distance d = 110 m avant de s’arrˆeter d’apresles traces de pneu. En supposant, pour simpliﬁer, que l’acceleration de la voiture est constantependant le derapage, calculer la vitesse de la voiture juste avant le freinage.On donne le coeﬃcient de frottement dynamique : µd = 0, 6.4Attention au virageUne voiture roule, a vitesse constante en norme v0, dans un virage de rayon R = 50 m sur uneroute horizontale.a Si la voiture ne derape pas et suit donc la courbe de la route, quelle est la nature desfrottements sur les roues ? Que se passerait-il si les roues se bloquaient coup de frein brutal ?b Calculez le coeﬃcient de frottement minimal pour que la voiture ne glisse pas.A.N. : v0 = 50 km h1 et v0 = 80 km h1.c De quel angle faut-il relever le virage pour qu’il n’y ait aucun frottement transverse av0 = 50 km h1 ? On suppose que la voiture roule a une altitude constante.5Le saut de l’angeUn parachutiste aimant les sensations fortes se laisse tomber le plus longtemps possible avantd’ouvrir son parachute. Lors de sa chute, que l’on supposera verticale pour simpliﬁer, le parachutisteest soumis a une force de frottement due a l’air de la forme :⃗f = 12 Cx ρ A v2 ⃗vvou ρ = 1.2 kg/m3 est la masse volumique de l’air, Cx un coeﬃcient de resistance aerodynamiquequi depend essentiellement de la forme du corps, ⃗v la vitesse de chute du parachutiste et A l’airede sa section perpendiculaire a ⃗v.a Montrer que le parachutiste atteint une vitesse limite. Etablir l’expression de cette vitesselimite.b Estimer cette vitesse limite pour un homme de masse m = 80 kg equipement compristombant en position horizontale du saut de l’ange Cx 1 puis en position tˆete en avantCx 0.7.

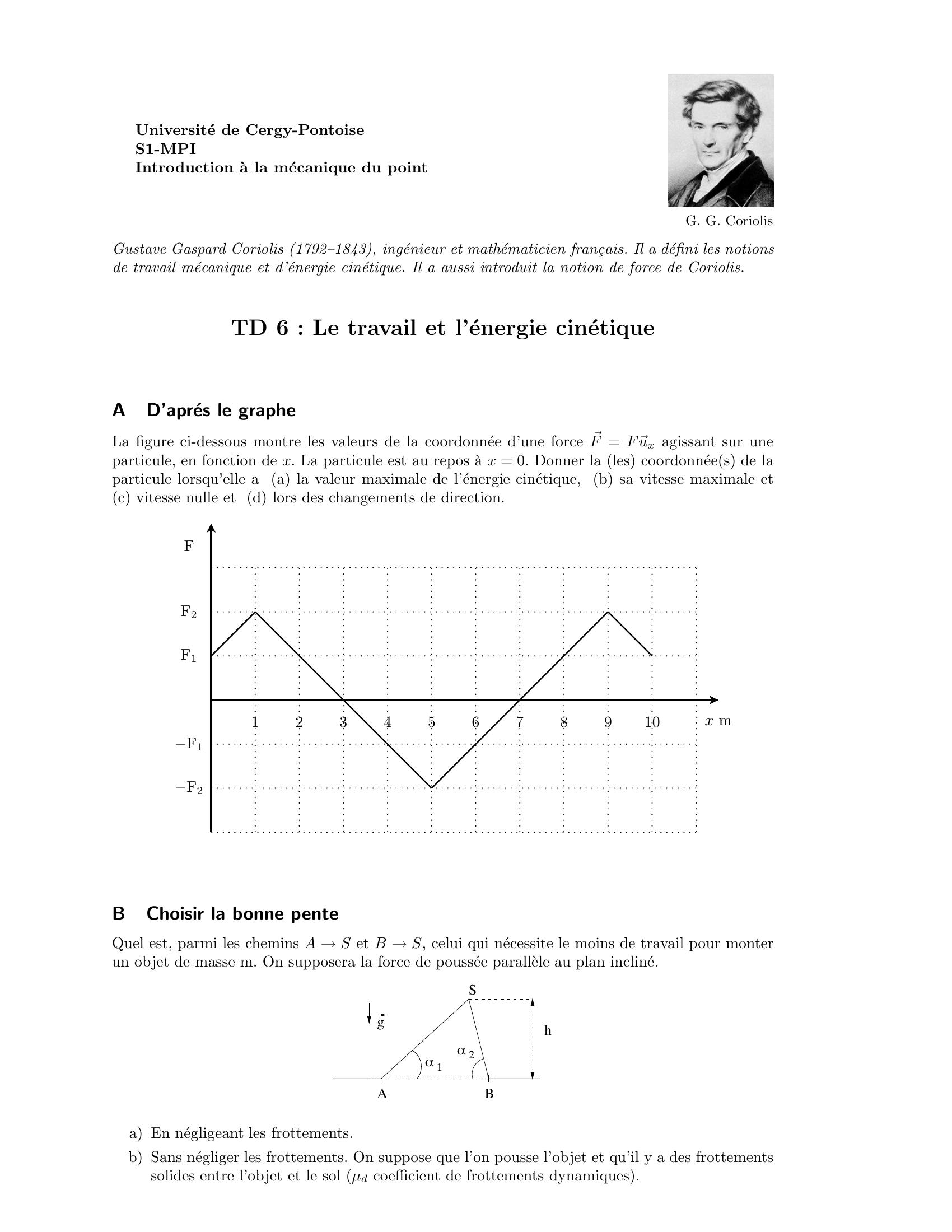
Page 15 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointG. G. CoriolisGustave Gaspard Coriolis 1792–1843, ingenieur et mathematicien fran¸cais. Il a deﬁni les notionsde travail mecanique et d’energie cinetique. Il a aussi introduit la notion de force de Coriolis.TD 6 : Le travail et l’energie cinetiqueAD’apres le grapheLa ﬁgure ci-dessous montre les valeurs de la coordonnee d’une force ⃗F = F⃗ux agissant sur uneparticule, en fonction de x. La particule est au repos a x = 0. Donner la les coordonnees de laparticule lorsqu’elle a a la valeur maximale de l’energie cinetique, b sa vitesse maximale etc vitesse nulle et d lors des changements de direction.FF1F2F1F212345678910x mBChoisir la bonne penteQuel est, parmi les chemins A →S et B →S, celui qui necessite le moins de travail pour monterun objet de masse m. On supposera la force de poussee parallele au plan incline.S! 2h!gBA1a En negligeant les frottements.b Sans negliger les frottements. On suppose que l’on pousse l’objet et qu’il y a des frottementssolides entre l’objet et le sol µd coeﬃcient de frottements dynamiques.

Page 16 : CMatelot navigue sous les ﬂotsUn sous-marin, de masse m, est initialement immobile. Ses ballasts d’eau sont remplis de fa¸con ace que la poussee d’Archimede compense exactement son poids. A l’instant t = 0, les turbines dusous-marin se mettent en marche, et exercent une poussee horizontale Ft = f eωt pour t 0f et ω sont des constantes positives. Les frottements du sous-marin dans l’eau sont visqueux etvalent approximativement γ⃗v cette approximation est valable tant que la vitesse n’est pas tropgrande ou γ est une constante positive. On pose ω0 = γm, et l’on suppose que ω0 ω.a Montrer que, pour t 0, la vitesse du sous-marin peut s’ecrire : vt = veωt eω0t, ouvest une constante que l’on determinera. Decrire le mouvement du sous-marin.b Calculer le travail de chacune des forces qui s’exercent sur le sous-marin pendant son deplacement.Commentaire.DQue la force soit avec vous !Soit un objet, suppose ponctuel, se deplacant sur un plan, dans le champ de force ⃗F :⃗Fx, y = x ay ⃗ux + 3y 2x ⃗uy.ou ⃗ux, ⃗uy est la base canonique associee aux coordonnees cartesiennes x,y. a est une constante.a Par l’action conjointe d’autres forces, l’objet se deplace du point O0,0 au point A2,4.Calculer le travail re¸cu par l’objet de la part du champ de force ⃗F dans les cas suivants :i L’objet se deplace en ligne droite du O a A.ii L’objet se deplace de O a A suivant le trajet OBA, avec B2,0.iii L’objet se deplace de O a A suivant le trajet OCA, avec C0,4.b Pour quelles valeurs de a le travail re¸cu dans les trois cas precedents est-il le mˆeme ?EVitesse de liberationLa force d’attraction lunaire sur un objet de masse m est donnee par :⃗F = GMLmr2⃗ur,ou G est une constante universelle, ML est la masse de la lune et r est la distance du centre de lalune.a Calculer le travail de cette force pour aller de r = RL a r →selon la direction radiale.b En deduire la vitesse initiale qu’il faudrait donner a un objet pour qu’il s’echappe de l’at-traction gravitationnelle lunaire.On donne : G = 6,67 × 1011 Nm2kg2, ML = 7,36 × 1022 kg, RL = 1,74 × 106 m.c Mˆeme question pour qu’il s’echappe de l’attraction gravitationnelle terrestre.On donne : MT = 6, 0 × 1024 kg et RT = 6, 4 × 106 m.

Page 17 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointH von HelmholtzHermann von Helmholtz 1821–1894, physicien allemand qui a deﬁni l’energie potentielle et for-mule le principe de conservation de l’energie mecanique.TD 7 : L’energie potentielle et l’energie mecaniqueALe pendule asymetrique Voir video en ligneUn pendule de longueur l et masse m est attache comme le montre la ﬁgure. Il est lˆache sans vitesseinitiale d’un angle α0 avec la verticale.Calculer l’angle atteint par m a gauche de l’obstacle de longueur l0 l cos α0.α0l0lBLes ressortsUn objet ponctuel de masse m se deplace sur une piste horizontale et sans frottement, en faisantdes aller-retours entre deux ressorts de mˆeme raideur k, ﬁxes aux extremites de la piste. Au debutdu mouvement le corps a une energie cinetique E0c et il est en contact avec le ressort de gauche,lequel est comprime d’une longueur d. Calculez les longueurs de compression maximale des ressorts.kkm

Page 18 : CPistolet a ressort Exo Examen 2009Un bloc de masse m est pose sur un ressort vertical, comme indique sur la ﬁgure. Lorsque le blocest au repos, le ressort est comprime d’une distance d.mka Que vaut la raideur du ressort, k ? Quelle est l’unite S.I. de k ?b On pousse le bloc vers le bas d’une distance d′, puis on lˆache le bloc, sans vitesse initiale.Jusqu’a quelle hauteur h mesuree a partir du point de lˆacher remonte le bloc ? On supposeraque le bloc quitte le ressort.DMouvement circulaireUn corps est attache a une tige rigide de longueur l. L’autre extremite de la tige est attachee a unplan incline formant un angle de 300 avec l’horizontale, comme le montre la ﬁgure.Calculer la perte d’energie cinetique lorsque le corps va de A vers B, dans le cas a de frottementsnuls, b d’un coeﬃcient de frottement dynamique µd. c Dans chaque cas, quelle est la vitesseminimale initiale qu’il faudrait donner au corps pour qu’il atteigne B.ABELe looping Voir video en ligneUne masse m glisse sur une piste dont la partie terminale est un demi-cercle de rayon R.a S’il n’y a pas de frottement, de quelle hauteur h doit-on lˆacher m sans vitesse pour qu’elleatteigne le sommet S de la piste avec une vitesse de norme vS ? on supposera le mouvementpossible cf. cb On constate qu’il y a des frottements et qu’il faut en fait lˆacher m sans vitesse de la hauteur2 h pour qu’elle atteigne le sommet S de la piste avec la vitesse de norme vS. En deduire lavaleur du travail des forces de frottement sur l’ensemble du trajet.c Le mouvement des questions precedentes n’est possible que si la masse m ne quitte pas lapiste avant S. On appelle v0 la valeur minimale possible de vS. Donnez d’abord v0 a unfacteur pres, en utilisant des arguments d’homogeneite. Ensuite, calculez v0 exactement.En deduire la condition sur h pour que la masse m atteigne S s’il n’y a pas de frottements ?mSghR

Page 19 : FAllers-retours Exo Examen 2009Un bloc de masse m glisse sur une piste ayant une partie centrale horizontale de longueur D voirﬁgure. Les parties incurvees de la piste sont sans frottement, mais le coeﬃcient de frottementdynamique de la partie horizontale vaut µd = 0.2. On lˆache le bloc, sans vitesse initiale, d’unehauteur h au-dessus de la partie horizontale.hDma Quelle est la hauteur minimale a laquelle on doit lˆacher le bloc pour qu’il traverse au moinsune fois toute la partie horizontale?b On lˆache le bloc d’une hauteur h = D/2. A quelle hauteur h1 remonte le bloc apres le premierpassage sur la partie horizontale?c Au bout de combien de passages sur la partie horizontale le bloc s’immobilise-t-il ? Et ou lebloc s’immobilise-t-il ?GPuits de potentielUne particule se deplace suivant la direction x de l’espace dans un champ de forces derivant del’energie potentielle Epx Epx est une fonction paire dont le graphe est represente sur la ﬁgure.E1E4E3E2Epxxa Quels sont les points d’equilibre? Discutez leur stabilite.b Quels sont les points ou la force est maximale en norme ?c Decrire le mouvement de la particule d’energie E1, E2, E3 et E4.

Page 20 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointChristiaan HuygensChristiaan Huygens 1629 – 1695, physicien nerlandais qui a etabli les lois des chocs elastiques.Il est le premier a avoir l’idee d’utiliser le mouvement du pendule pour fabriquer des horloges. Ilest aussi connu pour ses travaux en optique.TD 8 : Les systemes de particules et les chocsALe pingouinUn pingouin est debout sur le bord gauche d’un traˆıneau voir ﬁgure. Le traˆıneau repose sur laglace, et par la suite on negligera les frottements. La masse du traˆıneau est distribuee de fa¸conuniforme sur sa longueur, L. La masse du pingouin et celle du traˆıneau sont les mˆemes.a Ou se trouve le centre de masse du traˆıneau?b A quelle distance du centre de masse du traˆıneau se trouve le centre de masse du systemepingouin+traˆıneau?Le pingouin maintenant avance vers le bord du traˆıneau situe a droite.c Le centre de masse du systeme traˆıneau+pingouin s’est deplace vers la droite, la gauche ouest reste stationnaire ?d A quelle distance et de quel cˆote du centre de masse du systeme se trouve le centre de massedu traˆıneau?e De quelle distance s’est deplace le pingouin par rapport au traˆıneau?f De quelle distance s’est deplace le pingouin par rapport au centre de masse du systemepingouin+traˆıneau? Et le traˆıneau?TraineauUn pingouin !Glace : pas defrottementBExplosion d’une piece pyrotechniqueUne piece pyrotechnique, de masse M = 3 m, lancee horizontalement a la vitesse ⃗v, v = 8 ms1explose en 3 fragments de mˆeme masse m. Le premier fragment continue horizontalement a vitesse⃗v1 v1 = 16 ms1. Le deuxieme est lance vers le haut suivant un angle de 450 et le troisiemesuivant le mˆeme angle, mais vers le bas. Soit τ la duree de l’explosion, supposee tres courte.a Faire le bilan des forces exterieures appliquees au systeme. Pourquoi peut-on, au moment del’explosion, negliger la force de gravitation?b Quelles sont, apres l’explosion, les vitesses ⃗v2 et ⃗v3 ?c Comparer les energies cinetiques du systeme avant et apres l’explosion. Que peut-on conclure ?

Page 21 : CCollisions1Collision elastique frontale Voir video en ligneDeux enfants s’amusent a faire entrer en collision deux palets de masse m1 et m2, dans une petiterigole rectiligne, creusee dans la glace. Les deux palets s’approchent l’un de l’autre avec les vitessesinitiales respectives v1 et v2.a Etablir l’expression des vitesses v′1 et v′2 de chaque palet apres leur collision supposee frontaleet parfaitement elastique. Discuter les cas : m1 = m2, m1 m2 et m1 m2.b Dans le cas ou v2 est nulle cible immobile il y a transfert d’une partie de l’energie cinetiquedu palet 1 au palet 2. Le coeﬃcient τ = E′c,2/Ec,1 caracterise ce transfert.Etablir l’expression de τ en fonction des masses. Discuter les cas : m1 = m2, m1 m2 etm1 m2.2Le joueur de tennisUn joueur de tennis joue seul contre un mur. Il lance sa balle d’une hauteur h avec une vitesseinitiale faisant un angle α avec l’horizontale. On suppose la collision de la balle contre le murelastique.a Tracer qualitativement la trajectoire de la balle.b S’il lance sa balle d’une distance d du mur, a quelle distance d′ doit-il se placer pourreceptionner sa balle ? On suppose qu’il maintient sa raquette a la mˆeme hauteur h.3Le super rebond Voir video en ligneOn aligne une petite balle de masse m directement au-dessus d’un ballon de masse M les 2balles sont separees par un mince espace. On les laisse tomber simultanement d’une hauteur hon supposera h tres grand devant les rayons des 2 balles. On suppose que le ballon rebondit demaniere elastique sur le sol et que la balle rebondit elle aussi de maniere elastique sur le ballon.On prendra la limite M m pour simpliﬁer les calculs.Jusqu’a quelle hauteur a exprimer en fonction de h remonte la petite balle apres la collision ?4Le rebond d’une balle molleUne balle de masse m, assimilee a un point materiel, tombe a la verticale sur le sol d’une hauteurh. La balle rebondit a la hauteur h′ h.a La collision balle-sol est-elle elastique?b Determiner les quantites de mouvement de la balle juste avant et juste apres la collision.c Quelle est la force moyenne exercee par le sol sur la balle en supposant que la duree du chocest τ ? Comparer cette force a la force gravitationnelle.d Determiner le coeﬃcient de restitution en energie ε.On donne : m = 100 g, h = 2 m, h′ = 1,5 m et τ = 102 s.5Pendule balistique : choc inelastique Voir video en lignePour mesurer la vitesse d’une ﬂechette, on utilise un bloc de bois, de masse M, suspendu a l’aidede deux cordes de longueur d. Une ﬂechette de masse m, se depla¸cant avec une vitesse horizontale⃗v, frappe le bloc et s’y loge. On considere que le choc est instantane.a Quelles sont, au moment du choc, les forces exterieures appliquees au systeme bloc +ﬂechette ? En deduire l’expression de la vitesse ⃗vf du systeme a la ﬁn de la collision, enfonction de m, M et ⃗v.b Quel est l’angle maximal de deviation - apres le choc - du systeme bloc + ﬂechette ?c L’energie du systeme est-elle conservee pendant l’experience? Expliquer.d Discuter le cas particulier m M.

Page 22 : Universite de Cergy-PontoiseS1-MPIIntroduction a la mecanique du pointPartiels et ExamensAnnees 2011/2012 et 2012/2013

Page 23 : Universite de Cergy-PontoiseOctobre 2011Introduction a la mecanique du pointS1 - MPIPartiel : duree 1hdocuments, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 3 ptsUne loi de mecanique s’ecrit : T 2 =4π2GM + m a3, ou T est une periode, G laconstante de gravitation universelle, M et m des masses.Quelle est la dimension de la grandeur a ?Exercice 2 4 ptsUne masse m est soumise aux quatre forces representees sur la ﬁgure ci-dessous,⃗F etant une force horizontale.NmgfF!La masse m etant a l’equilibre, calculer les normes des forces ⃗f et ⃗N en fonctionde ⃗F, α et m.Exercice 3 7 ptsa On frappe un ballon du sol avec une vitesse initiale ⃗v0 = v0x⃗ux+v0y⃗uy. Calculerla hauteur du sommet de la trajectoire du ballon.b Comparer les durees des deux trajectoires 1 et 2 du ballon representees ci-dessous le ballon est lance avec deux vitesses initiales diﬀerentes.2yx01Exercice 4 6 ptsOn tire un bloc de glace de masse m sur un sol horizontal avec deux forces ⃗F1et ⃗F2 comme indique sur la ﬁgure. On supposera que le bloc de glace glisse sansfrotter.!F12Fa Calculer l’acceleration du bloc en fonction de ⃗F1, ⃗F2, α et m.b Calculer la force exercee par le sol sur le bloc en fonction de ⃗F1, ⃗F2, α etm.c On augmente ⃗F1 progressivement. Quelle est la condition sur cette normepour que le bloc reste sur le sol ?

Page 24 : Universite de Cergy-PontoiseOctobre 2012Introduction a la mecanique du pointS1 - MPIPartiel : duree 1hdocuments, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 3 ptsLe graphique ci-dessous represente le mouvement en fonction du temps d’un objetse depla¸cant le long de l’axe des x.xta L’objet se deplace dans le sens des x 0 ou dans le sens des x 0 ?b Son mouvement est-il accelere ou ralenti ?Exercice 2 6 ptsUne masse m est soumise aux trois forces representees sur la ﬁgure ci-dessous, ⃗Fetant une force horizontale et les angles valant α = π/4 et β = π/6.!"mgFTCalculer les normes des forces ⃗T et ⃗F en fonction de m et g pour que la resultantedes forces soit nulle.Exercice 3 4 ptsUne voiture se depla¸cant avec une vitesse de norme egale a v0 freine avec uneacceleration constante ⃗a0 de norme a0. La trajectoire de la voiture est rectiligne.a Quel est le sens de ⃗a0 ?b Calculer la distance d’arrˆet de la voiture en fonction de v0 et a0.Exercice 4 8 ptsUn joueur de basket lance un ballon du point A jusqu’au centre du panier situeau point B, selon la trajectoire representee sur la ﬁgure ci-dessous. Le ballonest lance du point A avec une vitesse ⃗v0 de norme v0 et faisant un angle α avecl’horizontale. Le point B, centre du panier, se trouve a une distance horizontaled et a une hauteur h au-dessus du point A.A.N. : α = 45◦, v0 = 72 m.s1, h = 2 m et g = 10 m.s2.!"&'+,-a Calculer la distance d a laquelle le joueur doit se placer pour que le ballon entredans le panier en B ?b Calculer la tangente de l’angle que fait le vecteur vitesse du ballon en B avecl’horizontale.

Page 25 : Universite de Cergy-PontoiseJanvier 2012Introduction a la mecanique du pointS1 - MPIExamen : duree 2hdocuments, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 4 ptsUn bloc de masse m glisse sur la piste illustree sur la ﬁgure. Il est lˆache sans vitesseinitiale d’une hauteur h au-dessus du plan horizontal ou se trouve un ressort deraideur k et de longueur a vide l0 et ﬁxe au mur vertical.On suppose qu’il n’y a pas de frottements.k,lmh0Calculer la distance de compression maximale du ressort.Exercice 2 5 ptsUne balle de fusil de masse m arrive avec une vitesse ⃗v0 sur un bloc de masse Mimmobile comme illustre sur la ﬁgure. La balle reste dans le bloc apres la collisionet le bloc glisse sur le sol sur une distance d avant de s’arrˆeter on suppose que lemouvement du bloc est rectiligne. Le coeﬃcient de frottement dynamique entrele bloc et le sol est µd.mv0M1. Calculer ⃗v1, la vitesse du bloc juste apres la collision.2. Trouver la relation entre ⃗v1et d.3. En deduire la relation entre ⃗v0et d.Exercice 3 5 ptsJean passe pres de Marie dans son vaisseau spatial a la vitesse v = 0, 6c !.Marie mesure que la longueur et la hauteur du vaisseau spatial de Jean sontrespectivement de 8 m et 1,5 m.1. Calculer la longueur et hauteur du vaisseau mesurees dans le referentiel deJean. A.N.2. Jean met 20 s sur la montre de Marie pour passer entre deux bornes. Combiende secondes se sont ecoulees sur la montre de Jean ? A.N.3. Marie met 20 s sur la montre de Jean pour passer entre deux bornes. Combiende secondes se sont ecoulees sur la montre de Marie ? A.N.Exercice 4 7 ptsDeux blocs de masses m1 et m2 sont reliees par une corde ideale tendue qui passesur une poulie ideale comme indique sur la ﬁgure. Ils reposent sur deux plans, unplan incline faisant un angle α par rapport a l’horizontale et un plan horizontal.Les deux blocs sont initialement immobiles et on les lˆache.!m1m21. On suppose qu’il n’y a aucun frottement entre les blocs et les plans. Calculerl’acceleration des blocs. Calculer le module de la tension de la corde.2. On suppose maintenant que seul le bloc de masse m1 frotte et que le coeﬃcientde frottement dynamique entre le bloc de masse m1 et le plan incline vautµd .On observe que les deux blocs glissent.Calculer l’acceleration des blocs.Calculer le module de la tension de la corde.

Page 26 : Universite de Cergy-PontoiseJanvier 2013Introduction a la mecanique du pointS1 - MPIExamen : duree 2hdocuments, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 6 ptsUn pendule est forme de deux blocs de masses M et m respectivement comme lemontre la ﬁgure. Ce systeme M +m est lˆache d’une hauteur h par rapport a saposition a la verticale et lors du passage au point le plus bas de son oscillation,le bloc de masse m se detache du pendule.1. Quelle est alors la hauteur maximale h′ toujours par rapport a sa positiona la verticale atteinte par la masse M ?2. Le bloc de masse m est lˆache d’une hauteur H du sol. Tracer qualitativementsa trajectoire. Quelle distance d parcourt-il sur l’horizontale ?Exercice 2 4 ptsOn depose une piece de monnaie de masse m sur un tourne-disque horizontal aune distance r de son centre. Le tourne disque tourne avec une vitesse angulaireω constante et la piece ne glisse pas. On notera µs le coeﬃcient de frottementstatique entre la piece et le tourne-disque.1. Exprimer les normes de la vitesse et de l’acceleration de la piece en fonctiondes donnees du probleme. Les representer sur un schema.2. Calculer la force de frottement qui s’exerce sur la piece norme et direction.La representer sur un schema.3. Quelle est la condition sur la distance r pour que la piece ne glisse pas ?Exercice 3 5 ptsOn lance un bloc de masse m sur un plan incline faisant un angle α avec l’horizontaleavec une vitesse ⃗v0 parallele au plan et dirigee vers le haut cf ﬁgure. On noteraµd le coeﬃcient de frottement dynamique entre le bloc et le plan incline.m!0vCalculer la distance parcourue par le bloc jusqu’a son point le plus haut.Exercice 4 5 ptsUn ressort de masse negligeable, de longueur a vide lo et de raideur k, est pose surune table horizontale, suivant la direction Ox. Une de ses extremite est attacheea un mur et l’autre extremite est libre. Un bloc en bois de masse M qui peutglisser sans frottements est pose sur la table. Un projectile en acier de masse mm M, de vitesse ⃗vo dirigee suivant Ox vient alors heurter la masse M. Onsupposera la collision elastique.m0k,lM0v1. Determiner la vitesse ⃗V du bloc de bois juste apres la collision en fonctiondes donnees du probleme. Montrer que la masse m repart bien vers la gaucheapres la collision.2. En deduire la distance de compression maximale atteinte par le ressort dansla suite du mouvement.Aide : les etudiants n’ayant pas repondu a la question 1. peuvent quandmˆeme exprimer la distance de compression maximale du ressort en fonctionde ⃗V , la vitesse du bloc de bois juste apres la collision, et des donnees duprobleme.

Page 27 : Universite de Cergy-PontoiseJuin 2012Introduction a la mecanique du pointS1 - MPIExamen session 2 : duree 1h30documents, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 4 ptsOn lance une balle A sans vitesse initiale d’une hauteur h au-dessus du sol. Aumˆeme instant, on lance une balle B avec une vitesse horizontale de la mˆemehauteur h.Quelle balle touche le sol en premier ? Justiﬁer votre reponse : tracer qualitative-ment les deux trajectoires - calculer les durees de chaque trajectoire - comparer.Exercice 2 5 ptsUn bloc de masse m est pose sur un plan incline faisant un angle α par rapport al’horizontale. Le coeﬃcient de frottement dynamique entre le bloc et le plan vautµd.On tire le bloc m a l’aide d’une force ⃗F parallele au plan comme indique sur laﬁgure.Om!F1. Calculer le module de la force ⃗F qui permettrait de deplacer le bloc m versle haut avec une vitesse constante.2. Application numerique : m = 1 kg, α = π/6, µd = 1/3, g = 10 m.s2.Exercice 3 5 ptsUn bloc de masse m est lˆache sans vitesse initiale d’une hauteur h au-dessus duplan horizontal. Il glisse sur la piste illustree sur la ﬁgure et parcourt une distanced sur la portion horizontale de la piste avant de s’arrˆeter. On suppose que le blocglisse sans frotter sauf sur la portion horizontale indiquee en gris sur la ﬁgure, oule coeﬃcient de frottement dynamique vaut µd.µhmddCalculer la distance d’arrˆet d du bloc.Exercice 4 6 ptsDeux objets de mˆeme masse m et de vitesses ⃗v1 et ⃗v2 comme indique sur la ﬁgure,entrent en collision parfaitement inelastique. Apres la collision, les deux objetssont lies et se deplacent a la mˆeme vitesse ⃗v indiquee sur la ﬁgure.2m!vmv2m"v11. Tracer la trajectoire du centre de masse G du systeme forme par les deuxmasses m. Justiﬁer votre reponse.2. On suppose que l’on a : ⃗v1= ⃗v2= v0 et ⃗v= v0/2. Calculer les anglesα et β.

Page 28 : Universite de Cergy-PontoiseJuin 2013Introduction a la mecanique du pointS1 - MPIExamen session 2 : duree 1h30documents, calculettes, portables interditsLes exercices sont independants. Le bareme indique est approximatif.Exercice 1 8 ptsOn considere un plan incline d’un angle α = π/6 par rapport a l’horizontale.Sur ce plan est pose un bloc 1 de masse m1 qui, d’un cˆote, est attachea un mur par une corde B et, de l’autre cˆote, est relie a un bloc 2 demasse m2 par une corde A passant sur une poulie. Les cordes ainsi quela poulie sont sans masse, les cordes sont tendues et inextensibles et onsuppose qu’il n’y a aucun frottement.1corde Acorde B2!6ga Exprimer les tensions TA et TB des deux cordes en fonction des donneesdu probleme.b On coupe maintenant la corde B reliant le bloc 1 au mur. Exprimerla tension de la corde A ainsi que l’acceleration des blocs en fonction desdonnees du probleme.Exercice 2 7 ptsUn bloc de masse m est pose sans vitesse initiale sur un plan incline aupoint A, comme indique sur la ﬁgure. On notera µs et µd les coeﬃcientsde frottement statique et dynamique entre le bloc et la piste µs µd.BhA!a Quelle est la condition sur l’angle α pour que le bloc glisse sur le planincline ?b On suppose que le bloc glisse. Calculer la vitesse du bloc au point B.Le bloc atteint-il toujours le point B ? Justiﬁer.Exercice 3 5 ptsUn bloc de bois de masse M est pose sur une ouverture ciculaire. Lecentre de masse G du bloc se trouve au-dessus du centre de l’ouverture.Une balle de masse m frappe le bloc au niveau de G avec une vitesse ver-ticale de norme Vo et reste liee au bloc de bois apres la collision collisionparfaitement inelastique.Quelle est la hauteur maximale a laquelle va monter le bloc de bois ?On negligera les frottements de l’air.