TD

Posté le 07/02/2025

Chargé de TD/CM : D. Physique.

32 min de lecture

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Page 1 : CY Cergy Paris Universite2023 – 2024CY TechPreIng 2Travaux diriges d’ElectromagnetismeCe document est disponible en ligne— 1/24 —

Page 2 : Table des matieres1. Calculs de charges et forces electromagnetiques5I.Applications de cours . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5II.Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .62. Champ electrostatique7I.Loi de Coulomb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7II.Calculs de flux de champ electrique . . . . . . . . . . . . . . . . . . . . . . . . . . . .8III.Calcul de champ electrique avec le theoreme de Gauss . . . . . . . . . . . . . . . . . .8IV.Lignes de champ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9V.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .93. Potentiel electrostatique10I.Gradient et champ electrique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10II.Calcul de potentiel et de champ electrique pour diverses symetries . . . . . . . . . . .10III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .104. Conducteurs a l’equilibre electrostatique12I.Proprietes des conducteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12II.Calcul de la capacite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .12III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .135. CForce de Lorentz14I.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .156. Champ magnetostatique16I.Loi de Biot et Savart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16II.Calcul de champ magnetique avec le theoreme d’Ampere . . . . . . . . . . . . . . . .16III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .177. Equations de Maxwell18I.Consequences des equations de Maxwell. . . . . . . . . . . . . . . . . . . . . . . . .18II.Applications des equations de Maxwell . . . . . . . . . . . . . . . . . . . . . . . . . .188. Induction20I.Phenomenes d’induction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20II.Inductance mutuelle. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21III.Circuits couples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21IV.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .229. Electrocinetique23I.Association de resistances. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23II.Loi des mailles. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .24III.Circuit RL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .24— 2/24 —

Page 3 : Plan du coursElectrostatiqueForce entre deux chargesChamp electriqueTheoreme de superposition et symetriesTheoreme de GaussPotentiel electrostatiqueConducteurs en equilibre electrostatiqueMagnetostatiqueChamp magnetique - Force de LorentzLoi de Biot et Savart - Theoreme de superposition et symetriesInduction electromagnetismeElectrodynamique des regimes quasi stationnairesIntensite et tensionEquations caracteristiques des principaux dipˆolesLois de KirchoffEquations de MaxwellEquations de MaxwellEquations de Maxwell dans le vide— 3/24 —

Page 4 : Contact— Enseignants charges du cours magistral : Emilie Dupont et Abdelaziz Boumiz— Bureau : Bˆatiment Cauchy Etage 3 CY 308— E-mail : emilie.dupont@cyu.fr— E-mail : abdelaziz.boumiz@cyu.frL’equipe pedagogiqueCours Magistral CM : Emilie Dupont Cergy, Abdelaziz Boumiz ; et Lucie Desplat PauTravaux diriges TD :Panayotis Akridas Cergypanayotis.akridas-morel@cyu.frAbdelaziz Boumiz Cergyabdelaziz.boumiz@cyu.frLucie Desplat Paulucie.desplat@cyu.frEmilie Dupont Cergyemilie.dupont@cyu.frFabien Piguet Cergyfabien.piguet@cyu.frQuelques referencesListe non exhaustive de livres recommandes pour ce cours.— Jose-Philippe Perez, Robert Carles, Robert Fleckinger : « Electromagnetisme : Fondements etapplications », Dunod ; 4e edition 20 janvier 2020— « Le Cours de physique de Feynman »titre original : Feynman Lectures on Physics de RichardFeynman, Robert B. Leighton en et Matthew Sands en, Electromagnetisme 1.— Jerˆome Majou : « Super manuel de physique », MPSI, PCSI, PTSI, BrealConsultez le site du cours sur la plateforme.Allez voir aussi les sites : http://cpinettes.u-cergy.fr/S3-Electromag.html, https://etienneklein.fr/ ethttps://www.physagreg.fr/electromagnetisme1.php.Regarder la chaˆıne youtube sciences etonnantes... Il y a beaucoup de ressources en ligne, apprenez achoisir les bonnes et bien sˆur gare aux fakesciences— 4/24 —

Page 5 : 1Calculs de charges et forceselectromagnetiquesLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Applications de coursExercice 1 – Calculs d’aire et de volumeEn choisissant le systeme de coordonnees approprie :1/ Calculer, en utilisant une integrale double, la surface d’un disque de rayon R.2/ Calculer, en utilisant une integrale double, la surface de la paroi laterale d’un cylindre dehauteur h et de rayon R.3/ Calculer, en utilisant une integrale triple, le volume d’un cylindre de hauteur h et de rayon R.Exercice 2 – Calculs de charge totaleEn choisissant le systeme de coordonnees approprie :1/ Calculer la charge totale contenue dans un fil de longueur L uniformement charge dont ladensite lineique vaut λ0.2/ Calculer la charge totale contenue dans un disque de rayon R uniformement charge en surfacedont la densite surfacique vaut σ0.3/ Calculer la charge totale contenue dans une boule de rayon R uniformement chargee en volumedont la densite volumique vaut ρ0.ExercicesExercice 3 – Charge totale d’une distribution surfaciqueOn considere une sphere de centre O et de rayon R portant en sa surface une densite de chargesσ = σ01 + cos θou θ = →Oz, →OPCalculer la charge totale portee par la distribution.Exercice 4 – Noyaux atomiques Du point de vue du potentiel et du champ electrique qu’ils creent, les noyaux de certains atomes legerspeuvent ˆetre modelises par une distribution volumique de charge a l’interieur d’une sphere de centreO et de rayon a. On designe par →r = →OP, le vecteur position d’un point P quelconque de l’espace.Pour r a, la charge volumique ρP qui represente le noyau varie en fonction de r suivant la loi :ρr = ρ01 r2a2— 5/24 —

Page 6 : ou ρ0 est une constante positive.1/ Donner les symetries et invariances de cette distribution de charges.2/ Exprimer la charge totale Q du noyau.Pour aller plus loinExercice 5 – Masse volumique de la TerreOn peut supposer, dans un modele grossier, que la repartition de la masse de la Terre assimilee a unesphere de rayon R n’est pas uniforme : le noyau terrestre, principalement forme de fer et de nickel,est plus dense que la croˆute. La masse volumique ρ depend donc de la distance r au centre C :ρr = ρ01 r2RDonnees : la densite du fer vaut environ 8 et celle des roches granitiques vaut environ 4.1/ Exprimer la masse M de la Terre en fonction de R et ρ0.2/ Calculer numeriquement la masse volumique au centre et a la surface de la Terre. Commenter.On donne M = 6.0 × 1024 kg et R = 6.4 × 103 km— 6/24 —

Page 7 : 2Champ electrostatiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Loi de CoulombExercice 1 – Distribution discrete de charges ponctuellesQuatre charges electriques ponctuelles, de valeur absolue q, sont placees aux sommets d’un carreABCD. Ce carre a pour cˆote 2a, centre O et appartient au plan Oxz, comme le montre la figureci-dessous.Determiner l’expression de la force subie par la charge electrique Q placee en un point M quelconquede l’axe Oy.— 7/24 —

Page 8 : Calculs de flux de champ electriqueExercice 2 – Symetrie spheriqueSoit une sphere, de rayon R, chargee uniform´ement.En commen¸cant par une ´etude de sym´etrie et d’invariance, calculerle flux de →E a travers la surface Σ d’une sphere de rayon r. Lesdeux spheres ont le mˆeme centre.Exercice 3 – Sym´etrie cylindriqueSoit un cylindre, de rayon R et de hauteur suppos´ee infinie, charg´euniform´ement.En commen¸cant par une ´etude de sym´etrie et d’invariance, calculerle flux de →E a travers la surface Σ d’un cylindre de rayon r et dehauteur h. Les deux cylindres ont le mˆeme axe.Exercice 4 – Sym´etrie planeSoit un plan infini charg´e uniform´ement de densit´e σ.En commen¸cant par une ´etude de sym´etrie et d’invariance, calculerle flux de →E a travers la surface Σ d’un cylindre de rayon r et dehauteur h. L’axe du cylindre est perpendiculaire au plan charg´e.il serait int´eressant de prendre h/2 de part et d’autre du plan.Calcul de champ ´electrique avec le th´eoreme de GaussExercice 5 – Sphere uniform´ement charg´ee en volumeUne boule de centre O et de rayon R porte une densit´e volumique de charge uniforme ρ.1/ Quelle est l’expression de la charge totale, not´ee Q, contenue dans la sphere ?2/ Calculer le champ ´electrostatique →E M en consid´erant le point M :a a l’interieur de la sphere : r Rb a l’ext´erieur de la sphere : r R3/ Le champ est-il continu a la travers´ee de la sphere ? A commenter.4/ Tracer l’allure de Er.Exercice 6 – Sphere uniform´ement charg´ee en surfaceUne sphere de centre O et de rayon R porte une densit´e surfacique de charge uniforme σ.1/ Quelle est l’expression de la charge totale, not´ee Q, sur la sphere ?2/ Calculer le champ ´electrostatique →E M en consid´erant le point M :a a l’interieur de la sphere : r Rb a l’ext´erieur de la sphere : r R3/ Le champ est-il continu a la travers´ee de la sphere ? A commenter.4/ Tracer l’allure de Er.— 8/24 —

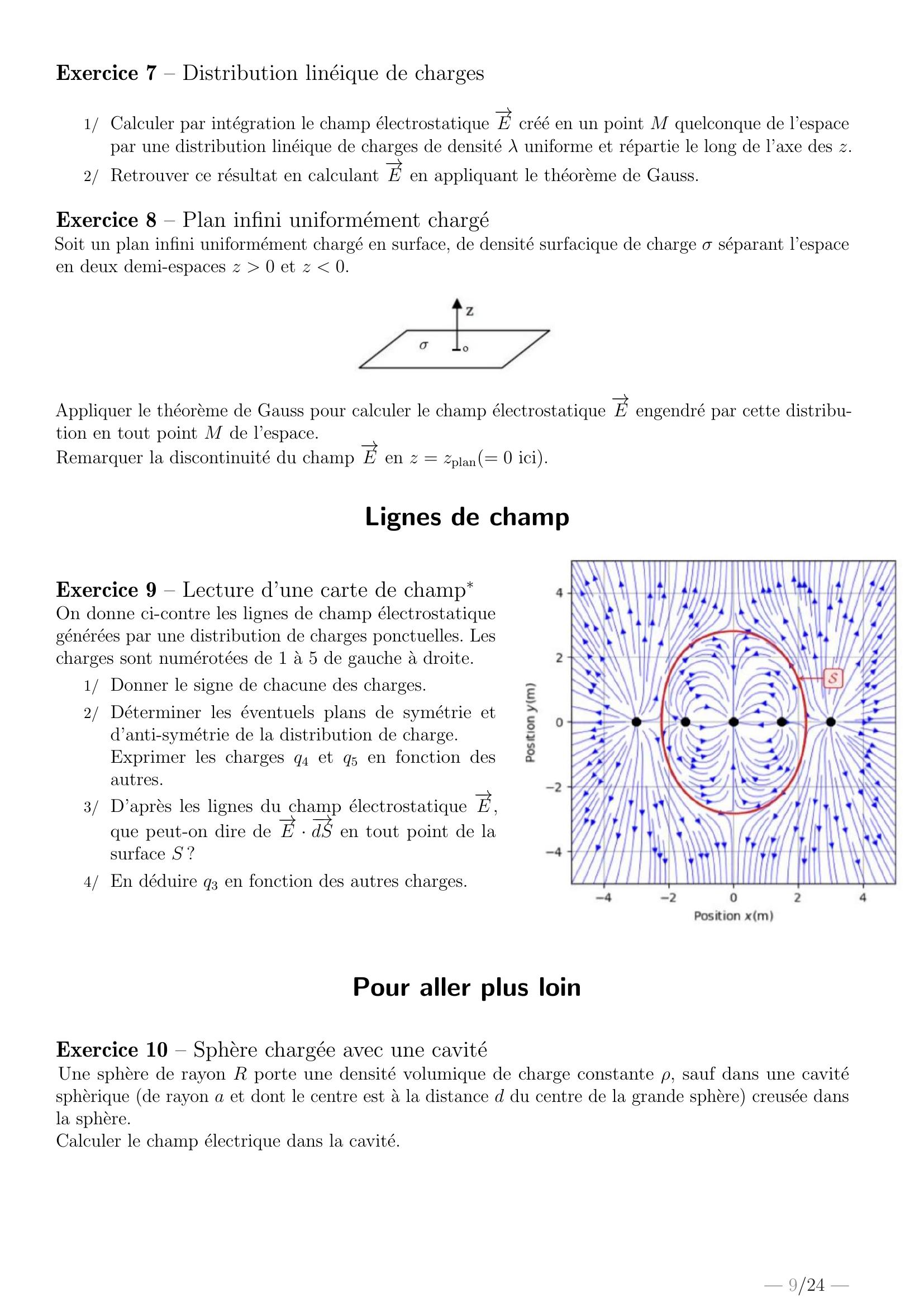
Page 9 : Exercice 7 – Distribution lin´eique de charges1/ Calculer par int´egration le champ ´electrostatique →E cr´e´e en un point M quelconque de l’espacepar une distribution lin´eique de charges de densit´e λ uniforme et r´epartie le long de l’axe des z.2/ Retrouver ce r´esultat en calculant →E en appliquant le th´eoreme de Gauss.Exercice 8 – Plan infini uniform´ement charg´eSoit un plan infini uniform´ement charg´e en surface, de densit´e surfacique de charge σ s´eparant l’espaceen deux demi-espaces z 0 et z 0.Appliquer le th´eoreme de Gauss pour calculer le champ ´electrostatique →E engendr´e par cette distribu-tion en tout point M de l’espace.Remarquer la discontinuit´e du champ →E en z = zplan= 0 ici.Lignes de champExercice 9 – Lecture d’une carte de champOn donne ci-contre les lignes de champ ´electrostatiqueg´en´er´ees par une distribution de charges ponctuelles. Lescharges sont num´erot´ees de 1 a 5 de gauche a droite.1/ Donner le signe de chacune des charges.2/ D´eterminer les ´eventuels plans de sym´etrie etd’anti-sym´etrie de la distribution de charge.Exprimer les charges q4 et q5 en fonction desautres.3/ D’apres les lignes du champ ´electrostatique →E ,que peut-on dire de →E · →dS en tout point de lasurface S ?4/ En d´eduire q3 en fonction des autres charges.Pour aller plus loinExercice 10 – Sphere charg´ee avec une cavit´eUne sphere de rayon R porte une densit´e volumique de charge constante ρ, sauf dans une cavit´espherique de rayon a et dont le centre est a la distance d du centre de la grande sphere creus´ee dansla sphere.Calculer le champ ´electrique dans la cavit´e.— 9/24 —

Page 10 : 3Potentiel ´electrostatiqueLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Gradient et champ ´electriqueExercice 1 – Calcul de potentiel ´electriqueLe potentiel cr´e´e par une charge ponctuelle en un point M, situ´e a la distance r de la charge q, est aune constante additive pres :V M =14πε0qrCalculer le champ ´electrostatique →E qui d´erive du potentiel V .Calcul de potentiel et de champ ´electrique pour diversessym´etriesExercice 2 – Sym´etrie cylindriqueSoit un cylindre de rayon R et de hauteur infinie. D´eterminer le potentiel ´electrostatique cr´e´e par ladistribution surfacique de charges de densit´e σ r´epartie uniform´ement sur la surface de ce cylindre.Exercice 3 – Sym´etrie sph´eriqueSoit une sphere de centre O et de rayon R cf. exercice 6 du TD2. D´eterminer le potentiel ´electrostatiquecr´e´e par la distribution surfacique de charges de densit´e σ r´epartie uniform´ement sur la surface decette sphere.Exercice 4 – Sym´etrie axiale Un champ de vecteur →E d´erive d’un potentiel V qui a la sym´etrie de r´evolution autour de l’axe Oz.On se place dans un plan contenant l’axe Oz. Dans ce plan, on adopte les coordonn´ees polaires, etl’on pose θ = →Oz, →OM. Le potentiel V a alors pour expression :V =Kr3 3 cos2 θ 1D´eterminer les composantes du champ →E .Pour aller plus loinExercice 5 –D´eterminer les coordonn´ees de →gradf ou f est le champ scalaire suivant :1/ fx, y, z = xy2 yz2— 10/24 —

Page 11 : 2/ fx, y, z = xyz × sinxy3/ On donne le champ scalaire fx, y, z = x2 + y2 + z2. Calculer →gradf.Discuter les sym´etries et invariances des champs f et →gradf.— 11/24 —

Page 12 : 4Conducteurs a l’´equilibre ´electrostatiqueLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Propri´et´es des conducteursExercice 1 – Conducteur creuxSoit A, un conducteur creux.On place en son sein un second conducteur not´e B portant une charge +Q :1/ Retrouver le fait que QA,int = QB = Q en utilisant le th´eoreme de Gauss. On note QA,int :charge surfacique pr´esente au niveau de la surface int´erieure de A.2/ Calculer la charge ext´erieure QA,ext i.e. charge surfacique pr´esente au niveau de la surfaceext´erieure de A dans les cas suivants :a A est isol´e et initialement neutre.b A porte une charge initiale qCalcul de la capacit´eExercice 2 – Condensateur planUn condensateur plan, plac´e dans le vide ε0, est constitu´e de deux armatures conductrices planes desurface S, paralleles entre elles, et s´epar´ees d’une distance e l’une de l’autre.Dans cette ´etude, on se place dans l’approximation d’un condensateur plan infini.— 12/24 —

Page 13 : 1/ En utilisant le th´eoreme de Gauss, d´eterminer le champ ´electrostatique →E cr´ee par un planinfini charg´e avec une densit´e de charge surfacique uniforme +σ.2/ D´eduire le champ entre les deux armatures du condensateur en fonction de la charge surfacique+σ puis en fonction de la charge totale +Q port´ee par l’armature n◦1.3/ En d´eduire la diff´erence de potentiel V = V1 V2 entre les armatures n◦1 et n◦2, puis lacapacit´e C du condensateur en fonction de S, e et ε0.4/ Application num´erique :Pendant un orage, la surface de la Terre et la surface inf´erieure des nuages forment, avec uneassez bonne approximation, un condensateur plan. On suppose que le nuage se trouve a 1000metres d’altitude et qu’il couvre une surface d’environ 20 km2.Quelle est la valeur de la capacit´e du condensateur form´e par le systeme « Terre Nuage » ?Donn´ees : ε0 = 8.85 × 1012 SIExercice 3 – Condensateur cylindriqueUn condensateur cylindrique a air est form´e de deux armatures coaxiales, de rayons not´es R1 et R2avec R1 R2. Ces deux cylindres infinis coaxiaux sont uniform´ement charg´es en surface avec unecharge Q1 et Q2 respectivement, telles que Q1 = Q2 = Q.1/ On suppose ici que ce conducteur est de longueur infinie. D´eterminer →E en un point M situ´e ala distance r de l’axe, avec R1 r R2.2/ En d´eduire l’expression de la capacit´e C de ce condensateur. A.N. : R2 = 20 cm, R1 = 10 cmet h = 50 cm.3/ Que devient l’expression de la capacit´e C lorsque les rayons sont voisins c-a-d : R2 R1 = e R1.Pour aller plus loinExercice 4 – On considere deux boules conductrices de rayons R1 et R2 dont les centres sont a une distance dgrande devant R1 et R2. Elles portent les charges respectives Q1 et Q2, distribu´ees uniform´ement.1/ Calculer les potentiels V1 et V2 de chacune des boules, en leur centre.2/ On relie les boules par un fil conducteur. Calculer les charges Q1′ et Q2′, ainsi que les potentielsnot´es V1′ et V2′.3/ En d´eduire la capacit´e de ce conducteur constitu´e des deux boules reli´ees par le fil conducteur.— 13/24 —

Page 14 : 5Force de LorentzLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Exercice 1 – Force magn´etique sur une charge en mouvement1/ Un proton se d´eplace vers la droite a 3000 m/s dans un champ de 10 G orient´e dans la directionindiqu´ee sur la figure.Quelle est la force sur ce proton ? Donner l’expression litt´erale de cette force puis sa valeurnum´erique.2/ Une charge de 1 µC se d´eplace dans une r´egion ou le champ magn´etique est uniforme etconstant.Elle ne subit pas de force quand elle se dirige avec une vitesse de 5 m/s dans la direction del’axe des x positifs. Elle subit cependant une force de 107 N dans la direction de l’axe des zpositifs quand elle a une vitesse de →v = 3→i + 4→j m · s1.Les vecteurs unitaires de la base cart´esienne sont : →i vecteur unitaire de l’axe x, →j vecteurunitaire de l’axe y et →k vecteur unitaire de l’axe z.Quel est le champ magn´etique ?Exercice 2 – Force de LorentzUn proton q = 1,60 × 1019 C, m = 1,67 × 1027 kg se trouve dans un champ magn´etique uniformed’intensit´e B = 0,5 T. On appelle x l’axe qui pointe dans la direction de ce champ.A t = 0 s, le proton a une vitesse →v avec vxt = 0 = 1,5 × 105 m · s1, vyt = 0 = 0 m · s1 etvzt = 0 = 2,0 × 105 m · s1. De plus, on est au point 0, 0, 0.1/ ´Ecrire la deuxieme loi de Newton pour le proton a t = 0 s.A t 0 s, le proton a d´esormais une vitesse →v a 3 composantes non nulles. →B est toujours uniforme,constant orient´e suivant x.2/ ´Ecrire les ´equations diff´erentielles du premier ordre pour vx, vy et vz a t 0 s. On notera→Ω= qm→B ,3/ ´Etablir les deux ´equations diff´erentielles du second ordre pour vy et vz.4/ Montrer que la trajectoire du proton est une h´elice qui a pour axe la droite parallele a xd’´equation z = 0; y = R, pour rayon R = vzt = 0Ωet de pas vxt = 02πΩ.— 14/24 —

Page 15 : Exercice 3 – Spectrometre de masseOn envoie un atome de krypton ionis´e 1 fois avec une vitesse de 40 000 m · s1 dans un spectrometrede masse ou regne un champ magn´etique uniforme et constant de 0,6 T. L’atome frappe la plaque aune distance de 11,044 cm du point d’entr´ee de l’atome.1/ Quelle est la masse de l’atome ?2/ De quel isotope de l’atome pourrait-il s’agir ?Pour aller plus loinExercice 4 – Particule dans des champs ´electrique et magn´etiqueUne particule de masse m et de charge q p´enetre avec une vitesse →v 0 = v0→u x dans une zone ou existentun champ ´electrique →E = E0→u y et un champ magn´etique →B = B0→u z uniformes et stationnaire.1. A quelle condition le vecteur vitesse de la particule reste-t-il inchang´e ?2. Expliquer comment ce dispositif peut ˆetre adapt´e en s´electeur de vitesse.Exercice 5 – Particule dans des champs ´electrique et magn´etiqueOn considere un point mat´eriel de charge q 0 et de masse m, de vitesse initiale →v 0 a l’entr´eed’une zone ou regnent un champ ´electrique →E ou un champ magn´etique →B . On suppose ces champsuniformes et ind´ependants du temps, et on n´eglige toute autre force que celles provoqu´ees par ceschamps.La particule d´ecrit une droite et possede une acc´el´eration constante a.1. D´eterminer la direction et la norme du ou des champs qui provoquent cette trajectoire.2. D´eterminer la position du point mat´eriel en fonction du temps.La particule d´ecrit une trajectoire circulaire de rayon R0 dans un plan xOy.1. D´eterminer la direction du ou des champs qui provoquent cette trajectoire.2. D´eterminer la norme du champ en fonction de v0 et R0.— 15/24 —

Page 16 : 6Champ magn´etostatiqueLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Loi de Biot et SavartExercice 1 – Fil rectiligne infiniment long1/ Calculer, par int´egration en utilisant la loi de Biot et Savart, le champ magn´etique →B cr´e´e enun point M quelconque par un fil rectiligne infiniment long et d´efini par l’axe Oz.2/ Retrouver ce champ magn´etique →B en appliquant le th´eoreme d’Ampere.Exercice 2 – Calcul de flux du champ magn´etique pour un filD´eterminer l’expression du flux Φ→B du champ magn´etique →B cr´e´e par un fil rectiligne infini parcourupar un courant d’intensit´e I, a travers un rectangle dont le plan contient le fil, de dimension h paralleleau fil et b perpendiculaire au fil.Le cˆot´e le plus proche du fil se trouvant a la distance a. a b hExercice 3 – SpireCalculer, par int´egration en utilisant la loi de Biot et Savart, le champ magn´etique →B direction, senset module cr´e´e en un point M de l’axe de r´evolution d’une spire de centre O et de rayon R parcouruepar un courant d’intensit´e I constante.Calcul de champ magn´etique avec le th´eoreme d’AmpereExercice 4 – Sol´eno¨ıde fini On considere un sol´eno¨ıde fini de longueur L et comprenant N spires, chacune ´etant parcouruepar un courant d’intensit´e I constante. Ces spires sont circulaires de rayon R et sont r´egulierementenroul´ees sur un cylindre de r´evolution autour de l’axe z′z.On cherche a d´eterminer completement le champ magn´etique →B M en un point M quelconque del’axe z′z. Le courant et l’axe z′z sont orient´es de maniere directe regle du tire-bouchon.1/ Soit une longueur ´el´ementaire dz de l’axe z′z ou se trouve le sol´eno¨ıde. Quel nombre ´el´ementairedN de spires se trouvent entre la cote z et z + dz ?2/ Calculer le champ ´el´ementaire d→B M cr´e´e au point Mpar ces dN spires ?3/ En d´eduire la valeur Bz du champ magn´etique au point Mz. On fera apparaˆıtre les anglesα1 et α2 sous lesquels on voit, du point M, la spire d’entr´ee et la spire de sortie du sol´eno¨ıde.4/ Retrouver l’expression du champ magn´etique →B M a l’int´erieur d’un sol´eno¨ıde infinimentlong, en utilisant le r´esultat pr´ec´edent.— 16/24 —

Page 17 : 5/ Retrouver l’expression du champ magn´etique →B M a l’int´erieur et a l’ext´erieur d’un sol´eno¨ıdeinfiniment long en utilisant le th´eoreme d’Ampere.Pour aller plus loinExercice 5 – Tore circulaireOn veut ´etudier le champ magn´etique cr´e´e par une distribution de courants pr´esente sur un torecirculaire de rayon R a section circulaire de rayon a. On note O le centre du tore et Oz son axe der´evolution. Une chambre a air gonfl´ee, de v´elo par exemple, constitue un tel tore.La distribution de courants est constitu´ee par un enroulement d’un grand nombre de N spires jointivescirculaires de rayon a enroul´ees sur toute la surface du tore, le sens du courant ´etant donn´e sur lafigure. On n´egligera l’´epaisseur des fils.Soit M un point quelconque de l’espace ou l’on cherche le champ magn´etique →B cr´e´e par cettedistribution.1/ ´Etude qualitativea Quel est le domaine de d´efinition du champ magn´etique ? Dans toute la suite, on considereque M appartient a ce domaine.b Quelle est la direction de →B en M ? Justifier la r´eponse.c Que vaut →B au point O ?d Justifier le choix du systeme de coordonn´ees cylindriques d’axe O, z. De quelles coor-donn´ees d´epend le module →B du champ ?2/ Montrer qu’en tout point situ´e a l’ext´erieur du tore, →B est nul.3/ D´eterminer l’expression de →B en un point quelconque de l’int´erieur du tore.— 17/24 —

Page 18 : 7´Equations de MaxwellLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Cons´equences des ´equations de MaxwellExercice 1 – ´Equations de Poisson´Etablir les ´equations de Poisson vues en cours.V + ρε0= 0→→A + µ0→j = →0Exercice 2 – Cylindre parcouru par un courantEn utilisant les ´equations locales de Maxwell, d´eterminer le champ magn´etique cr´e´e par un cylindreplein, infiniment long, de rayon R, parcouru par un courant uniforme I, suivant sa longueur.Exercice 3 – Champ ´electriqueDans le demi-espace vide x 0, il regne un champ ´electrique →E →r , t = E0cosωt kz.→e x, encoordonn´ees cart´esiennes, avec ω et k deux constantes positives.1. Calculer div→E . Justifier le r´esultat obtenu.2. Calculer →rot→E et donner l’expression de l’´equation de Mawxell faisant intervenir la quantit´e→rot→E .3. D´eterminer ainsi le champ magn´etique →B →r , t. On supposera que →B n’a pas de terme constant.4. V´erifier la valeur de sa divergence.5. D´eterminer la relation entre les constantes ω et k, a l’aide d’une autre ´equation de Maxwell,exprim´ee dans le vide.Applications des ´equations de MaxwellExercice 4 – Conservation de la chargeUne sphere creuse, de rayon interne R/2 et de rayon externe R, est charg´ee, avec une charge dedensit´e volumique de charge ρr. La charge totale port´ee par cette sphere est ´egale a Q. Le champ´electrostatique cr´e´e a la distance r du centre O, pour R/2 r R a pour expression →E = kαrR→u rou →u r est le vecteur unitaire radial de la base de coordonn´es sph´eriques. Le milieu est assimilable auvide.1. Exprimer →E 0.— 18/24 —

Page 19 : 2. Etablir l’expression de →E r pour 0 r R/2 a partir des ´equations locales de Maxwell. End´eduire la valeur de α.3. Etablir la loi ρr. Calculer la charge totale et d´eduire la valeur de k.4. A l’ext´erieur de la sphere, les r´esultats obtenus sont-ils compatibles avec le th´eoreme de Gauss ?Exercice 5 – Cylindre conducteurSoit un cylindre conducteur de conductivit´e σ, de longueurh consid´er´ee comme infinie, parcouru par un courant sta-tionnaire uniform´ement r´eparti, dans la direction de son axe,d’intensit´e I.1. D´eterminer le champ ´electromagn´etique en tout point de l’espace.2. En d´eduire le vecteur de Poynting en tout point de l’espace et son flux a travers la surfacecylindrique du conducteur. Commenter le r´esultat obtenu.3. V´erifier l’´equation locale de Poynting en tout point. Commenter.— 19/24 —

Page 20 : 8InductionLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Ph´enomenes d’inductionExercice 1 – Roue de BarlowUn disque conducteur de rayon a est libre de tourner autour de son axe horizontal passant par O. Uncourant constant d’intensit´e i arrive en son centre O et repart par le point A, sur la p´eriph´erie. Laroue est plac´ee dans un champ magn´etique horizontal, d’intensit´e B, uniforme et permanent.Calculer le moment Σ en O de la force de Laplace exerc´ee sur le disque conducteur.Exercice 2 – Rail de LaplaceLa barre AB, de longueur a et de masse m, de centre de masse d’abscisse xt et de vitesse →v = v→uxavec v = ˙x est lanc´ee avec une vitesse initiale v0 sur des rails m´etalliques sur lesquels elle glisse sansfrottement.Elle constitue avec les rails de r´esistance n´egligeable un circuit rectangulaire C de r´esistance Rconstante et d’inductance n´egligeable et dont la surface a l’instant t est St = axt.Ce circuit est plac´e dans un champ magn´etique permanent →B = B→uz d’origine ext´erieure a C.1/ D´eterminer la f´em induite.2/ En d´eduire l’expression du courant induit qui circule dans la barre.3/ ´Etablir l’´equation diff´erentielle de vt et en d´eduire l’expression de la solution en tenant comptedes conditions initiales.4/ Montrer que l’´energie cin´etique initiale de la barre se dissipera totalement en chaleur par effetJoule dans la r´esistance.— 20/24 —

Page 21 : Inductance mutuelleExercice 3 – Tore circulaireSur un tore engendr´e par la rotation d’un cercle de rayon asont bobin´ees N spires. On suppose que le rayon R moyen dutore est grand devant a. Sur cet enroulement P, une bobine Ccomportant n spires de rayon a est constitu´ee.Calculer le coefficient d’inductance mutuelle des deux enroule-ments P et C.A.N : N = 1600, n = 20, R = 15 cm, a = 3 cm.Exercice 4 – Inductance mutuelle de deux spiresSoient deux spires, l’une de rayon R et d’axe Oz et uneseconde spire de mˆeme axe et de rayon a R.Ces deux spires sont a une distance d l’une de l’autre.1/ Calculer M1→2.2/ En d´eduire M2→1.Circuits coupl´esExercice 5 – Plaque de cuisson a induction Le chauffage du fond m´etallique des casseroles et autres poˆeles de cuisson peut ˆetre r´ealis´e par effetJoule des courants induits directement dans le fond de la casserole par un champ magn´etique variable,les courants de Foucault.Log´e dans une table support en c´eramique, un bobinage aliment´e en courant sinuso¨ıdal, appel´einducteur, g´enere ce champ.L’inducteur a un rayon de 5 cm et compte vingt spires de cuivre de r´esistance ´electrique R1 = 18 mΩet d’auto-inductance L1 = 30 µH. Il est aliment´e par une tension harmonique v1 de pulsation ω.Du point de vue ´electromagn´etique, on mod´elise le fond de casserole par une spire circulaire unique,ferm´ee sur elle-mˆeme, appell´ee induit.L’induit a une r´esistance R2 = 8.3 mΩet une auto-inductance L2 = 0.24 µH. Le transfert d’´energie´electrique s’effectue par couplage inductif entre l’inducteur et l’induit d’inductance mutuelle M = 2 µH.1/ En s’appuyant sur un sch´ema ´electrique ´equivalent, ´etablir les ´equations ´electriques relativesaux deux circuits.— 21/24 —

Page 22 : 2/ En d´eduire l’expression litt´erale de la fonction de transfert H = I2I1.3/ En d´eduire l’imp´edance d’entr´ee Ze = V1I1du systeme.4/ La pulsation ω est choisie bien plus grande que R1/L1 et R2/L2. Simplifier les deux expressionspr´ec´edentes et calculer num´eriquement leur module.5/ On souleve la casserole. Indiquer qualitativement comment varie l’amplitude du courant appel´epar l’inducteur.Pour aller plus loinExercice 6 – Cadre de cuivre Un cadre de cuivre filiforme, de r´esistance R, de forme carr´ee de cˆot´e a, de masse m, est accroch´e aun ressort vertical de raideur k et de masse n´egligeable.Le plan du cadre est vertical et, a l’´equilibre, la moiti´e inf´erieure du cadre est situ´e dans un champmagn´etique uniforme de module B, stationnaire et perpendiculaire au cadre.1/ On abaisse le cadre d’une hauteur a/2 et on le lˆache sans vitesse initiale. ´Etablir l’´equationdiff´erentielle du mouvement du cadre rep´er´e par sa position par rapport a l’´equilibre.2/ On donne k = 0, 4 N.m1, B = 0, 1 T, g = 10 m.s1, R = 0, 5 mΩ, m = 50 g et a = 10 cm.D´eterminer la nature de la loi horaire.— 22/24 —

Page 23 : 9´Electrocin´etiqueLes exercices ou questions marqu´es d’une ´etoile sont d’un niveau sup´erieur a celui exigible auxexamens.Rappels :La masse, dans un circuit ´electrique, est la branche de r´ef´erence despotentiels ´electriques. C’est-a-dire qu’on peut mesurer une tension´electrique = diff´erence de potentiel a partir de cette partie conductrice.Voici le symbole couramment utilis´e pour la masse :La mise a la terre permet ensuite d’annuler ou au minimum de r´eduireles risques de d´echarges ´electriques dans les installations industrielles,domestiques, et autres. Son potentiel est constant et sa valeur estconventionnellement fix´ee a 0 volt.Pour saisir la diff´erence entre la masse et la terre, il faut comprendre que la connexion de massepermet l’´equipotentialit´e, c’est-a-dire la mise au mˆeme potentiel de plusieurs appareils, circuits etstructures m´etalliques, alors que la terre permet de maintenir ce potentiel a z´ero volt. La masse estdonc une n´ecessit´e technique, alors que la terre est un imp´eratif de s´ecurit´e.Association de r´esistancesExercice 1 – G´en´erateur de courantSoit le circuit suivant compos´e d’un g´en´erateur de courant I et de deux r´esistances. Quelle est lavaleur de la tension V aux bornes du g´en´erateur de courant ?Exercice 2 – R´esistance ´equivalenteSoit le r´eseau de r´esistances suivant :Calculer la valeur de la r´esistance ´equivalente not´ee RAB entre A et B.— 23/24 —

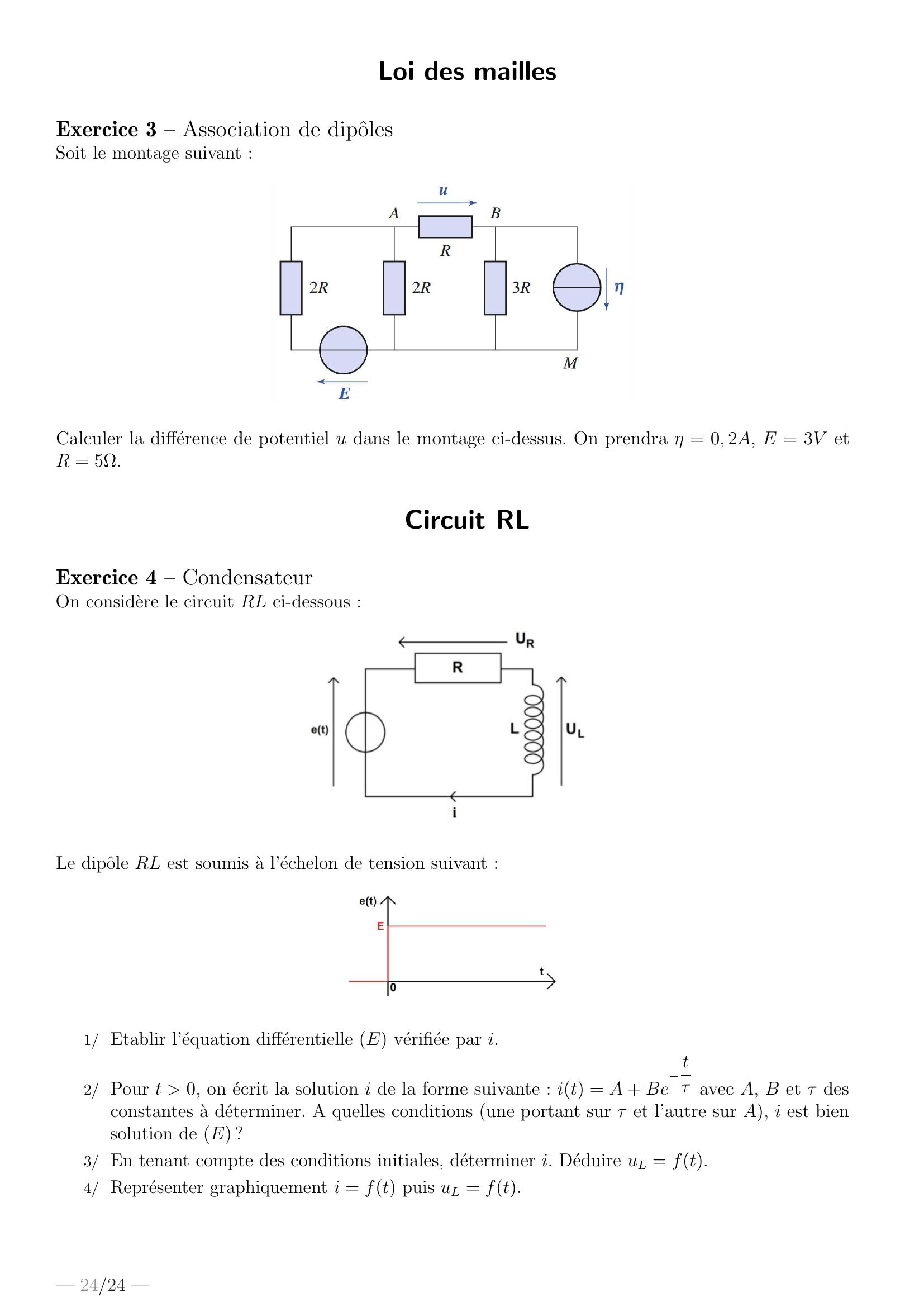
Page 24 : Loi des maillesExercice 3 – Association de dipˆolesSoit le montage suivant :Calculer la diff´erence de potentiel u dans le montage ci-dessus. On prendra η = 0, 2A, E = 3V etR = 5Ω.Circuit RLExercice 4 – CondensateurOn considere le circuit RL ci-dessous :Le dipˆole RL est soumis a l’´echelon de tension suivant :1/ Etablir l’´equation diff´erentielle E v´erifi´ee par i.2/ Pour t 0, on ´ecrit la solution i de la forme suivante : it = A + Betτ avec A, B et τ desconstantes a d´eterminer. A quelles conditions une portant sur τ et l’autre sur A, i est biensolution de E ?3/ En tenant compte des conditions initiales, d´eterminer i. D´eduire uL = ft.4/ Repr´esenter graphiquement i = ft puis uL = ft.— 24/24 —