TD

Télécharger le TD en pdf

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

Page 1 : CY Cergy Paris Universite2023 – 2024CY TechPreIng 1Travaux diriges de Panorama sur laPhysiqueCe document est disponible en ligne— 1/38 —

Page 2 : Table des matieres1. Rappels6I.Unites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6II.Prefixes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8III.Alphabet grec . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8IV.Prerequis de Mathematiques pour la physique . . . . . . . . . . . . . . . . . . . . . .92. Geometrie11I.Proprietes geometriques usuelles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11II.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123. Analyse dimensionnelle13I.Analyse dimensionnelle et unites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .13II.Trouver les exposants d’une formule . . . . . . . . . . . . . . . . . . . . . . . . . . . .13III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .144. La lumiere16I.Generalites. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16II.Effet photoelectrique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16III.Indice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16IV.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .175. Optique geometrique18I.Dioptres plans et spheriques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18II.Lentilles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .19III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .196. Rappel : reperage et cinematique21I.Nature et reperage de l’espace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21II.Cinematique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .227. Reperage et Vecteurs25I.Reperage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25II.Addition de vecteurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25III.Produit scalaire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .26IV.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .268. Cinematique28I.Definition des vitesses et acceleration . . . . . . . . . . . . . . . . . . . . . . . . . . .28II.Trajectoire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .29III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .30IV.Annexe : Derivees des fonctions scalaires . . . . . . . . . . . . . . . . . . . . . . . . .319. Lois de Newton32I.Trajectoires paraboliques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32II.Bilan de forces. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .33III.Lois de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34— 2/38 —

Page 3 : IV.Deuxieme loi de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3410.Lois de Newton suite36I.Divers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36II.Frottements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36III.Pour aller plus loin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37— 3/38 —

Page 4 : Plan du coursIntroductionLes grands domaines de la physiqueLes differentes echellesLes differentes « ecoles de pensees »Introduction a la « pensee scientifique »La methode scientifiqueDimensions, unites, analyse dimensionnelleOptique : l’etude de la lumiereLes modeles decrivant la lumiereOptique geometriqueCinematique : la description du mouvementReperage dans l’espace et le tempsRappels et + : Calcul vectoriel, DeriveeLes grandeurs cinematiquesMecaniqueLes 3 lois de NewtonLes differentes forcesTravail et energie— 4/38 —

Page 5 : Contact— Enseignant charge du cours magistral : Emilie Dupont— Bureau : Bˆatiment Cauchy Etage 3 CY 308— E-mail : emilie.dupont@cyu.frL’equipe pedagogiqueCours Magistral CM : Emilie Dupont Cergy ; et Lucie Desplat PauTravaux diriges TD :Panayotis Akridas Cergypanayotis.akridas-morel@cyu.frAbdelaziz Boumiz Cergyabdelaziz.boumiz@cyu.frLucie Desplat Paulucie.desplat@cyu.frEmilie Dupont Cergyemilie.dupont@cyu.frFabien Piguet Cergyfabien.piguet@cyu.frQuelques referencesListe non exhaustive de livres recommandes pour ce cours.— « Le Cours de physique de Feynman » titre original : Feynman Lectures on Physics de RichardFeynman, Robert B. Leighton en et Matthew Sands en, volume I— Jean-Marie Brebec : « H-prepa Optique-1re Annee MPSI-PCSI-PTSI », Collectif Hachette— Lucien Quaranta : « Optique », ELSEVIER-MASSON— P. Brenders, M. Sauzeix : « precis d’Optique physique MP PC PSI PT », Breal— Halliday, Resnick, Walker : « Physique 1. Mecanique », Dunod— Hecht : « Physique 1 : Mecanique », de Boeck— Alonso, Finn : « Physique generale 1 », InterEditions— Giancoli : « Physique generale 1 », De Boeck Universite— Seguin : « Physique : Mecanique », de Boeck— Gie, Sarmant : « Mecanique 1ere Annee », Tec et Doc— Jose-Philippe Perez : « Mecanique : Fondements et applications », Masson— Jean Marc Levy-Leblonc : « La physique en question : mecanique », Vuibert— Luc Valentin : « L’univers mecanique », Hermann— Bernard Salamito et al. : « Physique PCSI - Tout-en-un - 5e edition », Dunod— Jerˆome Majou : « Super manuel de physique », MPSI, PCSI, PTSI, BrealConsultez le site du cours sur la plateforme.Allez voir aussi les sites http://cpinettes.u-cergy.fr/S1-Meca et https://etienneklein.fr/.Regarder la chaˆıne youtube sciences etonnantes... Il y a beaucoup de ressources en ligne, apprenez achoisir les bonnes et bien sˆur gare aux fakesciences— 5/38 —

Page 6 : 1RappelsUnitesLe Systeme International SIEn 1960, lors de la onzieme Conference generale des poids et mesures CGPM, apparaˆıt le SystemeInternational d’unites, le SI, qui comprend aujourd’hui deux classes d’unites : les unites de base, aunombre de sept et les unites derivees.En 2018, lors de la 26eme CGPM, a eu lieu une redefinition de quatre des sept unites de base, cettereforme est entree en vigueur le 20 mai 2019. Cet evenement marque un tournant important pour laphysique, puisque les etalons materiels sont maintenant remplaces par la donnee de sept constantesphysiques. Ce procede avait commence des 1983, en fixant la valeur de c, la vitesse de la lumiere,c’est au tour de h, la constante de Planck, de e, la charge electrique de l’electron, de k, la constantede Boltzman, et de NA , la constante d’Avogadro, d’ˆetre desormais gravees dans les tables du SI,sans oublier νCs la frequence de la transition hyperfine de l’atome de cesium 133 et Kcd l’efficacitelumineuse d’un rayonnement monochromatique.Cette methode est tres elegante, mais elle comporte un risque...reflechissez y ! Et n’hesitez pas a lirepar exemple :https://lejournal.cnrs.fr/articles/ces-constantes-qui-donnent-la-mesureLes unites de baseI.1. Le metre mLe metre est la longueur du trajet parcouru dans le vide par la lumiere pendant une duree de1/299792458 de seconde.I.2. Le kilogramme kgAvant octobre 2018 : le kilogramme est la masse du prototype en platine iridie qui a ete sanctionnepar la Conference generale des poids et mesures tenue a Paris en 1889 et qui est depose au BureauInternational des Poids et Mesures.Apres le 20 mai 2019 : le kilogramme, unite de masse du SI, est defini en prenant la valeur numeriquefixee de la constante de Planck, h, egale a 6, 62607015 × 1034 lorsqu’elle est exprimee en J·s, uniteegale a kg·m2·s1, le metre et la seconde etant definis en fonction de c et de νCs.Pour mesurer la constante de Planck h, les chercheurs ont utilise une balance du watt ou de Kibblede quoi produire une valeur de h avec une incertitude relative de 5, 7.108 conforme aux prescriptionsdu CIPM Comite international des poids et mesures .I.3. La seconde sLa seconde est la duree de 9192631770 periodes de la radiation correspondant a la transition entre lesdeux niveaux hyperfins de l’etat fondamental de l’atome de cesium 133, νCs.— 6/38 —

Page 7 : I.4. L’ampere AAvant octobre 2018 : l’ampere est l’intensite d’un courant electrique constant qui, maintenu dans deuxconducteurs paralleles, rectilignes, de longueur infinie, de section circulaire negligeable et places a unedistance de un metre l’un de l’autre dans le vide, produirait entre ces conducteurs une force de 2.107newton par metre de longueur.Apres le 20 mai 2019 : l’ampere, unite de courant electrique du SI, est defini en prenant la valeurnumerique fixee de la charge elementaire, e, egale a 1, 602176634 × 1019 lorsqu’elle est exprimee enC, unite egale a A·s.I.5. Le kelvin KAvant octobre 2018 : le kelvin est la fraction 1/273,16 de la temperature thermodynamique du pointtriple de l’eau.Apres le 20 mai 2019 : le kelvin, unite de temperature thermodynamique du SI, est defini en prenantla valeur numerique fixee de la constante de Boltzmann, k, egale a 1, 380649 × 1023 lorsqu’elle estexprimee en J·K1, unite egale a kg·m2·s2·K1.I.6. La candela cdAvant octobre 2018 : le candela est l’intensite lumineuse, dans une direction donnee, d’une source quiemet un rayonnement monochromatique de frequence 540, 1012 hertz et dont l’intensite energetiquedans cette direction est 1/683 watt par steradian.Apres le 20 mai 2019 : le candela est l’unite du SI d’intensite lumineuse dans une direction donnee.Elle est definie en prenant la valeur numerique fixee de l’efficacite lumineuse d’un rayonnementmonochromatique de frequence 5401012 Hz, Kcd , egale a 683 lorsqu’elle est exprimee en lm·W1,unite egale a cd·sr·W1, ou cd·sr·kg1·m2·s3 , le kilogramme, le metre et la seconde etant definis enfonction de h, c et νCs.I.7. La mole molAvant octobre 2018 : la mole est la quantite de matiere d’un systeme contenant autant d’entiteselementaires qu’il y a d’atomes dans 0, 012 kilogramme de carbone 12.Apres le 20 mai 2019 : la mole est la quantite de matiere d’un systeme contenant NA = 6, 022140761023entites elementaires atomes, ions, molecules, etc. . ., NA etant la constante d’Avogadro.Ces donnees viennent des sites web suivants :— http://www.metrologie-francaise.fr/fr/si/unites-mesure.asp ,— https://www.bipm.org/fr/worldwide-metrology/metre-convention/.N’hesitez pas a les consulter, vous y trouverez bien d’autres informations, et de jolies histoires. . . Carcomme c’est explique sur ce site : “...il ne faudrait pas croire que ce systeme, une fois etabli, reste fige.Les progres de la science et des technologies, les nouveaux besoins de la societe, et par consequence lesnouveaux besoins en terme d’exactitude accrue, amenent le LNE et l’ensemble des instituts nationauxde metrologie a ameliorer, de fa¸con constante et continue, la realisation pratique de l’ensemble desunites du SI. Cette preoccupation concerne aussi bien les references que les moyens de transfert versles utilisateurs, pour permettre de repondre au mieux a ces nouveaux besoins. Il est donc parfoisnecessaire de faire evoluer les definitions des unites ou d’en introduire de nouvelles.”Pour regarder une video sur la redefinition du kilogramme :https://www.youtube.com/watch?v=pBUdM30qmgM&feature=youtu.be— 7/38 —

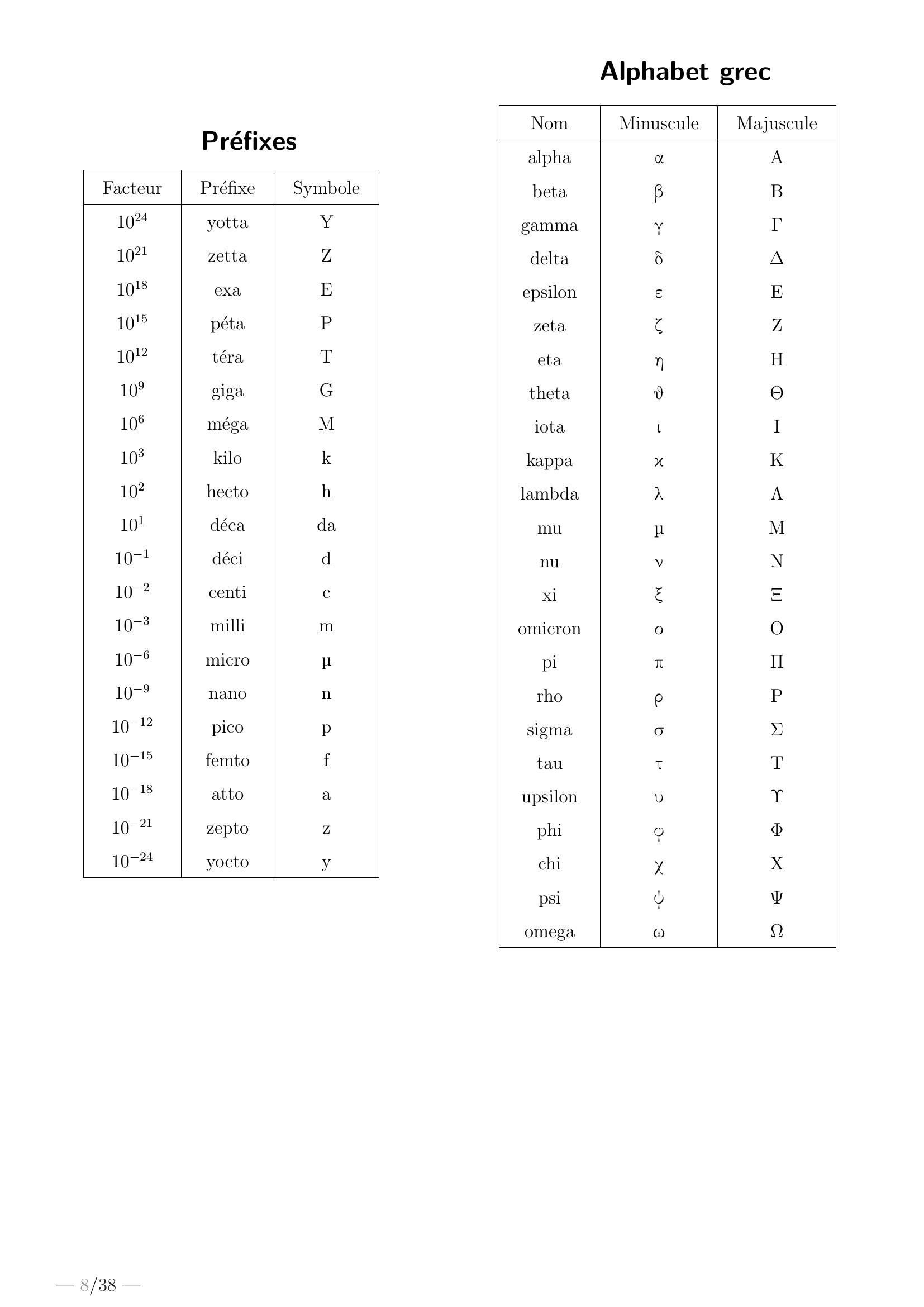
Page 8 : PrefixesFacteurPrefixeSymbole1024yottaY1021zettaZ1018exaE1015petaP1012teraT109gigaG106megaM103kilok102hectoh101decada101decid102centic103millim106microµ109nanon1012picop1015femtof1018attoa1021zeptoz1024yoctoyAlphabet grecNomMinusculeMajusculealphaαΑbetaβΒgammaγΓdeltaδΔepsilonεΕzetaζΖetaηΗthetaθΘiotaιΙkappaκΚlambdaλΛmuµΜnuνΝxiξΞomicronοΟpiπΠrhoρΡsigmaσΣtauτΤupsilonυΥphiφΦchiχΧpsiψΨomegaωΩ— 8/38 —

Page 9 : Prerequis de Mathematiques pour la physiqueExercice 1 – Definition d’un angleθRLθUn arc de cercle de rayon R = 2m a pour longueur L = 4m. Quelle est la valeur de l’angle θ ? Plusieursreponses possibles.1/ 2 rd2/ 360/π o3/ 0, 5 rd4/ 8 rd5/ π/90 o6/ 180π o7/ Il n’y aucune reponse juste.Exercice 2 – Lecture sur le cercle trigonometriqueθ1adbcθRelier correctement le nom du segment a sa valeur :1/ a1 sin θ2/ b2 cotan θ3/ c3 cos θ4/ d4 tan θExercice 3 – les angles dans un triangleβπα/6— 9/38 —

Page 10 : 1/ Determiner l’angle α en radian et en degre.2/ Determiner l’angle β en radian et en degre.Exercice 4 – Theoreme de Thalesx41,86Sachant que les deux segments en gras sont paralleles que vaut x :1/ 2, 72/ 23/ 34/ 3, 85/ On ne peut pas conclure.Exercice 5 – Formules d’addition des cosinus et sinusRelier correctement :1/ cosa + b1 cos a cos b + sin a sin b2/ sina + b2 cos a cos b sin a sin b3/ cosa b3 sin a cos b + cos a sin b4/ sina b4 sin a cos b cos a sin bExercice 6 – Derivee des cosinus et sinus en 0Relier correctement :1/ cos′ 01 π/22/ sin′ 02 03 14 1— 10/38 —

Page 11 : 2GeometrieProprietes geometriques usuellesExercice 1 – Somme des angles dans un triangleOn considere le triangle ABC et on appelle α, β et γ ses trois angles internes. On trace la parallelea la droite AB passant par C.1/ Determiner les deux angles notes « ? » sur la figure.2/ En deduire la valeur de la somme des trois anglesinternes d’un triangle.αβγ??ACBExercice 2 – Triangle inscrit dans un cercleOn considere C un point quelconque sur le cercle de centre O et de diametre AB. On appelle αl’angle interne en A au triangle ABC, et β celui en B.1/ Determiner les deux angles notes « ? » sur la figure.2/ En deduire la valeur de l’angle interne en C au triangle ABC.3/ Trouver les valeurs des deux derniers angles des triangles AOCet OBC.ABCα ?β?OExercice 3 – Theoreme de PythagoreSoit un triangle rectangle dont l’hypotenuse est de longueur 1dans l’unite de mesure choisie.On appelle a et b les longueurs de ses deux autres cˆotes a pour le plus petit.ab11/ On dilate ce triangle d’un facteur h. On a ainsi obtenu un triangle semblable au precedent.Rappeler ce que cela signifie, qu’ont en commun les deux triangles ? Quelles sont les longueursdes trois cˆotes du triangle dilate a exprimer en terme de h, a et b ?2/ On trace la hauteur de l’angle droit vers l’hypotenuse.Montrer que les deux petits triangles interieurs sont semblables autriangle initial.En deduire les longueurs de tous les cˆotes de ces deux petits triangles.a exprimer en terme de h, a et bh3/ On trace la hauteur de l’angle droit vers l’hypotenuse.Montrer que les deux petits triangles interieurs sont semblables autriangle initial. En deduire les longueurs de tous les cˆotesde ces deux petits triangles.a exprimer en terme de h, a et b.h4/ En deduire le theoreme de Pythagore.5/ On appelle α et β les angles du premier triangle rectangle considere.Quel lien existe-t-il entre les angles α et β ?Exprimer les longueurs a et b en fonction de α, puis de β.Quelle formule de trigonometrie peut-on deduire directement de laquestion c ?On suppose que l’angle α devient tres petit, vers quoi tendent l’angle β et les longueurs a et b ?ab1αβ— 11/38 —

Page 12 : Pour aller plus loinExercice 4 – Triangle equilateralSoit A1A2A3 un triangle equilateral de centre O et de cˆote a.1/ Calculer d la distance du centre a l’un des sommets.2/ Calculer α l’angle interne du triangle en l’un des sommets.Exercice 5 – « Je vois le sinus de l’angle double »A, B, C et A, B, D sont deux triangles semblables, ils sont tout deux rectangles en B et leurhypotenuse est de longueur 1.CH en pointilles sur la figure est une hauteur du triangle ADC.α1αACHBD1/ Que vaut l’angle en C entre la hauteur et le cˆote CD ?2/ Calculer la longueur CH de deux fa¸con differente et en deduirela formule du sinus de l’angle double.— 12/38 —

Page 13 : 3Analyse dimensionnelleLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Analyse dimensionnelle et unitesExercice 1 – Dimension et unite de grandeur1/ La force magnetique →F exercee sur un porteur de charge electrique q en mouvement a la vitesse→v dans un champ magnetique →B est donnee par la relation de Lorentz : →F = q→v →B estun produit vectoriel et α est l’angle forme par les vecteurs →v et →B .Exprimer la dimension de la grandeur B.2/ L’expression du champ magnetique a l’interieur d’un long soleno¨ıde est B = µ0Nl I ou µ0permeabilite du vide, N nombre de spires, l longueur du soleno¨ıde, I intensite du courant.En deduire la dimension et l’unite S.I. de µ0.3/ Determiner la dimension et l’unite S.I. de la constante de Planck h sachant qu’a toute ondeelectromagnetique de frequence ν, on associe des photons d’energie E = hν.Exercice 2 – Obtention d’une formule1/ On lance, verticalement, vers le haut et depuis le sol, un objet de masse m avec une vitesseinitiale v0. On veut trouver par une analyse dimensionnelle une expression de la hauteur hau-dessus du sol que l’objet atteindra on negligera tout frottement.Quelles sont les grandeurs pertinentes du probleme ? En deduire une expression pour la hauteurh a l’aide d’une analyse dimensionnelle.2/ On lˆache sans vitesse initiale un objet de masse m d’une hauteur h au-dessus du sol. On veuttrouver par une analyse dimensionnelle une expression de sa vitesse finale vf en negligeant toutfrottement.Quelles sont les grandeurs pertinentes du probleme ? En deduire une expression pour la vitessevf a l’aide d’une analyse dimensionnelle.Trouver les exposants d’une formuleExercice 3 – Poussee d’ArchimedeTrouver a l’aide d’une analyse dimensionnelle, la formule donnant la poussee d’Archimede, sachantque cette force est fonction du volume du corps immerge V , de la masse volumique ρ du fluide et del’acceleration de la pesanteur g.Aide : on cherchera les valeurs des exposants α, β et γ satisfaisant l’equation PA = C V α ρβ gγ, Cetant une constante numerique sans dimension.1/ Donner les dimensions des parametres du probleme.— 13/38 —

Page 14 : 2/ Quelles sont les valeurs des exposants α, β et γ.Exercice 4 – Corde de guitareOn considere une corde de guitare tendue. La corde est homogene, de masse m et de longueur l ; onmesure sa tension T. On pince la corde et l’elongation se propage le long de la corde a la vitesse v.1/ Quelles sont les grandeurs pertinentes du probleme.2/ Deduire, a l’aide d’une analyse dimensionnelle, une expression pour la vitesse v en fonction desgrandeurs pertinentes du probleme.Exercice 5 – Pendule simpleUn pendule simple est un fil sans masse de longueur l au bout duquel est attachee une masse m. Apriori, la periode des oscillations d’un tel pendule notee T peut dependre de g, l, m et θmax, l’anglede deviation maximale par rapport a la verticale.1/ Montrer par analyse dimensionnelle que T ne peut pas dependre de m et trouver sa dependanceen fonction de l et g.2/ Pourquoi ne vous demande-t-on pas la dependance en fonction de θmax ?Remarque : Galilee est le premier a s’ˆetre rendu compte experimentalement que la periode nedepend que tres faiblement de θmax quand cet angle est petit.Exercice 6 – Trajectoires possiblesUne bille de masse m est lancee au bas d’une piste cylindrique de rayon R avec une vitesse initialev0. Si v0 est faible la bille oscillera autour de sa position initiale tout en bas de la piste. Pour v0tres grande la bille fera une rotation complete. Enfin pour une valeur intermediaire de la vitesse, elledecollera de la piste.1/ Donner les dimensions de chacun des parametres du probleme m, R . . . .2/ Trouver a l’aide d’une analyse dimensionnelle a quelle grandeur doit ˆetre comparee v0 pourparler de « faible » ou « grande » vitesse l’acceleration de la pesanteur g est bien sur connue.Pour aller plus loinExercice 7 – Analyse dimensionnelle d’une explosionOn raconte que c’est grˆace a une simple analyse dimensionnelle que Geoffrey Ingram Taylor a puestimer l’energie E degagee par l’explosion d’une bombe atomique, alors que cette information etaitencore classee secret-defense. Un film de l’explosion avait en effet ete rendu public, permettant deconnaˆıtre la taille r du champignon atomique apres un temps t suivant l’explosion de la bombe.1/ Justifier par un argument de dimension, qu’une relation entre E, r et t met necessairement enjeu une autre grandeur dimensionnee.On comprend d’ailleurs facilement qu’une caracteristique du milieu dans lequel l’explosion alieu intervient ; on choisi la masse volumique de l’air ρ.2/ En utilisant une analyse dimensionnelle, trouver une expression de r en fonction de t, faisantintervenir E et ρ et une constante sans dimension.Exercice 8 – L’effet CasimirComme on peut le lire sur Wikipedia : « L’effet Casimir, tel que predit par le physicien neerlandaisHendrik Casimir en 1948, est une force attractive entre deux plaques paralleles conductrices et nonchargees. Cet effet, dˆu aux fluctuations quantiques du vide . . . »Precisons-le bien, la force dont il est ici question se manifeste alors que les plaques conductrices sontdans le vide.— 14/38 —

Page 15 : Le phenomene etant fondamentalement d’origine quantique, nous supposerons que cette force dependde la constante de Planck h celle permettant de connaˆıtre l’energie d’un photon de frequence ν :E = h ν.Le caractere conducteur des plaques indique que des proprietes electromagnetiques sont en jeu, etnous supposerons donc aussi que cette force depend de c, la vitesse de la lumiere.1/ Donner les dimensions de chacun des parametres du probleme h, ν, c . . . .2/ En utilisant une analyse dimensionnelle, trouver une expression de la force par unite de surfaces’exer¸cant entre ces plaques en fonction de h, c et a, la distance separant les plaques.Exercice 9 – Masse d’un trou noir A partir des lois de Newton, il est possible de retrouver la troisieme loi de Kepler donnant la periodede rotation T d’une planete situee a une distance R du soleil de masse MS :T =s4π2R3GMS.1/ Montrer que le terme a droite de l’egalite est bien homogene a un temps.2/ A partir de vos connaissances et de la troisieme loi de Kepler, donner un ordre de grandeur dela masse du Soleil.3/ A partir de la figure ci-dessous, donner un ordre de grandeur de la masse de ce trou noir situeau centre de notre galaxie.Trajectoire d’une etoile entre janvier 1992 et juillet 2006.Exercice 10 – Rayon de Schwarzschild La vitesse de liberation d’un corps est la vitesse minimale a communiquer a ce corps pour echapper al’attraction gravitationnelle d’un astre de masse M. A partir de la conservation de l’energie, on peutmontrer que la vitesse de liberation v verifie l’equation :12mv2 GmMR= 0,3.1ou m est la masse du corps dont on cherche la vitesse et R est le rayon de l’astre en question.1/ Sur Terrea Exprimer v en fonction des donnees du probleme.b Calculer la vitesse de liberation d’une fusee sur Terre.2/ Un trou noir est caracterise par son rayon de Schwarzschild RS : la distance en-dessous delaquelle mˆeme la lumiere ne peut s’echapper du trou noir. Calculer puis donner la valeur durayon de Schwarzschild du trou noir precedemment etudie.— 15/38 —

Page 16 : 4La lumiereLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.On donne :-la valeur de la vitesse de la lumiere dans le vide c = 299 792 458 m/s 3 108m/s.-les longueurs d’onde dans le vide des rayonnements visibles : rouge 620-700 nm, orange 580-620nm, jaune 575-580 nm, vert 500-575 nm, bleu 450-500 nm et violet 400-450 nm.-la valeur approchee de la constante de Planck h = 6,626 070 15 1034J s.GeneralitesExercice 1 – Experience de FresnelOn place un disque opaque derriere un petit trou a travers lequel emerge de la lumiere. On observesur un ecran l’ombre ainsi creee par ce disque. Qu’observe-t-on au centre de cette ombre ? Expliquer.Exercice 2 –La puissance par unite de surface de la lumiere solaire, a la surface terrestre, vaut environ 1400 W/m2.En admettant que l’energie moyenne des photons solaires correspond a la couleur orange, calculer lenombre de photons frappant une surface de 1 cm2 a chaque seconde.Effet photoelectriqueExercice 3 – Travail d’extractionLa longueur d’onde maximale pour observer l’effet photoelectrique en eclairant du potassium est deλ1 = 564 nm.1/ Calculer le travail d’extraction ϕ energie minimale pour extraire un electron.2/ Si la longueur d’onde de la lumiere utilisee est de λ2 = 400 nm, determiner l’energie cinetiquemaximale des electrons extraits.Exercice 4 –Sachant que le travail d’extraction du zinc vaut ϕ = 4,33 eV, peut-on observer l’effet photoelectriqueavec de la lumiere visible ? On donne 1 eV = 1,6 1019 J.IndiceExercice 5 –Quel est la difference de temps de propagation de la lumiere dans le vide et dans une fibre optique delongueur 1000 km et d’indice n = 1,62 ?— 16/38 —

Page 17 : Exercice 6 – Dioptre planUn rayon lumineux de longueur d’onde dans le vide λ = 589 nm passe de l’atmosphere a une cuved’eau. La vitesse de propagation de la lumiere dans l’eau est de 2,25 108m/s.1/ Quel est l’indice optique n associe a ce rayon lumineux dans l’eau ?2/ Quelle est la frequence de ce rayon lumineux ? Depend-elle du milieu ?3/ Quelle est la longueur d’onde de ce rayon dans l’eau ?4/ Quelle couleur voit un observateur si ce rayon lumineux lui parvient dans l’air ? Mˆeme questions’il lui parvient dans l’eau ?Exercice 7 – Dioptre planOn considere un rayon lumineux traversant le plan separant deux milieux homogenes 1 et 2 d’indicesde refraction respectifs n1 = 1,5 et n2 = 1.1/ Donner un exemple de milieux ayant ces indices.2/ On suppose que le rayon incident arrive sur le plan depuis le milieu 1 sous un angle d’incidenceα1 = π/6. Calculer l’angle α2 sous lequel il est refracte dans le milieu 2. Tracer les rayonsincidents et refractes.3/ Reprendre la question precedente pour un angle d’incidence β1 = π/3.4/ Reprendre les questions precedentes si l’on suppose maintenant que le rayon incident arrive surle plan depuis le milieu 2.Pour aller plus loinExercice 8 – Stigmatisme On considere le dioptre plan d’un milieu plus refringent verre d’indice n = 1,5 a un milieu moinsrefringent air d’indice n = 1.On considere trois rayons issus d’un point objet A reel : le rayon AH normal au dioptre, le rayon AItombant sous une incidence de 10o sur le dioptre et le rayon AJ tombant sous une incidence de 40osur le dioptre. Les droites support des trois rayons emergents se coupent-elles en un mˆeme point ?Commenter le resultat.Exercice 9 – Truite Une truite nage dans la riviere a la profondeur h.1/ Comment la surface de l’eau lui apparaˆıt-elle : lumineuse, sombre, les deux ?2/ A quelle condition peut-elle apercevoir un pˆecheur qui se tient sur la rive de cette riviere ? Onprendra l’indice n de l’eau egal a 1,33.Exercice 10 – Un pˆecheur situe sur le bord d’une riviere regarde un poisson nageant entre deux eaux parallelementa la surface de l’eau. La surface de l’eau sera assimilee a un dioptre plan.Le pˆecheur voit-il le poisson plus haut, dans sa position reelle ou plus bas ? Justifier votre reponse al’aide d’un schema.— 17/38 —

Page 18 : 5Optique geometriqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Dioptres plans et spheriquesExercice 1 – Lois de DescartesDeux milieux transparents homogenes et isotropes mthi d’indices respectifs n1 et n2 sont separes parun dioptre plan. On appelle A un point dans le milieu 1, B un point dans le milieu 2 et I un pointsur le dioptre.1/ Exprimer le chemin optique L de A a B passant par I.2/ A et B etant donnes, montrer que L est extremal lorsque I est tel que la loi de la refractionest verifiee.3/ Sur quel principe d’optique s’appuie-t-on pour affirmer que L est extremal ?4/ Etablir de la mˆeme fa¸con la loi de la reflexion.Exercice 2 – Espace objet et espace imageConstruire quelques rayons lumineux traversant un systeme optique centre avec1/ un objet a l’infini dans la direction α et un point image virtuel,2/ un objet a l’infini dans la direction α et une image a l’infini dans la direction β,3/ un point objet virtuel et une image a l’infini dans la direction de l’axe optique.Exercice 3 – Stigmatisme1/ Montrer que le miroir plan est stigmatique pour tous les points de l’espace.2/ Le point image d’un point objet reel est-il reel ou virtuel ?3/ L’image d’un objet etendu lui est-elle superposable ?Exercice 4 –Une personne de hauteur h, dont les yeux se trouvent a une distance d au dessous du sommet ducrˆane, desire se voir entierement dans un miroir plan.1/ Faire un schema avec les rayons necessaires.2/ Quelle est la taille minimale du miroir dans le sens de la hauteur ?3/ Comment la personne doit-elle poser son miroir ? A quelle distance doit-elle le placer ?Exercice 5 –Un catadioptre est constitue de trois miroirs plans perpendiculaires deux a deux plans Oxy , Oyzet Ozx , par exemple.Determiner les directions des rayons reflechis successifs et caracteriser la direction du rayon emergentdu catadioptre rayon qui a donc subi au plus trois reflexions.— 18/38 —

Page 19 : 1/ Si le rayon incident arrive sur le miroir Oxy parallellement a la direction Oz.2/ Si le rayon incident arrive sur le miroir Oxy parallellement au plan Ozx.3/ Si le rayon incident arrive sur le miroir Oxy sous une incidence quelconque.4/ Quel vous semble pouvoir ˆetre l’interˆet d’un tel dispositif ?LentillesExercice 6 – Lentilles mincesOn considere des lentilles minces utilisees dans les conditions de Gauss pour construire des images.1/ Pour une lentille convergente lorsque l’objet est i reel, ii virtuel, les images obtenues sont-ellesreelles ou virtuelles ?2/ En deduire les conditions dans lesquelles une lentille convergente donne une image i plusgrande que l’objet, ii virtuelle, iii non renversee, iv de grandissement +1 ou -1.3/ Reprendre les mˆemes questions pour une lentille divergente.Exercice 7 – Deux lentilles convergentesSoit un systeme forme de deux lentilles minces convergentes L1 et L2 respectivement de foyers objetsF1 et F2, de foyers images F ′1 et F ′2, de focales f ′1 = 5 cm et f ′2 = 10 cm, et de centres O1 et O2. Ellessont disposees de fa¸con a former un systeme afocal les rayons venant de l’infini repartent a l’infini.1/ Faire un schema du dispositif.2/ On veut former une image reelle A′B′ d’un objet reel de hauteur 1 cm. On place l’objet ABtel que O1A = 6cm et AB orthogonal a l’axe optique. Construire l’image A’B’ justifierl’utilisation des conditions de Gauss. Cette image est-elle reelle ?3/ Tracez un faisceau de rayons issu de B a travers ce systeme optique.4/ Calculer le grandissement transversal de ce systeme optique pourquoi peut-on definir ungrandissement pour ce systeme optique ?.Pour aller plus loinExercice 8 – Lentille epaisse On considere une lentille d’epaisseur e, elle est constituee d’un mthi d’indice n ayant la forme d’uneboule de rayon R tronquee pour avoir une face plane. On l’utilise dans l’air.1/ Partie A Un rayon lumineux arrive de l’infini parallelement a l’axe optique, il a un angled’incidence α au point I sur le dioptre spherique, il traverse la lentille comme indique sur lafigure :a Donner les trois relations permettant de determiner les angles β, γ et δ a partir des donnees.b Obtenir dans cet ordre a partir des donnees les distances suivantes : hi, Li, HJ, HI, hfet Lf.c Simplifier les resultats obtenus aux questions precedentes si l’on suppose α 1. Quepeut-on dire du point F ′ dans ces conditions ?d Simplifier les resultats obtenus aux questions 1/ et 2/ si l’on suppose maintenant α = π/3et n =3. Conclure sur le stigmatisme.— 19/38 —

Page 20 : hfihLiLfβ γδαReIJHF’2/ Partie B Un autre rayon lumineux arrive de l’infini parallelement a l’axe optique, en sensinverse. Il est a une hauteur h au dessus de l’axe optique, il traverse la lentille comme indiquesur la figure :ehRabLa A quelle condition sur les donnees y a-t-il en effet un rayon qui sort a gauche de la lentille ?b On suppose h R, calculer L. Comparer avec Lf question Ac quand e devient petitdevant R.Exercice 9 – Miroir spherique concave Un œil se regarde dans un miroir spherique concave le milieu de œil se situe sur l’axe optique dumiroir. Place a 24 cm du miroir, il se voit a l’endroit, agrandi d’un facteur 3.1/ Faire un schema en representant l’œil par deux points A et B convenablement choisis.2/ L’image A′B′ de l’œil par le miroir est-elle reelle ou virtuelle ?3/ Determiner les positions des foyers objet F et image F ′ du miroir.4/ Calculer le rayon de la calotte spherique reflechissante le miroir.5/ Comment varie le grandissement transversal lorsque l’œil s’approche du miroir ?6/ Que voit-on si l’œil est a 36 cm du miroir ? stigmatisme, agrandissement et orientation del’image— 20/38 —

Page 21 : 6Rappel : reperage et cinematiqueLa mecanique est l’etude du mouvement des corps, elle comporte une partie descriptive la cinematiqueet une partie d’analyse des causes et des lois la dynamique.Avant d’aborder les questions du mouvement, nous devons preciser la nature de l’espace physiquedans lequel il a lieu.Nature et reperage de l’espaceDans une assez bonne approximation, pour les phenomenes ayant lieu a notre echelle, l’espace physiquepeut ˆetre identifie a un espace plat de dimension trois.Un point M de l’espace peut donc ˆetre repere par trois nombres reels x1, x2, x3, appeles lescoordonnees du point M.Le nombre des systemes de coordonnees possibles est infini et le choix d’utiliser l’un plutˆot que l’autren’a pour objet que la simplification technique du probleme.Si le mouvement etudie est plan, deux coordonnees sont alors suffisantes pour reperer un point, et lessystemes usuels de coordonnees sont alors les systemes cartesien et polaire :MOxyMOxyrθxysystème cartésien: x, yθsystème polaire: r, Remarque On peut bien entendu relier les coordonnees cartesiennes et polaires d’un point M par :x = r cos θ et y = r sin θUn point M peut aussi ˆetre repere, a partir de l’origine O, par son vecteur position, encore appelerayon vecteur : →r = →OM.Ce vecteur peut lui-mˆeme ˆetre defini par trois autres nombres reels : ses composantes X1, X2, X3dans une base →e1, →e2, →e3 :→r = X1 →e1 + X2 →e2 + X3 →e3.A un systeme de coordonnees, x1, x2, x3, on peut associer en chaque point de l’espace, decoordonnees x1, x2, x3, une base normee →u1, →u2, →u3, dite base canonique associee, de la fa¸consuivante :La direction et le sens de →u1 sont obtenus en fixant les valeurs de x2 et x3 et en faisant croˆıtre x1.En rajoutant que →u1 est unitaire →u1 = 1 on le determine tout a fait. On procede de mˆeme pourconstruire →u2 et →u3.Pour les systemes de coordonnees du plan que nous avons presentes, nous trouvons :— 21/38 —

Page 22 : MOxyMOxyrθsystème polairexysystème cartésienuuuuyxrθPour ces deux systemes usuels la base associee est orthonormee, ce qui simplifie les calculs.On note qu’en general la base associee n’est pas uniforme : les vecteurs sont differents pour differentschoix du point M. Seuls les systemes cartesiens ont une base uniforme.La table suivante donne pour trois systemes de coordonnees usuels les coordonnees d’un point M etles composantes du rayon vecteur sur la base associee :systeme de coordonneescoordonnees de Mrayon vecteur →r = →OMcartesien de dimension 3x, y, z→r x, y, z = x →ux + y →uy + z →uzcartesien de dimension 2x, y→r x, y = x →ux + y →uypolairer, θ→r r, θ = r →urCinematiqueToute description du mouvement necessite au prealable d’avoir decide de ce qui ne bouge pas ! Lemouvement est en effet une grandeur relative par essence. Il faut donc choisir un corps solide dereference, le referentiel , pour reperer tous les mouvements.A ce corps solide de reference, on associe alors a chaque instant un espace du type decrit precedemmentet l’on peut ainsi decrire la position de tous les points materiels.La trajectoire d’un point materiel M est la courbe de l’espace physique decrite par M au cours dutemps.L’equation horaire du point materiel M est la donnee de sa position en fonction du temps Mt.La grandeur rendant compte du mouvement est la vitesse , c’est a dire la mesure de la variation de laposition au cours du temps.On definit ainsi :-la vitesse moyenne du point materiel M entre les instants t1 et t2 :→Mt1Mt2t2 t1=→r t2 →r t1t2 t1.-et la vitesse instantanee au temps t : →v t = ˙→r t = d→rdt = limt→0→r t + t →r tt.Pour decrire le mouvement, on definit aussi l’acceleration : mesure de variation de vitesse au coursdu temps.L’acceleration moyenne entre les instants t1 et t2 est donc :→v t2 →v t1t2 t1.— 22/38 —

Page 23 : la vitesse moyenne tend vers la vitesseinstantanée lorsque t diminue vers 0OxxtytyvtrtMtθtttt12Figure 6.1. exemple de trajectoire plane d’un point materiel ML’acceleration instantanee au temps t etant : →γ t = ˙→v t = d→vdt = limt→0→v t + t →v tt.Si l’on a choisi de decrire la position du point materiel M a chaque instant par les composantes deson rayon vecteur sur une base, en general les composantes et la base sont fonctions du temps :→r t = X1t →e1t + X2t →e2t + X3t →e3t.Ainsi la vitesse de M est :→v t = ˙X1t →e1t + ˙X2t →e2t + ˙X3t →e3t + X1t ˙→e1t + X2t ˙→e2t + X3t ˙→e3t.Pour obtenir les composantes de →v sur la base, il faut donc connaˆıtre celles des vecteurs ˙→e1t, ˙→e2tet ˙→e3t.vitesse en cartesienIci →e1 = →ux, →e2 = →uy.Sachant que la base cartesienne est uniforme : ˙→ux = ˙→uy = →0 .On obtient donc les composantes de →v sur la base cartesienne, en partant de →r = x →ux + y →uy :→v t = ˙x →ux + ˙y →uyvitesse en polaireIci →e1 = →ur, →e2 = →uθ.Sachant que →ur = cos θ→ux + sin θ→uy et →uθ = sin θ→ux + cos θ→uy,on trouve d→urdθ = →uθ et d→uθdθ = →ur.Donc en composant par la fonction θt : ˙→ur = d→urθtdt= dθdtd→urdθ θt = ˙θ →uθet de mˆeme ˙→uθ = d→uθθtdt= dθdtd→uθdθ θt = ˙θ →ur.On obtient donc les composantes de →v sur la base polaire, en partant de →r = r →ur :→v t = ˙r →ur + r ˙→ur = ˙r →ur + r ˙θ →uθacceleration en cartesienOn a vu que →v t = ˙x →ux + ˙y →uy.En derivant encore une fois par rapport au temps on obtient donc les composantes de →a sur la basecartesienne :→a t = ¨x →ux + ¨y →uy— 23/38 —

Page 24 : acceleration en polaireOn a vu que →v t = ˙r →ur + r ˙θ →uθ.En derivant encore une fois par rapport au temps on obtient donc les composantes de →a sur la basepolaire :→a t=¨r →ur + ˙r ˙→ur + ˙r ˙θ →uθ + r ¨θ →uθ + r ˙θ ˙→uθ=¨r →ur + ˙r ˙θ→uθ + ˙r ˙θ →uθ + r ¨θ →uθ r ˙θ2 →ur=¨r r ˙θ2 →ur + 2 ˙r ˙θ + r ¨θ →uθConsiderons le cas particulier du mouvement circulaire sur un cercle de rayon R ; on trouve :→r=R →ur→v=R ˙θ →uθ→a t=R ˙θ2→ur + R ¨θ →uθOn trouve en particulier que la valeur algebrique de la vitesse dans un mouvement circulaire estv = R ˙θ et on peut donc aussi ecrire →a t = v2R→ur + R ¨θ →uθ.— 24/38 —

Page 25 : 7Reperage et VecteursLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.ReperageExercice 1 – Reperage dans un planA et B sont deux points du plan.1/ On donne les coordonnees cartesiennes des points A = 1, 3 et B = 3, 2. Trouver leurscoordonnees polaires. Donner l’equation de la droite passant par ces points en coordonneescartesiennes. Ecrire cette equation en coordonnees polaires.2/ On donne les coordonnees polaires des points rA = 4, θA = 120o et rB = 10, θB = 330o, trouverleurs coordonnees cartesiennes. Trouver une courbe d’equation r = a θ + b en coordonneespolaires passant par ces points a et b sont deux nombres a determiner. Tracer cette courbe.Exercice 2 – Representation de vecteurs dans un planRepresenter sur un graphique les vecteurs :→a = 3→ux 4→uy, →b = →ux 5→uy, 12→a , →a + →b et→a →b→a .Addition de vecteursExercice 3 – Petites Questions1/ Si →V = →V 1+→V 2, V = →V est-il necessairement plus grand que V1 = →V 1 et/ou V2 = →V 2 ?2/ La somme de deux vecteurs de normes differentes peut-elle ˆetre nulle ie egale au vecteur nul ?Est-ce possible avec la somme de trois vecteurs de normes differentes ?3/ Indiquer si la somme des vecteurs sur les figures suivantes peut avoir une resultante nulle.— 25/38 —

Page 26 : Exercice 4 – En forceO1 et O2 sont deux points de l’espace. Un point materiel M du plan subit deux forces : →F1 = k →r1due a O1 et →F2 = k →r2 due a O2 k est une constante et les vecteurs positions →ri = →OiM reperent Mpar rapport a chacun des deux points O1 et O2.1/ Calculer la force totale →F = →F1 + →F2 subie par M.2/ Faire un schema pour plusieurs positions du point M.Produit scalaireExercice 5 – Composantes cartesiennes de vecteursTrouver les composantes cartesiennes des vecteurs suivants et les indiquer sur le diagramme la normedes vecteurs est indiquee en unites arbitraires.Pour le cas c projeter les vecteurs sur les axes x′, y′ indiques sur la figure :Exercice 6 – Produit scalaire1/ On donne une base quelconque du plan usuel : →e1, →e2. On appelle x1, x2 les composantesd’un vecteur →x dans cette base.Calculez →x · →e1 et la norme de →x .2/ Si →a .→b = 0 ceci implique-t-il que →a et →b sont perpendiculaires ? Et la reciproque ?3/ Si →a .→b = →a .→c ceci implique-t-il que →b = →c ? Et la reciproque ?4/ En utilisant la definition du produit scalaire de deux vecteurs, calculer les produits scalairesdes vecteurs de base des reperes cartesien et polaire.5/ En utilisant la propriete de distributivite du produit scalaire sur l’addition, montrer que :si →a = ax→ux + ay→uy + az→uz et →b = bx→ux + by→uy + bz→uz, alors : →a .→b = axbx + ayby + azbz.En deduire l’expression de a = →a on rappelle que →a 2 = →a .→a .6/ Trouver l’angle forme par les vecteurs : →a = 3→ux + 2→uy →uz et →b = →ux + 2→uz.Pour aller plus loinExercice 7 – Composantes polaires de vecteurs On donne les coordonnees cartesiennes des points A = 1, 3 et B = 3, 2 ainsi que les composantescartesiennes des vecteurs →VA = 3 →ux + →uy et →VB = 5 →ux →uy.1/ Trouvez les composantes polaires du vecteur →VA sur la base polaire au point A.2/ Trouvez les composantes polaires du vecteur →VB sur la base polaire au point B.— 26/38 —

Page 27 : Exercice 8 – Vol de la mouche Une mouche vole d’un coin d’une chambre de dimensions 5m × 4m × 3m jusqu’au coin oppose sur ladiagonale du parallelepipede.1/ Quelle est la norme de son vecteur deplacement total ? Choisir un systeme de coordonnees etdonner les composantes de ce vecteur. Le representer graphiquement.2/ La longueur de la trajectoire du vol de la mouche peut-elle ˆetre inferieure superieure ou egalea la norme du vecteur deplacement total ?3/ Si la mouche marchait sur le sol et les murs au lieu de voler, quelle serait la trajectoire laplus courte pour le mˆeme deplacement total ? Astuce : Le plus court chemin sur un plan vousconnaissez...alors pensez a deplier le parallelepipede. Attention, il y a plus d’une fa¸con de lefaire.Exercice 9 – Et pour terminer Une roue d’un rayon de R = 45 cm roule sans glissement d’un demi-tour. On repere le point de contactavec le sol a t = 0 avec la lettre P.1/ Trouver la norme du vecteur deplacement du point P lors de ce deplacement.2/ Trouver l’angle par rapport au sol du vecteur deplacement du point P lors de ce deplacement.— 27/38 —

Page 28 : 8CinematiqueLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Definition des vitesses et accelerationExercice 1 – On commence en vitesse moyenne1/ Le record de vitesse au service d’une balle de tennis est de 263km/h. Elle parcours environ25 m avant de toucher le sol. Quel est le temps de vol de la balle ?2/ Un pilote de chasse s’exerce au vol en dessous des radars. Il vole horizontalement a une altitudede 35 m a une vitesse de 1300 km/h. Subitement il rencontre un terrain qui a une pente de4, 3o. Cette pente est suffisamment douce pour ˆetre difficile a detecter. De combien de tempsdispose le pilote pour ne pas s’ecraser ?Exercice 2 – Et on accelere1/ Un electron avec une vitesse initiale de v0 = 1, 50 × 105 ms1 rentre dans une region longue de1 cm ou il est accelere electriquement. Il sort avec une vitesse de 5, 70 × 105 ms1. Supposantque l’acceleration est constante, quelle est sa valeur ?2/ L’ascenseur a l’hˆotel Marriott peut monter de 190 m. Il a une vitesse maximale de 305 m/minet son acceleration et deceleration sont constantes et de mˆeme norme : a0 = 1, 22 ms2.a Quelle distance est parcourue par l’ascenseur dans la phase d’acceleration : repos →vitessemaximale ?b Combien de temps faut-il pour faire le trajet de 190 m, commen¸cant et terminant aurepos ?c Tracer les graphes de at, vt et zt des acceleration, vitesse et position de l’ascenseuron orientera l’axe des z positivement vers le haut.Exercice 3 – Le lapinLe graphique de la figure ci-dessous represente la position en fonction du temps d’un lapin courant enligne droite dans un tunnel.1/ Quelle est sa vitesse moyenne entre t = 0 et t = 20s et entre t = 40s et t = 50s ?2/ Estimez sa vitesse instantanee a t=10s et a t=30s.3/ La vitesse du lapin est-elle constante a certaines periodes de temps ? Si oui, indiquez lesquelles.4/ A quel moment le lapin atteint-il une vitesse maximale ?5/ Le lapin s’arrˆete-t-il a un moment quelconque ? Si oui lequel ?6/ Pendant la periode illustree sur la figure, le lapin court-il toujours dans le mˆeme sens ?7/ Tracer les graphes de at et vt, acceleration et vitesse du lapin en fonction du temps.— 28/38 —

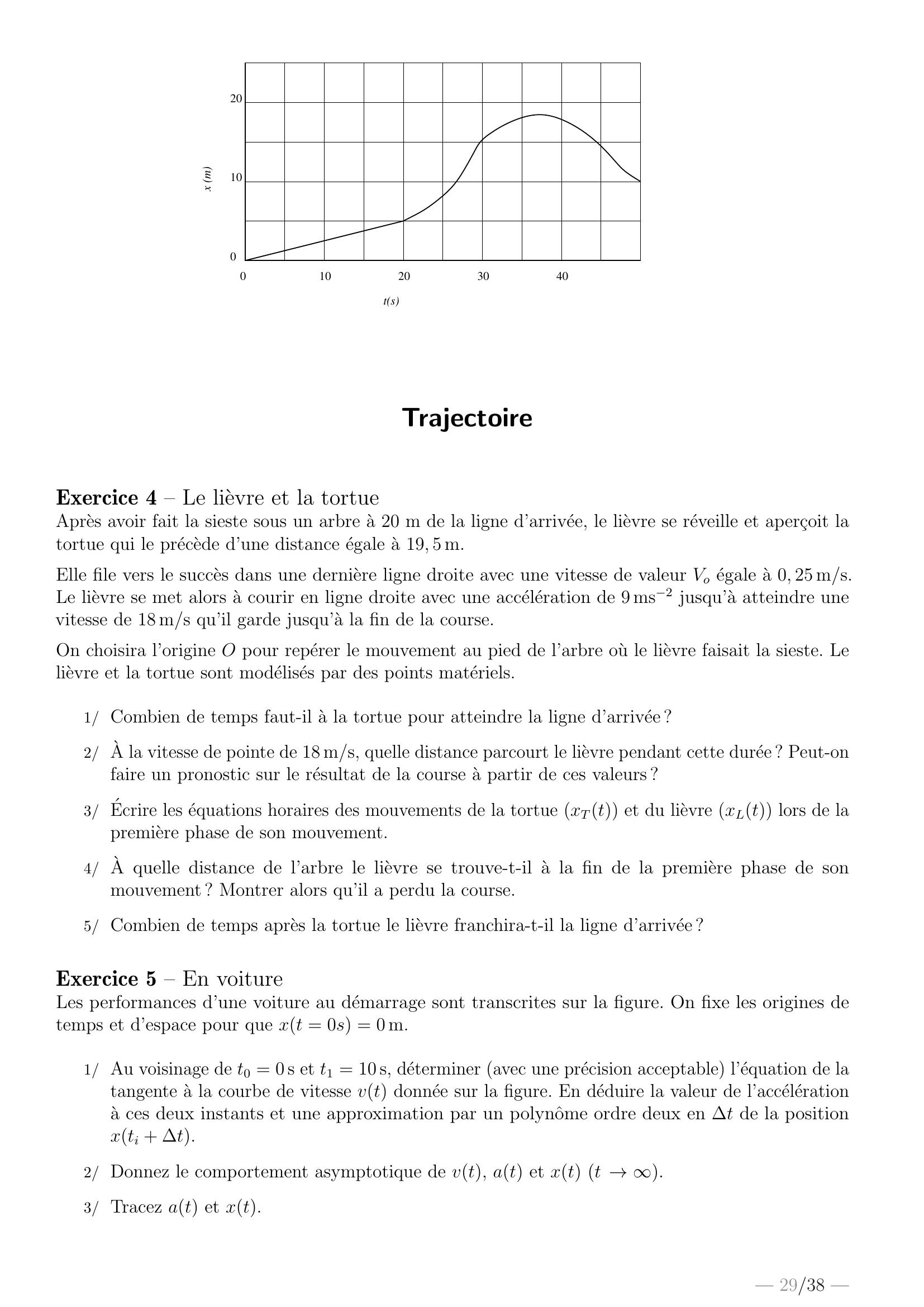
Page 29 : 010204001020tsx m30TrajectoireExercice 4 – Le lievre et la tortueApres avoir fait la sieste sous un arbre a 20 m de la ligne d’arrivee, le lievre se reveille et aper¸coit latortue qui le precede d’une distance egale a 19, 5 m.Elle file vers le succes dans une derniere ligne droite avec une vitesse de valeur Vo egale a 0, 25 m/s.Le lievre se met alors a courir en ligne droite avec une acceleration de 9 ms2 jusqu’a atteindre unevitesse de 18 m/s qu’il garde jusqu’a la fin de la course.On choisira l’origine O pour reperer le mouvement au pied de l’arbre ou le lievre faisait la sieste. Lelievre et la tortue sont modelises par des points materiels.1/ Combien de temps faut-il a la tortue pour atteindre la ligne d’arrivee ?2/ A la vitesse de pointe de 18 m/s, quelle distance parcourt le lievre pendant cette duree ? Peut-onfaire un pronostic sur le resultat de la course a partir de ces valeurs ?3/ Ecrire les equations horaires des mouvements de la tortue xTt et du lievre xLt lors de lapremiere phase de son mouvement.4/ A quelle distance de l’arbre le lievre se trouve-t-il a la fin de la premiere phase de sonmouvement ? Montrer alors qu’il a perdu la course.5/ Combien de temps apres la tortue le lievre franchira-t-il la ligne d’arrivee ?Exercice 5 – En voitureLes performances d’une voiture au demarrage sont transcrites sur la figure. On fixe les origines detemps et d’espace pour que xt = 0s = 0 m.1/ Au voisinage de t0 = 0 s et t1 = 10 s, determiner avec une precision acceptable l’equation de latangente a la courbe de vitesse vt donnee sur la figure. En deduire la valeur de l’accelerationa ces deux instants et une approximation par un polynˆome ordre deux en t de la positionxti + t.2/ Donnez le comportement asymptotique de vt, at et xt t →.3/ Tracez at et xt.— 29/38 —

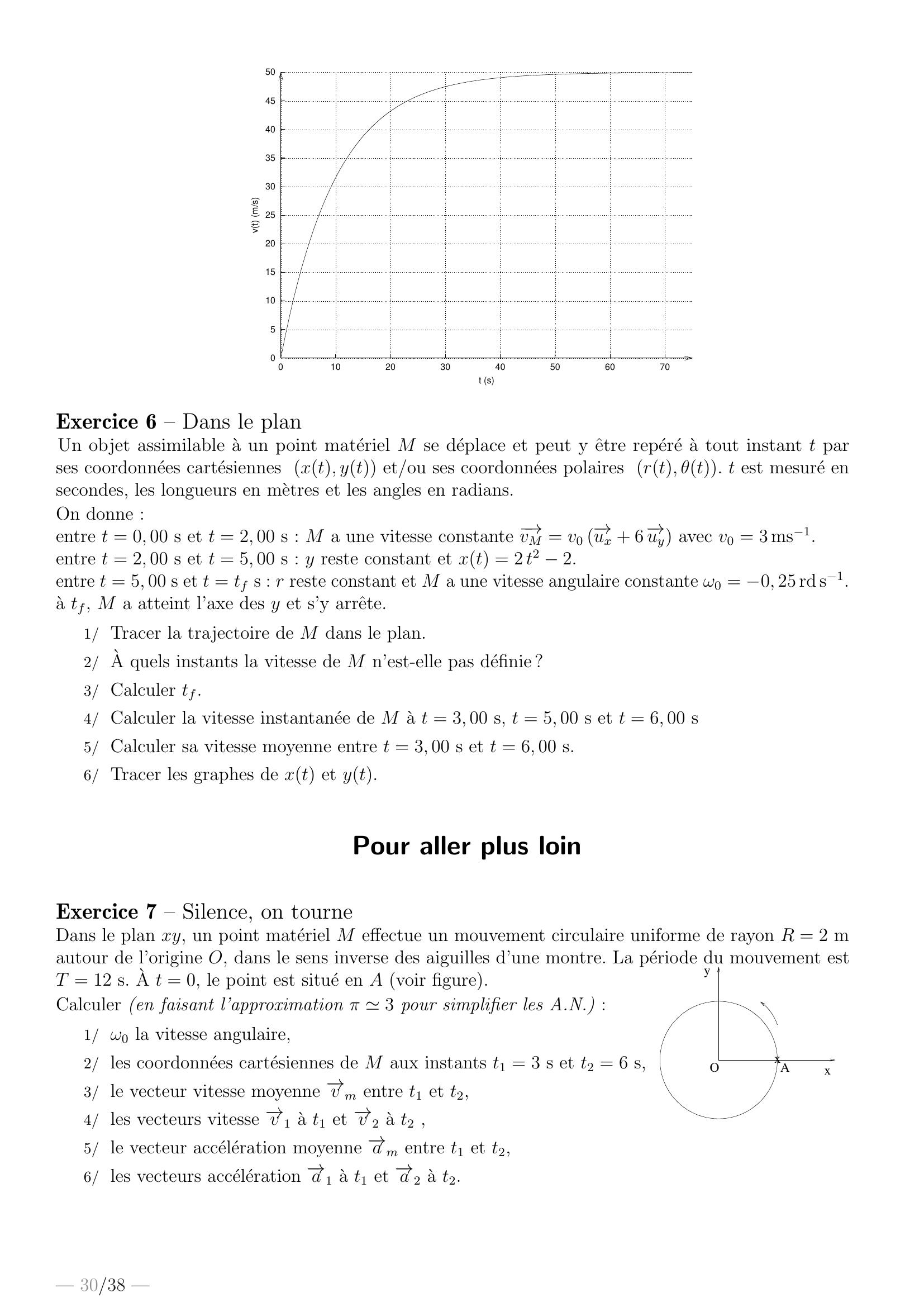
Page 30 : 05101520253035404550010203040506070vt m/st sExercice 6 – Dans le planUn objet assimilable a un point materiel M se deplace et peut y ˆetre repere a tout instant t parses coordonnees cartesiennes xt, yt et/ou ses coordonnees polaires rt, θt. t est mesure ensecondes, les longueurs en metres et les angles en radians.On donne :entre t = 0, 00 s et t = 2, 00 s : M a une vitesse constante →vM = v0 →ux + 6 →uy avec v0 = 3 ms1.entre t = 2, 00 s et t = 5, 00 s : y reste constant et xt = 2 t2 2.entre t = 5, 00 s et t = tf s : r reste constant et M a une vitesse angulaire constante ω0 = 0, 25 rd s1.a tf, M a atteint l’axe des y et s’y arrˆete.1/ Tracer la trajectoire de M dans le plan.2/ A quels instants la vitesse de M n’est-elle pas definie ?3/ Calculer tf.4/ Calculer la vitesse instantanee de M a t = 3, 00 s, t = 5, 00 s et t = 6, 00 s5/ Calculer sa vitesse moyenne entre t = 3, 00 s et t = 6, 00 s.6/ Tracer les graphes de xt et yt.Pour aller plus loinExercice 7 – Silence, on tourneDans le plan xy, un point materiel M effectue un mouvement circulaire uniforme de rayon R = 2 mautour de l’origine O, dans le sens inverse des aiguilles d’une montre. La periode du mouvement estT = 12 s. A t = 0, le point est situe en A voir figure.xyOAxCalculer en faisant l’approximation π 3 pour simplifier les A.N. :1/ ω0 la vitesse angulaire,2/ les coordonnees cartesiennes de M aux instants t1 = 3 s et t2 = 6 s,3/ le vecteur vitesse moyenne →v m entre t1 et t2,4/ les vecteurs vitesse →v 1 a t1 et →v 2 a t2 ,5/ le vecteur acceleration moyenne →a m entre t1 et t2,6/ les vecteurs acceleration →a 1 a t1 et →a 2 a t2.— 30/38 —

Page 31 : Exercice 8 – Le TGV Le TGV a une vitesse moyenne de 216 km h1 en service normal. Si le train prend un virage a cettevitesse, contante en norme, il est stipule que les passagers ne doivent pas subir une accelerationsuperieure a 0, 05g :1/ Puisque le TGV a une vitesse contante en norme de quelle acceleration parle-t-on ? La representersur un schema a plusieurs instants, representer aussi la vitesse a ces mˆemes instants.2/ Obtenir l’expression sur la base polaire des vecteurs position, vitesse et acceleration du TGVpendant le virage.3/ Quel est le rayon le plus petit pour la courbe ? prendre g = 9, 8 ms2.4/ A quelle vitesse le train doit-il prendre un virage de rayon 1 km ?Exercice 9 – Le piston On considere un systeme articule en A et constitue de deux barres identiques OA et AB assujetties arester dans le plan x, y. O est fixe et B glisse le long de l’axe x et l’angle entre OA et l’axe x, φ, varietel que φ = ωt. Chaque barre est de longueur 2b.1/ Determiner l’equation cartesienne de la trajectoire du milieu, M, de AB.Decrire cette trajectoire.2/ Determiner la vitesse et l’acceleration du point M.3/ Determiner les expressions des coordonnees du point B en fonction du temps.4/ La vitesse maximale du point B est de 12 m/s et b = 1 cm. Determiner la vitesse de rotationen tour/min du point A dans son mouvement de rotation autour de O.Annexe : Derivees des fonctions scalairesExercice 10 –Calculer la derivee des fonctions reelles de variable reelle suivantes :1/ y1x = 2 x + 32/ y2x = cos2x3/ y3x = 3 sin x 2 x4/ y4x = 2x3 + 1x5/ y5x = x3 + 2 x2 + 16/ y6x = x3 + 2x2 + 17/ y7x = 3e3 x + ln x8/ y8x = sin2 x + x3Exercice 11 –Soit la courbe d’equation catesienne y = 2 x2 + 5 x+1. La tracer schematiquement. Quel est sonminimum et en quels points s’annule-t-elle ?Exercice 12 –Ecrire la forme developpee des polynˆomes x + ϵn pour n = 1, 2 et 3.Expliquer le lien avec la derivee de la fonction x 7→xn. En deduire l’equation de la tangente a lacourbe d’equation y = xn au point de coordonnees cartesiennes 1, 1.— 31/38 —

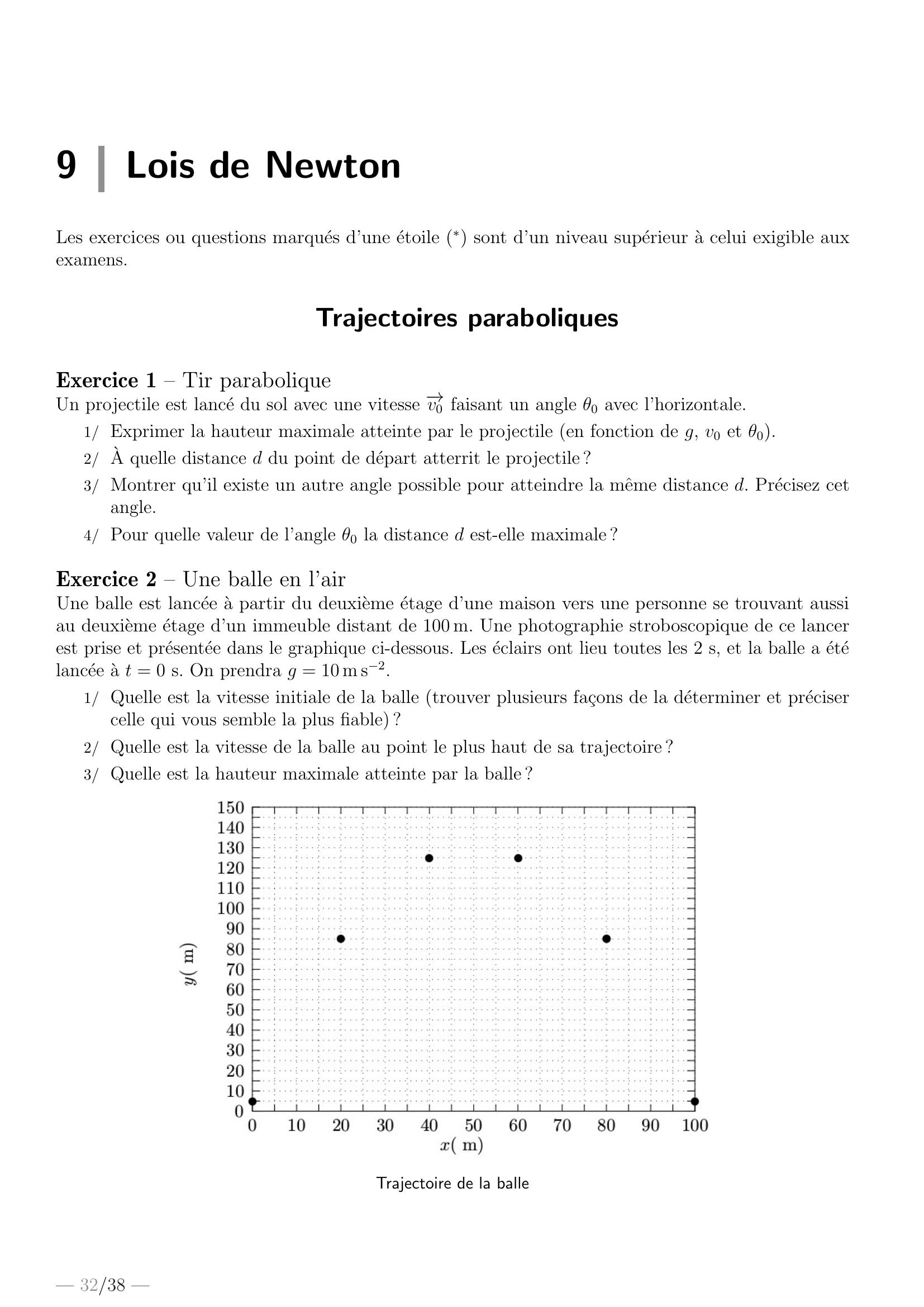
Page 32 : 9Lois de NewtonLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.Trajectoires paraboliquesExercice 1 – Tir paraboliqueUn projectile est lance du sol avec une vitesse →v0 faisant un angle θ0 avec l’horizontale.1/ Exprimer la hauteur maximale atteinte par le projectile en fonction de g, v0 et θ0.2/ A quelle distance d du point de depart atterrit le projectile ?3/ Montrer qu’il existe un autre angle possible pour atteindre la mˆeme distance d. Precisez cetangle.4/ Pour quelle valeur de l’angle θ0 la distance d est-elle maximale ?Exercice 2 – Une balle en l’airUne balle est lancee a partir du deuxieme etage d’une maison vers une personne se trouvant aussiau deuxieme etage d’un immeuble distant de 100 m. Une photographie stroboscopique de ce lancerest prise et presentee dans le graphique ci-dessous. Les eclairs ont lieu toutes les 2 s, et la balle a etelancee a t = 0 s. On prendra g = 10 m s2.1/ Quelle est la vitesse initiale de la balle trouver plusieurs fa¸cons de la determiner et precisercelle qui vous semble la plus fiable ?2/ Quelle est la vitesse de la balle au point le plus haut de sa trajectoire ?3/ Quelle est la hauteur maximale atteinte par la balle ?Trajectoire de la balle— 32/38 —

Page 33 : Exercice 3 – Un colis venu des airsUn avion humanitaire vole a une vitesse de 290 km h1 et plonge sur sa cible a un angle de π/6 endessous de l’horizontale. Le pilote lˆache un colis a 700 m de sa cible distance au sol.1/ Quel est le temps de vol du colis ?2/ Quelle etait l’altitude de l’avion lorsque le colis a ete lˆache ?Exercice 4 –Un gamin veut lancer une pierre sur un chat perche dans un arbre. Des qu’il tire, le chat se laissetomber. Comment le gamin doit-il viser ? direction de la vitesse initiale et condition sur sa normeBilan de forcesExercice 5 –Mettre en evidence les forces agissant sur chacun des trois systemes : bloc m seul, table seule, bloc ettable ensemble cf.figure 9.1. Pour chacune de ces forces indiquer sa reaction associee au sens : pairede forces action-reaction d’une interaction.On supposera qu’il n’y a pas de frottements entre la table et le bloc m.mtableFigure 9.1. Bloc sur une tableExercice 6 –Deux blocs en contact peuvent glisser sans frottement sur une surface horizontale. Une force constante→F s’exerce sur le bloc A entraˆınant un mouvement d’ensemble des deux blocs cf. figure 9.2.1/ La force exercee par B sur A est-elle egale en module a la force exercee par A sur B ?2/ La force exercee par le bloc A sur le bloc B est-elle egale a →F ?3/ Reprendre ces questions lorsque les blocs s’immobilisent contre le mur.FABFigure 9.2. Blocs en mouvementExercice 7 – Masse suspendueUne masse m de 10 kg est suspendue a deux cordes identiques, accrochees au plafond, comme lemontre la figure cf. figure 9.3..Calculer la tension dans les cordes.On donne α = π/6 et β = π/3.Figure 9.3. Masse suspendue— 33/38 —

Page 34 : Lois de NewtonExercice 8 –Un vieux fermier attache son ˆane a son chariot et essaye de le faire avancer. Mais l’ˆane, qui vient delire les « Principia Mathematica » de Newton, lui dit : « Il est inutile que j’essaye de faire bouger lechariot. Etant donne que l’action et la reaction sont de mˆeme module mais de sens opposes, le chariottirera sur moi autant que je tirerai sur lui et aucun de nous n’avancera ».Etant donne votre maˆıtrise des principes de Newton et sachant que vous n’ˆetes pas un ˆane, pourriez-vousconvaincre l’ˆane « erudit » de bouger ?Exercice 9 –1/ On pese une cage contenant un oiseau. L’indication de la balance est-elle modifiee suivant quel’oiseau est au repos sur son perchoir ou volete dans la cage ?2/ On pese un aquarium contenant un poisson. L’indication de la balance est-elle modifiee suivantque le poisson est pose au fond de l’aquarium ou en train de nager horizontalement ?Deuxieme loi de NewtonExercice 10 – Bloc de glaceOn tire un bloc de glace le long d’un sol plan avec deux forces, →F1 et →F2, comme indique sur lafigure 9.4. On peut negliger les forces de frottement entre le bloc de glace et le sol. Les deux forcessont choisies pour que la vitesse de glissement reste constante.Si l’angle θ est diminue, pour garder la vitesse constante faut-il augmenter, diminuer ou garderconstante la norme de la force →F 2 ?Figure 9.4. Bloc de glaceExercice 11 – Bloc contre blocOn supposera les frottements negligeables, le fil inextensible, et la poulie et le fil de masses negligeables.Calculer la valeur de sa masse pour que le m1 se deplace :1/ a vitesse constante.2/ avec une acceleration vers la gauche de g/2 pour α = π/4.m12mαgFigure 9.5. Deux blocs— 34/38 —

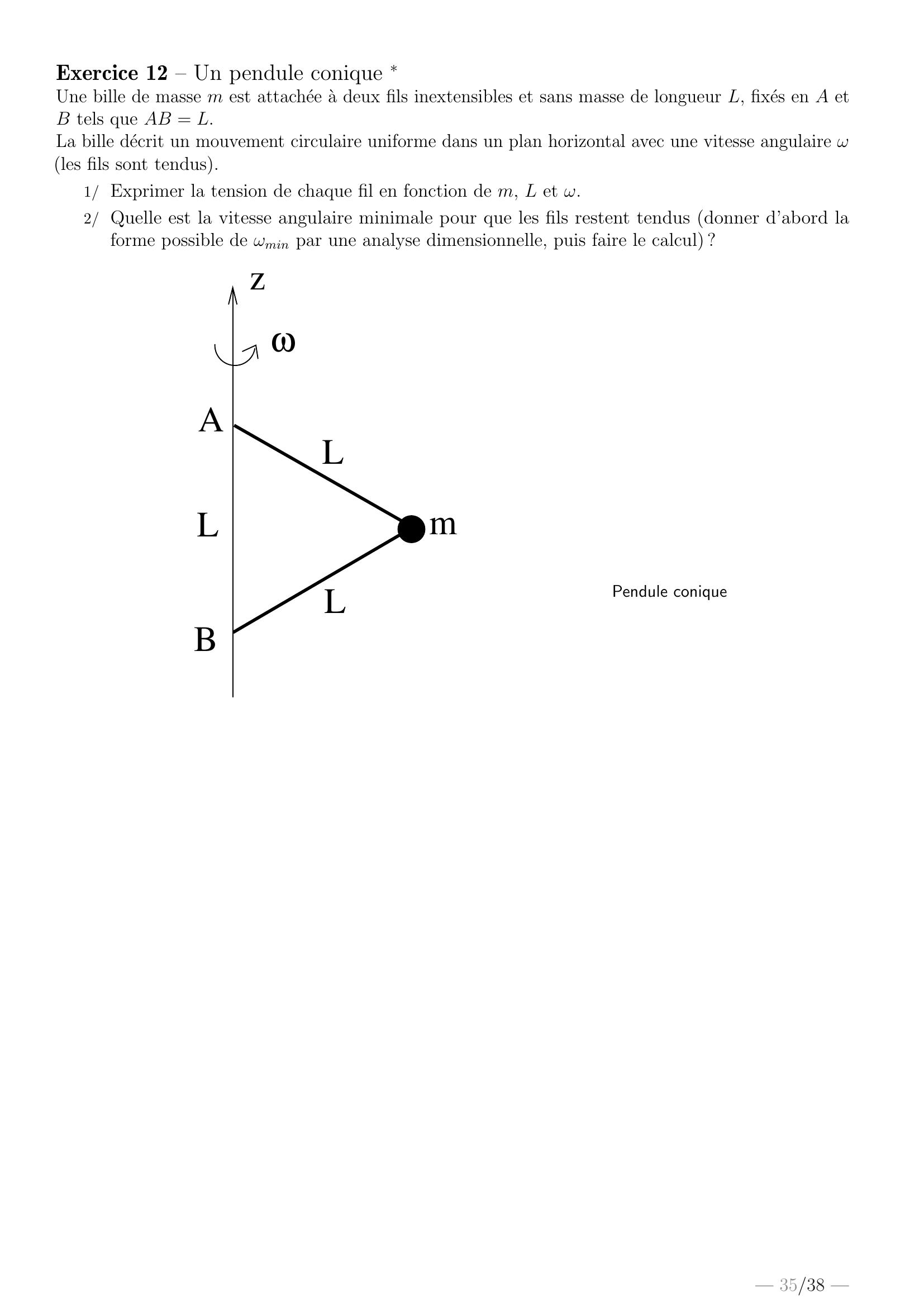
Page 35 : Exercice 12 – Un pendule conique Une bille de masse m est attachee a deux fils inextensibles et sans masse de longueur L, fixes en A etB tels que AB = L.La bille decrit un mouvement circulaire uniforme dans un plan horizontal avec une vitesse angulaire ωles fils sont tendus.1/ Exprimer la tension de chaque fil en fonction de m, L et ω.2/ Quelle est la vitesse angulaire minimale pour que les fils restent tendus donner d’abord laforme possible de ωmin par une analyse dimensionnelle, puis faire le calcul ?AzωmLLBLPendule conique— 35/38 —

Page 36 : 10Lois de Newton suiteLes exercices ou questions marques d’une etoile sont d’un niveau superieur a celui exigible auxexamens.DiversExercice 1 – Chute libre sur la LuneSur la lune le temps de chute verticale d’un objet sur une hauteur h = 1 m est t = 1, 1 s. En deduirela masse ML de la Lune sachant que son rayon est RL = 1, 75 × 103 km.On donne : G = 6, 67 × 1011 N.m2.kg2.Exercice 2 –Une barque contenant des cailloux flotte dans une piscine. Trouvez une relation entre le volumeimmerge, la masse de la barque et celle des cailloux. Si l’on jette les cailloux dans l’eau, que devient leniveau de l’eau de la piscine ?FrottementsExercice 3 – Glissera, glissera pas ?Un bloc de masse m est pose sur un plan faisant un angle α avec l’horizontale. On notera µs lecoefficient de frottement statique entre le bloc et le plan. Quel est l’angle α limite pour que le bloc semette en mouvement ?Exercice 4 – Bloc frottantUn bloc est tire a l’aide d’une corde avec une force →F , indiquee sur la figure, qui fait un angle θ avecl’horizontale.Bloc sur une tableSi le bloc est au repos et θ augmente, quelles sont les quantites qui augmentent, decroient, ou restentles mˆemes parmi :1/ Fx la composante horizontale de la force,2/ fs la force de frottement statique,3/ N la force normale,4/ fs,max la force de frottement statique maximale.5/ Si, par contre, le bloc est en mouvement, et θ est augmente, est-ce que la force de frottementaugmente, diminue ou reste la mˆeme ?— 36/38 —

Page 37 : Exercice 5 –Une voiture bloque ses roues. Elle derape sur une distance d = 110 m avant de s’arrˆeter d’apres lestraces de pneu. En supposant, pour simplifier, que l’acceleration de la voiture est constante pendantle derapage, calculer la vitesse de la voiture juste avant le freinage.On donne le coefficient de frottement dynamique : µd = 0, 6.Exercice 6 – Attention au virageUne voiture roule, a vitesse constante en norme v0, dans un virage de rayon R = 50 m sur une routehorizontale.1/ Si la voiture ne derape pas et suit donc la courbe de la route, quelle est la nature des frottementssur les roues ? Que se passerait-il si les roues se bloquaient coup de frein brutal ?2/ Calculez le coefficient de frottement minimal pour que la voiture ne glisse pas.A.N. : v0 = 50 km h1 et v0 = 80 km h1.3/ De quel angle faut-il relever le virage pour qu’il n’y ait aucun frottement transverse av0 = 50 km h1 ? On suppose que la voiture roule a une altitude constante.Pour aller plus loinExercice 7 – Le saut de l’ange Un parachutiste aimant les sensations fortes se laisse tomber le plus longtemps possible avant d’ouvrirson parachute. Lors de sa chute, que l’on supposera verticale pour simplifier, le parachutiste est soumisa une force de frottement due a l’air de la forme :→f = 12 Cx ρ A v2 →vvou ρ = 1.2 kg/m3 est la masse volumique de l’air, Cx un coefficient de resistance aerodynamique quidepend essentiellement de la forme du corps, →v la vitesse de chute du parachutiste et A l’aire de sasection perpendiculaire a →v .1/ Montrer que le parachutiste atteint une vitesse limite. Etablir l’expression de cette vitesselimite.2/ Estimer cette vitesse limite pour un homme de masse m = 80 kg equipement compris tombanten position horizontale du saut de l’ange Cx 1 puis en position tˆete en avant Cx 0.7.Exercice 8 – Ressort Dans cet exercice la gravite n’intervient pas.Une masse m est accrochee a un ressort, de longueur a vide l0 et de raideur k, lui-mˆeme fixe a unmur. Initialement m est au repos, le ressort ayant sa longueur a vide.On tire m dans la direction du ressort x avec une force constante →F .1/ Determinez la longueur du ressort quand m a une acceleration nulle, puis quand m faitdemi-tour.2/ On suppose maintenant que deux masses identiques m/2 sont attachees aux extremites duressort et que l’on tire dans la direction x chacune d’entre elles avec une force d’intensite F/2.m/2m/2F/2F/20xxtxt— 37/38 —

Page 38 : Initialement les deux masses sont au repos et le ressort a sa longueur a vide. La symetrie dusysteme assure que le milieu du ressort est immobile et que les masses peuvent ˆetre repereespar xt et xt respectivement.Reprendre les questions precedentes pour les masses m/2.— 38/38 —

Pages : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38